Calibration of the Shear Wave Speed-Stress Relationship in Ex Vivo Tendons

Abstract

It has recently been shown that shear wave speed in tendons is directly dependent on axial stress. Hence, wave speed could be used to infer tendon load provided that the wave speed-stress relationship can be calibrated and remains robust across loading conditions. The purpose of this study was to investigate the effects of loading rate and fluid immersion on the wave speed-stress relationship in ex vivo tendons, and to assess potential calibration techniques. Tendon wave speed and axial stress were measured in 20 porcine digital flexor tendons during cyclic (0.5, 1.0 and 2.0 Hz) or static axial loading. Squared wave speed was highly correlated to stress (r²_avg = 0.98) and was insensitive to loading rate (p = 0.57). The constant of proportionality is the effective density, which reflects the density of the tendon tissue and additional effective mass added by the adjacent fluid. Effective densities of tendons vibrating in a saline bath averaged 1680 kg/m³ and added mass effects caused wave speeds to be 22% lower on average in a saline bath than in air. The root-mean-square error between predicted and measured stress was 0.67 MPa (6.7% of maximum stress) when using tendon-specific calibration parameters. These errors increased to 1.31 MPa (13.1% of maximum stress) when calibrating based on group-compiled data from ten tendons. These results support the feasibility of calculating absolute tendon stresses from wave speed squared based on linear calibration relationships.

Introduction

Knowledge of tissue loading is inherently important to the study of musculoskeletal disorders. This is particularly true for tendon, which transmits muscle forces to the skeleton, and thereby facilitates human movement. Unfortunately, it remains challenging to assess in vivo tendon loading during movement. Modeling approaches can provide estimates of tendon loading based on measured kinematics and external forces, but rely on many assumptions regarding muscle coordination, musculoskeletal geometry, and tissue morphology (Buchanan et al., 2004; Crowninshield and Brand, 1981; Delp et al., 2007; Erdemir et al., 2007; Seireg and Arvikar, 1975). Direct measurement is more favorable, but conventional approaches (e.g., buckle transducers (Fleming and Beynnon, 2004; Komi et al., 1987), optic fiber technique (Finni et al., 1998; Komi et al., 1996)) are highly invasive, and thus have limited applicability for human use.

We recently introduced a technique for non-invasive measurement of tendon loading based on shear wave propagation speed (Martin et al., 2018). Our technique is related to ultrasound shear wave elastography (SWE), which uses ultra-high framerate imaging to track tissue shear wave speed, and subsequently computes an estimate of tissue elasticity (Bercoff et al., 2004). Prior studies have shown that tendon shear wave speed increases markedly when the tendon is stretched (Aubry et al., 2013; DeWall et al., 2014; Hug et al., 2013; Slane et al., 2017). This phenomenon has most often been attributed to strain-stiffening behavior, where wave speed increases are caused by a load-dependent increase in tendon shear elastic modulus. However, a tensioned beam model reveals that bulk shear wave speed in tendon exhibits a direct dependence on tensile stress that is independent of nonlinearity in the shear modulus, and that this effect may be dominant as loading is increased (Martin et al., 2018). Thus, shear wave speed could potentially serve as a non-invasive indicator of tendon loading.

Certain aspects of the tendon wave speed-stress relationship require further study to confirm that wave speed can be a dependable indicator of tendon loading. Tendons are known to be viscoelastic, and so it is unclear whether tendon stresses estimated from wave speed will be sensitive to loading rate. This is important because functional activities generally impose a range of loading rates on in vivo tendons. Additionally, it must be determined whether tendon-specific calibration is preferable to a generic relationship for estimating absolute tendon stresses from wave speed. It is theorized that differences between in vivo calibrations may arise due to anatomical differences in the adjacent medium, including tissue and fluid, which can add to the effective mass of the tendon and affect wave propagation speed (Martin et al., 2018).

Here we addressed these issues in the simplified case of ex vivo porcine digital flexor tendons. The purpose of this work was threefold. First, we evaluated whether the wave speed-stress relationship was independent of loading rate, such that a sensor based on this phenomenon would be applicable for use during movements at varying rates. Next, we examined the potential for predicting tendon stress based on calibrations determined from tendon-specific and group-compiled data. Finally, we assessed how the adjacent medium affected the tendon wave speed-stress relationship in a simple ex vivo case as a first step toward understanding the in vivo case.

2. Methods

2.1. Tensioned beam model

Tendon shear wave propagation was modeled using a tensioned Timoshenko beam (Ginsberg, 2001) assuming locally linear elastic material properties. At higher vibration frequencies, shear motion becomes dominant, and shear wave speed (c) is dependent on a shear correction factor (k’) based on the finite shape of the cross-section, the tangential shear modulus (μ), the axial stress acting on the tendon cross-section (σ), and the effective density of the tendon (ρ_eff) (Martin et al., 2018):

$$c^2=\frac{k^{\prime }\mu +\sigma }{{\rho }_{eff}}$$ (1)

Rearranging this expression and assuming a unity shear correction factor results in a linear prediction model for tendon stress from squared wave speed:

$$\sigma ={\rho }_{eff}{c}^2-\mu$$ (2)

Given simultaneous measurements of tensile stress and shear wave speed, one can estimate the effective density, ρ_eff, and the shear modulus, μ. The effective density in vivo would be dependent on both the tissue density and the additional effective mass due to entrained motion of the adjacent tissue and fluid. The current study considers an ex vivo loading situation where a tendon with elliptical cross-section is vibrating in a saline-filled bath, such that the surrounding fluid results in an added mass effect. It has previously been shown that a beam vibrating in a viscous fluid, e.g., in atomic microscopy (Allen et al., 2009), has an effective density, ρ_eff, given by:

$${\rho }_{eff}={\rho }_t+{\rho }_f\left(\frac{b}{a}\right){\Gamma }_r\text{(Re)}$$ (3)

where ρ_t is the tendon density, ρ_f is the fluid density, Γ_r (Re) is a hydrodynamic function of the Reynolds number (Sader, 1998), a is the major cross-sectional axis and b is the minor axis, which is aligned perpendicular to the direction of vibrational motion. In a fluid bath that extends infinitely in all directions, the hydrodynamic function, Γ_r, is similar for circular and elliptical cross-sections over the Reynolds numbers (~700–7000) seen in this study. For this study, we used a constant value for Γ_r (1.07) that is the mid-range (1.03–1.11) value for a beam with a circular cross-section over the relevant Reynolds numbers. The diameter was set as the mean minor axis width (b).

Combining Eqns. 1 and 3, one can derive an estimate for shear wave speed in a tendon immersed in a fluid bath:

$$c^2=\frac{k^{\prime }\mu +\sigma }{{\rho }_t+{\rho }_f\cdot \left(\frac{b}{a}\right)\cdot {\Gamma }_r}$$ (4)

This expression can be used to predict wave speeds when a tendon is vibrating in water (ρ_f=ρ_w) or in air (ρ_f=ρ_a). Recognizing that the added mass effect of air will be negligible (ρ_a<<ρ_t), the model would suggest that the ratio of tendon shear wave speed at a given stress in water, c_w, versus in air, c_a, should be:

$$\frac{c_w}{c_a}=\sqrt{\frac{{\rho }_t}{{\rho }_t+{\rho }_w\left(\frac{b}{a}\right){\Gamma }_r}}$$ (5)

2.2. Ex vivo experiments

The theoretical relationship between shear wave speed and axial stress was tested in ex vivo porcine tendons.

2.2.1. Tendon specimens

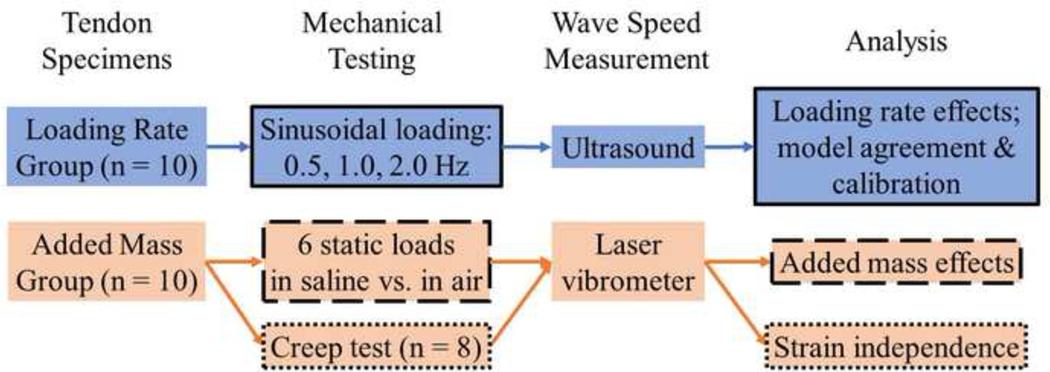
Porcine digital flexor tendon specimens (n=20) were excised from 6–10-month-old porcine feet from approximately 2 cm past the distal muscle-tendon junction to the bony distal insertion. Excised specimens were wrapped in normal saline (9 g-NaCl/L) soaked gauze and frozen until the time of testing. Ten tendons were tested in a saline bath and used to assess the suitability of a tensioned beam model to describe wave speed-stress relationships across a range of loading rates (Loading Rate Group; Fig. 1). The other ten tendons were used to assess added mass effects of tendon vibration in saline relative to air (Added Mass Group).

Figure 1.

Workflow diagram describing experimental design. Color indicates specimen group (see “Tendon Specimens”); outline style indicates experiment (see “Analysis”).

2.2.2. Mechanical testing

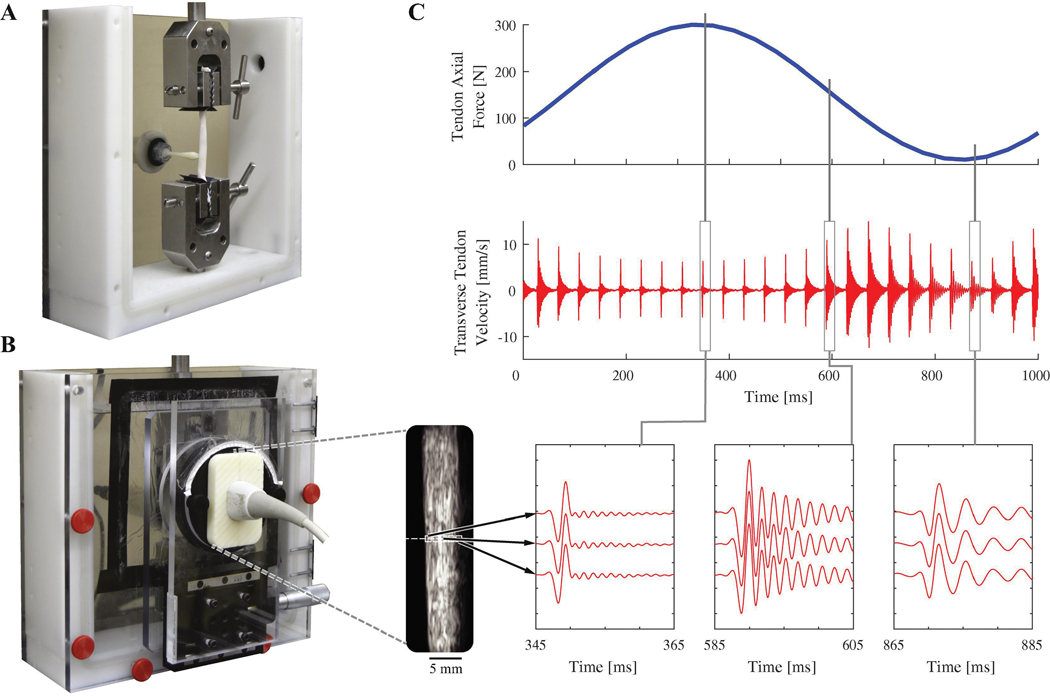
Tendon specimens were placed in a custom mechanical testing bath (Fig. 2), gripped at each end using waveform grips (G240KSS, Test Resources, Shakopee, MN), and immersed in normal saline. For the Loading Rate Group, axial loads were applied sinusoidally (0.5, 1.0, 2.0 Hz) from 10–300 N using an electrodynamic mechanical testing system (Acumen 3, MTS, Eden Prairie, MN). Specimens were preconditioned with 10 loading cycles and allowed to rest for 7 minutes prior to data collection. Data were then collected during the final 5 out of 10 additional loading cycles. Tendon stress was calculated by dividing applied force by undeformed cross-sectional area. Cross-sections were assumed to be elliptical, and average area was calculated using the width of the major and minor axes at three locations evenly spaced along the tendon (Table 1). For the Added Mass Group, six static axial loads were applied between 50 and 300 N (50 N increments). Tendons in this group were tested immersed in saline and in air. During in-air testing, tendons were covered with saline-soaked towels between trials to maintain hydration. Tendons were not given recovery time between trials (Duenwald et al., 2010) since strain is theorized to have no effect on wave speed. To test the independence from strain, a constant-load creep test was performed on tendons from the Added Mass Group. Tendon deformation displacements were measured while tendons were loaded to 300 N for a period of 100 seconds.

Figure 2.

A: Porcine digital flexor tendon loaded in mechanical testing bath. A tapping device is used to generate shear waves in the tendon. B: Ultrasound imaging is performed through an acoustic window and is used to track transverse tendon velocity for 0.5 mm long kernels (white boxes on ultrasound image, enlarged for clarity). C: Transverse tendon velocity measured during cyclic loading as waves are induced at 25 Hz. Vibration frequency increases with axial tendon loading.

Table 1.

Tendon specimen dimensions.

	Minor axis [mm]	Major axis [mm]	Area [mm2]	Length [mm]
Loading Rate Group	4.2 ± 0.6	6.8 ± 1.0	22.6 ± 5.2	79.3 ± 6.8
Added Mass Group	3.9 ± 0.6	8.4 ± 0.7	25.2 ± 3.5	58.3 ± 7.9

2.2.3. Shear wave generation

Shear waves were generated using a piezoelectric stack actuator (PK4JQP1, Thorlabs Inc, Newton, NJ) housed in a custom 3D-printed tapping device that mechanically interfaced with the tendon (Fig. 2). The actuator was driven by 1 ms pulses delivered at a 25 Hz repetition rate to generate a displacement of 17.8 μm at the contact point. The signals were generated using a function generator (SDG1025, Siglent, Solon, OH), and amplified using an open-loop piezo controller (MDT694B, Thorlabs Inc, Newton, NJ). The contact point was located 22 mm above the lower grip for the Loading Rate Group and 10 mm for the Added Mass Group.

2.2.4. Measurement of tendon motion

For the Loading Rate Group, a 38 mm linear array ultrasound transducer (L14–5W/38, BK Medical, Peabody, MA) was affixed to a mechanical testing bath and aligned with the long axis of the tendon (Fig. 2). A research ultrasound system (SonixTOUCH Research, BK Medical, Peabody, MA) was then used to collect high framerate (14100 fps) radiofrequency (RF) data from a single transducer element located 42 mm from the bottom grip. The spatial resolution of the RF signal was 19 μm as determined by the 40 MHz RF sample rate and a nominal 1560 m/s speed of sound for tendon. RF signals were upsampled by a factor of 4 using a polyphase antialiasing filter (resample, MATLAB). A 1D speckle-tracking algorithm was then used to determine tendon transverse velocity for 0.5 mm-long kernels of RF data located within the tendon boundaries (Chernak and Thelen, 2012; Martin et al., 2018). Frame-to-frame kernel displacements were calculated by finding the spatial shift between two frames that would maximize cross-correlation between the two signals. Cosine interpolation was used to compute sub-pixel displacements (Céspedes et al., 1995). Kernel velocities were calculated by multiplying frame-to-frame displacements by the framerate (Fig. 2). Tendon velocity data were acquired for 2 seconds during each cyclic loading trial.

For the Added Mass Group, laser vibrometry was used to facilitate measurements of tendon motion both in and out of the saline bath. Tendon motion was measured using a 660 nm wavelength laser Doppler vibrometer (PDV-100, Polytec, Inc., Irvine, CA). The laser was focused on the surface of the sample 20 mm above the bottom grip. The sensitivity and bandwidth of the vibrometer were set to 5 mm/s/V and 22 kHz, respectively. Tendon velocity data were acquired for 2 seconds at each static load, and for 2 seconds at each of 10 evenly spaced time points during creep tests.

2.2.5. Vibration frequencies and wave speeds

For each tap, transverse tendon velocity data were band pass filtered (50–2000 Hz) using a second-order, zero-lag, Butterworth filter to eliminate signal not associated with the tapper-induced vibration. For the Loading Rate Group, velocity trajectories were averaged across the measurement kernels through the depth of the tendon. A fast Fourier transform (FFT) was performed on the averaged (Loading Rate Group) or surface (Added Mass Group) velocity data. The vibration frequency, f, was determined by finding the peak magnitude of the FFT spectrum, which was assumed to be the first mode of vibration. Wave speed was calculated from vibration frequency as c=2fL, where L is the grip-to-grip tendon length.

2.3. Data analysis

Separate analyses were performed on data collected from tendons in the Loading Rate Group and the Added Mass Group to address the objectives of this study. The suitability of a tensioned beam model to describe the wave speed-stress relationship (Eqn. 2) and sensitivity to loading rate were assessed using data from the Loading Rate Group. Additionally, data from these tendons were used to estimate tendon effective density and shear modulus, and to assess model prediction errors based on trial-specific, tendon-specific and group-compiled calibration where all trials were included. Data from trials with different loading rates were considered together for tendon-specific and group-compiled analyses since loading rate did not have a significant effect on wave speed (see 3.1). The added mass effect caused by immersion of tendons in a saline bath was assessed using data from the Added Mass Group. Tendons in this group were additionally used to test whether tendon creep affects wave speed.

2.3.1. Sensitivity of wave speed to loading rate

A two-way repeated measures analysis of variance (ANOVA; p = 0.05) was used to examine the effects of varying loading rate and tendon stress on tendon wave speed. Wave speed data from all tendons were compiled and separated into 10 bins based on axial stress (0 to 10 MPa by 1 MPa) such that stress could be considered as a discrete variable.

2.3.2. Linearity of the squared wave speed-stress relationship

The coefficient of determination (r²) was used to assess the linearity of the squared wave speed-stress relationship. Linearity was assessed for trial-specific, tendon-specific, and group-compiled data.

2.3.3. Tendon effective density and shear modulus

Linear fits were performed on squared wave speed versus stress and were used to estimate tendon effective density and shear modulus (Eqn. 2). Fits were performed using trial-specific, tendon-specific, and group-compiled data.

2.3.4. Error between predicted and applied stress

Tendon wave speeds were used to predict tendon stresses using Eqn. 2 with estimated tendon effective densities and shear moduli from trial-specific, tendon-specific, and group-compiled data. The accuracy of predicted stresses was assessed using the root-mean-square error (RMSE) compared with the applied stresses.

2.3.5. Added mass effect of tendon immersion in saline bath

The added mass effect caused by immersion of the tendon was assessed by comparing tendon wave speeds for trials in saline versus in air. A two-way repeated measures ANOVA (p = 0.05) was used to examine the effects of immersion and varying axial load on wave speed. Wave speed data were averaged across 2 second trials at each of 6 static loads (see 2.2.2). The ratio of wave speeds measured in immersed tendons versus tendons tested in air was computed and compared to the predicted ratio for each tendon (Eqn. 5).

2.3.5. Effect of tendon creep on wave speed

Wave speeds measured during creep tests were compared with axial deformation displacements under constant tendon loading. Wave speeds measured for each sample were normalized to the average wave speed for the sample across the ten 2-second collections. Normalized wave speed data were then combined across tendons and the mean and standard deviation were computed for each 2-second collection. Tendon creep displacements were calculated by subtracting displacement occurring during initial ramp loading from total displacement measured during each trial. Creep displacements were normalized to the maximum value observed during the trial, and mean and standard deviation of the normalized creep displacement data were computed across tendon specimens. One tendon yielded unusable wave speed data during the creep test, while another slipped out of the grips and was damaged. Both were excluded from analysis.

3. Results

3.1. Sensitivity of wave speed to loading rate

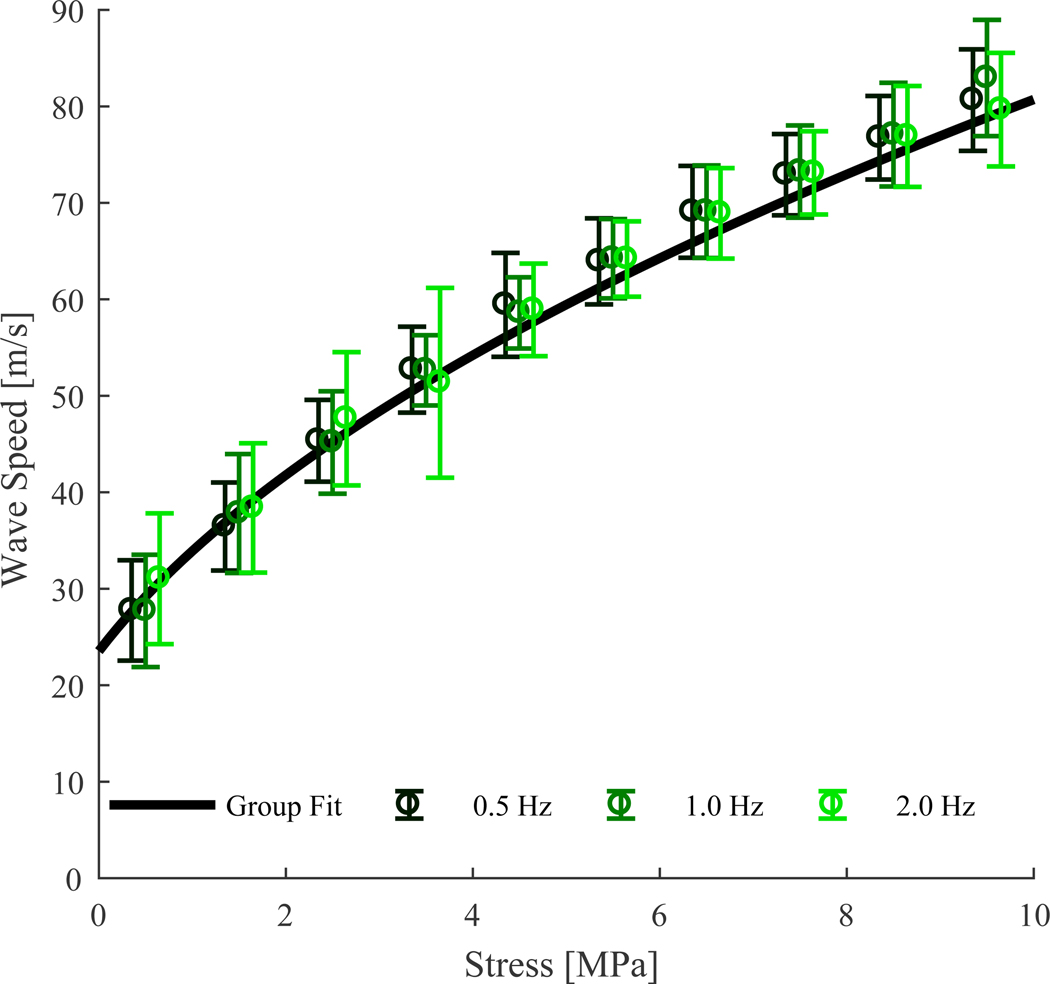
Shear wave speed was not significantly dependent on loading rate (p = 0.565, Fig. 3). Wave speed was significantly dependent on tendon stress (p < 0.001), and no rate-by-stress interaction effects were observed (p = 0.998).

Figure 3.

Binned mean (± 1 s.d.) shear wave speed versus stress for three cyclic loading rates performed on 10 tendons. Also shown is a fit calculated for group-compiled stress versus squared wave speed data.

3.2. Linearity of the squared wave speed-stress relationship

The relationship between squared wave speed and stress was highly linear for all individual trials in isolation (r² = 0.98±0.03). Tendon-specific data showed similar correlation (r² = 0.97±0.02). When data from all trials on all tendons were compiled and considered together, variance in wave speed squared predicted slightly less of the variance in stress (r² = 0.92).

3.3. Tendon effective density and shear modulus

Based on trial-specific linear fits of tendon stress versus squared wave speed, tendon effective density was estimated as 1680±240 kg/m³ and tendon shear modulus was estimated as 940±450 kPa. Similar estimates for effective density and shear modulus were found when performing fits on tendon-specific or group-compiled data (Table 2).

Table 2.

Results from analyses on trial-specific, tendon-specific, and group-compiled data. Correlation between tendon stress and squared wave speed, estimated tendon effective density (ρ_eff) and shear modulus (μ), and error between stress predicted from wave speed and applied stress.

Regression	r2	ρ eff [kg/m3]	μ [MPa]	RMSE [MPa]
Trial-Specific	0.98 ± 0.03	1680 ± 240	0.94 ± 0.45	0.61 ± 0.44
Tendon-Specific	0.97 ± 0.02	1670 ± 240	0.91 ± 0.38	0.67 ± 0.46
Group-Compiled	0.921	1680	0.93	1.31 ± 0.64

3.4. Error between predicted and applied stress

Root-mean-square errors were low when predicting stresses using trial-specific (RMSE = 0.61±0.44 MPa) and tendon-specific (RMSE = 0.67±0.46 MPa) calibrations (Table 2). Errors were approximately twice as high when using group-compiled calibrations to predict stress (RMSE = 1.31±0.64 MPa). These average RMS errors ranged from 6–13% of the maximum stress.

3.5. Added mass effect of tendon immersion in saline bath

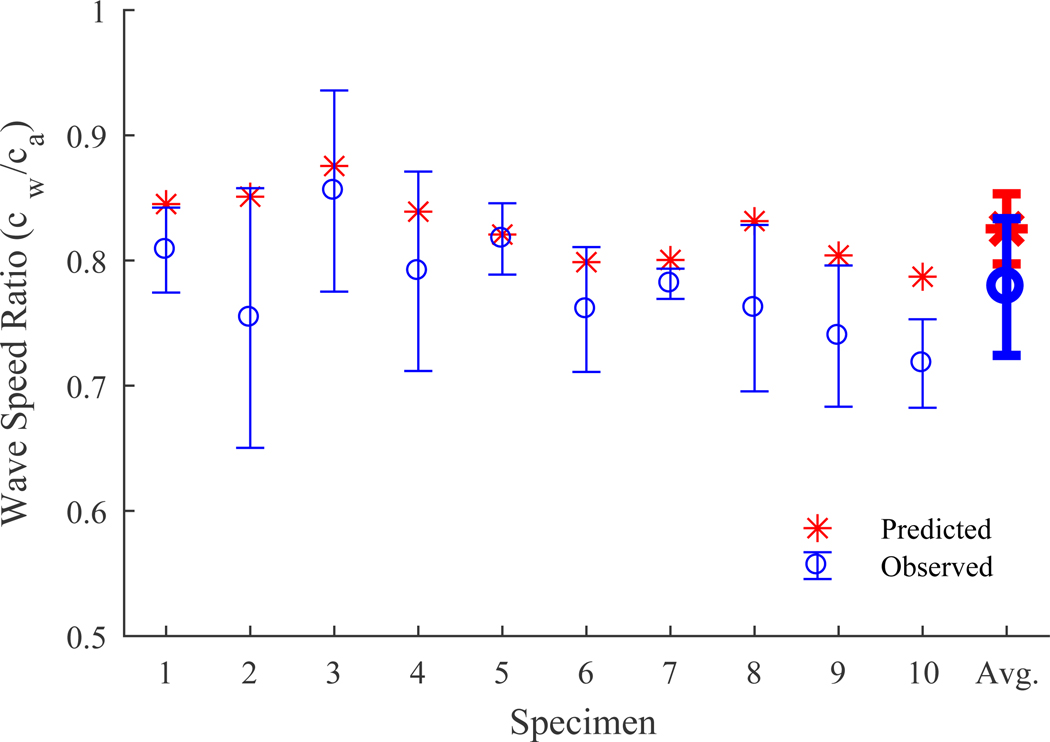
A two-way repeated-measures ANOVA revealed that wave speed was significantly affected by both tendon stress (p < 0.001) and immersion in saline (p < 0.001). No significant interaction effect was observed (p = 0.768). The predicted ratio for tendon wave speed in saline versus air (Eqn. 5) was 0.83±0.04 (mean ± s.d.) across the 10 tendons tested. The mean observed ratio was 0.78±0.04. The saline bath’s effects on wave speed were consistently greater than predicted, but prediction error averaged only 6% (Fig. 4).

Figure 4.

Ratio between tendon wave speed in a saline bath versus air as predicted using the model (Eqn. 5) and experimentally observed (mean ± s.d.) for individual specimens across 6 static loads.

3.5. Effect of tendon creep on wave speed

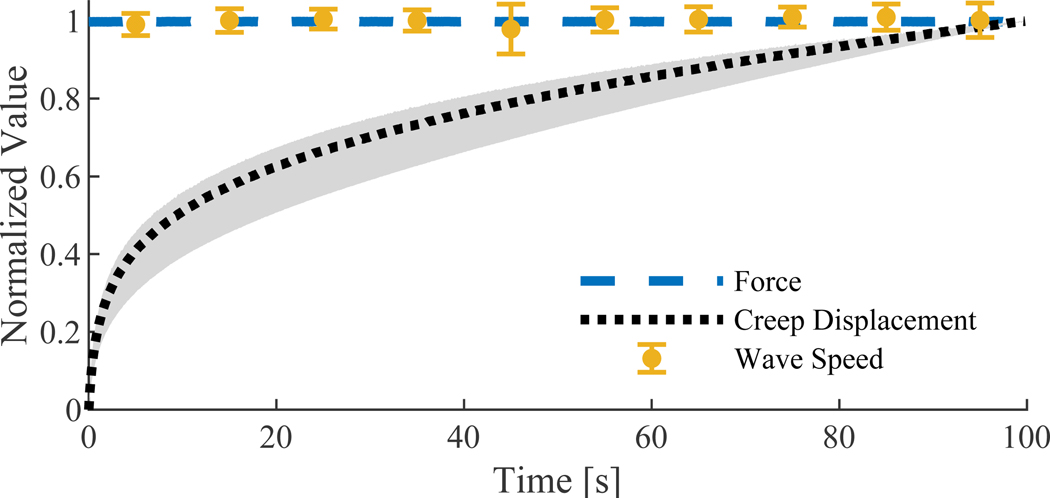
Normalized wave speed was within one standard deviation of unity at all time points, whereas creep displacement was readily observable (Fig. 5). Creep displacement was 0.9±0.4% of initial tendon length across specimens (mean ± s.d.), and accounted for 22±7% of the total displacement occurring during the test.

Figure 5.

Normalized force (mean), creep displacement (mean ± s.d.) and wave speed (mean ± s.d.) during a 100 second constant load (300 N) creep test.

3. Discussion

The objective of this study was to examine the suitability of a tensioned beam model to describe the relationship between axial stress and shear wave speed in ex vivo tendons. The high observed correlation between stress and wave speed squared is consistent with model predictions. The constant of proportionality is the tendon effective density, which was shown to be relatively constant across specimens and across a range of loading rates. These data demonstrate that tendon shear wave speed is primarily a function of load magnitude, which supports the use of shear wave speed to estimate tendon stress under functional conditions (Martin et al., 2018).

Shear wave speeds reported here for ex vivo tendons were considerably higher than seen in in vivo tendons at comparable loads (Martin et al., 2018). Wave speeds in the range of 4 to 16 m/s have been measured in unloaded and lightly loaded in vivo Achilles tendons (Helfenstein-Didier et al., 2016; Slane et al., 2017). While we did not directly measure unloaded tendon wave speed in this ex vivo study, linear fits of stress versus wave speed squared yielded an average intercept of 24 m/s. Our measured wave speeds increased considerably under loading, reaching ~80 m/s under ~10 MPa stresses, which is as high or higher than peak in vivo Achilles tendon wave speeds of ~50–80 m/s during walking where tendon stress is substantially greater (Finni et al., 1998; Martin et al., 2018). The lower in vivo tendon wave speeds are most likely attributable to entrained motion of the adjacent tissues and fluid, which could increase the tendon’s effective density and slow wave propagation. In this study we showed that wave propagation speed was reduced in a saline bath when compared to air (Fig. 4). The added mass effect associated with entrained motion of the surrounding water can be modeled, such that we were able to predict reduced wave speeds in the bath with less than 6% error on average (Fig. 4). In vivo tendon motion is additionally affected by entrained motion of adjacent tissues, which represents a more complex condition to model. It is likely that the connectivity of the surrounding tissue in the in vivo case evokes a greater added mass effect than the fluid bath studied here. Future work will address this by examining the wave speed-stress relationship in in situ cadaver tendons with the adjacent tissue intact and removed.

This study demonstrates how the stress-wave speed relationship can be calibrated in ex vivo tendons. Calibration is more challenging for the in vivo case where stress measures are not readily available. One can measure joint torques during isometric exertions, and then estimate tendon stress given measures of tendon moment arms, cross-sectional areas and assumed muscle force distributions (Dick et al., 2016; Herzog et al., 1991; Maganaris and Paul, 2002). Tendon-specific calibrations could thus be performed using an isokinetic dynamometer and imaging to measure tendon geometry (Maganaris and Paul, 2002). Longer term, one might be able to estimate tendon effective density and shear modulus from normative data. The RMSE values we report for ex vivo tendon stresses predicted from wave speeds were encouragingly low and give precedence to the idea of using linear fits of normative data. Thus, it is feasible that normative data could be collected for cadaveric muscle-tendon units in which wave speeds are measured while known loads are applied to intact tendons. We are currently evaluating effective density in in situ cadaver tendons from data collected during simulated gait and isometric contractions. More data is needed to estimate load-dependent variations in tendon shear modulus, μ. Prior studies have shown that ligament shear modulus increases to 1.7 MPa with large shear strain (Weiss et al., 2002), but it hasn’t yet been determined whether similar strain-stiffening increases in shear modulus occur with axial loading.

We computed tendon wave speed from vibration frequency, in contrast with the transient wave propagation measurements employed in SWE (Bercoff et al., 2004) and in our shear wave tensiometers (Martin et al., 2018). The effective pin-pin boundary conditions created by the upper and lower grips caused standing waves to emerge, whereas waves apparently dissipate in the adjacent muscle in the in vivo condition. Standing waves likely reflect the average stress over the tendon cross-section and length. On the other hand, transient wave analyses may be dependent on local stresses, which could vary through the cross-section or along the length of the tendon. We are undertaking a laser vibrometry study to investigate consistency of wave speeds evaluated from transient and standing wave analyses.

A prior study by Revel et al. used laser vibrometry to measure rabbit calcaneus communis tendon vibration frequencies under similar axial loading conditions (Revel et al., 2003). In contrast to the results presented here, Revel et al. showed only minor increases in vibration frequency with increasing axial stress (approximately 45–60 Hz from 0–8 MPa). Here, we observed vibration frequencies upwards of 500 Hz at ~8 MPa. The source of this discrepancy is unclear.

The theoretical wave speed-stress relationship examined by this study (Eqn. 1) does not explicitly account for viscoelasticity in the shear modulus term, but viscoelastic effects should only affect the shear modulus term, which becomes less important with greater axial stress. Others have shown that shear wave speeds differ with varied excitation frequencies and can be used to estimate tendon viscosity in lightly loaded tendon (Cortes et al., 2015). Our theoretical model predicts that wave speed is insensitive to frequency-dependent changes in shear modulus at loads of interest. Hence, it appears that it would be difficult to use wave speed to study viscoelasticity in loaded tendons.

The results of this study support a tensioned beam model prediction that tendon shear wave speed is primarily dependent on tendon stress under functional loads. Ultimately, our goal is to robustly estimate in vivo tendon stresses during dynamic activity. The independence of the wave speed-stress relationship to loading rate is important in this regard, since loading rates vary widely for different activities, or during different phases of an activity (e.g., walking). Further, the results support the idea of calibrating wave speed-stress relationships under simple loading conditions, and subsequently using such calibrations to estimate in vivo stresses under more complex loading scenarios. In total, the results of this study are an important step towards the development of a robust, non-invasive method for estimating dynamic in vivo tendon stresses.