Abstract
An integrative model is proposed to describe the dependence of the transverse relaxation rate of blood water protons (R2blood = 1/T2blood) on hematocrit fraction (Hct) and oxygenation fraction (Y). This unified model takes into account (i) the diamagnetic effects of albumin, hemoglobin, and the cell membrane; (ii) the paramagnetic effect of hemoglobin; (iii) the effect of compartmental exchange between plasma and erythrocytes under both fast and slow exchange conditions that vary depending on field strength and compartmental relaxation rates; (iv) the effect of diffusion through field gradients near the erythrocyte membrane. To validate the model, whole blood and lysed blood R2 data acquired previously using Car-Purcell-Meiboom-Gill (CPMG) measurements as a function of inter-echo spacing τCP at magnetic fields of 3.0T, 7.0T, 9.4T and 11.7T were fitted to determine the life times (field independent physiological constants) for water diffusion and exchange, as well as several physical constants, some of which are field independent (magnetic susceptibilities) and some are field dependent (relaxation rates for water protons in solutions of albumin and oxygenated and deoxygenated hemoglobin, i.e. blood plasma and erythrocytes, respectively). This combined exchange-diffusion model allowed excellent fitting of the curve of the τCP dependent relaxation rate dispersion at all four fields using a single average erythrocyte water life time, τery = 9.1±1.4 ms and an averaged diffusional correlation time, τD = 3.15±0.43 ms. Using this model and the determined physiological time constants and relaxation parameters, blood T2 values published by multiple groups based on measurements at magnetic field strengths of 1.5T and higher could be predicted correctly within error. Establishment of this theory is a fundamental step for quantitative modeling of the BOLD effect underlying functional MRI.
Keywords: Blood T2, Hematocrit, Oxygenation fraction, Exchange, Diffusion, τcp dependence, Hemoglobin, Albumin
Introduction:
The transverse relaxation rate of blood water protons (R2blood) is sensitive to the physiological conditions of the blood, especially the oxygenation fraction (Y) and the hematocrit fraction (Hct). In vivo, the capillary and venous oxygenation are determined by the perfusion and metabolic functioning of the tissue. For instance, an increase in local cerebral blood flow (CBF) during brain activation causes a reduction in the oxygen extraction fraction (OEF)1. This in turn reduces the arteriovenous oxygenation fraction difference (Ya-Yv) and R2blood in the capillaries and veins, a phenomenon known as the BOLD effect2-6. Quantification of whole-brain or local OEF has been done by measuring R2blood in draining venous compartments and comparing it with available calibration curves7-19 that relate R2blood to Hct and Y. Such data can be combined with a measured CBF to determine the cerebral metabolic rate of oxygen20-25. The development of an exact theory for R2blood is needed to provide a foundation for physiological theories for the BOLD effect5,6,26-31 and for BOLD-based applications for determining physiological parameters. However, while many models have been proposed for the description of R2blood7,8,10,12,15,17,32-39, an inclusive and conclusive theory that allows its prediction as a function of Hct and Y at multiple magnetic field strengths B0 has remained elusive. This is not surprising as, contrary to R1blood 40-49, the rate R2blood depends not only on the concentration of blood proteins and their diamagnetic and paramagnetic relaxivities, but also on the correlation times describing the exchange of water protons between compartments with different magnetic susceptibility and their diffusion through magnetic field gradients within or around such compartments. The sensitivity of R2blood to these correlation times becomes apparent when varying the inter-echo spacing (τcp) in a multi-echo Carr Purcell Meiboom Gill (CPMG) experiment, or even just the echo time (TE) in a single echo experiment, and this R2blood dispersion effect has a strong field dependence. The goal of this work is to establish a universal theory that can be used to predict R2blood as a function of physiological conditions (Y, Hct), MRI parameters (TE, τcp) and field strength B0. This theory is evaluated using a recently published large experimental R2blood data set.50 Development of such a theory for blood is important, because even gradient echo based blood transverse relaxation changes contribute substantially to the total BOLD effect, especially at lower field. For instance, during visual activation, extravascular BOLD signal change fractions are approximately 45±13%, 70±11% and 91±11% at 1.5, 3.0 and 7.0 T, respectively.51,52
Previous studies5,7,8,12,16,17,32,33,36-39,48,53-61 have already provided much insight into the relationship between R2blood, Hct, Y, and τcp. The rate R2blood is usually described as the sum of a τcp-independent term R20,blood (the intercept of the R2blood-τcp dispersion curve at infinitely short τcp) and a τcp-dependent relaxation enhancement due to either chemical exchange, as previously described by the Luz and Meiboom (LM)62 or the more general Allerhand and Gutowsky (AG) models63, or diffusion though local field gradients models, as proposed by Jensen and Chandra (JC model)32 or by Ziener et al. (Ziener model)33. Previously, when fitting R2blood dispersion data versus the rate 1/τcp, the intercept R20,blood has been considered either as a free fitting parameter without any quantitative relationship with Hct and Y, or just assumed to be the R2blood value at the shortest available experimental τcp7,8,12,15,17,36-39. However, both of these approaches could induce errors due to residual diffusion contributions, especially under deoxygenated conditions at high magnetic fields (Fig. 1), and make it difficult to predict R2blood from the blood physiological parameters. Here, we will instead start from basic principles for plasma and erythrocyte water proton relaxation rates based on albumin and hemoglobin protein solutions, respectively. This is possible because of the recent availability of relaxation data for plasma and lysed blood,50 in which the cell sequestration of hemoglobin is broken and the membranes removed. This lysed blood was mixed with plasma to perform hemoglobin concentration dependent studies, which also allowed determination of the “intracellular” water relaxation rate R2ery. Studying R2ery as a function of Y allowed estimation of the diamagnetic and paramagnetic water relaxivities for this hemoglobin solution.
Figure 1.
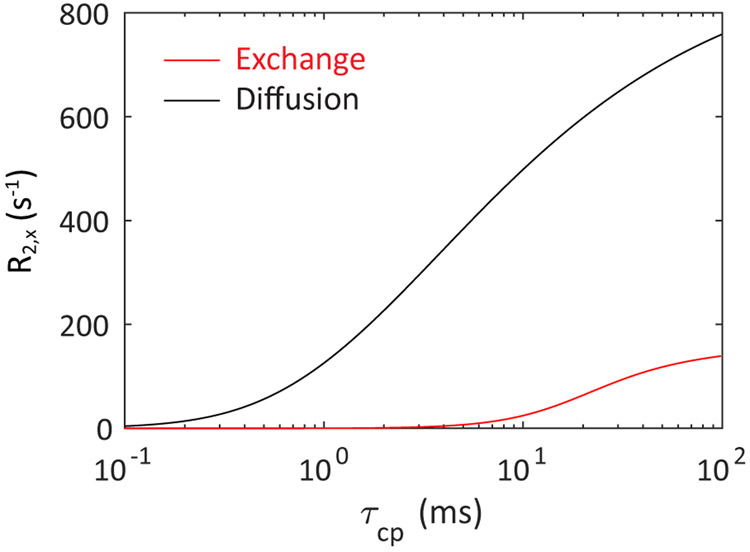
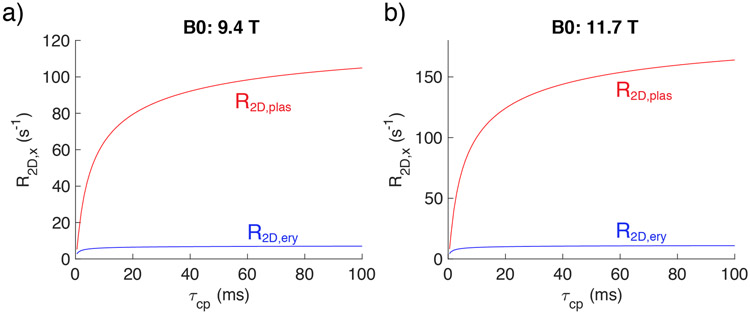
Comparison between the R2blood contributions at 11.7 T from diffusion (Jensen-Chandra model) and exchange (Luz-Meiboom model) as a function of τcp for a Hct of 0.4 and a chemical shift difference between intracellular and extracellular water of 0.1 ppm. It can be seen that the estimated diffusion contribution is substantial even at τcp values below a few ms, which is the approximate length of the 180° pulses on typical human scanners.
When fitting the R2blood dispersion as a function of echo spacing τcp, previous studies have been limited mainly to single-mechanism descriptions based on either water exchange between compartments7,8,10,12,15,17,36-39,57,58 or diffusion through field gradients within compartments32,33,64-68, sometimes including arguments why one would be better than the other. However, it is important to realize that both mechanisms affect the blood transverse relaxation enhancement, each with a characteristic τcp-dependent dispersion32,36 that depends on the correlation times representative for these distinct processes (Fig. 1). Evidence of problems with using one mechanism comes from the fact that while both approaches are generally able to provide excellent curve fits at each field strength, it is difficult to get consistent erythrocyte life times (τery) and diffusional correlation times (τD) between fields17. For instance, a gradual decrease in τery is found when going to higher fields using the fast exchange models and in τD using the diffusion models, while correlation times should in principle not be field dependent parameters. We propose here that a further improvement can be made by combining exchange and diffusion models to characterize the blood transverse relaxation rate and finding appropriate starting values for model fitting by separating out data from experimental conditions where either exchange or diffusion contributions dominate. For instance, the effect of diffusion becomes apparent already at very short τcp (< 2ms) under conditions of large field gradients around the cell membrane, such as for venous oxygenations at high magnetic fields, while, due to the relatively long lifetime of water in the erythrocyte (τery ~ 10 ms), compartmental exchange contributions are still minimal under such conditions (Fig. 1). A further improvement that we will implement is the use of the general exchange model69,70 that not only covers all exchange regimes (fast, slow and intermediate), but can also be adjusted to include compartmental relaxation rates for the erythrocyte and plasma water (R2ery and R2plas, respectively). This is crucial, because the exchange regime changes with field strength and oxygenation fraction. Finally, with regards to diffusion, water protons in the plasma and erythrocyte may experience different shape effects of the erythrocyte membrane. If so, they will contribute in different proportions, the magnitude of which we will assess. The resulting analytical expression thus combines the intrinsic relaxation of protein solutions with the relaxation enhancements due to exchange between and diffusion around compartments with different magnetic susceptibilities. This expression, together with the field-dependent inherent relaxivities determined from our fits allows one to predict R2blood at different Hct, Y, TE and τcp as a function of magnetic field strength.
Theory
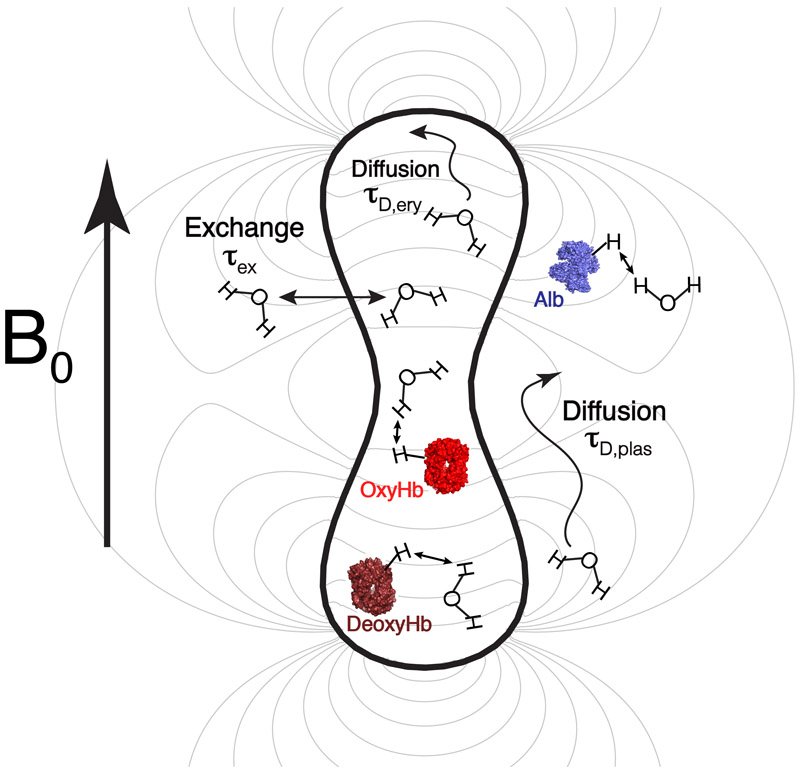
Blood is composed predominantly of plasma and erythrocytes. The plasma consists mainly of buffered water and albumin, while the intracellular volume of the erythrocyte consists mainly of buffered water and a high concentration of hemoglobin. As illustrated in Fig. 2, R2blood is affected by these protein-water interactions both at the molecular level and the cell level71. At the molecular level, a protein molecule (albumin or hemoglobin) enhances the overall relaxation of water protons because of fast chemical exchange between exchangeable protons in proteins and water protons in bulk water72. At the cell level, a magnetic susceptibility difference is induced by the diamagnetic hemoglobin and paramagnetic deoxyhemoglobin molecules being confined to the erythrocyte with its bi-concaved shape. This will generate a B0 field gradient and a chemical shift difference between water protons in the erythrocyte and in plasma. When water molecules diffuse in the field gradient or exchange across the erythrocyte membrane, the field gradient/chemical shift difference will result in a loss of phase coherence for the transverse proton magnetization. This R2blood enhancement can be mediated by the interplay between τcp and the correlation time of exchange (τex) or diffusion (τD). A CPMG sequence with a τcp that is short compared to τex or τD can promptly refocus the local chemical shift evolution of water protons before the molecule moves to a position with different spatial frequency, and thus minimizes the relaxation enhancement. When increasing τcp, more and more water protons change their positions either between the two compartments or over a larger range of field variance due to the presence of a gradient, and experience a larger relaxation enhancement. When τcp is much longer than τex and τD, the water molecules have experienced most possible compartmental positions and thus the full range of field variance. At this point the relaxation will not enhance anymore when further increasing the τcp. However, this situation of full mixing (theoretically analogous to fast exchange) is generally not reached for the case of blood over the typical range of echo times TE used for in vivo experiments. Therefore, in addition to blood parameters such as the hemoglobin concentration in the erythrocyte (cHb), albumin concentration in plasma (cAlb), the volume ratio taken by the erythrocyte (Hct), and the oxygenation fraction (Y), the experimentally measured R2blood depends on the chosen τcp. If τcp is not kept constant while the echo time TE is varied, such as in a TE-dependent single spin-echo relaxation measurement, R2,blood even varies with TE.
Figure 2.
Two-compartment model used to describe the transverse relaxation rate of blood water protons, R2blood. The magnetic field line (gray line) simulated based on the biconcave shape of erythrocyte shows the smaller gradient inside the erythrocyte.
To characterize R2blood, we propose the model shown in Fig. 2. The water in the blood is divided into two pools: (i) the erythrocyte water proton pool with relaxation rate R2ery, having contributions from the hemoglobin solution relaxation rate R2Hb and a diffusion relaxation enhancement R2D,ery (ii) the plasma pool with the rate R2plas with contributions from the albumin solution relaxation rate R2Alb and a diffusion relaxation enhancement R2D,plas. Then the whole-blood relaxation rate R2blood is calculated by including the water exchange effect across the erythrocyte membrane described using a previously established general exchange model69,70, erythrocyte shape factors (β), and a cell membrane component accounting for relaxation enhancement due to the presence of the erythrocyte membrane.
Transverse Relaxation in Hemoglobin and Albumin Solutions
As shown in a previous study72, the transverse relaxation of water in a protein solution measured by CPMG experiments can be well approximated in terms of chemical exchange between free water protons and exchangeable protein protons. To quantitatively describe the transverse relaxation consequences of this chemical exchange process, the general exchange model developed by Carver and Richards69 and modified by Davis et al.70 (Appendix 1) has to be used. The reason is that the transverse relaxation rate of exchangeable protein protons without exchange (R2b,prot) is much faster than that of bulk water protons in buffered solution (R2buf) and the regular expressions of Luz and Meiboom62 or Allerhand and Gutowsky63 are not applicable73 (See Appendix 2 for requirements). Therefore, the transverse relaxation rates of the water protons in hemoglobin solution and albumin solution (plasma) are expressed as69:
R2prot =
| [1a] |
| [1b] |
| [1c] |
| [1d] |
| [1e] |
| [1f] |
| [1g] |
in which kprot is the dissociation rate for protein-bound exchangeable protons and kbuf is the association rate onto the protein of protons from the free solution pool. While R2buf and kbuf are orders of magnitude smaller than R2b,prot and kprot, respectively, and could in principle be neglected, we include them as R2buf is available from direct measurements and kbuf can be calculated (Eq. 1c). In this paper we use cgs units for chemical shifts and magnetic susceptibilities. The chemical shift difference (rad/s) between exchangeable protein protons and solution water protons, Δωprot, can be calculated for each field strength using the averaged chemical shift difference (Δδprot, ppm) between the protein protons and the water protons:
| [2] |
Pprot is the proton fraction of the number of exchangeable protein protons () relative to the number of bulk water protons () and can be estimated as
| [3] |
where is the number of exchangeable protein protons per molecule and cprot the molar concentration (mol/L) of protein. The bulk water volume fraction, fV,water of a protein solution depends on the protein concentration and is [1 - 0.3/(332g/L) × cHb(g/L)] for Hb inside erythrocyte and [1 - 0.05/(50g/L) × cAlb(g/L)] for Alb in plasma. For normal blood, where cHb is 332g/L inside the erythrocyte and cAlb is 50g/L in the plasma, fV,water is a constant of 0.774 and 0.9575 for Hb and Alb respectively. However, for the hemoglobin solutions of different concentration, the number has to be calculated appropriately. The water concentration in solution is 55.6 M and, because there are two protons for each water molecule, a pre-factor 2 is used to calculate the bulk water proton number. The term in the denominator of Eq. [3] was neglected when deriving the final expression on the right hand side.
The hemoglobin solution is a mixture of deoxygenated and oxygenated hemoglobin. Assuming minimal conformational changes from the oxygenated to the deoxygenated state, we use the same proton dissociation rate (kprot) and the same number of exchangeable protons (). However, the exchangeable protons in the deoxygenated and oxygenated hemoglobins have different chemical shifts (Δδprot) and relaxation rates (R2b,prot) because the iron ion in oxygenated hemoglobin is diamagnetic, while it is paramagnetic in deoxygenated hemoglobin. Therefore, the overall relaxation rate (R2Hb) of water protons in the hemoglobin solution is expressed as17,36:
| [4] |
where the rates of the oxygenated (R2OxyHb) and deoxygenated (R2DeoxyHb) hemoglobin contributions can be calculated based on Eqs. 1-3 using their particular chemical shift differences ΔδOxyHb and ΔδDeoxyHb for their exchangeable protons.
Membrane Relaxation Enhancement
The lipid bilayers of the erythrocyte may also enhance the transverse relaxation of blood water76,77 as for instance demonstrated by the short T2 of myelin water78. Following our previous paper50, we assume the transverse relaxation enhancement of the membrane (R2mem) to be the same inside and outside the cell. However, this enters in different proportions in the equations for the plasma and erythrocyte contributions, because the intracellular contribution is always the same (concentration of exchangeable protons in the membrane inside the erythrocyte does not change), while the extracellular concentration of exchangeable membrane protons increases proportional to the Hct. In addition, the total effect for blood water has to include the appropriate water fractions for the erythrocyte (fery) and plasma, fplas = (1 – fery), which depend on the protein concentrations in these compartments. Thus:
R2blood total enhancement from the cells:
| [5a] |
R2blood total enhancement from plasma:
| [5b] |
where R2mem is a field dependent relaxation rate. The relationship between Hct and fery is defined in the whole-blood relaxation section below (Eq. [17]). Notice that Eq. [5b] correctly reflects that there will be no additional membrane water relaxation contribution to whole blood from plasma, both for pure plasma (Hct = 0 and fery = 0) and pure cells (Hct = 1 and fery = 1).
Oxygenation Dependence of the Magnetic Susceptibility
The volume magnetic susceptibilities of the hemoglobin solution inside the erythrocyte and the albumin solution (plasma) are given by79:
| [6a] |
| [6b] |
in which χ and χM indicate volume and molar magnetic susceptibilities, respectively; mL/mole is the molar magnetic susceptibility of hemoglobin in its quaternary form80 and mL/mole is the molar paramagnetic contribution due to a single deoxygenated heme81. This value corresponds to a magnetic moment of 5.435 Bohr magneton (B.M.), which agrees well with Pauling’s measurement 5.46 B.M82. χH2O is the volume magnetic susceptibility of water (−0.719×10−6), is the molar volume of the quaternary hemoglobin (M/ρ = 64.5×103 [g/mole]/1.335 [g/mL])83, and cHb is the total concentration of the quaternary hemoglobin inside the erythrocyte. For albumin, which has a molecular weight of 66.5×103 g/mol42, we assume the same molar susceptibility and density as for quaternary hemoglobin, while cAlb is 0.752 mM in the plasma. Substitution of these values gives:
| [6c] |
| [6d] |
| [6e] |
In previous papers, this susceptibility difference was written as
| [7a] |
A Δχdeoxy of 0.253 ppm is in the typical range found in recent measurements38,84, but interestingly the oxygenation-dependent term derived in Eq. [6e] is not (1-Y) but correctly reflects the fact that the magnetic susceptibility difference transitions from being negative (diamagnetic) in the arteries and arterioles to positive (paramagnetic) when oxygenation decreases. The theoretical prediction indicates this transition happens at Y = 0.937, but for a more general description we define an oxygenation value for this diamagnetic-to-paramagnetic susceptibility difference transition (Yoff):
| [7b] |
Meanwhile, it is important to note that the water proton chemical shift difference between the plasma and the hemoglobin solution inside the erythrocyte is not naturally equivalent to the bulk susceptibility difference between inside and outside the erythrocyte. This chemical shift difference mainly comes from two parts: 1. The average proton chemical shift of water protons will change due to the fast exchange with the exchangeable protons of proteins in solution. As discussed above in the transverse relaxation in hemoglobin and albumin solutions, this chemical shift difference contribution can be expressed as
| [8] |
in which Pery and Pplas are the fractions of the number of exchangeable protein protons relative to the number of bulk water protons; 2. the chemical shift difference generated by the bulk susceptibility difference between the erythrocyte and plasma85. This is very similar to the bulk susceptibility corrections for the chemical shift measurement when an external standard solution was used in a sealed capillary that is coaxially inserted in the sample86. Because this chemical shift difference is proportional to the bulk susceptibility difference and depends on the erythrocyte’s shape and its orientation relative to the main magnetic field, a shape factor βEx will be introduced. Therefore, combing Eq. 7b and 8, the average chemical shift difference experienced between water protons inside and outside the erythrocyte becomes:
| [9] |
in which all Δδ values are also on the order of 10−6. In the fitting of the whole blood values we will start with using 0.937 (Eq. 6e) as the starting value for Yoff.
Diffusion-based Relaxation Enhancement due to the Presence of a Cell Membrane
In whole blood, the susceptibility difference between erythrocytes and plasma generates an inhomogeneous magnetic field both inside and outside the erythrocytes. Jensen and Chandra.32 derived an analytical solution for the diffusion relaxation enhancement based on a weak field approximation:
| [10] |
where
| [11] |
The diffusional correlation time is defined to describe the process of water proton diffusion through a gradient that they experience,32,33,87 in which D is the translational diffusion constant of water, and rc is the length scale of the inhomogeneities (i.e. expected to be approximately on the order of the erythrocyte size). G0 can be considered as a square of local gradient, which is obtained by averaging the square of the local field inhomogeneity (Eq. 27 in Ref. 32). If we assume the erythrocyte to be spherical from the view of a molecule close to the membrane, the value of G0 can be approximated as 17,32
| [12a] |
However, the deviation of the erythrocyte’s bi-concaved shape from spherical leads to a different field pattern and different diffusion-based relaxation enhancements. We therefore need to add a shape factor β.
| [12b] |
The term η is the volume that experiences the gradient. In the plasma, we approximate this by the volume occupied by the erythrocyte (η = Hct). Therefore, the diffusion relaxation enhancement in the plasma can then be calculated as
| [13] |
In this study, the water diffusion contribution inside the erythrocyte is neglected due to the magnetic field homogeneity inside the erythrocyte. In fact, if we assume the erythrocyte to be an oblate ellipsoid of rotation, the magnetic field inside the erythrocyte will be fully homogeneous88. Under this uniform magnetic field, the spin dephasing does not depend on position and not contribute to R2 measured by CPMG experiments. Certainly, the erythrocyte’s shape is not perfectly ellipsoid, but as shown by the simulation based on the real erythrocyte’s shape (Figure 2), the magnetic field inside the erythrocyte is very homogeneous compared to the magnetic field outside the erythrocyte. Therefore, the water diffusion contribution inside the erythrocyte is neglected.
Whole-blood Relaxation Including Exchange-based Relaxation Enhancement
To describe transverse relaxation in the two-compartment model for blood (Fig. 2), the contributions from the individual compartments now can be written out using equations 1-4 for the hemoglobin and albumin solutions (R2Hb and R2Alb) and equation 13 for the diffusion enhancement in the plasma. The water proton transverse relaxation rates for the water protons in the plasma (R2plas) and erythrocyte (R2ery) then are:
| [14a] |
| [14b] |
The permeability of the erythrocyte membrane limits the life time of the water molecules in the erythrocyte to about 10 ms.89 As a consequence, water molecules experience the different precession frequencies in the erythrocyte and plasma, leading to dephasing and a relaxation enhancement. Previously, this exchange-based enhancement has been described using the Luz-Meiboom (LM) Model62,90, but this model implicitly assumes91 that: (i) the R2 rates in the erythrocyte and in the plasma are of the same order of magnitude, which need not be always valid because the intrinsic relaxation rates and diffusion relaxation enhancements are very different inside and outside the erythrocyte, especially at lower oxygenations; (ii) the chemical shift difference between erythrocyte and plasma Δω is much smaller than the exchange rate, i.e. fast exchange on the NMR time scale, which is not fulfilled at high magnetic field17. Therefore, again the general exchange model (Appendix 1)69,70 needs to be used to calculate the blood transverse relaxation rate:
| [15a] |
| [15b] |
| [15c] |
| [15d] |
| [15e] |
| [15f] |
| [15g] |
in which kery and kplas are the water exchange rate constants from the erythrocyte to the plasma and from the plasma to the erythrocyte, respectively. They can be related to water life time in the erythrocyte τery through the equations:
| [16a] |
| [16b] |
in which the water fraction in the erythrocyte fery is42
| [17] |
The exchange life time for the two-compartment system is defined by
| [18] |
Equations 15[a-g] may appear to be different from the widely used Luz-Meiboom (LM) fast exchange model62, where the intrinsic relaxation rate contributions of protein solutions in erythrocyte and plasma were appropriately proportioned through multiplication with the appropriate water fractions17. It is important to realize that, while not intuitive, the effect of these fractions is included appropriately in the current equations too. To show that the fractions are in there, one can take the limit of fast exchange and retrieve the equations used in previous studies where fast exchange was assumed (Supplementary S4).
Methods
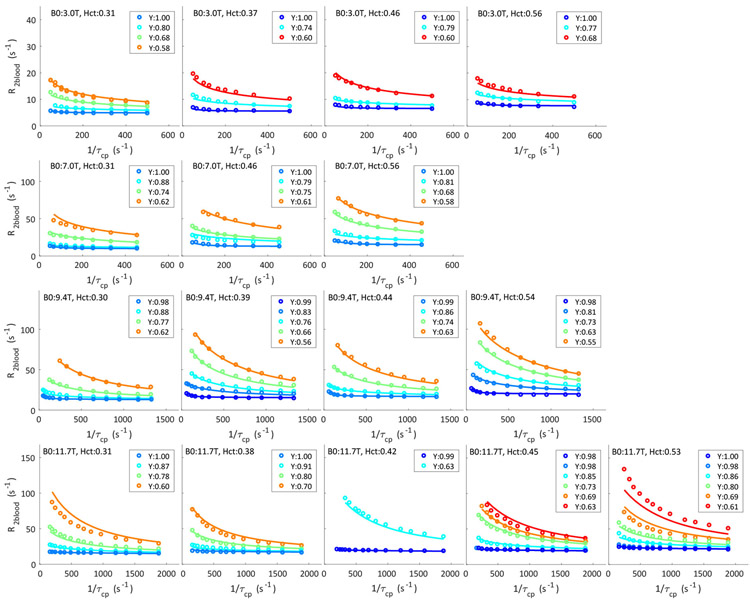
To verify the model, we used the isolated plasma, lysed blood and whole blood R2 data measured by Grgac et al.50 as a function of Hct, Y, and τcp at 3.0 T, 7.0 T, 9.4 T and 11.7 T. The fitting approach is described in Figure 3. As discussed above, the whole blood R2 includes contributions arising from the hemoglobin and albumin solutions (R2Hb and R2Alb), the erythrocyte membrane, and relaxation enhancements from water exchanging between inside and outside of the erythrocyte and diffusing around the erythrocyte. Therefore, we first fitted the isolated plasma and lysed blood R2 data to obtain the parameters for calculating R2Alb and R2Hb, respectively. These were subsequently used for the fitting of whole blood R2 values50 for obtaining the parameters describing the membrane, diffusion and exchange relaxation enhancements. In the latter fitting, we started with baseline Yoff = 0.937 (Eq. 6e) and obtained further initial parameters by focusing on data acquired at short τcp and high Y, where the diffusional contributions dominate, before performing the final whole-blood fitting.
Figure 3:
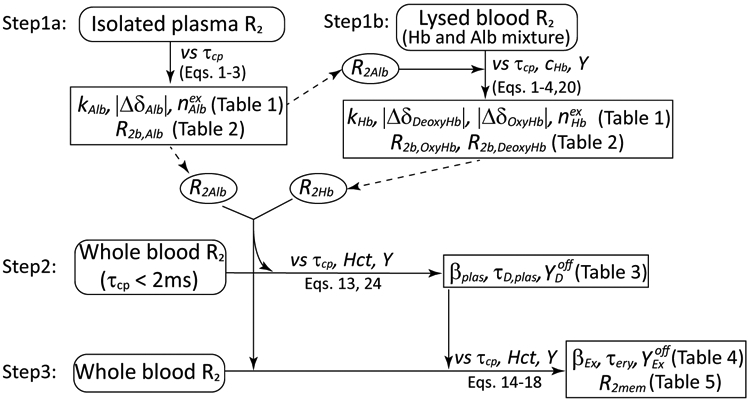
Flow chart illustrating the fitting process.
Data Used in the Model Fitting
We used the isolated plasma, lysed blood and whole blood R2 data measured by Grgac et al.50, but several corrections were made. First, the length of refocusing pulse in the CPMG pulse sequence needs to be accounted for to have a correct τcp, using the equation92:
| [19] |
in which pw is the length of refocusing pulse. This was previously done for the long pulses used at 3.0 T and 7.0 T, but due to the short pw (microsecond) on the high resolution vertical bore NMR scanners, the data at 9.4 T and 11.7 T in previous paper50 were not corrected. The now corrected data for 9.4 T and 11.7 T are listed in Supplementary Tables S1, S2 and S3. Notice that the use of a corrected (shorter) τcp for refitting the TE-dependence of the experimental curves will lead to slightly larger relaxation rates than the original ones in reference50 (Supplementary S5). Second, the previous paper contained multiple measurements of plasma at 9.4 T, with some larger differences for some of the inter-echo spacings (Table 2c in previous paper50). We therefore re-measured the τcp dependence of R2plas at 9.4 T (Supplementary Table S1) using the same approach as for the previous paper50, and the new data only were used in the current fitting. Third, we acquired several new data at 3.0 T using the same method as previous paper50, and found that the previous data with Hct of 0.45 and 0.56, which were measured at the same day, had significantly higher R2blood at long τcp than the new data. This could indicate some experimental problems in the blood preparation. Therefore, we used only new data for this Hct range (new Hct values 0.46 and 0.56) at 3.0 T (Supplementary Table S3a). Fourth, we only included the data with Hct smaller than 0.58. This is because the irregular bi-concave shape of the erythrocyte can not effectively fill the space and Hct can not be over 0.58 without changing the shape and thus magnetic field gradient properties of the erythrocyte93. This should not be problematic for use of the model, because the normal range of Hct in vivo is 0.36-0.5375 which is covered in our fitting. Fifth, we only include data with Y higher than 0.55. Low oxygenation fractions greatly increase the susceptibility of the erythrocyte and thus the signal decay rate. As a consequence, we have limited data for such oxygenation fractions at high field and for consistency removed these Y-values also at lower fields. Since Y of venous blood is about 0.60-0.65, we are basically limiting the fitting of our data to the physiological range. All the data used in the fitting are listed in Supplementary Tables S1-S3.
Transverse Relaxation of Hemoglobin and Albumin Solution
To determine the parameters causing the exchange relaxation enhancement of water protons in albumin solution, the isolated plasma data were described using R2plas = R2Alb(B0,τcp,R2b,Alb,cAlb,kAlb,,ΔδAlb). These data measured as a function of τcp at 3.0, 7.0, 9.4, and 11.7 T (supplementary Table S1) were then fitted for R2b,Alb, kAlb, , and ΔδAlb using Eqs. 1-3 through minimizing the relative error ∣R2.exp-R2,fitted∣/R2,exp, A value of 0.36 s−1 was used for the bulk water relaxation rate (R2buf = R2saline) across all magnetic fields50; the albumin concentration was 0.752 mM42 and the bulk water volume fraction fV,water was 0.95, based on the fact that the albumin takes 5% volume in the solution75. To improve the accuracy of the fitting, the ranges of the fitted parameters were limited based on existing knowledge. The typical chemical shift ranges for exchangeable NH protons and OH protons are from 6.6 to 8.8 ppm94 and from 5.4 to 6.2 ppm95, respectively, while the proton chemical shift of bulk water is about 4.8 ppm. Therefore, ΔχAlb was limited from 0.6 ppm to 4 ppm in the fitting. The upper limit for the number of exchangeable protons in albumin () was taken from the deuterium exchange experiments96 by Benson et al. which showed a maximum of about 910 96. The lower limit of was estimated as 350 by directly counting the number of NH and OH groups in the accessible side chains (such as the side chains rich in lysine, arginine and threonine) of the albumin sequence72. The lower limit of the proton dissociation rate (kAlb) was assumed to be 1000 s−1, based on the experimental finding of the lack of large R2plas changes with τcp shortening in our measured τcp range (0.5 ms – 20 ms). In the fitting, the plasma data at 9.4 T and 11.7 T were used first to estimate the field-independent parameters (kAlb, and ΔδAlb) and the field-specific R2b,Alb, because the τcp dependence of R2plas at 3.0 T and 7.0 T was too small compared to the experimental noise (Table S1). The kb,Alb, and ΔδAlb estimated this way were subsequently used to fit the 3.0 T and 7.0 T data for the R2b,Alb values at these fields.
The parameters causing the exchange relaxation enhancement of water protons in hemoglobin solution were determined from fitting the lysed blood data available for mixtures of packed erythrocytes and plasma (Supplementary Tables S2a-d). To account for the addition of albumin, Eq. 4 was modified as:
| [20] |
where R2Alb was calculated based on the fitted parameters above, and the Hct was estimated from the ratio of the hemoglobin concentration in the lysed blood sample and in the erythrocyte (332g/L = 5.15 mM): 97,98
| [21] |
Because the hemoglobins occupy 30% of the volume in solution74, Pery in Eq. 3 can be calculated from
| [22] |
It is worthy to note that the hemoglobin concentrations for several of the lysed packed erythrocyte samples were higher than 5.15 mM, probably because the erythrocytes shrink during the centrifugation in the preparation of packed erythrocytes. For these cases, the Hct was set to one, and the Pery modified to:
| [23] |
assuming that the volume occupied by the hemoglobins is proportional to the hemoglobin concentration.
Similar to the fitting of isolated plasma data, the lysed blood data at 9.4 T and 11.7 T were fitted first to obtain the global parameters (kHb, ΔδDeoxyHb and ΔδOxyHb) and R2b,OxyHb and R2b,DeoxyHb for each field. The fitting ranges of the global parameters were set the same as for albumin because both are globular proteins with comparable molecular weight (66.5 vs 64.5 kDa, respectively). The parameters kHb, , ΔδDeoxyHb and ΔδOxyHb from the fitting of 9.4 T and 11.7 T data were subsequently used as the constants in Eqs. 1-3 to fit the 3.0 T and 7.0 T data for determining the field-specific R2b,Oxy and R2b,Deoxy values.
Transverse Relaxation of Whole Blood
In the parameter fitting of the whole blood, R2blood data obtained for various Hct and Y values at 3.0 T, 7.0 T, 9.4 T, 11.7 T (Supplementary Tables S3a-d) were fitted using Eqs. 14 and 15 through minimizing the relative error ∣R2.exp-R2,fitted∣/R2,exp. The transverse relaxation rates of albumin solution in plasma (R2Alb) and hemoglobin solution in the cytoplasm of erythrocytes (R2Hb) were calculated based on Eq. 1 using an albumin concentration of 0.752 mM42, a hemoglobin concentration of 5.15 mM in the erythrocyte97,98, R2buf = 0.36 s−1 at all fields50, and the values of kAlb, , ΔχAlb kHb, , ΔδDeoxyHb, ΔδOxyHb, and the protein specific R2b values as given by the field dependency equation (Eq. 31) derived from the previous fits of the isolated plasma and lysed blood data. Having the R2Hb and R2Alb available, the remaining parameters to be fitted from the whole blood data were τery, βplas, τD,plas, βEx, Yoff, and R2mem, among which τery, βplas, τD,plas, βEx, and Yoff are expected to be magnetic field independent and thus set to be the same across all magnetic fields. R2mem was fitted separately for each field.
To minimize the uncertainty of multi-parameter fitting (many possible fitting minima and co-dependent parameter changes for the diffusion and exchange life time), we first fit only the short τcp (< 2ms) data at high fields (9.4 T and 11.7 T), assuming contributions only from the albumin and hemoglobin solutions and the diffusion effects in plasma (Eq. 13). This is reasonable because for the exchange contribution, the water life time in the erythrocyte (~10ms) is much longer than the τcp (< 2ms) of these fitted data, thus the water exchange has little contribution compared with the diffusion contribution in the plasma which has the diffusional correlation time (~3ms estimated based on the erythrocyte size) close to τcp of these data (Fig. 1). Therefore, to fit the data acquired at short τcp (< 2ms), only the diffusion-based relaxation, the intrinsic protein solution relaxation, and the membrane relaxation contributions were used:
| [24] |
where fery was calculated from the Hct using Eq. 17; R2Hb and R2Alb were pre-calculated using Eqs. 1-4 based on the parameters (Tables 1 and 2) obtained from the fits of lysed blood and plasma. Starting with this equation, the values of the parameters and accuracy of the fits were judged and the equations further adjusted by removing superfluous parameters (negligible contributions) and adding additional parameters, the logic of which is described in the results. As similar approach was used when subsequently fitting the whole blood values. From these fits it became clear that there was a need to have separate Yoff parameters for diffusion and exchange ( and ), which are about 5% bigger and smaller, respectively, than the theoretically derived value of 0.937 (Eq. 6e). Thus:
| [7c] |
| [7d] |
Table 1.
Protein proton dissociation rates, number of exchangeable protons, and chemical shift differences relative to the bulk water protons.*
| kprot (s−1) | ∣Δδprot∣ (ppm) |
|||
|---|---|---|---|---|
| Albumin | (11.6±5.8)×103 | 806±418 | 1.21±0.76 | |
| Hemoglobin | Oxy | (14.6±6.4)×103 | 499±206 | 0.614±0.304 |
| Deoxy | 1.11±0.51 |
Table 2.
Transverse relaxation rates for the exchangeable protein protons (R2b,prot)
Therefore, in total 7 parameters, i.e. three unifield parameters (τery, and βEx) and four R2mem (one R2mem for each field) were fitted using 130 R2blood values at 3T, 104 R2blood values at 7T, 191 R2blood values at 9.4T and 285 R2blood values at 11.7T. In the fitting, the τery range was limited from 8 ms to 20 ms based on previous literature89,99-105. was limited from 0.8 to 1.0. The chemical shift shape factor βEx was limited from −10 to 10. The nonlinear fitting function “fmincon” in matlab was used in the fitting. To alleviate the problem of local minimum, a series of 126 initial values was sampled using τery values of [8.0, 10.0, 12.0, 14.0, 16.0, 18.0] ms, βEx values of [−4, −2, −1, 0, 1, 2, 4] and values of [0.85, 0.9, 0.95].
To compare our model with previous models, the same data set was fitted with
-
The Luz-Meiboom (LM) fast exchange model 62
where τex defined in Eq. 18 and Δωery–plas defined in Eq. 9 were used for the fitting; The R20 is a weighted average of the relaxation rates of the hemoglobin solution inside the erythrocyte (Eq. 1a) and the albumin solution outside the erythrocyte (Eq. 1a) combined with the membrane contribution:[25] [26] Therefore, in total 7 parameters (3 unifield parameters βEx, , τery and four R2,membrane, one for each field) will be fitted.
- The Allerhand-Gutowsky (AG) exchange model 63
[27a] [27b] [27c]
where Sr and Si are the real and imaginary parts of S respectively and R20 is described by Eq. 26. Similar to the Luz-Meiboom (LM) fast exchange model, in total 7 parameters (3 unifield parameters βEx, , τery and four R2,mem, one for each field) will be fitted.[27d] -
The Ziener diffusion model33:
[28a]
where η is the occupied volume by the erythrocyte in the plasma (η = Hct), Fn(η), λn(η) are the expansion coefficients related to η and can be calculated as shown in Supplementary S6, and R20 is described by Eq. 26. Therefore, in total 7 parameters (3 unifield parameters βplas, , τD,plas and four R2mem, one for each field) will be fitted.[28b] The Akaike information criterion (AIC)106-108, which penalizes the goodness of fit with the number of free parameters, was used to compare the fitting goodness of the different models. The AIC with a correction for finite sample sizes was calculated as 109:
where RSS is residue sum of square, n is the number of data points and k is the number of fitting parameters plus one. To interpret the calculated AIC values as conditional probabilities, the Alkaike weights were calculated using 109:[29]
where wi(AIC) and AICi are the ith model’s Alkaike weights and AIC value, and AICmin is the smallest AIC value among all the models.[30]
Results
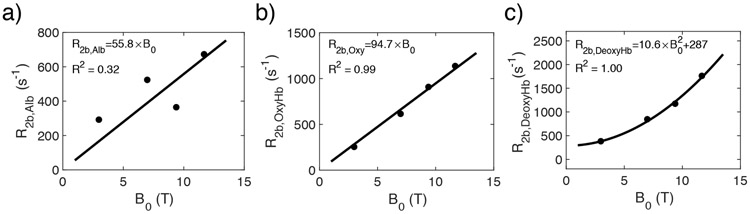
The fits of the relaxation data of isolated plasma and lysed blood used to determine the relaxation contributions of albumin and hemoglobin molecules, respectively, are shown in Figs. 4 and 5. The fitted number of exchangeable protons, the dissociation rate, the chemical shift difference relative to bulk water, and the transverse relaxation rates without exchange (R2b,prot) are listed in Tables 1 and 2. The field dependencies of these rates are plotted in Fig. 6, where linear (including point 0,0) and quadratic functions were used to fit the diamagnetic and paramagnetic rates, respectively:
| [31a] |
| [31b] |
| [31c] |
Figure 4:
Fits of R2 of isolated plasma at multiple fields used to determine the unknown contributions to R2Alb, namely kAlb, , and ΔδAlb as well as the R2b,Alb values at the four different fields (Tables 1,2).
Figure 5.
Fits of R2 of lysed blood samples at multiple fields ((a) 3.0T; (b) 7.0T; (c) 9.4T; (d) 11.7T) to determine the unknown contributions to R2Hb, namely kHb, , and ΔΔHb, as well as the R2b,Hb values at these four different fields (Tables 1,2).
Figure 6.
The B0 dependence of the transverse relaxation rates of the exchangeable protons in albumin(a), oxygenated hemoglobin (b) and deoxygenated hemoglobin (c).
Based on these field dependencies, we also predicted the relaxation times of albumin and hemoglobin at 1.5 T, 2.35T, and 4.7 T (Table 2) to be used below for prediction of blood relaxation data at these field strengths and comparison with measured values in the literature. Due to the low relaxation rates in plasma, the error in the measured R2b,Alb is expected to be larger than for R2b,OxyHb and R2b,DeoxyHb, which becomes clear when comparing the fit in Fig. 6a with the fits in Figs. 6b and c. When predicting literature values, we will therefore use Eqns. 31a-c (now part of the model) and not the individual numbers listed in Table 2.
To simplify the whole blood R2 fitting through the use of appropriate data-based starting values, we exploited the fact that the diffusion contribution dominates at short inter-echo spacing (see Fig. 1). We did this by first fitting only the R2blood data measured at short τcp (< 2ms) at 9.4T and 11.7T and considering only the protein solution R2 values, the membrane relaxation contribution and the diffusion effect in the plasma (Eq. 24). In the determination of the diffusion contribution the susceptibility difference between inside and outside the erythrocyte ((Δχery–plas) is very important. Except for a few studies38,84, Δχery–plas has usually been described by Δχdeoxy(1 – Y), while we now have a theoretical derivation based on magnetic protein properties, Δχery–plas = 0.253×(0.937-Y) ppm (Eq. 6e), indicating that there is an oxygenation value Yoff unequal to unity to account for the transition from diamagnetic to paramagnetic cell susceptibility. To test for the correctness of the theoretical value, two fits were conducted, one using Eq. 6e (Model 1 in supplementary S7), and another introducing a diffusion-specific fitting parameter into Eq. 7b, leading to ppm, corresponding to Model 2 in supplementary S7. The results (Table 3 and Supplementary Figs. S7.1 and S7.2) show that the fitting with decreased the relative error by about 30%. To assess whether it is proper to neglect the intracellular diffusion contribution, we also estimated the intracellular diffusion contribution R2D,ery using a form similar to extracellular diffusion contribution above (Eq. 13) as
| [32] |
in which Hct dependence in Eq. 13 was dropped because the gradient is felt throughout the cytoplasm in the small erythrocyte, leading to the assumption of no Hct dependence for R2D,ery. We then incorporated R2D,ery into Eq. 24 (model 3 in supplementary S7):
| [33] |
Table 3:
Fitted parameters for the short τcp (< 2ms) whole blood data at 9.4 T and 11.7 T using the three models and Equation. 24 (Model 1, 2) and Equation 33 (Model 3)
| Model 1 | Model 2 | Model 3 | |
|---|---|---|---|
| τD,plas (ms) | 3.30±0.43 | 3.15±0.43 | 4.04±1.58 |
| βplas | 0.778±0.013 | 0.661±0.027 | 0.608±0.054 |
| 0.985±0.015 | 0.984±0.015 | ||
| τD,ery (ms) | 0.376±1.80 | ||
| βery | 0.641±0.980 | ||
| Relative Error | 6.75% | 4.58% | 4.57% |
When fitting this model, we found that the fitted diffusional correlation time outside the erythrocyte (τD,plas) was about ten times larger than inside (τD,ery) (Table 3 and Fig. 7), corresponding to a diffusion contribution in the plasma that is much larger than inside the erythrocyte. Moreover, the results in Table 3 show that this new model had a fitting error (4.57%) very similar to the model (Eq. 24) without the intracellular diffusion contribution (4.58%), but even though there were two more fitting parameters (τD,ery and βery), the fitting error for the τD,plas was dramatically increased. This provided further support for neglecting the intracellular diffusion contribution and therefore Eq. 24 only was used to fit the data acquired at short τcp (< 2ms) (Table 3 and Supplementary Fig. S7.2) and all further fits were done without considering the diffusion contribution in the erythrocyte.
Figure 7.
The τcp dependence of R2D,plas (red) and R2D,ery (blue) for venous blood at Hct = 0.43 and Y=0.65 using the parameters fitted based on Model 3 in Supplementary 7.
In the analysis of the complete whole blood data set with all τcp values, the τD,plas (3.15 ms), βplas (0.661) and (0.985) fitted from short τcp data (Table 3) were used for the diffusion contribution and not adjusted further. This , was initially also used in the exchange contribution (Eq. 9). However, we found that this approach could not fit the whole blood R2 at high oxygenation fraction values and high magnetic field (9.4 T and 11.7T) and therefore needed to introduce a parameter in the exchange susceptibility equation. Fig. 8 shows the fitting results of the whole data set using our general model (including eqns. 31a-c). As a comparison, the same data set was fitted with the LM exchange model62 (Supplementary Fig. S8.1), the AG exchange model63 (Supplementary Fig. S8.2), the JC diffusion model32 (Supplementary Fig. S8.3) and the Ziener diffusion model33 (Supplementary Fig. S8.4). The values of fitted parameters for each model are presented in Tables 4 and 5. The determined water residence times in the erythrocyte (τery) fitted using the LM and AG exchange models are much shorter than τery fitted in our general model, while the exchange-based shape factors (βEx) fitted in the LM and AG exchange models are much larger than those fitted in our general model. Notice the large deviations at long τcp, especially at low field for the fits in Supplementary Figs. S8.1 and S8.2, indicating that the fit of the exchange contributions is not very good using these two models. The diffusion correlation time (τD,plas) fitted in our general model is similar to the JC results and about 50% larger than the Ziener diffusion model. The diffusion shape factor βplas fitted by our general model is a bit larger than the results fitted by the JC model but much smaller than Ziener model. Most importantly, the fits in the Supplementary Figs. S8.1 - S8.4 show that none of the single-mechanism models can consistently fit the correct curve shapes at all fields, while our general model can. Table 6 presents the average relative error (R2-R2,fit)/R2 along with AIC analysis to compare the performance of different models. In line with the visual inspection of the curve fits, the average relative error in our general model is the best, and the calculated AIC values, which penalize the goodness of fit with the number of fitting parameters, also show the same trend as the relative error. Meanwhile, the Akaike weights calculated based Eq. 30, which represent the model likelihood in the comparison of the given models, shows that our model has a dominant advantage to fit the data.
Figure 8:
Results of multi-variant fits of whole blood R2 at multiple fields with different Hct, Y and τcp using our general model (Eq. 15a-g)
Table 4.
Fitted parameters for the whole blood R2 model
| This paper | LM | AG | JC | Ziener | |
|---|---|---|---|---|---|
| τD,plas (ms) | 3.15±0.43 | 3.42±0.22 | 2.26±0.09 | ||
| βplas | 0.661±0.027 | 0.490±0.012 | 1.02±0.03 | ||
| 0.985±0.015 | 1.00±0.01 | 1.00±0.01 | |||
| τery (ms) | 9.13±1.43 | 0.792±0.032 | 0.790±0.030 | ||
| βEx | −1.20±0.20 | 3.22±0.090 | 3.29±0.088 | ||
| 0.889±0.019 | 0.979±0.010 | 0.972±0.009 |
The error indicates 95% confidence interval of fitting.
Table 5.
Membrane relaxation rate R2mem (s−1) as a function of magnetic field strength for whole blood obtained from fits with five different models
| 3.0 T | 7.0 T | 9.4 T | 11.7 T | |
|---|---|---|---|---|
| This paper | 2.65±0.87 | 2.27±1.01 | 3.33±0.75 | 1.29±0.63 |
| Luz-Meiboom | 2.79±1.06 | 2.60±1.19 | 2.54±1.02 | 0.00±0.97 |
| Allerhand-Gutowskey | 2.78±1.04 | 2.64±1.16 | 2.92±0.98 | 0.00±0.92 |
| Jensen-Chandra | 2.81±0.97 | 2.15±1.13 | 2.28±0.97 | 0.00±0.94 |
| Ziener | 2.26±0.09 | 2.38±1.21 | 2.58±1.04 | 0.00±1.00 |
The error indicates 95% confidence interval of fitting.
Table 6.
Summary of goodness of fit for the different models.
| Model | Relative Error | No. of Parameters |
AIC | w(AIC) |
|---|---|---|---|---|
| This paper | 4.2% | 10 * | 1563 | 100% |
| Luz-Meiboom | 6.5% | 7 | 1876 | 0% |
| Allerhand-Gutowskey | 6.5% | 7 | 1844 | 0% |
| Jensen-Chandra | 6.2% | 7 | 1756 | 0% |
| Ziener | 7.0% | 7 | 1874 | 0% |
Of these 10, only 7 were varied in the fitting of all data as βplas, τD,plas and τD,plas and were kept constant.
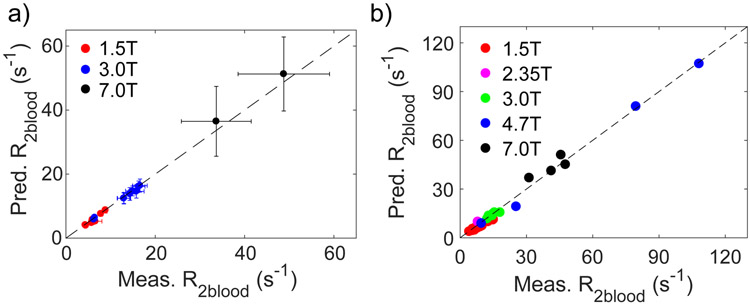
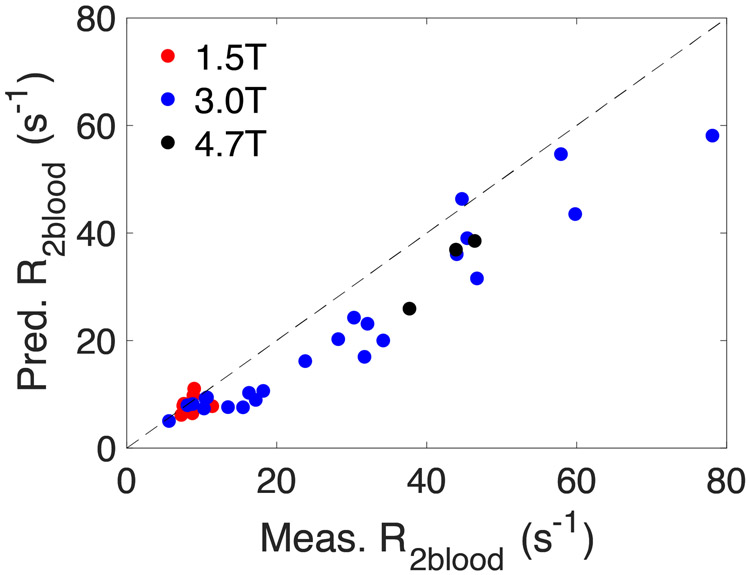
Finally, our general model was used to predict the CPMG-based T2 value of human blood at normal Hct for commonly used human field strengths (1.5T, 3T, and 7T). These results are compared with the literature values for CPMG measurements in Table 7 and Fig. 9a. We then did a similar prediction for all field strengths at which either T2 of human or bovine blood samples was measured in vitro and the results are shown in Table 8 and Fig. 9b. Both comparisons show outstanding agreement between the model prediction and actual experimental determinations.
Table 7.
Comparison between literature values of human blood T2 measured in vivo at different common field strengths and blood T2 predicted# by our model.
| B0 | τcp (ms) |
Hct | Y | Measured T2 (ms) |
Predicted T2 (ms) # |
|
|---|---|---|---|---|---|---|
| Adult (Ref. 12) | 1.5T | 6 | 0.43* | 0.67 | 168 | 172 |
| Adult (Ref. 12) | 1.5T | 25 | 0.43* | 0.62±0.04 | 128±9 | 131±14 |
| Adult (Ref. 12) | 1.5T | 25 | 0.43* | 0.82±0.04 | 174±18 | 209±14 |
| Adult (Ref. 11) | 1.5T | 6 | 0.43* | 0.45±0.05 | 113±6 | 114±12 |
| Adult (Ref. 11) | 1.5T | 6 | 0.43* | 0.67±0.05 | 166±15 | 172±15 |
| Adult (Ref. 7) | 1.5T | 24 | 0.43* | 0.97 | 230 | 242 |
| Adult (Ref. 7) | 1.5T | 24 | 0.43* | 0.77±0.05 | 152±34 | 190±19 |
| Adult (Ref. 59) | 1.5T | 6 | 0.43* | 1.0 | 224.5±5.3 | 253 |
| Male (Ref. 14) | 3T | 10 | 0.45* | 0.61±0.03 | 61.4±5.3 | 61.9±6.4 |
| Female (Ref. 14) | 3T | 10 | 0.40* | 0.62±0.04 | 63.4±7.0 | 68.4±9.8 |
| Adult (Ref. 14) | 3T | 10 | 0.43* | 1.0 | 155±10 | 155 |
| Adult (Ref. 10) | 3T | 10 | 0.35-0.42 | 1.0 | 140-180 | 158-180 |
| Adult IVJ (Ref. 19) | 3T | 10 | 0.43* | 0.65±0.04 | 70±7 | 72.4±10.4 |
| Adult SSS (Ref. 19) | 3T | 10 | 0.43* | 0.63±0.03 | 67±7 | 67.7±7.1 |
| Adult SS (Ref. 19) | 3T | 10 | 0.43* | 0.68±0.04 | 77±9 | 80.1±11.5 |
| Male Normoxia (Ref. 124) | 3T | 10 | 0.45* | 0.605±0.036 | 60.3±5.9 | 60.9±7.6 |
| Male Hyperoxia (Ref. 124) | 3T | 10 | 0.45* | 0.689±0.037 | 77.2±8.3 | 80.3±10.5 |
| Male Normoxia (Ref. 124) | 7T | 5 | 0.45* | 0.600±0.056 | 20.5±4.3 | 19.5±4.4 |
| Male Hyperoxia (Ref. 124) | 7T | 5 | 0.45* | 0.690±0.061 | 29.7±6.9 | 27.4±8.2 |
The reference didn’t mention Hct, so Hct was assumed as the average value based on published of 0.45+/−0.05 for males, 0.40+/−0.04 for females and 0.43+/−0.08 for adult humans125
Figure 9.
Comparison of predicted CPMG-based R2blood values with literature values for (a) in vivo human data (Table 7) and (b) in vitro human and bovine blood data (Table 8).
Table 8.
Comparison of predicted T2 with literature values for human and bovine blood.
| B0 | τcp (ms) |
Hct | Y | Literature T2 (ms) |
Predicted T2 (ms) |
|
|---|---|---|---|---|---|---|
| Human blood (Ref. 16) | 1.5T | 10# | 0.512 | 0.93 | 181# | 212 |
| Human blood (Ref. 16) | 1.5T | 10# | 0.512 | 0.87 | 156# | 201 |
| Human blood (Ref. 16) | 1.5T | 10# | 0.512 | 0.72 | 129# | 159 |
| Human blood (Ref. 16) | 1.5T | 10# | 0.512 | 0.66 | 111# | 142 |
| Human blood (Ref. 16) | 1.5T | 10# | 0.512 | 0.62 | 102# | 131 |
| Human blood (Ref. 16) | 1.5T | 10# | 0.512 | 0.48 | 80.0# | 98.1 |
| Human blood (Ref. 16) | 1.5T | 10# | 0.512 | 0.43 | 68.0# | 88.6 |
| Human blood (Ref. 16) | 1.5T | 10# | 0.512 | 0.42 | 67.1# | 86.9 |
| Bovine blood (Ref. 12) | 1.5T | 10 | 0.43# | 0.65# | 149# | 156 |
| Bovine blood (Ref. 12) | 1.5T | 20 | 0.43# | 0.65# | 136# | 145 |
| Human blood (Ref. 35) | 1.5T | 15 | 0.43* | 0.719±0.026 | 181±20 | 174±10 |
| Human blood (Ref. 35) | 1.5T | 15 | 0.43* | 0.967±0.016 | 254±24 | 245±1 |
| Human blood (Ref. 17) | 2.35T | 10 | 0.43# | 0.65# | 128# | 98.9 |
| Bovine blood (Ref. 10) | 3T | 5 | 0.43# | 0.65# | 82.6# | 84.0 |
| Bovine blood (Ref. 10) | 3T | 10 | 0.43# | 0.65# | 69.4# | 72.4 |
| Bovine blood (Ref. 10) | 3T | 15 | 0.43# | 0.65# | 68.0# | 66.7 |
| Bovine blood (Ref. 10) | 3T | 20 | 0.43# | 0.65# | 64.9# | 63.2 |
| Human blood (Ref. 34) | 3T | 10 | 0.43# | 0.65# | 78.1# | 72.4 |
| Human blood (Ref. 34) | 3T | 20 | 0.43# | 0.65# | 55.9# | 63.2 |
| Bovine blood (Ref. 48) | 4.7T | 10# | 0.40 | 0.254 | 12.6# | 12.2 |
| Bovine blood (Ref. 48) | 4.7T | 10# | 0.40 | 1.00 | 105# | 110 |
| Bovine blood (Ref. 48) | 4.7T | 10# | 0.40 | 0.718 | 39.7# | 51.5 |
| Bovine blood (Ref. 48) | 4.7T | 10# | 0.40 | 0.014 | 9.26# | 9.1 |
| Human blood (Ref. 17) | 7T | 10# | 0.43# | 0.65# | 22.0# | 19.4 |
| Human blood (Ref. 9) | 7T | 5 | 0.34 | 0.65# | 32.2# | 27.0 |
| Human blood (Ref. 9) | 7T | 5 | 0.42 | 0.65# | 24.3# | 24.1 |
| Human blood (Ref. 9) | 7T | 5 | 0.54 | 0.65# | 21.1# | 22.0 |
For the references in which only fitted R2blood models were given and the measured R2blood values were not listed, the R2blood values were calculated using their fitted model. In the calculation, if τcp was not specified in their model, 10ms was used, if Hct was not specified, the averaged adult Hct 0.43 was used and if Y was not specified, a typical venous oxygenation 0.65 was used.
The reference didn’t mention Hct, so Hct was assumed as the average value based on published of 0.45+/−0.05 for males, 0.40+/−0.04 for females and 0.43+/−0.08 for adult
Discussion
We designed a general mechanistic model for transverse relaxation of blood water that takes into account the effects of τcp, Hct, Y, and hemoglobin and albumin concentration, and validated it on R2blood data measured previously using a CPMG sequence50. Our approach differs from previous studies7,8,12,15,17,36-39, in which the R2 contribution of proteins (albumin and hemoglobin) was assumed to be a τcp independent term R20 that was determined from whole blood R2 fitting either by extrapolating to infinitely small τcp or by using the whole blood R2 values measured at the shortest attainable τcp. However, the lysed blood and isolated plasma data50 (Supplementary Tables S1 and S2) clearly have a τcp dependence, which could result from either diffusion or exchange effects. However, as reviewed by Kiselev and Novikov71, the protein molecule has a relatively small spatial scale, and the diffusional correlation time around the gradient induced by the protein molecule is much shorter than that cause by for instance the erythrocyte membrane. Because the diffusion contribution to water R2 is roughly proportional to the correlation time, the diffusion contribution for proteins in solution is very small. Therefore, the fast exchange contribution dominates the τcp dependence of R2 in the protein solutions, which is different from the whole blood case, where between-compartment water exchange is on a much slower time scale than direct exchange between protein and water. This latter exchange R2 contribution can be interpreted in terms of either (i) the sub-millisecond exchange between exchangeable protein protons and bulk water protons72, (ii) the millisecond exchange between water in hydration shell of protein and bulk water110, or (iii) the cross relaxation between proteins protons and bulk water protons111. Based on previous studies showing that the R2 of water in protein solution is enhanced at characteristic pH values corresponding to the pKa of NH or OH protons of the protein112, we concluded that the fast exchange between exchangeable protein protons and bulk water protons is the main source of relaxation enhancement for proteins solutions and modeled this contribution following the work of Hills et al.72. Certainly, the exchange rate for exchangeable protons often is indeed very fast and will not induce a noticeable τcp dependence of R2 of whole blood for typical longer TEs (longer τcp) used in vivo. However, as measured by previous proton-deuterium exchange experiments96, large proteins like albumin and hemoglobin have hundreds of exchangeable protons with exchange correlation times in the millisecond range. Therefore, the albumin and hemoglobin solutions will have a high microsecond to low millisecond range τcp dependence. This fast exchange contribution to the intercept at long 1/τcp in a plot of whole-blood relaxation versus 1/τcp is relevant for a complete theory. Due to the fact that τcp cannot be very short because of machine-based limitations in the refocusing pulse length, we did not observe the characteristic R2 jump with increasing 1/τcp when 1/τcp is comparable to the proton exchange rate, but the fitting results with small error (3.1%) at the available τcp range provided a reasonable estimate of the protein relaxation contributions as a function of Hct, Y and B0, which were subsequently used in the fitting of the whole blood R2 data. The B0 dependencies of these protein solution relaxation rates due to the presence of exchangeable protons (R2b,Alb R2b,OxyHb and R2b,DeoxyHb) were determined in Fig. 6 (Eqs. 31a-c). Following suggestions in the work of Gardener et al.17, the R2b values for the diamagnetic proteins (R2b,Alb and R2b,OxyHb) were fitted using a linear model, while those of the paramagnetic protein (R2b,DeoxyHb) were fitted using a quadratic model. Due to the range of relaxation rates, the fitted R2b,Alb had a large fluctuation, but considering its small contribution of plasma R2 to the whole blood relaxation, this is not detrimental and the fitted linear curve provides a good estimate. These field dependencies can now be used to predict the hemoglobin solution (cytoplasm) and albumin solution (plasma) R2b values beyond the magnetic fields investigated here.
Once the albumin solution parameters R2b,Alb, kAlb, , ΔδAlb and the hemoglobin solution parameters R2b,oxyHb, R2b,DeoxyHb, kHb, , ΔδOxyHb, ΔδDeoxyHb are available (Tables 1,2 and Eqs. 31a-c) from the data fits for isolated plasma and lysed blood, the number of unknown parameters to be determined by fitting the whole blood R2 to Eqs. 14 and 15 is reduced to the exchange-based, diffusion-based, and membrane-based relaxation enhancements, with the latter very small. Thus, with the magnetic susceptibility differences calculated from basic principles and related to oxygenation through Equation 7b, the task is much simplified, with the only unknowns remaining being the field-independent parameters τD,plas, τery, , , βplas, , βEx and the field-dependent parameter R2mem. We then exploited the dominant contribution of diffusion through field gradients in the plasma at high field and short τcp to determine the values for τD,plas, and βplas and thus further reduce the number of the unknown parameters. In this process, we neglected the intracellular diffusion contribution as explained in Theory section and supported by our fitting estimates (Fig. 7) showing that the intracellular diffusion contribution was one order of magnitude smaller than that in plasma (Fig. 7), in agreement with recent simulation results88. It is important to realize that the assumption of a negligible relaxation enhancement from intracellular diffusion does not conflict with a previous observation at 7 Tesla that the width of the water proton peak in blood NMR spectra is the same at low Hct (0.42) and high Hct (0.69) for the same oxygenation (Y = 0.6) 113. In fact, using our theory, the blood T2 (τcp=10ms) values are predicted as 16.1 ms and 15.8 ms for these two samples, respectively. At first this seems counter-intuitive to cytoplasm having a small diffusion contribution, because one would then expect R2blood (linewidth) to decrease with an increasing fraction of cytoplasm (Hct). However, R2blood at low oxygenation has a parabolic Hct dependence with the highest value at Hct of about 0.55, as shown by Thulborn et al.36. This phenomenon can be explained by the fact that although the extracellular diffusion contribution is proportional to Hct (Eq. 13a), this contribution will be counteracted by the plasma’s water fraction (about 1-Hct, more precisely 1 – fery) when accounting for total blood water. Therefore, the previous proton linewidth equivalence finding is not proof for equivalence of intracellular and extracellular diffusion contributions39,113.
Most interesting in the correlation time dependent fit limited to diffusion was the finding that differed from the one predicted from theory (Yoff = 0.937). When fitting the whole-blood data with the predicted Yoff, we noticed that we could not satisfactorily match the curve shapes at all fields unless we assumed individual values for diffusion () and exchange (). While this appeared illogical at first, we later concluded that this is not unreasonable based on the known physiological phenomenon that the erythrocyte membrane has a much higher affinity to the deoxygenated Hb114-116 and that this binding to the erythrocyte membrane coincides with a strong shift of the hemoglobin’s Hb-O2 saturation curve to the right115,117. This means that the membrane will bind a certain amount deoxygenated hemoglobin even if the blood oxygenation is high. These bound deoxygenated hemoglobins will largely determine the magnitude of the magnetic field gradient near the membrane and it is thus not surprising to find that Yoff for diffusion differs from that in the theoretical calculation (Eq. 6e) for which the distribution of deoxygenated hemoglobin is assumed to be homogeneous. Thus, the reflects the susceptibility difference that water protons experience for the average compartments, while accounts for the field gradients being affected by phenomena changing close to the membrane.
In the fitting results related to the exchange process, the fitted water residue time in the erythrocyte τery was found to be 9.13 ± 1.43 ms, which is in the range of 6.0 to 9.6 ms measured by others at 37 °C 89,100,103,105. Using the fitted τD,plasma of 3.15 ± 0.43 ms and the water diffusion coefficient at 37 °C (2.9 μm2/ms) 118, the effective radius of the erythrocyte rc can be estimated to be 3.02 μm through the equation 32,33,87. While this is on the correct order of magnitude for the erythrocyte, for which the short and long radii are about 1 μm and 4 μm, respectively, it appears to be on the high side. On the other hand, this may be explained by the diffusion constant of the viscous plasma water being smaller than that of neat water119.
The shape factors βplas and βEx were introduced to account for the effect of the erythrocyte’s bi-concaved donut shape on the magnetic field gradient experienced in the plasma close to the membrane and the average field inside the cell, respectively. As pointed out in Theory Section, the need to include a shape effect in the diffusion contribution results from the fact that the erythrocyte shape is too complicated to find an analytical result for the pre-coefficient in the JC model. The fitted βplas (0.661) is close to the theoretical derivation by Kiselev and Novikov64 (~0.8 from their Fig. 2) which assumes the erythrocyte as a disk with height-to-radius radio of 0.5. This also agrees with Sukstanskii and Yablonskiy’s work67 (~0.8 from their Fig. 3) if the erythrocyte is assumed as an ellipsoid with a long-to-short axis ratio of 4. In the exchange contribution, the shape factor is needed because the susceptibility difference between inside and outside the erythrocyte will induce magnetism on the external boundary of the erythrocyte and generate a demagnetization field that depends on the shape of the cell. In our fitting, the theoretically calculated susceptibility difference between deoxygenated and oxygenated hemoglobin (Δχdeoxy) was used as the value in Eq. 6e and the introduction of shape factors for diffusion and exchange will correct the fitting uncertainty of using Δχdeoxy, which is just based on solution susceptibility values. The fitted βEx (−1.20) value is also close to the theoretically predicted value (−1.62, Supplementary S9). The small deviation could result from the discrepancy between our assumed cylinder shape and the erythrocyte’s bi-concaved shape. The membrane contributions fitted here are smaller than found in our previous paper50. Interestingly, we did not find a B0 dependence for the membrane relaxivity. Therefore, the average of R2mem of all four fields in Table 4 (2.39 s−1) was used to predict blood R2.
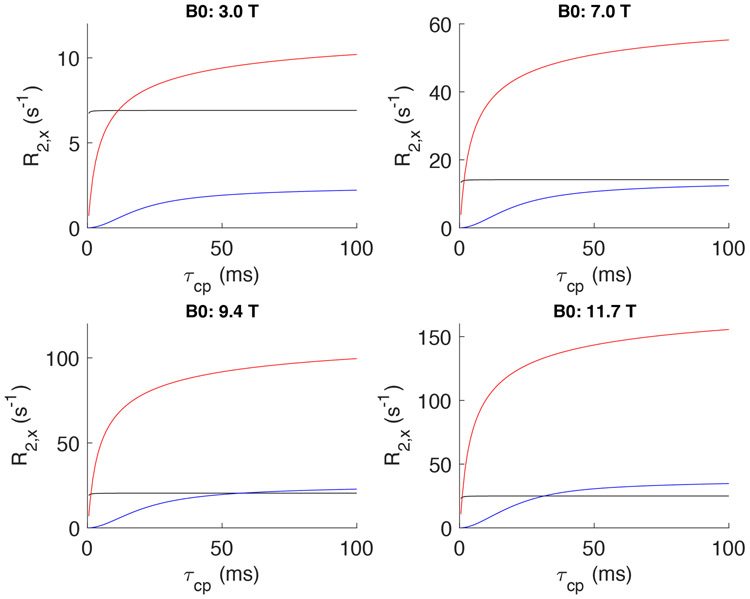
Using the fitted parameters, we can determine the contributions from different relaxation mechanisms, which are shown in Fig. 10. These calculations show that the relaxation rates of hemoglobin and albumin solutions (black curves), which have a weak proton-exchange based dependence on τcp, have a large contribution at low field (3T) that even dominates at very short τcp. However, at higher fields, the compartmental exchange and diffusion relaxation enhancements, which result from the sequestration of the hemoglobin solution by the erythrocyte membrane, increase with a quadratic dependence on B0. Interestingly, the compartmental exchange contribution does not become much larger than that of the individual protein solutions, but the compartmental diffusion contribution dominates, being a factor of about five larger than the compartmental exchange contribution at every field. The data show that with increasing field, the chemical shift difference inside and outside the erythrocyte is changing from 264 rad/s−1 (3T) to 1017 rad/s−1 (11.7T). Given that the water exchange rate (kery + kplas in Eq. 15) can be calculated to be 154 s−1 at a Hct of 0.43, the exchange goes from the intermediate regime at 3T to the slow exchange regime at 11.7T. Therefore, the LM and AG models, based on fast exchange, are not able to fit the data with a consistent erythrocyte lifetime at all fields. Meanwhile, while the diffusion relaxation enhancement dominates at short τcp, and the JC and Ziener models should be able to fit such data with consistent correlation times between fields, the exchange contribution cannot be neglected at longer τcp, where these two models will therefore fail to give consistent life times.
Figure 10.
The τcp dependence of intrinsic relaxation contribution R20 (black), exchange relaxation enhancement R2ex (blue) and diffusion relaxation enhancement in the plasma R2D,plas (red) for venous blood at Hct = 0.43 and Y=0.65.
For all our fittings, we minimized the relative error (i.e. (R2,exp-R2,fit)/R2.exp) rather than the absolute error ∣R2,exp-R2,fit∣. This is because the experimental errors induced by the fluctuation of samples conditions such as oxygenation will be larger at the higher magnetic field and lower oxygenation due to the quadratic dependence of R2 on the B0 and susceptibility. The minimization of relative error can alleviate the effect of these experimental errors. This also may explain that we had larger deviations for some low oxygenation fittings at 11.7 T (Fig. 8). As shown in Supplementary S10, these deviations can possibly be explained by <5% oxygenation error. Certainly, other factors such as the aggregation and alignment of erythrocytes120 and imperfection of the model also could introduce these deviations.
We also compared our model with pure exchange models (LM model and AG model) and diffusion models (JC model and Ziener model). Our model performed best as judged from the AIC statistics for current R2 data set. Actually, as already commented upon by Thulborn et al.36, both exchange and diffusion are expected to contribute to the τcp dependent relaxation enhancement. As measured and analyzed by previous studies, the correlation times for these two kinds of water displacements are very different (~10ms vs ~3ms), and their τcp dependent correlation function is different32 because exchange is water jumping between two environments with different chemical shifts while diffusion is water moving randomly through a continuously changing field. Therefore, it is very difficult to just use a single model with a single correlation time to fully characterize the τcp dependence of R2blood. As shown in Fig. 10, the diffusion relaxation enhancement in the plasma dominates the R2blood measured by a CPMG experiment. This is the reason that the exchange correlation time (Eq. 18 τex = τery/(1-fery)) fitted from LM and AG model is closer to the water diffusion correlation time and much shorter than the water residue time measured by membrane permeability experiments. However, the exchange contribution can not be ignored for an accurate estimation of blood R2. For example, the experimental R2blood is 22.7 s−1 for Hct=0.44, Y = 0.99, τcp = 16.05 ms at 9.4T (Table S3c). Using our model including exchange, the predicted value is 22.4 s−1, while using the JC model, the predicted value is 17.6 s−1, indicating a ~20% error. Even more important than just accuracy (which represents a summary of both short and long inter-echo spacings) is the curve shape for the JC model versus our universal model at lower fields, physiological Hct, arterial oxygenation and small 1/τcp (longer τcp), the range important for typical fMRI experiments. This is clear in Figs. 8 and S8.3 and amplified in Supplementary Fig. S11 for convenience. The JC model cannot faithfully represent the curve and instead shows a straight line. Meanwhile, we found the fitted βplas and τD,plas (Table 4) by JC model to be closer to our model than the Ziener model. This probably results from the Ziener model assuming erythrocytes to be impermeable solid spheres with water diffusion outside the erythrocyte being restricted, while the JC model assumes unrestricted water diffusion. However, because the diffusion R2 contribution is positively correlated with τD,plas and βplas, the shorter τD,plas and larger βplas obtained from the Ziener model will not cause significant deviation of the fitted R2blood results. Therefore, our combined model that considers both the exchange and diffusion effects and both the water inside and outside the erythrocyte can better depict the τcp dependence of blood R2.
Our model also supplies the constants and equations to predict R2blood at arbitrary Hct, Y and τcp at multiple fields. Figs. 9a-b (Tables 7, 8) show that the CPMG-based T2blood values predicted by our model agree well with both the in vitro and in vivo CPMG blood T2 measured at 1.5T, 2.35T, 3T, 4.7T and 7T by other groups. Since the model has many constants and terms and since the predicted and measured relaxation times will also depend on the length of the 180° RF pulses in the CPMG experiment, we have made available a website (Blood T1 T2 Calculation at http://godzilla.kennedykrieger.org/) that can be used for these predictions.
As a comparison, the JC model was also applied to predict the blood CPMG-based T2 values, which are compared with literature numbers in Supplementary Tables S12a,b and Figs. S12a,b. Compared to the general model, we found that the JC model had a significantly larger averaged relative error for both in vivo measurements (0.67 s−1 (6.4%) vs 1.21 s−1 (13.2%)) and in vitro measurements (1.8 s−1 (13.4%) vs 2.7 s−1 (17.7%)). This further confirms that our model has better performance.
We also attempted to predict single-echo based blood T2 measurements. As clear from Jensen and Chandra’s work32 and the exchange theories and as observed by Golay et al.12 and in line with the model, T2 values measured by CPMG experiments are always longer than T2 values measured by single spin echo experiment. To predict T2 values for single spin echo experiments, we use our model to calculate the magnetization intensity at each TE by setting TE = τcp for a range of 10 – 200 ms, followed by fitting the single-echo based T2 from these intensities. As shown in Fig. 11 (Supplementary Table S13), however, these predicted R2blood values are still smaller (T2blood longer) by a systematic offset of a few Hz than the values reported previously in the literature12,15,18,38. Several phenomena could explain such a deviation. One possibility is that the spin dephasing by background field gradients (either due to unidirectional flow or diffusion effects) cannot be effectively refocused in the single spin echo and induce an extra relaxation contribution121. We also performed a comparison with the JC model for these single echo-based measurements, also shown in Supplementary Table S13. Again our general model showed a better averaged relative error (6.3 s−1 (24%) vs 9.4 s−1 (35%)), confirming the CPMG-based comparison above.
Figure 11.
Comparison of our predicted single-echo (SE) based R2blood values with the literature values measured for human and bovine blood (Table S13 in Supplementary)
The work here should also be considered in the context of several limitations. First, the model we built considers the compartmental exchange and diffusion as two separated processes based on the assumption that water diffusion is much faster than water exchange between inside and outside the erythrocyte. However, the diffusional correlation time is not short enough (as shown in Table 3) to clearly separate it from the exchange process. We also could approximate the water motion in the whole blood as a free diffusion process which implies that the membrane is fully permeable for water diffusion, and use current diffusion theories such as the JC diffusion model to calculate blood R2. However, the capacity of the erythrocyte membrane to regulate water transport could cause the larger deviation for the JC model found in our comparisons above. A recent study shows that such a restricted diffusion by the permeable membrane can be described by the disorder-averaged diffusion propagator using a scattering approach122. However, further study is still needed to derive an analytical equation to describe the R2 relaxation contribution from this restricted diffusion. Meanwhile, the derivation of the analytical equation (Eq. 41 in Ref 32) used to calculate whole blood R2 in the JC model inherently implies that the erythrocyte is impermeable (shown in Supplementary S14). Therefore, we used this equation to calculate the diffusion contribution in the plasma. Furthermore, in Reference 32, after fitting the JC model to red blood cells, the data were interpreted invoking the “random sphere” assumption (Eq. 41 in Ref 32), which inherently implies that the whole blood R2 is proportional to Hct, in conflict with the experimental observation36. Several studies64,65 have justified this by adding a multiplication factor (1-Hct), but further investigation is still needed to establish this justification as shown in supplementary S15. Therefore, although the diffusion-based theory32,33,64-68,122 to describe R2 in biological tissue has undergone significant developments in recent years, a perfect analytical model is still missing and we here addressed the need to build a working theory for the blood R2. In this theory, the continuous water diffusion and jump-like water exchange were considered to be non-interfering processes based on the fact that the exchange correlational time is three times longer than the diffusion correlational time. The isolated diffusion contribution was then calculated based on the classic JC model32 and incorporated into the general exchange model69,70 to calculate the whole blood R2.
A second limitation of our general model is that the JC model terms we used for diffusion are based on a weak field approximation and as a consequence, the accumulated phase by water spins at the time scale of diffusion should be much smaller than 1. If we assume the frequency induced by the erythrocyte to be at the scale of , the accumulated phase64,66 α during the diffusion correlation time τc is . As shown in Supplementary Fig. S16, all our fitting samples have α values ranging from 0 – 0.6, and thus there is higher probability of large fitting errors when increasing α. Third, in our fitting, we aimed to minimize the total relative error ∣R2.exp-R2,fitted∣/R2,exp of all the samples using the nonlinear fitting function from MATLAB, which has the risk to accidentally end in a local minimum. As shown in the Methods, we used 126 initial values sampled in the physiological ranges of fitting parameters to alleviate this process. Fourth, the oxygenation of all our fitting samples was higher than 0.55. Further work should be done for lower oxygenation cases.
Conclusion
We derived a comprehensive general model for the effects of hemoglobin concentration, hematocrit fraction, oxygenation fraction and albumin concentration on the water proton transverse relaxation time of blood, and determined the relaxation constants and relevant diffusional and exchange correlation times in the equations using previously published whole blood R2 data at multiple Hct and Y values at 3T, 7T, 9.4T and 11.7T. The fitted parameters presented here provided a good calibration for calculating CPMG based human blood T2 as a function of field strength, as demonstrated by excellent agreement with human blood T2 measured in vivo and in vitro in other studies. A website was made available to use this theory for calculating blood T2 (Blood T1 T2 Calculation at http://godzilla.kennedykrieger.org/).
Supplementary Material
Acknowledgement
We are grateful for grant support from the National Institutes of Health (NIH P41EB015909 and K25 HL145129). We thank Joseph Gillen’s help with the parallel calculation and making the webpage for calculating blood T2.
Grant support: NIH: P41 EB015909 and K25 HL145129
Abbreviations:
- Hct
hematocrit fraction
- Y
oxygenation fraction
- τcp
inter-echo spacing in a multi-echo Carr Purcell Meiboom Gill (CPMG) experiment
- τery
water life times in erythrocyte
- τD
water diffusional correlation times
- cHb
hemoglobin concentration in the erythrocyte
- cAlb
albumin concentration in plasma
the number of exchangeable protons in albumin
- ΔδAlb
the averaged chemical shift difference between bulk water protons and exchangeable protons in albumin
- kAlb
the averaged dissociation rate of exchangeable protons in albumin
the number of exchangeable protons in hemoglobin
- kH
the averaged dissociation rate of exchangeable protons in hemoglobin
- ΔδDeoxyHb
the averaged chemical shift difference between bulk water protons and exchangeable protons in the deoxygenated hemoglobin
- ΔδOxyHb
the averaged chemical shift difference between bulk water protons and exchangeable protons in the oxygenated hemoglobin
- fv,water
the bulk water volume fraction
- fery
the erythrocyte water fraction in whole blood
- fplas = (1 – fery)
the plasma water fraction in whole blood
- Δχdeoxy
volume magnetic susceptibility difference between erythrocyte and plasma at fully deoxygenated state
- Δχery-plas
volume magnetic susceptibility difference between erythrocyte and plasma
- Yoff
the oxygenation value at which the volume magnetic susceptibility difference between erythrocyte and plasma changes from diamagnetic to paramagnetic, i.e. at which the volume magnetic susceptibility of plasma and erythrocyte is equal.
- Δωery-plas
the chemical shift difference between inside and outside the erythrocyte
- Pery
the fractions of the number of exchangeable protein protons relative to the number of bulk water protons in the erythrocyte
- Pplas
the fractions of the number of exchangeable protein protons relative to the number of bulk water protons in the plasma
- βplas
the shape factor that corrects the difference between the field gradient generated by the sphere we assumed in the model and the field gradient generated by the real shape of the erythrocyte
- βEx
the shape factor that corrects the difference between bulk susceptibility difference and the real chemical shift effect generated by the erythrocyte
- R2blood
whole blood transverse relaxation rate of water
- R2b,Alb
the averaged relaxation rates of exchangeable protons in albumin without exchange
- R2b,OxyHb
the averaged relaxation rates of exchangeable protons in oxygenated hemoglobin without exchange
- R2b,DeoxyHb
the averaged relaxation rates of exchangeable protons in deoxygenated hemoglobin without exchange
- R2mem
the transverse relaxation enhancement of water due to presence of the cell membrane
- R2Hb
the transverse relaxation rate of water in the hemoglobin solution in the cytoplasm of erythrocytes
- R2Alb
the transverse relaxation rate of water in the albumin solution in plasma
- R2D,plas
diffusion-based relaxation enhancement for plasma water
- R2D,ery
diffusion-based relaxation enhancement for erythrocyte water
- R2ery
intracellular water relaxation rate for erythrocytes in blood
- R2plas
extracellular water relaxation rate for plasma in blood
APPENDICES
Appendix 1: General expressions for R2 based on Carver-Richards chemical exchange model
The general form of the τcp dependence of R2 for exchange between two sites can be obtained from the Bloch equation derived by Woessner123 and Allerhand and Gutowsky91
| [A1a] |
| [A1b] |
| [A1c] |
| [A1d] |
in which “b” refers to bound, which we will use here for the exchangeable protein protons in protein solution and erythrocyte cytoplasm water protons in blood. On the other hand, “f“ refers to free, which we will use for water protons in solution in protein solutions and plasma water in blood. Following the derivation by Carver and Richards69 and Davis et al.70, this Bloch equation can be solved analytically and obtain
| [A2a] |
| [A2b] |
| [A2c] |
| [A2d] |
| [A2e] |
| [A2f] |
| [A2g] |
Notice that kb and kf have the relationship that kb × Pb = kf × Pf and that Pb + Pf = 1 where P is the proton fraction for the protons of interest in protein solution. We replace this by water fraction (fi, with i = ery or plas) in the blood. The term Δω is chemical shift difference between the sites in the two compartments.
Appendix 2: Fast exchange versus general exchange requirements
The derivation of Luz-Meiboom model62,91 assumes that the exchange rate must be much faster than the chemical shift difference between two exchange sites; also the relaxation times at two exchange sites in the absent of the exchange must be of the same order of magnitude.
The modeled developed by Allerhand and Gutowsky63 has expanded the suitable exchange rate range to the range that is comparable or slower than the chemical shift difference between two exchange sites, but it still requires the relaxation times at two exchange sites in the absence of the exchange must be of the same order of magnitude.
References
- 1.Fox PT, Raichle ME. Focal physiological uncoupling of cerebral blood flow and oxidative metabolism during somatosensory stimulation in human subjects. Proc Natl Acad Sci U S A. 1986;83:1140–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci U S A. 1990;87(24):9868–9872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ogawa S, Lee T-M, Nayak AS, Glynn P. Oxygenation-sensitive contrast in magnetic resonance image of rodent brain at high magnetic fields. Magn Reson Med. 1990;14:68–78. [DOI] [PubMed] [Google Scholar]
- 4.Buxton RB, Uludağ K, Dubowitz DJ, Liu TT. Modeling the hemodynamic response to brain activation. Neuroimage. 2004;23:S220–S233. [DOI] [PubMed] [Google Scholar]
- 5.Van Zijl PCM, Eleff SM, Ulatowski JA, Oja JME, Ulug AM, Traystman RJ, Kauppinen RA. Quantitative assessment of blood flow, blood volume and blood oxygenation effects in functional magnetic resonance imaging. Nat Med. 1998;4:159–167. [DOI] [PubMed] [Google Scholar]
- 6.Uludaǧ K, Müller-Bierl B, Uǧurbil K, Uludag K, Müller-Bierl B, Uğurbil K. An integrative model for neuronal activity-induced signal changes for gradient and spin echo functional imaging. Neuroimage. 2009;48(1):150–165. [DOI] [PubMed] [Google Scholar]
- 7.Wright GA, Hu BS, Macovski A. Estimating oxygen saturation of blood in vivo with MR imaging at 1.5 T. J Magn Reson Imaging. 1991;1(3):275–283. [DOI] [PubMed] [Google Scholar]
- 8.Oja JM, Gillen JS, Kauppinen RA, Kraut M, van Zijl PC. Determination of oxygen extraction ratios by magnetic resonance imaging. J Cereb blood flow Metab. 1999;19(12):1289–1295. [DOI] [PubMed] [Google Scholar]
- 9.Krishnamurthy LC, Liu P, Xu F, Uh J, Dimitrov I, Lu H. Dependence of blood T(2) on oxygenation at 7 T: in vitro calibration and in vivo application. Magn Reson Med. 2014;71(6):2035–2042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lu H, Xu F, Grgac K, Liu P, Qin Q, van Zijl P. Calibration and validation of TRUST MRI for the estimation of cerebral blood oxygenation. Magn Reson Med. 2012;67(1):42–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Foltz WD, Merchant N, Downar E, Stainsby JA, Wright GA. Coronary venous oximetry using MRI. Magn Reson Med. 1999;42(5):837–848. [DOI] [PubMed] [Google Scholar]
- 12.Golay X, Silvennoinen MJ, Zhou J, Clingman CS, Kauppinen RA, Pekar JJ, van Zij PC. Measurement of tissue oxygen extraction ratios from venous blood T(2): increased precision and validation of principle. Magn Reson Med. 2001;46(2):282–291. [DOI] [PubMed] [Google Scholar]
- 13.Lu H, Ge Y. Quantitative evaluation of oxygenation in venous vessels using T2-Relaxation-Under-Spin-Tagging MRI. Magn Reson Med. 2008;60(2):357–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Qin Q, Grgac K, van Zijl PCM. Determination of whole-brain oxygen extraction fractions by fast measurement of blood T(2) in the jugular vein. Magn Reson Med. 2011;65(2):471–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Silvennoinen MJ, Clingman CS, Golay X, Kauppinen RA, van Zijl PCM. Comparison of the dependence of blood R2 and R2* on oxygen saturation at 1.5 and 4.7 Tesla. Magn Reson Med. 2003;49(1):47–60. [DOI] [PubMed] [Google Scholar]
- 16.Stefanovic B, Pike GB. Human whole-blood relaxometry at 1.5 T: Assessment of diffusion and exchange models. Magn Reson Med. 2004;52(4):716–723. [DOI] [PubMed] [Google Scholar]
- 17.Gardener AG, Francis ST, Prior M, Peters A, Gowland P a. Dependence of blood R2 relaxivity on CPMG echo-spacing at 2.35 and 7 T. Magn Reson Med. 2010;64(4):967–974. [DOI] [PubMed] [Google Scholar]
- 18.Zhao JM, Clingman CS, Närväinen MJ, Kauppinen RA, van Zijl PCM. Oxygenation and hematocrit dependence of transverse relaxation rates of blood at 3T. Magn Reson Med. 2007;58(3):592–597. [DOI] [PubMed] [Google Scholar]
- 19.Wehrli FW, Rodgers ZB, Jain V, Langham MC, Li C, Licht DJ, Magland J. Time-resolved MRI oximetry for quantifying CMRO(2) and vascular reactivity. Acad Radiol. 2014;21(2):207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.An H, Lin W. Cerebral oxygen extraction fraction and cerebral venous blood volume measurements using MRI: effects of magnetic field variation. Magn Reson Med. 2002;47(5):958–966. [DOI] [PubMed] [Google Scholar]
- 21.An H, Sen S, Chen Y, Powers WJ, Lin W. Noninvasive Measurements of Cerebral Blood Flow, Oxygen Extraction Fraction, and Oxygen Metabolic Index in Human with Inhalation of Air and Carbogen using Magnetic Resonance Imaging. Transl Stroke Res. 2012;3(2):246–254. [DOI] [PubMed] [Google Scholar]
- 22.Xu F, Ge Y, Lu H. Noninvasive quantification of whole-brain cerebral metabolic rate of oxygen (CMRO2) by MRI. Magn Reson Med. 2009;62(1):141–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fujita N, Matsumoto K, Tanaka H, Watanabe Y, Murase K. Quantitative study of changes in oxidative metabolism during visual stimulation using absolute relaxation rates. NMR Biomed. 2006;19(1):60–68. [DOI] [PubMed] [Google Scholar]
- 24.Liu P, Xu F, Lu H. Test-retest reproducibility of a rapid method to measure brain oxygen metabolism. Magn Reson Med. 2013;69(3):675–681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jain V, Langham MC, Wehrli FW. MRI estimation of global brain oxygen consumption rate. J Cereb Blood Flow Metab. 2010;30(9):1598–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ogawa S, Menon RS, Tank DW, Kim SG, Merkle H, Ellermann JM, Ugurbil K. Functional brain mapping by blood oxygenation level-dependent contrast magnetic resonance imaging. A comparison of signal characteristics with a biophysical model. Biophys J. 1993;64(3):803–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Buxton RB, Wong EC, Frank LR. Dynamics of blood flow and oxygenation changes during brain activation: The balloon model. Magn Reson Med. 1998;39(6):855–864. [DOI] [PubMed] [Google Scholar]
- 28.Davis TL, Kwong KK, Weisskoff RM, Rosen BR. Calibrated functional MRI: Mapping the dynamics of oxidative metabolism. Proc Natl Acad Sci. 1998;95(4):1834–1839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lu H, Zhao C, Ge Y, Lewis-Amezcua K. Baseline blood oxygenation modulates response amplitude: Physiologic basis for intersubject variations in functional MRI signals. Magn Reson Med. 2008;60(2):364–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lu H, Golay X, Pekar JJ, van Zijl PCM. Sustained Poststimulus Elevation in Cerebral Oxygen Utilization After Vascular Recovery. J Cereb Blood Flow Metab. 2004;24(7):764–770. [DOI] [PubMed] [Google Scholar]
- 31.Hua J, Stevens RD, Huang AJ, Pekar JJ, van Zijl PCM. Physiological origin for the BOLD poststimulus undershoot in human brain: vascular compliance versus oxygen metabolism. J Cereb Blood Flow Metab. 2011;31:1599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jensen JH, Chandra R. NMR relaxation in tissues with weak magnetic inhomogeneities. Magn Reson Med. 2000;44(1):144–156. [PubMed] [Google Scholar]
- 33.Ziener CH, Kampf T, Jakob PM, Bauer WR. Diffusion effects on the CPMG relaxation rate in a dipolar field. J Magn Reson. 2010;202(1):38–42. [DOI] [PubMed] [Google Scholar]
- 34.Bush A, Borzage M, Detterich J, Kato RM, Meiselman HJ, Coates T, Wood JC. Empirical model of human blood transverse relaxation at 3 T improves MRI T2 oximetry. Magn Reson Med. 2017;77:2364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Barth M, Moser E. Proton NMR relaxation times of human blood samples at 1.5 T and implications for functional MRI. Cell Mol Biol. 1997;43(5):783–791. [PubMed] [Google Scholar]
- 36.Thulborn KR, Waterton JC, Matthews PM, Radda GK. Oxygenation dependence of the transverse relaxation time of water protons in whole blood at high field. Biochim Biophys Acta. 1982;714:265–270. [DOI] [PubMed] [Google Scholar]
- 37.Ye FQ, Allen PS. Relaxation enhancement of the transverse magnetization of water protons in paramagnetic suspensions of red blood cells. Magn Reson Med. 1995;34(5):713–720. [DOI] [PubMed] [Google Scholar]
- 38.Spees WM, Yablonskiy DA, Oswood MC, Ackerman JJH. Water Proton MR Properties of Human Blood at 1.5 Tesla : Magnetic Susceptibility, T1 , T2 , T*2, and Non-Lorentzian Signal Behavior. Magn Reson Med. 2001;45:533–542. [DOI] [PubMed] [Google Scholar]
- 39.Gillis P, Petö S, Moiny F, Mispelter J, Cuenod C. Proton transverse nuclear magnetic relaxation in oxidized blood: a numerical approach. Magn Reson Med. 1995;33(1):93–100. [DOI] [PubMed] [Google Scholar]
- 40.Li W, Grgac K, Huang A, Yadav N, Qin Q, van Zijl PCMM. Quantitative theory for the longitudinal relaxation time of blood water. Magn Reson Med. 2016;76(1):270–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lu H, Clingman C, Golay X, van Zijl PCM. Determining the longitudinal relaxation time (T1) of blood at 3.0 Tesla. Magn Reson Med. 2004;52(3):679–682. [DOI] [PubMed] [Google Scholar]
- 42.Grgac K, van Zijl PCM, Qin Q. Hematocrit and oxygenation dependence of blood (1)H2O T1 at 7 tesla. Magn Reson Med. 2013;70:1153–1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Silvennoinen MJ, Kettunen MI, Kauppinen RA. Effects of hematocrit and oxygen saturation level on blood spin-lattice relaxation. Magn Reson Med. 2003;49(3):568–571. [DOI] [PubMed] [Google Scholar]
- 44.Shimada K, Nagasaka T, Shidahara M, Machida Y, Tamura H. In vivo measurement of longitudinal relaxation time of human blood by inversion-recovery fast gradient-echo MR imaging at 3T. Magn Reson Med Sci. 2012;11(4):265–271. [DOI] [PubMed] [Google Scholar]
- 45.De Vis JB, Hendrikse J, Groenendaal F, de Vries LS, Kersbergen KJ, Benders MJNL, Petersen ET. Impact of neonate haematocrit variability on the longitudinal relaxation time of blood: Implications for arterial spin labelling MRI. NeuroImage Clin. 2014;4:517–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Rane SD, Gore JC. Measurement of T1 of human arterial and venous blood at 7T. Magn Reson Imaging. 2013;31(3):477–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Janick P, Hackney D, Grossman R, Asakura T. MR Imaging Various Oxidation States of Intracellular and Extracellular Hemoglobin. Am J Neuroradiol. 1991;12(5):891–897. [PMC free article] [PubMed] [Google Scholar]
- 48.Meyer M-EE, Yu O, Eclancher B, Grucker D, Chambron J. NMR relaxation rates and blood oxygenation level. Magn Reson Med. 1995;34(2):234–241. [DOI] [PubMed] [Google Scholar]
- 49.Rooney WD, Johnson G, Li X, Cohen ER, Kim S-G, Ugurbil K, Springer CS. Magnetic field and tissue dependencies of human brain longitudinal 1H2O relaxation in vivo. Magn Reson Med. 2007;57(2):308–318. [DOI] [PubMed] [Google Scholar]
- 50.Grgac K, Li W, Huang A, Qin Q, van Zijl PCM. Transverse water relaxation in whole blood and erythrocytes at 3T, 7T, 9.4T, 11.7T and 16.4T; determination of intracellular hemoglobin and extracellular albumin relaxivities. Magn Reson Imaging. 2017;38:234–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Donahue MJ, Hoogduin H, Van Zijl PCM, Jezzard P, Luijten PR, Hendrikse J. Blood oxygenation level-dependent (BOLD) total and extravascular signal changes and ΔR2* in human visual cortex at 1.5, 3.0 and 7.0 T. NMR Biomed. 2011;24(1):25–34. [DOI] [PubMed] [Google Scholar]
- 52.Lu H, van Zijl PCM. Experimental measurement of extravascular parenchymal BOLD effects and tissue oxygen extraction fractions using multi-echo VASO fMRI at 1.5 and 3.0 T. Magn Reson Med. 2005;53(4):808–816. [DOI] [PubMed] [Google Scholar]
- 53.Gomori J, Grossman R, Yuip C, Asakura T. NMR relaxation times of blood: dependence on field strength, oxidation state, and cell integrity. J Comput Assist Tomogr. 1987;11(4):684–690. [PubMed] [Google Scholar]
- 54.Brooks RA, Vymazal J, Bulte JW, Baumgarner CD, Tran V. Comparison of T2 relaxation in blood, brain, and ferritin. J Magn Reson Imaging. 1995;4:446–450. [DOI] [PubMed] [Google Scholar]
- 55.Bryant RG, Marill K, Blackmore C, Francis C. Magnetic relaxation in blood and blood clots. Magn Reson Med. 1990;13(1):133–144. [DOI] [PubMed] [Google Scholar]
- 56.Chen JJ, Pike GB. Human whole blood T2 relaxometry at 3 Tesla. Magn Reson Med. 2009;61(2):249–254. [DOI] [PubMed] [Google Scholar]
- 57.Matwiyoff NAA, Gasparovic C, Mazurchuk R, Matwiyoff G. The line shapes of the water proton resonances of red blood cells containing carbonyl hemoglobin, deoxyhemoglobin, and methemoglobin: implications for the interpretation of proton MRI at fields of 1.5 T and below. Magn Reson Imaging. 1990;8(3):295–301. [DOI] [PubMed] [Google Scholar]
- 58.Fabry ME, Eisenstadt M. Water exchange between red cells and plasma. Measurement by nuclear magnetic relaxation. Biophys J. 1975;15(11):1101–1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Noseworthy MD, Kim JK, Stainsby JA, Stanisz GJ, Wright GA. Tracking oxygen effects on MR signal in blood and skeletal muscle during hyperoxia exposure. J Magn Reson Imaging. 1999;9(6):814–820. [DOI] [PubMed] [Google Scholar]
- 60.Gasparovic C, Matwiyoff NA. The magnetic properties and water dynamics of the red blood cell: A study by proton-NMR lineshape analysis. Magn Reson Med. 1992;26(2):274–299. [DOI] [PubMed] [Google Scholar]
- 61.Stanisz GJ, Li JG, Wright GA, Henkelman RM. Water dynamics in human blood via combined measurements of T2 relaxation and diffusion in the presence of gadolinium. Magn Reson Med. 1997;39(2):223–233. [DOI] [PubMed] [Google Scholar]
- 62.Luz Z, Meiboom S. Nuclear Magnetic Resonance Study of the Protolysis of Trimethylammonium Ion in Aqueous Solution—Order of the Reaction with Respect to Solvent. J Chem Phys. 1963;39(2):366. [Google Scholar]
- 63.Allerhand A, Gutowsky HS. Spin-echo studies of chemical exchange. II. closed formulas for two sites. J Chem Phys. 1965;42(5):1587. [DOI] [PubMed] [Google Scholar]
- 64.Kiselev VG, Novikov DS. Transverse NMR relaxation as a probe of mesoscopic structure. Phys Rev Lett. 2002;89(27):2–5. [DOI] [PubMed] [Google Scholar]
- 65.Novikov DS, Kiselev VG. Transverse NMR relaxation in magnetically heterogeneous media. J Magn Reson. 2008;195(1):33–39. [DOI] [PubMed] [Google Scholar]
- 66.Sukstanskii AL, Yablonskiy DA. Gaussian approximation in the theory of MR signal formation in the presence of structure-specific magnetic field inhomogeneities. Effects of impermeable susceptibility inclusions. J Magn Reson. 2004;167(1):56–67. [DOI] [PubMed] [Google Scholar]
- 67.Sukstanskii AL, Yablonskiy DA. Gaussian approximation in the theory of MR signal formation in the presence of structure-specific magnetic field inhomogeneities. J Magn Reson. 2003;163(2):236–247. [DOI] [PubMed] [Google Scholar]
- 68.Sukstanskii AL, Yablonskiy DA. Theory of FID NMR signal dephasing induced by mesoscopic magnetic field inhomogeneities in biological systems. J Magn Reson. 2001;151(1):107–117. [DOI] [PubMed] [Google Scholar]
- 69.Carver JP, Richards RE. A general two-site solution for the chemical exchange produced dependence of T2 upon the carr-Purcell pulse separation. J Magn Reson. 1972;6(1):89–105. [Google Scholar]
- 70.Davis DG, Perlman ME, London RE. Direct measurements of the dissociation-rate constant for inhibitor-enzyme complexes via the T1 rho and T2 (CPMG) methods. J Magn Reson Ser B. 1994;104:266–275. [DOI] [PubMed] [Google Scholar]
- 71.Kiselev VG, Novikov DS. Transverse NMR relaxation in biological tissues. Neuroimage. 2018;182(December 2017):149–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Hills BP, Takacs SF, Belton PS. The effects of proteins on the proton NMR transverse relaxation time of water I. Native bovine serum albumin. Mol Phys. 1989;67(4):903. [Google Scholar]
- 73.McLaughlin A, Leigh J Relaxation times in systems with chemical exchange: Approximate solutions for the nondilute case. J Magn Reson. 1973;9(2):296–304. [Google Scholar]
- 74.Kageyama K, Onoyama Y, Kogawa H, Goto E, Tanabe K. The maximum and minimum water content and cell volume of human erythrocytes in vitro. Biophys Chem. 1989;34(1):79–82. [DOI] [PubMed] [Google Scholar]
- 75.Chanarin I, Brozovic M, Tidmarsh E, Waters D. Blood and Its Disease. New York: Churchill Livingstone; 1984. [Google Scholar]
- 76.Doherty T, Hong M. 2D 1H–31P solid-state NMR studies of the dependence of inter-bilayer water dynamics on lipid headgroup structure and membrane peptides. J Magn Reson. 2009;196(1):39–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Lee J, Barry JA. Influence of membrane lipid packing on T2-weighted magnetic resonance images: study of relaxation parameters in model membrane systems. Magn Reson Med. 1996;36(3):420–426. [DOI] [PubMed] [Google Scholar]
- 78.Alonso-Ortiz E, Levesque IR, Pike GB. MRI-based myelin water imaging: A technical review. Magn Reson Med. 2015;73(1):70–81. [DOI] [PubMed] [Google Scholar]
- 79.Cerdonio M, Morante S, Vitale S. Magnetic susceptibility of hemoglobins. Methods Enzymol. 1981;76(C):354–371. [DOI] [PubMed] [Google Scholar]
- 80.Cerdonio M, Morante S, Torresani D, Vitale S, DeYoung A, Noble RW. Reexamination of the evidence for paramagnetism in oxy- and carbonmonoxyhemoglobins. Proc Natl Acad Sci U S A. 1985;82:102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Taylor DS, Coryell CD. The magnetic susceptibility of the iron in ferrohemoglobin. J Am Chem Soc. 1938;60(5):1177–1181. [Google Scholar]
- 82.Pauling L, Coryell CD. The magnetic properties and structure of hemoglobin, oxyhemoglobin and carbonmonoxyhemoglobin. Proc Natl Acad Sci. 1936;22(4):210–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Cerdonio M, Congiu-Castellano a, Calabrese L, Morante S, Pispisa B, Vitale S. Room-temperature magnetic properties of oxy- and carbonmonoxyhemoglobin. Proc Natl Acad Sci U S A. 1978;75(10):4916–4919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Jain V, Abdulmalik O, Propert KJ, Wehrli FW. Investigating the magnetic susceptibility properties of fresh human blood for noninvasive oxygen saturation quantification. Magn Reson Med. 2012;68(3):863–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Chu SC, Xu Y, Balschi JA, Springer CS. Bulk magnetic susceptibility shifts in NMR studies of compartmentalized samples: use of paramagnetic reagents. Magn Reson Med. 1990;13(2):239–262. [DOI] [PubMed] [Google Scholar]
- 86.Live DH, Chan SI. Bulk susceptibility corrections in nuclear magnetic resonance experiments using superconducting solenoids. Anal Chem. 1970;42(7):791–792. [Google Scholar]
- 87.Yablonskiy DA, Haacke EM. Theory of NMR signal behavior in magnetically inhomogeneous tissues: The static dephasing regime. Magn Reson Med. 1994;32(6):749–763. [DOI] [PubMed] [Google Scholar]
- 88.Wilson GJ, Springer CS, Bastawrous S, Maki JH, Jr CSS, Bastawrous S, Maki JH. Human whole blood 1H2O transverse relaxation with gadolinium-based contrast reagents: Magnetic susceptibility and transmembrane water exchange. Magn Reson Med. 2017;77:2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Conlon T, Outhred R. Water diffusion permeability of erythrocytes using an NMR technique. Biochim Biophsica Acta. 1972;288:354–361. [DOI] [PubMed] [Google Scholar]
- 90.Luz Z, Meiboom S. Proton relaxation in dilute solutions of cobalt(II) and nickle(II) ions in methanol and the rate of methanol exchange of the solvation sphere. J Chem Phys. 1964;40(9):2686. [Google Scholar]
- 91.Allerhand A, Gutowsky HS. Spin-echo NMR studies of chemical exchange. I. Some general aspects. J Chem Phys. 1964;41(7):2115–2126. [DOI] [PubMed] [Google Scholar]
- 92.Foltz WD, Stainsby JA, Wright GA. T2 accuracy on a whole-body imager. Magn Reson Med. 1997;38(5):759–768. [DOI] [PubMed] [Google Scholar]
- 93.Burton AC. Physiology and Biophysics of the Circulation. Year book medical publishers, Inc; 1965. [Google Scholar]
- 94.Wuthrich K NMR of Proteins and Nucleic Acids. Wiley; 1991. [Google Scholar]
- 95.Liepinsh E, Otting G, Wuthrich K. NMR spectroscopy of hydroxyl protons in aqueous solutions of peptides and proteins. J Biomol NMR. 1992;2(5):447–465. [DOI] [PubMed] [Google Scholar]
- 96.Benson ES, Hallaway BE, Lumry RW. Deuterium-hydrogen transitions exchange in bovine analysis of pH-dependent plasma albumin. J Biol Chem. 1964;239(1):122. [PubMed] [Google Scholar]
- 97.The Blood Gas Handbook. Denmark: Radiometer Medical; 2011. [Google Scholar]
- 98.Kokholm G Simultaneous measurements of blood pH, pCO2, pO2 and concentrations of hemoglobin and its derivates-a multicenter study. Scand J Clin Lab Invest Suppl. 1990;203:75–86. [DOI] [PubMed] [Google Scholar]
- 99.Benga G Water Exchange through the Erythrocyte Membrane. Int Rev Cytol. 1989;114:273–316. [DOI] [PubMed] [Google Scholar]
- 100.Herbst MD, Goldstein JH. A review of water diffusion measurement by NMR in human red blood cells. Am J Physiol. 1989;256(5):1097–1104. [DOI] [PubMed] [Google Scholar]
- 101.Andrasko J Water diffusion permeability of human erythrocytes studied by a pulsed gradient NMR technique. Biochim Biophys Acta - Gen Subj. 1976;428(2):304–311. [DOI] [PubMed] [Google Scholar]
- 102.Fabry ME, Eisenstadt M. Water exchange across red cell membranes: II. measurement by nuclear magnetic resonance T1, T2, and T12 hybrid relaxation. The effects of osmolarity, cell volume, and medium. J Membr Biol. 1978;42:375–398. [DOI] [PubMed] [Google Scholar]
- 103.Morariu V V, Benga G. Evaluation of a nuclear magnetic resonance technique for the study of water exchange through erythrocyte membranes in normal and pathological subjects. Biochim Biophys Acta. 1977;469(3):301–310. [DOI] [PubMed] [Google Scholar]
- 104.Chien DY, Macey RI. Diffusional water permeability of red cells independence on osmolality. Biochim Biophys Acta - Biomembr. 1977;464(1):45–52. [DOI] [PubMed] [Google Scholar]
- 105.Shporer M, Civan MM. NMR study of 17O from H217O in human erythrocytes. Biochim Biophys Acta - Gen Subj. 1975;385(1):81–87. [DOI] [PubMed] [Google Scholar]
- 106.Akaike H A new look at the statistical model identification. IEEE Trans Autom Control. 1974;19(6):716–723. [Google Scholar]
- 107.Burnham KP, Anderson DR. Multimodel inference: understanding AIC and BIC in model selection. Sociol Methods Res. 2004;33(2):261–304. [Google Scholar]
- 108.Glatting G, Kletting P, Reske SN, Hohl K, Ring C. Choosing the optimal fit function: Comparison of the Akaike information criterion and the F-test. Med Phys. 2007;34(11):4285–4292. [DOI] [PubMed] [Google Scholar]
- 109.Burnham KP, Anderson DR. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach (2nd Ed) Vol 172; 2002. [Google Scholar]
- 110.Zhong J, Gore JC, Armitage IM. Relative contributions of chemical exchange and other relaxation mechanisms in protein solutions and tissues. Magn Reson Med. 1989;11(3):295–308. [DOI] [PubMed] [Google Scholar]
- 111.Koenig SH, Bryant RG, Hallenga K, Jacob GS. Magnetic cross-relaxation among protons in protein solutions. Biochemistry. 1978;17(20):4348–4358. [DOI] [PubMed] [Google Scholar]
- 112.Denisov VP, Halle B. Hydrogen exchange rates in proteins from water H-1 transverse magnetic relaxation. J Am Chem Soc. 2002;124(35):10264–10265. [DOI] [PubMed] [Google Scholar]
- 113.Brooks R a, Brunetti A, Alger Di JR, Chiro G On the origin of paramagnetic inhomogeneity effects in blood. Magn Reson Med. 1989;12(2):241. [DOI] [PubMed] [Google Scholar]
- 114.Tsuneshige A, Imai K, Tyuma I. The binding of hemoglobin to red cell membrane lowers its oxygen affinity. J Biochem. 1987;101(3):695–704. [DOI] [PubMed] [Google Scholar]
- 115.Walder JA, Chatterjee R, Steck TL, Low PS, Musso GF, Kaiser ET, Rogers PH, Arnone A. The interaction of hemoglobin with the cytoplasmic domain of band 3 of the human erythrocyte membrane. J Biol Chem. 1984;259(16):10238–10246. [PubMed] [Google Scholar]
- 116.Chu H, McKenna MM, Krump NA, Zheng S, Mendelsohn L, Thein SL, Garrett LJ, Bodine DM, Low PS. Reversible binding of hemoglobin to band 3 constitutes the molecular switch that mediates O2regulation of erythrocyte properties. Blood. 2016;128(23):2708–2716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Chu H, Breite A, Ciraolo P, Franco RS, Low PS. Characterization of the deoxyhemoglobin binding site on human erythrocyte band 3: Implications for O2 regulation of erythrocyte properties. Blood. 2008;111(2):932–938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Holz M, Heil R, Sacco A, Chemie P, Karlsruhe U, Karlsruhe D, Foggia U, Napoli V. Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1 H NMR PFG measurements. Phys Chem Chem Phys. 2000;2:4740–4742. [Google Scholar]
- 119.Kotitschke K, Kimmich R, Rommel E, Parak F. NMR study of diffusion in protein hydration shells. Prog Colloid Polym Sci. 1990;83:211–215. [Google Scholar]
- 120.Kuchel PW, Durrant CJ, Chapman BE, Jarrett PS, Regan DG. Evidence of red cell alignment in the magnetic field of an NMR spectrometer based on the diffusion tensor of water. J Magn Reson. 2000;145(2):291–301. [DOI] [PubMed] [Google Scholar]
- 121.Waluch V, Bradley WG. NMR even echo rephasing in slow laminar flow. J Comput Assist Tomogr. 1984;8(4):594. [DOI] [PubMed] [Google Scholar]
- 122.Novikov DS, Fieremans E, Jensen JH, Helpern JA. Random walks with barriers. Nat Phys. 2011;7(6):508–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Woessner DE. Nuclear transfer effects in nuclear magnetic resonance pulse experiments. J Chem Phys. 1961;35(1):41–48. [Google Scholar]
- 124.Jain V, Magland J, Langham M, Wehrli FW. High temporal resolution in vivo blood oximetry via projection-based T2 measurement. Magn Reson Med. 2013;70(3):785–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Hoffman R, Furie B, McGlave P, Silberstein, Leslie E Shattil SJ, Benz EJJ, Heslop H Normal blood values: selected reference values for neonatal, pediatric, and adult populations. In: Hematology: Basic Principles and Practice. 2008 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.