Abstract
Accurate force-field (FF) parameters are key to reliable prediction of properties obtained from molecular modeling (MM) and molecular dynamics (MD) simulations. With ever-widening applicability of MD simulations, robust parameters need to be generated for a wider range of chemical species. The CHARMM General Force Field and program (CGenFF, https://cgenff.umaryland.edu/) is a tool for obtaining initial parameters for a given small molecule based on analogy with the available CGenFF parameters. However, improvement of these parameters is often required and performing their optimization remains tedious and time consuming. In addition, tools for optimization of small molecule parameters in the context of the Drude polarizable FF are not yet available. To overcome these issues, the FFParam package has been designed to facilitate the parametrization process. The package includes a graphical user interface (GUI) created using Qt libraries. FFParam supports Gaussian and Psi4 for performing QM calculations and CHARMM and OpenMM for MM calculations. A Monte Carlo Simulated Annealing (MCSA) algorithm has been implemented for automated fitting of partial atomic charge, atomic polarizabilities and Thole scale parameters. The LSFITPAR program is called for automated fitting of bonded parameters. Accordingly, FFParam provides all the features required for generation and analysis of CHARMM and Drude FF parameters for small molecules. FFParam-GUI includes a text editor, graph plotter, molecular visualization and text to table converter to meet various requirements of the parametrization process. It is anticipated that FFParam will facilitate wider use of CGenFF as well as promote future use of the Drude polarizable FF.
Keywords: molecular dynamics, quantum mechanics, polarizable force field
Introduction
The performance of molecular modeling (MM) or molecular dynamics (MD) simulations in predicting the properties of chemical and biological systems depends on the algorithms, on the size of the systems, and the accuracy of the underlying force-field (FF) parameters that describe the molecular system. The FF parameters should be able to describe molecular structure, conformational energies and intermolecular interactions as well as macroscopic properties such as hydration free energies. CHARMM,1 AMBER,2 OPLS,3,4 and GROMOS5 are the most widely used FFs in the context of biological systems. The parameters for these biological systems, including nucleic acids, proteins, carbohydrates, lipids etc., are carefully optimized in these FFs such that both microscopic and macroscopic properties are well reproduced. Nonetheless, MD simulations of molecules outside this scope, e.g. applications in drug design, require new parameters for a much wider range of chemical space. There are a few automated tools to extend FFs to novel molecules. Examples of these include the CHARMM General Force Field (CGenFF),6 which is an extension of CHARMM additive FF and LigParGen for generation of parameters consistent with the OPLS-AA FF.7 Antechamber8 is another such program that generates parameters consistent with the AMBER FF, referred to as the Generalized Amber Force Field (GAFF).9,10 These programs typically generate initial parameters based on the analogy to atom types and the associated parameters available in the respective FF or through parameter estimation algorithms as in GAFF211.
A fundamental problem with both analogy and interpolation-based approaches in developing missing FF parameters is the limited accuracy in the assignment of approximate parameters to a specific molecule. CGenFF provides penalty scores to the parameters reflecting the extent of analogy with the atom types associated with existing parameters. This offers a metric for selecting a parameter for further optimization. Typically, only new parameters generated by analogy, as indicated by the assignment of penalty scores, are optimized. This maintains the hierarchical fashion of the FF and allows continuous development.6 However, for a specific project it may be necessary to optimize parameters already available in the FF to achieve the accuracy required for the study. In either case, optimization of the selected parameters represents a tedious and time-consuming task. Currently, a loosely codified protocol developed in our lab exists to generate such parameters. The process involves a tremendous amount of manual file handling, including extracting information from output files, performing calculations on properly aligned molecules, optimizing the parameters and checking their performance by iterating these processes.
ffTK12 is an automated parameter optimization tool designed for the development of CGenFF parameters directly from first principles.12 It is provided as a plugin to the VMD program.13 ffTK facilitates the generation of parameters through a GUI by assisting input file generation for QM and molecular mechanics (MM) calculations, extracting the results from output files, and displaying the performance of the optimized parameters. In addition, it also provides automated algorithms such as Monte-Carlo Simulated Annealing (MCSA) for improving the parameters. ffTK supports NAMD14 as the MM engine and creates input files compatible with the Gaussian software15 for the required QM calculations. While ffTK is a great tool to improve the CHARMM additive parameters, its capabilities have not been extended to the Drude polarizable FF. Another limitation of ffTK was its design, as it was developed as a plugin rather than a standalone package that contains all the required capabilities to complete the optimization process.
The inclusion of polarizability in empirical FFs has been attracting significant attention from the scientific community. Our lab in collaboration with Roux and coworkers has developed the classical Drude Polarizable FF,16,17 which addresses induced electronic polarization within a MM framework by attaching an auxiliary particle (Drude particle or oscillator) to each polarizable atom via a harmonic spring. The polarization response is obtained by distributing the charge on the atomic nucleus and Drude particle, based on the magnitude of the atomic polarizability, alpha, and the force constant on the harmonic spring. The position of the Drude particle is then optimized in response to the surrounding electric field with the fixed atomic nuclei, corresponding to self-consistent field (SCF) calculation that satisfies the Born-Oppenheimer approximation. The magnitude of the charges on the atom and Drude particle also accounts for the partial atomic charge. For the improvement of intramolecular dipole-dipole interactions, Thole scaling factors are introduced that dictate the magnitude of 1,2 and 1,3 interactions,18 thereby optimizing the treatment of molecular polarizability.17,19 Atom-based anisotropic polarizability terms improve the treatment of intermolecular interactions as a function of orientation.20 Lone pairs (LP) are an integral part of the Drude FF which further diverges the centrosymmetric-nature common to most additive FFs. While the Drude FF still uses the Lennard-Jones term to treat van der Waals interactions, the inclusion of LJ parameters on LP and Drude particles introduces an effective asymmetry into the vdW representation.21,22 In addition, LJ parameters for specific atom pairs, termed atom-pair specific LJ parameters (i.e. NBFIX in CHARMM nomenclature) have been used extensively to improve the treatment of non-bond interactions.17 Using these capabilities the Drude FF has been shown to perform better on halogenated species and on protein-halogen interactions as compared to additive FF.22 However, the Drude FF is relatively young in comparison to additive FFs and the range of chemical space covered is mainly associated with large biomolecules. Therefore, a significant extension of the Drude polarizable FF to a much wider range of chemical space is required.
In view of the preceding issues, we have developed a standalone cross-platform GUI-based package, FFParam, to facilitate the parametrization of both CHARMM additive and polarizable Drude FFs. The aim of this package is not only to minimize the manual work usually involved in parametrization but also to automate parameter fitting based on robust algorithms. FFParam currently supports Gaussian15 and Psi423 as QM engine file formats for performing QM calculations. The latter is distributed as open-source software and its python-based API integrates well with FFParam since it is also based on python. Apart from creating input files, FFParam can run both MM and QM calculations either on the local workstation or on a remote cluster. Current engines supported for the corresponding MM calculations are CHARMM24 and OpenMM25 programs. Similar to Psi4, OpenMM is an open-source MD package with a python-based API. This allows FFParam to become an operating-system independent platform. Automatic fitting of electrostatic parameters is supported by FFParam using a Monte Carlo Simulated Annealing (MCSA) method26 implemented directly in the current program. For automatic fitting of bonded parameters, FFParam supports the least square fitting method of Vanommeslaeghe and MacKerell,27 LSFITPAR, which was specifically developed to produce robust FF parameters. FFParam also facilitates parametrization by organizing its modules in separate tabs in the GUI, arranged according to the parametrization workflow. In addition, the ability to display and edit text, display graphs, do simple mathematical operations and perform 3D molecular visualization reduces the dependency on external programs. Thus, FFParam is a single unified platform allowing users of all levels to rapidly improve the parameters for small molecules.
Structure of FFParam
The FFParam package includes Python modules for performing parametrization, integrated with a Graphical User Interface (GUI) designed using PyQt5 libraries. Since the entire package is written in Python, it may be readily downloaded and installed through Anaconda (https://www.anaconda.com). PyQt is Python binding for the Qt cross-platform C++ framework, which enables the development of a cross-platform portable GUI. FFParam-GUI has a modular structure divided into two sections (Figure 1). The top section of the GUI allows various operations and calculations to be performed through tabs which are aligned horizontally in accordance with their sequential access during the course of parametrization. These tabs are InitializeSystemSetup, CreateQMInput, QMCalculations, ExtractQMResult, MMCalculations, CompareMMvsQM and AutoFit:ChargeAlpThol. The name of these tabs is suggestive of their capabilities. All the above-mentioned tabs other than InitializeSystemSetup, QMCalculations, and CompareMMvsQM tab are initially inactive to prevent unwanted errors. Once a file containing a topology and parameters (referred to as toppar stream file henceforth) is loaded into InitializeSystemSetup tab, all the inactive tabs become active and share relevant information extracted from the toppar stream file, such as atom names, atom types, total charge, partial atomic charges and the atomic connectivity of the molecule. FFParam promotes use of atom names rather than atom types with which a non-expert user will be more familiar. The Settings pull down menu allows users to provide the paths to Gaussian, CHARMM, LSFITPAR, CGenFF, as well as connection with a remote server (Figure 1).
Figure 1.
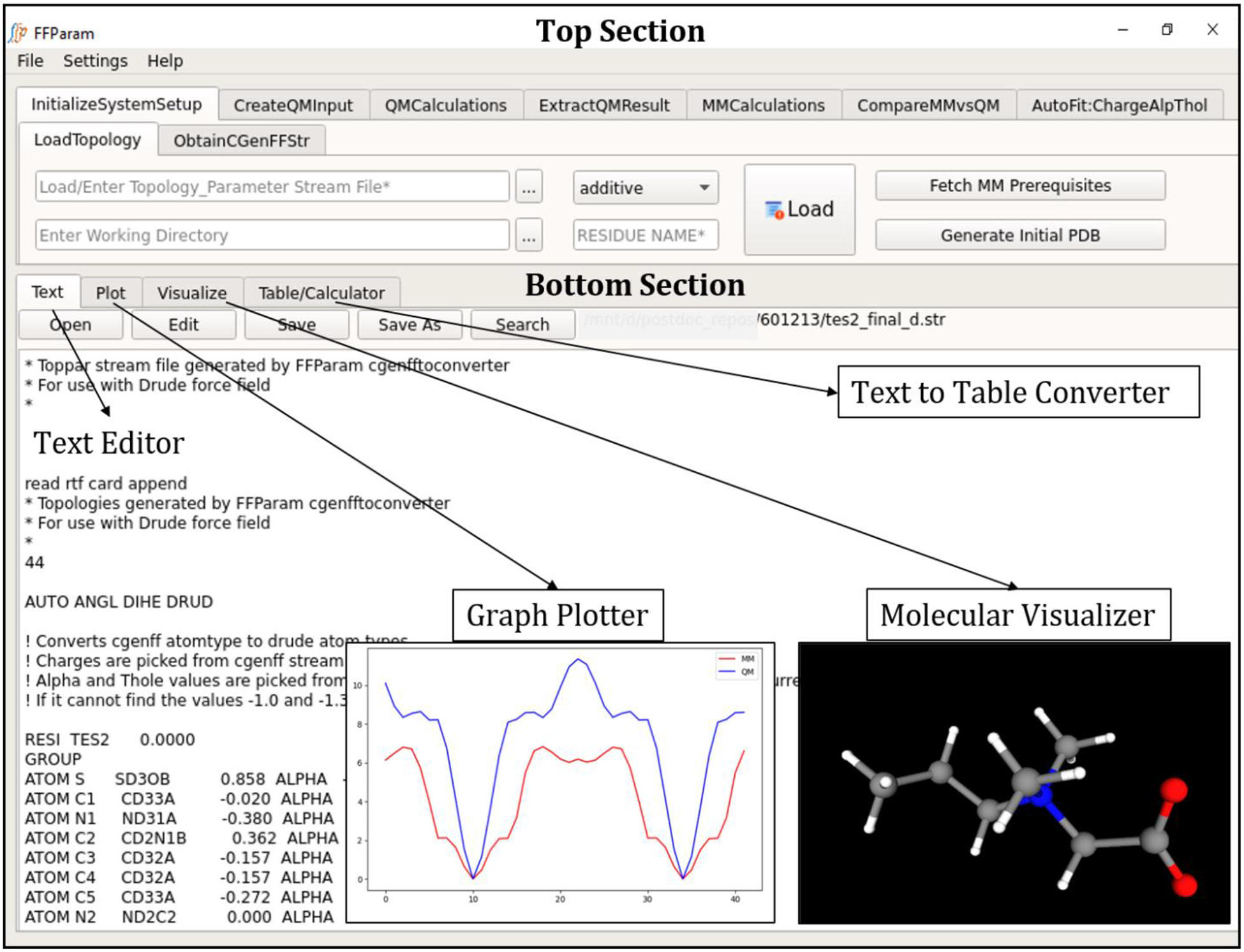
The front display of FFParam-GUI with expanded view of the top section of the GUI.
FFParam maintains a unique directory structure for performing parameter optimization on a specific “model” compound. The toppar stream file associated with the model compound should be placed in the top-level (parent) directory, which can be set with the working directory field. A CHARMM input script required for MM calculations in CHARMM and toppar/toppar_drude subdirectory containing all the standard CHARMM additive and Drude topology and parameter files are placed by FFParam in the parent directory. This is performed by a push-button named “Fetch MM Prerequisites” located in InitializeSystemSetup tab. All the files created during parametrization are placed in the parent directory and its subdirectories based on the type of data. For example, all the QM input and output files are placed in qmfiles subdirectory. Other subdirectories are created to store related data, including dipolar for the dipole moments and molecular polarizability, charges for the water interaction energies, intcoor for the geometries and pesscan for the potential energy scans.
Producing robust parameters requires visual inspection of text, graph and 3D structures. The bottom section of the FFParam-GUI is designed for displaying the various data and files produced during the parametrization process. A Qt-based text editor is embedded for the ease of displaying, editing and saving text input or output. Common text editor features like cut, copy, and paste are enabled. Most of output generated during the steps of the parametrization process are directed to the text-editor by default. It is also possible to open, edit, save and search through a text file independently by clicking “Open”, “Edit” “Save”, “Save as” and “Search” buttons. The analysis of PES requires plotting the QM and MM energies as a function of the internal coordinate. To perform this, a graph plotter has been designed using matplotlib libraries28 which enables the display, manipulation (features) and saving (images) of the graphs. It is connected with the CompareMMvsQM tab, wherein energy values contained in the supplied QM and MM text files are plotted. However, “Plot” tab supports graph plotting of any csv file-format containing columns of numeric data. The molecular visualizer has been designed with the PyOpenGL libraries (cross-platform Python binding to OpenGL). This visualizer is especially useful because it has been customized to display any format containing molecular coordinates produced during the parametrization process including .pdb, .crd, .xyz, .mol2, .com (Gaussian input), .log(Gaussian output), and .out (Psi4 output) files. The water interaction input files generated by this package under “CreateQM” tab involves both Cartesian and Z-matrix specification in a single file. The customized molecular visualizer reads these files, helping the user to inspect water-model compounds interaction geometries before performing QM calculations. More importantly, multiple geometries may be visualized simultaneously by selecting and opening the respective files together. This feature may be exploited to compare QM and MM geometries, various input/output of water interaction files, etc. Distance, angle and dihedral values may be measured by choosing the atoms (double-click on atomic position to select), with the values displayed in a pop-up message box. The structures can be rotated using mouse movements while left-click of the mouse is pressed. Zooming may be performed by scrolling the mouse. A translation feature is not enabled in the visualizer as the small model compounds for which it was designed are centered in the visualization screen. An image saving feature is also provided to facilitate preparation of reports. The features of elements such as color and covalent radii used are those suggested by Open-Babel library (http://openbabel.org/). The “Table/Calculator” tab is developed using table widget in PyQt for assisting in simple addition operations on numeric entries in a text file. Although the bottom section of the package is independent of the top section, any output obtained after an MM operation in the top section is automatically displayed on Text or Plot tabs provided in the bottom section. Various capabilities of the FFParam package will be further discussed in the context of their usage at different stages of parametrization process of test cases.
System Initialization
Parametrization in FFParam is initialized by uploading the toppar stream file containing both CHARMM topology and parameters of the model compound, providing the residue name and the type of FF (additive or Drude). Use of the residue name allows for the toppar stream file to contain topologies and parameters for multiple residues, which may be useful when optimizing parameters for larger target molecules that requires the use of multiple model compounds, as presented below and in the supporting information. The primary source of a toppar stream file is the CGenFF program. The CGenFF program, which requires molecular information in mol2 format, is hosted by the ParamChem website (https://cgenff.umaryland.edu/). It may also be obtained as a standalone program from SilcsBio LLC (http://silcsbio.com/) and is currently free of charge to non-profit users. FFParam provides an option to link to a locally compiled version of the CGenFF program. Since the Drude analog of the CGenFF program is not available currently, FFParam includes a module for converting the additive toppar stream file into Drude FF format. It is recommended that users check the correctness of this Drude FF toppar stream file.
Based on the atom and bond description in the toppar stream file, all the valence angles and dihedrals are deduced by the package. It can also generate a psf file for a given residue which may be useful during OpenMM calculations. The lone pairs are ignored while determining the angles and dihedrals. During the course of parametrization, QM and MM engines often require atom indices instead of atom names; therefore, FFParam keeps track of atom indices along with their atom names. It allows users to make selections using atom names while the program assigns the atom indices. With Drude toppar stream files, FFParam atom indices considers the presence of Drude particles after each non-hydrogen atom. This allows the use of coordinate files which may or may not contain Drude particles or lone pairs by automatically assigning the correct mapping of atom names to atom indices.
As mentioned above, CGenFF generates a toppar stream file on the basis of coordinate and bond information provided in mol2 file. In practice, the user may want to rename or reorder atoms in the toppar stream file. For organization of the parametrization process, it is necessary to maintain the atom names and order present in the toppar stream file in all remaining files. In view of this, FFParam allows for the construction of 3D coordinates of the concerned molecule from the topology information in the toppar stream file using RDKit libraries.29 This initial set of coordinates should be minimized using the MM engine with the initial set of parameters in the toppar stream file. The resulting minimized geometry may then be used for generating QM input file in Gaussian or Psi4 format. This reduces time spent on geometry optimization in the QM engine and also ensures that the QM optimized geometry will have the same conformation as it would have after the MM minimization. However, for complex molecules it is recommended that the MM minimized geometry be checked to assure that a physically-correct geometry is obtained.
FFParam Workflow and data structure overview
This section presents an overview of the parametrization workflow of a model system in FFParam (Scheme 1). After system initialization, stage one involves generation of all the required QM data before proceeding with the parametrization. These target data are used for fitting the MM parameters such that the MM model closely reproduces the QM target data. In addition, initially generating all the required target data avoids switching back-and-forth amongst various steps of parametrization. The QM target data can be broadly divided into three categories. These include geometry optimization (source of QM optimized geometry and associated electronic properties like dipole moment and molecular polarizability), conformational energies (adiabatic potential energy scans (PES) of bonds, angles or dihedrals), and interaction energies with individual water molecules. FFParam can generate QM input files in both Gaussian and Psi4 formats to calculate the above-mentioned types of QM target data. Default levels of theory and basis sets are suggested by the GUI that are commonly used during additive and Drude parametrization, although users may change them according to their specific requirements. These default levels are presented in Table S8 of Supplementary Information.
Scheme 1:
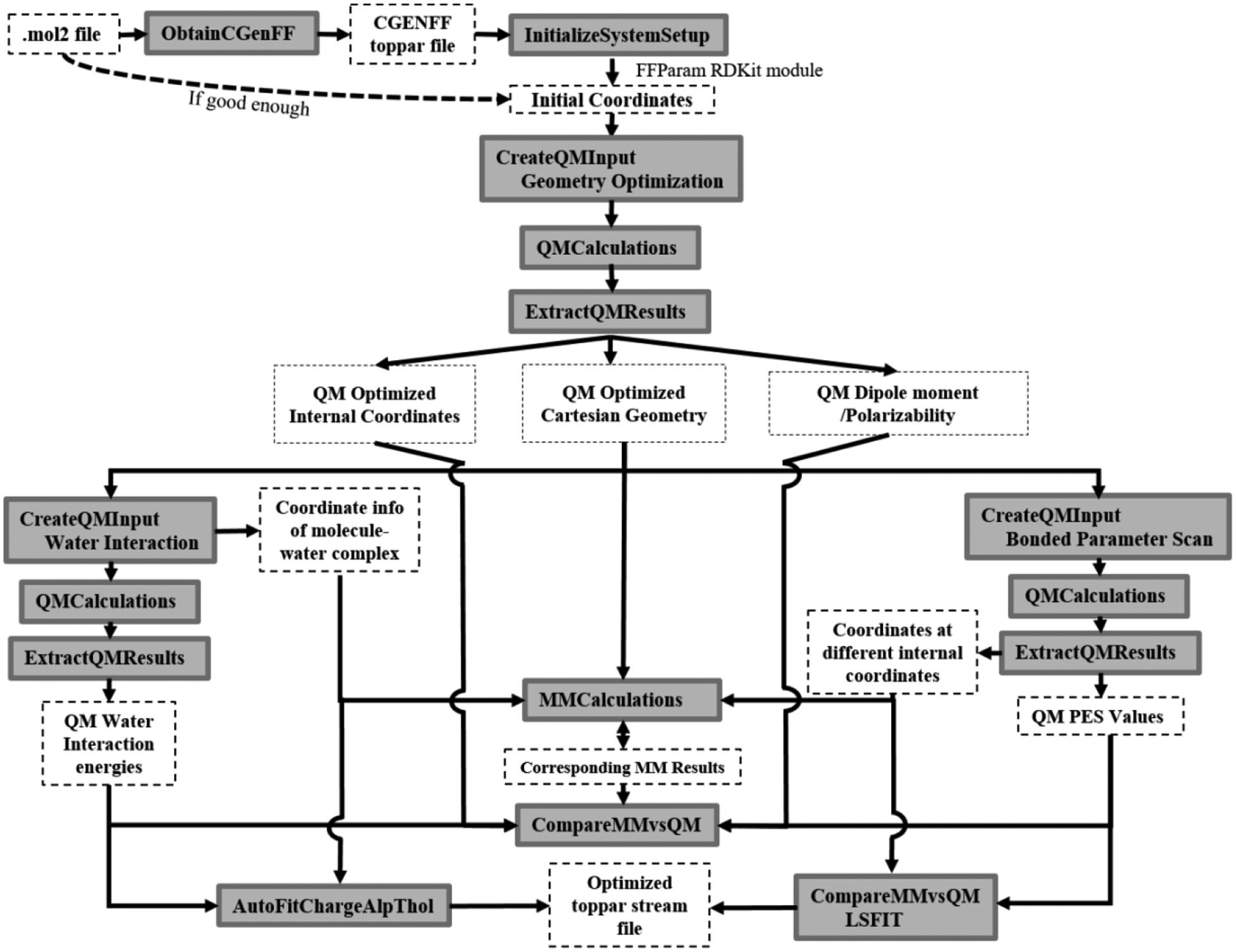
Flow Chart of the workflow of parameterization of electrostatic and bonded parameters using FFParam-GUI. The text in grey boxes correspond to the tabs in FFParam-GUI and text in dashed boxes is the data obtained upon execution of the corresponding action.
Apart from syntactical differences between Psi4 and Gaussian input files, the QM input files created for Psi4 calculations, especially for the water-interaction and bonded parameter scans, are structured differently than for Gaussian calculation. This is required to address three main issues in Psi4. These are the lack of support for z-matrix optimization (required for partial optimization of water and model compound in a desired orientation), convergence issues in bonded parameter scans and absence of functions to calculate molecular polarizability at the MP2 level of theory. Therefore, the following additions to the protocol have been incorporated in the Psi4 input files. For the calculation of water-model compound interaction energies, a series of coordinates are generated by varying the distance between the model compound and the water molecule, which are then used in a single-point energy calculation. Similarly, for a PES calculation, coordinates are generated for each step along the scan by changing the value of the concerned internal coordinate in the model compound. Modifications to the internal coordinates are made using RDKit and stored in a format that is accepted by the QCElemental package in Psi4. A Psi4 calculation on the input files created by FFParam involves geometry optimization with the selected internal coordinates constrained to the specified value. Of special notice is the calculation of the molecular polarizabilities, for which a finite-difference method has been explicitly implemented.30 With these additions, both Psi4 and Gaussian may be used to generate the full range of QM target data required for the optimization process.
Evaluation of molecular properties such as the dipole moment or molecular polarizability are performed on the QM optimized geometry by the QM engine. Interaction energy evaluations and adiabatic PES are subsequently performed with the QM optimized structure. In addition to the user running the QM calculations outside of FFParam, the program allows QM calculations to be run through the GUI. If the user wants to run a Gaussian calculation through the FFParam GUI, the path of the Gaussian executable should be provided to the GUI (under Settings in Figure 1), while if Psi4 calculations are desired, the path to Psi4 library should be added to the user’s PYTHONPATH environment variable. The package also provides the capabilities to establish a remote connection, execute client commands on a remote machine, and exchange input and output files between the remote server and client. This empowers FFParam to be launched from any workstation and perform expensive QM calculations seamlessly on a remote server. Output from the QM calculations should be placed in the subdirectory qmfiles for further processing by FFParam.
Once the QM calculations are complete, the relevant target data is extracted from the QM output files. Assuming that default input keywords are used while creating the QM input files, FFParam can extract the optimized geometry, internal coordinates, dipole moment and molecular polarizability from the geometry optimization output. The optimized structure is placed in the parent directory, internal coordinates are placed in the intcoor subdirectory and both the dipole moments and molecular polarizabilities are maintained in the dipolar subdirectory. In the case of water interaction energy evaluations, the monomer energies are subtracted from the total complex energy, where both complex and monomer energies should be calculated at same level of theory and basis set. The resulting data is stored in the charges subdirectory. From the QM PES outputs, the geometries optimized at each requested bond, angle or dihedral value and their corresponding energies are extracted and deposited in pesscan subdirectory.
The MM calculations performed through CHARMM or OpenMM are designed to yield MM data that can then be compared with the previously extracted QM target data. At this stage, the user can select appropriate parameters for optimization based on associated penalty scores or based on the comparison of the QM and MM data. Such analysis is facilitated by the text and plotting capabilities of FFParam-GUI. Optimization of parameters may be performed either manually by changing them in the toppar stream file using the text editor and Table/Calculator capabilities, or in an automated fashion using MCSA or LSFITPAR capabilities in FFParam. The optimization of bonded and non-bonded parameters can be targeted separately. Electrostatic parameters are parameterized using the QM optimized structure as a basis for MM water-interaction calculations (Scheme 1). This is based on the fact that water interaction calculations are a function of molecular coordinates and assumes that the final MM optimized structure of the model compound will be similar to the QM structure. On the other hand, the bond, angle and dihedral parameters are optimized to maximize the agreement between the MM and QM intramolecular geometries and PES. The final parameters, comparison of the QM and MM results along with graphs and the associated data may then be extracted for report preparation.
Model compound preparation for FFParam
Successful application of FFParam is facilitated by selection of the appropriate “model” compound for the optimization. This decision needs to take into account the need for QM calculations as well as issues associated with a large number of rotatable bonds. For example, most drug-like molecules contain two or more ring systems connected by flexible linkers. An example target compound (ZINC ID: ZINC601213) obtained from the ZINC database31 is shown in Figure 2a. The full target compound (2a) contains two ring systems (Figure 2b and 2d) connected via a chain (Figure 2c) that contains multiple rotatable bonds. While applying FFParam to the full molecule is possible, it is ill advised given the computational demands of the QM calculations and the molecular flexibility. Accordingly, it is suggested that the system be separated into three model compounds capped with methyl groups, (compounds 2b, 2c and 2d) and the parametrization be performed on those individually.
Figure 2.
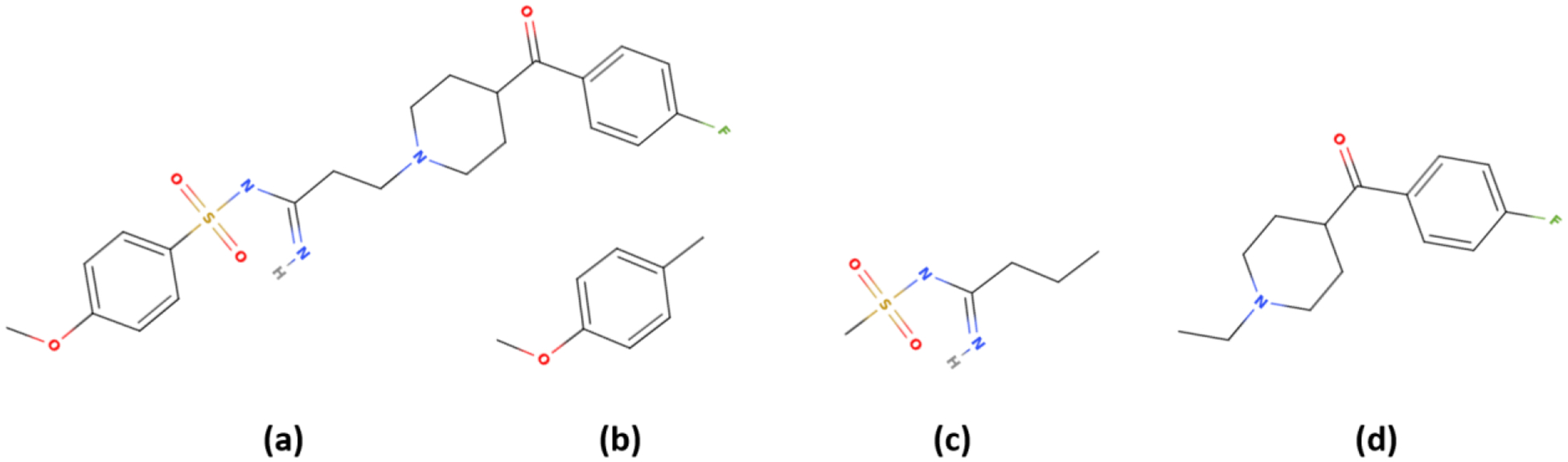
a. Target compound for parameter optimization and model compounds b, c and d extracted from the target compound that will be individually parametrized with the resulting parameters combined to model the full target compound.
Once the parameters have been optimized individually for the three model compounds, they can be combined together resulting in a parameter set for the full target compound (Figure 2a). In many cases, only electrostatic parameters (charge, Alpha and Thole factors) and dihedrals around rotatable bonds need to be optimized, which is demonstrated using fragment 2c as a model compound in the following sections. Additional details of the parameter optimization strategy are presented in the Supporting Information along with the initial CGenFF and final optimized parameters for the compounds in Figure 2. As described in the supporting information, parameters associated with 2b and 2d did not require optimization while both electrostatic and bonded parameters for 2c were optimized and then transferred to the full target compound.
Optimization of Electrostatic Parameters
Electrostatic parameter optimization for the additive FF focuses on the interaction energies of the model compound with water, supplemented by dipole moments. In the case of the Drude FF gas phase dipole moments and molecular polarizabilities are the primary target data supplemented by water-model compound interaction energies. This approach is consistent with the standard CGenFF and Drude optimization protocols.32–34 For interactions with water, emphasis is placed on polar sites in the model compound wherein O, N, S and P atoms are considered H-bond acceptors, while hydrogen atoms covalently linked to acceptor atoms are considered as H-bond donors. In order to capture maximum interaction of water with these sites, the water molecule is placed at a distance and orientation relative to these sites (Figure 3) in accordance with VESPR-theory.35 FFParam allows users to pick the atoms of interest for water interactions or select all possible atomic sites in the molecule for creating a precursor file that contains information on the sites and orientations of water around those sites (da file). The da file is subsequently used for creating QM or MM model compound-water input files. The QM calculation on these input files involves a scan in 0.05 Å increments along the direction of approach to find the minimum interaction energy of model compound-water complexes. The minimum value of interaction energies and corresponding distances between water and each of the chosen sites are extracted in a text file. In the case of the additive FF, the QM interaction energies are scaled by a factor of 1.16 for polar, neutral species as previously discussed.36
Figure 3.
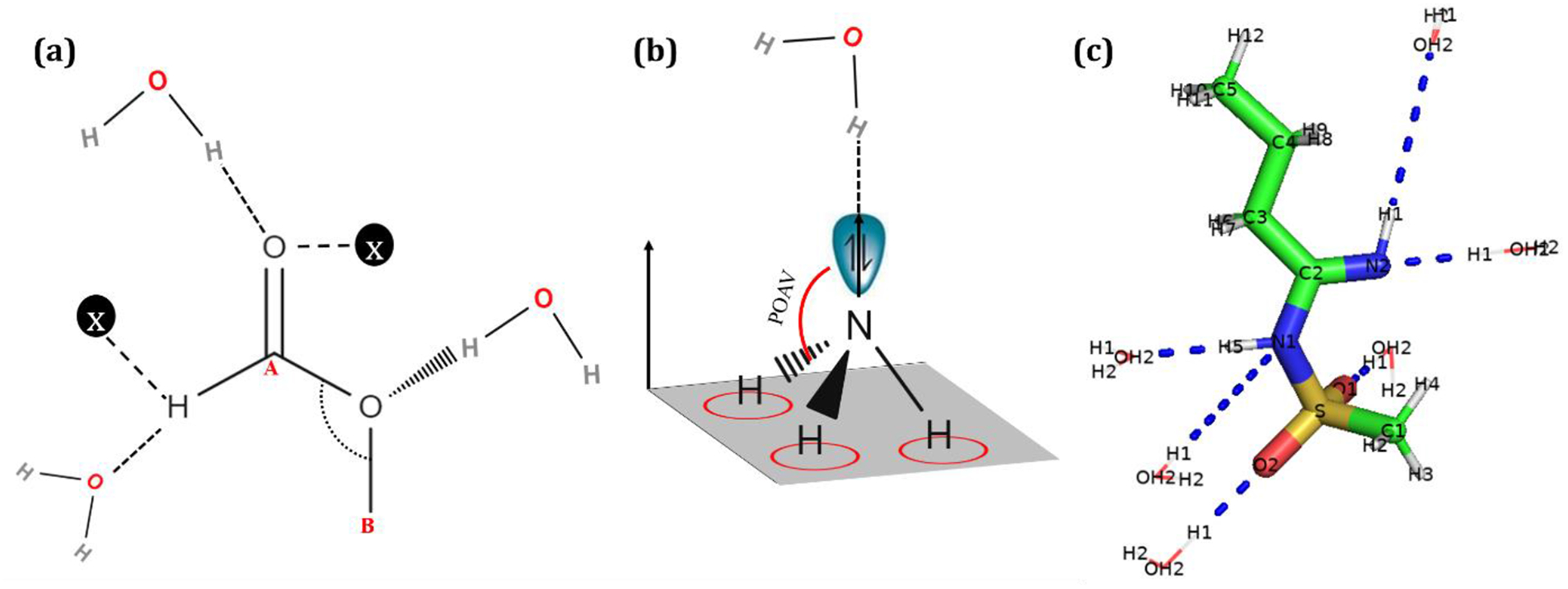
(a) Representative orientations of water molecules with model compounds based on the donor and acceptor atoms. A and B are adjacent host atoms which may be required to place water molecule in correct position. X indicates virtual atoms used to define the relative orientation of the model compound and water. (b) In the case of sp3 hybridized nitrogen and phosphorus, POAV angle is determined for placing the water molecule. In accordance to the figure, it is the angle between plane created by N-H-H atoms and normal vector to the plane created by H-H-H atoms. (c) Different water-interactions studied for model compound 2c as mentioned in Table 1.
The MM optimized distances and interaction energies can be obtained from CHARMM or OpenMM for the same set of model compound-water complexes using the precursor da file. Here, the MM water-interaction energies are obtained using the partial atomic charges present in the toppar stream file of the model compound along with the remaining parameters in the respective FFs. In the case of the Drude FF, the SCF optimization of the Drude particles on isolated water and model compound is taken into account while calculating the interaction energies. The CompareMMvsQM tab allows for comparison of the MM and QM minimum interaction energies and distances. The difference between MM and QM interaction energies for selected atoms can be minimized by manipulating the appropriate electrostatic properties. For example, with the additive FF, users can manipulate the atomic charges manually and examine its effect on interaction energies by editing the toppar stream file in the Table/Calculator tab, which has the capability to sum the charge in a selected column to facilitate checking of the total charge of the model compound, which needs to be maintained as an integer. Manual manipulation is an iterative process, wherein the user fits the interaction energies and distances by changing the desired charges, ensuring that the sum of all atomic charges is equal to total charge, running the MM calculation with the adjusted charges, and comparing the new MM values against the QM target values.
The Drude polarizable FF contains extra terms, in addition to the atomic charges, associated with the explicit treatment of polarizability on non-hydrogen atoms. These include the alpha and Thole scale factors. Although, polarizability is a molecular property, the alpha values on individual atoms are adjusted to primarily target the components of the QM polarizability tensor as well as the dipole moment. While the MM molecular polarizability values are sensitive to the alpha values, additional fine tuning can be performed by adjusting the Thole scale factors (range: 0–2.6).37 While the Drude electrostatic model is more complex than the additive model, the optimization of the model is actually more well-defined. This is because initial electrostatic parameter optimization with the Drude model can directly target gas phase QM dipole moments and molecular polarizabilities (typically scaled by 0.85) of the model compound in conjunction with the water interaction data. The following sub-sections describe the details of automated fitting of charge, Alpha and Thole values in FFParam. In a recent article, a machine learning model based on neural nets was presented to obtain atomic charges and atomic polarizabilities for model compounds.38 This type of approach will be incorporated in the program to automatically generate initially topologies and parameters for the Drude FF.
Automatic fitting of Electrostatic parameters
Manual fitting of charges can be tedious and time consuming especially when multiple atomic charges require simultaneous adjustments. In light of this, a module for performing MCSA has been developed as a part of FFParam to optimize the atomic charges. The MCSA algorithm acceptance ratio, r, is based on the Metropolis-Hastings algorithm (Eq. 1a), where the penalty function is the root-mean square error (RMSE) discussed below.
| (Eq. 1a) |
| (Eq. 1b) |
| (Eq. 1c) |
In equation 1, Tstart is the initial annealing temperature, Ti is the annealing temperature at ith MCSA step out of a total of Nsteps. Starting from the initial annealing temperature, the instantaneous temperature, Ti, decays exponentially to zero over the number of specified MCSA steps. The use of variable Tscaled ensures gradual cooling over the specified number of MCSA steps, such that Ti attains values less than ~0.03 only towards the end of all the MCSA steps, Nsteps. This avoids getting trapped in local minima, a phenomenon known as simulated quenching. The current implementation also determines the initial annealing temperature, Tstart , using average of first five RMSE values of the given system (Eq. 2).
| (Eq. 2a) |
| (Eq. 2b) |
The penalty function for use in the Metropolis criteria in the MCSA algorithm is the RMSE between QM and MM water interaction energies, Eint, dipole moments, di, or molecular polarizabilities, Pi. The RMSE value may be expressed as a weighted sum of individual RMSE values:
| (Eq. 3) |
where wint, wDip and wPol are weights given to RMSE values of water-interaction energy, dipole moment and molecular polarizability, respectively. The variable, n, is the number of interaction energy data points, and the summation, “i”, in dipole moment and polarizability goes over their individual components (dx, dy, dz, Pxx, Pyy, and Pzz ) as well as their total magnitude. The MCSA optimization of charge parameters in the additive FF may be performed on the basis of water-interaction energies or dipole moment or a combination of both. In the case of Drude FF, Alpha and Thole values can be optimized by targeting the individual components of QM dipole moment and molecular polarizability values. In the case of a combination of the two or more data types (interaction energy, dipole moment and polarizability), the individual RMSE values are weighted equally by the MCSA algorithm, although the capability to weight them differently is available.
During MCSA optimization the values of the electrostatic parameters are changed randomly in each step, resulting in a new RMSE value. The amount of change in the charges is restricted to 10% of the initial charge on the atoms, except for non-polar atoms not adjacent to heteroatoms and non-polar hydrogens which remain fixed by default. For Alpha and Thole values, the default allowed change is restricted to 10% and 100%, respectively, of the initial value obtained from the toppar stream file. The default percentage change in the above-mentioned electrostatic parameters may be modified as needed. Assignment of a percent change of zero effectively constrains the value of the electrostatic parameter to its initial value.
Performance of the current algorithm in fitting atomic charges of model compound 2c is shown in Figure 4a. A total of 5000 MCSA steps was requested with Tstart = 10 to fit to QM interaction energy data of all the non-duplicate donor-acceptor atoms. The slow decay of Tstart yields smooth convergence of the RMSE, where acceptance of uphill moves is initially high. As the total number of MC cycles increases the extent and number of the unfavorable moves decreases in accord with the decreased temperature. Convergence was attained in approximately 3200 steps. If the RMSE remains unchanged for 100 consecutive steps, it is considered to have converged to the best possible value for given initial conditions. Further improvement in the MM interaction energies was achieved by re-optimizing the optimized charges for an additional 600 steps (not shown). The initial (from CGenFF) and final set of MM interaction energies and distances can be observed in Table 1 against their QM analogs. A Drude analog of model compound 2c was created using the converter module in ObtainCGenFF tab for the purpose of demonstrating the MM Alpha and Thole factor optimization targeting the polarizability with the Drude FF (Table S7 of the supporting information). As shown in Figure 4b, a total of 5000 MCSA steps were requested with Tstart = 10, to fit to QM dipole moment and molecular polarizability data, with convergence achieved after 4000 steps. It is evident from Table 2 that the molecular polarizability values match much better with their QM analogs than those obtained using initial set of parameters leading to an overall decrease in the RMSE.
Figure 4.
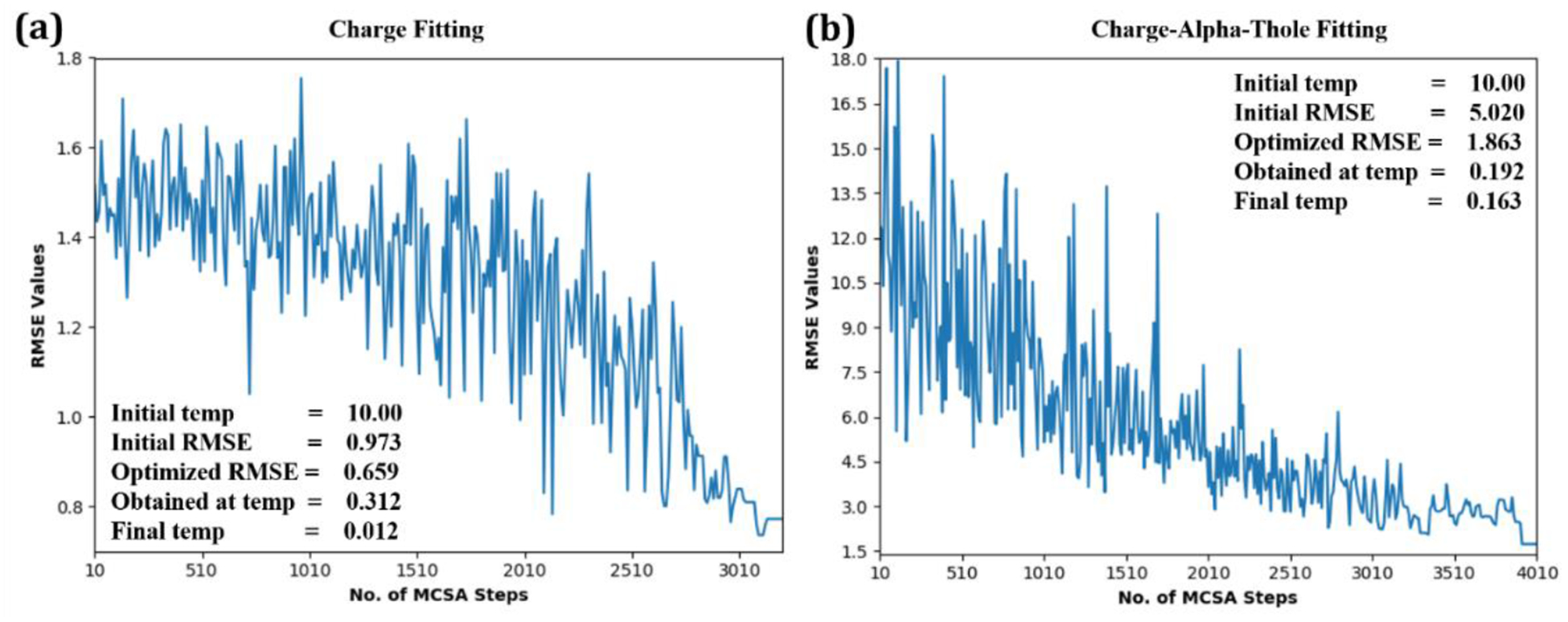
Plot of RMSE (averaged over every 10 steps) as a function of the number of MCSA steps between (a) QM and MM water-interaction values with the additive FF and (b) QM and MM dipole-polarizability values with the Drude FF for model compound 2c (Figure 2).
Table 1.
QM and MM Water Interaction Energies before and after MCSA fitting. E denotes energy and D denotes distance of the water molecule closest atom to the donor or acceptor atom in the molecule. See figure 3c for orientation of water molecule relative to their host atoms.
| Type | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| O1_WAT | −5.61 | −5.87 | −5.66 | −0.26 | −0.05 | 2.10 | 1.83 | 1.81 | −0.27 | −0.29 |
| O2_WAT | −4.37 | −3.80 | −4.18 | 0.57 | 0.18 | 2.12 | 1.86 | 1.83 | −0.26 | −0.29 |
| N1_WAT | −0.84 | −1.96 | −1.60 | −1.12 | −0.76 | 3.99 | 3.42 | 3.5 | −0.57 | −0.49 |
| H1_WAT | −2.02 | −2.25 | −1.08 | −0.22 | 0.94 | 3.34 | 3.12 | 3.29 | −0.22 | −0.05 |
| N2_WAT | −3.73 | −2.55 | −4.02 | 1.18 | −0.29 | 2.27 | 2.05 | 1.98 | −0.22 | −0.29 |
| H5_WAT | −6.50 | −8.11 | −6.75 | −1.61 | −0.25 | 2.02 | 1.80 | 1.84 | −0.22 | −0.18 |
| RMSE | 0.97 | 0.52 |
Table 2.
QM and MM Dipole and Molecular Polarizability values before and after applying MCSA fitting.
| Data Type | QM Values | MMinit Values | MMopt Values | Δ(MMinit - QM) | Δ(MMopt - QM) |
|---|---|---|---|---|---|
| Dipx | 7.444 | −0.565 | 5.527 | −8.008 | −1.916 |
| Dipy | 0.771 | −1.297 | −1.010 | −2.069 | −1.781 |
| Dipz | −1.234 | 3.766 | 3.190 | 5.000 | 4.424 |
| Diptot | 7.585 | 4.023 | 6.461 | −3.562 | −1.124 |
| Polxx | 17.532 | 13.489 | 17.486 | −4.042 | −0.046 |
| Polyy | 15.900 | 10.544 | 15.675 | −5.356 | −0.225 |
| Polzz | 14.215 | 9.034 | 14.054 | −5.181 | −0.161 |
| Poltot | 15.882 | 11.023 | 15.738 | −4.860 | −0.144 |
| RMSE | 5.020 | 1.863 |
Lennard-Jones and NBThole Parameters
LJ parameters are typically optimized targeting condensed phase properties such as pure solvent heats of vaporization and densities or crystal heats of sublimation and unit cell geometries. The capabilities to perform such optimizations are not currently supported by FFParam, with the corresponding LJ parameters being directly transferred from the atom type already available in CGenFF or the Drude FF. The one exception to this is the potential to optimize atom pair-specific LJ parameters based on model compound-water interactions. Performing this would require the specific parameter, in the form of an NBFIX, be manually added to the toppar stream file followed by manual adjustments using FFParam’s text editing capabilities. Similar are the availability of through-space nonbond Thole scale factors (NBTHOLE) between specific atoms in the Drude FF.39 These again can be optimized targeting specific water-model compound interactions. While it is anticipated that the capability to optimized pair-specific LJ and NBTHOLE parameters will be rarely used in the context of small model compounds, its availability is of worth noting given their important contribution to the Drude FF.17 Future extensions of FFParam will be designed to automate the optimization of the LJ parameters as well.
Parametrization of Bonded Parameters
Bonded parameters (bond, angle and dihedral parameters) and molecular symmetry dominate the geometrical and conformational properties of a molecule. In both CGenFF and the Drude FF once the atom types are assigned, bonded parameters are allocated. If a bonded parameter does not exist in the parent FF, the value of the parameter is assigned from existing bonded parameter for which the atom types have the closest analogy. Similar to charge parameters, bonded parameters are assigned penalty values reflecting the analogy of the atom types in that specific parameters with those of the existing parameters40,41. This allows for initial identification of parameters for optimization. Additional prioritization of parameters can be made based on the difference between the QM and MM data. The force constants and equilibrium values for bond and angle parameters are optimized by fitting MM and QM PES of selected bonds and angles. While, in the case of dihedrals, force constants, phase and multiplicities are optimized to minimize the difference between the MM and QM dihedral PES. The use of PES is convenient as it allows for individual degrees of freedom associated with specific parameters to be investigated. In FFParam, this approach replaces vibrational spectra as target data, whose use is complicated by non-unique nature of the assignment of normal modes.42
Drop-down menus in FFParam-GUI allow for rapid selection of the targeted bond, angle or dihedral. FFParam-GUI assigns a default range and step-size for the QM PES, but users can change the suggested values as required. As mentioned above, the QM input file for relaxed PES of the chosen internal coordinate is created in Gaussian or Psi4 format. The QM calculation yields energies of a range of geometries at specified values of the selected internal coordinate. An analogous MM potential energy scan is performed on these locally optimized QM geometries with the targeted internal coordinate restrained. FFParam plotting capabilities can be utilized for visual comparison of MM and QM PES. In addition, the initial and final RMSE between the MM and QM relative energies is reported.
Manual fitting of bond and angle parameters is relatively simple, as they can easily be fitted to the QM PES by changing the equilibrium value and force constants which control the minimum values and curvature of the MM PES, respectively. Fitting of dihedral parameters can be achieved by modifying force constant, multiplicity and phase of the targeted parameter. As the dihedral parameters are treated as a Fourier series, this process includes the addition or removal of terms with selected multiplicities, as discussed in more detail below. While manual fitting of bonded parameters is accessible in FFParam, this procedure may be time consuming, especially in the case of dihedral parameters.
Automated Fitting of Bonded Parameters
Automation of the fitting bonded parameters in FFParam relies on an external program, LSFITPAR.43 This program applies a least square fitting approach wherein harmonic restraints are applied on the existing parameters to fit to the QM data. The novel fitting procedure implemented in LSFITPAR is capable of producing robust parameters via a non-iterative procedure, with minimal impact on well-behaved parameters. Despite of its robustness, use of this program has been limited mainly because of the effort required to generate the initial data and the input files. For example, to fit a given dihedral parameter, the MM PES needs to be generated in the presence of all the FF terms except the parameter corresponding to the dihedral being fitted, whose force constants are set to zero. In addition, LSFITPAR can simultaneously fit more than one bonded parameter, by providing QM target data for additional bonds, angles or dihedrals that may be generated in a multi-dimensional PES. These surfaces then need to be combined in the exact order for both QM and MM with headers and other information written to each file for the program. To facilitate the use of LSFITPAR, FFParam provides easy to use options for creating the initial set of QM and MM data as well as creating the input file containing a minimal set of arguments required to run the fitting program. The path to the LSFITPAR executable may be set using the Setting pull-down menu allowing execution of the program directly from FFParam. Once the optimization is complete, the optimized parameters from LSFITPAR need to be transferred to the toppar stream file to validate their performance in the context of the full energy function. This step is required as LSFITPAR performs the optimization by simply altering the energy contribution from the parameter being optimized to the total potential energy that is compared to the target QM data. Accordingly, inserting the optimized parameters into the toppar stream file and recalculating the MM PES using the full force field is required to validate the new parameters. At this step it is useful to check the values of the actual parameters to assure that they are consistent with similar values in the FF.
Optimization of the dihedral parameters requires additional care. The parameter for each dihedral may be treated as a Fourier series that is essentially a sum of contributions from terms with multiplicities ranging from 1 to 6. By default, FFParam includes the multiplicities initially assigned to the dihedral by the CGenFF program. However, if the quality of the optimized parameters from LSFITPAR are not satisfactory i.e. Plot tool displays large difference between MM and QM PES, then the user can gradually modify the multiplicities included for the fitting and repeat the optimization step using LSFITPAR. Multiplicities 1, 2 and 3 should initially be used, possibly supplemented with a 6-fold term, while 4 and 5-fold terms are typically not used, though they may be added if deemed necessary. Once a satisfactory fit is achieved, the resulting force constants for all the multiplicities should be reexamined to identify those approaching values of zero. Such multiplicities should then be removed and LSFITPAR fitting should be repeated. Alternatively, if large force constants are obtained for multiple terms (eg. > 5 kcal/mol), then contributions from different multiplicities may be cancelling each other’s effect. After removing redundant multiplicity terms, refitting should be performed with minimal number of multiplicities that can accurately reproduce the QM PES. This procedure avoids overfitting of the dihedral parameters, yielding parameters that are typically more transferable to similar molecules. Multiple cycles of refitting makes fitting of bonded-parameter relatively less automated than electrostatic parameter fitting, which will be improved in future releases.To exemplify the optimization procedure an exercise was carried out for parametrization of bonded parameters of model compound 2c, details of which are presented in the supporting information. Figure 5 demonstrates PES of different dihedrals in the model compound obtained from QM and MM calculations, with the concerned dihedral highlighted in green in the 2D structure of the molecule. The X-axis represents various dihedral values involved in the scan, while the Y-axis shows QM and MM PES relative potential energy values (note the different energy scales). The large deviation between QM and initial MM PES indicates the need to revisit the CGenFF obtained parameters. For all the dihedrals shown in Figure 5, few rounds of optimization using LSFITPAR, starting from CGenFF assigned dihedral parameters, yields good agreement with QM target data. The optimized MM PES in Figure 5 are those obtained once the improved parameters are added to the toppar stream file and the full MM PES is recalculated.
Figure 5.
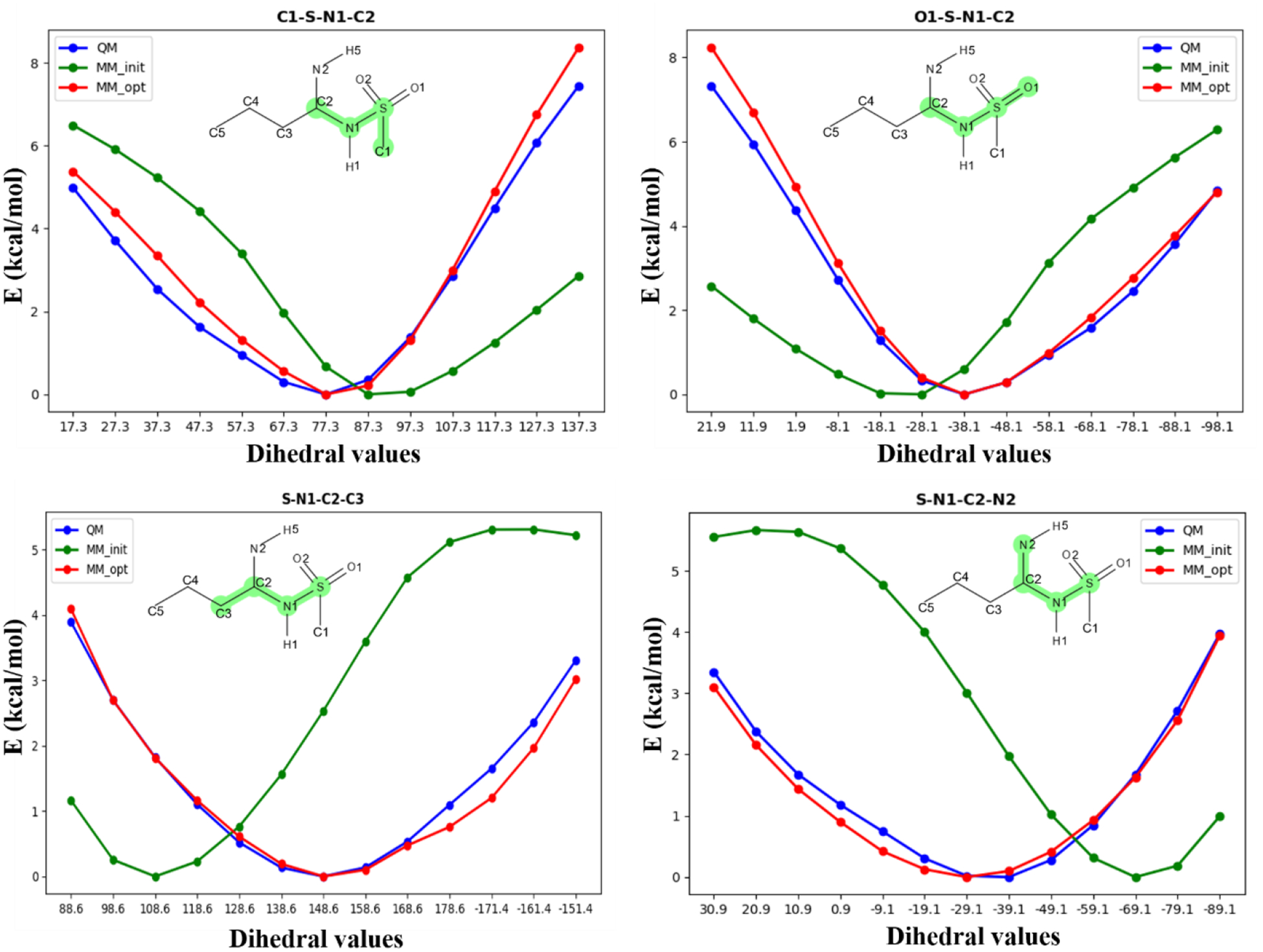
Plot of QM and PES against dihedral values for four different dihedrals, highlighted within the figure, for model compound 2c. Blue line represents QM data points, green represents the initial MM data points from CGenFF obtained dihedral parameters, and red represents MM data points obtained after fitting the dihedral parameters.
Conclusions
FFParam has been developed as a standalone python package designed for facilitating the parametrization of the CHARMM additive and polarizable Drude force fields. The program includes a graphical user interface (GUI) created using Qt libraries and is thus cross-platform compatible. The required QM and MM calculations are performed during parameter optimization. QM calculations may be performed using either Gaussian or Psi4, while the CHARMM or OpenMM packages may be used for the MM calculations. Psi4 and OpenMM offer the advantage of being open source that are accessible as python libraries, making FFParam completely independent of any external compiled software. Implementation of MCSA-based automated charge, alpha and Thole scale factor parameter fitting allows for improving electrostatic modeling. For the bonded parameters the capabilities of the LSFITPAR program allow for robust automated fitting, a process greatly facilitated by the input capabilities of FFParam. Thus, the strength of FFParam lies in the range of core capabilities that provide almost all the features required during a typical small molecule parametrization procedure, shielding the user from many of the labor-intensive steps traditionally present in FF optimization. The current package is expected to be useful to both expert and non-expert users in achieving high quality CHARMM additive and polarizable Drude parameters for the molecules required as part of their ongoing research efforts. The FFParam program and related tutorial may be obtained from the MacKerell laboratory website at http://mackerell.umaryland.edu/software.shtml.
Supplementary Material
Acknowledgements
This work was supported by National Institutes of Health grant GM131710. The University of Maryland Computer-Aided Drug Design Center is acknowledged for its generous allocations of computer time. Our lab members and colleagues, Dr. Abhishek Kognole, Dr. Asaminew Aytenfisu, Dr. Saad Raza, Ms. Payal Chatterjee, Dr. Mattia Turchi, and Dr. Miroslava Nedyalkova are acknowledged for testing FFParam package for different molecular systems of interest.
Footnotes
More details of the parameter optimization process and the toppar stream file containing topologies and parameters of test model compounds can be found in the Supporting Information.
Conflict of Interest
ADM Jr. is cofounder and CSO of SilcsBio LLC.
References
- 1.Brooks BR; Brooks CL 3rd; Mackerell AD Jr.; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M J Comput Chem 2009, 30(10), 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Case DA; Cheatham TE 3rd; Darden T; Gohlke H; Luo R; Merz KM Jr.; Onufriev A; Simmerling C; Wang B; Woods RJ J Comput Chem 2005, 26(16), 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jorgensen WL; Maxwell DS; Tirado-Rives J Journal of the American Chemical Society 1996, 118(45), 11225–11236. [Google Scholar]
- 4.Van Der Spoel D; Lindahl E; Hess B; Groenhof G; Mark AE; Berendsen HJ J Comput Chem 2005, 26(16), 1701–1718. [DOI] [PubMed] [Google Scholar]
- 5.Christen M; Hunenberger PH; Bakowies D; Baron R; Burgi R; Geerke DP; Heinz TN; Kastenholz MA; Krautler V; Oostenbrink C; Peter C; Trzesniak D; van Gunsteren WF J Comput Chem 2005, 26(16), 1719–1751. [DOI] [PubMed] [Google Scholar]
- 6.Vanommeslaeghe K; MacKerell AD Jr. J Chem Inf Model 2012, 52(12), 3144–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dodda LS; Cabeza de Vaca I; Tirado-Rives J; Jorgensen WL Nucleic Acids Research 2017, 45(W1), W331–W336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sousa da Silva AW; Vranken WF BMC Res Notes 2012, 5, 367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ozpinar GA; Peukert W; Clark T J Mol Model 2010, 16(9), 1427–1440. [DOI] [PubMed] [Google Scholar]
- 10.Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA J Comput Chem 2004, 25(9), 1157–1174. [DOI] [PubMed] [Google Scholar]
- 11.Vassetti D; Pagliai M; Procacci P Journal of Chemical Theory and Computation 2019, 15(3), 1983–1995. [DOI] [PubMed] [Google Scholar]
- 12.Mayne CG; Saam J; Schulten K; Tajkhorshid E; Gumbart JC J Comput Chem 2013, 34(32), 2757–2770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Humphrey W; Dalke A; Schulten K Journal of Molecular Graphics 1996, 14(1), 33–38. [DOI] [PubMed] [Google Scholar]
- 14.Phillips JC; Braun R; Wang W; Gumbart J; Tajkhorshid E; Villa E; Chipot C; Skeel RD; Kale L; Schulten K J Comput Chem 2005, 26(16), 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Frisch MJ; Trucks GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Scalmani G; Barone V; Petersson GA; Nakatsuji H; Li X; Caricato M; Marenich AV; Bloino J; Janesko BG; Gomperts R; Mennucci B; Hratchian HP; Ortiz JV; Izmaylov AF; Sonnenberg JL; Williams; Ding F; Lipparini F; Egidi F; Goings J; Peng B; Petrone A; Henderson T; Ranasinghe D; Zakrzewski VG; Gao J; Rega N; Zheng G; Liang W; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Vreven T; Throssell K; Montgomery JA Jr.; Peralta JE; Ogliaro F; Bearpark MJ; Heyd JJ; Brothers EN; Kudin KN; Staroverov VN; Keith TA; Kobayashi R; Normand J; Raghavachari K; Rendell AP; Burant JC; Iyengar SS; Tomasi J; Cossi M; Millam JM; Klene M; Adamo C; Cammi R; Ochterski JW; Martin RL; Morokuma K; Farkas O; Foresman JB; Fox DJ: Wallingford, CT, 2016. [Google Scholar]
- 16.Baker CM; Anisimov VM; MacKerell AD Jr. J Phys Chem B 2011, 115(3), 580–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Baker CM; Lopes PE; Zhu X; Roux B; MacKerell AD Jr. J Chem Theory Comput 2010, 6(4), 1181–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Harder E; Anisimov VM; Whitfield T; MacKerell AD Jr.; Roux B J Phys Chem B 2008, 112, 3509–3521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Harder M; Kuhn B; Diederich F ChemMedChem 2013, 8(3), 397–404. [DOI] [PubMed] [Google Scholar]
- 20.Harder E; Anisimov VM; Vorobyov IV; Lopes PEM; Noskov S; MacKerell AD Jr.; Roux B J Chem Theory Comp 2006, 2, 1587–1597. [DOI] [PubMed] [Google Scholar]
- 21.Lemkul JA; MacKerell AD The Journal of Physical Chemistry B 2016, 120(44), 11436–11448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lin FY; MacKerell AD Jr. J Chem Inf Model 2019, 59(1), 215–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Parrish RM; Burns LA; Smith DGA; Simmonett AC; DePrince AE; Hohenstein EG; Bozkaya U; Sokolov AY; Di Remigio R; Richard RM; Gonthier JF; James AM; McAlexander HR; Kumar A; Saitow M; Wang X; Pritchard BP; Verma P; Schaefer HF; Patkowski K; King RA; Valeev EF; Evangelista FA; Turney JM; Crawford TD; Sherrill CD Journal of Chemical Theory and Computation 2017, 13(7), 3185–3197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Brooks BR; Brooks CL 3rd; Mackerell AD Jr.; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M Journal of computational chemistry 2009, 30(10), 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Eastman P; Swails J; Chodera JD; McGibbon RT; Zhao Y; Beauchamp KA; Wang L-P; Simmonett AC; Harrigan MP; Stern CD; Wiewiora RP; Brooks BR; Pande VS PLOS Computational Biology 2017, 13(7), e1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Guvench O; MacKerell AD Jr. Journal of molecular modeling 2008, 14(8), 667–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vanommeslaeghe K; Yang M; MacKerell AD Jr. J Comput Chem 2015, 36(14), 1083–1101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hunter JD Computing in Science & Engineering 2007, 9(3), 90–95. [Google Scholar]
- 29.McGuire RF; Momany FA; Scheraga HA The Journal of Physical Chemistry 1972, 76(3), 375–393. [DOI] [PubMed] [Google Scholar]
- 30.Anisimov VM; Lamoureux G; Vorobyov IV; Huang N; Roux B; MacKerell AD J Chem Theory Comput 2005, 1(1), 153–168. [DOI] [PubMed] [Google Scholar]
- 31.Sterling T; Irwin JJ Journal of chemical information and modeling 2015, 55(11), 2324–2337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vanommeslaeghe K; Hatcher E; Acharya C; Kundu S; Zhong S; Shim J; Darian E; Guvench O; Lopes P; Vorobyov I; Mackerell AD Jr. J Comp Chem 2010, 31(4), 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lin F-Y; MacKerell AD Journal of Chemical Theory and Computation 2018, 14(2), 1083–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lemkul JA; MacKerell AD Jr J Comp Chem 2018, 39, 2624–2646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gillespie RJ Journal of Chemical Education 2004, 81(3), 298. [Google Scholar]
- 36.MacKerell AD Jr. J Comp Chem 2004, 25, 1584–1604. [DOI] [PubMed] [Google Scholar]
- 37.Thole BT Chem Phys 1981, 59, 341–350. [Google Scholar]
- 38.Heid E; Szabadi A; Schroder C Phys Chem Chem Phys 2018, 20, 10992–10996. [DOI] [PubMed] [Google Scholar]
- 39.Luo Y; Jiang W; Yu H; MacKerell AD Jr.; Roux B Faraday Discussions 2013, 160, 135–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Vanommeslaeghe K; MacKerell AD Jr. J Chem Inf Model 2012, 52(12), 3144–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Vanommeslaeghe K; Raman EP; MacKerell AD Jr. J Chem Inf Model 2012, 52(12), 3155–3168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pulay P; Fogarasi G; Pang F; Boggs JE J Am Chem Soc 1979, 101, 2550–2560. [Google Scholar]
- 43.Vanommeslaeghe K; MacKerell AD Jr. J Comp Chem 2015, 36 1083–1101. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


