Six-dimensional quantitative DCE MR Multitasking of the entire abdomen: Method and application to pancreatic ductal adenocarcinoma

Abstract

Purpose:

To develop a quantitative DCE MRI technique enabling entire-abdomen coverage, free-breathing acquisition, 1-second temporal resolution, and T₁-based quantification of contrast agent concentration and kinetic modeling for the characterization of pancreatic ductal adenocarcinoma (PDAC).

Methods:

Segmented FLASH readouts following saturation-recovery preparation with randomized 3D Cartesian undersampling was used for incoherent data acquisition. MR Multitasking was used to reconstruct 6-dimensional images with 3 spatial dimensions, 1 T₁ recovery dimension for dynamic T₁ quantification, 1 respiratory dimension to resolve respiratory motion, and 1 DCE time dimension to capture the contrast kinetics. Sixteen healthy subjects and 14 patients with pathologically confirmed PDAC were recruited for the in vivo studies, and kinetic parameters v_p, K^trans, v_e, and K_ep were evaluated for each subject. Intersession repeatability of Multitasking DCE was assessed in 8 repeat healthy subjects. One-way unbalanced analysis of variance (ANOVA) was performed between control and patient groups.

Results:

In vivo studies demonstrated that v_p, K^trans, and K_ep of PDAC were significantly lower compared with nontumoral regions in the patient group (P = .002,.003, .004, respectively) and normal pancreas in the control group (P = .011, <.001, <.001, respectively), while v_e was significantly higher than nontumoral regions (P < .001) and healthy pancreas (P < .001). The kinetic parameters showed good in vivo repeatability (interclass correlation coefficient: v_p, 0.95; K^trans, 0.98; v_e, 0.96; K_ep, 0.99).

Conclusion:

The proposed Multitasking DCE is promising for the quantification of vascular properties of PDAC. Quantitative DCE parameters were repeatable in vivo and showed significant differences between normal pancreas and both tumor and nontumoral regions in patients with PDAC.

1 |. INTRODUCTION

Pancreatic cancer is the third leading cause of cancer-related deaths in the United States.^1,2 Pancreatic ductal adenocarcinoma (PDAC) represents 95% of malignant pancreatic cancers.³ It has an unusual microenvironment characterized by a highly desmoplastic stroma encompassing up to 90% of the tumor; regions with hypoxic tissue; interstitial hypertension; and heterogeneous vascularization, including low microvascular density (MVD) and reduced blood flow in the lesion area and high MVD in the surrounding area, which is inherently resistant to treatment.⁴ Due to technical challenges for early detection,^5–8 approximately 60% of patients at the first diagnosis are deemed unable to receive macroscopic complete tumor resection, which remains the only curative treatment option for PDAC.⁹ Those patients who are ineligible for surgery will receive neoadjuvant chemotherapy or radiotherapy. However, the lack of effective approaches for early assessment of response to these therapies prevents optimization of the treatment design for each individual. These reasons contribute to a dismal 5-year survival rate of 8%.³

Because of its superior soft-tissue contrast, MRI plays a key role in the detection, staging, and treatment management of PDAC.^10–12 The clinical MRI protocol for PDAC characterization consists of T₁-weighted (T1W) gradient-echo (GRE) imaging, T₂-weighted (T2W) turbo spin-echo (TSE) imaging, diffusion-weighted imaging (DWI), and gadolinium (Gd)-enhanced multiphasic T1W GRE imaging at pre-contrast phase, arterial phase (20–40 seconds after the start of injection), venous phase (45–65 seconds), and equilibrium phase (3–5 minutes).^5,10 Gd-enhanced multiphasic T1W imaging has shown great tumor delineation and high sensitivity in the detection of PDAC. However, it is a qualitative technique that is subject to coil positioning, sequence parameters, and interobserver and interscanner variability.¹³ In addition, 4 phases are not sufficient to assess the vascular features of PDAC lesions.¹⁴

Quantitative DCE MRI has been proposed to evaluate the enhancement pattern and vascular properties of tissues. DCE MRI involves the fast acquisition of a series of T1W images at high temporal resolution during Gd-based contrast agent (CA) administration. Dynamic signal enhancement curves are then extracted per pixel or from regions of interest (ROIs) and analyzed with an appropriate pharmacokinetic model to estimate several kinetic parameters, including fractional plasma volume (v_p), transfer constant (K^trans), fractional extravascular extracellular volume (v_e), and rate constant (K_ep). Several investigations have shown that K^trans and v_e are positively correlated with MVD and fibrosis in PDAC, respectively.^4,15 Other studies have shown that quantitative DCE MRI can characterize PDAC and monitor treatment response.^16,17

Despite these encouraging results, DCE MRI of PDAC continues to face demanding technical challenges.^15–17 First, imaging of the pancreas is subject to respiratory motion artifacts, which can significantly degrade image quality and affect kinetic quantification. To alleviate this problem, respiratory-triggered acquisition, sophisticated motion registration schemes,^18,19 and/or patient cooperation such as prone positioning, shallow breathing, or breath-holding are usually required. Second, there is typically a trade-off among spatial resolution, temporal resolution, and spatial coverage. Third, most existing DCE techniques linearly transform the dynamic signal intensity from T1W MRI to estimate CA concentration for kinetic modeling. However, the nonlinearity between T1W MRI signal and CA concentration can introduce errors in the quantification of kinetic parameters, especially in tissues with high-contrast uptake such as blood.²⁰ Another approach is to nonlinearly calculate the CA concentration based on a separately acquired pre-contrast T₁ map and dynamic T1W signal, but this requires an additional scan and is subject to misregistration between separate imaging series.^21,22

In this work, we propose a novel DCE technique based on our newly developed MR Multitasking framework²³ to address the aforementioned limitations. This Multitasking DCE technique performs 6-dimensional (6D) quantitative imaging with 3 spatial dimensions, a saturation recovery dimension, a respiration dimension, and a DCE time dimension. It achieves respiratory motion–resolved, high-temporal-resolution T₁ quantification of the entire abdomen in a 10-minute free-breathing scan, followed by the derivation of CA concentration and kinetic modeling. To our knowledge, this is the first abdominal DCE MRI method that simultaneously allows for 3D true free-breathing acquisition, 1-second temporal resolution, and dynamic T₁ mapping.

2 |. METHODS

2.1 |. Sequence design

Three-dimensional segmented FLASH readouts following periodic nonselective saturation-recovery (SR) preparation were used to acquire data at various saturation recovery times for dynamic T₁ quantification.²⁴ Fat signal was suppressed using water excitation for the FLASH readouts. Images were acquired in a transversal orientation, covering the abdomen from the liver dome to the iliac crest. A 3D Cartesian trajectory with randomized Gaussian reordering in both phase (k_y) and partition (k_z) encoding was implemented to incoherently undersample k-space.²⁴ In the Multitasking framework, training data are usually acquired frequently at the center k-space line to capture the multidimensional dynamics and estimate the temporal basis functions.²³ In this work, the collection of 1 center k-space line was interleaved with the collection of 7 imaging lines, yielding a sampling period of 45 ms for the training data. The orientation of the center k-space line was modified to the superior–inferior direction (partition encoding direction, k_x = k_y = 0) for the improved capture of respiratory motion.

2.2 |. Image reconstruction

2.2.1 |. Multitasking image model

Our 6D quantitative DCE technique is based on the recently developed MR Multitasking framework,²³ which uses a low-rank tensor (LRT) image model to exploit the high correlation between images along multiple time dimensions,^25,26 vastly accelerating the acquisition. The LRT model is a multidimensional extension of low-rank matrix models,^27–30 which rely on the partial separability between spatial and temporal image dimensions to decrease the degrees of freedom and accelerate acquisition.

The abdominal DCE image is expressed as a 6D image a(x,τ,t_r,t_d), a function of 3 spatial dimensions (x=[x,y,z]^T) and 3 time dimensions (saturation recovery time τ, respiration motion t_r, and DCE time course t_d). The strong correlation between images along and across time dimensions induces a to be partially separable in the combination of space x=[x,y,z]^T, τ, t_r, and t_d:

$$a\left(\mathbf{x},\tau ,t_{\text{r}},t_{\text{d}}\right)=\sum _{\mathcal{l}=1}^L\sum _{m=1}^M\sum _{n=1}^N\sum _{p=1}^P{g}_{\mathcal{l}mnp}{u}_{\mathcal{l}}(\mathbf{x})v_m(\tau )w_n\left(t_{\text{r}}\right)q_p\left(t_{\text{d}}\right),$$ (1)

where u_𝓁(x) is the 𝓁th of L spatial coefficient maps; v_m(τ) is the mth of M saturation recovery basis functions; w_n(t_r) is the nth of N respiratory motion basis functions; q_p(t_d) is the pth of P DCE basis functions; g_𝓁mnp are the elements of the core tensor. This implies that the 4-way tensor $\mathcal{A},$ which has modes corresponding to voxel location x and each time dimension, τ, t_r and t_d, is low-rank. This low-rank tensor model can be expressed in matrix notation as

$${\mathbf{A}}_{(1)}=\mathbf{U}{\mathbf{G}}_{(1)}{(\mathbf{Q}\otimes \mathbf{W}\otimes \mathbf{V})}^T,$$ (2)

where the columns of U, V, W, and Q contain the basis functions for each dimension; ⊗ denotes the Kronecker product; the subscript (i) denotes the mode-i flattening of the tensor.³¹ The separation of the spatial and temporal factors decouples the tradeoff between spatial and temporal resolution, providing an avenue for accelerated acquisition. The reconstruction strategy for recovering the undersampled low-rank tensor used in this work is a factored, explicit low-rank strategy, which reconstructs the image tensor by sequentially determining each of its factors.²³

2.2.2 |. Single-time-dimension reconstruction

To allow respiratory motion identification, dynamic images with a single time dimension were first generated using an explicit low-rank matrix imaging strategy, with 1 temporal dimension t (elapsed time) representing a mixture of saturation recovery times, respiratory states, and dynamic contrast changes:

$$a(\mathbf{x},t)=\sum _{\mathcal{l}=1}^L{u}_{\text{rt},\mathcal{l}}(\mathbf{x}){\varphi }_{\text{rt},\mathcal{l}}(t),$$ (3)

where the single-time-dimension temporal basis function ${\left\{{\varphi }_{\text{rt},\mathcal{l}}(t)\right\}}_{\mathcal{l}=1}^L$ was estimated from the singular value decomposition (SVD) of the training data. Following this, the spatial coefficients ${\left\{u_{\text{rt},\mathcal{l}}(\mathbf{x})\right\}}_{\mathcal{l}=1}^L$ were recovered by fitting the ${\left\{{\varphi }_{\text{rt},\mathcal{l}}(t)\right\}}_{\mathcal{l}=1}^L$ the collected imaging data using a conjugate gradient least-squares algorithm.²⁷

2.2.3 |. Respiratory-motion compensation

The respiratory motion was binned into 6 states, as specified in the Supporting Information Section A and Supporting Information Figure S1. To enhance the correlation between images across different respiratory bins with minimal increase in the computational complexity, interbin translational registration was applied to the k-space data. To estimate translational motion, a template image of each bin was first obtained by averaging the single-time-dimension images within each respiratory state. The template image from end-expiration was set to be the reference, denoted as a_ref; the template images from the other 5 bins are denoted as a_i, i∈1, 2,…, 5. The translation vector b_i between the moving bin i and the reference was estimated as

$${\widehat{b}}_i=\arg \underset{b_i}{\max }Mt\left({\mathbf{F}}^{-1}\left(\mathbf{P}\left(b_i\right)°\left(\mathbf{F}W{\mathbf{a}}_i\right)\right),{\mathbf{a}}_{\text{ref}}\right),$$ (4)

with spatial Fourier transform F, a weighting window W that emphasizes the signal from moving organs of interest and reduces the signal from surrounding static muscle, linear phase modulator P(b_i) (the k-space operation equivalent to image-domain translation), and mutual information metric Mt(⋅,⋅). The k-space data were then directly compensated by applying P(b_i) to all k-space lines corresponding to the ith respiratory bin.

We note that the purpose of respiratory-motion compensation was not to erase the difference of images between respiratory bins, but to increase the image correlation by moving them to a similar location, thereby improving image quality.³² The superiority of respiratory-motion compensation was tested by comparing the SNR in the pancreas and sharpness of the pancreas boundary with and without compensation using a one-tailed t-test. The sharpness of the boundary was estimated using the rise-distance method.³³

2.2.4 |. Tensor subspace estimation

Following respiratory-motion identification and compensation, the next stage is to recover the multidimensional temporal factor $\mathbf{\Phi }={\mathbf{G}}_{(1)}{(\mathbf{Q}\otimes \mathbf{W}\otimes \mathbf{V})}^T$ from the training data. This was divided into 2 steps: (1) predetermine the T₁ recovery basis functions in V from a dictionary of SR signal curves; and (2) estimate the respiratory basis functions in W, DCE basis functions in Q, and the core tensor $\mathcal{G}$ from the training data.

In the first step, a dictionary of feasible SR signal curves was generated ahead of time for a range of T₁ values and B₁ inhomogeneities based on the Bloch equations.²⁴ The dictionary consisted of 101 T₁ values logarithmically spaced from 100 ms to 3000 ms, 17 flip angles from 6° to 14° in half-degree increments, and 21 saturation pulse angles linearly spaced from 60° to 120°. The T₁ recovery factor V was directly extracted from the SVD of this dictionary.

In the second step, the training data were reshaped into a 4-way tensor D_tr with 1 k-space readout mode and 3 temporal modes: τ, t_r, and t_d. The training data were not available from every combination of respiratory state, saturation recovery time, and DCE phase, so the training data tensor was highly undersampled. In addition, a motion-removal scheme described in our previous work²⁴ was implemented to further remove outlier readouts corresponding to abrupt motion. The undersampled training data tensor was completed by solving

$$\begin{array}{l}{\widehat{D}}_{\text{tr}}=\arg \underset{{\mathbf{D}}_{\text{tr},(2)}\mathrm{\in range}(\mathbf{v})}{\min }{\Vert {\mathbf{d}}_{\text{tr}}-M\left({\mathcal{D}}_{\text{tr}}\right)\Vert }_2^2\\ +\lambda \sum _{i=1,3,4}{\Vert {\mathbf{D}}_{\text{tr},(i)}\Vert }_{*}+R\left({\mathcal{D}}_{\text{tr}}\right),\end{array}$$ (5)

where d_tr is the collected training data; M(⋅) applies the training data sampling pattern; ‖⋅‖∗ denotes the nuclear norm; D_tr,(i) denotes the mode-i matricization of the tensor $D_{\text{tr}};R(\cdot )$ is an optional additional regularization functional, which in this work was chosen as temporal total variation (TV) along the respiratory and DCE dimensions: $R\left({\mathcal{D}}_{\text{tr}}\right)={\lambda }_3{\Vert \nabla {\mathbf{D}}_{\text{tr},(3)}\Vert }_1+{\lambda }_4{\Vert \nabla {\mathbf{D}}_{\text{tr},(4)}\Vert }_1,$ where ∇ is the finite-difference operator. With the completed Dtr, the core-tensor $\mathcal{G}.$ respiratory basis functions W, and DCE time-course basis functions Q can be extracted using the higher-order SVD (HOSVD),³⁴ which provides $\mathbf{\Phi }={\mathbf{G}}_{(1)}{(\mathbf{Q}\otimes \mathbf{W}\otimes \mathbf{V})}^T.$

2.2.5 |. Spatial coefficient recovery

With a known temporal subspace spanned by the rows of $\mathbf{\Phi },$ the spatial factor U can be recovered by solving the following optimization problem:

$$\widehat{\mathbf{U}}=\arg \underset{\mathbf{U}}{\min }\Vert \mathbf{d}-\text{Ω}(\mathbf{F}SU\text{Φ}){\Vert }_2^2+R(\mathbf{U}),$$ (6)

with acquired imaging data d, undersampling operator Ω, spatial Fourier transform F, coil sensitivity operator S, and an optional regularization functional R (⋅). In this work, we used an anisotropic spatial TV regularizer to integrate compressed sensing into the low-rank framework $R(\mathbf{U})=\lambda \sum _{\mathcal{l}}\left(\frac{1}{\Delta x}{\Vert {\nabla }_x\left\{u_{\mathcal{l}}(\mathbf{r})\right\}\Vert }_1+\frac{1}{\Delta y}{\Vert {\nabla }_y\left\{u_{\mathcal{l}}(\mathbf{r})\right\}\Vert }_1+\frac{1}{\Delta z}{\Vert {\nabla }_z\left\{u_{\mathcal{l}}(\mathbf{r})\right\}\Vert }_1\right),$ where, for example, Δx is the voxel width in x and ∇_x {⋅} is the finite-difference operator along. The final result of the reconstruction produces the 6D image with full T₁ recovery curves for every combination of the respiratory states and multiple DCE phases. The MATLAB (R2018a, MathWorks, Natick, MA) p-code for the reconstruction is available upon request.

2.3 |. Dynamic T₁ quantification and kinetic modeling

Pixelwise dynamic T₁ quantification was performed following image reconstruction. Here, signal intensity is a function of R₁ t_d = 1∕T₁ t_d (the relaxation rate at a specific DCE time point t_d), amplitude A, SR pulse efficiency parameter B, FLASH readout interval T_R, flip angle, and recovery time point n = 1, 2, …, N (N = 84 per SR period) such that τ = nT_R. The signal intensity at a given pixel is

$$\begin{array}{l}s\left(A,\alpha ,B,n,R_1\left(t_{\text{d}}\right)\right)\\ =A\frac{1-e^{-T_{\text{R}}\cdot R_1\left(t_{\text{d}}\right)}}{1-e^{-T_{\text{R}}\cdot R_1\left(t_{\text{d}}\right)}\cos \alpha }\left[1+(B-1){\left(e^{-T_{\text{R}}\cdot R_1\left(t_d\right)}\cos \alpha \right)}^n\right]\sin \alpha ,\end{array}$$ (7)

the signal intensity vector s for an entire SR period can be expressed as

$$\mathbf{s}\left(A,\alpha ,B,R_1\left(t_{\text{d}}\right)\right)={\left[s\left(A,\alpha ,B,1,R_1\left(t_{\text{d}}\right)\right),\dots ,s\left(A,\alpha ,B,N,R_1\left(t_{\text{d}}\right)\right)\right]}^T,$$ (8)

and the 2D dynamic signal matrix S representing all DCE time bins t_d from 0 to T_d is

$$\mathbf{S}\left(A,\alpha ,B,{\mathbf{r}}_1\right)=\left[\mathbf{s}\left(A,\alpha ,B,R_1(0)\right),\dots ,\mathbf{s}\left(A,\alpha ,B,R_1\left(T_{\text{d}}\right)\right)\right],$$ (9)

Where r₁ is the vector of R₁ values containing R₁(t_d), t_d = 0, 1, …, T_d, and where t_d = 0 represents the pre-contrast time point. For each pixel and respiratory state, the dynamic relaxation curve R₁(t_d), t_d = 0, 1, …, T_d was fitted from the reconstructed (τ, t_d)-space signal using lsqnonlin (nonlinear least-square solver) in MATLAB. According to the relaxivity, the dynamic contrast agent concentration curve Ct for each pixel was directly derived as

$$C_{\text{t}}\left(t_{\text{d}}\right)=\frac{R_1\left(t_{\text{d}}\right)-R_1(0)}{\gamma },$$ (10)

with the relaxivity rate being γ = 4.0 L · mmol⁻¹ ·s⁻¹ in this work.^35,36 Subsequently, the vascular properties were evaluated with the two-compartment extended Tofts model.³⁷ Details of the kinetic modeling are available in Supporting Information Section B. A computational simulation in Supporting Information Section C demonstrates the improved accuracy in kinetic parameter quantification resulting from the Multitasking T₁-mapping–based approach over a conventional linear approach.

2.4 |. Imaging experiments

2.4.1 |. Imaging protocol

All studies were performed on a 3T clinical MR scanner (Biograph mMR, Siemens Medical Solutions, Erlangen, Germany) with a 12-channel phase array surface coil. In the imaging session, a routine protocol was first acquired for pancreas delineation and tumor definition. It included 3D T1W volumetric interpolated breath-hold examination (VIBE) with Dixon fat suppression in axial orientation, multi-slice T2W half-Fourier acquisition single-shot turbo spin echo (HASTE) in axial and coronal orientations, and multi-slice single-shot (SS) EPI DWI. A 2D MOLLI³⁸ sequence in oblique planes covering as much PDAC tumor mass as possible was obtained as the reference for in vivo T₁ mapping. Following these sequences, the Multitasking DCE sequence was performed. The protocol was designed to cover the entire abdomen from the dome of the liver to the iliac crest. Each SR period was 500 ms, with saturation times from 5.6 ms to 470.4 ms with an increment of 5.6 ms for T₁ quantification. The SR period was repeated 1200 times in a scan of 10 minutes. The DCE bin duration was selected to be 1 second by combining 2 SR periods, striking a balance between temporal resolution and SNR.²⁴ Gd-based contrast agent (Gadavist, 0.1 mmol/kg; Bayer Schering Pharma, Berlin, Germany) was administrated intravenously 2 minutes into the scan at a rate of 2 mL/s, followed by a 20-mL saline flush at the same rate. Immediately at the end of this sequence, post-contrast MOLLI at the same slice location as pre-contrast MOLLI was collected. Detailed imaging parameters for the protocols are summarized in Table 1.

TABLE 1.

List of imaging parameters

Parameters	T1W VIBE	T2W HASTE	MOLLI	SS-EPI DWI	Multitasking DCE
Slice thickness (mm)	3	5	5	6	3
Slice resolution	50%	—	—	—	50%
Number of slices	72	86	1	60	120
Gap	—	1	—	1	—
TR (ms)	4.15	1000	280.56	4500	5.60
TE (ms)	1.39/2.65	99	1.12	47	2.45
Number of averages	1	1	1	6	1
FOV (mm2)	350 × 247	330 × 226	390 × 390	339 × 306	380 × 268
In-plane resolution (mm2)	1.2 × 1.2	1.3 × 1.3	2.0 × 2.0	2.0 × 2.3	1.2 × 1.2
Flip angle (º)	9	105	35	90	10

Abbreviations: HASTE, half-Fourier acquisition single-shot turbo spin echo; MOLLI, modified Look-Locker inversion recovery; SS-EPI, single-shot EPI; VIBE, volumetric interpolated breath-hold examination.

2.4.2 |. Phantom study

The phantom study was performed on the ISMRM/NIST MRI system phantom (model 130; High Precision Devices, Boulder, CO)³⁹ to validate the T₁ mapping accuracy of the proposed Multitasking DCE technique. The T₁ layer with T₁ varying from 50 ms to 2000 ms was selected for data analysis. As a reference, a standard 2D inversion-recovery spin-echo (IR-SE) sequence with TR = 10 000 ms and 7 different inversion times (23, 100, 400, 900, 1600, 2200, and 3000 ms) was also acquired at the center of the T₁ layer with parameters: FOV = 220 × 220 mm², in-plane spatial resolution = 1.2 mm, and slice thickness = 6 mm. Two experiments with the same protocols were conducted on 2 separate days to assess the intersession repeatability of T₁ measurements in Multitasking DCE.

2.4.3 |. In vivo study

The in vivo study was approved by the local institutional review board. Written informed consent was obtained from all participating subjects before scanning. The study population included both healthy subjects (as the control group) and patients with PDAC. Sixteen volunteers (8 females, age range, 23 to 60 years) without a history of pancreatic disease were recruited as the control group, 8 of whom were able to come back for a second scan with the same protocol on a different day (with at least 1 week apart from the first scan) for the assessment of intersession repeatability.

For the patient study, the inclusion criteria were the presence of pathologically confirmed PDAC and tolerance to MRI and Gd-based contrast agent. Patients who had previously undergone pancreatic surgery were excluded from the study. The final patient group included 14 patients (7 females, age range, 51 to 77 years). The mean size of the tumors, defined as the largest diameter in axial CT images according to RECIST 1.1 criteria, is 3.9 cm, ranging from 1.6 cm to 6.7 cm. The detailed size and location information of the tumors in the patient group are provided in Supporting Information Table S4. The previous clinical contrast-enhanced CT scans and diagnosis reports for all patients were also obtained for tumor definition.

2.5 |. Image analysis

Post-processing was performed off-line in MATLAB. The pancreas boundary of each subject was defined based on the T1W VIBE images from the same session. Dynamic T₁ fitting and kinetic modeling were performed on all slices involving the pancreas, for all subjects.

In the control group, the kinetic parameters v_p, K^trans, v_e, and K_ep obtained for each subject are the mean values of all voxels within the pancreas throughout multiple slices. For the patient group, the tumor boundary was identified by a radiologist (L.W.) with 11 years of experience in reading MR images for PDAC, by cross-referencing T1W VIBE, T2W HASTE, SS-EPI, and clinical contrast-enhanced CT images. The kinetic parameters for PDAC were the mean from all voxels within the tumor. The region of interest for the nontumoral area included all voxels in the pancreas but outside the tumor.

2.6 |. Statistical analysis

Statistical analysis was conducted in SPSS version 24 (IBM, Armonk, NY). The T₁ measurement agreement between the Multitasking DCE and reference methods for both phantom and in vivo studies was evaluated by the intraclass correlation coefficient (ICC) and paired t-tests. The intersession repeatability of the proposed technique was assessed on the repeated data from the 8 healthy volunteers who were scanned twice on separate days. Bland-Altman analysis, ICC, and coefficient of variation (CoV) of the 4 kinetic parameters v_p, K^trans, v_e, and K_ep were obtained.

A significance test using one-way unbalanced analysis of variance (ANOVA) was applied to identify the significant difference of each kinetic parameter obtained between (1) PDAC tumor mass and nontumoral pancreatic tissue in the patient group, (2) PDAC tumor mass in the patient group and normal pancreatic tissue in control group, and (3) nontumoral pancreatic tissue in the patient group and normal pancreatic tissue in control group. Holm-Bonferroni correction was also implemented to correct the familywise error in this multi-group test.

3 |. RESULTS

3.1 |. Phantom measurements

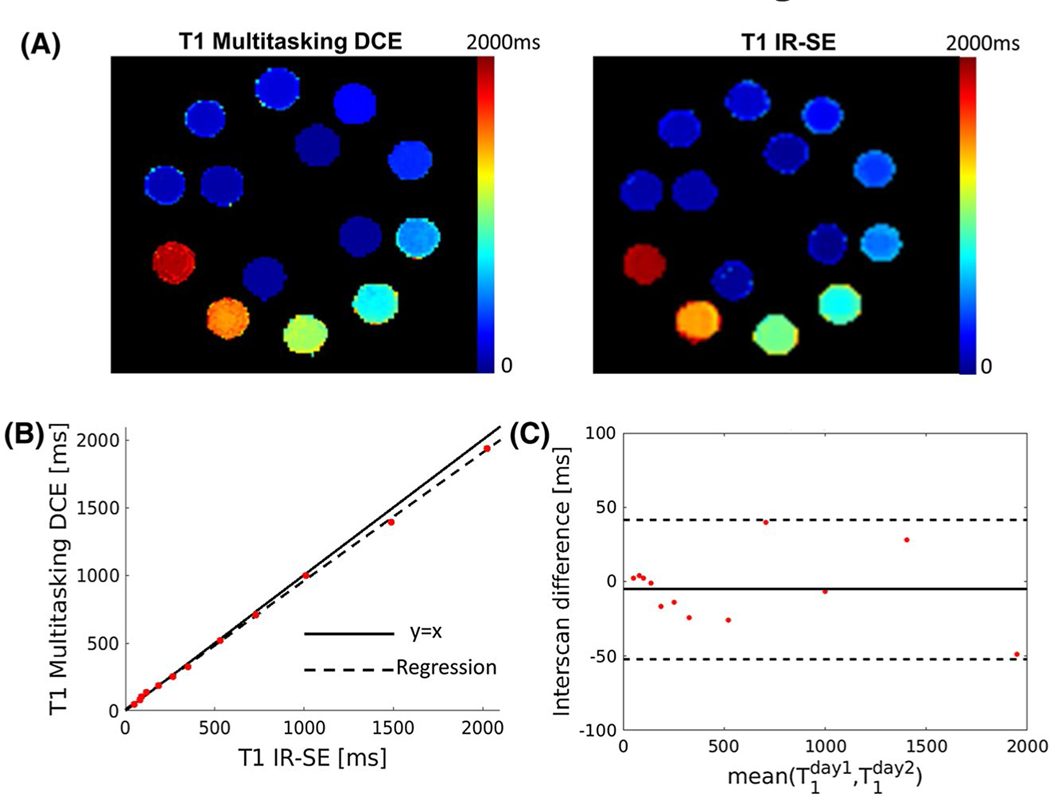
The color maps in Figure 1A display the T₁ maps from the Multitasking DCE and reference IR-SE sequence. Figure 1B shows the linear regression of the T₁ measurements between the 2 methods, indicating that the T₁ values from Multitasking DCE were in good agreement with reference values (linear regression slope = 0.972, R² = 0.970, ICC = 0.999). Across all spheres in the phantom, the T₁ measured using Multitasking DCE shows no significant difference with the T₁ measured by IR-SE (P = .073). The intersession repeatability of the T₁ mapping in Multitasking DCE was illustrated in Figure 1C. The mean absolute interscan differences were 2.55% with a relatively low CoV (9%), indicating that the T₁ mapping of Multitasking DCE is repeatable.

FIGURE 1.

Phantom measurements. (A) T₁ maps from the Multitasking DCE and reference inversion-recovery spin-echo (IR-SE) sequence of the T₁ layer of ISMRM/NIST MRI system phantom. (B) Regression of T₁ of the proposed Multitasking DCE versus IR-SE. The solid line represents y = x, whereas the dashed lines represent the regression of the T₁ from 2 methods (R² = 0.970). (C) The Bland–Altman plot shows intersession repeatability of the T₁ measurement of the Multitasking DCE measured on 2 different days. The solid line and dashed lines indicate the mean value and 1.96 of the SD of the T₁ between different measurements, respectively

3.2 |. Numerical simulation

Supporting Information Figure S2 shows true CA concentration curves as well as estimated concentration curves for blood, normal pancreas, and PDAC using both the T₁-based Multitasking approach and the conventional linear approach in a numerical simulation. The linear approach has a fundamental bias in the estimation of kinetic parameters, as it does not account for the nonlinearity of T1W signal intensity as a function of CA concentration, whereas the T₁-based Multitasking approach provides estimated parameters consistent with the true parameters, as listed in Supporting Information Table S2. Supporting Information Figure S3 and Supporting Information Table S3 compare the kinetic parameter estimates from a Multitasking patient case using Multitasking and linear approaches, showing the same trends as the numerical simulation.

3.3 |. Effect of respiratory-motion compensation

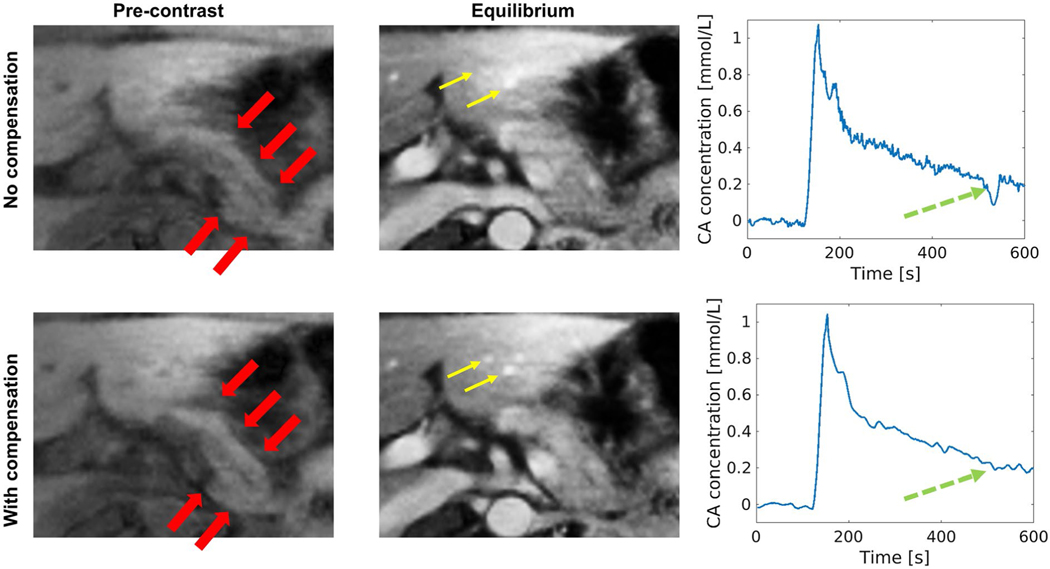
The respiratory-motion compensation scheme was applied to all subjects. Figure 2 compares the image quality and CA concentration curves in the pancreas with and without respiratory-motion compensation in a representative subject. The subject had an irregular respiratory pattern with nonu-niformly distributed bins, resulting in poor image quality at bins with fewer image lines. In this example, respiratory-motion compensation increased the interbin image correlation and therefore improved image quality. The CA concentration curve with motion compensation is much cleaner with less oscillation from respiratory motion. The SNR and sharpness measurements before and after motion compensation for both pre-contrast and equilibrium phases (t_d = 4 minutes) are listed in Table 2 for comparison. A one-tailed t-test shows that motion compensation produced significantly superior SNR in the pancreas and sharpness of the pancreas boundary (P = .006, .008, .013, <.001, respectively).

FIGURE 2.

Effect of respiratory-motion compensation. The images without and with respiratory compensation are shown at 2 DCE phases: 1 pre-contrast phase and 1 equilibrium phase (t_d = 4 minutes). The contrast agent (CA) concentration curve of the pancreas is displayed. Images with compensation show less artifacts and improved structure delineation. The red thick arrows mark the pancreas, which is much sharper with less artifacts on images with compensation. The yellow thin arrows mark small vessels, which show clearer boundary and improved contrast on images with compensation. The green dashed arrows point out that the CA concentration curve with compensation is much cleaner with far less oscillation

TABLE 2.

Comparison of SNR and sharpness without motion compensation and with motion compensation over all subjects (N = 30)

	SNR pre-contrast	SNR equilibrium	SHP pre-contrast (mm−1)	SHP equilibrium (mm−1)
NMC	29.83 ± 14.21	35.22 ± 13.07	0.39 ± 0.15	0.49 ± 0.16
MC	33.95 ± 17.09	40.50 ± 16.10	0.47 ± 0.15	0.59 ± 0.18
P-value	.006	.008	.013	<.001

Note: One-tailed t-tests were performed and the p-values are listed in the table. The equilibrium phase is t_d = 4 minutes, where t_d is the time since injection. Abbreviations: MC, motion compensation; NMC, no motion compensation; SHP, sharpness.

3.4 |. In vivo measurements

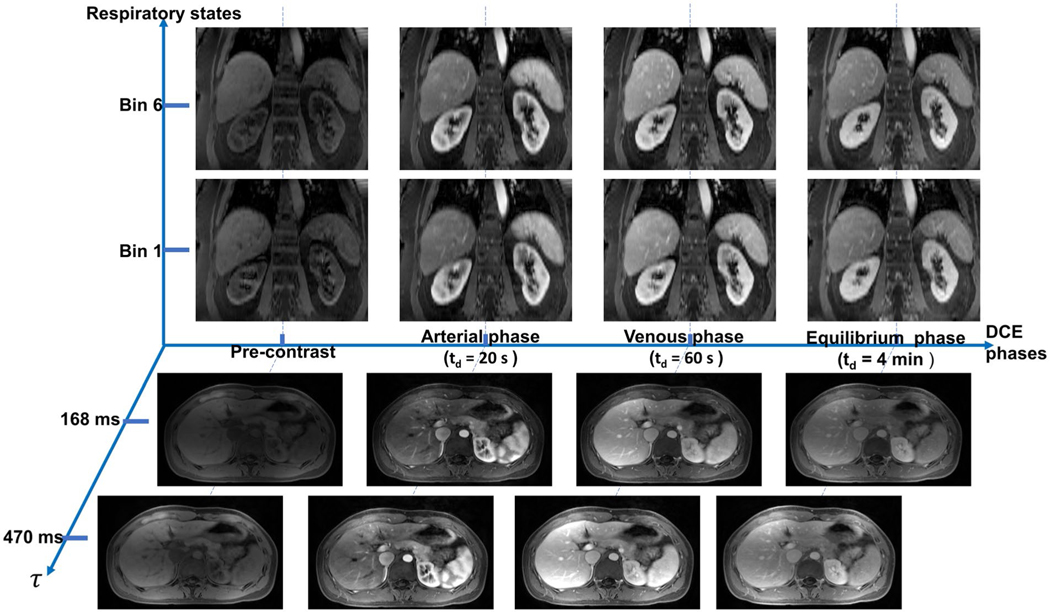
The in vivo protocol including the conventional sequences and Multitasking DCE was successfully applied to all healthy volunteers and patients. A demonstration of the 6D images from Multitasking DCE is shown in Figure 3. As described previously, the DCE bin duration in the reconstruction was chosen to be 1 second, yielding 600 DCE phases, each of which contains 84 saturation times. Combined with 6 respiratory bins, the reconstructed image tensor possesses a total of 600 × 84 × 6 = 302 400 timepoints, each corresponding to a 3D (3 spatial dimensions) image volume. Figure 3 displays the images in either coronal or axial orientation at 4 key DCE phases (pre-contrast phase, arterial phase with t_d = 20 seconds, venous phase with t_d = 60 seconds, and equilibrium phase with t_d = 4 minutes) at 2 saturation times and 2 respiratory states. Coronal orientation provides an appropriate view of the respiratory motion, while axial orientation shows excellent pancreas delineation. Supporting Information Video S1 further demonstrates the 6D images from Multitasking DCE.

FIGURE 3.

Representative 6D images with 3 spatial dimensions, a saturation-recovery (SR) dimension, a respiratory dimension, and a DCE time course. Images are displayed at pre-contrast phase, arterial phase (t_d = 20 seconds), venous phase (t_d = 60 seconds), and equilibrium phase (t_d = 4 minutes). For each DCE phase, images of end-inspiration (bin 1) and end-expiration (bin 6) phases at τ = 470 ms are shown in coronal orientation; images of different τs (τ = 168 ms and τ = 470 ms) at end-expiration phase are shown in transversal view with clear pancreas delineation

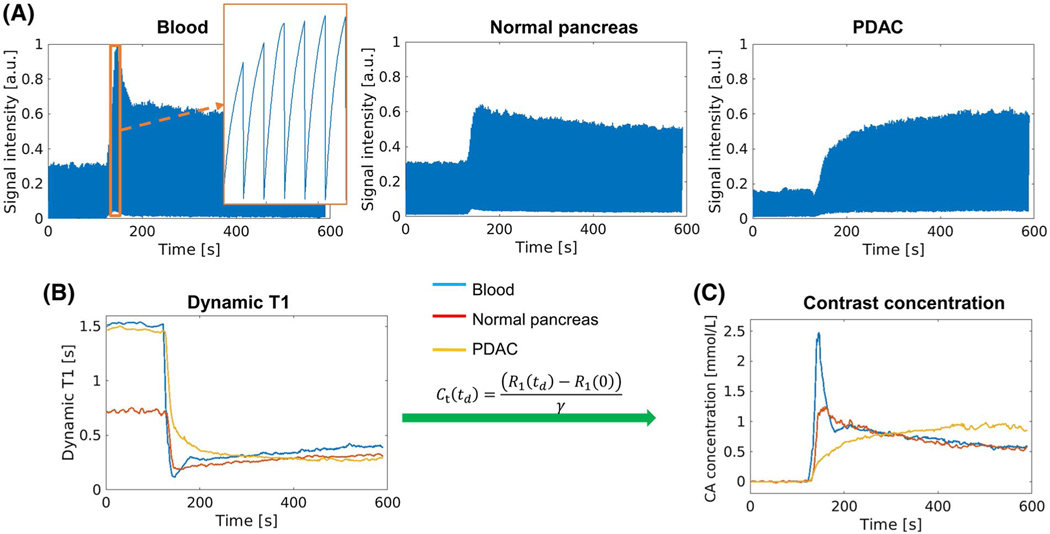
The typical process of the conversion from dynamic signal to CA concentration is illustrated in Figure 4. Figure 4A displays example signal intensity curves over all saturation times and DCE phases at end-expiration, displaying blood, normal pancreas, and PDAC mass. Figure 4B,C shows the corresponding dynamic T₁ curves and CA concentration curves for each of these tissues. The shape of the concentration curves is consistent with the findings in other studies.¹⁵

FIGURE 4.

Transformation from signal intensity to CA concentration. (A) Representative signal profiles of blood, normal pancreas, and pancreatic ductal adenocarcinoma (PDAC) displayed at end-expiration. The zoomed-in area in the image of blood signal shows the SR curves during the peak enhancement. (B) Dynamic T₁ mapping based on SR periods. (C) Contrast agent (CA) concentration curves derived directly from the T₁ mapping according to contrast media relaxivity

The agreement of in vivo T₁ measurements between Multitasking DCE and MOLLI was assessed for normal pancreas in the control group (denoted as control), PDAC mass in the patient group (denoted as tumor), and nontumoral areas (denoted as non-tumor) in the patient group (Table 3). The ICC of the 3 categories for pre-contrast T₁ (ICC = 0.820, 0.904, and 0.973, respectively) and post-contrast T₁ (ICC = 0.924, 0.958, and 0.922, respectively) indicate good agreement of in vivo T₁ measurements between Multitasking DCE and MOLLI; the p-values given by paired t-tests for the 3 categories are 0.024, 0.180, and 0.428, respectively, for pre-contrast T₁, and <.001, .013, and .043, respectively, for post-contrast T₁.

TABLE 3.

Comparison of in vivo T₁ measurements between Multitasking DCE and MOLLI

		Multitasking (ms)	MOLLI (ms)	ICC	Paired t-test (p-value)
Pre-contrast	Control	757 ± 55	818 ± 46	0.820	.024
	Tumor	1571 ± 210	1621 ± 171	0.904	.180
	Non-tumor	1183 ± 338	1245 ± 352	0.973	.428
Post-contrast	Control	419 ± 74	470 ± 80	0.924	<.001
	Tumor	386 ± 63	426 ± 56	0.958	.013
	Non-tumor	417 ± 58	460 ± 49	0.922	.043

Note: The mean values and SD of pre-contrast and post-contrast T₁ from Multitasking DCE and MOLLI are listed for normal pancreas in control group, tumor, and nontumoral regions in patients. The ICC and p-value by paired t-test between T₁ measured by MOLLI and Multitasking are provided. The ICC of each category indicates good agreement of in vivo T₁ measurement between Multitasking DCE and MOLLI.

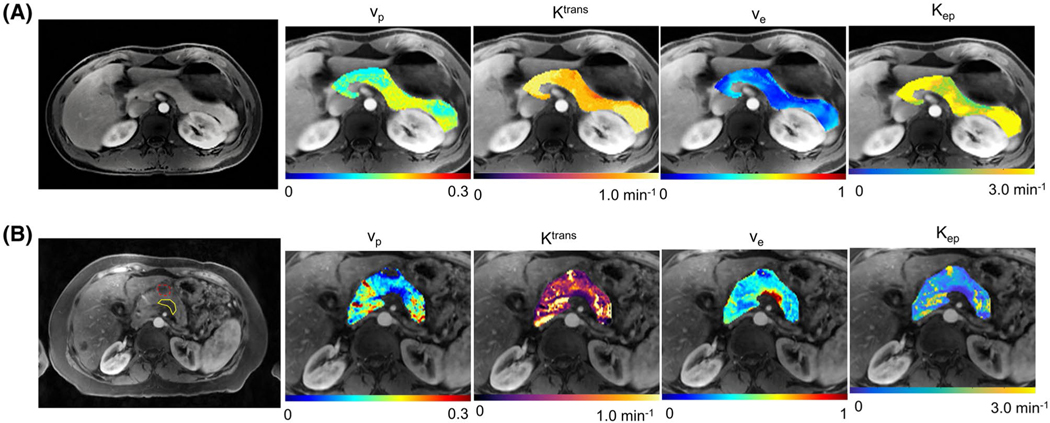
Examples of the kinetic parametric maps are shown in Figure 5. Figure 5A shows a healthy subject with a normal pancreas. The gray-scale images display the anatomical structure of a representative slice at the last saturation time of the arterial phase. The overlaid color voxels show the results of parametric mapping. Figure 5B represents a PDAC case with tumor located within the pancreatic body. The tumor mass was marked by a yellow boundary on the gray-scale images by the radiologist, and a benign cyst is marked by a dashed red boundary.

FIGURE 5.

Representative maps of kinetic parameters of a 32-year-old subject in control group (A) and a 57-year-old subject with PDAC marked by a yellow boundary (B). The gray-scale image in each case is a representative slice with excellent pancreas delineation at the arterial phase. The overlaid color maps display v_p, K^trans, v_e, and K_ep of the pancreas. In (B), the tumor region has lower v_p, K^trans, and K_ep, and higher v_e than the surrounding nontumoral regions. A hypo-enhancing cyst in (B) is marked by a dashed red boundary

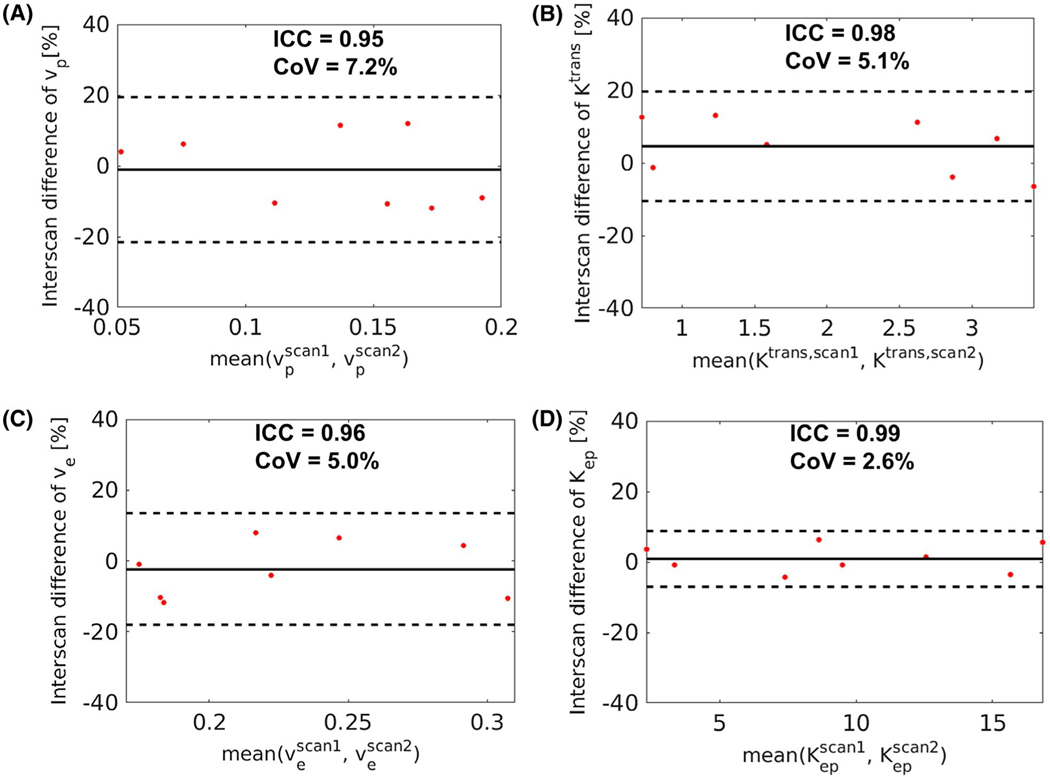
The intersession repeatability of the kinetic parameters from the proposed Multitasking DCE method was also evaluated, with Bland-Altman plots shown in Figure 6. The ICC of v_p, K^trans, v_e, and K_ep were 0.95, 0.98, 0.96, and 0.98, respectively. The CoV of the 4 parameters were 7.2%, 5.1%, 5.0%, and 2.6%, respectively.

FIGURE 6.

Bland-Altman plots evaluating the in vivo intersession repeatability of the kinetic parameters from Multitasking DCE on the 8 subjects in the control group who received the scan twice on separate days. The solid lines indicate the mean bias, and the dashed lines indicate the 95% limit of agreement. The interclass correlation coefficient (ICC) and coefficient of variation (CoV) of each parameter are listed on top of the corresponding plot

Figure 7 contains a bar graph showing the mean and SD measurements of v_p, K^trans, v_e, and K_ep from the control, tumor, and nontumoral regions. The results for all categories were in general agreement with published values from literature.^4,15–17 An ANOVA analysis with Holm-Bonferroni correction indicated that all 4 parameters were significantly different between tumor with non-tumor (P = .002, .003, <.001, and .004, respectively) and between tumor and control (P = .0011, <.001, <.001, and <.001, respectively). The K^trans, v_e, and K_ep between non-tumor and control also showed a significant difference (P < .001, <.001, and =.003, respectively). Detailed results of the statistical analyses are listed in Supporting Information Table S1. Supporting Information Figure S4 shows the correlation between the size of PDAC and each kinetic parameter estimated by Multitasking DCE.

FIGURE 7.

Bar graph showing the mean value and SD of v_p, K^trans, v_e, and K_ep for control group, tumor, and nontumoral regions in the patient group. The p-values between each pair of categories by one-way unbalanced ANOVA with Holm-Bonferroni correction are marked on top of the bar graph. All 4 parameters were significantly different in the comparison between tumor and control and between tumor and non-tumor. The K^trans, v_e, and K_ep between control and non-tumor also showed a significant difference

4 |. DISCUSSION

DCE MRI has been widely applied in the study of permeability properties of lesions in oncology, especially in tumors of breast and pelvic organs.^40–44 Investigations have reported that permeability parameters derived from DCE MRI are associated with the histologic criteria.^{15,17,40–42} However, only a limited number of studies have performed DCE MRI in the upper abdomen due to the challenges of adequate anatomical coverage, sufficient temporal resolution, as well as the challenges posed by respiratory motion. In this study, we presented a 6D quantitative DCE MRI technique based on MR Multitasking and demonstrated its feasibility of the characterization of PDAC. Multitasking DCE enables 3D free-breathing acquisition, whole-abdomen coverage, high DCE temporal resolution of 1 second, and dynamic T₁ mapping in a single 10-minute scan, which overcomes all the aforementioned challenges and potentially facilitates the wide application of quantitative assessment of vascular properties in PDAC, including tumor characterization and treatment-response monitoring.

The coverage in head–foot direction of Multitasking DCE is 360 mm from the liver dome to the iliac crest. The potential utility of the large coverage includes the evaluation of vasculature involvement of PDAC as well as the detection of abdominal metastasis of PDAC,^45–47 which are vital information in the diagnosis and staging of the disease.

Sufficient temporal resolution is crucial to the quantification of DCE MRI. Othman et al reported that a temporal resolution of at least 10 seconds/phase is required for the accurate diagnosis of cancer.⁴⁸ Several recent investigations have also shown that the acquisition of the arterial input function, which usually changes more rapidly than the tissue of interest, requires a temporal resolution on the order of 1 second.^49,50 To achieve satisfactory temporal resolution, a tradeoff usually has to be made by reducing either the coverage or spatial resolution. For example, Akisik et al used 2D-T1W acquisition for 3 axial slices and 1 sagittal slice with 4.4-second temporal resolution.¹⁷ Kim et al implemented the k-space weighted image-contrast (KWIC) technique, which allows k-space data sharing to reconstruct 3D images with high-spatial/low-temporal resolution or vice versa in one DCE session.¹⁶ In this work, the proposed technique can achieve adequate coverage and spatial resolution with a high temporal resolution that can be retrospectively set based on the choice of DCE bin duration. Here it was retrospectively set to be 1 second to balance temporal resolution and SNR, as a similar temporal resolution also yielded the highest intersession repeatability when evaluated in our previous work.²⁴

In addition, the CA concentration in the proposed technique is directly quantified from dynamic T₁ mapping to avoid the error introduced by linear approximation from T1W signal intensity. The feasibility of dynamic T₁ fitting in Multitasking DCE has been assessed by numerical simulations in our previous work.²⁴ For the in vivo study, the pre-contrast T₁ shows no significant difference between the MOLLI and Multitasking measurements for tumor and non-tumoral regions in the PDAC group; a less than 10% difference (P = .024) was shown in controls, which may be due to known differences between various T₁ mapping sequences.⁵¹ The post-contrast T₁ measured by Multitasking is systematically 10% shorter than the T₁ from the MOLLI scan collected after Multitasking for all tissue types (P < .001, P = .013, and P = .043, respectively). One possible reason is that contrast washout lengthened T₁ during the time gap between the T₁ measurement in the last DCE phase in Multitasking DCE and the subsequent MOLLI scan, especially in cases where subjects moved during the scan and relocalization of the pancreas was required before the post-contrast MOLLI scan.

Another feature of the proposed Multitasking DCE is the capability to resolve respiratory motion. Respiration-induced motion artifacts are a major source of degraded image quality in abdominal MRI. Acquisition with breath-holds is the most common way to reduce these artifacts, which is often unreliable and in many cases infeasible. Radial sampling patterns are more robust to motion, but take longer for image reconstruction and can still result in blurring or streaking artifacts. XD-GRASP is a technique that separates respiratory motion states and uses sparsity constraints along different time dimensions. A recent publication of DCE MRI in liver using XD-GRASP described a protocol with 3D coverage and reasonable spatial resolution but a relatively low temporal resolution of 13 seconds and no T₁ quantification.⁵²

The estimates of the kinetic parameters v_p, K^trans, v_e, and K_ep of control and patient groups are generally in line with the values published in the literature.^15,16 K^trans and v_e have been shown to correlate with the MVD and fibrosis in PDAC lesions, respectively, and therefore can be used as imaging markers of the perfusion properties of tumor.^4,15 In the TK model, K^trans is dominated by the tissue blood flow and the capillary permeability–surface area and can have different physiological interpretations depending on the balance between the 2 factors.³⁷ In the context of PDAC, the microvessels in the lesions are leaky and in low density, leading to high permeability and limited blood flow, in which case K^trans is approximately equal to plasma flow per unit volume of tissue.³⁷ This is a possible pathological reason behind the decrease of K^trans value observed in malignant tumors compared with the nontumoral area in the patient group and normal tissue in the control group. The v_e in the DCE MRI represents fractional extravascular extracellular volume. The higher v_e in malignant tumor possibly results from the changes in the interstitial space due to the increased collagen content in the extracellular matrix. The nontumoral area in patients with PDAC are commonly associated with chronic obstructed pancreatitis also characterized by atrophy of the distal end toward the tail, reduced blood, and increased fibrosis,^53,54 which may contribute to decreased K^trans and increased v_e in nontumoral tissues in the patient group compared with the normal tissues in the control group.^55–58 Figure 5 suggests regional differences of kinetic parameters in the control group, which may be caused by the intrinsic heterogeneous tissue compositions in different parts of the pancreas.⁵⁹ Previous studies have shown that some imaging biomarkers such as ADC differ significantly between the head, body, and tail of the pancreas.⁶⁰

Our study had several limitations. All of the patients recruited for this pilot study were undergoing chemotherapy at the time of the study. Chemotherapy may change the microvascular structures and thus the kinetic parameters, which limits the value of the current data to represent the vascular properties of untreated PDAC tumors. In addition, this pilot study had a relatively small number of subjects for both control and patient groups. With the encouraging findings of this work, further studies to validate the clinical utility of the proposed technique in a larger patient cohort with first diagnosed PDAC are warranted. Furthermore, tumor histological validation was not available for this pilot study. Instead, the capability of Multitasking DCE in quantitatively assessing tumor vascular properties was evaluated by the intersession repeatability of the kinetic parameters. The kinetic parameters are consistent with the values in the published literatures. In future studies, the correlation between the kinetic parameters and the histological parameters including the MVD and fibrosis should be assessed.

5 |. CONCLUSIONS

A novel Multitasking abdominal DCE technique was developed, enabling free-breathing and respiratory motion–resolved image acquisition, entire-abdomen coverage, 1-second temporal resolution, dynamic T₁ quantification, and kinetic modeling. Quantitative DCE parameters from the preliminary in vivo study were repeatable and showed significant differences among normal pancreas, tumor, and nontumoral regions in patients with PDAC.

Supplementary Material

supp

FIGURE S1 Respiratory binning scheme. (A) A narrow bar-shaped region of interest (ROI) in the head–foot direction was manually drawn on top of the liver–air interface. (B) The signal at each last saturation time within the ROI was averaged over left–right direction as a 1-dimensional (1D) projection. The 1D projection over the duration of the scan formed a 2D spatial-temporal profile showing the location changes of the liver dome. (C) The position of the liver dome was extracted and then divided into 6 respiratory bins

FIGURE S2 Simulated CA concentration curves and estimated CA concentration curves using the linear approach (LA) and T₁-based Multitasking approach (MT) for all tissues. The CA concentration curves estimated by LA are different from the simulated curves, whereas the curves estimated by MT are the same with the simulated curves. The zoomed-in area in the image of the signal intensity of MT shows the SR curves for PDAC

FIGURE S3 CA concentration curves derived by LA and MT from a Multitasking DCE patient case for all tissues. The zoomed-in area in the image of the signal intensity of MT shows the SR curves for PDAC

FIGURE S4 Correlation between the size of PDAC and v_p, K^trans, v_e, and K_ep estimated by Multitasking DCE. The R and the p-value of the correlation are attached to the corresponding graph. No significant correlation (P = .35, .78, .41, and .54 for v_p, K^trans, v_e, and K_ep, respectively) was found for this data set

TABLE S1 Statistical result of v_p, K^trans, v_e, and K_ep for control group, tumor, and nontumoral regions in the patient group

TABLE S2 True value of v_p, K^trans, v_e, and K_ep in the simulation and the mean and SD measurement of each kinetic parameter estimated using LA and MT

TABLE S3 Values of v_p, K^trans, v_e, and K_ep estimated using LA and MT from a Multitasking DCE patient case

TABLE S4 Size and location of the tumor for all patients. The size of the tumor is defined as the largest diameter in axial CT images according to RECIST 1.1 criteria

2

VIDEO S1 Demonstration of the 6-dimensional images (3 spatial dimensions, 1 SR dimension, 1 respiratory dimension, and 1 DCE time dimension)