Using Serology with Models to Clarify the Trajectory of the SARS-CoV-2 Emerging Outbreak

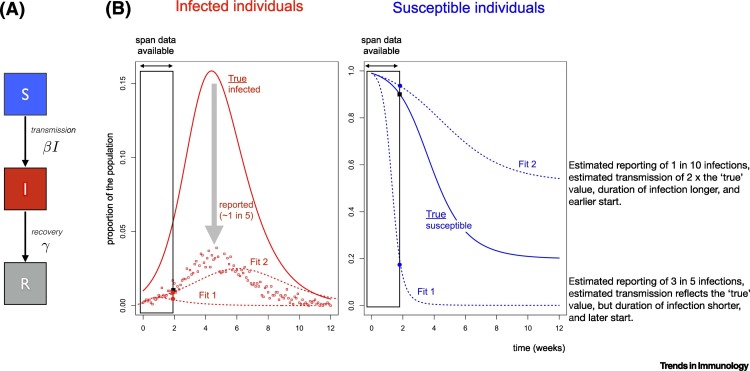
Coronavirus disease 2019 (COVID-19) presents an unprecedented international public health challenge. Policy has frequently been informed by mathematical models of infectious disease transmission, particularly in this outbreak [1]. Such models show that epidemics such as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection are driven by the interaction of three dynamic variables (Figure 1A): the number or density of infectious individuals; previously unexposed susceptibles; and recovered (partly or fully immune) individuals [2]. While a time series of estimated cases arises directly from epidemic surveillance, susceptible and immune classes can only be directly identified by serology, which is less routinely carried out. Thus, mathematical models are typically structured around the likely phases of infectiousness, with parameters being estimated by fitting models to reported numbers of cases or deaths (Figure 1B). From these parameter estimates, researchers can project the expected trajectory of cases, opening the way to characterizing the urgency of interventions and their likely impact. However, as we illustrate below using a toy model (Figure 1), if such inference is based only on cases, it may lack robustness for a novel pathogen, as both disease parameters and surveillance intensity remain unclear. Therefore, direct estimation of the susceptible fraction by using serology or other immunological measures to identify the proportion of the population that is susceptible could greatly clarify our understanding of epidemic dynamics and control [3,4].

Figure 1.

Grounding Mathematical Models of Infection Using Serology.

(A) A classic Susceptible–Infected–Recovered model, where individuals start as susceptible (S, assumed to initially reflect everyone for SARS-CoV-2), become infectious (I) at a rate defined by the encounter rate between susceptible and infectious individuals, and the rate of infection on encounter (defined by the parameter β; and then eventually recover (R, at rate γ). (B) Resulting trajectories of infections (left) with β = 2 and γ = 1 week (solid line, ‘true’ cases), and the associated observed cases (points), simulated from a binomial distribution around this line with probability of being reported of ρ = 0.2. If we assume that only case data (points) are available, and only for the first 2 weeks of the pandemic (indicated by ‘span data available’, i.e., here, the scenario considered reflects an early phase of the pandemic), then several different parameter sets (denoted as Fit1 and Fit2) are compatible with the data. Compatibility can be measured via any metric describing the distance between the observed cases (points) and the projected numbers of reported cases (dashed lines). However, the two different parameter sets yield different longer term trajectories (dashed lines, higher curve Fit2 corresponds to β = 4, γ = 0.6 ρ = 0.01 with a starting point 1 week earlier than the simulated ‘true’ start of the outbreak, and the lower curve Fit1 corresponds to β = 2, γ = 1.5 ρ = 0.6 and a starting point 1 week later than the ‘true’ fit). Different parameter sets can yield similar projections of numbers of cases through time as a function of the assumed time of the start of the outbreak (difficult to know with precision), the case reporting rate, and parameters such as the magnitude of transmission and duration of infection. Yet, in the same time frame (early time span), these different parameter sets yield different proportions of susceptible individuals (right hand plot, solid line: ‘true’ values based on the hypothetical simulated example (solid line in the first panel); dashed lines: the two different estimates, Fit1 and Fit2). While the differences between numbers of cases for the different scenarios is largely overlapping, the proportions susceptible are different, and thus, information on serology could be important for grounding model fitting because it provides clear discrimination between the different models described here. (Note that for simplicity, we assume SIR, dynamics, with no exposed class, and short term strong immunity). See https://labmetcalf.shinyapps.io/serol1/ to explore the dynamics.

By using data on reported numbers of cases or deaths, mathematical models allow estimation of infectious disease parameters such as the magnitude of transmission, or duration of infection that will govern the time course of the outbreak. This is achieved by identifying the combinations of parameters that result in a projected numbers of cases (or deaths) that best matches the observed. However, cases are generally under-reported, infections may vary in terms of their detectability (i.e., children may be less symptomatic [5]), and case definitions may change over the epidemic time course [6]. Challenges in identifying cause of death, and variability in mortality across different groups can lead to similar issues. This can make it challenging to pin down parameters which define the growth in the number of infections and timing of the peak of an outbreak. For instance, even if only under-reporting is at play, different combinations of parameters can yield the same trajectory of cases in the short term (Figure 1B). This is important because the trajectory associated with parameters that match the numbers of cases over the short term might deviate considerably over the longer term. Slight differences in the magnitude of transmission, or the speed at which infectious individuals recover, can compound into substantially large differences in terms of the degree to which the size of the susceptible population is depleted and thus, the number of cases that will occur. Furthermore, if under-reporting changes over time (e.g., via increased testing), the true drivers of dynamics are further obscured.

Measurement of immunological features such as serological status provides a crucial extra layer of information to address this problem. In the depicted example (Figure 1), a model fitted to early case data could erroneously indicate that a 75% reduction in transmission would be needed to avert a second wave of infection – yet in reality (i.e., according to the true parameters used in the simulation), transmission would need to be reduced by only 50%. The discrepancy arises because the true magnitude of transmission (used in the simulation) is lower than that estimated based on reported cases. In turn, a lower magnitude of transmission translates into a smaller fraction by which transmission must be reduced to ensure that the number of infections generated per infected individual is <1 (the condition for the outbreak to decline in size). Repeated estimates of susceptibility through time could both ensure greater precision in estimation of the magnitude of transmission: predictions from Fit1 and Fit2 differ substantially in terms of susceptibility, even early on during the outbreak (Figure 1). Furthermore, such measures give us more power to dissect complexities such as behavioral and seasonal changes in transmission, or age-specific heterogeneities in immunity and transmission.

There are, of course, many important caveats. Serology too has an error rate, and we are still uncertain as to how SARS-CoV-2 serology can be interpreted in terms of immunity (including the degree to which it wanes or is partial), and recent work suggests potentially rapid loss of seropositive status, particularly in asymptomatic individuals [7]. Cell-mediated immunity may be of greater importance than antibodies for some infections, making serological measurements less likely to reflect relevant immune status, although this aspect of immunity is still unclear for SARS-CoV-2. Yet, since being seropositive is indicative of having been infected at a point in the past, serology measures an integral of past infection. This means that an appropriate sample tested serologically has greater power to capture the state of the system than a test for active infection, which only provides a snapshot of the present moment. In other words, serological data can dramatically narrow down the range of plausible epidemic scenarios by calibrating the model to empirical observations of susceptible depletion, while by contrast, this information is simply missing in traditional case-based surveillance.

To conclude, while testing of active infections is and should remain a priority, more widely available serological data will provide powerful discrimination between different sets of parameters and plausible epidemic trajectories, as illustrated in Figure 1. Increasingly, serological tests are becoming available, enabling the identification of individuals bearing antibodies suggestive of past infection [8,11]; this can allow us to complete our window into the drivers of outbreaks beyond a measure of infection, to include susceptible and recovered individuals (Figure 1). As serology becomes more widespread in our efforts to meet the current pandemic, there is significant potential to lay the foundations towards making serology a routine part of public health. This could enhance various aspects of vigilance, from situational awareness of vaccine preventable infections [9] to pandemic preparedness [10].

Disclaimer Statement

This article does not necessarily represent the views of the National Institutes of Health or US Government.