Highlights
-
•
Standard TSP instances are not suitable for generalized conclusions.
-
•
Although good for TSPs, GPUs are not well suited for explored supply chain problem.
-
•
25.4x speed-up was achieved on CPU compared to its sequential counterpart.
-
•
148x speed-up was achieved on Xeon Phi compared to its sequential counterpart.
Keywords: Transportation network optimisation, Ant Colony Optimization, Parallel ACO on Xeon Phi/GPU
Abstract
Ant Colony algorithm has been applied to various optimisation problems, however, most of the previous work on scaling and parallelism focuses on Travelling Salesman Problems (TSPs). Although useful for benchmarks and new idea comparison, the algorithmic dynamics do not always transfer to complex real-life problems, where additional meta-data is required during solution construction. This paper explores how the benchmark performance differs from real-world problems in the context of Ant Colony Optimization (ACO) and demonstrate that in order to generalise the findings, the algorithms have to be tested on both standard benchmarks and real-world applications. ACO and its scaling dynamics with two parallel ACO architectures – Independent Ant Colonies (IAC) and Parallel Ants (PA). Results showed that PA was able to reach a higher solution quality in fewer iterations as the number of parallel instances increased. Furthermore, speed performance was measured across three different hardware solutions – 16 core CPU, 68 core Xeon Phi and up to 4 Geforce GPUs. State of the art, ACO vectorisation techniques such as SS-Roulette were implemented using C++ and CUDA. Although excellent for routing simple TSPs, it was concluded that for complex real-world supply chain routing GPUs are not suitable due to meta-data access footprint required. Thus, our work demonstrates that the standard benchmarks are not suitable for generalised conclusions.
1. Introduction and motivation
Supply chain optimisation has become an integral part of any global company with a complex manufacturing and distribution network. For many companies, inefficient distribution plan can make a significant difference to the bottom line. Modelling a complete distribution network from the initial materials to the delivery to the customer is very computationally intensive. With increasing supply chain modelling complexity in ever-changing global geo-political environment, fast adaptability is an edge. A company can model the impact of currency exchange rate changes, import tax policy reforms, oil price fluctuations and political events such as Brexit, Covid-19 before they happen. Such modelling requires fast optimisation algorithms.
Mixed Integer Linear Programming (MILP) tools such as Cplex are commonly used to optimise various supply chain networks (Esmaeilikia et al., 2016). Although MILP tools can obtain an optimum solution for a large variety of linear models, not all real-world supply chain models are linear. Furthermore, MILP is computationally expensive and on large instances can fail to produce an optimal solution. For that reason, many alternative algorithmic approaches (heuristics, meta-heuristics, fuzzy methods) have been explored to solve large-complex SC models (Esmaeilikia et al., 2016). One of these algorithms is the Ant Colony Optimization (ACO), which can be well mapped to real-world problems such as routing (Schyns, 2015) and scheduling (Zhang, Zhang, & Feng, 2014). Supply Chain Optimization Problem (SCOP) includes both, finding the best route to ship a specific order and finding the most optimal time to ship it, such that it reaches expected customer satisfaction while minimising the total cost occurred. Although other metaheuristics algorithms exist in the literature for solving SCOPs, such as Genetic Algorithm (GA) (Azad et al., 2019, Yeh and Chuang, 2011) and Simulated Annealing (SA; Fathollahi-Fard et al., 2019, Mohammed and Duffuaa, 2019), ACO was chosen due to the long history of the algorithm applied to various vehicle routing (Kalayci and Kaya, 2016, Zhang et al., 2019) and supply chain (Bottani et al., 2019, Panicker et al., 2018) problems with great solution quality and speed. Also, a recent study in (Valdez, Moreno, & Melin, 2020) concluded that compared to GA and SA, the ACO performs the best for routing problems such as the Travelling Salesman Problem (TSP).
Ant colony algorithms try to mimic the observed behaviour of ants inside colonies to solve a large range of optimisation problems. Since the introduction by Marco Dorigo in 1992, many variations and hybrid approaches of Ant Colony algorithms have been explored (Wang et al., 2009, Kıran et al., 2012). Most ant colony algorithms consist of two distinct stages – solution construction and pheromone feedback to other ants. Typically, an artificial ant builds its solution from the pheromone left from previous ants, therefore allowing communication over many iterations via a pheromone matrix and converges to a better solution. The process of solution creation and pheromone update is repeated over many iterations until the termination criterion is reached; this can be either total number of iterations, total computation time or dynamic termination.
Researchers in (Wang & Lee, 2015) compared an industrial optimisation-based tool – IBM ILOG Cplex with their proposed ACO algorithm. It was concluded that the proposed algorithm covered 94% of optimal solutions on small problems and 88% for large-size problems while consuming significantly less computation time. Similarly, (Wong & Moin, 2017) compared ACO and Cplex performance on multi-product and multi-period Inventory Routing Problem. On small instances, ACO reached 95% of the optimal solution while on large instances performed better than time-constrained Cplex solver. Furthermore, ACO implementations of Closed-Loop Supply Chain (CLSC) have been proposed; CLSC contains two parts of the supply chain – forward supply and reverse/return. (Vieira, Vieira, Gomes, Barbosa-Póvoa, & Sousa, 2015) solved CLSC models, where the ACO implementation outperformed commercial MILP (Cplex) on nonlinear instances and obtained 98% optimal solution with 40% less computation time on linear instances.
Academic literature suggests that Graphical Processing Units (GPUs) are very suitable for solving benchmark routing problems such as Travelling Salesman Problem (TSP), with speedups of up to 60x (Yelmewad, Kumar, & Talawar, 2019) and even 172x (Zhou, He, & Zhang, 2017) when compared to the sequential CPU implementation. This paper aims to explore if the same ACO architectures that are so well suited for TSP can be applied for a real-world supply chain optimisation problem. Furthermore, investigate what hardware architectures are the best suited for the supply chain problem solved.
The paper is structured as follows: Section 2 explores the current state of the art parallel implementations of ACO across CPU, GPU and Xeon Phi; Section 3 introduces the hardware and software solutions used; Section 4 described the real-world problem being solved; Section 5 details the parallel ACO implementations and Section 6 compares the results. Finally, Section 7 concludes the paper.
2. Parallel Ant Colony Optimization
Since the introduction of ACO in 1992, numerous ACO algorithms have been applied to many different problems, and many different parallel architectures have been explored previously. (Randall & Lewis, 2002) specifies 5 of such architectures:
-
•
Parallel Independent Ant Colonies – each ant colony develop their solutions in parallel without any communication in-between;
-
•
Parallel Interacting Ant Colonies – each colony creates a solution in parallel and some information is shared between the colonies;
-
•
Parallel Ants – each ant builds solution independently, then all the resulting pheromones are shared for the next iteration;
-
•
Parallel Evaluation of Solution Elements – for problems where fitness function calculations take considerably more time than the solution creation;
-
•
Parallel Combination of Ants and Evaluation of Solution Elements – a combination of any of the above.
Researchers have tried to exploit the parallelism offered from recent multi-core CPUs (Prakasam & Savarimuthu, 2016), along with clusters of CPUs (Gülcü et al., 2018, Weidong et al., 2015) and most recently GPUs (Tan & Ding, 2016) and Intel’s many-core architectures such as Xeon Phi (Sato, Tsutsui, Fujimoto, Sato, & Namiki, 2014). Breakdown of the strategies and problems solved are shown in Table 1 .
Table 1.
ACO architecture and hardware configurations explored. LAC - Longest Common Subsequence Problem, MKP - Multidimensional Knapsack Problem, TSP - Travelling Salesman problem. IAC – Independent Ant Colonies, IntAC – Interactive Ant Colonies, PA – Parallel Ants.
| Task parallelism, IAC | Task parallelism, IntAC | Task parallelism, PA | Data parallelism, PA | |
|---|---|---|---|---|
| CPU | Scheduling (Thiruvady, Ernst, & Singh, 2016) | Scheduling (Thiruvady, Ernst, & Singh, 2016) | TSP (Guerrero et al., 2014, Yang et al., 2016) Scheduling (Thiruvady, Ernst, & Singh, 2016) Supply chain [this paper] |
TSP (Zhou, He, Hou, & Qiu, 2018) Supply chain [this paper] |
| GPU | n/a | n/a | Protein folding (Llanes, Vélez, Sánchez, Pérez-Sánchez, & Cecilia, 2016) TSP (Guerrero, Cecilia, Llanes, García, Amos, & Ujaldón, 2014) MKP (Fingler, Cáceres, Mongelli, & Song, 2014) LAC (Markvica, Schauer, & Raidl, 2015) |
TSP (Zhou et al., 2018, Cecilia et al., 2018, Skinderowicz, May 2020) Edge detection (Dawson & Stewart, 2014) Supply chain [this paper] |
| CPU cluster | Scheduling (Huo & Huang, 2016) | TSP (Randall & Lewis, 2002) | TSP (Weidong, Jinqiao, Yazhou, Hongjun, & Jidong, 2015) | n/a |
| Xeon Phi | n/a | n/a | Supply chain[this paper] | TSP (Tirado et al., 2015, Tirado et al., 2017, Lloyd and Amos, 2017) Supply chain[this paper] |
During the search, an Ant has to keep track of the existing state meta-data, for instance Travelling Salesman Problem only need to keep the record of what cities have been visited as part of problem constraint. However, real-life problems have a lot more constraints and therefore requires a lot of meta-data storage during solution creation. This paper explores such problem in the supply chain domain. Table 2 shows the most common problems solved by ACO and their corresponding associated constraints/meta-data required during solution creation.
Table 2.
Meta-data required during solution creation based on problem type.
| Problem | Meta-data required during solution creation | Comment |
|---|---|---|
| Scheduling | 2 | Resource and precedence constraints |
| TSP | 1 | Has the city been visited |
| Protein Folding | 1 | Has the sequence been visited |
| MKP | 1 | Total weight per knapsack |
| LAC | 1 | Tracking of current position in string |
| Edge detection | 1 | Has edge already been visited |
| Supply chain (this paper) | 3 | Capacity, daily order, freight weight constraints |
2.1. CPU
Parallel ACO CPU architectures have been applied to various tasks – for example, (Thiruvady, Ernst, & Singh, 2016) applied ACO for supply chain scheduling problem in mining domain. Authors managed to reduce the execution time from one hour (serial) to around 7 min. Both (Seshadri, 2015) and (Aslam, Khan, & Beg, 2015) used ACO for image edge detection with varying results, (Seshadri, 2015) achieved a speedup of 3–5 times while (Aslam et al., 2015) managed to reduce sequential runtime by 30%. Most commonly, ACO has been applied to the Travelling Salesman Problem (TSP) benchmarks. For instance, (Yang, Fang, & Duan, 2016) proposed ACO approach with randomly synchronised ants, the strategy showed a faster convergence compared to other TSP approaches. Moreover, authors in (Zhou, He, Hou, & Qiu, 2018) proposed a new multi-core Single Instruction Multiple Data (SIMD) model for solving TSPs. Similarly, both (Chitty, 2018) and (Ismkhan, 2017) tries to solve large instances of TSP (up to 200 k and 20 k cities, respectively) where the architectures are limited to the size of the pheromone matrix. (Ismkhan, 2017) discusses such limitations and proposes a new pheromone sharing for local search – effective heuristics ACO (ESACO), which was able to compute TSP instances of 20 k. In contrast, authors in (Chitty, 2018) eliminate the need for pheromone matrix and store only the best solutions similar to the Population ACO. Furthermore, researchers implement a Partial Ant, also known as the cunning ant, where ant takes an existing partial solution and builds on top of it. Speedups of as much as 1200x are achieved compared to sequential Population ACO.
Generally, CPU parallel architecture implementations come down to three programming approaches - Message Passing Interface (MPI) parallelism, OpenMP parallelism (Abouelfarag, Aly, & Elbialy, 2015) and data parallelism with the vectorisation of SIMD. For instance, (Li, Lu, Shan, & Zhang, 2015) explored both master–slave and coarse-grained strategies for ACO parallelisation using MPI. It was concluded that fine-grained master–slave policy performed the best. (El Baz, Hifi, Wu, & Shi, 2016) used MPI with ACO to accelerate Maximum Weight Clique Problem (MWCP). The proposed algorithm was comparable to the ones in literature and outperformed Cplex solver in both – time and performance. Moreover, authors in (Huo & Huang, 2016) implemented parallel ACO for solving Flow shop scheduling problem with restrictions using MPI. Compared to the sequential version of the algorithm, 93 node cluster achieved a speedup of 16x. (Mehne, 2015) compared ACO parallel implementation on MPI and OpenMP on small vector estimation problem. It was found that maximum speedup of OpenMP was 24x while MPI – 16x. Furthermore, (Zhou, He, Hou, & Qiu, 2018) explored the multi-core SIMD CPU with OpenCL and compared it to the performance of the GPU. It was found optimised parallel CPU-SIMD version can achieve similar solution quality and computation time than the state of art GPU implementation solving TSP.
2.2. Xeon Phi
Intel’s Xeon Phi Many Integrated Core (MIC) architecture offers many cores on the CPU (60–72 cores per node) while offering lower clock frequency. Few researchers have had the opportunity to research ACO on the Xeon Phi architecture. For instance, (Tirado, Urrutia, & Barrientos, 2015) showed how utilising L1 and L2 cache on Xeon Phi coprocessor allowed a speedup of 42x solving TSP compared to sequential execution. Due to the nature of SIMD features such as AVX-512 on Xeon Phi, researchers in both (Tirado, Barrientos, González, & Mora, 2017) and (Lloyd & Amos, 2017) proposed a vectorisation model for roulette wheel selection in TSP. In the case of (Lloyd & Amos, 2017), a 16.6x speedup was achieved compared to sequential execution. To the best of the authors' knowledge, Xeon Phi and ACO parallelism have not been explored to any other problem except TSP.
2.3. GPUs
General Purpose GPU (GPGPU) programming is a growing field in computer science and machine learning. Many researchers have tried exploiting latest GPU architectures to speed optimise the convergence of ACO. ACO GPU implementation expands to many fields, such as edge detection (Dawson and Stewart, 2014, Dawson, 2015), protein folding (Llanes, Vélez, Sánchez, Pérez-Sánchez, & Cecilia, 2016), solving Multidimensional Knapsack Problems (MKPs) (Fingler, Cáceres, Mongelli, & Song, 2014) and Vertex colouring problems (Murooka, Ito, & Nakano, 2016). Moreover, researchers have used GPU implementations of ACO for classification (Tufteland et al., 2016, Gao et al., 2016) and scheduling (Kallioras et al., 2015, Wang et al., 2015) with various speedups compared to the sequential execution.
However, the majority of publications are solving Travelling Salesman Problems (Khatri & Kumar Gupta, 2015), although useful for benchmarking and comparison, little characteristics transfer to other application areas. For instance, highly optimised local memory on GPU (Compute Unified Device Architecture - CUDA) can significantly speed up the execution for TSP. However, when applied to real-life problems where additional restrictions and metadata is required to build a solution, most of the data needs to be stored on much slower global memory. Authors in (Guerrero et al., 2014) did extensive research comparing server, desktop and laptop hardware solving TSP instances on both CUDA and OpenCL. Although there are a couple of ACO OpenCL implementations on GPU (Markvica et al., 2015, NSharma and Garg, 2015), the majority of studies use CUDA. For instance, (Wagh & Nemade, 2017) implemented a GPU-based ACO and achieved a speedup of 40x compared to sequential ACS. Similarly, a 22x speedup was obtained in (Uchida, Ito, & Nakano, 2014) solving pr1002 TSP and 44x on fnl4461 TSP instance in (Zhou, He, & Qiu, 2017). However, there are also various hybrid approaches for solving TSP - (O. U. B and R. Tarnawski, 2018) uses parallel Cultural ACO (pCACO) (a hybrid of genetic algorithm and ACO). Research showed that pCACO outperformed sequential and parallel ACO implementations in terms of solution quality. Furthermore, (Bali, Elloumi, Abraham, & Alimi, 2017) solved TSP instances using ACO-PSO hybrid and authors in (Llanes et al., 2016) explored heterogeneous computing with multiple GPU architectures for TSP. Finally, authors in (Skinderowicz, 2020) explored six different min–max ACO architectures on GPU and their performance on the TSP.
Although task parallelism has potential for a speedup, (Cecilia, García, Nisbet, Amos, & Ujaldón, 2013) showed how data parallelism (vectorisation) on GPU could achieve better performance by proposed Independent Roulette wheel (I-Roulette). Authors then expanded the I-Roulette implementation in (Cecilia, Llanes, Abellán, Gómez-Luna, Chang, & Hwu, 2018), where SS-Roulette wheel was introduced. SS-Roulette stands for Scan and Stencil Roulette wheel. It mimics a sequential roulette wheel while allowing higher throughput due to parallelism. First, the Tabu list is multiplied by the probabilities and the results stored in a choice vector (scan). Then a stencil pattern is applied to the choice vector based on a random number to select an individual (stencil). Further, (Zhou, He, & Zhang, 2017) implements a G-Roulette – a grouped roulette wheel selection based on I-Roulette, where cities in TSP selection are grouped in CUDA warps1 . An impressive speedup of 172x was achieved compared to the sequential counterpart.
2.4. Comparing hardware performances
Fairly comparing parallel performances of different hardware architectures is by no means trivial. Most research compares a sequential CPU ACO implementation to one of the parallel GPUs, which is hardly fair (Skinderowicz, 2016). In addition, unoptimised sequential code is compared to highly optimised GPU code. Such comparisons result in misleading and inflated speedups (Tan & Ding, 2016). Furthermore, (Markvica, Schauer, & Raidl, 2015) argues that often the parameter settings chosen for the sequential implementation is biased in favour of GPU. (Tan & Ding, 2016) proposes criteria to calculate the real-world efficiency of two different hardware architectures by comparing the theoretical peak performances of GPU and CPU. While the proposed method is more appropriate, it still does not account for real-life scenarios where memory latency/speed, cache size, compilers and operating systems all play a role of the final execution time. Therefore, two different systems with similar theoretical floating-point operations per second running the same executable can have significantly different execution times.
Furthermore, in some instances, only execution time or solution quality is compared, rarely both are taken into consideration when analysing results.
3. Background
This section briefly covers the tools and hardware-specific languages used in the implementation.
3.1. Parallel processing with OpenMP
OpenMP2 is a set of directives to a compiler that allows a programmer to create parallel tasks as well as vectorisation (Single Instruction Multiple Data - SIMD) to speed up execution of a program. A program containing parallel OpenMP directives starts as a single thread. Once directive such as #pragma omp parallel is reached, the main thread will create a thread pool and all methods within the #pragma region will be executed in parallel by each thread in the thread group. Moreover, once the thread reaches the end of the region, it will wait for all other threads to finish before dissolving the thread group and only the main thread will continue.
Furthermore, OpenMP also supports nesting, meaning a thread in a thread-group can create its own individual thread-group and become the master thread for the newly created thread-group. However, thread-group creation and elimination can have significant overhead and therefore, thread-group re-use is highly recommended (Rohit Chandra, Dagum, & Kohr, 2000).
This paper utilises both omp parallel and omp simd directives.
3.2. CUDA programming model
Compute Unified Device Architecture (CUDA) is a General-purpose computing model on GPU developed by Nvidia in 2006. Since then, this proprietary framework has been utilised in the high-performance computing space via multiple Artificial Intelligence (AI) and Machine Learning (ML) interfaces and libraries/APIs. CUDA allows writing C programs that take advantage of any recent Nvidia GPU found in laptops, workstations and data centres.
Each GPU contains multiple Streaming Multiprocessors (SM) that are designed to execute hundreds of threads concurrently. To achieve that, CUDA implements SIMT (Single Instruction Multiple-Threads) architecture, where instructions are pipelined for instruction-level parallelism. Threads are grouped in sets of 32 – called warps. Each warp executes one instruction at a time on each thread. Furthermore, CUDA threads can access multiple memory spaces – global memory (large size, slower), texture memory (read only), shared memory (shared across threads in the same SM, lower latency) and local memory (limited set of registers within each thread, fastest)3 .
A batch of threads is grouped into a thread-block. Multiple thread-blocks create a grid of thread blocks. The programmer specifies the grid dimensionality at kernel launch time, by providing the number of thread-blocks and the number of threads per thread-block. Kernel launch fails if the program exceeds the hardware resource boundaries.
3.3. Xeon Phi knights landing architecture
Knights Landing is a product code name for Intel’s second-generation Intel Xeon Phi processors. First-generation of Xeon Phi, named Knights Corner, was a PCI-e coprocessor card based on many Intel Atom processor cores and support for Vector Processing Units (VPUs). The main advancement over Knights Corner was the standalone processor that can boot stock operating systems, along with improved power efficiency and vector performance. Furthermore, it also introduced a new high bandwidth Multi-Channel DRAM (MCDRAM) memory. Xeon phi support for standard x86 and x86-64 instructions, allows majority CPU compiled binaries to run without any modification. Moreover, support for 512-bit Advanced Vector Extensions (AVX-512) allows high throughput vector manipulations.
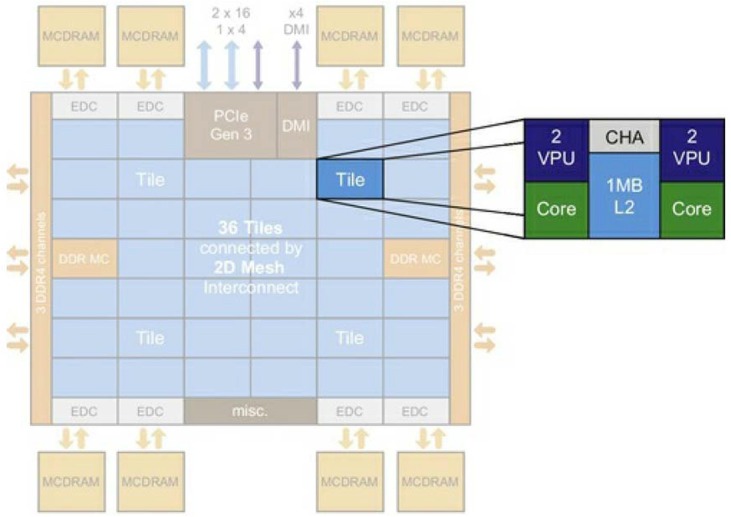
The Knights Landing cores are divided into tiles (typically between 32 and 36 tiles in total). Each tile contains two processor cores and each core is connected to two vector processing units (VPUs), shown in Fig. 1 . Utilising AVX-512 and two VPUs, each core can deliver 32 dual-precision (DP) or 64 single-precision (SP) operations each cycle (Sodani, 2016). Furthermore, each core supports up to four threads of execution – hyper threads where instructions are pipelined.
Fig. 1.
Knights Landing tile with a larger processor die (Sodani, 2016).
Another introduction with the Knights Landing is the cluster modes and MCDRAM/DRAM management. The processor offers three primary cluster modes4 – All to all mode, Quadrant mode and Sub-Numa Cluster (SNC) mode and three memory modes – cache mode, flat mode and hybrid mode. For a detailed description of the Knights Landing Xeon Phi architecture refer to (Sodani, 2016).
4. Problem description
A real-world dataset of an outbound logistics network is provided by a global microchip producer. The company provided demand data for 9216 orders that need to be routed via their outbound supply chain network of 15 warehouses, 11 origin ports and one destination port (see Fig. 2 ). Warehouses are limited to a specific set of products that they stock, furthermore, some warehouses are dedicated for supporting only a particular set of customers. Moreover, warehouses are limited by the number of orders that can be processed in a single day. A customer making an order decides what sort of service level they require – DTD (Door to Door), DTP (Door to Port) or CRF (Customer Referred Freight). In the case of CRF, the customer arranges the freight and company only incur the warehouse cost. In most instances, an order can be shipped via one of 9 couriers offering different rates for different weight bands and service levels. Although most of the shipments are made via air transport, some orders are shipped via ground – by trucks. The majority of couriers offer discounted rates as the total shipping weight increases based on different weight bands. However, a minimum charge for shipment still applies. Furthermore, faster shipping tends to be more expensive, but offer better customer satisfaction. Customer service level is out of the scope of this research.
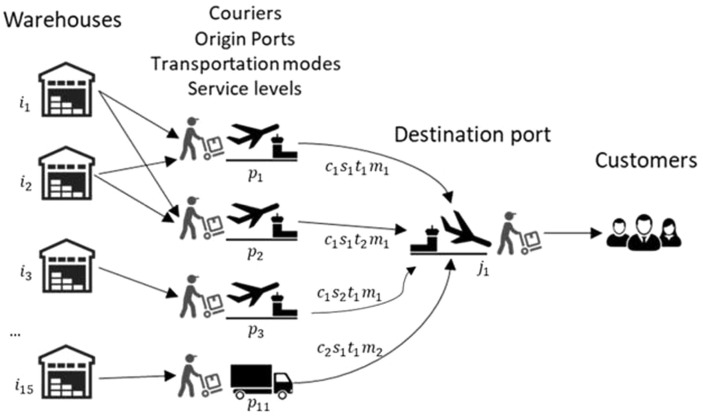
Fig. 2.
Graphical representation of the outbound supply chain. Each warehouse i is connected to one or many origin ports p. The shipping lane between origin port p and destination port j is a combination of courier c, service level s, delivery time t and transportation mode m.
Fig. 2 shows a simplified example case of the supply chain model. Warehouses and can be supplied by either origin ports or . In contrast, warehouse can only be supplied via origin port and warehouse can be only supplied by origin port . In the example shipping lane is chosen between and destination port with courier , service level , delivery time and transportation mode .
4.1. Dataset
Dataset (Ivars Dzalbs) is divided into seven tables, one table for all orders that need to be assigned a route – OrderList table, and six additional files specifying the problem and restrictions. For instance, the FreightRates table describes all available couriers, the weight gaps for each lane and rates associated. The shipping lane refers to courier-transportation mode-service level combination between two shipping ports. The PlantPorts table describes the allowed links between the warehouses and shipping ports in the real world. Furthermore, the ProductsPerPlant table lists all supported warehouse-product combinations. The VmiCustomers contains all edge cases, where the warehouse is only allowed to support specific customer, while any other non-listed warehouse can supply any customer. Moreover, the WhCapacities lists warehouse capacities measured in the number of orders per day and the WhCosts specifies the cost associated in storing the products in a given warehouse measured in dollars per unit.
4.2. Fitness function
The main goal of optimisation is to find a set of warehouses, shipping lanes and couriers to use for the most cost-effective supply chain. Therefore the fitness function is derived from two incurred costs – warehouse cost and transportation cost in Eq. (1). The totalling cost is then calculated across all orders in the dataset.
| (1) |
where is warehouse cost for order at warehouse and is transportation cost for order between warehouse port and customer port , the total number of orders
| (2) |
where warehouse cost for order at warehouse is calculated in (2), by the number of units in order multiplied by the warehouse storage rate (WhCosts table).
Furthermore, transportation cost for a given order k and chosen line between origin port p and destination port j is calculated by the algorithm in Fig. 3 :
Fig. 3.

Pseudocode for calculating order transportation cost.
where is the service level for order , – origin port, – destination port, – courier, – service level, – delivery time, – transportation mode. Furthermore, is the minimum charge for given line , is the weight in kilograms for order . is the freight rate (dollars per kilogram) for given weight gap based on the total weight for the line (FreightRates table).
The algorithm first checks what kind of service level the order requires, if the service level is equal to CRF (Customer Referred Freight) – transportation cost is 0. Furthermore, if order transportation mode is equal to GROUND (order transported via truck), order transportation cost is proportional to the weight consumed by the order () in respect of the total weight for given line and the rate charged by a courier for full track . In all other cases, the transportation cost is calculated based on order weight and the freight rate . The freight rate is determined based on total weight on any given line and the corresponding weight band in the freight rate table. Furthermore, a minimum charge is applied in cases where the air transportation cost is less than the minimum charge.
4.3. Restrictions
The problem being solved complies with the following constraints:
| (3) |
where = 1 if order was shipped from warehouse and 0 otherwise. is the order limit per day for warehouse (WhCapacities table).
| (4) |
where is the weight in kilograms for order shipped from warehouse port to customer port via courier using service level , delivery time and transportation mode . is the upper weight gap limit for line (FreightRates table).
| (5) |
where product for order belongs to supported products at warehouse (ProductsPerPlant table). Warehouses can only support given customer in the VmiCustomers table, while all other warehouses that are not in the table can supply any customer. Moreover, the warehouse can only ship orders via supported origin port, defined in PlantPorts table.
5. Methods and implementation
To solve the transportation network optimisation problem, we are using an Ant Colony System algorithm first proposed by (Dorigo & Gambardella, 1997). Because ACO is an iterative algorithm, it does require sequential execution. Therefore, the most naïve approach for parallel ACO is running multiple Independent Ant Colonies (IAC) with a unique seed for the pseudo-random number generator for each colony (high-level pseudocode in Fig. 4 ). Due to the stochastic nature of solution creation, it is, therefore, more probabilistic to reach a better solution than a single colony. This approach has the advantage of low overhead as it requires no synchronisation between the parallel instances during the search. At the very end of the search, the best solution of all parallel colonies is chosen as the final solution. The main disadvantage of IAC is that if one of the colonies finds a better solution, there is no way to improve all the other colony’s fitness values.
Fig. 4.
High-level pseudocode for Independent Ant Colonies (IAC) search algorithm.
Alternatively, the ACO search algorithm could also be letting the artificial ant colonies synchronise after every iteration. Therefore, all parallel instances are aware of the best solution and can share pheromones accordingly. High-level pseudocode of such Parallel Ant (PA) implementation is shown in Fig. 5 . The main advantage of this architecture is that it allows efficient pheromone sharing, therefore converging faster. However, there is a high risk of getting stuck into local optima as all ants start iteration with the same pheromone matrix. Furthermore, synchronisation of all parallel instances after every iteration is costly.
Fig. 5.
High-level pseudocode Parallel Ants (PA) search algorithm.
Both IAC and PA implementations are exploiting task parallelism – each parallel instance (thread) gets a set of tasks to complete. An alternative approach would be to look at data parallelism and vectorisation. In such a strategy, each thread processes a specific section of the data and cooperatively complete the given task. Due to the highly sequential parts of ACO, it would not be practical to only use vectorisation alone. A more desirable path would be to implement vectorisation in conjugate to the task parallelism. In case of CPU, task parallelism can be done by the threads, while vectorisation is done by Vector Processing Units (VPUs) based on Advanced Vector Extensions 2 (AVX2) or AVX512. Moreover, in the case of GPU and CUDA – task parallelism would be done at a thread-block level while data parallelism would exploit WARP structures. Parallel Ants with Vectorisation (PAwV) expands on the Parallel Ants architecture by introducing data-parallelism of solution creation and an alternative roulette wheel implementation – SS-Roulette, first proposed in (Cecilia et al., 2018). Local search in Fig. 6 expands on the implementation in Fig. 5 (lines 3–7). First, the choiceMatrix is calculated by multiplying the probability of the route to be chosen with the tabuList – a list of still available routes (where 0 represents not available and 1 – route still can be selected). A random number between 0 and 1 is generated to determine if a given route will be chosen based on exploitation or exploration. In the case of exploitation, the choiceMatrix is reduced to obtain the maximum and the corresponding route index. Furthermore, in the case of exploration, the route is chosen based on the SS-Roulette wheel described by (Cecilia et al., 2018).
Fig. 6.
High-level pseudocode for Parallel Ants with Vectorization (PAwV) search algorithm. Expanding on Fig. 5′ lines 3–7.
The main advantage of IAC is that it requires to synchronise between threads only at the start of the search and at the very end of the search, therefore keeping synchronisation overhead low. However, as there is no pheromone sharing, new better solutions cannot be shared across the parallel instances. In contrast, both PA and PAwV offers sharing of the best performing ants’ pheromone before the next iteration begins. The potential drawback is that search might get stuck in local optimum as all parallel instances share the same pheromone starting point. Furthermore, pheromone sharing and therefore, synchronisation between threads is costly overhead, especially if performed after each iteration. The PAwV architecture exploits the use of SIMD instructions for further data parallelism inside the Ant’s solution construction. Table 3 summarises these architectural features.
Table 3.
Comparison of Independent Ant Colonies (IAC), Parallel Ants (PA) and parallel Ants with Vectorisation (PAwV) architectures.
| IAC | PA | PAwV | |
|---|---|---|---|
| Synchronisation between threads during search | No | Yes | Yes |
| Pheromone sharing between parallel instances | No | Yes | Yes |
| Data parallelism | No | No | Yes |
6. Experiments
A sequential implementation of ACO described in (Dorigo & Gambardella, 1997) is adapted from (Veluscek, Kalganova, Broomhead, & Grichnik, 2015) by altering the heuristic information calculation for a given route – defined as a proportion of order’s weight and the maximum weight gap (see Eq. (2)). Furthermore, the ACO set of parameters were obtained from both work in (Veluscek, Kalganova, Broomhead, & Grichnik, 2015) and empirical experimentation. Table 4 summarises these algorithm hyperparameters. Moreover, we then implement three different Parallel ACO architectures – Independent Ant Colonies (IAC), Parallel Ants (PA) and Parallel Ants with Vectorisation (PAwV) in C++ and CUDA C.
Table 4.
Ant Colony System set of parameters for all configurations and architectures.
| Parameter | Value |
|---|---|
| Pheromone evaporation rate (rho) | 0.1 |
| Weight on pheromone information (α) | 1 |
| Weight on heuristic information (β) | 8 |
| Exploitation to exploration ratio (q0) | 0.9 |
Experiments were conducted on three different hardware configurations – CPU, GPU and Xeon Phi.
Hardware a - CPU
-
•
CPU: AMD Ryzen™ Threadripper™ 1950X (16 cores, 32 threads), running at 3.85 GHz.
-
•
RAM: 64 GB 2400 MHz DDR4, 4 channels.
-
•
OS: Windows 10 Pro, version 1703
-
•
Toolchain: Intel C++ 18.0 toolset, Windows SDK version 8.1, x64
Hardware B - Xeon Phi
-
•
CPU: Intel® Xeon Phi™ Processor 7250F (68 cores, 272 hyper-threads), running at 1.4 GHz. Clustering mode set to Quadrant and memory mode set to Cache mode.
-
•
RAM: 16 GB on-chip MCDRAM and 96 GB 2400 MHz DDR4 ECC.
-
•
OS: Windows Server 2016, version 1607
-
•
Toolchain: Intel C++ 18.0 toolset, Windows SDK version 8.1, x64, KMP_AFFINITY = scatter
Hardware C - GPU
-
•
CPU/RAM/OS – see host Hardware A.
-
•
GPUs: 4x Nvidia GTX1070, 8 GB GDDR5 per GPU, 1.9 GHz core, 4.1 GHz memory. PCIe with 16x/8x/16x/8x.
-
•
Toolchain: Visual Studio v140 toolset, Windows SDK version 8.1, x64, CUDA 9.0, compute_35, sm_35
Hardware architecture C shares the same host CPU as Hardware A.
6.1. Benchmarks
It is crucial to consider both elapsed time and solution quality when referring to speed optimisation of optimisation algorithms. One could get superior convergence within iteration but, take twice as long to compute. Similarly, one could claim that the algorithm is much faster at completing a defined number of iterations but sacrifice solution quality. Furthermore, there is little point comparing sequential execution of one hardware platform to parallel implementation of another. A comparison should take into consideration all platform strengths and weaknesses and set up the most suitable configuration for a given platform.
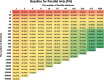
To obtain a baseline fitness convergence rate at a various number of parallel instances, we create Iterations vs Parallel Instances matrix for all architectures. An example of such matrix for Parallel Ants is shown in Table 5 . The matrix is derived by averaging the resulting fitness obtained from 10 independent simulations with a unique seed value for each given Parallel Instances configuration. All configurations are run for x number of iterations, where x is based on the total number of solutions explored and is a function of the number of Parallel Instances. The total number of solutions explored is set to 768 k. The number of Parallel Instances is varied by with maximum n of 11, i.e. 1024 parallel instances. The best value after every 5 iterations is also recorded.
Table 5.
Parallel Ants fitness value baseline for different configurations of the number of parallel instances and the number of iterations. Each Parallel Instance data point is an average of 10 individual runs (table derived from 11*10 = 110 runs). Expressed as a percentage of the proximity of the best-known solution (2,701,367.58). Colour-coded from worse – in red, to the best – in green.
 |
We then compute the number of iterations required to reach a specific solution quality for different ACO architectures in Table 6 , expressed as proximity to the best-known optimal solution. For the particular problem and dataset, the best solution is the total cost of 2,701,367.58. There are six checkpoints of solution quality ranging from 99% to 99.9%. Although at first 1% gain might not seem significant, one must remember that global supply chain costs are measured in hundreds of millions, and even 1% savings do affect the bottom line. Empty fields (-) represent instances where the ACO was not able to converge to given solution quality.
Table 6.
The number of iterations required to reach a specific solution quality. Each data point in the table is an average of 10 individual runs. Empty fields (-) represent instances where ACO did not obtain specified solution quality in 768 k solutions explored. The solution quality is expressed as a percentage of the proximity of the best-know solution (2,701,367.58).
|
The number of iterations required to reach specific solution quality | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Checkpoint of optimal solution | The number of parallel instances |
|||||||||||
| Architecture | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | |
| Independent Ant Colonies | 99.00% | 30 | 30 | 35 | 30 | 30 | 35 | 30 | 30 | 25 | 25 | 25 |
| 99.25% | 45 | 45 | 40 | 40 | 45 | 40 | 40 | 35 | 35 | 35 | 35 | |
| 99.50% | 31,685 | 31,055 | 29,550 | 28,895 | 29,075 | 15,910 | 10,950 | – | – | – | – | |
| 99.60% | – | – | – | – | – | – | – | – | – | – | – | |
| 99.75% | – | – | – | – | – | – | – | – | – | – | – | |
| 99.90% | – | – | – | – | – | – | – | – | – | – | – | |
| Parallel Ants | 99.00% | 30 | 25 | 25 | 25 | 25 | 25 | 20 | 15 | 15 | 15 | 15 |
| 99.25% | 45 | 40 | 40 | 35 | 35 | 35 | 35 | 35 | 30 | 30 | 30 | |
| 99.50% | 31,685 | 2590 | 65 | 60 | 60 | 55 | 55 | 55 | 55 | 50 | 50 | |
| 99.60% | – | – | 9190 | 2640 | 195 | 170 | 230 | 70 | 70 | 65 | 65 | |
| 99.75% | – | – | – | – | – | – | – | 685 | 310 | 140 | 135 | |
| 99.90% | – | – | – | – | – | – | – | – | – | 800 | 675 | |
| Parallel Ants with 5 sequential ant local search | 99.00% | 20 | 15 | 15 | 15 | 15 | 10 | 10 | 10 | 10 | 10 | 5 |
| 99.25% | 30 | 30 | 30 | 30 | 30 | 25 | 30 | 25 | 20 | 25 | 20 | |
| 99.50% | 400 | 65 | 55 | 55 | 50 | 50 | 50 | 50 | 45 | 45 | 45 | |
| 99.60% | – | 7715 | 160 | 135 | 90 | 65 | 60 | 65 | 60 | 55 | 55 | |
| 99.75% | – | – | – | – | 6630 | 205 | 150 | 155 | 130 | 125 | 125 | |
| 99.90% | – | – | – | – | – | – | – | – | 460 | 255 | 160 | |
On all experiments, IAC was able to obtain solution quality only below 99.6%. In contrast, PA and PA with 5 ant local search were able to achieve above 99.9% solution quality with 512 and 1024 parallel instances. Furthermore, IAC did not see any significant benefit of adding more parallel instances for 99% and 99.25% checkpoints.
In contrast, PA does benefit from the increase in the number of parallel instances. For instance, PA can obtain the same solution quality in half the number of iterations at 99% checkpoint (scaling of 2x for sequential vs 1024 parallel instances). Scaling of 633.7x in case of 99.5% checkpoint for sequential counterpart. Similarly, PA with 5 ant sequential local search has the same dynamics, with scaling of 4x at 99% checkpoint compared to sequential and 140x at 99.6% checkpoint compared to 2 and 1024 parallel instances. One can also note that at increased solution quality and a little number of parallel instances, PA with 5 ant local search also offers improved efficiency in terms of total solutions explored. For example, at the 99.5% checkpoint with 2 parallel instances, PA takes 2590 iterations, while PA with 5 ant local search only requires 65 (decrease of 40x iterations or 8x total solutions explored). However, in most instances, PA without any local search is more efficient.
6.2. Speed performance
To evaluate speed performance, we ran each given configuration and parallel architecture for 500 iterations or 10 min wall-clock time (whichever happens first) and recorded the total number of iterations and wall-clock time for three independent runs. Then, average wall-clock time per iteration was calculated. It is essential to measure the execution time correctly, just purely comparing computation per kernel/method may not show the real-life impact. For that reason, total time is measured from the start of the memory allocation to the freeing of the allocated memory, however it does not include the time required to load the dataset into memory. This allows us to estimate, with reasonable accuracy, what is the wall-clock time needed to run a specific architecture and configuration to converge to a given fitness quality. Although running each given architecture and configuration 10 times would produce more accurate convergence rate estimates, it would also require significantly more computation time. Furthermore, all vectorised implementations went through iterative profiling and optimisation process to obtain the fastest execution time. To the best of the authors’ knowledge, all vectorised implementations have been fully optimised for the given hardware.
6.2.1. CPU
ACO implementation of IAC, PA and PAwV was implemented in C++ and multiple experiments of the configurations are shown in Table 7 . Intel C++ 18.0 with OpenMP 4.0 was used to compile the implementation. KMP5 (an extension of OpenMP) config was varied based on total hardware core and logical core count (16c,2t = 32 OpenMP threads).
Table 7.
Hardware A wall-clock time per iteration, in seconds. KMP config is environment variable set as part of KMP_PLACE_THREADS, for all instances KMP_AFFINITY = scatter, optimisation level /O3, favour speed /Ot.
|
Hardware A - CPU computation time per iteration (in seconds) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Configuration |
The number of Parallel Instances |
|||||||||||
| KMP config | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | |
| IAC, double precision | 16c,1t | 0.078 | 0.081 | 0.083 | 0.085 | 0.112 | 0.196 | 0.372 | 0.691 | 1.368 | 2.661 | 5.263 |
| 16c,2t | 0.148 | 0.277 | 0.517 | 1.002 | 2.014 | 4.093 | ||||||
| PA, double precision | 16c,1t | 0.082 | 0.084 | 0.085 | 0.090 | 0.115 | 0.205 | 0.383 | 0.705 | 1.411 | 2.743 | 5.483 |
| 16c,2t | 0.153 | 0.288 | 0.539 | 1.044 | 2.088 | 4.220 | ||||||
| PAwV, double precision, AVX2 | 16c,1t | 0.050 | 0.053 | 0.057 | 0.058 | 0.075 | 0.131 | 0.233 | 0.426 | 0.805 | 1.547 | 3.101 |
| 16c,2t | 0.107 | 0.189 | 0.351 | 0.749 | 1.536 | 3.095 | ||||||
| PAwV, single precision, AVX2 | 16c,1t | 0.049 | 0.050 | 0.052 | 0.055 | 0.066 | 0.111 | 0.206 | 0.367 | 0.699 | 1.355 | 2.664 |
| 16c,2t | 0.088 | 0.152 | 0.275 | 0.501 | 1.006 | 1.975 | ||||||
| PAwV, single precision, AVX2, with 5 sequential ant local search | 16c,1t | 0.212 | 0.218 | 0.227 | 0.241 | 0.264 | 0.484 | 0.918 | 1.722 | 3.380 | 6.759 | 13.461 |
| 16c,2t | 0.347 | 0.645 | 1.222 | 2.369 | 4.659 | 9.704 | ||||||
Very similar results were obtained for both IAC double precision and PA double precision, with PA having around 5% overhead compared to IAC. In both instances, running 32 OpenMP threads offered around 24% speed reduction compared to 16 threads. Furthermore, PAwV with double precision vectorisation using AVX2 offered speed reduction of 26%, while scaling from 16 OpenMP threads to 32 offered almost no scaling at 256 parallel instances upwards.
The nature of ACO pheromone sharing and probability calculations does not require double precision and therefore can be substituted with single-precision calculations.
AVX2 offers 256-bit manipulations, therefore increasing theoretical throughput by a factor of 2, compared to double precision. 36% decrease in execution time was obtained, as not all parts of the code can take advantage of SIMD.
Furthermore, doing 5 ant sequential local search within each parallel instance increases time linearly and produces little time savings in terms of solutions explored. The overall scaling factor at 1024 parallel instances compared to sequential execution at PAwV (single precision with AVX2 and 16c2t) is therefore 25.4x.
6.2.2. Xeon Phi
Similar experiments were also conducted on the Xeon Phi hardware, Table 8 . Due to the poor convergence rate and search capability, the execution time for IAC was not measured. Xeon Phi differs from Hardware A with the ability to utilise up to 4 hyper-threads per core and AVX512 instruction set. Although Hardware B has 68 physical cores, for more straightforward comparison on base 2, only 64 were used in experiments. At 1024 parallel instances on double-precision PA, having 2 threads and 4 threads per core does offer speedup of 30% and 42% respectively, compared to 1 thread per core. Moving to the vectorised implementation of 256-bit AVX2, gains additional speedup of around 37% across all parallel instances, however, did not benefit from 4 hyper-threads. Furthermore, exploiting the AVX512 instruction set offers a further 24% speedup compared to AVX2. In this configuration having 4 hyper threads per core worsens the speed performance (3.644 s vs 3 s). Like Hardware A, PAwV was explored with single precision and offered near-perfect scaling on 1024 parallel instances with 4 hyper-threads per core, or 40% overall speed improvement compared to PAwV with double precision (3 s vs 1.804 s). Alike Hardware A, having 5 sequential local ants does not provide any time savings and time increases linearly. The overall scaling factor at 1024 parallel instances compared to sequential execution at PAwV (single precision with AVX512 and 64c4t) is therefore 148x.
Table 8.
Hardware B wall-clock time per iteration, in seconds. KMP config is environment variable set as part of KM_PLACE_THREADS, for all instances KMP_AFFINITY = scatter, optimisation level /O3, favour speed /Ot.
|
Hardware B - Xeon Phi computation time per iteration (in seconds) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Configuration |
The number of Parallel Instances |
|||||||||||
| KMP config | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | |
| PA, double precision | 64c,1t | 0.687 | 0.687 | 0.725 | 0.726 | 0.726 | 0.729 | 0.734 | 1.417 | 2.787 | 5.941 | 11.089 |
| 64c,2t | 1.014 | 1.974 | 3.845 | 7.669 | ||||||||
| 64c,4t | 1.087 | 1.606 | 3.226 | 6.438 | ||||||||
| PAwV, double precision, AVX2 | 64c,1t | 0.408 | 0.411 | 0.430 | 0.431 | 0.433 | 0.434 | 0.438 | 0.818 | 1.578 | 3.094 | 6.114 |
| 64c,2t | 0.563 | 1.047 | 2.022 | 3.964 | ||||||||
| 64c,4t | 0.625 | 1.101 | 2.072 | 4.082 | ||||||||
| PAwV, double precision, AVX512 | 64c,1t | 0.304 | 0.309 | 0.326 | 0.326 | 0.327 | 0.332 | 0.335 | 0.608 | 1.152 | 2.242 | 4.404 |
| 64c,2t | 0.446 | 0.809 | 1.535 | 3.000 | ||||||||
| 64c,4t | 0.494 | 0.982 | 1.913 | 3.644 | ||||||||
| PAwV, single precision, AVX512 | 64c,1t | 0.261 | 0.266 | 0.282 | 0.284 | 0.284 | 0.287 | 0.288 | 0.521 | 0.970 | 1.900 | 3.806 |
| 64c,2t | 0.359 | 0.646 | 1.210 | 2.361 | ||||||||
| 64c,4t | 0.412 | 0.542 | 0.957 | 1.804 | ||||||||
| PAwV, single precision, AVX512, with 5 sequential ant local search | 64c,1t | 1.105 | 1.123 | 1.195 | 1.200 | 1.205 | 1.205 | 1.215 | 2.342 | 4.601 | 9.136 | 18.844 |
| 64c,2t | 1.489 | 2.915 | 5.743 | 11.815 | ||||||||
| 64c,4t | 1.553 | 2.225 | 4.428 | 9.054 | ||||||||
6.2.3. GPUs
A further set of experiments were also conducted for GPU, Table 9 . The implementation with no vectorisation (Blocks x1), uses 1 thread per CUDA block to compute one solution, therefore 1024 parallel instances require 1024 blocks. Similarly, for (Blocks x32), 32 threads are used per block, each thread computing its own solution independently. For parallel instances of 32, only 1 block would be used with 32 threads. The implementation of no vectorisation utilises no shared memory; however, all static problem metadata is stored as textures. A single kernel is launched, and the best solution across all parallel instances is returned.
Table 9.
Hardware C wall-clock time per iteration, in seconds. The total number of parallel instances are adjusted for the thread-block dimensions. Compiled with CUDA 9.0. 1x, 2x and 4x correspond to the number of devices used to compute.
|
Hardware C - GPU computation time per iteration (in seconds) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Configuration | The number of Parallel Instances |
||||||||||
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | |
| 1x GPU no vectorisation (Blocks × 1) | 46.792 | 47.634 | 47.610 | 47.499 | 47.458 | 48.914 | 50.811 | 53.474 | 60.845 | 126.897 | 229.080 |
| 1x GPU no vectorisation (Blocks × 32) | – | – | – | – | – | 108.316 | 110.571 | 112.512 | 113.214 | 114.512 | 115.219 |
| 1x GPU with vectorisation (Blocks x32) | – | – | – | – | – | 49.890 | 52.457 | 54.180 | 55.409 | 58.802 | 64.569 |
| 1x GPU with vectorisation (Blocks x64) | – | – | – | – | – | – | 57.139 | 58.586 | 59.676 | 61.031 | 65.840 |
| 2x GPU with vectorisation (Blocks x32) | – | – | – | – | – | – | 50.048 | 52.634 | 55.471 | 55.509 | 60.856 |
| 4x GPU with vectorisation (Blocks x32) | – | – | – | – | – | – | – | 50.062 | 52.702 | 54.406 | 55.879 |
Vectorized version implements architecture described in (Cecilia et al., 2018), storing the route choice matrix in shared memory and utilising local warp reduction for sum and max operations. Each thread-block builds its solution, while the extra 32 threads assist with the reduction operations, memory copies and fitness evaluation. Table 9 shows a comparison between the two implementations. Implementation without vectorisation performs on average two times slower compared to the vectorised version. Furthermore, 64 threads per block (Blocks x64) performs slower than 32 threads per block (Block x32).
Next, scaling across multiple GPUs were explored. Each device takes a proportion of 1024 instances with unique seed values and after each iteration, the best overall solution is reduced. In the case of 2 GPUs and 1024 parallel instances, each device will compute 512 parallel instances concurrently. Scaling across 2 (2x) and 4 GPUs (4x) did not provide any significant speedup (only 10%). This is due to the fact that each iteration consumes at least 50 s and scaling across multiple GPUs adds almost no overhead. The maximum number of parallel instances might need to be increased to fully utilise all 4 GPUs to the point where all Streaming Multiprocessors (SMs) are saturated and increasing block count increases the computation time linearly.
GPU implementation is, therefore, one magnitude of order slower than that of CPU. However, this could be explained by the nature of the problem and not be specific to ACO architecture, as there have been a lot of success on GPUs solving simple, low memory footprint TSP instances (Uchida et al., 2014, Cecilia et al., Mar. 2018, Li, 2014). However, the problem addressed in this paper requires a lot of random global memory access to check for all restrictions such as order limits, capacity constraints and weight limits, which are too big to be stored on the shared memory.
6.3. Hardware comparison and speed of convergence
If both convergence rate of the architecture and the speed of the hardware is considered, an estimate can be made on what would be the average wall-clock time to converge to specific solution quality. The fastest configuration for both Hardware A (Table 7) and Hardware B (Table 8) was chosen and then multiplied by the number of iterations required to reach a specific solution quality (Table 6) to obtain an estimate of the compute time required (Table 10 ). Therefore, a fairer real-life impact can be derived.
Table 10.
Estimated time (in seconds) required to converge to specific solution quality. Calculated by multiplying the number of iterations by the time taken for iteration for individual best performing hardware configuration. Solution quality is expressed as a percentage of the proximity of the best-know solution (2,701,367.58).
|
Estimated time required (in seconds) to reach specific solution quality | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Architecture | Checkpoint of optimal solution | The number of parallel instances |
||||||||||
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | ||
| Hardware A - TR1950x | 99.00% | 1.46 | 1.24 | 1.30 | 1.39 | 1.64 | 2.19 | 3.04 | 4.13 | 7.52 | 15.10 | 29.63 |
| 99.25% | 2.19 | 1.99 | 2.07 | 1.94 | 2.29 | 3.06 | 5.31 | 9.64 | 15.03 | 30.19 | 59.25 | |
| 99.50% | 1539.02 | 128.82 | 3.37 | 3.33 | 3.93 | 4.81 | 8.35 | 15.14 | 27.56 | 50.32 | 98.75 | |
| 99.60% | 476.40 | 146.33 | 12.78 | 14.88 | 34.92 | 19.27 | 35.07 | 65.42 | 128.38 | |||
| 99.75% | 188.60 | 155.33 | 140.91 | 266.63 | ||||||||
| 99.90% | 805.20 | 1333.13 | ||||||||||
| Hardware B - Xeon Phi 7250F | 99.00% | 7.84 | 6.66 | 7.04 | 7.09 | 7.10 | 7.18 | 5.76 | 6.18 | 8.13 | 14.36 | 27.06 |
| 99.25% | 11.76 | 10.65 | 11.27 | 9.92 | 9.94 | 10.05 | 10.08 | 14.42 | 16.26 | 28.71 | 54.12 | |
| 99.50% | 8282.30 | 689.67 | 18.31 | 17.01 | 17.04 | 15.79 | 15.84 | 22.66 | 29.81 | 47.85 | 90.20 | |
| 99.60% | 2588.73 | 748.49 | 55.39 | 48.80 | 66.26 | 28.84 | 37.94 | 62.21 | 117.26 | |||
| 99.75% | 282.22 | 168.02 | 133.98 | 243.54 | ||||||||
| 99.90% | 765.60 | 1217.70 | ||||||||||
| Hardware C - GPU | 99.00% | 1404 | 1191 | 1190 | 1187 | 1186 | 1223 | 1001 | 751 | 791 | 816 | 838 |
| 99.25% | 2106 | 1905 | 1904 | 1662 | 1661 | 1712 | 1752 | 1752 | 1581 | 1632 | 1676 | |
| 99.50% | 1,482,595 | 123,373 | 3095 | 2850 | 2847 | 2690 | 2753 | 2753 | 2899 | 2720 | 2794 | |
| 99.60% | 437,536 | 125,398 | 9254 | 8315 | 11,511 | 3504 | 3689 | 3536 | 3632 | |||
| 99.75% | 16,338 | 7617 | 7544 | |||||||||
| 99.90% | 43,525 | 37,719 | ||||||||||
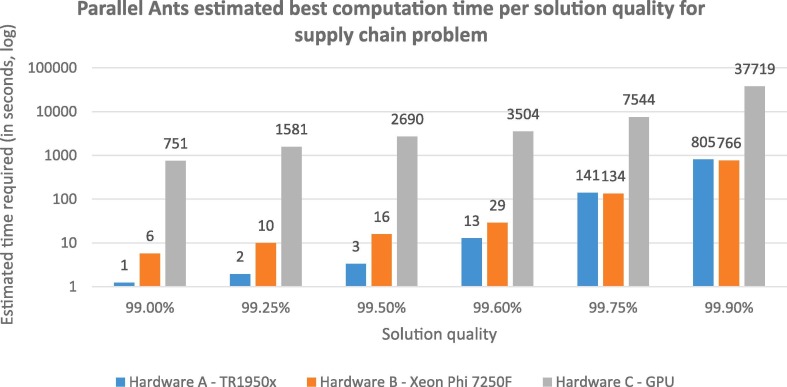
If one only considers the best time to converge to 99% solution quality, Hardware A can do that in 1.24 s on average while Hardware B would take 6.66 s. Furthermore, if we look at 99.5% solution quality, Hardware A would take 3.33 s while Hardware B − 17.01 s. Faster clock speed for Hardware A gives an advantage over Hardware B at lower solution quality checkpoints. In contrast, at 99.75% and 99.9% solution quality, Hardware B outperforms. More experimentation is required to determine if exploring more than 768 k solutions at lower Parallel Instance count affects the dynamics at the 99.75–99.9% range. In addition, best computation time to achieve specific solution quality was also compared in Fig. 7 , where the estimated best computation time required (in logarithmic) is plotted against three tested architectures across various solution quality checkpoints. Fig. 7 clearly shows that GPU results (Hardware C) were considerably slower and therefore, authors conclude that GPUs are not suitable for the supply chain problem solved.
Fig. 7.
Parallel Ants best estimated computation time per solution quality for supply chain problem to converge to specific solution quality. Solution quality is expressed as a percentage of the proximity of the best-know solution (2,701,367.58).
6.4. Comparisons using the travelling salesman problem
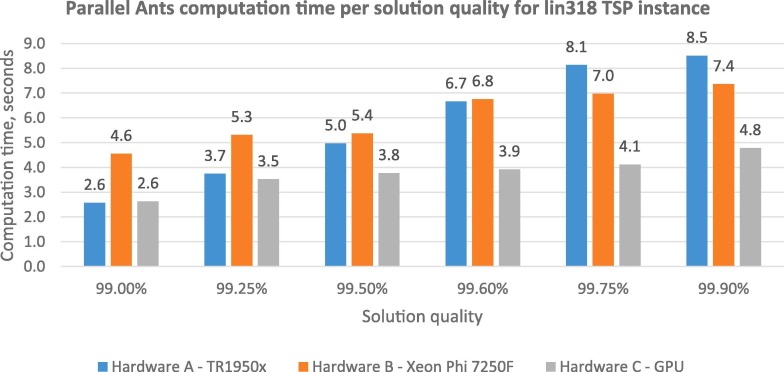
In addition to the real-world supply chain problem, a single TSP instance with 318 cities (lin318) is selected for comparison. The lin318 instance is small enough such that all experiments can be computed quickly but large enough to see measurable differences between hardware architectures explored. Like in the supply chain problem, solution quality checkpoints against optimal fitness value of 42,029 were recorded during the convergence process. Moreover, just like in supply chain problem, PA outperformed IAC architecture for solving lin318. The lin318 computation time was plotted against various hardware solutions and solution quality checkpoints in Fig. 8 .
Fig. 8.
Parallel Ants computation time per solution quality for lin318 TSP to converge to specific solution quality. Solution quality is expressed as a percentage of the proximity of the best-know solution (a distance of 42029).
When solving the lin318 TSP instance, Hardware A performs faster than Hardware B for solution quality between 99.0 and 99.6% and slower for higher solution quality, similar to the supply chain problem results in Fig. 7. Although Hardware C - GPU performed magnitudes slower in supply chain problem, for the TSP instance it was able to converge faster than Hardware A and Hardware B. Therefore, authors can confirm the findings of (Uchida et al., 2014, Cecilia et al., Mar. 2018, Li, 2014), that suggest that GPUs offer speedup over CPU counterpart when routing simple TSPs. However, authors also acknowledge that these dynamics do not apply for a more complex real-world routing problem where GPU is magnitudes slower than CPU counterparts (Hardware A or Hardware B) due to the additional meta-data required to be stored during solution creation.
7. Conclusions & further work
Nature-inspired meta-heuristic algorithms such as Ant Colony Optimization (ACO) have been successfully applied to multiple different optimisation problems. Most work focuses on the Travelling Salesman Problem (TSP). While TSPs are a good benchmark for new idea comparison, the dynamics of the proposed algorithms for benchmarks do not always match to a real-world performance where the problem has more constraints (more meta-data during solution creation). Furthermore, speed and fitness performance comparisons are not always completely fair when compared to a sequential implementation. This work explored the dynamics of different ACO architectures applied to benchmark and real-world problem. The experimental results demonstrate that the results obtained from the TSP benchmarks cannot be generalised to the real-world applications, especially in terms of hardware performance and usage. Therefore, our findings demonstrate that in order to achieve the generalisable conclusions, the experimental work has to be completed on both: standard benchmarks and real-world applications.
Furthermore, our work solves a real-world outbound supply chain network optimisation problem and compares two different ACO architectures – Independent Ant Colonies (IAC) and Parallel Ants (PA). It was concluded that PA outperformed IAC in all instances, as IAC failed to find any better solution than 99.5% of optimal. In comparison, PA was able to find a near-optimal solution (99.9%) in fewer iterations due to effective pheromone sharing across ants after each iteration. Furthermore, PA shows that it consistently finds a better solution with the same number of iterations as the number of parallel instances increase.
Moreover, a detailed speed performance was measured for three different hardware architectures – 16 core 32 thread workstation CPU, 68 core server-grade Xeon Phi and general-purpose Nvidia GPUs. Results showed that although GPUs can scale when solving simple TSP (as confirmed by multiple other studies), those scaling dynamics do not transfer to more complex the real-world problem. Memory access footprint required to check capacity limits and weight constraints did not fit on small shared memory on GPU. Thus, it performed 29 times slower than the other two hardware solutions even when running 4 GPUs in parallel. Therefore, authors consider this finding a new knowledge with surprise value.
When compared to a real-life impact on the time required to reach a specific solution quality, both CPU and Xeon Phi optimised-vectorised implementations showed comparable speed performance; with CPU taking the lead with lower Parallel Instances count due to the much higher clock frequency. At near-optimal solution (99.75%+) and 1024 parallel instances, Xeon Phi was able to take full advantage of AVX512 instruction set and outperformed CPU in terms of speed. Therefore, compared to an equivalent sequential implementation at 1024 parallel instances, CPU was able to scale 25.4x while Xeon Phi achieved a speedup of 148x.
Since PA fitness performance increases as the number of parallel instances increase, it would be worth looking into scaling above 1024 instances using either cluster of CPUs or clusters of Xeon Phi’s, which will be part of the future work. Furthermore, Field Programmable Gate Arrays (FPGAs) might have the potential to take advantage of highly vectorised ACO, which is another area of possible future research.
CRediT authorship contribution statement
Ivars Dzalbs: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing - original draft, Writing - review & editing, Visualization. Tatiana Kalganova: Conceptualization, Resources, Writing - review & editing, Visualization, Supervision, Project administration, Funding acquisition.
Acknowledgement
Authors would like to thank Intel Corporation for donating the Xeon Phi hardware and for partially sponsoring this research.
Biographies
Ivars Dzalbs is a second year PhD student at Brunel University London. His area of expertise is intelligent systems and artificial intelligence. Furthermore, Ivars holds Bachelors degree in Electronic and Computer engineering.
Dr Tatiana Kalganova (BUL: PI:TK) BSc (Hons), PhD, is a Reader in Intelligent Systems and ECE Postgraduate Research Director in ECE at Brunel. She has over 20 years of experience in design and implementation of applied Intelligent Systems. Her research into Ant Colony Optimization (ACO) and graph mathematics have been deployed into Caterpillar’s GEMSTONE supply chain optimization process leading to multiple internal and external international awards, including the 2016 Caterpillar Chairman’s Award for Process/Business Innovation, the 2016 Global Excellence in Analytics Award by the International Institute of Analytics, and 2017 Finalist for the INFORMS Innovation in Analytics prize.
Footnotes
Groups of 32 threads, are known as CUDA warps. For information refer to: https://devblogs.nvidia.com/using-cuda-warp-level-primitives/
OpenMP API website and documentation https://www.openmp.org/
CUDA documentation https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html.
Detailed description of Xeon Phi memory and cache modes available at: https://software.intel.com/en-us/articles/intel-xeon-phi-x200-processor-memory-modes-and-cluster-modes-configuration-and-use-cases
OpenMP Thread Affinity Control https://software.intel.com/en-us/articles/openmp-thread-affinity-control
Supplementary data to this article can be found online at https://doi.org/10.1016/j.cie.2020.106610.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- Abouelfarag A.A., Aly W.M., Elbialy A.G. Performance analysis and tuning for parallelization of ant colony optimization by using openmp. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 2015;9339:73–85. doi: 10.1007/978-3-319-24369-6_6. [DOI] [Google Scholar]
- Aslam, A., Khan, E., & Beg, M. M. S., (2015). Multi-threading based implementation of Ant-Colony Optimization algorithm for image edge detection. In 2015 Annual IEEE India Conference (INDICON), 2015, vol. 151, no. 2005, pp. 1–6, doi: 10.1109/INDICON.2015.7443603.
- Azad, N., Aazami, A., Papi, A., & Jabbarzadeh, A. (2019). A two-phase genetic algorithm for incorporating environmental considerations with production, inventory and routing decisions in supply chain networks. In Proceedings of the genetic and evolutionary computation conference companion on - GECCO ’19, pp. 41–42, doi: 10.1145/3319619.3326781.
- Bali O., Elloumi W., Abraham A., Alimi A.M. ACO-PSO optimization for solving TSP problem with GPU acceleration. Adv. Intell. Syst. Comput. 2017;557:559–569. doi: 10.1007/978-3-319-53480-0_55. [DOI] [Google Scholar]
- Bottani E., Murino T., Schiavo M., Akkerman R. Resilient food supply chain design: Modelling framework and metaheuristic solution approach. Computer Industrial Engineering. 2019;135:177–198. doi: 10.1016/j.cie.2019.05.011. October 2018. [DOI] [Google Scholar]
- Cecilia J.M., García J.M., Nisbet A., Amos M., Ujaldón M. Enhancing data parallelism for Ant Colony Optimization on GPUs. Journal of Parallel and Distributed Computing. 2013;73(1):42–51. doi: 10.1016/j.jpdc.2012.01.002. [DOI] [Google Scholar]
- Cecilia J.M., Llanes A., Abellán J.L., Gómez-Luna J., Chang L.-W., Hwu W.-M.W. High-throughput Ant Colony Optimization on graphics processing units. Journal of Parallel and Distributed Computing. Mar. 2018;113:261–274. doi: 10.1016/j.jpdc.2017.12.002. [DOI] [Google Scholar]
- Cecilia J.M., Llanes A., Abellán J.L., Gómez-Luna J., Chang L.W., Hwu W.M.W. High-throughput ant colony optimization on graphics processing units. Journal of Parallel and Distributed Computing. 2018;113:261–274. doi: 10.1016/j.jpdc.2017.12.002. [DOI] [Google Scholar]
- Chitty D.M. Applying ACO to large scale TSP instances. Adv. Intell. Syst. Comput. 2018;650:104–118. doi: 10.1007/978-3-319-66939-7_9. [DOI] [Google Scholar]
- Dawson, L., & Stewart, I. A. (2014). Accelerating ant colony optimization-based edge detection on the GPU using CUDA. In 2014 IEEE congress on evolutionary computation (CEC), pp. 1736–1743, doi: 10.1109/CEC.2014.6900638.
- Dawson, L. (2015). Generic techniques in general purpose gpu programming with applications To Ant Colony and Image Processing Algorithms.
- Dorigo M., Gambardella L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Transactions on Evolutionary Computation. Apr. 1997;1(1):53–66. doi: 10.1109/4235.585892. [DOI] [Google Scholar]
- El Baz, D., Hifi, M., Wu, L., & Shi, X. (2016). A parallel ant colony optimization for the maximum-weight clique problem. In 2016 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), pp. 796–800, doi: 10.1109/IPDPSW.2016.111.
- Esmaeilikia M., Fahimnia B., Sarkis J., Govindan K., Kumar A., Mo J. Tactical supply chain planning models with inherent flexibility: Definition and review. Annals of Operations Research. 2016;244(2):407–427. doi: 10.1007/s10479-014-1544-3. [DOI] [Google Scholar]
- Fathollahi-Fard A.M., Govindan K., Hajiaghaei-Keshteli M., Ahmadi A. A green home health care supply chain: New modified simulated annealing algorithms. J. Clean. Prod. 2019;240:118200. doi: 10.1016/j.jclepro.2019.118200. [DOI] [Google Scholar]
- Fingler H., Cáceres E.N., Mongelli H., Song S.W. A CUDA based solution to the multidimensional knapsack problem using the ant colony optimization. Procedia Computer Science. 2014;29(30):84–94. doi: 10.1016/j.procs.2014.05.008. [DOI] [Google Scholar]
- Gao J., Chen Z., Gao L., Zhang B. 2016 8th workshop on hyperspectral image and signal processing: Evolution in remote sensing (WHISPERS) 2016. GPU implementation of ant colony optimization-based band selections for hyperspectral data classification; pp. 1–4. [DOI] [Google Scholar]
- Guerrero G.D., Cecilia J.M., Llanes A., García J.M., Amos M., Ujaldón M. Comparative evaluation of platforms for parallel ant colony optimization. Journal of Supercomputing. 2014;69(1):318–329. doi: 10.1007/s11227-014-1154-5. [DOI] [Google Scholar]
- Gülcü Ş., Mahi M., Baykan Ö.K., Kodaz H. A parallel cooperative hybrid method based on ant colony optimization and 3-Opt algorithm for solving traveling salesman problem. Soft Computing. 2018;22(5):1669–1685. doi: 10.1007/s00500-016-2432-3. [DOI] [Google Scholar]
- Huo Y., Huang J.X. IEEE international parallel and distributed processing symposium workshops (IPDPSW) 2016. Parallel ant colony optimization for flow shop scheduling subject to limited machine availability; pp. 756–765. [DOI] [Google Scholar]
- Ismkhan H. Effective heuristics for ant colony optimization to handle large-scale problems. Swarm and Evolutionary Computation. 2017;32:140–149. doi: 10.1016/j.swevo.2016.06.006. [DOI] [Google Scholar]
- Ivars Dzalbs, T. K. Supply chain logistics problem dataset. [Online]. Available: https://brunel.figshare.com/articles/Supply_Chain_Logistics_Problem_Dataset/7558679.
- Kalayci C.B., Kaya C. An ant colony system empowered variable neighborhood search algorithm for the vehicle routing problem with simultaneous pickup and delivery. Expert Systems with Applications. 2016;66:163–175. doi: 10.1016/j.eswa.2016.09.017. [DOI] [Google Scholar]
- Kallioras N.A., Kepaptsoglou K., Lagaros N.D. Transit stop inspection and maintenance scheduling: A GPU accelerated metaheuristics approach. Transp. Res. Part C Emerg. Technol. 2015;55:246–260. doi: 10.1016/j.trc.2015.02.013. [DOI] [Google Scholar]
- Khatri K., Kumar Gupta V. Research on solving travelling salesman problem using rank based ant system on GPU. Compusoft. 2015;4(5):2320. [Google Scholar]
- Kıran M.S., Özceylan E., Gündüz M., Paksoy T. A novel hybrid approach based on particle swarm optimization and ant colony algorithm to forecast energy demand of Turkey. Energy Conversion Management. 2012;53(1):75–83. doi: 10.1016/j.enconman.2011.08.004. [DOI] [Google Scholar]
- Li F. GACO: A GPU-based high performance parallel multi-ant colony optimization algorithm. Journal of Information Computing Science. 2014;11(6):1775–1784. doi: 10.12733/jics20103218. [DOI] [Google Scholar]
- Li B.H., Lu M., Shan Y.G., Zhang H. Parallel ant colony optimization for the determination of a point heat source position in a 2-D domain. Applied Thermal Engineering. 2015;91:994–1002. doi: 10.1016/j.applthermaleng.2015.09.002. [DOI] [Google Scholar]
- Llanes A., Cecilia J.M., Sánchez A., García J.M., Amos M., Ujaldón M. Dynamic load balancing on heterogeneous clusters for parallel ant colony optimization. Cluster Computation. 2016;19(1):1–11. doi: 10.1007/s10586-016-0534-4. [DOI] [Google Scholar]
- Llanes A., Vélez C., Sánchez A.M., Pérez-Sánchez H., Cecilia J.M. Parallel ant colony optimization for the HP protein folding problem. In: Ortuño F., Rojas I., editors. Lecture notes in computer science (including subseries lecture notes in artificial intelligence and lecture notes in bioinformatics) Springer International Publishing; Cham: 2016. pp. 615–626. [Google Scholar]
- Lloyd H., Amos M. A highly parallelized and vectorized implementation of max-min ant system on Intel® Xeon PhiTM. 2016 IEEE Symp Ser. Comput. Intell. SSCI. 2017;2016 doi: 10.1109/SSCI.2016.7850085. [DOI] [Google Scholar]
- Markvica D., Schauer C., Raidl G.R. CPU versus GPU parallelization of an ant colony optimization for the longest common subsequence problem. In: Moreno-Díaz R., Pichler F., Quesada-Arencibia A., editors. Lecture notes in computer science (including subseries lecture notes in artificial intelligence and lecture notes in bioinformatics) Springer International Publishing; Cham: 2015. pp. 401–408. [Google Scholar]
- Mehne H.H. Evaluation of parallelism in ant colony optimization method for numerical solution of optimal control problems. J. Electr. Eng. Control Comput. Sci. JEEECCS. 2015;1(2):15–20. [Google Scholar]
- Mohammed, A., & Duffuaa, S. (2019). A meta-heuristic algorithm based on simulated annealing for designing multi-objective supply chain systems. In 2019 Industrial & systems engineering conference (ISEC), pp. 1–6, doi: 10.1109/IASEC.2019.8686517.
- Murooka, R., Ito, Y., & Nakano, K. (2016). Accelerating ant colony optimization for the vertex coloring problem on the GPU. In 2016 Fourth International Symposium on Computing and Networking (CANDAR), pp. 469–475, doi: 10.1109/CANDAR.2016.0088.
- NSharma, S., & Garg, V. (2015). Multi colony ant system based solution to travelling salesman problem using OpenCL. Int. J. Comput. Appl., vol. 118, no. 23, pp. 1–3, May 2015, doi: 10.5120/20882-3637.
- O. U. B and R. Tarnawski, Machine Learning, Optimization, and Big Data, vol. 10710. Cham: Springer International Publishing, 2018.
- Panicker V.V., Reddy M.V., Sridharan R. Development of an ant colony optimisation-based heuristic for a location-routing problem in a two-stage supply chain. International Journal of Value Chain Management. 2018;9(1):38. doi: 10.1504/IJVCM.2018.091109. [DOI] [Google Scholar]
- Prakasam A., Savarimuthu N. Metaheuristic algorithms and probabilistic behaviour: A comprehensive analysis of ant colony optimization and its variants. Artificial Intelligence Review. 2016;45(1):97–130. doi: 10.1007/s10462-015-9441-y. [DOI] [Google Scholar]
- Randall M., Lewis A. A parallel implementation of ant colony optimization. Journal of Parallel and Distributed Computing. 2002;62(9):1421–1432. doi: 10.1006/jpdc.2002.1854. [DOI] [Google Scholar]
- Rohit Chandra R., Dagum Leo, Kohr David. Parallel programming in OpenMP. Elsevier. 2000 [Google Scholar]
- Sato, M., Tsutsui, S., Fujimoto, N., Sato, Y., & Namiki, M. (2014). First results of performance comparisons on many-core processors in solving QAP with ACO, pp. 1477–1478, doi: 10.1145/2598394.2602274.
- Schyns M. An ant colony system for responsive dynamic vehicle routing. European Journal of Operational Research. 2015;245(3):704–718. doi: 10.1016/j.ejor.2015.04.009. [DOI] [Google Scholar]
- Seshadri, C. S, H. S., & Lokesha, V. (2015). An effective parallelism topology in ant colony optimization algorithm for medical image edge detection with critical path methodology (PACO-CPM). International Journal Recent Contribution from Engineering Science IT, vol. 3, no. 4, pp. 12, doi: 10.3991/ijes.v3i4.5139.
- Skinderowicz R. The GPU-based parallel Ant Colony System. Journal of Parallel and Distributed Computing. 2016;98:48–60. doi: 10.1016/j.jpdc.2016.04.014. [DOI] [Google Scholar]
- Skinderowicz R. Implementing a GPU-based parallel MAX–MIN ant system. Futur. Gener. Comput. Syst. May 2020;106:277–295. doi: 10.1016/j.future.2020.01.011. [DOI] [Google Scholar]
- Sodani, J. J. R. (2016). Intel xeon phi processor high performance programming: Knights landing edition, Edition 2. Morgan Kaufmann.
- Tan Y., Ding K. A survey on GPU-based implementation of swarm intelligence algorithms. IEEE Transactions on Cybernetics. 2016;46(9):2028–2041. doi: 10.1109/TCYB.2015.2460261. [DOI] [PubMed] [Google Scholar]
- Thiruvady D., Ernst A.T., Singh G. Parallel ant colony optimization for resource constrained job scheduling. Annals of Operations Research. 2016;242(2):355–372. doi: 10.1007/s10479-014-1577-7. [DOI] [Google Scholar]
- Tirado F., Barrientos R.J., González P., Mora M. Efficient exploitation of the xeon phi architecture for the ant colony optimization (ACO) metaheuristic. Journal of Supercomputing. 2017;73(11):5053–5070. doi: 10.1007/s11227-017-2124-5. [DOI] [Google Scholar]
- Tirado, F., Urrutia, A., & Barrientos, R. J. (2015). Using a coprocessor to solve the ant colony optimization algorithm. In 2015 34th international conference of the chilean computer science society (SCCC), vol. 2016-Febru, pp. 1–6, doi: 10.1109/SCCC.2015.7416584.
- Tufteland, T., Ødesneltvedt, G., & Goodwin, M. (2016). Optimizing PolyACO training with GPU-based parallelization. In International series in operations research and management science, vol. 272, pp. 233–240.
- Uchida, A., Ito, Y., & Nakano, K. (2014). Accelerating ant colony optimisation for the travelling salesman problem on the GPU. International Journal of Parallel, Emergent and Distributed Systems, vol. 29, no. 4. Taylor & Francis, pp. 401–420, doi: 10.1080/17445760.2013.842568.
- Valdez, F., Moreno, F., & Melin, P. (2020). A comparison of ACO, GA and SA for solving the TSP problem, pp. 181–189.
- Veluscek M., Kalganova T., Broomhead P., Grichnik A. Composite goal methods for transportation network optimization. Expert Systems with Applications. May 2015;42(8):3852–3867. doi: 10.1016/j.eswa.2014.12.017. [DOI] [Google Scholar]
- Vieira P.F., Vieira S.M., Gomes M.I., Barbosa-Póvoa A.P., Sousa J.M.C. Designing closed-loop supply chains with nonlinear dimensioning factors using ant colony optimization. Soft Computing. 2015;19(8):2245–2264. doi: 10.1007/s00500-014-1405-7. [DOI] [Google Scholar]
- Wagh A., Nemade V. Query optimization using modified ant colony algorithm. International Journal of Computers and Applications. Jun. 2017;167(2):29–33. doi: 10.5120/ijca2017914185. [DOI] [Google Scholar]
- Wang K.-J., Lee C.-H. A revised ant algorithm for solving location–allocation problem with risky demand in a multi-echelon supply chain network. Applied Soft Computing. 2015;32:311–321. doi: 10.1016/j.asoc.2015.03.046. [DOI] [Google Scholar]
- Wang P., Li H., Zhang B. A GPU-based parallel ant colony algorithm for scientific workflow scheduling. Int. J. Grid Distrib. Comput. 2015;8(4):37–46. doi: 10.14257/ijgdc.2015.8.4.04. [DOI] [Google Scholar]
- Wang J., Osagie E., Thulasiraman P., Thulasiram R.K. HOPNET: A hybrid ant colony optimization routing algorithm for mobile ad hoc network. Ad Hoc Networks. 2009;7(4):690–705. doi: 10.1016/j.adhoc.2008.06.001. [DOI] [Google Scholar]
- Weidong G., Jinqiao F., Yazhou W., Hongjun Z., Jidong H. 2015 8th international conference on intelligent computation technology and automation (ICICTA) 2015. Parallel performance of an ant colony optimization algorithm for TSP; pp. 625–629. [DOI] [Google Scholar]
- Wong L., Moin N.H. Ant colony optimization for split delivery inventory routing problem. Malaysian Journal of Computing Science. 2017;30(4):333–348. doi: 10.22452/mjcs.vol30no4.5. [DOI] [Google Scholar]
- Yang Q., Fang L., Duan X. RMACO :A randomly matched parallel ant colony optimization. World Wide Web. 2016;19(6):1009–1022. doi: 10.1007/s11280-015-0369-6. [DOI] [Google Scholar]
- Yeh W.-C., Chuang M.-C. Using multi-objective genetic algorithm for partner selection in green supply chain problems. Expert Systems with Applications. 2011;38(4):4244–4253. doi: 10.1016/j.eswa.2010.09.091. [DOI] [Google Scholar]
- Yelmewad P., Kumar A., Talawar B. 2019 10th international conference on computing, communication and networking technologies (ICCCNT) 2019. MMAS on GPU for large TSP instances; pp. 1–6. [DOI] [Google Scholar]
- Zhang Z., Zhang N., Feng Z. Multi-satellite control resource scheduling based on ant colony optimization. Expert Systems with Applications. 2014;41(6):2816–2823. doi: 10.1016/j.eswa.2013.10.014. [DOI] [Google Scholar]
- Zhang S., Zhang W., Gajpal Y., Appadoo S.S. Ant colony algorithm for routing alternate fuel vehicles in multi-depot vehicle routing problem. Springer Singapore. 2019:251–260. [Google Scholar]
- Zhou Y., He F., Hou N., Qiu Y. Parallel ant colony optimization on multi-core SIMD CPUs. Future Generation Computing Systems. 2018;79:473–487. doi: 10.1016/j.future.2017.09.073. [DOI] [Google Scholar]
- Zhou Y., He F., Qiu Y. Dynamic strategy based parallel ant colony optimization on GPUs for TSPs. Sci. China Inf. Sci. Jun. 2017;60(6):068102. doi: 10.1007/s11432-015-0594-2. [DOI] [Google Scholar]
- Zhou W., He F., Zhang Z. 2017 IEEE 21st international conference on computer supported cooperative work in design (CSCWD) 2017. A GPU-based parallel MAX-MIN Ant System algorithm with grouped roulette wheel selection; pp. 360–365. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.