Abstract
American Southwest (ASW) megadroughts represent decadal-scale periods of dry conditions, the near-term risks of which arise from natural low-frequency hydroclimate variability and anthropogenic forcing. A large single-climate-model ensemble indicates anthropogenic forcing increases near-term ASW megadrought risk by a factor of 100, however, accurate risk assessment remains a challenge. At the global-scale we find that anthropogenic forcing may alter the variability driving megadroughts over 55% of land-areas, undermining accurate assessments of their risk. For the remaining areas, current ensembles are too small to characterize megadroughts’ driving variability. For example, constraining uncertainty in near-term ASW megadrought risk to 5 percentage points with high confidence requires 287 simulations. Such ensemble sizes are beyond current computational and storage resources and these limitations suggest that constraining errors in near-term megadrought risk projections with high confidence-even in places where underlying variability is stationary-is not currently possible.
1. INTRODUCTION
Decadal-to-multidecadal periods of meteorological drought (hereinafter drought will be used to refer to meteorological drought), or megadroughts, are a robust feature of the Common Era paleoclimate record, particularly in the American Southwest (ASW-32°N-41°N; 125°W-105°W; e.g. Cook et al. 2016). Quantifying the risk of a megadrought occurring in the future is critical: past megadroughts in the ASW, for instance, were sufficiently intense to decrease the Colorado basin’s runoff by 15% on multidecadal timescales (Meko et al. 2007). If such a drought were to occur again, it would greatly affect water availability and present stresses for people and ecosystems. At the same time, megadroughts represent natural hydroclimate change on the very timescales over which projections of future hydroclimate are made to inform decision-making (e.g. IPCC AR5-Stocker et al. 2014).
Hydroclimate conditions at the end of the 21st century are likely to be dominated by anthropogenic radiative forcing, with severe drying projected for the ASW (Cook et al. 2014a; 2015). Over the near-term decades, however, hydroclimate change will involve a significant contribution from low-frequency internal variability, which likely played a role in driving real-world megadroughts (e.g. Coats et al., 2016, Ault et al., 2014, 2015, Woodhouse and Lukas, 2006, Ho et al., 2016). The varied ways in which anthropogenic forcing and internal variability could interact over the coming decades will determine near-term future hydroclimate (e.g. Mankin et al., 2015), and therefore, megadrought risk.
Accurately projecting near-term future megadrought risk necessitates estimating the frequency of megadrought occurrence from climate models forced with the most likely future trajectories of exogenous boundary conditions. Complicating this estimate over the near-term future, however, are two issues: First, is whether climate models can simulate megadroughts with the correct atmosphere-ocean dynamical drivers (e.g. Coats et al. 2013; 2015; Ault et al. 2013; 2014). Second, megadroughts are necessarily rare events. Estimating future megadrought risk, therefore, requires a robust characterization of the future mean and variability in hydroclimate.
“Large” ensembles of a single climate model represent a new tool motivated, in part, by the goal of having an ensemble large enough to robustly sample internal variability in a nonstationary climate (Kay et al. 2015; Deser et al. 2012). In the context of estimating future megadrought risk, for instance, a large ensemble should allow for a robust characterization of both mean hydroclimate and the distribution around this mean in the future-with the caveat that such an ensemble can only characterize that model’s representation of the climate system. Importantly, producing a large ensemble requires considerable computational and storage resources, with each additional ensemble member in the National Center for Atmospheric Research (NCAR) Community Earth System Model (CESM) large ensemble project taking three weeks to run on their Yellowstone supercomputer (e.g., Kay et al. 2015). This considerable computational expense necessitates an understanding of the number of simulations required to robustly sample internal variability in different climate variables and on different timescales.
Along these lines, recent work suggests that a statistically-derived ensemble based on the statistical moments of an unforced control simulation can produce the same range of future precipitation and temperature trends as a forced large single-model ensemble (Thompson et al. 2015). Such a conclusion, however, is predicated on a problematic assumption: It assumes that the statistics of internal variability in the future will be the same as in the present. Yet there is evidence that forcing can project onto internal modes of variability (e.g. Palmer 1993, Cai et al. 2014, 2015), violating this assumption. Projections from process-based large single-model ensembles, on the other hand, are dynamically derived, allowing for nonstationary internal variability. These model-based projections also provide information on the atmosphere-ocean dynamics underlying climate features-which may change in the future even if the statistics of internal variability are unchanged. Finally, if we regard the single-model ensemble mean as the model’s ‘forced response’ (e.g., Deser et al. 2012; Thompson et al. 2015), then the estimate of the forced response itself is a function of the number of ensemble members included in its calculation. Large single-model ensembles thus provide a more robust estimate of a model’s forced response.
Given this context, projections from large single-model ensembles are clearly valuable and we leverage such an ensemble (Kay et al. 2015) in a perfect model framework, which uses variability in a long unforced model simulation as ground truth, to analyze the challenge of accurately estimating future megadrought risk. Specifically, we ask three related questions: (1) Where do the statistics of internal hydroclimate variability remain unchanged with forcing (i.e., where do the assumptions of a perfect model framework hold)? (2) For places where the perfect model framework’s assumptions hold, how many model ensemble members are necessary to accurately estimate future megadrought risk? And (3) What is the marginal value of each additional model ensemble member towards accurately estimating future megadrought risk? We answer these questions by analyzing future megadrought risk in the ASW, but also generalize our results globally for those locations where the perfect model framework applies (see Methods section 2.3). Given uncertainties in our physical understanding of real-world megadroughts, however, these questions can only inform our understanding of the size of contemporary model ensembles and highlight the difficulties of using these ensembles to project future megadrought risk.
2. METHODS
2.1. Climate model data
All model output is from the NCAR CESM Large Ensemble project (hereinafter LENS, Kay et al. 2015). We utilize 30 LENS ensemble members over the period 2006–2040 C.E., as well as the full 1100-year CESM control simulation (hereinafter the CESM control simulation). The former runs employ the RCP8.5 emissions scenario of the Coupled Model Intercomparison Project phase 5 (“CMIP5”, Taylor et al. 2012). Uncertainty in our physical understanding of real-world megadroughts precludes a validation of megadroughts within the model. Nevertheless, Figure S1 provides a validation of temperature and precipitation over the ASW. The climatology and variability of temperature and precipitation over the ASW, as well as teleconnections to the ASW are well produced by the NCAR CESM.
2.2. Megadrought estimation
The hydroclimate variable used herein is the Palmer Drought Severity Index (PDSI, Palmer 1965), which was chosen to maintain consistency with both the paleoclimate record of hydroclimate over North America (Cook et al. 2007; Cook et al. 2014b) and previous studies (Cook et al. 2014a; 2015). PDSI is an offline estimate of soil moisture balance, and has been established as a robust estimator of soil moisture variability that compares well to other soil moisture metrics (e.g. the Standardized Precipitation Evapotranspiration Index (SPEI), Vicente Serrano et al. 2010; Cook et al. 2014a) and model soil moisture (Cook et al. 2014a; 2015; Smerdon et al. 2015). PDSI is calculated from supply via precipitation and losses due to evapotranspiration (ET), with ET estimated by means of scaling potential evapotranspiration (PET) using a beta function. PET is estimated herein using the Food and Agriculture Organization (FAO) of the United Nations (Allen et al. 1998) formulation of the Penman-Monteith (PM) function (Penman 1948; Xu and Singh 2002). Precipitation, surface pressure, surface temperature, vapor pressure and surface net radiation model fields are utilized. Wind speed and ground heat flux are set to constant values of 1 and 0, respectively, because PDSI calculated using PM PET is not highly sensitive to them (Cook et al. 2014a). Soil moisture capacities are set at the standard values of 25.4 mm and 127 mm for the top and bottom layers. PDSI is calculated using this formulation for all 30 LENS ensemble members and the 1100-year CESM control simulation (years 400–1499) with all PDSI values standardized against the full CESM control simulation. Hydroclimate timeseries are produced by taking an area-weighted average of the grid point PDSI over the ASW (32°N-41°N; 125°W-105°W) for the ASW results, and at the grid-point scale for the global results.
Megadroughts in the PDSI timeseries are defined using the multidecadal megadrought definition of Ault et al. (2014), in which the 35-year mean is at least 0.5 standard deviations below the mean (for the ASW this is −0.99 PDSI). While Ault et al. (2014) use precipitation in their analyses, our megadrought definition is qualitatively consistent, with the main difference being the inherent 12–18 month memory timescale of PDSI. Using this definition megadrought risk is then the percent of 35-year periods with mean PDSI of less than −0.5 standard deviations, with the standard deviation defined over the full CESM control simulation. Hereinafter mean PDSI over a 35-year period will be referred to as a 35-year hydroclimate state.
2.3. Perfect model framework
A perfect model framework is used to answer questions (2) and (3) of the introduction. In particular, future megadrought risk is defined by calculating megadrought risk using all 35-year hydroclimate states from the CESM control simulation shifted by the mean of the 30 LENS ensemble members between 2006–2040 C.E. (an estimate of the CESM’s forced response to RCP8.5). This will be the “perfect” baseline by which we determine if future megadrought risk has been accurately projected. Importantly, this definition of future megadrought risk assumes that statistics of internal variability are unchanged in the future. To explicitly test this assumption we will use a two-sample Kolmogorov-Smirnov (K-S) test, a nonparametric test of the similarity of distributions. Specifically, the K-S test is used to compare the 35-year hydroclimate states from the CESM control simulation to the 35-year hydroclimate states (2006–2040 C.E.) from LENS. In a K-S test small p-values indicate that the null-hypothesis that the two samples come from populations with the same distribution can be rejected. Rejecting the null hypothesis implies that forced internal variability is different from unforced internal variability and the future megadrought risk as defined herein is likely incorrect. By consequence, for grid points or regions with p-values greater than 0.5, we do not attempt to answer questions (2) and (3) of the introduction. It is important to note that despite satisfying this criterion, the statistics of internal variability still may have changed at the analyzed grid points or regions. While it is not possible to project this source of error onto the analysis of megadrought risk, we caution that it could cause the answer to question (2) to be either too large or too small. A direct assessment of the impact of this issue over the ASW is included in Figure 3 and Section 3.3.
Figure 3:
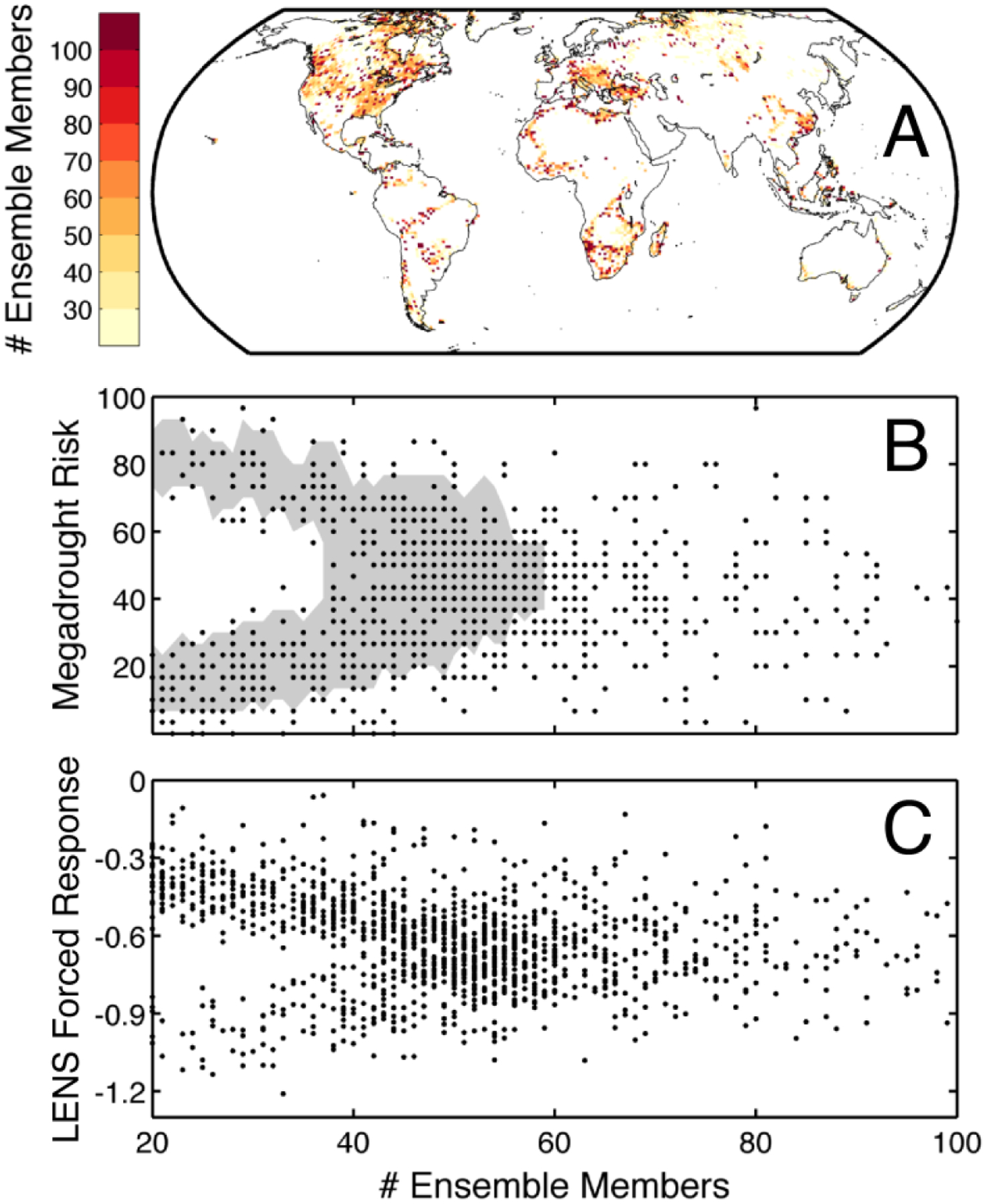
(Panel A) The number of ensemble members necessary to achieve 5 pp error in the median using the same analysis as Fig. 1b. (Panel B) The values in Panel A (x-axis) plotted against future megadrought risk from the perfect model framework (y-axis). The grey shaded region is the range for the same plot but randomly subsampling the CESM control simulation to calculate number of ensemble members instead of using surrogate timeseries based on the LENS. (Panel C) The values in Panel A (x-axis) plotted against the ensemble mean PDSI of the 30 LENS ensemble members between 2006–2040 C.E. (an estimate of the forced response to RCP8.5-y-axis). (Panel A, B and C) Values are only shown for grid points with a p-value greater than 0.5 in Fig. 2a, an increase in future megadrought risk (2006–2040 C.E.), and a future megadrought risk (2006–2040 C.E.) that is less than 100%.
2.4. Timeseries modeling
The timeseries modeling we pursue is a means to test how the accuracy of megadrought risk estimation varies with ensemble size. We statistically generate many realizations of hydroclimate with random time evolutions but preserving the spectral characteristics, mean, and magnitude of the LENS. These timeseries are surrogate hydroclimate realizations with the same characteristics as the LENS. These surrogates allow estimates of the number of LENS ensemble members needed to accurately estimate future megadrought risk (defined using the perfect model framework, as described above).
All timeseries modeling uses a power law rescaling of uncorrelated white noise following Ault et al. (2014) to match the LENS’ spectral and statistical characteristics. This involves: (1) calculating the discrete Fourier transform of a white noise timeseries that has been scaled to have the same variance as the LENS. (2) Rescaling the Fourier coefficients to be power-law distributed (with a predefined value of β) before taking the real part of the inverse Fourier transform. In this case β is determined by estimating the spectra of PDSI from each LENS member using the multitaper method (Thomson 1982) and then estimating the linear least squares fit in log-frequency, low-power space.
3. RESULTS and DISCUSSION
3.1. Perfect model framework and future megadrought in the ASW
The CESM’s pre-industrial climate (from the CESM control simulation) indicates no megadrought risk in the ASW (Methods section 2.2). Megadroughts are rare events, and thus might not be expected to occur in an 1100-year simulation. However, the lack of megadroughts may also be related to a wet bias over the ASW in the CESM model (Figure S1). Nevertheless, the 35-year hydroclimate states from the CESM control simulation are normally distributed, passing a Mann-Whitney test of normality at the 5% level. The area under the normal fit to these 35-year hydroclimate states less than −0.5 standard deviations of PDSI, i.e., the percentage of 35-year hydroclimate states that are expected to be megadroughts given an infinite sampling of the model’s internal variability, gives 0.2%. Although the analyses herein represent a perfect model framework (Methods section 2.3), it is interesting to note that megadrought risk in the North American Drought Atlas (Cook et al. 2014b), a tree-ring based reconstruction of hydroclimate variability over the Common Era, is 1.0% in the ASW.
Fig. 1a shows the ten-bin histogram of mean hydroclimate over the period 2006–2040 C.E. from LENS. Superposed on this histogram is the normal fit to the data (red) as well as the normal fit to the 35-year hydroclimate states from the CESM control simulation (Figure S2) shifted by the ensemble mean of the 30 LENS ensemble members between 2006–2040 C.E. (blue). This latter distribution is the expected distribution of 35-year hydroclimate states in the future given the model’s internal variability superposed on the shift in mean hydroclimate produced by the RCP8.5 forcing scenario. Importantly, this is the expected future distribution of 35-year hydroclimate states if forcing does not project onto the internal modes of variability to make certain 35-year hydroclimate states more or less likely and thus represents the perfect model framework against which the LENS is compared. Using this perfect model framework suggests that anthropogenic forcing increases future megadrought risk in CESM from 0% to 23%. Interestingly, this large change in megadrought risk results almost entirely from a shift in the atmospheric demand for moisture (Figure S3), with very little impact of a change in the mean of precipitation. The two distributions in Fig. 1a are similar; nevertheless, small differences can lead to large errors in the estimate of future megadrought risk. In the LENS, for example, future megadrought risk is 20%. The absolute value of the difference between the perfect model framework and the LENS megadrought risk estimates is the error in future megadrought risk. Using this definition, the error in the LENS’s future megadrought risk estimate is 3 percentage points (pp).
Figure 1:
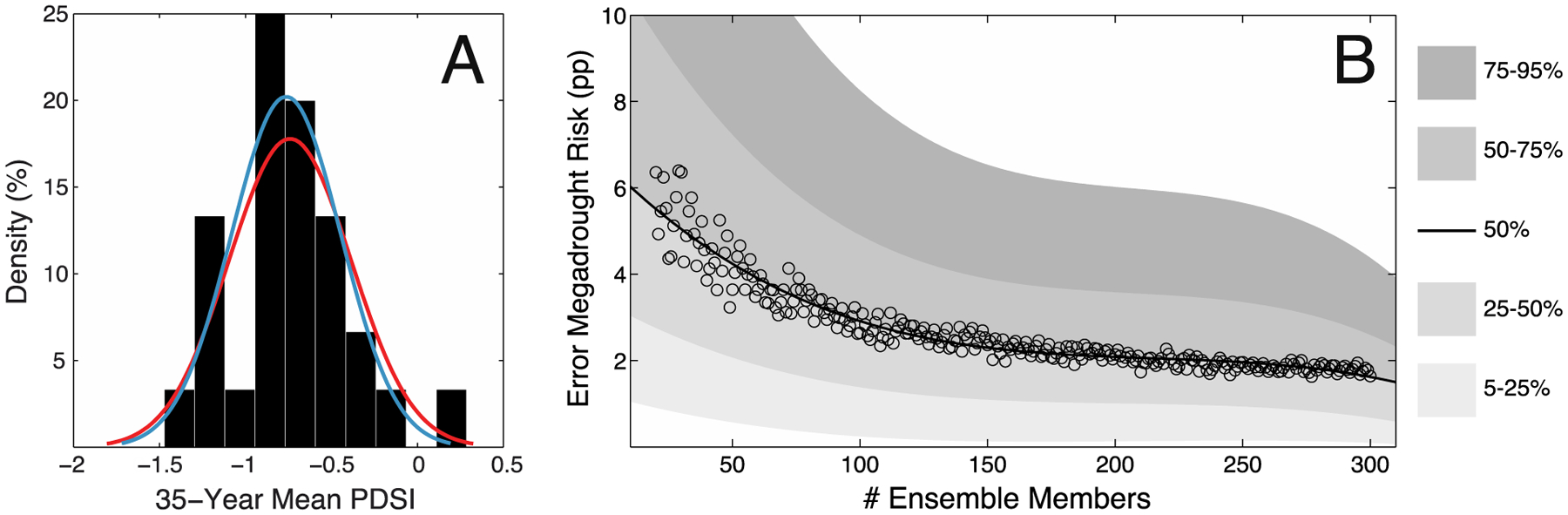
(Panel A) Ten-bin histogram of mean PDSI over the ASW (32°N-41°N; 125°W-105°W) between 2006–2040 C.E. from the 30 LENS ensemble members with a normal distribution fit (red curve). The blue curve in Panel B is the normal distribution fit to all 35-year periods from the 1100-year CESM control simulation (35-year hydroclimate states) shifted by the ensemble mean of the LENS between 2006–2040 C.E. (the distribution was originally centered on 0). The distributions are not significantly different based on a two-sample nonparametric K-S test. (Panel B) Future megadrought risk is defined using all 35-year hydroclimate states from the CESM control simulation shifted by the mean of the LENS between 2006–2040 C.E. (the perfect model framework-blue curve in Panel A). Error (y-axis) is the difference between this future megadrought risk and the future megadrought risk estimated from an ensemble of 35-year surrogate timeseries based on LENS (Methods). The surrogate timeseries ensembles are varied in size from 20 to 300 members (# Ensemble Members) and each sized ensemble is produced 1000 times. The black circles are the median values of error for the 1000 ensembles of each size, with the black line being a third order polynomial fit to the median values. The gray shaded regions represent the range of error. For instance, the upper bound of the darkest gray shaded region is the third order polynomial fit to the 95th percentile of error for each sized ensemble.
There are three possible sources of this error: (1) the LENS may not be large enough (i.e. not enough ensemble members) to accurately estimate the distribution around the mean of 35-year hydroclimate states; (2) the differences in the distributions themselves can be the result of randomness; and/or most notably, (3) the forcing in LENS may have changed the distribution around the mean of 35-year hydroclimate states. The relationship between error and these three possible sources will be explored in the next section.
3.2. Sources of error in megadrought risk estimates
To test if forcing has projected onto internal modes of variability to change the distribution around the mean of 35-year hydroclimate states we will use the K-S test outlined in Methods section 2.3. The p-value in this case is 0.94, suggesting that the distribution around the mean of 35-year hydroclimate states is likely unchanged in the ASW in the future.
Given the lack of evidence for future changes to the statistics of internal variability in the ASW, the 35-year hydroclimate states from the CESM control simulation shifted by the ensemble mean of LENS between 2006–2040 C.E. (as in Fig. 1a) can be used to define future megadrought risk (Methods section 2.3). Congruent with this perfect model framework, we then ask how many LENS ensemble members are necessary to accurately estimate future megadrought risk. To do this we use ensembles of surrogate climate realizations, or timeseries (Methods section 2.4), to assess error in the estimation of future megadrought risk as a function of number of ensemble members from 20 to 300 (Fig. 1b). We calculate error as the absolute value of the difference in future megadrought risk estimated from each surrogate timeseries ensemble as compared to the future megadrought risk from the perfect model framework. The sets of surrogates will be produced 1000 times, however, and the percentile ranges of error will be recorded (Fig. 1b).
For example, to constrain error in future megadrought risk for the ASW to 5 pp with median confidence requires 30 ensemble members. The error in future megadrought risk for the actual LENS is smaller than this despite the ensembles being the same size. This indicates that, by chance, the LENS is more successful at estimating future megadrought risk than would be expected given its size. In order to constrain error to 5 pp with a high-degree of confidence (95th percentile), would require 287 ensemble members. Such a target is unrealistic given the current state of computational and data storage resources. Additionally, the marginal value of an additional ensemble member to reducing error at every percentile range falls to nearly zero around 150 ensemble members, suggesting that for the purposes of accurately estimating future megadrought risk in the ASW, an ensemble larger than this would not be worth the computational expense.
3.2. Forced changes in variability?
As for the ASW, we test whether the statistics of internal variability are unchanged in the future using the same analysis as above (Methods section 2.3) but at each grid point globally. In many regions the distribution around the mean of 35-year hydroclimate states changes in the future, as indicated by the areas with small p-values in Fig. 2a and, more generally there is a large degree of spatial heterogeneity in this value. For reference, the null hypothesis that the distributions are the same can be rejected for 12% and 6% of grid points at the 90th and 95th confidence limits, respectively.
Figure 2:
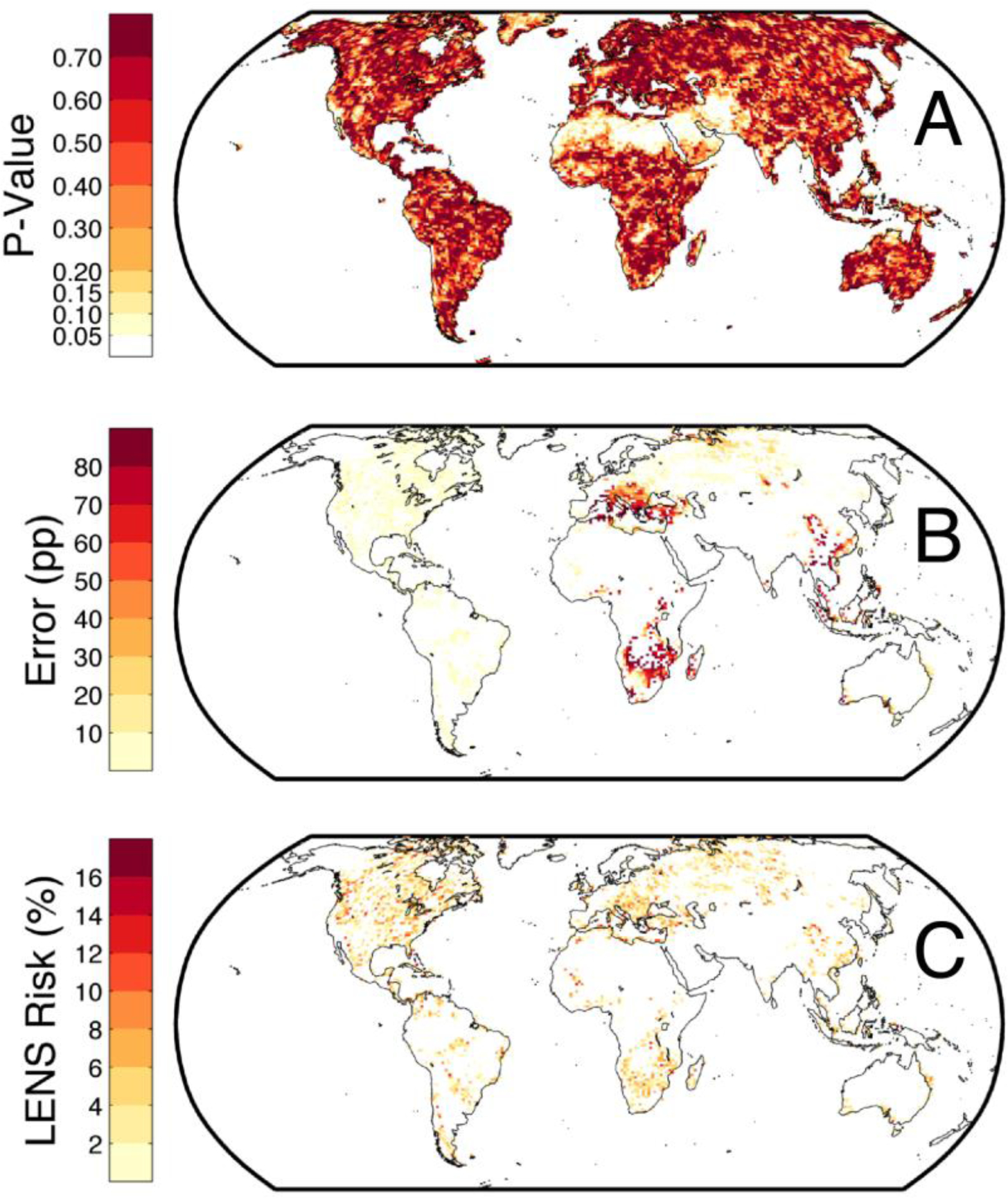
(Panel A) At each grid point we calculate the p-value from a two-sample K-S test between the 35-year hydroclimate states from the CESM control simulation and the 30 35-year hydroclimate states (2006–2040 C.E.) from the LENS. (Panel B) The error (pp) in future megadrought risk from the LENS relative to the perfect model framework and (Panel C) estimate of future megadrought risk (2006–2040 C.E.) from the LENS. (Panel B and C) Values are only shown at grid points with a p-value greater than 0.5 (Panel A), an increase in future megadrought risk (2006–2040 C.E.), and a future megadrought risk (2006–2040 C.E.) that is less than 100%:
While a full treatment of the reasons underlying changes to the statistics of internal variability in the future is outside the scope of this paper, there are regions with robust changes that are worth discussing. For instance, while the distribution around the mean of 35-year hydroclimate states does not appear to change in the future when averaging over the ASW, the California coast and the southern ASW has small p-values in Fig. 2a. For the former region this is consistent with expected changes in water season hydroclimate (Simpson et al. 2015). The latter region is the portion of the ASW that has summer hydroclimate variability driven by the North American Monsoon, and more generally, many monsoon regions appear to have changing statistics of internal variability in the future. This includes those regions encompassed by the East and West African monsoons, the Indian monsoon and the Malaysian-Australian monsoon. These changes are consistent with model-projected increases in monsoon strength (with increased atmospheric moisture content compensating for weakening circulation) and the length of the monsoon season, particularly associated with a delay in monsoon retreat (IPCC AR5, Chapter 14-Stocker et al. 2014). Another area with a robust change in the statistics of internal variability in the future is the subtropics at or near the northern descending branch of the Hadley Cell (e.g. ~30°N in Fig. 2a). While this is potentially consistent with model-projected weakening and poleward expansion of the Hadley cell (e.g. Lu et al. 2007), it could be related to the use of PDSI, which may struggle to represent drought variability over the subtropical deserts.
3.3. Constraining uncertainty in future megadrought risk
If the distribution around the mean of 35-year hydroclimate states changes in the future then we cannot use a perfect model framework to assess error in future megadrought risk. We therefore focus on grid points with p-values of more than 0.5 in Fig. 2a (45% of grid points globally), as such values indicate a lower likelihood of the statistics of internal variability changing in the future. To further simplify interpretation we will also require that the analyzed grid points have an increase in megadrought risk in the future (relative to the CESM control simulation), and a future megadrought risk that is less than 100%. For these grid points, Fig. 2b shows the estimate of future megadrought risk from the LENS and Fig. 2c and 2d compares this to future megadrought risk from the perfect model framework.
Fig. 3a indicates the impact of the size of the ensemble on error by showing the number of ensemble members necessary to constrain error to 5 pp in the median (using the same methodology as in Fig. 1b). While there is a large degree of spatial heterogeneity in this value, there appears to be a straightforward relationship between number of ensemble members and future megadrought risk (Fig. 3b). For future megadrought risks greater than 50%, the number of ensemble members necessary to constrain error to 5 pp in the median decreases as future megadrought risk increases, the opposite is true of values less than 50%. The reason for this relationship is intuitive: it takes more ensemble members to constrain error if attempting to discern differences in probabilities in the center of mass of the statistical distribution.
Importantly, because future megadrought risk is a function of both the distribution around the mean and the change in the mean, this implies that the magnitude of the radiatively forced change in the mean is itself a strong control on the number of ensemble members necessary to accurately estimate future megadrought risk (Fig 3c).
In Fig. 3b the same analysis is also completed by randomly subsampling the CESM control simulation instead of using surrogate timeseries based on the LENS (the range for the randomly sampled CESM control simulation is the shaded region in Fig. 3b). Randomly subsampling the CESM control simulation provides an estimate of how many ensemble members are necessary to reproduce the distribution of 35-year hydroclimate states that is used to define future megadrought risk (in the perfect model framework). By consequence, any differences between the shaded region and points in Fig. 3b likely indicates that there are changes to the statistics of internal variability in the future at the analyzed grid points (despite the relatively large p-values in Fig. 2a). In some cases, these changes increase the number of ensemble members necessary to accurately estimate future megadrought risk by nearly two times, in part, because the distribution used to define future megadrought risk is not the true future distribution of 35-year hydroclimate states.
4. CONCLUSIONS
The LENS suggests that even over the near-term decades (2006–2040 C.E.) anthropogenic forcing increases megadrought risk in the ASW by 20 pp or at least 100 times relative to pre-industrial conditions in a CESM control simulation. Over this same time period, anthropogenic forcing can increase megadrought risk in some regions by 100 pp (0.5% of grid points-not shown). Although estimated from a single climate model, these stark changes in megadrought risk over the near-term decades suggest a need to better understand the capability of state-of-the-art climate models to estimate future megadrought risk. Along these lines, there are a number of results herein that are generalizable to this question. For starters, the statistics of internal variability within the CESM model changes in some regions and not in others-with monsoon regions and the subtropics at or near the descending branch of the Hadley Cell in the Northern Hemisphere being notable examples of the former. The ASW, however, is a region where the statistics of internal variability appear not to change in the future and we can use this behavior to determine the marginal value of each ensemble member to accurately estimating future megadrought risk.
We find there is little value beyond 150 ensemble members, suggesting that running additional ensemble members is not worth the computational expense when estimating future megadrought risk in the ASW. Nevertheless, running 150 ensemble members is already beyond the scope of current computational and storage resources and these limitations suggest that targets such as constraining error in megadrought risk projections in the ASW to 5 pp with high confidence is not possible. In a global sense, there is spatial heterogeneity in the number of ensemble members necessary to accurately estimate future megadrought risk. This heterogeneity is largely explained by differences in the magnitude of the radiatively forced shift in mean hydroclimate, thereby providing a strong control on the number of ensemble members necessary to accurately estimate future megadrought risk.
It is important to note that the experiment set up herein is a simple (and likely a baseline) estimate for the number of ensemble members necessary to accurately estimate future megadrought risk. We have only asked how many ensemble members are necessary to constrain the future distribution of 35-year hydroclimate states as defined by the models’ own internal variability superposed on its’ own forced response.
In the real world, the distribution of 35-year hydroclimate states is not known nor is the possibility of forcing projecting onto internal modes of variability well defined. Models are likewise biased, with these biases being correlated across models, and in the real world models are attempting to reproduce a distribution of 35-year hydroclimate states that may be inconsistent with their own dynamics-including, and perhaps most importantly, their sensitivity to forcing-which is itself uncertain in the future. By consequence, using the CMIP5 multi-model ensemble to estimate future megadrought risk represents a much more difficult endeavor than the perfect model framework used herein. Additionally, the question of how many ensemble members are necessary to sample internal variability will differ depending on the climate feature of interest-the results herein only apply to estimating future megadrought risk. Nevertheless, the framework introduced herein is generalizable to other climate features and further work will be important to better understand how many ensemble members are necessary to robustly sample internal variabilit
Supplementary Material
ACKNOWLEDGEMENTS
The authors would like to thank the National Center for Atmospheric Research’s CESM1 (CAM5) Large Ensemble Community Project (LENS) and supercomputing resources provided by Stanford Center for Computational Earth and Environmental Science in the School of Earth, Energy, and Environmental Sciences at Stanford University. The model output employed from the LENS can be accessed at https://www2.cesm.ucar.edu/models/experiments/LENS. Our work was supported by the Center for International Security and Cooperation (CISAC) at Stanford University and the Earth Institute Fellowship at Columbia University to JSM and the Cooperative Institute for Research in Environmental Sciences at the University of Colorado, Boulder and Dr. Kristopher B. Karnauskas to SC.
Footnotes
Publisher's Disclaimer: This article has been accepted for publication and undergone full peer review but has not been through the copyediting, typesetting, pagination and proofreading process which may lead to differences between this version and the Version of Record.
Contributor Information
Sloan Coats, Cooperative Institute for Research in Environmental Sciences, University of Colorado, Boulder, Colorado.
Justin S. Mankin, Ocean & Climate Physics, Lamont-Doherty Earth Observatory, Columbia University, Palisades, New York NASA Goddard Institute for Space Studies, New York, New York.
REFERENCES
- Allen RG, Pereira LS, Raes D and Smith M, 1998. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO, Rome, 300(9), p.D05109. [Google Scholar]
- Ault TR, Cole JE, Overpeck JT, Pederson GT, St. George S, Otto-Bliesner B, Woodhouse CA. and Deser C, 2013. The continuum of hydroclimate variability in western North America during the last millennium.Journal of Climate, 26(16), pp.5863–5878. [Google Scholar]
- Ault TR, Cole JE, Overpeck JT, Pederson GT and Meko DM, 2014. Assessing the risk of persistent drought using climate model simulations and paleoclimate data. Journal of Climate, 27(20), pp.7529–7549. [Google Scholar]
- Cai W, Borlace S, Lengaigne M, Van Rensch P, Collins M, Vecchi G, Timmermann A, Santoso A, McPhaden MJ, Wu L and England MH, 2014. Increasing frequency of extreme El Niño events due to greenhouse warming. Nature Climate Change, 4(2), pp.111–116. [Google Scholar]
- Cai W, Wang G, Santoso A, McPhaden MJ, Wu L, Jin FF, Timmermann A, Collins M, Vecchi G, Lengaigne M and England MH, 2015. Increased frequency of extreme La Niña events under greenhouse warming. Nature Climate Change, 5(2), pp.132–137. [Google Scholar]
- Coats S, Smerdon JE, Seager R, Cook BI and González-Rouco JF, 2013. Megadroughts in Southwestern North America in ECHO-G Millennial Simulations and Their Comparison to Proxy Drought Reconstructions*.Journal of Climate, 26(19), pp.7635–7649. [Google Scholar]
- Coats S, Smerdon JE, Cook BI and Seager R, 2015. Are Simulated Megadroughts in the North American Southwest Forced?*. Journal of Climate, 28(1), pp.124–142. [Google Scholar]
- Coats S, Smerdon JE, Karnauskas KB, and Seager R The improbable but unexceptional occurrence of North American megadrought clustering during the Medieval Climate Anomaly, Environmental Research Letters, 117, 074025, 10.1088/1748-9326/11/7/074025. [DOI] [Google Scholar]
- Cook BI, Smerdon JE, Seager R and Coats S, 2014a. Global warming and 21st century drying. Climate Dynamics, 43(9–10), pp.2607–2627. [Google Scholar]
- Cook BI, Smerdon JE, Seager R and Cook ER, 2014b. Pan-Continental Droughts in North America over the Last Millennium*. Journal of Climate,27(1), pp.383–397. [Google Scholar]
- Cook BI, Ault TR and Smerdon JE, 2015. Unprecedented 21st century drought risk in the American Southwest and Central Plains. Science Advances, 1(1), p.e1400082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook BI, Cook ER, Smerdon JE, Seager R, Williams AP, Coats S, Stahle DW and Díaz JV, 2016. North American megadroughts in the Common Era: reconstructions and simulations. Wiley Interdisciplinary Reviews: Climate Change. [Google Scholar]
- Cook ER, Seager R, Cane MA and Stahle DW, 2007. North American drought: reconstructions, causes, and consequences. Earth-Science Reviews, 81(1), pp.93–134. [Google Scholar]
- Deser C, Phillips A, Bourdette V and Teng H, 2012. Uncertainty in climate change projections: the role of internal variability. Climate Dynamics,38(3–4), pp.527–546. [Google Scholar]
- Ho M, Lall U and Cook ER, 2016. Can a paleo-drought record be used to reconstruct streamflow? A case-study for the Missouri River Basin. Water Resources Research, doi: 10.1002/2015WR018444. [DOI] [Google Scholar]
- Kay JE, Deser C, Phillips A, Mai A, Hannay C, Strand G, Arblaster JM, Bates SC, Danabasoglu G, Edwards J and Holland M, 2015. The Community Earth System Model (CESM) large ensemble project: A community resource for studying climate change in the presence of internal climate variability. Bulletin of the American Meteorological Society, 96(8), pp.1333–1349. [Google Scholar]
- Lu J, Vecchi GA and Reichler T, 2007. Expansion of the Hadley cell under global warming. Geophysical Research Letters, 34(6). [Google Scholar]
- Mankin Justin S., et al. , 2015. The potential for snow to supply human water demand in the present and future. Environmental Research Letters 1011, 114016. [Google Scholar]
- Palmer TN, 1993. A nonlinear dynamical perspective on climate change. Weather, 48(10), pp.314–326. [Google Scholar]
- Penman HL, 1948, April Natural evaporation from open water, bare soil and grass In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences (Vol. 193, No. 1032, pp. 120–145). The Royal Society. [DOI] [PubMed] [Google Scholar]
- Meko DM, Woodhouse CA, Baisan CA, Knight T, Lukas JJ, Hughes MK and Salzer MW, 2007. Medieval drought in the upper Colorado River Basin. Geophysical Research Letters, 34(10). [Google Scholar]
- Simpson IR, Seager R, Ting M and Shaw TA, 2015. Causes of change in Northern Hemisphere winter meridional winds and regional hydroclimate.Nature Climate Change, doi: 10.1038/nclimate2783. [DOI] [Google Scholar]
- Smerdon JE, Cook BI, Cook ER and Seager R, 2015. Bridging Past and Future Climate across Paleoclimatic Reconstructions, Observations, and Models: A Hydroclimate Case Study*. Journal of Climate, 28(8), pp.3212–3231. [Google Scholar]
- Stocker TF ed., 2014. Climate change 2013: the physical science basis: Working Group I contribution to the Fifth assessment report of the Intergovernmental Panel on Climate Change. Cambridge University Press. [Google Scholar]
- Taylor KE, Stouffer RJ and Meehl GA, 2012. An overview of CMIP5 and the experiment design. Bulletin of the American Meteorological Society,93(4), pp.485–498. [Google Scholar]
- Thomson DJ, 1982. Spectrum estimation and harmonic analysis.Proceedings of the IEEE, 70(9), pp.1055–1096. [Google Scholar]
- Thompson DW, Barnes EA, Deser C, Foust WE and Phillips AS, 2015. Quantifying the role of internal climate variability in future climate trends. Journal of Climate, 28(16), pp.6443–6456. [Google Scholar]
- Vicente-Serrano SM, Beguería S, López-Moreno JI, Angulo M and El Kenawy A, 2010. A new global 0.5 gridded dataset (1901–2006) of a multiscalar drought index: comparison with current drought index datasets based on the Palmer Drought Severity Index. Journal of Hydrometeorology,11(4), pp.1033–1043. [Google Scholar]
- Xu CY and Singh VP, 2002. Cross comparison of empirical equations for calculating potential evapotranspiration with data from Switzerland. Water Resources Management, 16(3), pp.197–219. [Google Scholar]
- Woodhouse C and Lukas J, 2006. Multi-Century Tree-Ring Reconstructions of Colorado Streamflow for Water Resource Planning. Climatic Change, 78(2–4), 293–315, doi: 10.1007/s10584-006-9055-0. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


