Exposure Measurement Error in Air Pollution Studies: The Impact of Shared, Multiplicative Measurement Error on Epidemiological Health Risk Estimates

Abstract

Spatiotemporal air pollution models are increasingly being used to estimate health effects in epidemiological studies. Although such exposure prediction models typically result in improved spatial and temporal resolution of air pollution predictions, they remain subject to shared measurement error, a type of measurement error common in spatiotemporal exposure models which occurs when measurement error is not independent of exposures. A fundamental challenge of exposure measurement error in air pollution assessment is the strong correlation and sometimes identical (shared) error of exposure estimates across geographic space and time. When exposure estimates with shared measurement error are used to estimate health risk in epidemiological analyses, complex errors are potentially introduced, resulting in biased epidemiological conclusions. We demonstrate the influence of using a three-stage spatiotemporal exposure prediction model and introduce formal methods of shared, multiplicative measurement error (SMME) correction of epidemiological health risk estimates. Using our three-stage, ensemble learning based nitrogen oxides (NO_x) exposure prediction model, we quantified SMME. We conducted an epidemiological analysis of wheeze risk in relation to NO_x exposure among school-aged children. To demonstrate the incremental influence of exposure modeling stage, we iteratively estimated the health risk using assigned exposure predictions from each stage of the NO_x model. We then determined the impact of SMME on the variance of the health risk estimates under various scenarios. Depending on the stage of the spatiotemporal exposure model used, we found that wheeze odds ratio ranged from 1.16 to 1.28 for an interquartile range increase in NO_x. With each additional stage of exposure modeling, the health effect estimate moved further away from the null (OR=1). When corrected for observed SMME, the health effects confidence intervals slightly lengthened, but our epidemiological conclusions were not altered. When the variance estimate was corrected for the potential “worst case scenario” of SMME, the standard error further increased, having a meaningful influence on epidemiological conclusions. Our framework can be expanded and used to understand the implications of using exposure predictions subject to shared measurement error in future health investigations.

1. INTRODUCTION

Uncertainties common in air pollution exposure assessment result in various error structures that can be categorized as shared and/or unshared exposure measurement error, where unshared error assumes independence between errors and exposure (true or measured) while shared error does not [1]. Measurement error can also take the form of Berkson or Classical. Classical error is associated with random errors of measurement commonly related to instrument noise, while Berkson error results from assigning the local spatial and/or temporal area mean measurement to individuals (i.e., assigning highly aggregated exposure values) [1]. A fundamental challenge of exposure measurement error in air pollution assessment is the strong correlation and sometimes identical (shared) error of exposure estimates across geographic space and time. Berkson and Classical errors can be shared and/or unshared depending on the nature of the association between the error magnitude with measured (in a Berkson error model) or true (in a Classical error model) exposure. Although subject to exposure measurement error [2], environmental epidemiologists utilize spatiotemporal air pollution exposure predictions in health risk models to determine associations between air pollution and health outcomes. Because measurement error is common and unavoidable in spatiotemporal exposure predictions, health risk models are therefore subject to questions of precision and/or bias [3, 4]. Customary understanding of the implications of unshared error types on epidemiological inference recognize that Berkson error will impact estimate precision, while classical error will induce bias in the observed health estimates towards the null [4, 5]. When exposure estimates with shared measurement error are used to estimate risk in epidemiological analyses, complex errors are potentially introduced, resulting in biased epidemiological conclusions [6, 7], where magnitude of bias is influenced by the strength (size) of the epidemiological association [7, 8].

Only through knowing the variances of the errors can proper correction of biased epidemiological conclusions be made [9]. Shared measurement error results in biased variance estimates, and is of most concern when the shared error is multiplicative [10]. A multiplicative error structure, common in air pollution exposure estimates, can alter the shape of the exposure-response curve (over and/or under estimation) and occurs when the error is proportional to the true exposure [11]. In simulation work focusing on air pollution measurement error, Szpiro and Pacorick [6] demonstrate the use of the nonparametric bootstrap to account for shared measurement error and show bias in variance estimates. Butland et al [12] demonstrate a consistent inflation of variance estimates due to shared measurement error. Although shared (Berkson) multiplicative error (with constant variance) is understood not to bias epidemiological risk estimates, correcting for shared error will provide refined confidence intervals and hence, better support epidemiological inference.

While several methods have been developed to address unshared exposure measurement error in epidemiological investigations [9, 13–18] ,existing methods, such as regression calibration, are not applicable in situations where the errors are shared across space and time [10, 19] and only few investigations focusing on shared exposure measurement error have been considered in the context of air pollution epidemiology [6, 7]. Often correlated errors are accounted for, but little work has demonstrated the independent influence of shared error. Each exposure model produces estimates with a complex combination of error types that warrant consideration when interpreting epidemiological risk estimates.

NO_x (NO + NO₂), a byproduct of fuel combustion and precursor gas involved in the secondary formation of ozone and particulate matter, and other air pollutants have been implicated in respiratory health [20–22], especially in children. NO_x exposure has been causally linked to airway inflammation [23, 24] and shown to trigger asthma exacerbations such as cough or wheeze in children [25–27]. Asthma is a costly, inhibiting and complex multifactorial disease characterized by airway hyper responsiveness, bronchial constriction and symptoms such as cough, chest tightness, and wheeze. Wheezing in early life, primarily characterized by airway obstruction or narrowing in the lungs, is a common symptom of asthma that has been shown to be associated with asthma development later in life [28, 29]. Further, wheezing is an important symptom to investigate as studies have revealed that lung function is reduced among children with persistent wheeze [30]. Although wheeze is a symptom implicated in numerous obstructive pulmonary diseases, the most common diagnosis associated with wheeze in infants and children is asthma [31].

Previous work in the southern California Children’s Health Study (CHS), a longitudinal cohort designed to assess the influence of air pollution on child respiratory outcomes, has demonstrated associations of proxy measures of traffic related air pollution (TRAP) exposure, such as residential proximity to major roads [32] and more sophisticated NO_x line source dispersion (CALINE-4) model estimates [33] with asthma risk . Similarly, CHS research has found negative associations between respiratory function and development with direct and indirect NO_x exposures, including proximity to major roads, measurements from regional monitors, CALINE-4 estimates [34], and land use exposure model estimates [35]. Associations of NO_x and respiratory health in the CHS are consistent with other studies in Los Angeles [36], California [37] and around the world [28, 38, 39]. To date, no investigations of respiratory health using our newly developed three stage spatiotemporal NO_x model has been carried out in the CHS cohort.

In our previous work [40], we developed methods based on radiation dosimetry exposure measurement error by Stram and Kopecky [10] to identify, quantify, and characterize spatial and temporal shared and unshared, multiplicative and additive (SUMA) exposure measurement error [40] under a Berkson model in a novel three-stage ensemble learning spatiotemporal nitrogen oxides (NO_x) model with constrained optimization [41]. This paper will build on our previous work inspired by radiation epidemiology [10] to assess the independent impact of shared multiplicative error on the observed epidemiological associations between residential NO_x exposure and pediatric wheeze events in the CHS[42]. We will evaluate the the variance of our health effect estimate across each stage of our spatiotemporal NO_x model to evaluate the influence of exposure modeling improvements on health risk estimates.

2. METHODS

2.1. Population and Health Outcomes

This work utilized cohort E, the most recent wave of the CHS [42, 43] which began enrolling school aged children (5–6 years of age) in 2002/2003 and administered yearly questionnaires for 12 years to assess respiratory outcomes (among others). Wheeze information was reported by parents or guardians in questionnaires indicating if the child experienced wheeze symptoms within the last 12 months (“Has your child had wheezing or whistling in the chest in the last 12 months?”). Children in the CHS were recruited from within specific communities across southern California, selected to represent a range of air pollution exposures by design [42]. Using information from longitudinal address confirmation, residential history questionnaires and birth certificates, lifetime residential timelines were assembled (with prenatal periods starting in 1992) for each participant and biweekly NO_x exposure was assigned to these times and locations based on our spatiotemporal model [41].

2.2. Exposure Assessment

Details on our high-resolution 1992–2013 Southern California NO_x model are described in Li et al. (2017) [41]. Briefly, the model uses a flexible 3 stage framework that utilizes routine measurements collected over a long time period from regional monitoring stations to inform temporal basis functions with singular value decomposition to capture long term and seasonal temporal variations [44]. In addition to the routine measurements, this model used data from short-term spatially dense measurement campaigns, to account for local variability across the CHS study domain. Stage 1 is a mixed effect spatiotemporal model that uses temporal parameters, long term mean concentrations from regional monitoring stations, short term sampling concentration measurements, and local spatiotemporal predictors including traffic variables, population density, meteorological parameters, and spatial effects to model bi-weekly NO_x concentrations. Spatial effects were specified both as random effects based on 500-meter aggregate distance Thiessen polygons and nonparametric additive terms. This first stage is comparable to a typical spatiotemporal exposure prediction model. Stage 2 uses ensemble learning to produce 120 individual mixed-effect models (also known as ensembles) that produce biweekly predictions by iteratively sampling 90% of the spatiotemporally-referenced predictors from stage 1 for training and a random subset of around 63% of the observations to test against the remaining ~ 37% of the data set in each ensemble. The estimates from the 120 trained models (ensembles) are then averaged using weights based on model performance to output location and time specific optimized biweekly NO_x predictions (referred to as stage 2 predictions). Methods used in stage 2 produce predictions that are less prone to investigator bias regarding covariates selection due to the ensemble learning process which eliminates forced covariate inclusion and inflated variance of predictions, which are typical in other spatiotemporal models. To minimize the influence of missing spatiotemporal covariates and better estimate time series of NO_x concentrations, stage 3 uses constrained optimization according to the temporal basis functions and known physical constraints (e.g. decreasing temporal trend of NO_x over study years, higher cool season concentrations compared to warm season, concentration limits, and seasonal ranges) to adjust stage 2 NO_x predictions. The constrained optimization output is averaged up to monthly NO_x estimates at the residence of each CHS participant [41, 45] for use in the epidemiologic analyses (referred to as stage 3 predictions).

2.3. Quantifying SUMA error components

In our previous work we demonstrate the utility of obtaining the 120 ensembles from the second stage of the NO_x prediction modeling (prior to calculating the weighted average) and apply a radiation dosimetry statistical framework originally developed by Stram and Kopecky [10] to quantify SUMA exposure measurement error. This method assumes that the 120 ensembles are not independent and come from the distribution of true exposure given the known exposure determinants for each location in time. As our spatiotemporal model is a point based model, the assumption that the 120 ensembles come from the distribution of true exposure implies that any important missing covariate from the exposure model and the degree of smoothing within the model is random and the final spatiotemporal model is agreed upon by experts who developed the model and conditional upon the information that is available to the experts who developed the model. Our model [41], relies on expert judgment and our resultant exposure surfaces can be regarded as the best subjective judgement of these implications that is consistent with the opinion of the experts about the uncertainties of NO_x surface modeling.

The SUMA model for shared and unshared Berkson error is written as follows for each time-space specific point of interest, i:

$$X_i={ϵ}_{\mathit{\text{SM}}}{ϵ}_{\mathit{\text{Mi}}}{Z}_i+ {ϵ}_{\mathit{\text{SA}}}+{ϵ}_{\mathit{\text{Ai}}}$$ (1)

where X_i is the true exposure for estimate of interest, Z_i is the estimated exposure (a weighted mean of the ensembles). ϵ_SM and ϵ_Mi are the shared and unshared multiplicative errors with mean equal to 1 and variances ${\sigma }_{SM}^2$ and ${\sigma }_M^2$ respectively, and ϵ_SA and ϵ_Ai are the shared and unshared additive errors, with mean equal to 0 and variances ${\sigma }_{SA}^2$ and ${\sigma }_A^2$ respectively. Stram and Kopecky’s [10] methods to estimate the following variance terms ${\sigma }_{SM}^2$, ${\sigma }_M^2$, ${\sigma }_{SA}^2$ , and ${\sigma }_A^2$ from air pollution exposure estimates are detailed in our previous work [40]. We focus on the variance of the shared multiplicative error component $\left({\sigma }_{SM}^2\right)$ because this variance term is what primarily affects the behavior of variance estimates and confidence intervals for the risk estimate in a standard regression analysis[8]. Briefly, to calculate ${\sigma }_{SM}^2$ , for every pair of NO_x predictions, referred to as i and j, the covariance term using realized values X_i and X_j over the 120 ensembles is called C_ij. We performed simple ordinary least squares (OLS) regression of C_ij on the product of the mean of the realized values X_i and X_j (stage 2 exposure predictions as explained earlier), called Z_iZ_j (product mean), to fit the model

$$C_{ij} = a_0+ a_1{Z}_i{Z}_j + {\epsilon }_{ij}$$ (2)

where Stram and Kopecky note that the slope term (a₁) corresponds to $\widehat{{\sigma }_{SM}^2}$, which is the estimate of ${\sigma }_{SM}^2$.

2.4. Influence of Shared Multiplicative Error on Variance of Epidemiological Health Risk Estimates

If the SUMA model holds true (eq. 1, see also eq. 10 in Stram and Kopecky [10] for derivations), then the true variance of a slope estimate $\widehat{b}$ from a regression of disease, D, on observed exposure, W, will be approximately equal to the usual (naïve) estimate SE(b)² of the variance of $\widehat{b}$ , ignoring the effect of shared multiplicative measurement error (SMME) captured by the term $b^2{\sigma }_{SM}^2$.

$$\mathit{\text{Var}}\left(\widehat{b}\right)= \mathit{\text{SE}}{\left(b\right)}^2 + b^2 {\sigma }_{\mathit{\text{SM}}}^2$$ (3)

Using eq. 3, the variance of $\widehat{b}$ can be adjusted to account for ${\sigma }_{SM}^2$, resulting in more accurate confidence intervals. Eq. 3 implicitly assumes any adjustment variables included in the model of the regression of D on W are not associated with exposure error.

2.5. A Demonstration of the Influence of SMME in a Cross-Sectional Epidemiological Analysis

A mixed effect logistic regression model was used to predict pediatric wheeze risk in relation to NO_x exposure in the one year prior to study enrollment [46]. Because children in the CHS were recruited from within specific communities by design [42], the model includes a random effect for community to account for correlation among individuals living in the same study community. The following covariates were obtained at baseline and considered for inclusion as fixed effects to adjust for potential confounding (nominally defined by a change of approximately 10% or more in the effect estimate of NO_x on wheeze risk and further confirmed with directed acyclic graphs): CHS community, sex, gestational age, age, body mass index, maternal education, maternal race, maternal/paternal allergy history, sibling crowding, tobacco smoke exposure, gas stove use, maternal marital status, season of conception, day care attendance, and asthma diagnosis. Because of the high missing proportion of self-reported income, geocoded residential address was used to determine median household income as an additional measure of socioeconomic status at the census block group level from the American Community Survey 2005 [47].

The logistic mixed effects model was repeatedly fit using the output from the various stages of the spatiotemporal NO_x model [41] averaged for the 12 months prior to questionnaire completion. As described earlier, the 120 individual outputs from stage 2 ensembles, a single averaged output of the 120 stage 2 NO_x outputs (Mean of stage 2), and a single constrained optimization NO_x output from stage 3 were used as the main exposure in each iteration of fitting the logistic mixed effects model repeatedly. By using the 120 stage 2 NO_x outputs separately in the health models, we aim to demonstrate the possible range of variability in health effect estimates that could have been observed had we built a single stage model with a fixed set of inputs (approximated by assuming any one of the 120 ensembles could have been the final, single-stage exposure model).

The observed health effect estimates were standardized for an interquartile range increase in NO_x and subsequently adjusted for SMME, via applied correction information methods of calculating the “corrected” variance, Eq. 3 [10], to incrementally understand the influence of the multiple exposure model output stages and the influence of SMME on the estimate and variance of the epidemiological health risk estimate of the odds of recent wheeze per interquartile range increase in annual average ambient NO_x exposure. This variance correction method ultimately can assess the impact of SMME on the standard errors of the parameters of interest. The corrected variance of the effect estimate is calculated using Eq. 3. Once a new corrected variance is calculated, new confidence intervals can be calculated to reflect the true precision of the health effect estimates independently accounting for SMME [10]. Furthermore, because SMME correction was developed for linear models and the logistic wheeze model is not strictly linear, we investigated the accuracy of a Taylor series approximation of the logistic model over the observed range of NO_x predictions (and extrapolated ranges to display the shape of the curve) found in our study in a sensitivity analysis.

3. RESULTS

Of the 5,106 children included in the most recent cohort (E) of the CHS, 761 cases of wheeze were reported by parents at study entry (57% with doctor diagnosed asthma). Characteristics of the cases and non-cases are shown in Table 1. The majority of CHS participants are of Hispanic (white or black) ethnicity (57.6%), living with one or two other children in the same home (63%), approximately 6 years old at study entry, with a mean BMI of 16 kg/m². NO_x exposure (stage 2 and stage 3) estimates were not statistically different between wheeze cases and non-cases. We observed significant differences in race/ethnicity, gestational age, sex, BMI, maternal education, number of siblings living in the same home, and paternal allergy history by wheeze status. A higher proportion of premature (15.4%), male (58.9%) children reported wheezing. We observed a greater proportion of children with reported history of wheeze living with no other children in the home (16.2%) and having parents with reported allergy history (52.8%).

Table 1:

Descriptive Statistics of Exposures and Sociodemographics in the southern California Children’s Health Study (CHS) Participants at Baseline

	Full CHS Cohort (n=5,106)	Wheeze Cases (n=761)
	Mean (SD) or N (%)	Mean (SD) or N (%)	p-value1
Exposure
Annual Average Stage2 Predicted NOx (ppb)a	37.52 (15.31)	37.87 (14.53)	0.495
Annual Average Stage 3 Predicted NOx (ppb)b	37.03 (14.86)	37.48 (14.05)	0.364
Race/Ethnicity			<0.0001
White Non-Hispanic	1,627 (31.5)	263 (34.6)
Hispanic	2,867 (57.6)	375 (49.4)
Black (African American)	176(3.0)	44 (5.8)
Asian/Hawaiian/Pacific Islander	157 (3.1)	20 (2.6)
Other	255 (4.6)	57 (7.5)
Missing	24 (0.5)	2 (0.2)
Premature Birthc			<0.0001
Yes	547 (10.7)	116(15.4)
No	4,467 (87.4)	633(83.1)
Missing	92 (1.8)	12 (1.6)
Child Sex			<0.0001
Male	2,615 (51.2)	448 (58.9)
Female	2,489 (48.7)	312 (41.0)
Body Mass Index (kg/m2)	16.65 (2.69)	16.99 (3.07)	0.004
Missing	417 (8.1)	81 (10.6)
Age of Child (months)	72.41 (7.92)	72.06 (8.09)	0.206
Maternal Education
Less than 12th grade	1,084 (21.2)	112 (14.7)	<0.0001
Completed High School	955 (18.7)	135 (17.7)
Some college or technical school	1857 (36.3)	359 (47.2)
Completed 4 years of College	550 (10.7)	71 (9.3)
Some graduate training	446 (8.7)	64 (8.4)
Missing	214 (4.2)	20 (2.6)
Number of Other Children Living in Same Homed			<0.001
0	656 (12.8)	123 (16.2)
1–2	3,218 (63.0)	484 (63.6)
3+	1,076 (21.0)	137 (18.0)
Missing	156 (3.0)	17 (2.2)
Maternal or Paternal Allergy Historye			<0.001
Yes	1,927 (37.8)	402 (52.8)
No	3,179 (60.1)	339 (44.5)
Missing	108 (2.1)	20 (2.6)

¹Pearson Chi-square test (categorical variables) and F-test (continuous variables) examining the differences between wheeze cases and non-wheeze cases within CHS, cohort E.

^aStage 2 Spatiotemporal NO_x modeled using ensemble learning methods; 12 month average.

^bStage 3 Spatiotemporal NO_x modeled the same as stage 2 with additional constrained optimization applied to predictions;12 month average.

^cParent or guardian report if study participant was born premature.

^dParent or guardian report number of individuals less than 18 years of age living in the same home as the study participant.

^eMaternal or paternal allergy history present if biologic mother and/or father report doctor diagnosed allergy or hay fever.

Distributions of annual average NO_x assigned to CHS participants in the epidemiological analysis were very similar between stage 2 and 3, with a Pearson correlation of 0.994. Stage 2 NO_x predictions had a higher maximum with slightly higher standard deviation. The difference between annual stage 2 and 3 NO_x exposure ranged between −10.42 and 10.96 ppb. Upon mapping these differences, we observed the largest differences between stage 2 and 3 NO_x exposure estimates at geographic locations in the communities of Anaheim and Upland, two communities with generally higher traffic relative to the other CHS communities (Figure 1). We also found evidence of spatial clustering (Moran’s Index p-value <0.0001) in these locations with greatest difference between stage 2 and 3 NO_x.

Figure 1:

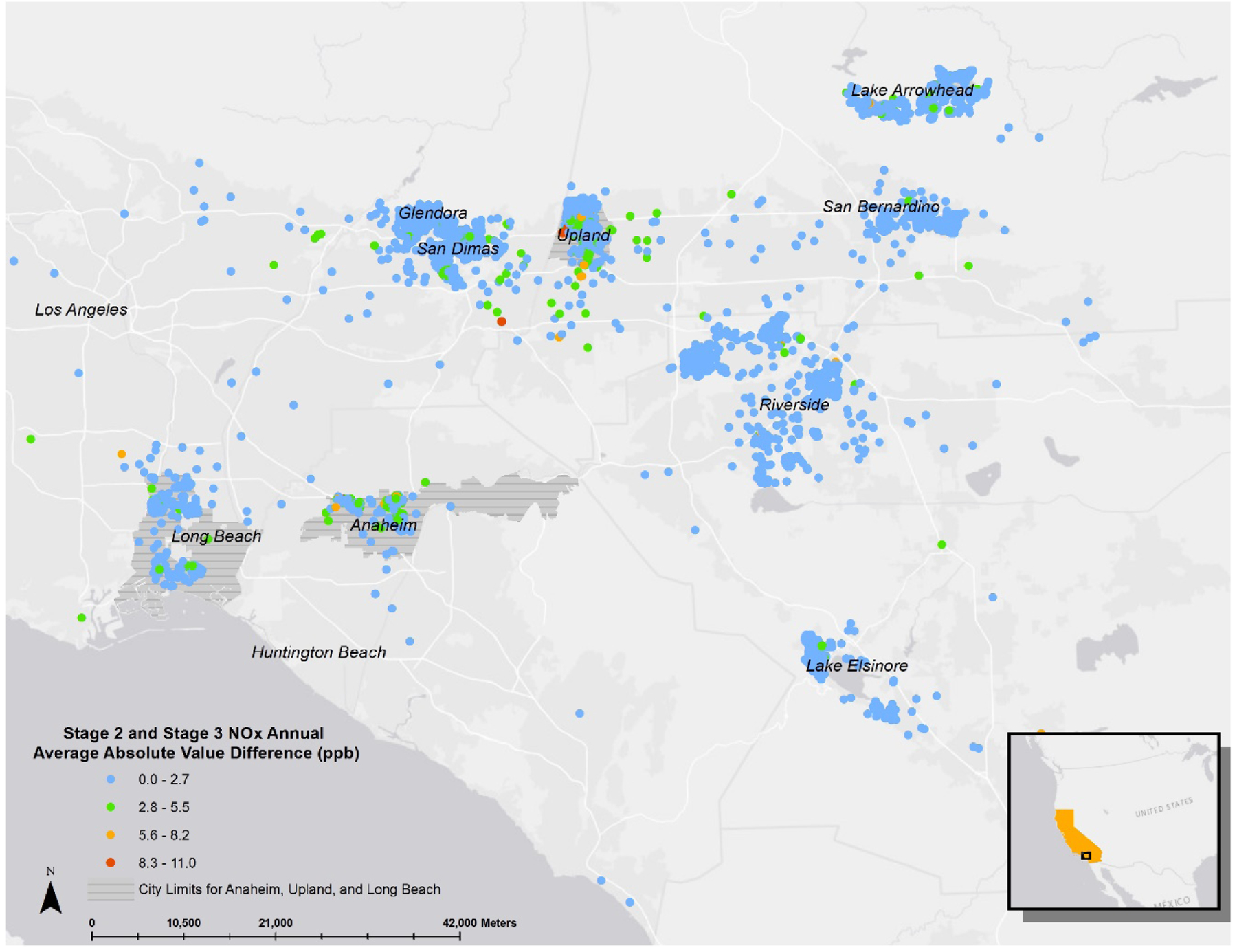
Geographic Distribution of the Absolute Value of the Difference Between Stage 2 and Stage 3 Annual Average NOx (ppb). Santa Barbara and Alpine is not shown in the map as the geographic distribution of these absolute differences was unremarkable and the values were very small.

The SMME estimate $\left({\sigma }_{SM}^2\right)$ was 0.00029 across all CHS prediction locations and time (1992–2013), as determined from our previous work [40]. We also identified significant spatial variation of SMME across the CHS region with certain prediction locations exhibiting SMME values seven times higher than the average SMME in our earlier analysis. Similarly, because our epidemiological analysis is based on baseline data of CHS participants, we conducted an SMME analysis by baseline community of the CHS and for this particular time period (2002–2003). We found that the SMME estimate was 0.00023, and that the highest SMME occurred in the community of Long Beach, CA (Table 3).

Table 3:

Shared Multiplicative Measurement Error (SMME) Estimates by Children’s Health Study (CHS) community (2002–2008).

	n (biweekly-location-person specific)	Covariance Range (minimum, maximum)	Covariance Average (Standard Deviation)	Product Mean Range (minimum, maximum)	Product Mean Average (Standard Deviation)	SMME	p-value
All Communities	144,588	−60.8, 339.0	0.3 (1.7)	37, 29,266	1,524 (1,423)	0.00023	<0.0001
Alpine	9,705	−10.0, 96.7	1.5 (1.9)	84, 8,925	1,020 (690)	0.00134	<0.0001
Anaheim	10,679	−109.3, 364.4	2.2 (4.3)	202, 31,886	3,373 (2,435)	0.00080	<0.0001
Glendora	12,892	−11.1, 73.5	0.7 (1.3)	136, 28,954	1,632 (1,171)	0.00043	<0.0001
Lake Elsinore	9,143	−2.9, 26.0	0.2 (0.5)	33, 3,948	375 (258)	0.00065	<0.0001
Lake Gregory	9,781	−1.6, 10.8	0.3 (0.4)	35, 3,127	272 (172)	0.00128	<0.0001
Long Beach	10,093	−60.9, 387.9	4.1 (14.2)	186, 27,127	3,252 (2,523)	0.00669	<0.0001
Mira Loma	13,748	−11.6, 43.0	0.9 (1.3)	93, 26,732	2,068 (1,317)	0.00054	<0.0001
Riverside	11,881	−48.3, 110.5	0.6 (1.2)	117, 27,439	1,869 (1,411)	0.00039	<0.0001
San Bernardino	9,639	−24.6, 158.2	1.9 (2.3)	186, 17,336	2,263 (1,409)	0.00092	<0.0001
San Dimas	11,201	−43.7, 71.8	1.1 (1.8)	19, 27,363	2,720 (2,075)	0.00046	<0.0001
Santa Barbara	12,696	−23.3, 170.0	0.5 (1.5)	16, 1,4784	784 (660)	0.00083	<0.0001
Santa Maria	11,399	−4.0, 33.9	2.4 (2.1)	57, 7,038	616 (367)	0.00420	<0.0001
Upland	11,731	−14.5, 80.6	0.9 (1.5)	104, 25,244	1,937 (1,508)	0.00046	<0.0001

Odds Ratios (ORs) and 95% Confidence Intervals (CIs) for recent wheeze and exposure to an interquartile range (IQR) increase (24 ppb) of NO_x in the previous 12 months using the output from each of 120 ensembles, stage 2 NO_x model output and stage 3 NO_x model output are shown in Figure 2 (Table 4), and the health risk estimate is corrected for SMME where applicable. Independent tests of the OR for an IQR increase in NO_x exposure using any of the 120 ensembles ranged from 1.17–1.29. Ten percent of the lower confidence limits did not cross the null value of OR =1, p<0.05. The variances of the OR ranged from 0.000020 to 0.000026. The average OR across the 120 ensembles was 1.23 (standard deviation = 0.028). Using the stage 2 NO_x output, the OR was 1.24 (95% CI: 0.976, 1.569). By applying the correction information methods for SMME, the standard error increased from 0.004964 to 0.004966 and the corrected 95% CI remained the same (0.976, 1.569). Because in our previous work we found significant spatial variations of SMME [40], with NO_x predictions in the city of Long Beach showing the highest SMME values, we wanted to evaluate a “worst case scenario” by applying the Long Beach specific SMME correction to the variance of the CHS-wide health effect estimate. Despite the SMME in Long Beach being approximately 29 times greater than that of the entire cohort, the new stage 2 based confidence interval (corrected for Long Beach specific SMME) minimally lengthened to (0.974, 1.573).

Figure 2:

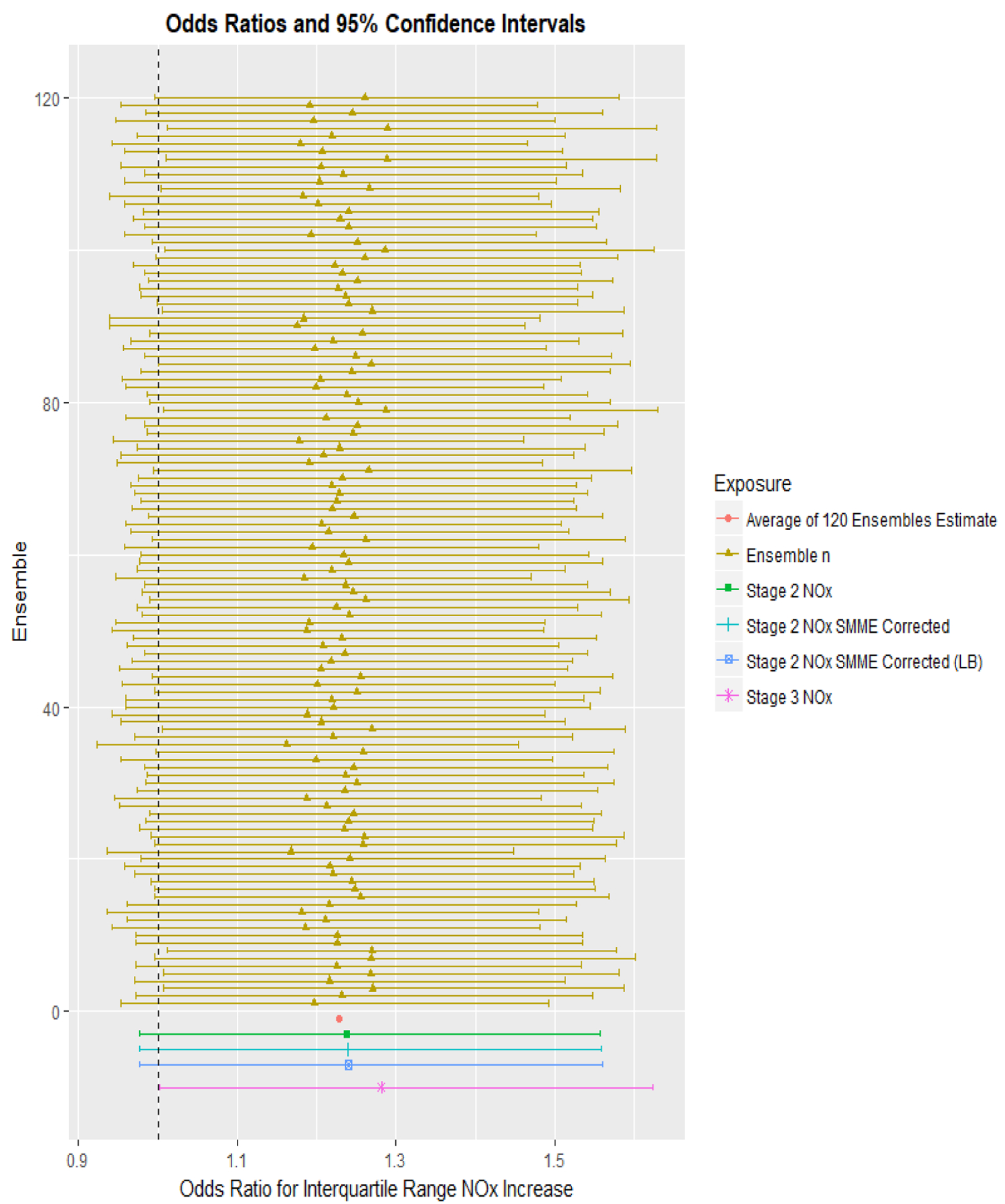
Odds Ratio (OR, corrected for SMME where applicable) and 95% Confidence Interval (CI) of Recent Wheeze for an Interquartile Range Increase in Residential NOx Exposure as Estimated by the Different Stages (1–3) of the Li et al. (2017) [41] Spatiotemporal Model. Mixed-effect models were used to determine ORs and 95% CI for recent wheeze using exposure predictions from the individual 120 ensembles (yellow). The mean OR was calculated (red) to represent the average health effect estimate of stage 1 of the spatiotemporal model. Health models using stage 2 (green) and stage 3 (purple) NOx estimates were included for comparison. Health effect estimates from stage 2 corrected for SMME are shown in blue. All models were adjusted for maternal race, premature birth, child sex, baseline community, child age, child body mass index, maternal education, crowding in home, maternal and paternal allergy history.

Table 4:

Odds Ratio (OR) and 95% Confidence Interval (CI, original and corrected for SMME where applicable) from the Epidemiological Analysis of the Risk of Recent Wheeze in Relation to an Interquartile^a Increase in Residential NO_x as Estimated by the Different Stages of the Li et al. (2017)[41] Spatiotemporal Model

	Odds Ratioa,b (OR)	95 % Confidence Intervala,b	Standard Error b	p-value	BIC	AIC
Range of ORs and their standard errors from the 120 individual ensembles	1.167–1.291		0.0045–0.0051
Mean of 120 RRs from ensembles	1.234
OR based on stage 2 NOx	1.235	(0.9763, 1.5696)	0.004964	0.078	3766	3568
OR based on stage 2 NOx corrected for SMMEc	1.235	(0.9762, 1.5697)	0.004966
OR based on stage 2 NOx corrected for Long Beach Specific SMMEc	1.235	(0.9739, 1.5734)	0.005015
OR based on stage 3 NOx	1.283	(1.0014, 1.6396)	0.005126	0.0471	3766	3568
OR based on stage 3 NOx corrected for SMMEc	1.283	(1.0013, 1.6365)	0.005136
OR based on stage 3 NOx corrected for Long Beach Specific SMMEc	1.283	(0.9982, 1.6415)	0.005200

^aResults displayed for an interquartile range increase; Interquartile range for stage 2 and 3 NO_x is 24.2 and 24.5 respectively, n=4,380

^bModels adjusted for maternal race, premature birth, child sex, baseline community, child age, child body mass index, maternal education, crowding in home, maternal and paternal allergy history.

^cShared Multiplicative Exposure Measurement Error (SMME) correction adjusts the variance of the health estimate using eq. 3.

SUMA error components could not be calculated using stage 3 NO_x exposure prediction model outputs (a single monthly prediction following constrained optimization) and therefore, the SMME correction of variance from stage 2 NO_x was applied to the stage 3 based health estimate. Using stage 3 output from the NO_x exposure model, the OR for an IQR increase in NO_x was marginally associated with recent wheeze episodes (OR: 1.28; 95% CI: 1.001, 1.640). We did observe lengthening of the confidence interval across the null when applying the Long Beach SMME correction (95% CI: 0.998, 1.642). Compared to the stage 2 effect estimate, the stage 3 effect estimate moved away from the null, and the variance increased. The AIC and BIC were comparable between the model using stage 2 and 3 NO_x predictions (AIC: 3568; BIC: 3766).

In our sensitivity analysis to assess linearity, we found that the Taylor series approximation of the logistic model was linear for the range of the annual NO_x values in our data (Figure 3), supporting our approach to apply these correction information methods in this context given that these methods are developed based on linear models.

Figure 3: Comparison of the Logistic Wheeze Expit Function and the Taylor Series Linear Approximation.

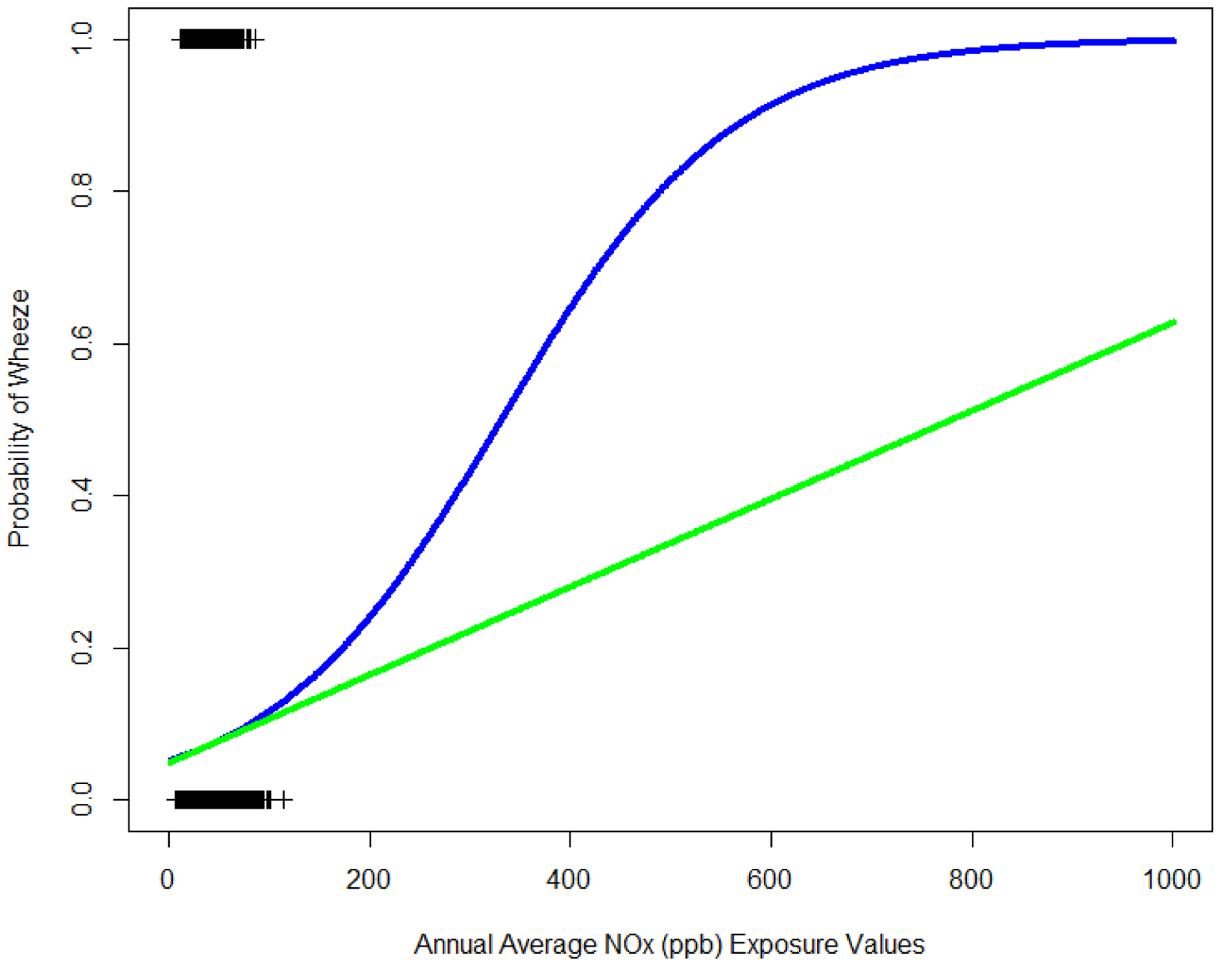
Expit Function (Blue) and it’s Taylor Series Linear Approximation (Green) for NO_x levels ranging from 0 to 1,000 ppb. Observed annual average NO_x values in southern California Children’s Health Study (CHS) indicated on plot with “+”. Observed and extrapolated NO_x values (x-axis) and wheeze status (y-axis) displayed. Focus should be given to the observed range of NO_x.

4. DISCUSSION

We have shown that the Stram and Kopecky [10] framework, originally developed for radiation dosimetry, can be applied to ensemble based air pollution epidemiological evaluations to formally assess the influence of SMME on the variance of observed health effect estimates. By applying SMME correction in our epidemiological analysis using wheeze as a health outcome, we found that specifically for this outcome and exposure combination, SMME was not a major concern in our epidemiological models using stage 2 NO_x as it did not influence the variance of the effect estimate in a meaningful way (altering statistical significant of the effect estimate), but we did see that epidemiological conclusions were altered as the confidence intervals crossed the null, when adjusting the stronger health effect estimates derived using stage 3 NO_x estimates for the “worst case scenario” (Long Beach specific) SMME.

We conducted a cross-sectional epidemiological analysis to estimate the association between NO_x exposure and the risk of wheeze in the previous year to assess the impact of the SMME on the observed health effect conclusions. Further, by repeatedly fitting the same epidemiological model using different estimates of NO_x exposure from each stage of the Li et al. (2017) model [41], we also quantified the additional influence of the ensemble learning and constrained optimization stage in the exposure model on epidemiological conclusions. Our findings highlight the benefit of using a 3-stage spatiotemporal model with ensembles and constrained optimization for NO_x prediction, as we observed stronger health effects with each additional stage of our Li et al. (2017) [41] NO_x exposure model, largely because of the addition of constrained optimization.

We highlight the influence of exposure model specification on health effect estimates by fitting the health model to each exposure prediction ensemble (n=120). Although there is some variation in the effect estimate between exposure ensembles (between −6% and 5% variability from the final stage 2 estimate), overall the resulting estimate consistently demonstrates positive associations between NO_x and wheeze. This analysis is limited as we do not have the gold standard health effect estimate to formally assess bias, but we assume the true health effect is most similar our final stage 3 NO_x based on our confidence in this model and the consensus of previous literature. More notable is the meaningful changes in precision across the health estimates between exposure ensembles, as only 10% of the confidence intervals did not cross the null. In this setting, we see that accuracy and consistency (guided by covariate inclusion) of in spatiotemporal exposure models had a meaningful influence on the precision of (exposure estimates, see Figure S1, and Table 4) epidemiological conclusions. By averaging across ensembles (stage 2), the error of exposure prediction should be theoretically reduced resulting in decreased variance and bias. We found that the measure of association moved away from the null using the stage 2 output and further shifted away from the null using the stage 3 output. The stage 3 output adjusted exposure predictions represent real-life physical constraints. This results in more realistic exposure predictions further reduce variability of exposures. Although the measure of association shifted away from the null, we did see an increase in the standard error, indicating that although we reduced variance in the exposure predictions, there may be increased variance in the epidemiological measures of association obtained using exposure predictions with applied constraints. We found significant spatial autocorrelation of the difference between stage 2 and 3 NOx estimates, indicating that the constrained optimization was more important in specific geographic areas. We note that the largest difference between the stage 2 and 3 annual average NOx estimates was observed among some predictions within high NOx communities, but this was not seen in all high NOx communities.

Through this work, we gain useful information regarding the additional uncertainty of epidemiological inferences resultant from shared exposure error. Although we found that shared additive error was larger in magnitude than SMME in our earlier work [40], we focused our adjustment of epidemiological effects on SMME as other work has indicated minimal influence of shared additive error on epidemiological results in a Berkson model [48]. Shared error differs from traditional measurement error as the errors are not independent, which is common in air pollution exposure models since the dynamic and fine scale variability of true air pollution can’t fully be captured in models that rely on spatial and temporally aggregated covariates. There has been work showing that exposure bias is actually greatest from shared error within predictions compared to bias due to shared error between predictions [49]. Our work only focuses on the shared error between predictions and future studies that can classify shared within and between exposure measurement error will be integral in identifying factors contributing to shared measurement error.

The utility of this work in the epidemiological setting is to adjust confidence intervals to account for SMME. SMME artificially shortens confidence intervals ([10, 12, 50]) and therefore adjustment will lengthen confidence intervals so that environmental epidemiologist can provide inferences with increased precision. The assessment of SMME in exposure estimates alone is not meaningful to epidemiologists without comparison to the epidemiological effect estimate (b) and the naïve variance (SE(b)²). Further, SMME is negligible if $b^2 {\sigma }_{SM}^2$ is small relative to the variance of the epidemiological estimate, SE(b)² (see eq.3).

The observed variable influence of SMME across health models is related to the magnitude of the beta effect estimate. The stage 2 effect estimate was small and only marginally significant, therefore, the influence of SMME on the variance of the estimate was small and did not create a meaningful bias in the variance estimate. However, for the stage 3 effect estimate, SMME was more influential due to the magnitude of the association. The influence of SMME is determined by the nature of the association of exposure estimates W on outcome D. Methods used from this investigation may be carried over to other health outcomes to assess the influence of SMME on epidemiological inferences, but our conclusions regarding the effect of SMME from this exposure model cannot be generalized to other investigations assessing other health outcomes Other sophisticated methods have been developed to assess shared Berkson-like error using bootstrap methodology (parameter and non-parametric)[50]; however, these methods require modeling exposure and health risk together in a two-stage model. Often epidemiologists utilize already developed spatiotemporal models with the same or similar spatial and temporal domain corresponding to their research sampling frame. In these situations, our methods become a feasible option for SMME assessment. It is important to note the scope of this work is only to assess the influence of SMME on confidence intervals, other types of measurement error could still have additional and important effects on the health effect estimates.

In the provided wheeze epidemiological analysis, the SMME variance was very small compared to the health effect estimate and therefore did not have meaningful impact on conclusions. But in settings where the SMME is more similar to the magnitude of the epidemiological effect estimate, confidence intervals will meaningfully lengthen (as we have seen using the Long Beach specific SMME). To demonstrate this point, using equation 3, we have determined the influence of increasing value of SMME on the p-value of the epidemiological estimate using a Wald-like test. This was carried out on both the stage 2 and stage 3 effect estimates and we were able to identify the SMME value where significant findings should be questioned (see Supplement Figure S2).

We also note that this epidemiological analysis was cross-sectional, utilizing exposure measures of the annual average prior to the baseline entry year of this CHS cohort. This time corresponds to years 2002–2003, which correspond to exposure prediction time period where we observed relatively lower shared multiplicative error [40] (compared to earlier years in the first paper). If this analysis focused on early life exposure of CHS participants, the magnitude of SMME would be larger and could be more influential on epidemiological conclusions between NO_x and wheeze risk, depending on the observed association. These types of insights can be gained from conducting a similar, formal measurement error evaluation in future health analyses. By quantifying the shared variances, we gain useful information regarding the additional uncertainty of epidemiological inferences resultant from shared measurement error, common to spatiotemporal exposure models. Overall, it is both the magnitude of SMME in the complex spatiotemporal model and the magnitude of the epidemiological association which will determine the influence of SMME on epidemiological conclusions.

This work focuses only on the formal SMME adjustment of variance estimates without regard to the influence on the effect estimates. Traditional understanding of Berkson error focuses on precision while accuracy is not of critical concern (unless variance is non-constant). Previous works that focuses on Berkson/Berkson-like error in exposure, found that bias can be introduced in epidemiological estimates [51], but this bias is overall very small [7]. It should be noted that there has been new work in simulations that has shown that when Berkson/Berkson-like error (low ratio of variance of modeled to true exposure) is very large, a nontrivial bias away from the null was observed [12] . We did informally assess bias in our effect estimate across stages of the exposure prediction model. Although we do not know the true association, the literature supports a consistent association between NO₂ and NO_x exposure and asthma symptoms including wheeze [52]. Further work formally assessing bias in the effect estimate across the stages of the exposure model are needed.

Stram and Kopecky’s [10] methods of SMME correction are based on linear models. We used logistic regression health models; therefore, the appropriateness of application was of concern. To our knowledge, analytic methods to correct for SMME in non-linear models do not yet exist. To determine appropriateness, we compared the model to the Taylor Series approximation of logistic model and found a nearly perfect linear fit for the range of our data. The fit is no longer linear when annual NO_x levels increase to 200 ppb or greater, a value beyond the range of our exposure assignments (Figure 3). We also found nearly identical calculated probabilities of association when running this model as a linear and logistic model. This SMME correction method could be used in any epidemiological study design which utilizes exposure measures with multiple realizations such as ensemble-based exposures with a linear association and where errors are assumed to be normal. Although we have demonstrated, by using a Taylor Series approximation of the linear, this method can also be applied to non-linear models, a formal investigation should be conducted to confirm that these methods could be used in a non-linear situation.

Our work is limited in scope as it is based on a Berkson error model without consideration of the impacts of classical/classical-type error. Although we use exposure estimates derived from a sophisticated model that is designed to capture fine scale spatial and temporal variability, our model same as all models remains subject to shared Berkson error due to spatial misalignment and other factors [53]. Further, it has been shown that classical error becomes Berkson-like error in spatiotemporal models due to smoothing [53].We are also not considering the measurement error introduced by our assumption that outdoor residential NO_x exposure accurately represents true personal exposures which we know are impacted by time-activity and mobility patterns of individuals. However, we did account for residential mobility in the form of moves or changes in residential address. Lastly, we do not assess health effects or error in a multipollutant framework, a growing interest in the field of environmental epidemiology.

We adjusted for common confounders used when regressing risk of childhood wheeze on residential NO_x exposure. As we do not account for the variables of adjustment used in our epidemiological model, the SMME adjustment method used in this exercise ( Eq. 3) assumes that any adjustment variables used in the epidemiological model are not associated with exposure error. We believe this assumption is reasonable to a certain extent since our study takes place among an urban population. As a design variable, we adjusted for CHS community of recruitment, a variable we believe may be associated with error. But this variable was included in the epidemiological model only because it is a study design variable and when we carried out this exercise without it, we found almost identical results. We caution future use of this method to expand Eq. 3 to account for variables of adjustment in the epidemiolocal model.

Overall, we used quantified SUMA error from our previously published spatiotemporal exposure model [41] to formally evaluate the impact of SMME on health effect estimates using an example epidemiological analysis. In conclusion, we showed that sophisticated spatiotemporal models that are employing machine learning techniques are preferable for use as they yield overall better exposure estimates through improvements in bias and precision. Even with the use of such improved exposure models, we found that non-trivial effects of measurement error on epidemiological conclusions are still present. Epidemiologist, exposure scientist, data scientist, and statisticians must work together, rather than in parallel to fully understand implications of using these refined exposure models within the epidemiological context [12].

Table 2:

Distribution of Average Annual NO_x Exposure (ppb) by Stage of the Ensemble Learning Spatiotemporal Model Output

Model Output Stage	Minimum	Mean	Standard Deviation	Median	Maximum
Stage 2	6.44	37.52	15.31	37.84	113.41
Stage 3	7.15	37.03	14.86	37.69	108.12
Difference (Stage 2-Stage3)	−10.42	0.50	1.6	0.43	10.96