Modelling of reproduction number for COVID-19 in India and high incidence states

Abstract

Background

Since the onset of the COVID-19 in China, forecasting and projections of the epidemic based on epidemiological models have been in the centre stage. Researchers have used various models to predict the maximum extent of the number of cases and the time of peak. This yielded varying numbers. This paper aims to estimate the effective reproduction number (R) for COVID-19 over time using incident number of cases that are reported by the government.

Methods

Exponential Growth method to estimate basic reproduction rate R₀, and Time dependent method to calculate the effective reproduction number (dynamic) were used. “R0” package in R software was used to estimate these statistics.

Results

The basic reproduction number (R₀) for India was estimated at 1.379 (95% CI: 1.375, 1.384). This was 1.450 (1.441, 1.460) for Maharashtra, 1.444 (1.430, 1.460) for Gujarat, 1.297 (1.284, 1.310) for Delhi and 1.405 (1.389, 1.421) for Tamil Nadu. In India, the R at the first week from March 2–8, 2020 was 3.2. It remained around 2 units for three weeks, from March 9–29, 2020. After March 2020, it started declining and reached around 1.3 in the following week suggesting a stabilisation of the transmissibility rate.

Conclusion

The study estimated a baseline R₀ of 1.379 for India. It also showed that the R was getting stabilised from first week of April (with an average R of 1.29), despite the increase in March. This suggested that in due course there will be a reversal of epidemic. However, these analyses should be revised periodically.

1. Introduction

Since the onset of the COVID-19 in China, forecasting and projections of the epidemic based on epidemiological models have been in the centre stage for planning and implementations of strategies to mitigate the epidemic. There has been a great dependence of these due to the unprecedented nature and uncertainties of the disease. Researchers have used various models to predict the maximum extent of the number of cases and the time of peak. However, the rate of new cases over time, referred to as incidence, serves as a proxy for risk but does not contribute as a metric for the epidemic progression or prediction of its evolution.^{1 , 2} There are other measures that could serve as proxy for disease progression. One measure of viral spread is the R₀, which refers to the average number of secondary infections caused by a primary case and is commonly used to characterize the transmissibility potential of a disease in a completely susceptible population.² At the beginning of an epidemic, from a couple of days to 1–2 weeks, “Basic reproduction number” (R₀) can be estimated. During an ongoing epidemic for few weeks to months, “Time dependent” reproduction number which is otherwise called as effective reproduction number (R) can be estimated. The effective reproductive number (R) can be used to characterize transmissibility once a certain proportion of the population has been infected and is resistant or immune.³ It determines the potential for epidemic spread at a specific time t under the control measures in place. Regular and frequent computation of effective reproduction number in different settings is essential to understand the trajectory and real time assessment of the magnitude of the epidemic. Besides, it is an important parameter to evaluate the effectiveness of current public health interventions and plan additional interventions as required.⁴

The measure of disease transmissibility can be estimated through generation time interval which is the time difference between the infection time of an infected person and the infector. Serial interval time is the time between the start of symptoms in the primary patient (infector) and onset of symptoms in the patient receiving that infection from the infector (the infectee).⁵ The serial interval is observable, while the generation interval usually is not. Therefore, researchers use serial interval time to calculate the reproduction number. Considering the importance, the paper aims to estimate the effective reproduction number (R) of COVID-19 for India and selected high incidence states over time using incident number of cases that are reported by the government.

2. Methods

The basic and time-dependent effective reproduction number, $R_0$ and $R$ are the most important parameters to quantify the transmission potential and track the subsequent evolution of transmission of an epidemic over a period of time. The R₀ is the average number of secondary infections produced by a typical case of an infection in a population where everyone is susceptible. For example, if the R₀ for HINI in a population is 15, then we would expect each new case of HINI to produce 15 new secondary cases (assuming everyone around the case was susceptible). R₀ excludes new cases produced by the secondary cases.

The basic reproductive number is affected by several factors such as the rate of contacts in the host population, the probability of infection being transmitted during contact, and the duration of infectiousness. A population will rarely be totally susceptible to an infection in the real world. Some contacts will be immune, for example developing immunity due to prior infection or as a result of previous immunisation. Therefore, not all contacts will become infected and the average number of secondary cases per infectious case will be lower. This is measured by the effective reproductive rate (R). Essentially, R₀ must be > 1 for an epidemic to occur in a susceptible population. If R > 1, the number of cases will increase, such as at the start of an epidemic. Where R = 1, the disease is endemic, and where R < 1 there will be a decline in the number of cases. To successfully eliminate a disease from a population, R needs to be less than 1.

There are various methods to estimate the basic reproduction number and effective reproduction number, such as attack rate (AR), exponential growth (EG), maximum likelihood method (ML), sequential Bayesian method (SB) and the Time dependent method (TD). We used exponential and time dependent method to estimate basic and effective reproduction number respectively.

2.1. Exponential growth method (EG)

Wallinga & Lipsitch explained the relationship between basic reproduction number and exponential growth rate (r), which is defined by per capita change in number of new cases per unit of time.⁶ This is defined as,

$$\frac{1}{R_0}=\underset{0}{\overset{\infty }{\int }}{e}^{-rt}w\left(t\right)dt$$

Where

• $R_0$ is basic reproduction number,

• $r$ is exponential growth rate and

$w\left(t\right)$ is generation interval distribution which is defined by the time lag between infection in a primary case and a secondary case but it cannot be observed directly, so it is often substituted with the serial interval distribution that measures time between symptoms onsets. The $R_0$ is derived from the above equation and

$$R_0=\frac{1}{M_T\left(-r\right)},$$

Provided $M_T\left(-r\right)$exists.Where, $M_T\left(-r\right)$ is moment generating function of serial interval time T and it is finite for all $r\in \left[-a,a\right];$a is a positive constant.⁷

2.2. Time dependent method

Time dependant calculation of reproduction number (R) was proposed by Wallinga and Teunis in 2004.³ In this method, the effective reproduction number $R$ is computed by arithmetic mean over the effective reproductive number of the case $\left(R_j\right)$ for all those cases who show the first symptoms of illness on day t.

$$R_t=\frac{1}{N_t}\sum _{j=1}^{N_t}{R}_j$$

Where, $N_t$ is number of cases reported in the time unit $t$ and the $R_j$ is

$$R_j=\sum _{k=1}^n{p}_{k,j}$$

$p_{k,j}$ is probability that the case $k$ infected by the case $j$ and is computed by,

$$p_{k,j}=\frac{w(t_k-t_j|\theta )}{{\sum }_{m=1,m\ne k}^{n}w(t_k-t_m|\theta )}$$

The confidence interval of $R_t$ can be obtained by simulation. The data for India and other states were taken from the crowd sourced database available on https://www.covid19india.org, which is given in Appendix 1. Additional details about the derivation of these equations are provided in Appendix 2. The reproduction number was estimated using “R0” package in R software version 3.6.2.⁵ We assume that the serial interval distribution follows gamma distribution with mean (sd) was 4 (2) which was given by Hwang et al.⁸

3. Results

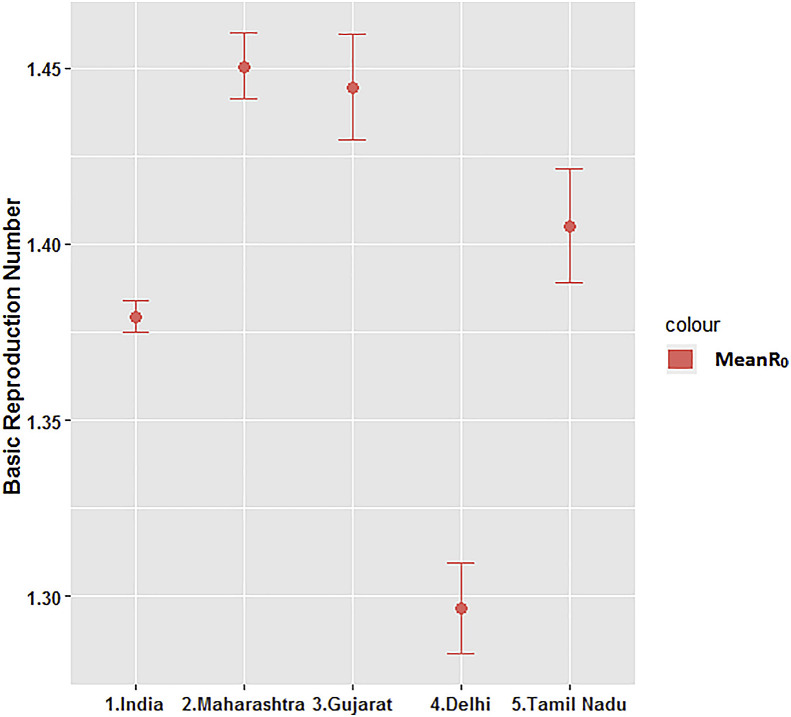
The basic reproduction number (R₀) for India was estimated at 1.379 (95% CI: 1.375, 1.384). This was 1.450 (95% CI: 1.441, 1.460) for Maharashtra, 1.444 (95% CI: 1.430, 1.460) for Gujarat, 1.297 (95% CI: 1.284, 1.310) for Delhi and 1.405 (95% CI: 1.389, 1.421) for Tamil Nadu. Maharashtra and Gujarat had higher basic reproduction rate as compared to other states. Delhi had lower R₀ 1.297 as compared to other states. The diagrammatic representation of basic reproduction number, R₀ is presented in Fig. 1 .

Fig. 1.

Graphical Representation of Basic Reproduction Number (R₀) using Exponential Growth Method.

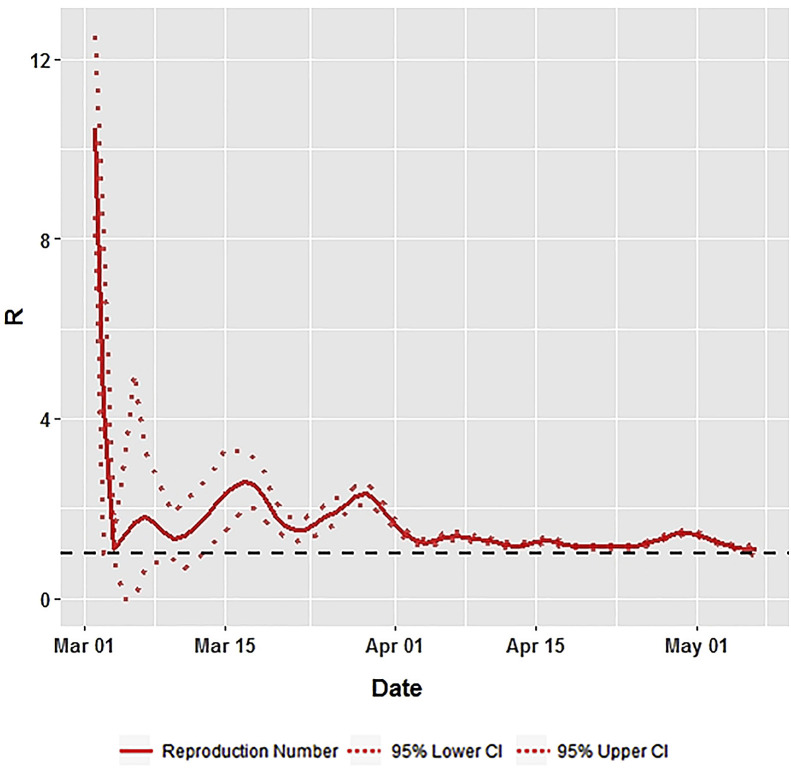
The average effective reproduction number R over 7 days with 95% CI, for India and high incidence states is presented in Table 1 . The state specific details are presented diagrammatically in Fig. 2, Fig. 3 . In India, the R at the first week from March 2–8, 2020 was 3.2. It remained around 2 units for three weeks, from March 9–29, 2020. After March 2020, it started declining and reached around 1.3 in the following week suggesting a stabilisation of the transmissibility rate. In Maharashtra, the effective R was about 2.0 from March 9 to April 5, 2020. This declined and remained at 1.5 till April. In Gujarat, from March 16–22, 2020 the R remained at 3 and declined thereafter to reach about 2 on April 19, 2020. It further declined to around 1 during the 2^nd week of May 2020. In Delhi, though the starting R was about 4.5, it declined and reached one on April 19, 2020, and then increased and stabilised at 1.5. In Tamil Nadu, the 3^rd and 4^th week of March, starting from 16th–29th March, showed an average R of about 3.4. It declined thereafter and remained at about 1 until April 26, 2020, and thereafter increased to 2.

Table 1.

Average Effective Reproduction Number (R) over 7 days and 95% CI using Time Dependent Method.

From	To	Week	Average Effective Reproduction Number R (95% CI)
			India	Maharashtra	Gujarat	Delhi	Tamil Nadu
02-03-2020	08-03-2020	1	3.20 (1.64, 5.15)	–	–	–	–
09-03-2020	15-03-2020	2	1.70 (1.01, 2.48)	2.00 (0.89, 3.26)	–	–	–
16-03-2020	22-03-2020	3	2.12 (1.66, 2.60)	1.82 (0.71, 3.07)	2.76 (1.63, 4.04)	–	3.39 (2.00, 5.00)
23-03-2020	29-03-2020	4	1.94 (1.70, 2.20)	1.95 (1.31, 2.68)	1.18 (0.42, 2.09)	4.49 (2.72, 6.40)	3.64 (2.23, 5.19)
30-03-2020	05-04-2020	5	1.57 (1.46, 1.68)	1.82 (1.50, 2.16)	2.21 (1.15, 3.51)	1.82 (1.46, 2.18)	1.62 (1.32, 1.92)
06-04-2020	12-04-2020	6	1.30 (1.23, 1.38)	1.44 (1.27, 1.61)	2.13 (1.67, 2.59)	1.46 (1.19, 1.74)	0.94 (0.73, 1.15)
13-04-2020	19-04-2020	7	1.22 (1.16, 1.28)	1.41 (1.28, 1.54)	1.66 (1.45, 1.86)	1.00 (0.78, 1.22)	1.05 (0.78, 1.32)
20-04-2020	26-04-2020	8	1.16 (1.11, 1.21)	1.18 (1.09, 1.26)	1.09 (0.96, 1.22)	1.40 (1.20, 1.61)	1.43 (1.15, 1.73)
27-04-2020	03-05-2020	9	1.37 (1.32, 1.42)	1.36 (1.27, 1.44)	1.23 (1.11, 1.35)	1.47 (1.31, 1.64)	2.27 (2.03, 2.51)
04-05-2020	07-05-2020	10	1.13 (1.06, 1.20)	1.11 (0.99, 1.22)	1.05 (0.84, 1.26)	1.16 (0.94, 1.38)	1.53 (1.34, 1.72)

Fig. 2.

Effective Reproduction Number (R) for India using Time Dependent Method.

Fig. 3.

Effective Reproduction Number (R) for High Incidence States in India using Time Dependent Method.

4. Discussion

In our study, we estimated the basic and time-dependent reproductive number for COVID-19 in India which is critical for developing and assessing the interventions. Though empirical data driven estimates are ideal, this study has attempted to estimate parameters using daily incidence of COVID-19 cases. It is estimated that at effective reproduction rate of 2.5, 90% the ongoing pandemic can be controlled if 80% of the contacts can be traced and quarantined or isolated effectively. If the effective reproduction number could be brought down to less than 1.5, higher level of control can be achieved with lower level of contact tracing and; if it reaches 3.5 or more then the trajectory of the epidemic will be very rapid.⁹

While estimating reproduction number, it is assumed that the number of secondary infections produced by a single case has no variations. However, several factors such as super-spreading events, changing disease control strategies, their effectiveness and other social interventions result in drastic changes in the transmission pattern in countries and within countries within a short time period. As a result, the effective reproductive number is also constantly modified during the epidemic. We estimated the weekly reproduction number, considering the reported median incubation period of 5–6 days.¹⁰ The weekly estimation could be useful to monitor and assess the impact of the virus; develop timely and appropriate strategies; and assess the effectiveness of control measures in India and different states.

Everyday cases support the fact that state wise analyses are essential, as the trend of R changes over time which are different between states. Therefore we were able to study the trend in R in the high burden states. The state specific analyses suggested that it is critical to have state specific mitigation strategies as the transmission dynamics vary between states. Stratification of data would be able to provide a better estimate on which control measures and duration would work best and provide the best benefit for specific states. Some reasons that might explain the observed differences include climatic factors (e.g., temperature variation and humidity), demographic and biosecurity factors (e.g., presence of filtered farms).¹ Moreover, underreporting due to asymptomatic cases and the lack of testing among this sub population may have provided a lower estimate of R. However, if underreporting is constant over a period of time, it might not affect the results. As there has been no method that could explicitly account for under-reporting during the course of the epidemic and there are no published methods for R calculations that can account for such issues, we assumed the underreporting to be constant in time, thus not dramatically affecting results.

According to the study, almost all the states indicated a significant change in R during March 15–31, 2020. In India, R was higher during this time period that could be due to a known cluster of around 5000 cases and many of them travelled from the neighbouring countries. It affected the situation in many other states as well. In Tamil Nadu, another cluster was identified in a city vegetable market that served as an epicentre, which became a source for many infections in the state. Due to this, the R in Tamil Nadu increased significantly in the first week of May 2020.

Regarding the serial time interval, the data are restricted to online reports of confirmed cases and therefore may be biased towards more severe cases in areas with a high-functioning healthcare and public health infrastructure. The rapid isolation of such cases may have prevented longer serial intervals, potentially shifting our estimate downwards compared to serial intervals that might be observed in an uncontrolled epidemic.¹¹

Second, the identity of each infector and the timing of symptom onset were presumably based on individual recollection of past events. If recall accuracy is impeded by time or trauma, cases may be more likely to attribute infection to recent encounters (short serial intervals) over past encounters (longer serial intervals). Therefore there may be under estimation in the serial time interval estimation. However, in order to adjust for bias we need to do a rapid empirical study to validate our estimation.⁷

As limitations, at the state level in our study, it is always difficult to observe the initial cases in any new outbreak or epidemic like COVID-19. This will likely to result in overestimation of initial reproduction numbers due to under reporting or delay in reporting of cases. To address this challenge, we have decided not to consider reported numbers of cases for the first 4 weeks starting from January 30, 2020, when summarizing these data. The estimated CIs using the time-dependent method could be wider because of few observed cases at times.

5. Conclusion

The study estimated a baseline R₀ of 1.379 for India. It indicated an increasing trend in the R, when there was an eventuality in the states. It also showed that the R was getting stabilised from first week of April and remained at the same level about 1.29, which implies that intensive interventions that include aggressive tracing and testing coupled with appropriate clinical management of the infected are essential to control the transmissibility of the disease.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Ethical approval

Not required.

Declaration of competing interest

None of the authors have conflicts of interest to report.