Magnetic resonance fingerprinting with quadratic RF phase for measurement of T₂* simultaneously with δ_f, T₁, and T₂

Abstract

Purpose:

This study explores the possibility of using a gradient moment balanced sequence with a quadratically varied RF excitation phase in the magnetic resonance fingerprinting (MRF) framework to quantify T₂* in addition to δ_f, T₁, and T₂ tissue properties.

Methods:

The proposed quadratic RF phase-based MRF method (qRF-MRF) combined a varied RF excitation phase with the existing balanced SSFP (bSSFP)-based MRF method to generate signals that were uniquely sensitive to δ_f, T₁, T₂, as well as the distribution width of intravoxel frequency dispersion, Γ. A dictionary, generated through Bloch simulation, containing possible signal evolutions within the physiological range of δ_f, T₁, T₂, and Γ, was used to perform parameter estimation. The estimated T₂ and Γ were subsequently used to estimate T₂*. The proposed method was evaluated in phantom experiments and healthy volunteers (N = 5).

Results:

The T₁ and T₂ values from the phantom by qRF-MRF demonstrated good agreement with values obtained by traditional gold standard methods (r² = 0.995 and 0.997, respectively; concordance correlation coefficient = 0.978 and 0.995, respectively). The T₂* values from the phantom demonstrated good agreement with values obtained through the multi-echo gradient-echo method (r² = 0.972, concordance correlation coefficient = 0.983). In vivo qRF-MRF-measured T₁, T₂, and T₂* values were compared with measurements by existing methods and literature values.

Conclusion:

The proposed qRF-MRF method demonstrated the potential for simultaneous quantification of δ_f, T₁, T₂, and T₂* tissue properties.

1 |. INTRODUCTION

Transverse relaxation time T₂* is an MR tissue property that provides insight into underlying tissue physiology and pathology. The clinical value of such insight has led to the incorporation of T₂* contrast-dependent methods such as MR-SWI and BOLD contrast-based techniques within various clinical protocols. The T₂* tissue property is affected by tissue iron concentration, making it sensitive to iron containing blood products, and has been observed to change in several disease states. Parkinson’s disease is associated with increased iron in the substantia nigra, globus pallidus, and hippocampus.^1–4 Alzheimer’s disease has been associated with increased iron stores in the basal ganglia, as well as hippocampal and cortical regions of the brain.^1,5,6 Huntington’s disease has been associated with increased iron concentration in the globus palladus and putamen.³ Outside of the brain, T₂*-sensitive techniques are used to monitor iron overload of the liver and heart in transfusion-dependent patients.^7,8 Iron nanoparticle-based MR contrast agents have also been engineered for versatile biological specificity that rely on MR T₂*-sensitive methods for detection.⁹

Empirically, T₂* is the exponential decay time constant of the tissue MR signal. This time constant can be decomposed into two components described by the following relationship:

$$\frac{1}{T_2^{*}}=\frac{1}{T_2}+\frac{1}{{T^{\prime }}_2}$$ (1)

where T₂ is the time constant of non-refocusable transverse magnetization decay, and T′₂ is the time constant of refocusable transverse magnetization decay arising from intravoxel frequency dispersion. Although both T₂ and T′₂ properties are affected by tissue iron concentrations, neither property alone is specific to pathologies affecting tissue iron.¹⁰ For example, T₂ is also affected by tissue water content, and T′₂ is also affected by macroscopic field inhomogeneities and other sources of tissue susceptibility.⁸ Thus, MR methods capable of simultaneous quantification of T₂, T′₂, and T₂* properties may provide greater sensitivity and specificity to pathology. For this reason, methods such as the GESFIDE (Gradient-Echo Sampling of Free Induction Decay and Echo)¹¹ sequence have been developed. These methods require relatively long acquisition times because they must sample both refocused and non-refocused signal echoes, and as a result, have not yet gained widespread adoption.

Magnetic resonance fingerprinting (MRF) is a recently developed framework for the simultaneous quantification of multiple tissue properties.¹² In its initial implementation, the framework was applied to reduce quantification time for brain tissue T₁ and T₂ relaxation properties by incorporating spatial and temporal incoherence to transient signals in a balanced SSFP-based pulse sequence (bSSFP-MRF).¹² Other MRF implementations have since been developed to increase measurement robustness,¹³ be applied to other organ systems,^14,15 or quantify additional tissue properties.^16,17 Application of the MRF framework to T₂* quantification may enable fast and robust quantification of T₂* along with other tissue properties within a clinical exam. However, the initially proposed bSSFP-MRF method has only slight T₂* sensitivity.¹⁸

This work introduces the novel quadratic RF phase-based MRF (qRF-MRF) method for the robust measurement of tissue T₂* simultaneously with tissue T₁, T₂, and off-resonance (δ_f) properties within a single acquisition. The method was adapted from the original bSSFP-MRF method because of its sensitivity to T₁, T₂, and off-resonance ( δ_f) properties.¹² The qRF-MRF T₂* sensitivity is obtained using a varied RF phase scheme that is able to generate both high signal amplitude and signal dependence to intravoxel variations in δ_f. These properties are exploited to generate unique signal evolutions with high SNR within the MRF framework for robust and rapid quantification.

2 |. THEORY

Traditional bSSFP experiments have a well-characterized amplitude and phase behavior.^19,20 Typical acquisition parameters in bSSFP experiments include constant high flip angle (FA), constant short TR, constant (linear) increment in RF excitation phase (PH), and zero net gradient moment per TR. The signal observed from isochromats are highly dependent on the relative RF phase increment, defined as the difference between the PH increment and the phase accumulated over the duration of a TR due to δ_f precession.

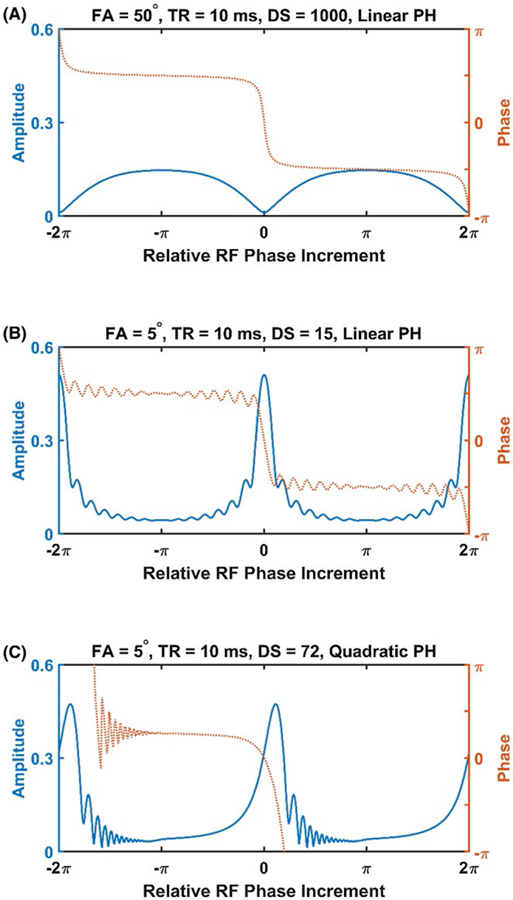
Figure 1A shows the amplitude and phase profiles for isochromats with different relative RF phase increments. When using large flip angles, isochromats with a relative RF phase increment approximately equal to an odd multiple of π have high amplitudes and similar phase values at sampling time TE. Signals from such isochromats are coherent during bSSFP experiments, regardless of the presence or absence of δ_f variations, due to their similar phase values. Without sensitivity to δ_f variations, the generated signals by these isochromats are not sensitive to T′₂. Isochromats with relative phase increments close to an even multiple of π behave differently. Such isochromats have a steep phase profile, allowing for δ_f variation-dependent signal attenuation through phase cancelation. However, these isochromats have low signal amplitude, and signals from them cannot be reliably detected. Without signal regimes with both high amplitude and steep phase profile, the traditional bSSFP experiment is not sensitive to T′₂, and therefore is not appropriate for T₂* quantification.

FIGURE 1.

Amplitude and phase responses during variations of balanced SSFP (bSSFP)-type sequences. Responses are plotted as functions of the relative phase increment between consecutive RF phase from a rotating reference frame locked to the isochromat precession frequency. Traditional bSSFP (A) with high flip angle (FA), many preparation dummy scans (DS), and linear RF phase increment (PH) generates high signal amplitude with flat phase response when PH increment is an odd multiple of π. Low FA bSSFP with low DS (B) shows high signal amplitude with steep phase response for PH increments near even multiples of π. Low FA with a quadratic PH evolution (C) shows a similar response profile as low-FA bSSFP. High amplitude and steep phase response is maintained regardless of DS number with quadratic RF phase

Adjustments to the typical acquisition parameters during a bSSFP experiment can substantially increase T′₂ sensitivity. Figure 1B shows the amplitude and phase profiles corresponding to a bSSFP experiment with a low FA and a reduced number of preparation pulses. Here, isochromats with an even multiple of π RF phase increment maintain the steep phase profile necessary for generation of T₂*-weighted signal through intravoxel signal dephasing, but will transiently develop a large transverse amplitude before its steady state. In fact, this amplitude may surpass 50% of M₀, even greater than those encountered in traditional bSSFP experiments.

Approaches using such acquisition parameters for T₂*-weighted signal generation in bSSFP experiments have been explored previously.²¹ These approaches depend on the selection of acquisition parameters such that the resulting δ_f frequencies with steep phase profile coincide with the imaging regions of interest. The δ_f frequencies associated with this band, with the potential for T₂*-weighted signal generation, is dependent on the choice of PH and TR used. Since PH and TR may be varied across imaging frames within an experiment, the frequency positions of this band, during the n_th frame, is approximately given by

$${\delta }_{f\left(n\right)}\approx \frac{P{H}_{\left(n\right)}-P{H}_{\left(n-1\right)}-2N\pi }{T{R}_{\left(n\right)}*2\pi },$$ (2)

where N is any integer. As traditional bSSFP experiments use constant PH and TR parameters, the resulting band is also constant. The T₂* sensitive regimes may be limited due to the macroscopic field inhomogeneity would the imaging FOV. By using a varied PH or TR between frames, the band can vary accordingly and allow for greater FOV coverage.

In the proposed method, a quadratic RF phase increment was selected such that PH was constantly varied. As a result, high-amplitude T₂*-weighted signal bands were swept through different δ_f values. Figure 1C shows the transient amplitude and phase profiles of an experiment with a quadratic RF phase, demonstrating preserved high amplitude and steep phase characteristics necessary for T′₂ and T₂* sensitivity. In this way, macroscopic field inhomogeneity would not limit the sensitive FOV.

3 |. METHODS

3.1 |. Pulse sequence design

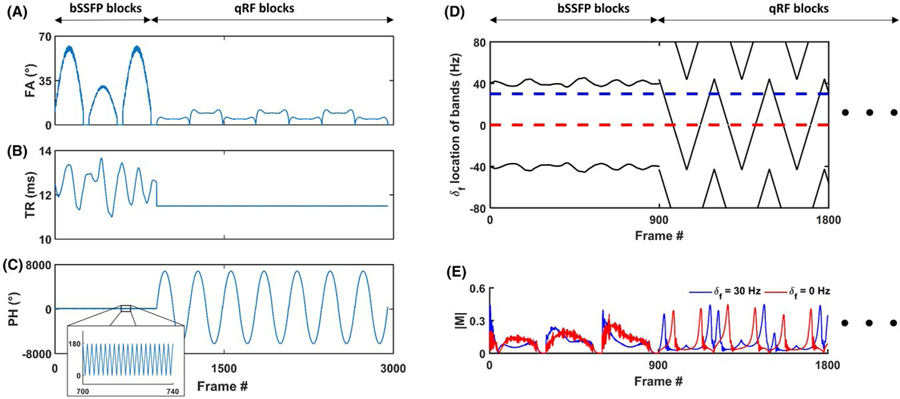
The proposed acquisition strategy used in qRF-MRF is based on a bSSFP-type sequence with a varied FA, TR, and PH. Pulse sequence FAs, TRs, and PHs were selected to generate unique signal shapes for combinations of δ_f, T₁, T₂, and intravoxel frequency dispersion properties within clinically relevant ranges. Figure 2A–C shows the FAs, TRs, and PHs used in the proposed method. Because bSSFP-MRF already fulfills both pulse sequence design criteria for the subset of δ_f, T₁ and T₂ properties, the initial 900 time frames of the proposed qRF-MRF method were performed using the identical FA, TR, and PH scheme as the bSSFP-MRF method,¹² organized into 3 “bSSFP blocks” of 300 frames each.

FIGURE 2.

Pulse sequence description. The FA (A), TR (B), and RF PH (C) used during acquisition of each time frame of the proposed method are shown. During the first 900 time frames, three bSSFP-based blocks of excitations are using parameters identical to previously established bSSFP-MRF, including the use of alternated phase cycling. During the latter 2100 time frames, seven quadratic RF (qRF) blocks of excitations are acquired using low FA, constant TR, and quadratic PH acquisition parameters. The resulting off-resonance frequency position of high T₂*-sensitive bands (D), calculated using Eq. (2), are shown for the first 1800 frames. Two example signal evolutions (E), differing only in δ_f value, are shown to illustrate signal behavior caused by the addition of quadratic phase RF. During quadratic RF lobes, high-amplitude signals from isochromats develop whenever resonance bands intersect the respective δ_f value

For the remaining frames, a new scheme of acquisitions, using seven repeated “qRF blocks” dedicated toward intravoxel frequency dispersion sensitivity, was performed by using low FA with quadratically varied PH increment. The FA pattern (Figure 2A) of each qRF block consisted of a smoothly varied base shape that ranged from 0°–6° for odd-numbered blocks, and 0°–12° for even-numbered blocks. The qRF blocks used a constant 11.5-ms TR (Figure 2B). Within the first and second halves of each qRF block, the PH (Figure 2C) of the piecewise n_th frame is given by

$$PH\left(n\right)=-1.24*n^2+180n$$ (3)

and

$$PH\left(n\right)=-1.24*n^2-180n,$$ (4)

respectively. Each qRF block consisted of only 293 frames to reduce repetition of combinations of the sampled gradient trajectory with the FA, TR, and PH acquisition parameters used throughout the method. Finally, 49 frames, acquired with 0° FA excitation, were appended to the end of the sequence, such that a total of 3000 frames were acquired in the method, consistent with the bSSFP-MRF method.

Figure 2D shows the corresponding frequency positions of T₂*-sensitive bands during different frames of the method, as calculated by Eq. (2). These bands remain relatively stationary near ≈ ±40 Hz during the initial 900 frames, where constant alternated RF phase is used. Minor fluctuations in the position of resonance bands during these frames occurs as a result of the variations in TR. However, isochromats with δ_f values near bands during these frames develop the signal voids typically associated with bSSFP null-bands due to the relatively high FA. After the qRF blocks are initiated, the bands linearly traverse the full span of possible δ_f values. During these frames, isochromats develop transverse magnetization amplitude during particular frames, depending on δ_f value, an example of which is shown in Figure 2E. For frames in which a band traverses through a given isochromat’s δ_f value, a high transverse magnetization is developed.

A variable-density spiral trajectory²² designed with zeroth-moment and first-moment nulling was used to acquire data. The spiral trajectory required 24 and 48 interleaves to fully sample the inner and outer region of k-space, respectively. One spiral interleaf was sampled each frame, resulting in highly undersampled k-space data per frame. Previous MRF methods used a constant rotation of 7.5° of the spiral trajectory between frames to obtain spatial incoherence. In the current method, incoherence was further increased by adopting a bit-reversed ordering of sampled spiral interleafs that repeated itself every 48 frames. All acquisitions were single slice with FOV = 300 × 300 mm², matrix size = 256 × 256 (in-plane pixel size of 1.2 × 1.2 mm²), and slice thickness of 5 mm. All 3000 frames for each single 2D slice were acquired in 35 seconds.

3.2 |. Dictionary

A dictionary-based approach was used to perform parameter estimation for δ_f, T₁, T₂, and T₂* properties from undersampled image frame data following reconstruction. The dictionary used for parameter estimation was generated in two steps. First, a base dictionary, S_base (n, δ_f, T₁,T₂, describing the signal at each of the 3000 frames, n, for different combinations of δ_f, T₁ and T₂ values, was simulated using the Bloch equation as described previously.¹² This base dictionary was calculated for a wide range of 421 possible δ_f values, 89 possible T₁ values, and 99 possible T₂ values. Values for δ_f ranged from ±70 Hz with 0.33-Hz step size. Values for T₁ ranged from 50 ms to 3700 ms with a variable step size, in which each value was 5% greater than the value immediately smaller than it. Values for T₂ ranged from 5 ms to 135 ms with a constant step size of 3 ms, and then 135 ms to 2000 ms with a variable step size, each with a value 5% greater than the value immediately smaller than it.

This base dictionary was then convolved by a shape function, L(δ_f, Γ), to generate the full dictionary, S(n, δ_f, T₁,T₂,Γ), such that

$$S\left(n,{\delta }_f,T_1,T_2,\Gamma \right)=\left(S_{base}\left(n,{\delta }_f,T_1,T_2\right)*L\left({\delta }_f,\Gamma \right)\right)\left[{\delta }_f\right].$$ (5)

In the current work, the shape function was limited to a Lorentzian distribution, parameterized by the Γ value that represents the FWHM of the distribution as described by

$$L\left({\delta }_f,\Gamma \right)=\frac{\frac{\Gamma }{2}}{{{\delta }_f}^2+{\left(\frac{\Gamma }{2}\right)}^2}.$$ (6)

Although the Lorentzian distribution may not precisely reflect the underlying distribution in vivo, this shape was chosen such that the pulse sequence simulation of a gradient-echo (GRE)-type pulse sequence would generate a monoexponentially decaying transverse signal evolution. Curve-fitting this simulated signal evolution would yield the decay time constant, T₂*, given by

$$\frac{1}{T_2^{*}}=\frac{1}{T_2}+\pi \Gamma .$$ (7)

Shapes, given by L(δ_f, Γ), were generated for 52 different values of Γ. Values for Γ ranged from 0 (the Dirac delta function) to 40 Hz. Between the values of 0 Hz and 0.825 Hz, Γ varied with a constant step size of 0.075 Hz. Between 0.825 Hz and 40 Hz, Γ increased with a variable step size that increased 10% per value. Before the convolution step in Eq. (5), each Lorentzian shape was truncated to span ±20 Hz and normalized. After computation, S(TR, δ_f, T₁,T₂,Γ) was decimated to 1-Hz resolution in δ_f values to reduce memory requirements. The final dictionary, consisting of 30 251 520 entries, spanned 101 values for δ_f that ranged from ±50 Hz. Dictionary generation was implemented in MATLAB (The MathWorks, Natick, MA) using custom-developed code.

3.3 |. Pattern recognition

The inner-product-based pattern recognition method used in this work has been described previously.^12,13 For each pixel, the calculated dictionary and measured time course signals were normalized to their sum-squared magnitudes. The inner products between each pixel and dictionary entry was calculated, and the entry corresponding to the maximum value of the inner product was taken to represent the closest signal evolution to the acquired pixel. The estimated values for δ_f, T₁, T₂, and Γ were then derived from this entry. Relative proton density was derived from the scaling factor between the measured pixel signal and the matched dictionary entry. The value of T₂* for each pixel was calculated from match-derived T₂ and Γ values using Eq. (7).

3.4 |. Phantom experiments

To evaluate the accuracy of qRF-MRF, a phantom study was performed. All studies were performed using a 16-channel head receiver array on a Siemens Magnetom Skyra 3T system (Siemens AG Medical Solutions, Erlangen, Germany). The accuracy of T₁ and T₂ were compared against traditional Cartesian spin-echo methods. Both phantom composition and traditional spin-echo methods have been described previously.²³ Briefly, the phantom consisted of 10 cylindrical compartments with different concentrations of gadopentate dimeglumine (Magnevist) and agarose (Sigma-Aldrich, St. Louis, MO). Reference T₁ values were measured using an inversion-recovery spin echo (8 log-spaced TIs ranging from 21 ms-3500 ms with 12-ms TE and 10-second TR). The T₂ values were measured using a repeated spin-echo sequence (7 log-spaced echoes that ranged from 13 ms-203 ms using a TR of 10 seconds). Reference T₂* values used the multi-echo GRE method (25° FA excitation using 15 linearly spaced echoes ranging from 4 ms-152 ms with a TR of 200 ms). T₁ values were calculated pixel-wise by solving the equation S(TI) = a + bexp(-TI/T₁) using a 3-parameter nonlinear least-squares fitting routine. The T₂ values were determined pixel-wise by solving the equation S(TE) = aexp(-TE/T₂) using a 2-parameter nonlinear least-squares fitting routine. The T₂* values were fit similarly to T₂. The concordance correlation coefficient (CCC)²⁴ was used to assess measurement accuracy.

To assess how the number of frames affected quantification, the values for T₁, T₂, and T₂* were obtained from the dictionary pattern-recognition process using different numbers of frames. The number of frames was varied from 200–3000 frames with a 200-frame increment.

3.5 |. In vivo experiments

In vivo volunteer brain data were acquired in an internal review board-approved study, with written informed consent obtained before each scan. The proposed qRF-MRF method was performed in five volunteers. For comparison of quantified δ_f, T₁, and T₂ properties, bSSFP-MRF²⁵ maps were acquired using 3000 time frames. For T₂* measurement validation, a multi-echo GRE method using Cartesian-based sampling (25° FA excitation using 11 echoes ranging from 4 ms-80 ms using a TR of 200 ms) was acquired. Quantified properties were assessed for each method in manually drawn regions of interest corresponding to the gray matter, white matter, the substantia nigra, and the red nucleus. The CCC²⁴ was used to assess agreement between quantified maps by qRF-MRF, bSSFP-MRF, and multi-echo GRE methods.

3.6 |. Postprocessing

The postprocessing for all fingerprinting data was consistent with previous methods.¹² Acquired spiral data were reconstructed as described previously.¹³ Briefly, the nonuniform fast Fourier transform,²⁶ using measured spiral trajectories,²⁷ was used to separately reconstruct each undersampled time frame from each coil. These frames were combined using the adaptive coil combination method.²⁸ Finally, all time frames were normalized to the combined coil sensitivity map.²⁹

4 |. RESULTS

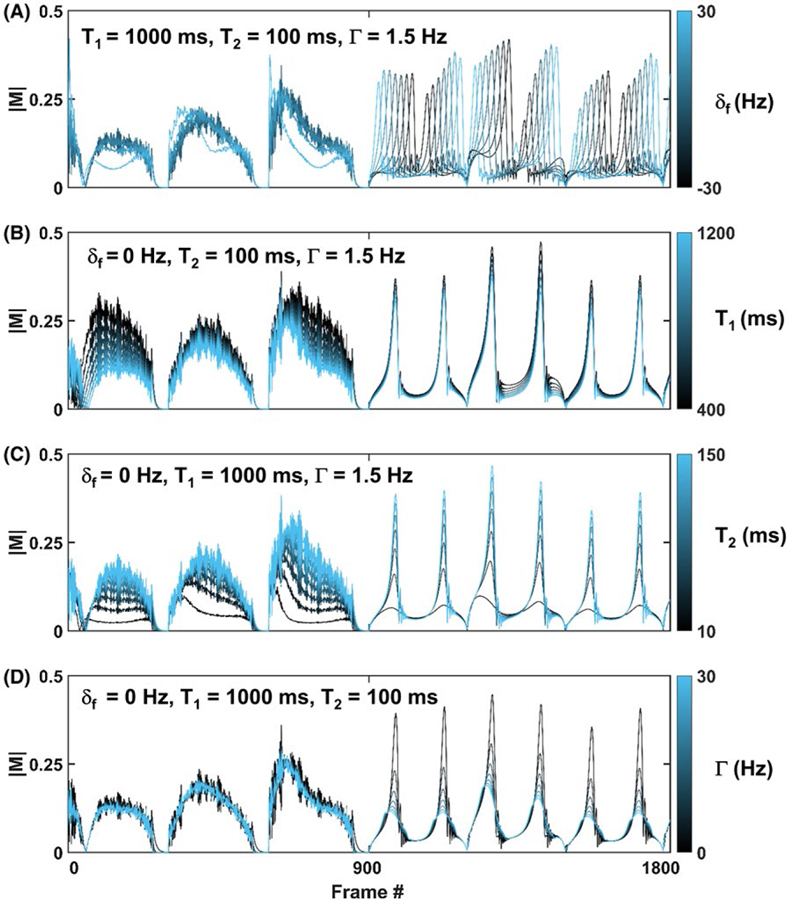
Figure 3 shows example entries from the qRF-MRF dictionary. In each plot, the first 1800 of 3000 total frames of representative signal evolutions are shown. Shown in each subplot are seven signal evolutions that differ in only 1 of the 4 of the varied dictionary properties, δ_f, T₁, T₂ and Γ, while the other 3 properties are held constant. During the first 900 frames of the qRF-MRF method, changes in the shape of signal evolutions due to each property of δ_f, T₁, and T₂ are apparent. This is expected, as the FA, TR, and PH scheme in these frames are identical to bSSFP-MRF. However, only subtle differences can be observed due to variations of the Γ property. Starting from the 901st frame, a different scheme of low FA, constant TR, and quadratic PH starts. During these acquisition blocks, substantial signal shape variations can be observed due to δ_f, T₂, and Γ properties. As shown in Figure 3A, the frames with high signal during qRF blocks depends on δ_f value. Despite the signal now arising from the sum of a distribution of δ_f values, high signal frames are still band-dependent. Changes in T₁ (Figure 3B) during qRF blocks are not as apparent as changes during bSSFP blocks. Changes in T₂*, either by a decrease in T₂ (Figure 3C) or increase in Γ value (Figure 3D), result in blunting of high-amplitude signal response during qRF blocks due to the dephasing.

FIGURE 3.

Sets of representative dictionary entries. In each plot, only 1 of the 4 matched dictionary properties is varied (color bar), whereas the remaining 3 are fixed (values shown in insets). The 4 matched dictionary properties are δ_f (A), T₁ (B), T₂ (C), and intravoxel frequency dispersion Γ (D)

Figure 4 shows the quantitative maps from phantom experiments. Figure 4A–E displays the maps obtained directly through the qRF-MRF dictionary-matching process. The δ_f map, shown in Figure 4A, shows substantial variation across the imaging FOV due to in-plane B₀ field inhomogeneity. For most phantom compartments, the δ_f variation was restricted between ±40 Hz. For these phantom compartments, T₁ and T₂ maps showed homogenous quantification. Pixels that mapped to +40 Hz in δ_f also showed errors in T₁ and T₂ quantification. This is due to the null-band behavior of bands for ±40 Hz during bSSFP acquisition blocks. The Γ maps were smooth within phantom compartments, but differed in spatial distribution as compared with T₁, T₂, or δ_f maps. The Γ in compositionally homogenous phantoms primarily represented the summed effects of in-plane and through-plane B₀ field inhomogeneity. The edges of phantom compartments, in which susceptibility differences near air interfaces can be expected to introduce intravoxel frequency variation, mapped to large matched Γ values. Relative M₀ maps calculated from the ratio between measured and matched signal evolutions are shown in Figure 4E. The relative M₀ map was smooth with the exception of pixels with propagated T₁ and T₂ errors at +40 Hz δ_f. Figure 4F shows the corresponding T₂* map. The reference multi-echo GRE T₂* map is shown in Figure 4G. The CCC between qRF-MRF-measured and GRE-measured T₂* maps was 0.90.

FIGURE 4.

Values of δ_f (A), T₁ (B), T₂ (C), Γ (D), and relative M₀ (E) are shown for phantom with varied concentrations of gadopentate dimeglumine and agarose generated using qRF-MRF. The resulting qRF-MRF T₂* map (F) shown was derived from T₂ and Γ maps using Eq. (7). The comparison multi-echo gradient-echo (GRE) quantified T₂* map (G) is also shown

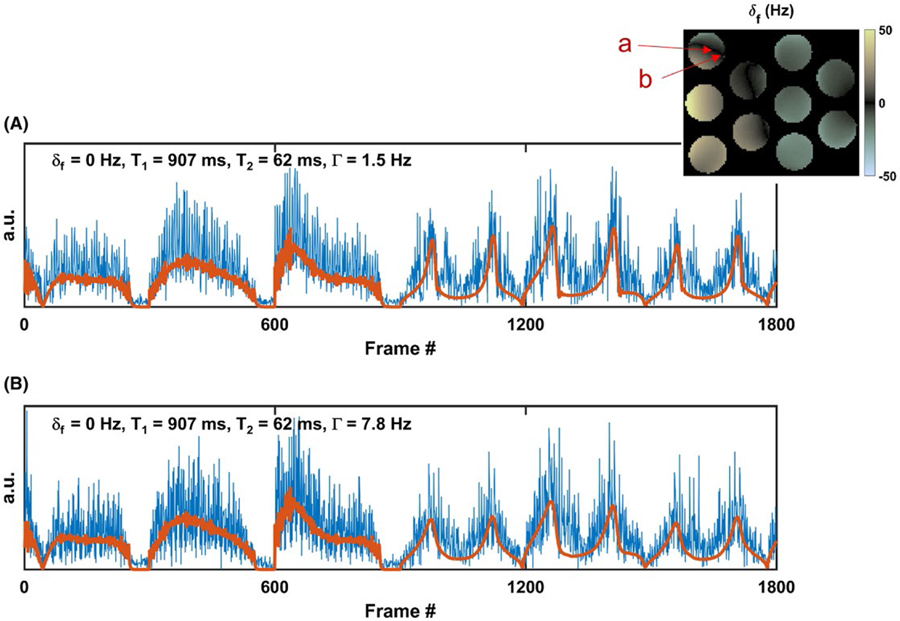
Figure 5 shows two example signal evolutions from the phantom experiment with superimposed corresponding matched fingerprints. Both signal evolutions originated from pixels within the same compartment. Dictionary matching of both signals obtained the same δ_f, T₁, and T₂ values but different Γ values, and thus different T₂* values, due to local variations in intravoxel B₀ field homogeneity. High-amplitude noise-appearing undersampling artifacts are apparent within the measured signal evolutions. However, the matching process was still able to recognize the best matching dictionary shape and extract the corresponding δ_f, T₁, T₂, and Γ properties.

FIGURE 5.

Example undersampled time-frame data, with best matching dictionary entries, from two pixels originating within the same homogenous phantom compartment shown in Figure 4 ( δ_f subfigure reproduced in inset). Differences in underlying signal shapes represent differences primarily caused by local field homogeneity within pixels. Property values extracted from the best dictionary matches are shown in inset

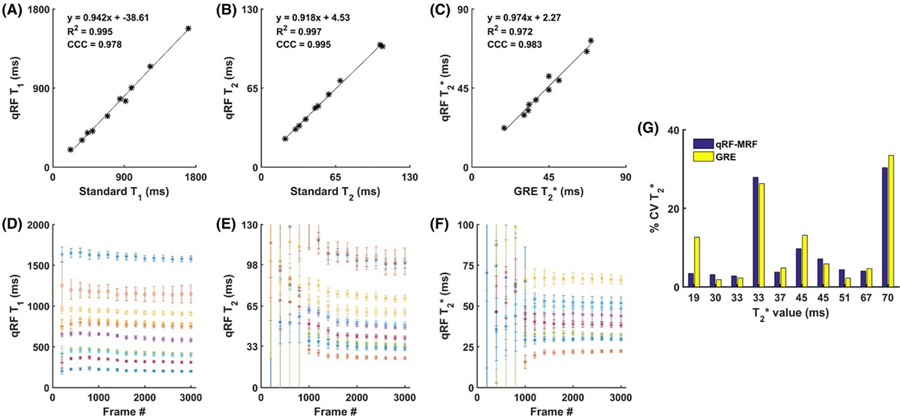
Figure 6A–C shows the correlation of quantified T₁, T₂, and T₂* values obtained using all 3000 frames qRF-MRF against standard spin-echo and GRE methods, along with their corresponding linear regression, R² coefficient of determination, and concordance correlation results. Figure 6D–F shows the mean and SD of quantified T₁, T₂, and T₂* values according to the number of frames used in the matching process. Quantification of T₁ required fewer frames than T₂ and T₂* to accurately quantify. Dictionary matching using less than 900 frames, before the qRF acquisition blocks, showed unreliable T₂ and T₂* quantification. After the 900th frame, the SD of the T₂ and T₂* measurements decreased. Slight changes in the mean and SD of the quantification of T₁, T₂, and T₂* values was observed as the number of frames increased. Coefficient of variation, defined as the ratio between the SD and the mean of the measurements, for T₂* within each compartment is shown in Figure 6G. Due to differences in local B₀ inhomogeneity between phantom compartments, the coefficient of variation between compartments varied considerably between compartments. However, within the same phantom compartment, the qRF-MRF and GRE methods showed comparable coefficient of variations, with the exception of the shortest T₂* compartment. In this compartment, the TEs used for the GRE method insufficiently covered the T₂* decay curve, which led to a variability in quantification.

FIGURE 6.

Accuracy and reproducibility of qRF-MRF. The values of T₁ (A) and T₂ (B) values were measured within each phantom compartment using qRF-MRF against spin-echo methods. The T₂* (C) values were measured within each phantom compartment using qRF-MRF against the multi-echo GRE method. The mean and SD of T₁ (D), T₂ (E), and T₂* (F) measured within each compartment are shown with increasing number of time frames used during the dictionary-matching process. G, Coefficient of variation given by the SD divided by the mean, for T₂* measurement for both qRF-MRF and GRE methods against the GRE-measured mean T₂* value. The 2 compartments with large CV variation caused by poor local field homogeneity were excluded from (F) and plotted using circle markers in (D) and (E). Abbreviations: CCC, concordance correlation coefficient; CV, coefficient of variation

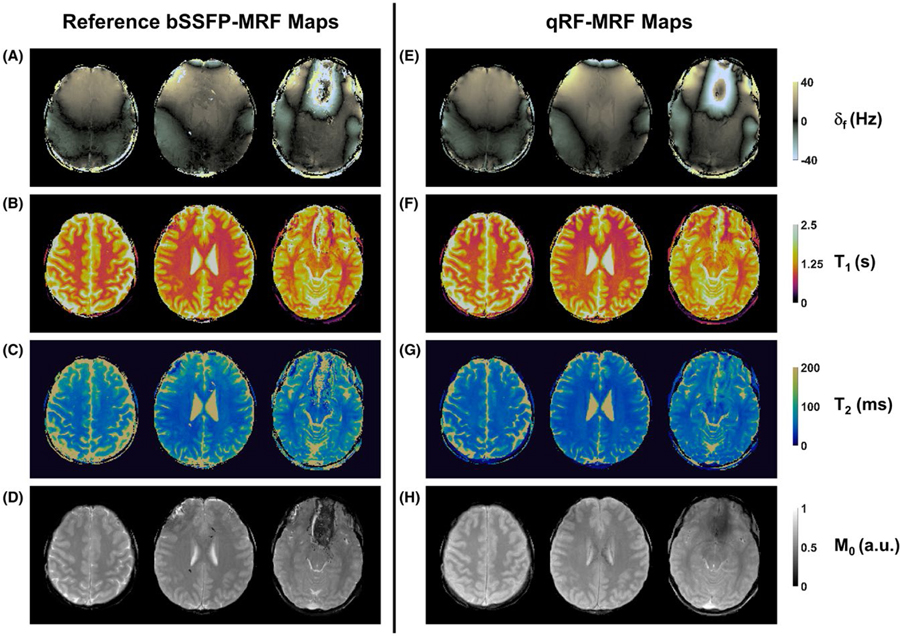
Figure 7 shows representative reference bSSFP-MRF and qRF-MRF maps acquired in vivo. Visually, the qRF-MRF quantitative maps agreed well with maps from comparison bSSFP-MRF. The δ_f maps obtained using both qRF-MRF and bSSFP-MRF showed similar macroscopic B₀ field distributions. Vessels were visible in δ_f maps obtained by both bSSFP-MRF and qRF-MRF. Compared with bSSFP-MRF, the qRF-MRF δ_f map showed smoother matching results. Similar to phantom experiments, errors in T₁ and T₂ can be observed in pixels at ±40 Hz δ_f in both qRF-MRF and bSSFP-MRF methods. The CCCs between the shown bSSFP-MRF and qRF-MRF maps were 0.45 ± 0.11, 0.89 ± 0.03, and 0.60 ± 0.05 for δ_f, T₁, and T₂ properties, respectively. The CCC between all bSSFP-MRF and qRF-MRF maps was 0.35 ± 0.13, 0.83 ± 0.06, and 0.53 ± 0.11 for δ_f, T₁ and T₂ properties, respectively.

FIGURE 7.

Representative in vivo tissue property maps. Maps were acquired using both reference (left) and the qRF-MRF method (right) in healthy volunteers. Reference maps for δ_f (A), T₁ (B), T₂ (C), and relative M₀ (D) were generated using the bSSFP-MRF method with the same number of time frames as the qRF-MRF method. The qRF-MRF method simultaneously generated δ_f (E), T₁ (F), T₂ (G), and relative M₀ (H) maps are shown using the same scale as references maps. The total acquisition time for each scan was 38 seconds and 35 seconds per slice for each bSSFP-MRF and qRF-MRF scan, respectively

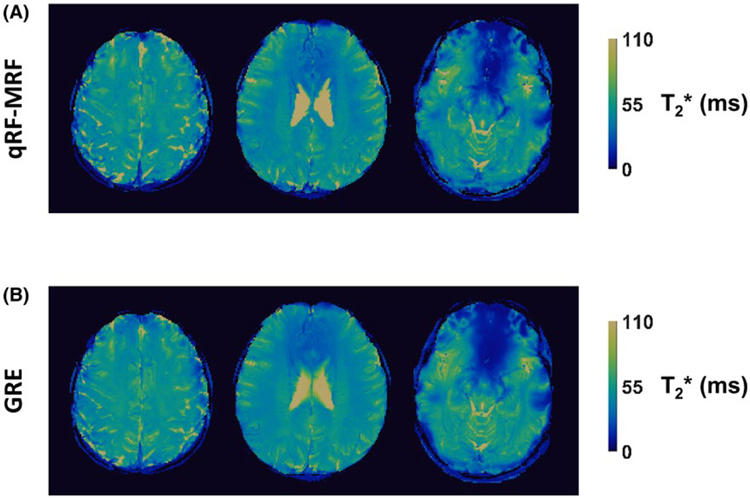
Figure 8 shows the qRF-MRF quantified T₂* maps, corresponding to the same images as in Figure 7, above their respective GRE T₂* maps. Vessels are visible in T₂* maps obtained by both GRE and qRF-MRF, due to the paramagnetic properties of iron in blood. The CCCs between the qRF-MRF and GRE-estimated T₂* maps was 0.82 ± 0.06 for the shown maps, and 0.77 ± 0.11 across all maps. The simultaneously acquired δ_f, T₁, T₂, relative M₀, and T₂* maps by qRF-MRF alongside the corresponding reference method acquired maps can be seen in Supporting Information Figure S1. Results of the region of interest analysis for in vivo δ_f, T₁, T₂, and T₂* values are listed in Table 1.

FIGURE 8.

Representative in vivo T₂* maps. The qRF-MRF T₂* maps (A), generated simultaneously with other tissue property maps shown in Figure 7, are shown above their corresponding multi-echo GRE-measured reference T₂* map (B). The GRE maps were acquired in 51 seconds each

TABLE 1.

Region of interest analysis for in vivo T₁, T₂, and T₂* values

		qRF-MRF	Reference methoda	Literature10,13,45–48
White matter (ms)	T1	988 ± 66	917 ± 60	~690–1100
	T2	44 ± 4	42 ± 5	~56–80
	T2*	43 ± 4	46 ± 7	~45–48
Gray matter (ms)	T1	1395 ± 227	1210 ± 351	~1286–1393
	T2	63 ± 10	76 ± 9	~78–117
	T2*	51 ± 9	49 ± 10	~42–52
Substantia nigra (ms)	T1	1081 ± 69	978 ± 130	1147
	T2	34 ± 2	38 ± 7	~42–47
	T2*	25 ± 5	26 ± 6	~22–28
Red nucleus (ms)	T1	1057 ± 97	958 ± 156
	T2	39 ± 6	42 ± 8	~46–48
	T2*	32 ± 6	31 ± 6	~24–31

^aMeasured using bSSFP-MRF for T₁ and T₂ multi-echo GRE for T₂*.

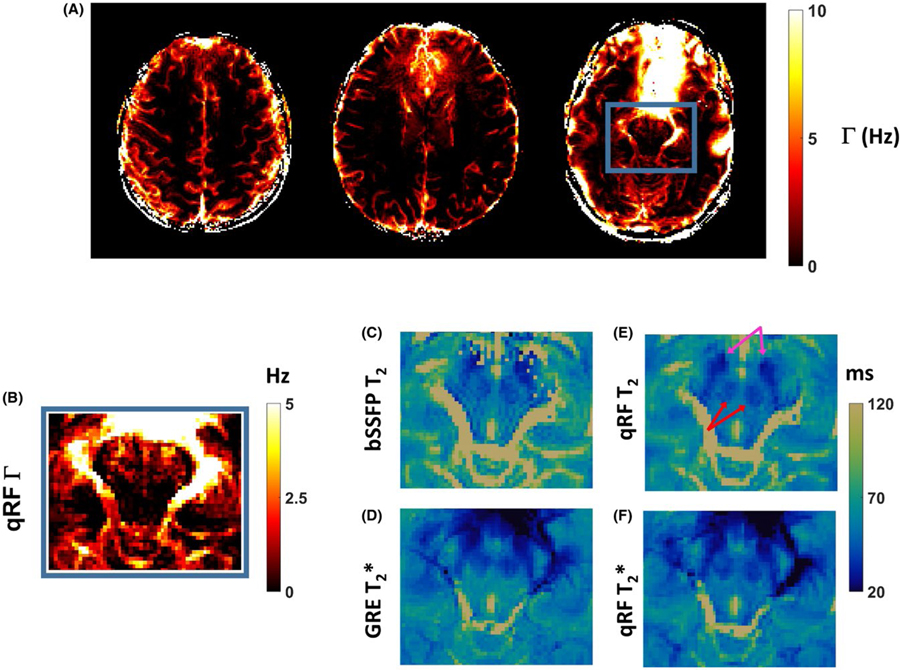
Quantitative Γ maps are shown in Figure 9A. Anatomical regions near air–tissue interfaces exhibited large Γ values. Blood vessels exhibited moderate Γ values. A zoomed-in Γ map of axial slice through midbrain structures is shown in Figure 9B. The corresponding T₂ and T₂* maps are reproduced in Figure 9C–F using a shared scale and color map. Higher Γ values and decreased T₂ and T₂* values within substantia nigra and red nucleus can be observed, due to higher tissue iron content within these tissues. The contrast of fine structures was preserved between qRF-MRF and reference maps.

FIGURE 9.

A, The Γ maps acquired using the qRF-MRF method from the same experiments shown in Figures 7 and 8. B, Zoomed-in FOV of the Γ map to the midbrain structures. C,D, Corresponding zoomed maps from reference T₂ (C) and T₂* (D) maps. E-F, Corresponding zoomed maps from qRF-MRF-acquired T₂ (E) and T₂* (F) methods. The same scale and color map used for the T₂ and T₂* maps are shown. The lower T₂ value associated with substantia nigra (pink arrows) and red nucleus (red arrows) can be observed across all methods for both T₂ and T₂* values

5 |. DISCUSSION

In this work, the proposed qRF-MRF method allowed the simultaneous quantification of δ_f, T₁, and T₂* tissue properties in 35 seconds per slice. The accuracy of the method was demonstrated in a phantom and in healthy volunteers. The ability to rapidly, robustly, and simultaneously quantify δ_f, T₁, T₂, relative M₀, and T₂* properties has many potential applications. For instance, through the knowledge of δ_f, T₁, T₂* and relative M₀ properties, synthetic SWI³⁰ may be possible, alongside synthetic T₁-weighted and T₂-weighted images that require knowledge of T₁, T₂, and relative M₀ properties. Another application lies in improving contrast agent sensitivity. Because MR contrast agents typically induce changes in multiple tissue T₁, T₂ and T′₂ properties, simultaneous detection of these properties may be able improve accuracy in contrast agents’ detection and quantification.³¹ Mapping of T₂ and T₂* tissue properties within midbrain structures may also enhance tissue iron quantification. This may lead to the increased capacity to diagnose and monitor the diseases that are known to accumulate iron in these structures. However, the potential of the proposed qRF-MRF method for each of these applications must still be demonstrated.

The unique signal evolution that develops during qRF acquisition blocks has several beneficial properties for tissue property quantification. With respect to the components of T₂* quantification, the imaging frames with highest SNR also have the highest T₂ and Γ sensitivity. Additionally, qRF-MRF appeared to quantify δ_f more robustly as compared with bSSFP-MRF. Both in the current and previous³² works, bSSFP-MRF, using direct pattern matching, was observed to be susceptible to locally discontinuous δ_f quantification errors. These errors had the potential to propagate to errors in T₁ and T₂ quantification. The qRF-MRF method appears to be more robust to this type of error.

Previously, a Cartesian EPI readout-based MRF method (MRF-EPI) was proposed for simultaneous measurement of T₁ and T₂* tissue properties.³³ The MRF-EPI method differed substantially from the current method in the use of a series of parallel imaging-based single-shot readouts with spoiled GRE acquisitions using variable FA, TE, and TR to generate image series that were sensitive to T₁ and T₂* values. Although the MRF-EPI method quantified relatively fewer tissue properties using a lower resolution and matrix size, MRF-EPI only required 10 seconds per slice. Future studies may seek to combine the approach of MRF-EPI with the current proposed method to further enhance robustness and speed of T₂* quantification.

Currently, the underlying frequency dispersion distribution during the dictionary-generation process was limited to Lorentzian shapes. This choice was made because simulation of a multi-echo GRE experiment would produce the consistent mono-exponential decay signal behavior assumed during GRE quantification. This assumption may not be accurate or appropriate in various situations. For instance, white matter has been shown to have a myelin signal component with both distinct rapid T₂* relaxation and substantial frequency shift.³⁴ Incorporation of the underlying causes of tissue-susceptibility differences due to vessel geometry or myelin into the signal model has previously been shown to enable potential quantification of these properties.^16,17,35 The qRF-MRF method may be sensitive to these properties as well. Although modeling these additional properties would result in an exponentially larger dictionary size, compression methods have been developed that may enable exploring this potential in the future.^36–39

Several limitations remain in the proposed method. The first 900 frames of bSSFP-MRF were maintained at the beginning of the qRF-MRF acquisition. This was done because simulations showed decreased signal-shape differences with respect to changes in T₁ during qRF blocks as compared with bSSFP blocks. However, as a result of these high FA bSSFP blocks, the current qRF-MRF method was still susceptible to banding artifacts near ±40 Hz, coinciding with the off-resonance position of the bands during the first 900 frames, as shown in Figure 2D. Examples of these artifacts can clearly be seen in the phantom results (Figure 4B–D) corresponding to pixels with off-resonance value near 40 Hz (Figure 4A). Alternative banding-free schemes with sensitivity for T₁, such as FISP-MRF,¹³ will be investigated in the future.

Another limitation of qRF blocks was the relative temporal sparseness of qRF-MRF signals as compared with bSSFP-MRF signals. The choices used in the current method were selected to increase incoherence of aliasing artifacts with respect to the signal evolution. The assessment of the number of frames necessary for accurate tissue-property measurements suggested that after approximately 2000 frames, accuracy of T₁, T₂, and T₂* quantification largely stabilized. However, matching precision improved up through the complete 3000 frames. Further improvements to accuracy and robustness may be made by optimizations to the acquisition parameters (FA, TR, and PH choices) or property estimation method, such as by adopting an iterative reconstruction method,^32,40–42 which may improve robustness to aliasing artifacts. These kinds of improvements would enable further reduction in acquisition time, by reducing the number of frames necessary for robust quantification.

Like all quantitative methods, property estimation depends on the accuracy of the underlying signal model. Although qRF-MRF quantification of T₁, T₂, and T₂* properties in phantom was shown to be accurate, several discrepancies appeared during in vivo experiments. Gray and white matter T₂ was consistently lower, as measured through qRF-MRF, as compared with both reference bSSFP and literature values. However, T₂* measurements in the same regions agreed well with the reference and literature values. Because T₂* is directly derived from quantified T₂ and Γ values, this suggests a corresponding underestimation of Γ values in gray and white matter. In one literature study, reports for R₂′ values (theoretically related to Γ by scaled factor of π) varied from 2.7 s^–1 to 3.5 s^–1 for gray matter, and 2.8 s^–1 to 4.3 s^–1 for white matter, depending on the quantification method used.⁴³ Although none of the literature quantification methods can be considered a gold standard, the reported values appear to be consistent with an underestimation of Γ in gray and white matter in the current work. Several reasons may explain the accurate T₂* measurement yet biased T₂ and Γ measurements in vivo, which are not present in phantom experiments such as magnetization transfer effects.⁴⁴ Flow is another possible explanation, as none of the gradients used in the current method were flow compensated. Fresh spins flowing into the imaging plane likely have an additional effect on measured signal evolutions. Given that T₂ and Γ represent the irreversible and reversible components of signal decay, respectively, it is also likely that many other “irreversible” effects in vivo that are not currently in the signal model, including diffusion, motion, magnetization transfer, or eddy current effects, may manifest preferentially as an apparent shortening in T₂ value. These considerations are topics of careful future evaluation.

6 |. CONCLUSIONS

In this work, we proposed a novel MR method, developed within the MRF framework, that can be used to simultaneously quantify δ_f, T₁, T₂, and T₂* properties. Using the flexibility of MRF experiment design, a quadratic RF phase was incorporated in a novel scheme to develop transient signals with high amplitude and a frequency-dependent phase. As a result, signals become uniquely sensitive to intravoxel susceptibility-induced field variation. Combined with Bloch equation-based template-matching approaches, intravoxel field variation can be estimated from measured signals, alongside other tissue properties. Accurate quantification of T₁, T₂, and T₂* tissue properties was achieved in phantom experiments at the current pixel sizes in 35 seconds per slice. In vivo experiments showed robust and artifact-free property maps, with good agreement in T₂* quantification with the gold-standard multi-echo GRE method.

Supplementary Material

supplementary material

FIGURE S1 Representative in vivo tissue property maps. Tissue property maps shown in figures 7 and 8 are shown together here for ease of visualization and comparison. Reference bSSFP-MRF maps (a-d) and GRE method (e) show good visual agreement with acquired qRF-MRF maps (f-j) in volunteers. Total acquisition time per 2D slice for each scan was 38, 51 and 35 sec per slice for each bSSFP-MRF, GRE, and qRF-MRF scan, respectively.