Abstract
The storm water management model (SWMM) is a widely used tool for urban drainage design and planning. Hundreds of peer-reviewed articles and conference proceedings have been written describing applications of SWMM. This review focuses on collecting information on model performance with respect to calibration and validation in the peer-reviewed literature. The major developmental history and applications of the model are also presented. The results provide utility to others looking for a quick reference to gauge the integrity of their own unique SWMM application. A gap analysis assesses the model’s ability to perform water-quality simulations considering green infrastructure (GI)/low impact development (LID) designs and effectiveness. It is concluded that the level of detail underlying the conceptual model of SWMM versus its overall computational parsimony is well balanced—making it an adequate model for large and medium-scale hydrologic applications. However, embedding a new mechanistic algorithm or providing user guidance for coupling with other models will be necessary to realistically simulate diffuse pollutant sources, their fate and transport, and the effectiveness of GI/LID implementation scenarios.
Introduction
SWMM (Rossman 2004) is one of the most widely used urban watershed hydrology and water-quality models in the world (Obropta and Kardos 2007). Historically, what sets SWMM apart from other urban watershed models is its emphasis on engineered water conveyance systems for stormwater runoff and wastewater management, considering both combined and sanitary sewer design and performance. As this review will highlight, SWMM has been used for a wide variety of sewer planning, analysis, and design applications, in addition to flood analysis, primarily as a result of sewer system backup, and evaluating the performance of stormwater green infrastructure (GI) strategies. With concern growing for how climate change is affecting already degrading urban water infrastructure in many areas (Grimm et al. 2008; Rosenberg et al. 2010) and interest increasing for adopting GI alternatives as a potentially cost-effective stormwater management option (Marsalek and Chocat 2002; Pataki et al. 2011), SWMM likely already is, and probably will be, the go-to simulation tool for addressing such needs in at least the near-term future. Historically, SWMM has been used most often by consulting engineers to help address the unique design needs of municipal and regional planning projects. Therefore, most reports using SWMM do not pass through the scientific peer-review processes. As such, it is at present difficult to gauge the integrity of previous work with respect to model performance and utility. The objective in this paper is to conduct such a review of the scientific literature pertaining to the reported application and performance of SWMM. The level of effort put forth to collate an up-to-date and comprehensive accounting of SWMM applications, including highlighting reported model performance data, would benefit the user community as a quick reference for gauging the relative integrity of existing and new projects that are using SWMM.
Previous reviews of SWMM have been primarily associated with comparisons to other models (Dietz 2007; Elliott and Trowsdale 2007; Obropta and Kardos 2007; Tsihrintzis and Hamid 1997). This paper aims to (1) provide an overview of SWMM’s development history; (2) summarize the modeling methods and research findings for many of the more than 150 peer-reviewed articles returned by the search, and provide a quantitative assessment of model performance from different application categories; and (3) describe the key strengths and weaknesses of SWMM to identify gaps and suggest some improvements. The intent was to cover most of the peer-reviewed articles published on the application of SWMM for a variety of problems. The decision to include a paper in the review was based on the level of detail provided about the model application. Descriptions in some articles were not detailed enough to extract a complete understanding of the application or the model performance; these were excluded. Finally, because conference proceedings do not undergo rigorous peer review, these were not referenced in the collation of model performance data.
SWMM Development History
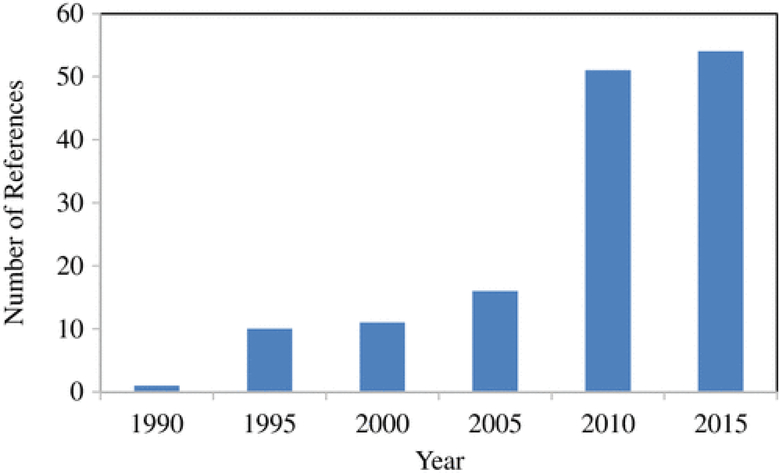
The U.S. Environmental Protection Agency (USEPA) developed SWMM as a public domain software in 1971 to meet the need for rainfall runoff quantity and quality simulations in urban environments, coincident with the signing into law of the Clean Water Act in the United States (Metcalf and Eddy 1971). Since then, there have been four major software and user manual iterations. The search of peer-reviewed literature illustrated a dramatic rise in the publication rate of studies using the model as a primary tool or evaluating its utility in urban hydrology applications over the last 10 years since the release of the most recent version, SWMM 5 (Fig. 1).
Fig. 1.
Trends of SWMM publications in water resources subject (data from Web of Science 2016)
The first version of SWMM (SWMM I) was produced as a joint project among the USEPA, Metcalf & Eddy, the University of Florida, and Water Resources Engineers (Metcalf and Eddy 1971). The model was written in FORTRAN and consisted of a series of blocks: Executive, Runoff, Transport, Storage, and Receiving Water. The latter four are the computational blocks; each block contains multiple subroutines. The Runoff block was limited to Horton’s equations for pervious infiltration, whereas the Manning’s equations and continuity equations were used for overland flow approximations. Flow routing within the Transport block was done using the kinematic wave method. There were several computing limitations for SWMM I, and applications were limited to watersheds with surface area ranging from 10 to 5,000 acres (4 to 2,023 ha).
SWMM was upgraded to version II in 1975. The Combine block was added to merge output data for processing by individual computational blocks. This feature allowed SWMM to be applicable to larger urban basins. Erosion prediction was also added by incorporating the Universal Soil Loss Equation. The modeling capability for pollutants, including 5-day biological oxygen demand (BOD5BOD5), nitrogen (N) and orthophosphate (PO4PO4), was also added (Huber et al. 1975).
With the release of SWMM 3 in 1981, the model could be used for both planning and design considerations. A formal Statistics block was created to perform frequency analysis by evaluating the time-step output, and a Graph block consisted of multiple subroutines that allowed for hydrographs and pollutographs to be plotted with appropriate scaling, ranges, and labeling. Continuous simulations on monthly and annual time scales could also be conducted. Metric units were also supported for the first time in the Runoff, Transport, and Storage/Treatment blocks. The Green-Ampt equation for infiltration expanded surface-water generation capabilities. Scour and deposition procedures were added to the Transport block. Most significantly, a full dynamic wave method (Extran) for routing flows through the conveyance network was added. However, explicit limitations were still imposed that limited the number of elements that could be modeled.
When the fourth iteration, SWMM 4, was released in 1988, several additional alterations were made. Rain and Temp service blocks were created for the input of long-term, continuous precipitation and temperature data, respectively. A groundwater module and irregular channel cross section geometry were also added. Computational improvements were made to the hydraulic routines to eliminate convergence problems.
Finally, with the release of SWMM 5 in 2005, the model’s engine was completely re-engineered in the C language, and a separate graphical user interface was added. There was no longer any limit on the number of elements that could be included in a model. The fully interactive graphical user interface (GUI) improved user access to all model features and their respective options. The ability to import background images to aid in constructing the model was added to the GUI; the user could also construct his or her own map within the software. The current version of SWMM (5.1.010) allows users to simulate GI through low-impact development (LID) components, such as rain barrels, porous pavement, and infiltration trenches. Best management practices (BMPs) can be incorporated in wash-off load reduction simulations. The U.S. Soil Conservation Service curve number (CN) method for modeling infiltration was added in addition to support for custom closed-conduit shapes. Improvements were made to the hydraulic routines and a very flexible rule-based approach for controlling, e.g., pumps and gates, was implemented. The current version of the model can be downloaded from http://www2.epa.gov/water-research/storm-water-management-model-swmm?#downloads.
With its long open-source history and well-supported commercial options, SWMM has become a robust piece of software. Its potential uses include developing sizing rules for devices, planning of land use in catchments and urban areas, and preliminary design of regional controls, subdivisions, or sites (Elliott and Trowsdale 2007). In the following sections, SWMM’s process models are reviewed from the literature to show how SWMM has been used in practice, and to assess its calibration and validation accuracy.
SWMM Process Models
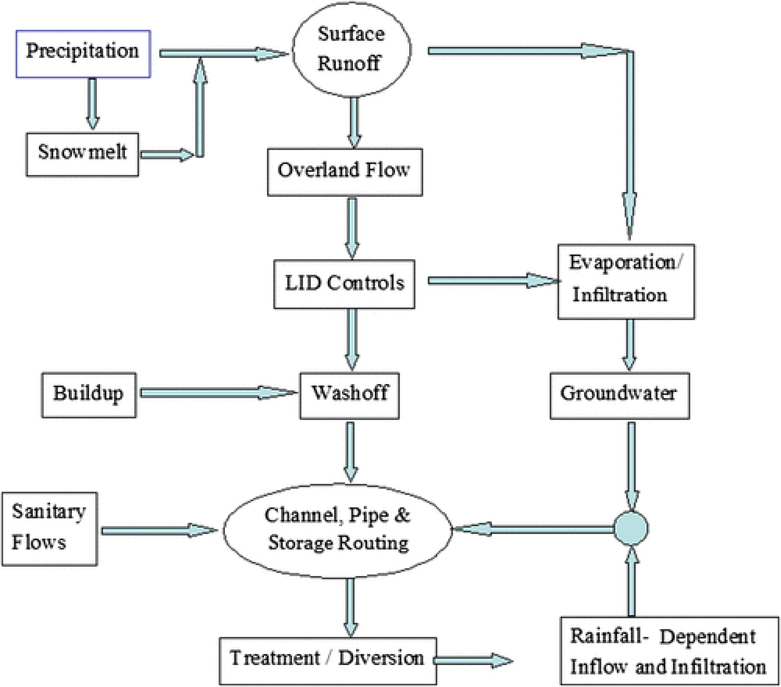
SWMM’s processes and their governing equations have been described in a number of past publications (e.g., Huber et al. 1988; Rossman 2015). However, for potential newcomers to the model, the core processes that SWMM was built upon and the assumptions used in developing the governing equations are included. Fig. 2 shows the model’s represented processes and their interactions. A modeling project can be constructed using six primary environmental components: (1) external forcing data including precipitation, temperature, and evaporation; (2) a land surface runoff component; (3) a subsurface groundwater component; (4) a conveyance system of pipes, channels, flow regulators, and storage units; (5) contaminant buildup, wash-off, and treatment; and (6) LID controls. These components are described subsequently. Not all of these components need to be included in a project (i.e., most literature include just precipitation, surface runoff, and conveyance system hydraulics).
Fig. 2.
Processes considered in the SWMM model
External Forcing Data
Both single-event and long-term precipitation time series can be used in SWMM. Single events representing a design storm can be used to simulate the runoff and pollutant loads. Temperature data are needed for simulation of snowmelt. SWMM can approximate the daily temperature fluctuations by using temperature minimums and maximums. Evaporation data can be introduced to the program in various forms of a single constant value, a set of monthly average values, time-series daily data, or calculated based on temperature using the Hargreaves method (Hargreaves and Samani 1985). Wind speeds are used for snowmelt modeling, and they can be provided as average monthly values or as daily time series. Precipitation is considered to be in the form of snow when the temperature is below a certain threshold, specified by the user. Snow accumulation and melting are computed with the National Weather Service’s SNOW-17 model (Anderson 2006).
Land-Surface ComponentSurface Runoff
A SWMM project divides an area to be modeled into one or more subcatchments. Each is represented as an idealized rectangular basin with a uniform slope where overland flow occurs parallel to one of the major axes of the rectangle. A water balance is made by considering each subcatchment as a nonlinear reservoir (Shubinski et al. 1973), in which the change in depth of overland flow with respect to time is simply the difference between precipitation input and the sum of evaporation, infiltration, and runoff flow losses. The latter is computed as a function of depth using the Manning’s equation.
Each subcatchment can be divided into three zones, including a pervious area and two impervious areas, one with and one without depression storage. By default, each of the zones will contribute independently (in parallel) to the conveyance system or a downstream subcatchment. However, there are options to reroute fractions of runoff generated on each zone to other zones.
Infiltration
SWMM computes infiltration using either Horton’s method (Horton 1940), the Green-Ampt method (Green and Ampt 1911), or an incremental form of the curve number method (Akan and Houghtalen 2003). Horton’s method expresses infiltration capacity as an empirical exponentially decreasing function of time after the start of the precipitation. SWMM can also use the Mein and Larson (1973) formulation of the Green-Ampt method. It assumes the formation of a sharp wetting front during infiltration and uses Darcy’s law to relate the velocity of this front to the soil’s hydraulic conductivity, the capillary suction along the front, and the depth of the saturated zone. The incremental curve number model is based on an empirical equation that relates cumulative infiltration to cumulative precipitation through the well-known Soil Conservation Service (SCS) curve number that has been tabulated for various types of land covers (Cronshey 1986).
Subsurface Component
SWMM can account for infiltration causing a rise in the water table beneath a subcatchment with a subsequent slow release of groundwater back into the conveyance system. This feature allows the program to reproduce the long recession periods associated with runoff hydrographs for unlined and natural channels. Subsurface flow is modeled by assigning two reservoirs to each subcatchment: one representing the vadose zone and the second representing a deeper groundwater zone. The moisture content in the upper (vadose zone) compartment is assumed to be uniformly distributed, whereas the lower (groundwater) layer is assumed to be fully saturated. The depth of the groundwater layer is variable depending on the total storage. Water is directed from the vadose zone compartment into the groundwater compartment. The water in the groundwater layer can then be directed into the conveyance system or percolate downward. Evapotranspiration can affect both reservoirs, with its rate being dependent on the depth of each reservoir. While solving the model, a water balance is performed on the two reservoirs to model the dynamics of storage and flow from each.
Conveyance System Component
There are two primary options for modeling flow routing in SWMM: kinematic wave routing and dynamic wave routing. The kinematic wave routing model is based on solving the continuity equation in which the friction slope along a conduit is assumed to equal its bottom slope. This method is not able to account for pressurized flow, flow reversal, or backwater effects, and is only applicable to dendritic conveyance networks. The dynamic wave model solves the full St. Venant equations for conservation of mass and momentum, and therefore does not have the aforementioned restrictions. The St. Venant equations are solved by expressing them in a finite-difference form that makes the flow in conduit a function of the nodal heads at either end of the conduit. Another set of continuity equations accounts for the change in nodal head as a function of the net nodal inflow and the surface area of the connecting conduits. These two sets of equations are solved together to provide an updated hydraulic solution at each time step.
Contaminant Buildup, Fate, and Transport
The user selects the functional relationship governing pollutant buildup and wash-off based on specific pollutant characteristics. Buildup on surfaces is modeled according to a power, exponential, or Langmuir saturation function. Pollutant wash-off is a rate limited mobilization process, whose rate constant is a power function of the overland flow rate and is proportional to the pollutant mass remaining. Alternatively, wash-off can be modeled with a rating curve in which the mobilization is solely a function of flow, independent of buildup, or as a constant concentration (the so-called event mean concentration or EMC). The effect of street sweeping can be modeled by specifying a frequency or noting specific times and by selecting the fraction of pollutants removed during each event. Pollutant treatment (as a result of settling or filtration) can be modeled as a removal rate at each node, making it a function of water depth, hydraulic residence time, and other variables. The fate and transport of pollutants in the conveyance system is then modeled based on mass balance and advection. Pollutant decay can be modeled as a first-order reaction whose rate constant is supplied by the user.
LID Controls
LID modeling features were added to the 2010 version of SWMM 5 (Rossman 2015, 2004). LIDs are modeled as a number of interconnected, fully mixed layers representing the surface, pavement, soil, storage, and underdrain portions of a LID unit. Infiltration, drainage, and overflow control the storage in each of the layers dynamically. SWMM can explicitly model bioretention cells, infiltration trenches, porous pavement, rain barrels, vegetated swales, green roofs, and street planters. The infiltration rate in the soil layers is determined by assuming an exponential relationship between the hydraulic conductivity and moisture content. The saturated hydraulic conductivity and conductivity slope (i.e., the slope of the relationship between the logarithm of conductivity and moisture content) are provided by the user. Infiltration into the growth media of bioretention cells and green roofs is modeled with the Green-Ampt equation. Outflow from the storage zone into the native soil beneath the unit proceeds at a constant user-supplied rate. Underdrain flow is represented by an orifice-type equation. The presence and absence of each layer type depends on the type of LID. For example, a vegetative swale only has the surface layer, whereas bioretention systems can have surface, soil, storage, and underdrain layers.
SWMM ApplicationsUrban Drainage Flooding Analysis
Studies on the use of SWMM for flooding analysis have been published throughout the period of 1987–2014, but most have been published since 2013 with the growing interest in the effects of climate change (Dasgupta et al. 2013; Gersonius et al. 2013; Kirshen et al. 2014; Ranger et al. 2011). Earlier use of continuous simulation for design flood estimation within urban catchments was performed in the 1960s and 1970s as reviewed by Rawls et al. (1980). Flooding analysis for land-use change is also a great concern (Camorani et al. 2005; Huong and Pathirana 2013). Study areas have included coastal regions, for which the additional consideration of sea level rise (Huong and Pathirana 2013; Ranger et al. 2011) and typhoon-driven waves (Chen et al. 2011) have been considered. Flooding analyses in the literature have often been performed on large scales, including watershed, country (Chen et al. 2011), province, and mega-city (Dasgupta et al. 2013; Hsu et al. 2000; Ranger et al. 2011). Internationally, a number of existing megacities and peri-urban areas have experienced largely unplanned growth, have sparse sewer networks, and are geographically at risk from climate change and extreme events (Dasgupta et al. 2013). Numerous smaller-scale studies have also been undertaken by city and county governments in the United States, and in provinces or districts internationally. Because of the scope of this review, these papers have not been included, but database searches for conference proceedings (ASCE Library) using the keywords of flooding and SWMM returned 261 results.
In residential areas, the motivation for detailed flooding predictions is often because flood warnings and evacuations may need to be planned, rescues performed, species protected, ecosystem services maintained, and resources best allocated (Ford et al. 2002). The questions to be answered include, is there a risk? And if so, what kind, and where? The concept of flood risk is typically defined as the product of flood damage and the probability of its occurrence (Morita 2014); it may also combine estimates of hazard exposure and vulnerability (Patel et al. 2005; Ranger et al. 2011). Pairing risk analyses with various rainfall scenarios and infrastructure configurations is a common problem in the literature, for which SWMM has served a role. By modeling the urban drainage network, the role that infrastructure plays can be understood, and plans for improvement to mitigate risk can be made. Flooding analyses using SWMM have produced inundation maps, helped to determine the areas with the greatest risk, and found weak points in sewer networks (Banks et al. 2014; Chen and Herr 2010; Ford et al. 2002; Fu et al. 2011; Gersonius et al. 2013; Huong and Pathirana 2013).
Another common trend has been for modelers to combine the SWMM model with other hydrologic models, to better account for complex hydraulic or hydrologic flooding regimes from multiple sources in larger spatial scale regions. Examples include HEC-1 (Chen et al. 2011), the soil and water assessment tool (SWAT) (Dasgupta et al. 2013), HEC-RAS (Dasgupta et al. 2013), a combination of HEC, HEC-2, and HEC-RAS for channel monitoring (Ford et al. 2002), the open-source two-dimensional (2D) model BreZo (Huong and Pathirana 2013), and geographical information system (GIS)-based flood damage prediction tool (FDPM) (Morita 2014).
In fact, the spatial resolution of most of the relevant studies was low, while the modeled areas were located within larger basins or megacities. Although specific lot sizes were rarely addressed, this level will be a focus for understanding how GI implementation may affect local flooding risks. This requires modeling at subhourly time steps, especially for catchments affected by short-duration high-intensity rainfalls (Olsson et al. 2009), and this is a strength of SWMM.
Water Quality and Transport of Contaminants
Twenty-one relevant papers were found in the literature search on SWMM and water quality during the period of 1988–2014. Notably, a review of stormwater quality modeling tools other than SWMM was provided by Borah and Bera (2004). A variety of water quality constituents have been investigated using SWMM, including total suspended solids (TSS) (Borris et al. 2014; Chang et al. 2008; Chow et al. 2012), nitrogen compounds (Burian et al. 2001, 2002; Chang et al. 2008; Jia et al. 2014), heavy metals (Borris et al. 2014; Fallah Shorshani et al. 2014), dissolved oxygen (DO) and biochemical oxygen Demand (BOD) (Kirshen et al. 2014), and phosphorous (Chow et al. 2012; Jia et al. 2014). The water quality constituents considered in these studies are summarized in Tables 1 and 2. Most papers had investigated multiple constituents at once, and a number reported generalized assessment of SWMM output regarding pollutants rather than specifically discussing constituent fate and transport modeling results.
Table 1.
Brief Description and Sensitive Parameters in SWMM Applications Used in the Review
| Study area | |||||
|---|---|---|---|---|---|
| Reference | Catchment (s) | Location | Drainage area (km2km2) | Indicatora | Sensitive parametersb |
| Alfredo et al. (2010) | Laboratory green roof prototypes | — | 7.442×10−77.442×10−7 | Runoff | — |
| Lee et al. (2008) | Scott Creek | Adelaide, Australia | 26.8 | Runoff | — |
| Ashbolt et al. (2013) | Upper Yaun Creek | Coomera, Australia | 3.61 | Runoff | — |
| Baffaut and Delleur (1989) | 4 catchments Ross Ade | Florida; West Lafayette, Indiana | —; 0.117 | Runoff | — |
| Baffaut and Delleur (1990) | 9 experimental plots | Lakewood, Colorado | 0.00009 | TSS, TP,c Pb, Zn | Washoff C1&C2 (exp), Buildup C1&C2 (exp) |
| Balascio et al. (1998) | — | New Castle County, Delaware | 0.23 | Runoff | %Imperv, Dstore-Imperv, % Zero-Imperv, Width, % Slope, N-Imperv, N-Perv, Dstore-perv, MaxRate, MinRate, Decay |
| Barco et al. (2008) | Ballona Creek | California | 217 | Runoff | Dstore-Imperv, Dstore-Perv |
| Blumensaat (2012) | 3 catchments | Saxony, Germany; North-Rhine Westphalia, Germany; Western Ukraine | 1.97–52.08 | Runoff | Width |
| Borris et al. (2014) | City of Skelleftea | Sweden | 2.35 | Runoff | Dstore-Imperv, Dstore-Perv |
| Burszta-Adamiak and Mrowiec (2013) | 3 green roof platforms | Wroclaw, Poland | 2.88×10−62.88×10−6 | Runoff | InitSat |
| Camorani et al. (2005) | Po river | Bologna, Italy | 76.1 | Runoff | — |
| Cermola et al. (1979) | City of New Haven (2 catchments) | Connecticut | 20 | Runoff | %Imperv, Width |
| BOD, TSS | CoFractc | ||||
| Chang et al. (2008) | Yong-Kong industrial park (2 catchments) Guan-Tian industrial park (1 catchment) | Taiwan | 0.115–0.28 | Runoff | — |
| Blumensaat (2012) | BOD, COD, TSS, TS, TKN, TN | — | |||
| Chen and Adams (2006) | Upper East Don | Toronto, Canada | 0.161 | Runoff | Area; % Slope, Dstore-Imperv, Dstore-Perv; N-Imperv, N-Perv, MinRate, MaxRate |
| TSS, TS, TKN, TP; COD, BOD, Cu, Fe, Zn | Buildup C1&C2 (exp), Washoff C1&C2 (exp) | ||||
| Chen and Goldscheider (2014) | Hochifen-Gottesacker area, Alps | Austria/Germany | 35 | Runoff | — |
| Chen et al. (2002) | Love River | Kaohsiung City, Taiwan | 154 | Runoff | — |
| Chiang et al. (2010) | Yu-Cheng | Taipei, Taiwan | 16.45 | Runoff | — |
| Choi and Ball (2002) | Centennial Park | Sydney, Australia | 1.327 | Runoff | — |
| di Pierro et al. (2006) | Upper Bukit Timah | Singapore | 6.11 | Runoff | — |
| Chow et al. (2012) | 3 catchments | Skudai, Malaysia | 0.044–0.342 | Runoff | %Imperv, Width, Dstore-Imperv, N-Imperv |
| TSS, TP | Buildup C1&C2 (exp), Washoff C1&C2 (exp) | ||||
| Chung et al. (2011) | Mokgamcheon | South Korea | 56 | Runoff | N-Perv, N-Imperv, Dstore-Imperv, Dstore-Perv, Rough, Conduct, FC, UMC, Ks, Ps, CET, DP |
| BOD, TSS | Buildup C1&C2&C3 (Pow), Washoff C1&C2 (exp) | ||||
| Fang and Ball (2007) | Centennial Park | Sydney, Australia | 1.327 | Runoff | — |
| Ferreri et al. (2010) | Laboratory experiment | — | — | Runoff | — |
| Fioretti et al. (2010) | Green roof system | University of Genova, Italy | 0.001 | Runoff | Dstore-Imperv, N-Imperv |
| Gaume et al. (1998) | Quebec City | Canada | — | TSS | — |
| Ghosh and Hellweger (2012) | Faneuil Brook subbasin, lower Charles River watershed | Boston, Massachusetts | — | Runoff | — |
| Gülbaz and Kazezyılmaz-Alhan (2013) | Sazlidere | Istanbul, Turkey | 165 | Runoff | Rough,N-Imperv,N-Perv, Conduct, InitDef, Dstore-Imperv, Dstore-Perv |
| Hsu et al. (2000) | Taipei City | Taiwan | — | Runoff | N-Imperv |
| Jat et al. (2009) | Ajmer City (2 catchments) | Rajasthan, India | 40.80–58.20 | Runoff | — |
| Karamouz and Nazif (2013) | Tehran | Iran | 110 | Runoff | — |
| Kazezyılmaz-Alhan and Medina (2007) | Duke University West Campus | Durham, North Carolina | 0.22 | Runoff | — |
| Koudelak and West (2008) | Liepaja | Latvia | — | Runoff | — |
| Krebs et al. (2013) | Taapelipolku | Finland | 0.0587 | Runoff | Dstore-Imperv, Rough |
| Krebs et al. (2014) | City of Lahti (3 catchments) | Finland | 0.0663–0.1259 | Runoff | %Imperv, Dstore-Imperv, Dstore-Perv, N-Imperv, N-Perv, Rough, Suction, Conduct, InitDef |
| Lee et al. (2010) | Nogok Stream | Korea | 51 | Runoff | — |
| BOD, TN, TP | — | ||||
| Lei and Schilling (1994) | Hakden | Zurich, Switzerland | — | Runoff | %Imperv |
| Lenz et al. (2003) | Central Park | New York City, New York | 3.428 | Runoff | — |
| TP, TN, TSS, BOD, ON, NN, AN, OP, ORP | — | ||||
| Liong et al. (1993) | Upper Bukit Timah | Singapore | 6.11 | Runoff | — |
| Liong et al. (2001) | Upper Bukit Timah | Singapore | 6.11 | Runoff | — |
| Liong et al. (1991a) | Upper Bukit Timah | Singapore | 6.11 | Runoff | — |
| Liong et al. (1991b) | Upper Bukit Timah | Singapore | 6.11 | Runoff | — |
| Liong et al. (1995) | Upper Bukit Timah | Singapore | 6.11 | Runoff | — |
| Liu et al. (2013) | Dry run | Columbus, Ohio | 17.4 | Runoff | — |
| SC | — | ||||
| Madarang and Kang (2014) | Gwangju City | South Korea | 0.0025 | Runoff | — |
| TSS | buildup rate (buildup function not specified) | ||||
| Mahajan et al. (2014) | — | Cincinnati, Ohio | — | Runoff | — |
| Mailhot et al. (1997) | — | Quebec City, Canada | 1.81 | TSS | Buildup C1&C2 (exp),Washoff C1&C2 (exp) |
| Mancipe-Munoz et al. (2014) | Western Hills | Cincinatti, Ohio | 6.77 | Runoff | %Imperv, Width, % Slope, N-Imperv, Dstore-Imperv, N-Perv, Dstore-Perv; If imperviousness <20%<20%: Suction, Conduct, InitDef |
| Muhaisen et al. (2009) | City of Granada | Spain | 3 | Runoff | — |
| Muschalla et al. (2014) | — | Quebec City, Canada | 0.153 | Runoff | — |
| Obropta et al. (2008) | Teaneck Creek Conservatory site | New Jersey | 0.1862 | Runoff | — |
| Ouyang et al. (2012) | — | Beijing | 0.01 | Runoff | — |
| COD, TSS, TP | — | ||||
| Park et al. (2008) | — | — | — | Runoff | — |
| TSS, BOD | — | ||||
| Park et al. (2010) | Boeun (2 catchments) | Chungbukdo, South Korea | 0.177–0.182 | Runoff | — |
| BOD, TSS | — | ||||
| Peterson and Wicks (2006) | Devil’s Icebox/Connor’s Cave system | Missouri | — | Runoff | Rough, Length, Width-C |
| 17β-estradiol | |||||
| Petrucci et al. (2013) | Seine-Saint-Denis county; Orge River/ Seine River basins | France | 207–100,000 | Runoff | — |
| Petrucci and Bonhomme (2014) | City of Sucy-en-Brie | Paris, France | 2.3 | Runoff | — |
| TSS | — | ||||
| Piro et al. (2010) | Liguori | Cosenza, Italy | 4.136 | Runoff | — |
| TSS | — | ||||
| Qin et al. (2013) | Guang-Ming New District | Shenzhen, China | 0.6 | Runoff | Height, Vratio, Thick, Ksat |
| Sabouri et al. (2013) | City of Guelph (2 catchments); City of Kitchener (2 catchments) | Ontario, Canada | 0.194–0.79 (Gulph); 0.051–0.358 (Kitchener) | Runoff | — |
| Scholz and Kazemi Yazdi (2009) | Experimental site | University of Edinburgh, Scotland | 0.00064 | Runoff | — |
| Selvalingam et al. (1987) | Bukit Timah | Singapore | 27.4 | Runoff | — |
| Shrestha et al. (2013) | Zenne River | Belgium | 1162 | Runoff | — |
| Slys and Stec (2012) | City of Przemysl | Poland | 6.3288 | Runoff | — |
| Smith et al. (2005) | Reesor Creek | Toronto, Canada | 35 | Runoff | — |
| Smith et al. (2007) | City of Costa Mesa | Orange County, California | — | Runoff | — |
| TSS, Cd, Cu, Zn | — | ||||
| Cho and Seo (2007) | Jangcheon | Youngrang Lake | 4.7 | Runoff | — |
| BOD, COD, TSS, TP | |||||
| Sun et al. (2014a) | CSO 027 | Syracuse, New York | 0.588 | Runoff | N-Imperv, N-Perv, Dstore-Imperv, Dstore-Perv; Width, Rough |
| Sun et al. (2014b) | CSO 044 and CSO 027 (2 catchments) | Syracuse, New York | 0.1775–0.4676 | Runoff | Dstore-Imperv, N-Imperv, Rough |
| Taeuk and Sangho (2014) | Milyang Dam | South Korea | 94.39 | Runoff | — |
| (Talei and Chua 2012) | Kranji Reservoir | Singapore | 5.6 | Runoff | — |
| Talei et al. (2010) | Kranji basin | Singapore | 5.6 | Runoff | — |
| Tan et al. (2008) | — | Singapore | 5.6 | Runoff | Width, %Imperv, % Slope, N-Imperv |
| Temprano et al. (2006) | Santander | Spain | 0.56 | Runoff | %Imperv, % Slope, Width, N-Imperv, N-Perv |
| TSS, COD, TKN | Buildup C1&C2 (exp), Washoff C1&C2 (exp), CoFractc | ||||
| Tillinghast et al. (2011) | House Creek | Piedmont, North California | 0.431 | Runoff | — |
| Tran and Kang (2013) | Gwangju City | South Korea | 0.0025 | Runoff | — |
| TSS | — | ||||
| Tsihrintzis and Hamid (1998) | 4 catchments | South Florida | 0.0597–0.2357 | Runoff | Dstore-Imperv, Rough, N-Imperv, N-Perv, Dstore-Perv, Suction, Conduct, InitDef |
| BOD, TSS, TKN, Pb | — | ||||
| Tsihrintzis and Sidan (2008) | 4 catchments | South Florida | 0.0597–0.2357 | Runoff | — |
| Tsihrintzis et al. (2007) | Vassova Lagoon | North Greece | 2.7 | Runoff | Rough |
|
Valeo and Ho (2004) |
McKenzie Lake community | Calgary, Canada | 0.2548 | Runoff | — |
| van der Sterren et al. (2014) | 2 rainwater tank systems | Sydney, Australia | 0.000144–0.000170 | Runoff | — |
| TP, TN, TS | Buildup C1 (lin), Washoff C2 (exp)c, IC | ||||
| Walsh et al. (2014) | Chollas Creek | San Diego, California | 30.7 | Runoff | — |
| Wang and Altunkaynak (2012) | Cascina Scala | Pavia, Italy | 0.1135 | Runoff | — |
| Warwick et al. (1991) | Bachman Branch | Dallas, Texas | 25.9 | Runoff | %Imperv |
| TSS, BOD, ORP | — | ||||
| Wicke et al. (2012) | 15 experimental boards | Christchurch, New Zealand | 5.625×10−75.625×10−7 | TSS, Zn, Cu Pb | Buildup C1&C2 (exp), Buildup C1&C2 (Sat), Washoff C1(exp) |
| Wu et al. (2008) | Shuifang Spring | Chongqing, China | — | Runoff | % Slope, Dstore-Imperv, Dstore-Perv, rough, Length, Width-C, CurveNo |
| Wu et al. (2013) | 5 catchments | Polk County, Iowa | 0.618–2.698 | Runoff | — |
| Xiong et al. (2005) | Laboratory experiment | University of Illinois Urbana Champaign | 0.0001488 | Runoff | — |
| Xiong et al. (2005) | 25 hypothetical catchments | — | 0.046458 | Runoff | %Imperv, Width, Dstore-Imperv, Dstore-Perv, N-Imperv, N-Perv, % Slope, Length, Rough, MaxRate, MinRate, Decay |
| Zaghloul and Abu Kiefa (2001) | 3 hypothetical catchments | — | 0.0324–0.0486 | Runoff | — |
| Zaghloul and Al-Shurbaji (1991) | Kuwait City | Kuwait | 0.48 | Runoff | Dstore-Imperv, Width, N-Imperv |
| Zhang and Shuster (2014) | North Appalachian (2 catchments) | Coshocton, Ohio | 0.0047–0.0065 | Runoff | — |
| Zhao et al. (2009) | Yalianfang | Macau, China | 0.1365 | Runoff | — |
| Zhao et al. (2008) | Yalianfang | Macau, China | 0.1365 | Runoff | Des-Imperv; %Imperv, N-Imperv, Widt |
Note: The parameter abbreviations are as follows:
Hydrologic parameters: Dstore-Imperv, depth of depression storage on the impervious portion of the subcathcment; Dstore-perv, depth of depression storage on the pervious portion of the subcathcment; %Imperv, percent of land area that is impervious; Width, characteristic width of the overland flow path for the sheet flow runoff; %Slope, average percent slope of the subcatchment; N-Imperv, Manning’s nn for overland flow over the impervios porion of the subcatchment; N-Perv, Manning’s nn for overland flow over the pervious portion of the subcatchment; %Zero-Imperv, percent of the impervious area with no depression storage; Area, area of subcatchment; Rough, Manning’s nn for conduit/open channel; Length, length of conduit/open channel; Width-C, width of conduit/open channel.
Infiltration parameters: InitSat, percent to which the LID unit’s soil layer or storage layer is initially filled with water; MaxRate, maximum infiltration rate on Horton infiltration; MinRate, minimum infiltration rate on Horton infiltration; Decay, decay rate constant of Horton infiltration; Suction, soil capillary suction in Green-Ampt infiltration; Conduct, soil saturated hydraulic conductivity in Green-Ampt infiltration; InitDef, initial soil moisture deficit in Green-Ampt infiltration; CurveNo, SCS curve number.
Groundwater parameters: FC, soil field capacity; UMC, unsaturated zone moisture content at start of simulation; Ps, slope of soil tension versus moisture content curve; Ks, slope of the logarithm of hydraulic conductivity versus moisture deficit; CET, maximum evapotranspiration rate assigned to the upper zone; DP, coefficient for unquantified losses.
LID parameters: Height, thickness of storage layer; Thick, thickness of soil layer/permeable pavement; Vratio, void ratio; Ksat, soil’s saturated hydraulic conductivity, initial concentration.
Buildup/washoff parameters: Buildup C1&C2 (exp), coefficients of buildup exponential function C1 (maximum buildup possible) and C2 (buildup rate constant); Buildup C1&C2 (Sat), coefficients of buildup saturation function C1 (maximum buildup possible) and C2 (half-saturation constant); Buildup C1&C2&C3 (Borah et al.), coefficients of buildup power function C1 (maximum buildup possible) and C2 (buildup rate constant) and C3 (time exponent); Buildup C1 (lin), coefficient of buildup linear function C1 (maximum buildup); Washoff C1&C2 (exp), coefficients of washoff exponential function C1 (washoff coefficient) and C2 (washoff exponent); CoFract, fraction of co-pollution.
Indicator abbreviations: TSS, total suspended solids; TS, total solids; BOD, biochemical oxygen demand; COD, chemical oxygen demand; Pb, lead; Cu, copper; Zn, Zinc; NN, nitrate nitrogen; AN, ammonia nitrogen; TKN, total kjeldahl nitrogen; TN, total nitrogen; ON, organic nitrogen; ORP, ortho-phosphate; OP, organic phosphorus; SC, specific conductance.
Parameters that are specified by sensitivity analysis.
Inferred.
Table 2.
Calibration/Validation Methodology and Performance Measures for the SWMM Applications Used in the Review
| Calibration | Validation | ||||
|---|---|---|---|---|---|
| Reference | Methoda | Time period | Performanceb | Time period | Performanceb |
| Alfredo et al. (2010) | Manually | 1 event | RMSEQc = 25.1–185.5 mL/min25.1–185.5 mL/min | 1 event | RMSEQc = 50.2–222.3 mL/min50.2–222.3 mL/min |
| Lee et al. (2008) | Manually | Continuous for 12 yearsc | Visually | — | — |
| Ashbolt et al. (2013) | Shuffled complex evolution algorithm | Continuous for 12 months | NSEQ = 0.78 (hourly), 0.81 (daily) | Continuous for 6 months | NSEQ = 0.33 (hourly), 0.75 (daily) |
| Baffaut and Delleur (1989) | Expert system | 6 events | (Florida) REPTc = −6.3–(−0.2) min−6.3–(−0.2) min, REV=−8.9–10.0%REV=−8.9–10.0%, REP=−27.3–9.7%REP=−27.3–9.7% | 3 events | (Florida) (Eddy and Engineers) REPTc = −9.2–1.9 min−9.2–1.9 min, REV = 2.4–25.3%, REP = 4.0–17.6% |
| (Ross Ade) REPTc = −0.2–169.2 min−0.2–169.2 min, REV=−59.0–33.0%REV=−59.0–33.0%, REP=−38.0–36.0%REP=−38.0–36.0% | (Ross Ade) REPTc = −0.1–4.3 min−0.1–4.3 min, REV%=−5.0–64.1%REV%=−5.0–64.1%, REP=−116–68.5%REP=−116–68.5% | ||||
| Baffaut and Delleur (1990) | Expert system | — | −20%<REL<20%−20%<REL<20% | — | — |
| Balascio et al. (1998) | Genetic algorithm | 2 events | MOF = 0.90–0.92 | 2 events | MOF = 0.85–0.94 |
| Barco et al. (2008) | Complex method | 5 events | REV = 16–100%, REP = 25–51% | 5 events | REV = 3–54%, REP = 8–32% |
| Blumensaat (2012) | Manually | Continuous for 3 weeks | — | Continuous for 3 weeks | NSEQ>0.5NSEQ>0.5, REVc<10%<10% |
| Borris et al. (2014) | Manually | 8 events | REV<10%REV<10%, REP<20%REP<20% | 6 events | R2V = 0.99, R2P = 0.95 |
| Burszta-Adamiak and Mrowiec (2013) | Manually | 13 events | NSEQ=−6.59–0.49NSEQ=−6.59–0.49, REV=−6–4%REV=−6–4%, REP = 19–1931% | — | — |
| Camorani et al. (2005) | Manually | 1 event | REP<8%REP<8% | 1 event | REP<8%REP<8% |
| Cermola et al. (1979) | Manually | 2 events | REV=−4.4%REV=−4.4% | 2 events | REV=−14.3%REV=−14.3% |
| Manually | 1 event | REL=−2.3%REL=−2.3% (BOD), 6.4% (TSS) | 1 event | Visually | |
| Chang et al. (2008) | PCSWMM2000 | 1 event | NSEQ = 0.84–0.97 | 2 events | NSEQ = 0.8–0.94 |
| — | — | — | 26 events | — | |
| Chen and Adams (2006) | Manually | 11 events | R2V = 0.94 | — | — |
| Manually | 17 events | R2L = 0.86–0.93 | — | — | |
| Chen and Goldscheider (2014) | Genetic algorithm | Continuous July–October 2012 | COFc | Continuous July–October 2012 | RMSEQ=0.073–0.320 m3/sRMSEQ=0.073–0.320 m3/s, NSEQ = 0.916–0.946, REV=2–4% |
| Chen et al. (2002) | PCSWMM 2000 | — | — | — | — |
| Chiang et al. (2010) | Manuallyc | 14 events | CCD = 0.96–0.98 | — | — |
| Choi and Ball (2002) | Manuallyc | 3 events | REP=−1.45%REP=−1.45%, RMSEP=0.03 m3/sRMSEP=0.03 m3/s, RED = 0.24%, RMSED = 0.01 mm | 3 events | REP = 4.75%, RMSEP=0.02 m3/sRMSEP=0.02 m3/s, RED=−1.24%RED=−1.24%, RMSED = 0.02 mm |
| di Pierro et al. (2006) | Genetic algorithm | 4 events | REV = 0.20–21.29%, REP = 0.00–49.10% | — | — |
| Chow et al. (2012) | Manually | 8–10 events | RED=−9.47–1.5%RED=−9.47–1.5%, ARED = 3.6–9.47%, NOFD = 0.062–0.099, NSED = 0.968–0.996, R2D = 0.987–0.998, CCD = 0.967–1.075 | 7 events | RED=−8.28–2.78%RED=−8.28–2.78%, ARED = 2.60–8.47%, NOFD = 0.01–0.292, NSED = 0.910–0.996, R2D = 0.966–0.999, CCD = 0.814–1.017 |
| REP=−7.33–(−1.46%)REP=−7.33–(−1.46%), AREP = 5.60–10.61%, NOFP = 0.061–0.177, NSEP = 0.924–0.992, R2P = 0.916–0.992, CCP = 0.930–0.989 | REP=−17.54–11.74%REP=−17.54–11.74%, AREP = 5.26–18.97%, NOFP = 0.045–0.272, NSEP = 0.885–0.998, R2P = 0.980–0.998, CCP = 0.799–1.005 | ||||
| Manually | 6–9 events | REL=−10.72–13.31%REL=−10.72–13.31%, AREL = 12.46–23.09%, NOFL = 0.063–0.379, NSEL = 0.714–0.99, R2L = 0.761–0.99, CCL = 0.745–1.111 | 6–7 events | REL=−14.12–4.70%REL=−14.12–4.70%, AREL = 15.26–28.11%, NOFL = 0.195–0.359, NSEL = 0.747–0.969, R2L = 0.737–0.965, CCL = 0.769–1.137 | |
| REC=−2.59–13.70%REC=−2.59–13.70%, AREC = 10.44–20.51%, NOFC = 0.018–0.244, NSEC = 0.753–0.992, R2C = 0.285–0.999, CCC = 0.737–1.099 | REC=−9.80–3.00%REC=−9.80–3.00%, AREC = 13.10–23.16%, NOFC = 0.101–0.353, NSEC = 0.570–0.919, R2C = 0.249–0.956, CCC = 0.914–1.172 | ||||
| REPC=−13.82–3.69%REPC=−13.82–3.69%, AREPC = 8.16–21.06%, NOFPC = 0.037–0.177, NSEPC = 0.840–0.994, R2PC = 0.858–0.997, CCPC = 0.774–1.120 | REPC=−4.26–12.53%REPC=−4.26–12.53%, AREPC = 9.60–24.37%, NOFPC = 0.086–0.327, NSEPC = 0.661–0.958, R2PC = 0.710–0.982, CCPC = 0.794–0.993 | ||||
| Chung et al. (2011) | Manually | 26 events | NSEQ = 0.919, RMSEQ=1.318 m3/sRMSEQ=1.318 m3/s, RMAEQ = 0.139 | 22 events | NSEQ = 0.648, RMSEQ=0.607 m3/sRMSEQ=0.607 m3/s, RMAEQ = 0.303 |
| Manually | 25 events (BOD), 20 events (TSS) | NSEC = 0.678 (BOD), 0.735 (TSS), RMSEC=3.957 mg/LRMSEC=3.957 mg/L (BOD), 34.652 mg/L34.652 mg/L (TSS), RMAEC = 0.15 (BOD), 0.189 (TSS) | 21 events (BOD), 14 events (TSS) | NSEC = 0.635 (BOD), 0.861 (TSS), RMSEC=3.913 mg/LRMSEC=3.913 mg/L (BOD), 4.661 mg/L4.661 mg/L (TSS), RMAEC = 0.156 (BOD), 0.103 (TSS) | |
| Fang and Ball (2007) | Genetic algorithm | 3 events | RMSEQ = 0.0715–0.0880, standard deviation of RMSEQ = 0.0010–0.0014 | — | — |
| Ferreri et al. (2010) | Manuallyc | — | REQc = 7.5–38.3% | — | — |
| Fioretti et al. (2010) | Manuallyc | 1 event | REV = 15%, REP = 2.6% | 1 events | REV = 14.4%, REP = 17% |
| Gaume et al. (1998) | Powell method | 8 events | COFc = 409921–759239 | — | — |
| Ghosh and Hellweger (2012) | PCSWMM 2000 | 50 events | Visuallyc | — | — |
| Gülbaz and Kazezyılmaz-Alhan (2013) | Manually | 2 events | — | 3 events | — |
| Hsu et al. (2000) | — | — | — | 1 event | Visually |
| Jat et al. (2009) | Manually | Continuous June 1–September 30 2000 | R2Q = 0.99 | Continuous for 4 months | — |
| Karamouz and Nazif (2013) | Manuallyc | 1 event | REP = 3%, RETc = 20% | — | — |
| Kazezyılmaz-Alhan and Medina (2007) | Manually | 30 events | — | 1 event | Visually |
| Koudelak and West (2008) | InfoWorks CS | 2 events | Visually | Continuous May–July 2005 | Visually |
| Krebs et al. (2013) | NSGAII | 6 events | NSEQ = 0.88, CCQ = 0.94, REP=−13.6%REP=−13.6%, REV = 7.0% | 11 events | NSEQ = 0.84, CCQ = 0.92, REP=−5.0%REP=−5.0%, REV = 5.1% |
| Krebs et al. (2014) | NSGAII | 8 events | NSEQ = 0.42–0.98, CCQ = 0.82–1.00 | 19 events | NSEQ = 0.53–0.96, CCQ = 0.75–0.99 |
| Lee et al. (2010) | Manuallyc | 7 events | RMSEQ = 0–0.05, NSEQ = 0.12–0.97, R2Q = 0.52–0.97 | — | — |
| Manuallyc | RMSEL=0.77–63.06 kg/dayRMSEL=0.77–63.06 kg/day (BOD), 0.50–57.54 kg/day0.50–57.54 kg/day (TN), 0.03–4.09 kg/day0.03–4.09 kg/day (TP), NSEL = 0.08–0.86 (BOD), 0.29–0.97 (TN), 0.04–0.79 (TP), R2L = 0.21–0.82 (BOD), 0.23–0.93 (TN), 0.22–0.75 (TP), REL = 6.46–34.26% (BOD), 2.68–34.18% (TN), 3.15–32.04% (TP) | — | — | ||
| Lei and Schilling (1994) | — | — | — | — | — |
| Lenz et al. (2003) | Manuallyc | 6 events | Visually | — | — |
| Manuallyc | Visually | — | — | ||
| Liong et al. (1993) | KBSWMM2 | 3 events | R2Q = 0.99–1.00 | 3 events | — |
| Liong et al. (2001) | Shuffled complex evolution | 2 events | COF<1%COF<1% | — | — |
| Liong et al. (1991a) | KBSWMM | 2 events | REV = 5–8%, REP = 6–9% | 2 events | REV = 9–11%, REP = 11–37% |
| Liong et al. (1991b) | KBSWMM | 5 events | AREV<10%AREV<10%, AREP<10%AREP<10% | — | — |
| Liong et al. (1995) | Genetic algorithm | 3 events | REP=−1.339–0.045%REP=−1.339–0.045% | 3 events | REP = 1.767–7.265% |
| Liu et al. (2013) | Manuallyc | Continuous July–August 2011 | Visually | — | — |
| Manuallyc | — | Visually | — | — | |
| Madarang and Kang (2014) | Box complex method | 17 events | NSEV = 0.93 | — | — |
| Manually | 17 events | NSEL = 0.35 | — | — | |
| Mahajan et al. (2014) | Manuallyc | Continuous January–July 2001 | — | Continuous July–December 2001 | RMSEV=26006.4 m3RMSEV=26006.4 m3, RMSEDQ = 913.8 min, R2V = 0.91 |
| Mailhot et al. (1997) | Metropolis Monte Carlo algorithm | 5 events | COFc = 409921–759239 | — | — |
| Mancipe-Munoz et al. (2014) | PEST | Continuous for 10 months | NSEQ = 0.6, REV = 432% | Continuous for 5 months | NSEQ = 0.62, REV = 18% |
| Muhaisen et al. (2009) | Manually | 474 events | Visually | — | — |
| Muschalla et al. (2014) | — | — | — | 2 events | Visually |
| Obropta et al. (2008) | Manuallyc | 2 events | — | — | — |
| Ouyang et al. (2012) | Manuallyc | — | — | 4 events | REDc = −0.13%−0.13%, REVc = −2.65%−2.65% |
| — | — | — | RELc = −5.03%−5.03%, REPCT=−20%REPCT=−20% | ||
| Park et al. (2008) | Manually | 1 event | R2Q = 0.78 | 1 event | — |
| Manually | 1 event | R2L = 0.79 | 1 event | — | |
| Park et al. (2010) | XP-SWMMc | — | — | 1 event | R2V = 0.79–0.90 |
| — | — | — | — | R2Cc = 0.94–0.97 (BOD), 0.87–0.97 (TSS) (Villarreal et al.) | |
| Peterson and Wicks (2006) | — | Continuous for 1 day | REQ = 10% | — | — |
| — | Continuous for 1 day | REC = 14% | — | — | |
| Petrucci et al. (2013) | Genetic algorithm | Continuous: 2/3 of data; October–December 2009 and May–July 2010 | NSEQ = 0.56–0.78 | Continuous: 1/3 of data; October–December 2009 and May–July 2010 | NSEQ = 0.48–0.77 |
| Petrucci and Bonhomme (2014) | Genetic algorithm | Continuous; April–May 2012 | NSEQc = 0.79–0.84 | Continuous October–December 2012 | NSEQc = 0.60–0.76 |
| Genetic algorithm | — | NSECc<0.5<0.5 | — | NSECc<0.35<0.35 | |
| Piro et al. (2010) | Calibrated before | 8 events | R2Q>0.8R2Q>0.8 | — | — |
| — | — | R2C>0.78R2C>0.78 | — | — | |
| Qin et al. (2013) | Manuallyc | 1 event | RMSEQ=0.021 m3/sRMSEQ=0.021 m3/s | 1 event | RMSEQ=0.084 m3/sRMSEQ=0.084 m3/s, REQ = 1–10%, REP = 6.7%, REPT = 0% |
| Sabouri et al. (2013) | PCSWMM | 25 events (Guleph); 28 events (Kitchener) | — | — | — |
| Scholz and Kazemi Yazdi (2009) | Manually | — | Visually | Continuous June–November 2006 | Visually |
| Selvalingam et al. (1987) | Manuallyc | 1 event | Visually | 1 event | Visually |
| Shrestha et al. (2013) | Manuallyc | Continuous January 2007–January 2008 | REQ=−6%REQ=−6% and >4%>4% | Continuous January 2008–January 2009 | REQ=−6%REQ=−6% and >4%>4% |
| Slys and Stec (2012) | Manuallyc | — | REV = 18% | — | — |
| Smith et al. (2005) | PCSWMMc | — | REV=−28.2%REV=−28.2%, R2Q = 0.868 | — | — |
| Smith et al. (2007) | Manuallyc | 4 events | REP<5–10%REP<5–10% | — | — |
| Manuallya | — | — | — | — | |
| Cho and Seo (2007) | Genetic Algorithm | Continuous June–August 2005 | — | — | — |
| Sun et al. (2014a) | GLUE | 20 events | — | — | — |
| Sun et al. (2014b) | GLUE | 12 events | Visually | 8 events | Visually |
| Taeuk and Sangho (2014) | Shuffled complex evolution | 3 events | NSEQ = 0.87–0.99, REQ=−4.32–5.04%REQ=−4.32–5.04%, REP=0.05–16.27 m3/sREP=0.05–16.27 m3/s, REPT = 0–10 h | 2 events | NSEQ = 0.74–0.85, REQ = 8.23–18.65%, REP=61.37–146.07 m3/sREP=61.37–146.07 m3/s, REPT = 0–1 h |
| Talei and Chua (2012) | — | — | — | 62 events | NSEQ = 0.642, R2Q = 0.770, RMSEQ=2.648 m3/sRMSEQ=2.648 m3/s, REP = 34.8% |
| Talei et al. (2010) | Calibrated before | 15 events | NSEQ = 0.6275–0.6342, REP = 31.3–37.2% | — | — |
| Tan et al. (2008) | PEST | Continuous at May 2005 + 10 events | (Event-based and continuous) NSEQ = 0.7392–0.9445, REV=−4.7–22.7%REV=−4.7–22.7%, REP = 1.2–19.1%, REPT = 0–10 min | 66 events | Event-based: NSEQ = 0.1943–0.9309, REV=−51.4–49.2%REV=−51.4–49.2%, REP = 0.016–0.687%, REPT = 0–50 min; Continuous simulation: NSEQ = 0.2120–0.9517, REV=−63.9–45.3%REV=−63.9–45.3%, REP = 0.014–0.706%, REPT = 0–55 min |
| Temprano et al. (2006) | Manually | 1 event | REP<30%REP<30%, REMinQ<30%REMinQ<30%, REV<10%REV<10% | 2 events | Visually |
| Manually | 1 event | REMinC<30%REMinC<30%, REPC<30%REPC<30%, CAT<10 minCAT<10 min, REL<30%REL<30% | 1 event | Visually | |
| Tillinghast et al. (2011) | PCSWMM | Continuous: 35% of data June 2007–April 2008 | R2P = 0.9263, RMSEP=0.1262 m3/sRMSEP=0.1262 m3/s | Continuous 65% of data June 2007–April 2008 | — |
| Tran and Kang (2013) | Box complex method | 17 events | NSEV = 0.93 | — | — |
| Box complex method | — | NSEL = 0.35, REL=−14%REL=−14% | — | — | |
| Tsihrintzis and Hamid (1998) | Manuallyc | 58 events | — | 16 events | CCP = 0.62–0.92, CCD = 1.05–2.62, CCPT = 1.02–1.66, CCT = 0.38–1.05 |
| Tsihrintzis and Sidan (2008) | — | 72 events | REPc = −16.49–13.14%−16.49–13.14%, CCP = 0.74–0.97, R2P = 0.76–0.98 | 26 events | REPc = −37.41–1.10%−37.41–1.10%, CCP = 0.62–0.92, R2P = 0.52–0.99 |
| REDc = 16.12–206.42%, CCD = 1.06–1.95, R2D = 0.56–0.93 | REDc = −2.93–129.79%−2.93–129.79%, CCD = 1.05–2.62, R2D = 0.47–0.98 | ||||
| REPTc = 65.25–108.11%, CCPT = 1.07–1.68, R2PT = 0.29–0.99 | REPTc = 6.28–125.00%, CCPT = 1.02–1.66, R2PT = 0.38–0.99 | ||||
| RET = 13.59–75.21%, CCT = 1.02–1.59, R2T = 0.23–0.91 | RET=−8.51–57.94%RET=−8.51–57.94%, CCT = 0.38–1.05, R2T = 0.75–1.00 | ||||
| Tsihrintzis et al. (2007) | Manually | 1 event | R2Q = 0.86–0.91, R2D = 0.57–0.80 | 3 events | R2Q = 0.62–0.72, R2D = 0.77–0.91 |
| Valeo and Ho (2004) | Manuallyc | — | — | Continuous 3 weeks | REV = 0.1%, NSEV = 12, REP = 50–61% |
| van der Sterren et al. (2014) | Manuallyc | Continuous October 2008–April 2009 | RMSED = 0.09, RMSEP<0.09 L/sRMSEP<0.09 L/s, REP=−12–0.5%REP=−12–0.5%, DE = 0.5%, NSEP=−0.25NSEP=−0.25, 0.98, NSED=−0.25NSED=−0.25, 0.98 | Continuous October 2008–October 2009 | REP=−7.2%REP=−7.2%, RMSEP=0.05 L/SRMSEP=0.05 L/S, CCP = 0.51, RMSED = 486 mm, CCD = 0.56, CCV=−0.06CCV=−0.06 |
| Manuallyc | Continuous October 2008–April 2009 (TS); April–September 2009 (TN & TP) | CCC = 0.25–0.4 (TS), 0.64–0.89 (TP), REC = 0.2–38% (TP), 58–98% (TN) | Continuous April–September 2009 (TS); September–October 2009 (TN & TP) | RECc = −52%−52% (TP), −7.1–97%−7.1–97% (TN), −44–(−17%)−44–(−17%) (TS) | |
| Walsh et al. (2014) | Manually | — | — | 7 events | REV = 5%, REP = 3.1%, REQ = 20% |
| Wang and Altunkaynak (2012) | Rosenbrock’s method | 35 events | — | 35 events | — |
| Warwick et al. (1991) | Manuallyc | 3 events | NSEV≥0.50NSEV≥0.50, NSEP≥0.40NSEP≥0.40 | 9 events | — |
| — | — | — | 1 events | Visually | |
| Wicke et al. (2012) | Excel solver | 5 events | R2L = 0.82–0.95 (TSS), 0.68–0.92 (Zn), 0.60–0.90 (Cu), 0.85–0.94 (Pb) | — | — |
| Wu et al. (2008) | — | 1 event | NSEQ = 0.95 | 1 event | NSEQ = 0.92 |
| Wu et al. (2013) | Manually | 1 event | R2Q = 0.73–0.89, NSEQ = 0.25–0.80 | 1 event | R2Q = 0.39–0.92, NSEQ = 0.23–0.91 |
| Xiong et al. (2005) | — | — | — | 68 events | REP=−35.777–8.491%REP=−35.777–8.491%, REPT=−65.288–(−7.623%)REPT=−65.288–(−7.623%), REV=−28.501–14.608%REV=−28.501–14.608%, NSEQ=−0.7109–0.9569NSEQ=−0.7109–0.9569 |
| Zaghloul (1983) | — | — | — | — | — |
| Zaghloul and Abu Kiefa (2001) | Neural network | 69 events | — | 12 events | — |
| Zaghloul and Al-Shurbaji (1991) | Manuallyc | 1 event | Visually | 3 events | visually |
| Zhang and Shuster (2014) | Manuallyc | Continuous March–October 1990–1995 (except 1994) | — | Continuous March–October 1996–2003 | REV = 4–218%, CCQ = 0.63–0.66, MOF = 0.6–143 |
| Zhao et al. (2009) | Manually | 1 event | NSEQ = 0.92, REQ = 2.0%, RMSEQ=0.005 m3/sRMSEQ=0.005 m3/s, REP = 7.2%, REPT = 1 min | 1 event | NSEQ = 0.86, REQ = 2.5%, RMSEQ=0.004 m3/sRMSEQ=0.004 m3/s, REP = 21.7%, REPT = 0 min |
| Zhao et al. (2008) | GLUE | 1 event | NSEQ>0.7NSEQ>0.7, −20%<REQ<20%−20%<REQ<20%, CCQ>0.9CCQ>0.9, the best 10% of RMSEQ | 1 event | NSEQ>0.7NSEQ>0.7, −20%<REQ<20%−20%<REQ<20%, CCQ>0.9CCQ>0.9, the best 10% of RMSEQ |
Calibration method abbreviations: GLUE, generalized likelihood uncertainty estimation; NSGAII, genetic multiobjective optimization algorithm; PEST, model independent parameter estimation.
Performance abbreviations are listed in Table 3.
Inferred.
Researchers have taken two approaches to modeling water quality within SWMM. The first is to make an assumption about the link between runoff volumes generated by a model simulation and water quality values for a particular constituent. For example, it is sometimes assumed that the TSS load is directly proportional to runoff volumes (e.g., Blumensaat 2012; Choi et al. 2006). Generally speaking, this indicates that water quality investigations take place in postprocessing, outside of SWMM. In some cases, other water quality models have been linked to SWMM to perform these analyses, using input data from SWMM (Burian et al. 2002; Choi et al. 2006). The second approach uses the water quality modules within SWMM (Tables 1 and 2).
The purpose of water quality investigations using SWMM have included (1) determining the effects from nonpoint pollution (Jia et al. 2014; Lee et al. 2010; Oraei Zare et al. 2012; Choi et al. 2006), (2) BMP/LIDs treatment (Chang et al. 2008; Jia et al. 2014; Oraei Zare et al. 2012; Van der Sterren et al. 2014), (3) air quality interactions (Burian et al. 2001, 2002; Fallah Shorshani et al. 2014), (4) climate/land use change effects (Borris et al. 2014), (5) first flush effects (Chang et al. 2008; Ouyang et al. 2012; Young et al. 2010), (6) monitoring the program design (Talei et al. 2010), (7) traditional stormwater management structure performance (Borris et al. 2014), and (8) spatial resolution effects (Fallah Shorshani et al. 2014; Park et al. 2008; Warwick et al. 1991).
SWMM and Total Maximum Daily Load Implementation Plans
There were 18 references on the topic of SWMM and total maximum daily loads (Toddles), from the time period of 1999–2015. Most of these papers discussed SWMM in their introduction, and only five of them chose to apply SWMM. Some researchers chose to create improved models that were based on SWMM, or they sought to simplify it for their application (Chen et al. 1999; Chin 2011; Ha and Stenstrom 2008; Kuzin and Adams 2008; Petersen et al. 2005). The data heaviness and complexity of SWMM were cited in these cases (Ha and Stenstrom 2008; Petersen et al. 2005). No bacterial TMDL studies conducted using SWMM were found among these peer-reviewed journal publications.
SWMM models were not necessarily used as stand-alone methods for assessing TMDL implementation plans. They were used in larger studies to determine the main sources of nonpoint pollution and the effect of reduction measures (e.g., BMPs). One study combined a SWMM model with another water quality model, and additional models, into a larger risk-management decision-making tool (Chen and Herr 2010).
Four other papers applied SWMM in looking at sediment and heavy metals (Lee et al. 2010; McGarity 2013; McPherson et al. 2005; Smith et al. 2007). Event mean concentrations (EMCs) were used to assess TMDLs. The models were calibrated using previously collected monitoring data. Although in all cases, the hydrology closely matched, in one paper the agreement between modeled and measured data was weaker (R2 between 0.5 and 0.7) (McPherson et al. 2005).
In one of these papers, BMPs were optimized afterward by using a mixed-integer linear program (Smith et al. 2007). That particular model required ambient monitoring data to estimate loadings at each of the inlets. The authors mentioned that the model was robust. They also stated that the practice was data intensive, and as a city might consider, significant capital expenditure is required for getting the information needed to rigorously perform such analysis.
Overall, the number of applications of SWMM in assessing TMDL plans was few. However, as seen in the literature, a large number of watersheds with existing SWMM models can easily be added onto these models to optimize pollution reduction plans and to meet regulatory requirements. Where capital has already been invested in collecting geographic and monitoring data, SWMM would be a great tool. When TMDL assessment is the goal, uncertainly analysis is important to determine the reliability of projections and to choose appropriate margins of safety.
Land Use and Climate Change Effects
Many of the more recent studies using SWMM were performed to consider the effects of land use and climate change. Researchers have performed simulations to understand better the effects on stream ecological health and the hydraulics of sewer systems. Particular concerns for these studies have included overflows, flooding frequency, and water quality. Studies that considered climate change have primarily modeled changes in precipitation, and effects on stream flow, peak discharge, flashiness, and transport of contaminants. Studies that considered land use change have primarily modeled changes to imperviousness to predict effects on flooding. Land use change applications have also considered changing demands for urban sewage and water treatment and changing inflows. There were nine studies that fell into the category of addressing water quantity, compared with five that addressed water quality concerns.
Considering those papers that addressed water quality concerns, models were used to predict effects on a range of measures, including total phosphorus (TP) (Kovács and Clement 2009; Ouyang et al. 2012), TSS (Borris et al. 2014; Doglioni et al. 2009; Ouyang et al. 2012), chemical oxygen demand (COD) (Doglioni et al. 2009; Ouyang et al. 2012), biochemical oxygen demand (BOD) (Doglioni et al. 2009), and temperature (Sabouri et al. 2013). The type of land use change that was used in the models was increasing imperviousness. Gradually increasing imperviousness scenarios were used by the studies reviewed. Results from land use change included higher runoff, pollutant transport, and temperatures. For just under half of these studies, SWMM was used in conjunction with other models, including WetSpa (Kovács and Clement 2009), SWAT (Kim et al. 2011), the urban drainage model (Doglioni et al. 2009), and the land use change model (Doglioni et al. 2009).
Considering those papers that addressed water quantity concerns, models were used to predict effects on flood risk (Camorani et al. 2005; Huong and Pathirana 2013), drainage needs (Denault et al. 2006), total runoff (Kim et al. 2011; Ouyang et al. 2012), surface flow (Kim et al. 2011; Ouyang et al. 2012), and groundwater discharge rates (Kim et al. 2011). These studies also used changes to impervious cover and precipitation pattern changes, in addition to sea level rise (Huong and Pathirana 2013). The effect of sea level rise was studied by integrating SWMM with a 2D inundation model. Results included greater flood risk, increased inundation areas, increased maximum flood depth, increased stream flow, increased channel dimensions, increases in total runoff and surface flow, and decreases in groundwater discharge rates. Again, just under half of the time, SWMM was combined with other models, including SWAT (Kim et al. 2011), BreZo (Huong and Pathirana 2013), Dinamica-Environment for Geoprocessing Objects (an urban growth model) (Huong and Pathirana 2013), and a National Oceanic and Atmospheric Administration (NOAA) atmospheric and land surface model (Huong and Pathirana 2013).
In most cases, climate and land uses changes are both occurring, but only one study attempted to address the interrelated changes. Urich (2013) reviewed a hypothetical sewer system’s overflow efficiency and surface flooding for a 20-year period. As factors representing the effect of climate change were increased, combined sewer overflows and surface flooding increased between 20 and 30% in 2030.
There was a single study that focused on the effects on ecologic stream health. Wu et al. (2013) used the kinematic wave method for five watersheds in Iowa. The authors indicated in the study that SWMM was able to model some watersheds more accurately than others [Nash-Sutcliffe efficiency (NSE) ranged from 0.23 to 0.91]. There was also one paper that looked at adapting infrastructure. In Gainesville, Florida, this was done by retrofitting an area with more pervious surfaces. According to the predictions made by the model, the addition of some 2.0 m linear infiltration reactors would lead to reductions of phosphorous, nitrogen, and TSS (Sansalone et al. 2013).
Hypothetical Analysis
Generally speaking, the strength of SWMM is how it facilitates the determination of the best sewer designs in complex situations, and finds the most sensitive parameters with regard to flooding and water quality issues. This theme carries through those papers that created hypothetical watersheds and hypothetical sewer or water treatment systems. In some of these cases, real parameters were used to simulate the performance of a designed system in a particular location. These applications have been undertaken to determine sewer designs with appropriate pipe sizes, manhole locations, and system pressurization. Applications of hypothetical watersheds within SWMM have also included designing optimum systems for handling suspended solids, and testing numerical methods and parameters. A total of 14 papers included in this review chose to model hypothetical watersheds.
Two papers among the 14 focused on applying SWMM to explain results from laboratory experiments. Ferreri et al. (2010) used laboratory testing to evaluate system pressurization through a conduit. They found that SWMM was able to adequately capture the pressurization. Xiong et al. (2005) created three watershed experimentation systems in a laboratory. They exported the results for use in SWMM to estimate the water quality based on the kinematic wave model and SWMM’s nonlinear reservoir modeling. They found that the kinematic wave modeling more closely captured peak flow than SWMM’s nonlinear reservoir model for all experiments.
Guo and Urbonas (2009) constructed a hypothetical sewer system to determine appropriate pipe sizes. Blumensaat (2012) created a hypothetical system including SWMM and consisting of a one-dimensional (1D) river and a 2D aquifer to evaluate the water flux within the Poltva catchment in Ukraine. Urich et al. (2013) created virtual infrastructure benchmarking (VIBe) computer-generated cities for use with the biophysical model (BPM). SWMM 5 was used in this study to evaluate the combined sewer overflow and surface flooding. Todeschini et al. (2012) created a hypothetical catchment to evaluate multiple sewer network designs for installation in Pavia, Italy. They used SWMM 5 to compare the performance of stormwater detention tanks, flow regulators, and bypass devices for total volume and TSS discharge concentrations. They found that a detention tank with flow regulators provided the most optimal performance.
SWMM was also used to create semihypothetical systems to evaluate wastewater treatment plant design (Doglioni et al. 2009; Schindler et al. 2010). Guo and Urbonas (2009) constructed cascading planes of watersheds to determine different kinematic wave shape factors. These factors were then incorporated into SWMM 5’s nonlinear reservoir model to translate a natural watershed into its equivalent rectangular shape. Steffen et al. (2013) applied SWMM to a hypothetical watershed to understand the effect of weather pattern trajectory on peak flow, and found that downstream storm movement generally produced greater peak flows than upstream storm movement. The authors were able to show that these additional physical factors are important to take into consideration when applying SWMM to predict flow rates.
Effects of Spatial Discretization
The effect of the spatial resolution of subcatchment discretization and the corresponding sewer network setup on SWMM output has been investigated in multiple studies (Fallah Shorshani et al. 2014; Ghosh and Hellweger 2007; Krebs et al. 2014; Park et al. 2008; Sun et al. 2014a). Fallah Shorshani et al. (2014) provided one of the most complete analyses in which they investigated the effect of different configurations and model structures, including an increasing quantity of geographical information, on both water quantity and water quality predictions for a 2.3-km2 catchment in a suburb of Paris, France. Results for water quantity showed that the inclusion of basic geographical information, particularly land uses, improves the performance. They also stated that uncalibrated models with sufficient land use information can reach prediction performances comparable to those of calibrated models. On the other hand, inclusion of high-resolution data on improving model prediction performance is far more uncertain when considering calibrated models. This may be because the model calibration compensates for the lack of high spatial resolution for model setup. Ghosh and Hellweger (2007) found that the total outflow volume was relatively insensitive to spatial resolution in their study watershed, whereas peak flows were more sensitive, and the level depended on the size of the storm. Sun et al. (2014a) showed that both the model parameterization and model prediction were sensitive to spatial scale of the delineation for moderate-sized watersheds in New York. Krebs et al. (2014) showed that although the runoff volume was mostly unaffected by input spatial resolution, lower resolutions resulted in overestimation of peak flows as a result of excessively short times of concentration.
Generally, the conclusions about the effect of spatial resolution have been widely variable, from finding insignificant effects to significant dependence of model predictions on it. Model prediction clearly depends on spatial resolution in all cases; however, no definitive conclusion can be made on the optimal resolution required to achieve the most accurate prediction of runoff and water quality, as it depends highly on the accuracy and availability of the data used to build the model at finer resolution.
Combined Sewer System Overflows
Combined sewer systems are a form of urban drainage system that is common in medium and large-sized U.S. cities. They are also internationally prevalent. When excess runoff occurs in these systems, overflows commonly result, in which the contents of sanitary and storm sewers are mixed and released out of a common outlet, typically to a natural water body. Sixteen studies were found in the literature that focused exclusively on modeling combined sewer systems or improving methods to model these types of systems in SWMM. Fifty-five conference proceedings were found on this application (ASCE Library), but were not included in this review.
The most common trend in these studies was the focus on the designing and planning of sewer systems, either to avoid combined sewage overflows (CSOs) or to adapt current systems to reduce existing overflow problems. Kirshen et al. (2014) took a lowest-cost and risk-based net-benefits approach, considering adaptation strategies that included the following: underground storage, LID applied throughout the watershed, sewer separation, and a combination of sewer separation and LID. Koudelak and West (2008) developed a new master plan for the city of Liepaja, Latvia. The combined sewers were sized to provide protection against internal flooding of properties.
Some additional studies modeled LIDs and investigated their performance in reducing runoff in CSOs. Abi Aad et al. (2009) used the new LID features in SWMM 5 to model the effects of rain barrels and rain gardens. The overarching goal was to reduce CSOs by reducing peak flow, and to time the outflow using detention techniques. Muhaisen et al. (2009) studied detention basin design for a specific flood control target and performed storm modeling based on the extreme value theory (EVT) copula (Gudendorf and Segers 2010). The purpose of this study, which took place in Spain, was to avoid CSO expansion by designing detention basins with minimized cost.
Two studies looked in a more in-depth manner at water quality in combined sewers. In one study, Park et al. (2010) sought to characterize the discharge of storm runoff pollution (COD, TSS, total nitrogen, and total phosphorus) from urban catchments with combined sewers in Korea, and to estimate the probability of mass first flush (MFFn) by using SWMM and probability density functions. The authors found that the most reliable MFFn could be achieved when the representative rainfall characteristics including rainfall depth and duration are statistically representative. Another study looked at pathogen loadings from CSOs in a hypothetical river basin (Mahajan et al. 2014). The authors estimated these by superimposing a simulation of overflow discharges on raw sewage enteric pathogen concentration.
Consideration of the effects of climate change on CSOs and increasing CSOs was another trend in the literature. Abi Aad et al. (2009) included climate change as a concern in the introduction of their study. Kirshen et al. (2014) performed a vulnerability assessment and an evaluation of adaptation strategies for the effects of climate change on urban drainage flooding and CSOs. Fu et al. (2011) developed a general framework for sewer flood estimation that enables simultaneous consideration of two types of uncertainty: randomness from rainfall data represented using imprecise probabilities, and imprecision from model parameters represented by fuzzy numbers that were used as a simplified representation of probability.
Overall, SWMM, and particularly because of its combined mechanistic conveyance network modeling capability and algorithm for overland flow simulation, provides a powerful tool to evaluate the effects of various management practices on reducing the risk or frequency of CSO overflow into receiving waters.
LID Effectiveness
Because of the relatively recent addition of LID capabilities to SWMM, the number of papers reporting the LID application in urban stormwater modeling is small. Tillinghast et al. (2012) used these features to evaluate the effects of LID practices on stream geomorphic stability in Chapel Hill, North Carolina. They examined the effect of implementing nine different scenarios of wet ponds. Jia et al. (2014) used SWMM’s LID capability to predict the effectiveness of bioretention cells, permeable pavement, and infiltration ponds to reduce the risk of flooding in the city of Suzhou in eastern China. Chaosakul et al. (2013) applied SWMM to evaluate the effectiveness of LIDs including bioretention cells, vegetative swales, rain barrels, porous pavement, and infiltration trenches in Bangkok, Thailand. McCutcheon and Wride (2013) applied the SWMM bioretention component to runoff data collected during a single event from two rain gardens, one turf and one clay, and found a reasonable agreement between the simulated and measured results.
Most of the other studies currently published on LID effectiveness using SWMM have not used the LID features of the program; instead, they have used its conventional flow routing capabilities. In many applications, the effect of LIDs on runoff generation in a region is modeled using conventional rainfall-runoff capabilities of SWMM by adjusting the percentage of pervious surface or the depression storage (Muhaisen et al. 2009) and runoff coefficient (Alfredo et al. 2010). Others who have used the conventional capabilities of SWMM have represented green infrastructure as subcatchments receiving water from the adjacent impervious or pervious subcatchments (Jawdy et al. 2010). In a few studies, retention-based BMPs are modeled simply as storage units (Muhaisen et al. 2009). Some researchers have coupled SWMM with other models representing the LIDs. In one example of this, Jia et al. (2012) coupled SWMM with the best management practice decision support system (BMPDSS) system to evaluate the effectiveness of several scenarios of LID improvement in Beijing’s Olympic Village.
One study indicated the co-benefits of using a continuous simulation (CS) model, like SWWM, with a design storm (DS) model. Lucas (2010) applied SWWM and HydroCAD in the design of a bioretention planter/trench infiltration-detention system for a large-scale urban retrofit project. By incorporating bioretention systems, comprising 0.8% the drainage area and stone trench comprising another 3.4%, the volume of flows exceeding the CSO threshold were decreased by 90%. HydroCAD and SWMM were used to model the system separately, with near-identical results. A few key modifications were required in SWMM. The benefits of the CS model were in seeing the entire picture and refining the DS models, whereas the DS models’ flexibility allows for the exploration of alternative designs and stakeholder input. Lucas and Sample (2015) applied the SWMM LID component to evaluate the long-term performance of different types of LIDs, including free discharge and controlled outlet green and gray (primarily storage) infrastructure. They concluded that in terms of hydraulic performance, green LIDs with controlled outflow rate performed substantially better than gray stormwater control measures (SCMs).
Acknowledging the necessity for modifications to model LIDs appropriately in the SWMM 5.0, Zhang et al. (2010) proposed and tested two SWMM representation schemes for bioretention and porous pavement. Schemes like these would allow for more uniform applications.
Optimization
Single and multiobjective optimization techniques (outside of those used for calibration discussed previously) have been used with SWMM by several researchers to meet the optimal design criteria for the stormwater conveyance system or LID design and placement. Tobio et al. (2014) optimized design rainfall (the depth of precipitation expected to be captured). They found that the runoff volume reduction of a system is directly proportional to the storage volume to surface area (SV/SA) ratio. However, the optimal design rainfall was also dependent on the amount of rainfall during a storm event. For the TSS load reduction of the system, no significant relationship with the rainfall was found, but the TSS reduction was found to be directly proportional to the SV/SA ratio. Li et al. (2015) investigated the optimal design of detention tanks, under the constraints of local flooding control criteria, with the aim of developing an efficient and robust method for the design of tank networks. A modified particle swarm optimizer was adopted to find nondominated solutions to minimize both the engineering cost and flooding risks.
Karamouz and Nazif (2013) proposed an optimization model for selecting BMPs to improve system performance and reliability in dealing with urban flash floods in a case study in Tehran (110 km2). They further enhanced the method to perform multi-objective optimization nondominated sorting genetic algorithm-II (NSGA-II) to investigate multiple factors including flooding damage risk and cost of BMP implementation (Karamouz and Nazif 2013; Oraei Zare et al. 2012). System for Urban Stormwater Treatment and Analysis Integration (SUSTAIN) is a framework to evaluate optimal location, type, and cost of stormwater best management practices. SUSTAIN consists of a land simulation module, a conveyance module, and a BMP module. It is also equipped with a cost analysis and an optimization module for finding the optimal types and placement of BMPs. It is built on an ArcGIS platform that provides spatial analysis needed for watershed delineation and the BMP sitting tool. The land simulation module and conveyance module are based on the SWMM engine, whereas the sediment transport is based on the HSPF sediment algorithm. The BMP module is custom-based and considers the following processes to reduce land runoff volume and attenuate peak flows: evaporation of standing surface water, infiltration of ponded water into the soil media, deep percolation of infiltrated water into groundwater, and outflow through weir or orifice control structures (Lee et al. 2012). The BMP sitting tool is equipped with an NSGA-II multi-objective algorithm to find the best placement of BMPs to meet water quantity and quality objectives.
The automatic optimization studies usually rely on a highly hypothetical representation of the constraints on placement of stormwater management and treatment devices. In reality, there are practical, including regulatory, constraints that substantially limit the choices of locations and types of facilities, and these are not easily implemented into the automatic optimization algorithms. When the number of plausible choices is limited because of these practical constraints, sometimes performing a simple scenario analysis is more effective than computationally costly optimization.
Comparison of SWMM with Other Models
The studies in the literature comparing SWMM with other models can be divided into three major groups: (1) SWMM compared with data-driven models, (2) SWMM used to evaluate the accuracy of the proposed analytical formulations or numerical process-based methods for stormwater quantity and quality, and (3) SWMM compared with available hydrological and hydraulic models. The last category is the most relevant to the scope of the study and is reviewed chronologically as follows.
Pandit and Gopalakrishnan (1997) compared the average annual total nitrogen stormwater loads in multiple sites in Tampa, Florida, as predicted by multiple models. They found close model predictions for the continuous simulation method (CSM) and SWMM Level I (developed in 1976). Bhaduri et al. (2001) applied long-term hydrologic impact analysis (L-THIA) and SWMM to two watersheds in Chicago (89 and 38 ha) and found that L-THIA predicts the annual average runoff as being between 1.1 and 23.7% higher than SWMM’s predictions. The model’s results were better for larger watersheds. Calabrò and Maglionico (2002) compared runoff and water quality (Villarreal et al. 2002) (TSS) predictions between SWMM and two other models—urban pollution simulator (UPSIM) and conceptual simplified model for sewer system simulation (COSMOSS). The tests were performed for two catchments in Italy, Parco d. Orleans (9.6 ha) and Fossolo (40.71 ha), and one catchment in Yugoslavia, Milijakovac (211 m2). All of the models’ results were found to be sufficiently accurate and reliable; however, the models were sensitive to the parameters used to simulate the buildup and wash-off processes. Valeo and Ho (2004) applied multiple methods/models, including the urban snow model (USM) and SWMM to predict the snow melt flow from a small residential community (25.48 ha) located in Calgary, Canada. They found that the USM performed better than SWMM as measured by time to peak, peak flow rate, and model efficiency. The SWMM model fared poorly and was unable to simulate peak flow rates in most cases, although it predicted the time to peak moderately well.
Xiong et al. (2005) compared the nonlinear reservoir routing for overland flow in SWMM, and the kinematic wave routing method as applied in the dynamic watershed simulation model (DWSM) using data collected from a laboratory experiment conducted using smoothed aluminum rectangles with the overall size of 12.2×12.2 m. They found that DWSM generally provides more accurate results. The results of SWMM were acceptable only for storms with durations longer than the watershed’s time of concentration. Tsihrintzis et al. (2007) calibrated the Illinois Urban Drainage Area Simulator ILLUDAS (ILUDRAIN) and the Penn State runoff quality model (PSRM-QUAL) to predict flow from multiple urban sites in south Florida (5.97–23.57 ha). They compared the modeling results with three other tested methods/models: the runoff CN method combined with the Santa Barbara urban hydrograph method (SCS-SBUH), SWMM, and the U.S. Geological Survey (USGS) distributed routing rainfall-runoff model (DR3M). The predictions from all models showed agreement with the observed data, but better predictions were obtained for cases with more impervious areas. Overall, it was found that ILUDRAIN matched the runoff depth and peak flow more closely than the other models, the SCS-SBUH method resulted in better predictions for the time to peak, and the time base of the hydrograph was estimated more accurately by SWMM and PSRMQUAL.
Guo and Urbonas (2009) compared SWMM 5 and CUHP runoff predictions for a 74-ha watershed in Denver and found that both models predict the peak flows well. Lee et al. (2010) evaluated the applicability of the SWMM and hydrologic simulation program-FORTRAN (HSPF) models to simulate the flow and water quality [BOD5, TP, total nitrogen (TN)] at the Nogok stream watershed (51 km2) in South Korea. They found that both models adequately simulated the field data. Cantone and Schmidt (2001) used the Illinois urban hydrologic model (IUHM) to model the runoff from the Calumet Drop Shaft 52 (CDS-51) catchment (316 ha), located in the village of Dolton, Illinois. They found that IUHM is capable of predicting runoff with a similar accuracy as the more tedious InfoSWMM model. Zhang and Shuster (2014) assessed the performance of SWMM and the gridded surface-subsurface hydrologic analysis (GSSHA) in simulating two catchments in Ohio (0.65 and 0.47 ha). They found that with simple calibration, GSSHA outperformed SWMM; however, SWMM achieved better results using a priori parameter values obtained based on the literature. This can be indicative of the more complex and therefore flexible model being able to reproduce the data by adjusting the parameters, and not reflective of GSSHA better representing the underlying processes.
Although watershed hydrology models such as SWAT (Pisinaras et al. 2010), HSPF (Ackerman et al. 2005), and HEC-HMS (Emerson et al. 2005) have been used for modeling urban stormwater systems, they clearly lack features specifically needed for urban environments, such as the ability to model flow in a complex sewer network that can operate under partially free-surface and partially pressurized flow, and can experience backwater conditions, or subwatersheds, consisting of pervious and impervious areas with specific configuration of connection to the sewer network. They also lack the ability to implement LIDs that are specifically used in urban areas such as green roofs, bioretention systems, and infiltration trenches among others with the level of detail needed for such areas.
Interfacing SWMM with Other Models
SWMM has been interfaced or coupled with other models. In these cases, its output has been exported to other models for integrated modeling. The coupled models include GIS, SWAT, and other models designed for specific applications such as river water quality, groundwater, air quality, LID, and urban planning.
Barco et al. (2008) used SWMM version 4.3 with GIS to manage and process input and output data. Dongquan et al. (2009) proposed an automatic GIS approach for the catchment discretization in SWMM and successfully tested it to model runoff in Macau, China (13.65 ha). They showed that their proposed approach results in more meaningful parameters compared with manual catchment discretization. Jat et al. (2009) coupled SWMM and GIS externally to compute the change in surface runoff characteristics, for groundwater analysis to simulate the change in groundwater level and quality.
Kim et al. (2011) integrated SWAT and SWMM to assess the effects of urbanization on the White Rock Creek watershed (169 km2) in Texas. SWMM simulated runoff from urban areas, while the runoff from the other land uses was modeled by SWAT. Shrestha and Buchberger (2012) developed the open modeling interface (OpenMI) to simulate sediment dynamics at the River Zenne in Belgium (basin area of 1,162 km2). The OpenMI integrated SWAT to model water and sediment fluxes from rural areas of watershed, and SWMM to model the hydraulics of the river, canal, and sewer systems from urban areas of watershed, in addition to new codes for sediment transport and stream water temperature that were developed to complement SWMM.
Chen et al. (2002) assessed the effect of stormwater overflow on DO levels in an urban river system, using the Lover River in Taiwan (154 km2) as a case study. They used a Web-based platform that integrated calibrated the SWMM and Lover River hydrodynamic and water quality (LRHWQ) models. They fed the rainfall data to SWMM and the storm runoff and BOD loading to LRHWQ to dynamically predict the DO levels.
Blumensaat (2012) coupled the hydrogeological OpenGeoSys model with SWMM and tested this river-aquifer model in the Poltva River catchment (1,500 km21,500 km2) in the Ukraine. The SWMM solved the 1D dynamic wave equations in the river compartment, and OpenGeoSys solved a 2D groundwater flow equation in the aquifer compartment. Shon et al. (2012) combined SWMM and the Tank model (Sugawara 1969) to simulate flow at the Big Ning River basin in China (3,720 km23,720 km2). They modeled surface hydrological processes through SWMM, and interflow and groundwater hydrological processes using the Tank model. The combined model prediction for three storm events resulted in flood peak predictions with relative errors ranging between 20 and 30%.
Burian et al. (2001) coupled the California Institute of Technology (CIT) airshed model for wet and dry deposition and SWMM to simulate the fate and transport of nitrogen species through the atmosphere and storm drainage system of the Ballona Creek watershed (300 km2300 km2) in Los Angeles, California.
Jia et al. (2012) coupled the SWMM and BMPDSS models and applied this framework to simulate and optimize LID-BMP scenarios for Beijing’s Olympic Village (36 ha) in China. They used SWMM to generate time series data of surface runoff from different types of land use, and to simulate pipe network hydraulics for the case study. The runoff series data were then used as inputs to BMPDSS to analyze BMPs’ placement and optimization.
Sansalone et al. (2013) used the SWMM and USGS VS2D models to simulate the behavior of green infrastructures—cementitious permeable pavement and biofiltration area reactors in controlling the flow and pollution from impervious surfaces. VS2D was used to model the flow and transport in the substrate mediums (represented as 2D systems) that are not able to use SWMM’s LID component. Their study, conducted in Gainesville, Florida, used SWMM to compute the recharge periods and inflow fluxes to the green infrastructures. They found that only a fraction of the LID media is used during storms. The reduction in the effectiveness of LIDs as a result of short-circuiting has been reported by others (DeBusk and Wynn 2011; Jones and Davis 2013; Trowsdale and Simcock 2011).
SWMM’s Performance
A formal model evaluation process is deemed to be critical to the integrity of a SWMM modeling project. The conducted search of the peer-reviewed literature returned 93 publications that have presented model evaluation formally. These findings are summarized in Tables 1 and 2. With the information provided in these tables, a user now has a reference to compare the relative performance of his or her unique application.
Over half of the SWMM model evaluation statistics reported in the literature were completed on small watersheds with areas <5 km2 (51 papers out of 93). The SWMM output for midsized watersheds (5–40 km2) was evaluated in 18 of the papers reviewed, whereas 12 papers reported evaluation statistics for basins larger than 40 km2. These numbers are likely biased toward smaller catchments, as this review focuses solely on peer-reviewed publications; including all practical applications of SWMM may result in a different outcome. Runoff prediction was the endpoint for model evaluation in most of the reviewed papers (67 papers out of 93). Only 26 of the papers formally evaluated water quality endpoints. When water quality was the focus, those specific studies also evaluated runoff (22 papers). Among the water quality indicators, TSS and BOD were modeled more often in 22 and 11 studies, respectively. Other water quality indicators evaluated included (with number of studies in parenthesis) total phosphorus (8), chemical oxygen demand (5), total Kejldahl nitrogen (4), total nitrogen (4), Zn (4), Cu (3), Pb (3), total solids (3), oxidation reduction potential (ORP) (2), and other indicators of SC, Cd, Fe, Organic-N, Nitrate-N, Ammonia-N, OP, and 17β-estradiol with just 1 literature reference.
Sensitivity Analysis
Sensitivity analysis is a model evaluation technique used to identify the parameters or inputs to which the model results are most sensitive. The results of sensitivity analysis can be particularly useful in assessing the effects of the uncertainties associated with each parameter. Sensitivity analysis is also performed to find the most effective parameters for consideration during model calibration.
Because the outputs of SWMM are often in the form of time series rather than single scalar quantities (e.g., hydrographs or pollutographs), aggregate quantities are usually extracted from the outputs before the sensitivity analysis. These aggregate quantities are usually discharge, peak discharge, peak discharge time, total volume, total depth, and time base for runoff simulations; for water quality modeling, they include pollution load and concentration, peak concentration, and peak concentration time. In a sensitivity analysis, each parameter is perturbed (changed) from a default value, and the change (typically in percent) in model aggregate outputs is quantified. In a few studies, these aggregates are also quantified in terms of a sensitivity coefficient (Boon et al. 2008; Chow et al. 2012; Lei and Schilling 1994). Although the sensitivity analysis is typically performed manually by changing one variable at a time, automatic sensitivity analysis is available in some commercial versions of SWMM (van der Sterren et al. 2014; James et al. 2002).
Although relative sensitivities of SWMM input parameters are highly project-specific, commonly reported sensitive parameters fell within three categories: conduit, land surface, and water quality parameters. For conduits, the parameters that describe the conduit geometry and orientation are usually assumed to be known and fixed. However, in a few studies, the conduit length and width were found to be sensitive (Ghosh and Hellweger 2012; Peterson and Wicks 2006; Wu et al. 2008; Zaghloul 1998), in addition to conduit slope (Ghosh and Hellweger 2012). More frequently, the Manning’s roughness coefficient for conduits has been reported sensitive in the literature (Burszta-Adamiak and Mrowiec 2013; Ghosh and Hellweger 2012; Gülbaz and Kazezyılmaz-Alhan 2013; Krebs et al. 2014; Lee et al. 2010; Peterson and Wicks 2006; Sun et al. 2014a; Tsihrintzis and Hamid 1997, 1998; Zaghloul 1983).
SWMM model predictions are typically found to be sensitive to parameters that are related to characteristics of impervious surfaces such as impervious percentage (Barco et al. 2008; Cermola et al. 1979; Chow et al. 2012; Jia et al. 2014; Kim et al. 2011; Mancipe et al. 2011; Song et al. 1983; Zaghloul 1983), impervious depression storage (Barco et al. 2008; Boon et al. 2008; Calabrò and Maglionico 2002; Chen and Adams 2006; Obropta and Kardos 2007; Sun et al. 2014a; Tsihrintzis and Hamid 1998; Xiong et al. 2005; Zaghloul and Al-Shurbaji 1991; Zhao et al. 2008), and Manning’s roughness coefficient for impervious surfaces (Chen and Adams 2006; Chow et al. 2012; Gülbaz and Kazezyılmaz-Alhan 2013; Jia et al. 2014; Krebs et al. 2014; Mancipe et al. 2011; Schoenfelder et al. 2006; Sun et al. 2014a; Xiong et al. 2005; Zhao et al. 2008; Zhao and McEnroe 2000). Moreover, a number of studies found output to be sensitive to overland flow width (Boon et al. 2008; Cermola et al. 1979; Chow et al. 2012; Jia et al. 2014; Mancipe et al. 2011; Marsalek 1983; Sun et al. 2014a; Zaghloul and Al-Shurbaji 1991; Zhao et al. 2008) and average slope (Boon et al. 2008; Calabrò and Maglionico 2002; Chen and Adams 2006; Krebs et al. 2014; Mancipe et al. 2014; Wu et al. 2008). Width and slope along with Manning’s roughness coefficient for impervious surfaces are the inputs to the Manning’s equation for computing overland flow rate and velocity. Guo and Urbonas (2009) explicitly derived a method to determine the most representative catchment width and slope as a function of watershed lateral and longitudinal slopes, relative location of the drainage channel, and width of overland flow.
Pervious surfaces of a watershed can also contribute to stormwater runoff and pollution when most of a watershed’s surface consists of pervious surfaces during large storms. Of the 34 studies that presented a sensitivity analysis of SWMM, 13 identified the pervious surface characteristics (i.e., Manning coefficient or depression storage) or infiltration parameters to be sensitive to SWMM predictions. Mancipe-Munoz et al. (2014) identified infiltration parameters as being sensitive if the impervious surface covers less than 20% of a watershed. Valeo and Ho (2004) found snowmelt from pervious surfaces to be sensitive. Chung et al. (2011) modeled a 56-km2 watershed in South Korea during the monsoon season. They identified Manning’s roughness coefficient and the depression storage of both pervious and impervious areas, and the saturated hydraulic conductivity of the soil among the sensitive parameters. Gülbaz and Kazezyılmaz-Alhan (2013) modeled a 165-km2 watershed in Turkey, finding that hydraulic conductivity and the initial soil moisture were sensitive. Sun et al. (2014a) found that runoff predictions were insensitive to lawn parameters of depression storage and Manning’s coefficient. However, and although the total runoff volume was insensitive to tree area, the peak runoff predictions were slightly sensitive to depression storage and Manning’s coefficient of tree area. Krebs et al. (2014) found that predicted peak runoff flow was sensitive to infiltration parameters only for a catchment (19% imperviousness area) with the lowest urbanization of the three modeled. Borris et al. (2014) concluded that pervious areas can have an influence on stormwater runoff and TSS load.
SWMM water quality predictions are sensitive to the choice of buildup and wash-off functions and their parameters as shown by Baffaut and Delleur (1990), Calabrò and Maglionico (2002), Chung et al. (2011), Ouyang et al. (2012), Temprano et al. (2006), Tsihrintzis and Hamid (1998), and Van der Sterren et al. (2014). Although the exponential wash-off model was found to be the only model for sensitivity analysis of water quality (eight studies), various functions have been used for sensitivity analysis of the buildup parameters including exponential (six studies), whereas the linear, saturation, and power function were sensitive in a single study each.
Calibration and ValidationCalibration
Traditionally, SWMM calibration has been performed manually by changing one parameter at a time and comparing the SWMM predictions with observations. This trial-and-error method has been used extensively by researchers (Blumensaat et al. 2012; Chung et al. 2011; Gülbaz and Kazezyılmaz-Alhan 2013; Temprano et al. 2006; Scholz and Kazemi Yazdi 2009; Zaghloul and Abu Kiefa 2001; Calabrò 2002; Park et al. 2008; Walsh et al. 2014; Warwick and Tadepalli 1991; Wu et al. 2013). Out of the papers reviewed reporting calibration statistics (84 studies), 44 did it manually. As a common practice, sensitive parameters are initially assigned a value within the range reported in the SWMM manual or in the literature, and are then ae subject to perturbation (or tweaking). This approach is time-consuming, especially when a larger number of parameters are considered. Furthermore, there is no guarantee that the optimal parameter values will result. Automatic calibration algorithms exist to overcome this limitation and are essentially optimization or search algorithms. Optimization algorithms are based on gradient-based methods (e.g., steepest descent, conjugate gradient), combinatorial methods (e.g., the simplex method), heuristic approaches, or evolutionary algorithms (e.g., genetic algorithms, shuffled complex evolution algorithms). Gradient-based methods typically need a smaller number of model runs to find the optimal values of the parameters; however, they are prone to getting trapped in local minima if the initial guess is not appropriately chosen (Abrishamchi et al. 2010; Mancipe-Munoz et al. 2014). Heuristic approaches are better able to identify the global minima, but require a large number of model runs (Duan et al. 1994; Shie-Yui Liong 1993).
Commercial versions of SWMM (KBSWMM, used in three studies; PCSWMM, used in six studies; and XPSWMM, used in one study) provide automatic model calibration capabilities, based on one or more of the aforementioned optimization algorithms. Furthermore, there have been multiple algorithms/methods coupled with SWMM, but not as an embedded feature. These include shuffled complex evolution algorithms used in three studies, Box’s complex method used in three studies, generalized likelihood uncertainty estimation (GLUE) used in three studies, PEST parameter estimation code used in two studies, genetic algorithms used in eight studies, expert systems used in two studies, and genetic multiobjective optimization algorithm (NSGA-II) used in two studies. Other optimization algorithms used include the Metropolis Monte Carlo algorithm, Powell method, and Rosenbrock’s method. Because different studies have used different measures to determine the goodness of fit, it is not possible at this time to draw a conclusion about whether automatic calibration techniques result in better model performance compared with manual calibration methods. Regardless, calibration tools allow a user to perform the calibration task more effectively while trying more combinations of parameter values in less time, potentially resulting in better calibration.
Although 10 of the studies reported in Tables 1 and 2 evaluated the calibration process qualitatively by visualizing hydrograph characteristics, such as arrival time, magnitude of peak flow rate, and the overall shape of the hydrograph, the rest used measures of goodness of fit to quantify the results of the calibration process. A summary of the goodness of fit measures reported in Tables 1 and 2 (including both calibration and validation measures) is presented in Table 3. Some studies have used more than one goodness of fit measure. Description, ranges, advantages, and deficiencies of various goodness of fit measures are discussed elsewhere (Krause et al. 2005; Legates and McCabe Jr. 1999). The results presented in Table 3 indicate that relative error is the most common statistical measure of goodness of fit and has been used 83 times in the literature. The next most popular statistic is the Nash-Sutcliff efficiency NSE (38 times). For evaluating the runoff processes, runoff discharge is the most popular calibration endpoint, used 54 times. Other popular runoff-based calibrants include peak discharge (45 times), total runoff volume (32 times), depth (19 times), peak discharge time (10 times), and time base (5 times). For water quality modeling, the contaminant load is the most popular calibration endpoint (20 times), followed by contaminant concentration (18 times), peak concentration (7 times), and time-to-peak concentration (1 time).
Table 3.
Description of Abbreviated Calibration and Validation Parameters Used in Tables 1 and 2 with Their Literature Counts in Parentheses
| Parametera | Runoff | Contaminants | Total counts (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Discharge (Q) | Peak discharge (P) | Peak discharge time (PT) | Volume (V) | Depth (D) | Time base (T) | Load (L) | Concentration (C) | Peak concentration (PC) | Peak concentration time (PCT) | ||
| Relative error (RE) | REQ (8) | REP (26) | REPT (7) | REV (21) | RED (4) | RET (2) | REL (7) | REC (3) | REPC (2) | REPCT (1) | 81 (38.8%) |
| Absolute relative error (ARE) | — | AREP (2) | — | AREV (1) | ARED (1) | — | AREL (1) | AREC (1) | AREPC (1) | — | 7 (3.3%) |
| Nash-Sutcliff efficiency (NSE) | NSEQ (21) | NSEP (3) | — | NSEV (4) | NSED (2) | — | NSEL (4) | NSEC (3) | NSEPC (1) | — | 38 (18.2%) |
| (Linear) correlation coefficient (CC) | CCQ (4) | CCP (5) | CCPT (2) | CCV (1) | CCD (5) | CCT (2) | CCL (2) | CCC (2) | CCPC (1) | — | 24 (11.5%) |
| Coefficient of determination (R2) | R2Q (9) | R2P (4) | R2PT (1) | R2V (4) | R2D (3) | R2T (1) | R2L (4) | R2C (3) | R2PC (1) | — | 30 (14.4%) |
| Root mean square error (RMSE) | RMSEQ (9) | RMSEP (3) | — | RMSEV (1) | RMSED (2) | — | RMSEL (1) | RMSEC (1) | — | — | 17 (8.1%) |
| Other parametersb | — (4) | — (1) | — | — | — (1) | — | — (1) | — (4) | — (1) | — | 12 (5.7%) |
| Total counts (%) | 55 (26.3%) | 44 (21.1%) | 10 (4.8%) | 32 (15.3%) | 18 (8.6%) | 5 (2.4%) | 20 (9.6%) | 17 (8.1%) | 7 (3.3%) | 1 (0.5%) | 209 (100%) |
The following two parameters were excluded from the analysis: multiobjective function (MOF) and combinatory objective function (COF).
Other parameters include root mean absolute error of discharge (RMAEQ) and concentration RMAEC, normalized objective function of peak discharge (NOFP), depth NOFD, load NOFL, concentration NOFC and peak concentration NOFPC, relative error of minimum discharge (REMinQ), root mean square of overflow duration (RMSEDQ), relative error of minimum concentration (REMinC), concentration appearance time (CAT), and standard deviation of RMSEQ.
Validation
Validation pertains to verifying the accuracy of a model for a time period separate from that used for calibration. SWMM validation was performed in numerous studies (59 studies in Tables 1 and 2). Model performance for the validation period is usually quantified using the same measures of goodness of fit that was used for calibration process. A comparison among studies in Tables 1 and 2, in which both calibration and validation performance were reported using similar measures, shows that SWMM validation performance is more often weaker than calibration performance, indicating a lower confidence for the extrapolation capacity of the model. This highlights the need to perform the validation, to ensure that it is not substantially inferior to the model performance for the calibration period.
In an attempt to summarize the bulk of the information provided on goodness of SWMM model fits listed in Tables 1 and 2, a box and whisker distributional diagram was prepared from the most commonly reported statistics (Fig. 3). To be conservative, when values were reported as a range, the lower end of the range was taken. NSE, coefficient of determination (R2), and relative error (RE) goodness of fits (GOFs) for runoff discharge and peak discharge were combined (QP), as were those for concentration load and peak concentration (CLP). A box and whisker plot for the former provides a general view of how the model performs relative to hydrology, and the latter generalizes model performance with respect to water quality (Fig. 3). NSEs and R2s above 0.6 (in which a maximum of 1 means the best fit) are typical and slightly higher for calibration than validation periods for flow variables. For the water quality variables reported, model fits using NSE and R2 are slightly lower than flow, but still mostly above 0.5. The central tendencies among the REs reported for both calibration and validation periods for QP fall between ±10%, as does the calibration period results for CLP variables. However, the validation period results found for CLP variables suggest a strong negative bias for SWMM simulations, but this is based only on seven values found in the literature and is not consistent with respect to water quality constituents. Taken together, the values reported in Tables 1 and 2 and generalized in Fig. 3 suggest that SWMM can be effectively calibrated to simulate flows and water quality that closely match reality over a wide range of urban catchment sizes.
Fig. 3.
Summary of NSE, R2, and RE GOF statistics obtained from the literature review (all data taken from Tables 1 and 2). QP, gray boxes; CLP, white boxes; lowercase “c” and solid boxes, GOF statistics reported for the calibration period; lowercase “v” and hashed boxes, values reported for a validation period; numbers above the median line of each box in the diagram are the sample size
The time period over which the model is calibrated is potentially an important consideration for model performance. Continuous simulation lasting from just one day (e.g., Peterson and Wicks 2006) up to a year or more (e.g., Ashbolt et al. 2013; Zhang and Shuster 2014), and event-based simulations from just one storm event (e.g. Alfredo et al. 2010; Fioretti et al. 2010; Wu et al. 2008) up to tens of storm events (Muhaisen et al. 2009; Wang and Altunkaynak 2012; Zaghloul and Abu Kiefa 2001; Tsihrintzis and Hamid 1998; Tsihrintzis and Sidan 2008) have all been used in the literature. The event-based calibration approach is more popular in the literature (61 studies) as compared with continuous calibration (20 studies). However, no comprehensive study exists that compares the continuous and event-based simulations over different climatic and hydrological conditions. However, the event-based approach was found by Boon et al. (2008) to provide more accurate results in terms of overall hydrograph shape, time to peak, and peak flow rate, whereas the continuous approach performed better in the runoff volume estimation. This study suggested that continuous calibration should still be implemented when runoff volume is the main concern.
Continuous-event calibrations are susceptible to potential inaccuracies in the rain-intensity input data, particularly when the rain gauge location is not close to the catchment centroid. These inaccuracies are mostly in the form of deviations from the actual temporal patterns, so that when event total runoff volumes are used for calibration the inaccuracies are averaged out and better agreements between modeled and observed runoff can be obtained.
Uncertainty Analysis
Uncertainty analysis refers to evaluating the effects of estimation errors associated with the values used for model setup, variance in the external forcing data, and model structural (or epistemic) uncertainty as a result of simplification of real-world phenomena. These uncertainties can propagate to the model output (Sun et al. 2014a). When the models are calibrated using observed data, there are additional uncertainties associated with the measurement errors (Gaume et al. 1998). It becomes desirable and necessary to integrate these uncertainties into the modeling processes to quantify the overall confidence in model predictions (Sun et al. 2014a). The uncertainty assessments performed on the SWMM model can be classified into two general approaches, here referred to as “forward uncertainty assessment” and “inverse uncertainty analysis.” The goal of forward uncertainty assessment is to evaluate model output uncertainty as a result of parameter and external forcing uncertainties (Gaume et al. 1998; Lei and Schilling 1994; Mailhot et al. 1997; Wu et al. 2013). Typically, a prior range or a prior distribution is assumed for the model parameters, and a Monte Carlo (MC) simulation is performed to find the ranges of possible model predictions. Forward model uncertainty analysis involves identification and quantification of the sources of uncertainty, and the propagation of the uncertainty through the model.
In contrast, the goal of inverse uncertainty analysis is to use observed data to find the ranges or the probability distributions of model input parameters that represent the plausible parameter values, resulting in model predictions close to the observed data. The parameter uncertainty can be expressed as joint probability distributions, plausible regions, or 95% confidence intervals. The methods used for inverse uncertainty analysis can be classified into MC-based approaches, such as Markov chain Monte Carlo (MCMC) methods based on Bayesian inference, generalized likelihood uncertainty estimation (GLUE) (Beven and Binley 1992), and methods based on local sensitivity. The methods based on local sensitivity are more efficient in the sense that they require a significantly smaller number of model runs compared with MC based methods; however, they are based on the assumption of a linear response surface between the parameters and the model outputs, and the results can be inaccurate when the relationship is nonlinear. Both MC-based approaches and local sensitivity-based approaches have been used to perform uncertainty analysis in SWMM (Sun et al. 2014b; Zhao et al. 2008).
Lei and Schilling (1994) proposed a strategy to reduce the computational cost of forward uncertainty propagation analysis using first-order analysis, sensitivity analysis, statistical linearization, and MC analysis. As an example, parameter uncertainty propagation analysis in the runoff block of the HYSTEM-EXTRAN model (a modification of SWMM) was performed for the Halden subcatchment in Zurich, Switzerland. They found that the type of probability density function had little effect on the results of the error propagation analysis, given a fixed mean and standard deviation of the input parameters. Wu et al. (2013) studied uncertainty of model prediction stemming from parameters including subcatchment width, Manning’s roughness coefficient for pervious surfaces, and natural channels, by changing one of these parameters at a time while holding all others constant. Their uncertainty analyses showed that these parameters have little effect on model prediction as measured by aggregate statistics.
Among the papers that have described inverse uncertainty assessment, Sun et al. (2014a) used GLUE with a high-resolution SWMM developed for a highly urbanized sewershed in Syracuse, New York (58.8 ha). The results showed that the sampling importance resampling (SIR) method (Rubin 1988) was a more effective alternative than the conventional threshold sampling method. They also examined the effect of catchment discretization resolution, showing that the posterior parameter sets calibrated based on a more refined watershed delineation (i.e., microdelineation) resulted in a lower uncertainty of flow predictions for the entire hydrograph, compared with the cases in which rougher subwatershed delineation (i.e., macrodelineation) was used.
Zhao et al. (2008) integrated SWMM with the Latin hypercube sampling technique (Hossain et al. 2006) based on a combined objective aiming to reduce the uncertainty of model outputs to obtain more accurate predictions. They applied their model to the Yalianfang catchment in Macau, China (13.65 ha), and found that the combined objective method could reduce the uncertainties of both the model parameters and the predictions. Mailhot et al. (1997) used the Metropolis Monte Carlo algorithm to investigate the effects of the amount of observed data and data uncertainty on the uncertainty associated with the estimated parameters. They did this using the water quality component of SWMM and data collected from Quebec City’s sewer system. Their analysis showed that even when a large amount of data is available, the uncertainties in predictions of the suspended solid concentration can remain significant. Gaume et al. (1998) focused on the estimation and interpretation of the parameter uncertainties, finding that the local sensitivity-based methods, based on the second-order approximation of the shape of the objective function in the vicinity of the optimum parameter set, provide an inaccurate estimate of the uncertainty, and suggested using global approaches. In general, however, forward and reverse uncertainty analysis has been rarely performed in the different applications of SWMM.
Gap Analysis
The need for high computational speed when modeling hydrological and contaminant transport in complex sewersheds consisting of interconnected subcatchments, conveyance systems, and LIDs makes it inevitable that the processes be represented in a simplified way. This is a strength of SWMM that has led to its widespread application to address a multitude of design, policy decision making, and planning problems in urban systems. In most hydrologic applications, the simplified representation has proven justifiable not only because of the necessity to keep the computational burden manageable, but also to make parameterization and calibration doable and reduce the risk of misuse. However, this strength can also be considered a limitation pending the modeling goal. Options for users to represent urban drainage features with a higher degree of process-level detail are called for, but for model refinement to be justified it needs to be supported by field data and adequate scientific understanding.
Five areas that—based on authors’ experience in the field and given the results returned by the peer-reviewed literature—suggest that gaps in the current model structure are limiting SWMM’s utility as a comprehensive stormwater management decision support model are identified. These include (1) lack of embedded algorithm and/or user guidance for parameter estimation, sensitivity analysis, automated calibration, and uncertainty assessment; (2) inadequate provision and criteria for specifying the surface spatial heterogeneity in the overland flow simulation; (3) no mechanistic multicomponent reactive fate and transport processes for contaminants (particularly nutrients) during buildup and wash-off simulation, in transport as overland flow or in the conveyance system, and inside LIDs and storage structures; (4) limited options for direct simulation of urban land management operations; and (5) the need for more explicit handling of interflow and groundwater flow pathways for water quality loading. Clearly, these aspects do not represent vital features needed for common catchment-scale hydrologic applications, but rather would provide options for users to evaluate smaller-scale processes in more detail and would allow SWMM to be used more specifically for risk-based water quality management in urban environments.
Parameter Estimation, Model Sensitivity and Calibration, and Uncertainty Assessment
Better handling of model parameter estimation facilitates proper use of the model and could occur along two lines. One includes updated user guidance for choosing appropriate parameter values during model setup, including characteristic ranges and nonsensical values. For instance, the addition of an internal urban soils database with selection criteria would offer more refined estimates of infiltration parameters. This is important because urban soils do not behave like natural soils; therefore, inferring infiltration-based parameter values from Natural Resources Conservation Service (NRCS) soil distribution maps, for example, is inaccurate. Second, inverse modeling procedures can be used to estimate parameter values when detailed observational/monitoring data is available to support such a goal. Statistical tools that allow users to approach this aspect quantitatively should be explored and considered for inclusion in the SWMM package.
Provided computationally efficient optimization algorithms for characterizing model structural uncertainty, model sensitivity analysis, and calibration can be conducted in a more automated manner. Commercially available SWMM packages (e.g., PCSWMM) already offer such a framework. However, little methodological guidance is available for the use of such a framework, and there is little support to SWMM model users for evaluating the results. Furthermore, it has been suggested by a few studies (e.g., Baffaut and Delleur 1990; Blackler and Guo 2014; di Pierro et al. 2006; Qin et al. 2013; Warwick et al. 1991) that calibration processes might be sensitive to the selection of event(s) for event-based simulation; thus, different model performance might be observed for low and high-intensity events that are used for calibration. In addition, calibration is subjective to the form of the objective function, which should formally be defined based on a presumed error structure for observation. A systematic study on how different objective functions for model calibration results in which features of hydrographs or pollutographs (e.g., total volumes, peak volumes, base flows, total loads) are reproduced better or worse would be useful in guiding users in selecting appropriate objective functions for different applications.
Finally, formal model uncertainty analysis is critical for probabilistic risk management. Uncertainty analysis not only allows the user to characterize the generated output in terms of a confidence range, but it also allows for estimation of relative risk, such as risk of flooding, or violating a water quality standard. Quantifying the uncertainty of the calibrated model after LID or BMP scenarios have been simulated is critical to weighting the significance of such management scenarios, and therefore to decisions about management alternatives. However, the review returned only a few articles that had demonstrated such a quantitative uncertainty estimation approach to the decisions related to model output or management scenario analysis. Forward or reverse uncertainty analysis has rarely been performed (section “Uncertainty Analysis”). The reason stems from the fact that SWMM lacks a built-in functionality to perform uncertainty assessment. Coupling SWMM with external uncertainty analysis programs to perform this task requires special skills foreign to most practitioners. Because of the popularity of SWMM in the urban drainage design community, adding a built-in feature to perform forward and inverse uncertainty analysis would help move the whole community in the direction of making uncertainty analysis a standard practice for stormwater management modeling.
Hydrologic Simulation Improvements
Overland flow for urban surfaces encounters heterogeneity in perviousness, slopes, and in the particular formations of preferential flow paths that are designed to quickly transfer runoff to the conveyance system. Although the same hydraulic phenomena happen in nonurban watersheds, it is more pronounced in urban environments because of the presence of curbs, gutters, roofs, sidewalks, catch-basins, and parking lots. This level of heterogeneity has implications related to both water quantity and quality.
The current version of SWMM represents the overland flow formation on subcatchments using a single reservoir, with the outflow rate assumed to be a function of average storage per area and assuming a single roughness. This simplification, particularly when a coarse subcatchment delineation is considered, can result in high bias in the peak flow simulation and in the flow rates during transition periods at the beginning and the end of storm events (Xiong et al. 2005). In addition to the heterogeneities of surface roughness and connectivity, the heterogeneity in infiltration plays a very important role in controlling the ultimate surface runoff. In urban catchment, the infiltration is usually far from something that can be represented using a uniform Green-Ampt equation, but rather is more appropriately governed by a matrix of Green-Ampt models with a spectrum of saturated hydraulic conductivities. Yu (1998) showed that the SCS method can be theoretically derived by considering a distribution of saturated hydraulic conductivities. When observed flow rates are used for calibration, the effect of lumping the parameters can be compensated (to some degree) by adjusting the parameter values such as Manning’s roughness coefficient and depression storage. However, further field and modeling studies are needed to evaluate how well the single reservoir approach reproduces observed hydrographs on small catchments. It is also beneficial to find parsimonious alternatives to the single reservoir representation that can capture the urban surface heterogeneity. Because of the large number of alternatives for representing the urban mosaic in SWMM and the potential effect the spatial discretization approach can have on the model results, better guidance to help modelers best match simulation objectives with the spatial resolution of model setup would be useful.
Although adding a 2D surface runoff modeling feature to SWMM would represent a complex undertaking, additional studies that compare the performance of SWMM to an existing 2D model run in parallel would also prove useful to understanding the conditional reliability of the existing SWMM modeling approach. These model comparison studies could be accompanied by tracer study protocols that would inform the real travel time distributions over a catchment and help in model refinement (Harman and Kim 2014). Studying how to best approach overland flow simulation could also help to improve SWMM for more realistic evaluation of the effects of potential flooding or flash floods that require incorporation of the effect of structures.
Model prediction clearly depends on spatial resolution in all cases. However, no definitive conclusion can be made on the optimal resolution required to achieve the most accurate prediction of runoff and water quality, as it depends highly on the accuracy and availability of the data used to build the model at finer resolution.
Water Quality Improvements
The capability of SWMM in predicting pollutographs is substantially inferior to hydrographs (Tables 1 and 2). It is known that the buildup and wash-off algorithms used in the model are gross simplifications of the real heterogeneous physiochemical processes at play. Contaminant buildup rates are highly dependent on site locations and land management practices (i.e., turf grass fertilization rates). Similarly, the nature and rates of wash-off are expected to depend on the characteristics of the surfaces where pollutants accumulate. As opposed to water quantity, for which the main external forcing data (i.e., precipitation) are widely available with a relatively good accuracy, the forcing data for water quality are mostly lacking. This makes the predictive use of the model uncertain in the absence of monitoring data. Generally, a critical gap is that biogeochemically driven nutrient fate and transport processes of any kind are not available for simulation. Multicomponent reactive transport as affected by the aerobic/anoxic conditions of mediums encountered in the built stormwater conveyance system, stream channels, and LIDs is a requirement for watershed-scale nutrient TMDL development and implementation.
First Flush and Sediment Transport
Although the buildup and wash-off modules in SWMM are flexible enough to represent a wide range of pollutants, several studies show that first-flush phenomena is specific to the physiochemical properties of the pollutant; some pollutants may have an affinity for binding to sediments, whereas others are solubilized quickly (e.g., Kim et al. 2011; Massoudieh et al. 2008). At this time, there are no provisions in the model to represent loosely versus tightly bound pollutant fractions. This is important because understanding the first-flush phenomena may be critical to effectively sizing BMPs or LIDs (Massoudieh et al. 2011; Razmkhah et al. 2010; Stenstrom and Kayhanian 2005). First-flush behavior also relates to basin size, surface characteristics, rain intensity, and temporal rain dynamics. The relative importance among these parameters needs further study. Adding a multirate modeling feature to SWMM would allow users to consider first flush by distributing the built-up pollutants into classes (or bins) with different levels of mobilization potential. Although adding this feature to the current version of SWMM is relatively easy in terms of implementation, research is needed to parameterize such a component. Once pollutants are released to the overland flow, there is no provision to allow for sedimentation or resuspension. Such an addition would be a useful feature, particularly in the context of modeling the effect of conveyance system clogging as a result of sedimentation and sediment-contaminant interactions affecting water quality.
Soluble and Particle Bound Pollutants, Aqueous-Solid Mass Exchange
In SWMM, pollutants are represented as single entities. In reality, some pollutants of importance in urban environments, such as heavy metals, some organics, and to some degree phosphorus species, have various degrees of affinity to solid colloidal (or fine particles) and can undergo solid-aqueous phase mass transfer as a result of physical, chemical, or biological processes (Pitt and Clark 2008). For example, Pb or Zn bound to particulate matter can be immobilized as a result of sedimentation in the sewer system, filtration, or settling in BMPs, but then they can gradually be released back into the runoff as a result of solid-aqueous phase mass exchange. An external link of SWMM to other numerical codes is required to accurately model the solids (Shrestha et al. 2013). However, better understanding of the interactions between pollutants and suspended solids in urban setting requires further study. To make SWMM capable of considering such processes, contaminants should be allowed to be present at different phases (particulate and aqueous), and the mass transfer between the phases should be incorporated into the model.
Transformation
First-order decay of pollutants can be modeled in SWMM. However, in the case of some pollutants undergoing microbial-mediated transformations, such as nitrogen species and organic matter, the fate is affected by the presence and concentration of other constituents such as dissolved organic carbon (DOC) and oxygen (in the case of nitrogen). Denitrification occurs primarily under anoxic condition, and the rate of mineralization of organic matter depends on the redox conditions. In streams and sewer networks, anoxic conditions can prevail in the sediment layer and lead to some level of denitrification. In such cases, flow rate can be a controlling factor in the size of anoxic zones forming. There is no provision in SWMM to consider these interactions. Allowing the user to define reaction rates as a function of a few constituents would be a useful add-in feature that will allow more realistic modeling of the fate of contaminants undergoing microbial-mediated transformations.
Urban Land Management and LID Representation
SWMM provides an option for users to schedule street sweeping activity, which reduces the buildup of contaminants on impervious surface. There are several other types of rather routine urban land management operations that would be useful to be simulated, especially when it comes to water quality considerations related to nutrients. Examples include lawn fertilizer application rates, pesticide spray programs, and grass cutting or leaf mulching. These are potentially important sources of pollutants or excess organic loads in many low and medium-density urban environments that currently can only be implicitly accounted for through input of a known pollutant runoff time series, assigning contaminant loads to specific subcatchments manually, or through event mean concentration estimation.
With interest continuing to grow in the application of LID/GI as a cost-effective and aesthetic alternative to gray infrastructure for managing stormwater, there is a great need for research that formally evaluates SWMM’s ability to accurately simulate these management alternatives. Currently, the way LID performance is modeled in SWMM is relatively simple: Each LID is represented as a few fully mixed layers. The effect of the additional hydraulic head as a result of the surface ponding is not considered, and the maximum Darcy flux that can be achieved is equal to the saturated hydraulic conductivity. This simple representation is suitable for the most widely used application of the model, which is to analyze hydrological fluxes at a catchment scale. However, the user cannot simulate important processes internal to LIDs, such as the sedimentation of solids and the pollutants bound to them. Processes such as clogging of the substrate in LIDs can result in the decline of the unit performance, as is prevalent in porous pavement, sand filters, infiltration trenches, and other bioretention systems. In addition, when the fate and transport of pollutants with high affinity to the solid phase is modeled, it is important to consider processes like adsorption and desorption to the substrate or soil media in the LIDs. Sorption can cause significant retardation of pollutant transport in LID media; however, the pollutant front still moves in the media, which can lead to a decline in the pollutant reduction capability of some LIDs over time.
The typical scale of SWMM applications probably does not warrant modeling these process-level details, especially considering that many LID types are meant to be distributed spatially at multiple locations throughout a catchment. Having such utility when a more detailed analysis is needed of a certain LID option over a smaller area would be invaluable to improving the performance and adoption rate of such practices. Therefore, including the level of detail needed to consider many of the processes affecting fate, transport, and remobilization of contaminants in LIDs—such as the effect of redox conditions, colloid, or particle-assisted transport and settling—and remobilization dynamics would probably best be implemented in a stand-alone model, whose results could be used as input to an existing SWMM application.
Groundwater
Placing emphasis on GI/LID simulation as a major utility of SWMM in the future dictates that the subsurface modeling component be re-evaluated and likely upgraded, especially with respect to water quality simulation. Although SWMM can account for important groundwater hydrologic effects, such as delayed runoff as a result of base flow entering the conveyance system or open channels, this water—pending its source and path taken to the discharge point—could be laden with pollutants. For example, infiltrating rainfall on pervious areas like lawns and flower beds can solubilize soil nutrients and pesticides that are subsequently carried to receiving streams in delayed fashion. The ability to explicitly model important chemical transformation and physical processes in the shallow groundwater (or vadose zone) may be necessary for SWMM to simulate in-stream water quality effects, if a significant portion of pollutants flux through this compartment. In addition, because of the reservoir-based representation of subsurface, SWMM is unable to model regional groundwater flow, as it requires considering coupled interaction between adjacent reservoirs representing the groundwater underneath each subcatchment. The base-flow can play an important role in determining the temporal pattern of the falling limb of hydrographs; therefore, adding the ability to model groundwater in a more rigorous way to SWMM can be beneficial in some applications. Adding the ability of the subsurface components underneath subcatchments to interact with each other through a Darcy-type relationship would allow better representation of the base flow and processes like the groundwater mounding underneath infiltration-based LIDs.
Conclusions
The search of peer-reviewed scientific literature and evaluation of the over 150 articles returned that the use of the SWMM model to help solve water management issues in urban environments highlights the relevance of the model to drainage design and planning. The analysis focused on reporting model performance data for both hydrologic and water quality endpoints. From the articles reviewed, the relevant information on sensitive parameters, calibration methods, and calibration/validation statistics were extracted. From this collection (Tables 1 and 2), SWMM was found to be applied to a wide range of problems related to urban stormwater, which can be attributed to it being a flexible and parsimonious simulation tool for urban hydrology and water quality that is adequate for most of its intended applications. It fosters end-user ease of use that has made it one of the most widely used models for urban water management in the world. It performs better simulations of hydrologic endpoints compared with water quality constituents, but the latter could definitely be improved upon by relatively simple embedded component additions or with a model run in parallel. Opportunities for automated calibration and uncertainty analysis are quickly becoming a reality for SWMM, and these will enhance its use as a tool for managing risks in urban environments that are undergoing rapid alterations in response to both climate change and a growing urban populace. Although much work has focused on modeling methods that support automated optimization of management alternatives to help support urban planning studies, this should not be of critical importance because of practical limitations that are unique to each urban watershed model construct. The focus for SWMM improvement over the next few years should be placed on developing and validating methods that integrate LID/GI alternatives in terms of hydrologic continuity and water quality management.
Acknowledgments
The authors acknowledge the helpful comments, corrections, and feedback from Lewis Rossman (formerly USEPA and principal scientist for EPA-SWMM 5 operation and maintenance), Michelle Simon (USEPA), Srinivas Panguluri (CB&I Federal Services), and Christopher Impellitteri (USEPA). The U.S. Environmental Protection Agency, through its Office of Research and Development, funded and managed the research described in this paper. It has been subjected to the Agency’s peer and administrative review and has been approved for external publication. Any opinions or ideas expressed in this paper are those of the author(s) and do not necessarily reflect the official positions and policies of the USEPA. Any mention of trade names or commercial products does not constitute endorsement or recommendation for use.
Contributor Information
Mehran Niazi, Food and Drug Administration, 10903 New Hampshire Ave., Silver Spring, MD 20993; formerly, National Risk Management Research Laboratory, Water Supply and Water Resources Division, U.S. EPA, 26 W. MLK Dr., Cincinnati, OH 45268.
Chris Nietch, National Risk Management Research Laboratory, Water Supply and Water Resources Division, U.S. EPA, 26 W. MLK Dr., Cincinnati, OH 45268.
Mahdi Maghrebi, Dept. of Civil Engineering, Catholic Univ. of America, Washington, DC 20064.
Nicole Jackson, National Risk Management Research Laboratory, Water Supply and Water Resources Division, U.S. EPA, 26 W. MLK Dr., Cincinnati, OH 45268.
Brittany R. Bennett, Dept. of Civil Engineering, Catholic Univ. of America, Washington, DC 20064.
Michael Tryby, National Risk Management Research Laboratory, Water Supply and Water Resources Division, U.S. EPA, 26 W. MLK Dr., Cincinnati, OH 45268.
Arash Massoudieh, Dept. of Civil Engineering, Catholic Univ. of America, Washington, DC 20064.
References
- Abi Aad M, Suidan M, and Shuster W (2009). “Modeling techniques of best management practices: Rain barrels and rain gardens using EPA SWMM-5.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000136, 434–443. [DOI] [Google Scholar]
- Abrishamchi A, Massoudieh A, and Kayhanian M (2010). “Probabilistic modeling of detention basins for highway stormwater runoff pollutant removal efficiency.” Urban Water J, 7(6), 357–366. [Google Scholar]
- Ackerman D, Schiff KC, and Weisberg SB (2005). “Evaluating HSPF in an arid, urbanized watershed.” J. Am. Water Resour. Assoc, 41(2), 477–486. [Google Scholar]
- Akan AO, and Houghtalen RJ (2003). Urban hydrology, hydraulics, and stormwater quality: Engineering applications and computer modeling, Wiley, Hoboken, NJ. [Google Scholar]
- Alfredo K, Montalto F, and Goldstein A (2010). “Observed and modeled performances of prototype green roof test plots subjected to simulated low- and high-intensity precipitations in a laboratory experiment.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000135, 444–457. [DOI] [Google Scholar]
- Anderson EA (2006). “Snow accumulation and ablation model–SNOW-17.” 1–61. [Google Scholar]
- Ashbolt S, et al. (2013). “Can stormwater harvesting restore pre-development flows in urban catchments in South East Queensland?” Water Sci. Technol, 67(2), 446–451. [DOI] [PubMed] [Google Scholar]
- Baffaut C, and Delleur J (1989). “Expert system for calibrating SWMM.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)0733-9496(1989)115:3(278), 278–298. [DOI] [Google Scholar]
- Baffaut C, and Delleur JW (1990). “Calibration of SWMM runoff quality model with expert system.” J. Water Resour. Plann. Manage, 116(2), 247–261. [Google Scholar]
- Balascio CC, Palmeri DJ, and Gao H (1998). “Use of a genetic algorithm and multi-objective programming for calibration of a hydrologic model.” Trans. ASAE, 41(3), 615–619. [Google Scholar]
- Banks JC, Camp JV, and Abkowitz MD (2014). “Adaptation planning for floods: A review of available tools.” Nat. Hazards, 70(2), 1327–1337. [Google Scholar]
- Barco J, Wong KM, and Stenstrom MK (2008). “Automatic calibration of the US EPA SWMM model for a large urban catchment.” J. Hydraul. Eng, 10.1061/(ASCE)0733-9429(2008)134:4(466), 466–474. [DOI] [Google Scholar]
- Beven K, and Binley A (1992). “The future of distributed models: Model calibration and uncertainty prediction.” Hydrol. Process, 6(3), 279–298. [Google Scholar]
- Bhaduri B, Minner M, Tatalovich S, and Harbor J (2001). “Long-term hydrologic impact of urbanization: A tale of two models.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)0733-9496(2001)127:1(13), 13–19. [DOI] [Google Scholar]
- Blackler GE, and Guo JCY (2014). “Field test of paved area reduction factors using a storm water management model and water quality test site.” J. Irrig. Drain Eng, 10.1061/(ASCE)IR.1943-4774.0000680. [DOI] [Google Scholar]
- Blumensaat F, Wolfram M, and Krebs P (2012). “Sewer model development under minimum data requirements.” Environ. Earth Sci, 65(5), 1427–1437. [Google Scholar]
- Boon S, et al. (2008). “Performances of rainfall-runoff models calibrated over single and continuous storm flow events.” J. Hydrol. Eng, 13(7), 597–607. [Google Scholar]
- Borah D, Weist J, Wall J, and Powell D (2009). “Watershed models for storm water management: Comparing hydrologic and hydraulic procedures” World Environmental and Water Resources Congress 2009: Great Rivers, ASCE, Reston, VA, 1–10. [Google Scholar]
- Borah DK, and Bera M (2004). “Watershed-scale hydrologic and nonpoint-source pollution models: Review of applications.” Trans. ASAE, 47(3), 789–803. [Google Scholar]
- Borris M, Viklander M, Gustafsson A-M, and Marsalek J (2014). “Modelling the effects of changes in rainfall event characteristics on TSS loads in urban runoff.” Hydrol. Process, 28(4), 1787–1796. [Google Scholar]
- Burian SJ, Nix SJ, Durrans SR, and Pitt RE (2002). “Analysis of the long-term performance of storage/release systems using linked watershed-water body modeling.” Proc., 9th Int. Conf. on Urban Drainage—Global Solutions for Urban Drainage, ASCE, Reston, VA. [Google Scholar]
- Burian SJ, Streit GE, McPherson TN, Brown MJ, and Turin H (2001). “Modeling the atmospheric deposition and stormwater washoff of nitrogen compounds.” Environ. Modell. Software, 16(5) 467–479. [Google Scholar]
- Burszta-Adamiak E, and Mrowiec M (2013). “Modelling of green roofs’ hydrologic performance using EPA’s SWMM.” Water Sci. Technol, 68(1), 36–42. [DOI] [PubMed] [Google Scholar]
- Calabrò P, and Maglionico M (2002). “Comparison between a detailed model and two simplified models in urban stormwater quality simulation.” Proc., 9th Int. Conf. on Urban Drainage (9ICUD), ASCE, Reston, VA, 1–14. [Google Scholar]
- Camorani G, Castellarin A, and Brath A (2005). “Effects of land-use changes on the hydrologic response of reclamation systems.” Phys. Chem. Earth, Parts A/B/C, 30(8–10), 561–574. [Google Scholar]
- Cantone J, and Schmidt A (2001). “Potential dangers of simplifying combined sewer hydrologic/hydraulic models.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000023, 596–605. [DOI] [Google Scholar]
- Cermola JA, El-Baroudi HM, Sachdev DR, and DeCarli S (1979). “SWMM application to combined sewerage in new haven.” J. Environ. Eng. Div., 150(6), 1035–1048. [Google Scholar]
- Chang C-H, Wen C-G, and Lee C-S (2008). “Use of intercepted runoff depth for stormwater runoff management in industrial parks in Taiwan.” Water Resour. Manage, 22(11), 1609–1623. [Google Scholar]
- Chaosakul T, Koottatep T, and Irvine K (2013). “Application of low impact development (LID) scenarios to assess localized flood reduction: A case study of Rattanakosin Village, Thailand.” Pragmatic modeling of urban water systems, monograph 21, James W, et al. , eds., Computational Hydraulics International, Guelph, ON, Canada. [Google Scholar]
- Chen AS, Hsu M-H, Huang C-J, and Lien W-Y (2011). “Analysis of the Sanchung inundation during Typhoon Aere, 2004.” Nat. Hazards, 56(1), 59–79. [Google Scholar]
- Chen C, and Herr J (2010). “Simulating the effect of sulfate addition on methylmercury output from a wetland.” J. Environ. Eng, 10.1061/(ASCE)EE.1943-7870.0000176, 354–362. [DOI] [Google Scholar]
- Chen C, Herr J, Ziemelis L, Goldstein R, and Olmsted L (1999). “Decision support system for total maximum daily load.” J. Environ. Eng, 10.1061/(ASCE)0733-9372(1999)125:7(653), 653–659. [DOI] [Google Scholar]
- Chen CL, Scanlin J, Chang NB, and Feng A (2002). “Simulating the fate of diazinon in castro valley watershed by SWMM.” Proc., 9th Int. Conf. on Urban Drainage—Global Solutions for Urban Drainage, ASCE, Reston, VA. [Google Scholar]
- Chen J, and Adams B (2006). “Analytical urban storm water quality models based on pollutant buildup and washoff processes.” J. Environ. Eng, 10.1061/(ASCE)0733-9372(2006)132:10(1314), 1314–1330. [DOI] [Google Scholar]
- Chen Z, and Goldscheider N (2014). “Modeling spatially and temporally varied hydraulic behavior of a folded karst system with dominant conduit drainage at catchment scale, Hochifen-Gottesacker, Alps.” J. Hydrol, 514, 41–52. [Google Scholar]
- Chiang YM, Chang LC, Tsai MJ, Wang YF, and Chang FJ (2010). “Dynamic neural networks for real-time water level predictions of sewerage systems-covering gauged and ungauged sites.” Hydrol. Earth Syst. Sci, 14(7), 1309–1319. [Google Scholar]
- Chin D (2011). “Quantifying pathogen sources in streams by hydrograph separation.” J. Environ. Eng, 10.1061/(ASCE)EE.1943-7870.0000394, 770–781. [DOI] [Google Scholar]
- Cho JH, and Seo HJ (2007). “Parameter optimization of SWMM for runoff quantity and quality calculation in a eutrophic lake watershed using a genetic algorithm.” Water Sci. Technol, 7(5), 35–41. [Google Scholar]
- Choi KS, and Ball JE (2002). “Investigation of model complexity and structure on the calibration process.” Proc., 9th Int. Conf. on Urban Drainage—Global Solutions for Urban Drainage, ASCE, Reston, VA, 1–9. [Google Scholar]
- Choi SC, Jung DI, Won CH, and Rim JM (2006). “Calculation of intercepted volume of sewer overflows: A model for control of nonpoint pollution sources in urban areas.” J. Ocean Univ. China, 5(4), 317–321. [Google Scholar]
- Chow MF, Yusop Z, and Toriman ME (2012). “Modelling runoff quantity and quality in tropical urban catchments using storm water management model.” Int. J. Environ. Sci. Technol, 9(4), 737–748. [Google Scholar]
- Chung E-S, Hong W-P, Lee KS, and Burian SJ (2011). “Integrated use of a continuous simulation model and multi-attribute decision-making for ranking urban watershed management alternatives.” Water Resour. Manage, 25(2), 641–659. [Google Scholar]
- Cronshey R (1986). “Urban hydrology for small watersheds.” U.S. Dept. of Agriculture, Soil Conservation Service, Engineering Division, Washington, DC. [Google Scholar]
- Dasgupta S, Gosain AK, Rao S, Roy S, and Sarraf M (2013). “A megacity in a changing climate: The case of Kolkata.” Clim. Change, 116(3–4), 747–766. [Google Scholar]
- DeBusk K, and Wynn T (2011). “Storm-water bioretention for runoff quality and quantity mitigation.” J. Environ. Eng, 10.1061/(ASCE)EE.1943-7870.0000388, 800–808. [DOI] [Google Scholar]
- Denault C, Millar RG, and Lence BJ (2006). “Assessment of possible impacts of climate change in an urban catchment.” J. Am. Water Res. Assoc, 42(3), 685–697. [Google Scholar]
- Dietz ME (2007). “Low impact development practices: A review of current research and recommendations for future directions.” Water Air Soil Pollut, 186(1–4), 351–363. [Google Scholar]
- di Pierro F, Khu ST, and Savić D (2006). “From single-objective to multiple-objective multiple-rainfall events automatic calibration of urban storm water runoff models using genetic algorithms.” Water Sci. Technol, 54(6–7), 57. [DOI] [PubMed] [Google Scholar]
- Doglioni A, Primativo F, Laucelli D, Monno V, Khu ST, and Giustolisi O (2009). “An integrated modelling approach for the assessment of land use change effects on wastewater infrastructures.” Environ. Modell. Software, 24(12), 1522–1528. [Google Scholar]
- Dongquan Z, Jining C, Haozheng W, Qingyuan T, Shangbing C, and Zheng S (2009). “GIS-based urban rainfall-runoff modeling using an automatic catchment-discretization approach: A case study in Macau.” Environ. Earth Sci, 59(2), 465–472. [Google Scholar]
- Duan Q, Sorooshian S, and Gupta VK (1994). “Optimal use of the SCE-UA global optimization method for calibrating watershed models.” J. Hydrol, 158(3–4), 265–284. [Google Scholar]
- Elliott A, and Trowsdale S (2007). “A review of models for low impact urban stormwater drainage.” Environ. Modell. Software, 22(3), 394–405. [Google Scholar]
- Emerson CH, Welty C, and Traver RG (2005). “Watershed-scale evaluation of a system of storm water detention basins.” J. Hydrol. Eng, 10.1061/(ASCE)1084-0699(2005)10:3(237), 237–242. [DOI] [Google Scholar]
- Fallah Shorshani M, Bonhomme C, Petrucci G, Andre M, and Seigneur C (2014). “Road traffic impact on urban water quality: A step towards integrated traffic, air and stormwater modelling.” Environ. Sci. Pollut. Res. Int, 21(8), 5297–5310. [DOI] [PubMed] [Google Scholar]
- Fang T, and Ball JE (2007). “Evaluation of spatially variable control parameters in a complex catchment modelling system: A genetic algorithm application.” 9(3), 163–173. [Google Scholar]
- Ferreri GB, Freni G, and Tomaselli P (2010). “Ability of Preissmann slot scheme to simulate smooth pressurisation transient in sewers.” Water Sci. Technol, 62(8), 1848–1858. [DOI] [PubMed] [Google Scholar]
- Fioretti R, Palla A, Lanza LG, and Principi P (2010). “Green roof energy and water related performance in the Mediterranean climate.” Build. Environ, 45(8), 1890–1904. [Google Scholar]
- Ford D, McFadden D, and Hilmes-Robinson M (2002). “Early warning.” Civ. Eng, 72(8), 62–67. [Google Scholar]
- Fu G, Butler D, Khu ST, and Sun SA (2011). “Imprecise probabilistic evaluation of sewer flooding in urban drainage systems using random set theory.” Water Resour. Res, 47(2), W02534. [Google Scholar]
- Gaume E, Villeneuve J-P, and Desbordes M (1998). “Uncertainty assessment and analysis of the calibrated parameter values of an urban storm water quality model.” J. Hydrol, 210(1–4), 38–50. [Google Scholar]
- Gersonius B, Ashley R, Pathirana A, and Zevenbergen C (2013). “Climate change uncertainty: Building flexibility into water and flood risk infrastructure.” Clim. Change, 116(2), 411–423. [Google Scholar]
- Ghosh I, and Hellweger F (2007). “Effects of spatial resolution in urban hydrologic simulations.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000405, 129–137. [DOI] [Google Scholar]
- Ghosh I, and Hellweger FL (2012). “Effects of spatial resolution in urban hydrologic simulations.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000405, 129–137. [DOI] [Google Scholar]
- Green WH, and Ampt G (1911). “Studies on soil physics. 1: The flow of air and water through soils.” J. Agric. Sci, 4(1), 1–24. [Google Scholar]
- Grimm NB, et al. (2008). “Global change and the ecology of cities.” Science, 319(5864), 756–760. [DOI] [PubMed] [Google Scholar]
- Gudendorf G, and Segers J (2010). “Extreme-value copulas.” Copula theory and its applications, Jaworski P,Durante F, K.Härdle W, and Rychlik T, eds., Springer, Berlin, 127–145. [Google Scholar]
- Gülbaz S, and Kazezyılmaz-Alhan CM (2013). “Calibrated hydrodynamic model for sazlidere watershed in Istanbul and investigation of urbanization effects.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000600, 75–84. [DOI] [Google Scholar]
- Guo J, and Urbonas B (2009). “Conversion of natural watershed to kinematic wave cascading plane.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000045, 839–846. [DOI] [Google Scholar]
- Ha S, and Stenstrom M (2008). “Predictive modeling of storm-water runoff quantity and quality for a large urban watershed.” J. Environ. Eng, 10.1061/(ASCE)0733-9372(2008)134:9(703), 703–711. [DOI] [Google Scholar]
- Hargreaves GH, and Samani ZA (1985). “Reference crop evapotranspiration from temperature.” Appl. Eng. Agric, 1(2), 96–99. [Google Scholar]
- Harman CJ, and Kim M (2014). “An efficient tracer test for time-variable transit time distributions in periodic hydrodynamic systems.” Geophys. Res. Lett, 41(5), 1567–1575. [Google Scholar]
- Horton RE (1940). “The infiltration-theory of surface-runoff.” Eos, Trans. Am. Geophys. Union, 21(2), 541. [Google Scholar]
- Hossain F, Anagnostou EN, and Bagtzoglou AC (2006). “On Latin Hypercube sampling for efficient uncertainty estimation of satellite rainfall observations in flood prediction.” Comput. Geosci, 32(6), 776–792. [Google Scholar]
- Hsu M-H, Chen SH, and Chang T-J (2000). “Inundation simulation for urban drainage basin with storm sewer system.” J. Hydrol, 234(1), 21–37. [Google Scholar]
- Huber WC, Dickinson RE, Barnwell TO Jr., and Branch A (1988). Storm water management model; version 4, Environmental Protection Agency, Washington, DC. [Google Scholar]
- Huber WC, Heaney JP, Medina MA, Peltz WA, and Sheikh H (1975). Storm water management model: User’s manual, version II, Environmental Protection Agency, Washington, DC. [Google Scholar]
- Huong HTL, and Pathirana A (2013). “Urbanization and climate change impacts on future urban flooding in Can Tho city, Vietnam.” Hydrol. Earth Syst. Sci, 17(1), 379–394. [Google Scholar]
- James W, Robert C, Wan B, and James W (2002). “Implementation in PCSWMM using genetic algorithms for auto calibration and design-optimization.” Proc., 9th Int. Conf. on Urban Drainage—Global Solutions for Urban Drainage, ASCE, Reston, VA, 1–10. [Google Scholar]
- Jat MK, Khare D, Garg PK, and Shankar V (2009). “Remote sensing and GIS-based assessment of urbanisation and degradation of watershed health.” Urban Water J, 6(3), 251–263. [Google Scholar]
- Jawdy C, Reese A, and Parker J (2010). “The potential for green infrastructure practices to reduce combined sewer overflows as examined in Nashville, Tennessee.” Proc., World Environ. Water Resources Congress 2010: Challenges of Change, ASCE, Reston, VA, 3452–3461. [Google Scholar]
- Jia H, Lu Y, Yu SL, and Chen Y (2012). “Planning of LID-BMPs for urban runoff control: The case of Beijing Olympic Village.” Sep. Purif. Technol, 84, 112–119. [Google Scholar]
- Jia H, Ma H, Sun Z, Yu S, Ding Y, and Liang Y (2014). “A closed urban scenic river system using stormwater treated with LID-BMP technology in a revitalized historical district in China.” Ecol. Eng, 71, 448–457. [Google Scholar]
- Jones PS, and Davis AP (2013). “Spatial accumulation and strength of affiliation of heavy metals in bioretention media.” J. Environ. Eng, 10.1061/(ASCE)EE.1943-7870.0000624, 479–487. [DOI] [Google Scholar]
- Karamouz M, and Nazif S (2013). “Reliability-based flood management in urban watersheds considering climate change impacts.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)WR.1943-5452.0000345, 520–533. [DOI] [Google Scholar]
- Kazezyılmaz-Alhan CM, and Medina MA (2007). “Kinematic and diffusion waves: Analytical and numerical solutions to overland and channel flow.” J. Hydraul. Eng, 10.1061/(ASCE)0733-9429(2007)133:2(217), 217–228. [DOI] [Google Scholar]
- Kim NW, Won YS, Lee J, Lee JE, and Jeong J (2011). “Hydrological impacts of urban imperviousness in white rock creek watershed.” Trans. ASABE, 54(5), 1759–1771. [Google Scholar]
- Kirshen P, Caputo L, Vogel RM, Mathisen P, Rosner A, and Renaud T (2014). “Adapting urban infrastructure to climate change: A drainage case study.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)WR.1943-5452.0000443. [DOI] [Google Scholar]
- Koudelak P, and West S (2008). “Sewerage network modelling in Latvia, use of InfoWorks CS and Storm Water Management Model 5 in Liepaja city.” Water Environ. J, 22(2), 81–87. [Google Scholar]
- Kovács A, and Clement A (2009). “Impacts of the climate change on runoff and diffuse phosphorus load to Lake Balaton (Hungary).” Water Sci. Technol, 59(3), 417–423. [DOI] [PubMed] [Google Scholar]
- Krause P, Boyle D, and Bäse F (2005). “Comparison of different efficiency criteria for hydrological model assessment.” Adv. Geosci, 5, 89–97. [Google Scholar]
- Krebs G, Kokkonen T, Valtanen M, Koivusalo H, and Setälä H (2013). “A high resolution application of a stormwater management model (SWMM) using genetic parameter optimization.” Urban Water J, 10(6), 394–410. [Google Scholar]
- Krebs G, Kokkonen T, Valtanen M, Setala H, and Koivusalo H (2014). “Spatial resolution considerations for urban hydrological modelling.” J. Hydrol, 512, 482–497. [Google Scholar]
- Kuzin S, and Adams B (2008). “Probabilistic approach to estimation of urban storm-water total maximum daily loads: Unregulated catchment.” J. Irrig. Drain. Eng, 10.1061/(ASCE)0733-9437(2008)134:5(579), 579–588. [DOI] [Google Scholar]
- Lee A, Hewa G, Pezzaniti D, and Argue JR (2008). “Improving stream low flow regimes in urbanised catchments using water sensitive urban design techniques.” Aust. J. Water Resour, 12(2), 121–132. [Google Scholar]
- Lee J, Heaney J, and Pack C (2010). “Frequency methodology for evaluating urban and highway storm-water quality control infiltration BMPs.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)0733-9496(2010)136:2(237), 237–247. [DOI] [Google Scholar]
- Lee JG, et al. (2012). “A watershed-scale design optimization model for stormwater best management practices.” Environ. Modell. Software, 37, 6–18. [Google Scholar]
- Lee SB, Yoon CG, Jung KW, and Hwang HS (2010). “Comparative evaluation of runoff and water quality using HSPF and SWMM.” Water Sci. Technol, 62(6), 1401–1409. [DOI] [PubMed] [Google Scholar]
- Legates DR, and McCabe GJ Jr. (1999). “Evaluating the use of ‘goodness-of-fit’ measures in hydrologic and hydroclimatic model validation.” Water Resour. Res, 35(1), 233–241. [Google Scholar]
- Lei J, and Schilling W (1994). “Parameter uncertainty propagation analysis for urban rainfall runoff modelling.” Water Sci. Technol, 29(1–2), 145–154. [Google Scholar]
- Li F, Duan H-F, Yan H, and Tao T (2015). “Multi-objective optimal design of detention tanks in the urban stormwater drainage system: Framework development and case study.” Water Resour. Manage, 29(7), 2125–2137. [Google Scholar]
- Liong S, ShreeRam J, and Ibrahim Y (1995). “Catchment calibration using fractional-factorial and central-composite-designs-based response surface.” J. Hydraul. Eng, 10.1061/(ASCE)0733-9429(1995)121:6(507), 507–510. [DOI] [Google Scholar]
- Liong SY, Chan WT, and Law CL (1991a). “An expert system for storm water management modelling, and its application.” Eng. Appl. Artif. Intell, 4(5), 367–375. [Google Scholar]
- Liong SY, Chan WT, and Lum LH (1991b). “Knowledge-based system for SWMM runoff component calibration.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)0733-9496(1991)117:5(507), 507–524. [DOI] [Google Scholar]
- Liong SY, Van Nguyen VT, Gautam TR, and Wee L (2001). “Alternative well calibrated rainfall-runoff model: Genetic programming scheme” World Water and Environmental Resources Congress 2001 (CD-ROM), ASCE, Reston, VA, 777–787. [Google Scholar]
- Liong S-Y, Tat W, and Liang C (1993). “Computer-aided catchment-calibration model.” Adv. Eng. Software, 17(3), 147–154. [Google Scholar]
- Liu G, Schwartz FW, and Kim Y (2013). “Complex baseflow in urban streams: An example from central Ohio, USA.” Environ. Earth Sci, 70(7), 3005–3014. [Google Scholar]
- Lucas WC (2010). “Design of integrated bioinfiltration-detention urban retrofits with design storm and continuous simulation methods.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000137, 486–498. [DOI] [Google Scholar]
- Lucas WC, and Sample DJ (2015). “Reducing combined sewer overflows by using outlet controls for green stormwater infrastructure: Case study in Richmond, Virginia.” J. Hydrol, 520, 473–488. [Google Scholar]
- Madarang KJ, and Kang J-H (2014). “Evaluation of accuracy of linear regression models in predicting urban stormwater discharge characteristics.” J. Environ. Sci, 26(6), 1313–1320. [DOI] [PubMed] [Google Scholar]
- Mahajan R, Uber JG, and Eisenberg JNS (2014). “A dynamic model to quantify pathogen loadings from combined sewer overflows suitable for river basin scale exposure assessments.” Water Qual. Exposure Health, 5(4), 163–172. [Google Scholar]
- Mailhot A, Gaume E, and Villeneuve JP (1997). “Uncertainty analysis of calibrated parameter values of an urban storm water quality model using metropolic Monte Carlo algorithm.” Water Sci. Technol, 36(5), 141–148. [Google Scholar]
- Mancipe N, Buchberger S, and Makram S (2011). Calibration of distributed rainfall-runoff model in Hamilton County, Ohio, CHI Press, Toronto. [Google Scholar]
- Mancipe-Munoz NA, Buchberger SG, Suidan MT, and Lu T (2014). “Calibration of rainfall-runoff model in urban watersheds for stormwater management assessment.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)WR.1943-5452.0000382, 05014001. [DOI] [Google Scholar]
- Marsalek J (1983). “Discussion of ‘SWMM model and level of discretization’ by Nabil A. Zaghloul (November, 1981).” J. Hydraul. Eng, 10.1061/(ASCE)0733-9429(1983)109:12(1773), 1773–1776. [DOI] [Google Scholar]
- Marsalek J, and Chocat B (2002). “International report: Stormwater management.” Water Sci. Technol, 46(6–7), 1–17. [PubMed] [Google Scholar]
- Massoudieh A, Abrishamchi A, and Kayhanian M (2008). “Mathematical modeling of first flush in highway storm runoff using genetic algorithm.” Sci. Total Environ, 398(1–3), 107–121. [DOI] [PubMed] [Google Scholar]
- Massoudieh A, Sharifi S, and Kayhanian M (2011). “Predicting highway stormwater pollutographs using a hybrid evolutionary data driven modeling framework” World Environmental and Water Resources Congress 2011: Bearing Knowledge for Sustainability, ASCE, Reston, VA, 3669–3678. [Google Scholar]
- McCutcheon M, and Wride D (2013). “Shades of green: Using SWMM LID controls to simulate green infrastructure.” J. Water Manage. Model, R246–15, 289–301. [Google Scholar]
- McGarity A (2013). “Watershed systems analysis for urban storm-water management to achieve water quality goals.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)WR.1943-5452.0000280, 464–477. [DOI] [Google Scholar]
- McPherson T, Burian S, Stenstrom M, Turin H, Brown M, and Suffet I (2005). “Trace metal pollutant load in urban runoff from a Southern California watershed.” J. Environ. Eng, 10.1061/(ASCE)0733-9372(2005)131:7(1073), 1073–1080. [DOI] [Google Scholar]
- Mein RG, and Larson CL (1973). “Modeling infiltration during a steady rain.” Water Resour. Res, 9(2), 384–394. [Google Scholar]
- Metcalf and Eddy. (1971). “Storm water management model.” Univ. of Florida, Water Resources Engineers, U.S. EPA, U.S. Government Printing Office, Washington, DC. [Google Scholar]
- Morita M (2014). “Flood risk impact factor for comparatively evaluating the main causes that contribute to flood risk in urban drainage areas.” Water, 6(2), 253–270. [Google Scholar]
- Muhaisen OS, Osorio F, and García PA (2009). “Two-copula based simulation for detention basin design.” Civ. Eng. Environ. Syst, 26(4), 355–366. [Google Scholar]
- Muschalla D, Vallet B, Anctil F, Lessard P, Pelletier G, and Vanrolleghem PA (2014). “Ecohydraulic-driven real-time control of stormwater basins.” J. Hydrol, 511, 82–91. [Google Scholar]
- Nazif S, and Karamouz M (2011). “Simulation of streamflow to reservoirs using a data based mechanistic model: A case study” Proc., World Environmental and Water Resources Congress 2011, ASCE, Reston, VA, 1535–1542. [Google Scholar]
- Nestor A, Mancipe-Munoz SGB, Makram TS, and Ting L (2014). “Calibration of rainfall-runoff model in urban watersheds for stormwater management assessment.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)WR.1943-5452.0000382. [DOI] [Google Scholar]
- Obropta C, Kallin P, Mak M, and Ravit B (2008). “Modeling urban wetland hydrology for the restoration of a forested riparian wetland ecosystem.” Urban Habitats, 5(1). [Google Scholar]
- Obropta CC, and Kardos JS (2007). “Review of urban stormwater quality models: Deterministic, stochastic, and hybrid approaches1.” J. Am. Water Resour. Assoc, 43(6), 1508–1523. [Google Scholar]
- Olsson J, Berggren K, Olofsson M, and Viklander M (2009). “Applying climate model precipitation scenarios for urban hydrological assessment: A case study in Kalmar City, Sweden.” Atmosph. Res, 92(3), 364–375. [Google Scholar]
- Oraei Zare S, Saghafian B, and Shamsai A (2012). “Multi-objective optimization for combined quality-quantity urban runoff control.” Hydrol. Earth Syst. Sci, 16(12), 4531–4542. [Google Scholar]
- Ouyang W, Guo B, Hao F, Huang H, Li J, and Gong Y (2012). “Modeling urban storm rainfall runoff from diverse underlying surfaces and application for control design in Beijing.” J. Environ. Manage, 113, 467–473. [DOI] [PubMed] [Google Scholar]
- Pandit A, and Gopalakrishnan G (1997). “Estimation of annual pollutant loads under wet-weather conditions.” J. Hydrol. Eng, 10.1061/(ASCE)1084-0699(1997)2:4(211), 211–218. [DOI] [Google Scholar]
- Paolo S, and Calabrò MM (2002). “Comparison between a detailed model and two simplified models in urban stormwater quality simulation.” Proc., 9th Int. Conf. on Urban Drainage—Global Solutions for Urban Drainage, ASCE, Reston, VA, 1–14. [Google Scholar]
- Park I, Kim H, Chae S-K, and Ha S (2010). “Probability mass first flush evaluation for combined sewer discharges.” J. Environ. Sci, 22(6), 915–922. [DOI] [PubMed] [Google Scholar]
- Park SY, Lee KW, Park IH, and Ha SR (2008). “Effect of the aggregation level of surface runoff fields and sewer network for a SWMM simulation.” Desalination, 226(1–3), 328–337. [Google Scholar]
- Pataki DE, et al. (2011). “Coupling biogeochemical cycles in urban environments: Ecosystem services, green solutions, and misconceptions.” Front. Ecol. Environ, 9(1), 27–36. [Google Scholar]
- Patel CC, Grossi P, and Kunreuther H (2005). Catastrophe modeling: A new approach to managing risk, Vol. 25, Springer, New York. [Google Scholar]
- Petersen T, Rifai H, Suarez M, and Stein A (2005). “Bacteria loads from point and nonpoint sources in an urban watershed.” J. Environ. Eng, 10.1061/(ASCE)0733-9372(2005)131:10(1414), 1414–1425. [DOI] [Google Scholar]
- Peterson EW, and Wicks CM (2006). “Assessing the importance of conduit geometry and physical parameters in karst systems using the storm water management model (SWMM).” J. Hydrol, 329(1–2), 294–305. [Google Scholar]
- Petrucci G, and Bonhomme C (2014). “The dilemma of spatial representation for urban hydrology semi-distributed modelling: Trade-offs among complexity, calibration and geographical data.” J. Hydrol, 517, 997–1007. [Google Scholar]
- Petrucci G, Rioust E, Deroubaix J-F, and Tassin B (2013). “Do stormwater source control policies deliver the right hydrologic outcomes?” J. Hydrol, 485, 188–200. [Google Scholar]
- Piro P, Carbone M, Garofalo G, and Sansalone JJ (2010). “Management of combined sewer overflows based on observations from the urbanized Liguori catchment of Cosenza, Italy.” Water Sci. Technol, 61(1), 135–143. [DOI] [PubMed] [Google Scholar]
- Pisinaras V, Petalas C, Gikas GD, Gemitzi A, and Tsihrintzis VA (2010). “Hydrological and water quality modeling in a medium-sized basin using the soil and water assessment tool (SWAT).” Desalination, 250(1), 274–286. [Google Scholar]
- Pitt R, and Clark S (2008). “Integrated storm-water management for watershed sustainability.” J. Irrig. Drain. Eng, 10.1061/(ASCE)0733-9437(2008)134:5(548), 548–555. [DOI] [Google Scholar]
- Qin HP, Li ZX, and Fu G (2013). “The effects of low impact development on urban flooding under different rainfall characteristics.” J. Environ. Manage, 129, 577–585. [DOI] [PubMed] [Google Scholar]
- Ranger N, et al. (2011). “An assessment of the potential impact of climate change on flood risk in Mumbai.” Clim. Change, 104(1), 139–167. [Google Scholar]
- Rawls WJ, Stricker V, and Wilson K (1980). “Review and evaluation of urban flood flow frequency procedures.” USDA Science and Education Administration, Agricultural Research Center West, Beltsville, MD, 62. [Google Scholar]
- Razmkhah H, Abrishamchi A, and Torkian A (2010). “Evaluation of spatial and temporal variation in water quality by pattern recognition techniques: A case study on Jajrood River (Tehran, Iran).” J. Environ. Manage., 91(4), 852–860. [DOI] [PubMed] [Google Scholar]
- Rosenberg EA, et al. (2010). “Precipitation extremes and the impacts of climate change on stormwater infrastructure in Washington State.” Clim. Change, 102(1–2), 319–349. [Google Scholar]
- Rossman L. (2015). Storm water management model reference manual volume I—Hydrology I, U.S. Envrionmental Protection Agency, Office of Research and Developement, National Risk Management Laboratory, Cincinnati. [Google Scholar]
- Rossman LA (2004). SWMM (stormwater management model), version 5, user manual, Environmental Protection Agency, Washington, DC. [Google Scholar]
- Rubin DB (1988). “Using the SIR algorithm to simulate posterior distributions.” Bayesian Stat, 3(1), 395–402. [Google Scholar]
- Sabouri F, Gharabaghi B, Mahboubi AA, and McBean EA (2013). “Impervious surfaces and sewer pipe effects on stormwater runoff temperature.” J. Hydrol, 502, 10–17. [Google Scholar]
- Sansalone J, et al. (2013). “Retrofitting impervious urban infrastructure with green technology for rainfall-runoff restoration, indirect reuse and pollution load reduction.” Environ. Pollut, 183, 204–212. [DOI] [PubMed] [Google Scholar]
- Schindler N, Tranckner J, and Krebs P (2010). “Extreme value statistics for river quality simulations.” Water Sci. Technol, 61(2), 397–406. [DOI] [PubMed] [Google Scholar]
- Schoenfelder C, Kenner S, and Hoyer D (2006). “Hydraulic model of the Belle Fourche Irrigation District using EPA SWMM 5.0” World Environmental and Water Resource Congress 2006: Examining the Confluence of Environmental and Water Concerns, ASCE, Reston, VA, 1–10. [Google Scholar]
- Scholz M, and Kazemi Yazdi S (2009). “Treatment of road runoff by a combined storm water treatment, detention and infiltration system.” Water Air Soil Pollut, 198(1–4), 55–64. [Google Scholar]
- Shie-Yui Liong YL, Chan WT, and Law CL (1993). “Computer-aided catchment-calibration model.” Adv. Eng. Software, 17(3), 147–154. [Google Scholar]
- Shon TS, Kim SD, Cho EY, Im JY, Min KS, and Shin HS (2012). “Estimation of NPS pollutant properties based on SWMM modeling according to land use change in urban area.” Desalin. Water Treat, 38(1–3), 267–275. [Google Scholar]
- Shrestha M, and Buchberger S (2012). “Role of satellite water tanks in intermittent water supply system” World Environmental and Water Resources Congress 2012, ASCE, Reston, VA, 944–951. [Google Scholar]
- Shrestha NK, Leta OT, De Fraine B, van Griensven A, and Bauwens W (2013). “OpenMI-based integrated sediment transport modelling of the river Zenne, Belgium.” Environ. Modell. Software, 47, 193–206. [Google Scholar]
- Shubinski RP, Roesner LA, and Union AG (1973). Linked process routing models, American Geophysical Union, Washington, DC. [Google Scholar]
- Slys D, and Stec A (2012). “Hydrodynamic modelling of the combined sewage system for the city of Przemysl.” Environ. Prot. Eng, 38(4), 99–112. [Google Scholar]
- Smith CS, Lejano RP, Ogunseitan OA, and Hipp JA (2007). “Cost effectiveness of regulation-compliant filtration to control sediment and metal pollution in urban runoff.” Environ. Sci. Technol, 41(21), 7451–7458. [DOI] [PubMed] [Google Scholar]
- Smith D, Li J, and Banting D (2005). “A PCSWMM/GIS-based water balance model for the Reesor Creek watershed.” Atmosph. Res, 77(1–4), 388–406. [Google Scholar]
- Song C, Cardie J, and Leung K (1983). “Transient mixed-flow models for storm sewers.” J. Hydraul. Eng, 10.1061/(ASCE)0733-9429(1983)109:11(1487), 1487–1504. [DOI] [Google Scholar]
- Steffen J, Jensen M, Pomeroy CA, and Burian SJ (2013). “Water supply and stormwater management benefits of residential rainwater harvesting in U.S. cities.” J. Am. Water Res. Assoc, 49(4) 810–824. [Google Scholar]
- Stenstrom MK, and Kayhanian M (2005). “First flush phenomenon characterization.” Rep. No. CTSWRT0573, Sacramento, CA. [Google Scholar]
- Sugawara M (1967). “The flood forecasting by a series storage type model” Int. Symp. on Floods and Their Computation, IAHS Publ. 85, IAHS Press, Wallingford, U.K., 1–6. [Google Scholar]
- Sun N, Hall M, Hong B, and Zhang L (2014a). “Impact of SWMM catchment discretization: Case study in Syracuse, New York.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000777, 223–234. [DOI] [Google Scholar]
- Sun N, Hong B, and Hall M (2014b). “Assessment of the SWMM model uncertainties within the generalized likelihood uncertainty estimation (GLUE) framework for a high-resolution urban sewershed.” Hydrol. Process, 28(6), 3018–3034. [Google Scholar]
- Taeuk K, and Sangho L (2014). “Modification of the SCE-UA to include constraints by embedding an adaptive penalty function and application: Application approach.” Water Resour. Manage, 28(8), 2145–2159. [Google Scholar]
- Talei A, and Chua LHC (2012). “Influence of lag time on event-based rainfall–runoff modeling using the data driven approach.” J. Hydrol, 438–439, 223–233. [Google Scholar]
- Talei A, Hock L, Chua C, and Quek C (2010). “Expert systems with applications a novel application of a neuro-fuzzy computational technique in event-based rainfall–runoff modeling.” Exp. Syst. Appl, 37(12), 7456–7468. [Google Scholar]
- Tan S, Chua L, Shuy E, Lo E, and Lim L (2008). “Performances of rainfall-runoff models calibrated over single and continuous storm flow events.” J. Hydrol. Eng, 10.1061/(ASCE)1084-0699(2008)13:7(597), 597–607. [DOI] [Google Scholar]
- Temprano J, Arango Ó, Juan C, Joaquín S, and Iñaki T (2006). “Stormwater quality calibration by SWMM: A case study in Northern Spain.” Water SA, 32(1), 55–63. [Google Scholar]
- Tillinghast E, Hunt W, and Jennings G (2011). “Relating stormwater control measure (SCM) discharge design standards to stream erosion in Piedmont North Carolina: Case studies in Raleigh and Chapel Hill, North Carolina” Proc., World Environmental and Water Resources Congress, ASCE, Reston, VA, 509–518. [Google Scholar]
- Tillinghast E, Hunt W, Jennings G, and D’Arconte P (2012). “Increasing stream geomorphic stability using storm water control measures in a densely urbanized watershed.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000577, 1381–1388. [DOI] [Google Scholar]
- Tobio JAS, Maniquiz-Redillas MC, and Kim L-H (2014). “Optimization of the design of an urban runoff treatment system using stormwater management model (SWMM).” Desalin. Water Treat, 53(11), 3134–3141. [DOI] [PubMed] [Google Scholar]
- Todeschini S, Papiri S, and Ciaponi C (2012). “Performance of stormwater detention tanks for urban drainage systems in northern Italy.” J. Environ. Manage, 101, 33–45. [DOI] [PubMed] [Google Scholar]
- Tran D, and Kang JH (2013). “Optimal design of a hydrodynamic separator for treating runoff from roadways.” J. Environ. Manage, 116, 1–9. [DOI] [PubMed] [Google Scholar]
- Trowsdale SA, and Simcock R (2011). “Urban stormwater treatment using bioretention.” J. Hydrol, 397(3–4), 167–174. [Google Scholar]
- Tsihrintzis VA, and Hamid R (1997). “Modeling and management of urban stormwater runoff quality: A review.” Water Resour. Manage, 11(2), 136–164. [Google Scholar]
- Tsihrintzis VA, and Hamid R (1998). “Runoff quality prediction from small urban catchments using SWMM.” Hydrol. Process, 12(2), 311–329. [Google Scholar]
- Tsihrintzis VA, and Sidan CB (2008). “ILLUDAS and PSRM-QUAL predictive ability in small urban areas and comparison with other models.” Hydrol. Process, 22(17), 3321–3336. [Google Scholar]
- Tsihrintzis VA, Sylaios GK, Sidiropoulou M, and Koutrakis ET (2007). “Hydrodynamic modeling and management alternatives in a Mediterranean, fishery exploited, coastal lagoon.” Aquacult. Eng, 36(3), 310–324. [Google Scholar]
- Urich C, et al. (2013). “Modelling cities and water infrastructure dynamics.” Proc. Inst. Civ. Eng, 166(5), 301–308. [Google Scholar]
- Valeo C, and Ho CLI (2004). “Modelling urban snowmelt runoff.” J. Hydrol, 299(3–4), 237–251. [Google Scholar]
- van der Sterren M, Rahman A, and Ryan G (2014). “Modeling of a lot scale rainwater tank system in XP-SWMM: A case study in Western Sydney, Australia.” J. Environ. Manage, 141, 177–189. [DOI] [PubMed] [Google Scholar]
- Villarreal E, Bengtsson L, Niemczynowicz J, and Zhang L (2002). “Extension of storm water system at Östra Torn, Lund.” Proc., 9th Int. Conf. on Urban Drainage (9ICUD): Global Solutions for Urban Drainage, ASCE, Reston, VA, 1–11. [Google Scholar]
- Walsh TC, Pomeroy CA, and Burian SJ (2014). “Hydrologic modeling analysis of a passive, residential rainwater harvesting program in an urbanized, semi-arid watershed.” J. Hydrol, 508, 240–253. [Google Scholar]
- Wang K-H, and Altunkaynak A (2012). “Comparative case study of rainfall-runoff modeling between SWMM and fuzzy logic approach.” J. Hydrol. Eng, 10.1061/(ASCE)HE.1943-5584.0000419, 283–291. [DOI] [Google Scholar]
- Warwick J, Tadepalli P, and Warwick BJJ (1991). “Efficacy of SWMM application.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)0733-9496(1991)117:3(352), 352–366. [DOI] [Google Scholar]
- Warwick JJ, and Tadepalli P (1991). “Efficacy of SWMM application.” J. Water Resour. Plann. Manage, 10.1061/(ASCE)0733-9496(1991)117:3(352), 352–366. [DOI] [Google Scholar]
- Web of Science. (2016). “Citation database.” ⟨http://webofknowldege.com/⟩ (May 15, 2016).
- Wicke D, Cochrane TA, and O’Sullivan A (2012). “Build-up dynamics of heavy metals deposited on impermeable urban surfaces.” J. Environ. Manage, 113, 347–354. [DOI] [PubMed] [Google Scholar]
- Wu JY, Thompson JR, Kolka RK, Franz KJ, and Stewart TW (2013). “Using the storm water management model to predict urban headwater stream hydrological response to climate and land cover change.” Hydrol. Earth Syst. Sci, 17(12), 4743–4758. [Google Scholar]
- Wu Y, Jiang Y, Yuan D, and Li L (2008). “Modeling hydrological responses of karst spring to storm events: Example of the Shuifang spring (Jinfo Mt., Chongqing, China).” Environ. Geol, 55(7), 1545–1553. [Google Scholar]
- Xiong Y, Melching C, Asce AM, and Asce M (2005). “Comparison of kinematic-wave and nonlinear reservoir routing of urban watershed runoff.” J. Hydrol. Eng, 10.1061/(ASCE)1084-0699(2005)10:1(39), 39–49. [DOI] [Google Scholar]
- Young KD, Younos T, Dymond RL, Kibler DF, and Lee DH (2010). “Application of the analytic hierarchy process for selecting and modeling stormwater best management practices.” J. Contemp. Water Res. Educ, 146(1), 50–63. [Google Scholar]
- Yu B (1998). “Theoretical justification of SCS method for runoff estimation.” J. Irrig. Drain. Eng, 10.1061/(ASCE)0733-9437(1998)124:6(306), 306–310. [DOI] [Google Scholar]
- Zaghloul N (1998). “Flow simulation in circular pipes with variable roughness using SWMM-EXTRAN model.” J. Hydraul. Eng, 10.1061/(ASCE)0733-9429(1998)124:1(73), 73–76. [DOI] [Google Scholar]
- Zaghloul NA (1983). “Sensitivity analysis of the SWMM runoff-transport parameters and the effects of catchment discretisation.” Adv. Water Resour, 6(4), 214–223. [Google Scholar]
- Zaghloul NA, and Abu Kiefa MA (2001). “Neural network solution of inverse parameters used in the sensitivity-calibration analyses of the SWMM model simulations.” Adv. Eng. Software, 32(7), 587–595. [Google Scholar]
- Zaghloul NA, and Al-Shurbaji A-R (1991). “A storm water management model for urban areas in Kuwait.” Water Resour. Bull, 26(4), 563–575. [Google Scholar]
- Zhang G, Hamlett JM, and Saravanapavan T (2010). “Representation of low impact development scenarios in SWMM” Dynamic Modeling of Urban Water Systems Monograph, CHI Press, Guelph, ON, Canada, 18. [Google Scholar]
- Zhang Y, and Shuster W (2014). “The comparative accuracy of two hydrologic models in simulating warm-season runoff for two small, Hillslope catchments.” J. Am. Water Resour. Assoc, 50(2), 434–447. [Google Scholar]
- Zhao D, Chen J, Wang H, and Tong Q (2008). “Application of a sampling based on the combined objectives of parameter identification and uncertainty analysis of an urban rainfall-runoff model.” J. Irrig. Drain. Eng, 10.1061/(ASCE)IR.1943-4774.0000522, 66–74. [DOI] [Google Scholar]
- Zhao D, Chen JHW, Tong Q, Cao S, and Sheng Z (2009). “GIS-based urban rainfall-runoff modeling using an automatic catchment-discretization approach: A case study in Macau.” Environ. Earth Sci, 59(2), 465–472. [Google Scholar]
- Zhao H, and McEnroe B (2000). “Lag times for urban and developing watersheds in Kansas.” Joint Conf. on Water Resource Engineering and Water Resources Planning and Management 2000: Building Partnerships, ASCE, Reston, VA, 1–8. [Google Scholar]