Abstract
Polarizable force fields are emerging as a more accurate alternative to additive force fields in terms of modeling and simulations of a variety of chemicals including biomolecules. Explicit treatment of induced polarization in charged species such as phosphates and sulfates offers the potential for achieving an improved atomistic understanding of the physical forces driving their interactions with their environments. To help achieve this, in this study we present balanced Drude polarizable force-field parameters for molecular ions including phosphates, sulfates, sulfamates and oxides. Better balance was primarily achieved in the relative values of minimum interaction energies and distances of the anionic model compounds with water at the Drude and quantum mechanical (QM) model chemistries. Parametrization involved reoptimizing available parameters as well as extending the force field to new molecules with the goal of achieving self consistency with respect to the Lennard-Jones and electrostatic parameters targeting QM and experimental hydration free energies. The resulting force fields parameters achieve consistent treatment across the studied anions, facilitating more balanced simulations of biomolecules and small organic molecules in the context of the classical Drude polarizable force field.
Keywords: Molecular ions, polarizable force field, CHARMM, molecular dynamics, molecular modeling
Graphical Abstract
Introduction
Over last three decades there has been significant increase in computational modeling and simulations of biomolecules to investigate various problems that are experimentally difficult to explore.[1–4] The field has been significantly dependent on empirical potential energy functions that are based on non-polarizable, additive force fields.[5–14] However, the fixed charges on the atoms is these models restrict the investigation of inductive effects on molecules that arise in diverse condensed-phase environments. A notable example of a limitation in additive forces is the inability to correctly treat the distribution of atomic ions at air–water interfaces,[15–17] an issue that was overcome by the explicit inclusion of polarizability in the force field.[18–21] This and other examples,[22–28] point towards the need for polarizable force fields of high accuracy that encompass a wide range of chemical species. While there are a handful of polarizable force fields including induced point dipole or fluctuating charge models [29–31] our lab is focused on development of the CHARMM Drude Force Field based on the classical Drude oscillator.
Phosphate and sulfate moieties occur in a wide range of biomolecules including carbohydrates, glycoproteins, nucleic acids, and lipids. Specifically, phosphates and sulfates play important roles in cellular function including protein-protein interactions facilitated by phosphorylation.[32, 33] Anions such as sulfamates and oxides are present in drug-like molecules and various oxides are intermediates of enzymatic reactions, such as proteolysis.[34, 35] Accordingly, accurate, consistent treatment of molecular anions is essential for a comprehensive force field that will be of utility for modeling and simulation studies of heterogeneous chemical and biomolecular systems.
Our laboratory has been involved in the development of a comprehensive polarizable force field based on the classical Drude Oscillator model; alternative approaches and efforts to treat electronic polarization have been extensively reviewed elsewhere.[20, 36–40] Details of the Drude energy function, parameterization strategies and methodological information for various classes of molecular have been reported in previous studies.[41–47] Notably, the availability of the Drude model in different simulation packages including CHARMM[48], NAMD[49], GROMACS[50], OpenMM[51, 52] and ChemShell QM/MM[53–55] have made it convenient to run polarizable simulations into the microsecond time scale.
The current Drude polarizable force field has a limited number of molecular anions and their optimization in the context of different applications has led to some inconsistencies in the parameters for those molecules. For example, the phosphate parameters were initially developed in the context of the nucleic acids[56] while alternate Lennard-Jones (LJ) and electrostatic parameters were developed in the context of phospholipids.[57, 58] Further, the atom types from nucleic acids were recently used to parameterize the methyl phosphate ions and their interactions with magnesium ions.[59] The imbalance in the force field could cause a divergent effect as future molecules are parameterized with machine learning approaches being developed to predict the parameters for new small molecules. In this work, to achieve more balanced parameters for the Drude molecular anions as well as extend the coverage of the force field for this class of molecules, optimization of sulfate, phosphate, sulfamate and selected oxides are presented and discussed. The molecular anions studied are listed on Table 1 along with their abbreviations.
Table 1.
Molecular anions and their abbreviations studied in this work. Molecules not previously in the Drude force field are indicated by *. Molecules ACET, PHET, MES and ETS were optimized in recent study by Lin et. al.[42]
| Molecule names | Formula | Abbreviations (Residue ID) |
|---|---|---|
| Dimethylphosphate | (CH3)2PO4 | DMP |
| Methylphosphate (neutral) | CH3PO4H2 | MP_0 |
| Methylphosphate (anionic) | CH3PO4H− | MP_1 |
| Methylphosphate (dianionic) | CH3PO42− | MP_2 |
| Phosphate (anionic) | H2PO4− | HP_1* |
| Phosphate (dianionic) | HPO42− | HP_2 |
| Sulfate | SO42− | SO4* |
| Methylsulfate | CH3SO4− | MSO4* |
| Methylsulfonate | CH3SO3− | MSNA* |
| N-methylsulfamate | CH3NHSO3− | NMSM* |
| N-ethylsulfamate | C2H5NHSO3− | NESM* |
| Methoxide | CH3O− | MEO* |
| Ethoxide | C2H5O− | ETO* |
| Acetate | CH3COO− | ACET |
| Phenolate | C6H5O− | PHET |
| Methanethiolate | CH3S− | MES |
| Ethanethiolate | C2H5S− | ETS |
Computational Methods
Quantum Mechanical (QM) calculations were performed with the PSI4 [60] and Gaussian 03.[61] programs. Solute-water interaction geometries were constructed based on the donor-acceptor properties of the model compound by placing a single water at distances from 1.5 to 5.0 Å in steps of 0.05 Å in selected orientations (Figure 1 and S1–10). Monomer geometries were obtained from gas phase optimizations done at the MP2/6–31G(d) model chemistry to default tolerances. Then single point interaction energies of the model compound-water dimers as well as the individual monomers were calculated at the MP2/cc-pVQZ model chemistry with counterpoise correction for basis set superposition error (BSSE) using the gas phase monomer geometries of the model compounds with the SWM4-NDP geometry for water.[62–64] Interaction energies were obtained based on the difference between the total energy of the dimer and that of the individual monomers in the gas phase. Dipole moments were determined for MP2/6–31+G(d) gas phase optimized structures followed by MP2/cc-pVQZ single point calculations using Gaussian 03.[61] The gas phase molecular polarizabilities were estimated using the finite difference method[65] at the RIMP2/cc-pVQZ//MP2/6–31G(d) model chemistry using Psi4 inputs generated by the program FFParam.[60, 66]
Figure 1.
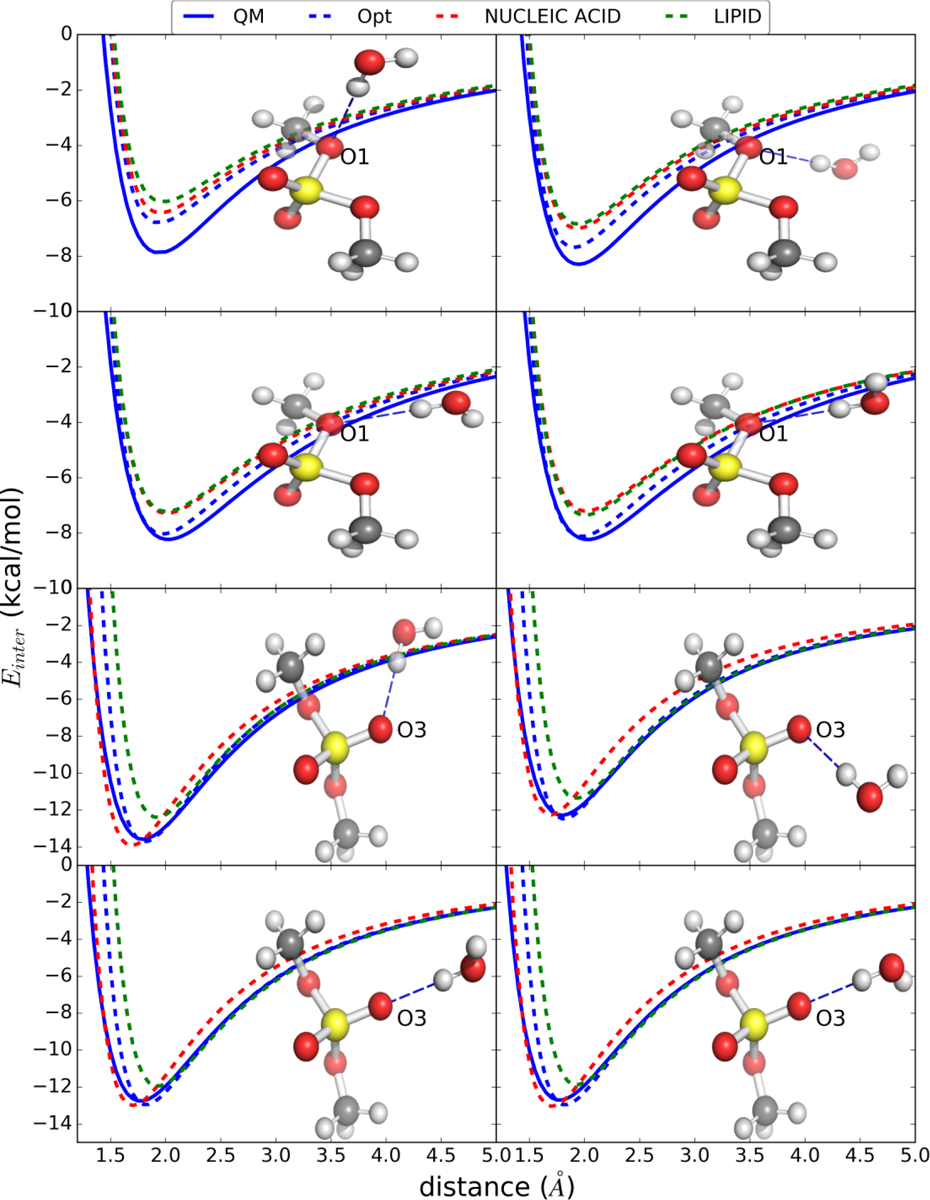
Water interaction energy surfaces as a function of distance from the QM and Drude models with dimethylphosphate (DMP). Distances are between the hydrogen (H) on the water model and the respective model compound oxygens as shown. Comprehensive interaction energy figures are included in the supplement Figure S1–11. Images rendered using PyMol.[75]
Molecular Mechanics (MM) calculation with Drude polarizable force field involved energy minimization of the model compounds in the gas phase to a tolerance of 10−5 kcal·mol−1 ·Å−1. Model compound-water interaction energies were obtained by relaxing the Drude particles via minimization by steepest-descent (SD) algorithm for 200 steps followed by an adopted-basis Newton–Raphson (ABNR) algorithm for 500 steps to a final gradient of 10–5 kcal·mol–1·Å–1 with the atomic positions restrained with a force constant of 107 kcal·mol–1·Å–2 to the QM gas phase optimized geometry. Interaction energies were again obtained based on the difference between the total energy of the dimer and that of the individual monomers in the gas phase. Dipole moments and molecular polarizabilities were calculated using the QM optimized geometries with only relaxation of the Drude particles as described above. FFParam was used to setup all the calculations above and analyze the results from QM and MM.[66]
Adiabatic dihedral potential energy scans (PES) were performed by geometry optimization at the MP2/6–31G(d) level with the target dihedral constrained followed by RIMP2/cc-pVQZ single point energies (i.e., RIMP2/cc-pVQZ//MP2/6–31G(d) QM model chemistry) using the Psi4 program.[60] PES were performed in 15° increments resulting in 24 conformations for 1D and 576 conformations for 2D surfaces. Analogous adiabatic MM PES were then computed with the target dihedral constrained to the QM values using the Drude force field.[47] Selected dihedral parameters were optimized, including the C-O-P-O dihedral parameter in dimethylphosphate (DMP). Once the QM target PES was calculated the analogous adiabatic MM PES was computed with targeted dihedral force constant set to zero and the MM PES calculated. The energy difference between the MM and QM (MM-QM) PES was then targeted for the fitting of the dihedral parameters using the least-square fitting program developed in this laboratory specifically for use in parameter optimization.[67] During fitting multiplicities n of 1, 2, 3, 4, 5 and 6 were included and the phase angle, δ, was limited to 0 and 180° as required to insure applicability of the parameters to stereoisomers about a chiral center.
The hydration free energy of molecular anions was calculated through alchemical free energy perturbation (FEP) simulations.[68] Final hydration free energies were based on three individual calculations (condensed phase, gas phase and long-range correction (LRC)), described and established in previous work by Lin et al.[41, 42] In short, for the condensed phase first the molecule was solvated in a box of SWM4-NDP [62] water and equilibrated for 100 ps in the NPT ensemble at 298.15 K and 1 atm using CHARMM[69]. Then the alchemical FEP was implemented applying coupling parameters to calculate the contributions to free energy by repulsive, dispersive and electrostatic terms based on the approach of Deng and Roux.[70] Each window was equilibrated for 100 ps and data was collected over 200 ps for the production runs. For the charged molecules a contribution arising from the Galvani potential Φ generated from the vacuum/water interface was added as a correction[71, 72], along with an entropic correction term (dScorr)[73] as shown in equations 1, 2 and 3.
| (1) |
| (2) |
| (3) |
In eq.1 ΔGhyd is the final calculated value of the hydration free energy. ΔGaq and ΔGgas are calculated as sums of the non-polar and electrostatic () contributions (Eq. 2 and 3), where the non-polar contribution is divided into dispersive () and repulsive () components associated with the vdW term. The zfΦ term corresponds to interfacial correction where z is the charge on the molecule, f is Faraday’s constant and Φ is Galvani potential. For SWM4-NDP water model Φ = −0545 V.[72] LRC is the long-range correction calculated according to Baker et. al.[74] MD simulations with the Drude model were performed as described in previous studies.[41–43] All molecular mechanics, MD simulations and FEP calculations were performed with the program CHARMM[69].
Results and Discussion
Parameter optimization efforts were designed to extend the treatment of molecular anions in the Drude force field as well as overcome divergent parameters that were developed during optimization of different aspects of the force field. This included divergence of the phosphate parameters based on DMP in nucleic acids versus in phospholipids. For example, the charges on the anionic oxygens in the nucleic acids was −0.776, while that in the lipids was −0.876; the final optimized charge being −0.856 from the present study. The LJ radii, Rmin/2 (i.e. 2−5/6 σ), on the anionic oxygens were 1.865, 1.970 and 1.865 Å in the nucleic acid, lipid and optimized models, respectively, while the LJ εmin parameter on the anionic oxygen for the nucleic acids was changed from −0.07 to the lipid value to −0.19 kcal/mol. Similarly, for the ester oxygen the nucleic acid εmin was adjusted from −0.02 to the lipid value of −0.17 kcal/mol. Accordingly, in the present work a unified model was developed that will be applied to various systems moving forward. In addition, when considering different molecular anions, optimization in the present study was performed to assure that the differences between the QM and Drude minimum interaction energies and distances were well balanced. For example, there was a tendency for the Drude minimum energy interactions to be more favorable and shorter than QM data involving interactions of water with the nucleic acid DMP anionic phosphates while the opposite occurred with the lipid DMP parameters as discussed in the next section. Accordingly, parameter optimization was focused on minimizing these differences, balancing the agreement between all the interaction orientations and reproducing the hydration free energies of the studied model compounds. Adjustment of the electrostatic parameters also considered the gas phase molecular dipole moments including their tensors.
Water-model compound interactions
Model compound-water interactions were analyzed for various orientations with respect to the different donor/accepter atoms in the compounds. In Figure 1 the example of water-DMP interactions are shown including results from the initial nucleic acid and lipid models, the final optimized model and from the QM calculation. The original nucleic acid parameters yielded minimum energies and distances that were slightly shorter and more favorable than the QM while the opposite was true for the lipid parameters. These differences are associated with both the partial atomic charges and the LJ parameters. The longer distances with the lipid model are associated with the larger Rmin/2 on the anionic oxygens, a problem that was fixed with the change from the value of 1.970 to the nucleic acid value 1.865 Å. Simultaneously, the change in εmin and the decrease in the magnitude of the charge from −0.876 to −0.856 corrects for the overestimation seen with the nucleic acid model. This yields the final optimized parameters that are in good agreement with the QM data for both the minimum interaction energies and distances (Table 1). Furthermore, during adjustment of the charge distribution the reproduction of target data on the dipole moment and hydration free energy were considered, as discussed below.
To preserve consistency across different species of molecular anions the diverse model compounds listed in Table 1 were selected and optimized applying the present well-balanced approach. The water-model compound interactions energy orientations along with the corresponding energy surfaces are presented in Figures 1 and S1–11. As shown, Drude energies were computed for the original, previously published parameters, when available, along with those optimized in this work. Of the model compounds in Table 1, HP_1, SO4, MSO4, MSNA, NMSM, NESM, MEO and ETO were not previously available in the Drude force field.
In the case of the phosphates, it was important to obtain balanced parameters that were applicable to DMP, methylphosphates (MP_0, MP_1 and MP_2) and phosphates (HP_1 and HP_2). We were able to bring consistency in the charges on the anionic oxygens of DMP, MP_1 and HP_1, which all have a total charge of −1. Also, in the previous parameters the charges on the anionic oxygens in MP_2, MP_1 and MP_0 decreased irregularly as the magnitude of the total charge decreased.[59] With re-optimization, there is now a consistent decrease in the anionic oxygen charges going from MP_2 to MP_1 to MP_0. Presented in Table 2 are results from the original and optimized models for DMP, all phosphate containing compounds excluding DMP and all non-phosphate containing compounds. The individual minimum interaction energies and distances are reported in Tables S1 to S3 of the supplemental information. As expected, the differences defined by the different metrics in Table 2 show improvements versus the original parameters were available.
Table 2.
Statistical analysis of the differences in the water-model compound minimum interaction energies (Emin, kcal/mol) and distances (Rmin, Å) for molecular ions between QM and Drude model (Drude). Complete lists of the water minimum interaction energies and distances can be found in Tables S1 to S3 of the supplemental information.
| DMP | All phosphate containing compounds excluding DMP |
Non-phosphate containing compounds |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Opt | Opt | Opt | ||||||||||
| R_min | R_min | R_min | R_min | R_min | R_min | |||||||
| AVG Difference | 0.01 | −0.01 | 0.01 | 0.07 | 0.01 | 0.01 | ||||||
| ABS_AVG Difference | 0.06 | 0.11 | 0.05 | 0.11 | 0.07 | 0.04 | ||||||
| STDEV Difference | 0.07 | 0.07 | 0.07 | 0.16 | 0.13 | 0.07 | ||||||
| RMS Difference | 0.11 | 0.15 | 0.08 | 0.17 | 0.13 | 0.07 | ||||||
Dipole moments
Molecular dipole moments were also included as target data for optimization of the electrostatic parameters. A summary of the results is presented in Table 3 with the differences with respect to QM in the dipole moments before and after optimization. Total dipoles as well as the X, Y and Z components for all the molecules are provided in the supporting Tables S4 and S5. Intramolecular geometries for the Drude model were the QM optimized geometry with only Drude particle positions minimized in the MM calculations. For model compounds in which the electrostatic parameters were optimized as part of the present study, dipole moments were computed for both the original and optimized parameters. Specifically, DMP shows significant improvement in total dipole moment with respect to the nucleic acid version and a slight compromise relative to the lipid version as that model was optimized more recently targeting similar QM data (Table S4). Similarly, MP_1, MP_2 and HP_2 show notable improvement compared to original parameters (Table S5). An excellent agreement with the QM data was also obtained with all the newly parameterized molecules that were not previously in the Drude force field showing an overall < 0.1 Debye absolute average difference in the total dipole moments (Table S5, legend).
Table 3.
Dipole moment differences between the Drude and QM models for molecules in which the electrostatic parameters were updated as part of the present study. QM data at the RIMP2/cc-pVQZ//MP2/6–31G(d) model chemistry. All values are in Debye.
| Differences = Drude - QM | DMP | Molecules previously in the Drude FF excluding DMP | |||
|---|---|---|---|---|---|
| Opt | Opt | ||||
| AVG Difference | 0.12 | 0.05 | |||
| ABS_AVG Difference | 0.03 | 0.16 | |||
| STDEV Difference | 0.24 | 0.23 | |||
| RMS Difference | 0.28 | 0.24 | |||
Molecular Polarizabilities
Comparisons were also made with respect to the molecular polarizabilities, though these were not considered directly as target data for the optimization. Table 4 includes the ratios of the Drude to QM molecular polarizabilities, with the Drude values based on the QM geometries. The absolute values of the molecular polarizabilites are in Table S7. Overall, the Drude polarizabilities are smaller than the QM values, consistent with the polarizability scaling used in the Drude FF.[76] With polar neutral species the ratios, or scaling factors, are typically close to 0.85 though smaller values have been obtained. With the anions the average ratio is 0.75. This smaller value may be associated with the more diffuse nature of the electron distribution associated with the negative ions in the gas phase versus neutral species. In the condensed phase the presence of molecules (eg. water) around the anions may limit the extent that the electron cloud can distort leading to smaller effective molecular polarizabilties. However, the approximation that the electric field of the atoms at their nucleic is used to determine the polarization response may also contribute to this effect.[77] Further studies are required to address this issue in detail.
Table 4.
Ratio of Drude and QM molecular polarizabilities and their tensors. QM data at the RIMP2/cc-pVQZ//MP2/6–31G(d) model chemistry.
| Molecule | Ratio: Drude/QM | |||
|---|---|---|---|---|
| XX | YY | ZZ | total | |
| DMP | 0.72 | 0.75 | 0.74 | 0.74 |
| MP_0 | 0.82 | 0.91 | 0.87 | 0.87 |
| MP_1 | 0.85 | 0.77 | 0.74 | 0.79 |
| MP_2 | 0.75 | 0.55 | 0.72 | 0.66 |
| HP_1 | 0.91 | 0.89 | 0.87 | 0.89 |
| HP_2 | 0.74 | 0.74 | 0.78 | 0.75 |
| SO4 | 0.71 | 0.71 | 0.71 | 0.70 |
| MSO4 | 0.69 | 0.77 | 0.82 | 0.76 |
| MSNA | 0.66 | 0.73 | 0.73 | 0.70 |
| NMSM | 0.87 | 0.78 | 0.81 | 0.82 |
| NESM | 0.75 | 0.82 | 0.84 | 0.80 |
| MEO | 0.56 | 0.56 | 0.57 | 0.56 |
| ETO | 1.00 | 0.61 | 0.59 | 0.74 |
| Average | 0.77 | 0.74 | 0.75 | 0.75 |
Conformational properties
While the majority of bonded parameters were already available in the Drude FF and not subjected to optimization, it was necessary to improve selected dihedral parameters in molecules that included O-methyl or O-ethyl moieties or hydroxyl groups. Presented in Figure 2 and 3 are the QM and Drude PES. In the case of DMP, a two-dimensional PES was performed for the dihedrals C1-O11-P-O12 and O11-P-O12-C2 to examine the relative stability of gauche-gauche (gg), gauche-trans (gt), and trans-trans (tt) conformations and the barriers between those minima. Figure 3 shows the heatmap of PES with respect to the lowest energy at gg conformation at +/− 75°. The gt and tt conformations have slightly unfavorable energies compared to gg, though both are comparable to each other as reported previously.[78, 79] As is evident the Drude PES are typically in very good agreement with the QM data, indicating that the overall conformations of the molecules and the barriers between low energy conformations are satisfactorily treated.
Figure 2.
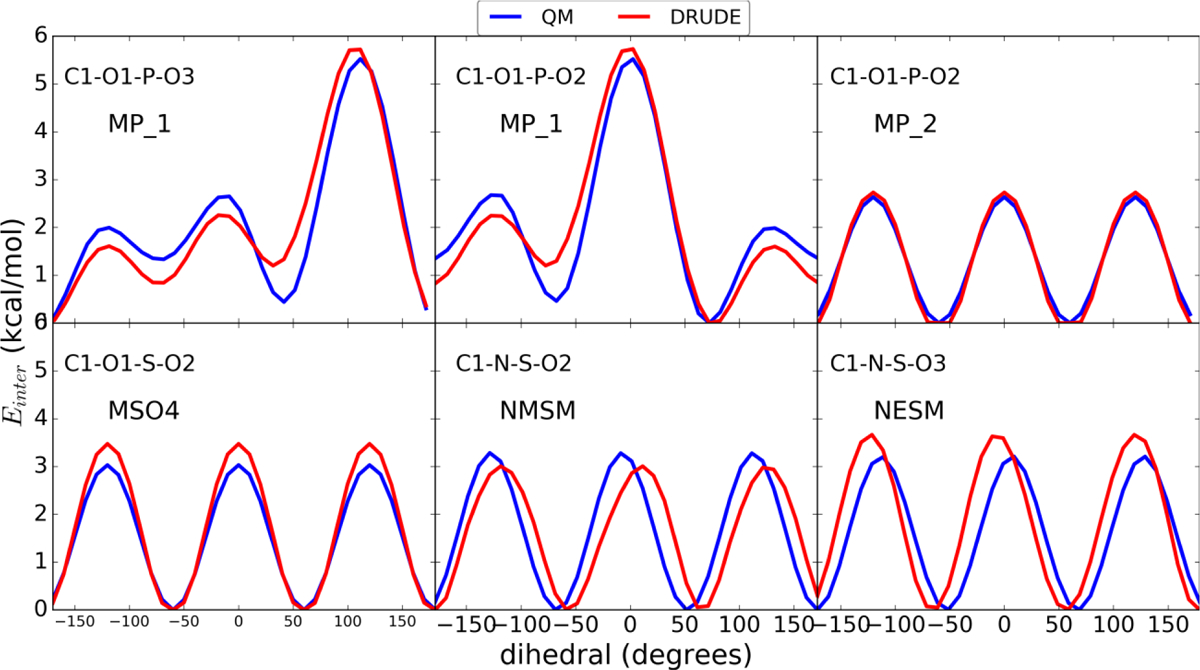
QM and optimized Drude torsional PES along with target dihedral labels.
Figure 3.
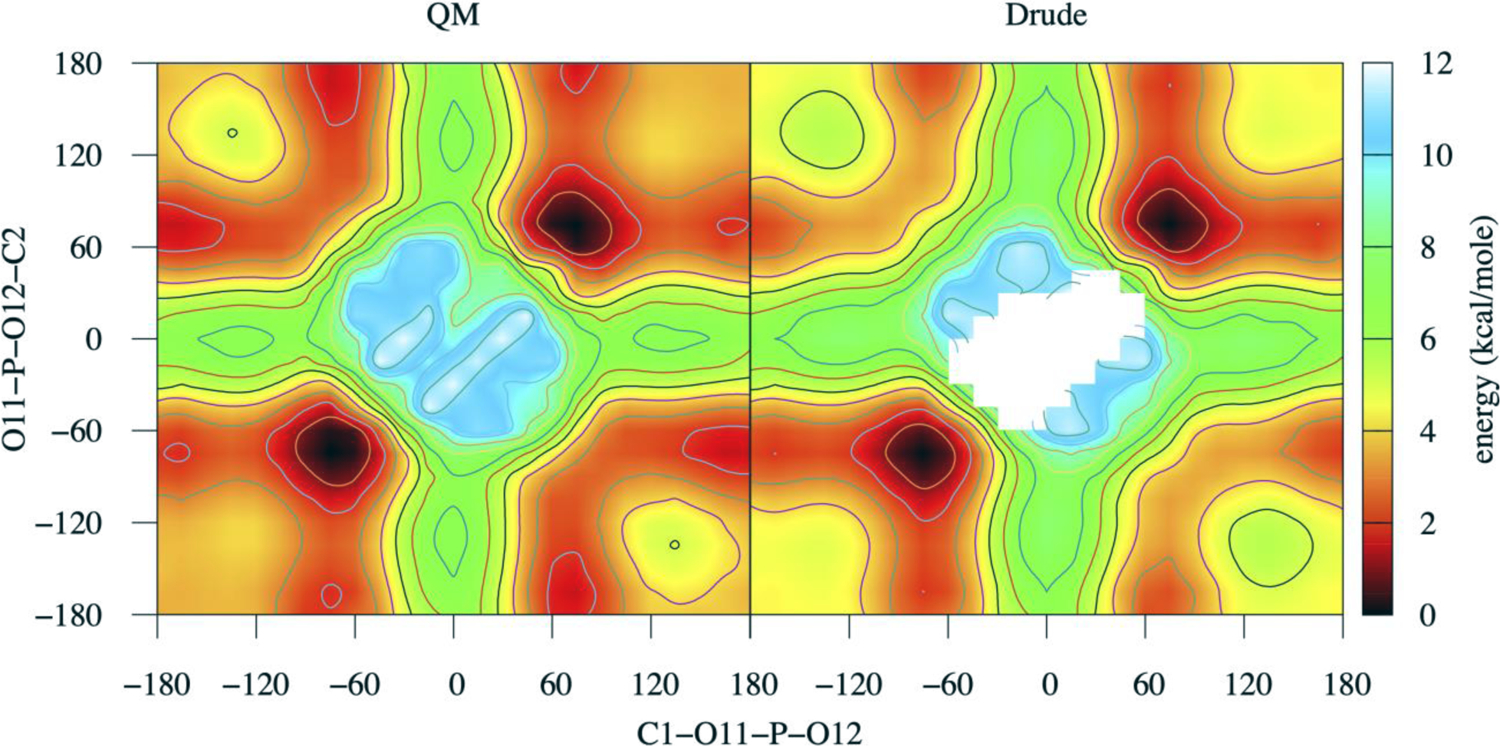
2D QM and MM conformational energies for DMP along C1-O11-P-O12 and O11-P-O12-C2 dihedrals. On the conformational surface, gg (global minima) lies on +/−75.0 degree.
Hydration free energies
The final target data were the hydration free energies, which were calculated using the free energy perturbation protocol established by Deng and Roux.[70] For all the anions, target hydration free energies were corrected to account for the vacuum/water interface, entropic terms and long-range dispersion corrections (Equation 1). Two methods for calculation of the correction for target data could be applied according to the type of experimental data where the hydration free energy is measured relative to an ion with the same charge or in the presence of a counterion.[41, 42]
| Method-1: |
| Method-2: |
Based on which approach was used in the experiments, the appropriate correction/offset is required using the corresponding coion/counterion. Accordingly, we have used Cl− (ΔGexpt = −74.60 kcal/mol and ΔGdrude = −78.40 kcal/mol), Na+ (ΔGexpt = −100.6 kcal/mol and ΔGdrude = −96.3 kcal/mol), and H+ (ΔGexpt = −265.9 kcal/mol and ΔGdrude = −258.8 kcal/mol) to define the target data. For DMP a true experimental value is unavailable and an estimation of ΔGexpt = −76.0 ± 4.0 kcal/mol provided by Klauda et. al.[80] has been used as reference value in this study. Since the estimation uses H+ as counterion we calculated the target data for DMP using the same; however, the uncertainty in the ΔGexpt estimation is high, limiting its utility. For HP_1 three different experimental data are available ranging from −68 to −111 kcal/mol. To be consistent, we have used ΔGexpt values −76.0 and −299.0 kcal/mol for HP_1 and HP_2, respectively, from the same study, which uses Na+ as counterion in the experimental evaluation.[81]
Presented in Table 5 are the experimental and calculated hydration free energies. The overall level of agreement with the Drude model to reproduce the hydration free energies is agreeable (considering the unavailability/ambiguity in experimental data) with an overall RMS difference of 1.33 kcal/mol, excluding the compound HP_2. The hydration free energy of HP_2 was sacrificed to obtain more accurate reproduction of that of HP_1, which is within 1.0 kcal/mol of the target value. Only in the case of HP_2 is the hydration free energy in poorer agreement with the target data as compared to the previous parameters.
Table 5.
Calculated, experimental and target free energies of hydration for the molecular anions. Detailed distribution of calculated free energies are provided in Table S6 of the supplemental information. All values are in kcal/mol. Values in parenthesis for DMP corresponds to the calculated hydration free energy based on the current Drude nucleic acid parameters. ΔG_drudeopt is average hydration free energy from 3 independent runs and with errors being standard errors calculated from the 3 independent runs.
| Molecule | ΔG_expt | ΔG_target | ΔG_drudeorig | ΔG_drudeopt | ΔG_Difforig | ΔG_Diffopt |
|---|---|---|---|---|---|---|
| DMP | −76.00[80] | −83.10a | −78.48 (−70.99) | −81.04 ± 0.08 | −3.32 (−10.81) | 2.06 |
| MP_0 | N A | −13.83 | −10.47 ± 0.22 | |||
| MP_1 | N A | −87.95 | −77.99 ± 0.29 | |||
| MP_2 | N A | −284.28 | −265.27 ± 0.25 | |||
| HP_1 | −76.00[81–84] | −79.70b | −80.25 ± 0.18 | −0.55 | ||
| HP_2 | −299.00[81, 82] | −302.70b | −294.15 | −275.54 ± 0.16 | −8.65 | 27.16 |
| SO4 | −258.25[83] | −262.05a | −263.19 ± 0.31 | −1.14 | ||
| MSO4 | N A | −67.83 ± 0.03 | ||||
| MSNA | N A | −70.51 ± 0.10 | ||||
| NMSM | N A | −72.83 ± 0.09 | ||||
| NESM | N A | −72.77 ± 0.26 | ||||
| MEO | −95.20[85] | −102.30c | −100.64 ± 0.11 | 1.66 | ||
| ETO | −91.20[85] | −98.30c | −95.62 ± 0.32 | 2.68 | ||
| ACET* | −77.3[85, 86] | −84.4c | −84.7 ± 0.1 | −0.3 | ||
| PHET* | −71.3[85, 86] | −78.4c | −78.2 ± 0.0 | 0.2 | ||
| MES* | −73.7[85, 86] | −80.8b | −80.6 ± 0.1 | 0.2 | ||
| ETS* | −71.8[85, 86] | −78.7c | −78.9 ± 0.1 | −0.2 |
Conclusions
The study presents an important refinement of the Drude polarizable FF parameters for modeling of various molecular anions. The effort focused on achieving a better balance in the Drude parameters for these species primarily with respect to their interactions with water while yielding good agreement with molecular dipoles and polarizabilities and the condensed phase hydration free energies. The most important of these were the modifications in the non-bonded parameters of the anionic oxygen of the phosphates, especially in DMP, which is critical for the treatment of nucleic acids and phospholipids. Importantly, the same LJ parameters are used for the methylphosphates, thereby simplifying the force field with respect to the number of atom types.
Final topologies and parameters are provided in the supporting information and can also be accessed from the MacKerell laboratory web site (http://mackerell.umaryland.edu/CHARMM_ff_params.html) with future releases of the program CHARMM and from the Drude Prepper module in the CHARMM-GUI.[87, 88] This includes inclusion of the developed Drude polarizable force field parameters for molecular anions with the remainder of the classical Drude polarizable force, including carbohydrates[46, 47, 89, 90], lipids[58], nucleic acids[91, 92] and proteins[93].
Supplementary Material
Acknowledgements
Financial support from the NIH (GM131710) and computational support from the University of Maryland Computer-Aided Drug Design Center are acknowledged.
Footnotes
Supporting Information
Figures and tables showing details of water interaction energy calculations, dipole moments, molecular polarization and final force field parameters for molecular anions.
Competing Financial Interests Statement
ADM Jr. is cofounder and CSO of SilcsBio LLC.
References
- 1.Whitford PC, Blanchard SC, Cate JH, Sanbonmatsu KY. Connecting the kinetics and energy landscape of tRNA translocation on the ribosome. PLoS Comput Biol. 2013;9(3):e1003003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dror RO, Pan AC, Arlow DH, Borhani DW, Maragakis P, Shan Y, et al. Pathway and mechanism of drug binding to G-protein-coupled receptors. Proc Natl Acad Sci U S A. 2011;108(32):13118–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shaw DE, Maragakis P, Lindorff-Larsen K, Piana S, Dror RO, Eastwood MP, et al. Atomic-level characterization of the structural dynamics of proteins. Science. 2010;330(6002):341–6. [DOI] [PubMed] [Google Scholar]
- 4.McCammon JA, Gelin BR, Karplus M. Dynamics of folded proteins. Nature. 1977;267(5612):585–90. [DOI] [PubMed] [Google Scholar]
- 5.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, et al. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J Am Chem Soc. 1995;117(19):5179–97. [Google Scholar]
- 6.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102(18):3586–616. [DOI] [PubMed] [Google Scholar]
- 7.MacKerell AD, Brooks B, Brooks CL, Nilsson L, Roux B, Won Y, et al. CHARMM: The Energy Function and Its Parameterization Encyclopedia of Computational Chemistry: John Wiley & Sons, Ltd; 2002. [Google Scholar]
- 8.Guvench O, Hatcher E, Venable RM, Pastor RW, MacKerell AD. CHARMM Additive All-Atom Force Field for Glycosidic Linkages between Hexopyranoses. J Chem Theory Comput. 2009;5(9):2353–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.MacKerell AD Jr., Banavali N, Foloppe N. Development and current status of the CHARMM force field for nucleic acids. Biopolymers. 2000;56(4):257–65. [DOI] [PubMed] [Google Scholar]
- 10.Pastor RW, Mackerell AD, Jr. Development of the CHARMM Force Field for Lipids. J Phys Chem Lett. 2011;2(13):1526–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. Evaluation and Reparametrization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. J. Phys. Chem. B 2001;105(28):6474–87. [Google Scholar]
- 12.Damm W, Frontera A, Tirado–Rives J, Jorgensen WL. OPLS all-atom force field for carbohydrates. J Comput Chem. 1997;18(16):1955–70. [Google Scholar]
- 13.Soares TA, Hunenberger PH, Kastenholz MA, Krautler V, Lenz T, Lins RD, et al. An improved nucleic acid parameter set for the GROMOS force field. J Comput Chem. 2005;26(7):725–37. [DOI] [PubMed] [Google Scholar]
- 14.Pol-Fachin L, Rusu VH, Verli H, Lins RD. GROMOS 53A6GLYC, an Improved GROMOS Force Field for Hexopyranose-Based Carbohydrates. J Chem Theory Comput. 2012;8(11):4681–90. [DOI] [PubMed] [Google Scholar]
- 15.Jungwirth P, Tobias DJ. Molecular Structure of Salt Solutions: A New View of the Interface with Implications for Heterogeneous Atmospheric Chemistry. J. Phys. Chem. B 2001;105(43):10468–72. [Google Scholar]
- 16.Chang T-M, Dang LX. Recent Advances in Molecular Simulations of Ion Solvation at Liquid Interfaces. Chem Rev. 2006;106(4):1305–22. [DOI] [PubMed] [Google Scholar]
- 17.Jungwirth P, Tobias DJ. Specific Ion Effects at the Air/Water Interface. Chem Rev. 2006;106(4):1259–81. [DOI] [PubMed] [Google Scholar]
- 18.Warshel A, Kato M, Pisliakov AV. Polarizable Force Fields: History, Test Cases, and Prospects. J Chem Theory Comput. 2007;3(6):2034–45. [DOI] [PubMed] [Google Scholar]
- 19.Freddolino PL, Harrison CB, Liu Y, Schulten K. Challenges in protein folding simulations: Timescale, representation, and analysis. Nat. Phys 2010;6(10):751–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lopes PEM, Roux B, MacKerell AD. Molecular modeling and dynamics studies with explicit inclusion of electronic polarizability: theory and applications. Theor Chem Acc. 2009;124(1):11–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhu X, Lopes PEM, MacKerell AD Jr. Recent developments and applications of the CHARMM force fields. WIREs Comput Mol Sci. 2012;2(1):167–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lemkul JA, Savelyev A, MacKerell AD Jr. Induced Polarization Influences the Fundamental Forces in DNA Base Flipping. J Phys Chem Lett. 2014;5(12):2077–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lemkul JA, MacKerell AD Jr. Polarizable force field for RNA based on the classical drude oscillator. J Comput Chem. 2018;39(32):2624–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Huang J, MacKerell AD Jr. Induction of peptide bond dipoles drives cooperative helix formation in the (AAQAA)3 peptide. Biophys J. 2014;107(4):991–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lin FY, MacKerell AD Jr. Improved Modeling of Cation-pi and Anion-Ring Interactions Using the Drude Polarizable Empirical Force Field for Proteins. J Comput Chem. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lemkul JA. Same fold, different properties: polarizable molecular dynamics simulations of telomeric and TERRA G-quadruplexes. Nucleic Acids Res. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang J, Cieplak P, Li J, Wang J, Cai Q, Hsieh M, et al. Development of polarizable models for molecular mechanical calculations II: induced dipole models significantly improve accuracy of intermolecular interaction energies. J Phys Chem B. 2011;115(12):3100–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wang J, Cieplak P, Cai Q, Hsieh MJ, Wang J, Duan Y, et al. Development of polarizable models for molecular mechanical calculations. 3. Polarizable water models conforming to Thole polarization screening schemes. J Phys Chem B. 2012;116(28):7999–8008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shi Y, Xia Z, Zhang J, Best R, Wu C, Ponder JW, et al. The Polarizable Atomic Multipole-based AMOEBA Force Field for Proteins. J Chem Theory Comput. 2013;9(9):4046–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Patel S, Brooks CL, III CHARMM Fluctuating Charge Force Fields for Proteins: I Paramaterization and application to bulk organic liquid simulations. J Comp Chem. 2004;25(1):1–16. [DOI] [PubMed] [Google Scholar]
- 31.Wang ZX, Zhang W, Wu C, Lei H, Cieplak P, Duan Y. Strike a balance: optimization of backbone torsion parameters of AMBER polarizable force field for simulations of proteins and peptides. J Comput Chem. 2006;27(6):781–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Westheimer FH. Why nature chose phosphates. Science. 1987;235(4793):1173–8. [DOI] [PubMed] [Google Scholar]
- 33.Kehoe JW, Bertozzi CR. Tyrosine sulfation: a modulator of extracellular protein-protein interactions. Chem Biol. 2000;7(3):R57–R61. [DOI] [PubMed] [Google Scholar]
- 34.Winum J-Y, Scozzafava A, Montero J-L, Supuran CT. Sulfamates and their therapeutic potential. Med Res Rev. 2005;25(2):186–228. [DOI] [PubMed] [Google Scholar]
- 35.Rami M, Dubois L, Parvathaneni N-K, Alterio V, van Kuijk SJA, Monti SM, et al. Hypoxia-Targeting Carbonic Anhydrase IX Inhibitors by a New Series of Nitroimidazole-Sulfonamides/Sulfamides/Sulfamates. J Med Chem. 2013;56(21):8512–20. [DOI] [PubMed] [Google Scholar]
- 36.Halgren TA, Damm W. Polarizable force fields. Curr Opin Struct Biol. 2001;11(2):236–42. [DOI] [PubMed] [Google Scholar]
- 37.Lemkul JA, Huang J, Roux B, MacKerell AD Jr. An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem Rev. 2016;116(9):4983–5013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cieplak P, Dupradeau FY, Duan Y, Wang J. Polarization effects in molecular mechanical force fields. J Phys Condens Matter. 2009;21(33):333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ponder JW, Case DA. Force fields for protein simulations. Adv Protein Chem. 2003;66:27–85. [DOI] [PubMed] [Google Scholar]
- 40.Baker CM. Polarizable force fields for molecular dynamics simulations of biomolecules. WIREs Comput Mol Sci. 2015;5(2):241–54. [Google Scholar]
- 41.Lin FY, MacKerell AD Jr. Polarizable Empirical Force Field for Halogen-Containing Compounds Based on the Classical Drude Oscillator. J Chem Theory Comput. 2018;14(2):1083–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lin FY, Lopes PEM, Harder E, Roux B, MacKerell AD Jr. Polarizable Force Field for Molecular Ions Based on the Classical Drude Oscillator. J Chem Inf Model. 2018;58(5):993–1004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Small MC, Aytenfisu AH, Lin F-Y, He X, MacKerell AD. Drude polarizable force field for aliphatic ketones and aldehydes, and their associated acyclic carbohydrates. J Comput Aided Mol Des. 2017:1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lemkul JA, MacKerell AD Jr. Polarizable Force Field for DNA Based on the Classical Drude Oscillator: II. Microsecond Molecular Dynamics Simulations of Duplex DNA. J Chem Theory Comput. 2017;13(5):2072–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lemkul JA, Lakkaraju SK, MacKerell AD Jr. Characterization of Mg(2+) Distributions around RNA in Solution. ACS Omega. 2016;1(4):680–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yang M, Aytenfisu AH, MacKerell AD Jr. Proper balance of solvent-solute and solute-solute interactions in the treatment of the diffusion of glucose using the Drude polarizable force field. Carbohydr Res. 2018;457:41–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Aytenfisu AH, Yang M, MacKerell AD Jr. CHARMM Drude Polarizable Force Field for Glycosidic Linkages Involving Pyranoses and Furanoses. J Chem Theory Comput. 2018;14(6):3132–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lamoureux G, Roux B. Modeling Induced Polarization with Drude Oscillators: Theory and Molecular Dynamics Simulation Algorithm. J Chem Phys. 2003;119(6):3025–39. [Google Scholar]
- 49.Jiang W, Hardy DJ, Phillips JC, Mackerell AD, Schulten K, Roux B. High-performance scalable molecular dynamics simulations of a polarizable force field based on classical Drude oscillators in NAMD. J Phys Chem Lett. 2011;2(2):87–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lemkul JA, Roux B, van der Spoel D, MacKerell AD Jr. Implementation of extended Lagrangian dynamics in GROMACS for polarizable simulations using the classical Drude oscillator model. J Comput Chem. 2015;36(19):1473–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Eastman P, Friedrichs MS, Chodera JD, Radmer RJ, Bruns CM, Ku JP, et al. OpenMM 4: A Reusable, Extensible, Hardware Independent Library for High Performance Molecular Simulation. J Chem Theory Comput. 2013;9(1):461–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Huang J, Lemkul JA, Eastman PK, MacKerell AD Jr. Molecular dynamics simulations using the drude polarizable force field on GPUs with OpenMM: Implementation, validation, and benchmarks. J Comput Chem. 2018;39(21):1682–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Metz S, Kästner J, Sokol AA, Keal TW, Sherwood P. ChemShell—a modular software package for QM/MM simulations. WIREs Comput Mol Sci. 2014;4(2):101–10. [Google Scholar]
- 54.Lu Y, Farrow MR, Fayon P, Logsdail AJ, Sokol AA, Catlow CRA, et al. Open-Source, Python-Based Redevelopment of the ChemShell Multiscale QM/MM Environment. J Chem Theory Comput. 2019;15(2):1317–28. [DOI] [PubMed] [Google Scholar]
- 55.Sherwood P, de Vries AH, Guest MF, Schreckenbach G, Catlow CRA, French SA, et al. QUASI: A general purpose implementation of the QM/MM approach and its application to problems in catalysis. Journal of Molecular Structure: THEOCHEM. 2003;632(1):1–28. [Google Scholar]
- 56.Savelyev A, MacKerell AD Jr. All-atom polarizable force field for DNA based on the classical drude oscillator model. J Comput Chem. 2014;10:1652–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Li H, Chowdhary J, Huang L, He X, MacKerell AD Jr., Roux B. Drude Polarizable Force Field for Molecular Dynamics Simulations of Saturated and Unsaturated Zwitterionic Lipids. J Chem Theory Comput. 2017;13(9):4535–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Chowdhary J, Harder E, Lopes PE, Huang L, MacKerell AD Jr., Roux B. A polarizable force field of dipalmitoylphosphatidylcholine based on the classical Drude model for molecular dynamics simulations of lipids. J. Phys. Chem. B 2013;117(31):9142–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Villa F, MacKerell AD Jr., Roux B, Simonson T. Classical Drude Polarizable Force Field Model for Methyl Phosphate and Its Interactions with Mg(2). J Phys Chem A. 2018;122(29):6147–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Parrish RM, Burns LA, Smith DGA, Simmonett AC, DePrince AE 3rd, Hohenstein EG, et al. Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability. J Chem Theory Comput. 2017;13(7):3185–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, et al. Gaussian 03. Revision B.04 ed. Pittsburgh, PA: Gaussian, Inc; 2003. [Google Scholar]
- 62.Lamoureux G, Harder E, Vorobyov I, Roux B, MacKerell AD Jr. A polarizable model of water for molecular dynamics simulations of biomolecules. Chem Phys Lett. 2006;418:245–9. [Google Scholar]
- 63.Boys SF, Bernardi F. The Calculation of Small Molecular Interaction by the Differences of Seperate Total Energies. Some Procedures with Reduced Errors. Mol Phys. 1970;19:553–66. [Google Scholar]
- 64.Ransil B Studies in molecular structure. IV. Potential curve for the interaction of two helium atoms in single-configuration LCAO MO SCF approximation. J Chem Phys. 1961;34:2109. [Google Scholar]
- 65.Anisimov VM, Lamoureux G, Vorobyov IV, Huang N, Roux B, MacKerell AD Jr. Determination of electrostatic parameters for a polarizable force field based on the classical Drude oscillator. J Chem Theory Comput. 2005;1(1):153–68. [DOI] [PubMed] [Google Scholar]
- 66.Kumar A, Yoluk O, MacKerell AD Jr. FFParam: Standalone package for CHARMM additive and Drude polarizable force field parametrization of small molecules. J Comput Chem. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Vanommeslaeghe K, Yang M, MacKerell AD Jr. Robustness in the fitting of molecular mechanics parameters. J Comp Chem. 2015;36(14):1083–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Kollman PA. Free Energy Calculations: Applications to Chemical and Biochemical Phenomena. Chem Rev. 1993;93:2395–417. [Google Scholar]
- 69.Brooks BR, Brooks III CL, MacKerell AD Jr., Nilsson L, Petrella RJ, Roux B, et al. CHARMM: the biomolecular simulation program. J Comput Chem. 2009;30(10):1545–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Deng Y, Roux B. Hydration of amino acid side chains: nonpolar and electrostatic contributions calculated from staged molecular dynamics free energy simulations with explicit water molecules. J Phys Chem B. 2004;108:16567–76. [Google Scholar]
- 71.Harder E, Roux B. On the origin of the electrostatic potential difference at a liquid-vacuum interface. J Chem Phys. 2008;129(23):234706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Lamoureux G, Roux B. Absolute hydration free energy scale for alkali and halide ions established from simulations with a polarizable force field. J Phys Chem B. 2006;110(7):3308–22. [DOI] [PubMed] [Google Scholar]
- 73.Yu H, Whitfield TW, Harder E, Lamoureux G, Vorobyov I, Anisimov VM, et al. Simulating Monovalent and Divalent Ions in Aqueous Solution Using a Drude Polarizable Force Field. J Chem Theory Comput. 2010;6(3):774–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Baker CM, Lopes PE, Zhu X, Roux B, MacKerell AD Jr. Accurate Calculation of Hydration Free Energies using Pair-Specific Lennard-Jones Parameters in the CHARMM Drude Polarizable Force Field. J Chem Theory Comput. 2010;6(4):1181–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.PyMOL: The PyMOL Molecular Graphics System, Version 2.0 Schrödinger, LLC. [Google Scholar]
- 76.Baker CM, Mackerell AD Jr. Polarizability rescaling and atom-based Thole scaling in the CHARMM Drude polarizable force field for ethers. J Mol Model. 2010;16(3):567–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Schropp B, Tavan P. The polarizability of point-polarizable water models: density functional theory/molecular mechanics results. J Phys Chem B. 2008;112(19):6233–40. [DOI] [PubMed] [Google Scholar]
- 78.Kamitakahara A, Hsu C-L, Pranata J. Reexamination of the conformations of dimethyl phosphate anion in water. Journal of Molecular Structure: THEOCHEM. 1995;334(1):29–35. [Google Scholar]
- 79.Ibargüen C, Manrique-Moreno M, Hadad CZ, David J, Restrepo A. Microsolvation of dimethylphosphate: a molecular model for the interaction of cell membranes with water. Phys Chem Chem Phys. 2013;15(9):3203–11. [DOI] [PubMed] [Google Scholar]
- 80.Klauda JB, Venable RM, Freites JA, O’Connor JW, Tobias DJ, Mondragon-Ramirez C, et al. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J Phys Chem B. 2010;114(23):7830–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.George P, Witonsky RJ, Trachtman M, Wu C, Dorwart W, Richman L, et al. “Squiggle-H2O”. An enquiry into the importance of solvation effects in phosphate ester and anhydride reactions. Biochimica et Biophysica Acta (BBA) - Bioenergetics. 1970;223(1):1–15. [DOI] [PubMed] [Google Scholar]
- 82.Steinbrecher T, Latzer J, Case DA. Revised AMBER Parameters for Bioorganic Phosphates. J Chem Theory Comput. 2012;8(11):4405–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Marcus Y Thermodynamics of solvation of ions. Part 5.—Gibbs free energy of hydration at 298.15 K. J. Chem. Soc. Faraday Trans 1991;87(18):2995–9. [Google Scholar]
- 84.Li J, Zhu T, Hawkins GD, Winget P, Liotard DA, Cramer CJ, et al. Extension of the platform of applicability of the SM5.42R universal solvation model. Theor Chem Acc. 1999;103(1):9–63. [Google Scholar]
- 85.Kelly CP, Cramer CJ, Truhlar DG. Aqueous Solvation Free Energies of Ions and Ion-Water Clusters Based on an Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton. J. Phys. Chem. B 2006;110(32):16066–81. [DOI] [PubMed] [Google Scholar]
- 86.Kelly CP, Cramer CJ, Truhlar DG. SM6: A Density Functional Theory Continuum Solvation Model for Calculating Aqueous Solvation Free Energies of Neutrals, Ions, and Solute-Water Clusters. J Chem Theory Comput. 2005;1(6):1133–52. [DOI] [PubMed] [Google Scholar]
- 87.Park S-J, Lee J, Patel DS, Ma H, Lee HS, Jo S, et al. Glycan Reader is improved to recognize most sugar types and chemical modifications in the Protein Data Bank. Bioinformatics. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Lee J, Cheng X, Swails JM, Yeom MS, Eastman PK, Lemkul JA, et al. CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field. J Chem Theory Comput. 2016;12(1):405–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Patel DS, He X, MacKerell AD Jr. Polarizable empirical force field for hexopyranose monosaccharides based on the classical drude oscillator. J Phys Chem B 2015;119:637–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Jana M, MacKerell AD Jr. CHARMM Drude Polarizable Force Field for Aldopentofuranoses and Methyl-aldopentofuranosides. J Phys Chem B. 2015;119(25):7846–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Lemkul JA, MacKerell AD Jr. Polarizable Force Field for DNA Based on the Classical Drude Oscillator: I. Refinement Using Quantum Mechanical Base Stacking and Conformational Energetics. J Chem Theory Comput. 2017;13(5):2053–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Lemkul JA, MacKerell AD Jr. Balancing the Interactions of Mg(2+) in Aqueous Solution and with Nucleic Acid Moieties For a Polarizable Force Field Based on the Classical Drude Oscillator Model. J Phys Chem B. 2016;120(44):11436–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Lopes PEM, Huang J, Shim J, Luo Y, Li H, Roux B, et al. Polarizable Force Field for Peptides and Proteins Based on the Classical Drude Oscillator. J Chem Theory Comput. 2013;9(12):5430–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


