Feature Uncertainty Predicts Behavioral and Neural Responses to Combined Concepts

Abstract

The cognitive and neural structure of conceptual knowledge affects how concepts combine in language and thought. Examining the principles by which individual concepts (e.g., diamond, baseball) combine into more complex phrases (e.g., “baseball diamond”) can illuminate not only how the brain combines concepts but also the key ingredients of conceptual structure. Here we specifically tested the role of feature uncertainty in the modulation of conceptual brightness evoked by adjective-noun combinations (e.g., “dark diamond”) in male and female human subjects. We collected explicit ratings of conceptual brightness for 45 noun concepts and their “dark” and “light” combinations, resulting in a measure reflecting the degree of conceptual brightness modulation in each noun concept. Feature uncertainty was captured in an entropy measure, as well as in a predictive Bayesian model of feature modulation. We found that feature uncertainty (i.e., entropy) and the Bayesian model were both strong predictors of these behavioral effects. Using fMRI, we observed the neural responses evoked by the concepts and combinations in a priori ROIs. Feature uncertainty predicted univariate responses in left inferior frontal gyrus, and multivariate responses in left anterior temporal lobe were predicted by degree of conceptual brightness modulation. These findings suggest that feature uncertainty is a key ingredient of conceptual structure, and inform cognitive neuroscience theories of conceptual combination by highlighting the role of left inferior frontal gyrus and left anterior temporal lobe in the process of flexible feature modulation during comprehension of complex language.

SIGNIFICANCE STATEMENT The meaning of a word depends on the words surrounding it. The challenge of understanding how flexible meaning emerges in language can be simplified by studying adjective-noun phrases. We tested whether the uncertainty of a feature (i.e., brightness) in a given noun concept (e.g., diamond) influences how the adjective and noun concepts combine. We analyzed feature uncertainty using two probabilistic measures, and found that feature uncertainty predicted people's explicit interpretations of adjective-noun phrases (e.g., “dark diamond”). Using fMRI, we found that combined concepts evoked responses in left inferior frontal gyrus and left anterior temporal lobe that related to our measures of feature modulation and uncertainty. These findings reveal the cognitive and neural processes supporting conceptual combination and complex language use.

Introduction

Human language relies on a deep reservoir of conceptual knowledge. Words (e.g., “diamond”) refer to concepts (e.g., diamond) that contain information relating to knowledge about things in the world (e.g., diamonds are bright, sparkly, and expensive). Most utterances comprise many words strung together, and one must combine the meanings of the underlying concepts to generate an appropriate interpretation. This is complicated because the meaning of a word is often influenced by the words surrounding it (Frege, 1884). That is, the information activated to represent a concept (e.g., diamond) will be flexibly adjusted when the concept combines with other concepts in language (e.g., “dirty diamond,” “baseball diamond”). Here we use conceptual combination to explore the following: (1) aspects of conceptual structure that enable flexible activation of conceptual features, focusing on feature uncertainty, and (2) the neural regions that are involved in flexible feature modulation in complex language use.

The cognitive and neural representations of conceptual features are context-dependent (e.g., Halff et al., 1976; Yee and Thompson-Schill, 2016). We hypothesized that the uncertainty of a conceptual feature (e.g., brightness) within a concept (e.g., diamond) will influence the flexible activation of that feature when corresponding concepts combine (e.g., “dark diamond”). If a feature is present or absent in a concept with high certainty, activation of that feature might be less flexible in relevant verbal contexts: charcoal is almost always dark in color, so “light charcoal” might not induce much change in conceptual brightness. On the other hand, uncertainty in a conceptual feature allows this ambiguity to be resolved in combined concepts resulting in substantial feature change: the brightness of paint is very uncertain, so “light paint” might induce a substantial change in conceptual brightness. We analyzed feature uncertainty using information theory's measure of “entropy,” which reflects the uncertainty, or the informativity, of a signal (Shannon, 1948). In a behavioral experiment, we quantified the extent to which “dark” and “light” modifiers influenced the conceptual brightness of noun concepts, and found that feature uncertainty related to the flexible modulation of conceptual brightness.

Another approach to testing theories of conceptual structure and combination is to embed theoretical assumptions in different computational models and see how well those models predict behavioral or neural responses to combined concepts (e.g., Mitchell and Lapata, 2008, 2010; Baroni and Zamparelli, 2010; Baron and Osherson, 2011). We therefore also embedded feature uncertainty in a predictive Bayesian model of feature composition. This Bayesian model outperformed more traditional models that do not incorporate feature uncertainty. Probabilistic models of language composition have been explored in prior work (Lassiter and Goodman, 2013; Goodman and Frank, 2016); here we extend these ideas to the analysis of feature-based semantic composition.

We also aimed to characterize the neural regions involved in the flexible modulation of conceptual features in the “dark” and “light” adjective-noun phrases. Previous fMRI studies of conceptual knowledge and combination constrained our analyses to neural regions implicated in related cognitive processes. Left anterior temporal lobe (LATL) is consistently recruited in conceptual combination tasks (Baron et al., 2010; Baron and Osherson, 2011; Bemis and Pylkkänen, 2011, 2013a,b; Boylan et al., 2017). Left angular gyrus (LAG) has also been widely implicated in conceptual combination (Bemis and Pylkkänen, 2013a; Boylan et al., 2015, 2017; Price et al., 2016). Conceptual combination is similar to figurative language in that it involves the flexible selection and integration of conceptual features across concepts. Left inferior frontal gyrus (LIFG) is heavily implicated in figurative language comprehension, and has revealed sensitivity to flexible feature selection (Solomon and Thompson-Schill, 2017) and changes in metaphor familiarity over time (Cardillo et al., 2012). We also examined responses in left fusiform gyrus (LFUS), which is involved in semantic retrieval of visual features in language tasks (e.g., Martin, 2007) and might therefore be recruited to represent conceptual brightness in combined concepts. Our fMRI study implicates LATL and LIFG in the flexible modulation of conceptual features during comprehension of adjective-noun combinations.

Materials and Methods

Participants

In the behavioral experiment, 357 participants (49% female; mean ± SD age, 39.8 ± 13.4 years) completed online surveys on Amazon Mechanical Turk and were compensated according to standard rates. Participants were located within the United States. Consent was obtained for all participants in accordance with the University of Pennsylvania Institutional Review Board.

Adjective and noun stimuli

We focused on the single dimension of conceptual brightness to enable a tightly controlled analysis of how brightness information is modulated across verbal contexts. The adjectives “dark” and “light” were used to modulate the conceptual brightness of 45 noun concepts. These 45 noun concepts covered the full range of brightness values (e.g., diamond, snow, paint, shadow, charcoal; Fig. 1B). A full list of noun stimuli is shown in Table 1.

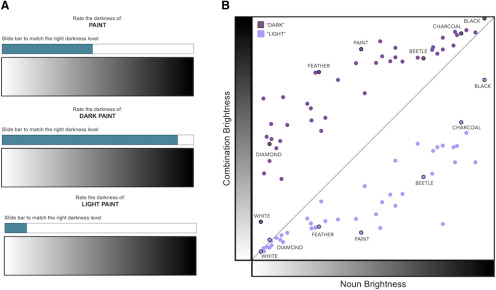
Figure 1.

Explicit measures of conceptual brightness. A, Participants used a visual scale to indicate the brightness of nouns and adjective-noun combinations. B, We calculated the extent to which conceptual brightness was modulated across the 45 noun concepts. Distance from the middle black line corresponds to increased modulation of conceptual brightness separately for the “dark” and “light” modifiers. The calculated ground-truth brightness modulation for each concept is the mean absolute distance between combination brightness and noun brightness across the two adjectives.

Table 1.

Noun concepts^a

white	sand	eyeshadow
paper	sky	mud
snow	feather	beetle
sugar	silver	shadow
diamond	coconut	asphalt
teeth	marble	chocolate
pearls	slippers	limousine
rice	paint	coffee
dove	gray	panther
bone	fur	cave
ivory	car	mascara
cloud	rock	charcoal
foam	jeans	night
shell	jacket	tuxedo
bread	rubber	black

^aThe 45 noun concepts used in the current study are displayed in order of conceptual brightness (light to dark).

Noun stimuli were normed for word length, frequency, and concreteness. Word frequency and concreteness data were extracted from Brysbaert et al. (2014); Spearman's correlation was used to assess relationships between variables. A significant negative association was found between word length and frequency ($\rho$ = −0.44, p = 0.002, R² = 19%); word concreteness was not associated with either word length (p > 0.7) or word frequency (p > 0.4).

We also tested whether these variables correlated with our behavioral measures of interest (see below). While no significant relationships were found between noun brightness and word frequency ($\rho$ = −0.24, p = 0.12) or concreteness (p > 0.3), we did observe a significant positive association between word length and noun brightness ($\rho$ = 0.35, p = 0.02, R² = 12%). It should be noted that none of our behavioral predictions related to explicit noun brightness; indeed, our analyses were designed precisely to orthogonalize brightness modulation and noun brightness. However, we do control for word length when analyzing neural sensitivity to noun brightness in our fMRI data. Most importantly, no relationships were found between brightness entropy and word length (p > 0.8), frequency (p > 0.6), or concreteness (p > 0.6), or between ground-truth modulation and word length (p > 0.7), frequency (p > 0.5), or concreteness (p > 0.2).

Experimental design

One group of online participants (N = 58) provided subjective ratings of brightness probability. Each of the 45 noun concepts was presented in a randomized order, and participants were asked “Is/are [noun] typically dark?” on a 5 point scale ranging from “This is always light” to “This is always dark.” Ratings were reliable across participants (Cronbach's $\alpha$ = 0.82). Responses were averaged across participants and scaled between 0 and 1 to reflect brightness probability (p) for each of the 45 noun concepts, in which values close to 0 indicate that a concept is likely light in color and values close to 1 indicate that a concept is likely dark in color.

Another group of participants (N = 100) rated the brightness of the unmodified noun concepts. For each of the 45 noun concepts, participants were asked to rate the darkness of each concept by sliding a bar corresponding to a visually presented scale transitioning from white to black (e.g., “Rate the darkness of: paint,” Fig. 1A). The numerical values of the visual scale ranged from 0 (white) to 50 (black) and were hidden to participants. Stimuli were presented in a randomized order. These brightness judgments were reliable (Cronbach's $\alpha$ = 0.80) and were averaged across participants, resulting in brightness values for each of the 45 unmodified nouns.

A final group of participants (N = 199) rated the brightness of the adjective-noun combinations. Stimuli were split into two lists such that each participant saw each noun modified by either “dark” or “light,” and participants performed the same task described above (e.g., “Rate the darkness of: dark paint”). Brightness judgments of the adjective-noun combinations were reliable within both stimulus lists (Cronbach's $\alpha$ = 0.76, $\alpha$ = 0.86). Responses were averaged across participants, resulting in brightness values for each of the 45 “dark” combinations and each of the 45 “light” combinations. These values were compared with the brightness values of the unmodified nouns to calculate the degree of brightness modulation caused by “dark” and “light” adjectives for each noun concept. We describe this method in more detail below.

Behavioral measure of brightness uncertainty

Information theory's measure of entropy (Shannon, 1948) is a measure of uncertainty that can be calculated using probability values. Here we use entropy as a measure of feature uncertainty for a particular feature-noun pair. More specifically, we want to know the uncertainty of brightness in the 45 noun concepts, such as diamond and paint. Given the brightness probability values described above, we defined brightness entropy (E) as follows:

where P_LIGHT = 1 – P_DARK. This was our behavioral measure of brightness uncertainty. Entropy is symmetrical around p = 0.5, where p = 0 and p = 1 indicate maximum lightness and darkness, respectively; each concept was thus assigned a single entropy value that captured the concept's brightness uncertainty on the light-dark spectrum (i.e., it makes no difference whether E is calculated based on P_LIGHT or P_DARK). We predicted that brightness uncertainty would positively relate to the degree to which conceptual brightness is modulated across the 45 noun concepts when paired with “light” and “dark” adjectives.

Ground-truth brightness modulation

One reason why we used the single dimension of conceptual brightness, along with both “dark” and “light” modifiers, is because it allowed us to completely disentangle brightness uncertainty from brightness probability: whereas the combined light and dark probabilities are always identical across concepts (P_DARK + P_LIGHT = 1), each concept has a unique entropy value that captures uncertainty within the brightness dimension. That is, brightness probability alone cannot predict any differences in brightness modulation when collapsed across “dark” and “light” adjectives, whereas brightness uncertainty does have the ability to predict variation in feature modulation across concepts. Thus, any relationship between brightness entropy and brightness modulation cannot be attributed to brightness probability in the noun concept.

To derive this measure of brightness modulation, we first determined the extent to which “dark” and “light” adjectives separately modulated brightness in each of the 45 items by calculating the difference in brightness between each noun concept and its associated adjective-noun combinations (Fig. 1B). For example, the diamond “dark” effect corresponds to the absolute difference between the brightness values of “diamond” and “dark diamond,” and the diamond “light” effect corresponds to the absolute difference between the brightness values of “diamond” and “light diamond.” The mean of these “dark” and “light” effects for each noun reflects the extent to which brightness can be modulated within a concept across language contexts. We refer to this measure as ground-truth brightness modulation.

Results

Behavioral results

Feature uncertainty predicts ground-truth modulation

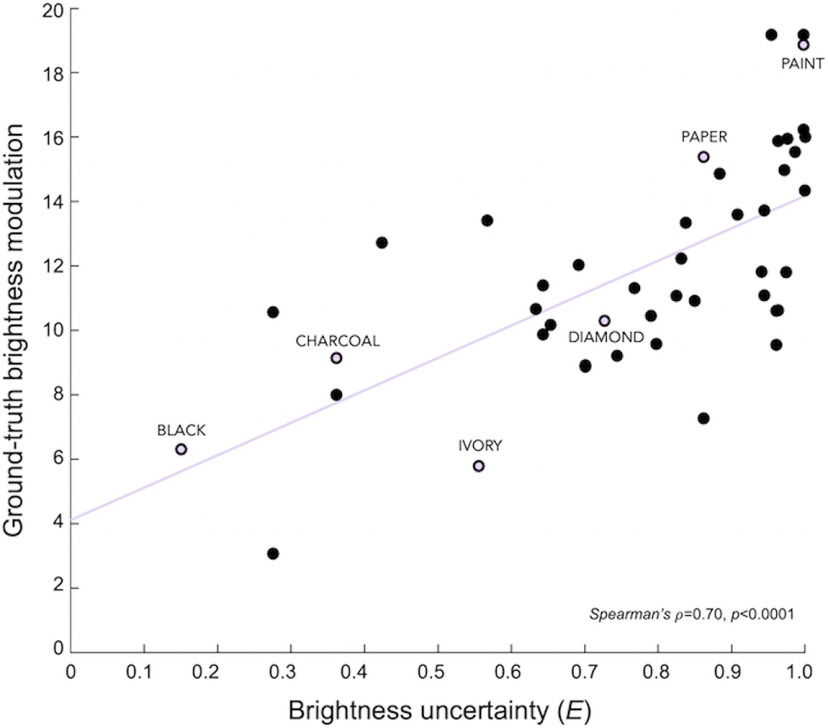
We used entropy to derive a measure of feature uncertainty, which specifically captured the uncertainty of conceptual brightness within each of our 45 noun concepts. We predicted that brightness uncertainty would positively predict the extent to which a concept's conceptual brightness could be modulated by related adjectives (i.e., “dark” and “light”). Consistent with this prediction, we observed a strong positive relationship between brightness uncertainty and ground-truth brightness modulation ($\rho$ = 0.70, p < 0.0001, R² = 49%), a result that supports the hypothesis that feature uncertainty is an aspect of conceptual structure that may influence processes of conceptual combination (Fig. 2).

Figure 2.

Brightness uncertainty predicts ground-truth brightness modulation in combined concepts. Brightness uncertainty was captured using entropy (E), based on the brightness probability of each noun concept. Brightness uncertainty positively predicted ground-truth brightness modulation ($\rho$ = 0.70, p < 0.001). Concepts characterized by low brightness uncertainty (e.g., charcoal) did not show large changes in brightness in “dark” and “light” combinations. Concepts with high brightness uncertainty (e.g., paint) showed large changes in brightness when modified by the same adjectives.

Observed relationship is not due to edge effects

Another reason why we combined across “dark” and “light” when analyzing ground-truth modulation was to reduce the influence of edge effects. By collapsing across “dark” and “light” modifiers, each concept has the same maximum potential movement on the brightness scale (i.e., 50 brightness units). When only one adjective is analyzed, some concepts have more of an opportunity to change than others due to the brightness of the unmodified nouns. For example, the darkness of charcoal (B_NOUN = 43) can only increase by 7 units when the “dark” modifier is used, whereas the darkness of snow (B_NOUN = 3) can potentially increase by 47 units. Collapsing across “dark” and “light” thus eliminates this particular concern.

However, to further confirm that the observed relationship between brightness uncertainty and modulation was not driven by noun concepts on the extreme edges of the bounded brightness scale, we removed the 15 darkest and 15 lightest noun concepts and ran the same correlation with the remaining 15 concepts. A positive relationship between brightness uncertainty and ground-truth modulation remained ($\rho$ = 0.78, p = 0.0006, R² = 61%). Indeed, this relationship still held when only the 9 middle-brightness noun concepts (gray, car, rock, marble, fur, slippers, paint, silver, coconut) were analyzed ($\rho$ = 0.74, p = 0.03, R² = 55%). These additional analyses support our claim that the relationship between feature uncertainty and feature modulation is not merely due to edge effects but does reflect something meaningful about how concepts are combined.

Modeling Methods

Predictive models of adjective-noun combination

To further understand how conceptual features are modulated in combined concepts, we created a set of predictive models that made different predictions about how concepts combine. Each model generates predictions reflecting the conceptual brightness of the adjective-noun combinations (B_COMBO) based on the conceptual brightness of the adjective (B_ADJ) and noun (B_NOUN); we tested the accuracy of these B_COMBO predictions in the analyses below. First, we tested an adjective model and a noun model, which provided baseline accuracy measures. Next, we tested an additive model that made B_COMBO predictions based on a weighted sum of the adjective and noun brightness representations, and a multiplicative model that made B_COMBO predictions based on the product of B_NOUN and a scaling parameter. Finally, we tested a Bayesian model that made B_COMBO predictions based on the product of adjective and noun brightness distributions. The Bayesian model was the only model that incorporated feature uncertainty.

Baseline models

The adjective and noun models are noncombinatorial and can therefore generate baseline predictions that the more interesting combinatorial models should outperform. A similar approach is found in distributional or vector-based semantics(e.g., Mitchell and Lapata, 2008, 2010; Chang et al., 2009). In the adjective model, the predicted brightness of the combined concept (e.g., “dark diamond”) is identical to the brightness of the adjective (e.g., “dark”) as follows:

where B_ADJ corresponds to either extreme end of the scale (B_DARK = 50; B_LIGHT = 0). When only one adjective is analyzed, the additive model does not predict differences in B_COMBO across the 45 nouns (see Fig. 4B) but does predict differences in B_CHANGE due to variation in B_NOUN. Importantly, however, this model does not predict any B_CHANGE variation across concepts when adjective effects are combined.

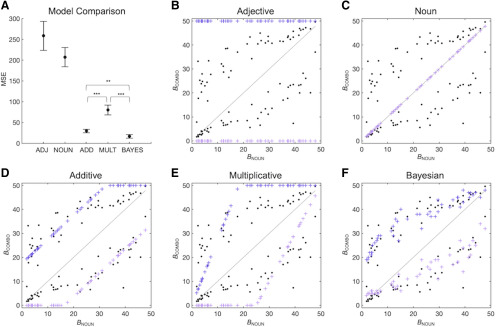
Figure 4.

Bayesian combinatorial model best predicts brightness of combined concepts. A, We compared the B_COMBO predictions of our five model against ground-truth B_COMBO data. The y axis indicates the MSE of the model predictions. Lower values indicate better performance. The Bayesian model outperformed both the additive models (t₍₄₄₎ = 2.93, p = 0.005) and multiplicative model (t₍₄₄₎ = 7.14, p < 0.001), providing further evidence that feature uncertainty is relevant for conceptual combination. Error bars indicate SEM. B–F, B_COMBO predictions of the 45 “dark” (dark purple) and 45 “light” (light purple) combinations for the adjective, noun, additive, multiplicative, and Bayesian models. Black dots represent the same ground-truth B_COMBO values presented in Figure 1B.

The second baseline model was a noncombinatorial noun model, in which the predicted brightness of the combined concept is identical to the brightness of the unmodified noun as follows:

The noun model predicts differences in B_COMBO across items (see Fig. 4C). It does not predict any variance in B_CHANGE in the “dark” and “light” combinations separately, nor when averaged together. Thus, like the adjective model, the noun model is also unable to capture variability in the extent to which brightness can be modulated across the 45 noun concepts.

Additive model

We constructed a combinatorial additive model in which the predicted brightness of a combined concept is a weighted sum of B_ADJ and B_NOUN. This model has been proposed as a candidate combinatorial mechanism in both cognitive (e.g., Smith et al., 1988) and computational models of distributional semantics (e.g., Mitchell and Lapata, 2010). The general form is as follows:

where W is a weight that scales B_ADJ. In our case, B_ADJ represents the extreme brightness values (B_DARK = 50; B_LIGHT = 0). Our implementation of the additive model makes separate predictions for “dark” and “light” combinations:

We optimized W between 0$\le W\le$1 (intervals of 0.01), separately for “dark” and “light” combinations (Fig. 3D). This resulted in a value of W_DARK (0.35) that minimized the mean squared error (MSE) of B_COMBO-DARK predictions relative to the explicit dark-combo brightness values, and a value of W_LIGHT (0.33) that similarly minimized the MSE of B_COMBO-LIGHT predictions. We used these optimized parameters to generate B_COMBO and B_CHANGE predictions for each concept. The additive model's B_COMBO predictions are shown in Figure 4D.

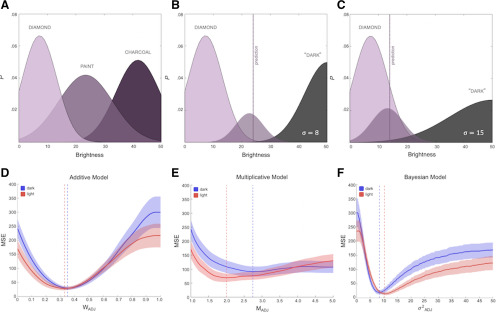
Figure 3.

Predictive combinatorial models. A, In our Bayesian model, conceptual brightness was represented as a probability distribution over brightness values for each noun concept. Greater values on the x axis indicate increased conceptual darkness. Each distribution is defined by a mean and σ, derived from our behavioral task (see Fig. 1). We defined the means of the “dark” and “light” distributions as the extreme ends of the brightness scale, and optimized for σ. B, C, Different “dark” $\sigma$ values result in different B_COMBO predictions for “dark diamond,” and our goal was to find the σ that generated the most accurate predictions of B_COMBO across the 45 noun concepts. D, In the additive model, we optimized the adjective weight for “dark” (W = 0.35) and “light” (W = 0.33) separately. E, In the multiplicative model, we optimized the parameter that scaled the noun concept for “dark” (M = 2.74) and “light” (M = 2.00) separately. F, In the Bayesian model, we optimized the σ of the “dark” ($\sigma$ = 8.42) and “light” ($\sigma$ = 10.27) distributions separately. We averaged the “dark” and “light” parameters within each model to analyze fMRI data.

Multiplicative model

We also constructed a combinatorial multiplicative model in which the predicted brightness of a combined concept is a product of B_NOUN and a scaling parameter that reflects the influence of the adjective. This model is interpreted as an integrative model in computational models of distributional semantics (e.g., Chang et al., 2009; Mitchell and Lapata, 2010). The general form is as follows:

where S is a parameter that determines the influence of “dark” and “light” modifiers on each noun concept. We optimized S between 0$\le S\le$5 (intervals of 0.01), separately for “dark” and “light” combinations (Fig. 3E). This resulted in a value of S_DARK (2.74) that minimized the MSE of B_COMBO-DARK predictions relative to the explicit dark-combo brightness values, and a value of S_LIGHT (2.0) that similarly minimized the MSE of B_COMBO-LIGHT predictions. Once the S parameter was optimized for each adjective, we used that parameter to generate B_COMBO and B_CHANGE predictions for each concept. The multiplicative model's B_COMBO predictions are shown in Figure 4E.

Bayesian model

We previously described how feature uncertainty can be reflected in an entropy measure, but feature uncertainty can also be embedded in probabilistic feature models. We thus constructed a combinatorial Bayesian model of adjective-noun combinations that incorporated brightness uncertainty. Brightness representations for adjective and noun concepts were captured in probability distributions over brightness values, in which the peak of the distribution reflects the mean brightness of the concept and the variance of the distribution reflects brightness uncertainty (Fig. 3A). A narrow brightness distribution indicates more certainty in the concept's brightness, and a wide brightness distribution indicates more uncertainty. In our Bayesian model, the predicted brightness of a combined concept is a function of the product of the constituent concepts' brightness distributions. If the brightness probability distributions for adjectives (P_ADJ) and nouns (P_NOUN) are Gaussian distributions defined by a mean ($\mu$) and SD ($\sigma$), then a Bayesian B_COMBO prediction is the maximum a posteriori estimate of the product of these distributions:

We derived the 45 P_NOUN distributions (e.g., for diamond, paint, charcoal) by fitting Gaussian distributions to histograms reflecting the frequency of responses in the explicit brightness judgment task. We do not have data corresponding to the P_ADJ distributions; for simplicity, we assumed that P_DARK$\mu$ = 50 and P_LIGHT$\mu$ = 0. We optimized separately for P_DARK$\sigma$ and P_LIGHT$\sigma$ (0$\le \sigma \le$50; intervals of 0.01). Two example P_DARK distributions with P_DARK$\sigma$ = 8 and P_DARK $\sigma$ = 15 are shown in Figure 3B,C. This procedure resulted in values for P_DARK$\sigma$ (8.42) and P_LIGHT$\sigma$ (10.27) that minimized the MSE of B_COMBO predictions relative to the explicit B_COMBO values (Fig. 3F). Once the P_ADJ$\sigma$ parameter was optimized for each adjective, we used that parameter to generate B_COMBO and B_CHANGE predictions for each concept. This enabled us to compare the relative accuracy of the additive, multiplicative, and Bayesian models, thereby determining whether the inclusion of feature uncertainty in a combinatorial model improves predictions of feature modulation. The Bayesian model's B_COMBO predictions are shown in Figure 4F.

Modeling Results

Bayesian model best predicts brightness of combinations

We tested the success of each of our models (i.e., adjective, noun, additive, multiplicative, Bayesian) at predicting the brightness of combined concepts (i.e., B_COMBO). The predictions of each model are shown in Figure 4B–F. For each model, we calculated the MSE for each of the 90 combinations, averaged across “dark” and “light” modifiers for each item, and then averaged across items to calculate the overall error for each model (Fig. 4A). As expected, the adjective model (MSE = 258.6) and noun model (MSE = 207.3) performed poorly relative to the combinatorial models. Restricting our analyses to the combinatorial models, a one-way ANOVA confirmed that overall MSE differed across the additive, multiplicative, and Bayesian models (F_(2,132) = 23.06, p < 0.001). Pairwise comparisons revealed that the multiplicative model performed worse than both the additive model (t₍₄₄₎ = 5.59, p < 0.001) and the Bayesian model (t₍₄₄₎ = 7.14, p < 0.001). Most interestingly, the Bayesian model also significantly outperformed the additive model (t₍₄₄₎ = 2.93, p = 0.005). The Bayesian model therefore made the most accurate predictions regarding the ground-truth conceptual brightness of adjective-noun combinations. The Bayesian model still outperformed the additive (t₍₄₄₎ = 2.29, p = 0.027) and multiplicative (t₍₄₄₎ = 7.65, p < 0.001) models when the optimized “dark” and “light” parameters were averaged within each model. This finding that the Bayesian combinatorial model, which incorporates feature uncertainty, outperformed the other combinatorial models further suggests that feature uncertainty contributes to feature modulation in conceptual combination.

fMRI Methods

Participants

Twenty-four participants (67% female; mean ± SD age, 25.6 ± 10.2 years) from the University of Pennsylvania community completed the fMRI study and were compensated $20/h for their time. All fMRI participants were right-handed, fluent speakers of English, with no self-reported neurologic disorders or damage. Consent was obtained for all participants in accordance with the University of Pennsylvania Institutional Review Board.

Experimental design

The fMRI study comprised six scanning runs; participants viewed the 45 unmodified noun concepts in the first two scans and the 90 adjective-noun combinations in the final four scans. Participants completed two tasks simultaneously: a conceptual color detection task (“color task”) and a fixation size-change detection task (“fixation task”).

In the unmodified noun scans (1 and 2), items were presented in an event-related design with 2 s stimulus presentation and a fixation interstimulus interval of 2-8 s. In the color task, participants were asked to press a button on a hand-held response box when an item referred to a cued color; the color cue (i.e., red or green) was presented before each block of trials. We thus interspersed filler items throughout each scan that were either typically red (e.g., “strawberry,” “ruby”), or typically green (e.g., “lettuce,” “frog”). This task was chosen to encourage visual imagery of the items without explicitly asking participants to think about conceptual brightness. Each run comprised one block of red-cued trials and one block of green-cued trials; the order of red/green blocks was pseudorandomized across runs. Each of the 45 target noun concepts was presented once per scan in a pseudorandomized order and was seen once in a red block and once in a green block across the experiment. To increase engagement with the stimuli, we included an additional fixation task in which participants were asked to press a different button on the response box when the fixation cross presented between the noun stimuli briefly changed in size, which happened at random intervals 8 times per scan (four per block).

In the combined concept runs (3-6), participants completed the same color task and fixation task described above. The fillers in the color task were combined concepts that are typically red (e.g., “dark blood,” “stop sign”) or green (e.g., “light moss,” “football field”). We included fillers that did not include “dark” and “light” modifiers to encourage participants to process the full combined phrases rather than focus on the final word alone. Each of the 45 noun concepts appeared (modified by “dark” or “light”) once per scan, resulting in two presentations of each specific combination across the experiment. Each combination (e.g., “dark diamond”) was seen once in a red block and once in a green block.

fMRI acquisition and analysis

fMRI data were collected on a 3-T Siemens Trio System equipped with a 64-channel array head coil. Structural data included axial T1-weighted localizer images with 160 slices and 1 mm isotropic voxels (TR = 1850 ms, TE = 3.91 ms, TI = 1100 ms, FOV = 240 mm, flip angle = 8°). Functional data included six acquisitions of echo-planar fMRI using a multiband sequence performed in 78 axial slices and 2 mm isotropic voxels (TR = 2000 ms, TE = 30 ms, FOV = 192 mm, flip angle = 75°).

Data were preprocessed and analyzed using FSL. Preprocessing included motion correction using MCFLIRT, spatial smoothing with a Gaussian kernel of FWHM 5 mm, and high-pass temporal filtering. Motion outliers were modeled as covariates of no interest. All scans were analyzed with a GLM, including item-level regressors modeling the individual TRs for each concept or combination contrasted against the fixation baseline. We added regressors for TRs in which filler items or instructions were presented, TRs in which the fixation cross changed size, and TRs in which participants made a response on the button box. These data were averaged across scans, resulting in whole-brain β maps for the 45 unmodified noun concepts, 45 dark combinations, and 45 light combinations for each participant. Individual subjects' data were transformed to MNI standard space using FLIRT linear regression in FSL, with a final isotropic voxel resolution of 2 mm. We excluded time points in which participants incorrectly responded to an experimental item from all subsequent analyses.

Defining a priori ROIs

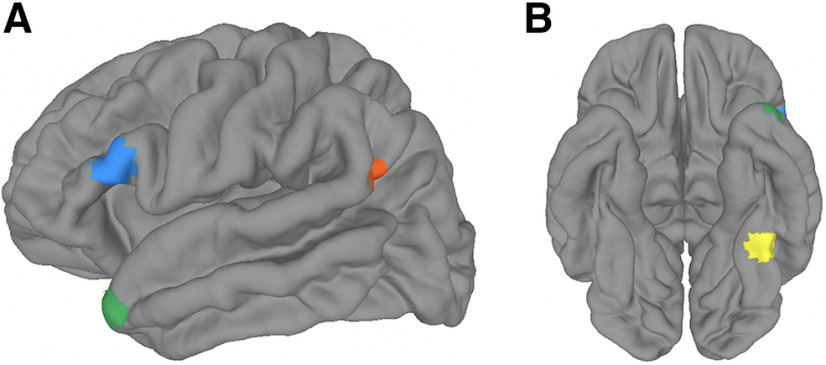
We analyzed neural responses to combined concepts within a priori ROIs. We selected four neural regions based on their association with theoretically relevant aspects of language comprehension and conceptual knowledge: LFUS, LAG, LATL, and LIFG. Each of these regions has been implicated in a cognitive process that could contribute to conceptual feature modulation in comprehension of combined concepts; instead of running multiple functional localizers, we referred to previous fMRI studies that report the peak voxel from an analysis that targeted one of these cognitive processes of interest (Fig. 5). Each of these spherical ROIs comprised 123 voxels, although we also report results of analyses performed in smaller and larger ROIs to confirm the robustness of our findings.

Figure 5.

A priori neural ROIs. We analyzed responses in four ROIs; each 123-voxel spherical ROI was drawn around the peak voxel reported in a prior study. The LIFG ROI (blue) was centered at MNI coordinates x = −54, y = 24, z = 10 based on an analysis of metaphor processing (Cardillo et al., 2012). The LATL ROI (green) was centered at x = −40, y = 16, z = −32 based on a multivoxel analysis of combined concepts (Baron and Osherson, 2011). The LAG ROI (orange) was centered at x = −52, y = −56, z = 22 based on an analysis of adjective-noun combinations (Price et al., 2015). The LFUS ROI (yellow) was centered at x = −38, y = −47, z = −14 based on an analysis of task-dependent color processing (Hsu et al., 2012). A, Left lateral view; B, ventral view, projected onto a cortical surface in MNI space.

The representation of a conceptual feature that has been modulated by or integrated within a combined concept could take place in the same neural region(s) that represent the conceptual feature in single concepts. While primary visual cortex is recruited for color and brightness perception (e.g., Rossi et al., 1996; Shapley and Hawken, 2011), LFUS is involved in semantic retrieval of color and other visual features in language tasks (e.g., Thompson-Schill et al., 1999; Hsu et al., 2011; Martin, 2007). Specifically, Hsu et al. (2011) observed increased activation in LFUS when the task required more detailed or specific color knowledge. Hypothesizing that this context-dependent activation of color information might correspond with context-dependent feature modulation in combined concepts, we drew our LFUS ROI around the peak voxel in the analysis reported by Hsu et al. (2011).

LAG has been widely implicated in studies of conceptual combination (Bemis and Pylkkänen, 2013a; Price et al., 2015, 2016; Boylan et al., 2015, 2017). Specifically, Price et al. (2015) observed increased activation in LAG for adjective-noun combinations that were more plausible (e.g., “plaid jacket” vs “fast blueberry”). Hypothesizing that this adjective-noun comprehension might correspond with feature modulation in our adjective-noun combinations, we drew our LAG ROI around the peak voxel reported by Price et al. (2015).

LATL has also been heavily implicated in conceptual combination (Baron et al., 2010; Baron and Osherson, 2011; Bemis and Pylkkänen, 2011, 2013a,b; Westerlund and Pylkkänen, 2014; Boylan et al., 2017). Specifically, Baron and Osherson (2011) observed that the multivoxel fMRI patterns evoked by combined concepts in LATL could be predicted by multiplicative and additive combinations of the patterns evoked by the constituent concepts. Hypothesizing that the integration of simple concepts in LATL might reflect the modulation of conceptual features, we drew our LATL ROI around the peak voxel reported by Baron and Osherson (2011). This ROI was less ventral, and/or more anterior, than the ATL sites considered by Lambon Ralph and colleagues to be a “semantic hub” (e.g., Pobric et al., 2007; Lambon Ralph et al., 2009; Visser and Lambon Ralph, 2011); our fMRI sequence was not optimized to account for the reduced FOV and signal quality to which these ventral ATL regions are susceptible (Visser et al., 2010).

LIFG has not yet been implicated in conceptual combination but is known to support related cognitive processes, such as semantic selection (Thompson-Schill et al., 1997, 1999) and figurative language comprehension (Rapp et al., 2004, 2007; Eviatar and Just, 2006; Lee and Dapretto, 2006; Stringaris et al., 2007; Bambini et al., 2011; Cardillo et al., 2012); we have previously reported LIFG sensitivity to the selection of conceptual features during metaphor processing (Solomon and Thompson-Schill, 2017). Conceptual combination is very similar to figurative language in that it involves the flexible selection and integration of conceptual features across concepts (Wisniewski, 1997; Estes and Glucksberg, 2000; Coutanche et al., 2020). Cardillo et al. (2012) observed that LIFG activation was tuned by metaphor familiarity, suggesting that LIFG is recruited during metaphor processing when it requires integrating constituent concepts on-the-fly. Hypothesizing that metaphor-related integration in LIFG might relate to modulation of conceptual features, we drew our LIFG ROI around the peak voxel reported by Cardillo et al. (2012).

Univariate fMRI modulation

We calculated a measure of univariate neural modulation (“univariate effects”) that captured the extent to which neural responses to the 45 noun concepts were modulated by “dark” and “light” adjectives. This measure is the neural analog of the ground-truth modulation measure described above. For each participant, the voxel responses to each of the 45 noun concepts were averaged across scans and then averaged within each ROI, resulting in one univariate response for each of the 45 nouns. These values were z-scored for each subject, such that the mean univariate response across all items in each ROI was set to 0 for each participant. These standardized responses to the 45 items were averaged across subjects, resulting in a univariate response to each of the 45 noun concepts. Identical methods were used to capture univariate responses to the 90 combinations, resulting in standardized activation values for the unmodified noun, dark combination, and light combination for each of the 45 items.

For each item, the univariate “dark” effect was the absolute value of the difference between the dark combination (e.g., “dark diamond”) and the noun (e.g., “diamond”); the univariate “light” effect was the absolute value of the difference between the light combination (e.g., “light diamond”) and the noun (e.g., “diamond”). These values were averaged to result in the univariate effect for each item, reflecting the extent to which neural responses to noun concepts are modulated by adjective-noun combinations. We discard the direction of change in fMRI analyses because there is no a priori reason why an increase in conceptual darkness would result in either an increase or decrease in neural response, and this directionality could potentially differ across ROIs. Furthermore, there is no reason to assume that these neural modulations reflect changes in representational brightness per se as opposed to processes involved in adjusting representations elsewhere in the brain.

We calculated the significance of relationships between our measures of interest and univariate effects in each ROI using Spearman's correlation and permutation testing. In each permutation analysis, we ran 10,000 permutations in which items were shuffled before correlating the behavioral and univariate measures, thereby generating a null distribution of correlation values. In all cases, we predicted positive relationships between behavioral and neural effects, and we considered negative relationships to be uninterpretable (e.g., increased conceptual change corresponding with decreased change in neural response). We thus assessed significance in a one-tailed design, such that the uncorrected significance threshold was the 95th percentile of permuted correlation values $(\alpha$ = 0.05). To correct for multiple comparisons across the four ROIs, the significance threshold was adjusted to the 98.75th percentile $(\alpha$ = 0.0125).

Multivariate fMRI modulation

We also calculated a measure of multivariate neural modulation (“multivariate effects”) that captured the extent to which multivoxel patterns (MVPs) corresponding to the 45 noun concepts were modulated by “dark” and “light” adjectives. Instead of averaging activity within each ROI, we analyzed the MVP across the 123 voxels. We calculated the Spearman's distance between MVPs evoked by the noun (e.g., “diamond”) and dark combination (e.g., “dark diamond”), as well as the distance between MVPs evoked by the noun and the light combination (e.g., “light diamond”), for each of the 45 items and separately for each subject. This distance measure corresponded to 1 – $\rho$, such that the distance values ranged from 0 (patterns are identical) to 2 (patterns are maximally different). These dark- and light-distance values were averaged across subjects, resulting in a multivariate dark and light effect for each item. These dark and light effects were summed for each noun concept, resulting in an overall multivariate effect for each of the 45 noun concepts. This measure captured the extent to which patterns of neural activity were modulated by the combined concepts in each of the ROIs.

Using combinatorial models to predict neural responses to combined concepts

In our analysis of univariate and multivariate fMRI data, we simplified the combinatorial models by averaging the optimized “dark” and “light” parameter estimates within each model. That is, for the additive model, we averaged the weight parameter W for “dark” and “light” and used the resulting W to generate B_CHANGE predictions for each combination. We similarly averaged the “dark” and “light” scaling parameters S for the multiplicative model, and the “dark” and “light” uncertainty parameters $\sigma$ for the Bayesian model.

The dark and light B_CHANGE predictions were averaged for each noun concept such that these B_CHANGE values were analogous to the ground-truth modulation measure. Averaging across modifiers is important because it enables us to interpret the B_CHANGE predictions as combinatorial; noncombinatorial models (i.e., the adjective and noun models) do not predict any differences in B_CHANGE across nouns when collapsing across “dark” and “light” combinations. Thus, the ability of these B_CHANGE measures to predict neural activity can be taken to reflect a combinatorial process, rather than a noncombinatorial process that may nevertheless influence neural responses (e.g., feature saturation effects).

Neural representations of conceptual brightness

We sought to determine whether any of the ROIs were sensitive to conceptual brightness in the unmodified noun concepts. In a univariate analysis, we used a regression analysis to determine whether explicit brightness ratings could predict mean univariate responses to the 45 noun concepts when controlling for word length. Because there was no a priori hypothesis for the directionality between mean neural activity and conceptual brightness, we used a two-sided regression analysis in a permutation test similar to that described above. We implemented this by testing for both a positive ($\alpha$ = 0.025) and negative ($\alpha$ = 0.025) relationship. However, to control for multiple ROI comparisons, the significance threshold was further reduced to assess both positive and negative correlations ($\alpha$ = 0.006).

In a multivariate analysis, we compared neural similarity spaces in each ROI to a brightness similarity model derived from the explicit brightness data. This brightness similarity model corresponded to a 45 × 45 matrix in which each cell corresponds to a pair of noun concepts. For each pair of concepts i and j, the value at matrix location (i,j) is the absolute difference of the brightness ratings of i and j. Identical methods were used to generate a word-length similarity matrix. The corresponding ROI similarity matrices were constructed by, for each subject, calculating the Spearman's distance between each of the 123-voxel patterns evoked by the 45 unmodified concepts; the resulting subject-specific similarity matrices were averaged into a concept similarity space for each ROI, and the diagonal and redundant similarity values (j,i) were removed. Because we were testing whether concepts with similar brightness values would evoke similar neural patterns, we used a one-sided positive regression in a permutation analysis to determine whether brightness of the noun concepts was reflected in patterns of neural activity in any of the ROIs, when controlling for similarity in word length $(\alpha$ = 0.0125).

fMRI Results

Univariate neural modulation

We determined whether our behavioral measures of interest (i.e., brightness uncertainty, ground-truth modulation) predicted univariate modulation evoked by combined concepts in our ROIs. No significant positive relationships were observed between LFUS univariate modulation and either brightness uncertainty or ground-truth modulation (p values > 0.9). Similarly, no positive relationships with these measures were observed in LAG (p values > 0.8) or LATL (p values > 0.2).

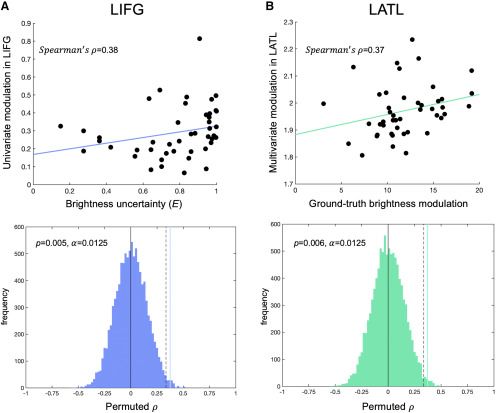
However, we observed a positive relationship between brightness uncertainty and univariate modulation in LIFG ($\rho$ = 0.38, R² = 14%), and permutation testing revealed this was significant while correcting for multiple comparisons (p = 0.005; $\alpha$ = 0.0125; Fig. 6A). This significant relationship held when the analysis was performed in smaller or larger ROIs (33 voxels: p = 0.012, 81 voxels: p = 0.004, 123 voxels: p = 0.005, 179 voxels: p = 0.009, 257 voxels: p = 0.017). We also observed a positive relationship between univariate modulation in LIFG and ground-truth modulation ($\rho$ = 0.33, R² = 11%), although this was not significant after controlling for multiple comparisons (p = 0.013; $\alpha$ = 0.0125). This result was consistent across a range of ROI sizes (81 voxels: p = 0.024, 179 voxels: p = 0.015, 257 voxels: p = 0.017). These results reveal LIFG sensitivity to behavioral measures of feature modulation, specifically feature uncertainty.

Figure 6.

fMRI results. Sensitivity to our combinatorial measures of interest were found in LIFG and LATL. A, Brightness uncertainty predicted univariate modulation in LIFG during comprehension of combined concepts ($\rho$ = 0.38; p = 0.005; $\alpha$ = 0.0125). Significance of Spearman's correlation was assessed in a permutation analysis (bottom). Blue histogram represents the permuted null distribution. Dashed line indicates the significance threshold $\alpha$ = 0.0125. Vertical blue line indicates the true correlation value, which exceeded the threshold. B, Ground-truth brightness modulation predicted multivariate modulation in LATL during comprehension of combined concepts ($\rho$ = 0.37; p = 0.006; $\alpha$ = 0.0125). Significance was assessed in a permutation analysis (bottom).

We also examined whether univariate modulation in our ROIs could be predicted by the additive, multiplicative, or Bayesian models. All of these models are combinatorial, but the Bayesian model incorporates feature uncertainty, whereas the other models do not. Univariate modulation did not positively correlate with additive model B_CHANGE in LFUS (p > 0.7), LAG (p > 0.9), or LATL (p = 0.17). However, univariate modulation in LIFG revealed a significant, positive relationship with the additive model's B_CHANGE predictions ($\rho$ = 0.36; R² = 13%; p = 0.008; $\alpha$ = 0.0125); this result was consistent across a range of ROI sizes (33 voxels: p = 0.036, 81 voxels: p = 0.016, 123 voxels: p = 0.008, 179 voxels: p = 0.011, 257 voxels: p = 0.019). Similar results were observed for the multiplicative model, in which B_CHANGE predictions did not correlate with univariate modulation in LFUS (p > 0.7), LAG (p > 0.9), or LATL (p = 0.19) but did correlate with univariate modulation in LIFG ($\rho$ = 0.34; R² = 12%; p = 0.011; $\alpha$ = 0.0125). As for the Bayesian model, B_CHANGE predictions did not positively correspond with univariate modulation in either LFUS (p > 0.8) or LAG (p > 0.4). However, we did observe evidence suggesting a positive relationship between Bayesian B_CHANGE predictions and univariate modulation in LIFG ($\rho$ = 0.29; R² = 8%; p = 0.027; $\alpha$ = 0.0125) and LATL ($\rho$ = 0.29; R² = 8%; p = 0.026; $\alpha$ = 0.0125). Although these results were not significant after controlling for multiple comparisons, they were robust across a range of ROI sizes in both LIFG (123 voxels: p = 0.027, 179 voxels: p = 0.022, 257 voxels: p = 0.016) and LATL (81 voxels: p = 0.03, 123 voxels: p = 0.03, 179 voxels: p = 0.021, 257 voxels: p = 0.034). These results strongly suggest that univariate responses to combined concepts in LIFG reflect a combinatorial process, whether or not this process incorporates feature uncertainty. These results also suggest that univariate responses in LATL may reflect a combinatorial process.

Multivariate neural modulation

We then determined whether our behavioral measures of interest (i.e., brightness uncertainty, ground-truth modulation) predicted multivariate modulation evoked by combined concepts in our ROIs. Multivariate modulation reflects the extent to which MVPs evoked by the noun concepts were influenced by the “dark” and “light” adjectives. No significant positive relationships were observed between LFUS multivariate modulation and either brightness uncertainty or ground-truth modulation (p values > 0.2). Similarly, multivariate modulation in LAG did not reveal a significant positive relationship with either brightness uncertainty (p > 0.9) or ground-truth modulation ($\rho$ = 0.24; R² = 6%; p = 0.059; $\alpha$ = 0.0125). In contrast with the univariate analyses above, we did not observe significant relationships between multivariate modulation in LIFG and brightness uncertainty (p > 0.3) or ground-truth modulation (p > 0.2).

In LATL, multivariate modulation was not predicted by brightness uncertainty (p = 0.17). However, we observed a positive relationship between ground-truth modulation and LATL multivariate modulation ($\rho$ = 0.37; R² = 14%; p = 0.006;$\alpha$ = 0.0125; Fig. 6B); this result was robust across a range of ROI sizes (33 voxels: p = 0.021, 81 voxels: p = 0.008, 123 voxels: p = 0.006, 179 voxels: p = 0.007, 257 voxels: p = 0.012). Thus, ground-truth behavioral modulation of conceptual brightness evoked by our adjective-noun combinations positively predicted the extent to which MVPs in LATL were influenced by those combinations. These results suggest that LATL represents the output of a conceptual combination process.

Neither the additive nor multiplicative model's B_CHANGE predictions predicted multivariate effects in LFUS (p values > 0.4), LAG (p values > 0.3), LATL (p values > 0.4), or LIFG (p values > 0.3). Similarly, the Bayesian model's B_CHANGE predictions did not significantly predict multivariate effects in LFUS (p > 0.6), LAG ($\rho$ = 0.29; R² = 8%; p = 0.067; $\alpha$ = 0.0125), LATL (p > 0.2), or LIFG (p > 0.5).

Neural representations of conceptual brightness

We did not observe representations of conceptual brightness in any of our ROIs. In LFUS, univariate responses did not positively (p > 0.3) or negatively (p > 0.6) relate to explicit brightness ratings when controlling for word length; similar results were observed in LAG (positive: p > 0.5; negative: p > 0.4), LATL (positive: p > 0.8; negative: p = 0.13), and LIFG (positive: p > 0.3; negative: p > 0.6). In the multivariate analysis, similarity of MVPs evoked by noun concepts did not reflect similarity in conceptual brightness when controlling for word length in LFUS (p = 0.11), LAG (p > 0.5), LATL (p > 0.4), or LIFG (p > 0.7).

Discussion

Here we explored how conceptual information is flexibly activated during comprehension of combined concepts using behavioral, modeling, and neuroimaging methods. We specifically targeted the feature dimension of conceptual brightness, which we modulated in adjective-noun combinations. We collected explicit ratings of conceptual brightness for unmodified nouns (e.g., “diamond,” “shadow”) and their “dark” and “light” combinations (e.g., “dark diamond,” “light diamond”), and used these data to characterize the extent to which conceptual brightness could be flexibly modulated within different noun concepts. We then explored whether brightness uncertainty related to these ground-truth modulation effects, and characterized the brain regions involved in this feature-based combinatorial process.

Feature uncertainty was quantified using entropy, a measure from information theory (Shannon, 1948) that reflects the uncertainty of an outcome or the potential informativity of a signal. If p is the probability of an outcome, entropy is highest when p = 0.5. For example, consider flipping a fair coin versus a biased coin. A flip of a fair coin has P_HEADS = 0.5 and P_TAILS = 0.5; the result of the coin flip is maximally uncertain. On the other hand, if a biased coin has P_HEADS = 0.8 and P_TAILS = 0.2, then the result of the flip is less uncertain, as it is likely to result in heads. We translated these ideas to the realm of conceptual knowledge to explore the flexible activation of features in conceptual combination. If the brightness of a noun concept is characterized by complementary values of P_DARK and P_LIGHT, then conceptual brightness will be most uncertain when both P_DARK and P_LIGHT = 0.5. Consider the concepts diamond and paint, which were characterized by P_DARK ∼ 0.2 and P_DARK ∼ 0.5, respectively. These values reflect the fact that diamonds are unlikely to be dark, whereas paint is equally likely to be dark or light in color. Because P_LIGHT = 1 – P_DARK, and because entropy is symmetrical around p = 0.5, each concept can be assigned a single brightness uncertainty value: diamond has a lower brightness uncertainty (0.73) than paint, which has very high brightness uncertainty (0.99).

We predicted that brightness uncertainty would positively correlate with the modulation of conceptual brightness across verbal contexts. For example, we predicted greater change in conceptual brightness for paint when modified by brightness adjectives (i.e., “dark paint,” “light paint”) than for diamond when paired with the same adjectives. Our results supported these predictions: we observed a strong positive relationship between brightness uncertainty and ground-truth brightness modulation across the 45 noun concepts. We also embedded feature uncertainty within a predictive Bayesian combinatorial model, in which a concept's conceptual brightness is represented as a probability distribution over brightness values. We assessed the ability of this Bayesian model to predict brightness modulations evoked by the adjective-noun combinations and compared its performance with more traditional additive and multiplicative models (Smith et al., 1988; Mitchell and Lapata, 2008, 2010). The Bayesian model outperformed the other models, highlighting the relevance of feature uncertainty in the conceptual combination process. Our behavioral and modeling results suggest that conceptual feature uncertainty influences how features are flexibly modulated when concepts combine.

In order to understand the neural correlates of this flexible combination process, we analyzed responses to the “dark” and “light” adjective-noun combinations within a priori ROIs, each of which has previously been implicated in a task requiring flexible conceptual or linguistic processing. We determined whether neural responses in any of these regions reflected feature uncertainty or flexible feature modulation. Our results reveal contributions of LIFG and LATL to these processes, which provide insights into the neural mechanisms of conceptual combination and flexible conceptual processing more generally.

LIFG was particularly sensitive to feature uncertainty during comprehension of combined concepts. Univariate modulation effects refer to the extent to which univariate responses, averaged within an ROI, were influenced by adjective-noun combinations relative to the noun alone. When the brightness of a noun concept was highly uncertain (e.g., paint), “dark” and “light” modifiers induced greater univariate modulation in LIFG. Additionally, univariate modulation in LIFG was positively predicted by additive and multiplicative models of adjective-noun combinations, further suggesting LIFG contributions to the feature-based combinatorial process induced by complex phrases. Weaker evidence also implied that univariate modulation in LIFG positively correlated with the ground-truth brightness modulation derived from behavioral data. LIFG is not typically associated with conceptual combination but plays a role in metaphor processing (Rapp et al., 2004, 2007; Eviatar and Just, 2006; Lee and Dapretto, 2006; Stringaris et al., 2007; Bambini et al., 2011; Cardillo et al., 2012; Solomon and Thompson-Schill, 2017). Figurative language and conceptual combination rely on similar conceptual devices (Wisniewski, 1997; Estes and Glucksberg, 2000), in that they both involve the selection and integration of conceptual features. The metaphor “His teeth are pearls” and the noun-noun combination “pearl teeth” both involve selecting the relevant conceptual features from the pearl concept (e.g., white, shiny) and mapping or integrating these features into the teeth concept. The feature is often preselected in adjective-noun combinations (e.g., “white teeth”), but integration of feature information is still required. Our current results suggest that LIFG is involved in the feature integration process during complex language comprehension, and we argue that this process is relevant for combined concepts, figurative language, and natural language use more generally. Our finding that LIFG is involved in modulating feature representations in combined concepts is consistent with broader claims that this region plays a crucial role in semantic selection and control (e.g., Thompson-Schill et al., 1997, 1999; Jefferies, 2013).

In LATL, multivariate responses reflected the degree of conceptual feature modulation evoked by the adjective-noun combinations. Our multivariate modulation analysis examined the extent to which MVPs evoked by a noun and its corresponding adjective-noun combinations differed from each other. For noun concepts with low brightness modulation (e.g., diamond), “dark” and “light” combinations evoked patterns in LATL that were similar to the patterns evoked by the noun alone. For noun concepts characterized by high brightness modulation (e.g., paint), “dark” and “light” combinations evoked patterns in LATL that were substantially different from the pattern evoked by the noun alone. That is, dark” and “light” modifiers did not influence patterns in LATL identically across nouns; the effect was modulated by degree of conceptual change. These results suggest that responses in LATL reflect an integration of conceptual features, rather than a superimposition of constituent concepts.

LATL has been widely implicated in neuroimaging studies of conceptual combination, in both fMRI (Baron et al., 2010; Baron and Osherson, 2011; Boylan et al., 2017) and MEG methodologies (Bemis and Pylkkänen, 2011, 2013a,b; Westerlund and Pylkkänen, 2014). The ATL also plays a central role in theories of conceptual knowledge more generally, such as the hub-and-spoke theory, a neurocomputational model in which ATL acts as a semantic “hub” that integrates featural representations from other regions (i.e., “spokes”). In this account, concepts in ATL are not represented in terms of their features, but rather in a high-dimensional semantic space (Rogers et al., 2004; Patterson et al., 2007; Lambon Ralph et al., 2010, 2017). In related work, Coutanche and Thompson-Schill (2015) find that representations in LATL reflect an integration of visual features (i.e., color and shape), but not the visual features themselves. We suggest that the integration of features (e.g., shiny, expensive) to form coherent concepts (e.g., diamond), and the integration of those concepts to form a combined concept (e.g., dark diamond), might recruit the same neural mechanisms. Our finding that LATL representations reflect the integration of conceptual brightness across concepts, but not conceptual brightness per se, is consistent with this theory that LATL integrates conceptual information within and between concepts in a high-dimensional semantic space.

We did not observe feature-based combinatorial responses in LAG, despite its role in combining concepts more generally (Graves et al., 2010; Bemis and Pylkkänen, 2013a; Boylan et al., 2015, 2017; Price et al., 2015, 2016). In particular, it has been argued that LAG is sensitive to the plausibility of adjective-noun combinations (Price et al., 2015), or to “relational” combinations that imply an event or relation between two concepts, rather than feature attribution (Boylan et al., 2015, 2017). The apparent lack of LAG response to feature-based combinations in our task is consistent with the theory that LAG is recruited for “relational” rather than “attributive” conceptual combinations (Boylan et al., 2015, 2017). We also found no evidence that LFUS is implicated in a feature-based combinatorial process, or that it represents conceptual brightness, despite previous findings that LFUS represents conceptual color (Martin et al., 1995; Simmons et al., 2007; Hsu et al., 2011, 2012). However, it is still an open question whether cortical regions that contain feature-based representations can also flexibly represent those features in combined concepts.

Here we characterized the computational and neural mechanisms underlying the flexible modulation of conceptual information during language comprehension. Using methods inspired by information theory and Bayesian modeling, we provide evidence that feature uncertainty plays a role in conceptual combination. Further, our analyses expose the LIFG and LATL as regions involved in this flexible combinatorial process. These findings are likely to extend more generally to complex language processing and flexible concept use.