Organ doses from CT localizer radiographs: Development, validation, and application of a Monte Carlo estimation technique

Abstract

Purpose:

The purpose of this study was to simulate and validate organ doses from different computed tomography (CT) localizer radiograph geometries using Monte Carlo methods for a population of patients.

Methods:

A Monte Carlo method was developed to estimate organ doses from CT localizer radiographs using PENELOPE. The method was validated by comparing dosimetry estimates with measurements using an anthropomorphic phantom imbedded with thermoluminescent dosimeters (TLDs) scanned on a commercial CT system (Siemens SOMATOM Flash). The Monte Carlo simulation platform was then applied to conduct a population study with 57 adult computational phantoms (XCAT). In the population study, clinically relevant chest localizer protocols were simulated with the x-ray tube in anterior-posterior (AP), right lateral, and PA positions. Mean organ doses and associated standard deviations (in mGy) were then estimated for all simulations. The obtained organ doses were studied as a function of patient chest diameter. Organ doses for breast and lung were compared across different views and represented as a percentage of organ doses from rotational CT scans.

Results:

The validation study showed an agreement between the Monte Carlo and physical TLD measurements with a maximum percent difference of 15.5% and a mean difference of 3.5% across all organs. The XCAT population study showed that breast dose from AP localizers was the highest with a mean value of 0.24 mGy across patients, while the lung dose was relatively consistent across different localizer geometries. The organ dose estimates were found to vary across the patient population, partially explained by the changes in the patient chest diameter. The average effective dose was 0.18 mGy for AP, 0.09 mGy for lateral, and 0.08 mGy for PA localizer.

Conclusion:

A platform to estimate organ doses in CT localizer scans using Monte Carlo methods was implemented and validated based on comparison with physical dose measurements. The simulation platform was applied to a virtual patient population, where the localizer organ doses were found to range within 0.4%−8.6% of corresponding organ doses for a typical CT scan, 0.2%−3.3% of organ doses for a CT pulmonary angiography scan, and 1.1%−20.8% of organ doses for a low-dose lung cancer screening scan.

1. INTRODUCTION

Computed tomography (CT) localizer radiographs (sometimes known as scout scans, scanograms, or topograms) are two-dimensional (2D) projection images that are acquired using the CT scanner prior to the full rotational CT acquisitions. The purpose of the localizer images is to acquire relevant information for tube current modulation,¹ patient positioning, and z-dimension coverage for the tomographic CT scan based on the measured 2D attenuation and visible patient anatomy. The 2D localizer acquisitions are usually performed in multiple orientations with respect to the patient, such as anterior-posterior (AP), posterior-anterior (PA), or lateral, depending on the protocol and the manufacturer. The radiation dose recorded from each of these orientations is sometimes characterized in terms of an orientation-agnostic volume CT dose index (CTDI_vol). For localizer series, CTDI-_vol² describes what the radiation burden would have been if a cylindrical phantom would have been rotationally imaged with the localizer-specific settings of collimation, table speed, and tube current (mAs). However, as the geometry of the localizer CT and rotational CT acquisitions are notably different, CTDI_vol is an inadequate descriptor of the radiation burden from a nonrotating exposure. Thus, there is a need to characterize radiation dose from CT localizer series using alternative metrics that allow for comparison between different localizer acquisition geometries in a patient relevant manner.

Several previous studies have characterized organ doses using metrics other than CTDI_vol. For example, localizer dose magnitude has been estimated as a range that is not specific to localizer geometry or particular organs of interest.^3,4 Other works have estimated an entrance dose for localizer scans, not focused on organ dose.^5,6 Schmidt et al.⁷ characterized organ doses for several acquisition geometries and body regions for a CT system using a physical anthropomorphic phantom, leading to the first comprehensive reporting of organ and effective doses. However, there is a need to go beyond a single anthropomorphic phantom and study the variation of organ doses across a patient population to ensure that the estimated radiation burden is personalized to patient characteristics. Previous studies have highlighted the need for personalized radiation dosimetry. A study by Li et al.⁸ found significant differences in effective dose estimates in tomographic CT scans between those calculated using DLP and k factors and those calculated from organ doses derived from patient-specific Monte Carlo simulations. Such studies highlight the need for patient-specific dosimetry to allow more personalized estimates of radiation burden. Furthermore, if patient-specific radiation burden can be quantified for localizer imaging, in addition to previous studies for tomographic imaging,⁹ it would allow the radiation burden quantification to include all image series associated with CT scanning.

The purpose of this study was to implement and validate a Monte Carlo simulation package for quantifying organ doses in localizer scans for a SOMATOM Definition Flash scanner (Siemens Healthineers) and to apply the simulation package to quantify the radiation burden from different CT localizer geometries for chest scans in a population of patients. Radiation dose was estimated at the organ level and compared with the dose magnitude for both a typical chest CT scan and a low-dose lung cancer screening scan to express the magnitude of localizer dose relative to full CT organ dose.

2. MATERIALS AND METHODS

This study consisted of three distinct parts including (a) development of a Monte Carlo method to calculate organ doses from localizer images, (b) validation of the localizer Monte Carlo method against a physical CT system, and (c) application of the localizer Monte Carlo code to a computational patient population (XCAT).

2.A. Development of Monte Carlo organ dose estimation

The organ dose estimation was performed using a previously developed Monte Carlo tool¹⁰ (based on PENELOPE, 2006), which has been validated for full rotation CT scans using the Definition Flash scanner¹¹ but not for localizer scans. A Monte Carlo methods table (according to the American Association of Physicists in Medicine Task Group 268¹²) describes aspects of this previously developed Monte Carlo code (Table I).

table I.

The Monte Carlo simulation details.

Item name	Description	References
Code	PENELOPE (2006)	13
Validation	The Monte Carlo code was previously validated for full rotation CT (for both axial and helical scans, see references). In the present study, the localizer validation is described in Section 2.B	10,11
Source Description	Particle type: x-ray Prebowtie: The source is modeled as a point source with an effective beam width to account for the penumbra of the beam. Prebowtie spectra are provided by the manufacturer in 0.5-keV bin increments for a 120-kVp tube potential. Postbowtie: The prebowtie spectrum is filtered by the bowtie using a method described in Section 2.A of the present paper, originally described by Li et al. (2014)	14,15
Cross sections	Cross sections are generated using the default material.f provided with PENELOPE, which has a large database of predefined common materials
Transport parameters	Transport of secondary electrons is not included
VRT or AEIT	Variance reduction was performed using the particle-splitting technique	10
Scored Quantities	The Monte Carlo scored quantity is Kerma (eV) in each organ per number of starting (prebowtie) photons
Number of histories	8.00E+07
Postprocessing	The postprocessing for the present study is described in Section 2.A

A previously validated model for the bowtie filter was incorporated into the Monte Carlo simulation.^11,16 The method uses the prebowtie energy spectra for the Flash scanner to perform the simulations. The bowtie filter is then implemented by scaling the deposited energy from each simulated photon (history) by an attenuation factor which is dependent on the photon energy and thickness of the bowtie along the trajectory for that specific simulated photon using a method described by Li et al.¹⁵ As such, the energy deposited by each simulated photon is scaled by an attenuation factor based on the Beer-Lambert Law of $e^{-\sum {\mu }_{m,E}{x}_m}$ where μ_m;E is the linear attenuation coefficient of the bowtie filter for each specific photon energy, x_m is the thickness of bowtie filter encountered by each simulated photon, and m is the bowtie material. The bowtie material is composed of filters with different materials m, and the method results in an angular dependent factor that essentially reduces the mAs along each trajectory according to the thickness of the bowtie, energy of the photon, and the materials along that trajectory. This implementation using attenuation factors allows for the bowtie to be incorporated into the model without a significant increase in Monte Carlo computation time.

The Monte Carlo simulation of localizer series required knowledge of the effective beam width for localizer image series. To calculate the effective beam width, the input information was the nominal localizer beam width of 3.6 mm and nominal focal spot size of 0.7 mm. Our previous study¹¹ characterized the effective beam width for the tomographic CT scan experimentally and found that the nominal beam width of 38.4 mm with a focal spot size of 1.2 mm was associated with 44.4 mm of effective beam width from the penumbra effect, resulting in an additional 6 mm from the nominal width. Given that the penumbra is independent of collimation and dependent on focal spot size, the localizer effective beam width was calculated by multiplying 6 mm by a ratio of focal spot sizes $\left(\frac{0.7\text{mm}}{1.2\text{mm}}\right)$ resulting in a calculated penumbra of 3.5 mm and an effective beam width of 7.1 mm for the localizer.

The output from the Monte Carlo code was used to obtain the energy deposited in each organ normalized by the number of photon histories generated at the source. The value of the energy deposited in each organ was then converted into units of absorbed dose (mGy) per starting photon by dividing the deposited energy in each organ by the mass of that organ. To remove the normalization by starting photon, the results were postprocessed so that the final value would be normalized by the console displayed mAs. To normalize the absorbed dose output by the mAs, it was necessary to establish a relationship between the mAs and the number of photon histories at the source [Eq. (2)].

Our previous study¹¹ characterized this relationship between the number of histories (n) per mAs for a semifan angle of 25° and effective beam width associated with beam collimation of 38.4 mm for a Definition Flash scanner. This relationship was previously characterized by using the Monte Carlo simulation platform to simulate energy deposited per number of starting photons in an ion chamber volume. Then, the corresponding physical ion chamber was used to measure energy deposited per mAs for a physical scanner. The ratio of simulated energy per starting photon was then divided by measured energy per mAs resulting in a final measurement of photons per mAs. For the present study, the number of histories (n) was modified to account for a different localizer effective beam width. The different effective beam widths were used to calculate a ratio of the areas of the field of view for the two collimation settings [incorporated into Eq. (2)].

To properly account for the number of photons produced at the source, an output correction factor (OCF) was implemented¹⁰ as

$$OCF=\frac{CTD{I}_{vol,\mathit{\text{measured}}}}{CTD{I}_{vol,\mathit{\text{sinulation}}}},$$ (1)

where CTDI_vol;measured is the CTDI_vol measured from a protocol with 120 kVp and 100 mAs and CTDI_{vol;simulation} is the corresponding CTDI_vol from the simulation platform. The CTDI_{vol;simulation} was generated by performing a Monte Carlo simulation with the CTDI phantom. The Monte Carlo simulation was used to estimate dose in the center and periphery of the phantom to then calculate a CTDI_vol. The OCF factor is essentially a scaling factor between the Monte Carlo simulations and the clinical scenario. The number of histories for the present study (n′) was calculated as

$$n^{\prime }=n\times OCF\times \frac{M_l}{M_c},$$ (2)

where M_l is the collimation size for the localizer scan settings and M_c is the collimation size for the full rotation CT scan settings (Table II).

table II.

A list of variables related to the Monte Carlo simulation.

Variable	Description	Method
μm,E	Bowtie linear attenuation coefficient	Provided by manufacturer
xm	Bowtie pathlengths as a function of fan angle	Provided by manufacturer
m	Bowtie material	Provided by manufacturer
CTDIVol,m	Measured CTDIvol for 120 kVp and 100 mAs	Previous clinical measurement
CTDIvol,s	Simulated CTDIvol for 120 kVp and 100 mAs	Monte Carlo derived
n	Number of photons per mAs for 38.4 mm collimation and 25-degree semifan angle. Used to translate between Monte Carlo histories and clinical number of photons	Previously Calculated
OCF	Ratio of CTDIvol,m to CTDIvol,s	Calculated
Mc	44.4 mm, effective beam size for 38.4 mm nominal collimation and 1.2 mm nominal focal spot size	Previous clinical measurement
Ml	7.1 mm, effective beam size for 3.6 mm nominal collimation and 0.7 mm nominal focal spot size	Calculated
N′	Number of photons per mAs for 3.6 mm nominal collimation	Calculated
OD	Energy (mJ) per starting photon deposited in each organ	Monte Carlo output
Dn	Normalized organ dose (mGy/mAs)	Calculated

The output of the Monte Carlo code in energy per starting photon was then converted to normalized organ dose D_n in mGy/mAs using

$$D_n\left(\frac{mGy}{mAs}\right)=OD\left(\frac{\mathit{\text{Energy}}(mJ)}{\mathit{\text{photons}}}\right)\times \frac{n^{\prime }\mathit{\text{photons}}}{\text{mAs}}\times \frac{1}{\mathit{\text{mass}}(kg)},$$ (3)

and finally the absorbed organ doses (mGy) for lung and breast for the localizer scan were calculated by multiplying D_n with the mAs for the localizer. A summary of the associted Monte Carlo variables in shown in Table II.

2.B. Monte Carlo validation

A validation study for localizer scans was performed for a commercial CT scanner (SOMATOM Definition Flash, Siemens Healthineers) by comparing dose estimation from a simulated scan with radiation dosimetry measurements from a physical scan. The physical measurements were performed using thermoluminescent dosimeters (TLDs) placed in an anthropomorphic phantom (model 701-D, CIRS, Norfolk, VA). The phantom was composed of 25-mm-thick axial slices containing cylindrical holes for placement of TLDs (Fig. 1). The TLDs (TLD-100, Thermoscientific, Oakwood Village, OH) were placed in a total of nine locations across six organs: thyroid, lung, heart, liver, spleen, and stomach. In each location, three TLDs were used to obtain a mean value and a standard deviation (used as a metric of uncertainty across different TLDs) for the absorbed dose at that location.

FIG. 1.

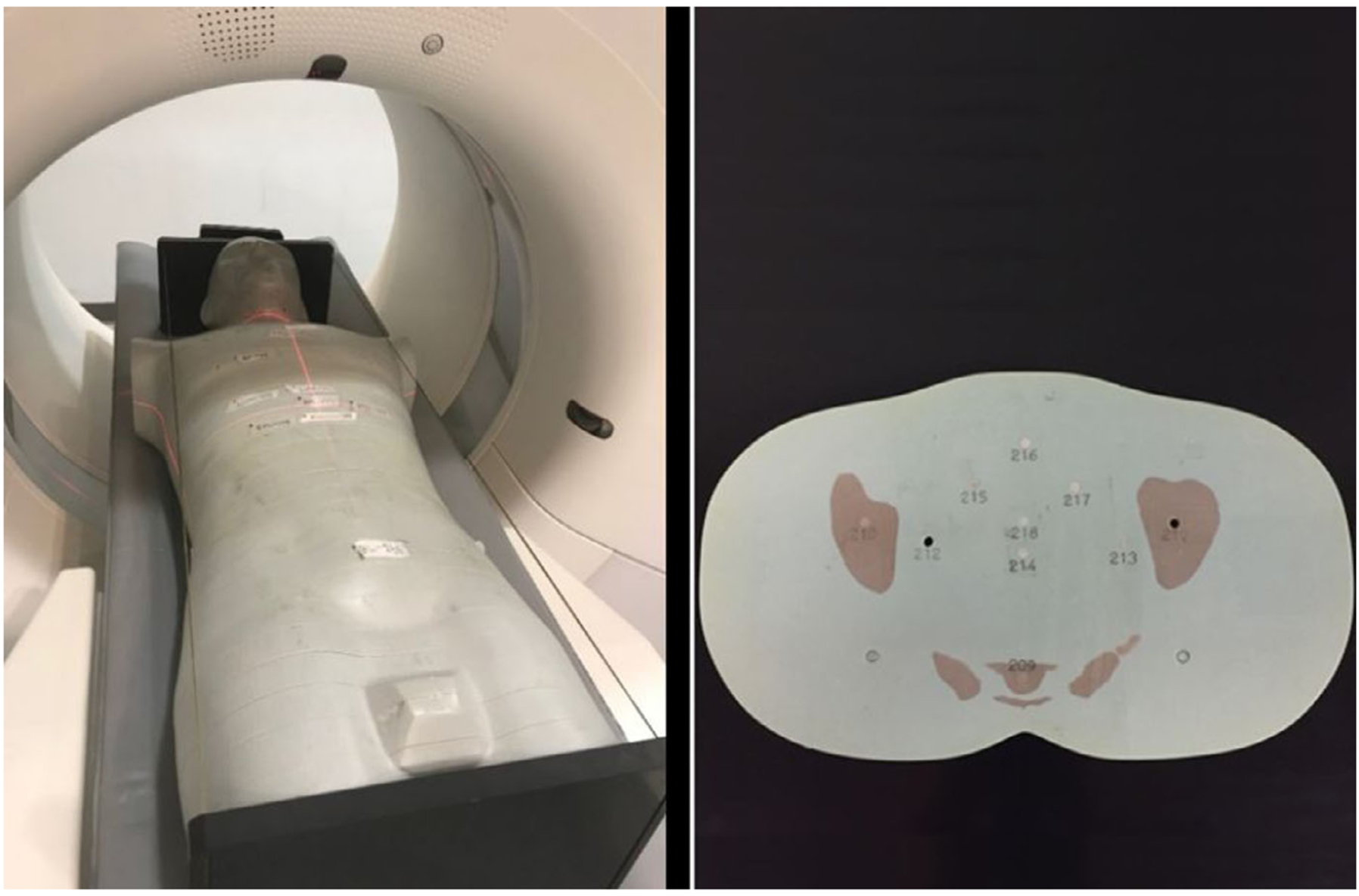
(Left) An adult male phantom (model 701-D, CIRS, Norfolk, VA) was scanned with a SOMATOM Definition Flash scanner (Siemens Healthineers). (Right) The phantom was composed of 25-mm axial slices which contained cylindrical holes for thermoluminescent dosimeters (TLDs) placement. In this study, TLDs were placed in locations corresponding to thyroid, lung, heart, liver, spleen, and stomach.

The phantom was scanned with a using the AP localizer geometry for a chest scan at 120 kVp, 100 mm/s table speed, and 3.6 mm nominal collimation (Table III). The protocol uses 35 mA per scan by default; however, the tube current was modified to 350 mA (i.e., increase of 10×), and scanning was repeated 50 times to improve the statistics of the TLD dose measurements. The TLDs were read and converted to units of absorbed dose. The dose measurements were divided by a factor of 1.2625 per their calibration against a Co-60 source.¹⁷ The calibration factor was computed for the effective energy of the beam corresponding with a 120-kVp beam exiting the center of the bowtie filter. The final TLD dose results were divided by a factor of 500 to adjust for the repeated scans (factor of 50) and increased mA (factor of 10) so that the dose represented the dose from a single chest localizer scan in AP orientation.

Table III.

Localizer protocol parameters.

Scanner	Siemens SOMATOM definition flash
Protocol	Chest
Start location	7 cm above lung
Stop location	14 cm below lung
kVp	120 kVp
mA	350 mA (validation), 35 mA (XCAT)
Table speed	100 mm/s
Nominal beam width	3.6 mm
Acquisition	AP (validation); AP, LAT, PA (XCAT)
Bowtie filter	Standard
CTDIVol	0.13 mGy

The images acquired on the scanner were reconstructed and segmented to construct a computational version of the phantom. The segmentation was performed using the method used to create the original XCAT phantoms.¹⁸ The resulting computational phantom had 3.45-mm isotropic voxel size and included segmented organs, segmented TLD locations as cylindrical volumes, and the CT table. A Monte Carlo simulation to match the physical scan was performed on this computational phantom and the absorbed dose in volumes corresponding to the location of the TLDs was estimated. The simulation was performed using 8×10⁷ histories uniformly distributed over the source trajectory, ensuring that the statistical uncertainty of the organ dose values in the field of view was <5%.

The simulation dose at TLD locations were compared to the measured TLD doses and a percent difference describing their disagreement was calculated as

$$PD=100\times \frac{S-M}{M},$$ (4)

where PD is the percent difference, S is the simulated dose (mGy), and M is the measured dose (mGy).

2.C. XCAT population study

The Monte Carlo simulation code was applied to a population of 57 adult extended cardiac-torso (XCAT) phantoms¹⁹ (age 18–78 yr, M/F 35/22). The phantoms were previously created by segmenting real patient CT datasets, morphing organs that were difficult to segment from existing templates, and then creating meshes from the organ segmentation.¹⁹ The phantoms were defined using nonuniform rational B-spline surfaces (NURBS), which allow the flexibility to manipulate the positioning of arms and legs. The arms were adjusted to be above the patients’ head for the chest protocol, similar to the corresponding real scans. The XCAT phantom heights ranged from 153 to 190 cm and weights ranged from 52 to 117 kg representing patients from 10th percentile to 97th percentile for height and weight. The XCAT models were voxelized for use in the Monte Carlo program with a 3.45-mm isotropic resolution, which was the resolution previously determined²⁰ to balance trade-offs of resolution and computation time. The attenuation from the CT examination table was accounted for by segmenting and voxelizing the table with the same voxel size from the images along with the patient anatomy.

For this study, we simulated a Definition Flash chest localizer protocol (Table III). Clinical data for 100 patients was used to calculate the mean start and stop location of the localizer scan with respect to the lungs. The table speed for this protocol was 100 mm/s with the nominal collimation width set to 3.6 mm (6 × 0.6 mm). The localizer scan was simulated separately for AP, PA, and right lateral orientations. The XCATs were centered in the simulation by calculating the center of each XCAT in the left-right and anterior-posterior directions and then positioning the center of each XCAT model at the isocenter.

The mean and standard deviation for each organ dose was quantified for all acquisition geometries (AP, PA, lateral) used in this study. The mean lung and breast (the key radiosensitive organs in the field of view for the scan) doses for the localizers were compared in greater detail across the three acquisition orientations (AP, PA, and lateral). The localizer organ doses for all XCAT organs were studied as a function of patient chest diameter by fitting an exponential relationship to characterize the dependence of organ doses on patient characteristics. An exponential relationship was chosen to match the relationship with exponential nature of x-ray attenuation in matter and is consistent with other works that use exponential fits to describe dosimetry variation with patient thickness.²¹ The exponential function used in the present study was of the form

$$\mathit{\text{OrganDose}}(mGy)=a\times e^{bd},$$ (5)

where a and b are fitting parameters and d is the mean patient chest diameter in the region of the scan which was calculated directly from the XCAT phantoms. The efficacy of each fit was evaluated using its R² value and a root-mean-square error (RMSE).

The localizer organ doses were then compared with full rotation CT breast and lung organ doses for three tube current modulated CT scans, the first at a typical dose for a chest scan (CTDI_vol = 4.1 mGy), the second at a lower dose of a lung cancer screening chest CT (CTDI_vol = 1.7 mGy), and the third at a higher dose representative of a CT pulmonary angiography scan (CTDI_vol = 10.8 mGy).²² The organ doses from the tomographic scans for each XCAT phantom were estimated using previously described method for calculating exponential factors, so-called h factors.⁹ The h factors were modeled exponentially based on the Beer-Lambert exponential relationship between attenuation and thickness. For the present study, the tomographic organ dose estimation was calculated using the XCATdose3 iPhone application²³ tube current modulation (TCM) coefficients which were originally calculated by Fu et al.²⁴ by simulating TCM profiles for a Siemens flash scanner of different modulation strengths, 0.25, 0.5, 0.75, and 1, with increasing number indicating increasing modulation strength. The inputs to the iPhone application are the patient diameter in the anatomical region of the scan, the TCM strength, and the CTDI_vol. For the present study, the XCAT patient thicknesses were input to the application, the modulation strength of 0.25 was chosen, and the two different CTDI_vol values were input as 4.1, 1.7, and 10.8 mGy. The organ doses from tomographic scans were then extracted and compared with organ doses localizer scans and were reported by comparing the localizer organ doses as percentages of organ doses from full rotation CT scans.

3. RESULTS

3.A. Validation results

The measured and simulated TLD doses (mGy) were found to be within ±20% (Table IV) of each other. The mean percent difference (PD) between the measured and simulated TLD doses was found to be −3.5% ± 5.8%, with the negative sign indicating that the simulated doses were less than the measured doses. All PDs were <10% except for the location in the spleen, which had a PD of −15.5% and was also the location that received the least amount of radiation dose.

Table IV.

The mean $\left(\overline{\mathrm{x}}\right)$ and standard deviation (σ) for measured TLD dose compared with the simulated TLD dose per location in the anthropomorphic phantom for AP localizer scan geometry. The percent difference (PD) between the mean measured and mean simulated value is shown.

	Measured $\overline{x}$ (mGy) ± σ (mGy)		Simulated $\overline{x}$ (mGy) ± σ (mGy)		PD (%)
Thyroid	0.496	0.004	0.517	0.009	4.35
Lung 1	0.293	0.006	0.284	0.009	−2.95
Lung 2	0.341	0.003	0.318	0.012	−6.75
Heart	0.320	0.0004	0.310	0.014	−3.13
Liver 1	0.140	0.002	0.141	0.009	1.24
Liver 2	0.194	0.003	0.196	0.010	1.18
Spleen	0.109	0.002	0.092	0.007	−15.50
Stomach 1	0.375	0.004	0.357	0.015	−4.84
Stomach 2	0.247	0.001	0.234	0.012	−5.31

3.B. XCAT population study results

The mean organ dose and associated standard deviation across the population of XCAT phantoms is shown in Table V. For some organs, such as breast and liver, the organ dose changed noticeably between the different acquisition geometries. For example, the AP acquisition resulted in the largest breast dose, and the lateral acquisition resulted in the largest liver dose. However, for other organs, including lungs, adrenal, and skin, the organ dose did not noticeably change between the different acquisition geometries (Table V).

TABLE V.

The mean $\left(\overline{\mathrm{x}}\right)$ and standard deviation (σ) for each organ dose and each localizer acquisition geometry across the population of XCAT phantoms (n=57).

Organ	AP $\overline{\mathrm{x}}$ (mGy) ± σ (mGy)		LAT $\overline{\mathrm{x}}$ (mGy) ± σ (mGy)		PA $\overline{\mathrm{x}}$ (mGy) ± σ (mGy)
Adrenal	0.127	0.032	0.121	0.027	0.171	0.037
Bladder	0.003	0.002	0.002	0.001	0.002	0.001
Bones	0.098	0.016	0.094	0.017	0.140	0.016
Brain	0.004	0.001	0.003	0.000	0.006	0.001
Breast	0.243	0.038	0.124	0.039	0.042	0.012
Esophagus	0.207	0.038	0.119	0.032	0.136	0.022
Eye	0.004	0.001	0.003	0.001	0.002	0.001
Gall bladder	0.263	0.083	0.280	0.074	0.056	0.019
Heart	0.315	0.041	0.125	0.037	0.101	0.020
Kidney	0.089	0.026	0.139	0.034	0.161	0.044
Large intestine	0.124	0.024	0.073	0.021	0.029	0.008
Larynx	0.289	0.058	0.032	0.010	0.073	0.017
Liver	0.214	0.051	0.309	0.043	0.097	0.020
Lung	0.217	0.029	0.161	0.034	0.177	0.022
Marrow	0.061	0.011	0.048	0.010	0.090	0.011
Ovaries	0.007	0.002	0.006	0.002	0.005	0.002
Pancreas	0.245	0.052	0.094	0.021	0.093	0.023
Prostate	0.002	0.001	0.001	0.001	0.002	0.001
Skin	0.048	0.006	0.050	0.006	0.042	0.004
Small intestine	0.184	0.048	0.048	0.016	0.041	0.013
Spleen	0.079	0.026	0.027	0.009	0.136	0.030
Stomach	0.284	0.062	0.054	0.014	0.081	0.018
Testes	0.0004	0.0002	0.0002	0.0001	0.0002	0.0001
Thymus	0.404	0.046	0.137	0.039	0.078	0.017
Thyroid	0.501	0.050	0.041	0.011	0.082	0.014
Trachea	0.286	0.039	0.132	0.035	0.143	0.020
Uterus	0.006	0.002	0.004	0.002	0.004	0.001
Vagina	0.0018	0.0005	0.0015	0.0005	0.0018	0.0006
Effective dose (mSv)	0.175	0.020	0.087	0.015	0.076	0.011

When the breast and lung doses were compared between the localizer views, the mean breast dose for PA scans was found to be less than AP and right lateral dose (Fig. 2). The mean lung dose was similar within uncertainty bars across the AP, PA, and right lateral localizer acquisitions (Fig. 2). The CTDI_vol for all three localizer acquisitions reported by this scanner manufacturer was a constant value of 0.13 mGy, regardless of the acquisition orientation.

FIG. 2.

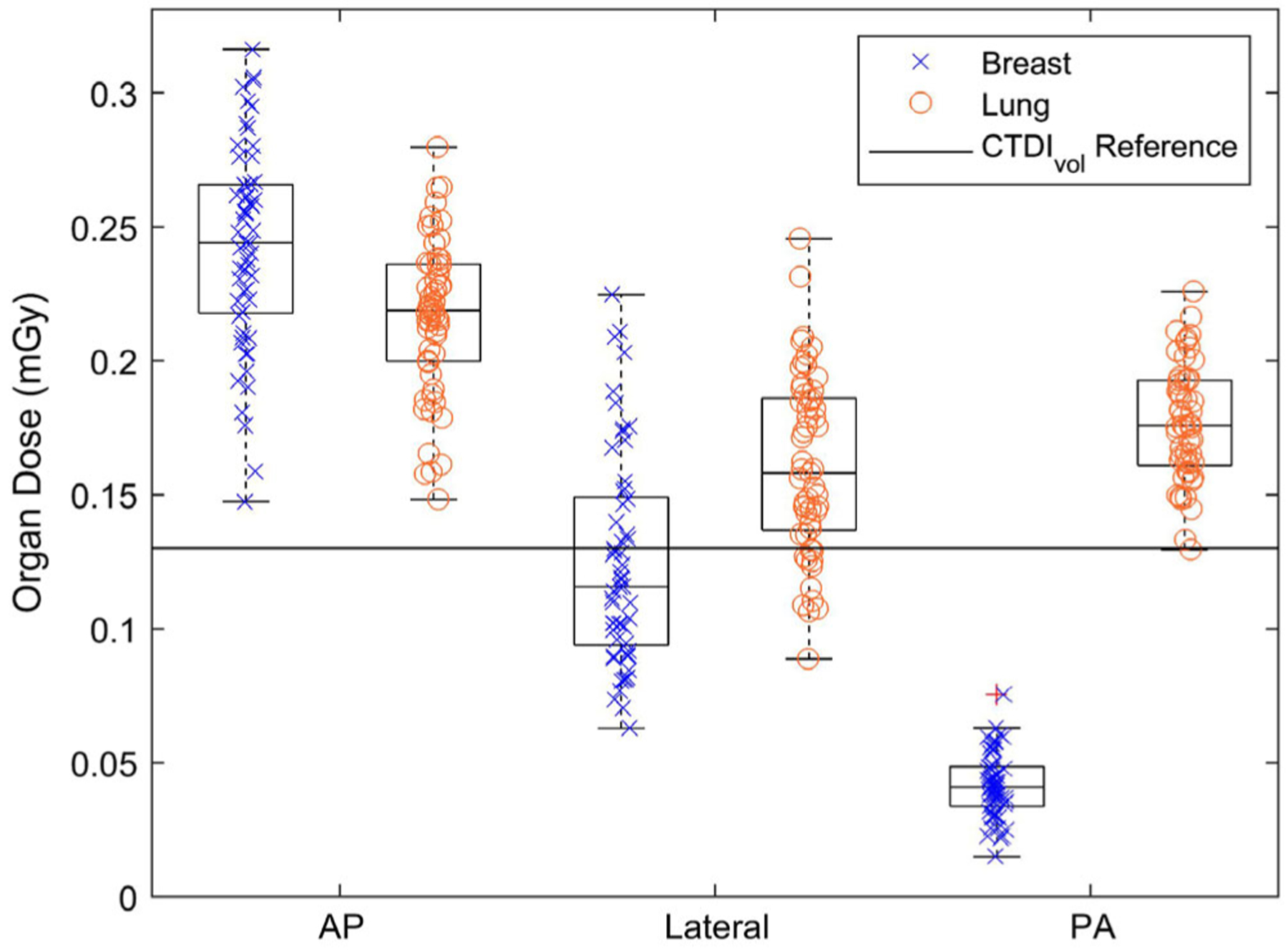
The breast (x) and lung (o) organ doses (mGy) for a population of human models (n = 57) corresponding to AP, right lateral, and PA localizer geometries. Outlier data points are shown with a red “+” symbol. The CTDI_vol (constant 0.13 mGy) is shown as a reference comparison dose index (solid line) to highlight the different information that can be understood by studying organ dose rather than a cylindrical phantom-based dose index.

The exponential decrease fitting parameters for each organ and each localizer geometry are shown in Table VI (AP and lateral) and Table VII (PA). The exponentially decreasing relationship partially describes the variation in organ dose for specific organ and geometry combinations. The R² and RMSE values for the exponential fits can be used as an indicator of precision in applying the exponential relationships to predicting organ doses for future patients. If the exponential relationships were to be applied to predict organ doses for patients, the RMSE can be used to create confidence intervals for the estimate of organ dose for a patient. An example exponential fit to breast dose as a function of patient thickness (Fig. 3) shows that the exponential fits better explain the patient to patient variation for PA geometry than lateral and AP geometries.

Table VI.

The fitting parameters (a, b), and the R² and root-mean-square from the residual (RMSE), for AP and lateral localizer acquisition geometries across the population of XCAT phantoms (n = 57).

Organ	AP				LAT
	a	B	R2	RMSE	a	b	R2	RMSE
Adrenal	1.461	−0.079	0.706	0.017	0.917	−0.065	0.608	0.017
Bladder	0.034	−0.074	0.186	0.001	0.024	−0.073	0.205	0.001
Bones	0.541	−0.055	0.806	0.007	0.494	−0.054	0.586	0.011
Brain	0.003	0.010	0.023	0.001	0.005	−0.017	0.077	0.000
Breast	0.465	−0.021	0.131	0.035	0.977	−0.067	0.305	0.033
Esophagus	1.205	−0.057	0.684	0.022	0.974	−0.068	0.446	0.024
Eye	0.001	0.059	0.371	0.001	0.002	0.017	0.039	0.001
Gall bladder	2.208	−0.069	0.338	0.068	1.088	−0.044	0.196	0.067
Heart	1.077	−0.040	0.642	0.025	1.983	−0.089	0.644	0.022
Kidney	1.493	−0.091	0.703	0.014	1.178	−0.069	0.568	0.022
Large intestine	0.411	−0.038	0.284	0.021	0.331	−0.049	0.202	0.019
Larynx	0.347	−0.006	0.006	0.058	0.184	−0.057	0.208	0.009
Liver	2.061	−0.073	0.650	0.030	0.991	−0.037	0.535	0.029
Lung	0.844	−0.044	0.771	0.014	0.987	−0.059	0.561	0.022
Marrow	0.440	−0.064	0.839	0.005	0.424	−0.070	0.765	0.005
Ovaries	0.032	−0.048	0.653	0.023	0.022	−0.046	0.348	0.029
Pancreas	1.835	−0.065	0.672	0.030	0.637	−0.062	0.557	0.014
Prostate	0.032	−0.048	0.653	0.023	0.022	−0.046	0.348	0.029
Skin	0.149	−0.036	0.625	0.004	0.151	−0.036	0.682	0.003
Small intestine	0.879	−0.050	0.276	0.041	0.833	−0.092	0.605	0.010
Spleen	1.400	−0.093	0.586	0.017	0.516	−0.096	0.603	0.006
Stomach	0.790	−0.033	0.164	0.058	0.390	−0.064	0.462	0.010
Testes	0.023	−0.045	0.653	0.023	0.017	−0.045	0.348	0.029
Thymus	0.999	−0.029	0.465	0.034	1.522	−0.078	0.536	0.027
Thyroid	1.053	−0.024	0.408	0.039	0.147	−0.041	0.181	0.010
Trachea	1.047	−0.042	0.653	0.023	0.810	−0.059	0.348	0.029
Uterus	0.023	−0.045	0.653	0.023	0.017	−0.045	0.348	0.029
Vagina	0.006	−0.042	0.653	0.023	0.006	−0.046	0.348	0.029

Table VII.

The fitting parameters (a, b), R², and root-mean-square from the residual (RMSE), for PA localizer acquisition geometry across the population of XCAT phantoms (n = 57).

Organ	PA
	a	b	R2	RMSE
Adrenal	1.377	−0.067	0.670	0.022
Bladder	0.025	−0.076	0.239	0.001
Bones	0.398	−0.034	0.622	0.010
Brain	0.004	0.009	0.023	0.001
Breast	0.897	−0.099	0.849	0.005
Esophagus	0.446	−0.038	0.398	0.017
Eye	0.001	0.020	0.050	0.001
Gall bladder	1.600	−0.109	0.678	0.011
Heart	0.622	−0.059	0.628	0.012
Kidney	2.629	−0.090	0.766	0.022
Large intestine	0.313	−0.077	0.534	0.006
Larynx	0.102	−0.011	0.014	0.017
Liver	0.468	−0.051	0.427	0.015
Lung	0.540	−0.036	0.602	0.014
Marrow	0.284	−0.037	0.656	0.006
Ovaries	0.018	−0.041	0.514	0.014
Pancreas	0.971	−0.076	0.661	0.013
Prostate	0.018	−0.041	0.514	0.014
Skin	0.114	−0.032	0.649	0.003
Small intestine	0.693	−0.091	0.632	0.008
Spleen	0.509	−0.042	0.257	0.026
Stomach	0.448	−0.055	0.411	0.014
Testes	0.017	−0.046	0.514	0.014
Thymus	0.384	−0.051	0.407	0.013
Thyroid	0.216	−0.031	0.240	0.012
Trachea	0.457	−0.037	0.514	0.014
Uterus	0.017	−0.046	0.514	0.014
Vagina	0.007	−0.046	0.514	0.014

FIG. 3.

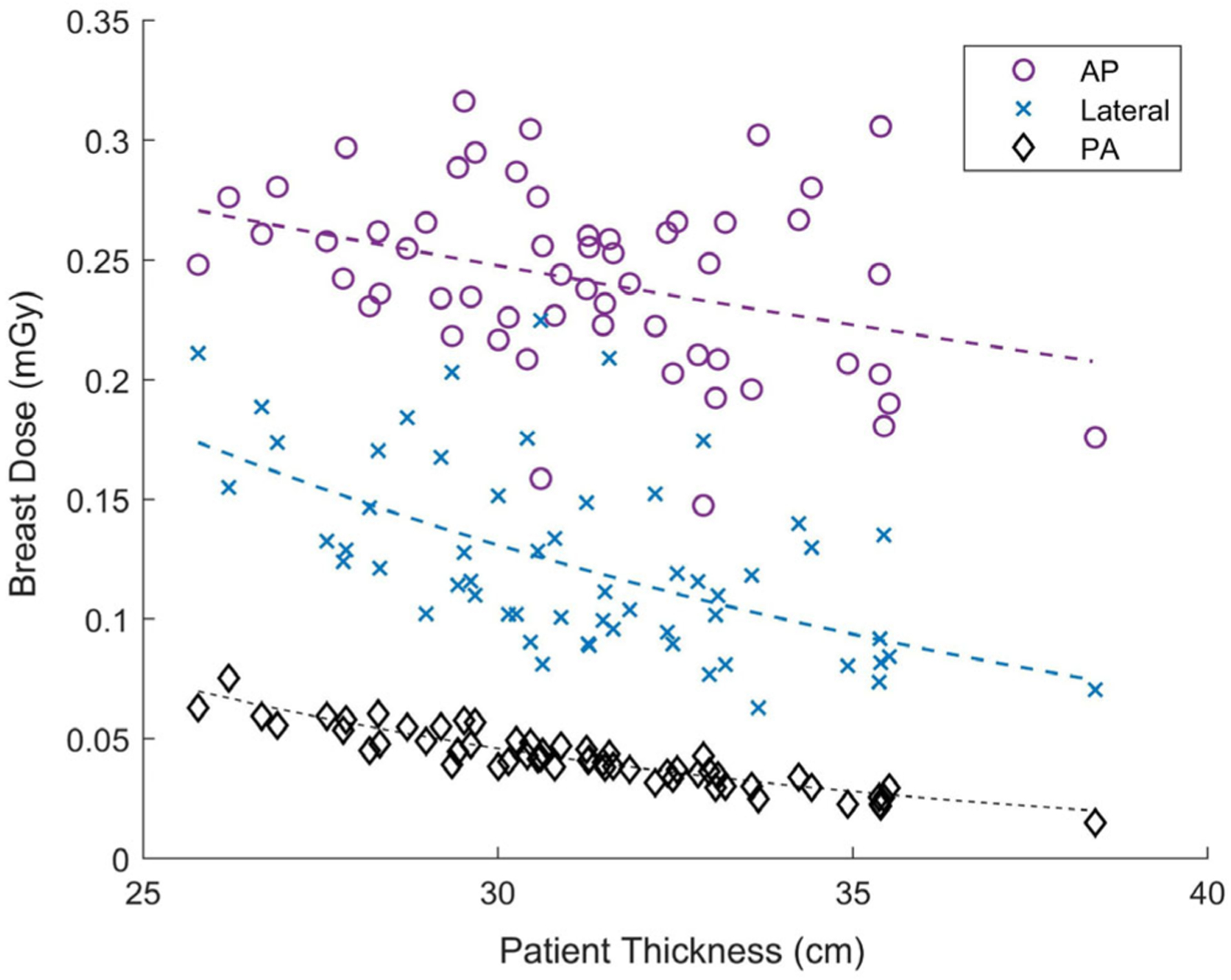
Breast dose (mGy) decreased exponentially for a population of patients (n = 57) for AP (circle), lateral (x), and PA (diamond) orientations. The exponential relationship with patient thickness explains most of the variation in breast dose for PA orientation, however, it does not explain as much of the variation for AP and lateral orientation. If results were used to predict future patient doses, the PA exponential relationship would result in more precise estimates of organ dose.

The breast and lung localizer doses were low (0.4%−8.6%) compared to the organ doses for a typical dose CT chest scan (CTDI_vol = 4.1 mGy) (Fig. 4). The breast and lung doses were in the range of 0.2%−3.3% of a CT Pulmonary Angiography (CTPA) scan (CTDI_vol = 10.8 mGy) (Fig. 4). However, the breast and lung localizer doses showed a higher maximum percentage (1.1%–20.8%) when compared with organ doses from a low-dose lung cancer screening chest CT (CTDI_vol = 1.7 mGy) (Fig. 4). The mean AP breast dose was 14.4% of the breast dose from a low-dose lung cancer screening scan. The mean combined PA and lateral organ dose was 9.8% for breast and 17.8% for lung as compared to corresponding breast and lung dose from a low-dose lung cancer screening scan. The PA and lateral doses were combined here because these acquisitions are often both performed prior to the tomographic series.

FIG. 4.

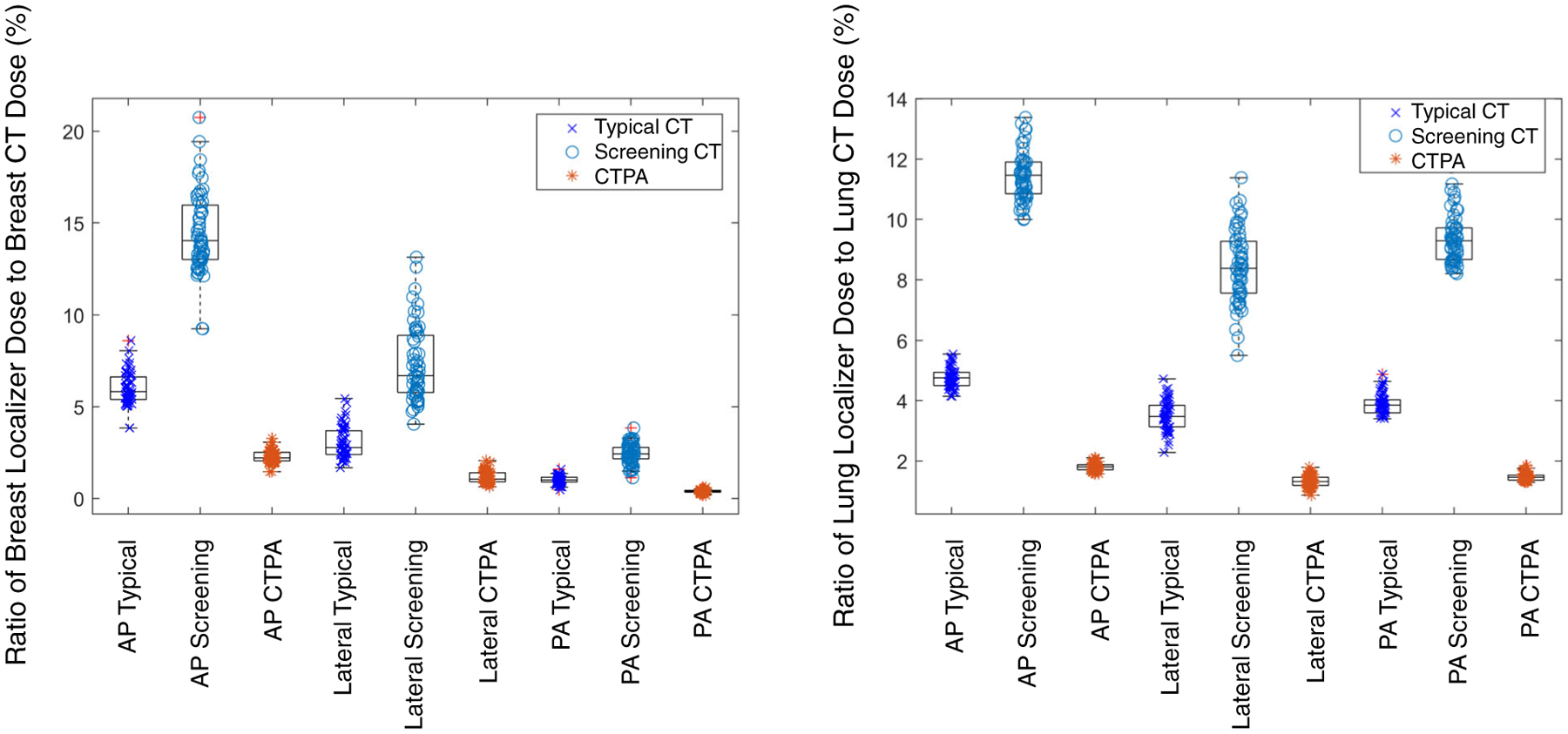
Breast dose (left) and lung dose (right) for a population of patients (n = 57) from the three localizer protocols (AP, lateral, and PA) used in this study expressed as a percentage of breast dose and lung dose for both a typical CT protocol dose (x), a low-dose lung cancer screening protocol (o), and a high-dose CTPA protocol (*). Outlier data points are shown with a red “+” symbol. The typical CT protocol dose scan had CTDI_vol = 4.1 mGy, low-dose lung cancer screening scan had CTDI_vol = 1.7 mGy, and the CTPA protocol had CTDI_vol = 10.8 mGy.

4. DISCUSSION

This study presents results that (a) demonstrate a Monte Carlo method to assess organ doses from localizer scans, (b) validate the estimated organ dose values against experimental measurements, and (c) quantify organ dose delivered to a population of patients for AP, PA, and lateral chest localizer scan geometries. The validation results show that the simulation platform matches a corresponding physical study with a mean difference of −3.5% across all TLD locations. The XCAT population study results showed that organ dose is dependent on the acquisition geometry and that it varies across a patient population, partially described by the mean chest diameter of the patient in the scan region. The exponentially decreasing relationships between organ dose and patient thickness demonstrate quantitatively the extent to which organ dose can be described by patient thickness for each organ and localizer geometry. Lastly, the results show that breast dose can be as high as 9% of breast dose for a typical dose CT scan and as high as 21% of breast dose for a low-dose lung cancer screening CT scan.

Based on prior literature and the multiple uncertainties inherent to a TLD dose measurement,^7,25 it was decided that the simulation platform would be considered validated if the measured and the simulated doses agreed within ±20%. For example, our previous paper for tomographic CT found that measured and simulated results agreed within −12% to 5%.¹¹ Since all results were within the 20% margin of error and were similar in magnitude to our own previous validation, we can consider the simulation platform to be validated. For most of the TLD locations, the simulation and physical results were within ±10%, except a location in the spleen for which the difference was observed to be −15.5%. The spleen location was also the location which received the least radiation dose, likely because the spleen is located toward the edge of the primary field for this scan. The spleen location may help explain why this organ location had the greatest percent difference. Given that the spleen is at the edge of the primary field and that the collimation is on the order of magnitude of the size of the TLD, small differences in the stop position of the scan may result in noteworthy differences in the measured and simulated TLD doses.

The XCAT population results of the study indicate that doses from localizer exams can be a non-negligible percentage of the full rotation CT and should be included when making estimates of patient doses for a CT exam. The exponentially decreasing results indicate that the variability in organ dose across a population of patients can be partially explained by changes in mean patient chest diameter (Tables VI and VII). The differences in organ doses for similarly sized patients are most likely due to differences in organ positioning and anatomical variations in organ size and shape. The RMSE values demonstrate that only some of the variability in organ dose can be explained by changes in patient diameter. If the size-dependent exponential relationship fully explained the variation, then the RMSE values would have been zero. The RMSE describes the precision of the exponential relationships and can be used to create confidence intervals for estimates of organ dose. The results for the breast exponential fits show that the RMSE for the PA fit is smaller than the RMSE for the AP and lateral fits. This result suggests that for projection imaging, the exponential fits are best applied when the organ of interest is on the opposite side of the patient from the x-ray source.

The results of this study are comparable with previous literature in that the localizer organ doses are within the estimated range of 0.25%−4% of the typical CT dose quoted by Yin et. al.³ However, this study goes further by calculating the radiation burden for a specific localizer acquisition for a population of patients, thereby making the estimates more patient and protocol specific. When compared with a previous (2013) localizer organ dose quantification for the same scanner,⁷ the organ doses from the present study are smaller, with percent differences from 6% to 146% for organ doses and differences of 48% to 67% for effective dose for similarly sized phantoms. We have confidence in our results as they are validated against experimental measurements. We thus suspect that the differences are due to unknown proprietary changes in the localizer protocol for the scanner, differences in phantoms studied, or differences in the localizer patient positioning. The results of the present study match well with another prior study (2016) which reported breast, heart, and lung localizer organ dose²⁶ in that both studies show that localizer breast dose is lower for PA localizer geometry when compared with AP, while the lung dose remains relatively consistent regardless of localizer acquisition geometry.

Prior studies^8,10 have characterized patient-relevant radiation dose by using Monte Carlo simulations to quantify organ dose. Organ dose is a metric that can be compared across different acquisition geometries and is most directly connected to radiation detriment to the patient. Although patient-specific organ dose estimates have been well characterized for full rotation CT exams for both fixed and modulated tube current,^8,9,20,27 they have not yet been quantified for a population of patients receiving CT localizer scans. A previous work on projection imaging²⁸ was similar to the present study in calculating factors relating patient size to organ dose. However, the results and methods were different because (a) the scan body coverage is not the same in localizers and projection radiography, (b) the localizer scan includes a bowtie filter not used in projection radiography, and (c) the source to patient distance is different between CT and radiography.

While the results of the study show that organ dose from a specific localizer geometry (e.g., PA) may be lower than that of another (e.g., AP), it is important to note that changing the localizer protocol can also affect the tube current modulation for the full rotation CT scan.^26,29,30 Furthermore, the localizer dose adds to the total CT dose by a small fraction. This addition is justified as the localizer scan is often used as the basis for tube current modulation to reduce radiation dose for the full rotation CT scan. However, the total patient dose from both the localizer scan and the full rotation CT scan should be considered together for purposes of optimizing tradeoffs in patient risk and image quality.

This study had a few limitations. One limitation is that the results were based on a single scanner and protocol. Other protocols and scanner models may utilize different kVp and bow tie filters which would likely result in different organ dose values. A second limitation of this work is that the photons per mAs were assumed to scale proportionally based on field size. While this is a fair assumption, the scaling may not be exact given that the anode heel effect might be more pronounced at larger field sizes. This study was also limited by the finite number of XCAT phantoms (n = 57) and by the fact that all phantoms were adult models. Finally, the exponential fits developed in this work are a step in the direction of personalizing radiation dosimetry estimates for specific patients; however, the results may not fulfill precision requirements for certain applications, depending on the specific RMSE for the given organ. In order to truly calculate personalized dosimetry with high precision, it would be necessary to have computational models for every possible patient and use those models as inputs to the Monte Carlo code.³¹

Future work should seek to characterize the localizer organ dose for a population of patients, including pediatric patients, for different regions of the body and different CT protocols beyond the chest protocol reported here. Future work should characterize localizer protocols from several different manufacturers to determine if they are similar enough to make these results generalizable to other scanners.

5. CONCLUSION

This study implemented and validated a Monte Carlo simulation platform for the purpose of estimating localizer organ dose and applied the simulation platform to a population of patients. The population study revealed that although the localizer dose for chest CT is small compared to the full CT dose, each localizer view can contribute as much as 21% of the total breast dose and this should be considered in the CT optimization process.