Abstract
Reinforcement learning models have proven highly effective for understanding learning in both artificial and biological systems. However, these models have difficulty scaling up to the complexity of real-life environments. One solution is to incorporate the hierarchical structure of behavior. In hierarchical reinforcement learning, primitive actions are chunked together into more temporally abstract actions, called ‘options’, that are reinforced by attaining a subgoal. These subgoals are capable of generating pseudo-reward prediction errors, which are distinct from reward prediction errors that are associated with the final goal of the behavior. Studies in humans have shown that pseudo-reward prediction errors positively correlate with activation of anterior cingulate cortex. To determine how pseudo-reward prediction errors are encoded at the single neuron level, we trained two animals to perform a primate version of the task used to generate these errors in humans. We recorded the electrical activity of neurons in anterior cingulate cortex during performance of this task, as well as neurons in lateral prefrontal cortex and orbitofrontal cortex. We found that the firing rate of a small population of neurons encoded pseudo-reward prediction errors and these neurons were restricted to anterior cingulate cortex. Our results provide support for the idea that anterior cingulate cortex may play an important role in encoding subgoals and pseudo-reward prediction errors in order to support hierarchical reinforcement learning. One caveat is that neurons encoding pseudo-reward prediction errors were relatively few in number, especially in comparison to neurons that encoded information about the main goal of the task.
Introduction
Reinforcement learning (RL) is one of the most influential learning models to date, and has had a dramatic impact on both artificial intelligence (Mnih et al., 2015) and our understanding of neural computation (Schultz, Dayan, & Montague, 1997). RL uses discrepancies between expected and actual reward outcomes to drive learning (Sutton & Barto, 1998). This estimation, known as a reward prediction error (RPE), is encoded by midbrain dopamine neurons (Hollerman & Schultz, 1998; Schultz et al., 1997 1997) and is thought to underlie how animals and humans learn behaviors necessary to acquire rewards from the environment (Dayan & Niv, 2008; Lee, Seo, & Jung, 2012). RPE-related neural signals are also found in lateral prefrontal cortex (LPFC) (Asaad & Eskandar, 2011) and anterior cingulate cortex (ACC) (Kennerley, Behrens, & Wallis, 2011). However, RL suffers from a problem of scaling (Botvinick, Niv, & Barto, 2009). While it performs well in relatively constrained learning environments, when the number of environmental states and actions increases, the amount of sampling required by the agent, and hence the amount of training time needed to acquire a behavior, scales as a positively accelerating function. Thus, an environment can quickly become too complex for RL to be a feasible learning solution.
Computational theoretical studies have proposed modifications to the conventional RL models in order to allow them to accommodate more complex hierarchical behavioral structure that is typical of the real word (Sutton, Precup, & Singh, 1999). Instead of reinforcing individual actions, hierarchical reinforcement learning (HRL) allows the chunking of actions into more temporally abstract behaviors, referred to as ‘options’. Each option terminates when a particular subgoal is attained, which generates an option-specific prediction error, referred to as a pseudo-reward prediction error (PPE). For example, when making a cup of coffee, one option might be adding milk, but individual actions that contribute to that option (e.g. getting the milk out of the fridge, opening the milk carton) would contribute solely to the PPE rather than the RPE generated by drinking the coffee.
The notion that complex behavior is organized hierarchically also has a long history in neuroscience. Hughlings Jackson, for example, emphasized the notion that the frontal lobe represented behaviors in a hierarchical manner (Phillips, 1973). Neuroimaging and neuropsychology studies have shown that progressively more complex behaviors are controlled by progressively more anterior regions of prefrontal cortex (Badre & D’Esposito, 2007; Badre, Hoffman, Cooney, & D’Esposito, 2009; Koechlin, Ody, & Kouneiher, 2003). Recent efforts have focused on determining the neural substrates of the algorithmic processes derived from computational theories of HRL (Badre & Frank, 2012; Frank & Badre, 2012; Holroyd & McClure, 2015; Ribas-Fernandes et al., 2011). However, to date there has been little attempt to study HRL at the level of individual neurons, which could provide insights into the specific computations performed by prefrontal neurons that support HRL. Therefore, we trained two monkeys to perform a primate version of a task that has been used in humans to study HRL (Ribas-Fernandes et al., 2011). The task required performing a sequence of lever movements in order to move a stimulus from a start position to a goal position, by way of an intermediate subgoal position. On a fraction of trials the position of the subgoal changed, thereby generating a PPE. In the human version of the task, the BOLD response in ACC positively correlated with the magnitude of the PPE. To examine whether this information was encoded at the level of single neurons, we recorded the electrical activity of single neurons in LPFC, ACC and orbitofrontal cortex (OFC) while animals performed the HRL task.
Materials and Methods
Subjects and behavioral task
Two male rhesus monkeys (Macaca mulatta) served as subjects (Q and R). Subjects were 5 and 6 years of age, and weighed approximately 7 and 9 kg at the time of recording. We regulated the daily fluid intake of our subjects to maintain motivation on the task. Subjects sat in a primate chair and viewed a computer screen. We used the MonkeyLogic system (Asaad & Eskandar, 2008) to control the presentation of the stimuli and the task contingencies. Eye movements were tracked with an infrared system (ISCAN). All procedures were in accord with the National Institute of Health guidelines and the recommendations of the University of California at Berkeley Animal Care and Use Committee.
Our behavioral task has previously been used to measure PPEs in humans (Ribas-Fernandes et al., 2011). The delivery task requires subjects to take the perspective of a delivery driver that has to choose between two jobs involving picking up a package (the subgoal) and delivering it to a customer (goal). After the subject selects one of the jobs, the position of the package sometimes changes, which generates a PPE. We trained two animals to perform a version of this task (Figure 1A). Subjects were required to fixate a central cue to initiate a trial, after which two stimulus configurations appeared on the left and right of the screen. Each configuration consisted of three colored dots which represented the start position (green), subgoal position (white), and goal position (blue). Subjects selected one of the configurations with a joystick movement. Once one of the two configurations was chosen, the other one disappeared and the subject had to make a series of joystick movements back-and-forth between the center location and the chosen side in order to move the green dot step-by-step from the start position to the goal position via the subgoal position. Each movement outwards caused the cursor to disappear, and then the movement back to the center caused the cursor to reappear 1° of visual angle closer to the subgoal or goal. The animal was allowed to make these movements as quickly as they desired. A juice reward was delivered once the green dot reached the goal position. The optimal choice was to select the shortest route, since this would lead to reward more quickly and with less physical effort.
Figure 1.
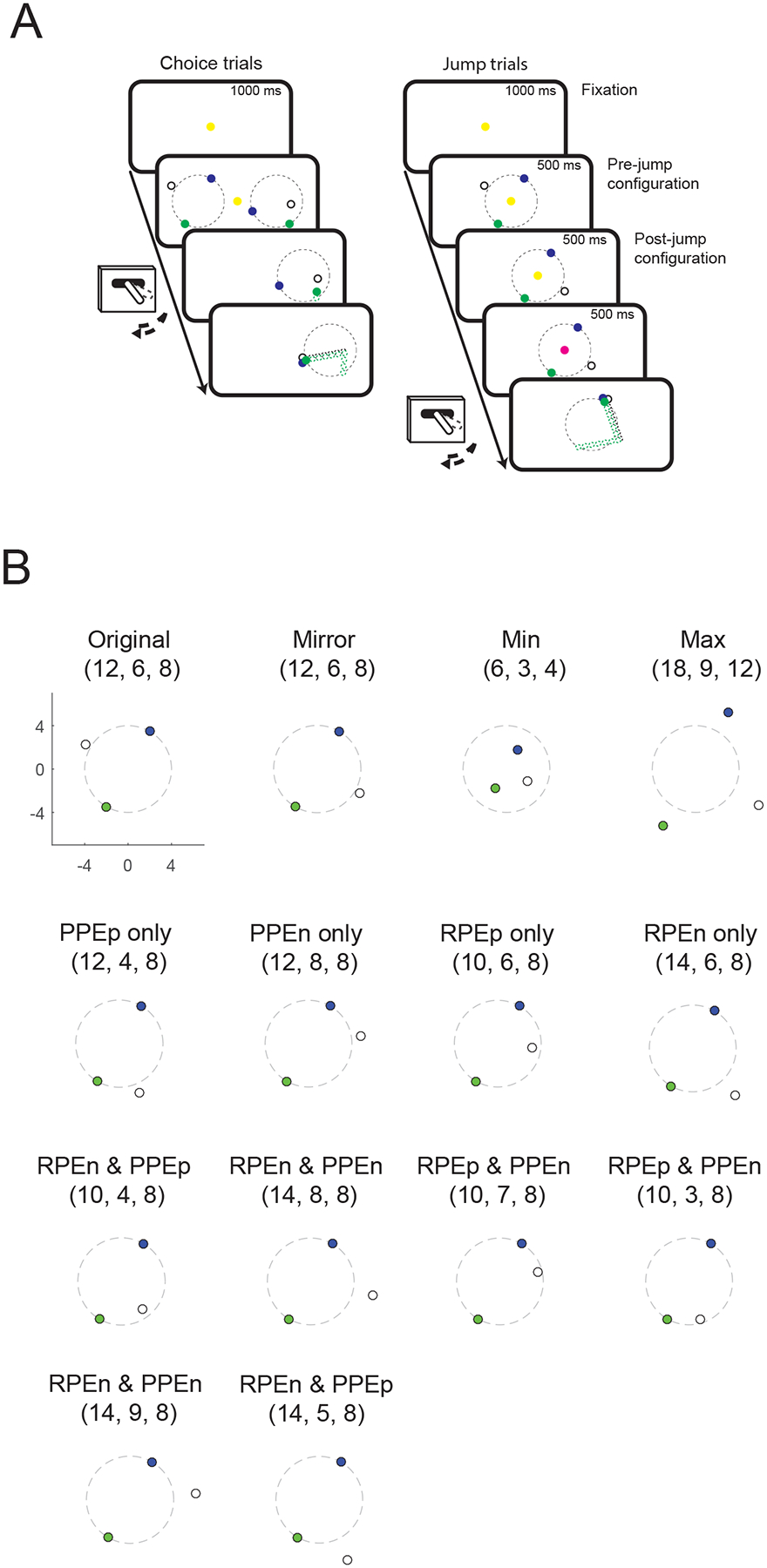
(A) Timeline of the behavioral task. On choice trials, subjects chose one of two stimulus configurations and then moved a joystick back-and-forth to move the green dot forwards on a green-white-blue route. The three dots were arranged on or within a circle of 8° (dashed black line) that was not visible to the subject. The optimal choice was to select the shortest route, since this would lead to reward more quickly and with less physical effort. On jump trials, a single configuration was presented, followed by a second configuration, which sometimes required updating the expectancy of how much work would be required to earn the reward because the position of the goal and/or subgoal changed. (B) Sample post-jump configurations. The original configuration is shown in the top left. Numbers above the configuration indicate the number of steps for TS, SG and SD. The subscript p and n refer to positive and negative prediction errors, respectively.
The start and goal positions in each original configuration were placed on the circumference of a circle 8° of visual angle in diameter. This circle was not visible to the animal. We manipulated two variables in each configuration: total steps (TS), the number of steps from the start position to the goal via the subgoal, and subgoal steps (SG), the number of steps from the start position to the subgoal. We also calculated the straight-line distance (SD), which is the degrees of visual angle in a straight line from the start position to the goal.
Once the animals had been trained on the choice task, we implanted the neurophysiological recording equipment and recorded neural activity. During recording sessions, only 10% of the trials were choice trials. The other 90% of trials, which we collectively refer to as ‘jump’ trials, began with the presentation of a single stimulus configuration for 500 ms in the center of the screen (pre-jump configuration), followed by a second configuration (post-jump configuration) for 500 ms. On 56% of the jump trials, the post-jump configuration contained no new information, either because it was identical to the pre-jump configuration, or because the subgoal changed position but remained the same distance from the start and goal positions (Figure 1B, ‘mirror’ condition). On the other 44% of the jump trials, the post-jump configuration generated a PPE (because the difference from the start position to the subgoal changed) and/or an RPE (because the total number of steps to the goal changed). These errors were the inverse of the number of steps, since fewer steps meant the animal would attain the reward with less effort. In other words, moving goals or subgoals closer would generate positive prediction errors while moving them further away would generate negative prediction errors. The fixation cue then changed color indicating to the subject whether they should make rightward or leftward joystick movements in order to move the green dot to the goal position. Table 1 describes the different combinations of experimental conditions and Figure 1B illustrates example configurations.
Table 1.
Relationship of jump configurations to parameters in the HRL model.
| Config. number |
TS | SG | SD | RPE | PPE | Notes |
|---|---|---|---|---|---|---|
| 1 | - | - | - | = | = | original |
| 2 | - | - | - | = | = | mirror |
| 3 | ↓ | ↓ | ↓ | + | + | min |
| 4 | ↑ | ↑ | ↑ | - | - | max |
| 5 | - | ↓ | - | = | + | PPEp only |
| 6 | - | ↑ | - | = | - | PPEn only |
| 7 | ↓ | - | - | + | = | RPEp only |
| 8 | ↑ | - | - | - | = | RPEn only |
| 9 | ↓ | ↓ | - | + | + | RPEp and PPEp |
| 10 | ↑ | ↑ | - | - | - | RPEn and PPEn |
| 11 | ↓ | ↑ | - | + | - | RPEp and PPEn |
| 12 | ↓ | ↓ | - | + | + | RPEp and PPEp |
| 13 | ↑ | ↑ | - | - | - | RPEn and PPEn |
| 14 | ↑ | ↓ | - | - | + | RPEn and PPEp |
Neurophysiological procedures
Our methods for neurophysiological recording have been reported in detail previously (Lara, Kennerley, & Wallis, 2009). Briefly, we implanted both subjects with a titanium head positioner for restraint and one recording chamber over each hemisphere, the position of which was determined using a 1.5 T magnetic resonance imaging (MRI) scanner. One recording chamber was positioned at an angle to allow access to LPFC and ACC, and the other was a vertical chamber to allow access to OFC. We recorded simultaneously from LPFC, ACC, and OFC using arrays of 6–14 tungsten microelectrodes (FHC Instruments). We determined the approximate distance to lower the electrodes from the MRI scans and advanced the electrodes using custom-built, manual microdrives until they were located just above the cell layer. We then slowly lowered the electrodes into the cell layer until we obtained a neuronal waveform, which were digitized and analyzed off-line (Plexon Instruments). We randomly sampled neurons; we did not attempt to select neurons based on responsiveness. This procedure aimed to reduce any bias in our estimate of neuronal activity thereby allowing a fairer comparison of neuronal properties between the different brain regions. We reconstructed our recording locations by measuring the position of the recording chambers using stereotactic methods. We plotted the positions onto the MRI sections using commercial graphics software (Adobe Illustrator). We confirmed the correspondence between the MRI sections and our recording chambers by mapping the position of sulci and gray and white matter boundaries using neurophysiological recordings. We traced and measured the distance of each recording location along the cortical surface from the lip of the ventral bank of the principal sulcus. We also measured the positions of the other sulci in this way, allowing the construction of unfolded cortical maps.
Statistical methods
Behavioral data analysis.
We conducted all statistical analyses using MATLAB (Mathworks). All data for behavioral analyses were from the choice trials. To determine how the parameters of the stimulus configurations affected choice behavior, we performed a formal model comparison. We predicted that configurations with fewer total steps should be considered more valuable than configurations with more steps and consequently should be chosen preferentially by the animals. We expected the position of the subgoal to have a smaller or negligible influence on choice behavior. We also included the straight line distance between the start and goal position, since this provided a complete description of the triangular arrangement of start, subgoal, and goal positions. We tested logarithmic transformations of the distances, in addition to linear distances, since we have previously observed a better fit between visual stimuli and reward value using logarithmic transformations (Rich & Wallis, 2014). We used these parameters to estimate the subjective value (SV) of the left and right choice options:
| (1) |
| (2) |
where TS is the total steps from the start position to the goal position by way of the subgoal, SG is the distance from the start position to the subgoal position, and SD is the straight line distance between the start and goal position. We then fit a logistic regression model using the discounted values (SVL - SVR) to predict PL, the probability that the subject chose the left configuration. We included a bias term, b, which accounted for any tendency of the subject to select the leftward configuration that was independent of the configurations’ values:
| (3) |
We estimated the weights of each parameters in the model by determining the values that minimized the log likelihood of the model. To fit the weights (w1 to w5), we used a maximum likelihood fitting (“fmincon” function in MATLAB) to find the set of parameters that best predicted the experimental data. To obtain fitted weights, we ran the maximum likelihood fitting function 100 times for each of 10 different randomly determined initial weights and then calculated the mean of the fitted weights. This helps to avoid accepting weights that reflect a local minimum in the fitting function. We compared models using Akaike’s Information Criterion (AIC) (Akaike, 1974).
Our other behavioral measure was the lever movement time, which we defined as the time taken to move the joystick from the center position to the chosen side and then back again following the movement of the green dot.
Neural data analysis.
All data for the neural analysis was from the jump trials. We visualized single neuron activity by constructing spike density histograms. We calculated the mean firing rate of the neuron across the appropriate experimental conditions using a sliding window of 100 ms. We then analyzed neuronal activity in two predefined epochs of 50–500 ms each, corresponding to the presentation of pre- and post-jump configurations. For each neuron, we calculated its mean firing rate on each trial during each epoch. To determine whether a neuron encoded an experimental factor, we used linear regressions to quantify how well the experimental manipulation predicted the neuron’s firing rate. Before conducting the regression, we standardized our dependent variable (i.e., firing rate) by subtracting the mean of the dependent variable from each data point and dividing each data point by the SD of the distribution. The standardization of firing rate was performed across all trials, pooling across conditions. We evaluated the significance of selectivity at the single neuron level using an alpha level of p < 0.05.
We examined how neurons encoded information about the pre-jump configuration by performing a linear regression on the neuron’s mean firing rate (F) during the pre-jump configuration presentation:
| (4) |
where SV denotes the subjective value of the pre-jump configuration calculated according to the weights derived from our behavioral model and LR was a dummy variable that indicated whether the start position was to the left or right of fixation. Selective neurons were defined as those in which Equation 4 significantly predicted the neuron’s firing rate (F-test evaluated at p < 0.05) and one or more of the beta coefficients (excluding b0) was significant (coefficient t-test evaluated at p < 0.05).
We examined how neurons encoded the post-jump configuration by performing a linear regression on the neuron’s mean firing rate (F) during the post-jump event with six predictors:
| (5) |
| (6) |
| (7) |
SV and LR are defined as for Equation 4. Another four predictors represented positive or negative reward prediction errors (RPE) or pseudo-reward prediction errors (PPE). We defined PPE as the difference between the original position of the subgoal and it’s position following the jump. Thus, we calculated this difference using the weighting that was ascribed to this parameter from the animal’s initial choice behavior (equations 1 and 2). Selective neurons were then defined in the same way as for Equation 4.
To quantify the strength of neural encoding, for each neuron, we calculated the coefficient of partial determination (CPD) for each parameter. This is the amount of variance in the neuron’s firing rate that can be explained by one predictor over and above the variance explained by other predictors included in the model. The CPD for predictor i is defined as:
| (8) |
where SSEX-i is the sum of squared errors in a regression model that includes all of the relevant predictor variables except i, and SSEX is the sum of squared errors in a regression model that includes all of the relevant predictor variables.
To examine the time course of the contribution of each predictor, we performed a “sliding” regression analysis to calculate the CPD at each time point for each neuron. We fit each regression model (Equation 4 for the pre-jump configuration and Equation 5 for the post-jump configuration) to neuronal firing for overlapping 200 ms windows, beginning with the 200 ms immediately prior to the task epoch and then shifting the window in 10 ms steps until we reached the end of task epoch. The sliding regression analysis requires a correction for multiple comparisons, since it involves performing a statistical test for each time point. We calculated this correction by calculating a false alarm rate. We applied the same statistical criterion to an equivalent analysis using shuffled neural data where significant parameters can only reflect noise. We preserved the firing patterns of individual neurons on individual trials, but shuffled the experimental conditions. The results of this analysis showed that a statistical criterion of three consecutive time bins where the regression parameter was significant at p < 0.005, yielded a false alarm rate less than 5%.
Results
Behavioral task performance
To examine the influence of the stimulus configurations, we performed a model comparison, as described in detail in the Methods. The full model included parameters for TS, SG and SD (w1, w2, and w3). Against this model we compared other models in which we tested subsets of these parameters. In addition, we evaluated whether choice behavior relied on linear or logarithmic estimates of distances. In both animals, the full model was clearly favored, although subject R favored logarithmic estimates of distance while subject Q favored linear estimates (Table 2 and Fig. 2A). For subject R, w1 = 3.2, w2 = 0.5 and w3 = 1.4, while for subject Q, w1 = 0.5, w2 = 0.4 and w3 = 1.1. Thus, for both subjects, the subgoal position had the smallest effect on choice behavior, although subject R based his choices more on TS, while subject Q used SD. These two variables were positively correlated (correlation coefficient = 0.91), which likely accounted for why either variable could be used to solve the task. Overall our models provided an excellent fit to choice behavior (Figure 2B), explaining 93% of the variance in subject R’s choice behavior, and 90% of the variance in subject Q.
Table 2.
AIC values for both subjects across all tested models.
| Subject | Distance estimate |
Parameters included in the model | ||||||
|---|---|---|---|---|---|---|---|---|
| TS SG SD |
TS SG |
TS SD |
SG SD |
TS | SG | SD | ||
| R | logarithmic | 700 | 706 | 703 | 735 | 709 | 902 | 763 |
| linear | 706 | 710 | 709 | 737 | 713 | 902 | 759 | |
| Q | logarithmic | 955 | 981 | 959 | 964 | 984 | 1112 | 979 |
| linear | 952 | 975 | 956 | 958 | 980 | 1107 | 972 | |
Figure 2.
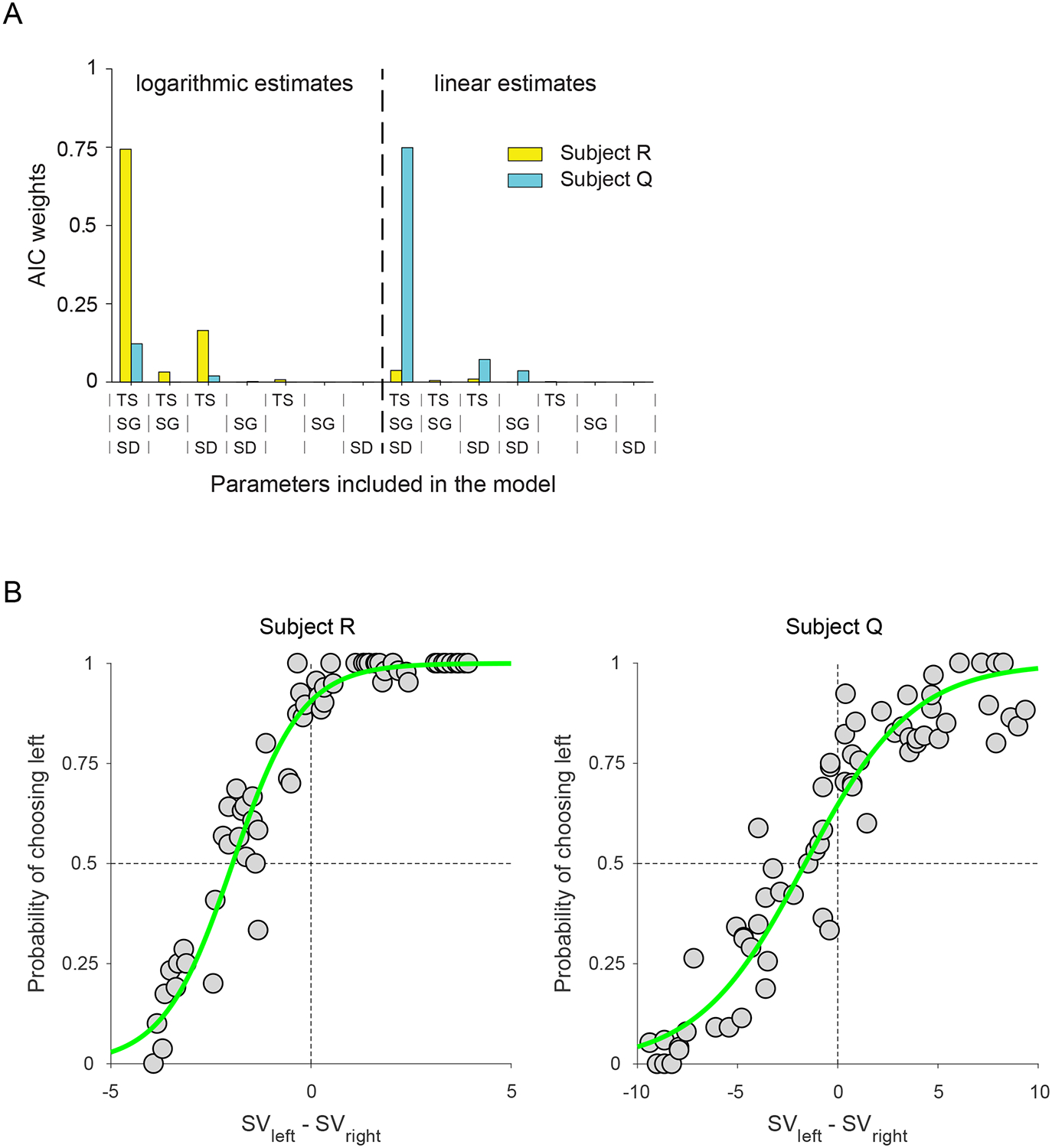
(A) AIC weights across the 14 tested models. The AIC weight is the relative likelihood of a given model within the set of tested models. The full model was clearly favored in both subjects, although a logarithmic transformation of distance was favored by subject R, whereas subject Q estimated distances linearly. (B) Behavioral performance during the choice trials. The probability of selecting the left configuration as a function of the difference in value of the left and right configurations as determined by Equations 1 and 2. Gray circles indicate actual data, whereas green lines indicate the best fitting model as determined by a formal model comparison.
Although the subgoal position only had a small effect on choice behavior, the model in which it was included clearly performed better than the model in which it was omitted in both animals. This indicated that the animals were not simply ignoring the subgoal. Further evidence was apparent in the lever movement times. Both animals showed a tendency to slow down as they approached both the subgoal and the goal, and to speed up again once the subgoal had been acquired (Figure 3A). This was evident when we looked at the change in movement time from one step to the next (Figure 3B). We found that subjects slowed down (positive values on the y-axis) on approaching the subgoal, and sped up (negative values on the y-axis) immediately after its attainment (one-way ANOVA, F(5, 227) = 17.62, p < 1 × 10−13 for subject R; F(5, 179) = 22.85, p < 1 × 10−16 for subject Q). In other words, subjects did pay attention to the subgoal position in the series of lever movements.
Figure 3.
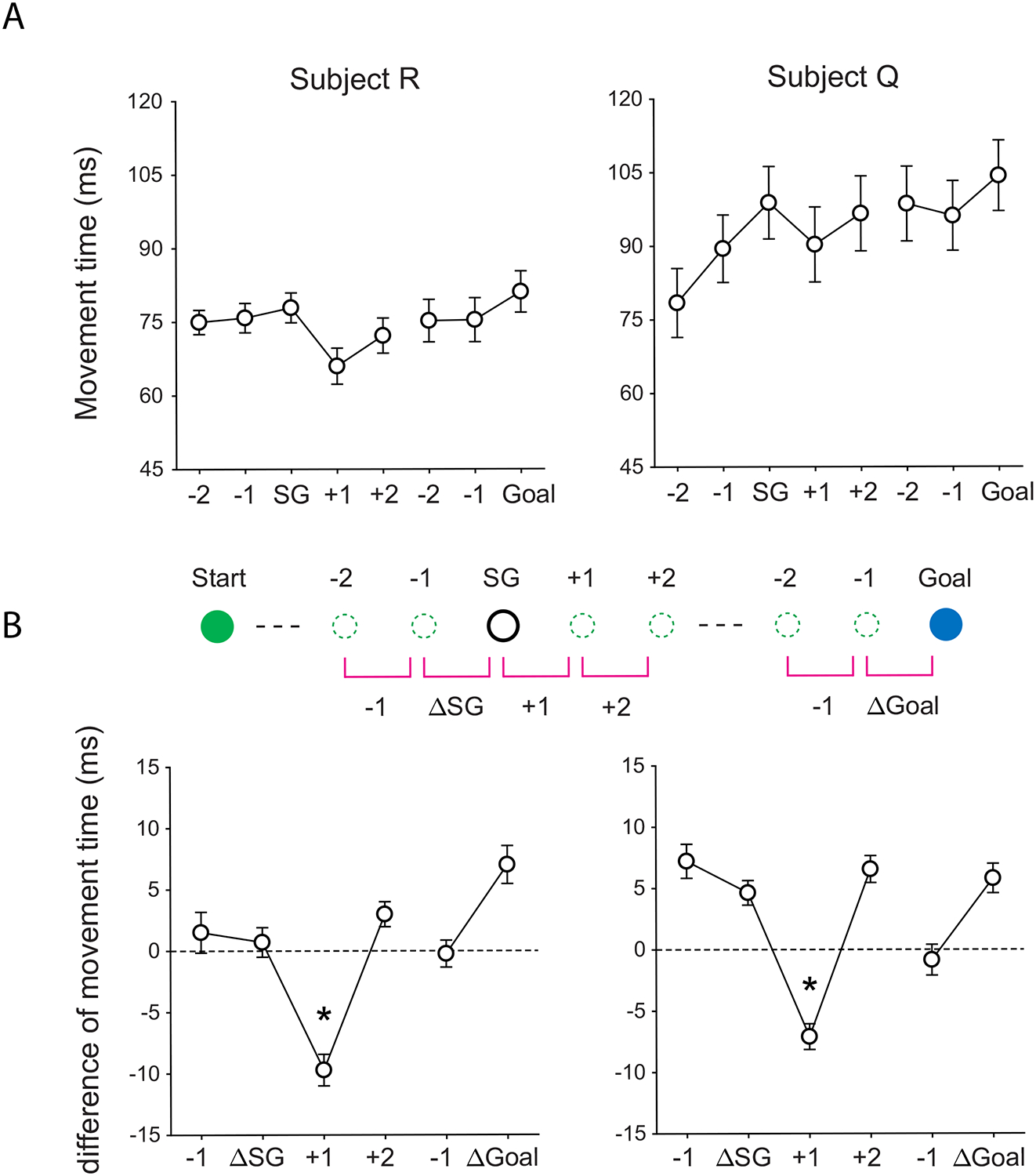
(A) Lever movement times for steps relative to subgoal or goal positions. (B) Movement times relative to the previous steps. The diagram indicates the specific movements referenced by the x-axis. Asterisks indicate that the values were significantly lower than any other values, using appropriate pairwise comparisons (p < 0.01, Bonferroni corrected).
Neural encoding
We recorded the activity of 308 neurons from LPFC (subject R 132; subject Q 176), 249 neurons from OFC (R 130; Q 119), and 212 neurons from ACC (R 106; Q 106). Recording locations are illustrated in Figure 4. We collected the data across 38 recording sessions for subject R and 30 sessions for subject Q. In order to obtain sufficient statistical power, the neurons from the two subjects were pooled. For all significant results, there were no qualitative differences between the two subjects (i.e. the effects were in the same direction), unless otherwise noted.
Figure 4.
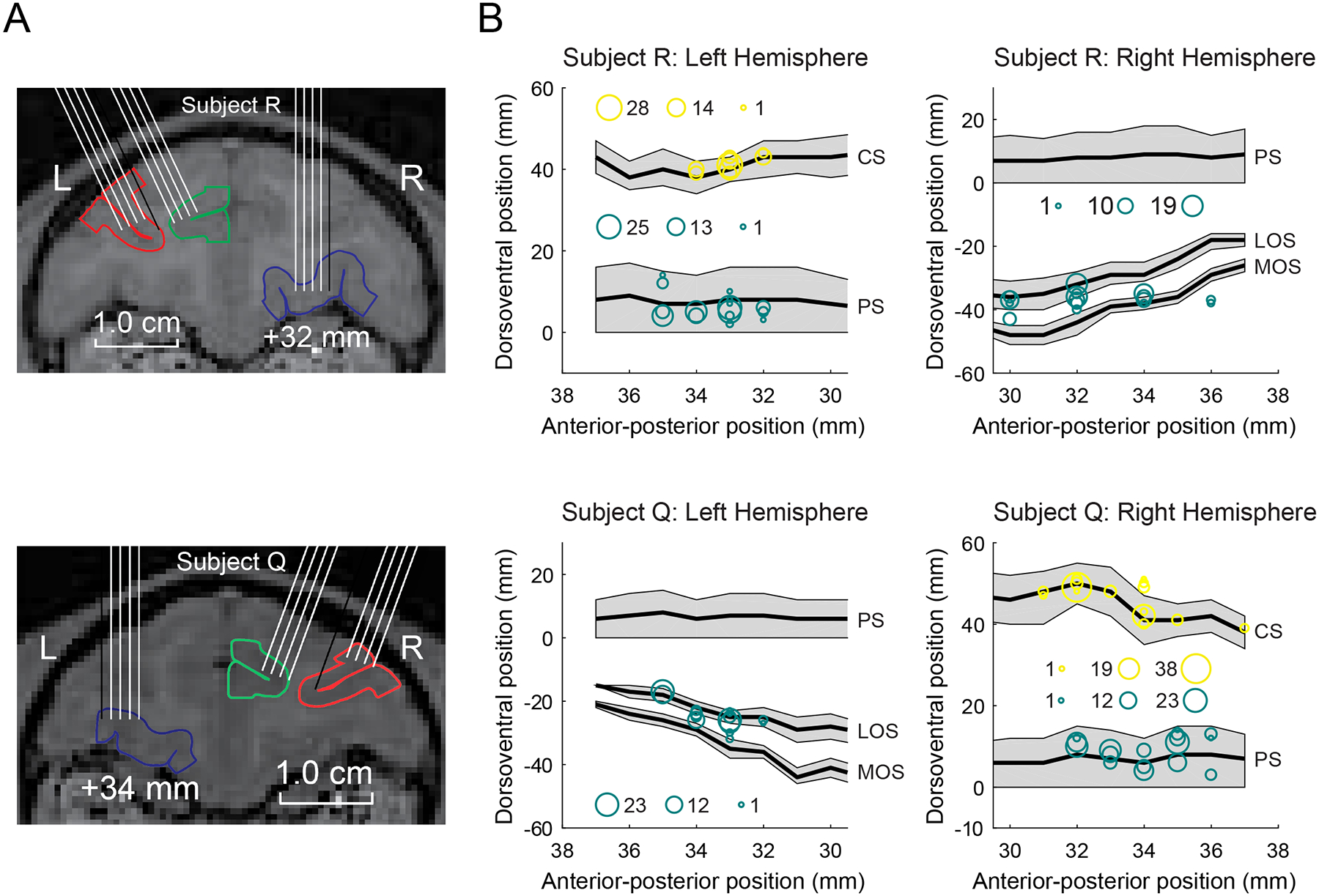
(A) Coronal MRI scans illustrating potential electrode paths. Red, green, and blue target areas indicate LPFC, ACC, and OFC, respectively. (B) Flattened reconstructions of the cortex indicating the locations of recorded neurons. The size of the circles indicates the number of neurons recorded at that location. We measured the anterior–posterior position from the interaural line (x-axis), and the dorsoventral position relative to the lip of the ventral bank of the principal sulcus (0 point on y-axis). Gray shading indicates unfolded sulci. LPFC recording locations were located within the principal sulcus. ACC recording locations were located within the cingulate sulcus. OFC recording locations were largely located within and between the lateral and medial orbital sulci. All recording locations are plotted relative to the ventral bank of the principal sulcus, which is a consistent landmark across animals. PS, principal sulcus; CS, cingulate sulcus; LOS, lateral orbital sulcus; MOS, medial orbital sulcus.
During the presentation of the pre-jump configuration the most prevalent encoding was the value of the configuration, and this was more prevalent in ACC relative to the other two areas (Figure 5). Figure 6A illustrates example neurons that encoded selectively the SV of the pre-jump configurations. Fewer neurons encoded sensory information about the stimulus configuration, i.e. LR, which is whether the start position was to the right or left of fixation. Since sensory encoding is not the focus of this report, we will not discuss LR encoding further. The time course of SV selectivity across the neural population is illustrated in Figure 7. There was no difference between the areas with respect to the onset of SV selectivity (median LPFC = 171 ms; median OFC = 166 ms; median ACC = 151 ms, 1-way ANOVA, F2,122 = 0.45, p > 0.05).
Figure 5.

Percentage of neurons in LPFC, OFC, and ACC that encode different predictors during the pre-jump and post-jump configurations. Shading indicates the proportion of neurons that encoded the variable with a given relationship: dark shading = positive, light shading = negative. For the post-jump configuration, gray color indicates the proportion encoding both positive and negative predictors, which was possible since we included these as separate regressors. None of the proportions significantly differed from the 50/50 split expected by chance (binomial test, p < 0.05, Bonferroni corrected for multiple comparisons). Asterisks indicate that the prevalence of neurons is significantly different between areas (chi-squared test, * = p < 0.05, ** = p < 0.01). Dotted line indicates the percentage of selective neurons expected by chance given our statistical threshold for selectivity.
Figure 6.

Spike density histograms illustrating selective neurons for subject value (SV) from three recording areas during the pre-jump (A) or post-jump (B) configurations. In each plot, the top panel indicates mean firing rate as a function of SV. The bottom panel indicates the coefficient of partial determination (CPD) for SV. This measure indicates the amount of variance in the neuron’s firing rate that is accounted for by SV and cannot be explained by any of the other parameters in the regression model (see Materials and Methods). Magenta data points indicate that SV significantly predicts neuronal firing rate. The gray lines indicate the onset and offset of the pre- and post-jump configurations.
Figure 7.

Encoding of the SV of the pre-jump configuration across the population in three prefrontal areas. Each horizontal line on the plot indicates the selectivity of a single neuron as measured using the coefficient of partial determination (see Materials and Methods). Neurons have been sorted according to the latency at which they first show selectivity. The vertical white lines indicate the onset and offset of the pre-jump configuration.
During the post-jump configuration, we also found that the most prevalent encoding was the encoding of the configuration’s value (Figure 5 and 6B). Note that some neurons encoded SV before the onset of the post-jump configuration, which indicates that they also encoded the SV of the pre-jump configuration. Some neurons also encoded RPE, and these neurons were most prevalent in ACC. In our task, rewards were fixed and delivered with certain probability, and so the RPE reflected changes in the amount of work that the animal needed to do, since the goal had moved either closer (positive RPE) or further (negative RPE) from the start position. In contrast, very few neurons encoded PPE, although the prevalence of such neurons did exceed chance in ACC (20/212 or 9.4%, binomial test, p < 0.01). However, the weak encoding of PPE relative to the other variables is evident in the population plots shown in Figure 8, where the robust encoding of SV contrasts with the weaker encoding of RPE and the virtually absent encoding of PPE.
Figure 8.

Encoding of predictors related to the post-jump configuration across the population in three prefrontal areas. Conventions are as in Figure 7.
Discussion
We developed a primate version of a task that has been previously used to study HRL in humans (Ribas-Fernandes et al., 2011). Animals had to use a lever to move a dot to a subgoal position and then on towards a goal position. Many prefrontal neurons encoded the value of the presented task configuration, as defined by the parameters that individual animals used to guide their choice behavior. This replicates our previous results (Kennerley, Dahmubed, Lara, & Wallis, 2009; Kennerley & Wallis, 2009), in which neurons encoded the number of lever presses that animals needed to make in order to earn a reward. Prefrontal neurons also encoded RPE, particularly in ACC, which is also consistent with our previous work (Kennerley et al., 2011). A novel aspect of our results is that these RPEs appeared to be driven by changes in effort rather than reward.
Both rodent lesion (Rudebeck, Walton, Smyth, Bannerman, & Rushworth, 2006) and human neuroimaging (Prevost, Pessiglione, Metereau, Clery-Melin, & Dreher, 2010) suggest that ACC may be particularly involved in effort-based decisions. Furthermore neurophysiology studies have shown a stronger dynamical interaction between ACC and LPFC for effort-based decisions compared to delay-based decisions, whereas the opposite is true for OFC and LPFC (Hunt, Behrens, Hosokawa, Wallis, & Kennerley, 2015). These ideas have been extended to include decisions about cognitive effort, which could be used to determine whether to exert cognitive control (Shenhav, Botvinick, & Cohen, 2013). If ACC is responsible for incorporating effort into value calculations, this would include calculating value prediction errors based on effort. An outstanding question is the role that dopamine plays in this process. Although dopamine neurons have long been associated with encoding reward predictions, the evidence for their involvement in effort calculations is more mixed. In an effort-based decision-making task, only a small minority of dopamine neurons incorporated effort information (Pasquereau & Turner, 2013). Future research should examine the precise role of dopamine in ACC prediction error calculations.
Very few neurons encoded PPEs, although those that did appear to be located in ACC. Neuroimaging studies in humans that used the same task showed that PPE correlated with increased BOLD activation in ACC (Ribas-Fernandes et al., 2011). Our data therefore appear to provide convergent evidence to support the HRL theoretical framework and a role for ACC in this process. However, an important caveat is that the degree of neural encoding that we observed in ACC was not particularly compelling. Only a handful of neurons showed significant encoding, and none of those neurons were particularly strongly tuned to PPE.
One possible explanation for the weak effects is that the animals were not paying sufficient attention to the task configurations, since the majority of trials did not require a choice. This explanation seems inadequate. In previous tasks where we have interleaved trials requiring a choice with those that did not require a choice, we have seen little difference in the response of prefrontal neurons to both types of trial (Rich & Wallis, 2016). In addition, in the current study, we observed robust encoding of the value of the stimulus configuration. Finally, both animals showed changes in reaction time on attaining the subgoal. Taken together, these results suggest that the animals were appropriately attending to the task and the subgoal.
Differences might also have arisen due to the way the task was represented across the two species. Humans bring context to the task in a way that monkeys cannot. For example, in humans, the description of the task involved a driver picking up a package and delivering it to a customer. This real-world knowledge might have contributed to humans approaching the task in a more hierarchical fashion compared to the relatively abstract representation that the animals experience. An additional difference between the two species relates to the value of acquiring the subgoal. In humans, there was no evidence that the subgoal influenced choice behavior, suggesting that acquiring the subgoal was not rewarding. In contrast, in the current study, the subgoal did influence the animals’ choice behavior, albeit to a smaller extent than the other stimulus parameters. Thus, we cannot rule out the possibility that the PPE that was generated in ACC simply reflected an RPE that was generated by the acquisition of the subgoal.
This raises a broader issue with the HRL framework. The original study examining HRL in humans emphasized that pseudo-rewards are distinct from primary rewards because attaining subgoals is not necessarily rewarding in and of itself (Ribas-Fernandes et al., 2011). An example is adding milk to coffee: the subgoal brings one closer to the first sip of coffee, but the act itself is not rewarding. However, traditional RL models can also account for the influence of non-rewarding subgoals on behavior, because reward values become progressively associated with earlier reward-predictive events, which would include attaining subgoals that are not in themselves necessarily rewarding. Thus, the critical difference between HRL and RL rests, not so much in the distinction between pseudo-rewards and primary rewards, but rather in the way in which behavior is organized, in particular, the unit of behavior that is reinforced. In RL, prediction errors are calculated for each individual action, whereas in HRL, individual actions are chunked into a subroutine that generates its own prediction error on completion. It is not clear whether the prediction error generated by the subroutine necessarily needs to involve a distinct neural signal compared to the prediction error generated by the primary reward.
How the brain determines the appropriate behavioral unit for reinforcement learning mechanisms is an area of active investigation. One idea is that the brain tends to group together mutually predictive stimuli and actions into a single event (Schapiro, Rogers, Cordova, Turk-Browne, & Botvinick, 2013). For example, driving to a restaurant and ordering a meal are both actions that can acquire an ultimate goal of eating a tasty meal, but behaviorally, the agent experiences a continuous stream of stimuli and actions. However, the act of driving involves many mutually predictive stimuli (e.g. steering wheel, traffic lights, seat belt) but only weakly predicts going to a restaurant, since one can drive to many alternate destinations. Likewise, ordering a meal involves many mutually predictive stimuli (e.g. server, menu, water), but may only weakly predict driving, since one could have also walked or caught the subway. Thus, the act of driving is grouped as a separate event from ordering the meal. The responses of prefrontal neurons are consistent with organizing behavior into these high-level events. For example, one of the major determinants of prefrontal firing rates is in which part of the task the agent is currently engaged (Sigala, Kusunoki, Nimmo-Smith, Gaffan, & Duncan, 2008). Prefrontal neurons also encode events at an abstract, high-level, incorporating categories (Freedman, Riesenhuber, Poggio, & Miller, 2001) and rules (Wallis, Anderson, & Miller, 2001). It may be that standard RL mechanisms operating on these high-level, behavioral events are sufficient to account for hierarchical behavior.
In summary, our results provide partial support for the involvement of ACC in HRL. In a task designed to use hierarchical behavior, we observed neurons in ACC whose firing rate correlated with PPE. However, there were caveats to this support, including the weak encoding, particularly in comparison to other signals that have been more firmly associated with ACC, such as predicted value and RPE, and whether HRL even requires a PPE signal distinct from RPE.
Acknowledgments
This work was funded by NIMH R01 MH097990 (to J.D.W.) and by Taiwan Top University Strategic Alliance Graduate Fellowship USA-UCB-100-S01 to (F-K.C.).
References
- Akaike H (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716–723. [Google Scholar]
- Asaad WF, & Eskandar EN (2008). A flexible software tool for temporally-precise behavioral control in Matlab. Journal of neuroscience methods, 174(2), 245–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asaad WF, & Eskandar EN (2011). Encoding of both positive and negative reward prediction errors by neurons of the primate lateral prefrontal cortex and caudate nucleus. Journal of Neuroscience, 31(49), 17772–17787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badre D, & D’Esposito M (2007). Functional magnetic resonance imaging evidence for a hierarchical organization of the prefrontal cortex. J Cogn Neurosci, 19(12), 2082–2099. [DOI] [PubMed] [Google Scholar]
- Badre D, & Frank MJ (2012). Mechanisms of hierarchical reinforcement learning in cortico-striatal circuits 2: evidence from FMRI. Cerebral cortex, 22(3), 527–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badre D, Hoffman J, Cooney JW, & D’Esposito M (2009). Hierarchical cognitive control deficits following damage to the human frontal lobe. Nat Neurosci, 12(4), 515–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botvinick MM, Niv Y, & Barto AC (2009). Hierarchically organized behavior and its neural foundations: a reinforcement learning perspective. Cognition, 113(3), 262–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P, & Niv Y (2008). Reinforcement learning: the good, the bad and the ugly. Current opinion in neurobiology, 18(2), 185–196. [DOI] [PubMed] [Google Scholar]
- Frank MJ, & Badre D (2012). Mechanisms of hierarchical reinforcement learning in corticostriatal circuits 1: computational analysis. Cerebral cortex, 22(3), 509–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman DJ, Riesenhuber M, Poggio T, & Miller EK (2001). Categorical representation of visual stimuli in the primate prefrontal cortex. Science, 291(5502), 312–316. [DOI] [PubMed] [Google Scholar]
- Hollerman JR, & Schultz W (1998). Dopamine neurons report an error in the temporal prediction of reward during learning. Nat Neurosci, 1(4), 304–309. [DOI] [PubMed] [Google Scholar]
- Holroyd CB, & McClure SM (2015). Hierarchical control over effortful behavior by rodent medial frontal cortex: A computational model. Psychol Rev, 122(1), 54–83. [DOI] [PubMed] [Google Scholar]
- Hunt LT, Behrens TE, Hosokawa T, Wallis JD, & Kennerley SW (2015). Capturing the temporal evolution of choice across prefrontal cortex. Elife, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennerley SW, Behrens TE, & Wallis JD (2011). Double dissociation of value computations in orbitofrontal and anterior cingulate neurons. Nature neuroscience, 14(12), 1581–1589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennerley SW, Dahmubed AF, Lara AH, & Wallis JD (2009). Neurons in the frontal lobe encode the value of multiple decision variables. J Cogn Neurosci, 21(6), 1162–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennerley SW, & Wallis JD (2009). Evaluating choices by single neurons in the frontal lobe: outcome value encoded across multiple decision variables. Eur J Neurosci, 29(10), 2061–2073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koechlin E, Ody C, & Kouneiher F (2003). The architecture of cognitive control in the human prefrontal cortex. Science, 302(5648), 1181–1185. [DOI] [PubMed] [Google Scholar]
- Lara AH, Kennerley SW, & Wallis JD (2009). Encoding of gustatory working memory by orbitofrontal neurons. J Neurosci, 29(3), 765–774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D, Seo H, & Jung MW (2012). Neural basis of reinforcement learning and decision making. Annual review of neuroscience, 35, 287–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, et al. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), 529–533. [DOI] [PubMed] [Google Scholar]
- Pasquereau B, & Turner RS (2013). Limited encoding of effort by dopamine neurons in a cost-benefit trade-off task. J Neurosci, 33(19), 8288–8300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips CG (1973). Proceedings: Hughlings Jackson Lecture. Cortical localization and “sensori motor processes” at the “middle level” in primates. Proc R Soc Med, 66(10), 987–1002. [PMC free article] [PubMed] [Google Scholar]
- Prevost C, Pessiglione M, Metereau E, Clery-Melin ML, & Dreher JC (2010). Separate valuation subsystems for delay and effort decision costs. J Neurosci, 30(42), 14080–14090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribas-Fernandes JJ, Solway A, Diuk C, McGuire JT, Barto AG, Niv Y, et al. (2011). A neural signature of hierarchical reinforcement learning. Neuron, 71(2), 370–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich EL, & Wallis JD (2014). Medial-lateral organization of the orbitofrontal cortex. J Cogn Neurosci, 26(7), 1347–1362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich EL, & Wallis JD (2016). Decoding subjective decisions from orbitofrontal cortex. Nat Neurosci, 19(7), 973–980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudebeck PH, Walton ME, Smyth AN, Bannerman DM, & Rushworth MF (2006). Separate neural pathways process different decision costs. Nat Neurosci, 9(9), 1161–1168. [DOI] [PubMed] [Google Scholar]
- Schapiro AC, Rogers TT, Cordova NI, Turk-Browne NB, & Botvinick MM (2013). Neural representations of events arise from temporal community structure. Nat Neurosci, 16(4), 486–492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W, Dayan P, & Montague PR (1997). A neural substrate of prediction and reward. Science, 275(5306), 1593–1599. [DOI] [PubMed] [Google Scholar]
- Shenhav A, Botvinick MM, & Cohen JD (2013). The expected value of control: an integrative theory of anterior cingulate cortex function. Neuron, 79(2), 217–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigala N, Kusunoki M, Nimmo-Smith I, Gaffan D, & Duncan J (2008). Hierarchical coding for sequential task events in the monkey prefrontal cortex. Proc Natl Acad Sci U S A, 105(33), 11969–11974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, & Barto AG (1998). Reinforcement learning: an introduction (adaptive computation and machine learning). Cambridge: MIT Press. [Google Scholar]
- Sutton RS, Precup D, & Singh S (1999). Between MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning. Artificial Intelligence, 112, 181–211. [Google Scholar]
- Wallis JD, Anderson KC, & Miller EK (2001). Single neurons in prefrontal cortex encode abstract rules. Nature, 411(6840), 953–956. [DOI] [PubMed] [Google Scholar]


