Modeling and numerical simulation of the bubble cloud dynamics in an ultrasound field for burst wave lithotripsy

Abstract

Modeling and numerical simulation of bubble clouds induced by intense ultrasound waves are conducted to quantify the effect of cloud cavitation on burst wave lithotripsy, a proposed non-invasive alternative to shock wave lithotripsy that uses pulses of ultrasound with an amplitude of O(1) MPa and a frequency of O(100) kHz. A unidirectional acoustic source model and an Eulerian-Lagrangian method are developed for simulation of ultrasound generation from a multi-element array transducer and cavitation bubbles, respectively. Parametric simulations of the spherical bubble cloud dynamics reveal a new scaling parameter that dictates both the structure of the bubble cloud and the amplitude of the far-field, bubble-scattered acoustics. The simulation further shows that a thin layer of bubble clouds nucleated near a kidney stone model can shield up to 90% of the incoming wave energy, indicating a potential loss of efficacy during the treatment due to cavitation. Strong correlations are identified between the far-field, bubble-scattered acoustics and the magnitude of the shielding, which could be used for ultrasound monitoring of cavitation during treatments. The simulations are validated by companion experiments in vitro.

1. INTRODUCTION

This paper provides a brief summary and overview of recent progress in modeling, numerical simulation, and experiments on cavitation bubble clouds that are nucleated in the human body during treatment using Burst Wave Lithotripsy (BWL) [1], a method of lithotripsy that uses pulses of high-intensity, focused ultrasound at a frequency of O(100) kHz and an amplitude of O(1–10) MPa to break kidney stones [7]. BWL is an alternative to standard shockwave lithotripsy (SWL) [8], which uses much higher amplitude shock waves delivered at a typically much lower rate. In both SWL and BWL, the tensile component of the pressure can nucleate cavitation bubbles in the human body. For SWL, cavitation is a significant mechanism in stone communition, but also causes tissue injury. By contrast, little is yet known about cavitation in BWL. A series of our studies has successfully identified the effects of cavitation on BWL; although they may be less injurious than cavitation in SWL, bubble clouds in BWL can scatter a large portion of the incoming wave energy that would otherwise be transmitted into the stone and thereby potentially cause loss of efficacy of stone comminution. The latest study reported in our article published in The Journal of the Acoustical Socity of America [6] suggests that the activities of cavitation in the human body and the resulting energy shielding could be identified by ultrasound monitoring in realtime during the treatment. We will review the results and their implication for future work.

2. MODELING AND NUMERICAL FRAMEWORK

Our initial experiment identified that diffuse bubble clouds with a size of O(1) mm are formed near the focal region during the passage of the burst wave in a water tank [5]. They are highly distinct from denser and larger bubble clouds observed in SWL. For simulation of the clouds in BWL, two numerical tools are developed: a model of ultrasound generation from a medical transducer [2], and a method of simulating clouds of cavitation bubbles in the focal region [3]. For the former, an analytical expression was derived to express acoustic source distribution on an arbitrary curvature of two-dimensional surface that generates a wave propagating in a favorable direction. For the latter, an Eulerian-Lagrangian method was introduced, in which the liquid phase is descritized on structured grids and bubbles are treated as spherical cavities that volumetrically oscillate at the sub-grid scale. The numerical framework enables large-scale simulation of the ultrasound-induced cavitation growth and collapse of individual bubbles, their mutual interactions, and the resulting bubble-scattered acoustic waves with and without a kidney stone.

3. ENERGY SHIELDING

A canonical study of the dynamics of isolated, spherical bubble clouds induced by intense ultrasound waves suggests that even diffuse bubble clouds in BWL can scatter a large portion of the incoming wave energy, and this can lead to loss of efficacy of stone comminution [4]. In order to quantify the energy shielding in the presence of a kidney stone, a combined numerical and experimental study has recently been conducted [6]. Figure 1 shows an overview of the study. In the experiment (Fig. 1a), 10 cycles of a burst wave with a peak maximum amplitude of 7 MPa and a frequency of 335 kHz was focused from a multi-element array medical transducer (Fig. 1b) on a cylindrical model kidney stone made of epoxy resin. A high-speed camera was used to capture bubble clouds nucleated in the proximal surface of the stone and bubble-scattered acoustic waves were measured by the transducer array that was used to generate the burst wave. In high speed images, we observed a thin layer of bubble clouds nucleated on the proximal surface of the stone (1c). The simulation successfully reproduced the experimental bubble clouds (Fig. 1d). Figure (1e) shows the correlation between the scattering factor, F, and the shielding factor, S, obtained from simulations with various values of the thickness and the initial void fraction of bubble clouds, β₀. The scattering factor is a function of the maximum value of the imaging functional, $\mathcal{I}$, a metric introduced to quantify the amplitude of the back-scattered acoustic waves from the bubbles and the stone. F is defined as

$$F=\frac{\text{max}[\mathcal{I}]}{\text{max}\left[{\mathcal{I}}_{ref}\right]},$$ (1)

where ${\mathcal{I}}_{ref}$ is the reference value of imaging functional without bubbles. Therefore, F quantifies the enhancement/decay of the scattered acoustic waves due to the presence of bubbles. The shielding factor is defined as

$$S=1-\frac{P}{P_{\text{ref}}},$$ (2)

where P is the total work done by the acoustic energy to the stone during each simulation. P_ref is the reference value of P obtained in the case without bubbles. Note that S = 0 and S = 1 indicate no shielding and perfect shielding (no energy transmission into the stone), respectively. Notably, the plot indicates a strong positive correlation between the shielding factor and the scattering factor over the global range of the data points, independent of the initial condition of bubbles. The shielding factor grows with increasing the scattering factor and reaches S ≈ 0.9 at F ≈ 4. The result indicates that up to 90% of the energy of the incident burst wave can be absorbed/scattered by bubbles that would otherwise be transmitted into the stone, and this can lead to significant loss of efficacy of stone comminution. An important implication of the correlation between the scattering factor and the shielding factor is that one may identify the magnitude of the strong energy shielding by measuring the scattered acoustic waves without directly observing the bubble clouds; cavitation and the shielding can be monitored during treatment using BWL. Extension of the numerical and experimental setups to model an in vivo environment is desirable to further quantify the energy shielding in practical conditions of BWL.

Figure 1:

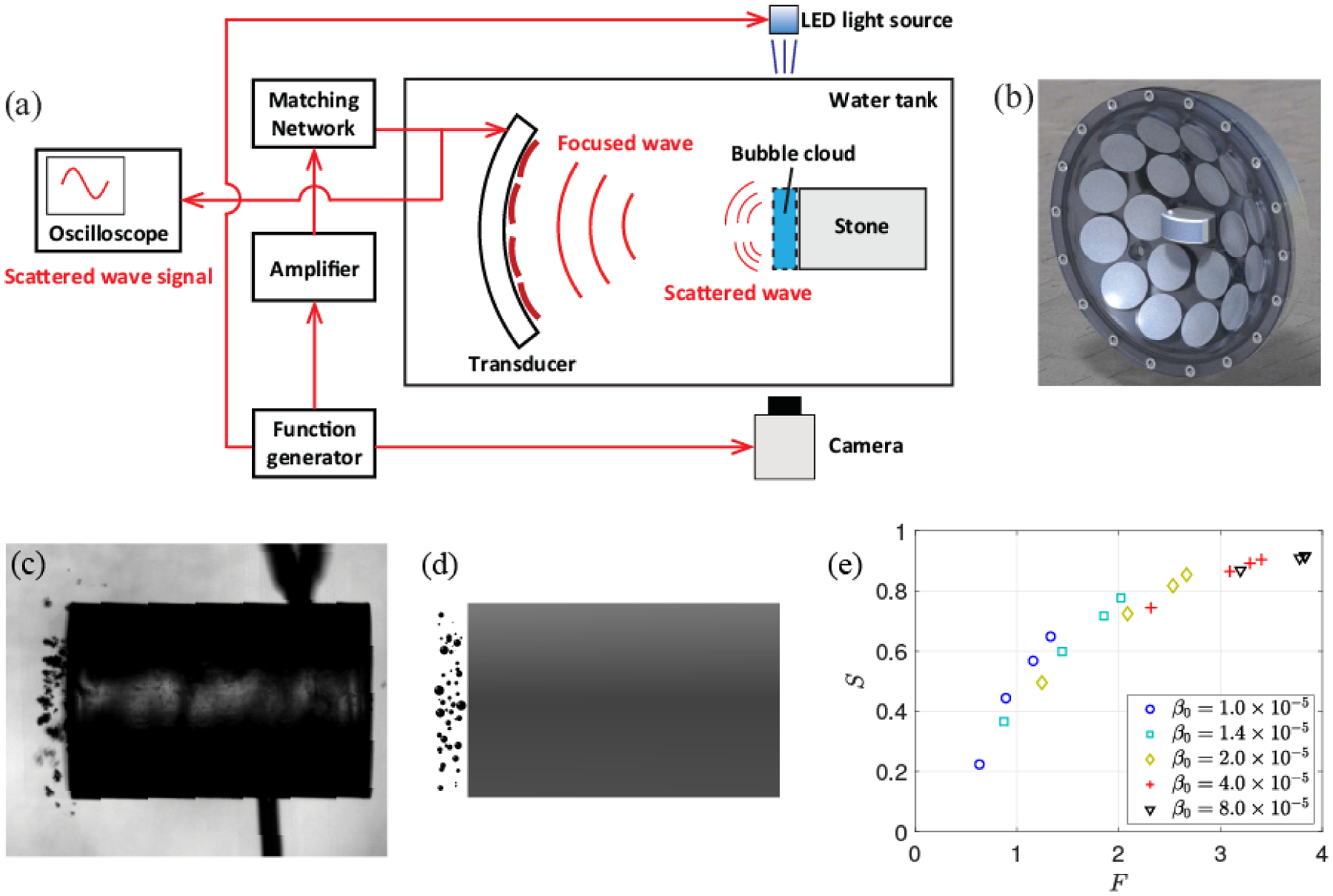
Overview of the study of the energy shielding of kidney stones by cavitation bubble clouds in BWL. (a) shows the schematic of the experimental setup. (b) shows the multi-element array medical transducer. (c) and (d) show images of representative bubble clouds observed during the passage of the burst wave from the high-speed imaging and the the simulation, respectively. The height and diameter of the stone are 10 and 6.25 mm. (e) shows the correlation between the scattering factor and the shielding factor obtained from simulations with various values of the thickness and the initial void fraction of bubble clouds, β₀. The figures are reproduced from [6].

4. CONCLUSION AND OUTLOOK

This series of combined numerical and experimental studies successfully identified the dynamics of cavitation bubble clouds in BWL and quantified the energy shielding of kidney stones by the bubbles, the latter of which may cause loss of efficacy of stone comminution. Recent work suggests that the magnitude of the energy shielding can be identified by scattered ultrasound waves. The results motivate future work to monitor and possibly control cavitation, and mitigate the energy shielding in real-time during clinical treatment. Such a strategy may lead to further precise, efficient, and safe methods of stone commminution for improved outcomes of BWL.