Self navigation for 3D multi-shot EPI with data-reference

Abstract

Purpose:

In this study, we sought to develop a self-navigation strategy for improving the reconstruction of diffusion weighted 3D multi-shot EPI. We propose a method for extracting the phase correction information from the acquisition itself, eliminating the need for a 2D navigator, further accelerating the acquisition.

Methods:

In-vivo acquisitions at 3T with (0.9mm)³ and (1.5mm)³ isotropic resolutions were used to evaluate the performance of the self-navigation strategy. Sensitivity to motion was tested using a large difference in pitch position of the head. Using a multi-shell diffusion weighted acquisition, tractography results were obtained at (0.9mm)³ to validate the quality with conventional acquisition.

Results:

The use of 3D multislab EPI with self-navigation enables 3D DW SE-EPI acquisitions that have the same efficiency as 2D single-shot acquisition. For matched acquisition time the image SNR between 3D and 2D acquisition is shown to be comparable for whole-brain coverage with (1.5mm)³ resolution and for (0.9mm)³ resolution the 3D acquisition has higher SNR than what can be obtained with 2D acquisitions using current state-of-art multiband techniques. The self-navigation technique was shown to be stable under inter-volume motion. In tractography analysis, the higher resolution afforded by our technique enabled clear delineation of the tapetum and posterior corona radiata.

Conclusion:

The proposed self-navigation approach utilized a self-consistent phase in 3D diffusion weighted acquisitions. Its efficiency and stability were demonstrated for a plurality of common acquisitions. The proposed self-navigation approach allows for faster acquisition of 3D multi-shot-EPI desirable for large FOV and/or higher resolution.

Introduction:

Diffusion weighted imaging (dMRI) provides the input for tractography algorithms used for the reconstruction of the complex axonal fiber architecture in the brain to infer ”structural connectivity” between gray matter regions (1–3) or to obtain information on the micro-structure of the underlying white matter tissue (4). The approach is one of the complementary magnetic resonance (MR) methods employed in the original Human Connectome Project (HCP) (3,5–7) launched in 2010 with the aim of generating the most (to date) accurate description of the connections among gray matter locations in the young-adult human brain. It continues to play a pivotal role in the more recent HCP-like initiatives aimed at creating large databases on human brain connectivity as a function of human lifespan (8–11), and diseased states (12–14)

Starting with the original HCP, the dMRI sequences incorporated transformative improvements based on volume coverage using simultaneous multislice (SMS) excitation with Multiband (MB) RF pulses (5,15–18)). These signal-to-noise (SNR) efficient, slice based approaches enabled significant improvements in spatial resolution, q-space sampling, and/or total time of data acquisition. For example, the original HCP generated high quality dMRI data with (1.25 mm)³ and (1.05 mm)³ isotropic resolution at 3 and 7 Tesla (T), respectively, with extensive q-space sampling in 53 min and 40 min of total data acquisition time respectively (3,5). In contrast, the UK Biobank (13) and the HCP-Lifespan (10) initiatives running with the same HCP sequences, opted for lower spatial resolution (2 and 1.5 mm isotropic, respectively). This substantially reduced the data acquisition times to ~7 and ~21 min, respectively, while still achieving extensive q-space sampling.

The dMRI implementations with the SMS/MB approach, however, run into limitations when whole brain coverage is targeted with much higher spatial resolution than those achieved in the HCP and its variants. The larger number of slices needed to cover the entire brain at higher resolutions leads to longer and SNR-inefficient volume acquisition times (VAT), which is the same as TR in slice based imaging. This can be remedied using higher slice accelerations (i.e. MB factors). Unfortunately maximal MB factors are severely limited in current dMRI implementations by power deposition and/or the unaliasing capabilities of currently available multichannel receive arrays. These limitations may be ameliorated by using parallel transmit techniques to manage power deposition with MB pulses employed in dMRI (19–21) and by higher number of receive channels to support a larger degree of aliasing due to multislice excitation (22). Instrumentation that enables such approaches, however, is not generally available at present. Alternatively, diffusion weighted (DW), three-dimensional (3D) volumetric encoding using multi-shot echo-planar imaging (multi-shot EPI) (23–26), Hadamard encoding (27) or simultaneous multislab acquisition with self-navigated RF-encoding (28) has been proposed to disentangle VAT and TR. This helps with reducing the effective TR between consecutive excitations of spins to a more SNR efficient domain.

For segmented DW-EPI, one of the main challenges is the presence of a spatiotemporally varying phase change of the magnetization (sometimes referred to as “diffusion-phase” (23)). Diffusion-phase is due to the application of diffusion gradients in the presence of physiological brain motion, cerebrospinal fluid pulsations or from non-identical B₀ fluctuations during the dephasing and rephasing parts of the diffusion weighting gradients. The inconsistency in this phase accrual for the different segments acquired in the “multi-shot” coverage of k-space, however, leads to a major degradation in the resulting images. This problem persists even when 3D encoding for dMRI is implemented by imaging multiple smaller slabs instead of whole-brain volumetric encoding (23–26). This is because encoding of the smaller slabs still often necessitates segmented EPI acquisitions. The solution employed to deal with this problem has been to employ an additional refocusing RF pulse followed by the acquisition of a 2D navigator. This allows for phase correction in order to correctly combine the multiple segments. However, a consequence of this approach is the lengthening of the total acquisition time by 30–50% (23). The approximation of the 3D diffusion phase with 2D navigator has been found to be sufficient for slabs less than 30mm at 3T (23,29–32). For thicker slabs, higher b-values or higher field strengths the use of 3D navigators as developed in (33) is one possible extension. Alternative strategies, such as using a SENSE reconstruction phase-consistency for PE-segmentation to obtain ghost-free images, as in the MUSE (34) or MUSSELS (35) techniques, also facilitate acquisitions without navigators.

In this study, we sought to develop a self-navigation strategy for the acquisition of DW 3D multislab multi-shot EPI for dMRI. We propose a method for extracting the required phase correction information from the acquisition itself, thus eliminating the need for additional RF pulse and the 2D navigator. The 3D dMRI obtained with this method for phase correction was compared in terms of SNR to 2D single-shot EPI dMRI serving as a gold standard. Furthermore, the robustness of our approach to inter-volume motion was evaluated to indirectly assess stability for eddy currents induced distortions.

Methods:

In the 3D multislab multi-shot EPI acquisition in this work the slab-selective RF pulses select a slab in one direction (taken as the z-direction). The resulting precessing magnetization is detected with a single 2D EPI echotrain encoded. It is encoded in the x and the y directions using a readout and a phase encoding gradient alongside a second phase encoding gradient applied in the z direction. The 2D encoded echotrain can be undersampled along the phase encoding dimension (in y) for reconstruction with parallel imaging (iPAT factor). We will refer to this phase encoding as the “in-plane” phase encoding. The excitation and subsequent detection is repeated with the second phase encoding gradient changing in amplitude. The number of repetitions is equal to the number of slices, including any oversampling, employed to resolve the slab in the z-direction. Fourier transform along the phase encoding in the z-direction divides the slab into multiple slices, including any oversampling. The slab may also be undersampled along the slice encoding direction (in z), and when the acquired 2D encoded echo-trains for individual k_z-plane are shifted relative to each other in the phase encoding dimension. This is referred to as 2D CAIPIRINHA(36) encoding.

TR refers to the time between the RF pulses applied to the same volume of the sample. Therefore, in multislab volume coverage using 3D multi-shot EPI, the minimum TR is determined by the number of slabs and the acquisition time of the (x, y) encoded data from the slab. The VAT required for covering the targeted volume is given by the number of slices, including oversampling slices, per slab, multiplied by the TR. In contrast, in 2D SMS/MB single-shot EPI, TR=VAT and the minimum TR is the number of slices required in the slice direction divided by the MB factor multiplied by the acquisition time of a single slice(37). For 3D multislab acquisitions SMS/MB acceleration means that multiple slabs are being excited and acquired simultaneously.

For a SE-EPI, the maximum signal will occur with a 90° excitation, a 180° refocusing pulse, and a TR greater than 5·T_1. But a long TR is not an SNR-efficient use of time, and better SNR can be achieved by averaging several less than fully relaxed acquisitions. The SNR is then maximized for a TR around 1.2·T₁. For TRs shorter than the optimum TR, the SNR can be preserved by increasing the excitation flip angle and maintaining the 180° refocusing flip angle(38) (see also Supporting Information Figure S2, S3, S4 and table S1 for theoretical, numerical and in-vivo discussion). Overflipping may seem counter intuitive, but the refocusing pulse converts an overflipped excitation into a magnetization that is more longitudinally relaxed than a 90° excitation. The ability to maintain the SNR for any TR much shorter than T₁ gets restricted. The RF excitation has a profile across both slabs and slices, and for adjacent slices the effective TR is less than the prescribed TR. This effect is minimized by acquiring the slices in an interleaved manner, thus maximizing signal (37). For SE-EPI with diffusion the eddy-currents from the diffusion gradients are typically modelled without directional history(39). For 2D imaging, the q-space value is changed between successive TRs necessitating a long TR relative to eddy-currents(40). For 3D and phase-encoding segmented EPI the q-space is only changed between successive VATs – composed of multiple TRs and with a linear ordering of the k_z planes, and the eddy-currents from the diffusion gradients. These gradients we modelled as consistent for the repetitions within a VAT.

Self-navigation:

In a DW 3D multi-shot EPI acquisition, the confounding and inconsistent variation in phase among the different shots or segments acquired for each TR can be corrected with the phase from a 2D navigator acquired at k_z=0 (i.e. without any phase encoding along the third dimension (23)). The relative phase-difference between each navigator acquired for different k_zs is then used for correcting the diffusion-phase induced in each echo. This is done by transforming both the navigator and the echo to a hybrid space (x,y,k_z,n_c), where n_c designates the different coils in the receive array, and by updating each k_z-plane with the addition of the phase from the navigator for each coil n_c. We propose an approach that is conceptually different from the navigator technique and which can be used without acquiring the temporal navigators at k_z=0. Although conceptually different its implementation does have similarities with the navigator technique.

The signal with a diffusion-phase can be expressed as

$$s\left(\overrightarrow{k},t\right)=\int \rho \left(\overrightarrow{x}\right)e^{i\overrightarrow{k}\cdot \overrightarrow{x}}{e}^{i{\varphi }_t\left(\overrightarrow{x}\right)}d\overrightarrow{x}=F\left(\rho \right)\otimes F\left(e^{i{\varphi }_t\left(\overrightarrow{x}\right)}\right),t=1\cdots k_z$$ [Eq. 1]

where $s\left(\overrightarrow{k},t\right)$ is the measured k-space data, $\rho \left(\overrightarrow{x}\right)$ the magnitude of the spin-distribution in the object, ${\varphi }_t\left(\overrightarrow{x}\right)$ the phase of the spin-distribution obtained for a discrete set of experimental conditions and F(·) the Fourier transform. These conditions are for each echo and includes both the dynamically varying diffusion-phase and the object phase. After sampling the discrete version $s\left(\overrightarrow{k},t\right)=F\left(\rho \right){\Phi }_t$ where Φ_t is a matrix that implements convolution with the Fourier transform of $e^{i{\varphi }_t\left(\overrightarrow{x}\right)}$, we propose to correct $s\left(\overrightarrow{k},t\right)$ such that the spatially induced diffusion-phase is formally replaced with a reference phase. This reference phase can be seen in the following equation

$$s^{\mathit{\text{corrected}}}\left(\overrightarrow{k},t\right)=F\left(\rho \right){\Phi }_t{\Phi }_t^{-1}{\Phi }_{\mathit{\text{reference}}}=F\left(\rho \right)\otimes F\left(e^{i{\varphi }_{\mathit{\text{reference}}}\left(\overrightarrow{x}\right)}\right)$$

The functions Φ_t, ${\Phi }_t^{-1}$, and, Φ_reference are each large convolutional operators, whose computations are generally nontrivial. Instead of obtaining explicit representations for ${\Phi }_t^{-1}$ and Φ_reference, the integrated effect of $\left({\Phi }_t^{-1}{\Phi }_{\mathit{\text{reference}}}\right)\left[k_z\right]$ for each hybrid plane is used for correcting [Eq. 1]. Similar to the 2D navigator technique, the effect of the diffusion phase ${\Phi }_t^{-1}{\Phi }_{\mathit{\text{reference}}}$ is assumed smooth in each plane of the hybrid space (x,y,k_z).

For DW 3D multi-shot EPI, a non-diffusion weighted acquisition, i.e. b=0 s/mm² acquisition, has the least amount of diffusion-phase. Thus we propose to use it as Φ_reference. In practice, even a non-diffusion weighted acquisition has “crusher gradients” around the 180° pulse that impart some diffusion weighting. Such gradients are very small in duration relative to the diffusion weighting gradients and are, therefore, generally ignored. As a first step, a channel-independent reference phase is estimated for each k_z plane

$$Dat{a}^{ref}\left(x,y,k_z\right)=\sum _{n_c=1}^N\overline{C_{n_c}\left(x,y\right)}{F}_{k_x,k_y}\left(s_{n_c}^{b=0}\left(k_x,k_y,k_z\right)\right)$$ [Eq. 2]

where $s_{n_c}^{b=0}$ is the acquired echo for b=0 s/mm^2, $F_{k_x,k_y}$ are the Fourier transformations along readout and phase-encoding directions, $\overline{C_{n_c}}$ the conjugate sensitivity profile for the slab obtained using an echo from k_z=0, and N the number of channels. The sensitivity profiles from the k_z=0 data are obtained by Fourier transforming along k_x and k_y, calculating the ratio of the individual channels normalized by the root sumof-squares (RSOS). After normalization the contrast-free images are spatially filtered along y and x with a Gaussian filter. This filter has full width half maximum (FWHM) of 4 pixels and a kernel width of 10 pixels. The same estimation is used for other diffusion weightings as

$$Dat{a}^{b_i}\left(x,y,k_z\right)=\sum _{n=1}^N\overline{C_n\left(x,y\right)}{F}_{k_x,k_y}\left(s_n^{b_i}\left(k_x,k_y,k_z\right)\right)$$ [Eq. 3]

Here b_i > 0 s/mm² where each echo train for every individual k_z-plane in $s_n^{b_i}$, is with different experimental conditions (diffusion-phase).

${\Phi }_t^{-1}{\Phi }_{\mathit{\text{reference}}}\left[k_z\right]$ represents the complex correction factor $e^{i\varphi \left(x,y,k_z\right)}$, which corresponds to the difference between the acquired phase and the reference phase

$$\varphi \left(x,y,k_z\right)=\angle \left(Dat{a}^{ref}\left(x,y,k_z\right),Dat{a}^{b_i}\left(x,y,k_z\right)\right),$$ [Eq. 4]

where Data^ref (x, y, k_z) is obtained from [Eq. 2] using a reference acquisition, Data^bi (x, y, k_z) is obtained from [Eq 3] using the diffusion weighted acquisition and ∠(·,·) denotes the angle between the two complex entities.

After obtaining the channel-independent correction phase $e^{i\varphi \left(x,y,k_z\right)}$, each channel is corrected with $e^{i\varphi \left(x,y,k_z\right)}$. The correction serves to impose a consistent object phase across all channels, while maintaining the channel specific phase-variations, such that the corrected channels ${\tilde{s}}_n^{b_i}$ are

$${\tilde{s}}_n^{b_i}=F_{x,y}\left(\left[F_{k_x,k_y}{s}_n^{b_i}\left(k_x,k_y,k_z\right)\right]e^{\varphi \left(x,y,k_z\right)}\right)$$

To reduce the influence of noise, the channel independent correction phase $e^{i\varphi \left(x,y,k_z\right)}$ is filtered with a Gaussian filter with FWHM=4 and width 10 for each k_z plane prior to application.

A schematic of the proposed algorithm is shown in Figure 1.

Figure 1:

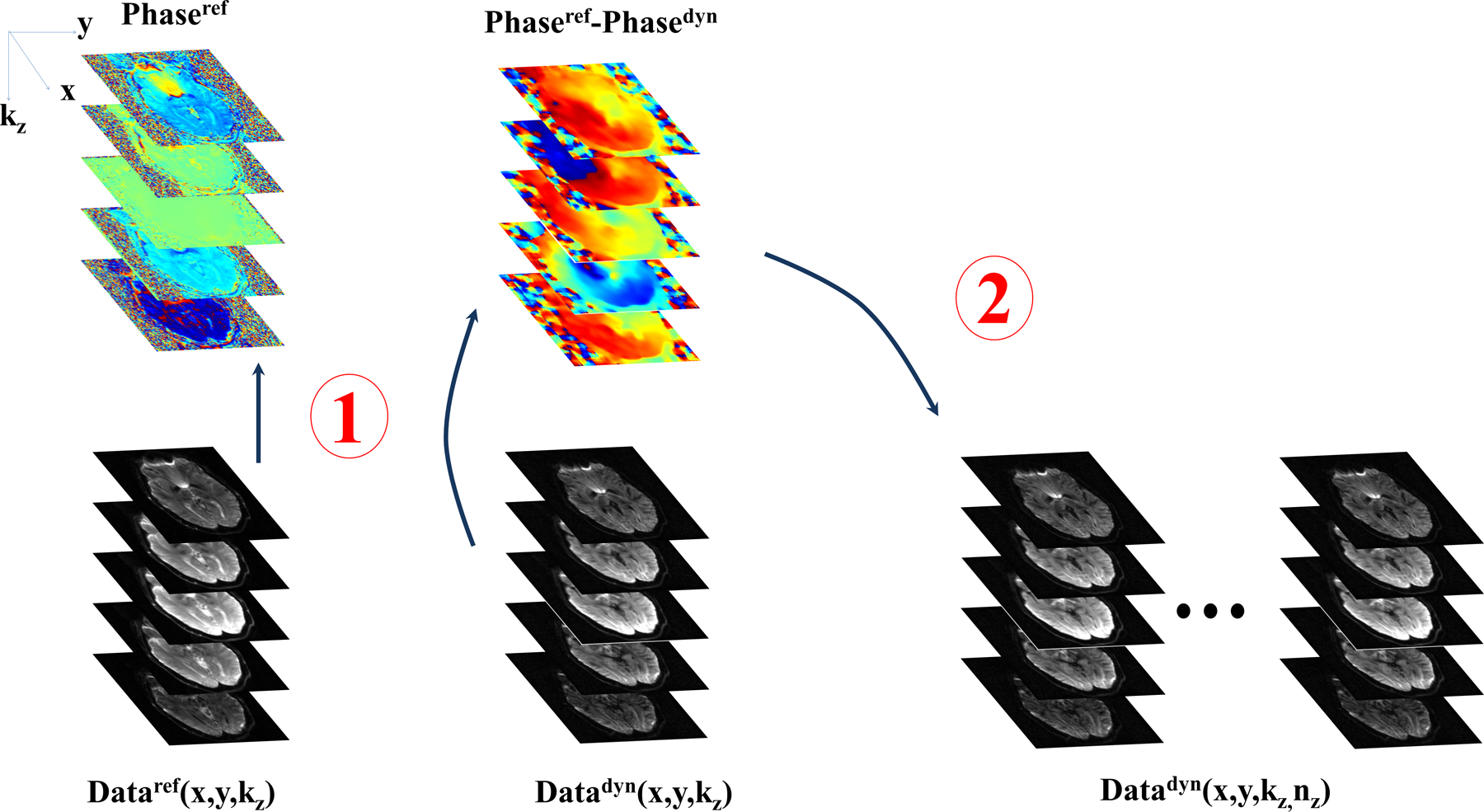
Flow diagram of the proposed self-navigation correction. For each k_z-plane of the reference acquisition, a channel combined image is calculated with [Eq. 2], as shown in bottom left. From the channel combined image, a reference phase for each k_z-plane is calculated, upper left. For the diffusion weighted image (bottom row, second column from left), a similar channel combined image is calculated, and the filtered phase-difference is obtained from [Eq. 4] and shown in the top row, second column. The resultant phase-difference is applied identically and independently to each channel in step 2, bottom row right.

Following the self-navigation correction and inverse Fourier transform along k_z, a weighted average (WA) was used to combine the data along slab boundaries, where the weights are determined using a slab profile estimate (23,41).

In Vivo Imaging

The diffusion-weighted data were acquired under an IRB approved protocol in 6 healthy volunteers (3 male,3 female, 40 ±19 years) using a 3T Siemens Magnetom Prisma (Siemens Healthcare, Erlangen, Germany) equipped with a 32-channel receiver head-coil and a 80 mT/m gradient system with a slew rate of 200 T/m/s. The SNR of a 3D multi-shot-EPI acquisition with self-navigation strategy was qualitatively compared with the gold-standard 2D single-shot-EPI for obtaining similar SNR for matched acquisition time. The 2D DW single-shot-EPI was acquired with the publicly available CMRR Multiband sequence. The sequence was developed originally for the HCP (5,42) using a pair of apodised sinc RF pulses for excitation and refocusing with flip angles set to 90° and 180° for deep brain structures (average flip angles of 78° and 160° respectively) and pulse durations set to 2.56 ms and 7.68 ms with RF bandwidth time product (BWTP) of 3.2 and 5.2, respectively. Slices are acquired with no gaps and in an interleaved fashion to minimize slice cross-talk from the imperfect slice profile of the RF-pulses. For 3D imaging, the excitation and refocusing pulses are typically chosen with high bandwidth time product (BWTP) in order to obtain both a good slab profile and low off-resonance sensitivity. As such, the 3D DW multi-shot EPI acquisition used a similar sequence design as the 2D. The main difference was the use of a Hyperbolic Secant (HS) frequency Swept SE-EPI (43) using HS1 pulses with a BWTP of 8 and 16 for excitation and refocusing respectively, both with 7680 μs duration. Slabs were excited in an interleaved fashion to minimize slab cross-talk from the RF-profile. Fat saturation was used on both 2D and 3D DW scans.

The different acquisition protocols for comparing 2D versus 3D acquisitions are summarized in Table 1 for the (1.5mm)³ and in Table 2 for the (0.9mm)³ acquisitions respectively, along with a brief description of the objective of the experiment. The lower resolution protocols compared SNR of 2D versus 3D under different conditions, as well as motion sensitivity of the self-navigated phase estimation. The higher resolution protocols were also used for SNR comparison between 2D and 3D, as well as among different choices of slab thicknesses and accelerations. Finally, a multi-shell multi-orientation DW acquisition for tractography was performed at this higher resolution using the proposed 3D approach with self-navigation.

Table 1.

Different scan parameters for the experiments used with (1.5mm)³ resolution. The flip angles in brackets are the nominal to obtain the listed flip angles in the center.

Objective	SNR comparison	SNR comparison	SNR comparison
	TR and avg. (matched TR to 3D)	TR and avg. (matched coverage to 3D)		Motion sensitivity
Protocol	A	A3	B	C
2D/3D	2D	2D	3D	3D
Resolution	(1.5 mm)3	(1.5 mm)3	(1.5 mm)3	(1.5 mm)3
TE(ms)	92.8	92.8	92.8	81.4
TR(ms)	1500	4000	1500	1520
FOV (mm3)	210×210×40.5	210×210×108	210×210×108	210×210×120
b-value	0/900/2000/3000	0/900/2000/3000	0/900/2000/3000	0/900
FOV shift	1/3	1/3	N/A	N/A
MB	3	3	1	1
iPAT	1	1	1	2
ESP (ms)	0.7	0.7	0.7	0.7
ETL (ms)	72.8	72.8	72.8	72.8
Partial Fourier	6/8	6/8	6/8	6/8
Average	12 (1 for b=0)	5 (1 for b=0)	1	1
VAT(s)	1.5	4	18	18
Slice/slab	27	72	8	8
Slab	1	1	9	10
Slab overlap (slice)	N/A	N/A	1	1
Slab oversampling	N/A	N/A	50%	50%
Total acq. time	56s	64 s	72s	36s
RF pulse used	Optimized Sinc	Optimized Sinc	HS1	HS1
RF BWTP	~3.2/ 5.2	~3.2/ 5.2	8/16	8/16
RF Duration (us)	2560/7680	2560/7680	7680/7680	7680/7680
Exc/Ref Flip angles	90°/180° (78°/160°)	90°/180° (78°/160°)	90°/180° (70°/160°)	90°/180° (70°/160°)

Table 2.

Different scan parameters for the experiments used with (0.9mm)³ resolution.

Objective	SNR comparison	SNR comparison	SNR comparison 3D	SNR comparison 3D	SNR comparison
	2D (MB = 2)	2D (MB = 3)	Thin Slab long TR	Thin Slab short TR (MB = 2)	Thick slab short TR	3D Multi-shell
Protocol	AA2	AA3	D1	D2	E	F
2D/3D	2D	2D	3D	3D	3D	3D
Resolution	(0.9 mm)3	(0.9 mm)3	(0.9 mm)3	(0.9 mm)3	(0.9 mm)3	(0.9 mm)3
TE(ms)	95.6	95.6	95.6	95.6	95.6	95.6
TR(ms)	12000	8000	3200	1600	1600	3050
FOV (mm3)	210*210*130	210*210*130	210×210×130	210*210*119	210×210×130	210×210×130
b-value	0/900/2000/3000	0/900/2000/3000	0/900/2000/3000	0/900/2000/3000	0/900/2000/3000	33 unique dir 17 for 1500, 16 for 3000 + 4(b=0)
FOV shift	1/2	1/3	N/A	N/A	N/A	N/A
MB	2	3	1	2	1	1
iPAT	2	2	2	2	2	2
ESP (ms)	0.93	0.93	0.93	0.93	0.93	0.93
ETL (ms)	80.9	80.9	80.9	80.9	80.9	80.9
Partial Fourier	6/8	6/8	6/8	6/8	6/8	6/8
Average	6	9 (1 for b=0)	2	2	1	1
VAT(s)	72	72	38	19	38	37
Slice/slab	72	72	8	8	16	8
Slab	1	1	18	16	9	18
Slab overlap (slice)	N/A	N/A	1	1	1	1
Slab over-sampling	N/A	N/A	50%	50%	50%	50%
Total acq. time	3m48s+ACS	3m44s + ACS	5m04s +ACS	2m32s +ACS+SBref	2m32s+ACS	22m12s
RF pulse family	Optimized Sinc	Optimized Sinc	HS1	HS2	HS1	HS1
Exc/Ref BWTP	~3.2/ 5.2	~3.2/ 5.2	8/16	8/12	8/16	8/16
Exc/Ref Duration (us)	2560/4480	2560/4480	7680/7680	7680/7680	7680/7680	7680/7680
Exc/Ref Flip angles	90°/180° (78°/160°)	90°/180° (78°/160°)	90°/180° (70°/160°)	90°/180° (70°/160°)	90°/180° (70°/160°)	90°/180° (70°/160°)

The 2D and 3D images were compared under conditions of different overall SNR as well as different “diffusion phase” achieved by using 3 different b values (b=900, 2000 and 3000 s/mm²); higher b values led to lower SNR but higher “diffusion phase”, thus increasing the demand on the performance of the proposed self-navigation procedure. Averaging of the 2D acquisition is performed on the complex phasecorrected SENSE-1 reconstructed images, where the phase-correction for each image was calculated as the smooth difference (using a Gaussian filter with FWHM=4 and width 10) of the phase of the individual image relative to the phase of the average image.

Protocols A and B were used to assess the SNR and image quality of the 3D multi-shot EPI acquisition (B), with the 2D SMS/MB ss-EPI acquisition (A) for matched TR, matched volume acquisition time, and resolution.

Protocols A3 and B were used to assess the SNR and image quality of the 3D multi-shot EPI acquisition (B), with the 2D SMS/MB ss-EPI acquisition (A3) for matched volume coverage, matched volume acquisition time, and resolution.

Protocol C was used to establish the robustness of the proposed self-navigation. The subject was asked to hold their head at the maximal pitch (head tilt) position during one acquisition, and subsequently at the minimal pitch position during a second otherwise identical acquisition. The absolute reference Data^ref from one acquisition was used for reconstruction using the data from the second pitch position, and compared with the use of the absolute reference Data^ref from the second pitch position.

The 2D protocols AA2 and AA3 and the 3D protocols D1, D2 and E are selected for comparing SNR of whole-brain acquisitions at (0.9mm)³ resolution for comparable acquisition time across different b-values. The 2D protocols AA2 and AA3 are with MB=2 and MB=3 respectively, and has a total acceleration of 4 and 6 respectively. Protocol D1 is a multislab acquisition with 18 slabs and a TR=3200ms. Protocol E is matched to protocol D1 for acceleration and VAT and acquired with 9 slabs, and TR=1600ms. Protocol D2 is matched to protocol D1 for coverage but with MB=2, TR/2 and VAT/2.

Protocol F was used for a high resolution multi-shell DW acquisition with 37 q-space values and b-values 1500 and 3000 s/mm² (17 for b=1500 s/mm², 16 for b=3000 s/mm² and 4 for b=0 s/mm², as a combined set following Caruyer(40)) to demonstrate the utility of 3D multi-shot EPI for high resolution white matter fiber orientation mapping.

We note that all protocols except protocol F, employed only one diffusion direction for each b-value and images were acquired for purposes of comparison under a particular set of conditions and not for generating tractography results. Only protocol F was meant as full multishell multi orientation dMRI.

Data Analysis

The equation for the signal intensity (25,31,38), S, in a SE-EPI is

$$S=M_0\text{ sin}\left({\theta }_{EX}\right){\text{sin}}^2({\theta }_{ref}/2)\frac{1+\left(\text{cos}\left({\theta }_{ref}\right)-1\right)e^{\left(-\left(TR-TE/2\right)/T_1\right)}-\text{cos}\left({\theta }_{ref}\right)e^{\left(-TR/T_1\right)}}{1-\text{cos}\left({\theta }_{ref}\right)\text{cos}\left({\theta }_{EX}\right)e^{\left(-TR/T_1\right)}}{e}^{\left(-TE/T_2\right)}$$ [Eq. 5]

where θ_EX and θ_ref are the excitation and refocusing flip angles respectively, and TE, TR and T₁ the relevant MR parameters. Eq. 5 is used for explaining the efficiency of different protocols (see also Supporting Information B).

For data analysis of images with different protocols, reconstruction with SNR units(44) is used. Thermal noise with the same covariance as the obtained data was added as a virtual volume and processed with the reconstructions pipeline. The standard deviation of the magnitude of the noise was calculated inside the part of the volume where there is sufficient signal, and multiplied by 1.54 to correct for the Rician behavior(45). The reconstructed images were normalized with the estimated average thermal noise level, which includes the average g-factor, listed in terms of the mean and maximal values and included for the high resolution data. In addition to the SNR used for the results, the tSNR for a set of relevant cross-comparisons are tabulated in Supporting Information Table S2 and discussed in the Supporting information. Unaliasing of each slice of the simultaneous multislab acquisitions was implemented with the slice-GRAPPA algorithm (17). For calibration of the convolution kernels, the k-space data from k_z=0 was used, and the slice-GRAPPA calibration estimated with slice-blocking (46). The SNR was estimated as above.

Results:

For a DW 3D multi-shot EPI with b=900 s/mm² the phases for Data^ref and the filtered Data^bi are shown in Figure 1. The reference phase Phase^ref, has both an anatomical and a smooth component. The filtered correction phase shows the outline of the underlying brain with fewer details relative to Phase^ref. Figure 2 depicts the individual slices in a slab, from the data shown in Figure 1, reconstructed with and without the correction phase. For the DW 3D multi-shot EPI without the phase-correction, there are significant signal variations from slice-to-slice through the slab with the underlying high-resolution anatomy being only partially identifiable. After the self-navigation phase correction there is a contiguous signal intensity variation from slice-to-slice through the slab and the underlying anatomy is clearly identifiable. Reduced signal intensity is also readily observed at the edges from both the RF excitation profile and the T₁ saturation caused by overlapping RF excitation from adjacent slabs.

Figure 2:

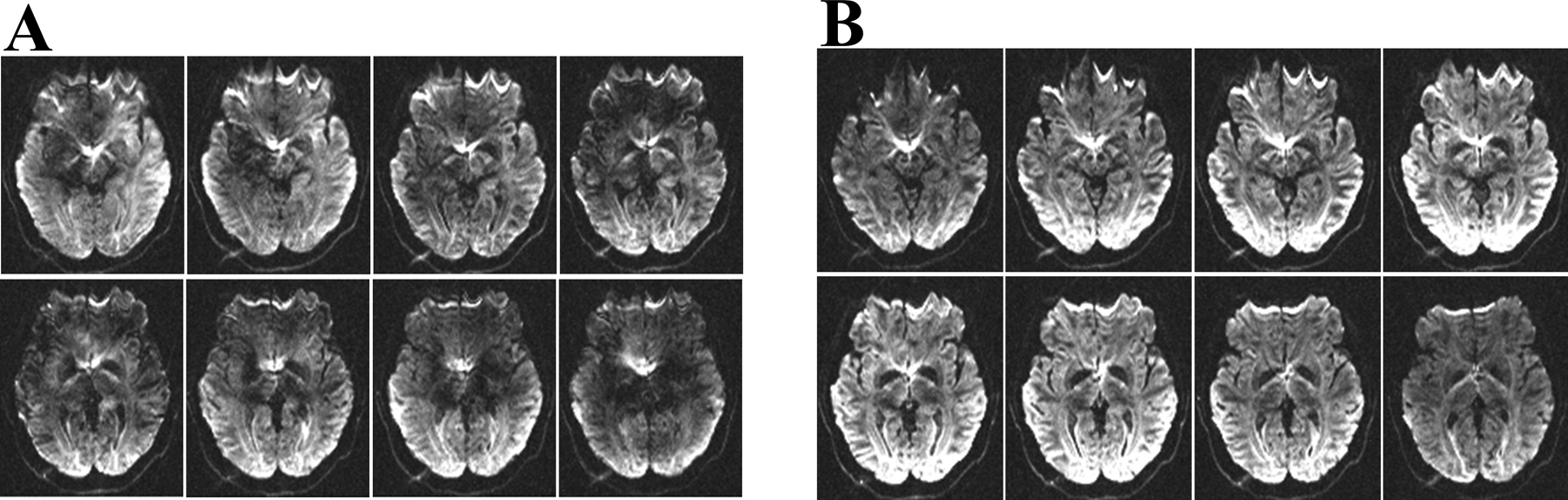
Contiguous slices in a 3D slab without (A) and with (B) the self-navigation correction, respectively, for DW 3D multi-shot EPI with b=900 s/mm². Images obtained without self-navigation display substantial signal intensity variation from slice to slice as well as signal loss throughout the brain. With self-navigation (B), the signal is contiguous from slice to slice. The edge slices have lower average signal intensity compared with the middle slices because of the RF-pulse profile.

Figure 3 shows a representative axial slice in SNR units from the 3D multi-shot EPI acquisition (protocol B). It also shows two different 2D single-shot EPI acquisitions (protocol A and A3) with TR=1.5s and TR=4s respectively. For the 2D acquisition with TR=1.5s, 1 and 12 averages are used and for TR=4s, 5 averages are used for comparable scan-time with the 3D acquisition. A quantitative comparison of SNR at b-values of 900, 2000, and 3000 s/mm² is shown using reconstruction in SNR units. Thus, when matched for acquisition time using 12 averages the 2D images look virtually the same for the 2D SMS/MB and 3D multi-shot EPI with self-navigation correction and the longer TR and whole brain acquisitions. The g-factor for protocol A is 1.08±0.05 (mean ± standard deviation), and for protocol A3 1.02±0.04 (mean ± standard deviation).

Figure 3:

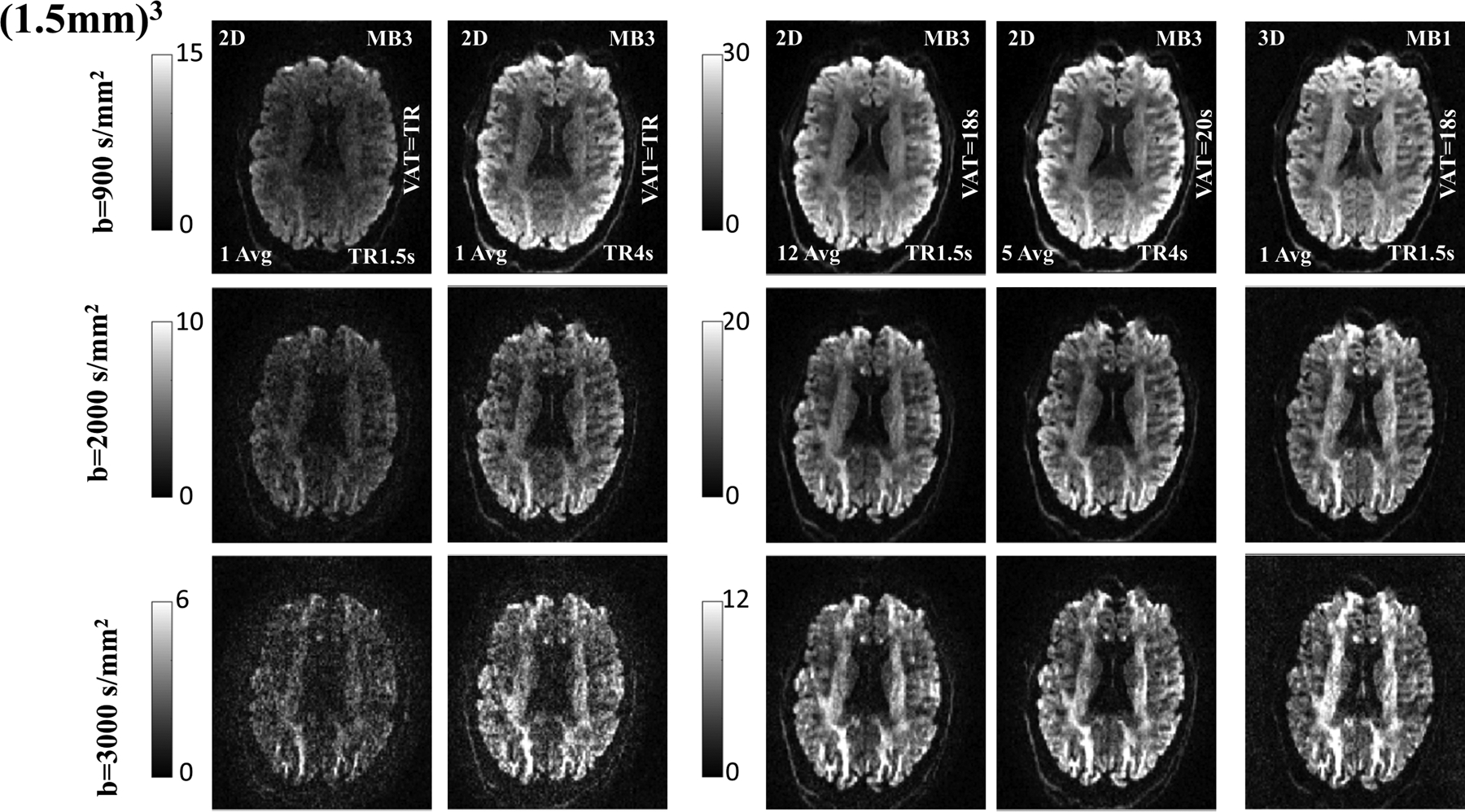
Comparison of the SNR in a 2D and 3D acquisition for b=900, 2000 and 3000 s/mm² at (1.5mm)³ isotropic resolution. The 3D multi-shot EPI in column 5 has a VAT=18 s (for a single volume) and acquired with TR of 1.5 s. This is compared with 2D acquisitions shown in column 3 with TR (and VAT) of 1.5 s and 12 averages for a VAT=18s and in column 4 with TR (and VAT) of 4 s and 5 averages for a VAT=20s respectively. Single average for 2D are shown in column 1 and 2 for TR=1.5s and TR=4 s respectively. The rows show the image SNR for b=900, 2000 and 3000 s/mm² respectively. Note that the 2D approach with the MB=3 slice acceleration and TR of 1.5s cannot cover the entire brain and for whole-brain coverage a TR of 4s is required (using only MB=3). Gray-scale images are in absolute SNR units, and adjusted for each row, and for short VAT and long VAT respectively.

Figure 4 depicts images acquired with protocol C for different pitch positions of the head relative to the laboratory reference frame, to assess the inter volume stability. The first and second row shows reconstructions where the calibrations (b=0) are at two different pitch positions without any purposeful intra volume motion. The first and second column shows reconstruction of DW data obtained with b=900 s/mm² from the two pitch positions respectively. For the lower left and upper right, there is a geometric difference between the pitch position of the calibration data and the pitch position of the DW data. Even though there is a 15–20 mm change in positioning, which is significantly larger than the difference in geometric distortion, the proposed phase correction approach is robust against such change. The signal drop in the visual cortex in this case is from a lack of signal for that part of a slab in the calibration volume.

Figure 4:

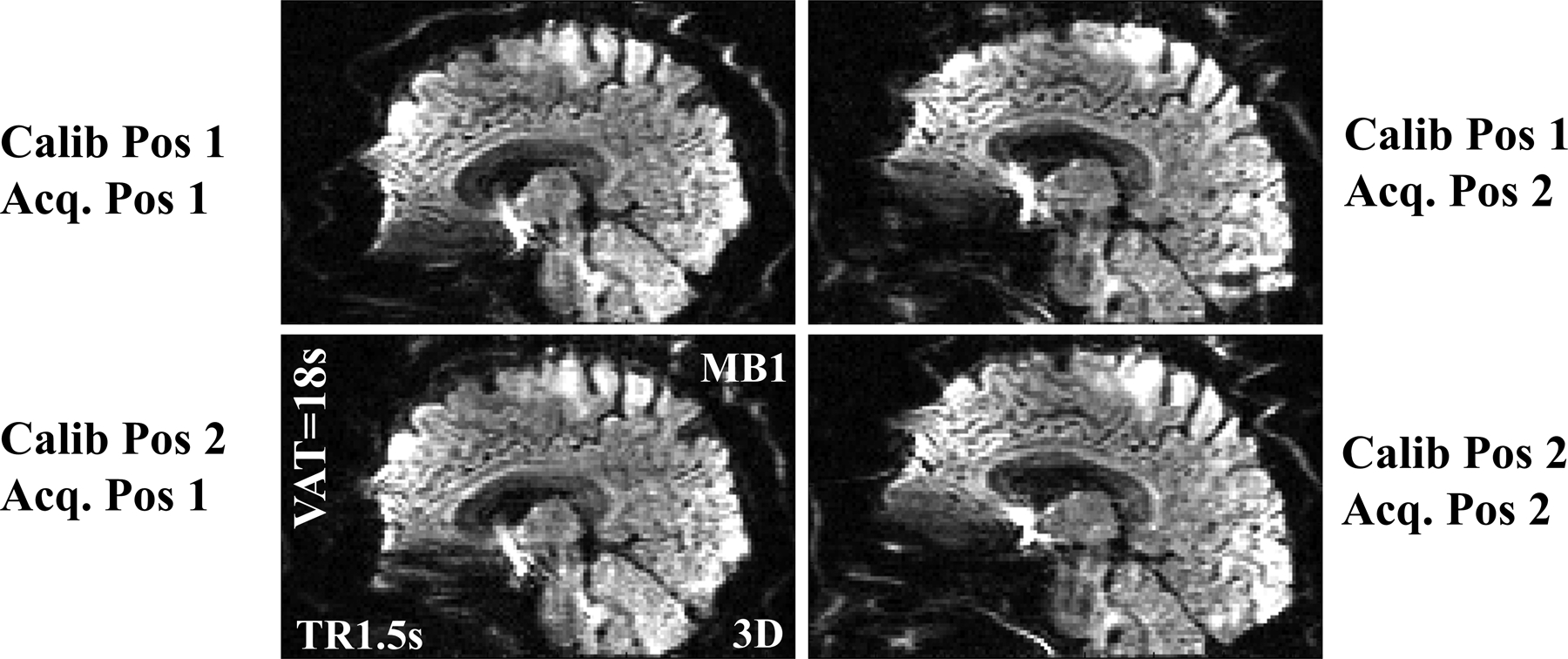
Sensitivity of the self-navigation correction to motion for reconstruction of DW with b=900s/mm² using two different pitch positions. The upper left and lower right images are reconstructions where the pitch during the reference phase calibration match with the DW image. For the lower left and upper right images, the DW is obtained for a different pitch position as the reference phase.

The SNR advantages of 3D multi-shot EPI acquisitions are expected to become larger for higher resolution images provided the diffusion phase problem can be properly eliminated. Figure 5A and B depicts axial DW 3D multi-shot EPI images obtained with both 2D and 3D protocols (AA2, AA3, D1 and D2) for matched z-coverage of 130mm, resolution of (0.9mm)³ and for b=900, and 3000 s/mm² respectively. The g-factor for these are [1.45±0.08], [1.44±0.09], [1.07±0.06] and [1.28±0.2] respectively. With (0.9 mm)³ resolution, in-plane undersampling of the EPI data becomes necessary to keep the echo-train length from getting too long. In this case undersampling by factor of 2 (iPAT=2) is employed. Column one row one and two for both figure 5A and 5B are single averages with a 2D SMS acquisition and MB factor 2 and 3 respectively, with the reconstruction in SNR units relative to the thermal noise level and shown with the leftmost gray-scale range. Column two, are the same acquisitions, with multiple averages for matching with the longer VAT of the 3D acquisition, also shown in SNR units and with the rightmost gray-scale range. Column three is the matched slice from a 3D acquisition with MB=1 or MB=2 respectively. The rightmost column is the 3D acquisition with 2 averages for scan time matched SNR comparison, all in SNR units with the rightmost gray-scale range. For Figure 5A the SNR of the images with b=900 s/mm² the grayscale is displayed with 2 times the range relative to Figure 5B, which shows similar images for b=3000 s/mm². For the 3D images, the top row third column is of matched duration to the bottom row right column, the former being acquired with MB=1 and the latter with MB=2. The number of slices/slab is the same for both, and the shortened TR for the MB=2, allows for 2 times the number of averages for the same scan-time. The second column, shows the achievable SNR with 2D accelerated acquisitions, relative to the 3D acquisition for comparable scan-times. With b=900 s/mm² the SNR for a 2D acquisition at (0.9mm)³ with MB3 (9 avg and VAT=72s), has a similar SNR to a 3D acquisition with MB=1 (1 avg. and VAT=38s) or MB=2 (2 avg. and VAT=38s) .With b=3000 s/mm² the SNR for a 2D acquisition at (0.9mm)³ with MB3 (9 avg and VAT=72s), has a similar SNR to a 3D acquisition with MB=2 (1 avg. and VAT=19s) and less than either a 3D acquisition with MB=1 (1 avg. and VAT=38s) or MB=2 (2 avg. and VAT=38s).

Figure 5:

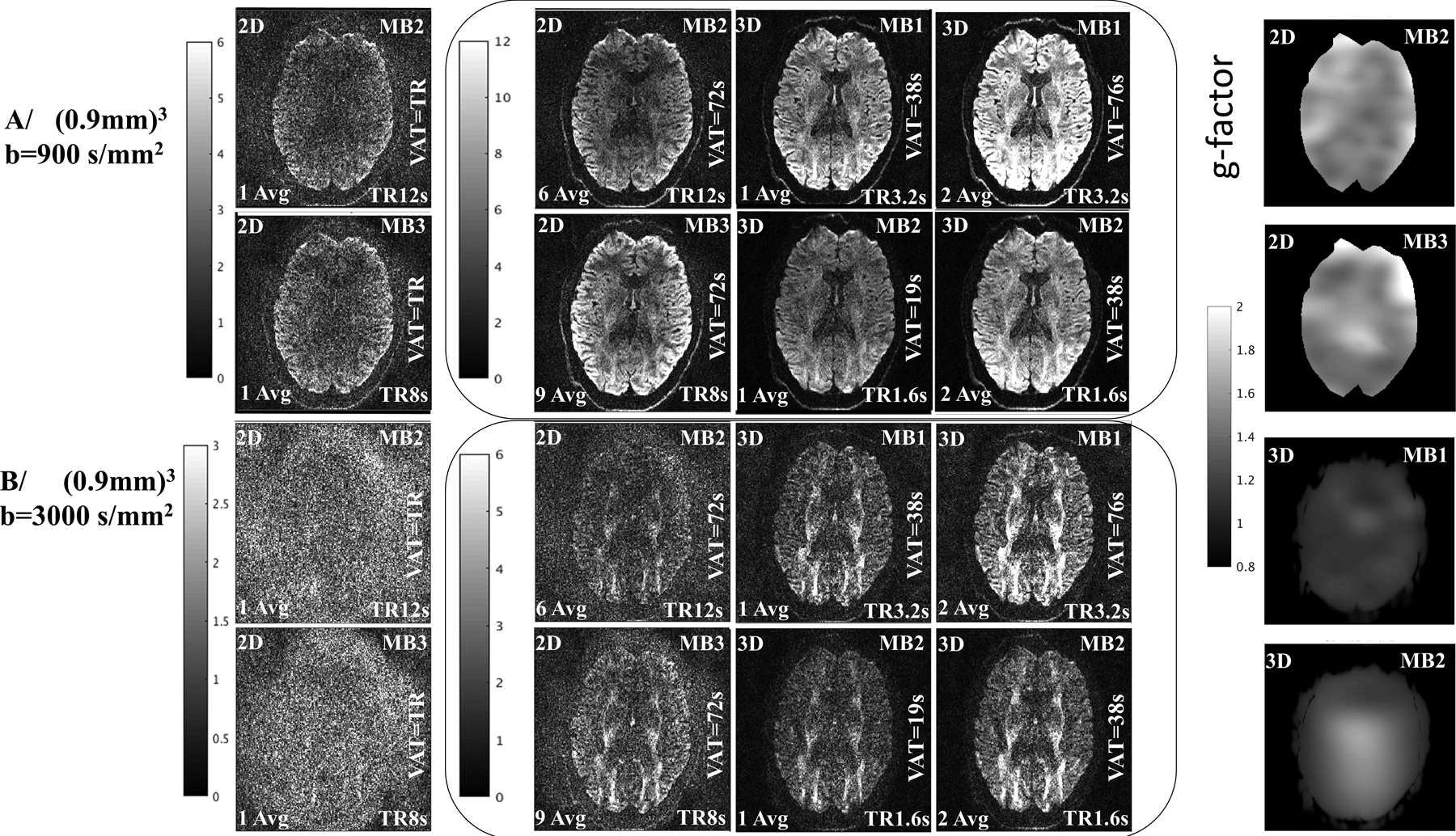
Comparison of the SNR in 2D and 3D acquisition for b=900 and 3000 s/mm² at (0.9mm)³ isotropic resolution. Column one in A/ and B/ are single average images obtained with 2D acquisitions using MB=2 (total acceleration 4) and MB=3 (total acceleration 6) respectively. The left column in the center figures in A/ and B/ are images obtained with the 2D acquisitions for VAT=72s obtained with averaging of complex valued signals. The center column in the center figures are images obtained with single averaged 3D acquisitions using MB=1(total acceleration 2, and VAT=38s) and MB=2(total acceleration 4 and VAT=19s) respectively. The right column in the center figures are images obtained with averaged 3D acquisitions using MB=1(total acceleration 2, and VAT=76s) and MB=2(total acceleration 4 and VAT=38s) respectively. The right column are images of g-factor maps for the corresponding slices obtained with the analytic g-factor method(61)

Discussion

In this study, we propose a self-navigation multi-shot EPI algorithm for determining and correcting the diffusion-phase in DW SE-EPI. The B₀ induced spin-phase variations in DW multi-shot EPI are strongly augmented by the applied diffusion gradients. The proposed algorithm corrects the induced phase-changes relative to a phase which is consistent, and specifically which can simply be measured with the same sequence without applying diffusion gradients. Such information is routinely obtained in any DW sequence, since this is the b=0 s/mm² volume, and used as reference for diffusion quantification with DW. The proposed method compares the coil-combined phase for each k_z-plane. As an alternative for estimating the diffusion-phase, the phase-difference can be calculated according to [Eq 4], and then weighted with the magnitude of the sensitivity profiles. When estimating the channel dependent phases the two approaches show little difference. The proposed self-navigation 3D DW multi-shot EPI approach was tested under varying SNR conditions (Figure 3 and Figure 5) and subject positions (Figure 4) to demonstrate that an absolute reference can indeed suffice for obtaining artifact-free DW images. The smoothened phasedifference between images with very different contrast do not exhibit high resolution anatomical phaseinformation. The accuracy of the proposed self-navigation method has also been evaluated on simulated “gold standard” images from magnitude data reconstructed with SENSE-1 acquired using 2D SMS-EPI. The gold-standard data have zero diffusion-phase and two diffusion volumes with a contrast from b=0 s/mm² and b=3000 s/mm², respectively. For the simulation data, illustrated in Supporting information Figure S1, most k_z planes have an estimated phase less than ±0.2, and for a few k_z-planes the phase has values over the ±π range. The simulated gold-standard data shows the potential for phase-variation for some k_z-planes, and the origin of the phase-errors in the simulated data warrants further evaluation. The k_z-planes that exhibit phase-errors correlate with slices with phase fluctuations outside the brain with a non-zero mean. For experimental data each k_z-plane has the same noise-level and the large phase-error from the simulation are not seen in the motion data, at (1.5mm)³ and (0.9mm)³. The TSNR data included in Supporting Information also do not show such variations, but the possibility for a large phase-error may exist, and can be increased by changing the local noise properties or can be reduced by spreading the signalenergy along k_z over more k_z planes which can be steered with the choice of RF-pulses.

The self-navigation method was evaluated for a whole brain acquisition with 1.5mm isotropic resolution. This was done using b-values of 900, 2000 and 3000 s/mm² with TR=1500ms and using parameters given as protocol B in Table 1 and compared with 2D acquisition using TR=1500ms and TR=4000ms in figure 3. Multi-shell acquisitions with relatively high b values (e.g. 3000 s/mm²) are commonly employed for white matter fiber orientation mapping and tractography. Hence the ability to accurately measure signal decay for high diffusion gradients and diminishing SNRs is critical. The performance of the self-navigated DW 3D multi-shot EPI was compared qualitatively with the gold-standard 2D-EPI (protocol A and A3) for conditions expected to match the SNR; and no significant difference in performance was identified. However, for the same SNR, the volume coverage in the slice direction (2D acquisition with protocol A) was significantly reduced with 3-fold slice acceleration (i.e. MB factor 3) and matched TR. The coverage was matched with the longer TR and 3-fold slice acceleration (2D acquisition with protocol A3).

dMRI acquisitions for tractography typically require minutes to tens of minutes (42). During such scans, the subject’s head may move. In order to evaluate whether the self-navigation is stable to such effects, two acquisitions with drastically different head positions were obtained with protocol C and shown in figure 4. The reconstruction was stable despite the acquisition of data with different head positions. The data was obtained without any noticeable intra-volume motion and a purposeful inter-volume motion. Brain areas where some loss could be seen are in regions where the reference scan did not have sufficient signal to accurately characterize a reference phase. For dMRI acquisitions, multiple b=0 s/mm² volumes are acquired intermittently to correct for motion. The self-navigation works with the same data, and the reference phase for the self-navigation can be updated dynamically with these reference volumes to account for smaller motion. In the presence of larger motion during an acquisition, the current approach is to discard such volumes, since the signal behavior has too much variability. This is a similar issue to cardiac/pulsation artifacts and the potential benefits of using cardiac-gated sequences. Most large-scale projects such as the Human Connectome Project (42) have indeed opted not to use cardiac-gating, since the data quantity far outweighs the data-quality with cardiac-gating. As such update of reference navigator should prove sufficient. Without intra-volume motion, the VAT should be kept short and the longest VAT=38s used in this paper should be susceptible to significant intra-volume motion if applied to a general population.

A 1D navigator (47) is commonly used in all EPI acquisitions with reversed readout gradients to account for differences in gradient delays, timing errors and other system parameters. A full-phase navigator is an EPI acquisition without phase-encoding gradients and used to correct errors during the EPI readout. These navigators are acquired soon after the excitation to ensure sufficient SNR, and in the case of a full-phase navigator is only acquired a single time. For the 2D navigators that conventionally are acquired (23), the navigators are obtained at k_z=0, to ensure sufficiently high SNR. So far, there have been no studies investigating if this technique is suitable for low SNR acquisitions, such as those encountered in high spatial resolution (e.g. (0.9mm)³ here) and high b-value (e.g. b=3000 s/mm² here) acquisitions in protocol D2 and E with short TR (TR~1.2·T₁). Moreover, the hypothesis that there is enough signal from each k_z-plane to perform a stable and correct reconstruction may not always hold, since the signal along k_z in general is rapidly vanishing for increasing slice phase-encoding. The sensitivity of a 3D acquisition under moderate diffusion weighting (b=900 s/mm²), as used for protocol B, exhibits a strong mixture of signal when uncorrected as shown in Figure 2. For the self-navigation, the reconstruction is stable even for the high resolution/low SNR acquisition with protocols D1 and D2, and as shown in figure 5, where the signal in the internal/external capsules and optic radiations is still clearly visible at the (b=3000 s/mm²) image relative to the rest of the brain.

The whole-brain multi-shell protocol F, despite its moderate angular resolution (33 directions), further illustrates (see supporting information Figure S9) the ability of the proposed method to generate detailed maps of the brain white matter. In particular, clear delineation of the tapetum and posterior corona radiata was observed, as well as identification of crossing fibers from the superior longitudinal fasciculus and internal capsule in the centrum semiovale.

For the cases of large volume and/or high-resolution imaging, which is the regime where 3D acquisitions have an advantage over 2D, the attainable TR is limited by the acquisition time after each excitation. The proposed self-navigation thus enables a reduced TR by eliminating the time spent in acquiring a second echo for navigation (23). This increases scan-efficiency, and minimizes scan-duration. The ability to acquire whole brain DWI SE-EPI with sub-second TR is illustrated in Supporting Information Figure S6 and S7. The effect of spin-history effects and sampling strategies to increase tSNR warrants further investigation, both for the sub-second TR regime and also for the SNR-optimal TR regime, since the SE-EPI tSNR is significantly affected by the spin-history at the edges of the slab/slice, and the overlap between slabs further exasperates this in the 3D setting. For all 3D multislab acquisitions, whether using navigator echoes or self-navigation, additional k_z-planes are acquired due to slab-oversampling. In this study, slab-oversampling was chosen as 50% (4 additional k_z-planes for 8sl/slab), and provided an increase in SNR while enabling simpler combination of adjacent slabs. This oversampling can be reduced for shortened scan-duration and in such case techniques such as NPEN (48) are attractive for enabling an iterative reconstruction that allows for a joint combination of the plurality of slabs. The increase in SNR is associated with a decreased q-space coverage, which will reduce the angular resolution. A comparison between low SNR acquisitions with high angular resolution versus much higher SNR acquisitions with low angular resolution warrants further investigation for 3D acquisitions. For most applications, it is preferable to distribute the total SNR over more q-space samples each with lower SNR versus few q-space samples with high SNR, since when estimating fiber orientation all data is used for the estimation of the underlying signal. With dictionary based model estimation using Bayesian techniques, such as BusineX (49,50), loss in angular sampling does not have a linear correspondence with angular resolution. In such case the effect of higher-quality data on the angular resolution warrants further investigation. For the (1.5mm)³ acquisitions the achievable SNR with the 3D can be matched with the 2D acquisition, and for most acquisitions at (1.5mm)³ it is not clear that there is benefit of the 3D relative to the 2D acquisition.

The combination of 3D multislab acquisition with simultaneous multiband (MB) imaging was demonstrated for a (0.9mm)³ isotropic acquisition in figure 5. For 2D imaging, the SNR loss from MB is SNR^full ·(g)⁻¹, where SNR^full is the unaccelerated 2D images and g the geometry factor. For 3D multislab the MB acceleration is applied in combination with either thinner slabs and the same TR, or the same slab thickness and shortened TRs. Depending on the specific TR values compared, the difference between these may be small as shown in Supporting information Figure S8, and specifically it is ${\left(\sqrt{R_{MB}}\right)}^{-1}$ for the same TR and thinner slabs when ignoring the necessary slab-oversampling. The inclusion of the MB encoding in the 3D multislab as such has an SNR loss of approximate $SN{R}^{\text{full}}\cdot {\left(\text{g}\right)}^{-1}\cdot {\left(\sqrt{R_{MB}}\right)}^{-1}$ where R_MB is the MB factor. Alternatively if MB for 3D multislab is being used to extend the FOV, then the SNR loss of the reference 3D multislab volume is SNR^full ·(g)⁻¹ (see also Supporting Information Figures S5, S6 and S7, for the ability using TR<1s). For low to moderate resolutions, such as the (1.5mm)³ in Figure 3, the SNR of a 2D multi-slice acquisition can be matched to the 3D multislab acquisitions for matched scan-time. Often the obtained SNR with the 3D acquisition will be much higher than what is necessary and the use of a faster 2D acquisition with less SNR or a 2D acquisition with different b-values provides better information. For the higher resolution of e.g. (0.9mm)³ the 2D acquisitions can be accelerated to 3×2 (MBxR_PE) with moderate g-factors and the SNR gain of the 3D acquisition is in such case about 40%−50%, while the required VAT for the 3D multislab with MB=2 is twice that of a 2D multi-slice acquisition. The benefit of the 3D multislab acquisition is as such for even higher resolutions, where the TR of the 2D multi-slice acquisition is even longer, and the TR inefficiency more pronounced (see Supporting Information B).For reduced VAT, the segmented 3D encoding for each slab can be undersampled through the slab. In the approaches presented here, the slabs are thin (<20mm) and the ability to perform through slab acceleration may benefit from 2D-CAIPIRINHA encoding, such that adjacent k_z-planes have different phase-encoded EPI readouts. For through slab undersampling the diffusion phase has to be corrected first, and in the proposed method with a correction in [x,y,k_z]-space this requires full encoding for each k_z-plane, reducing the efficiency of the 2D-CAIPIRINHA encoding. A reduced VAT will also limit the motion sensitivity of the 3D multislab acquisition, which for the higher resolution acquisition still exceed 19 seconds.

The phase-correction in the proposed self-navigation multi-shot EPI algorithm relies on “slab” sensitivity profiles for estimating a sensitivity-weighted (51,52) phase. Such data is already part of routine dMRI acquisitions, since sensitivity weighted reconstruction is preferred for analysis (51). The integration of the proposed algorithm is compatible with existing pipelines, without adding significant additional computation or reducing the speed of reconstruction. For the case of acquisitions with in-plane phase-encoding undersampling, GRAPPA can be applied to each k_z-plane independently and the self-navigation can be performed subsequently. Typically, the applied in-plane phase-encoding undersampling is less than 3, since with an undersampling of 3, one can easily reach 0.6 mm in-plane resolution on standard clinical system with an acceptable TE of less than 100 ms at moderate b-values. The long echo-train will result in blurring and distortion, necessitating either explicit or implicit ΔB₀ correction, or higher in-plane undersampling to reduce the distortion. In such case the SNR is often too low and segmented acquisitions are necessary. For the use of fully sampled phase-encoding segmented acquisitions, such as those in MUSE, the phase-consistency is applied in image-space, and it is not readily intuitive how 2D-MUSE could be applied to each k_z-plane. The low-rank constraint in MUSSELS defined for 2D imaging, might also be applicable for each k_z-plane, if the low-rank constraint is appropriately tuned for the low SNR observed with high-resolution, high- b-values and high k_z-encoding or any combination hereof. If the number of segments in the k_y phase-encoding direction is not too large, the self-navigation technique should be sufficient to train a joint GRAPPA reconstruction to reconstruct directly from the segmented acquisition with phase difference to combined segments without diffusion phase. This, however warrants further evaluation.

The self-navigation has also been applied to DW 3D multi-shot EPI obtained using standard sinc pulses for excitation and refocusing with both low and high bandwidth, and the use of frequency swept pulses for the DW 3D multi-shot EPI is not a necessary condition for the self-navigation (data not shown). For different combinations of excitation and refocusing pulses, the signal from the 3D slab will be more or less impacted by off-resonance sensitivity (31), and the refocusing pulse is often but not always chosen with a higher BWTP and calculated with the Shinnar-Le Roux algortihm to better define the slab. Broadening of the slab-selective profile reduces the SNR in multislab experiments and increased off-resonance sensitivity effectively widens the slab. More complex reconstructions are necessary to correctly combine slabs to account for both the RF-profile and the off-resonance effects (48). The use of frequency swept pulses here was used because of their known performance.

In order to capture the effects of physiological noise, tSNR is commonly used in fMRI, although its use has not received much attention in dMRI. In fMRI studies comparing 2D and single-slab 3D acquisitions (53–55), similar tSNR values were observed. These 3D acquisitions used as a single slab to avoid spin-history effects (56). For shortened TRs the difference in physiological noise contamination for GE-EPI between 2D and single-slab 3D acquisitions is reduced (56). Consistent signal representation, especially in the presence of slab overlaps (23–26,28,48,57), is important for performing volumetric co-registration but are not the same as spatially constant noise or tSNR. The data in the supplemental material shows that while slab overlap is beneficial to facilitate volumetric combination of slabs, it also adversely affects the tSNR. For standard Siemens pulses, the addition of slice-overlap reduces the tSNR by ~50%. Thus, while supporting information Table S2 shows that the SNR comparisons shown in Figure 3 and 5 between 2D and 3D acquisitions are not identically realized in the corresponding tSNR comparisons, the effect of slice-overlap is sufficient to account for the discrepancy. As a comparison metric between different 3D multislab acquisitions it would be useful to include the tSNR, warranting further understanding of the variability in the tSNR for multislab EPI in broader cohorts.

The proposed self-navigation multi-shot EPI algorithm also benefits more applications than the evaluated DW 3D multi-shot SE-EPI. For readout (RO) -segmented multi-shot EPI, the use of a 2D navigator is used to combine the different blades, and the proposed phase correction has also successfully been used (data not shown). Additionally, for 3D multi-shot GRE-EPI, which is increasingly used for e.g. high resolution fMRI (53,58), the dynamic data-correction may provide improved temporal stability. The segmentation correction may also benefit 3D segmented GRASE acquisitions for e.g. ASL where the segmentation fluctuations (59,60) limits the ability to capitalize on the otherwise superior SNR of the 3D technique relative to the 2D versions (10). However, such applications are beyond the scope of the current study, and warrant further evaluation.

Conclusion

The proposed self-navigation is an approach for generating self-consistent 3D acquisitions that tailor to the sequential nature that is used as data-acquisition in MRI. The proposed technique can provide a utility for other types of experiments, where current methodology requires more complex reconstruction approaches to generate self-consistent data.

Supplementary Material

Supp info

Figure S1: left column, central slice in a slab simulated reconstructed with self-navigation from 3D-EPI with the proposed self-navigation technique, using b=3000 s/mm² and reconstructed with SENSE-1. Second column; the relative difference between the original and the reconstruction with the estimated phase-difference. Third column, the phase difference between b=0 s/mm² and b=3000 s/mm² in hybrid space, shown with the specified ranges. Right column, the SSIM calculated for different kernel discretization and kernel shapes (FWHM).

Figure S2: Signal versus TR for SE-EPI. The columns in S1A show the effective SNR as a function of TR, for different T₁-values. The calculations are for a 180° refocusing pulse, and each color corresponds to a different excitation flip-angle. The two rows, show the SNR for two different ranges, [0:8000ms] and [0:18000ms]. The plots in the two rows of S1B, show the gain of a short TR acquisition relative to a 90° excitation pulse with TR=8000ms, and TR=18000ms respectively.

Figure S3: Experimental phantom validation of the theoretical predictions with [eq 5]. Supporting Information Figure S3A show the flip-angle for a slice in a spherical phantom. The flip-angle map is performed with a 60° GRE acquisition, and the color shows the spatial variations relative to the 60°. Supporting Information Figure S3B shows SNR measured for the square ROI highlighted on Supporting Information Figure S3A.

Figure S4: Experimental in-vivo validation of the theoretical predictions with [eq 5]. Supporting Information Figure S4A show the relative variation in flip-angle for an axial slice. The flip-angle map is performed with a 60° GRE acquisition. Supporting Information Figure S4B shows SNR measured different TRs and different excitation flipangles for the slice in Supporting Information Figure S4A.

Figure S5: Montage of all slices for (1.5mm)³, TR=1500ms, b=2000 s/mm², 8sl/slab and 9 slab (Protocol B) after slab combination

Figure S6: Montage of all slices for an acquisition with (1.5mm)³, TR=750ms, b=2000 s/mm², 16sl/slab and 4 slab; a short TR alternative to Protocol B for same scan time.

Figure S7: Reduced zFOV coverage and volume TR for (1.5mm)³, with b=2000 s/mm², TR=750ms, 8sl/slab, 4 Slab.

Figure S8: Comparison of image SNR for matched resolution with acquisition of thick slab with short TR (1.6 s) and 16 slices per slab (24 slices with oversampling) (Top row) and thin slab (8 slices per slab, 12 slices with oversampling) with long TR (3.2 s) (Bottom row), for b-values of 900, 2000 and 3000 s/mm². Top row is with protocol F, and bottom row is with protocol G. The same sagittal slice is shown for both protocol and for all b-values.

Figure S9: shows color-coded fiber orientations modulated with FA ((0.9mm)³ resolution) estimated by DTIFIT (upper panel), the sum of anisotropic fiber volume fractions estimated by the multishell BEDPOSTX (middle panel) and the corresponding color-coded multiple fiber orientations at high resolution (lower panel) at the ROIs highlighted in red in the middle panel (the centrum semi-ovale, tapetum and forceps major). The background in lower panel is the sum of anisotropic fiber volume fractions.

Table S1: Table of the common parameters used for obtaining the in-vivo experiments shown in Supporting Information Figure S3 and S4.

Table S2: Table of the tSNR comparison performed between 2D and 3D acquisitions for (1.5mm)³ and (0.9mm)³.