Trending on Social Media: Integrating Social Media into Infectious Disease Dynamics

Abstract

Social media plays an important role in alerting and educating the public during disease outbreaks. By increasing awareness of the disease and its prevention, it can lead to a modification of behaviour which then affects contact/incidence rates. Social media data may also be used when formulating, developing and parameterising models. As mobile technology continues to evolve and proliferate, social media is expected to occupy an increasingly prominent role in the field of infectious disease modelling to improve their predictive power. This article presents a review of existing models incorporating media in general and highlights opportunities for social media to enhance traditional compartmental models so as to make the best use of this resource in controlling the spread of disease.

Introduction

Social media and social networking sites such as Facebook, Instagram, WhatsApp, Pinterest and Twitter aided by the development of mobile technology have revolutionised the manner and the speed in which information is spread. Recent estimates indicate that there are more than 3.77 billion global internet users—more than half of the world’s population (Kemp 2017). Of these, 71% are social network users (Kemp 2017) with the ability to rapidly communicate with hundreds of other people. In terms of numbers, as of the third quarter of 2017, active Facebook users per month reached 2.07 billion with the average Facebook user having 155 friends (Knapton 2016), Statista 0118.

This paradigm shift in the way in which information is communicated has been utilised in diverse areas other than its familiar use in the marketing and promotion of products and as a source of market intelligence and customer engagement (Agnihotri et al. 2016). After the tragic 2013 explosions at the Boston Marathon, the FBI used online social networks to broadcast information about the suspects leading to their quick capture. Events such as the Arab Spring, the 2011 UK riots and the subsequent cleanup effort have also been fuelled by social media and have also demonstrated the ability of social media to influence collective behaviour (Baker 2012; McGarty et al. 2014).

The Centers for Disease Control and Prevention in the USA used Twitter for updates and to disseminate strategies for preventing the flu to help slow the spread of H1N1 influenza in 2009, with its network increasing from 2500 followers to 370,000 followers during the outbreak (Huo and Zhang 2016). YouTube and iTunes were also used to update and advise 1 million viewers in a similar manner (Merchant et al. 2011). During the 2014 ebola outbreak, social media was used to educate the public about Infection Prevention and Control (IPC) measures like barrier protection, hand washing and early reporting (Carter 2014; Gidado et al. 2015).

These practices—spurned on by social media—may play an important role in limiting the spread of the disease and may deeply influence the epidemic pattern. Apart from the generally beneficial role of social media in influencing behaviour, a strong correlation between social media data and actual reports has been found (Aramaki et al. 2011). This suggests that social media data has the potential to be used as a proxy to actual disease data and may be used in the detection and tracking of disease outbreaks.

Researchers are increasingly beginning to consider ways to incorporate social media into mathematical models. We limit this review of the use of social media in modelling to compartmental models implemented at the population level as opposed to those implemented at the individual level (i.e. using an Individual Based Model or Contact Network). We examine existing models incorporating media in general and highlight the opportunities for social media to enhance traditional infectious disease models and discuss challenges which may arise with its burgeoning addition to the infectious disease modelling suite. This paper is organised as follows: Sect.  2 describes the inclusion of behavioural aspects to modulate the dynamics of compartmental models while the use of social media data as an information source for the model is described in Sect. 3. Some challenges and observations are discussed in Sect. 4, and conclusions are summarised in Sect. 5.

Modelling Behaviour Change: The Dynamic Interaction of Media Reports and Behaviour Change

The role of human behaviour in mitigating the spread of infectious diseases is not to be underestimated, and social media is a valuable ally in these control efforts. Moreover, preventing the spread of disease through information as a form of nonmedical intervention is more economical than treating the disease via pharmaceutical interventions.

Traditional models employ a static approach to human behaviour—individuals meet and infect each other at random in what has been termed homogeneous mixing (Manfredi and D’Onofrio 2013). However, when people consciously change their behaviour and attitudes in response to external information such as details on vaccination and drug therapy or on self-protection measures such as physical distancing and hand washing, this may affect the rate at which people contact each other or get treatment. Consequently, this may influence the spread of the disease thus altering the course of the outbreak (Tchuenche and Bauch 2012).

Voluntary adaptive change in behaviour is well-documented in true epidemics (Epstein et al. 2008) and has been incorporated into traditional infectious disease models to allow for more realistic disease dynamics (Verelst et al. 2016). For example, in an epidemiological-economic model, susceptible people may weigh the pros and cons of reducing contacts to avoid contracting a costly infectious disease (Fenichel et al. 2011; Morin et al. 2013). These models generally known as behavioural change models are distinct from models where decision makers make recommendations or impose new regulations and expect the public to comply with those recommendations and regulations. Media, by increasing awareness of the disease, plays an important role in this modification of behaviour generally slowing the spread of disease. As pointed out in Agaba et al. (2017), Zhou et al. (2019), there are generally three ways of including this modification of behaviour. We will describe each of these in turn.

Media Functions

Up to date information about a disease has been shown to play an important role in reducing its spread (Manfredi and D’Onofrio 2013). When formulating a model, special consideration must be given to choice of incidence function describing the rate of flow from non-infected to infected compartments.

The behaviour modification induced by the media may be introduced as a reduction in the incidence function (via a so-called media function) with the underlying assumption that as the number of infections increases in a population and is reported by mass media, individuals who are susceptible will become more cautious and initiate protective measures which will then decrease their susceptibility. Hence, choices for the media functions are represented by decreasing functions of the number of infected, exposed or hospitalised people (Cui et al. 2008; Xiao et al. 2013; Sahu and Dhar 2015; Mitchell and Ross 2016; Lu et al. 2017). Common choices for these functions are a saturated Holling type-II functional response and an exponentially decreasing functional response as shown in Table 1.

Table 1.

Forms of the media function term modulating the incidence rate

References	Modification factor/media function
Cui et al. (2008), Liu et al. (2007), Tchuenche et al. (2011)	$e^{-mI(t)},e^{-m_{1}E\left(t\right)-m_{2}I\left(t\right)-m_{3}H\left(t\right)}$, $e^{-M\left(t\right)},$ where $M\left(t\right)=max\left\{0,,,a,I,+,b,\frac{\mathit{dI}}{\mathit{dt}}\right\}$.
Liu and Cui (2008), Tchuenche et al. (2011)	$\beta \left(I\right)={\beta }_1-{\beta }_2\frac{I}{m+I},$ where ${\beta }_1=$ contact rate before media alert, m measures impact of media coverage, and $\beta \left(I\right)=$ contact rate after media alert

For the purposes of comparison, let the parameter $m_i(t)$ represent the influence of the media. (E, I and H represent Exposed, Infected and Hospitalised Individuals)

Models introducing an exponential factor have demonstrated a wide variety of dynamical behaviour, including several endemic equilibria as well as Hopf and transcritical bifurcations. These models include SEI, SIHR and EIH models where the exponential decrease in the incidence rates is proportional to functions of the number of infected or exposed or hospitalised people (Tchuenche and Bauch 2012; Cui et al. 2008; Liu et al. 2007). Results from Cui et al. (2008) using a media function $e^{-mI(t)}$ reported the possibility of endemic equilibria as well as multiple outbreaks whose peaks as well as time to secondary peak of the disease decreased with increase in media influence.

Another popular modification of the incidence rate is reminscent of the Holling type-II functional response. While results using this functional response suggest that media exposure does not affect the basic reproductive number or eliminate the disease, media coverage is useful in controlling the spread of the disease by delaying the arrival of the infection (Liu and Cui 2008). Like the exponential function, this function reduces the transmission rate of the disease when the number of cases is high but eventually plateaus out as a result of media saturation, so that the contact rate remains constant regardless of increase in infections.

A comparison of these two media functions is shown in Fig. 1 for values of the media term $m=0.2$ and $m=2$. As shown, there may be a sharper decrease in number of infected people depending on the strength of the influence of the media term in each media function before they level off to become asymptotic towards the I-axis. One criticism of these functions is that in the initial stages of the disease when the number of infected is low, the public may not modify their behaviour as quickly as these functions suggest by their rate of decrease. It is only as the number of infectives increases and is reported by media and people become worried, that a change in behaviour may occur (Lu et al. 2017). Lu et al. (2017) suggested the use of a media function of the form $\frac{1}{1+m{I}^2}$ to describe this initially slow behaviour.

Fig. 1.

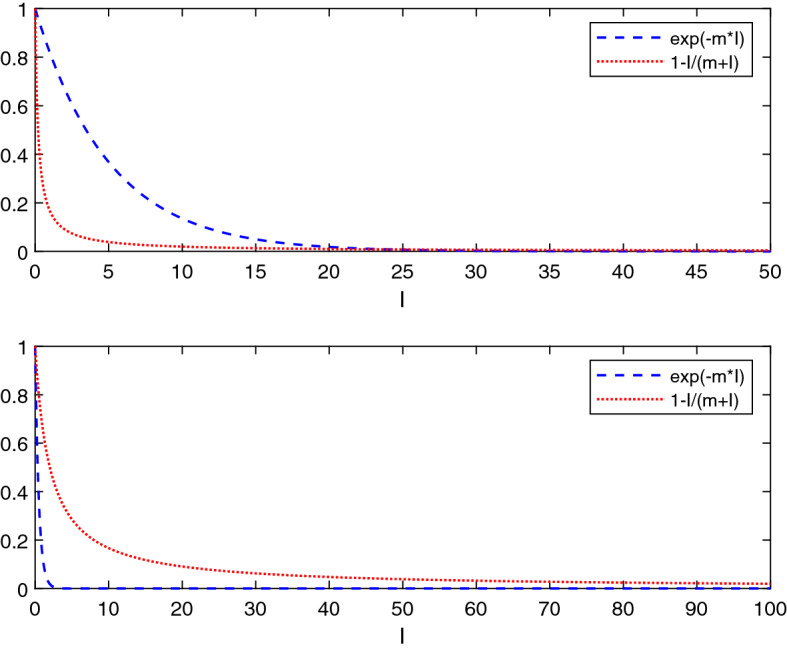
Comparison of media functions for different values of m ($m=0.2$ on top and $m=2$ at the bottom)

Collinson and Heffernan (2014) showed that key epidemic measurements used for planning and preparation peak number of infections, time of peak, end of epidemic and total number of infections depend on the choice of media function. Using a standard SEIR model, they generated epidemic curves without and with different media function and noted that the epidemic curve varied depending on the media function used. Consequently, though the role of media in influencing contact rate is evident, its mathematical incorporation into models (via the media function) appears ambiguous (Mitchell and Ross 2016) and requires a data-driven approach as described in Sect. 3.

Unaware/Aware and Media Compartments

The second approach entails the introduction of separate compartments representing the level of disease awareness in each subpopulation with transitions between unaware and aware individuals in some or all of the disease states (Agaba et al. 2017). These states may be denoted by unaware susceptible, infected and recovered individuals ($S_n$, $I_n$ and $R_n$) and aware susceptible, infected and recovered individuals ($S_a$, $I_a$ and $R_a$). Aware and unaware individuals are assigned distinct disease transmission parameters so that aware individuals may have lower susceptibility of acquiring infection.

Yet media reports can be considered as a distinct entity with its own influence on disease dynamics. Accordingly, the third way is to represent the media by a separate compartment, interaction with which results in the movement of unaware susceptibles to the aware population (Greenhalgh et al. 2015; Misra et al. 2011, 2013; Njankou and Diane 2017). This interaction may result from standard incidence (Misra et al. 2011, 2013), mass action incidence (Njankou and Diane 2017) or a Holling type-II functional form $\frac{M}{k+M}$ similar to that in Table 1 where the M represents a Media compartment.

As an example, we reference SIS models by (Misra et al. 2011; Greenhalgh et al. 2015) in Fig. 2. The susceptible population is divided into two subclasses—an aware susceptible and an unaware susceptible with the inclusion of a compartment M(t) representing the number of media awareness campaigns. The growth rate of this compartment is assumed to be proportional to the number of infective individuals $\frac{\mathrm{d}M}{\mathrm{d}t}=\mu I-{\mu }_{0}M$ where $\mu$ denotes the implementation of rate of awareness programs and ${\mu }_0$ the depletion rate of awareness programs due to ineffectiveness, social problems in the population and similar factors.

Fig. 2.

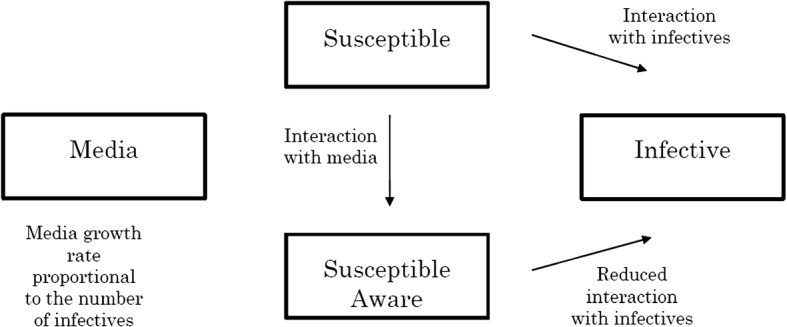
Effect of the inclusion of media compartment in an SIS model

Just as in the first approach where awareness programs run by media campaigns induce behavioural changes in the susceptibles, interaction with the M class will result in an “aware” class of susceptibles who may not interact with the infected class (Misra et al. 2011) or if they do, with reduced contact dependent on the media compartment (Greenhalgh et al. 2015). Some researchers (Liu et al. 2018; Greenhalgh et al. 2015) have included a time delay in the media compartment to highlight the differences in the dynamics of information and disease spread. This time delay may account for the lag between cases of disease occurring and mounting awareness programs (Greenhalgh et al. 2015) or the way information is spread via social media—not always directly but also by users forwarding tweets (Liu et al. 2018). Results from these modelling efforts generally confirm that media coverage can have a significant impact on the epidemic, such as delaying the peak and reducing the severity of the outbreak (Misra et al. 2011) and if multiple time delays are included may produce hopf bifurcations (Greenhalgh et al. 2015).

Combining Approaches

The above models considered the effects of media either as a reduction in the transmission rate of the disease (as a function of the number of infections—media function in Table 1) or by an interaction of susceptibles with a compartment which included the dynamics of media coverage (i.e. a media compartment as shown in Fig. 2). Some researchers have combined these two approaches by including the dynamics of media coverage (the number or percentage of tweets that report the disease for instance) in the media function (Pawelek et al. 2014; Huo and Zhang 2016; Zhou et al. 2019).

Recently, (Zhou et al. 2019) have investigated which factor—awareness of the number of infections or awareness of media reports, will have a greater influence on individual behaviour during an infectious disease outbreak, in an optimal control problem designed to seek the optimal reporting intensity of information to minimize the number of infected individuals (and costs). They adeptly combined the first and third approaches by formulating two new media functions similar to those in Table 1 which are functions of both the number of infected individuals and the intensity of mass media (obtained from a mass media compartment M). These functions $f_1(I,M)=e^{-{\alpha }_{1}I-{\alpha }_{2}M}$ and $f_2(I,M)=\frac{1}{1+{\alpha }_{1}I+{\alpha }_{2}M}$ where ${\alpha }_i$ are constants resulted in a modified incidence rate $f_i\beta SI,i=1,2$. In a similar manner to the model described in Fig. 2, the interaction with the media compartment M (inherent in the $f_i(I,M)$ terms) resulted in an exposed/susceptible aware compartment. Numerical simulations found that the epidemic curve did not depend on the media functions $f_1$ and $f_2$ and that the awareness of the number of infections will lead to greater reductions in the peak magnitude and the total number of infections.

Social Media Data as an Information Source for Models

Apart from its use in encouraging behaviour change, reports of symptoms and disease status shared in social media posts may be useful in detecting and even predicting the course of an epidemic. One of the earliest models (Pawelek et al. 2014) to utilise data from Twitter in a SEIT compartmental model (with an exponentially decreasing media function similar to that in Table 1) was able to reproduce the peaks of both the percentage of tweets and that of surveillance data showing number of infections. The percentage of tweets which included phrases like “have flu”, “have the flu”, “have swine flu”, and “have the swine flu” was used to parameterise and develop the mathematical model with the result that Twitter was found to have a significant influence on the emergence and spread of the disease. Since a Hopf bifurcation can occur, the model suggested the possibility of multiple outbreaks of influenza. However, the researchers noticed that the peak of the predicted percentage of tweets emerged later than the predicted peak of infectious people and concluded that although Twitter may not be useful as an early warning system, it may instead provide a good real-time assessment of the current outbreak.

Mitchell and Ross (2016) also used surveillance data in conjunction with Twitter data—flu-related tweets using phrases containing phrases such as “have flu”, “have the flu”, “have swine flu” and “have the swine flu”—as a proxy for an individual engaging with media about an influenza outbreak in a SEEIIR model (susceptibleexposedinfectedrecovered with media, with two compartments for exposed and infected individuals). They combined this data and traditional surveillance data to determine a media function $f_m=1-mI$ where m is a parameter to be fitted. Model results using this media function as well as those in Table 1 were compared with surveillance data, and this new functional response was found to generally result in a better fit.

Researchers are increasingly beginning to consider other ways to incorporate social media data into mathematical models. Traditionally, epidemiology has been based on data collected by public health agencies through health personnel in hospitals, doctors’ offices and out in the field. These data are generally presented as a time series of cases for a geographic region or for a demographic and may be difficult to collate or to obtain and analyse in a timely manner. Conversely, social media (Facebook, Twitter, LinkedIn, Instagram, Snapchat, Pinterest and Reddit) is abuzz with real-time information—all stored electronically and often in an accessible form.

A strong correlation between social media data and actual reports has been found (Aramaki et al. 2011). This suggests that social media data have the potential to be used as a proxy to actual disease data and may be used in the detection and tracking of disease outbreaks (Eysenbach 2009). Also, by analysing how people communicate and share health-related information, facets of a transmission/disease process not captured by this traditional surveillance such as behaviour, perception and awareness (Althouse et al. 2015) may be identified—especially at the beginning of an outbreak when epidemiological data are scarce. This information may prove useful when formulating and developing a model, especially when time is of the essence.

Social Media: Some Unique Features

With its increasing popularity, modellers are beginning to consider the dynamic effect of social media as distinct from traditional media sources. While the incorporation of media in mathematical models is increasingly being adapted for social media, it is important to recognise some important features of social media.

Unlike other traditional forms such as the newspaper, television or radio, social media allow a participatory exchange of information that is almost real-time (Yates and Paquette 2011) and user friendly, both of which contribute to its ease and rapidity of spread. As a result, information and experiences are continuously being shared and re-shared resulting in a more rapid modification of behaviour during the infectious disease outbreak.

Though this information spread may result in positive behaviour change, social media has also been implicated in fear mongering and misinformation (misleading, false and deceptive information). Recent examples include the 2014 Ebola outbreak (Towers et al. 2015; Fung et al. 2014), the recent Zika epidemic (Chandrasekaran et al. 2017) and the 2020 Covid-19 pandemic. The misinformation may negatively impact and undermine disease control efforts especially for emerging diseases such as Covid-19 where public health officials are dependent on behavioral measures such as quarantine, isolation and social distancing to reduce disease spread until a cure is found.

Attempts have been made to incorporate this “anti-information” into models. Huo and Zhang (2016) explored the use of twitter to negatively affect the mitigation of an influenza epidemic as a result of behaviour change after reading tweets about influenza (Huo and Zhang 2016). They divided the media compartment T(t) in two compartments—$T_1(t)$ and $T_2(t)$ representing the number of tweets that provide positive and negative information about influenza at time t, respectively. This was used to modify the contact rate given by $\beta SI{e}^{-\alpha T_1+\delta T_2}$ where $\alpha$ and $\delta$ represent parameters.

As social media becomes an increasingly dominant aspect of our lives with 2.56 billion global mobile social media users in 2017 (equaling 34% penetration) (Kemp 2017), its influence on the mathematical modelling of infectious disease cannot be ignored. The most common assumption when modelling the transmission dynamics of infectious diseases is homogenous mixing, i.e. the population mixes uniformly at random and each infectious individual (regardless of age, geographic location, etc.) has the same probability of coming in contact with any susceptible individual in the population. However, despite increased penetration, the population of social media users are a specific sample of the population where individuals must have an internet connection and be relatively tech savvy—these are characteristics of a younger demographic group (Jurdak et al. 2015). Thus, social media data may represent a population that is heterogeneous and age-stratified.

Conclusion: A Data-Driven Approach to Modeling

Traditional infectious disease models treat human behaviour as a fixed phenomenon that does not respond to disease dynamics—this we know is not the case. Systems containing an infectious disease spreading by biological contagion as well as a social contagion concerning the disease (a coupled “ disease-behaviour” system) can exhibit dynamics that do not occur when the two subsystems are isolated from one another (Bauch and Galvani 2013).

Social media represents a novel forum by which behavioural reactions can be observed and incorporated into the disease modelling process. Regardless of its veracity, it has been shown to play a role in influencing the population’s perception of risk and behaviour during the course of the outbreak (Fung et al. 2015). Despite some limitations and concerns, as mobile technology continues to evolve and access to smart devices proliferates, social media is expected to occupy an increasingly prominent role in the field of disease modelling. Accordingly, a better understanding of the behavioural change induced by social media can strengthen mathematical modelling efforts and assist in the development of public policy so as to make the best use of this increasingly ubiquitous resource in controlling the spread of disease.