Graphical abstract
Keywords: SNP heritability, Linear mixed model, REML, Method of moments, Summary statistics
Abstract
In GWAS studies, SNP heritability measures the proportion of phenotypic variance explained by all measured SNPs. Accurate estimation of SNP heritability can help us better understand the degree to which measured genetic variants influence phenotypes. Over the last decade, a variety of statistical methods and software tools have been developed for SNP heritability estimation with different data types including genotype array data, imputed genotype data, whole-genome sequencing data, RNA sequencing data, and bisulfite sequencing data. However, a thorough technical review of these methods, especially from a statistical and computational viewpoint, is currently missing. To fill this knowledge gap, we present a comprehensive review on a broad category of recently developed and commonly used SNP heritability estimation methods. We focus on their modeling assumptions; their interconnected relationships; their applicability to quantitative, binary and count phenotypes; their use of individual level data versus summary statistics, as well as their utility for SNP heritability partitioning. We hope that this review will serve as a useful reference for both methodologists who develop heritability estimation methods and practitioners who perform heritability analysis.
1. Introduction
A central quest in genetics is to understand the relative contribution of genetic factors and environmental factors to phenotypic variation – a quest commonly framed as the nature vs nurture debate. Elucidating the relative contribution of genetics versus environment for various diseases and disease-related complex traits can help us better understand the causal mechanism of disease etiology and facilitate resource prioritization for disease diagnosis and prevention. A key quantity to evaluate the contribution of genetics versus environment is heritability, which measures the proportion of phenotypic variance explained by genetic factors. Two types of heritability can be estimated. The broad-sense heritability () evaluates the proportion of phenotypic variance explained by all genetic factors, including additive effects, dominant effects, and epistasis effects. The narrow-sense heritability (), on the other hand, evaluates the proportion of phenotypic variance explained by additive genetic effects. Accurate estimation of heritability can show the degree to which genetic factors influence phenotypes and improve our understanding of the genetic basis of disease and disease-related complex traits. Indeed, heritability plays an important role across a range of genetic applications [1]: it is a key for understanding the evolutionary forces underlying natural selection; it determines how a population will respond to selection; it predicts, at least in part, gene mapping power in genome-wide association studies; it can estimate, quite accurately in some cases, the phenotypic value of an individual and thus facilitate genomic selection via predicted breeding values; and it provides an upper limit for the genetic prediction of phenotypes.
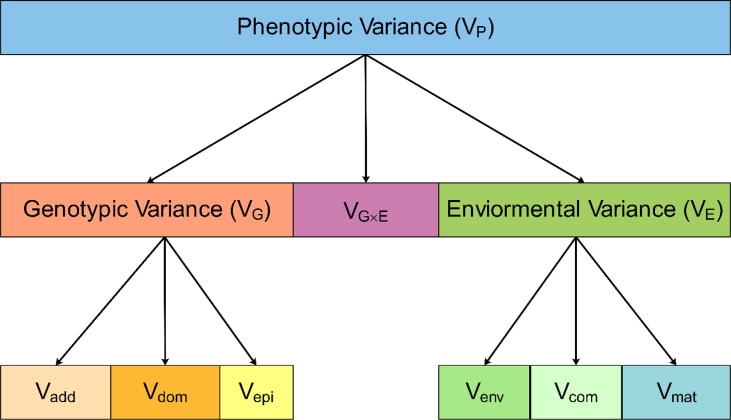
In the absence of genetic data, heritability estimation can be carried out in family/pedigree-based [2] or twin-based designs [3]. Recent reviews of heritability estimation in related individuals can be found from [4], [5]. Briefly, in family/pedigree-based studies, heritability is often estimated using the linear mixed model (LMM), also known as the variance component model. The LMM allows partitioning of the phenotypic variance into different components: a genetic variance component, an environmental component, and potentially a gene-environment (G × E) interaction component (Fig. 1). The genetic variance component captures the part of phenotypic variance explained by genetic factors and can usually be further partitioned into three parts: the additive, dominance, and epistatic parts. The environmental variance component captures the part of phenotypic variance explained by environmental factors and can also be further partitioned into three parts: the common environment part, the maternal influence part, and the residual stochastic environment part. The G × E interaction variance component captures the part of phenotypic variance explained by the interactions between genetic factors and environmental factors. Measuring the G × E component is often challenging as it requires the assessment of detailed environmental exposures obtained from appropriate study designs, with several recent analytic methods developed for modeling G × E interactions for heritability estimation [6]. In this review, we focus on the genetic variance components.
Fig. 1.
Partition of phenotypic variance. VG represents the phenotypic variance due to genetic effects; VE represents the phenotypic variance due to environmental effects; and VG×E represents the phenotypic variance due to gene-environment interactions. The genetic variance VG can be partitioned into three parts: Vadd that represents the additive genetic effects; Vdom represents the dominance genetic effects; and Vepi represents the epistatic effects. The environmental variance VE can also be partitioned into three parts: Vcom represents common environmental effects such as those due to residing in the same family; Vmat represents maternal effects such as nutritional intake during pregnancy; and Venv represents the residual stochastic environmental effects.
After obtaining the estimates for various components, we can compute the estimated ratio of genetic variance over the total phenotypic variance, which serves as an estimate for heritability. For data with a relatively simple, familiar structure, a method of moments (MoM) based algorithm is often employed for variance component estimation in the linear mixed model. For example, a regression between the offspring phenotypic value () and the average of phenotypic value for the two parents () can directly lead to the heritability estimate () [7]. Similarly, for studies involving monozygotic (MZ) twins and dizygotic (DZ) twins, Falconer’s formula is applied to obtain a heritability estimate, which equals twice the difference between the phenotypic correlation in MZ pairs and the phenotypic correlation in DZ pairs () [8], [9], [10]. For family studies with individuals of different levels of relationship, a likelihood-based inference procedure is often employed for variance component estimation in the linear mixed model. This procedure constructs a kinship matrix based on pedigree information and then obtains the maximum likelihood estimate (MLE) or the restricted maximum likelihood estimate (REML) for heritability. Regardless of the estimation algorithm, various early family-based studies have produced accurate heritability estimates for various quantitative traits. For example, it has been estimated that the narrow-sense heritability for height is around 80% in family-based studies [1], [11]. Heritability may vary across populations, across individual groups with different age or other characteristics, and may change over time. Similarly, heritability of livestock traits (e.g., milk yield) can sometimes double over a couple of decades through animal breeding programs [1].
The progress of array-based techniques, and more recently, whole-genome sequencing (WGS) techniques, have enabled accurate measurement of genotypes on millions of single nucleotide polymorphisms (SNPs) across the entire genome. These advances have subsequently enabled large-scale genome-wide association studies (GWASs) in apparently unrelated individuals. In the past decade, GWASs have identified many SNPs associated with various diseases and disease-related complex traits. However, the majority of identified SNPs only explain a small fraction of heritability for most traits, leading to a large fraction of unexplained heritability, commonly referred to “missing heritability”. Many explanations have been proposed for missing heritability. For example, it is possible the causal variants are not in complete linkage disequilibrium (LD) with the genotyped SNPs [12]. It is also possible that rare variants with large effects contribute disproportionately to the phenotypic variance. In addition, pedigree-based studies may have overestimated heritability [13]. A prominent hypothesis suggests that current GWASs are underpowered and that many causal SNPs remain undetected below the stringent genome-wide significant threshold, which can vastly underestimate the phenotypic variance. Therefore, it becomes critically important to estimate the heritability or phenotypic variance explained by all measured genome-wide SNPs. For example, in the seminal paper by Yang et al. [12], the heritability for height explained by significantly associated SNPs is only 10%, while that explained by all measured SNPs is near 50%, with an increase of 40%.
Several reviews have been recently written on SNP heritability estimation [4], [5], [14], [15], [16], [17], [18], [19], [20]. Most of these papers focus on the practical interpretation of SNP heritability and how it contributes to our understanding of missing heritability for various diseases and complex traits. In addition, these reviews are often targeted at experimental biologists, focus on quantitative traits, and have a narrow focus on a few existing statistical methods used for heritability estimation. To fill this critical gap, we provide a systematic review of various statistical methods that have been developed and used for SNP heritability estimation on quantitative traits, binary traits, and count phenotypes. Specifically, we included in our review all existing statistical methods that are developed for SNP heritability estimation. We did not include methods for heritability estimation in family/pedigree-based or twin-based designs. All methods in the review make use of genome-wide genotype data. Specifically, we focus on explaining the detailed modeling assumptions underlying various models, providing intuitions on how one would expect different models to work for traits with different genetic architectures. We include two commonly used algorithms -- the method of moments (MoM) and the restricted maximum likelihood (REML) -- the first of which allows estimation of SNP heritability using summary statistics. In addition, we include a broad category of methods that are suitable for modeling phenotypes in the form of traditional quantitative traits, ascertained case control status, and count measurements from recent genomic sequencing studies. We also include various methods for partitioning heritability across different SNP functional categories. We hope that our review can serve as a useful reference to the broad statistical genetics and computational biology communities on modeling and estimation of SNP heritability.
2. Heritability estimation for quantitative traits
2.1. Notations
First, we provide detailed notations and formulate the SNP heritability estimation problem into a statistical framework. We denote as the n-vector of quantitative trait measured on n individuals. We denote as the n by p matrix of genotypes for the same n individuals and p SNPs. These genotypes can be collected in different forms, including genotype array data, imputed genotype data, and whole genome sequencing data. The genotype for the -th individual and -th SNP, , is often coded as 0, 1, or 2, representing the number of reference alleles. For the genotype matrix, we assume that all missing genotypes have already been imputed with proper genotype imputation software; thus, will be in the range of 0 and 2. To simplify the algebra, we further assume that each column of (i.e., SNP) has been centered to have zero mean; the results will remain the same with or without centering [21]. It is also common to standardize the columns of to have unit variance, which corresponds to making an assumption that rarer variants tend to have larger effects than common variants and variant effect sizes tend to decay with the inverse of the genotype variance [22]. Therefore, standardizing the columns will affect the results, although previous studies have shown that its relative contribution to the genetic relatedness matrix (GRM, defined later) is the same and has minimal influence on the SNP heritability estimation [23]. Therefore, we also standardize each column of to have unit variance. We use the following linear regression to model the relationship between the phenotype vector and the genotype matrix ,
| (1) |
where is an -vector of genetic effect sizes and is the n-vector of residual errors with each entry . Note that centering of the phenotype and each column of genotype matrix allows us to ignore the intercept in equation (1).
Equation (1) is often used for estimating the proportion of phenotypic variance explained by all measured SNPs in GWAS, where Var denotes sample variance. This quantity is commonly referred to as the proportion of variance in phenotypes explained (PVE) by available genotypes or SNP heritability, denoted as . A simple approach to estimate SNP heritability is to select a candidate set of associated SNPs and then estimate PVE by these selected SNPs. For example, for a given trait, we can identify SNPs that are associated with the trait passing the genome-wide p-value significance threshold of . We can include all these significant SNPs, or further extract uncorrelated SNPs from the set through linkage disequilibrium (LD) pruning or clumping, into the model defined in equation (1). When the number of SNPs, , is small, we can easily estimate through ordinary least square estimation. When the selected SNPs are independent from each other, we can estimate the PVE as , where denotes the set of selected independent SNPs; when SNPs are correlated with each other, we can estimate the PVE using the definition . As noted above, such estimation may greatly underestimate the true SNP heritability because it ignores many SNPs that have not reached the stringent genome-wide threshold due to imperfect statistical power. For example, the top ~ 50 SNPs only explain 5–10% of phenotypic variance for height [24], [25], [26], [27] although, based on pedigree-based designs, height is a highly heritable trait with estimated heritability as high as 80% [1], [11].
2.2. Modeling assumptions on the effect sizes
When we include all genome-wide SNPs, the number of SNPs would exceed the number of individuals . Indeed, in a typical GWAS, is often on the order of a million to 100 million while typically ranges from a few thousand to half a million. When , the regression model defined in equation (1) becomes an underdetermined system. Therefore, we need to make certain modeling assumptions on the SNP effect sizes to complete the modeling specification. Various modeling assumptions have been proposed on the effect sizes . We describe a few commonly used modeling assumptions below.
Bayesian variable selection regression (BVSR). Perhaps the first attempt in the genetics field to estimate SNP heritability was BVSR. BVSR makes a sparse modeling assumption that a relatively small proportion of all genetic variants truly affect the phenotype [28], [29], [30], [31], [32], [33]. In particular, BVSR [32] assumes that the genetic effect size of each SNP follows a point-normal distribution
| (2) |
where is the variance component in the normal distribution and denotes a point mass at zero. The point normal is commonly referred to as a spike and slab prior. Based on the point-normal modeling assumption, with proportion , the SNP effect size is non-zero and follows a normal distribution; while with proportion , the SNP effect size is exactly zero. The proportion of non-zero effect SNPs, , is often assumed to be small. For example, BVSR [32] places a sparsity-inducing prior on and assumes that follows a uniform distribution a priori. The model defines a parameter to quantify PVE, , with as the number of non-zero . Given the observed data, BVSR relies on a Markov Chain Monte Carlo (MCMC) algorithm to obtain posterior samples from the approximate posterior distribution for SNP heritability. As an example, BVSR was applied to analyze a GWAS study with plasma C-reactive protein (CRP) and found that using all SNPs explained approximately 6% of variance in CRP, much higher than the previous estimates of 0.35%-0.4% using only significant SNPs [34], [35].
Linear mixed model (LMM). The second modeling assumption, which is most often used, is the normality assumption on the effect sizes. This modeling assumption is commonly referred to as LMM. LMM was first proposed by [12] for SNP heritability estimation, after which LMM became a standard method and one of the most effective approaches for the analytic task. LMM assumes that
| (3) |
Under this modeling assumption, all SNPs have non-zero effects with their effect sizes following a normal distribution. LMM is commonly used for heritability estimation as well as association analysis while accounting for family relatedness or population stratification. When a particular likelihood-based inference procedure REML (more details below) is used to perform parameter inference, LMM is also known as the ridge regression or Genome-based REML (GREML). In this review, the notations of LMM, GREML, REML, and GCTA [36] all represent this approach. In the LMM, the variance of total additive genetic effects can be defined as . The variance components and can be estimated using software such as GCTA [36] and GEMMA [37]. The SNP heritability estimate can be expressed as Note that, when the columns of the genotype matrix are not standardized, a scaling factor , where denotes the estimated genetic relatedness matrix (GRM) and is commonly computed as , is multiplied by , which leads to the SNP heritability estimate as [22].
Bayesian sparse linear mixed model (BSLMM). Because BVSR and LMM make completely different modeling assumptions, one may naturally expect that the two models work better for traits with different genetic architectures. Specifically, because of the sparse effect size assumption, BVSR is more accurate in estimating SNP heritability when a small proportion of SNPs truly has non-zero effects on the trait. In contrast, because of the polygenic effect size assumption, LMM is more accurate in estimating SNP heritability when truly a large proportion of SNPs have non-zero effects on the trait. Thus, BVSR tends to underestimate SNP heritability for polygenic traits while LMM tends to be imprecise for non-polygenic traits [22] – even though LMM produces unbiased estimates for traits with various genetic architectures [22], [38]. Unfortunately, the true genetic architecture of a phenotype is unknown a priori. Therefore, it is often unclear whether one should use LMM or BVSR to analyze a given trait.
Motivated by this methodological limitation, Zhou et al. [22] proposed a hybrid model of LMM and BVSR, which is referred to as Bayesian sparse linear mixed model (BSLMM). BSLMM places a mixture of two normal distributions on the effect sizes,
| (4) |
That is, with probability , tends to be small and follows a normal distribution with a small background variance of ; while with probability , tends to be large and follows a normal distribution with a large variance of , where is the additional variance on top of the background variance. Clearly, when , BSLMM reduces to LMM. When , BSLMM reduces to BVSR. By including both LMM and BVSR as special cases, BSLMM can take advantage of LMM and BVSR to adaptively infer the genetic architecture underlying the trait from the data at hand. In the BSLMM, the SNP heritability can be expressed as a population level parameter , the approximate expectation of PVE. Besides , BSLMM also defines a parameter as the approximate expectation of PGE, the proportion of genetic variance explained by the sparse effects. In addition, PVE can be estimated by while PGE can be estimated by , where is the random effect following . BSLMM relies on a Metropolis Hastings (MH) algorithm to perform posterior inference. BSLMM is also closely related to the recent omnigenic model hypothesis [39]. Specifically, the omnigenic model hypothesizes that all genes have non-zero effects, which is modeled in BSLMM by assuming that all SNPs have non-zero effects. In addition, the omnigenic model hypothesizes that a small proportion of genes, denoted as core genes, have additional effects. These additional effects are modeled by the normal component with a large variance in BSLMM. As an extension of BSLMM, Zhu and Stephens [40] provided a summary statistics-based version, Regression with Summary Statistics (RSS) likelihood. RSS likelihood allows BSLMM to be applied to large scale GWASs. By analyzing a summary-level GWAS with 253,288 individuals genotyped at 1.06 million SNPs using BSLMM, RSS likelihood obtained the heritability estimate for height as 52% [40].
Linkage disequilibrium adjusted kinships (LDAK). The above BVSR, LMM/GREML and BSLMM assume that the effect size for the j-th SNP, , does not depend on how many SNPs are in close linkage disequilibrium (LD) with the j-th SNP. In contrast, the Linkage Disequilibrium Adjusted Kinships (LDAK) [41], [42] assumes that depends on how j-th SNP is correlated with its neighborhood SNPs. Specifically, similar to LMM, LDAK assumes that follows a normal distribution . However, different from LMM that assumes the same variance , LDAK assumes that is j-th SNP specific and is related to minor allele frequency, LD score, and imputation information score of the SNP. The LD score of SNP is defined as , where is the sum of the squared Pearson’s correlation between SNP and all other SNP’s while represents the expectation of the summation under the null and a high value indicates that the j-th SNP is in high LD with many nearby SNPs. The imputation information score is a metric between 0 and 1 output from imputation software: a value of 1 indicates that there is no uncertainty in the imputed genotypes while a value of 0 means that there is complete uncertainty about the genotypes. Specifically, LDAK assumes that the effect size follows
| (5) |
where is the minor allele frequency of the SNP j; is a SNP-specific weight that is a function of the inverse of the LD score of SNP , so that the -th SNP effect size tends to be smaller if there are more SNPs in LD with the -th SNP; and is the imputation information score measuring genotype certainty, so that the j-th SNP effect size tends to be smaller for the genotype with higher uncertainty. The parameter determines the relationship between and . Specifically, indicates that does not depend on , an assumption commonly made in genetics; (e.g., ) indicates that decreases as increases; and (e.g., −0.75, −0.25) indicates that increases as increases. The default value of in LDAK is . LDAK relies on REML to estimate parameters. Because of different modeling assumptions of LDAK and LMM, different SNP heritability estimations are obtained by different methods in real data analysis. For example, if the underlying SNP effect size depends on LD in the same form as of LDAK, then methods, such as LMM that fails to model the effect size on LD score dependency, would generate downward biased estimates. Indeed, in a real data application, LDAK obtained an average of 43% SNP heritability estimation higher than that of LMM for 19 analyzed traits [42]. Certainly, while the naïve LMM does not account for the potential LD dependency, it also can be extended to do so by LD stratified analysis; such extensions are described in the SNP Heritability Partitioning section.
Besides these above methods, several other models can be used for SNP heritability estimation. Particularly, many phenotype prediction models developed elsewhere can be directly applied for SNP heritability estimation. For example, the Bayesian alphabet models assume that the genetic effect sizes follow either a t-distribution (BayesA) [43], [44], [45], [46], a mixture of t-distribution and a point mass at zero (BayesB, BayesD, BayesD) [43], [44], [45], [46], [47], or a mixture of two t-distributions (BayesC) [43], [45]. The Bayesian lasso assumes a double exponential distribution [28], [48]. BayesR assumes a mixture of three normal distributions and a point mass at zero [49]. NEG assumes a normal exponential gamma distribution [29]. BayesS assumes a point-normal distribution with SNP-specific variance as a function of MAF [50].
Dirichlet process regression (DPR). These aforementioned methods share a common feature of relying on a finite number of parameters to characterize the genetic effect distribution; that is, they all use parametric models. In contrast to the parametric model, Zeng and Zhou [51] developed a Bayesian non-parametric model, termed as the latent Dirichlet process regression (DPR). DPR assumes that follows a normal distribution, with a further unknown distribution G placed upon the variance parameter . DPR actively infers the unknown distribution G by assuming a non-parametric Dirichlet process (DP) prior on the distribution itself:
| (6) |
where the inverse gamma (IG) distribution is the base distribution and the concentration parameter determines how the distribution of G differs from the base distribution. By inferring the distribution G based on the data at hand, DPR is flexible and adaptive to a wide range of genetic architectures, resulting in accurate phenotype prediction and appreciable power gain for the transcriptome-wide association studies (TWAS) [52], [53], an integrative analysis of expression mapping studies and GWASs. Note that the above modeling assumption is also equivalent to assuming each element of follows a mixture of infinitely many normal distributions a priori,
| (7) |
Here, is the weight corresponding to the -th normal distribution; it is generated from a stick breaking process and determined by a latent proportion parameter that each follows a Beta prior. With the DPR modeling assumption, one can obtain the SNP heritability estimates via two algorithms: the Monte Carlo Markov Chain and the variational Bayesian algorithm.
3. SNP heritability estimation for case control studies and count phenotypes
Liability threshold model: REML. We have focused on estimation of SNP heritability for quantitative traits. More considerations are needed when the outcome is a disease phenotype obtained from case control studies. In this case, estimation of SNP heritability requires not only proper modeling of the binary nature of the outcome, but also proper controlling of the ascertainment occurred in case control studies. The binary nature of case control status suggests that the variance of the phenotype is a function of its mean, rendering invalid normality assumption on the residual errors. The normality assumption is commonly used in SNP heritability estimation for quantitative traits as described in previous sections. Ascertainment is a result of the case-control sampling design where the proportion of cases in the study is collected to be much higher than that in the population. Ascertainment effectively increases the associated SNP effect size estimates as compared to that in the population; it renders inaccurate effect size assumptions made in SNP heritability estimation for quantitative traits. Therefore, methods for quantitative traits are no longer applicable to case control studies. Instead, a liability threshold model is used to account for both the binary nature and ascertainment in case control studies.
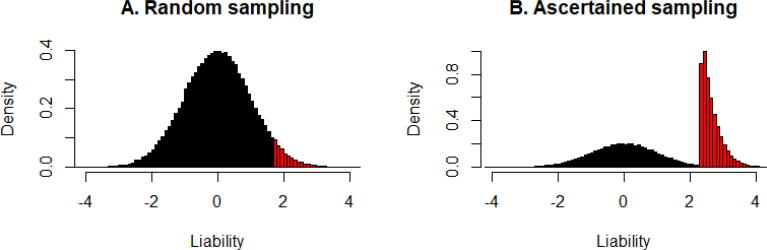
The liability threshold model was first introduced by [54]. It introduces a latent continuous variable for every individual i, termed as liability score . The liability score effectively measures the individual’s susceptibility to disease. The liability score, paired with the liability threshold value of , determines whether an individual is a case or a control: the individual i is a case when and is a control otherwise. The liability score is a continuous variable and assumed to follow the same linear model as in equation (1)
| (8) |
where represents the genetic contribution to liability and represents the environmental contribution to liability. As described in previous sections, different modeling assumptions can be made on the genetic effect sizes , though the common choice is the normal assumption. Under this assumption, the liability score follows a (multivariate) normal distribution in the population (Fig. 2A). The liability threshold , when paired with a distributional assumption on , effectively determines the prevalence of the disease. Certainly, due to ascertainment, the liability scores in the case control study no longer follow a normal distribution but are often enriched with large liability scores (Fig. 2B). To address the issue of nonnormality with liability score, Lee et al. [55] proposed a transformation procedure. In particular, the transformation procedure first treats the disease status (0/1) as a continuous outcome and fits an LMM described in equations (1), (3) using the REML algorithm to estimate the variance components. The resulting SNP heritability estimate is referred to as the SNP heritability estimated on the observed scale. Afterwards, the transformation procedure applies a linear transformation on and converts it to the SNP heritability estimate on the liability scale:
| (9) |
Fig. 2.
The distributions of liability score under random sampling and ascertained case-control sampling for unrelated individuals. Red represents cases while black represents controls. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
where is the standard normal density function, is the REML heritability estimates obtained by treating the case-control status (0/1) as a quantitative trait, represents the disease proportion in the population, and denotes the disease proportion in in the sample. The above transformation extends the Dempster and Lerner [56] formula which addresses the binary nature of case control outcome but does not account for ascertainment.
Liability threshold model: HE/PCGC. The detailed algorithmic derivation in Lee et al. [55] is complicated. Based on Taylor series expansion and approximation, Zhou et al. [22] provided an alternative derivation, which led to the same transformation equation described in equation [9]. However, the new derivation casts concern on the effectiveness of such transformation when paired with REML, as the approximation in equation [9] is only valid when SNP heritability is close to zero. When SNP heritability is not close to zero, the SNP heritability on the liability scale based on equation [9] will be underestimated [57], [58]. Golan et al. [58] provides a simple solution to the downward bias in SNP heritability estimation: instead of using REML estimates, one can use the Haseman-Elston (HE) regression to obtain the variance component estimates. The HE regression is also referred to as the phenotype correlation-genotype correlation (PCGC) regression relying on the equation , where is the phenotypic correlation between individual and and is the genotypic correlation between the two individuals. Here, is a function that relates SNP heritability and genetic correlation to the phenotypic correlation . The specific functional form of depends on the design of the study and the properties of the phenotype. In HE regression, the function is a simple product of the SNP heritability and genetic correlation; that is, . Instead of requiring low SNP heritability, HE/PCGC regression only requires each element in the kinship matrix close to zero. Consequently, it can be widely applied to data collected on unrelated individuals and provides approximately unbiased SNP heritability estimates on the liability scale in several GWASs [58]. The HE/PCGC regression is later recognized to be linked to the MINQUE (the minimal norm quadratic unbiased estimation) estimation proposed in the statistical literature and can be viewed from a method of moments (MoM) algorithm perspective [59]. The HE/PCGC regression is further extended to model ascertained case control studies using summary statistics [59], [60].
Generalized linear mixed model: PQLseq. Besides binary traits and case control studies, many complex traits are measured on various other data types through genomic sequencing studies. For example, RNA sequencing (RNAseq) studies have allowed accurate gene expression measurements across tens of thousands of genes. Bisulfite sequencing (BSseq) studies have enabled accurate methylation profiling across genome wide CpG sites. Understanding SNP heritability of these molecular traits, including gene expression levels and methylation levels, can facilitate our understanding of the causal or mediation mechanism underlying the SNP-trait associations. These two types of sequencing data have different data structures. Specifically, RNAseq studies collect one read count for each gene as its expression level. In contrast, BSseq studies collect two read counts for each CpG site – one methylated count and one total count – as the methylation level. The ratio between these two counts represents approximately the methylation proportion of the given CpG site. Both types of data are of count nature. The standard SNP heritability estimation method, LMM, has been recently applied to estimate heritability of gene expression [61], [62], [63], [64], [65], of methylation level [66], [67], [68], and of various other molecular traits [69]. However, LMM is specifically designed for analyzing quantitative traits. In genomic sequencing studies, the application of LMM requires a priori transformation of the count data to continuous data before heritability estimation [61], [70]. Transforming sequencing count data may fail to account for the sampling noise from the underlying count generating process and may inappropriately attribute such noise to independent environmental variation. As shown in Sun et al. [71], modeling count data with LMM can run into the risk of overestimating environmental variance and subsequently underestimating heritability. To mitigate the problem, Sun et al. [71] developed PQLseq, a penalized quasi-likelihood for sequencing count data, based on the generalized linear mixed models (GLMM), which directly model count data. For a given gene in an RNAseq study, PQLseq considers a Poisson mixed model (PMM) to directly model the count data for the -th individual, where is the number of reads mapped to the particular gene, is the total read counts (a.k.a read depth or coverage), and is an unknown Poisson rate parameter that represents the underlying gene expression level. For a given CpG site in a BSseq study, PQLseq considers a binomial mixed model (BMM) , where is the total read count for the -th individual, is the methylated read count constrained to be an integer value less than or equal to , and is an unknown parameter that represents the underlying proportion of methylated reads at the site. For either model, PQLseq transforms the unknown parameters into a latent variable : in PMM and in BMM. The latent variable is combined together into a vector, which is modelled as follows:
| (10) |
where represents the genetic contribution to the latent variable and represents the environmental contribution. PQLseq further relies on the penalized quasi-likelihood for parameter inference to obtain unbiased SNP heritability estimates.
4. Inference algorithms for LMM and the adaptation of summary statistics
All the methods described so far require individual-level genotypes and phenotypes data from all samples in the study. Because of consent and privacy concerns, and logistic limitations (e.g., large-scale data transfer and storage often require high-end computing infrastructure), it is increasingly difficult to access complete individual-level data from large-scale association studies. Indeed, sharing summary statistics such as the marginal z-scores across multiple studies, performing meta-analysis, and releasing results in terms of summary statistics has become a standard practice in most consortium studies. Requiring complete individual-level data restricts the use of many SNP heritability estimation methods and limits their benefits in many large-scale studies. In addition, the aforementioned methods are computationally expensive. For example, the REML algorithm in LMM or GLMM scales cubically with respect to the sample size. Similarly, both BVSR and BSLMM require computationally expensive Markov chain Monte Carlo methods for model fitting. To alleviate the computational concern and make use of summary statistics, several alternative statistical methods for SNP heritability have been recently developed.
A common method to estimate SNP heritability based on summary-statistics is LD Score regression (LDSC) [72]. For each SNP, LDSC first computes its LD score, , which is defined in the above LDAK section and captures approximately the number of genetic variants tagged by this SNP. LD score cannot be computed exactly due to the large number of genome-wide SNPs. Instead, it is typically estimated based on SNPs in an appropriate sliding window (e.g., 1 MB or 1 cM). After obtaining LD score, LDSC regresses the test statistic from GWAS on the per-SNP LD scores
| (11) |
where measures the confounding bias due to potential population stratification and cryptic relatedness. Here, population stratification refers to the presence of a systematic difference in allele frequencies between subpopulations in the data possibly due to different ancestry. Cryptic relatedness occurs when individuals in the study are more closely related to another than thought. Both population stratification and cryptic relatedness, if uncontrolled, can lead to upward biased SNP heritability estimation. By controlling for population stratification and cryptic relatedness using the parameter , LDSC can mitigate their influence for SNP heritability estimation. Thus, regressing the GWAS test statistics on per-SNP LD scores allows for estimation of . Unlike standard data-generative models (i.e., models that describe how the individual-level variables are generated based on genotypes of n samples), LDSC models the marginal test statistics for p SNPs. By modeling summary statistics, LDSC is not only applied to many data sets that previously cannot be analyzed for SNP heritability estimation, it also substantially improves computational speed and makes SNP heritability scalable to large data sets. LDSC was initially introduced without an underlying data-generative model. It was later found out that LDSC is fitting the LMM described in [59]. However, instead of applying the standard likelihood-based approach REML for fitting LMM, LDSC relies on a matching moments-based method. From this aspect, LDSC is closely related to HE/PCGC methods.
Zhou [59] developed MQS (MinQue for Summary statistics) and related it with LDSC and HE/PCGC. MQS is based on the MINQUE criterion, a conceptual framework based on MoM. For the case of one variance component, an analytic variance component estimation is as follows:
| (12) |
| (13) |
where is an n by n matrix. All choices of can lead to unbiased variance component estimates while different choices of can influence the estimation accuracy. In particular, the optimal choice with known leads to the most accurate variance component estimates. In practice, is unknown and the optimal choice of cannot be used. Therefore, we will need to make decisions on the choice of . Different choices of in MQS lead to different existing variance component estimation algorithms. Specifically, when and is updated through the above estimation equation in an iterative fashion, MQS becomes REML. When with a certain diagonal weighting matrix W, MQS becomes the weighted version of LDSC. When , MQS becomes HE/PCGC. MQS brings many seemingly unrelated methods – REML, HE/PCGC, LDSC – into the same unified statistical framework. With this new framework, MQS provides an alternative but mathematically equivalent form of HE/PCGC to allow for the use of summary statistics. MQS also provides an exact approximation of LDSC for yielding unbiased and statistically more efficient SNP heritability estimation. In addition, MQS can be easily extended to model multiple variance components or multiple phenotypes. Finally, while MQS requires computing q in equation [12] using all individuals, it can use only a subset of individuals to estimate without incurring accuracy loss for the final SNP heritability estimates. Such strategy of MQS, using a subset of individuals for estimating certain quantities while using all individuals for computing other quantities, is in line with the idea of stochastic approximation as in Robbins and Monro [73]. The stochastic estimation strategy used in MQS leads to computational speed improvement over standard methods by orders of magnitude.
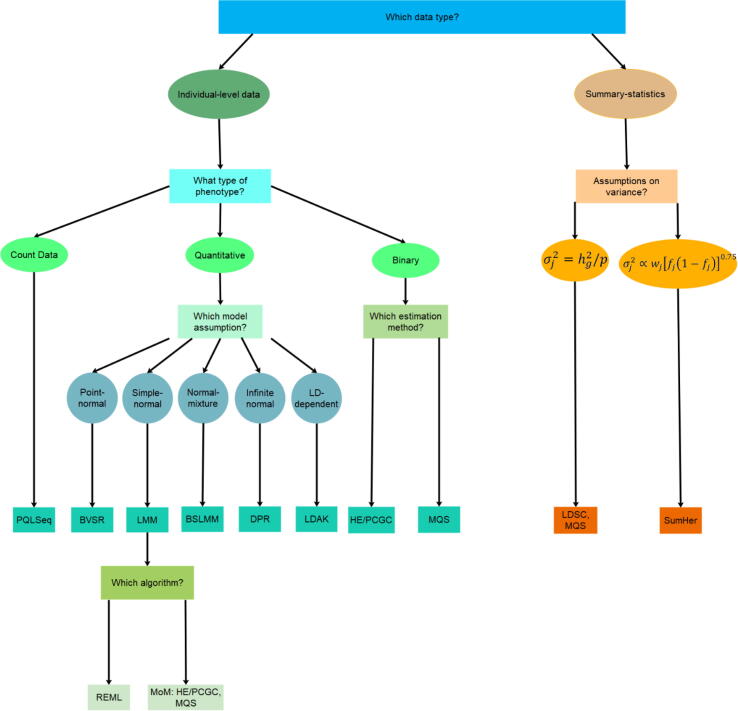
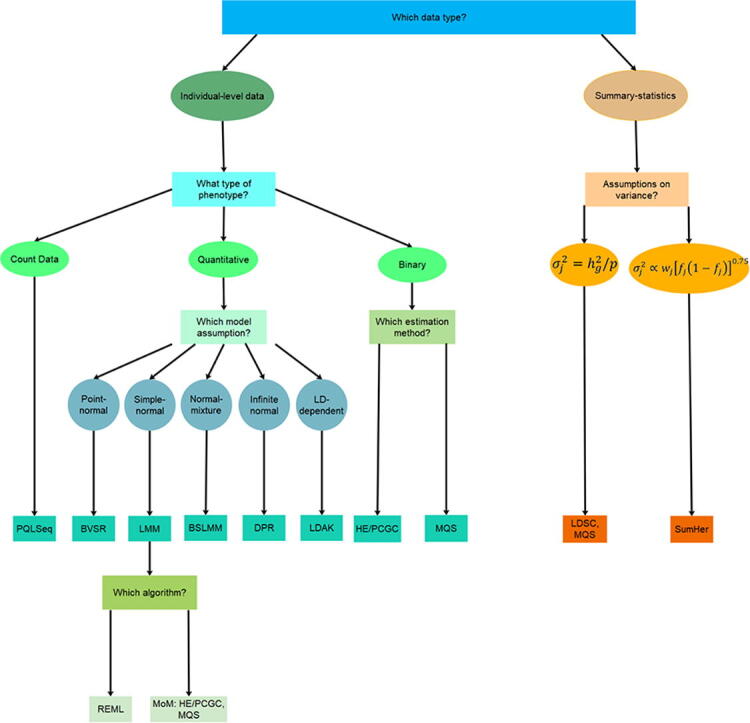
While both LDSC and MQS rely on the standard LMM assumption, the recently proposed SumHer [74] makes a different modeling assumption on the SNP effect sizes based on the LDAK model. SumHer effectively extends LDAK [41], [42] to use summary statistics. Another method extended from existing approach is PCGC-s [60], which extends the PCGC approach [58] to use summary statistics as well as the genetic correlations between two diseases. A summary of methods for estimating SNP heritability is shown in Table 1 and a corresponding decision tree is in Fig. 3.
Table 1.
A summary of methods for SNP heritability estimation.
| Main Text Sections | Methods | Modeling Assumptions | Estimation Algorithms | Trait Types | Software | Weblink | Comments | References |
|---|---|---|---|---|---|---|---|---|
| Modeling assumptions | BVSR | MCMC | Quantitative | GEMMA | https://github.com/genetics-statistics/GEMMA | Fast for large-scale data; Also useful for phenotype prediction and PRS construction; supports Mac and Linux platforms | [32], [33] | |
| BSLMM | MCMC | [22] | ||||||
| LMM/REML | REML | Quantitative | GEMMA/GCTA | https://github.com/genetics-statistics/GEMMAhttp://cnsgenomics.com/software/gcta/#Overview | Also useful for SNP association tests with LMM; supports Windows, Mac and Linux platforms | [12] | ||
| LDAK | REML | Quantitative | LDAK | http://dougspeed.com/ldak/ | Over 30 functions, importantly, SNP heritability estimation and SNP-based prediction models construction, supported for Mac and Linux platforms | [41], [42] | ||
| DPR | MCMC/VB | Quantitative | DPR | https://github.com/biostatpzeng/DPR | Mainly for robust genetic prediction and PRS construction of complex traits; supports Mac and Linux platforms | [51] | ||
| Case-control study | HE/PCGC | MoM | Binary | PCGC | https://data.broadinstitute.org/alkesgroup/PCGC/ | Mitigate biases in REML heritability estimation for ascertained case-control studies; supports Linux platform | [58] | |
| Count data | PQLseq | MCMC | Binary/Count | PQLseq | https://cran.r-project.org/web/packages/PQLseq/index.html | For heritability estimation of count data in RNAseq and Bisulfite seq studies; supports Windows, Mac and Linux platforms | [71] | |
| Summary statistics | LDSC | MoM | Quantitative/Binary | LDSC | https://github.com/bulik/ldsc | A command tool for estimating heritability and genetic correlation using GWAS summary statistics | [72] | |
| MQS | MoM | Quantitative/Binary | GEMMA | https://github.com/genetics-statistics/GEMMA | A general statistical framework for SNP heritability estimation using summary statistics; supports Mac and Linux platforms | [59] | ||
| SumHer | REML | Quantitative/Binary | SumHer | http://dougspeed.com/sumher/ | Heritability estimation using summary statistics under the LDAK assumption; supports Linux platform | [74] |
Table lists 10 methods described in the main text, with the first seven methods for analyzing individual level data and last three methods for analyzing summary statistics. Columns contain the main text section in which the method is described (1st column), method name (2nd column), modeling assumption on the SNP effect sizes (3rd column), estimation algorithms (4th column), phenotype type (5th column), implemented software (6th column), web link (7th column), additional comments (8th column) and references (9th column). In the 3rd column, denotes a point mass at zero; N(.,.) denotes a normal distribution with the mean and variance parameters; DP denotes a Dirichlet process. In the 4th column, MCMC represents Markov chain Monte Carlo method, VB represents variational Bayesian, REML represents restricted maximum likelihood method, and MoM represents method of moments. In the 8th column, PRS is short for polygenic risk scores.
Fig. 3.
A decision tree on what type of methods to use for SNP heritability estimation.
5. SNP heritability partitioning
In parallel to trait mapping efforts, large-scale functional genomic studies have yielded a rich source of SNP functional annotations [75], [76], [77], [78], [79]. Various discrete and continuous annotations are being developed to characterize the function of genetic variants [80], [81], [82]. For example, we can now classify genetic variants based on their genomic location (e.g., coding, intron and intergenic variants), role in protein structure and function (e.g., SIFT score [83] or PolyPhen score [84], ability to regulate gene expression (e.g., eQTL and ASE evidence [85], [86], biochemical function (e.g., DNase I hypersensitive sites, metabolomic QTL evidence, and chromatin states [87], [88], [89], evolutionary significance (e.g., GERP score [90], and/or a combination of all these annotations (e.g., CADD score [76] and Eigen score [91]. These functional annotations are important predictors for SNP effects. Previous studies have shown that SNPs in certain functional categories (e.g., in promoters and enhancers) are more likely to be causal [92], [93], tend to have larger effect sizes, and explain more heritability than SNPs in other categories (e.g., introns) [94], [95]. Along with SNP properties (e.g., MAF and LD), incorporating SNP functional annotation is expected to improve SNP heritability estimation accuracy. In this section, we will introduce methods that are developed to estimate and partition SNP heritability by different SNP properties (e.g., GREML-MS and GREML-LDMS) or by different functional genomic annotations (e.g., stratified LDSC, MQS, and SMART).
Lee et al. [96] and Yang et al. [13] categorize SNPs into different categories based on MAFs and MAFs with LD scores, respectively, and assume the following extended LMM modeling assumption
| (14) |
if -th SNP belongs to the -th functional category. In this way, SNPs inside each functional category have their own variance component . When the SNPs are categorized based on their MAFs, GREML-MS implements the REML approach for fitting the extended LMM. When the SNPs are categorized based on both MAFs and LD scores, GREML-LDMS implements the REML approach for fitting the extended LMM. Incorporating MAFs and LD scores is particularly useful for analyzing whole-genome sequencing data that collect SNPs in high density with an excessive number of rare variants. Indeed, some of the methods mentioned in previous sections may yield inaccurate heritability estimates in different data types when their corresponding modeling assumptions do not fit the genetic architecture of the trait. For example, in whole genome sequencing data, a naïve application of LMM may lead to underestimation of SNP heritability for traits whose underlying causal variants are mostly common. Instead, accurate SNP heritability estimation may require analysis in each MAF and/or LD stratum separately. To facilitate stratified analysis, GREML-MS stratifies the genetic variants based on their minor allele frequency into different MAF bins. That is, it estimates SNP heritability using SNPs in each MAF bin and then sums the estimates across bins. Similarly, GREML-LDMS stratifies the genetic variants based on both their MAF and LD and performs stratified heritability estimation. A previous study [13] had shown that, SNP heritability estimate for height was 52.3% by GREML-MS based on imputed data from 1,000 genome project reference. In the same data, SNP heritability estimate for height was 55.5% by using GREML-LDMS. Similar stratification ideas are applied for other methods, such as the stratified version of LD Score regression [97] or stratified LDSC, in which the SNP heritability is partitioned by functional annotations and estimated by using GWAS summary statistics. As introduced above, MQS [59] is based on a set of second moment matching equations determined by the MINQUE algorithm and has closed-form solutions for genetic variance components. MQS is also flexible in estimating heritability when SNPs are partitioned into different functional annotations. Hao et al. proposed SMART (Scalable Multiple Annotation integration for trait-Relevant Tissue) to mainly identify trait-relevant tissues by integrating multiple functional annotations jointly [98]. SMART modifies LMM to relate genetic effects with functional annotations by functionalizing the variant-specific variance components with respect to SNP annotations. The SNP heritability can be estimated based on the generalized estimation equation (GEE) that allows for only summary statistics.
6. Discussion
We have provided a technical review on a wide range of methods for SNP heritability estimation. We have focused on their modeling assumptions, their interconnected relationships, estimation algorithms, as well as their extensions towards different types of phenotypes and towards the use of summary statistics. Different methods have different benefits and may be preferred for heritability estimation of different traits or different data types. Indeed, heritability estimates for height in the literature vary depending on the particular methods used and depending on the datasets examined (Table 2). By detailing the technical properties of different methods, we hope that this review will serve as a useful reference for both methodologists who develop heritability estimation methods and practitioners who perform heritability analyses.
Table 2.
A summary of SNP heritability estimates for height using different methods.
| References | Dataset | Data Type | Sample Size | Number of SNPs | SNP type (applicable AF) | Methods | SNP heritability Estimates |
|---|---|---|---|---|---|---|---|
| [12] | Australian data | Individual | 35,189 | 294,831 | Array (>0.01) | LMM/REML | 0.449 |
| [22] | Australian data | Individual | 35,189 | 294,831 | Array (>0.01) | BSLMM | 0.41 |
| LMM/REML | 0.42 | ||||||
| BVSR | 0.15 | ||||||
| [59] | Australian data | Individual | 3,925 | 4,352,968 | Imputed (>0.01) | MQS | 0.28 |
| LMM/REML | 0.27 | ||||||
| HE | 0.25 | ||||||
| LDSC | 0.21 | ||||||
| [58] | Australian data | Individual | 35,189 | 294,831 | Array (>0.01) | PCGC/HE | 0.537 |
| LMM/REML | 0.510 | ||||||
| [74] | 24 Published GWAS | Summary | Average 121,000 | 4,555,718 | Imputed (>0.01) | SumHer | 0.46 |
| LDSC | 0.20 | ||||||
| [13] | UK10K | Individual | 44,126 | ~17 M | Imputed (>0.0003) | GREML-LDMS | 0.56 |
| GREML-MS | 0.523 |
Table lists SNP heritability estimates for height reported in the previous literature. Columns contain the references where the SNP heritability estimates are reported (1st column), dataset name (2nd column), data type in terms of individual-level data versus summary statistics (3rd column), sample size (4th column), number of SNPs (5th column), genotype data type in terms of array data versus imputed data (6th column), used methods (7th column) and the SNP heritability estimates (8th column). Note that the heritability estimates for height in the Austrian data using the imputed data [59] is smaller than that using the array data , which seems to be general phenomenon for many other traits.
As experimental technology develops and statistical methodology progresses, we are now able to achieve relatively robust and accurate SNP heritability estimation for many diseases and complex traits. For example, the estimates of SNP heritability for height is now above 50% [12], [40]. However, these SNP heritability estimates are still less than that estimated from pedigree studies where the heritability of height is estimated to be 80%. This phenomenon, (SNP heritability < family-based heritability), is referred to as “still-missing heritability” [17]. Many explanations on “still-missing heritability” exist. Pedigree-based heritability estimation may be upward biased due to gene-environment interactions [5], [6], [14], [15], [19], [99], [100]. In contrast, inaccurate genotype calling in sequencing or array-based studies may lead to an underestimation of SNP heritability. Accurate heritability estimation requires the statistical modeling assumption to match the underlying genetic architecture, which depends on the minor allele frequency distribution of causal variants, LD pattern, and the strength of environmental components, all of which can be population specific. Consequently, SNP heritability estimates may change across populations and may change over time within each population [7]. A recent study reports that heterogeneity across sampling populations and time may contribute to part of the “still-missing heritability” [101] as most existing studies are carried out on individuals of European ancestry [12], [59], [72], [74], [98]. Using LMM models on datasets from seven sampling populations, this study discovered that at least 20% of missing heritability for BMI and 37% for years of education can be explained by individual heterogeneity. Therefore, understanding how various genetic, environmental, as well as study design factors influence the estimation of SNP heritability is an important future direction.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
This study was supported by the National Institutes of Health (NIH) Grants R01HG009124 and the National Science Foundation (NSF) Grant DMS1712933.
References
- 1.Visscher P.M., Hill W.G., Wray N.R. Heritability in the genomics era—concepts and misconceptions. Nat Rev Genet. 2008;9(4):255–266. doi: 10.1038/nrg2322. [DOI] [PubMed] [Google Scholar]
- 2.Eaves L.J., Last K.A., Young P.A., Martin N.G. Model-fitting approaches to the analysis of human behaviour. Heredity. 1978;41(3):249. doi: 10.1038/hdy.1978.101. [DOI] [PubMed] [Google Scholar]
- 3.Keller M.C., Coventry W.L. Quantifying and addressing parameter indeterminacy in the classical twin design. Twin Research and Human Genetics. 2005;8(3):201–213. doi: 10.1375/1832427054253068. [DOI] [PubMed] [Google Scholar]
- 4.Tenesa A., Haley C.S. The heritability of human disease: estimation, uses and abuses. Nat Rev Genet. 2013;14(2):139. doi: 10.1038/nrg3377. [DOI] [PubMed] [Google Scholar]
- 5.J Mayhew A, Meyre D. Assessing the heritability of complex traits in humans: methodological challenges and opportunities. Current genomics. 2017;18(4):332-40. [DOI] [PMC free article] [PubMed]
- 6.Ober C., Vercelli D. Gene–environment interactions in human disease: nuisance or opportunity? Trends Genet. 2011;27(3):107–115. doi: 10.1016/j.tig.2010.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Laird N.M., Lange C. Springer Science & Business Media; 2010. The fundamentals of modern statistical genetics. [Google Scholar]
- 8.Rijsdijk F.V., Sham P.C. Analytic approaches to twin data using structural equation models. Briefings Bioinf. 2002;3(2):119–133. doi: 10.1093/bib/3.2.119. [DOI] [PubMed] [Google Scholar]
- 9.Sham P., Cherny S., Purcell S. Application of genome-wide SNP data for uncovering pairwise relationships and quantitative trait loci. Genetica. 2009;136(2):237–243. doi: 10.1007/s10709-008-9349-4. [DOI] [PubMed] [Google Scholar]
- 10.Falconer DS. Introduction to quantitative genetics. Introduction to quantitative genetics. 1960.
- 11.Silventoinen K., Sammalisto S., Perola M., Boomsma D.I., Cornes B.K., Davis C. Heritability of adult body height: a comparative study of twin cohorts in eight countries. Twin Res Human Genet. 2003;6(5):399–408. doi: 10.1375/136905203770326402. [DOI] [PubMed] [Google Scholar]
- 12.Yang J., Benyamin B., McEvoy B.P., Gordon S., Henders A.K., Nyholt D.R. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 2010;42(7):565. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yang J., Bakshi A., Zhu Z., Hemani G., Vinkhuyzen A.A., Lee S.H. Genetic variance estimation with imputed variants finds negligible missing heritability for human height and body mass index. Nat Genet. 2015;47(10):1114. doi: 10.1038/ng.3390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Eichler E.E., Flint J., Gibson G., Kong A., Leal S.M., Moore J.H. Missing heritability and strategies for finding the underlying causes of complex disease. Nat Rev Genet. 2010;11(6):446. doi: 10.1038/nrg2809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gibson G. Rare and common variants: twenty arguments. Nat Rev Genet. 2012;13(2):135. doi: 10.1038/nrg3118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wray N.R., Yang J., Hayes B.J., Price A.L., Goddard M.E., Visscher P.M. Pitfalls of predicting complex traits from SNPs. Nat Rev Genet. 2013;14(7):507. doi: 10.1038/nrg3457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Witte J.S., Visscher P.M., Wray N.R. The contribution of genetic variants to disease depends on the ruler. Nat Rev Genet. 2014;15(11):765. doi: 10.1038/nrg3786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yang J., Zeng J., Goddard M.E., Wray N.R., Visscher P.M. Concepts, estimation and interpretation of SNP-based heritability. Nat Genet. 2017;49(9):1304. doi: 10.1038/ng.3941. [DOI] [PubMed] [Google Scholar]
- 19.Timpson N.J., Greenwood C.M., Soranzo N., Lawson D.J., Richards J.B. Genetic architecture: the shape of the genetic contribution to human traits and disease. Nat Rev Genet. 2018;19(2):110. doi: 10.1038/nrg.2017.101. [DOI] [PubMed] [Google Scholar]
- 20.Evans L.M., Tahmasbi R., Vrieze S.I., Abecasis G.R., Das S., Gazal S. Comparison of methods that use whole genome data to estimate the heritability and genetic architecture of complex traits. Nat Genet. 2018;50(5):737. doi: 10.1038/s41588-018-0108-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Strandén I., Christensen O.F. Allele coding in genomic evaluation. Genet Select Evol. 2011;43(1):25. doi: 10.1186/1297-9686-43-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhou X., Carbonetto P., Stephens M. Polygenic modeling with Bayesian sparse linear mixed models. PLoS Genet. 2013;9(2) doi: 10.1371/journal.pgen.1003264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.de los Campos G, Vazquez AI, Fernando R, Klimentidis YC, Sorensen D. Prediction of complex human traits using the genomic best linear unbiased predictor. PLoS genetics. 2013;9(7). [DOI] [PMC free article] [PubMed]
- 24.Visscher P.M. Sizing up human height variation. Nat Genet. 2008;40(5):489. doi: 10.1038/ng0508-489. [DOI] [PubMed] [Google Scholar]
- 25.Weedon M.N., Lango H., Lindgren C.M., Wallace C., Evans D.M., Mangino M. Genome-wide association analysis identifies 20 loci that influence adult height. Nat Genet. 2008;40(5):575. doi: 10.1038/ng.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lettre G., Jackson A.U., Gieger C., Schumacher F.R., Berndt S.I., Sanna S. Identification of ten loci associated with height highlights new biological pathways in human growth. Nat Genet. 2008;40(5):584. doi: 10.1038/ng.125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gudbjartsson D.F., Walters G.B., Thorleifsson G., Stefansson H., Halldorsson B.V., Zusmanovich P. Many sequence variants affecting diversity of adult human height. Nat Genet. 2008;40(5):609. doi: 10.1038/ng.122. [DOI] [PubMed] [Google Scholar]
- 28.Yi N., Xu S. Bayesian LASSO for quantitative trait loci mapping. Genetics. 2008;179(2):1045–1055. doi: 10.1534/genetics.107.085589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hoggart C.J., Whittaker J.C., De Iorio M., Balding D.J. Simultaneous analysis of all SNPs in genome-wide and re-sequencing association studies. PLoS Genet. 2008;4(7) doi: 10.1371/journal.pgen.1000130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wu T.T., Chen Y.F., Hastie T., Sobel E., Lange K. Genome-wide association analysis by lasso penalized logistic regression. Bioinformatics. 2009;25(6):714–721. doi: 10.1093/bioinformatics/btp041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Logsdon B.A., Hoffman G.E., Mezey J.G. A variational Bayes algorithm for fast and accurate multiple locus genome-wide association analysis. BMC Bioinf. 2010;11(1):58. doi: 10.1186/1471-2105-11-58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Guan Y., Stephens M. Bayesian variable selection regression for genome-wide association studies and other large-scale problems. Annals Appl Statist. 2011;5(3):1780–1815. [Google Scholar]
- 33.Carbonetto P., Stephens M. Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies. Bayesian Anal. 2012;7(1):73–108. [Google Scholar]
- 34.Pankow J.S., Folsom A.R., Cushman M., Borecki I.B., Hopkins P.N., Eckfeldt J.H. Familial and genetic determinants of systemic markers of inflammation: the NHLBI family heart study. Atherosclerosis. 2001;154(3):681–689. doi: 10.1016/s0021-9150(00)00586-4. [DOI] [PubMed] [Google Scholar]
- 35.Lange L.A., Burdon K., Langefeld C.D., Liu Y., Beck S.R., Rich S.S. Heritability and expression of C-reactive protein in type 2 diabetes in the Diabetes Heart Study. Ann Hum Genet. 2006;70(6):717–725. doi: 10.1111/j.1469-1809.2006.00280.x. [DOI] [PubMed] [Google Scholar]
- 36.Yang J., Lee S.H., Goddard M.E., Visscher P.M. GCTA: a tool for genome-wide complex trait analysis. Am J Human Genet. 2011;88(1):76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhou X., Stephens M. Genome-wide efficient mixed-model analysis for association studies. Nat Genet. 2012;44(7):821. doi: 10.1038/ng.2310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wu Z., Sun Y., He S., Cho J., Zhao H., Jin J. Detection boundary and higher criticism approach for rare and weak genetic effects. Annal Appl Statist. 2014;8(2):824–851. [Google Scholar]
- 39.Boyle E.A., Li Y.I., Pritchard J.K. An expanded view of complex traits: from polygenic to omnigenic. Cell. 2017;169(7):1177–1186. doi: 10.1016/j.cell.2017.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhu X., Stephens M. Bayesian large-scale multiple regression with summary statistics from genome-wide association studies. Annal Appl Statist. 2017;11(3):1561. doi: 10.1214/17-aoas1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Speed D., Hemani G., Johnson M.R., Balding D.J. Improved heritability estimation from genome-wide SNPs. Am J Human Genet. 2012;91(6):1011–1021. doi: 10.1016/j.ajhg.2012.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Speed D, Cai N, Johnson MR, Nejentsev S, Balding DJ, Consortium U. Reevaluation of SNP heritability in complex human traits. Nature genetics. 2017;49(7):986. [DOI] [PMC free article] [PubMed]
- 43.Hayes B., Goddard M. Prediction of total genetic value using genome-wide dense marker maps. Genetics. 2001;157(4):1819–1829. doi: 10.1093/genetics/157.4.1819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Verbyla KL, Bowman PJ, Hayes BJ, Goddard ME, editors. Sensitivity of genomic selection to using different prior distributions. BMC proceedings; 2010: BioMed Central. [DOI] [PMC free article] [PubMed]
- 45.Verbyla K.L., Hayes B.J., Bowman P.J., Goddard M.E. Accuracy of genomic selection using stochastic search variable selection in Australian Holstein Friesian dairy cattle. Genet Res. 2009;91(5):307–311. doi: 10.1017/S0016672309990243. [DOI] [PubMed] [Google Scholar]
- 46.Hayes B.J., Pryce J., Chamberlain A.J., Bowman P.J., Goddard M.E. Genetic architecture of complex traits and accuracy of genomic prediction: coat colour, milk-fat percentage, and type in Holstein cattle as contrasting model traits. PLoS Genet. 2010;6(9) doi: 10.1371/journal.pgen.1001139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Habier D., Fernando R.L., Kizilkaya K., Garrick D.J. Extension of the Bayesian alphabet for genomic selection. BMC Bioinf. 2011;12(1):186. doi: 10.1186/1471-2105-12-186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Park T., Casella G. The bayesian lasso. J Am Stat Assoc. 2008;103(482):681–686. [Google Scholar]
- 49.Moser G., Lee S.H., Hayes B.J., Goddard M.E., Wray N.R., Visscher P.M. Simultaneous discovery, estimation and prediction analysis of complex traits using a Bayesian mixture model. PLoS Genet. 2015;11(4) doi: 10.1371/journal.pgen.1004969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zeng J., De Vlaming R., Wu Y., Robinson M.R., Lloyd-Jones L.R., Yengo L. Signatures of negative selection in the genetic architecture of human complex traits. Nat Genet. 2018;50(5):746. doi: 10.1038/s41588-018-0101-4. [DOI] [PubMed] [Google Scholar]
- 51.Zeng P., Zhou X. Non-parametric genetic prediction of complex traits with latent Dirichlet process regression models. Nat Commun. 2017;8(1):456. doi: 10.1038/s41467-017-00470-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gamazon E.R., Wheeler H.E., Shah K.P., Mozaffari S.V., Aquino-Michaels K., Carroll R.J. A gene-based association method for mapping traits using reference transcriptome data. Nat Genet. 2015;47(9):1091. doi: 10.1038/ng.3367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Gusev A., Ko A., Shi H., Bhatia G., Chung W., Penninx B.W. Integrative approaches for large-scale transcriptome-wide association studies. Nat Genet. 2016;48(3):245. doi: 10.1038/ng.3506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Falconer D.S. The inheritance of liability to certain diseases, estimated from the incidence among relatives. Ann Hum Genet. 1965;29(1):51–76. [Google Scholar]
- 55.Lee S.H., Wray N.R., Goddard M.E., Visscher P.M. Estimating missing heritability for disease from genome-wide association studies. Am J Human Genet. 2011;88(3):294–305. doi: 10.1016/j.ajhg.2011.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Dempster E.R., Lerner I.M. Heritability of threshold characters. Genetics. 1950;35(2):212. doi: 10.1093/genetics/35.2.212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chen G.-B. Estimating heritability of complex traits from genome-wide association studies using IBS-based Haseman-Elston regression. Front Genet. 2014;5:107. doi: 10.3389/fgene.2014.00107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Golan D., Lander E.S., Rosset S. Measuring missing heritability: inferring the contribution of common variants. Proc Natl Acad Sci. 2014;111(49):E5272–E5281. doi: 10.1073/pnas.1419064111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zhou X. A unified framework for variance component estimation with summary statistics in genome-wide association studies. Annal Appl Statist. 2017;11(4):2027. doi: 10.1214/17-AOAS1052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Weissbrod O., Flint J., Rosset S. Estimating SNP-based heritability and genetic correlation in case-control studies directly and with summary statistics. Am J Human Genet. 2018;103(1):89–99. doi: 10.1016/j.ajhg.2018.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tung J., Zhou X., Alberts S.C., Stephens M., Gilad Y. The genetic architecture of gene expression levels in wild baboons. Elife. 2015;4 doi: 10.7554/eLife.04729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Price AL, Helgason A, Thorleifsson G, McCarroll SA, Kong A, Stefansson K. Single-Tissue and Cross-Tissue Heritability of Gene Expression Via Identity-by-Descent in Related or Unrelated Individuals. Plos Genet. 2011;7(2). [DOI] [PMC free article] [PubMed]
- 63.Wright F.A., Sullivan P.F., Brooks A.I., Zou F., Sun W., Xia K. Heritability and genomics of gene expression in peripheral blood. Nat Genet. 2014;46(5):430–437. doi: 10.1038/ng.2951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Monks S.A., Leonardson A., Zhu H., Cundiff P., Pietrusiak P., Edwards S. Genetic inheritance of gene expression in human cell lines. Am J Hum Genet. 2004;75(6):1094–1105. doi: 10.1086/426461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Emilsson V., Thorleifsson G., Zhang B., Leonardson A.S., Zink F., Zhu J. Genetics of gene expression and its effect on disease. Nature. 2008;452(7186):423–U2. doi: 10.1038/nature06758. [DOI] [PubMed] [Google Scholar]
- 66.Banovich N.E., Lan X., McVicker G., van de Geijn B., Degner J.F., Blischak J.D. Methylation QTLs Are Associated with Coordinated Changes in Transcription Factor Binding, Histone Modifications, and Gene Expression Levels. Plos Genet. 2014;10(9) doi: 10.1371/journal.pgen.1004663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.McRae A.F., Powell J.E., Henders A.K., Bowdler L., Hemani G., Shah S. Contribution of genetic variation to transgenerational inheritance of DNA methylation. Genome Biol. 2014;15(5):R73. doi: 10.1186/gb-2014-15-5-r73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Bell J.T., Tsai P.C., Yang T.P., Pidsley R., Nisbet J., Glass D. Epigenome-Wide Scans Identify Differentially Methylated Regions for Age and Age-Related Phenotypes in a Healthy Ageing Population. Plos Genet. 2012;8(4):189–200. doi: 10.1371/journal.pgen.1002629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Cheng C.S., Gate R.E. Aiden AP. Genetic determinants of co-accessible chromatin regions in T cell activation across humans. BioRxiv. 2017 doi: 10.1038/s41588-018-0156-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wheeler H.E., Shah K.P., Brenner J., Garcia T., Aquino-Michaels K., Cox N.J. Survey of the Heritability and Sparse Architecture of Gene Expression Traits across Human Tissues. Plos Genet. 2016;12(11) doi: 10.1371/journal.pgen.1006423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Sun S., Zhu J., Mozaffari S., Ober C., Chen M., Zhou X. Heritability estimation and differential analysis of count data with generalized linear mixed models in genomic sequencing studies. Bioinformatics. 2018;35(3):487–496. doi: 10.1093/bioinformatics/bty644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Bulik-Sullivan B.K., Loh P.-R., Finucane H.K., Ripke S., Yang J., Patterson N. LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat Genet. 2015;47(3):291. doi: 10.1038/ng.3211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Robbins H, Monro S. A stochastic approximation method. The annals of mathematical statistics. 1951:400-7.
- 74.Speed D., Balding D.J. SumHer better estimates the SNP heritability of complex traits from summary statistics. Nat Genet. 2019;51(2):277. doi: 10.1038/s41588-018-0279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Genomes Project C, Abecasis GR, Auton A, Brooks LD, DePristo MA, Durbin RM, et al. An integrated map of genetic variation from 1,092 human genomes. Nature. 2012;491(7422):56-65. [DOI] [PMC free article] [PubMed]
- 76.Kircher M., Witten D.M., Jain P., O'Roak B.J., Cooper G.M., Shendure J. A general framework for estimating the relative pathogenicity of human genetic variants. Nat Genet. 2014;46(3):310–315. doi: 10.1038/ng.2892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Consortium GT. The Genotype-Tissue Expression (GTEx) pilot analysis: multitissue gene regulation in humans. Science. 2015;348(6235):648-60. [DOI] [PMC free article] [PubMed]
- 78.Roadmap Epigenomics C., Kundaje A., Meuleman W., Ernst J., Bilenky M., Yen A. Integrative analysis of 111 reference human epigenomes. Nature. 2015;518(7539):317–330. doi: 10.1038/nature14248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Consortium EP An integrated encyclopedia of DNA elements in the human genome. Nature. 2012;489(7414):57. doi: 10.1038/nature11247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Carithers L.J., Moore H.M. The Genotype-Tissue Expression (GTEx) Project. Biopreserv Biobanking. 2015;13(5):307–308. doi: 10.1089/bio.2015.29031.hmm. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Dixon J.R., Jung I., Selvaraj S., Shen Y., Antosiewicz-Bourget J.E., Lee A.Y. Chromatin architecture reorganization during stem cell differentiation. Nature. 2015;518(7539):331–336. doi: 10.1038/nature14222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Kellis M., Wold B., Snyder M.P., Bernstein B.E., Kundaje A., Marinov G.K. Defining functional DNA elements in the human genome. PNAS. 2014;111(17):6131–6138. doi: 10.1073/pnas.1318948111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Kumar P., Henikoff S., Ng P.C. Predicting the effects of coding non-synonymous variants on protein function using the SIFT algorithm. Nat Protoc. 2009;4(7):1073–1081. doi: 10.1038/nprot.2009.86. [DOI] [PubMed] [Google Scholar]
- 84.Adzhubei I, Jordan DM, Sunyaev SR. Predicting functional effect of human missense mutations using PolyPhen-2. Current protocols in human genetics / editorial board, Jonathan L Haines [et al]. 2013;Chapter 7:Unit7 20. [DOI] [PMC free article] [PubMed]
- 85.Pickrell J.K., Marioni J.C., Pai A.A., Degner J.F., Engelhardt B.E., Nkadori E. Understanding mechanisms underlying human gene expression variation with RNA sequencing. Nature. 2010;464(7289):768–772. doi: 10.1038/nature08872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Tung J, Zhou X, Alberts SC, Stephens M, Gilad Y. The genetic architecture of gene expression levels in wild baboons. eLife. 2015;4. [DOI] [PMC free article] [PubMed]
- 87.Pique-Regi R., Degner J.F., Pai A.A., Gaffney D.J., Gilad Y., Pritchard J.K. Accurate inference of transcription factor binding from DNA sequence and chromatin accessibility data. Genome Res. 2011;21(3):447–455. doi: 10.1101/gr.112623.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Ernst J., Kellis M. ChromHMM: automating chromatin-state discovery and characterization. Nat Methods. 2012;9(3):215–216. doi: 10.1038/nmeth.1906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.McVicker G., van de Geijn B., Degner J.F., Cain C.E., Banovich N.E., Raj A. Identification of Genetic Variants That Affect Histone Modifications in Human Cells. Science. 2013;342(6159):747–749. doi: 10.1126/science.1242429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Cooper G.M., Stone E.A., Asimenos G., Program N.C.S., Green E.D., Batzoglou S. Distribution and intensity of constraint in mammalian genomic sequence. Genome Res. 2005;15(7):901–913. doi: 10.1101/gr.3577405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Ionita-Laza I., McCallum K., Xu B., Buxbaum J.D. A spectral approach integrating functional genomic annotations for coding and noncoding variants. Nat Genet. 2016;48(2):214–220. doi: 10.1038/ng.3477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Pickrell J.K. Joint analysis of functional genomic data and genome-wide association studies of 18 human traits. Am J Hum Genet. 2014;94(4):559–573. doi: 10.1016/j.ajhg.2014.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Schork A.J., Thompson W.K., Pham P., Torkamani A., Roddey J.C., Sullivan P.F. All SNPs are not created equal: genome-wide association studies reveal a consistent pattern of enrichment among functionally annotated SNPs. PLoS Genet. 2013;9(4) doi: 10.1371/journal.pgen.1003449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Gusev A., Lee S.H., Trynka G., Finucane H., Vilhjalmsson B.J., Xu H. Partitioning heritability of regulatory and cell-type-specific variants across 11 common diseases. Am J Hum Genet. 2014;95(5):535–552. doi: 10.1016/j.ajhg.2014.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Kichaev G., Yang W.Y., Lindstrom S., Hormozdiari F., Eskin E., Price A.L. Integrating functional data to prioritize causal variants in statistical fine-mapping studies. PLoS Genet. 2014;10(10) doi: 10.1371/journal.pgen.1004722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Lee S.H., Yang J., Chen G.-B., Ripke S., Stahl E.A., Hultman C.M. Estimation of SNP heritability from dense genotype data. Am J Human Genet. 2013;93(6):1151–1155. doi: 10.1016/j.ajhg.2013.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Finucane H.K., Bulik-Sullivan B., Gusev A., Trynka G., Reshef Y., Loh P.-R. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat Genet. 2015;47(11):1228. doi: 10.1038/ng.3404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Hao X., Zeng P., Zhang S., Zhou X. Identifying and exploiting trait-relevant tissues with multiple functional annotations in genome-wide association studies. PLoS Genet. 2018;14(1) doi: 10.1371/journal.pgen.1007186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.van Rheenen W., Peyrot W.J., Schork A.J., Lee S.H., Wray N.R. Genetic correlations of polygenic disease traits: from theory to practice. Nat Rev Genet. 2019;1 doi: 10.1038/s41576-019-0137-z. [DOI] [PubMed] [Google Scholar]
- 100.Manolio T.A., Collins F.S., Cox N.J., Goldstein D.B., Hindorff L.A., Hunter D.J. Finding the missing heritability of complex diseases. Nature. 2009;461(7265):747. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Tropf F.C., Lee S.H., Verweij R.M., Stulp G., Van Der Most P.J., De Vlaming R. Hidden heritability due to heterogeneity across seven populations. Nat Hum Behav. 2017;1(10):757–765. doi: 10.1038/s41562-017-0195-1. [DOI] [PMC free article] [PubMed] [Google Scholar]