Abstract

Titanium dioxide (TiO2) photocatalysts in the form of thin films are of great interest due to their tunable optical band gaps, Eg’s, which are promising candidates for applications of visible-light photocatalytic activities. Previous studies have shown that processing conditions, dopant types and concentrations, and different combinations of the two have great impacts on structural, microscopic, and optical properties of TiO2 thin films. The lattice parameters and surface area are strongly correlated with Eg values, which are conventionally simulated and studied through first-principle models, but these models require significant computational resources, particularly in complex situations involving codoping and various surface areas. In this study, we develop the Gaussian process regression model for predictions of anatase TiO2 photocatalysts’ energy band gaps based on the lattice parameters and surface area. We explore 60 doped-TiO2 anatase photocatalysts with Eg’s between 2.280 and 3.250 eV. Our model demonstrates a high correlation coefficient of 99.99% between predicted Eg’s and their experimental values and high prediction accuracy as reflected through the prediction root-mean-square error and mean absolute error being 0.0012 and 0.0010% of the average experimental Eg, respectively. This modeling method is simple and straightforward and does not require a lot of parameters, which are advantages for applications and computations.
1. Introduction
Titanium dioxide, TiO2, shows great promises in several environmental applications due to its distinct properties over other materials, such as the nontoxicity, low cost, ease of preparation, water insolubility, superior acid resistance, and superhydrophilicity.1 Examples of application areas include the air purification, water treatment, renewable energy processes, solar cells, and conversion of CO2 to hydrocarbons.2−6 Among TiO2 polymorphs, anatase TiO2 is preferred over brookite and rutile because it has a higher surface energy of its {001} facets and better photocatalytic activities and is more stable than the other two forms. However, anatase TiO2 has a relatively wide band gap (∼3.20 eV), which only allows the material to absorb UV light. As UV light only accounts for merely 5% of solar photons, the large band gap of TiO2 limits the quantum yield in light-to-energy conversion.7−10
One effective way to modify the band gap of anatase TiO2 is chemical doping with foreign elements. Different elements, metals and nonmetals, affect the band gap in different ways. Metal ions, such as Zr, Cr, and W, are reported to inhibit the anatase-to-rutile phase transformation.11,12 Transition metals, such as Cu, and rare-earth metals, such as La, lead to the lattice deformation and the formation of oxygen vacancies, resulting in an impurity state in the TiO2 band gap, which improves the absorption of visible light by narrowing the band gap.13,14 Nonmetal doping, such as the nitrogen incorporation into the TiO2 lattice or on its surface, has been reported to benefit the improvement of photoefficiency under UV/visible light.1 Both single doping and codoping methods have been applied to the TiO2 photocatalyst fabrication by incorporating various elements into the crystal structure.10,13−24 The addition of foreign elements results in lattice distortions and changes in the Eg due to electronegativities, ionic radius differences, and introductions of impurity states.25 In addition to chemical doping, various preparation methods of TiO2 photocatalysts can influence the band gap narrowing differently. Typical fabrication methods include the coprecipitation, sol–gel process, spray pyrolysis, hydrothermal process, low-temperature solvothermal method, and plasma treatment.13,18,20,21 Processing parameters, including but not limited to the precursor materials, substrate temperature, deposition rate, and annealing temperature, affect the crystal structure and microstructure significantly. As a result, lattice parameters and the surface area are changed upon different combinations of synthesis steps.1,25−29 Previous research has demonstrated that the photocatalytic activity of TiO2 strongly depends on its phase structure, crystallinity, and morphology.30,31 Among various phases of TiO2, anatase is reported to have a better photocatalytic activity than the other two polymorphs.32 A good crystallinity is required to achieve the formation of an optimal amount of electron traps, which affects the photocatalytic efficiency. Lattice deformation caused by nonequilibrium crystal growth and chemical doping affects the electronic structure by modifying orbital hybridization and introducing additionally available electrons for conduction.33,34 Both the crystallinity and lattice deformation can be characterized by lattice parameters. Furthermore, other crystal defects, such as residual strain, impurities, dislocation densities, and defect energy, have significant influences on band gap structures and are correlated with surface morphology, which can be characterized by the surface area.35,36 High surface areas also promote quantum confinement effects in the semiconductor space charge and surface reaction, which greatly increase the photocatalytic efficiency.37 For example, N-doped TiO2 obtained by the reduction-nitridation method via the nonthermal plasma treatment is more favorable than the simple nitridation treatment, as the former promotes Ns doping and narrows the band gap more efficiently.38 Further, the recombination of photogenerated electron-hole pairs limits the photocatalytic activity. Some research has been carried out to reduce the recombination rate of the photoelectron–hole pairs and increase the interfacial charge-transfer efficiency. The surface microstructure, mainly characterized by the surface area, shows additional influences on photocatalyst quality and optical performance. The surface area is correlated with the residual strain, dislocation density, crystallinity, defect energy, impurities, and other structural defects and is shown to contribute to the band gap of TiO2 structures.35,36 Hence, with various synthesis methods and dopant selection, combination possibilities of TiO2 with the tunable Eg are enormous. It is, therefore, of great importance to investigate correlations among the tunability of the Eg, lattice parameters, and the surface area. Qualitative analysis on the effect of dopant types and levels on the Eg of TiO2 photocatalysts has been conducted through experiments.10,13−24 Quantitative analysis through thermodynamics models and first-principle models has been utilized to aid the understanding of the optical performance of these materials and facilitate the tuning of doped-TiO2Eg.39,40 However, these models require a significant amount of data inputs, such as variables for equations of state and orbital configurations, which can only be obtained by extensive measurements. The requirement of computational power also increases significantly when it comes to the codoping situation.
In this work, the Gaussian process regression (GPR) model is developed to elucidate the statistical relationship among the lattice parameters, a (Å) and c (Å), surface area, and energy band gap for doped-TiO2 anatase photocatalysts. Among the three descriptors, lattice parameters are structural parameters as direct representatives of the phase structure and crystallinity, and the surface area is the morphological parameter. Empirical studies show that crystal defects introduced by doping, such as foreign ions at substitutional or interstitial lattice positions, can shift the band gap toward the visible-light region. Depending on ionic radii, electronegativities, and valence, however, specific types and extents of crystal defects are difficult to estimate. Experimentally, crystal defects require significant amounts of analytical work to characterize, which eventually may be used as inputs into further theoretical work. First-principle simulations calculate the probability of each type of defects and their effects on the band gap tuning based on known atomic interactions, but these methods are known to be susceptible of underestimations of Eg values, particularly when the TiO2 lattices are doped with transition metals.41,42 Besides, effects of the morphological parameter, the surface area, on Eg values are difficult to incorporate into first-principle simulations. Although a high surface area is generally preferred, it is hard to quantify the required surface area while also considering lattice deformation in a practical application. Our GPR model, however, avoids depending on quantum mechanics theories for calculations, which may be susceptible to over- or underestimations due to unknown atomic interactions. In this method, the known experimental lattice parameters are used as macroscopic descriptors to find the relationship with experimentally measured Eg values. The model generalizes well in the presence of a few descriptive features, where intelligent algorithms are able to learn and recognize the patterns. This modeling approach demonstrates a high degree of accuracy and stability, contributing to efficient and low-cost estimations of the energy band gap of anatase TiO2 and understandings of which are based on the lattice parameters and surface area. As one of the computational intelligence techniques, the GPR model has already been utilized in other materials systems to predict significant physical parameters in different fields of applications.43−45 This model can serve as a guideline for searching for anatase TiO2 with tunable Eg when a specific range of band gaps is required for a practical application. It can also be used as part of machine learning to aid understandings of the effects of crystal structures and morphology on the optical performance of TiO2 photocatalysts.
The remaining of this work is organized as follows. Section 2 describes the data. Section 3 presents and discusses results, and Section 4 concludes. Section 5 contains details of the GPR model.
2. Description of Data Set
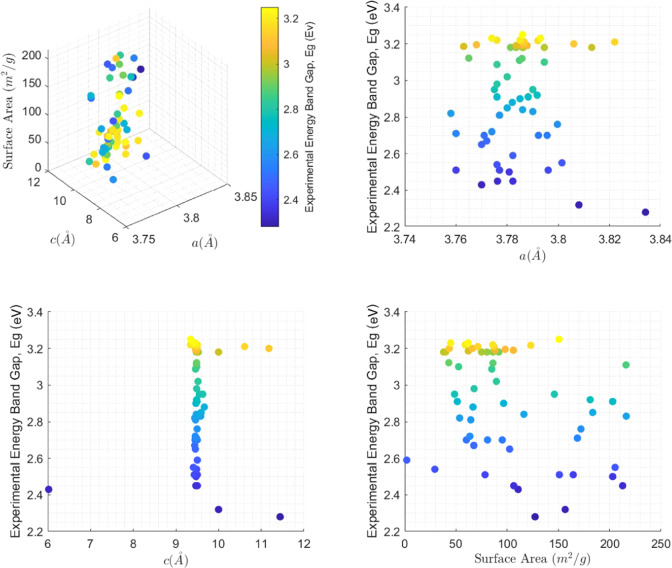
The experimental data used, shown in Table 1 (columns 1–5), are obtained from the literature.10,13−24 The data set covers a wide range of anatase TiO2 that are prepared through different synthesis methods and doped with various elements. A total of 60 TiO2 photocatalysts with the energy band gap, Eg, ranging from 2.280 to 3.250 eV are explored. The lattice parameters, a (Å) and c (Å), and measured surface area are used as descriptors. Eg values are calculated using the Tauc relationship13,22 after acquiring the transmittance data by the UV–vis spectrometer in each reference in Table 1. Data visualization in Figure 1 reveals nonlinear relationships, which are modeled through the GPR.
Table 1. Experimental Data and Predictionsa.
| sample | a (Å) | c (Å) | surface area (m2/g) | Eg (eV) | prediction | reference |
|---|---|---|---|---|---|---|
| pure TiO2 | 3.7650 | 9.4860 | 43.00 | 3.122 | 3.12198 | (21) |
| 1.0% Cu–3.5% In–TiO2 | 3.7760 | 9.4620 | 85.00 | 3.087 | 3.08695 | (21) |
| 5 mol % Cu-doped TiO2 (700°C) | 3.7700 | 6.0190 | 110.70 | 2.430 | 2.43004 | (15) |
| 5 mol % Cu-doped TiO2 (600°C) | 3.7960 | 9.4310 | 150.90 | 2.510 | 2.51004 | (15) |
| 5 mol % Cu, 15 mol % Zr co-doped TiO2 (700 °C) | 3.8340 | 11.4420 | 127.20 | 2.280 | 2.28005 | (15) |
| 5 mol % Cu, 15 mol % Zr co-doped TiO2 (600 °C) | 3.8080 | 10.0000 | 156.60 | 2.320 | 2.32005 | (15) |
| undoped-TiO2 | 3.7900 | 9.6300 | 146.07 | 2.950 | 2.94999 | (20) |
| S-doped TiO2 (K2S2O8/Ti = 0.25) | 3.7800 | 9.5900 | 183.45 | 2.850 | 2.84999 | (20) |
| S-doped TiO2 (K2S2O8/Ti = 0.5) | 3.7900 | 9.5800 | 216.22 | 2.830 | 2.83001 | (20) |
| pure TiO2 | 3.7740 | 9.4480 | 44.80 | 3.230 | 3.22994 | (10) |
| S0.05/TiO2 | 3.7750 | 9.5480 | 48.60 | 2.950 | 2.95000 | (10) |
| S0.05V0.001/TiO2 | 3.7770 | 9.4610 | 64.40 | 2.810 | 2.81002 | (10) |
| S0.05Fe0.001/TiO2 | 3.7820 | 9.6670 | 66.60 | 2.880 | 2.88001 | (10) |
| S0.05Zn0.001/TiO2 | 3.7930 | 9.4140 | 61.80 | 3.230 | 3.22997 | (10) |
| undoped-TiO2 | 3.7848 | 9.4826 | 216.00 | 3.110 | 3.10996 | (19) |
| V-doped TiO2 | 3.7882 | 9.4949 | 203.00 | 2.910 | 2.91000 | (19) |
| N-doped TiO2 | 3.7917 | 9.4868 | 181.00 | 2.920 | 2.91999 | (19) |
| V,N co-doped TiO2 | 3.7996 | 9.4976 | 172.00 | 2.760 | 2.76000 | (19) |
| pure TiO2 | 3.7860 | 9.5260 | 80.37 | 3.180 | 3.17999 | (13) |
| N–TiO2 | 3.7850 | 9.4710 | 96.49 | 2.900 | 2.90003 | (13) |
| La–TiO2 | 3.7800 | 9.5180 | 89.42 | 3.020 | 3.02000 | (13) |
| N/La–TiO2 | 3.7860 | 9.4780 | 116.25 | 2.840 | 2.84001 | (13) |
| undoped-TiO2 | 3.7760 | 9.4860 | 51.30 | 2.910 | 2.91001 | (18) |
| Ce-doped TiO2, “C0.03T1” | 3.7740 | 9.4540 | 63.52 | 2.720 | 2.72002 | (18) |
| Ce-doped TiO2, “C0.01T1” | 3.7720 | 9.4420 | 67.43 | 2.670 | 2.67002 | (18) |
| Ce-doped TiO2, “C0.05T1” | 3.7710 | 9.4500 | 60.14 | 2.700 | 2.70002 | (18) |
| Ce,Si co-doped TiO2, “C0.01T1S0.05” | 3.7700 | 9.4570 | 102.41 | 2.650 | 2.65006 | (18) |
| Ce,Si co-doped TiO2, “C0.01T1S0.5” | 3.7600 | 9.4620 | 164.48 | 2.510 | 2.51005 | (18) |
| Ce,Si co-doped TiO2, “C0.01T1S1” | 3.7600 | 9.4810 | 168.54 | 2.710 | 2.70997 | (18) |
| Ce-doped TiO2, “C0.005T1” | 3.7580 | 9.4420 | 53.57 | 2.820 | 2.82001 | (18) |
| undoped-TiO2 (475 °C) | 3.8220 | 10.6100 | 71.40 | 3.210 | 3.20997 | (14) |
| Ce(2%)Co(4%)–TiO2 (600 °C) | 3.8060 | 11.1800 | 43.60 | 3.200 | 3.19997 | (14) |
| Ce(2%)Co(4%)–TiO2 (700 °C) | 3.8130 | 10.0000 | 39.80 | 3.180 | 3.17997 | (14) |
| undoped-TiO2 | 3.7760 | 9.3410 | 85.93 | 3.220 | 3.21996 | (24) |
| 1% Nb-doped TiO2 | 3.7860 | 9.3470 | 150.61 | 3.250 | 3.24996 | (24) |
| pure TiO2 | 3.7760 | 9.4860 | 67.70 | 2.980 | 2.97994 | (17) |
| Ag-doped TiO2(400 °C) | 3.7822 | 9.5023 | 106.37 | 2.450 | 2.45006 | (17) |
| Ag-doped TiO2 (500 °C) | 3.7770 | 9.5010 | 78.40 | 2.510 | 2.51009 | (17) |
| Ag-doped TiO2 (600 °C) | 3.7760 | 9.4860 | 29.33 | 2.540 | 2.54004 | (17) |
| Ag-doped TiO2 (700 °C) | 3.7822 | 9.5023 | 1.93 | 2.590 | 2.59002 | (17) |
| undoped-TiO2 | 3.7945 | 9.5079 | 37.90 | 3.180 | 3.17997 | (16) |
| 1 wt % Mn-doped TiO2 | 3.7945 | 9.4860 | 52.59 | 3.100 | 3.10000 | (16) |
| 5 wt % Mn-doped TiO2 | 3.7956 | 9.4993 | 80.77 | 2.700 | 2.70002 | (16) |
| 10 wt % Mn-doped TiO2 | 3.7922 | 9.4546 | 95.19 | 2.700 | 2.70003 | (16) |
| 20 wt % Mn-doped TiO2 (TMA400) | 3.7762 | 9.4681 | 212.71 | 2.450 | 2.45003 | (16) |
| 20 wt % Mn-doped TiO2 (TMB400) | 3.7808 | 9.4720 | 203.00 | 2.500 | 2.50004 | (16) |
| 20 wt % Mn-doped TiO2 (TMN400) | 3.8014 | 9.4105 | 205.36 | 2.550 | 2.55003 | (16) |
| pure TiO2 | 3.7835 | 9.4907 | 86.11 | 3.180 | 3.18000 | (22) |
| 0.05 wt % W-doped TiO2 | 3.7858 | 9.4862 | 88.14 | 3.190 | 3.18997 | (22) |
| 0.1 wt % W-doped TiO2 | 3.7858 | 9.4817 | 86.08 | 3.120 | 3.12004 | (22) |
| 0.5 wt % W-doped TiO2 | 3.7813 | 9.4773 | 91.71 | 3.180 | 3.17996 | (22) |
| 1 wt % W-doped TiO2 | 3.7835 | 9.4817 | 88.18 | 3.190 | 3.18998 | (22) |
| pure TiO2 | 3.7850 | 9.5021 | 59.00 | 3.220 | 3.21998 | (23) |
| 0.1 mol % Sn-doped TiO2 | 3.7864 | 9.4958 | 66.00 | 3.200 | 3.19999 | (23) |
| 0.5 mol % Sn-doped TiO2 | 3.7863 | 9.4927 | 75.00 | 3.180 | 3.18000 | (23) |
| 1 mol % Sn-doped TiO2 | 3.7866 | 9.4915 | 87.00 | 3.210 | 3.20997 | (23) |
| 3 mol % Sn-doped TiO2 | 3.7878 | 9.4884 | 106.00 | 3.190 | 3.18996 | (23) |
| 2.0% In–TiO2 | 3.7630 | 9.4740 | 62.00 | 3.186 | 3.18597 | (21) |
| 3.5% In–TiO2 | 3.7680 | 9.4620 | 98.00 | 3.195 | 3.19494 | (21) |
| 5.0% In–TiO2 | 3.7920 | 9.4360 | 123.00 | 3.217 | 3.21696 | (21) |
| minimum | 3.7580 | 6.0190 | 1.93 | 2.280 | 2.28005 | |
| mean | 3.7843 | 9.5220 | 101.17 | 2.910 | 2.90962 | |
| median | 3.7842 | 9.4860 | 86.56 | 2.935 | 2.93499 | |
| maximum | 3.8340 | 11.4420 | 216.22 | 3.250 | 3.24996 | |
| standard deviation | 0.0141 | 0.5906 | 53.67 | 0.285 | 0.28542 | |
| correlation coefficient with Eg | 0.76% | 10.59% | –34.18% | 99.99% |
Figure 1.
Data visualization.
3. Results and Discussion
3.1. Computational Methodology
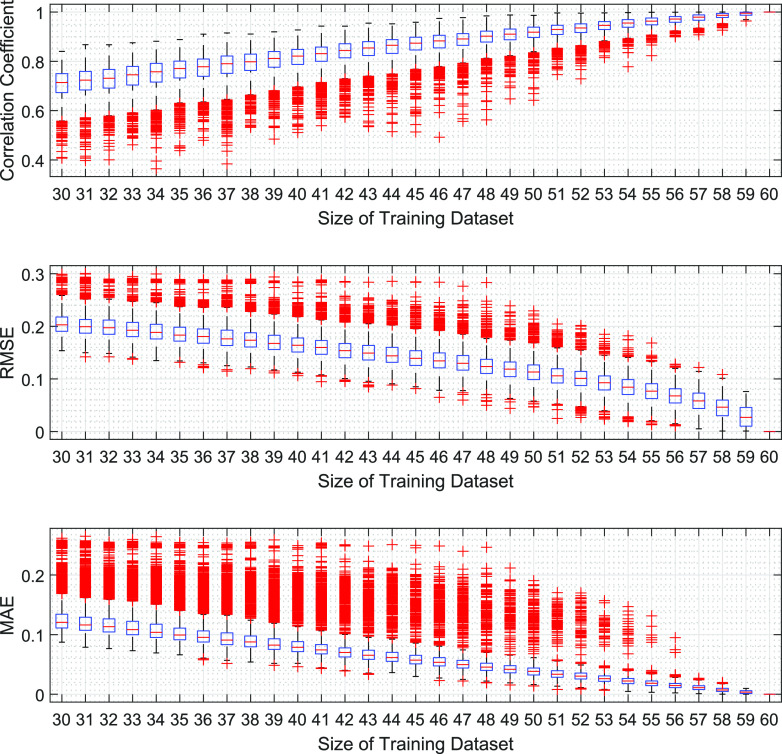
MATLAB is utilized for computations and simulations in this work. The relationship between model performance and training data sizes is investigated in Figure 2, which shows the benefit of training the GPR using all observations. The stability of the GPR approach is confirmed by bootstrap analysis in Section 3.3.
Figure 2.
Model performance and training data sizes. When the training data set size is between 30 and 57, 2000 random subsamples are drawn without replacements from the whole sample for model training. When the training data set size is 58, 59, or 60, 60C58, 60C59, or 60C60 subsamples are drawn without replacements from the whole sample based on exhaustive sampling for model training. Each trained model based on a certain subsample is used to score the whole sample and obtain the associated model performance. The GPR here uses the exponential kernel and constant basis function, with standardized predictors. Given a model performance measure, box plots show the median, 25th percentile, and 75th percentile. The whiskers extend to the most extreme values (i.e., ±2.7 standard deviation coverage) not considered as outliers, and the outliers are plotted using the “+” symbol.
3.2. Prediction Accuracy
Metal ions, such as Sn4+, Zr4+, and Cu2+, are incorporated into the anatase structure by the substitution of Ti4+ due to similar ionic radii, while Ag+ is favorably stabilized at an interstitial site. Nonmetal ions, such as N and S, are incorporated into the lattice and coexisted at both substitutional and interstitial sites. Changes in lattice parameters depend on ionic radii, electronegativities, valence, and incorporation mechanisms. On one hand, these crystal defects allow additional electronic levels to be created in the band structure, which effectively narrow the band gap, shift the absorption edge to the visible region, and enhance photocatalytic efficiency. On the other hand, excess additions of some dopants, such as N, may lead to the formation of the oxygen vacancy and Ti3+ due to charge imbalance, which increase the charge carrier recombination and hinder conversion efficiency. Hence, codoping is carried out to maintain the charge balance through charge compensation, add new electronic levels, suppress the recombination of charge carriers, and further increase photocatalytic efficiency. Besides, dopants also have an influence on the stability of the anatase phase and surface area. For example, dopants, such as Zr, Ag, W, Ce, and Nb, are found to inhibit the anatase-to-rutile phase transformation, while Mn, Cu, and Co are found to promote it. During the TiO2 synthesis, the high-temperature calcination is usually carried out to achieve high crystallinity, which, however, might lead to extensive grain coarsening and surface area reductions. Additions of dopants that inhibit the phase transformation to structure help stabilize the anatase phase at elevated processing temperature, hinder grain growth, decrease crystallite sizes, and thus increase the surface area. A high surface area indicates increased structural defects on the surface, such as unsaturated surface cations and surface hydroxyl groups, which favor the simultaneous absorption of organic molecules and enhance the photocatalytic efficiency. It should be pointed out that effects of modified lattices and surface areas on band gap tuning and photocatalytic properties are synergistic. There is no linear or monotonic relationship between lattice parameters, surface areas, and band gaps. In this work, the developed model is able to learn and capture the synergistic effects of the structure and morphology on Eg values.
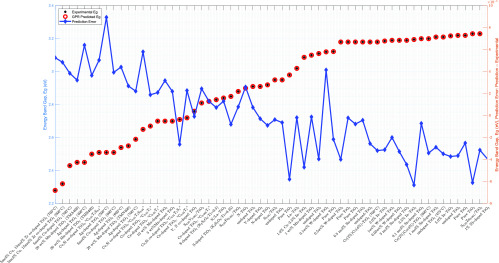
The final GPR model is detailed in Figure 3, which shows a good alignment between predicted and experimental data. The correlation coefficient (CC), root-mean-square error (RMSE), and mean absolute error (MAE) are 99.99%, 0.00003442 (0.0012% of the average experimental Eg), and 0.00002872 (0.0010% of the average experimental Eg), respectively, representing good prediction performance.
Figure 3.
Experimental vs predicted Eg. The final GPR model is built using the whole sample with the exponential kernel, constant basis function, and standardized predictors. It has a log-likelihood of −3.5784, β̂ of 2.8382, σ̂ of 0.0029, σ̂l of 0.2896, and σ̂f of 0.2939. Detailed numerical predictions are listed in Table 1 (column 6).
3.3. Prediction Stability
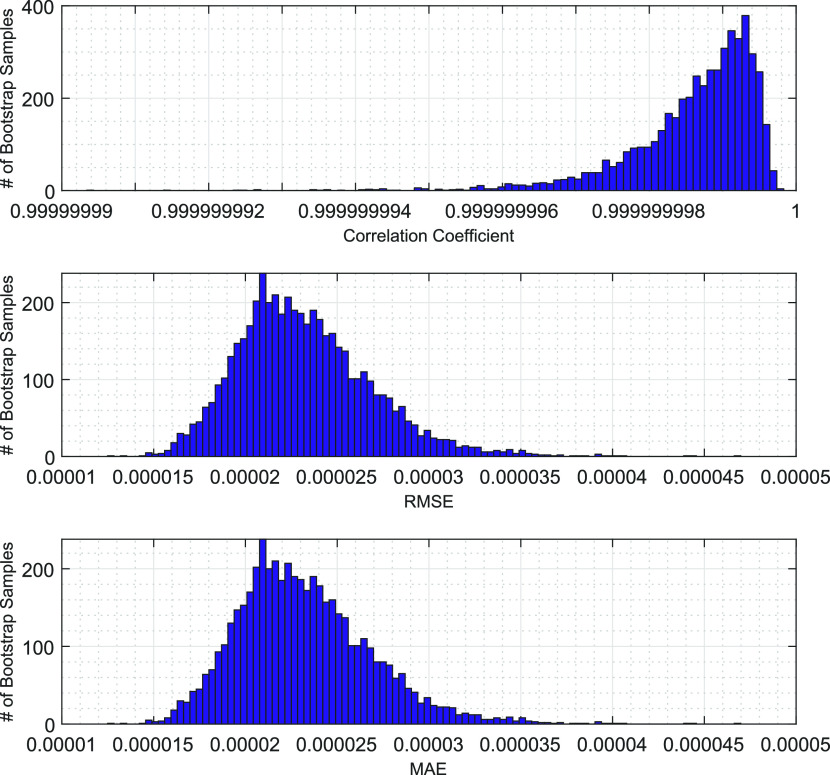
Given the relatively small sample size (see Table 1) used, the prediction stability of the GPR is assessed through bootstrap analysis in Figure 4, which shows that the modeling approach maintains high CCs, low RMSEs, and low MAEs over the bootstrap samples. This result suggests that the GPR might be generalized for Eg modeling of anatase TiO2 based on larger samples.
Figure 4.
Bootstrap analysis of GPR prediction stability. Five thousand bootstrap samples are drawn with replacements from the whole sample. Each bootstrap sample is used to train the GPR based on the exponential kernel, constant basis function, and standardized predictors and obtain the associate model performance. The histograms show distributions of CC, RMSE, and MAE over the 5000 bootstrap samples, whose averages are 99.99%, 0.00002320, and 0.00001782, respectively.
3.4. Prediction Sensitivity
Table 2 shows that the exponential kernel is generally the optimal choice among kernels considered. With the exponential kernel, prediction results are not sensitive to choices of basis functions except for the case of the empty basis function. Given the exponential kernel, the constant basis function is selected as the final specification for its simplicity, which usually is a benefit to model generalization, and its slight better performance as compared to more complicated basis functions, such as linear and pure quadratic.
Table 2. GPR Prediction Sensitivities to Choices of Kernels and Basis Functionsa.
| kernel | basis function | CC (%) | RMSE | RMSE/sample mean (%) | MAE | MAE/sample mean (%) |
|---|---|---|---|---|---|---|
| exponential | constant | 99.99 | 0.00003442 | 0.0012 | 0.00002872 | 0.0010 |
| exponential | empty | 82.38 | 0.17850737 | 6.1343 | 0.15125528 | 5.1978 |
| exponential | linear | 99.99 | 0.00003472 | 0.0012 | 0.00002926 | 0.0010 |
| exponential | pure quadratic | 99.99 | 0.00003554 | 0.0012 | 0.00002975 | 0.0010 |
| squared exponential | constant | 71.48 | 0.21057940 | 7.2364 | 0.18170821 | 6.2443 |
| matern 5/2 | constant | 99.99 | 0.00007681 | 0.0026 | 0.00005651 | 0.0019 |
| rational quadratic | constant | 99.98 | 0.00630021 | 0.2165 | 0.00459014 | 0.1577 |
The final GPR model is based on the exponential kernel and constant basis function, with standardized predictors.
4. Conclusions
In this study, we develop the Gaussian process regression (GPR) model for predictions of anatase TiO2 photocatalysts’ energy band gaps, Eg’s, based on the lattice parameters and surface area. Our model demonstrates a high correlation coefficient of 99.99% between predicted Eg’s and their experimental values. In addition, the model shows high prediction accuracy as reflected through the prediction root-mean-square error and mean absolute error being 0.0012 and 0.0010% of the average experimental Eg, respectively. Finally, model performance is illustrated to be stable. These results suggest that the GPR should be useful to model and understand relationships between structural and morphological parameters and Eg’s. This modeling method is simple and straightforward and does not require a lot of parameters, which are advantages for applications and computations. The model can be applied to a wide range of undoped and doped-TiO2 made by various synthesis methods and utilized to facilitate design and understandings of multidoped TiO2 photocatalysts with tunable Eg’s.
5. Proposed Methodology
5.1. Brief Description of Gaussian Process Regression
GPRs are nonparametric kernel-based probabilistic models. Consider
a training data set, {(xi, yi); i = 1, 2, ..., n} where 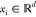 and
and 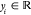 , from an unknown distribution. A trained
GPR predicts values of the response variable ynew given an input matrix xnew.
, from an unknown distribution. A trained
GPR predicts values of the response variable ynew given an input matrix xnew.
Recall a linear regression model, y = xTβ + ε, where ε ∼ N(0, σ2). A GPR aims at explaining y by introducing latent variables, l(xi) where i = 1, 2, ..., n, from a Gaussian process such that the joint distribution of l(xi)s is Gaussian and explicit basis functions, b. The covariance function of l(xi) captures the smoothness of y, and basis functions project x into a feature space of dimension p.
A GP is defined by the mean and covariance. Let m(x) = E(l(x)) be the mean function and k(x, x′) = Cov [l(x), l(x′)]
the covariance function and consider now the GPR model, y = b(x)Tβ + l(x), where l(x) ∼ GP(0, k(x, x′)) and 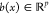 . k(x, x′) is often parameterized by
the hyperparameter,
θ, and thus might be written as k(x, x′|θ). In general, different algorithms estimate β, σ2, and θ for model training and would allow specifications
of b and k as well as initial values
for parameters.
. k(x, x′) is often parameterized by
the hyperparameter,
θ, and thus might be written as k(x, x′|θ). In general, different algorithms estimate β, σ2, and θ for model training and would allow specifications
of b and k as well as initial values
for parameters.
The current study explores four kernel functions,
namely exponential,
squared exponential, matern 5/2, and rational quadratic, whose specifications
are listed in eqs 1–eqs 1, respectively, where σl is the characteristic length scale defining how far apart x’s can be for y’s to become
uncorrelated, σf is the signal standard
deviation, 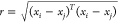 , and α is a positive-valued scale-mixture
parameter. Note that σl and σf should be positive. This could be enforced
through θ such that θ1 = log σl and θ2 = log σf.
, and α is a positive-valued scale-mixture
parameter. Note that σl and σf should be positive. This could be enforced
through θ such that θ1 = log σl and θ2 = log σf.
| 1 |
| 2 |
| 3 |
| 4 |
Similarly, four basis functions are investigated here, namely, empty, constant, linear, and pure quadratic, whose specifications are listed in eqs 5–eqs 5, respectively, where B = (b(x1), b(x2), ..., b(xn))T, X = (x1, x2, ..., xn)T, and
 |
.
| 5 |
| 6 |
| 7 |
| 8 |
To estimate β, σ2,
and θ, the marginal log-likelihood function in eq 9 is to be maximized, where K(X,X|θ) is the
covariance function matrix given by 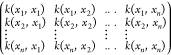 . The algorithm first computes β̂
(θ, σ2), maximizing the log-likelihood function
with respect to β given θ and σ2. It
then obtains the β-profiled likelihood, log {P(y|X, β̂(θ, σ2), θ, σ2)}, which is to be maximized
over θ and σ2 to compute their estimates.
. The algorithm first computes β̂
(θ, σ2), maximizing the log-likelihood function
with respect to β given θ and σ2. It
then obtains the β-profiled likelihood, log {P(y|X, β̂(θ, σ2), θ, σ2)}, which is to be maximized
over θ and σ2 to compute their estimates.
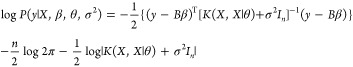 |
9 |
5.2. Performance Evaluation
Performance
of the proposed GPR models is evaluated using the root-mean-square
error (RMSE), mean absolute error (MAE), and correlation coefficient
(CC) in eqs 10–eq 9, respectively, where n is the
number of data points, aiexp and ai are the ith (i = 1, 2,
..., n) experimental and estimated energy band gap,
and 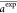 and
and 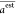 are their
averages.
are their
averages.
| 10 |
| 11 |
| 12 |
Acknowledgments
There is no funding received for this study.
The authors declare no competing financial interest.
References
- Devi L. G.; Kavitha R. Review on modified N-TiO2 for green energy applications under UV/visible light: selected results and reaction mechanisms. RSC Adv. 2014, 4, 28265–28299. 10.1039/C4RA03291H. [DOI] [Google Scholar]
- Bahnemann D. Photocatalytic water treatment: solar energy applications. Sol. Energy 2004, 77, 445–459. 10.1016/j.solener.2004.03.031. [DOI] [Google Scholar]
- Hay S. O.; Obee T.; Luo Z.; Jiang T.; Meng Y.; He J.; Murphy S. C.; Suib S. The viability of photocatalysis for air purification. Molecules 2015, 20, 1319–1356. 10.3390/molecules20011319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li K.; Peng B.; Peng T. Recent advances in heterogeneous photocatalytic CO2 conversion to solar fuels. ACS Catal. 2016, 6, 7485–7527. 10.1021/acscatal.6b02089. [DOI] [Google Scholar]
- Roose B.; Pathak S.; Steiner U. Doping of TiO2 for sensitized solar cells. Chem. Soc. Rev. 2015, 44, 8326–8349. 10.1039/C5CS00352K. [DOI] [PubMed] [Google Scholar]
- Parkin I. P.; Palgrave R. G. Self-cleaning coatings. J. Mater. Chem. 2005, 15, 1689–1695. 10.1039/b412803f. [DOI] [Google Scholar]
- Guo W.; Kirste R.; Bryan Z.; Bryan I.; Gerhold M.; Collazo R.; Sitar Z. Nanostructure surface patterning of GaN thin films and application to AlGaN/AlN multiple quantum wells: A way towards light extraction efficiency enhancement of III-nitride based light emitting diodes. J. Appl. Phys. 2015, 117, 113107 10.1063/1.4915903. [DOI] [Google Scholar]
- Sheikhi M.; Guo W.; Dai Y.; Cui M.; Hoo J.; Guo S.; Xu L.; Liu J.; Ye J. Mechanism of Improved Luminescence Intensity of Ultraviolet Light Emitting Diodes (UV-LEDs) Under Thermal and Chemical Treatments. IEEE Photonics J. 2019, 11, 1–8. 10.1109/JPHOT.2019.2950049. [DOI] [Google Scholar]
- Janczarek M.; Kowalska E. On the origin of enhanced photocatalytic activity of copper-modified titania in the oxidative reaction systems. Catalysts 2017, 7, 317 10.3390/catal7110317. [DOI] [Google Scholar]
- Lin Y.-H.; Tseng T.-K.; Chu H. Photo-catalytic degradation of dimethyl disulfide on S and metal-ions co-doped TiO2 under visible-light irradiation. Appl. Catal., A 2014, 469, 221–228. 10.1016/j.apcata.2013.10.006. [DOI] [Google Scholar]
- Hanaor D. A.; Sorrell C. C. Review of the anatase to rutile phase transformation. J. Mater. Sci. 2011, 46, 855–874. 10.1007/s10853-010-5113-0. [DOI] [Google Scholar]
- Ohtsuka Y.; Fujiki Y.; Suzuki Y. Impurity effects on anatase-rutile transformation. J. Jpn. Assoc. Mineral. Petrol. Econ. Geol. 1982, 77, 117–124. 10.2465/ganko1941.77.117. [DOI] [Google Scholar]
- Yu L.; Yang X.; He J.; He Y.; Wang D. One-step hydrothermal method to prepare nitrogen and lanthanum co-doped TiO2 nanocrystals with exposed {0 0 1} facets and study on their photocatalytic activities in visible light. J. Alloys Compd. 2015, 637, 308–314. 10.1016/j.jallcom.2015.03.035. [DOI] [Google Scholar]
- Ilkhechi N. N.; Alijani M.; Kaleji B. K. Optical and structural properties of TiO2 nanopowders with Co/Ce doping at various temperature. Opt. Quantum Electron. 2016, 48, 148 10.1007/s11082-016-0435-z. [DOI] [Google Scholar]
- Ilkhechi N. N.; Kaleji B. K.; Salahi E.; Hosseinabadi N. Comparison of optical and structural properties of Cu doped and Cu/Zr co-doped TiO2 nanopowders calcined at various temperatures. J. Sol-Gel Sci. Technol. 2015, 74, 765–773. 10.1007/s10971-015-3661-0. [DOI] [Google Scholar]
- Oseghe E. O.; Ndungu P. G.; Jonnalagadda S. B. Synthesis of mesoporous Mn/TiO2 nanocomposites and investigating the photocatalytic properties in aqueous systems. Environ. Sci. Pollut. Res. 2015, 22, 211–222. 10.1007/s11356-014-3356-z. [DOI] [PubMed] [Google Scholar]
- Lei X.; Xue X.; Yang H. Preparation and characterization of Ag-doped TiO2 nanomaterials and their photocatalytic reduction of Cr (VI) under visible light. Appl. Surf. Sci. 2014, 321, 396–403. 10.1016/j.apsusc.2014.10.045. [DOI] [Google Scholar]
- Hao C.; Li J.; Zhang Z.; Ji Y.; Zhan H.; Xiao F.; Wang D.; Liu B.; Su F. Enhancement of photocatalytic properties of TiO2 nanoparticles doped with CeO2 and supported on SiO2 for phenol degradation. Appl. Surf. Sci. 2015, 331, 17–26. 10.1016/j.apsusc.2015.01.069. [DOI] [Google Scholar]
- Gu D.-E.; Yang B.-C.; Hu Y.-D. V and N co-doped nanocrystal anatase TiO2 photocatalysts with enhanced photocatalytic activity under visible light irradiation. Catal. Commun. 2008, 9, 1472–1476. 10.1016/j.catcom.2007.12.014. [DOI] [Google Scholar]
- Niu Y.; Xing M.; Tian B.; Zhang J. Improving the visible light photocatalytic activity of nano-sized titanium dioxide via the synergistic effects between sulfur doping and sulfation. Appl. Catal., B 2012, 115–116, 253–260. 10.1016/j.apcatb.2011.12.039. [DOI] [Google Scholar]
- Tahir M.; Amin N. S. Photocatalytic CO2 reduction with H2 as reductant over copper and indium co-doped TiO2 nanocatalysts in a monolith photoreactor. Appl. Catal., A 2015, 493, 90–102. 10.1016/j.apcata.2014.12.053. [DOI] [Google Scholar]
- Oseghe E. O.; Ndungu P. G.; Jonnalagadda S. B. Photocatalytic degradation of 4-chloro-2-methylphenoxyacetic acid using W-doped TiO2. J. Photochem. Photobiol., A 2015, 312, 96–106. 10.1016/j.jphotochem.2015.07.014. [DOI] [Google Scholar]
- Rangel-Vázquez I.; Del Angel G.; Bertin V.; González F.; Vázquez-Zavala A.; Arrieta A.; Padilla J.; Barrera A.; Ramos-Ramirez E. Synthesis and characterization of Sn doped TiO2 photocatalysts: Effect of Sn concentration on the textural properties and on the photocatalytic degradation of 2, 4-dichlorophenoxyacetic acid. J. Alloys Compd. 2015, 643, S144–S149. 10.1016/j.jallcom.2014.12.065. [DOI] [Google Scholar]
- Kaleji B. K.; Hosseinabadi N.; Fujishima A. Enhanced photo-catalytic activity of TiO2 nanostructured thin films under solar light by Sn and Nb co-doping. J. Sol-Gel Sci. Technol. 2013, 65, 195–203. 10.1007/s10971-012-2924-2. [DOI] [Google Scholar]
- Ismail A. A.; Bahnemann D. W. Mesoporous titania photocatalysts: preparation, characterization and reaction mechanisms. J. Mater. Chem. 2011, 21, 11686–11707. 10.1039/c1jm10407a. [DOI] [Google Scholar]
- Schwartz J.; Koch C. C.; Zhang Y.; Liu X.. Formation of Bismuth Strontium Calcium Copper Oxide Superconductors. U.S. Patent US9773962B2 (2017). https://patents.google.com/patent/US9773962B2/en (accessed May 19, 2020).
- Zhang Y.; Johnson S.; Naderi G.; Chaubal M.; Hunt A.; Schwartz J. High critical current density Bi2Sr2CaCu2O x/Ag wire containing oxide precursor synthesized from nano-oxides. Supercond. Sci. Technol. 2016, 29, 095012 10.1088/0953-2048/29/9/095012. [DOI] [Google Scholar]
- Zhang Y.; Koch C. C.; Schwartz J. Formation of Bi2Sr2CaCu2O x/Ag multifilamentary metallic precursor powder-in-tube wires. Supercond. Sci. Technol. 2016, 29, 125005 10.1088/0953-2048/29/12/125005. [DOI] [Google Scholar]
- Zhang Y.; Koch C. C.; Schwartz J. Synthesis of Bi2Sr2CaCu2Ox superconductors via direct oxidation of metallic precursors. Supercond. Sci. Technol. 2014, 27, 055016 10.1088/0953-2048/27/5/055016. [DOI] [Google Scholar]
- Li F.; Li X.; Hou M.; Cheah K.; Choy W. Enhanced photocatalytic activity of Ce3+-TiO2 for 2-mercaptobenzothiazole degradation in aqueous suspension for odour control. Appl. Catal., A 2005, 285, 181–189. 10.1016/j.apcata.2005.02.025. [DOI] [Google Scholar]
- Yu J.; Jimmy C. Y.; Leung M. K.-P.; Ho W.; Cheng B.; Zhao X.; Zhao J. Effects of acidic and basic hydrolysis catalysts on the photocatalytic activity and microstructures of bimodal mesoporous titania. J. Catal. 2003, 217, 69–78. 10.1016/S0021-9517(03)00034-4. [DOI] [Google Scholar]
- Ovenstone J.; Yanagisawa K. Effect of hydrothermal treatment of amorphous titania on the phase change from anatase to rutile during calcination. Chem. Mater. 1999, 11, 2770–2774. 10.1021/cm990172z. [DOI] [Google Scholar]
- Yang S.; Gao L. Preparation of titanium dioxide nanocrystallite with high photocatalytic activities. J. Am. Ceram. Soc. 2005, 88, 968–970. 10.1111/j.1551-2916.2005.00151.x. [DOI] [Google Scholar]
- Addamo M.; Augugliaro V.; Di Paola A.; García-López E.; Loddo V.; Marci G.; Molinari R.; Palmisano L.; Schiavello M. Preparation, characterization, and photoactivity of polycrystalline nanostructured TiO2 catalysts. J. Phys. Chem. B 2004, 108, 3303–3310. 10.1021/jp0312924. [DOI] [Google Scholar]
- Munir S.; Shah S. M.; Hussain H.; et al. Effect of carrier concentration on the optical band gap of TiO2 nanoparticles. Mater. Des. 2016, 92, 64–72. 10.1016/j.matdes.2015.12.022. [DOI] [Google Scholar]
- Zhou J.; Xie L. Effect of net surface charge on particle sizing and material recognition by using phase Doppler anemometry. Appl. Opt. 2011, 50, 379–386. 10.1364/AO.50.000379. [DOI] [PubMed] [Google Scholar]
- Tian G.; Fu H.; Jing L.; Xin B.; Pan K. Preparation and characterization of stable biphase TiO2 photocatalyst with high crystallinity, large surface area, and enhanced photoactivity. J. Phys. Chem. C 2008, 112, 3083–3089. 10.1021/jp710283p. [DOI] [Google Scholar]
- Hu S.; Li F.; Fan Z. Preparation of visible light responsive N doped TiO2 via a reduction-nitridation procedure by nonthermal plasma treatment. Appl. Surf. Sci. 2011, 258, 1249–1255. 10.1016/j.apsusc.2011.09.085. [DOI] [Google Scholar]
- Zhou Z.; Li M.; Guo L. A first-principles theoretical simulation on the electronic structures and optical absorption properties for O vacancy and Ni impurity in TiO2 photocatalysts. J. Phys. Chem. Solids 2010, 71, 1707–1712. 10.1016/j.jpcs.2010.08.021. [DOI] [Google Scholar]
- Liu L.-Y.; Zhang Z.-X.; Gou X.-F.; Yang H.-X. Molecular modelling of the effect of loading rate on elastic properties of CNT-polyethylene nanocomposite and its interface. Mater. Res. Express 2020, 6, 1250d2 10.1088/2053-1591/ab61b2. [DOI] [Google Scholar]
- Ong S.Materials Project. https://www.materialsproject.org/wiki/index.php/GGA%2BU_calculations#cite_note-1 (2016; accessed May 19, 2020).
- Wang L.; Maxisch T.; Ceder G. Oxidation energies of transition metal oxides within the GGA+ U framework. Phys. Rev. B 2006, 73, 195107 10.1103/PhysRevB.73.195107. [DOI] [Google Scholar]
- Zhang Y.; Xu X. Yttrium barium copper oxide superconducting transition temperature modeling through Gaussian process regression. Comput. Mater. Sci. 2020, 179, 109583 10.1016/j.commatsci.2020.109583. [DOI] [Google Scholar]
- Zhang Y.; Xu X. Machine learning the magnetocaloric effect in manganites from lattice parameters. Appl. Phys. A 2020, 126, 341 10.1007/s00339-020-03503-8. [DOI] [Google Scholar]
- Zhang Y.; Xu X. Predicting the thermal conductivity enhancement of nanofluids using computational intelligence. Phys. Lett. A 2020, 384, 126500 10.1016/j.physleta.2020.126500. [DOI] [Google Scholar]