Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Jun 16;5(25):15301–15310. doi: 10.1021/acsomega.0c01337

Upgraded AMBER Force Field for Zinc-Binding Residues and Ligands for Predicting Structural Properties and Binding Affinities in Zinc-Proteins

Marina Macchiagodena †, Marco Pagliai †,*, Claudia Andreini †,‡, Antonio Rosato †,‡, Piero Procacci †,*
PMCID: PMC7331063  PMID: 32637803

Abstract

graphic file with name ao0c01337_0007.jpg

We developed a novel force field in the context of AMBER parameterization for glutamate and aspartate zinc(II)-binding residues. The interaction between the zinc ion and the coordinating atoms is represented by a spherical nonbonded parameterization. The polarization effect due to the zinc ion has been taken into account by redefining the atomic charges on the residues through accurate quantum mechanical calculations. The new zinc-binding ASP and GLU residues, along with the CYS and HIS zinc-binding residues, parameterized in a recent work [Macchiagodena M.;et al. J. Chem. Inf. Model. 2019, 59, 3803−3816], allow users to reliably simulate 96% of the Zn-proteins available in the Protein Data Bank. The upgraded force field for zinc(II)-bound residues has been tested performing molecular dynamics simulations with an explicit solvent and comparing the structural information with experimental data for five different proteins binding zinc(II) with GLU, ASP, HIS, and CYS. We further validated our approach by evaluating the binding free energy of (R)-2-benzyl-3-nitropropanoic acid to carboxypeptidase A using a recently developed nonequilibrium alchemical method. We demonstrated that in this setting it is crucial to take into account polarization effects also on the metal-bound inhibitor.

1. Introduction

Metalloproteins are essential in several fundamental cellular processes, such as protein synthesis and/or degradation, and in neurotransmission and are involved in diseases for public health, such as, for example, cancer and neurodegenerative disorders.1 Zinc is one of the essential metals, binding to a variety of different proteins in living cells.2−4 Classical molecular dynamics (MD) simulations at the atomistic level provide a powerful tool to understand speciation in proteins, their mechanism of action, and the basis for metal selectivity. The reliability of simulations is related to the availability of an accurate force field (FF) and of advanced enhanced sampling technologies. Several methods5−20 have been proposed to parameterize metals in biological systems in the context of nonpolarizable FFs (e.g., AMBER,21 CHARMM,22 OPLS23). The various strategies can be organized into classes that differ in the description of interactions between the metal ion and the protein residues that bind the metal: nonbonded, bonded, cationic dummy atom, and combined models. An exhaustive description of modeling strategies can be found in a recent review by Li et al.10

Here, we apply our exportable procedure24 to derive parameters for zinc(II)-binding glutamate and aspartate residues in the context of AMBER FF.21,25 The interactions between the metal ion and the binding residues are described using a nonbonded parameterization, which makes use of simple van der Waals and electrostatic atom–atom terms. The residues taken into account (GLU and ASP) together with the already reparameterized ones (CYZ, HDZ, and HEZ)24 allow around 96% of the Zn-proteins available in the Protein Data Bank (PDB) to be simulated.26 Using our protocol, we recalculated the atomic charges and the Lennard-Jones parameters taking into account the strong polarization effects induced by the zinc(II) cation on the coordinating ligands. The charges were evaluated on 23 high-quality zinc(II) protein structures (below 2 Å resolution) taken from the PDB. The selected structures harbor tetracoordinated zinc(II) with at least one glutamate and/or aspartate residue in the coordination sphere. The other interacting residues can be histidine, cysteinate, or water molecules. The new residues GLZ and ASZ (renamed consistently with the previously defined CYZ, HDZ, and HEZ) afford simulations where the three-dimensional (3D) structure of the zinc-binding site is in close agreement with experimental data. Furthermore, it was possible to reliably calculate the binding energy of (R)-2-benzyl-3-nitropropanoic acid to carboxypeptidase A, a zinc-binding enzyme, using a nonequilibrium (NE) alchemical method (for a detailed description of equilibrium and nonequilibrium alchemical techniques, the reader is referred to an excellent review, ref (27)). In particular, we showed that the correct binding free energies can be recovered only if one takes into account the polarization effects of the metal on all of the zinc-coordinating groups including the ligand, whose atomic charges (evaluated using the same protocol applied for GLZ and ASZ) differ from the standard AM1-BCC atomic charges of the ligand in bulk.

The advantages offered by our exportable reparameterization protocol include speed, convenience, and broad applicability granted by remaining in the context of existing nonpolarizable force field forms. Our nonbonded strategy with persistent polarization on metal-bound residues or ligands goes beyond the ability to reliably reproduce the mere structure for a fixed ligand environment to more readily enable quantitative thermodynamic comparison of different ligand environments around the metal in processes (whether real or alchemical) where these environments change.

2. Methods

2.1. Calculation of AMBER Parameters for GLZ and ASZ

Following the protocol developed in our previous paper,24 we selected a training set containing 23 structures of nonhomologous proteins that have at least one glutamate and/or one aspartate binding a tetracoordinated zinc(II) ion, for a total of 24 sites. The Zn···X distances in this set are representative of the statistics over the entire PDB.28 The structures have a high resolution (below 2 Å), and the coordination sphere can be characterized by a different combination of histidines, cysteinates, or water molecules in addition to aspartate and glutamate. Details are reported in Table 1, where the first coordination sphere compositions have been labeled as CxHyEzDk (one-letter code), adding H2O when present. We analyzed one site for each protein except for 1D8W, which has two sites.

Table 1. Protein Structures Used to Extract Complex Configurationsa.

PDB code resolution (Å) CxHyEzDk group
4YBG 1.60 C2HE
3C37 1.70 H3E
1I6N 1.80 HE2D
1D8W(1) 1.60 HED2
1D8W(2) 1.60 HED2
2DVT 1.70 H2ED
4E5V 1.75 H3E
2CDB 1.60 CHE-H2O
4GER 1.59 H2E-H2O
6FJ2 1.43 H2E-H2O
5ONR 1.39 H2E-H2O
4UFA 1.80 H2E-H2O
5AMA 1.80 H2E-H2O
3MS3 1.54 H2E-H2O
4TXD 1.80 C3D
2CS7 1.20 H3D
1V4Y 1.65 CH2D
4Z1D 1.80 CHED
3RZV 1.67 D2H2
1XRT 1.61 CH2D
1W5M 1.60 C2D-H2O
1KOL 1.65 CHD-H2O
1C7K 1.00 DH2-H2O
3F0D 1.20 DH2-H2O
Open in a new tab
a

For each protein, we report the PDB code, the resolution (Å), and the residue combination of the first coordination sphere. In bold are proteins used for validation.

For all of the structures of the training set (Table 1), we extracted the 3D coordinates of the zinc(II) ion and the coordinating residues. The amino acids were saturated by adding an OH moiety to the C=O and a H hydrogen to the N–H. The complexes thus obtained were used for the calculation of atomic charges with the Merz–Kollmann restrained electrostatic potential (RESP) scheme,29 applying selected constraints as described below. The charges of the carbonyl (C=O) and amino (N–H) groups were fixed at the standard AMBER21,25 values, while those of the saturating OH and H could vary freely. The total charge of the reparameterized residue (E and D) was fixed at the integer value of −1 e, and the zinc(II) charge was constrained to +2 e. The atomic charges were calculated using the CP2K suite of programs for each of the 24 complexes.30,31 The final renormalized charges on the GLZ and ASZ zinc-coordinating residues were obtained by an averaging procedure described in our previous paper.24 The σ Lennard-Jones parameter of the zinc(II)-binding oxygen atom of glutamate and aspartate has been increased by 0.1 Å, in agreement with the procedure adopted for the reparameterization of CYZ and HEZ/HDZ. The final value, using the GROMACS32,33 definition for the Lennard-Jones potential parameters, is σO = 3.05992 Å; the ϵO was kept to its AMBER standard value.

2.2. Molecular Dynamics Simulations

Molecular dynamics simulations and trajectory analyses were carried out using the GROMACS 2018.3 suite of programs.32,33 The simulations were performed in a cubic box with periodic boundary conditions, whose side length was chosen so that the minimum distance between protein atoms belonging to neighboring replicas was larger than 30 Å in any direction. Proteins were explicitly solvated with the extended simple point charge (SPC/E)34,35 water model at the standard density. The employed force field was amber99sb-ildn36 with our modifications.24 The system was initially minimized at 0 K with a steepest descent procedure and subsequently heated to 298.15 K in an NPT ensemble (P = 1 atm) using a Berendsen barostat37 and a velocity rescaling algorithm38 with an integration time step of 0.1 fs and a coupling constant of 0.1 ps for 500 ps. Production runs in the NPT ensemble were carried out for 50 ns imposing rigid constraints only on the X–H bonds (with X being any heavy atom) by means of the LINCS algorithm (δt = 2.0 fs).39 Electrostatic interactions were treated using the particle-mesh Ewald (PME)40 method with a grid spacing of 1.2 Å and a B-spline interpolation of order 4. As prescribed by the AMBER protocol, the cross-interactions for Lennard-Jones terms were calculated using the Lorentz–Berthelot41,42 mixing rules and we excluded intramolecular nonbonded interactions between atom pairs separated up to two bonds. The nonbonded interactions between one and four atoms involved in a proper torsion were scaled by the standard AMBER fudge factors (0.8333 and 0.5 for the Coulomb and Lennard-Jones, respectively).

2.3. Nonequilibrium Alchemical Method for Computing Inhibitor Constant

The inhibitor constant of (R)-2-benzyl-3-nitropropanoic acid against carboxypeptidase A (structure in Figure S1 of the Supporting Information) was calculated using a fast switching (FS) alchemical technique43−46 and compared with the experimental data.47 FS is the nonequilibrium variant of well-established alchemical technologies based on free energy perturbation or thermodynamic integration and implemented in popular MD programs.48−50 FS consistently performed well in blind challenges for binding free energy prediction such as SAMPL651,52 and SAMPL7.53 This technique is based on the production of canonical configurations of the bound and unbound states via the Hamiltonian replica-exchange method (HREM) and, starting from the HREM-sampled canonical configurations, on the subsequent “release of an entire flock of birds flying over the free energy surface (FES)”54 with a continuous alchemical decoupling of the ligand–environment interactions eventually producing bound and unbound work distributions. When the annihilation work distributions can be described by a normal distribution or by a simple mixture of Gaussian components, the annihilation free energies of the ligand when bound to the receptor and in bulk solvent can be obtained from the collection of NE work values using an unbiased estimate based on the Crooks theorem.55 In the case of non-normal distributions, the estimate of the annihilation free energy is obtained by the statistically boosted Jarzynski average,54 exploiting the decorrelation between the discharging and Lennard-Jones annihilation work values. The absolute binding free energies can be computed using

2.3. 1

where ΔGb and ΔGu are the annihilation free energies in the bound and unbound states, respectively. The ΔGbox is calculated as kBT ln(Vr/V0),56−58 where V0 is the standard state volume and Vr is evaluated from the distributions of the host–guest centers of mass (COM)–COM vector distance. ΔGfs is the finite size correction that must be added due to the annihilation of a net charge using PME.40,59 This term, accounting for the direct lattice Wigner self-potential,60 can be derived using the following equation:

2.3. 2

where QH and QG are the net charges on the host and guest molecules, respectively; Vboxb/u are the MD box volumes of the bound and unbound states; and α is the Ewald convergence parameter.

The ligand Cartesian coordinates were taken from the PDB structure of the carboxypeptidase A–(R)-2-benzyl-3-nitropropanoic acid complex (PDB code 2RFH). These coordinates were fed to the PrimaDORAC interface61 to assign the GAFF2 atom type to the inhibitor. For the atomic charges, we used two parameterizations: the standard AM1-BCC charges obtained using PrimaDORAC and those taking into account the zinc(II) polarization effect on the inhibitor when bound to the protein. In the last case, we reparameterized the atomic charges on the complex formed by the zinc ion, the interacting residues (two histidines and one glutamate), and the inhibitor (R)-2-benzyl-3-nitropropanoic acid. The structure to calculate atomic charges was extracted from the X-ray PDB (Figure S2 of the Supporting Information), and we followed the same procedure applied for the reparameterization of the zinc-bound residues (Section 2.1 and ref (24)). We have constrained the atomic charges of the phenyl group to those of GAFF2 evaluating the polarization response only for the moieties directly interacting with the cation. We used the restrained electrostatic potential (RESP) model29 implemented in NWChem62 with the BLYP63 functional and the pcseg-1 basis set,64 obtaining the result reported in Table S1 of the Supporting Information. The carboxypeptidase A enzyme was parameterized using the amber99sb-ildn force field with our parameterization for the zinc ion and interacting residues (HIE69, HIE192 e GLU72). For comparison, we also performed the calculation using the unmodified amber99sb-ildn for the protein and the standard AM1-BCC charges for the inhibitor. Therefore, the inhibitor constant affinity calculation was performed on three different models, as summarized in Table 2, allowing us to verify the quality of the proposed FF for glutamate and the zinc ion,24 as well as to assess the effects of zinc polarization on the ligand by comparing the results obtained with models B and C.

Table 2. Parameterization Used for Calculation of the Inhibitor Constant Affinity.

  enzyme Zn(II) Zn(II)-binding residues inhibitor
model A amber99sb-ildn amber99sb-ildn amber99sb-ildn GAFF2/AM1-BCC
model B amber99sb-ildn OUR OUR GAFF2/AM1-BCC
model C amber99sb-ildn OUR OUR GAFF2/OUR
Open in a new tab

In all MD simulations, the solvent was treated explicitly using the TIP3P model.65 Long-range electrostatic interactions were treated using the smooth particle-mesh Ewald (SPME) method,66 with an α parameter of 0.37 Å–1, a grid spacing in the direct lattice of about 1.2 Å, and a fourth-order B-spline interpolation for the gridded charge array.

As no counterions were included, charge neutralization in charged bound and unbound systems is implicitly done in SPME using a uniform neutralizing background plasma. Bond constraints were imposed on X–H bonds. The pressure was set to 1 atm using a Parrinello–Rahman Lagrangian67 with the isotropic stress tensor, while the temperature was held constant to 300 K using three Nosé–Hoover thermostats coupled to the translational degrees of freedom of the systems and to the rotational/internal motions of the solute and of the solvent. The equations of motion were integrated using a multiple time-step r-RESPA scheme68 with a potential subdivision specifically tuned for biomolecular systems in the NPT ensemble.69,70 The long-range cutoff for Lennard-Jones interactions was set to 13 Å in all cases.

The HREM simulations of the bound state were run by launching, in a single parallel job, eight replicas of independent Hamiltonian replica-exchange simulation with 36 batteries for a total of 288 MPI instances. The starting configuration is the X-ray structure. In each of the eight replica batteries, we used torsional tempering (including 14 nonbonded interactions) with a maximum scaling factor s = 0.2 corresponding to a torsional temperature of 1500 K. The “hot” region included all residues with at least one atom at a distance of less than 4.2 Å from any atom of the ligand. The scaling factors, sm, along the eight replica progressions are computed according to the protocol sm = s(m–1)/7. The ligand was weakly tethered in the binding site via a harmonic restraint potential between the COMs of the ligand and the protein, with the equilibrium distance corresponding to the experimental protein–ligand COM–COM distance and a force constant of 0.04 kcal mol–1 Å–2. Each HREM battery sampled 26 configurations taken at a regular interval of 12 ps, hence accumulating 968 solvated bound-state starting configurations in a total simulation time of 12 ns.

For setting up the starting configurations of the decoupled ligand in bulk, we first harvested 528 configurations of the isolated (gas-phase) molecule via an 8 ns (target state) HREM simulation using four replicas with torsional tempering with a minimum scaling factor of s = 0.1, corresponding to torsional temperature of 3000 K, and using the protocol sm = s(m–1)/3, m = 1, ..., 4 along the four replica progressions. The 580 sampled gas-phase ligand conformations, with random orientations and positions, were combined with a single equilibrated sample of about 1000 water molecules in standard conditions in a cubic box, producing 580 starting configurations of the decoupled (ghost) ligand in bulk.

For the ligand in the bound state (b state), alchemical annihilation simulations were performed starting from the λ = 1 (fully coupled) equilibrium configurations collected in the preceding HREM step. NE annihilation trajectories were run for 360 ps: in the first 120 ps, the electrostatic interactions were linearly switched off; in the following 120 ps, two-third of the Lennard-Jones potential was turned off; and in the last 120 ps, the one-third residual was finally switched off.

A time-inverted protocol was adopted for the ligand in the bulk state (u state); in this case, the alchemical fast-growth simulations were started from λ = 0 (fully decoupled) and NE trajectories were run for 360 ps. In the first 120 ps, one-third of the Lennard-Jones potential was turned on. In the following 120 ps, the Lennard-Jones potential was switched on completely. In the last 120 ps, the electrostatic interactions were linearly turned on. All of the simulations for computing the inhibitor constant were done using the program ORAC.71

3. Results and Discussion

3.1. FF for Zinc(II)-Binding Glutamate and Aspartate Residues

We report the atomic charges of the new GLZ and ASZ zinc-binding residues in Tables 3 and 4, obtained by averaging ab initio calculations on the training set listed in Table 1. For comparison, we also report the AMBER atomic charges (GLU and ASP residues). The main difference between reparameterized and AMBER atomic charges is in the redistribution of the negative charge on the two oxygen atoms of the carboxylate group. In our model for zinc-polarized ASZ and GLZ, the two oxygen atoms are not equivalent: the zinc-interacting atom has a higher negative charge, which contributes to preserving a monodentate interaction between Zn(II) and GLZ/ASZ. Indeed, as reported by Tamames et al.,72 the interaction Zn(II)···GLZ/ASZ involves only one oxygen atom. We reached the same conclusion by analyzing 13 785 aspartate and 9333 glutamate residues binding zinc(II) in structures with a resolution better than 1.8 Å (Figure 1). The majority of glutamate and aspartate residues interacts only with one oxygen atom (Oϵ1 or Oδ1), and the difference between the distances Zn···O1 (δ/ϵ) and Zn···O2 (δ/ϵ) is at least 1 Å. In the case of aspartate, the Oδ2 distance covers a higher range of values. The higher negative charge on the donor oxygen atom is in agreement with the corresponding increase of the Lennard-Jones parameter on the same atom.

Table 3. Atomic Charges for the Glutamate Residue (e): AMBER (GLU) and Reparameterized (GLZ)a.

atoms AMBER (GLU) GLZ
N –0.5163 –0.5163
H 0.2936 0.2936
CA 0.0397 0.1350
HA 0.1105 0.0566
CB 0.0560 –0.0325
HB1 –0.0173 –0.0005
HB2 –0.0173 –0.0005
CG 0.0136 0.2766
HG1 –0.0425 –0.0548
HG2 –0.0425 –0.0548
CD 0.8054 0.6926
OE1 –0.8188 –1.0627
OE2 –0.8188 –0.6870
C 0.5366 0.5366
O –0.5819 –0.5819
Open in a new tab
a

The atoms are labeled with AMBER atom names.

Table 4. Atomic Charges for the Aspartate Residue (e): AMBER (ASP) and Reparameterized (ASZ)a.

atoms AMBER (ASP) ASZ
N –0.5163 –0.5163
H 0.2936 0.2936
CA 0.0381 0.0422
HA 0.0880 0.0732
CB –0.0303 0.1549
HB1 –0.0122 –0.0052
HB2 –0.0122 –0.0052
CG 0.7994 0.7388
OD1 –0.8014 –1.1120
OD2 –0.8014 –0.6187
C 0.5366 0.5366
O –0.5819 –0.5819
Open in a new tab
a

The atoms are labeled with AMBER atom names.

Figure 1.

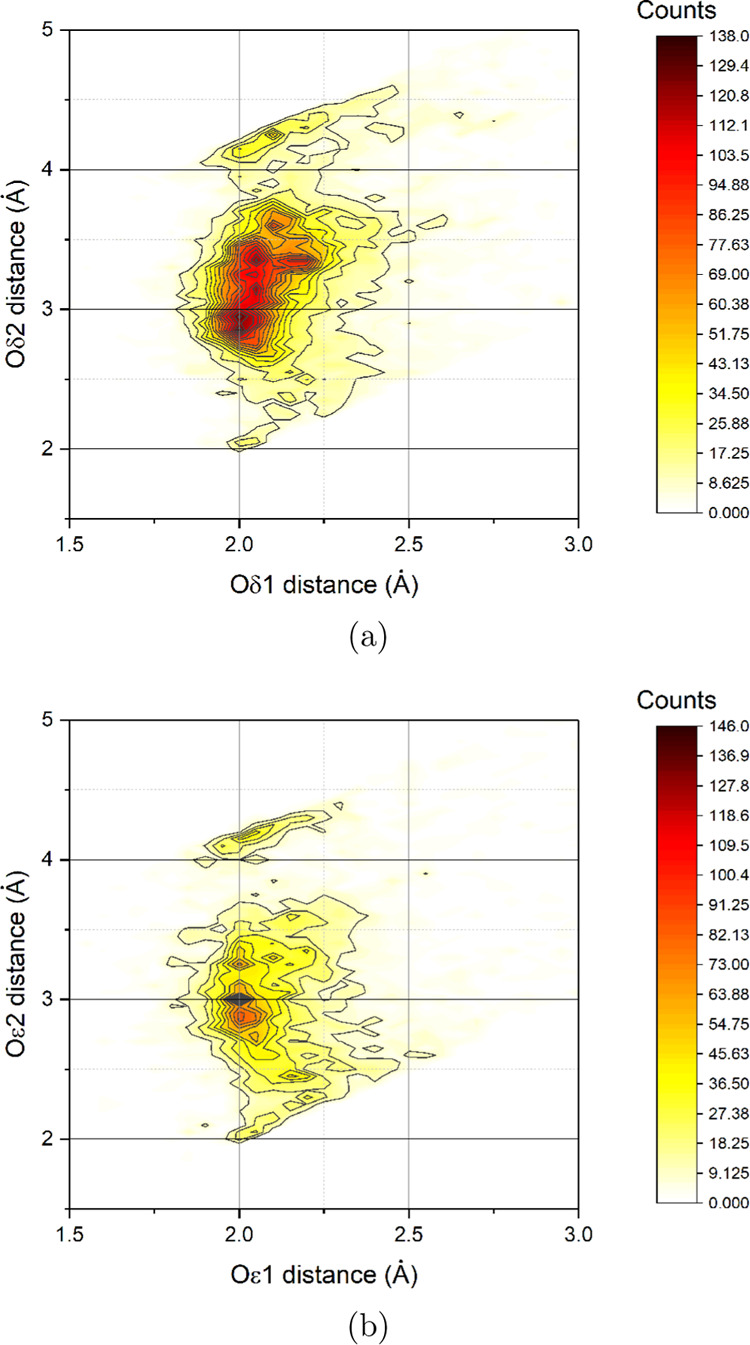
Figure 1

Open in a new tab

Combined distribution function between Zn(II)···Oδ1/Oδ2 and Zn(II)···Oϵ1/Oϵ2 distances for aspartate (a) and glutamate (b), respectively. In total, 13785 aspartate and 9333 glutamate residues binding zinc(II) were analyzed. By construction, we labeled with number 1 the oxygen atom closest to the metal ion. Only structures with a resolution better than 1.8 Å were included in the analysis.

3.2. Validation of GLZ and ASZ Parameters

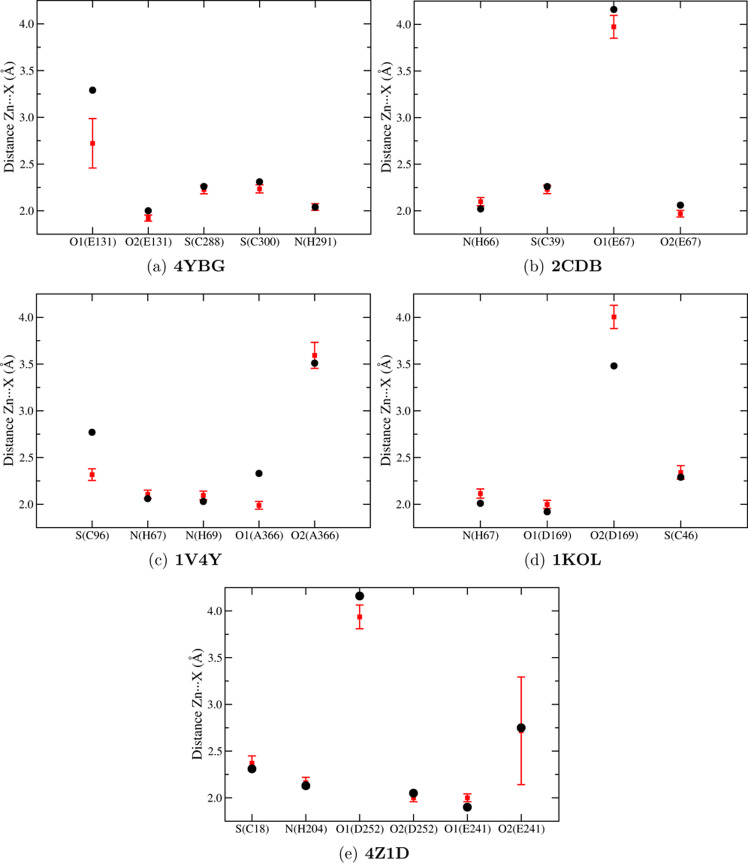
To investigate the structural properties of the zinc(II) sites applying our new FF, we performed MD simulation for five zinc(II)-proteins: 4YBG, 2CDB, 1V4Y, 1KOL, and 4Z1D (in bold in Table 1). The structures were chosen so as to include representative proteins of all CxHyEzDk groups. We calculated the radial distribution function (RDF) between Zn(II) and the oxygen-, nitrogen-, or sulfur-interacting atoms of GLZ and ASZ, HEZ/HDZ, or CYZ, respectively. Results are reported in Figure S3 of the Supporting Information along with reference values extracted from the X-ray structures. For all proteins, we obtained a good agreement between the X-ray distances and the maximum of RDF distribution as reported in Figure 2, in which RDF distribution averages are compared with experimental data. Our parameterization can differentiate the interactions between the zinc ion and the two oxygen atoms of the carboxylate group of glutamate and aspartate. This results in monodentate interactions (see also the Zn···O1 and Zn···O2 RDFs in Figure S3 in the Supporting Information) as experimentally observed (Figure 1). One exception was found for Zn···O2(E241) RDF (Figure S3e of the Supporting Information) of 4Z1D, which presents two peaks, around 2.2 and 3.5 Å, respectively. Although the two peaks differ from the experimental value (2.75 Å), the monodentate coordination is still preserved. The two RDF values are due to the presence of water molecules around glutamate 241. This interaction is also confirmed by analyzing the pair distribution function during the 50 ns of simulation between the zinc(II) ion and the interacting atoms, including the H-bond interactions with water (Figure 3). It is evident that the Zn···O2(E241) and O2(E241)···H(H2O) distances are correlated: when the O2 atom is H-bonded to water, the Zn···O2 distance is larger (3.5 Å).

Figure 2.

Figure 2

Open in a new tab

RDF average between zinc(II) and the interacting oxygen, nitrogen, or sulfur atom of glutamate, aspartate, histidine, or cysteinate, respectively (red squares). The error bar represents the standard deviation. The corresponding reference values extracted from X-ray structures are depicted with black dots. The comparison was performed for 4YBG (a), 2CDB (b), 1V4Y (c), 1KOL (d), and 4Z1D (e).

Figure 3.

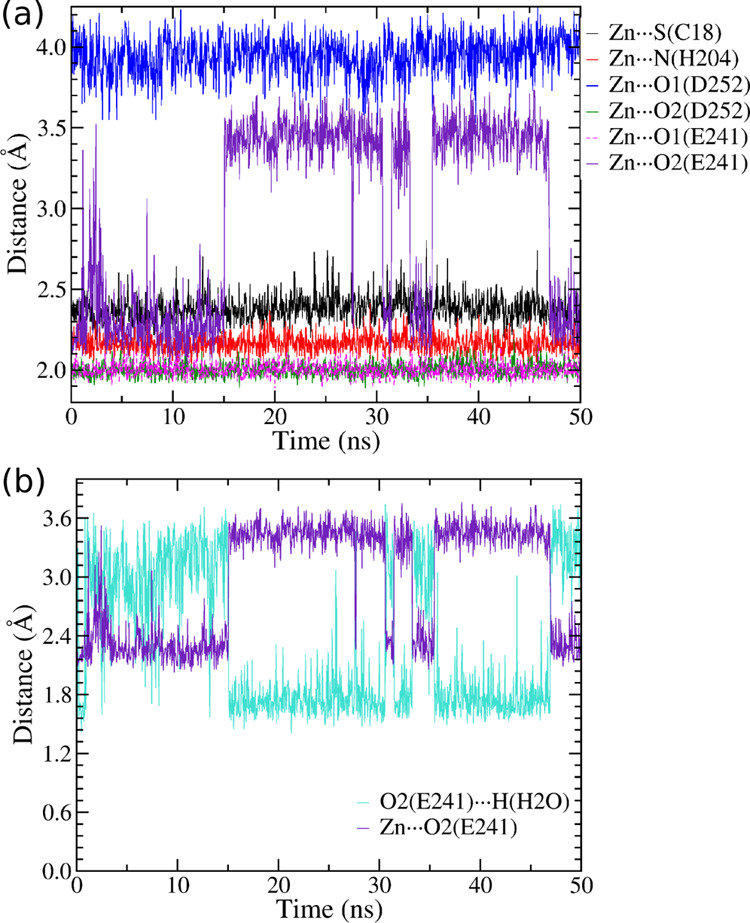
Figure 3

Open in a new tab

Pair distribution function between Zn(II) and interacting atoms for the 4Z1D protein. In (a), the distributions refer to protein atoms interacting with Zn(II); in (b) are those relative to Zn···O2(E241) and O2(E241)···H(H2O) distances.

The stability of the zinc(II) coordination during simulations was assessed by calculating the angle and monitoring the time evolution of the distances involved in the interaction with zinc(II). The results are reported in Table S2 and in Figure S4 of the Supporting Information. In Figure S5 of the Supporting Information, we show the root-mean-square deviation (RMSD) values for the metal-binding site (zinc(II) ion and the ligand residues) and the coordination sphere (zinc(II) ion and donor atoms) with respect to the PDB reference structure. The average RMSD values for the binding site and the bound atoms are ≈0.7 and ≈0.3 Å, respectively. For the backbone, all values are less than 2.5 Å; the high fluctuation found for 1KOL is attributable to the oscillation of a C-terminal α-helix.

3.3. Energy of Binding of (R)-2-Benzyl-3-nitropropanoic Acid to Carboxypeptidase A

As described in Section 2.1, we used three different models (Table 2) to calculate absolute binding energies. For each model, we calculated the distribution of the COM–COM distance between the inhibitor and the enzyme obtained from the HREM stage (Figure 4). The experimental ligand–protein COM–COM is shown as a vertical green line in Figure 4. The COM–COM distance distribution is consistently centered at lower values with respect to the reference experimental COM–COM distance, showing that the inhibitor lingers in the binding pocket for all three models. The spread of the COM–COM distributions obtained during the HREM stage, with COM–COM distances extending in a range of 2–3 Å, is an indication of the quality of sampling during the HREM stage. Model B exhibits a broad distribution, with the COM–COM distance ranging between 10 and 13 Å. Models A and C present a narrower distance distribution; in particular in model C, the inhibitor interacts strongly with the zinc(II) ion, as inferred by the steepness of the corresponding potential of mean force (PMF) in the binding region (inset of Figure 4a–c). The enhancement of the ligand binding in going from model B to model C is due to larger electrostatic contributions in the bound state of model C. Such enhanced contribution in model C was obtained via the renormalization of the atomic charges in the bound ligand, accounting for the polarization effects induced by the zinc(II) cation. As explained in ref (59), the PMF on the COM–COM distance distribution provides valuable indications for binding. Inspection of the PMFs reported in the insets of Figure 4 shows that model B yields the weakest enzyme–inhibitor interaction, while model A and model C are expected to produce higher and comparable binding strength.

Figure 4.

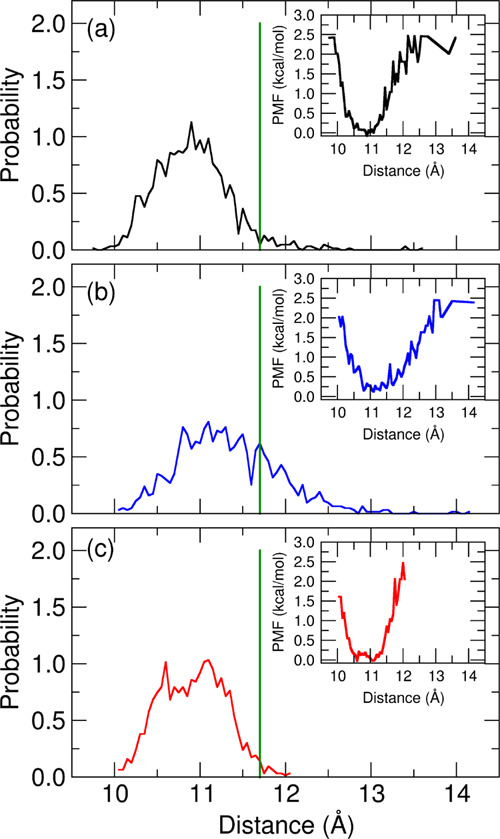
Figure 4

Open in a new tab

Probability distribution of the distance between the inhibitor and the carboxypeptidase A enzyme center of mass as obtained from the HREM simulations. (a) Model A; (b) model B; and (c) model C. The green line shows the distance extracted from the starting conformation of HREM simulation. In the inset is shown the relative potential mean field.

From the collection of annihilation and growth works for the bound and unbound states, respectively, we assessed the character of the distributions using the Anderson–Darling (AD) test statistic, A2.73,74 We further computed the correlation Pearson’s coefficients R between the discharging alchemical electrostatic (WQ) and Lennard-Jones (WLJ) works. Results for A2 and R are collected in Table 5. The work distribution for the common unbound state of all three models is non-normal with a high level of confidence. Concerning the bound-state distributions, model A and model B are found to be non-normal with a confidence level exceeding 99%. Model C is non-normal with a relatively low confidence level of 85%, corresponding to an AD test statistic of A2 = 0.58 (Table 5). On the other hand, the model C bound-state work distribution covers a range of more than 20 kcal mol–1, with the difference between the Jarzynski and Gaussian estimates for the annihilation free energy exceeding 12 kcal mol–1, a clear sign that the distribution is likely given by nontrivial mixtures of normal components. In this case, the Gaussian estimate is highly inaccurate, the only viable alternative being the standard Jarzynski estimate based on the exponential average e–βΔG = ⟨e–βΔW⟩. The latter, however, is imprecise due to its critical sensitivity to the poorly sampled left tails of the distributions.75,76 As explained in ref (54), we thus exploited the weak or negligible correlation (see Table 5, R values) between the discharging WQ and the Lennard-Jones annihilation work, WLJ, combining each value of the random variable (RV) WLJ with each value of the RV WQ, hence obtaining n2 work RVs W = WLJ + WQ instead of the original n. In this manner, we statistically boosted the exponential averages for all work distributions, increasing the number of points at low work values, thus obtaining more precise Jarzynski estimates. The standard and statistically boosted histograms of all bound-state annihilation work distributions and for the common unbound fast-growth work distribution (with an inverted sign) are shown in Figures 5 and 6.

Table 5. Anderson–Darling Test (A2) and Correlation Coefficient (R) between the Discharging Work and the Lennard-Jones Annihilation Work for the Bound State and the Common Unbound State of the Three Models.

model A2 (bound) A2 (unbound) R (bound) R (unbound)
A 4.06 4.92 –0.01 –0.09
B 2.37 4.92 –0.01 –0.09
C 0.58 4.92 –0.14 –0.09
Open in a new tab

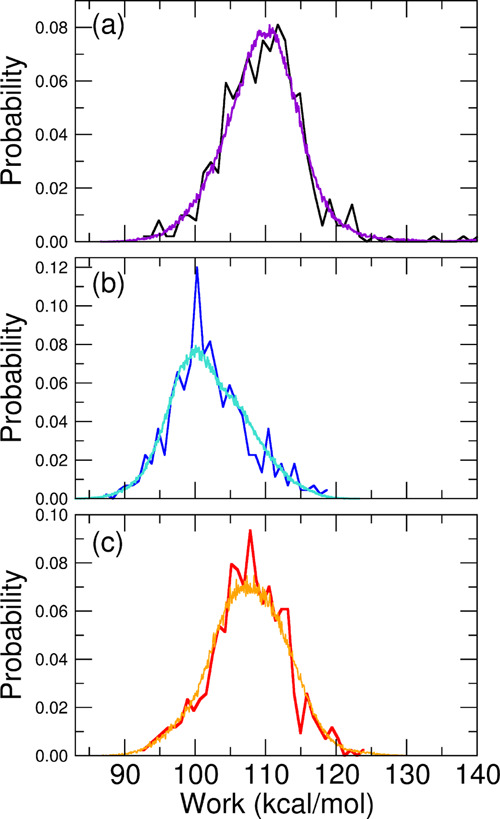
Figure 5.

Figure 5

Open in a new tab

Annihilation work distributions (W = WLJ + WQ) for the bound state obtained for model A (a), model B (b), and model C (c), with black, blue, and red lines representing standard distributions and violet, cyan, and orange lines representing the boosted ones.

Figure 6.

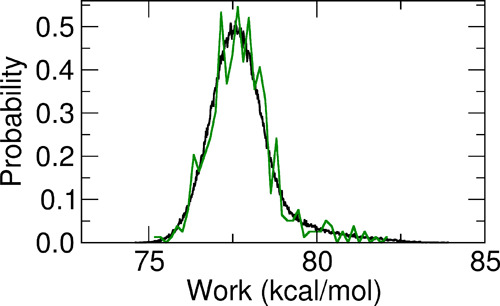
Figure 6

Open in a new tab

Standard (green line) and boosted (black line) growth work distributions (W = WLJ + WQ) for the unbound state.

As it can be seen, the boosted, more resolved histograms, computed on the 4802 discharging and Lennard-Jones combined work values, closely follow the standard noisy histograms as in a nonlinear regression fit. This is a consequence of the statistical independence of the two RVs associated with the discharging and Lennard-Jones annihilation works. When the corresponding R for the two RVs is close to zero, we trivially have P(W) = ∑iPLJ(Wi)PQ(W – Wi), namely, the boosted work distribution is given by the convolution of the Lennard-Jones and electrostatic work distributions.

In Table 6, we finally report the computed absolute dissociation free energies for the three models, where all bound and unbound annihilation free energies are calculated using boosted Jarzynski averages. The errors are standardly evaluated using bootstrap with resampling on the combined n2 work values. As it can be seen, model A, corresponding to a standard GAFF2 description of the ligand and the standard amber99sb-ildn FF for the zinc-protein, is quite accurate, overestimating the dissociation free energy by less than 1 kcal mol–1. Model B, on the other hand, where the ligand is parameterized with the standard GAFF2/AM1-BCC FF and where we used the modified (polarized) zinc-coordinating residues GLZ and HEZ replacing GLU and HIE in the amber99b-ildn FF, severely underestimates the binding strength of the ligand, yielding a dissociation free energy more than 5 kcal mol–1 below the experimental value. Such discrepancy is entirely due to neglecting the polarization effects of the zinc atoms on the zinc-coordinating groups of the ligand in the bound state, leading to a significant underestimation of the bound-state annihilation free energy. When, in model C, we replace the standard (GAFF2) AM1-BCC charges on the ligand with the new zinc-polarized charges (reported in Table S1 of the Supporting Information), polarization effects due to the zinc are restored, leading to a dissociation free energy that differs by less than 0.7 kcal mol–1 with respect to the experimental value. The remarkable improvement in going from model B to model C shows that the persistent polarization effects induced by the zinc atom in the bound state are important for all zinc-coordinating groups, including the ligand. Therefore, the ligand charge distribution must be coherently represented using the same computational protocol adopted for the zinc-coordinating HDZ, HEZ, GLZ, ASZ, and CYZ residues. On the other hand, our results show that the standard GAFF2/amber99sb-ildn approach, yielding Zn···O, Zn···N, or Zn···S distances well below the experimental values24 and neglecting completely polarization effects in the bound state, nonetheless produces a fairly accurate dissociation free energy, possibly due to a favorable compensation error. In summary, our new parameterization of ASP and GLU residues, together with the previous results for HIS and CYS, allows MD simulations to both correctly model the structural features of zinc(II)-binding sites and accurately compute the affinity constants of metal-binding inhibitors, with proper treatment of polarization effects while remaining in the context of a fixed-charge FF.

Table 6. Absolute Binding Free Energy Computed Using the Three Modelsa.

model ΔGb ΔGu ΔGbox ΔGfs ΔGCalc ΔGExp
A 93.63 ± 0.53 79.62 ± 0.03 –3.45 –0.23 –10.33 ± 0.56 –9.35
B 87.08 ± 0.87 79.62 ± 0.03 –3.53 –0.23 –3.70 ± 0.90 –9.35
C 91.49 ± 0.54 79.62 ± 0.03 –2.93 –0.23 –8.71 ± 0.57 –9.35
Open in a new tab
a

For each ΔGCalc, all of the contributions are reported following eq 1. The experimental value ΔGExp was obtained from ref (47). All values are in kcal mol–1.

4. Conclusions

In this work, we extended the protocol, successfully used to parameterize zinc-binding cysteinate and histidine residues,24 to zinc-binding glutamate and aspartate residues. The parameterization is based on a nonbonded model for the interaction between the metal ion and the protein. The polarization effects due to the zinc(II) ion have been included by defining new atomic charges for the residues, derived from accurate QM techniques on selected sites with a known 3D structure. Thus, we defined two new zinc(II)-coordinating residues, namely, GLZ (glutamate) and ASZ (aspartate).

We validated the FF by performing MD simulations on five zinc-proteins that belong to different superfamilies. These simulations produced stable structures for the metal site and were able to differentiate between the two Zn···Ox (O1 and O2) interactions with the carboxylate group. This reproduces well the monodentate coordination mode that is massively prevalent in all PDB structures of zinc-proteins.72 Importantly, this structural feature is not explicitly imposed by constraining metal–donor distances, as we are implementing a nonbonded model, and is entirely the result of the intrinsic characteristics of our FF.

We then evaluated the application of the new FF to the challenging computation of the inhibitor constant of (R)-2-benzyl-3-nitropropanoic acid against carboxypeptidase A, using the FS technique. On this specific example, our improved FF performed modestly better than the traditional AMBER FF. Interestingly, the comparison of the results obtained with different models for the ligand highlighted that the metal-induced local polarization effects in the bound state have a dramatic effect on the accuracy of the calculation when our FF for the protein is used. This can be regarded as a consequence of our FF directly taking into account the polarization effects on the group coordinating the metal in the bound state.

It must be stressed that both our protocol, with different environment-related polarized charges on the ligand, and the standard AMBER parameterization, with fixed charges in the bulk and bound states, provided good results for the binding affinity. It is possible that this is due to error compensation in the two legs of the alchemical thermodynamic cycle. Therefore, it will be important to systematically assess the performances of both approaches in other systems in which an organic ligand (e.g., inhibitor) is directly binding to a zinc(II) ion. This will define the reliability of our description in comparison to that of the AMBER FF and the importance of metal-induced charge reorganization effects on the coordinating residues and ligands.

Acknowledgments

This work was supported by the Università degli Studi di Firenze (grant “Computational chemistry of metalloproteomes to shed light on zinc ion simbiology”) and the Interuniversity Consortium of Magnetic Resonance of MetalloProteins (CIRMMP). The authors acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources and support (HP10C06ESW). The authors thank MIUR−Italy (“Progetto Dipartimenti di Eccellenza 2018-2022” allocated to Department of Chemistry “Ugo Schiff”) and Fondazione Cassa Risparmio di Firenze (project title “Caratteristiche strutturali dei siti metallici nelle macromolecole biologiche e loro impatto sui processi cellulari di salute umana”). This work was partly funded by the European Union’s Horizon 2020 research and innovation program under grant agreement no. 777536. We thank the anonymous reviewers for their constructive suggestions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c01337.

  • 2RFH and cluster structure; reparameterized atomic charges for inhibitor (R)-2-benzyl-3-nitropropanoic acid; angle and radial distribution functions between interacting atoms and zinc(II) calculated for 4YBG, 2CDB, 1V4Y, 1KOL, and 4Z1D proteins; pair distribution function between interacting atoms and zinc(II) for 4YBG, 2CDB, 1V4Y, and 1KOL proteins; RMSD values of the protein backbone, metal-binding site, and binding atoms calculated for 4YBG, 2CDB, 1V4Y, 1KOL, and 4Z1D proteins (PDF)

  • Compressed archive containing the topological and parameter files for the new residues GLZ and ASZ (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ao0c01337_si_001.pdf (2.8MB, pdf)
ao0c01337_si_002.zip (2.9KB, zip)

References

  1. Santos H. O.; Teixeira F. J.; Schoenfeld B. J. Dietary vs. Pharmacological Doses of Zinc: A clinical Review. Clin. Nutr. 2020, 1345–1353. 10.1016/j.clnu.2019.06.024. [DOI] [PubMed] [Google Scholar]
  2. Andreini C.; Bertini I.; Cavallaro G. Minimal Functional Sites Allow a Classification of Zinc Sites in Proteins. PLoS One 2011, 6, e26325 10.1371/journal.pone.0026325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bertini A.; Sigel I.; Sigel H.. Handbook on Metalloproteins; Marcel Dekker: New York, 2001. [Google Scholar]
  4. Frausto da Silva J. J. R.; Williams R. J. P.. The Biological Chemistry of the Elements: The Inorganic Chemistry of Life; Oxford University Press: New York, 2001. [Google Scholar]
  5. Tiraboschi G.; Gresh N.; Giessner-Prettre C.; Pedersen L. G.; Deerfield D. W. Parallel Ab Initio and Molecular Mechanics Investigation of Polycoordinated Zn(II) Complexes with Model Hard and Soft Ligands: Variations of Binding Energy and of Its Components with Number and Charges of Ligands. J. Comput. Chem. 2000, 21, 1011–1039. . [DOI] [Google Scholar]
  6. Gresh N.; Derreumaux P. Generating Conformations for Two Zinc-Binding Sites of HIV-1 Nucleocapsid Protein from Random Conformations by a Hierarchical Procedure and Polarizable Force Field. J. Phys. Chem. B 2003, 107, 4862–4870. 10.1021/jp022527z. [DOI] [Google Scholar]
  7. Sakharov D. V.; Lim C. Zn Protein Simulations Including Charge Transfer and Local Polarization Effects. J. Am. Chem. Soc. 2005, 127, 4921–4929. 10.1021/ja0429115. [DOI] [PubMed] [Google Scholar]
  8. Fracchia F.; Del Frate G.; Mancini G.; Rocchia W.; Barone V. Force Field Parametrization of Metal Ions from Statistical Learning Techniques. J. Chem. Theory Comput. 2018, 14, 255–273. 10.1021/acs.jctc.7b00779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Del Frate G.; Nikitin A. Including Electronic Screening in Classical Force Field of Zinc Ion for Biomolecular Simulations. ChemistrySelect 2018, 3, 12367–12370. 10.1002/slct.201802864. [DOI] [Google Scholar]
  10. Li P.; Merz K. M. Metal Ion Modeling Using Classical Mechanics. Chem. Rev. 2017, 117, 1564–1686. 10.1021/acs.chemrev.6b00440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Duarte F.; Bauer P.; Barrozo A.; Amrein B. A.; Purg M.; Åqvist J.; Kamerlin S. C. L. Force Field Independent Metal Parameters Using a Nonbonded Dummy Model. J. Phys. Chem. B 2014, 118, 4351–4362. 10.1021/jp501737x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Zhu T.; Xiao X.; Ji C.; Zhang J. Z. H. A New Quantum Calibrated Force Field for Zinc-Protein Complex. J. Chem. Theory Comput. 2013, 9, 1788–1798. 10.1021/ct301091z. [DOI] [PubMed] [Google Scholar]
  13. Seminario J. M. Calculation of Intramolecular Force Fields from Second-Derivative Tensors. Int. J. Quantum Chem. 1996, 60, 1271–1277. . [DOI] [Google Scholar]
  14. Nilsson K.; Lecerof D.; Sigfridsson E.; Ryde U. An Automatic Method to Generate Force-Field Parameters for Hetero-Compounds. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2003, 59, 274–289. 10.1107/S0907444902021431. [DOI] [PubMed] [Google Scholar]
  15. Norrby P.-O.; Liljefors T. Automated Molecular Mechanics Parameterization with Simultaneous Utilization of Experimental and Quantum Mechanical Data. J. Comput. Chem. 1998, 19, 1146–1166. . [DOI] [Google Scholar]
  16. Rydberg P.; Olsen L.; Norrby P.-O.; Ryde U. General Transition-State Force Field for Cytochrome P450 Hydroxylation. J. Chem. Theory Comput. 2007, 3, 1765–1773. 10.1021/ct700110f. [DOI] [PubMed] [Google Scholar]
  17. Hoops S. C.; Anderson K. W.; Merz K. M. Force Field Design for Metalloproteins. J. Am. Chem. Soc. 1991, 113, 8262–8270. 10.1021/ja00022a010. [DOI] [Google Scholar]
  18. Yu Z.; Li P.; Merz K. M. Extended Zinc AMBER Force Field (EZAFF). J. Chem. Theory Comput. 2018, 14, 242–254. 10.1021/acs.jctc.7b00773. [DOI] [PubMed] [Google Scholar]
  19. Li P.; Merz K. M. Taking into Account the Ion-Induced Dipole Interaction in the Nonbonded Model of Ions. J. Chem. Theory Comput. 2014, 10, 289–297. 10.1021/ct400751u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Panteva M. T.; Giambaşu G. M.; York D. M. Force Field for Mg2+, Mn2+, Zn2+, and Cd2+ Ions That Have Balanced Interactions with Nucleic Acids. J. Phys. Chem. B 2015, 119, 15460–15470. 10.1021/acs.jpcb.5b10423. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Ponder J. W.; Case D. A.. Protein Simulations; Advances in Protein Chemistry; Academic Press, 2003; Vol. 66, pp 27–85. [DOI] [PubMed] [Google Scholar]
  22. Vanommeslaeghe K.; Hatcher E.; Acharya C.; Kundu S.; Zhong S.; Shim J.; Darian E.; Guvench O.; Lopes P.; Vorobyov I.; Mackerell A. D. CHARMM General Force Field: A Force Field for Drug-Like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2010, 31, 671–690. 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Dodda L. S.; Vilseck J. Z.; Tirado-Rives J.; Jorgensen W. L. 1.14*CM1A-LBCC: Localized Bond-Charge Corrected CM1A Charges for Condensed-Phase Simulations. J. Phys. Chem. B 2017, 121, 3864–3870. 10.1021/acs.jpcb.7b00272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Macchiagodena M.; Pagliai M.; Andreini C.; Rosato A.; Procacci P. Upgrading and Validation of the AMBER Force Field for Histidine and Cysteine Zinc(II)-Binding Residues in Sites with Four Protein Ligands. J. Chem. Inf. Model. 2019, 59, 3803–3816. 10.1021/acs.jcim.9b00407. [DOI] [PubMed] [Google Scholar]
  25. Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. wwPDB consortium Protein Data Bank: the Single Global Archive for 3D Macromolecular Structure Data Nucleic Acids Res. 2019, 47, D520–D528. 10.1093/nar/gky949. [DOI] [PMC free article] [PubMed]
  27. Pohorille A.; Jarzynski C.; Chipot C. Good Practices in Free-Energy Calculations. J. Phys. Chem. B 2010, 114, 10235–10253. 10.1021/jp102971x. [DOI] [PubMed] [Google Scholar]
  28. Putignano V.; Rosato A.; Banci L.; Andreini C. MetalPDB in 2018: a Database of Metal Sites in Biological Macromolecular Structures. Nucleic Acids Res. 2018, 46, D459–D464. 10.1093/nar/gkx989. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Bayly C. I.; Cieplak P.; Cornell W.; Kollman P. A. A Well-behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: the RESP Model. J. Phys. Chem. A 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
  30. CP2K, version 6.1; CP2K Developers Group, 2018. CP2K is Freely Available from: https://www.cp2k.org/.
  31. Hutter J.; Iannuzzi M.; Schiffmann F.; VandeVondele J. CP2K: Atomistic Simulations of Condensed Matter Systems. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014, 4, 15–25. 10.1002/wcms.1159. [DOI] [Google Scholar]
  32. Pronk S.; Páll S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; van der Spoel D.; Hess B.; Lindahl E. GROMACS 4.5: a High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Van Der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A. E.; Berendsen H. J. C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
  34. Berendsen H. J. C.; Grigera J. R.; Straatsma T. P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. A 1987, 91, 6269–6271. 10.1021/j100308a038. [DOI] [Google Scholar]
  35. Pagliai M.; Macchiagodena M.; Procacci P.; Cardini G. Evidence of a Low-High Density Turning Point in Liquid Water at Ordinary Temperature under Pressure: A Molecular Dynamics Study. J. Phys. Chem. Lett. 2019, 10, 6414–6418. 10.1021/acs.jpclett.9b02724. [DOI] [PubMed] [Google Scholar]
  36. Lindorff-Larsen K.; Piana S.; Palmo K.; Maragakis P.; Klepeis J. L.; Dror R. O.; Shaw D. E. Improved Side-Chain Torsion Potentials for the Amber ff99SB Protein Force Field. Proteins 2010, 78, 1950–1958. 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Di Nola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  38. Bussi G.; Donadio D.; Parrinello M. Canonical Sampling Through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  39. Hess B.; Bekker H.; Berendsen H.; Fraaije J. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
  40. Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An N log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
  41. Lorentz H. A. Ueber die Anwendung des Satzes vom Virial in der Kinetischen Theorie der Gase. Ann. Phys. 1881, 248, 127–136. 10.1002/andp.18812480110. [DOI] [Google Scholar]
  42. Marcellin B. Sur Le Mélange Des Gaz. C. R. Acad. Sci. 1898, 126, 1703–1855. [Google Scholar]
  43. Procacci P. Dissociation Free Energies of Drug-receptor Systems Via Non-equilibrium Alchemical Simulations: a Theoretical Framework. Phys. Chem. Chem. Phys. 2016, 18, 14991–15004. 10.1039/C5CP05519A. [DOI] [PubMed] [Google Scholar]
  44. Nerattini F.; Chelli R.; Procacci P. II Dissociation Free Energies in Drug-receptor Systems Via Nonequilibrium Alchemical Simulations: Application to the FK506-related Immunophilin Ligands. Phys. Chem. Chem. Phys. 2016, 18, 15005–15018. 10.1039/C5CP05521K. [DOI] [PubMed] [Google Scholar]
  45. Procacci P.; Cardelli C. Fast Switching Alchemical Transformations in Molecular Dynamics Simulations. J. Chem. Theory Comput. 2014, 10, 2813–2823. 10.1021/ct500142c. [DOI] [PubMed] [Google Scholar]
  46. Sandberg R. B.; Banchelli M.; Guardiani C.; Menichetti S.; Caminati G.; Procacci P. Efficient Nonequilibrium Method for Binding Free Energy Calculations in Molecular Dynamics Simulations. J. Chem. Theory Comput. 2015, 11, 423–435. 10.1021/ct500964e. [DOI] [PubMed] [Google Scholar]
  47. Wang S.-H.; Wang S.-F.; Xuan W.; Zeng Z.-H.; Jin J.-Y.; Ma J.; Tian G. R. Nitro as a Novel Zinc-binding Group in the Inhibition of Carboxypeptidase A. Bioorg. Med. Chem. 2008, 16, 3596–3601. 10.1016/j.bmc.2008.02.010. [DOI] [PubMed] [Google Scholar]
  48. Harger M.; Li D.; Wang Z.; Dalby K.; Lagardère L.; Piquemal J.-P.; Ponder J.; Ren P. Tinker-OpenMM: Absolute and Relative Alchemical Free Energies Using AMOEBA on GPUs. J. Comput. Chem. 2017, 38, 2047–2055. 10.1002/jcc.24853. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Lee T.-S.; Cerutti D. S.; Mermelstein D.; Lin C.; LeGrand S.; Giese T. J.; Roitberg A.; Case D. A.; Walker R. C.; York D. M. GPU-Accelerated Molecular Dynamics and Free Energy Methods in Amber18: Performance Enhancements and New Features. J. Chem. Inf. Model. 2018, 58, 2043–2050. 10.1021/acs.jcim.8b00462. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Klimovich P. V.; Mobley D. L. A Python Tool to Set up Relative Free Energy Calculations in GROMACS. J. Comput.-Aided Mol. Des. 2015, 29, 1007–1014. 10.1007/s10822-015-9873-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Isik M.; Levorse D.; Mobley D. L.; Rhodes T.; Chodera J. D. Octanol-water Partition Coefficient Measurements for the SAMPL6 Blind Prediction Challenge. J. Comput.-Aided Mol. Des. 2020, 405–420. 10.1007/s10822-019-00271-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Rizzi A.; Murkli S.; McNeill J. N.; Yao W.; Sullivan M.; Gilson M. K.; Chiu M. W.; Isaacs L.; Gibb B. C.; Mobley D. L.; Chodera J. D. Overview of the SAMPL6 Host-guest Binding Affinity Prediction Challenge. J. Comput.-Aided Mol. Des. 2018, 32, 937–963. 10.1007/s10822-018-0170-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. The SAMPL7 Blind Prediction Challenges for Computational Chemistry, 2020. https://github.com/samplchallenges/SAMPL7 (accessed March 22, 2020).
  54. Procacci P. Accuracy, Precision, and Efficiency of Nonequilibrium Alchemical Methods for Computing Free Energies of Solvation. I. Bidirectional Approaches. J. Chem. Phys. 2019, 151, 144113 10.1063/1.5120615. [DOI] [PubMed] [Google Scholar]
  55. Crooks G. E. Nonequilibrium Measurements of Free Energy Differences for Microscopically Reversible Markovian Systems. J. Stat. Phys. 1998, 90, 1481–1487. 10.1023/A:1023208217925. [DOI] [Google Scholar]
  56. Gilson M. K.; Given J. A.; Bush B. L.; McCammon J. A. The Statistical-Thermodynamic Basis for Computation of Binding Affinities: A Critical Review. Biophys. J. 1997, 72, 1047–1069. 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Procacci P.; Chelli R. Statistical Mechanics of Ligand-Receptor Noncovalent Association, Revisited: Binding Site and Standard State Volumes in Modern Alchemical Theories. J. Chem. Theory Comput. 2017, 13, 1924–1933. 10.1021/acs.jctc.6b01192. [DOI] [PubMed] [Google Scholar]
  58. Zhang L.; Hermans J. Hydrophilicity of Cavities in Proteins. Proteins: Struct., Funct., Bioinf. 1996, 24, 433–438. . [DOI] [PubMed] [Google Scholar]
  59. Procacci P.; Guarrasi M.; Guarnieri G. SAMPL6 Host-guest Blind Predictions Using a Non Equilibrium Alchemical Approach. J. Comput.-Aided Mol. Des. 2018, 32, 965–982. 10.1007/s10822-018-0151-9. [DOI] [PubMed] [Google Scholar]
  60. Darden T.; Pearlman D.; Pedersen L. G. Ionic Charging Free Energies: Spherical Versus Periodic Boundary Conditions. J. Chem. Phys. 1998, 109, 10921–10935. 10.1063/1.477788. [DOI] [Google Scholar]
  61. Procacci P. PrimaDORAC: A Free Web Interface for the Assignment of Partial Charges, Chemical Topology, and Bonded Parameters in Organic or Drug Molecules. J. Chem. Inf. Model. 2017, 57, 1240–1245. 10.1021/acs.jcim.7b00145. [DOI] [PubMed] [Google Scholar]
  62. Valiev M.; Bylaska E.; Govind N.; Kowalski K.; Straatsma T.; Dam H. V.; Wang D.; Nieplocha J.; Apra E.; Windus T.; de Jong W. NWChem: A Comprehensive and Scalable Open-source Solution for Large Scale Molecular Simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. 10.1016/j.cpc.2010.04.018. [DOI] [Google Scholar]
  63. Becke A. D. Density-functional Exchange-energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  64. Jensen F. Segmented Contracted Basis Sets Optimized for Nuclear Magnetic Shielding. J. Chem. Theory Comput. 2015, 11, 132–138. 10.1021/ct5009526. [DOI] [PubMed] [Google Scholar]
  65. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  66. Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
  67. Parrinello M.; Rahman A. Crystal Structure and Pair Potentials: A Molecular-Dynamics Study. Phys. Rev. Lett. 1980, 45, 1196–1199. 10.1103/PhysRevLett.45.1196. [DOI] [Google Scholar]
  68. Tuckerman M.; Berne B. J.; Martyna G. J. Reversible Multiple Time Scale Molecular Dynamics. J. Chem. Phys. 1992, 97, 1990–2001. 10.1063/1.463137. [DOI] [Google Scholar]
  69. Procacci P.; Darden T. A.; Paci E.; Marchi M. ORAC: A Molecular Dynamics Program to Simulate Complex Molecular Systems with Realistic Electrostatic Interactions. J. Comput. Chem. 1997, 18, 1848–1862. . [DOI] [Google Scholar]
  70. Marchi M.; Procacci P. Coordinates Scaling and Multiple Time Step Algorithms for Simulation of Solvated Proteins in the NPT Ensemble. J. Chem. Phys. 1998, 109, 5194–5202. 10.1063/1.477136. [DOI] [Google Scholar]
  71. Procacci P. Hybrid MPI/OpenMP Implementation of the ORAC Molecular Dynamics Program for Generalized Ensemble and Fast Switching Alchemical Simulations. J. Chem. Inf. Model. 2016, 56, 1117–1121. 10.1021/acs.jcim.6b00151. [DOI] [PubMed] [Google Scholar]
  72. Tamames B.; Sousa S. F.; Tamames J.; Fernandes P. A.; Ramos M. J. Analysis of Zinc-ligand Bond Lengths in Metalloproteins: Trends and Patterns. Proteins 2007, 69, 466–475. 10.1002/prot.21536. [DOI] [PubMed] [Google Scholar]
  73. Anderson T. W.; Darling D. A. A Test of Goodness of Fit. J. Am. Stat. Assoc. 1954, 49, 765–769. 10.1080/01621459.1954.10501232. [DOI] [Google Scholar]
  74. Stephens M. A. Tests of Fit for the Logistic Distribution Based on the Empirical Distribution Function. Biometrika 1979, 66, 591–595. 10.1093/biomet/66.3.591. [DOI] [Google Scholar]
  75. Hummer G. Fast-growth Thermodynamic Integration: Error and Efficiency Analysis. J. Chem. Phys. 2001, 114, 7330–7337. 10.1063/1.1363668. [DOI] [Google Scholar]
  76. Gore J.; Ritort F.; Bustamante C. Bias and Error in Estimates of Equilibrium Free-energy Differences from Nonequilibrium Measurements. Proc. Natl. Acad. Sci. U.S.A. 2003, 100, 12564–12569. 10.1073/pnas.1635159100. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c01337_si_001.pdf (2.8MB, pdf)
ao0c01337_si_002.zip (2.9KB, zip)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES