Quantifying epileptogenesis in rats with spontaneous and responsive brain state dynamics

Abstract

There is a crucial need to identify biomarkers of epileptogenesis that will help predict later development of seizures. This work identifies two novel electrophysiological biomarkers that quantify epilepsy progression in a rat model of epileptogenesis. The long-term tetanus toxin rat model was used to show the development and remission of epilepsy over several weeks. We measured the response to periodic electrical stimulation and features of spontaneous seizure dynamics over several weeks. Both biomarkers showed dramatic changes during epileptogenesis. Electrically induced responses began to change several days before seizures began and continued to change until seizures resolved. These changes were consistent across animals and allowed development of an algorithm that could differentiate which animals would later develop epilepsy. Once seizures began, there was a progression of seizure dynamics that closely follows recent theoretical predictions, suggesting that the underlying brain state was changing over time. This research demonstrates that induced electrical responses and seizure onset dynamics are useful biomarkers to quantify dynamical changes in epileptogenesis. These tools hold promise for robust quantification of the underlying epileptogenicity and prediction of later development of seizures.

This work identified two novel electrophysiological biomarkers that quantify epilepsy progression in the tetanus toxin rat model: the response to periodic electrical stimulation and features of spontaneous seizure dynamics. Both biomarkers quantify the evolution of epileptogenesis over weeks.

Graphical Abstract

Graphical Abstract.

Introduction

Epileptogenesis is defined as the process by which a normally functioning brain network develops recurrent, spontaneous seizures. This process is incompletely understood, but likely involves a progression of biochemical, anatomical and physiological changes (Pitkanen et al., 2015). Understanding epileptogenesis and identifying biomarkers associated with it are two of the ‘Benchmarks for Epilepsy Research’ (Long et al., 2016). Current treatment for patients with epilepsy is to administer antiepileptic drugs after seizures begin, which may control the seizures but does not address the underlying pathology (Herman, 2006). This strategy is problematic in patients with post-injury epilepsy—epilepsy caused by a discrete brain insult (e.g. injury or infection)—as there is often a latent period before developing seizures in which it is unclear how to prevent epilepsy. It is hypothesized that medical interventions applied during the latent period could prevent epilepsy; however, the selection, timing and duration of anti-epileptogenic agents is difficult because the mechanisms and timing of epileptogenesis after brain insult are not well understood (Herman, 2002) and not all brain injuries result in epilepsy (Pitkanen and Immonen, 2014). Reliable biomarkers of epileptogenesis may help address these problems.

One of the foremost challenges in assessing epileptogenesis is that the primary outcome (seizures) is not present during the latent period. Even after seizures begin, it is hard to quantify epileptogenesis because seizures are infrequent. Molecular biomarkers have shown promise, but are still very difficult to acquire and analyse (Lukasiuk and Becker, 2014; Luna-Munguia et al., 2019). Others have used long-term electrophysiological recordings, showing that epileptic spikes often appear much earlier than the first seizure (Kadam et al., 2010; White et al., 2010) and that epileptogenesis is not a stepwise process; it progresses even after the first seizure (Dudek and Staley, 2011). These studies suggest that better biomarkers of epileptogenesis are required to characterize the pathology both before and after seizures begin.

In recent years, there has been great interest in predicting whether epilepsy will result after a brain insult. Recent studies using prolonged EEG recordings have shown several potential biomarkers: sleep stage features in the fluid percussion model (Andrade et al., 2017), spectral power variability in the ischaemia model (Milikovsky et al., 2017) and heart rate fluctuations in the malaria model (Bahari et al., 2018). These biomarkers have shown great promise for identifying epileptogenesis biomarkers that might predict if epilepsy will occur. This work takes a different approach: comparing two different biomarkers based upon the underlying brain dynamics. Both of these biomarkers are designed to assess the dynamics over the course of the entire seizure period. Such research is difficult because the brain undergoes changes over time, and it is hard to discern which changes are due to epilepsy versus normal aging or damage from the experiment. We therefore chose the tetanus toxin rat model. This model is unique because the brain develops epilepsy for several weeks then spontaneously remits, allowing us to compare the response of two different dynamical biomarkers over the entire course of epileptogenesis.

We utilize two electrophysiological methods to quantify epileptogenesis. One is to use electrical stimulation, or ‘probing’, to quantify neural excitability. Outside of epilepsy, previous research has shown that induced brain responses are good prognostic predictors of overall health condition after brain injury (Narayan et al., 1981; Carter and Butt, 2005). Within epilepsy, a range of probing methods (photic, electrical and transcranial magnetic stimulation) were found to be correlated with impending seizure onset, sleep-wake cycle, rate of interictal discharges and seizure onset location (Kalitzin et al., 2002; Kalitzin et al., 2005; Badawy et al., 2009; Freestone et al., 2011; Luttjohann et al., 2011; Badawy et al., 2013a, b; Medeiros et al., 2014; Wendling et al., 2016), but have not been tested through the full development of epilepsy. Thus, the response to probing stimulation has significant potential as a biomarker of epileptogenesis.

The second method is to track the brain system by characterizing seizures over time. While the current standard for seizure classification is based on clinical characteristics (Fisher et al., 2017), we utilize a scientifically based seizure classification system based on the first principles of dynamics theory (Jirsa et al., 2014; Saggio et al., 2017; Saggio et al., 2020). In short, this classification system characterizes seizures by focusing on the transition from normal (non-oscillatory state) brain activity to seizure (oscillatory state) activity. In dynamic systems, these types of transitions represent a sudden qualitative or topological change in the system, which is known mathematically as a bifurcation. The utility of this classification system lies in its potential ability to track changes in brain states and make rational predictions about certain constraints and behaviours likely to occur. For instance, within dynamic theory if a system produces a specific type of bifurcation at time point A, and then produces a different type of bifurcation at a later time point B, then it suggests the presence of a fundamental change in the system between time points A and B. Relating this to epileptogenesis, if we observe changes in the types of seizure transitions over time, then we can use that as a way to quantify brain state changes. From a practical standpoint, dynamical theory predicts that different bifurcations can be distinguished by analysing the spike amplitudes (SA), inter-spike intervals (ISI) and presence of baseline shifts (Jirsa et al., 2014). In addition, it also predicts that there will be different responses to perturbing stimuli when the brain is close to seizure threshold (Ranjan and Abed, 2000; Yaghoobi et al., 2001). In other words, the theory predicts that seizure dynamics and the response to probing stimuli are related. We hypothesize that, as the brain goes through the process of epileptogenesis, it will have different behaviours that can be measured by either characterizing the seizure dynamics or analysing the response to different probing stimulation.

To test this hypothesis, we performed a continuous, long-term study of electrically induced brain responses during epileptogenesis in an animal model. We measure the response to probing stimuli over the entirety of epileptogenesis, from before seizures began until after they resolved, a period of several weeks. We quantify the changes in both seizure onset dynamics and characteristics of interictal, electrically evoked responses throughout the course of the study. We find that these two measurements are closely linked, suggesting that the underlying brain state is changing during epileptogenesis, which produces alterations in seizure characteristics simultaneously with differences in the response to electrical stimulation. Most importantly, we find that the response to probing stimuli can help differentiate which subjects will later develop epilepsy.

Materials and methods

Animal model of epileptogenesis

This study uses the intra-hippocampal tetanus toxin rat model because it produces frequent, stereotyped, electro-clinical events that spontaneously remit 6–8 weeks after one stereotaxic toxin injection (0.1 g/l—30 ng of tetanus toxin dissolved in 300 nl solution) (Jefferys and Walker, 2006). For sham Control animals, the same procedure was performed with an injection of phosphate-buffered saline. The model can be characterized by three phases (Fig. 1). The Pre-seizure phase is the latency period, which is defined as the time between tetanus toxin injection and the first seizure. The Rising-seizure phase is marked by the emergence of seizures, where daily seizure rate (SR) begins small and increases as time progresses. The final, Falling-seizure phase begins when the SR reaches its maximum, known as the inflection point, and lasts until seizures have completely remitted. We postulate these three epochs of differing epileptic behaviour are representative of quantifiably different brain states, making the tetanus toxin model an ideal candidate for analysis. The experiments consisted of repeated, longitudinal measurements of the characteristics of spontaneous seizures as well as the response to a probing stimulation (see Fig. 2 for the data process pipeline). The experiments were approved by the St. Vincent’s Hospital (Melbourne) Animal Ethics Committee and were conducted in accordance with the ‘Australian Code for the Care and Use of Animals for Scientific Purposes, 8th Edition’ (2013).

Figure 1.

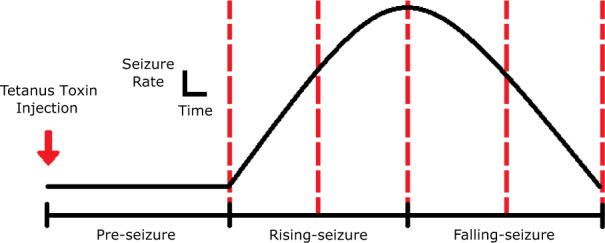
Progression of epileptogenesis—representation of an animal’s SR over time in the tetanus toxin model. The Pre-seizure period refers to the latency between the injection and the first observed seizure. The Rising-seizure period represents the emergence of seizures coupled with increasing SR before the inflection point. The Falling-seizure period starts at the inflection point and has a decreasing SR moving towards seizure remission. Dotted vertical lines represent a simple quarterly viewpoint beginning at the emergence of seizures.

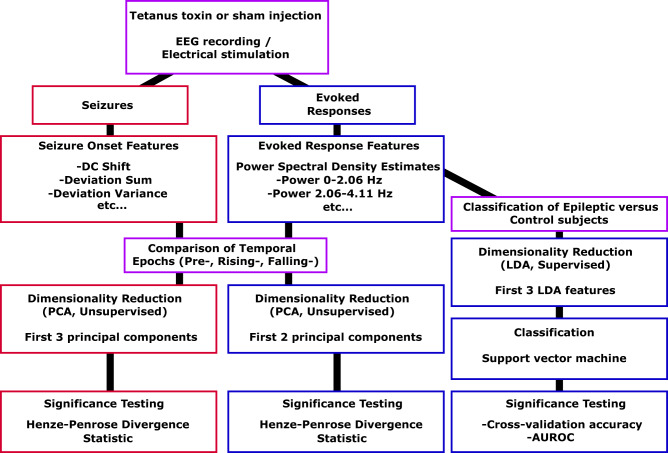
Figure 2.

Data pipeline diagram. All animals received an injection of either tetanus toxin or saline, then began EEG recording with the intermittent stimulation. EEG recordings from each animal contained data both from seizures (in the Experimental group) and from evoked responses (in both groups), which were analysed separately. Independent features are computed on seizures and evoked responses. For investigating changes within animals, dimensionality reduction is performed using unsupervised learning that maximizes the variance. We used divergence measures to test how separable the different groups were (e.g. Pre-seizure versus Rising-seizure versus Falling-seizure phases, early versus late seizures). For investigating changes between Experimental and Control evoked responses, supervised learning was used for dimensionality reduction. Classification accuracy was measured using both cross-validation and AUROC metrics. AUROC = area under the ROC curve; LDA = linear discriminant analysis; PCA = principal component analysis.

Stimulation paradigm

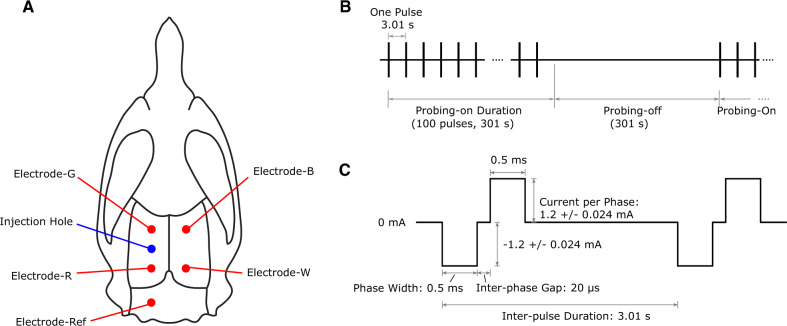
Five stainless steel epidural screw electrodes (major diameter: 1.524 mm, E363/20/SPC, wire length: 15 mm, Plastics One Inc., VA, USA), which included one reference, were implanted in each animal with a configuration shown in Fig. 3A. Setting the bregma reference point as the origin (0,0), the electrode locations (Anteroposterior, Mediolateral) were (in mm): B (−1.2, +3.0), W (−6.8, +3.0), G (−1.2, −3.0), R (−6.8, −3.0) and Ref (−10.6, −3.0). Note that our pilot animal (Control 1) had different anteroposterior coordinates for electrodes W (−5.6), R (−5.6) and Ref (−10.1), but these coordinates were changed in subsequent animals as the posterior electrodes were found to be too close to the anterior electrodes such that the anterior and posterior electrode pairs could not cover the length of the hippocampi along the sagittal planes at ±3.0 mm from the midline of the head. Electrodes B, W, G and R were connected to an off-the-shelf EEG acquisition system (Grael, Compumedics Ltd., VIC, Australia). Electrodes G and R were momentarily switched to be the stimulation source and sink, respectively, of electrical current for discharging one biphasic stimulus. These electrodes were chosen for stimulation as they were the closest to the tetanus toxin injection site, which is deemed to be the most representative of epileptic tissue. Stimulation began 2 days after tetanus toxin injection and comprised alternating probing-on and probing-off phases. The probing-on phase consisted of 100 biphasic pulses (phase-width 0.5 ms, current/phase: 1.2 ± 0.024 mA, interphase gap: 20 µs) over a 301 s period, with an inter-pulse interval of 3.01 s. The electrodes were tested via cyclic voltammetry in saline to ensure our stimulation parameters did not cause unwanted electrochemical reactions. It was found that these electrodes could handle up to 5 µC before having any potentially irreversible reaction. Our stimulation produces 0.6 µC per phase. The probing-off phase did not employ stimulation and was also set to a 301 s period (see Fig. 3B). Stimulation continued (∼5 min on, ∼5 min off) without interruption for the entire experiment except for 1-h daily check-ups. The same procedure was performed on the Control animals.

Figure 3.

Electrode placement and stimulation pattern—(A) Example rat skull diagram showing the tetanus toxin injection site and electrode placements. Electrodes G and R are also the stimulating electrodes. (B) Example of the pulse trains and timing of stimulation, which occurred every 3.01 s for a total Probing-on duration of 301 s. Each vertical line represents a single pulse waveform. (C) Waveform used for the stimulation.

Experimental procedure

Nine male Sprague-Dawley rats, obtained from the Animal Resources Centre (WA, Australia), were used for this experiment. Only male rats were used to avoid any effects that sex and the oestrous cycle might have on the probing responses. These rats were split into sham Control (3) and Experimental (6) groups. For each rat, a single, intra-hippocampal injection of tetanus toxin (Experimental) or phosphate-buffered saline (Control) was administered on Day −1 and subjects were transferred to the EEG recording room on Day 1, upon which recording and electrical probing protocols were immediately conducted. Data were recorded continuously in 23-h intervals, allowing a 1-h window for daily maintenance checks and data backup. Animals were under investigation for 9–10 weeks. All recordings were sampled at 2048 Hz with direct current (DC) coupling using an EEG acquisition system. The DC coupling assured that lower frequencies such as DC shifts were observed. Electrical probing was administered via a stimulator (neuroBi, custom built jointly by the University of Melbourne and Bionics Institute of Australia, VIC, Australia). More details about the stimulator have been published previously (Slater et al., 2015). The dark/light cycle in the recording room was controlled by a stand-alone timer with 8-h dark time and 16-h light time. The temperature inside the room was controlled within the range 21–26°C. Each rat was housed individually with ad libitum access to food and water.

Seizure detection

Seizures were marked by a custom-designed seizure detection algorithm, then verified by manual review. The EEG signal processing steps were as follows: (i) Every stimulation artefact was replaced by a line interpolating two end points of that artefact. This allowed the seizure detector to be stable, as stimulation artefact would always trip the detector. Later processing steps ignored the data from this interpolation, so it had no effect on final results. (ii) Signals were filtered by a third-order Butterworth IIR high-pass filter that had −3 dB cut-off frequency at 1 Hz. (iii) A spectrogram was generated with the following settings: 4096-point (2 s) Blackman-Harris window and 50% window length overlap. (iv) The 13–48 Hz band power was calculated by integrating the power spectral density between 13 and 48 Hz. Seizure activities contained higher than usual power across the whole available bandwidth. However, the frequency band below 13 Hz was contaminated by residual stimulation artefact and the 50 Hz frequency band was contaminated by power line noise. Therefore, the 13–48 Hz frequency band was chosen for seizure detection. (v) A 5-point median filter was applied on the 13–48 Hz band power. (vi) A 5 min (2.5 min before and 2.5 min after the current time point) moving average of 13–48 Hz band power was generated.

We used a sensitive algorithm to screen for potential seizures, then verified each detection manually. In this research, we define a single stand-alone seizure as a seizure that occurs at least 10 s after another seizure. A potential seizure event was detected if it fulfilled either of the following criteria: (i) the instantaneous 13–48 Hz band power was at least three times greater than the 5 min moving average for at least 9 s or (ii) the instantaneous 13–48 Hz band power was at least seven times greater than the 5 min moving average for at least 3 s. The event was classified as a seizure if it was detected on two or more electrodes simultaneously. Throughout this study, the term ‘seizure’ refers to either a clinical or subclinical epileptiform activity consistent with electrographic seizures.

In essence, the seizure detection algorithm is a sliding window calculated at every second, with a baseline comprised of the average data from 2.5 min before and after. The average seizure length was 42 s, though some lasted up to 173 s. Thus, the ‘baselines’ typically included data from during a seizure, but averaged with the data before or after the seizure as well. This has the effect of increasing the ‘baseline’ power, which means a detected event has a higher threshold to cross (i.e. after tuning the detector, a seizure detection had to be much higher than the true interictal data, since the calculated baseline includes seizure data). The output of the algorithm was then validated by a human reviewer assuring that every detected event (>7000) had epileptiform activity, although the precise time of seizure onset was not normalized across every file and a minority (<5%) had ambiguous onset times. Thus, it is possible that some of the onset/offset times were inaccurate. However, onset/offset times are notoriously inconsistent between experts as well. To account for this uncertainty, we analysed seizure onsets using an 8 s window centred on the estimated onset time (see Data Processing—Seizure Onsets). It should be noted that no seizures were observed in the Control group.

Data processing for evoked responses and seizure onsets

Only data from a single electrode were used to maintain reproducibility, reduce bias and ensure consistency between both evoked response and seizure onset analyses. Electrode-R (Fig. 3A) was chosen because seizure onsets were nearly identical across electrodes at any given time and it tended to have the most prominent seizure onsets (i.e. DC shift).

Evoked response

Responses from all 100 pulses were averaged for each pulse train to provide representative system responses at equal time points across the experiment. This analysis utilized the full 2048 Hz sampled data. To extract each individual evoked response within the pulse train, we examined the first 1000 data points (∼488 ms) starting at the second peak of each stimulus. The stimulation artefacts were simple to identify with a threshold detector, as they were much higher in amplitude than the rest of the recording and occurred at known intervals. The first four data points were primarily transients from the stimulation artefact and were redacted. The remaining evoked response data contained stimulation transient in addition to higher-frequency physiological responses. We controlled for the transient effect by comparing results within the same subject across time. Any averaged evoked responses that overlapped with seizures were removed from the analysis (range of 7–14% responses removed per animal with 10% average). The averaged evoked response amplitudes were then scaled between 0 and 1 to minimize the effect of changing electrode quality over the course of the study, thus emphasizing changes in frequency content. This analysis did not investigate any features of the probing-off period.

Seizure onset

Seizure onset data were captured using an 8 s window centred on the estimated seizure onset time obtained from the custom detector. In other words, each sample waveform included roughly 4 s of baseline and the first 4 s of seizure data. Seizure onsets that were uninterpretable due to stimulation artefacts were removed from the analysis (range of 6–12% seizures per animal removed with ∼9% average). Because the differences in seizure onset dynamics that we measured occur at frequencies <100 Hz (Jirsa et al., 2014), all onset samples were decimated to 204.8 Hz for easier data storage and administration.

Feature analysis of evoked responses and seizure onsets

Features from evoked responses and from seizure onset were independently extracted, normalized by subtracting the mean and dividing by standard deviation, and their dimensionalities reduced using standard principal component analysis (PCA).

Evoked response features

A frequency analysis was performed on each of the averaged evoked responses acquired for each stimulation period. A separate analysis was performed for every Probing-on epoch, and evaluated the averaged response of all 100 stimuli in that epoch. The analysis consisted of estimating the spectral power distribution over every ∼2 Hz increment from 0 to 1024 Hz. This was computed using the power spectrum density estimate (Welch’s power spectral density estimate, 996 sample window length, zero overlap, 996 digital Fourier transform points, 2048 Hz sampling frequency). Therefore, each evoked response had 499 features, where feature #1 is the power of the evoked response from 0 to 2.0562 Hz, feature #2 is the power of the evoked response from 2.0562 to 4.1124 Hz, etc.

Seizure onset features

A dynamical model based upon the first principles of dynamics (Jirsa et al., 2014) predicted that the brain’s transition from normal to seizure state (seizure onset) can be described using bifurcation theory and that there are four basic onset bifurcations: Saddle-node (SN), Saddle-node on an invariant cycle (SNIC), Supercritical Hopf (SupH) and Subcritical Hopf (SubH). These different bifurcations each have unique pairs of ISI and SA scaling laws that can be used to distinguish them (Jirsa et al., 2014; Saggio et al., 2017). SNIC bifurcations are characterized by non-zero SA scaling and a decreasing ISI trend (following, i.e. ‘scaled to’, a square root function). SubH bifurcations have no specific scaling laws for either ISI or SA. SN also has no specific scaling laws but can be accompanied by a DC shift. Finally, SupH bifurcations have no ISI scaling while the SA scales from zero as a square root function. True biological data are noisy and can be difficult to characterize exactly, so the primary goal of our analysis was not to ‘fit’ seizure onsets to any particular type of bifurcation. Instead, the analysis was a data-driven approach using the values of these basic features as a framework to quantify the seizures: analysing the presence of a DC shift and the scaling behaviour of the SA and ISI. Based upon this framework, we developed a set of features that focus on the key dynamical features. Each of the eight features is listed below in detail. As a reminder, the 8 s waveform of seizure onset data consists of 4 s of pre-onset baseline and 4 s of seizure data.

DC shift

We calculated the normalized area under the post-onset signal, as this feature estimates the relative prominence of the DC shift. This was performed by taking the following steps: (i) smooth the data with a 1-D, third-order median filter, (ii) subtract the median of the first 4 s of baseline from the entire signal, (iii) divide the entire signal by the maximum value of the signal and (iv) sum the result.

Deviation sum

This feature was developed to capture general trends post-onset. (i) Smooth the data with a 1-D, third-order median filter, (ii) truncate the initial 4 s of baseline, (iii) subtract the median of the remaining signal and (iv) sum the absolute value of the result.

Deviation variance

As with ‘Deviation Sum’, except Step 4 is replaced with taking the variance of the result.

Signal power

We quantified the power spectrum density estimate (Welch’s power spectral density estimate, 821 sample window length, zero overlap, 821 digital Fourier transform points, 204.8 Hz sampling frequency) of the seizure onset (i.e. the last 4 s of the data). The resulting power output corresponding to frequencies ≥2 Hz were summed.

Gamma band power

Like ‘Signal Power’, but only power corresponding to frequencies ≥32 Hz were summed.

Variance

To account for changes in electrode quality, we scaled the signal to be between 0 and 1. This was accomplished by first subtracting the minimum amplitude of the signal and then dividing by the new maximum amplitude. Finally, the variance of the scaled signal was taken.

Linear amplitude trend

Two linear models were fit to the data. First, a linear model was fit to the first 3.2 s of pre-onset baseline. Then, another linear model was fit to the last 3.2 s of seizure data. The slopes from both models were extracted and the baseline slope was subtracted from the seizure slope. This provided the relative linear amplitude trend of the seizure onset waveform with respect to baseline.

Burst count

This feature was designed to differentiate seizures that consisted of bursts from those that consisted primarily of spikes. We first performed high-degree, non-linear smoothing on the waveform (Savitsky-Golay filter, 11th order, 201 frame length). The resulting data were normalized between 0 and 1 by first subtracting the minimum amplitude then dividing by the new maximum amplitude. Finally, we found the peaks (‘findpeaks’ in MATLAB, Version 9.4.0.813654 R2018a, 0.3 minimum peak prominence) and counted them.

Statistical analysis

Definition of brain states for data labelling

As mentioned before, the tetanus toxin model consists of three epochs of epilepsy: (i) Pre-seizure, (ii) Rising-seizure and (iii) Falling-seizure. We analysed the evoked response and seizure onset characteristics independently across these epochs and then compared these results.

Recording started 2 days after injection (Day 1), which was prior to development of seizures in any animals, and continued every day until seizures had appeared and resolved, lasting several weeks. We defined the Pre-seizure epoch as all recordings done on days prior to the day of the first seizure. The Rising-seizure phase begins at the time of the first seizure and ends at the inflection point when the rate of seizures begins an overall decreasing trend. However, the SR was not necessarily unimodal and had considerable variability from day to day; thus, determination of a precise inflection point was ambiguous. Therefore, as an estimation, we determined the total number of seizures (N) that occurred in each animal and defined the Rising-seizure phase as the first N/2 seizures, and the Falling-seizure phase as the second N/2. This scheme assured that the two groups have similar size. We compared this method with results using the manually determined absolute maximum rate and there were no appreciable differences in any of the results. Analysis of the evoked responses included data from all three epochs. Obviously, seizure onset dynamics were only evaluated during the Rising-seizure and Falling-seizure epochs.

Using divergence to assess distinguishability

A major goal of this work is to characterize the brain states and determine if there are measurable differences between states. We used a data-science approach for this analysis, quantifying features of the data using algorithms and comparing the statistical distributions of those features. When feature distributions from different states can be distinguished completely, we refer to the distributions as fully ‘separable’, which in this case suggests that the different states produce fundamentally different brain activity. In practice, distributions typically have some overlap that reduces separability. If they are not separable, then either the brain states are not functionally distinct, or the chosen features are incapable of identifying any difference.

The method for distinguishing different groups is very important, especially for large datasets. With large numbers, simply finding the ‘statistical significance’ (often a P-value of a comparison test such as Student’s t-test) is not necessarily useful, as the populations may be ‘significantly different’ due to the large sample size but essentially indistinguishable in any meaningful way. A more robust method of distinguishing large groups is to use a test of divergence, which not only assesses significance but also separability. In this study, we utilized a measure related to the Henze–Penrose divergence (specifically using the quantity in Equation (5) in Berisha et al. (2016), which ranges between 1 (for completely separable distributions) to 0 (for completely indistinguishable distributions)). We denote this measure the Henze–Penrose statistic.

Comparing biomarker features across time

The primary measurements in this work are to assess whether the two electrical biomarkers (seizure dynamics and evoked responses) change over time, which we assessed by determining if the features changed significantly across different temporal epochs. This analysis was performed using unsupervised dimensionality reduction followed by a divergence measurement and bootstrapping (permutation test) to assess significance.

For seizure dynamics, we first reduced the dimensionality of the features by computing the first three principal components. Outliers whose principal component values exceeded 2 SD were removed from the analysis (removed data percentage ranged from 4.6% to 13.8%, avg. 9%), creating a more conservative measurement. We analysed these outliers and found that all were due to either inaccurate seizure onset time or motion artefact. For the features of seizure onset dynamics, there were only two groups to compare: the Rising-seizure and Falling-seizure epochs. We computed the Henze–Penrose statistic between the two distributions, providing a measure of their separability. To estimate the statistical significance of the separability, we performed a permutation test in which we randomly scrambled the labels of the original data groups and recomputed our divergence measurement. This permutation test was repeated 10 000 times for robustness.

For the evoked response data, the same analysis was performed with three exceptions. First, because the evoked response data encompassed all three epochs, we determined the separability between Pre- and Rising-seizure phases in addition to the Rising- and Falling-seizure phases. Second, only the first two principal components were used for the evoked response data, as these were sufficient for nearly full separability. Third, no principal component values were removed by thresholding from the analysis, as the evoked response data were not as noisy. In addition to testing differences in Experimental animals over time, we also investigated the change in the Control animals. Because Control animals had no pre-defined phases, we looked at the differences in evoked responses takes from the first 10 days (Days 1–10) and the final 10 days (Days 58–67).

Classification of Pre-seizure state using evoked responses

The evoked response experiment also allowed an analysis to determine if the Pre-seizure state could be detected, i.e. if it was possible to differentiate which animals would develop seizures. This independent analysis utilized the same features, but with a supervised classifier and cross-validation to determine how accurately these biomarkers can distinguish between the Control and Experimental animals even before seizures begin.

With the nine total animals, we developed a leave-one-out cross-validation in which eight animals are used for training and the classifier is tested on the held-out subject, repeated for each animal. For each of the nine iterations, we normalized the training data of each feature by subtracting the training group’s mean and dividing by the group’s standard deviation. The same mean and standard deviation were used to process the features within the test data as well. Focusing on the power band 0–203.57 Hz (i.e. the first 100 features), we implemented greedy linear discriminant analysis as a type of supervised learning for dimensionality reduction on the training data (eight subjects), then used the same transformation matrix to reduce dimensions on the test data. Only 100 features were used to limit over-fitting during the supervised learning process. We selected the top three linear discriminant analysis features that maximize linear separation between the Experimental and Control groups in the training data. These three linear discriminant analysis features were renormalized using their mean and standard deviation from the training data and then applied to the test data. The normalized linear discriminant analysis features from the training set were used to train a support vector machine classifier (Linear kernel function, scale factor of 1, MATLAB R2018a) to distinguish between the corresponding labels (i.e. Control or Experimental) for each individual evoked response (i.e. each 5 min data excerpt). We then tested the held-out data (i.e. all 5 min data excerpts from the current test animal) with the resulting classifier in each iteration of the cross-validation. The robustness of the cross-validation was assessed using two different metrics. First, we compared the total accuracy of the classifier to the theoretical accuracy of a random classifier. This is important metric, as it will determine if the classifier outperforms random guesses. To calculate the expected accuracy of a random classifier (i.e. the minimal success rate using only information about the distribution of class labels), we take the sum of the squares of the probability of each label occurrence. Only the first 10 days of evoked response Control data were used to mirror the general window of time the Pre-seizure phase occurred in the Experimental animals (mean: 6 days, range: 4–9 days). This first 10 days created a total sample size of 3977 samples across all three Control animals, which was comparable to 3915 samples across all Experimental animals, leading to a base rate probability of 50.00%. The second method to estimate robustness is to calculate the AUROC (area under the receiver operating characteristic curve) of the classifier. This metric is even more important as we seek to determine that the false-positive and true-positive classification rates are significantly above random chance. The AUROC ranges from 1 (perfect classification) to 0 (exactly wrong classification), with 0.5 being the outcome of a random classifier. Both cases provide an objective measure of the improvement over random guessing (i.e. the magnitude >50% accuracy or 0.5 AUROC).

Data availability

All data and associated scripts/tests can be found at the University of Michigan’s Deep Blue Library, as well as suggestions for alternate data processing parameters in future work (Crisp et al., 2019).

Results

Seizure onsets

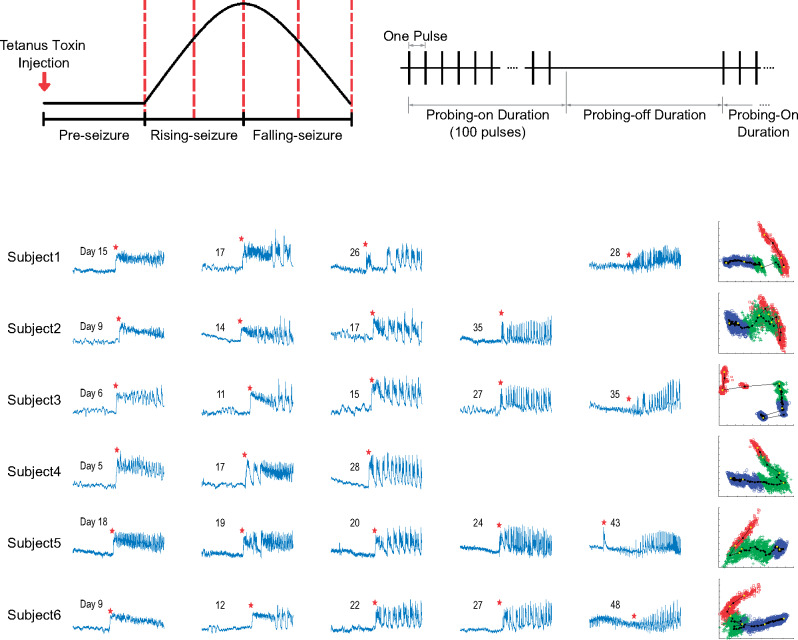
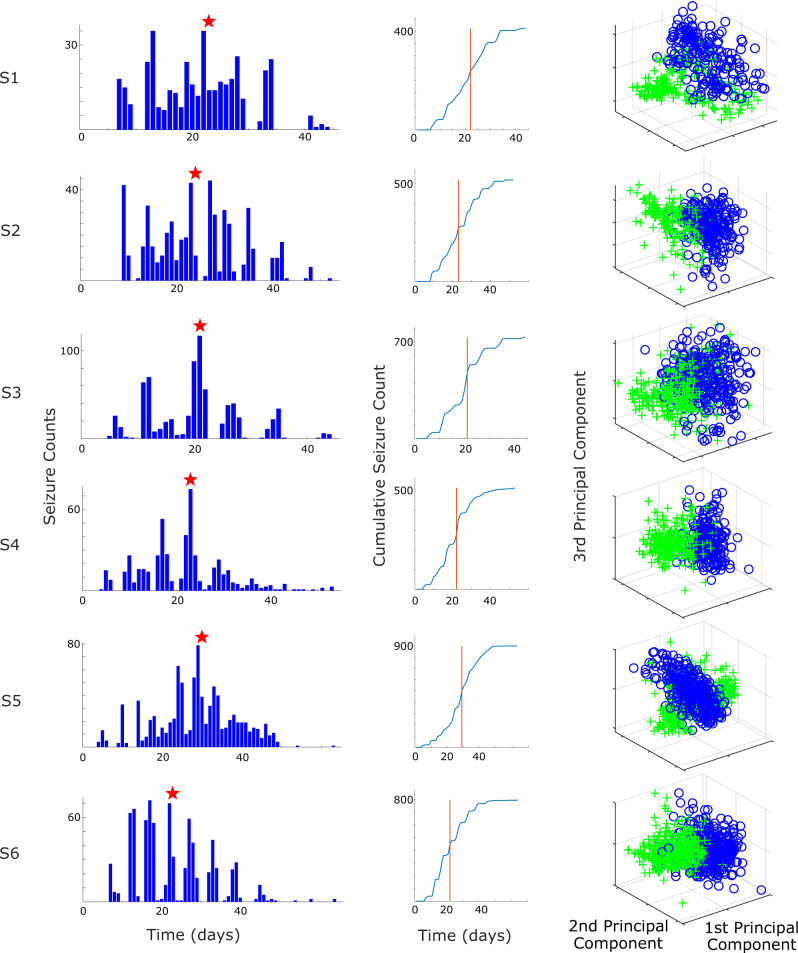
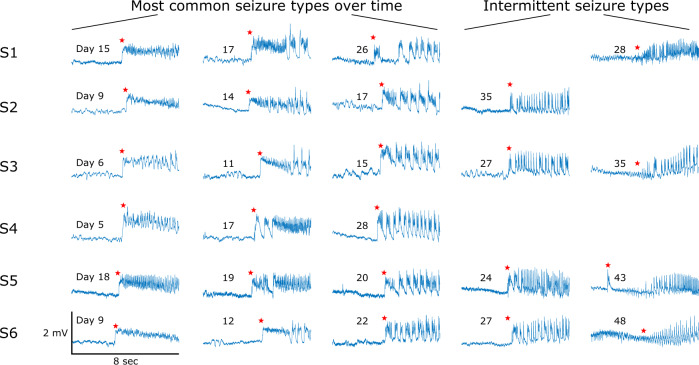
All six Experimental animals developed seizures after the tetanus toxin procedure. Seizures began after 6 ± 2 days and tended to increase in frequency for several days before reaching peak frequency (Fig. 4, column 1). Each animal also spontaneously remitted from seizures after several weeks. This time course is well-suited for epileptogenesis research as it includes a known trigger, a latent period, then a progressive course of seizures. We observed that there were clear differences in the seizures over this time course. We found that the seizure onset dynamics in a given animal changed over this period (Fig. 5). The first seizures to appear tended to have a DC shift (deflections that always occurred in the positive orientation) with fast spiking (Fig. 5, column 1). Over many days, the seizure features changed: the seizures began to have short clonic bursts with DC shifts (Fig. 5, column 2), then later they had bursts without DC shifts (Fig. 5, column 3). This transition represents a continuum from seizures that have features consistent with a SN onset (Jirsa et al., 2014) during the first seizures (DC shift, constant amplitude and frequency), transitioning to features from a SNIC or SubH onset (Saggio et al., 2017) during the last seizures (no DC shift, constant amplitude and increasing/arbitrary frequency). During the end of the recordings, there were two other patterns intermittently seen in some subjects. One was an onset with no DC shift, rising amplitude, and constant frequency (in 4/6 animals, Fig. 5, column 5), which was similar to a SupH onset. The other was an abrupt onset of discrete spike wave discharges, which is similar to a different type of SNIC/SubH bifurcation (in a different 4/6 animals, Fig. 5, column 4). Note that these different onset patterns were intermittent and variable: during the course of epileptogenesis a given animal alternated between these different types, but the overall collection of seizure dynamics was clearly altered from the beginning to the end of the experiment as illustrated in Fig. 5.

Figure 4.

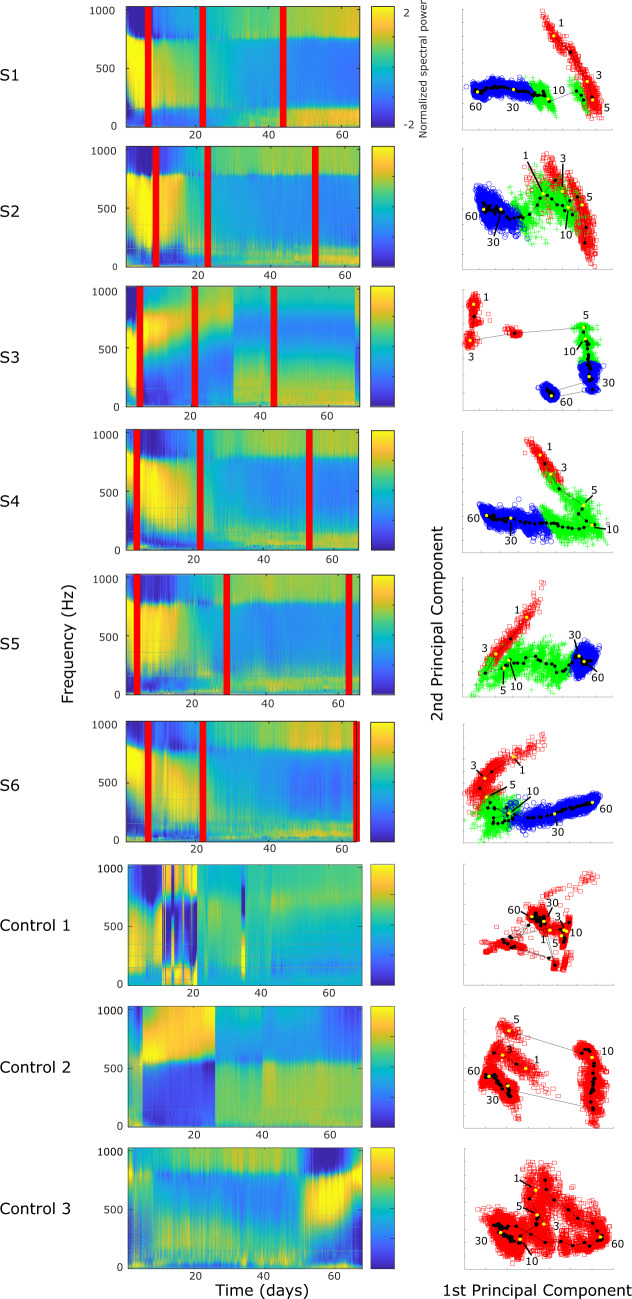
Seizure occurrences and divergence measurements—(Column 1) seizure occurrence over time for each animal. The x-axis time is based on the days since recording start (2 days after the tetanus toxin injection). The red star indicates the estimated inflection point, separating the Rising- and Falling-seizure phases. (Column 2) Cumulative seizure count over time for each animal. The red vertical line indicates the estimated inflection point (identical in meaning to the red star in Column 1). (Column 3) The corresponding principal components of the seizure onset features used for the divergence measurements between the Rising- and Falling-seizure phases. Green ‘+’ indicates seizure found in the Rising-seizure phase, while blue ‘O’ indicates seizure from the Falling-seizure phase. While the distributions in all six animals are not completely separable, there are clear differences between the two phases, which are manifest as high divergence measurements.

Figure 5.

Progression of seizure dynamics—examples of seizure onset dynamics over time in all six Experimental animals. Each row (labelled S1–S6) represents seizures in the indicated subject. The days shown mark the day since recording started on which each example seizure occurred. Hundreds of additional seizures were also present and are not shown. Over the course of epileptogenesis there was variation in seizure type, but the most common dynamic features at each time point changed. This figure demonstrates example seizures that have the most common morphology at different time points in the first three columns. In addition, the final two columns show intermittent morphologies that arose late in epileptogenesis in certain subjects. In each case, these different morphologies were not the dominant seizure type but are included here for comparison. Each waveform was downsampled to 204.8 Hz and lowpass filtered (Chebyshev Type 1 filter, normalized cut-off frequency of 0.08, passband ripple of 0.05 dB). Red stars indicate the seizure onset marked by a trained epileptologist.

Although assigning specific bifurcations would be possible at the extremes, there were many seizures during the course that would be difficult to assign to a single classification, as there are features from different types mixed together (e.g. some DC shift with increasing frequency). For this reason, we did not attempt to fit each seizure to specific classifications; rather, we used the features that distinguish the bifurcations as the input for the divergence analysis. Using the seizure features described in the Materials and Methods section, we calculated the first three principal components (Fig. 4, column 3) and used them to calculate the Henze–Penrose statistic between data from the two epochs (Rising-seizure and Falling-seizure). Note that a value of ‘1’ indicates complete separability, and ‘0’ means they are indistinguishable. The average Henze–Penrose statistic measurement over all six animals were 0.6157 ± 0.1983, all significantly larger than values computed for all 10 000 random permutations of the labels (P < 0.0001, permutation test). This demonstrates that the seizure onset features are not only significantly different, they also easily distinguish the two phases.

To further validate the changes occurring in the seizure onset data, we separated both the Rising- and Falling-seizure phases into halves (early and late), creating a total of four epochs (Fig. 1, see dotted vertical lines). We then computed the Henze–Penrose statistic between each neighbouring pair of the four smaller epochs. We found that seizure onset features from all six animals changed significantly between all compared phases (all P < 0.0001, permutation tests). Thus, about every 10 days the seizure onset patterns had changed significantly in each animal.

Evoked responses

Independent of the noticeable differences in seizure onset dynamics, we also found important differences in the response to provoking stimulation during interictal periods. We used a similar data-driven analysis to characterize these effects, though in this case we were also able to quantify the Pre-seizure phase.

There is a great clinical need for a biomarker that can inform clinicians about the state of the Pre-seizure phase, as there is potential for early treatment to avoid, diminish or prolong seizure development. However, this success is only available if clinicians can differentiate between a healthy brain and a brain progressing along the track of epileptogenesis without the obvious standard biomarker (seizures). Our analysis seeks to train a classifier to determine if incoming evoked responses come from a normal, healthy brain, or from a brain progressing along the track of epileptogenesis.

The stimulation continued at regular intervals for the entire weeks-long recording session. It spanned all behavioural states on every day, but the responses showed no clear dependence on time of day or behavioural state. We first used spectral features to quantify the dynamical effects as epileptogenesis progressed. We measured the features over the entire time course and found that the evoked responses were distinct during each phase of epileptogenesis (Fig. 6). The most visually obvious change was a consistent trend in amplitude (Fig. 6A); however, this effect was also noted in the Control animals, suggesting it was due to the experimental procedure. We found that the frequency response was more specific to the epileptic animals. We therefore normalized the amplitudes to focus the analysis on the frequency response to the stimulus, which primarily occurred in the first few milliseconds of the response (Fig. 6B and C). The Experimental animals began to have changes in the evoked responses immediately after the tetanus toxin injection. The changing nature persisted, and in each stage of epileptogenesis it was easy to distinguish the responses. Because there were so many measurements each day, we were able to quantify these responses and show how the distribution of the features changes over time, i.e. how ‘separable’ the distributions are. The full analysis combined many features, but to illustrate the strong separability in just one of the features, we highlight the temporal band power changes by normalizing via standard deviation each frequency component over time (Fig. 7, column 1). For five out of six animals, we see that changes in power bands separate into three distinct bands. Frequency ranges were similar enough for these animals to estimate by visual inspection: 0–169, 170–769 and 770–1024 Hz. The 0–169 and 770–1024 bands were similar in their power distribution across epochs. These bands started with minimal power in the Pre-seizure phase and gained power over time with increases in power correlating with transitions between each epileptogenic phase. The final frequency band, 170–769 Hz, displayed the opposite trend. Specifically, we see a high proportion of power during the Pre-seizure phase that decreases over time. One noticeable difference in this band compared to the others is that the trends in power distribution are highly subject-specific. One subject was distinct from the others (S3) and had a different time course, but also showed clear differences over the course of epileptogenesis.

Figure 6.

Evoked response visualization—each figure contains the evoked response from the first stimulation epoch occurring on Days 3, 15, 30 and 50 to show the temporal evolution (Electrode-R only). Data shown are from Experimental S1; similar results were present in all Experimental animals. (A) The average of 100 evoked responses from a single 5 min train of pulses. Note that on this long time scale the largest difference is the amplitude after stimulation. After normalization, the largest difference occurred in the first 0.01 s after stimulation (star, small bar), which are expanded in ‘B’. (B) Stimulation artefact is removed from the analysis. The average waveform is normalized between 0 and 1 (subtracting the minimum and dividing by the new maximum for each averaged tracing). This is done to minimize amplitude changes due to electrode variability over time. (C) The power spectrum density is computed for each averaged waveform. Temporal changes in the power spectrum density were highly consistent across time in the epileptic animals. Each Control was processed in the same way and there were some measurable differences over time, but they were not consistent with each other nor with the epileptic animals (see Fig. 8).

Figure 7.

Probing analysis—(Column 1) Power spectral density for each averaged electrically evoked response, plotted for each Experimental animal (S1–S6) and Control animals (Control 1–3) over the course of the study. The power bands were individually normalized by subtracting the mean and dividing by the standard deviation to highlight changes in a single frequency band over time. In each Experimental animal’s plot, there are three vertical lines. The first line corresponds to the day that seizures first commenced. The second indicates the point of inflection separating the Rising- and Falling-seizure phases. The third shows the day of the last recorded seizure. These lines were not included for the Control animals, as they did not have seizures. (Column 2) Frequency information from the analyses were investigated by PCA, and the first two principal components are plotted and labelled based on their epileptogenic phase membership (red ‘squares’ = Pre-seizure phase, green ‘+’ = Rising-seizure phase, blue ‘o’ = Falling-seizure phase). As seen in the figures, all three phases were quite distinct in all Experimental animals. The PCA was performed separately for each of the nine subjects. In order to demonstrate the temporal evolution of the induced responses, the first and second principal component values were segmented based on day and their centroids were calculated and plotted in the line-dot graph. Centroids from Days 1, 3, 5, 10, 30 and 60 are white and labelled. Days 21 and 22 for Control 1 were redacted from the figure, as they were corrupted by artefact.

To quantify these effects similar to our analysis of seizure onset dynamics, we computed the principal components (Fig. 7, column 2) and then investigated how well the evoked response features of the Experimental animals can be distinguished between the different phases of epileptogenesis. All phases were clearly distinguishable in all six animals (P < 0.0001, permutation test). Of particular interest is that in each of the six subjects, most of the change in principal components occurred within the first 10 days, suggesting that there is significant evolution in frequency response even before seizures begin.

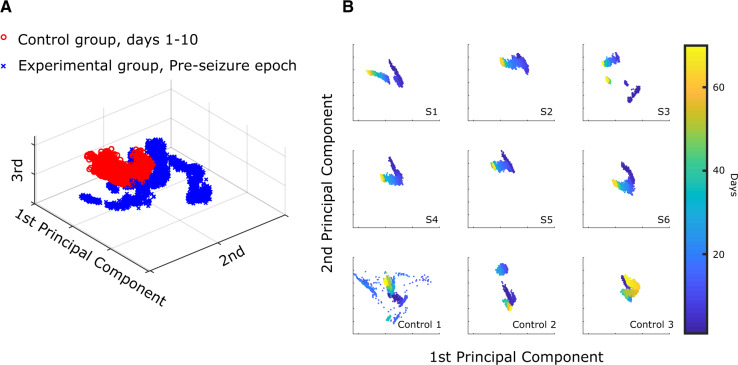
We also assessed the effect of stimulation on a healthy brain by performing the same analysis to compare data from the initial and final days of the Control animals (Days 1–10 and 58–67). The beginning and ending days were clearly distinguishable (Fig. 7) in all three Control animals (P < 0.0001, permutation test). This is not surprising, as the healthy brain received repeated electrical stimulation for the entirety of the experiment, and it is possible that implantation alone or even natural aging could produce changes over the course of the 2 month experiment. However, we hypothesized that changes in the brains of Experimental animals would be more substantial than changes in Control animals, given the added effects of epileptogenesis. In Fig. 7, column 1, the evoked responses of the Experimental animals have a high correlation with time and have very similar profiles. This is in great contrast to the Control animals, where each of the evoked responses had unique profiles and exhibited comparatively static features. However, to compare results across all animals we had to plot them in the same PCA space. The six Experimental animals were grouped and normalized (mean subtracted, divided by the standard deviation), and the dimensionality of their features were reduced using PCA. The same mean, standard deviation and PCA coefficients were used to project the features from the Control animals into the same PCA space. We first plotted these in PCA space for visualization. Each data point represents a single 5 min stimulation response. We noted differences between the Experimental and Control groups even in the first few days before seizures began (Fig. 8A). Evaluating the progression over the whole experiment, we noted that the Experimental animals tended to have a distinct shape to their PCA data, which was not present in the Controls (Fig. 8B). To quantify this effect, we fit the first two principal components of every sample from each of the nine animals to their corresponding days using a basic linear model (least sum of squares, linear fit). The R-squared value of the Experimental animals was found to be significantly higher than that of the Control animals (Experimental R-squared median: 0.85, Control R-squared median: 0.40, P = 0.0119, one-tailed Wilcoxon rank sum test). This indicates that while both groups experience changes over time, the Experimental animals had much higher correlation with time.

Figure 8.

Qualitative differences between Experimental and Control evoked responses—(A) aggregate of all evoked response data from the Pre-seizure phase of all Experimental animals (blue ‘x’) compared with all data up to Day 10 in the Control animals (red ‘o’). These data were plotted on the unsupervised PCA distribution formed from all nine subjects’ data. (B) The first two principal components generated by aggregating all six experimental animals were used as axes for all nine animals. S1–S6 refer to the Experimental subjects 1–6. The evoked responses are colorized according to the day of recording (1–70). Each of the Experimental animals has a clear temporal trend, while there is no consistent trend in the Control animals. Control 1 had many days with high variability but it, like all three Control animals, had similar responses at the beginning and end of the experiment. This figure is presented for illustrative purposes to show the differences between the groups using the same processing as prior figure; however, the actual classification used a different, supervised analysis with 9-fold cross-validation (see text). Days 21 and 22 for Control 1 were redacted from the figure, as they were corrupted by artefact.

These results led to a question with important clinical implications: would it be possible to distinguish Control versus Experimental animals in the period before seizures develop? Here, the results from the different groups must be compared across subjects. To be rigorous and avoid over-fitting, we approached this as a classification problem and implemented cross-validation. This analysis used the same spectral features but required a different approach with supervised dimensionality reduction and a support vector machine classifier. We used 9-fold leave-one-out cross-validation across all nine animals, individually classifying each 5 min-average evoked response from each animal.

We found that the classifiers utilizing evoked response features from the first 10 days (Controls) and Pre-seizure epoch (Experimental) were accurate in identifying which animals would later develop epilepsy (Experimental animals versus Control, overall 75.51% accuracy compared to 50% accuracy for random chance classification, leave-one-out cross-validation, AUROC: 0.8217). The classifier performed worse than random chance on only two (one Experimental, one Control) of the nine total animals. The poorly performing Experimental animal (S3—14.79% accuracy) exhibited strange, highly variable evoked response data that likely led to poor classification accuracy. In Control 2, the classifier performed slightly worse than random chance (48.94%). Interestingly, evoked responses from the first 5 days from Control 2 were all classified correctly. It was between Days 5 and 6 when the features of the evoked responses changed drastically and were classified incorrectly. The data from both these subjects can be seen in Fig. 8B as disconnected clusters of points in S3 and Control 2. We were unable to identify any other changes associated with these findings. However, in the remaining seven animals the results were quite remarkable: just a single evoked response train (5 min) could be classified as either Pre-seizure or Control much better than random chance.

Discussion

For the first time, both seizure onset dynamics and electrically induced brain responses were studied continuously over a long-term period to determine their roles as biomarkers for the epileptogenic brain. There has been some previous work for electrically induced brain responses in humans, though limited to shorter recordings and always for patients who are long past the epileptogenesis stage (Kalitzin et al., 2005; Freestone et al., 2011; Pigorini et al., 2015; Wendling et al., 2016). This tetanus toxin animal model provides a unique opportunity to study epileptogenesis from insult to epilepsy, and in this case also to remission. This study is unique because it compares two fundamentally different biomarkers simultaneously, through multiple stages of epileptogenesis.

Quantifying seizure dynamics

In both clinical and basic research, it is often necessary to describe seizure characteristics and attempt to compare them across different conditions. However, these comparisons have previously been limited to visual descriptions such as morphology and peak spiking frequency (Perucca et al., 2014; Lagarde et al., 2019). These methods of comparison are the basis of clinical epilepsy, but it is unclear when those differences comprise fundamental changes in the seizures themselves, e.g. is a 4 Hz versus a 7 Hz spike train really a different ‘type’ of seizure? The result is that it is very difficult to compare seizures across time and different subjects. In this work, we designed features based upon invariant aspects of seizure dynamics (Jirsa et al., 2014). In effect, these are the features that define when one seizure is ‘different’ from another, based upon principles of dynamics. Interestingly, this theory actually predicts that the spiking frequency is not important—only the temporal trend is. This robust method is designed to classify seizure dynamics, applicable to any seizure: computer model, experimental animal or human.

Our primary result was that there were clear differences in seizure dynamics over the course of epileptogenesis, as evidenced by the Henze–Penrose statistic results. These measures indicate that the epileptic tissue follows a fairly stereotyped dynamical pathway over the course of the tetanus toxin-induced epilepsy, tending to form seizures with fast, low amplitude spiking and DC shift at the beginning, versus seizures with repetitive bursts with increasing frequency at the end. While investigating the mechanisms underlying this change was beyond the scope of the current work, these results provide an intriguing guide for such research in the future. In effect, this type of analysis can quantify differences between seizures, identifying salient differences and providing rigour to future epileptogenesis research.

While not a main focus of the current research, it is also interesting to comment on the types of bifurcations seen over the course of epileptogenesis. In all animals, the initial seizures tended to have features consistent with SN bifurcations, while the final seizures more commonly were consistent with SNIC or SubH bifurcations. However, between these times, there was a range of different dynamics. There were two phenomena noted in all animals. First, each animal had seizures with different dynamics alternating over time, e.g. SN alternating with SNIC or SupH bifurcations. The relative frequency of each type changed over time, with SN being much more common in the Rising phase and SNIC/SubH more common by the end. Second, as shown in Fig. 5 (column 2), there were many seizures that did not conform to strict bifurcation types. Viewed collectively, it appears that many seizures between the early and late patterns (which clearly change from SN to SNIC/SubH) have mixed characteristics, as if the seizures make a slow transition from SN to SNIC/SubH over the course of weeks. This transition suggests a ‘map’ of brain states, wherein the progression of epileptogenesis slowly moves the dynamics from one region to another, as proposed by Saggio et al. (2017). Clearly, limiting to a low-dimensional model cannot explain all dynamical behaviour in the brain. Nevertheless, it is striking that despite limiting our analysis to the more parsimonious low-dimensional model, it still provides very strong separability, and even provides a strong rationale for explaining the evolution of seizure dynamics in Fig. 5.

Evoked responses

Quantifying the response to a perturbing stimulus has been very limited in epilepsy research but has shown intriguing results (Alarcon, 2005; David et al., 2010). This procedure has a robust history in other fields such as ecology, power systems and reservoirs (Chow et al., 1990; Kikani and Pedrosa, 1991; Heppell et al., 2000; Martı´nez et al., 2004; Ehrlén and Groenendael, 2008; Ma et al., 2012) but is difficult to perform in vivo. The basic theory is that perturbation is a probe of excitability and thus should change if the network is inherently ‘more epileptic’, i.e. closer to seizure threshold. In addition, perturbation can be used to assess proximity to specific bifurcations because it shows different responses when a SubH or a SupH bifurcation is nearby (Bryant and Wiesenfeld, 1986; Vohra et al., 1994; Yaghoobi et al., 2001). Because our system records at 2048 Hz, we are able to see a wide range of fast neuronal activity. There are many physiological phenomena in the 500–1000 Hz range: units, multi-units, high frequency oscillations, etc. Perhaps the most pertinent are ‘very high frequency waves’ produced by somatosensory evoked potentials, recorded with subdural electrodes very similar to this experiment (Amassian and Stewart, 2003).

Our data demonstrate that, like seizure dynamics, evoked responses show clear evolution over the course of epileptogenesis. As expected, there were also changes over time in the Control animals, but the effect was much more prominent in the Experimental animals. Perhaps the most important result is that these changes started even during the latency (i.e. Pre-seizure) period, and that evoked responses taken during this time can be used to help distinguish which animals are going to develop epilepsy. This outcome shows that this method may be a useful tool to assess the progression of epileptogenesis even prior to the first seizure. These results are limited because there were no evoked responses done prior to the tetanus toxin injection to establish the healthy baseline. Future studies will evaluate these potential confounds.

This study contains some important limitations. First, concerning the relationship between seizure dynamics and evoked responses, while we make the assumption that these measurements are independent, repeated stimulation has been found to affect the brain (Chen et al., 1997; Yamamoto et al., 2002). Therefore, it is possible that the stimulation affected the seizure dynamics, rather than disease progression; however, we note that the seizure progression found in these animals is wholly compatible with prior studies that did not have stimulation (Jefferys and Walker, 2006). Second, we did measure evoked response changes in the Control animals, which was likely due to some combination of aging, stimulation effect and implantation/experimental effect. Finding such differences was not surprising; the key aspect of our results was that the changes occurring in the Experimental animals were both qualitatively and quantitatively different than those occurring in the Control animals. Furthermore, our classification of Experimental versus Control in the first 10 days inherently controls for this change and was much better than a random classifier.

Summary

Treating epileptogenesis has been challenging due to the inherent heterogeneity of epilepsy as well as the temporal changes in molecular mechanisms. This has motivated research to develop biomarkers to track the disease progression in models of acute brain injury. Electrically induced evoked responses have been successful in diagnosing neural excitability to determine many epileptic characteristics. Additionally, a recent framework of seizure dynamics has been produced, creating a foundation and methodology for characterizing seizures based on signature dynamic manifestations. These two independent features hold great promise as biomarkers of epileptogenesis. This study investigates how the different stages of epileptogenesis modulate these features. We provide proof-of-concept evidence that these features change over time and can be used to inform the progression of the disease, in particular that the response to stimulation can help differentiate which subjects will develop epilepsy in the future. These features, in conjunction with other methodologies, can be used to better research progression of epilepsy as well as asses the efficacy of administered drugs post-injury.

Glossary

AUROC

= area under the receiver operating characteristic curve

DC

= direct current

ISI

= inter-spike interval

PSA

= principal component analysis

SA

= spike amplitude

SN

= saddle-node

SNIC

= saddle-node on the Invariant Cycle

SR

= seizure rate

SubH

= subcritical Hopf

SupH

= supercritical Hopf