Chemically Active Particles: From One to Few on the Way to Many

Abstract

Chemically active particles suspended in a liquid solution can achieve self-motility by locally changing the chemical composition of the solution via catalytic reactions at their surfaces. They operate intrinsically out of equilibrium, continuously extracting free energy from the environment to power the dissipative self-motility. The effective interactions involving active particles are, in general, nonreciprocal and anisotropic, even if the particles have simple shapes (e.g., Janus spheres). Accordingly, for chemically active particles a very rich behavior of collective motion and self-assembly may be expected to emerge, including phenomena such as microphase separation in the form of kinetically stable, finite-sized aggregates. Here, I succinctly review a number of recent experimental studies that demonstrate the self-assembly of structures, involving chemically active Janus particles, which exhibit various patterns of motion. These examples illustrate concepts such as “motors made out of motors” (as suggestively named by Fischer [Fischer, P. Nat. Phys. 2018, 14, 1072]). The dynamics of assembly and structure formation observed in these systems can provide benchmark, in-depth testing of the current understanding of motion and effective interactions produced by chemical activity. Finally, one notes that these significant achievements are likely just the beginning of the field. Recently reported particles endowed with time-dependent chemical activity or switchable reaction mechanisms open the way for exciting developments, such as periodic reshaping of self-assembled structures based on man-made internal clocks.

Introduction

Micrometer-sized chemically active particles suspended in a liquid solution can achieve self-motility (i.e., without requiring the action of external forces or torques) by producing local changes in the chemical composition of the solution in which they are suspended. This can be achieved, for example, by promoting catalytic chemical reactions on parts of the surface of the particle.^1,2 By means of distinct interactions between the particle and the various chemical species in the solution, the spatial variations of the chemical field (i.e., of the distribution of the number densities of the chemical species) induced by the particle are converted to the motion of the particle as well as to the hydrodynamic flow of the solution.^3,4 Consequently, such particles operate intrinsically out of equilibrium, continuously extracting free energy from the environment to power their motion against the dissipation within the solution.⁵ In many case, the velocities of the particle and of the flow around it are small (in the range of a few micrometer/s). Thus, remarkably, self-motility (swimming) is achieved in the regime of very low (vanishing) Reynolds numbers, in which inertia is negligible and the hydrodynamics is governed by the linear Stokes equations.

Following the first experimental reports, 15 years ago, of motile bimetallic rods operating via the catalytic decomposition of hydrogen peroxide,^1,2 the interest in active particles and active fluids, generically called active matter here, has been constantly increasing.⁵⁻⁷ Many types of chemically active particles have been proposed and studied experimentally.⁸⁻¹⁴ Concerning the mechanisms of motility, it is generally agreed that self-phoresis¹⁵⁻²⁴ applies to many of these particles, in particular, to the often-encountered Janus-type structures (bimetallic rods^25,26 and spheres,²⁷ catalyst-covered insulators^10,28−30 or semiconductor³¹⁻³⁴ spheres, and catalyst beads partially embedded in insulator spheres^24,35) powered by decomposing hydrogen peroxide in aqueous solution.³⁶ In brief, self-phoresis involves the coupling between the interactions of the molecular species in solution with the particle and the spatially nonuniform chemical composition of the solution (owing to the chemical reaction on the catalytic parts of the surface).^4,15−22 This coupling can often be well approximated as a prescribed actuation of the fluid solution by the surface of the particle (i.e., a slip velocity (relative motion of the fluid) proportional to the gradients along the surface in the concentrations of the molecular species (solutes) involved in the reaction).^4,15,17,20 The proportionality coefficient is the so-called phoretic mobility, which is determined by the local interactions of the solutes with the surface. This coefficient can be either positive or negative (i.e., the flow of the solution along the surface of the particle is toward or away from the active part, respectively). Accordingly, the motion of the particle is with the active part at the back or at the front, respectively. For Janus particles, which possess axial symmetry, this leads to drift along the symmetry axis (ballistic motion), with typical self-phoretic velocities of ∼1–20 μm/s. On time scales longer than the rotational diffusion time of the particle, the motion of a self-phoretic particle can be described as enhanced diffusion, emerging from the superposition between the self-phoretic drift and the rotational diffusion of the symmetry axis of the particle. Insightful reviews of these developments and exhaustive lists of references are provided in refs (17), (25), and (37−39.)

When a chemically active particle is in the vicinity of boundaries or other particles, either active or inactive, its chemical and hydrodynamic fields are disturbed. Since such disturbances couple back to the particle, in general leading to changes in its motion, chemically active particles have the means to sense and respond to their surroundings.⁴⁰ For example, chemically active particles moving near walls or fluid interfaces, situations which typically occur in experiments,^{1,15,31,41−44} are known to exhibit surface-bound steady states of “sliding”.⁴⁵⁻⁴⁸ These laid the foundation for guidance by topographical or chemical features.^{26,31,41,49−52} Furthermore, the chemical and hydrodynamic fields produced by one active particle induce the motion of nearby particles (i.e., an effective interaction), comprising drift by the hydrodynamic field and the phoretic response to the chemical field. For chemically active motile colloids, these nonequilibrium, effective interactions, which may also include the response of one particle to the electric field induced by the ionic cloud produced by another particle, are manifest in addition to the interactions that exist in equilibrium suspensions (i.e., DLVO forces, depletion interactions, magnetic or electrostatic dipolar interactions, capillary interactions, etc.). These effective interactions are long-ranged^{15,24,40,53,54} (they generically decay with the distance r from the particle as r^–2), have significant magnitude over length scales of a few particle radii, and can break the action–reaction principle (i.e., they are nonreciprocal⁵⁴). These complex effective interactions are expected to give rise to a very rich behavior of collective motion. (See studies considering only the interaction due to the chemical fields in refs (53) and (54).) Accordingly, chemically active particles seem to be excellent candidates for testing and developing methods of self-assembly or of programmed assembly (i.e., ensuring a specific outcome out of several possible scenarios of assembly via the choice of the shapes of particles and/or of a certain sequence of subassembly steps.)

Here I concisely review a number of recent reports of hierarchical functional structures with distinct patterns of motion (“motors made out of motors”⁵⁵), which emerge via self-assembly processes involving chemically active units.^34,56,57 In addition to their importance per se as paradigmatic proof of principle experiments, these systems can provide benchmark tests for the theoretical models of self-phoresis. This is so because these structures, in which the chemically active components are particles presumably moving by self-phoresis,^34,56,57 comprise a relatively small number of components such that detailed modeling and numerical analysis of the steps involved in their formation are, in principle, feasible.^58,59 An in-depth understanding of the effective interactions associated with the chemical activity and motility of the particle (as well as with its shape) will inform the design of particles with preconfigured assembly responses, a task which at this time is, more or less, a trial and error procedure guided solely by the experience, intuition, and inspiration of the researcher. This is particularly important from the perspective of exploring collective effects in systems in which the particle-level dynamics has time dependencies built in. The latter can be achieved by using particles with intrinsic time-dependent chemical activity⁶⁰⁻⁶² or by combining particles capable of promoting distinct reactions upon changes in externally controlled stimuli⁶³ with time-dependent variations of the stimuli. The reports of collective oscillations in macroscopic structures⁶⁰ and of active particles with an “internal clock”⁶² highlight the potential for very exciting future developments in this field.

Assembly with Motile, Chemically Active Particles

Before proceeding to the examples of the emergence of assembled, ordered structures involving chemically active particles with a relatively small number of components, which is the focus of this work, it is important to succinctly overview the dynamics observed in dense monolayers of active particles. This will provide the rationale both for the interest in the collective dynamics and for the approach to “few” (before studying “many”). One notes that there are only a few experimental studies involving large numbers of well-characterized, identical active particles.^{27,35,60,61,64−70} (This is in part due to the fact that the mass production of chemically active particles with regular, simple geometries, such as bimetallic Janus rods, Janus (catalyst-covered) spheres, and polymer-embedded hematite cubes, is still a demanding process. Additional difficulties arise due to issues concerning colloidal stability, such as irreversible aggregation and particles sticking to the walls.) Nevertheless, the outcomes of such studies have been remarkable; this is expected to encourage further significant efforts in this direction, for example, in the search for self-organized patterns of collective motion (“swarming”) of chemically active particles.

“Living” Crystals of Motile, Chemically Active Particles

A very interesting outcome of studies with dense monolayers of motile chemically active particles sedimented at a planar wall is the occurrence, at sufficiently large areal fractions of particles, of a microphase separation.³⁵ This out-of-equilibrium form of self-organization consists of “living” crystals (Figure 1); as their name suggests, the crystalline clusters are motile and dynamic in that they can reshape, break apart (“explode”), merge, or fragment.³⁵ This phenomenon has been observed for particles consisting of a chemically inert TPM (3-methacryloxypropyl trimethoxysilane) polymer sphere partially embedding a UV-photocatalytic hematite cube; they move with the hematite cube at the back via the (photo)catalytic decomposition of hydrogen peroxide.⁷¹

Figure 1.

Illustration of living crystals (colors added to identify the provenience of particles which belong(ed) to the four clusters visible in the left panel): rearranging, exchanging particles, merging (from left to right, panels 1 to 2 and 2 to 3) and “exploding” (blue cluster, panels 3 to 4). Adapted with permission from ref (35) (Figure 1). Copyright 2013 American Association for the Advancement of Science.

A somewhat similar dynamic steady state of clusters has been reported for two other systems;^27,64,67,72 however, the evolution of the clusters is different from that discussed above. For the Janus spheres consisting of Pt-covered Au particles and moving by the catalytic decomposition of hydrogen peroxide,^27,64 the aggregation and fragmentation of clusters involve mostly events in which monomers or dimers attach to, or detach from, an existing cluster.²⁷ The merging of clusters or the breakup of a large cluster (which is observed in panels 2 to 4 of Figure 1) seldom occurs in the study in ref (27). On the other hand, for the Janus spheres consisting of graphite-covered silica beads, which achieve motility via the demixing of a water-2,6-lutidine mixture close to the critical concentration (28 mass % lutidine) induced by the local heating of the graphite cap,⁷³ the findings are somewhat different from those in either of the two studies above.⁶⁷ While the formation of mobile clusters occurs upon increasing the areal density and/or the motility of the active particles, the dynamic evolution of the clusters differs: the merging of clusters is observed, but the fragmentation of a large cluster is not.⁶⁷ Accordingly, in this case it seems as if the system may eventually reach complete separation, with a large cluster in contact with a gas phase as the final state.

The studies discussed above highlight that the emergence of dynamic steady states of clusters (microphase separation), as well as the dynamic behavior at the mesoscopic level and the emerging cluster-size distributions, are system-dependent features. Therefore, the role played by the changes in the details of the chemical activity and of the physical properties of the surface of the particles must be understood. However, numerical simulations of such large systems, accounting for chemical activity and phoretic and hydrodynamic interactions between particles as well as between particles and the wall, are prohibitive in computational demands (memory and time), even when very simple models of active particles are employed.⁵⁸ Accordingly, such numerical studies will necessarily involve a certain degree of simplification. For example, Brownian dynamics simulations would require as an input the binary (or even few-body) effective interactions (potentials), which encode the phoretic and hydrodynamic effects noted above. From this perspective, the systems discussed in the following sections, which exhibit complex dynamic behaviors but involve a small number of particles, are better suited for detailed theoretical and numerical studies. Understanding and reproducing the experimental observations may play an important role in guiding the construction of effective, coarse-grained numerical simulations methods.

Chemically Active, Motile Janus Particles as Nucleation Sites

Perhaps the simplest, most straightforward strategy for self-assembly is to directly exploit the response of inert particles to the chemical and hydrodynamic fields induced by a chemically active one.^{24,34,74−76} Such assembly can be achieved with, e.g., an active particle with uniform activity over its whole surface immobilized at the wall.^24,74,75 Surprisingly, by suitably choosing the combination of inert and active particles, the nucleation of radially symmetric clusters of inert particles around an active particle is also possible for motile Janus particles³⁴ via a very complex dynamics of assembly, as illustrated in Figure 2. As intuitively expected, the spatial extent of these clusters can be controlled via the magnitude of the activity, for example, by increasing the amount of “fuel” (see inset in Figure 2(h)), i.e., the concentration of hydrogen peroxide, the light intensity for photocatalytic reactions, or both.^{24,34,63,74,75}

Figure 2.

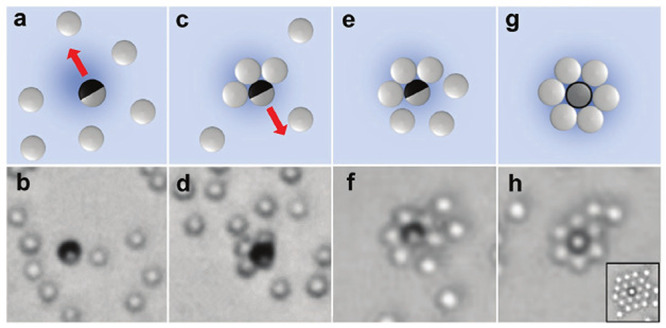
Illustration (top) of the experimentally observed (bottom) process of assembly of a ring of chemically inactive silica particles around a chemically active titania(black)/silica(gray) Janus particle. (a, b) Single-particle motion, with the titania cap at the front. (c, d) Capture and arrangement of inert particles in a half-ring structure around the active cap, followed by reversal of the direction of motion. (e, f) Completion of the ring structure by capture at the silica (inert) site. (g, h) Transition of the active particle from an axis parallel to the wall configuration to an axis perpendicular to the wall, active cap down, one. The inset in (h) illustrates that the size of the cluster increases upon increasing the UV light intensity, compared to that corresponding to the main panel. Reproduced with permission from ref (34) (Figure 4). Copyright 2017 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

In the case of the dynamic assembly reported in ref (34) and illustrated in Figure 2, the active particles are silica spheres half-covered (by e-beam evaporation) with a titania (anatase) film. These self-propel in hydrogen peroxide solutions when exposed to UV light of a suitable wavelength. The inert particles are silica spheres. Both the inert and the active particles are sedimented onto a glass slide. The motion of the Janus particles is influenced by the pH of the solution;³⁴ in that experimental study, the pH was adjusted such that a Janus particle, when it is far from other particles, moves with the active titania cap forward.

For low number densities of active and inert particles, once the activity of the titania/silica Janus particles is turned on (i.e., the UV light is on), the assembly process depicted in Figure 2 is observed. As noted in ref (34), the formation of the ring structure around the active particle “seed” involves a somewhat counterintuitive sequence of steps: (i) The motile particle first forms a half-ring of inert particles around the chemically active part; this ensemble (active particles plus the inert ones around the active cap) reverses the direction of motion (i.e., the Janus particle now moves with the active cap at the back (Figure 2(c,d)) and the inert particles follow it. (ii) Completion of a full ring of inert particles then occurs (Figure 2(e,f)); upon completion of this ring, the active particle exhibits a transition from the initial configuration, in which the symmetry axis of the particle is quasi-parallel to the wall, to a configuration with the cap down and the symmetry axis perpendicular to the wall. This configuration possesses axial symmetry (Figure 2(g,h)). (In the nomenclature of ref (45), a “hovering” state of the active particle becomes dynamically stable, instead of the initial “sliding” one.) Once the configuration in (h) occurs, the cluster is stable as long as the chemical activity is on; if the activity is turned off, then the cluster melts away.

Both the reversal of the direction of the motion and the transition from sliding to hovering are very distinct qualitative features of the dynamics. Accordingly, they provide benchmark tests for theoretical models and numerical studies of chemically active motile particles. More specifically, by carrying out Brownian dynamics simulations of the trajectories of the particles, with velocities calculated according to the chosen model of chemical activity (reaction scheme and products, etc.) and the mechanism of motility (i.e., self-diffusiophoresis, self-electrophoresis, etc.), it should be possible to capture and rationalize these transitions (eventually after accounting for short-ranged DLVO forces and gravitactic and phototactic effects).

Finally, further emphasizing the richness of even this simple strategy of assembly, one notes that not only the spatial extent of these clusters but also the crystalline symmetry (square, hexagonal, etc.) can be controlled. As illustrated in Figure 3, this can be achieved by using the size ratio of the active and inert spherical particles as the control parameter.

Figure 3.

Controlling the symmetry of the emerging cluster via the size ratio of the active and inert particles: square (a), pentagon (b), hexagon (c), and heptagon (d). Scale bars correspond to 5 μm. Reproduced with permission from ref (34) (Figure 6). Copyright 2017 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

Chemically Active Janus Particles and an Inert Microgear

The previous example of programmed assembly employed an active Janus particle as a nucleus for a cluster of chemically inactive ones. The opposite case, in which a topographically structured, chemically inactive particle acts as the scaffold for assembling motile, chemically active Janus particles in a spinning microgear, was reported in ref (56).

The system consists of a thin SU-8 photoresist microgear with strongly asymmetric teeth (the chemically inert component) and self-propelled spherical Janus particles, obtained by depositing Pt over half of the surface of a silica sphere (Figure 4). The active particles move by decomposing, on the Pt side, hydrogen peroxide in aqueous solution. The particles and the gears are sedimented at a glass slide, and the gears lie flat due to gravity.

Figure 4.

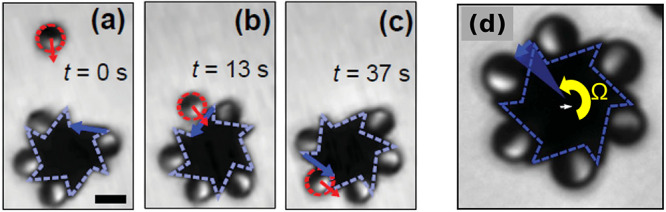
(a–c) Collision with the microgear, alignment along the long edge, and trapping at the vertex of the wedge for a motile Janus particle. The scale bar in (a) corresponds to 5 μm. (d) Self-assembled, steadily spinning (counterclockwise with angular velocity Ω) microgear. Adapted with permission from ref (56) (Figures 2 and 5). Copyright 2017 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

The inert gear, when alone, exhibits solely Brownian rotation and translation (as expected). Once the Janus particles are active, the assembly of a spinning gear follows upon collisions of the motile Janus particle with the inert gear (Figure 4(a–c)). The process exploits the concept of “guidance by the edge”,^31,44 and it requires an optimal choice of the ratio between the lengths of the long and short sides of a tooth such that only the long one is acting effectively in the guiding process. Crucially, the vertex of the wedge formed by a long and a short edge acts effectively as a trap for the Janus particle as long as the chemical activity is “on” (a phenomenon also reported in ref (44), Figure 2(d,e)). This is a key factor for achieving the complete occupation state shown in Figure 4(d) and steady spinning. The emergence of spinning can be understood by noting that the otherwise motile Janus particle is at rest with respect to the gear (i.e., it is stalled by the short edge of the tooth). Accordingly, a force, roughly along the normal to the short edge, is exerted on the tooth, and thus a torque acts on the gear.

This system also demonstrates that, owing to the operation under out-of-equilibrium conditions, the enhanced diffusion (active Brownian motion) of the individual Janus particles can be converted to a steady rotation of the ensemble, from which work can be extracted. As noted above, the key for the steady-state operation of this self-assembled structure is the dynamic trapping of a Janus particle by the vertex of the wedge. Capturing and rationalizing this distinct qualitative feature of the dynamics is another example of a benchmark test for theoretical models and numerical studies of chemically active motile particles.

Motor from Motors: Assembly of Motile Chemically Active Particles into Spinning Rotors

Probably the most significant result concerning the self-assembly of chemically active particles is that of hierarchical (super) structures of spinning rotors recently reported in ref (57) (Figure 5). The chemically active particles used in the study are TPM polymer spheres (Figure 5(a)) with a photocatalytic hematite cube partially embedded in the polymer (Figure 5(a)); these particles have also been employed in the studies in refs (35) (the living crystals; see Figure 1) and are well characterized.²⁴ The particles, sedimented at a glass wall, are chemically active and motile when immersed in hydrogen peroxide aqueous solutions and illuminated with blue-violet light of suitable wavelength. Their motion is with the hematite part in the back. In spatial gradients of light intensity, the particle reorients to align along the gradient direction, with the TPM part facing toward the region of high intensity (and, accordingly, the particle migrates toward the region of maximum light intensity).⁵⁷

Figure 5.

(a) Active particle consisting of a hematite cube and a TPM sphere. (b) Seven Janus particles self-assembled into a spinning rotor. (c) Dynamic superstructure of seven spinning rotors. (Inset) Melting of the structure upon turning off the activity. Adapted with permission from ref (56) (Figure 1). Copyright 2018, Springer Nature.

The phototactic characteristics mentioned above have been cleverly exploited to achieve the programmed self-assembly of a microstructure from a dilute suspension of active particles as follows. An in-plane radial gradient of light intensity was created by superposing a bright spot of a focused laser, shown from underneath the glass, over the background uniform illumination. This leads, due to the phototactic behavior, to an effective confinement of the motile particles in the vicinity of the bright spot and an enhanced rate of collisions between particles (owing to the biased motion of the particles within the laser spot toward its center).

As discussed in detail in ref (57), the first step in the assembly of the structure involves the transition of a motile active particle, as it crosses the center of the light pattern, from the sliding state to a nonmotile hovering state with the catalyst up (due to the illumination from below). In this state, the stalling of the active particle induces hydrodynamic flow oriented radially along the surface of the glass toward the particle. This acts as an effective radial attraction for the nearby motile particles, which is in addition to the attraction, due to the spatial pattern of illumination, toward the center of the spot. The second step of the self-assembly of the spinning rotor occurs by gathering six motile particles, with the TPM part oriented toward the center, around the hovering one. While these particles remain in a sliding configuration, a symmetry-breaking dynamic transition occurs. The state with in-plane radial symmetry, in which the axes of the six particles are aligned along radii from the central one and the ensemble is at rest, is replaced by one in which each of the six particles exhibits an in-plane tilting of its axis such that all six are either tilted to the right or tilted to the left of the radial direction (Figure 5(b)). Consequently, the ensemble spins counterclockwise or clockwise, respectively. (The two configurations occur with equal probability, as expected for a symmetry-breaking transition.)

As discussed in ref (57), the process is robust in that no other configuration (e.g., different spatial extent, with more than one spatial shell, or a different number of particles in the radial shell around the central one) occurs. Even more remarkable is that the self-assembled spinning rotor formed in this manner remains a stable structure upon turning off the radial light pattern, which was necessary for its formation for as long as the particles remain chemically active (i.e., hydrogen peroxide is present and the uniform illumination of a suitable blue-violet wavelength is on). (A comparison of this outcome with the living clusters (Figure 1) illustrates the concept of programmed self-assembly: while the motile particles are the same in both studies, the use of a certain spatial pattern of motility (the additional laser illumination) led to the formation of a new, distinct structure.) The symmetry-broken spinning state (six motile particles around the central hovering one) thus emerges as a stable attractor for the dynamics of the seven-particle structure, and the nonmotile state with in-plane radial symmetry is unstable. Rationalizing the emergence of this attractor provides another significant benchmark test for the models of chemical activity and self-motility; an even more challenging test is that of capturing the whole dynamics, involving the seven particles, of the process of assembly of the spinning rotor structure under the light pattern.

Impressively, the stable structures of spinning rotors can be now considered on their own as active building blocks for a new self-assembly process.⁵⁷ Thus, one can produce hierarchical superstructures such as the seven-rotor ensemble shown in Figure 5(c) and the three cospinning rotors in Figure 6 (one of the colored ensembles). The superstructures can be assembled on their own in higher-level blocks, such as the two co-rotating superstructures of three rotors (the yellow, orange, and red ones and the three blue ones, respectively, in Figure 6). This new assembly shows, in turn, certain self-organization properties, such as the emergence of a synchronization of the counterclockwise and clockwise rotations of the two three-rotor superstructures⁵⁷ (Figure 6).

Figure 6.

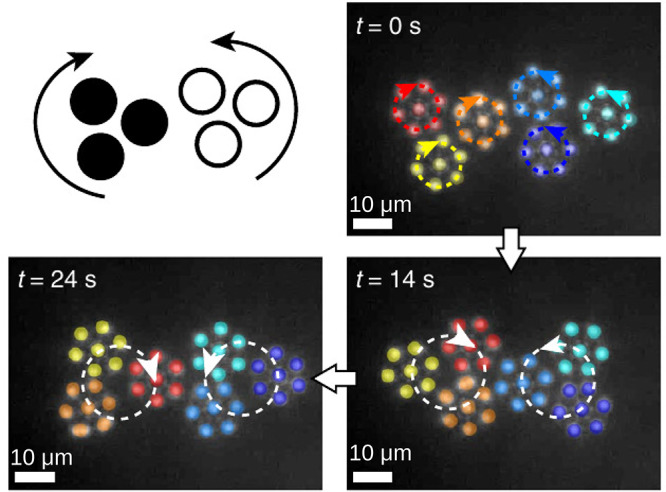
Two superstructures, each made out of three cospinning rotors, reach a state of synchronized rotations when brought close to each other. Adapted with permission from ref (57) (Figure 4). Copyright 2018 Springer Nature.

Modeling Self-Assembly Processes with Chemically Active Colloids

The technical challenges faced by theoretical and numerical models aimed at capturing collective effects in suspensions of active particles have been discussed in various contexts.^58,77−79 Accordingly, these will be only briefly discussed, with a focus on the context of small self-assembled structures reviewed in the previous section.

The main technical challenge faced by numerical studies involving many particles (active, passive, or mixtures of both) as well as confining surfaces (walls or interfaces) is that both the Laplace and the Stokes equations are to be solved in a three-dimensional domain with a complicated shape. Additionally, the domain involves moving boundaries (the surfaces of the particles), and the equations are subject to boundary conditions that are configuration-dependent (e.g., because the phoretic slip boundary condition involves the solution of the Laplace equation for the current arrangement of particles). Furthermore, the equations should be solved with high accuracy at both small length scales (i.e., within the narrow spaces between particles, when the particles are close to steric contact; e.g, Figures 2 and 4) as well as at large length scales, on the order of the particles radii (e.g., the chemical field around a particle located in the vicinity of an active one). Accordingly, irrespective of whether one employs finite element methods or exploits boundary element methods (in order to reduce the dimensionality of the spatial discretization), the memory demands of such studies strongly increase with the number of particles and quickly become prohibitive. (See, for example, the study in ref (58).) Similar conclusions can be drawn regarding the demands on CPU time concerning the accurate evaluation of the trajectories of many particles for sufficiently long times. It is then to be expected that, in what concerns the issue of collective motion, progress could eventually be made by involving numerical simulation methods with some degree of coarse-graining, such as lattice Boltzmann⁸⁰ or multiparticle collision (MPCD),^77,81,82 rather than by numerically solving the continuum equations. Such numerical simulation methods are well suited for scaling up the number of particles, but the implementation of the boundary conditions at the surfaces and, in particular, the chemical reaction is significantly more involved.⁸⁰ Therefore, systems of only a few particles, which can be approached by either type of numerical method, but exhibiting complex dynamics, such as the examples discussed in this review, are also very important from the perspective of the validation of complex, coarse-grained numerical simulation methods.

Furthermore, since the self-assembled structures of interest here involve small distances between the particles, far-field approximations cannot be a priori justified; consequently, analytical calculations are difficult, if not impossible, and have to be replaced by numerical studies. On the other hand, the small interparticle separations observed in the structures discussed above highlight the importance of the near-field details of the effective interactions. These are expected to depend significantly on the shapes of the particles. Accordingly, understanding these aspects can facilitate and guide the design of particles with optimal shapes for achieving a desired type of assembly.

In the case of bimetallic, chemically active particles, the mechanism of reaction and motility seems to be clear,¹⁷ and thus theoretical and numerical studies are limited only by technical challenges as noted above. On the other hand, the level of detail at which the modeling of catalyst/insulator chemically active particles is possible is currently limited by the insufficient knowledge of the precise chemical reaction(s) involved in the motility and, in particular, by the surprising possibility that electrochemical reactions might play a role.^83,84 The latter hypothesis is motivated by the fact that all of the various active particles involved in the examples discussed in the previous sections share the feature, initially discussed in the context of Pt/polystyrene particles,^83,84 that their motility is strongly reduced upon adding tiny amounts of salt to the solution (salt concentration above ∼10^–5 M). For the Pt/polystyrene particles, it was also established that the reduction in motility does not necessarily correlate with a reduction of the rate of hydrogen peroxide decomposition.⁸³ Although there is agreement that the addition of salt influences motility, the magnitude of these effects remains subject to debate; for example, a significantly weaker reduction (only a factor of 2) of the velocity of Pt-covered TPM colloids upon addition of salt at 1 mM concentration has been very recently reported in ref (85).

In order to explain the effect of salt on the motility, it has been argued^83,84,86 that, unexpectedly for a Pt-insulator particle, the mechanism of motility must be dominated by a self-electrophoretic component. Furthermore, in order to reconcile the reduction in motility with the lack of effects on the reaction rate,⁸³ it has been additionally argued that two reaction loops must be involved in the mechanism of motility. One of the reaction loops is electrochemical; it must have a spatially dependent rate over the surface of the particle in order to enable a self-induced electric field, and it contributes only minutely to the total rate of hydrogen peroxide decomposition.^83,86 The other reaction loop involves electrically neutral product species (oxygen and water), and it accounts for most of the rate of the hydrogen peroxide decomposition. The nature of the electrochemical reaction and the reason for spatial variations in its rate differ between the two proposals in refs (83) and (86).

The study in ref (83) attributes the spatial variations in the reaction rate to the dependence of the reaction rate on the thickness (when below 10 nm) of the Pt film, which is assumed to have varying thickness between the pole (thick) and the equator (thin) of the Janus sphere. This is motivated by the measured dependence of the rate of hydrogen peroxide decomposition on the thickness of a Pt catalyst film. On the other hand, the study in ref (86) attributes the spatial variations to a different factor, namely, the reaction being in the diffusion-limited kinetic regime. Thus, in this case the electrochemical loop should be active even for uniform Pt films of finite extent (e.g., a Pt disk). This conclusion explains the motility of the flat Pt twisted stars studied in ref (86), but it seems to be at odds with the observations reported in ref (87) that Pt disks, with uniform thickness and placed on insulator support, do not induce a response of nearby charged tracers. As suggested by ref (87), it may be possible to elucidate some of these issues by comparing the behavior of tracers in the vicinity of Pt disks which are imprinted on polystyrene, both for disks with uniform thickness, below and above 10 nm, as well as for disks with radially varying thickness, from thick (above 10 nm) to thin (below 5 nm).

Finally, additional unexpected features of the Pt-catalyzed decomposition of hydrogen peroxide have been revealed by the study of Pt/silica systems in ref (88). It has been observed that the hydrogen peroxide decomposition by Pt disks imprinted on silica walls induced a dramatically different motion of tracer particles depending on whether the surface of the Pt film was smooth or rough. In the former case, there was basically no response of the tracers, while in the latter the response was strong, with a direction that was dependent on the charge of the tracer. The latter feature was also interpreted as indicative of an electrochemical reaction, but what that reaction is remains unclear.

The features noted above reveal that the mechanism of motility for the chemically active catalyst/insulator particles is possibly much more involved than initially thought. The cost in time and computer resources for direct numerical studies of models that also accounts for eventual self-electrophoretic reactions with various possible products and (yet) unknown reaction rates is very high. From this perspective, it seems that at this time the better defined and more accessible question is that of whether the self-assembly processes discussed in the previous section can be captured by simple models of self-diffusiophoresis with slip velocity, as employed in previous studies of chemically active particles.^{15,18,21,45,49} Such studies should then be interpreted as employing heuristic models with phenomenological parameters (the phoretic or osmotic slip coefficients).

Numerical studies, using the boundary element method (BEM), of the dynamics of a few model active, spherical particles with a simple activity pattern (uniform over the surface) and phoretic mobility that is constant over the surface have been carried out already⁵⁸ (Figure 7). Extending these numerical schemes to account for the Janus character of the particles, for the confinement by a planar wall and for an osmotic slip at the wall, does not require major conceptual modifications. (There could be technical issues related to the calculation of the activity-induced osmotic slip along the wall.) Additional details, such as the weight and gyrotactic response of the Janus particles, can be addressed straightforwardly if the thickness of the catalyst film along the surface of the particle is known. As shown in a recent study,⁸⁹ such a thickness profile can be determined with very good accuracy by using focused ion beam slicing and image analysis of the corresponding micrographs.

Figure 7.

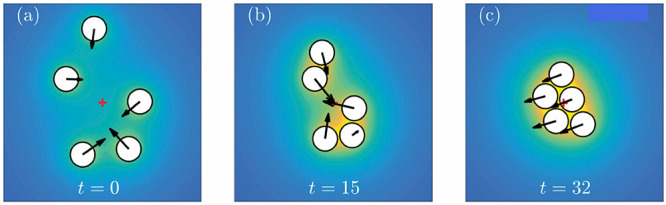
(a–c) Numerical solutions (BEM calculations) of the clustering of five identical chemically active spheres (located in the same plane) with the constant flux model chemical activity. The distribution of the product of the chemical activity is color-coded (deep blue, background (bulk) density; yellow, maximum density), and the arrows show the instantaneous configuration-dependent velocities of the particles. The red cross shows the position of the center of mass of the five particles. Adapted with permission from ref (58) (Figure 5). Copyright 2018 The Royal Society of Chemistry.

However, such BEM calculations remain challenging owing to the numerous degrees of freedom (i.e., the weakly three-dimensional motion of the sedimented particles, the in plane rotation of the axis of the particle, and the (eventually weak) out-of-plane rotation of the axis of the particle). (These are in addition to the technical aspects discussed at the beginning of this section.) Furthermore, the number of phenomenological parameters involved in the model should also be considered; not surprisingly, the larger the number of parameters and the smaller the number of constraints on them, the more time- and resource-demanding such a study will be. Consider, for example, the case of a titania/silica Janus particle assembling a cluster of silica particles, with all particles being sedimented near a glass wall. Assuming that the glass has properties similar to those of silica from which the particles are made, this setup then involves the minimum number of material parameters (i.e., a phoretic mobility coefficient for the titania part and one phoretic mobility coefficient for the silica surfaces). By choosing a very simple model of chemical activity, which is that of a constant-flux production boundary condition (over the active cap) of a single relevant solute species,^15,45 one more parameter (i.e., the boundary flux, which is related to the rate of the chemical reaction) is added to the description of the system. Thus, even in what can be considered the best-case setup described above, one arrives at the challenging issue of numerically exploring a three-dimensional parameter space in order to determine the state diagram of assembled structures emerging from the dynamics.

Accordingly, such studies are in much need of additional information about the phenomenological parameters. For example, the value of the self-phoretic velocity of the Janus particles when far from the surfaces, which can be determined by three-dimensional tracking during sedimentation,^29,32 provides a relation between the rate of reaction and the two phoretic mobility coefficients of the Janus particle. Furthermore, it may also be possible to estimate the phoretic mobilities for the various materials involved in an experiment by adapting the setups used to study the formation of depletion zones in the vicinity of perfluorinated polymer membrane materials such as Nafion.⁹⁰ For example, the formation of an exclusion zone for a dilute suspension of silica particles in aqueous hydrogen peroxide solution near a chemically active film of titania may be used to estimate the phoretic mobility coefficient of the silica. Such an estimate is obtained by equating the phoretic velocity at the edge of the exclusion zone with the sedimentation velocity. (The latter can be adjusted to be in the range of μm/s, which is expected to be relevant for phoresis simply by adjusting the size of the particle.)

In summary, there are still significant challenges faced by the theoretical modeling and numerical analysis/simulations of systems of chemically active particles. These are in part due to technical limitations, in part due to involving too many free parameters (not sufficiently characterized), and in part due to incomplete knowledge concerning the exact mechanisms of the chemical reactions involved in self-motility^83,84,86 (except, perhaps, in the case of the bimetallic Janus rods¹⁷). Accordingly, concerted efforts to elucidate the latter aspects, here including systematic investigations of the effects of salts on the motility of chemically active particles far from the walls, in the bulk solution (e.g., by using acoustic levitation⁹¹) are needed in order to make progress in understanding active self-assembly processes.

Outlook

The self-assembled structures that have been discussed here and, in particular, the beautiful motors made out of motors hierarchical organization show that after 15 years of intense effort the field of motile chemically active particles has reached maturity. I argue here that this is likely just the tip of the iceberg and that the potential for new developments is yet to be tapped. For example, the development of chemically active particles working with chemical reactions that do not produce gases, such as the recently reported enzyme-decorated Janus colloids,⁹²⁻⁹⁴ could enable systematic studies of collective behavior at high particle densities without the impact of spurious effects due to the formation of bubbles. Furthermore, the possibility of using components with time-dependent activity protocols, briefly mentioned below, is only one of the many potentially promising future directions.

Another interesting direction follows from the observation that the assembled structures are stable while they are active and that they melt when they become inactive. Accordingly, clusters of chemically inert particles assembled around a chemically active seed could be quasi-instantaneously disassembled or reconfigured by changing the nature of the out-of-equilibrium effective interactions from attractive to repulsive. This is possible by using photochemically active particles capable of promoting different reactions in the same solution when illuminated with light of different wavelengths, such as the recently reported Cu/titania Janus particles in aqueous peroxide solutions.⁶³ Furthermore, one may consider incorporating within such self-assembled structures particles with pulsating activity and motility (e.g., Ag/PMMA particles, which are periodically motile when immersed in hydrogen peroxide with KCl aqueous solution and UV illuminated; see ref (95) and Figure 8) to achieve self-assembled structures that periodically oscillate (“beating” structures).^60,61

Figure 8.

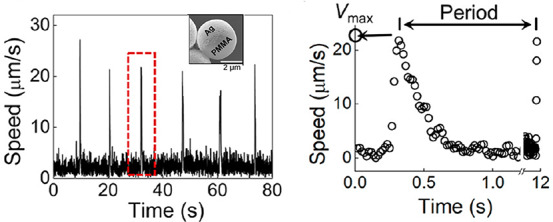
Velocity as a function of time for an Ag/PMMA Janus particle (inset) when immersed in hydrogen peroxide with KCl aqueous solution and UV illuminated. Adapted with permission from ref (95) (Figure 1). Copyright 2019 American Chemical Society.

The examples discussed in the previous sections deal with active particles of spherical (or quasi-spherical) shape and dynamics at the top of a planar wall. These systems exhibit complex behavior, yet the setup of spherical shapes and planar walls provides significant simplifications for theoretical and numerical studies. Accordingly, explaining in detail the various dynamic transitions and sequences of transitions occurring in these simpler systems is an essential first step in testing our current models of motile, self-phoretic, chemically active particles. However, as our understanding of these systems improves and the technical capabilities of manufacturing particles (e.g., three-dimensional printing) develop, it is to be expected that particles with more complex shapes will be employed in future studies and applications. Such particles would allow for more complex (i) patterns of motion at the single-particle level (ref (12)) and (ii) patterns of anisotropic interactions and of assembly upon collision. For example, for particles with complementary shapes, like pieces of a puzzle, a quasi-isotropic effective attraction at long range and an aligning, anisotropic near-range interaction can promote the right orientation for a collision in a lock-and-key configuration; such mechanisms would ensure robust and stable assembly. Another area of significant development could be that of collective motion and/or self-assembly for particles constrained to “live” on curved manifolds (e.g., active Janus particles trapped at the interface of a drop). While this topic has been less thoroughly explored, recent numerical studies of active particles on spheres^96,97 hint at the significant interplay between the curvature of the surface and the collective behavior of the particle. This may be very relevant in the context of active Pickering emulsions or active membranes.

Finally, one notes that the recent technological and computational advances have made it possible to track many particles and individually address them on the fly, quasi-simultaneously with narrow, focused laser beams.^98,99 This has provided the possibility to build spatial patterns of chemical activity for each particle and to implement protocols of turning the activity of each particle on and off according to man-made rules mimicking “quorum sensing”.⁹⁹ The ability to implement on demand both time protocols for chemical activity and artificial sensorial responses that otherwise may be challenging tasks for material science could lead to new forms of self-assembled active materials.

Biography

Mihail N. Popescu received his Ph.D. from Emory University and is currently working as a scientist at the Max-Planck-Institut für Intelligente Systeme (MPI-IS) in Stuttgart. His research interests are in the area of active matter, with a focus on chemically active particles, their behavior under confinement, and their response to spatially and temporally varying fuel fields.

The author declares no competing financial interest.