Abstract
The COVID-19 pandemic, which started at Wuhan, has shut down world economies, prompting governments to impose drastic lockdown measures of the economy and the society. As these measures are exhausted, non-COVID-19 related issues such as those associated with the mental and physical well-being of people under lockdowns became an emerging concern. As these issues are evident, not to mention the economic downturn, governments are currently looking at designing lockdown relaxation efforts by simultaneously considering both public health and economic restart. Without documented experiences to rely on, governments are resorting to trial-and-error approach in creating a lockdown exit strategy while preventing succeeding waves of cases that may overwhelm healthcare facilities. Thus, this work pioneers the use of the decision-making trial and evaluation laboratory (DEMATEL) method with intuitionistic fuzzy (IF) sets along with the domain of public health and the emerging COVID-19 pandemic. The DEMATEL handles the intertwined causal relationships among guideline protocols for the relaxation strategy. The intuitionistic fuzzy set theory addresses the vagueness and uncertainty of human judgments in the context of the DEMATEL. A case study of the Philippine government response for the lockdown exit is presented to evaluate the applicability of the proposed method. Findings reveal that compliance of minimum public health standards, limited movement of persons, suspension of physical classes, the prohibition of mass gatherings, non-operation of category IV industries, and non-operation of hotels or similar establishments are the most crucial protocols for such strategy. These findings offer practical insights for the government to allocate resources and impose measures to ensure their implementation, as well as for developing mitigation efforts to cushion their socio-economic impacts. Policy insights and avenues for future works are also discussed.
Keywords: COVID-19, Pandemic, Lockdown, Relaxed measures, DEMATEL, Intuitionistic fuzzy sets
Highlights
-
•
Lockdown relaxation protocols are managed to balance public health and economic restart.
-
•
It proposes intuitionistic fuzzy DEMATEL analysis in addressing the emerging COVID-19 pandemic.
-
•
The Philippine government response for the lockdown exit is presented to demonstrate the proposed method.
-
•
Findings reveal the six most crucial protocols for the lockdown exit strategy.
-
•
Policy insights are offered for the government to develop mitigation efforts to cushion adverse socio-economic impacts.
1. Introduction
While most countries were celebrating holidays during the second half of December 2019, the streets at Wuhan City in Hubei Province, China were at a brink of a disease outbreak caused by cases of pneumonia of unknown etiology. These cases are believed to be linked to Huanan Seafood Wholesale Market, which trades fish and wild animals, including bats [1]. Several claims traced the dates of the pneumonia cases back in November 2019, with the first confirmed case in Wuhan on 1 December [2]. However, the first case has no exposure to the Huanan seafood market, not until 10 December, when a case directly linked to the market was recorded [2]. The debate on these claims is still developing. Nonetheless, 27 cases were already documented on 31 December, which prompted the local health officials at Wuhan to inform the World Health Organization (WHO) about the developing disease [3]. The causative agent was identified as Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2), and the WHO named the disease as COVID-19 [3].
In just 30 days, COVID-19 quickly spread from Wuhan to the rest of China, pushing the public health services in Wuhan City and Hubei Province to their limits [4]. While some infected patients are asymptomatic, those with symptoms experience anywhere between mild ones (i.e., dry cough, sore throat, and fever) and more severe and fatal symptoms (i.e., organ failure, septic shock, pulmonary edema, severe pneumonia, and ARDS) which require hospitalization [3]. A review of its virology, epidemiology, clinical manifestations, diagnosis, treatment, and prevention can be found in Ref. [2]. [5] summarized why COVID-19 is such a threat: (1) it can kill adult people with existing health problems, and (2) its transmission is quite efficient. As the cases in China were gaining momentum, COVID-19 was starting to leak outside of its epicenter to the rest of the world. This prompted China on 23 January to implement an unprecedented lockdown in recent history, affecting a whopping 40–60 million people across Hubei province [3]. The measures are considered restrictive and drastic – curtailing some liberties of its citizens [6]. It suspended all forms of public transportation [3], implemented heightened mobility restrictions, limited social interaction, and canceled gatherings [7], and all public affairs within the city of Wuhan and other cities in Hubei were put off [8]. More aggressive measures were implemented in Wuhan after 7 February. These include locking down of residential buildings and compounds, strict self-quarantining for families, door-to-door inspection for suspected cases, quarantining suspected cases, and close contacts in quarantine spaces [9]. Along with these measures are the efforts to ramp up the construction of new hospitals and quarantine facilities to manage the surge of cases in the most affected areas [10].
Such drastic containment measures in China earned praises from the WHO and are considered crucial in curbing the spread of COVID-19 in mid-February [6,11]. The speed and the magnitude of these measures have never been implemented on such a large scale [4]. In the absence of antiviral drugs and vaccine, China focused on traditional public health outbreak response mechanisms of identifying cases, testing, isolation, contact tracing, social distancing, quarantine, and community containment [4,10,12]. It also recommended basic hand hygiene measures such as frequent hand washing and the use of PPE (e.g., face masks) [3]. These response initiatives were aimed at buying some time for science (e.g., development of vaccines and antiviral drugs, in-depth characterization) to catch up with the spread [4,13]. The timeline of the COVID-19 and the containment measures implemented in Wuhan can be found in Ref. [8]. Quantitatively identifying which of the stringent measures were most successful could not be carried out by present models [14,15]. What is known and apparent is that the totality of these measures has delayed COVID-19 spread in China [14]. Despite these efforts [3], outlined some of the lessons that China fell short in curbing the spread of COVID-19: lack of transparency, travel restriction delay, quarantine delay, public misinformation, emergency announcement delay, and research and development. Nonetheless, quantifying how these factors play in the viral spread and their long-term impact could not be determined yet and is open for discussion.
The staggering cases of the disease on a global scale prompted WHO on 11 March to declare COVID-19 a pandemic. Outside China, two enormous challenges are upfront: (1) effectively containing current and future outbreaks, and (2) treating the infected population promptly and safely [11]. The draconian measures imposed by China were, at a period, considered unpopular by other countries. Considered as the only way to truly control outbreaks, one-fifth of the world population is in lockdown [16]. In the absence of established measures to contain the COVID-19 spread at a scale, and no controlled experiment has taken place [17], countries resorted to trial-and-error initiatives with various strategies being explored to curb its transmission [18]. For instance, South Korea and Italy introduced lockdowns in early March [18]. On 24 March, the Indian government has announced a countrywide lockdown for three weeks [19]. Initially, the United Kingdom was entertaining the idea of “herd immunity”. It was later on obliged to change gears as the model published by an experienced team at Imperial College, London, predicted that at any response scenario, the number of cases requiring ICU would exceed the ‘surge capacity’ of healthcare facilities [20]. An unprecedented lockdown was then implemented on 23 March. In the Philippines, the government issued a lockdown in the form of an enhanced community quarantine on 12 March. Collectively, 188 countries have been on a pause, stopping religious meetings, sports events, and other social gatherings, while closing their borders and businesses including schools which affect 1.5 billion students [17].
The drastic measures and lockdowns implemented by most countries worldwide come at a high economic and socio-economic cost, creating ripples of economic shocks and disrupting the functioning of societies [21]. The economic costs are straightforward, but the social costs have far-reaching consequences [22]. Observed that the ongoing crisis had caused vulnerability to food insecurity for people who are already economically vulnerable. The lack of food shops in some countries (e.g., UK) has led people to be unable to acquire the food they need as stay-at-home measures compel them to go out or food supplies are not readily available [22]. [6] called for greater attention to the health of the people who are not infected by the virus during lockdowns. They highlighted that those who stopped working have worse mental and physical health conditions, as well as distress, and physically active people are more vulnerable to some well-being issues [6]. Another indirect effect is the growing cases of deteriorating mental health of people in lockdowns [23]. [23] identified some additional health problems such as stress, anxiety, symptoms of depression, insomnia, denial, anger, and fear at a global scale. With similar observation [24], surveyed the general public in China to assess their levels of psychological impact, anxiety, depression, and stress during the initial stage of the outbreak. They found out that more than half reported the psychological effect as moderate-to-severe, and about one-third rated moderate-to-severe anxiety. Collectively, these concerns may weaken the efficacy of the imposed measures to control the viral spread.
As of this writing [11 May 2020], the total number of COVID-19 cases worldwide is 4,117,684, with global deaths of 286,330 [25]. It is almost widely accepted that with the onset of current global drastic measures of testing, contact tracing, isolating, social distancing, and quarantining, COVID-19 can be contained, at least in its initial spread. However, the rapid acceleration of the disease in different countries and the near-collapse, if not total breakdown, of healthcare systems even in countries with more robust public health mechanisms indicate shortfalls of preparedness of countries in handling pandemics [15]. As confinement measures are not sustainable in the long run from an economic and social perspective, easing drastic containment measures is a way forward [26]. The decision to lift draconian measures comes with a trade-off between socio-economic costs and the potential resurgence of cases [27]. Cautioned that a premature relaxation of interventions and measures could lead to the second wave of cases, and governments must ensure that healthcare capacities are not pushed to its limits while the outbreaks are growing exponentially. A model developed by Ref. [27] suggests that a sudden and premature lifting of social distancing measures would yield higher health and economic loss. Even without a ‘premature’ relaxation, lifting altogether, the aggressive measures and lockdowns would cause cases to soar high at an exponential rate [28]. With a low community level of immunity, the attack rate of approximately 2% could initiate a rapid second wave [11]. In Taiwan, Hong Kong, and Singapore, lifting of lockdown measures has resulted in the second wave of cases, prompting these countries to enforce stricter measures than what was implemented [29]. With the sustained economic crash, which may result in more non-COVID-19 deaths and social despair linked to prolonged confinement, which may negatively affect people, a well-designed exit strategy is a significant step [26].
[17] further elaborated that a lockdown exit strategy must carefully consider the triangulation of “the health of their citizens, the freedoms of their population, and economic constraints”. These factors could be translated into three control knobs for governments: (1) isolation of patients and contact tracing, (2) border restrictions, and (3) social distancing [17]. Two primary defining criteria on when to turn these knobs for easing lockdown measures are the (1) testing capacity at a national level [30], and (2) healthcare capacity [15]. Upscaling of testing capacity is a precursor of efficient contact tracing, isolation, and quarantining, while the capacity of healthcare facilities dictates the allowable number of cases that require ICU beds for treatments. One plausible scheme which is a “drug holiday” approach [18], popularly adopted by Singapore and Hong Kong as the “suppress and lift” strategy [17]. In this approach, social distancing measures are eased out, and reimpose when cases start to climb again [17,18]. This strategy would create a series of small outbreaks within the threshold of the healthcare capacity and builds up immunity to the disease [18]. Another crucial feature of an exit strategy is to carefully monitor the real-time reproduction number (Rt) and the confirmed case fatality rate (cCFR) to inform strategy against a potential second wave to strike a balance between health and economic objectives [27]. As the resurgence of cases becomes inevitable brought about by relaxing drastic social distancing measures, governments must proactively prepare that the healthcare system has adequate labor, resources, and facilities to minimize mortality [15]. On the other hand, another exit strategy currently put forward by Ref. [26] is to release only immunized but virus-free people back to their normal lives to increase community immunity. When the pandemic subsides, younger people who are low risk but virus-free and not immune may be gradually considered. Such a strategy, as argued by Ref. [26]; would allow shifting from massive social-distancing measures to the testing of symptomatic cases only, isolation of confirmed cases, and contact tracing and quarantining, along with the release of immune people from containment. Despite these suggested post-lockdown relaxation insights, at present, there is no consensus in the scientific communities or guidance on developing an exit strategy with no agreed benchmarks on measuring safe conditions for returning to normal life [29].
As of 12 May, the Philippines has 11,086 COVID-19 cases, with 726 deaths [25]. Its largest metropolitan, Metro Manila, has been on a lockdown (i.e., locally termed as ‘enhanced community quarantine’ (ECQ)) since 12 March. After two months, Metro Manila and the other two large cities are still on a restrictive ECQ while the rest of the country is just recently under a relaxed ‘general community quarantine’ (GCQ). The guidelines of these two conditions are set forth by the Inter-Agency Task Force (IATF), which was formed by the Philippine government early this year to supervise and provide recommendations on all government actions regarding the COVID-19 pandemic. The GCQ status is a relaxation of the ECQ, with measures designed to restart economic activities. After a two-month lockdown of the entire country, the transition guidelines from ECQ to GCQ are provided in the [31]. The guidelines consist of a set of protocols with obvious overlaps that aim to maintain social distancing, proper hygiene, and minimal movement of people to curb the viral spread while gradually restoring some salient socio-economic activities. These protocols, as argued in the emerging literature, are under a trial-and-error approach with neither controlled experiments that would support the effectiveness of such protocols nor information from prior experience on a massive scale. Note also that current models fail to quantitatively identify which of the stringent measures were most successful in the China experience [14,15]. Nevertheless, the government's priority must be keeping mortality at a minimum, and amelioration measures are necessary to cushion the impact of economic collapse [21]; thus, a careful strike of balance is crucial.
Thus, this work offers a modeling approach based on network analysis on how these protocols are causally interrelated in an attempt to determine those protocols with high priority. Understanding these intertwined relationships provides insights to policymakers on key protocols, and at the same time, identifies those redundant protocols which can be relaxed. This information is crucial for efficient and effective resource allocation decisions that could strike a balance between maintaining public health and economic restart. To address this objective, an intuitionistic fuzzy decision-making trial and evaluation laboratory (DEMATEL) (IF-DEMATEL) is proposed in this work. DEMATEL, developed by the Science and Human Affairs Program of the Battle Memorial Institute of Geneva between 1972 and 1976, is a network analysis approach based on graph theory that handles a complex system of elements connected by causal relationships [32,33]. It achieves two objectives: (1) to determine the causal relationships among elements in a network (e.g., protocols in a set of protocols), and (2) to cluster the elements into the net cause and net effect groups. Due to the inherent uncertainty of eliciting judgments within the DEMATEL framework, an intuitionistic fuzzy set (IFS) theory is adopted in this work. IFS, proposed by Ref. [34]; is a generalization of the fuzzy set theory proposed by Ref. [35]; which handles vagueness and uncertainty in computing. While the classical fuzzy set theory introduces a membership function, the IFS extends this concept to include a non-membership function. The use of IF-DEMATEL is popular across different domain applications, such as strategic decisions in the insurance industry [36], sustainable solid waste management [37], critical factors in recycling industry [38], green supply chain [39], and project risk assessment [40]. Note that this list is not intended to be comprehensive. However, its application in public health is scant, most especially in the emerging COVID-19 pandemic. Thus, this work is the first of its kind in addressing (1) the use of IF-DEMATEL in the public health domain, and (2) the application of complexity mapping under uncertainty in the management of COVID-19 pandemic as a global public health emergency. It advances the evolving literature of COVID-19 by effectively identifying key protocols for a lockdown exit strategy, which may set as guidelines for relevant policy- and decision-making.
This paper is outlined as follows: Section 2 illustrates the emerging scenario of the Philippine COVID-19 outbreak. Section 3 presents a brief background of IF and DEMATEL. The proposed detailed methodology is described in Section 4. Section 5 details the results and the findings. Section 6 highlights the implications of these results. It ends with a conclusion and identification of future works in Section 7.
2. Emerging scenario of the Philippine COVID-19 outbreak
To date, the Philippines is experiencing one of the worst cases of the COVID-19 outbreaks as the second-highest confirmed cases and deaths in the ASEAN, next to Indonesia (COVID-19 Dashboard, 20200), amplified with its weak healthcare system. The COVID-19 outbreak in Wuhan has reached the Philippine media since December 2019. However, no concrete initiatives have been undertaken until the first COVID-19 case in the country, which was confirmed on 30 January with a 38-year-old female Chinese national [41]). Table 1 presents the timeline of events relevant to the response of the Philippine government to the COVID-19 outbreak. Note that all dates are adjusted to local times unless those declared by the WHO.
Table 1.
Summary of events in the Philippine COVID-19 outbreak.
| Date | Relevant events | Reference |
|---|---|---|
| 30 January |
|
[41]) [42] |
| 1 February |
|
[43] |
| 2 February |
|
[44]) |
| 4 February |
|
[45]) |
| 7 March |
|
[46]) |
| 9 March |
|
[47] |
| 11 March |
|
[48] |
| 12 March |
|
[49] |
| 16 March |
|
[50]) |
| 17 March |
|
[51] |
| 19 March |
|
[52]) |
| 25 March |
|
[53] |
| 12 April |
|
[54] |
| 24 April |
|
[55] |
| 30 April |
|
[31] |
| May 7, 2020 |
|
[56] |
The Philippine Congress, through the Bayanihan to Heal as One Act, allocates US$ 5.37 billion for the COVID-19 pandemic, where US$ 3.9 billion is allotted for the implementation of the emergency subsidy program, and US$ 1.4 for funding health requirements and other services [53]). The emergency subsidy program for two months covers the basic needs of the 18 million Filipino families [57]. The strict quarantine measures have put off public and private establishments that generate more than two-thirds of the overall GDP [58]). The inflation is expected to reach 2.2% in 2020, subsequently 2.4% in 2021 [58]. has projected GDP growth at 2% this year, with a strong recovery forecast of 6.5% growth in 2021 with the assumption that the pandemic will be curbed in June 2020. The Philippine government has been granted a loan of US$ 100 million from the World Bank to fund the emergency response project in addressing the healthcare needs for the COVID-19 pandemic, and improve public health preparedness [59]. Furthermore, the US government has also provided US$ 15.2 million in assistance to the country [60]. The Department of Labor and Employment highlighted that there are more than one million employees in the formal sector that were affected by temporary closures of businesses or flexible work arrangements (CNN Philippines, 2020). Employees in the manufacturing, hotel, restaurants, and tourism industry absorbed most of the impact [61]. [62] reported that the economy might lose between US$ 5.4 billion (best case) and US$ 49.5 billion (worse case) due to COVID-19 based on a Leontief input-output model. Specifically, the losses would come from transportation, storage, and communication sector (US$ 232.1–2.4 billion), manufacturing (US$ 1.6–16.9 billion), wholesale and retail (US$ 1.8–14.3 billion), and other services (US$ 823.2 million to 7 billion) [62].
As of April 2020, seventeen (17) testing centers for COVID-19 were constructed [63]. With the population of 109 million with a rapid increase of confirmed cases, the healthcare facilities are collapsing with just 89,000 hospital beds, of which 8,779 are isolation beds, 2,546 are ward beds, and only 1,249 are ICU beds, and 1,937 mechanical ventilators [64]). Currently, the Philippines has 129,000 doctors, of which only 50% are considered active [62]. As reported by Ref. [62]; the average age with COVID-19 cases in the Philippines is 53 years old, and the average age of mortality is 65 years old, 70% of which are male. 56% of the confirmed cases and 62% of reported deaths are concentrated in Metro Manila. On 24 April, the Philippine government decided to slowly lift the strict measures by announcing that lower risk community areas would be placed under GCQ [55]. The set of guidelines proposed on 7 May details the transition protocols from ECQ to GCQ. As long as an effective antiviral drug or vaccine remains unavailable, the government is looking at a future where provinces or cities are observing GCQ protocols. Table 2 summarizes the protocols issued by the IATF on 7 May. For easier recall, a code is assigned to each protocol. These protocols have inherent interrelationships, and redundancies are apparent to some extent. Each protocol requires resources and control measures that may overwhelm the government. Additionally, some protocols may be relaxed for economic and socio-economic purposes without undermining public health concerns over the pandemic. Thus, carefully identifying these protocols is a crucial task that requires attention.
Table 2.
The GCQ protocols with their corresponding codes.
| Codes | GCQ Protocols |
|---|---|
| P1 | compliance of minimum public health standards |
| P2 | limited movement of persons |
| P3 | 24-hr curfew of minors and senior citizens |
| P4 | work in government at full operational capacity |
| P5 | limited operational capacity of diplomatic missions and international organizations |
| P6a | full operational capacity of category I industries |
| P6b | minimum of 50% operational capacity of category II industries |
| P6c | maximum of 50% operational capacity of category III industries |
| P7 | limited operations of malls and shopping centers |
| P8 | allowed operation of essential public and private construction projects |
| P9 | non-operation of category IV industries |
| P10 | non-operation of hotels or similar establishments |
| P11 | suspension of physical classes |
| P12 | prohibition of mass gatherings |
| P13 | reduced capacity of public transportation |
3. Preliminaries
3.1. Intuitionistic fuzzy set (IFS) theory
[35] proposed the fuzzy set theory (FST) in handling vagueness and uncertainty in computing information. An extension of the FST is the intuitionistic fuzzy set (IFS) theory, which was introduced by Ref. [34]. IFS is characterized by a membership function, a non-membership function, and a hesitancy degree which express support, opposition, and neutrality in eliciting information [38]. This is an advantage over the FST as it can better handle the decision-maker's vagueness in the elicitation process, particularly when eliciting judgment [39]. Detailed three main advantages of the IFS theory. First, it offers the ability to model unknown information via the degree of hesitation. In the practical application (e.g., COVID-19 pandemic) where decision-makers are unsure about their preferences, IFS theory is more suitable in extracting opinion than the FST. Second, it is characterized by three grades of information that can better capture uncertainty comprehensively. Finally, the traditional FST only handles the degree of “agreement” but fails to represent the degree of “disagreement” which is often depicted in eliciting opinion. The following provides some fundamental concepts of the IFS relevant in this work.
Definition 1
[65]: Suppose is a finite, non-empty set, and . is a standard fuzzy set if a membership function such that . The set of 2-tuple is a fuzzy set where is a membership function of in .
Definition 2
[65]: A triangular fuzzy number can be defined as a triplet and the membership function is as follows:
(1)
Definition 3
[34]: Suppose is a finite, non-empty set. Then an IFS in is defined as
(2) where and such that . and represent the membership function and the non-membership function, respectively, of to . expresses the degree of lack of knowledge of every to , and . , , and follow Equation (3)
(3)
Definition 4
[66]: For a fixed universe , the IFS can be interpreted as a mapping , and it can be defined by a 2-tuple where for , denotes the degree of membership of and denotes the degree of non-membership of to ; and and satisfy the condition . The set is a standard fuzzy subset when . The crispification operation as a map is introduced. Here, for IFS.
Definition 5
[67]: Let be an IFS. By Definition 4, let be a crispification operator defined by . The procedure is described in two steps:
- (i)
transform into a (standard) fuzzy set;
- (ii)
evaluate the standard fuzzy set by using a defuzzification method.
For (i), the operator is defined as
(4) with . Note that is a standard fuzzy subset with a membership function
(5) In particular, is a solution of the minimization problem
(6) where denotes the Euclidean distance. With , the fuzzy set is characterized by a membership function
(7) For (ii), any defuzzification process can be adopted. The center of gravity (COG) method is a candidate.
3.2. The DEMATEL method
Developed between 1972 and 1976 by Battelle Memorial Institute of Geneva for a Science and Human Affairs Program, the DEMATEL method is a graph theoretic tool for analyzing a structural model or system characterized by elements (as vertices) and causal relationships among elements (as edges). It divides all elements into two categories: cause and effect. This categorization leads to superior understanding and better realization of the system's elements, which may offer solutions in convoluted problems [32,33]. Using concepts of graph theory and linear algebra, the following describes the computational process of the DEMATEL:
-
1.
Determine the system elements. This process can be obtained via different approaches, which may include a literature review on the domain topic, focus group discussion on the practical problem, expert decisions. Denote for these elements.
-
2.
Generate the direct-relation matrix. An expert group of members perform pairwise comparisons of the causal relationships between elements. This generates a direct-relation matrix for the member, . represents the casual influence of the element on element . An evaluation scale of 0, 1, 2, 3, and 4 is used for this causal influence, representing ‘no influence’, ‘low influence’, ‘medium influence’, ‘high influence’, and ‘very high influence’, respectively. The aggregate direct-relation matrix , , considering that is assigned to the importance of the member is described in Equation (8).
| (8) |
-
3.
Normalize the aggregate direction-relation matrix. The normalized direct-relation matrix is calculated using Equation (9) and Equation (10).
| (9) |
| (10) |
-
4.
Calculate the total relation matrix. Once is obtained, a continuous decrease in the system's indirect effects along with the powers of (i.e., ) guarantees convergent solutions to the matrix inversion. The total relation matrix is computed using Equation (11).
| (11) |
-
5.
Categorize the elements into the net cause and net effect. Compute for and using Equation (12) and Equation (13), respectively.
| (12) |
| (13) |
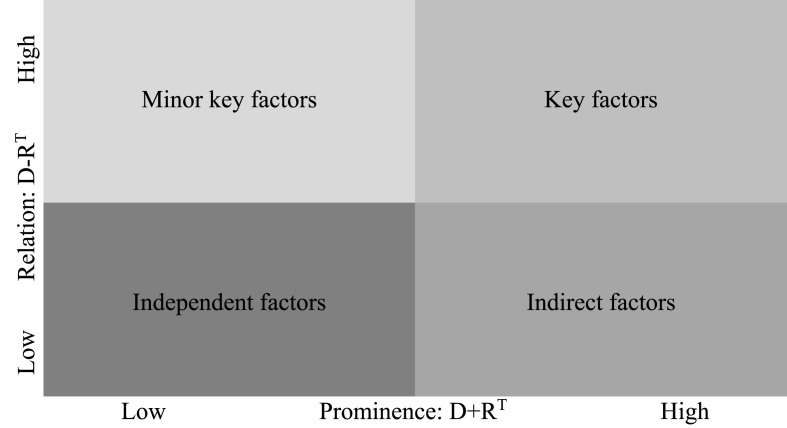
The vector (i.e., also known as the “prominence’ vector) represents the relative importance of each element. Those elements in the (i.e., also known as the “relation” vector) having belong to the net cause group, while those elements with belong to the net effect group.
-
6.
Construct the prominence-relation map. This map shows the mapping of the elements, as shown in Fig. 1 .
Fig. 1.
The prominence-relation map.
4. Proposed procedure: An IF-DEMATEL application to model the lockdown relaxation protocols of the Philippine government in response to the COVID-19 pandemic
The IF-DEMATEL approach in this work consists of the following steps:
Step 1: Identify the lockdown relaxation protocols.
The lockdown relaxation protocols in transitioning from ECQ to GCQ were extracted Executive Order No. 112 [31] of the Philippine government. They are considered the elements of the system in the DEMATEL approach. The summary of these protocols, along with their corresponding codes, is shown in Table 2. Note that there are 15 relaxation protocols identified in Table 2.
Step 2. Set up the direct-relation matrix.
The matrix was completed by a group of two academics and one infectious disease and public health expert with rich knowledge on the dynamics of systems, public health protocols, and local culture and conditions in the Philippines. In a focus group discussion, the group elicited values in IFS on consensus. Open discussions and careful deliberations were made to ensure that those judgments in the initial-direct relation matrix are not whimsical. The group was asked to provide the and values of on the causal influence of on . The values of are computed using Equation (3). Table 3 presents the initial direct-relation matrix in IFS. Each element is represented as a 2-tuple (as in Definition 4), i.e., .
Step 3. Obtain the corresponding membership function of the equivalent standard fuzzy subset
Table 3.
The initial direct-relation matrix in IFS.
| P1 | P2 | P3 | P4 | P5 | P6a | P6b | P6c | P7 | P8 | P9 | P10 | P11 | P12 | P13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 0 | <0.7,0> | <0.9,0> | <0.7,0.1> | <0.6,0.1> | <0.3,0.2> | <0.15,0.7> | <0.1,0.2> | <0.1,0.3> | <0.5,0.1> | <0.9,0> | <0.7,0.1> | <0.9,0> | <0.9,0> | <0.4,0.3> |
| P2 | <0.8,0> | 0 | <0.4,0> | <0.4,0.2> | <0.3,0.2> | <0.7,0.3> | <0.1,0.6> | <0.3,0.1> | <0.4,0.4> | <0.6,0.3> | <0.9,0> | <0.6,0> | <0.9,0> | <1,0> | <0.6,0.3> |
| P3 | <0.5,0> | <0.9,0> | 0 | <0,0.1> | <0,0.1> | <0,0.3> | <0.1,0.3> | <0.3,0.1> | <0,0.1> | <0,0.2> | <0,0> | <0,0> | <0.3,0> | <0,0> | <0.4,0> |
| P4 | <0.2,0.6> | <0.5,0.4> | <0.1,0.3> | 0 | <0.3,0> | <0.3,0 | <0.2,0> | <0.1,0> | <0.1,0.1> | <0.3,0> | <0,0> | <0.2,0.1> | <0.4,0> | <0,0.6> | <0,0.5> |
| P5 | <0.1,0.1> | <0.7,0.2> | <0,0.1> | <0.05,0.05> | 0 | <0,0> | <0,0> | <0,0> | <0,0.05> | <0,0> | <0,0> | <0,0> | <0.1,0> | <0.1,0.3> | <0.4,0.2> |
| P6a | <0.3,0.3> | <0.1,0.7> | <0.3,0.2> | <0.2,0> | <0,0> | 0 | <0.2,0> | <0.2,0> | <0.5,0.1> | <0.1,0> | <0,0.1> | <0,0.3> | <0,0> | <0,0.9> | <0,0.7> |
| P6b | <0.1,0.2> | <0.05,0.6> | <0.1,0.1> | <0.1,0> | <0,0> | <0.6,0> | 0 | <0.1,0> | <0.2,0.1> | <0.5,0.1> | <0,0> | <0,0.1> | <0,0> | <0,0.8> | <0.3,0.6> |
| P6c | <0.1,0.1> | <0.3,0.4> | <0,0> | <0.1,0> | <0,0> | <0,0> | <0.1,0> | 0 | <0.6,0.05> | <0,0.05> | <0,0> | <0,0.5> | <0,0> | <0.3,0.5> | <0.5,0.2> |
| P7 | <0.3,0.6> | <0.5,0.5> | <0.7,0> | <0.2,0> | <0,0> | <0.3,0.5> | <0.2,0.3> | <0.1,0.3> | 0 | <0,0.1> | <0,0.2> | <0,0> | <0,0> | <0.4,0.6> | <0.3,0.5> |
| P8 | <0.1,0.4> | <0.3,0.3> | <0,0> | <0.4,0> | <0,0> | <0.1,0> | <0.1,0> | <0,0> | <0.1,0> | 0 | <0,0.2> | <0,0.2> | <0,0> | <0.05,0.3> | <0.1,0.2> |
| P9 | <1,0> | <0.9,0> | <0.2,0> | <0.2,0.2> | <0,0> | <0,0.7> | <0,0.2> | <0,0.1> | <0.8,0> | <0,0.4> | 0 | <0.7,0> | <0,0> | <1,0> | <0.7,0> |
| P10 | <0.8,0.2> | <0.9,0.1> | <0.2,0> | <0.4,0.2> | <0,0.1> | <0.1,0.5> | <0.1,0.4> | <0,0.3> | <0,0> | <0,0.2> | <0.9,0> | 0 | <0,0> | <0.8,0.1> | <0.6,0.05> |
| P11 | <1,0> | <1,0> | <0.5,0> | <0.3,0> | <0.05,0.1> | <0,0> | <0,0> | <0,0> | <0,0> | <0,0> | <0,0> | <0,0> | 0 | <1,0> | <1,0> |
| P12 | <1,0> | <1,0> | <0.4,0> | <0,0.7> | <0,0.1> | <0,0.7> | <0,0.7> | <0.3,0.2> | <0.7,0.1> | <0,0.3> | <0.9,0> | <0.9,0> | <1,0> | 0 | <0.6,0> |
| P13 | <0.7,0.3> | <0.6,0.1> | <0.2,0> | <0,0.4> | <0.05,0.05> | <0,0.7> | <0.2,0.5> | <0.5,0.4> | <0.6,0.2> | <0.1,0.3> | <0,0> | <0,0> | <0.6,0> | <0.7,0.2> | 0 |
From Table 3, the next step is to deffuzify the IFS values. We adopted the two-step defuzzification process of [67]. The first step is to convert the IFS into corresponding standard fuzzy subsets using Equation (7). For instance,
Table 4 shows the initial-direct relation matrix in standard fuzzy subsets.
Step 4. Defuzzify the standard fuzzy subset values
Table 4.
The initial direct-relation matrix in standard fuzzy subsets.
| P1 | P2 | P3 | P4 | P5 | P6a | P6b | P6c | P7 | P8 | P9 | P10 | P11 | P12 | P13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 0 | 0.850 | 0.950 | 0.800 | 0.750 | 0.550 | 0.225 | 0.450 | 0.400 | 0.700 | 0.950 | 0.800 | 0.950 | 0.950 | 0.550 |
| P2 | 0.900 | 0 | 0.700 | 0.600 | 0.550 | 0.700 | 0.250 | 0.600 | 0.500 | 0.650 | 0.950 | 0.800 | 0.950 | 1.000 | 0.650 |
| P3 | 0.750 | 0.950 | 0 | 0.450 | 0.450 | 0.350 | 0.400 | 0.600 | 0.450 | 0.400 | 0.500 | 0.500 | 0.650 | 0.500 | 0.700 |
| P4 | 0.300 | 0.550 | 0.400 | 0 | 0.650 | 0.650 | 0.600 | 0.550 | 0.500 | 0.650 | 0.500 | 0.550 | 0.700 | 0.200 | 0.250 |
| P5 | 0.500 | 0.750 | 0.450 | 0.500 | 0 | 0.500 | 0.500 | 0.500 | 0.475 | 0.500 | 0.500 | 0.500 | 0.550 | 0.400 | 0.600 |
| P6a | 0.500 | 0.200 | 0.550 | 0.600 | 0.500 | 0 | 0.600 | 0.600 | 0.700 | 0.550 | 0.450 | 0.350 | 0.500 | 0.050 | 0.150 |
| P6b | 0.450 | 0.225 | 0.500 | 0.550 | 0.500 | 0.800 | 0 | 0.550 | 0.550 | 0.700 | 0.500 | 0.450 | 0.500 | 0.100 | 0.350 |
| P6c | 0.500 | 0.450 | 0.500 | 0.550 | 0.500 | 0.500 | 0.550 | 0 | 0.775 | 0.475 | 0.500 | 0.250 | 0.500 | 0.400 | 0.650 |
| P7 | 0.350 | 0.500 | 0.550 | 0.600 | 0.500 | 0.400 | 0.450 | 0.400 | 0 | 0.450 | 0.400 | 0.500 | 0.500 | 0.400 | 0.400 |
| P8 | 0.350 | 0.500 | 0.500 | 0.700 | 0.500 | 0.550 | 0.550 | 0.500 | 0.550 | 0 | 0.400 | 0.400 | 0.500 | 0.375 | 0.450 |
| P9 | 1.000 | 0.950 | 0.600 | 0.500 | 0.500 | 0.150 | 0.400 | 0.450 | 0.900 | 0.300 | 0 | 0.850 | 0.500 | 1.000 | 0.850 |
| P10 | 0.800 | 0.900 | 0.600 | 0.600 | 0.450 | 0.300 | 0.350 | 0.350 | 0.500 | 0.400 | 0.950 | 0 | 0.500 | 0.850 | 0.775 |
| P11 | 1.000 | 1.000 | 0.750 | 0.650 | 0.475 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0.500 | 0 | 1.000 | 1.000 |
| P12 | 1.000 | 1.000 | 0.700 | 0.150 | 0.450 | 0.150 | 0.150 | 0.550 | 0.800 | 0.350 | 0.950 | 0.950 | 1.000 | 0 | 0.800 |
| P13 | 0.700 | 0.750 | 0.600 | 0.300 | 0.500 | 0.150 | 0.350 | 0.550 | 0.700 | 0.400 | 0.500 | 0.500 | 0.800 | 0.750 | 0 |
The final step of the defuzzification process of [67] is to adopt a defuzzification function that would map . To carry out this step, the membership function values in Table 4 are assigned to a triangular fuzzy number = . See Definition 2. Using Equation (1) with , , , the following equation can be set up. Analogous to Equation (1), we have
| (14) |
where is the membership function value shown in Table 4, are parameters of a triangular fuzzy number and the is the corresponding crisp or defuzzified value. As an example,
The initial-direct relation matrix in crisp values is presented in Table 5 .
Step 5. Obtain the normalized direct-relation matrix.
Table 5.
The initial direct-relation matrix in crisp values.
| P1 | P2 | P3 | P4 | P5 | P6a | P6b | P6c | P7 | P8 | P9 | P10 | P11 | P12 | P13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 0 | 3.4 | 3.8 | 3.2 | 3.0 | 2.2 | 0.9 | 1.8 | 1.6 | 2.8 | 3.8 | 3.2 | 3.8 | 3.8 | 2.2 |
| P2 | 3.6 | 0 | 2.8 | 2.4 | 2.2 | 2.8 | 1.0 | 2.4 | 2.0 | 2.6 | 3.8 | 3.2 | 3.8 | 4.0 | 2.6 |
| P3 | 3.0 | 3.8 | 0 | 1.8 | 1.8 | 1.4 | 1.6 | 2.4 | 1.8 | 1.6 | 2.0 | 2.0 | 2.6 | 2.0 | 2.8 |
| P4 | 1.2 | 2.2 | 1.6 | 0 | 2.6 | 2.6 | 2.4 | 2.2 | 2.0 | 2.6 | 2.0 | 2.2 | 2.8 | 0.8 | 1.0 |
| P5 | 2.0 | 3.0 | 1.8 | 2.0 | 0 | 2.0 | 2.0 | 2.0 | 1.9 | 2.0 | 2.0 | 2.0 | 2.2 | 1.6 | 2.4 |
| P6a | 2.0 | 0.8 | 2.2 | 2.4 | 2.0 | 0 | 2.4 | 2.4 | 2.8 | 2.2 | 1.8 | 1.4 | 2.0 | 0.2 | 0.6 |
| P6b | 1.8 | 0.9 | 2.0 | 2.2 | 2.0 | 3.2 | 0 | 2.2 | 2.2 | 2.8 | 2.0 | 1.8 | 2.0 | 0.4 | 1.4 |
| P6c | 2.0 | 1.8 | 2.0 | 2.2 | 2.0 | 2.0 | 2.2 | 0 | 3.1 | 1.9 | 2.0 | 1.0 | 2.0 | 1.6 | 2.6 |
| P7 | 1.4 | 2.0 | 2.2 | 2.4 | 2.0 | 1.6 | 1.8 | 1.6 | 0 | 1.8 | 1.6 | 2.0 | 2.0 | 1.6 | 1.6 |
| P8 | 1.4 | 2.0 | 2.0 | 2.8 | 2.0 | 2.2 | 2.2 | 2.0 | 2.2 | 0 | 1.6 | 1.6 | 2.0 | 1.5 | 1.8 |
| P9 | 4.0 | 3.8 | 2.4 | 2.0 | 2.0 | 0.6 | 1.6 | 1.8 | 3.6 | 1.2 | 0 | 3.4 | 2.0 | 4.0 | 3.4 |
| P10 | 3.2 | 3.6 | 2.4 | 2.4 | 1.8 | 1.2 | 1.4 | 1.4 | 2.0 | 1.6 | 3.8 | 0 | 2.0 | 3.4 | 3.1 |
| P11 | 4.0 | 4.0 | 3.0 | 2.6 | 1.9 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 0 | 4.0 | 4.0 |
| P12 | 4.0 | 4.0 | 2.8 | 0.6 | 1.8 | 0.6 | 0.6 | 2.2 | 3.2 | 1.4 | 3.8 | 3.8 | 4.0 | 0 | 3.2 |
| P13 | 2.8 | 3.0 | 2.4 | 1.2 | 2.0 | 0.6 | 1.4 | 2.2 | 2.8 | 1.6 | 2.0 | 2.0 | 3.2 | 3.0 | 0 |
Using Equation (9) and Equation (10), the normalized direct-relation matrix is computed with . It is shown in Table 6 .
Step 6. Generate the total relation matrix
Table 6.
Normalized direct-relation matrix.
| P1 | P2 | P3 | P4 | P5 | P6a | P6b | P6c | P7 | P8 | P9 | P10 | P11 | P12 | P13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 0 | 0.08608 | 0.09620 | 0.08101 | 0.07595 | 0.05570 | 0.02278 | 0.04557 | 0.04051 | 0.07089 | 0.09620 | 0.08101 | 0.09620 | 0.09620 | 0.05570 |
| P2 | 0.09114 | 0 | 0.07089 | 0.06076 | 0.05570 | 0.07089 | 0.02532 | 0.06076 | 0.05063 | 0.06582 | 0.09620 | 0.08101 | 0.09620 | 0.10127 | 0.06582 |
| P3 | 0.07595 | 0.09620 | 0 | 0.04557 | 0.04557 | 0.03544 | 0.04051 | 0.06076 | 0.04557 | 0.04051 | 0.05063 | 0.05063 | 0.06582 | 0.05063 | 0.07089 |
| P4 | 0.03038 | 0.05570 | 0.04051 | 0 | 0.06582 | 0.06582 | 0.06076 | 0.05570 | 0.05063 | 0.06582 | 0.05063 | 0.05570 | 0.07089 | 0.02025 | 0.02532 |
| P5 | 0.05063 | 0.07595 | 0.04557 | 0.05063 | 0 | 0.05063 | 0.05063 | 0.05063 | 0.04810 | 0.05063 | 0.05063 | 0.05063 | 0.05570 | 0.04051 | 0.06076 |
| P6a | 0.05063 | 0.02025 | 0.05570 | 0.06076 | 0.05063 | 0 | 0.06076 | 0.06076 | 0.07089 | 0.05570 | 0.04557 | 0.03544 | 0.05063 | 0.00506 | 0.01519 |
| P6b | 0.04557 | 0.02278 | 0.05063 | 0.05570 | 0.05063 | 0.08101 | 0 | 0.05570 | 0.05570 | 0.07089 | 0.05063 | 0.04557 | 0.05063 | 0.01013 | 0.03544 |
| P6c | 0.05063 | 0.04557 | 0.05063 | 0.05570 | 0.05063 | 0.05063 | 0.05570 | 0 | 0.07848 | 0.04810 | 0.05063 | 0.02532 | 0.05063 | 0.04051 | 0.06582 |
| P7 | 0.03544 | 0.05063 | 0.05570 | 0.06076 | 0.05063 | 0.04051 | 0.04557 | 0.04051 | 0 | 0.04557 | 0.04051 | 0.05063 | 0.05063 | 0.04051 | 0.04051 |
| P8 | 0.03544 | 0.05063 | 0.05063 | 0.07089 | 0.05063 | 0.05570 | 0.05570 | 0.05063 | 0.05570 | 0 | 0.04051 | 0.04051 | 0.05063 | 0.03797 | 0.04557 |
| P9 | 0.10127 | 0.09620 | 0.06076 | 0.05063 | 0.05063 | 0.01519 | 0.04051 | 0.04557 | 0.09114 | 0.03038 | 0 | 0.08608 | 0.05063 | 0.10127 | 0.08608 |
| P10 | 0.08101 | 0.09114 | 0.06076 | 0.06076 | 0.04557 | 0.03038 | 0.03544 | 0.03544 | 0.05063 | 0.04051 | 0.09620 | 0 | 0.05063 | 0.08608 | 0.07848 |
| P11 | 0.10127 | 0.10127 | 0.07595 | 0.06582 | 0.04810 | 0.05063 | 0.05063 | 0.05063 | 0.05063 | 0.05063 | 0.05063 | 0.05063 | 0 | 0.10127 | 0.10127 |
| P12 | 0.10127 | 0.10127 | 0.07089 | 0.01519 | 0.04557 | 0.01519 | 0.01519 | 0.05570 | 0.08101 | 0.03544 | 0.09620 | 0.09620 | 0.10127 | 0 | 0.08101 |
| P13 | 0.07089 | 0.07595 | 0.06076 | 0.03038 | 0.05063 | 0.01519 | 0.03544 | 0.05570 | 0.07089 | 0.04051 | 0.05063 | 0.05063 | 0.08101 | 0.07595 | 0 |
The total relation matrix is obtained using Equation (11) and is shown in Table 7 . The corresponding and vectors are presented in Table 8 . Likewise, the categorization of protocols according to net cause or net effect is shown in Table 8. These vectors were computed following Equation (12) and Equation (13).
Step 7. Construct the prominence-relation map
Table 7.
Total relation matrix.
| P1 | P2 | P3 | P4 | P5 | P6a | P6b | P6c | P7 | P8 | P9 | P10 | P11 | P12 | P13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 0.34211 | 0.44113 | 0.39759 | 0.34902 | 0.33677 | 0.27659 | 0.23325 | 0.30408 | 0.33857 | 0.32014 | 0.40713 | 0.37274 | 0.42513 | 0.40042 | 0.36184 |
| P2 | 0.42360 | 0.35816 | 0.37401 | 0.32945 | 0.31709 | 0.28780 | 0.23369 | 0.31533 | 0.34639 | 0.31378 | 0.40520 | 0.37046 | 0.42276 | 0.40298 | 0.36826 |
| P3 | 0.33828 | 0.37019 | 0.24351 | 0.25971 | 0.25329 | 0.21227 | 0.20361 | 0.26207 | 0.27841 | 0.24009 | 0.29878 | 0.28102 | 0.32714 | 0.29362 | 0.30792 |
| P4 | 0.26312 | 0.29756 | 0.25221 | 0.19336 | 0.24728 | 0.22213 | 0.20716 | 0.23427 | 0.25635 | 0.24077 | 0.26611 | 0.25534 | 0.29670 | 0.23158 | 0.23660 |
| P5 | 0.29411 | 0.32929 | 0.26794 | 0.24875 | 0.19409 | 0.21373 | 0.20231 | 0.23806 | 0.26382 | 0.23469 | 0.27855 | 0.26252 | 0.29677 | 0.26306 | 0.27931 |
| P6a | 0.25155 | 0.23656 | 0.24092 | 0.22919 | 0.21279 | 0.14226 | 0.19068 | 0.21768 | 0.25007 | 0.21142 | 0.23471 | 0.21269 | 0.25111 | 0.19111 | 0.20140 |
| P6b | 0.26069 | 0.25235 | 0.24834 | 0.23501 | 0.22289 | 0.22585 | 0.14169 | 0.22347 | 0.24877 | 0.23467 | 0.25157 | 0.23300 | 0.26409 | 0.20757 | 0.23110 |
| P6c | 0.28332 | 0.29186 | 0.26402 | 0.24612 | 0.23561 | 0.20776 | 0.20240 | 0.18323 | 0.28389 | 0.22579 | 0.26811 | 0.23124 | 0.28285 | 0.25236 | 0.27457 |
| P7 | 0.25088 | 0.27666 | 0.25006 | 0.23428 | 0.21943 | 0.18524 | 0.18027 | 0.20662 | 0.19200 | 0.20811 | 0.24175 | 0.23699 | 0.26297 | 0.23511 | 0.23483 |
| P8 | 0.26016 | 0.28597 | 0.25481 | 0.25252 | 0.22814 | 0.20719 | 0.19720 | 0.22443 | 0.25468 | 0.17324 | 0.25063 | 0.23626 | 0.27311 | 0.24043 | 0.24757 |
| P9 | 0.40736 | 0.42097 | 0.34297 | 0.29926 | 0.29331 | 0.22136 | 0.22910 | 0.28205 | 0.35908 | 0.26381 | 0.29588 | 0.35527 | 0.36023 | 0.38246 | 0.36361 |
| P10 | 0.36980 | 0.39478 | 0.32379 | 0.29187 | 0.27282 | 0.22153 | 0.21303 | 0.25805 | 0.30619 | 0.25745 | 0.36431 | 0.25777 | 0.33935 | 0.35004 | 0.33833 |
| P11 | 0.41743 | 0.43481 | 0.36622 | 0.32195 | 0.30009 | 0.26237 | 0.24660 | 0.29672 | 0.33299 | 0.29153 | 0.35267 | 0.33175 | 0.32333 | 0.38934 | 0.38519 |
| P12 | 0.41729 | 0.43525 | 0.35923 | 0.27447 | 0.29350 | 0.22468 | 0.21065 | 0.29569 | 0.35597 | 0.27226 | 0.39045 | 0.36971 | 0.41038 | 0.30080 | 0.36887 |
| P13 | 0.33277 | 0.35220 | 0.29930 | 0.24360 | 0.25564 | 0.19113 | 0.19696 | 0.25530 | 0.29931 | 0.23738 | 0.29696 | 0.28005 | 0.33859 | 0.31533 | 0.24164 |
Table 8.
The prominence and relation vectors.
| Codes | GCQ Protocols | Rank | Rank | Category | ||||
|---|---|---|---|---|---|---|---|---|
| P1 | compliance of minimum public health standards | 5.30651 | 4.91247 | 10.21898 | 2 | 0.39403 | 2 | net cause |
| P2 | limited movement of persons | 5.26895 | 5.17773 | 10.44669 | 1 | 0.09122 | 7 | net cause |
| P3 | 24-hr curfew of minors and senior citizens | 4.16989 | 4.48491 | 8.65480 | 7 | −0.31502 | 14 | net effect |
| P4 | work in government at full operational capacity | 3.70056 | 4.00857 | 7.70912 | 11 | −0.30801 | 13 | net effect |
| P5 | limited operational capacity of diplomatic missions and international organizations | 3.86700 | 3.88275 | 7.74975 | 10 | −0.01574 | 8 | net effect |
| P6a | full operational capacity of category I industries | 3.27413 | 3.30188 | 6.57601 | 14 | −0.02775 | 9 | net effect |
| P6b | minimum of 50% operational capacity of category II industries | 3.48107 | 3.08861 | 6.56968 | 15 | 0.39246 | 3 | net cause |
| P6c | maximum of 50% operational capacity of category III industries | 3.73314 | 3.79703 | 7.53017 | 12 | −0.06389 | 10 | net effect |
| P7 | limited operations of malls and shopping centers | 3.41520 | 4.36649 | 7.78169 | 9 | −0.95129 | 15 | net effect |
| P8 | allowed operation of essential public and private construction projects | 3.58635 | 3.72513 | 7.31147 | 13 | −0.13878 | 11 | net effect |
| P9 | non-operation of category IV industries | 4.87670 | 4.60281 | 9.47951 | 4 | 0.27389 | 4 | net cause |
| P10 | non-operation of hotels or similar establishments | 4.55911 | 4.28682 | 8.84593 | 6 | 0.27229 | 5 | net cause |
| P11 | suspension of physical classes | 5.05299 | 4.87451 | 9.92750 | 3 | 0.17848 | 6 | net cause |
| P12 | prohibition of mass gatherings | 4.97918 | 4.45620 | 9.43539 | 5 | 0.52298 | 1 | net cause |
| P13 | reduced capacity of public transportation | 4.13615 | 4.44102 | 8.57716 | 8 | −0.30487 | 12 | net effect |
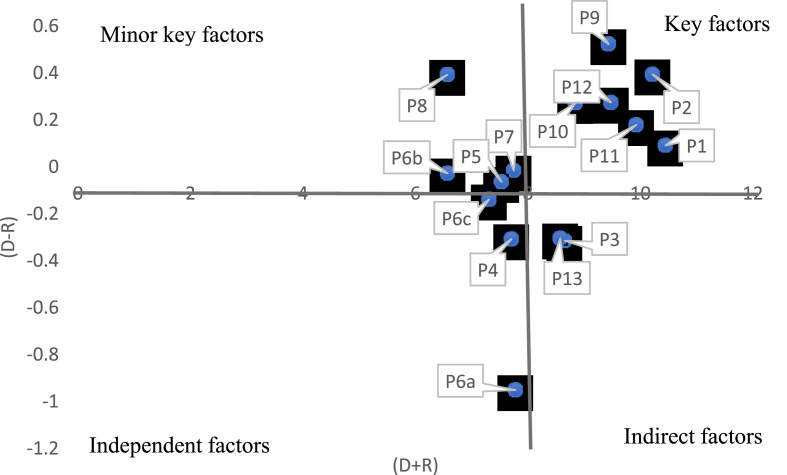
The prominence-relation map, similar to Fig. 1, is constructed based on coordinates. This map is illustrated in Fig. 2 .
Fig. 2.
The prominence-relation map of lockdown relaxation protocols for Philippine COVID-19 response.
5. Results and discussion
The results show that compliance of minimum public health standards (P1), limited movement of persons (P2), minimum of 50% operational capacity of category II industries (P6b), non-operation of category IV industries (P9), non-operation of hotels or similar establishments (P10), suspension of physical classes (P11), and prohibition of mass gatherings (P12) are categorized into a net cause group. They impact the entire set of guidelines, and their attainment or non-attainment affects the balance of public health and socio-economic performance. Thus, they should be given more attention by the IATF. These protocols in the net cause group have a more influential impact () than influenced impact (). On the other hand, the net effect group contains the 24-hr curfew of minors and senior citizens (P3), work in government at full operational capacity (P4), limited operational capacity of diplomatic missions and international organizations (P5), full operational capacity of category I industries (P6a), maximum of 50% operational capacity of category III industries (P6c), limited operations of malls and shopping centers (P7), allowed operation of essential public and private construction projects (P8), and reduced capacity of public transportation (P13). They tend to be easily influenced by other protocols as their values are negative, which implies that the influential impact () of these protocols are lower than their influenced impact ().
The scores describe the relative significance or prominence of the protocols. In this work, the limited movement of persons (P2) yields the highest score; thus, it must be considered as a relatively important for the lockdown exit strategy. This finding also implies that this protocol possesses the highest impact, both received and given. This protocol is central to the set of guidelines by the IAFT. Also, this result is supported by the insights of [7,68] on how China curb the disease spread. Most countries (e.g., South Korea) who have suppressed the first wave of cases found themselves in a situation where a spike of a new wave of cases emerges just days after they ease down the lockdown measures, particularly allowing people to move around on purpose beyond non-essential things such as leisure, going out to parks, restaurants, malls, bars, and opening of schools. The ranking of protocols according to the scores is described as follows: . The scores yield the following ranking: .
Overall, identifying the critical protocols must simultaneously consider both and vectors. To achieve this, we refer to Fig. 1 and categorize all protocols into four distinct categories: minor key factors (low prominence, high relation), key factors (high prominence, high relation, indirect factors (high prominence, low relation), and independent factors (low prominence, low relation. Based on Fig. 2, the minor key factors comprise limited operational capacity of diplomatic missions and international organizations (P5), minimum of 50% operational capacity of category II industries (P6b), limited operations of malls and shopping centers (P7), allowed operation of essential public and private construction projects (P8). The key factors include compliance of minimum public health standards (P1), limited movement of persons (P2), non-operation of category IV industries (P9), non-operation of hotels or similar establishments (P10), suspension of physical classes (P11), and prohibition of mass gatherings (P12). The indirect factors category is composed of 24-hr curfew of minors and senior citizens (P3) and reduced capacity of public transportation (P13). The independent factors consist of work in government at full operational capacity (P4), full operational capacity of category I industries (P6a), and maximum of 50% operational capacity of category III industries (P6c). We focus our attention on the key factors category and identify the most crucial protocols. In this category, the minimum public health standards protocol (P1) yields the most important one. Thus, the IATF must concentrate its resources and efforts to ensure that minimum public health standards are strictly observed during the GCQ. This finding is consistent with the observations of [3] on how China responded to the disease spread. Although those drastic lockdown measures are relaxed and people start to move around, relaxing public health standards (e.g., proper hygiene, wearing of masks, disinfecting public spaces, physical distancing) would stimulate a new surge of cases. The rank order of the key factors is as follows: .
6. Policy insights for the lockdown exit strategy
The Philippine government has become more efficient and transparent with the release of guidelines and protocols to curb the spread of COVID-19. The key factors in Fig. 2 represent the most crucial lockdown exit protocols, which would provide a balance between public health and economic restart. The government should allocate its resources and plan and implement strict control and monitoring mechanisms on these priority protocols as they impact other protocols for the successful attainment of GCQ's purpose. This work provides better insights to further streamline the lockdown exit strategy of the Philippine government.
The protocol on ensuring minimum public health standards (P1) yields the most critical protocol for implementing the GCQ. This protocol enforces social distancing, wearing of face masks, body temperature checks, provision of sanitation stations, immune system boosting, and disinfecting public spaces at all times. While the GCQ allows movements of people to restart the economy and the society, observing public health standards shields the general health of the community from such movements. It is straightforward to note that compliance to minimum health standards impacts most protocols and serves as a precursor in observing other protocols in the list. Thus, the IATF must establish control measures in those socio-economic activities allowed in the GCQ guidelines so that public health standards appropriate in responding to the COVID-19 pandemic are maintained. For instance, the DOH of the Philippine government has issued “Guidelines on the Risk-Based Public Health Standards for COVID-19 Mitigation” on 27 April [69] that guides the roles of various stakeholders in maintaining risk-based public health standards. Control measures must be heightened to ensure its strict implementation in the GCQ.
Closely linked to maintaining public health standards is the protocol that there must be limited movement of persons (P2). While P2 supports economic restart through cross-border movements, it also ensures that those movements are just related to essential activities to support the economy. P2 implies that public transportation is reduced, mall operations are limited, suspension of classes, and flexible work arrangements, among others. Managing food capacity and demand at a scale supports P2 by limiting the number of customers through booking and reservations to avoid long queues in supermarkets, retail stores, and food establishments. Establishments may venture into online platforms and delivery service as part of their augmented product. This protocol must be upheld and strictly monitored in GCQ by imposing measures that limit the movement of people. Note that people in lockdowns became impatient in responding to government measures that disrupt their daily lives. This stimulates people to go back to their pre-COVID-19 normal, which would drastically increase movements. Experiences in Hong Kong, Singapore, and South Korea reveal that after easing lockdown measures, the number of new cases surge in just a matter of days as the movement of people became uncontrollable.
The education sector absorbs a massive impact for these draconian measures. Suspension of physical classes (P11) has driven all academic institutions to shift towards online classes, distance learning, flexible learning, and other alternative modes of learning to cushion the disruption amidst the pandemic. With these platforms, some fundamental challenges become apparent for all stakeholders, including students, teachers, and administrators. Poor yet expensive internet connection in the Philippines, limited access to the internet in most rural communities, inadequate skills and experience of both teachers and students in such platforms, and the unavailability of those platforms on a school-wide basis are some of those challenges. Despite these challenges, suspension of physical classes must be maintained as a crucial protocol under GCQ conditions. As an augmentation, the government must support the establishment of necessary infrastructure to enable schools to venture for digital platforms in education as the new normal. The government, along with the academic institutions, must respond to these changes by promptly planning support services for all stakeholders, since personal interaction may not be possible without the availability of the COVID-19 vaccine. Issues in developing countries like the Philippines, such as Internet connectivity, availability of technologies (gadgets), and the technical capacity to go digital must be promptly addressed.
Gatherings such as conferences, festivals, concerts, sports events, and weddings, among others, would discourage social distancing, as huge crowds become uncontrollable. Thus, the prohibition of mass gatherings (P12) must be central to the lockdown exit strategy. To balance economic underpinnings, the government must implement a critical assessment on a per event basis. Permits to event organizers must be secured for proper response whether to suspend, cancel, or consider reducing the number of attendees. Recreation and leisure activities contribute to the overall mental and physical well-being of people under lockdowns [23,24]. However, the non-operation of category IV industries (P9) protocol discourages engagement of leisure activities, which induce sharing or touching of equipment that can spread the disease. To balance with economic goals, Category IV industries may work closely with the government to establish a comprehensive and robust risk assessment and management of activities during GCQ. With the travel restrictions imposed on global destinations beginning in January 2020, the tourism industry has been on a sore end, worsen with the uncertainty and stigma of tourists out of fear for safety. In support of the category IV industries, it can gradually operate some of the establishments such as museums, sightseeing, and some sports activities that do not involve sharing or touching of equipment and where social distancing can be easily implemented and monitored. Furthermore, the government must allocate subsidies toward destination promotion and may invest in virtual tourism during post-lockdown.
The non-operation of category IV industries (P9) is supported by the non-operation of hotels or similar establishments (P10) with the limited operation of the accommodation establishments due to travel restrictions and stigma. Hotels may position their core products in response to the GCQ conditions. For instance, hotels may shift towards highlighting their in-house restaurants through offering deliveries, take-out services, and catering bulk order delivery for small household gatherings. In the case of reopening hotels, content marketing can be adopted through the creation of initiatives that would build strong and profitable relationships with the market. For instance, hygiene standards in hotels and the safety measures of the hotel in response to the pandemic may be highlighted in the promotion campaign, as this is one of the major concerns of the traveling public. Moreover, the government must still strictly impose social distancing measures in hotels and monitor hygiene practices of these establishments as part of the new normal.
7. Conclusion and future works
As economic shutdowns were implemented and the mental and physical well-being of people under lockdowns in response to the COVID-19 pandemic becomes increasingly evident, governments around the world are already planning, if not implementing, relaxation efforts of those drastic measures implemented early this year. However, the emerging literature, as well as practical experiences of those countries who are already lifting those harsh measures, cautions the resurgence of a new wave of cases that may burden (again) the healthcare systems. Thus, a careful lockdown exit strategy is crucial for governments in order to balance the two conflicting objectives: (1) keep mortality at minimum, and (2) initiate an economic restart. Nevertheless, without controlled experiments and documented experience on such a massive scale, governments resort to trial-and-error approach on designing effectively a post-lockdown strategy. In this work, we demonstrate how network modeling helps in providing insights into the relaxation approach. To address those two objectives, as mentioned above, an intuitionistic fuzzy DEMATEL (IF-DEMATEL) approach is highlighted in this work. A case study in modeling the Philippine relaxation protocols is provided here to demonstrate the applicability of the IF-DEMATEL.
Transitioning from an ECQ (lockdown) status to a more relaxed GCQ status has been initiated by the Philippine government, and 15 GCQ protocols were introduced. This work aims to identify key protocols for the government to invest its resources and provide strict control measures to ensure its implementation. Results suggest that compliance of minimum public health standards, limited movement of persons, minimum of 50% operational capacity of category II industries, non-operation of category IV industries, non-operation of hotels or similar establishments, suspension of physical classes, and prohibition of mass gatherings protocols are part of the cause group which implies that they impact the rest of the guideline protocols, and they are influential in attaining the GCQ objectives. Findings also reveal that six important protocols must be given more attention, and more control measures are necessary. They include, according to priority degree of importance, compliance of minimum public health standards, limited movement of persons, suspension of physical classes, the prohibition of mass gatherings, non-operation of category IV industries, and non-operation of hotels or similar establishments. The Philippine government, through its pandemic task force, must ensure that these six protocols must receive more resources (e.g., funds, workforce) and strict measures must be put in place for their implementation, as well as for developing mitigation efforts to cushion their impacts on the economy and the society. These insights are crucial in resource allocation decisions and policy formulation for the government. Finally, this work reveals that the use of network modeling under uncertainty, specifically IF-DEMATEL, has considerable potential for public health studies in bringing in systemic insights for decision- and policymaking. This work, along with its use of the IF-DEMATEL, is the first of its kind in addressing the emerging COVID-19 pandemic.
Nevertheless, this work is not free from limitations. First, the limited number of experts sets a stage for future research which could handle a significant number of stakeholders, and decision- and policymakers. Future research may explore the same methodological approach to justify the validity of the findings of this work. Second, the proposed method is flexible if new protocols are introduced or removed from the current set of guideline protocols. Future work could address the sensitivity and the implications in the number and kind of protocols when changes are introduced to better respond to the evolving pandemic. Third, the application of the proposed approach is limited to a Philippine case with different culture, geography, political settings, and environment. The findings may not be extended directly to other countries or regions. Thus, future work could also adopt the proposed approach to other countries in developing their lockdown exit protocols. Fourth, the use of other fuzzy DEMATEL extensions (e.g., hesitant fuzzy sets, type-2 fuzzy sets, neutrosophic sets) could be explored and compared to the findings of this work. Fifth, other network modeling techniques such as system dynamics modeling, interpretative structural modeling technique, among others, could also be adopted in future works. Sixth, some predictive modeling techniques for assessing the impact of lockdown exit protocols, such as the adaptive neuro-fuzzy inference system [70,71], can be explored in future work. Finally, the use of multi-attribute decision-making techniques in prioritization problems along the domains of public health or the emerging COVID-19 pandemic is an interesting platform for future research.
CRediT authorship contribution statement
Lanndon Ocampo: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Software, Supervision, Validation, Writing - original draft, Writing - review & editing. Kafferine Yamagishi: Formal analysis, Visualization, Writing - original draft.
Biographies
Lanndon Ocampo is an Associate Professor in the Department of Industrial Engineering at Cebu Technological University (Philippines). He received his Ph.D. in Industrial Engineering from De La Salle University (Philippines) and his MEng and BSc (cum laude) degrees in Industrial Engineering as well as MSc in Mathematics from the University of San Carlos (Philippines). He has authored over 90 international peer-reviewed journal papers and has presented papers at over 30 research conferences. His research interests include optimization, multi-attribute decision-making, decision science, systemic risk analysis, and sustainable manufacturing. He is currently the Editor-in-Chief of the International Journal of Applied Industrial Engineering (IGI-Global). He is a 2017 Outstanding Young Scientist awardee by the National Academy of Science and Technology, Philippines (NAST PH), and a 2018 Outstanding Cebuano awardee in the field of Science and Technology. He is named as one of 2018 THE ASIAN SCIENTIST 100 – an annual listing of the region's top researchers, academics, and innovators. Most recently, he is conferred as the 2019 Achievement Awardee of the National Research Council of the Philippines (NRCP) under the Division of Engineering and Industrial Research.
Kafferine Yamagishi is an Assistant Professor, and currently the Chair of the Department of Tourism Management, College of Management and Entrepreneurship at Cebu Technological University, Philippines. She attained her Master of Management major in Tourism Management at the University of San Carlos (Philippines), where she is currently taking up her Doctor of Philosophy degree in Business Administration. She received her Certification in Professional Education and attained her Master of Arts in Education major in Administration and Supervision at Cebu Technological University. She graduated Bachelor of Science in Tourism (cum laude) at the University of San Jose-Recoletos, Philippines. Before joining academia, she worked both in the hospitality and tourism industry. She currently has four published articles in Scopus-indexed journals. Also, she has presented papers to research conferences throughout her academic career. Her research interests include tourism management, destination planning, tourism marketing, and events management.
References
- 1.Lu H., Stratton C.W., Tang Y.W. Outbreak of pneumonia of unknown etiology in wuhan China: the mystery and the miracle. J Med Virol. 2020;92(4):401–402. doi: 10.1002/jmv.25678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wu Y.C., Chen C.S., Chan Y.J. The outbreak of COVID-19: an overview. J Chin Med Assoc. 2020;83(3):217–220. doi: 10.1097/JCMA.0000000000000270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sohrabi C., Alsafi Z., O'Neill N., Khan M., Kerwan A., Al-Jabir A. World Health Organization declares global emergency: a review of the 2019 novel coronavirus (COVID-19) Int J Surg. 2020;76:71–76. doi: 10.1016/j.ijsu.2020.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wu Z., McGoogan J.M. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: summary of a report of 72 314 cases from the Chinese Center for Disease Control and Prevention. Jama. 2020;323(13):1239–1242. doi: 10.1001/jama.2020.2648. [DOI] [PubMed] [Google Scholar]
- 5.Gates B. Responding to covid-19—a once-in-a-century pandemic? N Engl J Med. 2020;382(18):1677–1679. doi: 10.1056/NEJMp2003762. [DOI] [PubMed] [Google Scholar]
- 6.Zhang S.X., Wang Y., Rauch A., Wei F. Unprecedented disruption of lives and work: health, distress and life satisfaction of working adults in China one month into the COVID-19 outbreak. Psychiatr Res. 2020;288:112958. doi: 10.1016/j.psychres.2020.112958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fisher D., Wilder-Smith A. The global community needs to swiftly ramp up the response to contain COVID-19. Lancet. 2020;395(10230):1109–1110. doi: 10.1016/S0140-6736(20)30679-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lin Q., Zhao S., Gao D., Lou Y., Yang S., Musa S.S. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int J Infect Dis. 2020;93:211–216. doi: 10.1016/j.ijid.2020.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Roda W.C., Varughese M.B., Han D., Li M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020;5:271–281. doi: 10.1016/j.idm.2020.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hopman J., Allegranzi B., Mehtar S. Managing COVID-19 in low-and middle-income countries. J Am Med Assoc. 2020;323(16):1549–1550. doi: 10.1001/jama.2020.4169. [DOI] [PubMed] [Google Scholar]
- 11.Salzberger B., Glück T., Ehrenstein B. Successful containment of COVID-19: the WHO-Report on the COVID-19 outbreak in China. Infection. 2020;48:151–153. doi: 10.1007/s15010-020-01409-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wilder-Smith A., Freedman D.O. Isolation, quarantine, social distancing and community containment: pivotal role for old-style public health measures in the novel coronavirus (2019-nCoV) outbreak. J Trav Med. 2020;27(2):1–6. doi: 10.1093/jtm/taaa020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Paital B., Das K., Parida S.K. Inter nation social lockdown versus medical care against COVID-19, a mild environmental insight with special reference to India. Sci Total Environ. 2020;728:1–18. doi: 10.1016/j.scitotenv.2020.138914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lau H., Khosrawipour V., Kocbach P., Mikolajczyk A., Schubert J., Bania J., Khosrawipour T. The positive impact of lockdown in Wuhan on containing the COVID-19 outbreak in China. J Trav Med. 2020 doi: 10.1093/jtm/taaa037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Xu S., Li Y. Beware of the second wave of COVID-19. Lancet. 2020;395(10233):1321–1322. doi: 10.1016/S0140-6736(20)30845-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hamzelou J. Vol. 7. 2020. (World in lockdown, new scientist). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kupferschmidt K. The lockdowns worked—but what comes next? Science. 2020;368(6488):218–219. doi: 10.1126/science.368.6488.218. [DOI] [PubMed] [Google Scholar]
- 18.Cohen J., Kupferschmidt K. Countries test tactics in ‘war’against COVID-19. Science. 2020;367(6484):1287–1288. doi: 10.1126/science.367.6484.1287. [DOI] [PubMed] [Google Scholar]
- 19.Pulla P. March 26). Covid-19: India imposes lockdown for 21 days and cases rise. BMJ. 2020;368:m1251. doi: 10.1136/bmj.m1251. [DOI] [PubMed] [Google Scholar]
- 20.Hunter D.J. Covid-19 and the stiff upper lip—the pandemic response in the United Kingdom. N Engl J Med. 2020;382(16):1–3. doi: 10.1056/NEJMp2005755. [DOI] [PubMed] [Google Scholar]
- 21.Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Loopstra R. Vulnerability to food insecurity since the COVID-19 lockdown. Preliminary Rep. 2020 https://foodfoundation.org.uk/wp-content/uploads/2020/04/Report_COVID19FoodInsecurity-final.pdf King’s College London. Retrieved from. [Google Scholar]
- 23.Torales J., O'Higgins M., Castaldelli-Maia J.M., Ventriglio A. The outbreak of COVID-19 coronavirus and its impact on global mental health. Int J Soc Psychiatr. 2020 doi: 10.1177/0020764020915212. [DOI] [PubMed] [Google Scholar]
- 24.Wang C., Pan R., Wan X., Tan Y., Xu L., Ho C.S., Ho R.C. Immediate psychological responses and associated factors during the initial stage of the 2019 coronavirus disease (COVID-19) epidemic among the general population in China. Int J Environ Res Publ Health. 2020;17(5):1–25. doi: 10.3390/ijerph17051729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.COVID-19 Dashboard . Johns Hopkins University; 2020. COVID-19 dashboard by the center for systems science and engineering (CSSE) at.https://coronavirus.jhu.edu/map.html Retrieved 11 May 2020, from. [Google Scholar]
- 26.Gilbert M., Dewatripont M., Muraille E., Platteau J.P., Goldman M. Preparing for a responsible lockdown exit strategy. Nat Med. 2020;26:643–644. doi: 10.1038/s41591-020-0871-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Leung K., Wu J.T., Liu D., Leung G.M. First-wave COVID-19 transmissibility and severity in China outside Hubei after control measures, and second-wave scenario planning: a modelling impact assessment. Lancet. 2020;395:1382–1393. doi: 10.1016/S0140-6736(20)30746-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kupferschmidt K., Cohen J. Can China's COVID-19 strategy work elsewhere? Science. 2020;367(6482):1061–1062. doi: 10.1126/science.367.6482.1061. [DOI] [PubMed] [Google Scholar]
- 29.Fadlallah R., El-Jardali F. K2P COVID-19 series: exiting the COVID-19 lockdown: a road map for action. Knowledge to policy (K2P) center, beirut, Lebanon, April. 2020;20:3. [Google Scholar]
- 30.Colbourn T. COVID-19: extending or relaxing distancing control measures. Lancet Pub Health. 2020;5(5):e236–e237. doi: 10.1016/S2468-2667(20)30072-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Official Gazette . 2020 April 30. Executive order No. 112, s. 2020.https://www.officialgazette.gov.ph/2020/04/30/executive-order-no-112-s-2020/ Retrieved May 9, 2020 from. [Google Scholar]
- 32.Gabus A., Fontela E. Battelle Geneva Research Centre; Switzerland, Geneva: 1972. World problems, an invitation to further thought within the framework of DEMATEL. [Google Scholar]
- 33.Gabus A., Fontela E. Battelle Geneva Research Centre; Switzerland Geneva: 1973. Perceptions of the world problematic: communication procedure, communicating with those bearing collective responsibility’, DEMATEL Report No. 1. [Google Scholar]
- 34.Atanassov K.T. Intuitionistic fuzzy sets. Fuzzy Set Syst. 1986;20(1):87–96. [Google Scholar]
- 35.Zadeh L.A. Fuzzy sets. Inf Control. 1965;8(3):338–353. [Google Scholar]
- 36.Nikjoo A.V., Saeedpoor M. An intuitionistic fuzzy DEMATEL methodology for prioritising the components of SWOT matrix in the Iranian insurance industry. Int J Oper Res. 2014;20(4):439–452. [Google Scholar]
- 37.Abdullah L., Zulkifli N., Liao H., Herrera-Viedma E., Al-Barakati A. An interval-valued intuitionistic fuzzy DEMATEL method combined with Choquet integral for sustainable solid waste management. Eng Appl Artif Intell. 2019;82:207–215. [Google Scholar]
- 38.Gan J., Luo L. Using DEMATEL and intuitionistic fuzzy sets to identify critical factors influencing the recycling rate of end-of-life vehicles in China. Sustainability. 2017;9(10):1873. [Google Scholar]
- 39.Govindan K., Khodaverdi R., Vafadarnikjoo A. Intuitionistic fuzzy based DEMATEL method for developing green practices and performances in a green supply chain. Expert Syst Appl. 2015;42(20):7207–7220. [Google Scholar]
- 40.Wu Y., Ke Y., Wang J., Li L., Lin X. Risk assessment in photovoltaic poverty alleviation projects in China under intuitionistic fuzzy environment. J Clean Prod. 2019;219:587–600. [Google Scholar]
- 41.World Health Organization Coronavirus disease (COVID-19) in the Philippines. 2020. https://www.who.int/philippines/emergencies/covid-19-in-the-philippines Retrieved May 9, from.
- 42.BBC News . 2020 January 31. Coronavirus declared global health emergency by WHO.https://www.bbc.com/news/world-51318246 Retrieved May 9, 2020 from. [Google Scholar]
- 43.Department of Health . 2020. March 21). DOH reports 1 COVID death and 3 new cases.https://www.doh.gov.ph/doh-press-release/DOH-REPORTS-1-COVID-DEATH-AND-3-NEW-CASES Retrieved May 9, 2020 from: [Google Scholar]
- 44.CNN Philippines . 2020 February 2. Duterte widens travel ban on mainland China, Hong Kong, Macau.https://cnnphilippines.com/news/2020/2/2/Duterte-travel-ban-mainland-China-Hong-Kong-Macau.html Retrieved May 9, 2020 from. [Google Scholar]
- 45.CNN Philippines . 2020. March 13 How a team of Filipino scientists developed a COVID-19 test kit.https://www.cnnphilippines.com/life/culture/2020/3/13/covid-test-kit-scientists.html Retrieved May 9, 2020 from. [Google Scholar]
- 46.Department of Health . 2020 March 7. DOH confirms local transmission of COVID-19 in PH; Reports 6TH case.https://www.doh.gov.ph/doh-press-release/doh-confirms-local-transmission-of-covid-19-in-ph Retrieved May 9, 2020 from. [Google Scholar]
- 47.Official Gazette . 2020. March 9). Proclamation no. 922 s. 2020.https://www.officialgazette.gov.ph/2020/03/08/proclamation-no-922-s-2020/ Retrieved May 9, 2020 from. [Google Scholar]
- 48.Gumbrecht Jamie, Howard Jacqueline. CNN Philippines; 2020 March 12. WHO declares novel coronavirus outbreak a pandemic.https://cnnphilippines.com/world/2020/3/12/WHO-COVID-19-pandemic.html?fbclid=IwAR3TGlDwCI-GRuRfTV7WcWCa0xymJi208ZaegQey_bTeKvthls7oMla8otU Retrieved from. [Google Scholar]
- 49.Esguerra Darryl John. Philippines upgrades coronavirus alert to Code Red Sublevel 2. Inquirer.net. 2020 March 12 https://newsinfo.inquirer.net/1240935/breaking-philippines-upgrades-covid-19-alert-to-code-red-sublevel-2 Retrieved from. [Google Scholar]
- 50.Official Gazette . 2020 March 16. Memorandum from the executive secretary on community quarantine over the entire luzon and further guidelines for the management of the coronavirus disease 2019 (COVID-19) situation.https://www.officialgazette.gov.ph/2020/03/16/memorandum-from-the-executive-secretary-on-community-quarantine-over-the-entire-luzon-and-further-guidelines-for-the-management-of-the-coronavirus-disease-2019-covid-19-situation/ Retrieved May 9, 2020 from. [Google Scholar]
- 51.Official Gazette . 2020. March 16) proclamation No. 929 s. 2020.https://www.officialgazette.gov.ph/2020/03/16/proclamation-no-929-s-2020/ Retrieved May 9, 2020 from. [Google Scholar]
- 52.Department of Foreign Affairs . 2020 March 19. Public advisory: on the temporary suspension of visa issuance and visa-free privilege.https://dfa.gov.ph/dfa-news/statements-and-advisoriesupdate/26385-public-advisory-on-the-temporary-suspension-of-visa-issuance-and-visa-free-privilege Retrieved May 9, 2020 from. [Google Scholar]
- 53.Atienza Luci, Charissa . Manila Bulletin; 2020 March 23. Villafuerte: Congress needs to authorize Duterte to realign P275 B to combat pandemic.https://news.mb.com.ph/2020/03/23/villafuerte-congress-needs-to-authorize-duterte-to-realign-p275-b-to-combat-pandemic/ Retrieved from. [Google Scholar]
- 54.Jalea Glee. CNN Philippines; 2020 April 12. Gov't requires public disclosure of information on COVID-19 cases.https://cnnphilippines.com/news/2020/4/12/COVID-19-mandatory-public-disclosure-IATF.html Retrieved May 9, 2020 from. [Google Scholar]
- 55.CNN Philippines ’General community quarantine’ to be implemented in low- or moderate-risk areas. 2020 April 24. https://www.cnnphilippines.com/news/2020/4/24/General-community-quarantine-GCQ-areas-guidelines.html Retrieved May 9, 2020 from.
- 56.Nakpil Danielle. 2020 May 7. Gov't issues new guidelines at workplace for enhanced, general community quarantine. CNN Philippines.https://www.cnn.ph/news/2020/5/7/new-guidelines-workplace-ECQ-GCQ.html Retrieved from. [Google Scholar]
- 57.Vitangcol Al. 2020 April 11. Social amelioration program should be for everyone, but in reality it's not. Manila Bulletin.https://www.manilatimes.net/2020/04/11/opinion/columnists/social-amelioration-program-should-be-for-everyone-but-in-reality-its-not/712356/ Retrieved from. [Google Scholar]
- 58.Asian Development Bank . 2020 April 3. Philippine GDP growth to slide in 2020 due to COVID-19, strong rebound seen in 2021 — ADB.https://www.adb.org/news/philippine-gdp-growth-slide-2020-due-covid-19-strong-rebound-seen-2021-adb Retrieved May 9, 2020 from. [Google Scholar]
- 59.The World Bank . 2020 April 23. Philippines: world Bank approves US$100M to support COVID-19 emergency response.https://www.worldbank.org/en/news/press-release/2020/04/23/philippines-world-bank-approves-usd100m-to-support-covid-19-emergency-response Retrieved May 9, 2020 from. [Google Scholar]
- 60.Gonzales Cathrine. US to provide additional P298-M to PH for COVID-19 response. Inquirer.net. 2020 May 7 https://globalnation.inquirer.net/187523/fwd-us-providing-additional-p298m-to-philippines-for-covid-19-response Retrieved May 9, 2020 from. [Google Scholar]
- 61.CNN Philippines . 2020 Apr 12. Over 1 million workers nationwide lose jobs due to COVID-19 quarantine – DOLE.https://www.cnnphilippines.com/news/2020/4/12/DOLE-COVID-quarantine-1-million-displaced-workers.html Retrieved May 9, 2020 from. [Google Scholar]
- 62.Abrigo M.R., Uy J., Haw N.J., Ulep V.G.T., Francisco-Abrigo K. 2020. Projected disease transmission, health system requirements, and macroeconomic impacts of the coronavirus disease 2019 (COVID-19) in the Philippines (No. 2020-15) [Discussion Paper Series] [Google Scholar]
- 63.Ferreras Vince. CNN Philippines; 2020. April 17). Philippines now has 17 COVID-19 testing centers.https://www.cnnphilippines.com/news/2020/4/17/Philippines-now-has-17-testing-facilities-COVID-19-.html Retrieved from. [Google Scholar]
- 64.Department of Health . 2020. Updates on novel coronavirus disease (COVID-19)http://www.doh.gov.ph/2019-nCoV Retrieved May 9, 2020 from. [Google Scholar]
- 65.Ocampo L.A. Applying fuzzy AHP–TOPSIS technique in identifying the content strategy of sustainable manufacturing for food production. Environ Dev Sustain. 2019;21(5):2225–2251. [Google Scholar]
- 66.Angelov P. Crispification: defuzzification of intuitionistic fuzzy sets. BUSEFAL. 1995;64:51–55. [Google Scholar]
- 67.Anzilli L., Facchinetti G. Novel developments in uncertainty representation and processing. Springer; Cham: 2016. A new proposal of defuzzification of intuitionistic fuzzy quantities; pp. 185–195. [Google Scholar]
- 68.Wang C.J., Ng C.Y., Brook R.H. Response to COVID-19 in Taiwan: big data analytics, new technology, and proactive testing. Jama. 2020;323(14):1341–1342. doi: 10.1001/jama.2020.3151. [DOI] [PubMed] [Google Scholar]
- 69.Department of Health . 2020 April 27. Guidelines on the risk-based public health standards for COVID-19 mitigation.https://www.doh.gov.ph/node/21466 Retrieved May 13, 2020 from. [Google Scholar]
- 70.Petković B., Petković D., Kuzman B. Biomass Conversion and Biorefinery; 2020. Adaptive neuro fuzzy predictive models of agricultural biomass standard entropy and chemical exergy based on principal component analysis. [DOI] [Google Scholar]
- 71.Petković B., Petković D., Kuzman B., Milovančević M., Wakil K., Ho L.S. Neuro-fuzzy estimation of reference crop evapotranspiration by neuro fuzzy logic based on weather conditions. Comput Electron Agric. 2020;173:105358. [Google Scholar]