Highlights
-
•
To investigate a multi-serotype disease alongside antibody-dependent-enhancement; ADE, this article is introducing two kinds of vaccination; primary and secondary vaccines.
-
•
Our framework dovetails mathematical epidemiological model; incorporating SVIRS epidemic model, with evolutionary decision dynamics.
-
•
The primary vaccine targets susceptible people, while the secondary one aims once infected but now recovered individuals letting them avoid ‘second infection’ which means critical situation.
-
•
We quantitatively argue, how effectively the primary and secondary vaccines to minimize such socially critical situation.
Keywords: Vaccination game, N-serovar, ADE factor, Secondary vaccination
Abstract
Records of epidemics acknowledge immunological multi-serotype illnesses as an important aspect of the occurrence and control of contagious diseases. These patterns occur due to antibody-dependent-enhancement (ADE) among serotype diseases, which leads to infection of secondary infectious classes. One example of this is dengue hemorrhagic fever and dengue shock syndrome, which comprises the following four serotypes: DEN-1, DEN-2, DEN-3, and DEN-4. The evolutionary vaccination game approach is able to shed light on this long-standing issue in a bid to evaluate the success of various control programs. Although immunization is regarded as one of the most accepted approaches for minimizing the risk of infection, cost and efficiency are important factors that must also be considered. To analyze the -serovar aspect alongside ADE consequence in voluntary vaccination, this study establishes a new mathematical epidemiological model that is dovetailed with evolutionary game theory, an approach through which we explored two vaccine programs: primary and secondary. Our findings illuminate that the ‘cost-efficiency’ effect for vaccination decision exhibits an impact on controlling -serovar infectious diseases and should be designed in such a manner as to avoid adverse effects. Furthermore, our numerical result justifies the fact that adopting ADE significantly boosted emerging disease incidence, it also suggest that the joint vaccine policy works even better when the complex cyclical epidemic outbreak takes place among multi serotypes interactions. Research also exposes that the primary vaccine is a better controlling tool than the secondary; however, introducing a highly-efficiency secondary vaccine against secondary infection plays a key role to control the disease prevalence.
1. Introduction
In the present study, we design on the strengths of existing research and considered the epidemic model and vaccination game and multi-serotype approaches, which in turn is based on evolutionary game theory and gives rise to the human decision-making process. The theoretical approach pioneered by Kermack and McKendrick (1927) and others (Anderson and May, 1979, Jones and Sleeman, 1983, Goffman and Newill, 1964) played an important role in epidemiology in terms of the control and prevention of contagious diseases. Recently, this area of study has been accentuated due to the advent of a new strain of pandemic diseases such as influenza, smallpox, SARS (severe acute respiratory syndrome), pneumonia, and dengue fever, among others. Precisely, if we are concerned more to control infectious diseases by immunization, pathogens become more robust to survive and developed new antigenic strains (Ferguson et al., 1999, Vaughn et al., 2000). One such ‘enhanced disease’ phenomenon is attributed to antibody-dependent enhancement (ADE), which gives rise to a bolstered viral growth rate in a secondary infection following recovery from a primary infection caused by a variety of serovars (Recker et al., 2009, Billings et al., 2007, Billings et al., 2008) (see Fig. 1 ). Antibody-dependent enhancement represents an evolutionary advancement in multi-strain viruses that makes vaccination difficult. More specifically, this enhancement presents obstacles to optimal immunization that includes all strains of a disease. The reason for this is that newly developed vaccines against only one serotype can increase the possibility of infection by a second serotype. This is particularly risky for people suffering from dengue fever and its related conditions, because infections in this case are particularly severe.
Fig. 1.
Schematic phase diagram of Antibody-Depending Enhancement (ADE) effect for four-serovars dengue disease: DEN 1, DEN 2, DEN 3 and DEN 4. The mechanism of ADE may be perceived when an individual who has previously infected (primary infected) with one serotype of the dengue infected again (secondary infected) months or years later with a different serotype. While an individual is infected with one serotype dengue disease (say DEN 1), the immune response developed antibodies against this particular serotype (DEN 1: green) dengue disease that prevents the virus from binding to macrophage cells. However, if another serotype of dengue virus: DEN 2/DEN 3/DEN 4 (orange/red/blue) infect the same individual, the immune system is misled because the four serotypes have similar surface antigens. The antibodies cannot recognize the surface protein of the newly attacked virus which proceeds to infect individual because it has not been inactivated by antibodies. This phenomenon is defined as Antibody-dependent enhancement (ADE) that creates the contagious disease much more terrible. The primary infected form mostly minor disease whereas the secondary infected is more likely to be associated with dengue hemorrhagic fever. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Among multi-serotypes epidemics, dengue fever, one of the most devastating mosquito-borne viral infections to humans, is a significant problem worldwide (Bhatt et al., 2013, Shepard et al., 2016). The disease is caused by infection with any of four virus serotypes: DEN-1, DEN-2, DEN-3, and DEN-4 (Ferrar et al., 2014). The virus affects more than 3.9 billion people in 128 countries in the tropical and subtropical regions of the world, and 52% of people are at risk in Asian and Latin American countries (Bhatia et al., 2013, Messina et al., 2014, Brady et al., 2012). While researchers and drug authorities are currently developing and testing several promising vaccines, one vaccine is currently commercially available for dengue fever (WHO, 2018, Thisyakorn, 2014). The world’s first dengue vaccine was CYD-TDV (brand name Dengvaxia). Created by Sanofi Pasteur (WHO, 2018, FDA, 2019) it was licensed in 2015 and commercially introduced in selected countries (Reuters, 2017, Susie, 2016, Zachri and Planasari, 2016). Recently, Takeda’s vaccine verified protection against virologically confirmed dengue (VCD), and vaccine trials ended (Biswal et al., 2019). The current form of all available dengue vaccines (Sanofi Pasteur and Takeda) target individuals previously infected (Biswal et al., 2019, WHO, 2018), and the vaccine aimed at avoiding second infection. However, for those who have not previously been infected, the vaccine is not as effective. Regarding current vaccination and serotype processes linked to dengue fever, the sequence of infection to which an individual is exposed should be considered. Strategies for self-protection from risk will greatly influence whether first and/or second infections occur. In the case of dengue fever, the most efficient protective measure is vaccination. In this context, the so-called vaccination game can be an effective approach for modeling such a complex and dynamic system, where epidemiological dynamics in society can be considered alongside the social evolution of individual decision-making for committing to vaccination in view of governmental policy.
The concept of the vaccination game relies on evolutionary game theory (EGT) alongside an epidemiological compartment model. EGT is a powerful framework for modeling the evolution of cooperation in biological and social sciences. It is the prevailing theoretical framework for understanding social and complex epidemic dynamics (Smith, 1974, Tanimoto, 2015, Tanimoto, 2019). Epidemiology with vaccination as a major issue in the study of evolutionary biology has been widely researched in the past few decades (Kabir et al., 2019a, Kabir and Tanimoto, 2019, Wang et al., 2016, Bauch and Earn, 2004, Kuga et al., 2019, Fukuda et al., 2014, Fukuda and Tanimoto, 2016, Iwamura and Tanimoto, 2018, Kabir et al., 2019b). More recently, a number of precursors used theoretical models to better understand epidemic dynamics in both local (single epidemic season) and global (repeated seasons) time scales, in order to explore how to control contagious diseases. Among them, notable studies include Kabir and Tanimoto (2019) for indicating a meta-population migration model, Kuga and Tanimoto (2018) for the imperfectness of vaccines using both a multi-agent simulation and theoretical approach, Tanaka and Tanimoto (2020) for presenting a subsidy model, Kabir et al., 2020, Kabir and Tanimoto, 2019 for the vaccination game approach with heterogeneous network and buzz effect, and Alam et al.’s (Kabir et al., 2019c) vaccination game model for introducing the secondary effect of a vaccine in repeated seasons. Additionally, Kabir and Tanimoto (2019) established a mathematical model of SVIR at a local time scale by allowing for the effectiveness of imperfect vaccination, whereas, Bauch and Bhattacharyya (2012) and others (Chen and Fu, 2018, Bauch, 2005) succeeded in establishing local time evolutionary epidemic models based on the social learning approach. Additionally, Kabir and Tanimoto (2019) studied the theoretical epidemic model by combining both vaccination and a treatment game approach to explain the impact of secondary provisions as a fail-safe effect. Recently, Arefin et al. (2019) presented the two-strain with two vaccinations game model by tracking repeated seasons.
Based on the literature, within the vaccination game framework, human decision-making and behavior is multi-modally affected by self-interest, vaccination cost, neighbors’ attitudes, and vaccination risk. All of these factors may play an important role in decreasing the risk for both vaccinated and non-vaccinated (free rider) individuals. However, all of the research noted above involving the vaccination game approach presumed vaccination as pre-emptive and lasting only one season. More importantly, the research adopted vaccines that were primarily aimed at treating influenza-like diseases. In the present study, we created a novel realistic model for the vaccination game approach for dengue-like disease treatment by taking into account ADE, where two vaccinations are introduced within a time sequence. Here, primary vaccination should be applied prior to initial infection, with the secondary vaccine following the first infection. Furthermore, spreading of the disease and updating the treatment strategy should be restructured using the same time scale, and the immunity lasts until it wanes.
The main goal of this work is to provide a benchmark for allowing the study of an epidemiological model for dengue transmission once vaccination has been affected. In doing so, the study focuses on representing the effect of ADE and n-serovar aspects within the evolutionary game framework. The two types of vaccinations, primary and secondary, were based on the respective dynamics of vaccination rate among individuals, which is affected by individual perceptions of both infection risk and cost burden. The model further allowed for investigating the relationship between ADE, serotypes, and cost-efficiency and how these might influence a vaccine within an evolutionary framework context.
The paper is ordered as follows. First, we formulate our model in detail. This is followed by introducing an evolutionary mechanism for the strategy-updating rule, i.e., modified replicator dynamics. After describing the model, we present simulation results and discuss their implications. Finally, we conclude the paper with a brief discussion of major findings in the conclusion section.
2. Model setup
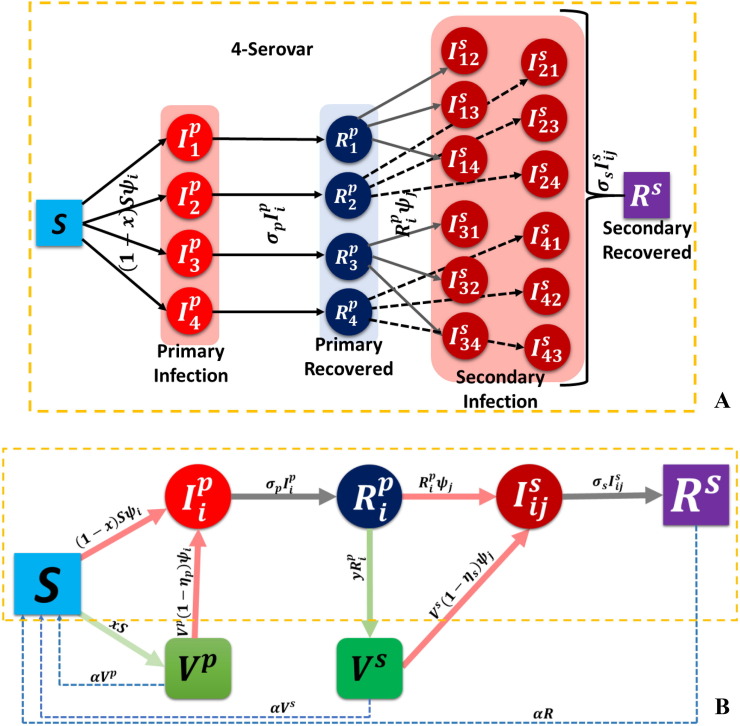
A modified SVIRS epidemic model in which primary and secondary vaccinations took place is proposed herein to study the influence of primary and secondary infection incidence (due to serotype). Based on the actual ADE mechanism of 4-serovars dengue disease presenting in Fig. 1, the proposed epidemic model assumed infection, vaccination, and recovered as primary and secondary states. The details of how an individual would ensue for four serotypes is shown in Fig. 2 (A). The model adopted a two-phase (epidemic and evolutionary) model to include an infinite and diverse population (Fig. 2(B)). It was presumed that an individual could choose whether to have the primary vaccine administered before primary infection and that the same choice was available for commitment to a secondary vaccination once primary recovery was complete but secondary infection had not yet occurred. Individual decisions arise from the evolution of expected payoff and whether a committing provision (primary or secondary vaccination) is perceived as beneficial. We assumed that a primary recovered state from initial infection with any one serotype provided natural life-long immunity against said serotype but led to the enhancement of other serotypes upon secondary infection. Under these circumstances, the total population was divided into seven states: susceptible, primary vaccinated , primary infected , primary recovered , secondary vaccinated , secondary infected , and secondary recovered . The set of dynamic equations presented in this work considered the mean field approximation method alongside a compartmental model. Here, S represents susceptible individuals (not yet infected), and denotes the fractions of primary infected and primary recovered individuals with serotypes, respectively, represents the fraction of secondary infected individuals with serotypes already recovered from serotype , and is the fraction of secondary recovered individuals defined as being in a final recovered state. Meanwhile, and are the fractions of primary and secondary vaccinated individuals from a susceptible and primary recovered state, specified by variables and , respectively, and defined as the incidental rate of vaccinators. The fraction of individuals in and decayed, respectively, since such an immunized state does not continue in perpetuity but returns to the susceptible state at the rate of . Furthermore, and represent infection rate ( serotype), primary recovery rate, and secondary recovery rate, respectively. The efficiency of vaccines is given as and , referring to the probability of immunity serving to avoid infection, despite receiving both primary and secondary vaccines. Regarding the schematic diagram in Fig. 2, the SVIRS model was designed as per the system of differential equations given below:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Fig. 2.
Schematic image of (A) the transfer chart for S-4 diseases and (B) the entire dynamic model. Relevant parameters are: (i) the probability that susceptible individuals will become infected, ; (ii) the probability that susceptible people will receive primary vaccination, ; (iii) the probability that a primary infected individual will recover, ; (iv) the probability that a primary recovered individual will again be infected, , due to the effect of ADE factor ; (iv) the probability that primary recovered people will be vaccinated, ; (v) the probability that secondary infected people will recover, ; (vi) the probability that vaccinated individuals will be infected due to the imperfectness of a vaccine in the case of primary and secondary vaccinations.
Referring to selected precursors (Recker et al., 2009, Billings et al., 2007, Billings et al., 2008) as a guideline, we introduce force of infection for serotypes, , defined as the ADE factor, where is given by:
| (8) |
As a general assumption, we analyzed the symmetric case defined by the setting of various contact rates and ADE factors of all serotypes, equal to: , and . A total primary and secondary infection groups existed; the possible number of infections an individual could contract was up to times. Here, we analyzed two cases for defined as 2-serovar (hereafter, S-2) and defined as 4-serovar (S-4) disease.
3. Dual decision-making processes
To explore the evolutionary trail arising from human decision-making processes related to vaccination uptake as a rational choice, we considered a modified replicator dynamic by referring to existing studies (Kabir and Tanimoto, 2019, Bauch and Bhattacharyya, 2012). In this context, individuals attempted to change their strategies using a probability proportional to the expected gain or loss of payoff. For the current context, in the evolutionary process, people incorporated two types of decision-making processes: primary and secondary vaccination. Here, an individual can become vaccinated against being susceptible to primary infection and receive secondary vaccination following primary recovery. The payoff in both instances depends on the difference between (a) the penalty of risking infection and (b) the drawbacks of being vaccinated. The drawback of the vaccine for primary and secondary vaccination can be quantified as and , and the penalty of being infected due to primary and secondary infection can be evaluated as and . This was derived from the premise that the relative expected cost of primary (secondary) vaccination was , where is the vaccination cost and is infection cost (here, . Consequently, the expression and quantifies the expected payoff gain for changing strategies and its sign controls whether the vaccination or non-vaccination option is preferred. The global dynamics of and can be depicted as follows:
| (9) |
| (10) |
where is the rate observed at time at which susceptible individuals become primarily vaccinated, and is the rate at which primary (temporal) recovered individuals become secondarily vaccinated. Furthermore, is the proportionality constant that alter the fraction of population into the transferring rate; throughout this study, we assumed.
The numerical simulation will be carried out for the stated equations (1–10) of the epidemic model by using the explicit finite difference method. Initially, we presumed the initial conditions for all simulations as, and . We also assumed that the initial incidental rate of vaccinators to be and .
4. Results and discussion
In this study, we investigated the diffusion of multi-serotype diseases based on the SVIRS epidemic model and the evolutionary game approach, where two vaccines were disseminated within a population. The stability of the model was reviewed by plotting timeline graphs based on the endemic equilibrium shown in Fig. 3 for the S-2 (solid line) and S-4 (dotted line) diseases. Panels A, B, C, D, E, F, and G, respectively, represent the portion of individuals for the following: susceptible, primary infection , secondary infection , primary vaccination (), secondary vaccination (), primary recovered and secondary recovered (). Moreover, we considered two combination of efficiency-cost cases as follows: for a less efficient and costly vaccine (blue) and for a highly efficient and cheaper vaccine (red), where and . For comparison, we included a case without vaccination (black). The numerical simulations were conducted using the following model parameter values: and , where and Throughout the numerical results provided below, we fixed and .
Fig. 3.
Dynamic behavior of a system comprising S-2 and S-4 diseases with and (blue), (red), and without vaccination (gray). Time series of (A) susceptible, (B) primary infection, (C) secondary infection, (D) primary vaccination, (E) secondary vaccination, (F) primary recovered, and (G) secondary recovered. Here, , , , , and . (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Comparing S-2 with S-4 diseases, we observed an increase in serotype diversity causing a subsequent rise in disease incidence (panels B and C). A similar tendency was also observed in the case of both vaccinated and secondary recovered individuals (panels D, E, and G). Enhancement of serotype diversity increased the portion of both vaccinated and secondary recovered groups. However, only one exception was observed for the primary recovered (panel F) group, suggesting that an increase in serotype diminished the portion of recovered individuals. This can be fully justified by the fact that a higher number of disease serotypes intensified the transmission from primary recovered to secondary infection. Additionally, Fig. 3 highlights that the impact of both vaccinations (primary and secondary) suppressed the spread of the disease when compared with non-vaccination or the default settings (no vaccination and evolutionary mechanism taking place). Furthermore, it appears that a higher efficiency at a cheaper cost delivered higher vaccination uptake, which in turn reduced infection for both primary and secondary incidences. The opposite tendency was observed in the case of less efficient and more expensive vaccines. According to results in general, even though more individuals will benefit from either primary or secondary vaccination, an epidemic cannot be eradicated by these two vaccination types as employed in the parameter settings noted here.
The discussion above nonetheless indicates that the model was successful, indicating an appropriate dynamic that is to some degree able to achieve a state of equilibrium. Thus, in the following discussion, we focus on the results observed at equilibrium for a variety of model parameters.
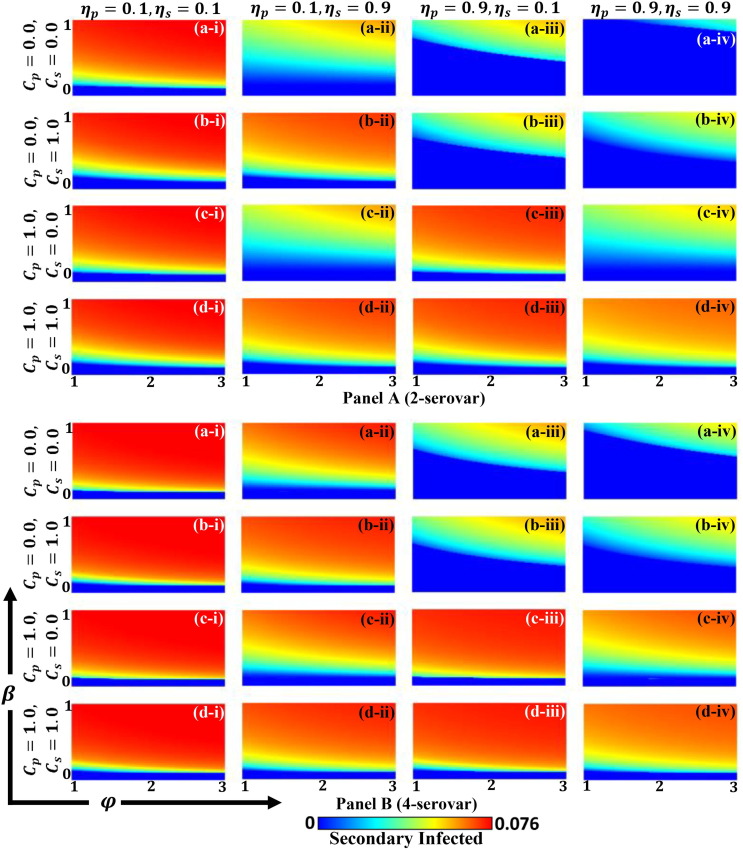
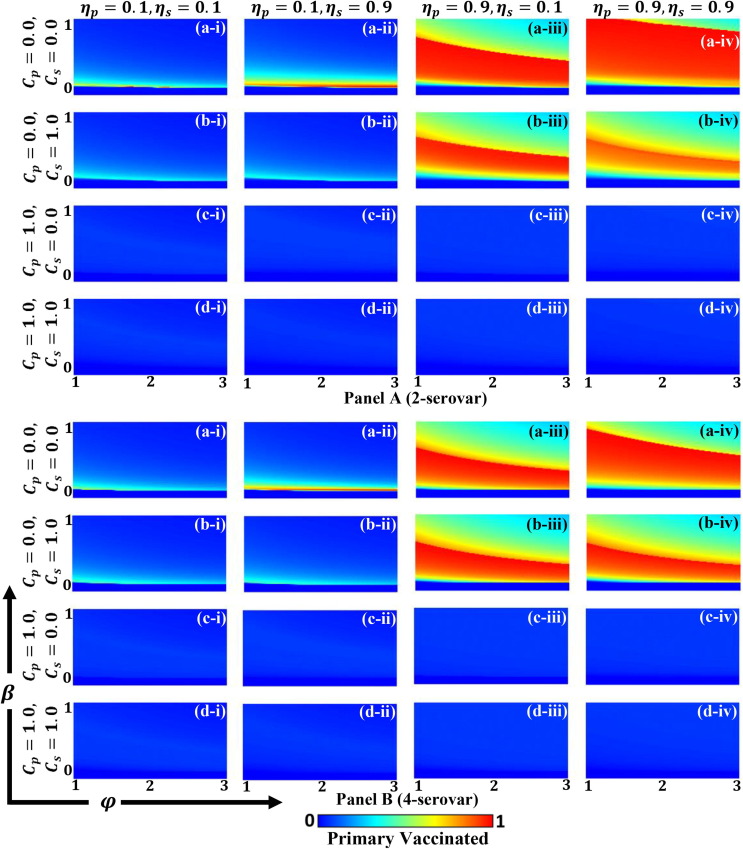
In order to derive an insightful understanding of how ADE factors and disease transmission function for two different serotypes (S-2 and S-4), we present a two-dimensional (2D) heat map of primary infected, secondary infected, primary vaccinated, and secondary vaccinated groups in Figs. 4 (a), (b) and 5 (a), (b), respectively. In each figure, panel A and panel B display the S-2 and S-4 disease for two vaccine efficiencies as (*-i) , (*-ii) , (*-iii) and (*-iv) and for their corresponding costs as (a-*) , (b-*), , (c-*) and (d-*) . Each sub-panel provides a 2D phase plane for the ADE factor, i.e., and for infection rate, i.e., . Throughout, we can see from Fig. 4 that the fraction of infected individuals increased as ADE factor increased. Since ADE factor defined quantifying enhancement of synergetic contact in the secondary infection rate, it was expected to play a significant role in increasing disease outbreaks. Meanwhile, it was observed that the outcome exhibited two equilibrium points, a disease-free state and an endemic state , where was the basic reproduction number defined as and, as already noted, we fixed . Accordingly, the disease will regress if presented by the deep blue region of Fig. 4, that also brings no vaccination area (Fig. 5). Another aspect that may also affect the fraction of both primary and secondary infected individuals is relevant vaccines cost and their efficiency being . From this result, three primary factors were observed, as discussed below.
Fig. 4.
(a): Phase diagrams of primary infection individuals along infection rate and ADE factor . Panels A and B present S-2 and S-4 diseases, respectively. Each panel shows the result of varying vaccination cost as (a-*) , (b-*) , (c-*) and (d-*) and the outcome of variable efficiency as (*-i) , (*-ii) , (*-iii) and (*-v) . Additional parameters are and . (b): Phase diagrams of secondary infection individuals along infection rate and ADE factor . Panels A and B present S-2 and S-4 diseases, respectively. Each panel shows the result of varying vaccination cost as (a-*) , (b-*) , (c-*) and (d-*) , and the outcome of varying efficiency as (*-i) , (*-ii) , (*-iii) and (*-v) . The remaining parameters are and .
Fig. 5.
(a): Phase diagrams for primary vaccination individuals along infection rate and ADE factor . Panels A and B present S-2 and S-4 diseases, respectively. Each panel shows the result of varying vaccination cost as (a-*) , (b-*) , (c-*) and (d-*) and the outcome of varying efficiency as (*-i) , (*-ii) , (*-iii) and (*-v) . The remaining parameters are and . (b): Phase diagrams of secondary vaccination individuals along infection rate and ADE factor . Panels A and B present S-2 and S-4 diseases, respectively. Each panel shows the result of varying vaccination cost as (a-*) , (b-*) , (c-*) and (d-*) and the outcome of varying efficiency as (*-i) , (*-ii) , (*-iii) and (*-v) . The remaining parameters are and .
First, the higher efficiency and lower cost for primary vaccination (sub-panels (a-iii), (a-iv), (b-iii), and (b-iv)) encouraged people to receive primary vaccination (Fig. 5(a)), which naturally led to a lower rate of primary infection (Fig. 4(a)).
Second, for one of the four combinations above (sub-panel (a-iv)), higher efficiency and lower cost were implemented not only for the first but also secondary vaccinations, the results indicating a lower rate of secondary vaccination (Fig. 5(b) (a-iv)). Therefore, we can state that this particular tendency is not uncommon but likely, since there were fewer people who were infected in the secondary infection group (Fig. 4(b) (a-iv)). These results indicate that primary vaccination worked effectively and so many people taking the primary immunization policy. As a result, there was no need to receive secondary vaccination.
Third, and similar to the first point, the higher efficiency and lower cost of the secondary vaccination (sub-panels (a-ii), (c-ii), and (c-iv)) encouraged people to commit to receiving secondary vaccination (Fig. 5(b)), which reduced the size of secondary infection (Fig. 4(b)). Although the case of (a-iv) should be one of above those, it does not indicate a high fraction of secondary vaccination. The reason why this happens was what we already discussed in the previous paragraph.
Visually comparing the S-2 and S-4 cases (as per comparison of panel A and panel B in Fig. 4, Fig. 5), shows the outcome likewise, where S-4 cases demonstrated relatively higher infectious situations but a smaller vaccinated region.
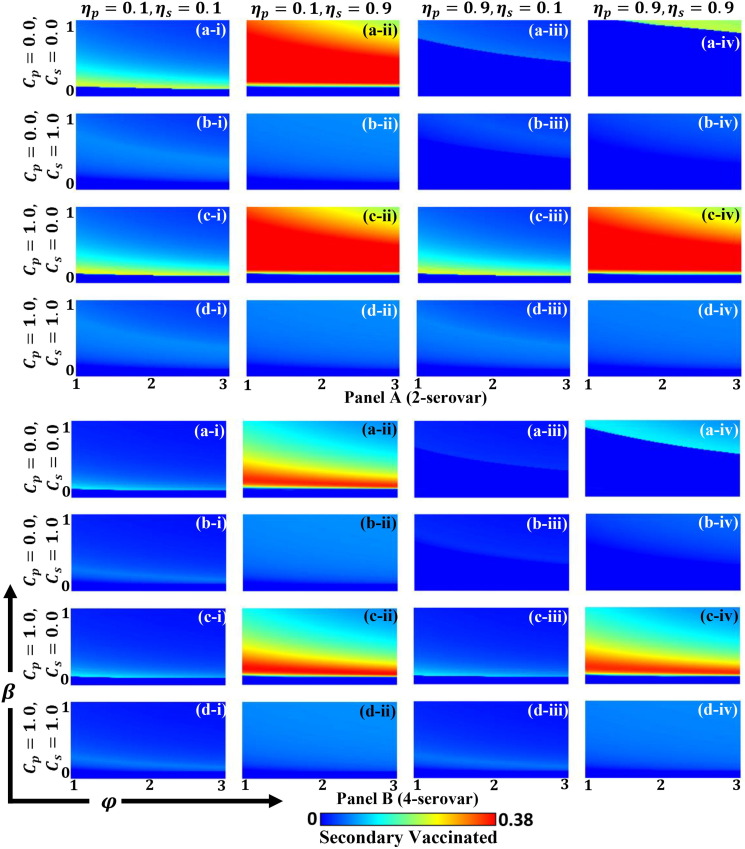
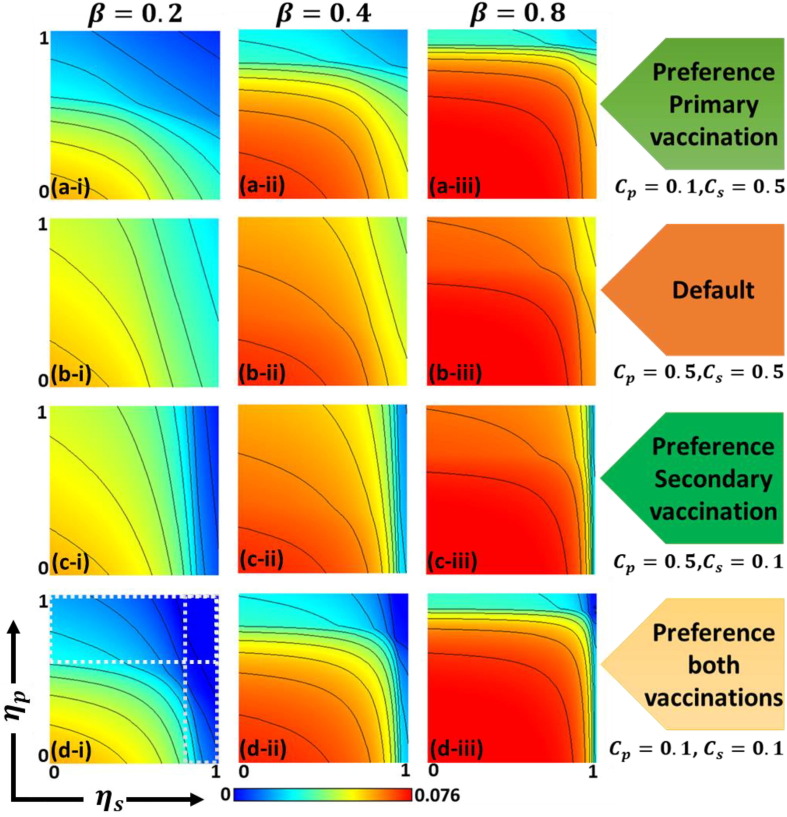
To establish appropriate provisions within society for exploring effective financial support policy (e.g., subsidy, discounts, or free-tickets) to control the spread of disease, we present another 2D heat map in Fig. 6 . The figure indicates secondarily infected (S-4) individuals () along with primary vaccine efficiency and secondary vaccine efficiency . In the case of dengue fever, a portion of secondary infected individuals will be exposed to danger of death; research is needed to effectively reduce this number. Here, sub-panels (a-*), (b-*), and (c-*) indicate preferences for primary vaccination , the default setting , and a preference for secondary vaccination . As a reference, sub-panel (d-*) indicates preference for both vaccinations . Here, we used the term ‘preference’ to imply the specific vaccination that the public health authority prioritized. For example, ‘preference of primary vaccination’ implies that governmental subsidy for encouraging primary vaccination (cheaper cost; Cp can be derived vis-a-vis the default case) exists. Additionally, sub-panels (*-i), (*-ii), and (*-iii) present the variation of infection rates for (), (), and 0.8 ().
Fig. 6.
Phase diagram for secondary infection individuals with S-4 along primary efficiency and secondary efficiency . The preference for primary vaccination as , default case as , preference for secondary vaccination as and preference for both vaccinations as are presented in sub-panels (a-*), (b-*), (c-*), and (d-*), respectively. Here, the infection rate is varied as (*-i) , (*-ii) and (*-iii) . The remaining parameters are and .
Deliberately observing all panels, we observed that the width of the blue region (from light to deep blue) shown in the Y-axis (extending in the -direction) was wider than in the X-axis (extending in the -direction); however, the extent of the blue color in the X-axis region was darker than in the Y-axis. This tendency was more evidently observed in the dotted box of panel (d–i) (presuming weaker infection rate and a preference for both vaccination types). This tendency can also be observed in other parameter settings.
The above observation implies the following. To suppress secondary infection, secondary vaccination requires high efficiency (reliability). However, if a higher can be realized, the effect will become significant. Contrastingly, the primary vaccination, despite not having higher efficiency for will still work reasonably effective in terms of suppressing secondary infection. This can be attributed to the secondary vaccination being introduced at a more downstream point within the process of infection dynamics, as shown in Fig. 2, compared to where primary vaccination is situated. Thus, a much more drastic effect is needed to subdue the spread of secondary infection. However, once this has been established, the impact of secondary vaccination will be significant.
The next step is to provide analogous phase diagrams for secondary infected (*-i), susceptible (*-ii), primary vaccinated (*-iii), and secondary vaccinated (*-iv) individuals against a S-4 according to variable infection rates (a-*) , (b-*) and (c-*) (see Fig. 7 ). In doing so, the assumption of a low-cost vaccine is made for both costs introduced above, in a case where both vaccinations are equally emphasized by the public health authority. It is worth noting that the dotted triangles for the weaker infection rate () display higher susceptibility but lower secondary infection, despite relatively lower coverage for both vaccinations. Referring to existing studies (Tanimoto, 2015, Tanimoto, 2019, Kabir et al., 2019a), this indicates that ‘free-riding’ on the so-called ‘herd immunity’ does occur, as a high efficiency for both vaccinations and relatively weaker infection rate only requires limited vaccination coverage within a society in order to stop the disease from spreading. This allows for a reasonable percentage of free-riders (no vaccination) to be present in the society.
Fig. 7.
Full phase diagrams of (*-i) secondary infection (*-ii), susceptible (*-iii), primary vaccination, and (*-iv) secondary vaccination individuals for S-4 disease along primary efficiency and secondary efficiency . Here, the infection rate is varied as (*-i) , (*-ii) and (*-iii) . The remaining parameters are , and .
5. Conclusion
Applying the vaccination game approach to epidemics, we proposed an n-serovar SVIRS disease model for studying the effect of ADE for two vaccination types, primary and secondary, as it relates to the control and preclusion of contagious diseases. Model investigations and numerical simulations were carried out by including two voluntary vaccination options with several parameters including vaccination cost, efficiency, and ADE factor for two serotypes (S-2 and S-4). Our model can easily be extended to a generalized n-serotype model for arbitrary infections. The model presumed modified replicator dynamics and a mean field approximation, i.e., an infinite and diverse population.
We found an established vaccination policy implemented by health authorities for controlling vaccination efficiency (investment required for improving vaccination efficiency) and the cost to individuals for being vaccinated (subsidies allowing for vaccination) to be crucial to infectious systems in which dual vaccinations are implemented. Additionally, the ADE effect also enhanced contagious disease where infections were involved.
We posited that secondary vaccination should be addressed if its efficiency can be established as being high. Secondary vaccination works at an immediately antecedent stage in the sequence of an infectious process; therefore, irrespective of how effective primary vaccination is, a highly efficient secondary vaccine will be able to minimize death casualties by, among others, dengue fever.
Contrastingly, if a highly efficient secondary vaccination is less conceivable, primary vaccination must take on the burden of stopping the disease from spreading. This implies that an appropriate combination of primary and secondary vaccinations will need to be designed.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Acknowledgments
This study was partially supported by Grant-in-Aid for Scientific Research from JSPS, Japan, KAKENHI (Grant No. JP19KK0262), SCAT (Support Center for Advanced Telecommunications Technology) Research Foundation, and I/O Data Foundation awarded to Professor Tanimoto. We would like to express our gratitude to them.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Author statement
Kabir K M Ariful conceived of the presented idea and established the theory and performed the computations. Jun Tanimoto encouraged Ariful Kabir to explore and supervised the findings of this work. All authors discussed the results and contributed to the final manuscript.
References
- Kermack W.O., McKendrick A.G. A Contribution to the mathematical theory of epidemics. Proc. Roy. Soc. Lond. A. 1927;115:700–721. [Google Scholar]
- Anderson R.M., May R.M. Population biology of infectious diseases: Part I. Nature. 1979;280:361–367. doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]
- Jones, D.S., Sleeman, B.D., 1983. Differential Equations and Mathematical Biology. London, Allen & Unwin.
- Goffman W., Newill V.A. Generalization of epidemic theory: an application to the transmission of ideas. Nature. 1964;204:225–228. doi: 10.1038/204225a0. [DOI] [PubMed] [Google Scholar]
- Ferguson, N., Anderson, R., Gupta, S., 1999. The effect of antibody-dependent enhancement on the transmission dynamics and persistence of multiple-strain pathogens. Poc. Natl. Acad. Sci. USA 96, 790–794. [DOI] [PMC free article] [PubMed]
- Vaughn D.W. Dengue viremia titer, antibody response pattern, and virus serotype correlate with disease severity. J. Infect. Dis. 2000;181:2–9. doi: 10.1086/315215. [DOI] [PubMed] [Google Scholar]
- Recker M., Blyuss K.B., Simmons C.P., Hien T.T., Wills B., Farrar J., Gupta S. Immunological serotype interactions and their effect on the epidemiological pattern of dengue. Proc. R. Soc. B. 2009;276:2541–2548. doi: 10.1098/rspb.2009.0331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Billings L., Schwartz I.B., Shaw L.B., McCrary M., Burke D.S., Cummings D.A.T. Instabilities in multiserotype disease models with antibody-dependent enhancement. J. Theor. Biol. 2007;246:18–27. doi: 10.1016/j.jtbi.2006.12.023. [DOI] [PubMed] [Google Scholar]
- Billings L., Fiorillo A., Schwartz I.B. Vaccinations in disease models with antibody-dependent enhancement. Math. Biol. 2008;211:265–281. doi: 10.1016/j.mbs.2007.08.004. [DOI] [PubMed] [Google Scholar]
- Bhatt, S., Gething, P.W., Brady, O.J., Messina, J.P., Farlow, A.W., Moyes, C.L., et al., 2013. The global distribution and burden of dengue. Nature 496, 504–507. [DOI] [PMC free article] [PubMed]
- Shepard, D.S., Undurraga, E.A., Halasa, Y.A., Stanaway, J.D., 2016. The global economic burden of dengue’ a systematic analysis. Lancet Infect. Dis. 16, 935–941. [DOI] [PubMed]
- Ferrar, J., Hotez, P.J., Junghanss, T., Kang, G., Lalloo, D., White, N.J., et al., 2014. Monson’s Tropical Infectious Diseases, Elsevier.
- Bhatia, R., Dash, A., Sunyoto, T., 2013. Changing epidemiology of dengue in South-East Asia. WHO-SEAJPH 2, 23–27. [DOI] [PubMed]
- Messina J.P., Brady O.J., Scott T.W. Global spread of dengue virus types: mapping the 70 years history. Trends Microbiol. 2014;22:138–146. doi: 10.1016/j.tim.2013.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brady, O.J., Gething, P.W., Bhatt, S., Messina, J.P., Brownstein, J.S., Hoen, A.G., et al., 2012. Refining the global spatial limits of dengue virus transmission by evidence-based consensus. PLoS Negl. Trop. Dis. 6 (8), e1760. [DOI] [PMC free article] [PubMed]
- Dengue vaccine: WHO position paper – September 2018, 2018. Weekly Epidemiol. Record 93 (36), 457–76.
- Dengvaxia, U.S. Food and Drug Administration (FDA), 2019. STN 125682.
- Thisyakorn, U., 2014. Latest developments and future directions in dengue vaccines. Therapeut. Adv. Vaccines 2 (1), 3–9. [DOI] [PMC free article] [PubMed]
- Sanofi's dengue vaccine approved in 11 countries. Reuters. 2017.
- Susie, E., 2016. World's first dengue fever vaccine launched in the Philippines, CNN
- Zachri, E., Planasari, S., 2016. Dengue Fever Vaccine Available in Indonesia, WIB, October 17, 2016
- Biswal B.M.D. Efficacy of a tetravalent dengue vaccine in healthy children and adolescents. N. Engl. J. Med. 2019;381:2009. doi: 10.1056/NEJMoa1903869. [DOI] [PubMed] [Google Scholar]
- World Health Organization; Dengue vaccine: WHO position paper – September 2018. Weekly Epidemiol. Record 93 (36), 457–76 (September 2018).
- Smith J.M. Theory of games and evolution of animal conflicts. J. Theor. Biol. 1974;47:209–221. doi: 10.1016/0022-5193(74)90110-6. [DOI] [PubMed] [Google Scholar]
- Tanimoto, J., 2015. Fundamental of Evolutionary Game Theory and its Applications, Springer.
- Tanimoto, J., 2019. Evolutionary Games with Sociophysics: Analysis of Traffic Flow and Epidemics, Springer.
- Kabir K.M.A., Kuga K., Tanimoto J. Analysis of SIR epidemic model with information spreading of awareness. Cha. Sol. Frac. 2019;119:118–125. [Google Scholar]
- Kabir K.M.A., Tanimoto J. Analysis of epidemic outbreaks in two-layer networks with different structures for information spreading and disease diffusion. Commun. Nonlinear Sci. Numer. Simul. 2019;72:565–574. [Google Scholar]
- Wang Z., Bauch C.T., Bhattacharyya S., d'Onofrio A., Manfredi P., Perc M., Perra N., Salathé M., Zhao D. Statistical physics of vaccination. Phys. Rep. 2016;664:1–113. [Google Scholar]
- Bauch, C.T., Earn, D.J., 2004. Vaccination and the theory of games. Proc. Natl. Acad. Sci. USA 101, 13391–13394. [DOI] [PMC free article] [PubMed]
- Kuga K., Tanimoto J., Jusup M. To vaccinate or not to vaccinate: a comprehensive study of vaccination-subsidizing policies with multi-agent simulations and mean-field modeling. J. Theor. Biol. 2019;469:107–126. doi: 10.1016/j.jtbi.2019.02.013. [DOI] [PubMed] [Google Scholar]
- Fukuda E., Kokubo S., Tanimoto J., Wang Z., Hagishima A., Ikegaya N. Risk assessment for infectious disease and its impact on voluntary vaccination behavior in social network. Cha. Sol. Frac. 2014;68:1–9. [Google Scholar]
- Fukuda E., Tanimoto J. Effects of stubborn decision-makers on vaccination and disease propagation in social network. Int. J. Autom. Logist. 2016;2:78–92. [Google Scholar]
- Iwamura Yoshiro, Tanimoto Jun. Realistic decision-making processes in a vaccination game. Phys. A Stat. Mech. Appl. 2018;494:236–241. [Google Scholar]
- Kabir K.M.A., Kuga K., Tanimoto J. Effect of information spreading to suppress the disease contagion on the epidemic vaccination game. Cha. Sol. Frac. 2019;119:180–187. [Google Scholar]
- Kabir K.M.A., Tanimoto J. Evolutionary vaccination game approach in metapopulation migration model with information spreading on different graphs. Cha. Sol. Frac. 2019;120:41–55. [Google Scholar]
- Kuga K., Tanimoto J. Which is more effective for suppressing an infectious disease: imperfect vaccination or defense against contagion? JSTATE Theory Exp. 2018;2 [Google Scholar]
- Tanaka M., Tanimoto J. Is subsidizing vaccination with hub agent priority policy really meaningful to suppress disease spreading? J. Theor. Biol. 2020;486 doi: 10.1016/j.jtbi.2019.110059. [DOI] [PubMed] [Google Scholar]
- Kabir K.M.A., Kuga K., Tanimoto J. The impact of information spreading on epidemic vaccination game dynamics in a heterogeneous complex network-a theoretical approach. Cha. Sol. Frac. 2020;132 [Google Scholar]
- Kabir K.M.A., Tanimoto J. Vaccination strategies in a two-layer SIR/V–UA epidemic model with costly information and buzz effect. Commun. Nonlinear Sci. Numer. Simul. 2019;76:92–108. [Google Scholar]
- Kabir, K.M.A., Jusup, M., Tanimoto, J., 2019. Behavioral incentives in a vaccination-dilemma setting with optional treatment, PRE 100, 062402. [DOI] [PubMed]
- Kabir K.M.A., Tanimoto J. Dynamical behaviors for vaccination can suppress infectious disease – a game theoretical approach. Cha. Sol. Frac. 2019;123:229–239. [Google Scholar]
- Bauch, C.T., Bhattacharyya, S., 2012. Evolutionary game theory and social learning can determine how vaccine scares unfold. PLoS Comp. Biol. 8 (4), e1002452. [DOI] [PMC free article] [PubMed]
- Chen, X., Fu, F., 2018. Social learning of prescribing behavior can promote population optimum of antibiotic use, Front. Phys. 6, 139.
- Bauch T.C. Imitation dynamics predict vaccinating behavior. Proc. R. Soc. B. 2005;272:1669–1675. doi: 10.1098/rspb.2005.3153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabir K.M.A., Tanimoto J. Modeling and analyzing the coexistence of dual dilemmas in the proactive vaccination game and retroactive treatment game in epidemic viral dynamics. Proc. R. Soc. A. 2019;475:20190484. doi: 10.1098/rspa.2019.0484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arefin, M.R., Masaki, T., Kabir, K.M.A., Tanimoto, J., 2019. Interplay between cost and effectiveness in influenza vaccine uptake: a vaccination game approach. Proc. R. Soc. A 475, 20190608. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.