Abstract
This letter describes a hybrid plug/compartment (HyPC) kinetic model to fit dynamic indocyanine green fluorescence data acquired in a porcine model of long bone traumatic fracture. Parametric images of periosteal blood flow, endosteal blood flow, total bone blood flow and fraction of endosteal-to-periosteal flow were obtained by applying the HyPC model on a pixel-by-pixel basis. Intraoperative discrimination between healthy and damaged bone could facilitate debridement reducing post-operative complications from non-union and infection. The ability to quantify periosteal and endosteal blood flow could inform nail vs. plate-and-screw decisions to avoid further compromising cortical blood supply.
Keywords: orthopaedic trauma, bone debridement, indocyanine green, tracer kinetics, bone blood flow
1. Introduction
Infection is common in orthopedic surgery, occurring in approximately 60% of open bone fractures, and represents a significant clinical challenge in military and civilian settings[1], [2]. The high incidence of infection is due to several factors, including contamination of open fractures, trauma to tissue, loss of soft tissue coverage, and secondary issues of long-term hospitalization. Regardless, failure to treat bone infection results in recurrent infection and dramatically increases the risk of repeat surgery, prolonged morbidity, loss of function and potential loss of limb [3]. Poor perfusion is thought to be a crucial determinant in development and persistence of bone infections, by preventing endogenous immune cells and antibiotics from reaching the traumatized tissues. When poorly perfused bone remains present during the setting of open fracture, it becomes a site of origin for biofilm formation and subsequent resistance to antibiotics. For these reasons, management of open fractures requires aggressive and extensive debridement to remove all poorly perfused bone. Unfortunately, there is currently no objective method to determine bone perfusion or guide the extent of debridement during surgery.
Indocyanine green (ICG) fluorescence imaging has been used to assess tissue perfusion in other surgical settings, such as in free flap reconstruction [4], [5]. In these cases, the dynamic ICG curves obtained from fluorescence imaging during wash-in and wash-out can be used to estimate blood perfusion. Because tissue flaps are optically homogeneous and more-or-less uniformly perfused, simple kinetic models can be used to assess underlying perfusion. However, bone blood supply consists of both periosteal and endosteal vessels that feed the interrogated bone cortex, requiring a specific kinetic model to separately parameterize these blood supplies.
In this letter, we describe a hybrid plug flow/compartment (HyPC) model that captures the two branched nature of the periosteal and endosteal components and articulates the slow-flow component of the endosteal medullary cavity. Separately endosteal and periosteal bone flow separately could provide important insight into selecting, for example, whether to apply fixation using an intermedullary nail, disturbing endosteal flow, or stripping the periosteum before applying a rigid plate. The recovered kinetic functions are compared against a model-independent nonparametric solution for validation under various flow-states during baseline and following severe bone trauma in a porcine model. This technical development informs future animal and patient studies examining the predictive value of these kinetic parameters with respect to injury status of bone and of outcome measures.
2. Materials and Methods
Theory
The time-dependent concentration of dye in a tissue, , at some position, , following a bolus injection is given by the convolution theory of tracer kinetics [6]:
| (1) |
where Ca(t) is the time-dependent concentration of dye in the arterial system, is the blood flow at position, , and is the impulse residue function (IRF) at position, . The IRF is defined as the fraction of dye remaining in the tissue at time, t, following an ideal bolus injection approximating a delta function. In the language of linear time-invariant systems, R(t) represents a ‘transfer function’ mapping Ca(t) to Q(t).
If at position, , there exists multiple quasi-independent vascular systems (locally independent with separate feeding arteries), then a “bulk” FR(t) can be defined as the superposition of the FR(t) functions from each capillary unit. Most indicator-dilution applications are found in 3D medical imaging (e.g., MRI, CT) and therefore, a voxel will cover a single vascular unit. If that vascular unit communicates with other interconnected compartments of tissue, a compartment model is used. Otherwise, if the dye remains in the intravascular space (IVS), a single compartment is considered, but may include parameter(s) to describe the distribution of capillary transit times.[7], [8]
Compact bone is supplied by the periosteal and endosteal blood vessels [9]. The periosteal vessels insert into the periosteum, a connective tissue that surrounds the bone. These vessels travel into the superficial compact bone providing blood flow from the exterior. The endosteal blood supply consists of the large nutrient vessels that insert through holes in the bone and run along the inside of the bone, branching off into central and perforating canals, and supplying blood from the interior to the inner two-thirds of the cortex as well as the medullary cavity [10]; the medullary cavity also contains the bone marrow, and porous blood vessels running through the marrow allow for new blood cells to enter the circulatory system [11].
When imaging volume units are large enough, such as in planar fluorescence imaging where light penetrates into 1-2 cm of cortical bone, a bulk FR(t) will be comprised of these two bifurcated periosteal and endosteal systems. To this end, we describe a novel, bone-specific kinetic model representing the superposition of a plug flow model (periosteal) and a two-compartment model (endosteal) with independent bolus arrival times, which we assign the name “hybrid plug/compartment” model, or “HyPC” for short.
Let there be two distinct tissue compartments, periosteal (P) and endosteal (E) that have a time-dependent tissue concentration of dye, QP(t) and QE(t), respectively. Within the HyPC model, representing the region of interrogation at , can be considered a summation of partial volumes of QP(t) and QE(t), such that:
| (2) |
where and are the fractional volumes interrogated by light when positioned at r, and the convolution
| (3) |
where iPBF and iEBF are the instrument-independent periosteal blood flow and quantitative endosteal blood flow (the actual physiologic blood flow in these regions independent of the type of instrument used to measure them). In practice, it is not always possible to determine the dP and dE. Therefore, we simplify from Eq. 2 to PBF and EBF, the periosteal and endosteal blood flows for a specific imaging geometry and assumed partial volume distribution. The aggregate FR(t) describing the sum of flow-scaled R(t)s in the periosteum and endosteum is defined as
| (4) |
For subjects with similar age and bone density, the iPBF will correlate with PBF, and iEBF will correlate with EBF.
The IRFs RP(r,t) and RE(r,t) are defined as:
| (5.1) |
| (5.2) |
Where is the arrival time of the bolus to the periosteal vasculature centered under , is the minimum time required for dye to travel across the periosteal vasculature, and is the arrival time of the bolus to the endosteal vasculature in the area of interrogation. Therefore, there are six parameters that are recovered by applying the HyPC model: , , , , , . Furthermore, we define the following calculated parameters: total bone blood flow, TBF = PBF + EBF; and EBF fractional flow, EFF = EBF / TBF.
Animal Experiment and Fluorescence Acquisition
A two pigs were used for this proof-of-concept study which was approved by Dartmouth’s Institutional Animal Care and Use Committee (IACUC) as part of protocol #00002150. Each pig was sedated and placed under general anesthesia using isoflurane. Peripheral veins were catheterized for administration of ICG. Once a deep plane of anesthesia was confirmed, the leg was surgically opened to expose the intact periosteum. A large artery, such as the superficial femoral artery, was blunt dissected and a piece of black cloth was placed between it and the leg to allow direct arterial input function (AIF) characterization [12]. Imaging was performed at baseline and after each of the following surgical manipulations: traverse tibial osteotomy at two locations, removal of proximal periosteum, and removal of distal periosteum. Imaging was performed using the Zeiss Pentero OPMI 800 operating in FLOW800 mode at a working distance of 300 mm. Infrared video was recorded to capture the injection of ICG, and its wash-in and wash-out of the tissue of interest.
Imaging Data Analysis
The ICG videos were transferred to a PC and loaded into MATLAB (TheMathWorks, Warrick, MA) and analyzed using an in-house developed implementation of the HyPC model. First videos were processed using the VideoReader function into a time series of images saved in a single array. Using the imfreehand tool, the region corresponding to the exposed artery was selected and saved as the AIF, Ca(t). The same tool was used to select regions-of-interest (ROIs) along the length of the bone. Each ROI was then fit with the HyPC model using a two-step approach to minimize the chance of overfitting. First, the initial wash-in slope (25% past the time of peak intensity) of the curve was fit using a plug-flow only model, to estimate PBF, TP and MP. These parameters were then used as priors for the plug component of the full model, which was fit to the whole curve to recover EBF, TE and k2. For both fitting procedures, fminsearchbnd was used. When applied on a pixel-by-pixel basis to produce parametric maps, the image stack was first median filtered with a 4x4 pixel window using medfilt2, and then reduced in size by 1/4. This was done to improve the signal-to-noise and reduce the time required to compute the maps.
To validate the recovered FR(t) function, a model-independent deconvolution was performed using the truncated SVD approach [13]. While FR(t) recovered this way will have oscillations expected with an SVD approach, if the HyPC model accurately represents the true FR(t), it should show agreement with the SVD function averaged over time.
3. Results
Figure 1 shows the results of the two-step fit of HyPC to the ICG curves extracted from ROI analysis of pig 1. For each curve, the recovered values for periosteal blood flow (PBF) and endosteal blood flow (EBF), and calculated total bone blood flow (TBF) and endosteal flow fraction (EFF) are shown. ROI analysis was performed on data from the two pigs, and values presented here are mean ± standard deviation. Periosteal damage results in marked decrease in PBF from baseline (6.8 ± 1.1 ml/min/100g of bone). The ROI adjacent to damaged periosteum decreased in PBF by 21.8 ± 22.3 %, and the ROI at the site of damage decreased by 83.8 ± 4.0%. The endosteal flow remained more or less constant, between 0.9 and 1.4 ml/min/100 g of bone; transection of the bone in two locations further reduced the PBF by 52.5 ± 17.6% and reduced the EBF by 73.5 ± 6.0%. The recovered flow-scaled IRFs show the degree to which the relative levels of BF compared to total blood flow (TBF) increased during the evolution of injury in Pig 1. With a baseline of 12.7 ± 0.1%, EFF increased to 42.5 ± 19.8% after periosteal damage, and remained at 30.1 ± 14.0% following transection of the bone.
Figure 1.
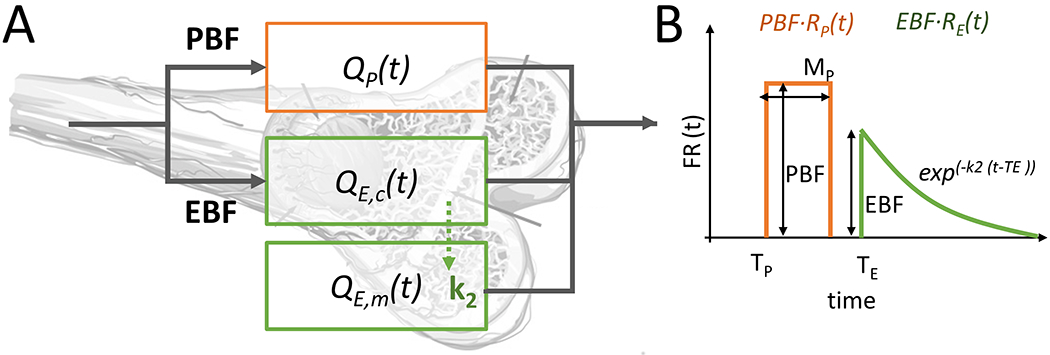
(A) A diagram showing the compartments of the HyPC model, overlaid onto the bone anatomy and how these compartments relate kinetically (QP, periosteal compartment; QE,c, endosteal capillary compartment; QE,m, endosteal medullary compartment) (B) The flow-scaled aggregate impulse residue function used in the HyPC model, showing the parameters recovered: PBF, EBF, TP, TE, MP, k2.
The nonparametric IRFs recovered using truncated SVD (TSVD) show good agreement with the HyPC fit recovered FR(t) functions from Pig 1 (Figure 2; bottom row). While the fairly dramatic oscillations are a feature of this type of highly unstable deconvolution [13], nevertheless, the center of these oscillations tracks very closely the HyPC FR(t), suggesting that the kinetic model is valid.
Figure 2.
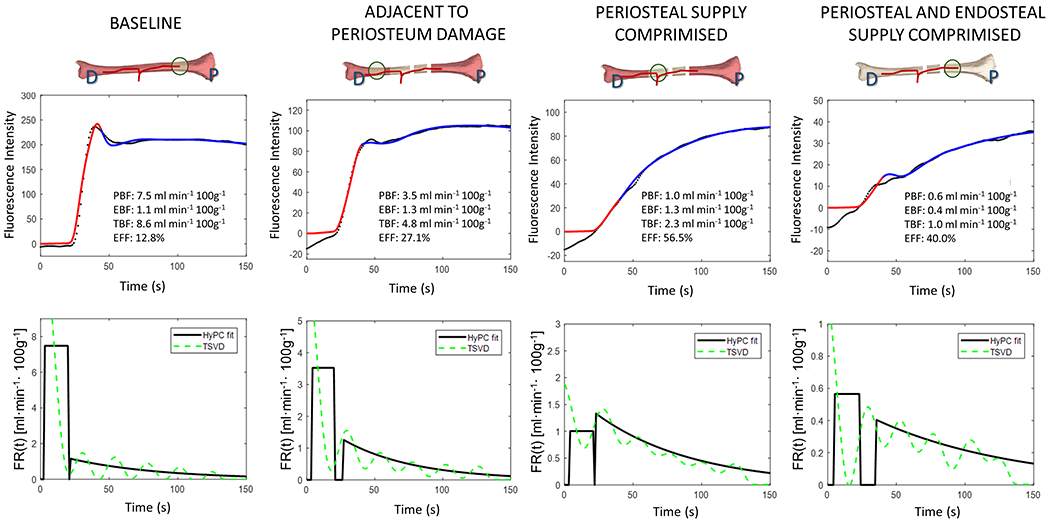
Top Row. ICG intensity (black dots) measured during baseline, after endosteal flow is disrupted and after both endosteal and periosteal flow is disrupted. Curve fitting is performed in two steps: first, a plug flow model is fit to the initial slope (red line) then the entire curve is fit using the hybrid plug and compartment (HyPC) model (blue line).
Bottom Row. The recovered flow-scaled impulse response functions, FR(t), corresponding to the curves in the top row are shown (black lines). For comparison, FR(t) estimated using Tikhonov deconvolution also shown (green lines).
In addition to ROI analysis, the HyPC model is effective at producing parametric maps. Using the procedure described previously, parametric maps of TBF and EFF were calculated for Pig 1 and are shown in Figure 3. For efficiency, the algorithm allows identification of an area of interest and calculates the values for those pixels first before populating the rest of the field of view in radom order, accounting for the speckled appearance of the adjacent tissue.
Figure 3.
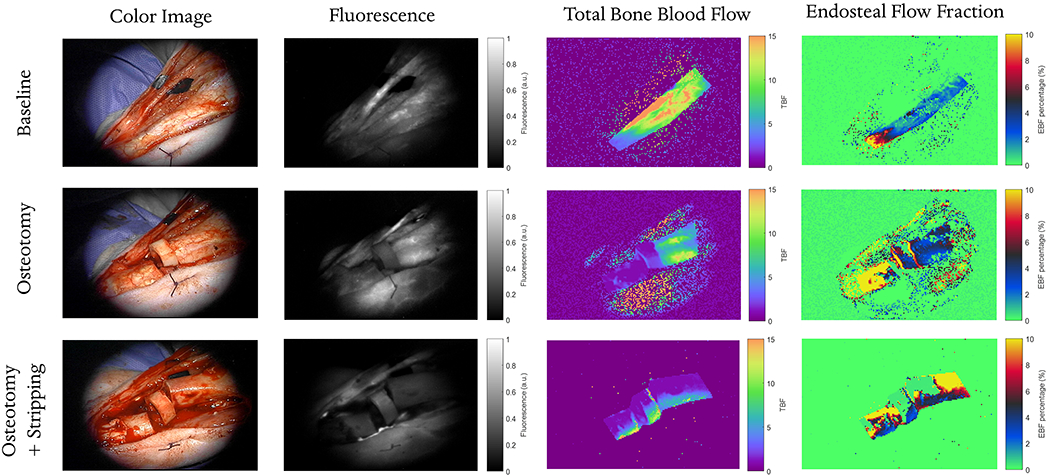
For each leg condition (baseline, osteotomy and osteotomy with full periosteum stripping), four images are shown: a white-light image acquired during surgery with the operating microscope, a fluorescence image acquired at a single time-point 30 s after ICG injection, parametric map of total bone blood flow (TBF) and the percent fraction of endosteal flow (EBF / TBF). Parametric maps are recovered by fitting the HyPC model on a pixel-by-pixel basis.
4. Discussion
While the use of existing techniques in MRI and PET have been explored to quantify bone blood flow [14], [15] , this manuscript presents the first bone-specific kinetic model that takes into account the unique interrogation volume of fluorescence imaging systems. Since the signal is acquired from both the superficial tissue and tissue 1-1.5 cm below the surface of the bone, changes in ICG fluorescence intensity over time will reflect the different wash-in and washout dynamics of the periosteal and endosteal blood supply. It was hypothesized that an appropriate model would need to exhibit the following criteria: 1) the difference in arrival times of dye in the periosteum and endosteal compartment, and 2) the porous nature of endosteal vessels which freely exchange material with the medullary cavity of the bone. The proposed HyPC model is related to the adiabatic approximation to the tissue homogeneity (AATH) model, which fulfills criterion #2, but HyPC is modified to decouple the fast and slow phase components, allowing for criterion #1.
While simple compartment models have been used in previous studies to quantify tumor kinetics [16], [17], for this unique orthopaedic application, we specifically developed a kinetic model to capture the unique bifurcated delivery of blood to cortical bone. A few of the recovered FR(t) functions in Figure 2 demonstrate the improved utility of this model compared with previous single input models like AATH [8] and GCTT [7]; in one case, the EBF was higher than the PBF, and in another, there was a gap between the exit of the dye in the periosteum and the arrival of the dye in the endosteum. Neither of these two scenarios would be allowed by previous models, or by a constrained nonparametric deconvolution [18]. The close tracking of the nonparametric deconvolution suggest the HyPC model is reasonably valid. Parametric maps of TBF and EFB fraction in Figure 3 clearly show the marked changes expected in bone flow following such disturbances. Total blood flow at baseline was about 10 ml/min/100g. Following osteotomy, TBF decreased markedly between transverse cuts due to the elimination of both endosteal and periosteal flow; distal to the cuts TBF was reduced mainly due to a disturbance in periosteal flow, suggesting transection of a supplying periosteal vessel. However, the endosteal flow remained intact. Subsequent stripping of the periosteum caused a reduction in TBF across the whole site, to levels around 3 ml/min/100g, and revealed the reduction in endosteal flow proximal to the transection.
As a proof-of-principle technical note, the most important limitation of this study is that only two pigs were used; a larger study is underway to support additional mechanistic investigations. There are some other limitations to this study that will be addressed in future work: First, the current method of obtaining the AIF is not practical in the clinical setting, and a pulse dye densitometer [19] would be better-suited to this purpose. Second, fluorescence should be corrected by the optical properties of the tissue for within-patient and between-patient comparisons. Additionally, using FEM to estimate the sensitivity to the periosteal and endosteal regions would improve quantitation. Notwithstanding these limitations, HyPC kinetic imaging, which could help surgeons to separately quantify the endosteal and periosteal supply during surgery, may enable discrimination between viable and non-viable tissue during debridement—an improvement which could reduce infection and non-union rates [20], [21]. Furthermore, the ability to directly quantify endosteal and periosteal blood flow may help the surgeon decide between an intramedullary nail or plate and screw fixation [22].
Acknowledgements
The authors would like to thank Dr. Eric Henderson for consulting on the study design, Dr. Karen Moodie for assisting with the animal experiment, and Alberto Ruiz and Benjamin Maloney for assisting in the data acquisition. Funding for this work was provided by a Dartmouth SYNERGY Grant (UL1TR001086) and salary support & training by NIH/NCI K99CA190890 (JTE). The authors have submitted US Provisional Patent Application No. 62/755,067 concerning the HyPC kinetic model and its implementation in orthopedic surgery.
References
- [1].Merritt K, “Factors increasing the risk of infection in patients with open fractures.,” The Journal of trauma, vol. 28, no. 6, pp. 823–827, 1988. [DOI] [PubMed] [Google Scholar]
- [2].Harris AM, Althausen PL, Kellam J, Bosse MJ, Castillo R, and L. E. A. P. (LEAP) S. Group, “Complications following limb-threatening lower extremity trauma,” Journal of orthopaedic trauma, vol. 23, no. 1, pp. 1–6, 2009. [DOI] [PubMed] [Google Scholar]
- [3].Gitajn IL et al. , “Deficits in preference-based health-related quality of life after complications associated with tibial fracture,” Bone Joint J, vol. 100, no. 9, pp. 1227–1233, 2018. [DOI] [PubMed] [Google Scholar]
- [4].Holm C, Tegeler J, Mayr M, Becker A, Pfeiffer UJ, and Mühlbauer W, “Monitoring free flaps using laser-induced fluorescence of indocyanine green: A preliminary experience,” Microsurgery: Official Journal of the International Microsurgical Society and the European Federation of Societies for Microsurgery, vol. 22, no. 7, pp. 278–287, 2002. [DOI] [PubMed] [Google Scholar]
- [5].Polom K, Murawa D, Rho Y, Nowaczyk P, Hünerbein M, and Murawa P, “Current trends and emerging future of indocyanine green usage in surgery and oncology: a literature review,” Cancer, vol. 117, no. 21, pp. 4812–4822, 2011. [DOI] [PubMed] [Google Scholar]
- [6].Meier P and Zierler KL, “On the theory of the indicator-dilution method for measurement of blood flow and volume,” Journal of applied physiology, vol. 6, no. 12, pp. 731–744, 1954. [DOI] [PubMed] [Google Scholar]
- [7].Schabel MC, “A unified impulse response model for DCE-MRI,” Magnetic resonance in medicine, vol. 68, no. 5, pp. 1632–1646, 2012. [DOI] [PubMed] [Google Scholar]
- [8].Lawrence KSS and Lee T-Y, “An adiabatic approximation to the tissue homogeneity model for water exchange in the brain: II. Experimental validation,” Journal of Cerebral Blood Flow & Metabolism, vol. 18, no. 12, pp. 1378–1385, 1998. [DOI] [PubMed] [Google Scholar]
- [9].McCarthy I, “The physiology of bone blood flow: a review,” JBJS, vol. 88, pp. 4–9, 2006. [DOI] [PubMed] [Google Scholar]
- [10].Rhinelander FW, “Circulation in bone,” The biochemistry and physiology of bone, vol. 2, pp. 1–77, 2012. [Google Scholar]
- [11].Reichert I, McCarthy I, and Hughes S, “The acute vascular response to intramedullary reaming. Microsphere estimation of blood flow in the intact ovine tibia,” The Journal of Bone and Joint Surgery. British volume, vol. 77-B, no. 3, pp. 490–493, May 1995. [PubMed] [Google Scholar]
- [12].Elliott JT et al. , “Image-derived arterial input function for quantitative fluorescence imaging of receptor-drug binding in vivo,” Journal of biophotonics, vol. 9, no. 3, pp. 282–295, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Østergaard L, Weisskoff RM, Chesler DA, Gyldensted C, and Rosen BR, “High resolution measurement of cerebral blood flow using intravascular tracer bolus passages. Part I: Mathematical approach and statistical analysis,” Magnetic resonance in medicine, vol. 36, no. 5, pp. 715–725, 1996. [DOI] [PubMed] [Google Scholar]
- [14].Dyke JP and Aaron RK, “Noninvasive methods of measuring bone blood perfusion,” Annals of the New York Academy of Sciences, vol. 1192, no. 1, pp. 95–102, Apr. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Heinonen I et al. , “Bone blood flow and metabolism in humans: Effect of muscular exercise and other physiological perturbations,” Journal of Bone and Mineral Research, vol. 28, no. 5, pp. 1068–1074, May 2013. [DOI] [PubMed] [Google Scholar]
- [16].Cuccia DJ et al. , “In vivo quantification of optical contrast agent dynamics in rat tumors by use of diffuse optical spectroscopy with magnetic resonance imaging coregistration,” Applied optics, vol. 42, no. 16, pp. 2940–2950, 2003. [DOI] [PubMed] [Google Scholar]
- [17].St Lawrence K et al. , “Kinetic model optimization for characterizing tumour physiology by dynamic contrast-enhanced near-infrared spectroscopy,” Physics in Medicine & Biology, vol. 58, no. 5, p. 1591, 2013. [DOI] [PubMed] [Google Scholar]
- [18].Yeung WTI, Lee T-Y, Maestro RFD, Kozak R, Bennett JD, and Brown T, “An absorptiometry method for the determination of arterial blood concentration of injected iodinated contrast agent,” Phys. Med. Biol, vol. 37, no. 9, p. 1741, 1992. [DOI] [PubMed] [Google Scholar]
- [19].Iijima T, Iwao Y, and Sankawa H, “Circulating blood volume measured by pulse dye-densitometry: comparison with (131)I-HSA analysis,” Anesthesiology, vol. 89, no. 6, pp. 1329–1335, Dec. 1998. [DOI] [PubMed] [Google Scholar]
- [20].Caudle RJ and Stern PJ, “Severe open fractures of the tibia.,” The Journal of bone and joint surgery. American volume, vol. 69, no. 6, pp. 801–807, 1987. [PubMed] [Google Scholar]
- [21].Gustilo RB, Mendoza RM, and Williams DN, “Problems in the management of type III (severe) open fractures: a new classification of type III open fractures,” Journal of Trauma and Acute Care Surgery, vol. 24, no. 8, pp. 742–746, 1984. [DOI] [PubMed] [Google Scholar]
- [22].Adams CI and Robinson CM, “CM Court-Brown, and M. M. McQueen,‘Prospective randomized controlled trial of an intramedullary nail versus dynamic screw and plate for intertrochanteric fractures of the Femur,’” Journal of orthopaedic trauma, vol. 15, no. 6, pp. 394–400, 2001. [DOI] [PubMed] [Google Scholar]


