Abstract
Motivation
Microbial communities have been proved to have close relationship with many diseases. The identification of differentially abundant microbial species is clinically meaningful for finding disease-related pathogenic or probiotic bacteria. However, certain characteristics of microbiome data have hurdled the accuracy and effectiveness of differential abundance analysis. The abundances or counts of microbiome species are usually on different scales and exhibit zero-inflation and over-dispersion. Normalization is a crucial step before the differential abundance test. However, existing normalization methods typically try to adjust counts on different scales to a common scale by constructing size factors with the assumption that count distributions across samples are equivalent up to a certain percentile. These methods often yield undesirable results when differentially abundant species are of low to medium abundance level. For differential abundance analysis, existing methods often use a single distribution to model the dispersion of species which lacks flexibility to catch a single species’ distinctiveness. These methods tend to detect a lot of false positives and often lack of power when the effect size is small.
Results
We develop a novel framework for differential abundance analysis on sparse high-dimensional marker gene microbiome data. Our methodology relies on a novel network-based normalization technique and a two-stage zero-inflated mixture count regression model (RioNorm2). Our normalization method aims to find a group of relatively invariant microbiome species across samples and conditions in order to construct the size factor. Another contribution of the paper is that our testing approach can take under-sampling and over-dispersion into consideration by separating microbiome species into two groups and model them separately. Through comprehensive simulation studies, the performance of our method is consistently powerful and robust across different settings with different sample size, library size and effect size. We also demonstrate the effectiveness of our novel framework using a published dataset of metastatic melanoma and find biological insights from the results.
Availability and implementation
The R package ‘RioNorm2’ can be installed from Github athttps://github.com/yuanjing-ma/RioNorm2.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Microbial communities have been proved to have close relationship with diseases such as diabetes (Kåhrström, 2012; Larsen et al., 2010), Crohn’s disease (Morgan et al., 2012), bacterial vaginosis (Ravel et al., 2011), eczema (Harris and Wagner, 2012), obesity (Turnbaugh et al., 2009) and metastatic melanoma (Matson et al., 2018). The identification of differentially abundant microbial species is clinically helpful for finding disease-related pathogenic or probiotic bacteria. It is a powerful means of understanding the contribution of the human microbiome to health and its potential as a target for therapeutic interventions.
Microbiome data are usually collected from marker gene surveys of DNA representing communities of microorganisms found in environmental samples. Our method focuses on the OTU table that is generated using 16S rRNA targeted sequencing (Dethlefsen et al., 2008; Shah et al., 2011; Venter et al., 2004). By studying the abundance level of OTUs from different conditions, it is possible to identify OTUs that are associated with conditions. However, the identification of differentially abundant OTUs (DA-OTUs) is difficult and complex due to zero-inflation and over-dispersion of microbiome data. Under-sampling causes the degree of sparsity to be high (Paulson et al., 2013). The zero count of an OTU does not necessarily mean the OTU is absent; it can be caused by under-sampling which makes the low abundant OTUs not detectable. Another issue related to microbiome data is its high variation. The microbiome data are known to contain a large amount of both biological and technical variation (Nayfach and Pollard, 2016). One source of biological variability is the natural diversity of bacterial species due to environment factors. Besides, the microorganisms vary over time; there is large variation of the same bacteria species among different samples. When detecting the DA-OTUs, we are only interested in the difference caused by specific conditions (e.g. health versus certain disease). Therefore, it is important to take the biological variation into consideration. Another type of variation is technical variation which is usually caused by equipment and experimental design. The library size is a major cause of the technical variation. It defines the number of random fragments generated and sequenced from a sample; with small library size, the low abundant OTUs are more difficult to be detected which causes the high variation in observed count numbers. Different library sizes also make count numbers incomparable across samples.
Due to the characteristics of metagenomics data, normalization is an essential first step for any downstream analysis. Some of the methods assume that counts distribution are equivalent up to a certain quantile across samples and aim to find the quantile for deriving the size factor. Total count normalization uses the sum of all counts within a sample as the size factor. Upper quartile normalization (Bullard et al., 2010) scales counts by the 75th percentile of each sample’s non-zero count distribution. MetagenomeSeq (Paulson et al., 2013) improves upper quartile method by proposing a project specific data-driven way to determine the exact percentile level (CSS). EdgeR (Robinson and Oshlack, 2010) uses TMM as the default normalization approach. The assumptions behind the TMM method are similar to the assumptions commonly made in quantile normalization. DESeq (Anders and Huber, 2010), originally designed for RNA-seq, creates quantile-adjusted ‘pseudodata’ by comparing each sample to an artificially created reference sample. These methods assume that OTUs whose counts are below this quantile are not differentially abundant among different conditions. However, the assumption might be controversial. A recent paper by Matson et al. (2018) points out that some DA-OTUs have relatively low and medium abundance levels. Therefore, the above quantile-based normalization approaches might include DA-OTUs when calculating the size factors. Besides, these approaches of rescaling counts are most appropriate for comparing OTU compositions from different conditions instead of identifying individual DA-OTUs. They will detect a large amount of false positives when the large differences in total abundances of DA-OTUs have caused proportions of non-DA-OTUs to change. RAIDA (Sohn et al., 2015) is developed to find individual DA-OTUs. It utilizes the ratio between features in a modified zero-inflated log-normal model to find size factors. It can solve the above-mentioned problems, but tends to have low power when the effect sizes are small. To avoid including DA-OTUs into size factor calculation and to account for proportion changes of non-DA-OTUs caused by abundance change of DA-OTUs, we propose a novel network-based method which finds a group of relatively invariant OTUs (riOTUs) across samples and conditions. The idea is inspired by the concept of housekeeping genes in microarray study. A gene is usually chosen as a housekeeping gene if it is uniformly expressed with low variation under both control and experimental conditions. The expression of one or multiple housekeeping genes is used as a reference or baseline for gene expression analysis of other genes. In microbiome data analysis, we cannot measure an OTU’s variation directly with the raw count data and we may not have prior knowledge on which OTUs having relatively stable abundance level across all samples. Therefore, we propose to find a group of OTUs whose relative abundance or relative change has low variation across all samples and conditions. The sum of counts of these riOTUs will serve as size factor for normalization. Our approach reduces the bias introduced by scaling raw counts by size factor that might incorporate DA-OTUs and at the same time performs well for detecting DA-OTUs.
After normalization, counts are brought to the same scale for differential abundance analysis. Methods which are developed for detecting differentially expressed genes using RNA-seq data such as edgeR, DESeq and DESeq2 (Love et al., 2014) have been applied to the microbiome setting. However, RNA-seq data does not exhibit as much zero-inflation as microbiome data. Other methods such as RAIDA, ANCOM (Mandal et al., 2015), Omnibus (Chen et al., 2018), MetagenomeSeq and Metastats (White et al., 2009) are differential abundance tests specially designed for microbiome data. RAIDA constructs a moderated t-statistics (Smyth, 2005) for the log-ratio of each feature using the estimated mean and variance. ANCOM performs statistical tests on point estimates of transformed OTU counts by an additive log ratio, where invariant taxa are chosen as the denominator. Omnibus performs differential abundance test by jointly testing the abundance, prevalence and dispersion. The test is built on a zero-inflated negative binomial (ZINB) regression model and winsorized count data to account for zero-inflation and outliers. MetagenomeSeq takes into account of zero-inflation by using a zero-inflated Gaussian distribution mixture model. Metastats applies non-parametric t-test for detecting high abundance DA-OTUs and separately handles sparsely-sampled features using Fisher’s exact test. The non-parametric part may lack of power when the sample size is small. In general, these approaches usually assume over-dispersion for all OTUs, which does not incorporate the individual difference.
In order to incorporate zero-inflation and to model over-dispersion with flexibility directly on count data, our second contribution is to propose a two-stage zero-inflated mixture count regression model. In the first stage, every OTU goes through a score test or bootstrap parametric test for testing over-dispersion. OTUs will be divided into two groups, i.e. with or without over-dispersion. In the second stage, OTUs without over-dispersion will be modeled using zero-inflated Poisson (ZIP) distribution and OTUs with over-dispersion will be modeled using ZINB distribution.
We evaluate our proposed framework, RioNorm2, through comprehensive simulation studies and compare the results with those of DESeq, DESeq2, metagenomeSeq, RAIDA and Omnibus. RioNorm2 consistently yields high power while controlling the false discovery rate (FDR). RioNorm2’s performance is robust and superior in simulated settings with small to medium effect size, library size and sample size. DESeq, DESeq2, RAIDA and Omnibus have very low power in detecting differential abundance when effect sizes are small or medium and the overall performance based on AUC is highly sensitive to the library size. Even though MetagenomeSeq has high power with small effect size, it also yields a large number of false positives. In the situation where some OTUs’ abundance level change without suppressing other OTUs’ abundance, RioNorm2 and RAIDA work the best. If the absolute abundance (count) is of interest rather than the relative abundance (i.e. proportion), it is dangerous to use DESeq, DESeq2, metagenomeSeq and Omnibus which tend to detect more false positives as the effect size increases.
We also apply RioNorm2 to a newly published dataset which studies the relationship between microbiome species and cancer treatment efficiency (Matson et al., 2018). The detected group of relatively invariants OTUs by RioNorm2 have similar phylogenetic tree information, which may imply that they have similar physical or genetic characteristics by sharing similar evolutionary paths from Kingdom to Genus level. Using this group of OTUs as reference OTUs has biological meanings. Besides, by separately modeling OTUs with and without over-dispersion by a two-stage model, RioNorm2 largely increases the power of detecting DA-OTUs.
2 Materials and methods
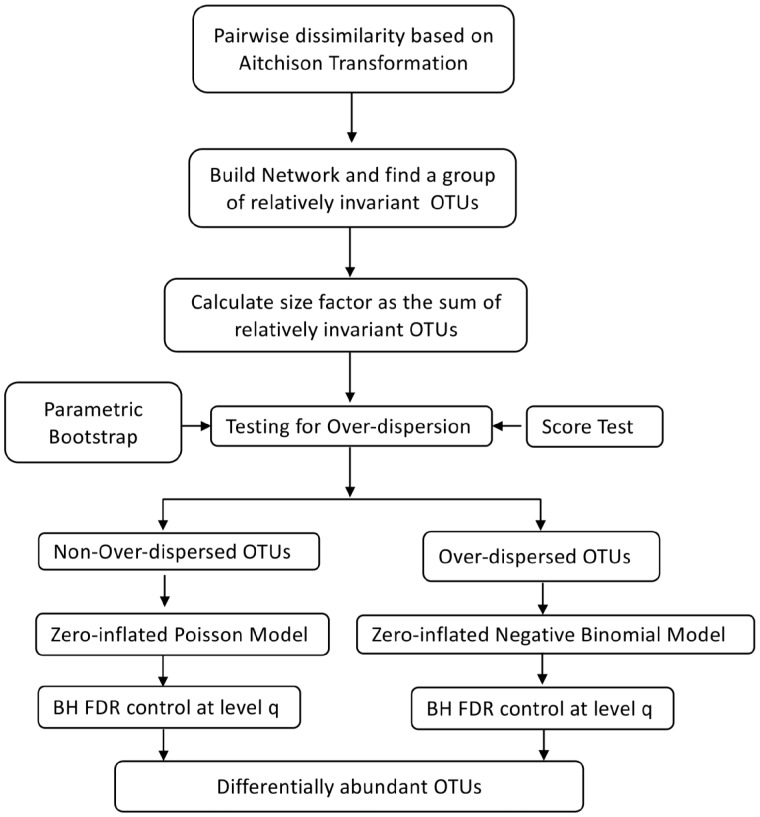
Figure 1 summaries the framework of our proposed method RioNorm2. The section is organized as follows. Section 2.1 gives detailed instruction on how to build taxa network for identifying riOTUs and use them to calculate size factors for normalization. Section 2.2 discusses the two-stage differential abundance test. Section 2.3 discusses the issues related to multiple testing correction.
Fig. 1.
Workflow of RioNorm2 (BH FDR represents BH FDR control procedure)
2.1 Normalization using riOTUs
Suppose the OTU count data are stored in a matrix C; the total number of OTUs is m and the total sample size is n. Let cij denote the observed raw count for OTU i from the jth sample, i = 1, 2,…, m, j = 1, 2,…, n and N0 denote the set of natural numbers {0, 1, 2,…}. To account for sampling biases, the first step is usually to normalize the count data of each sample with respect to some size factor Sj. Here, we use the total count normalization method as an example to illustrate the characteristics of such transformed data. Suppose . Then relative abundance of OTUs from sample j are calculated as . Due to the normalization, OTU abundance is no longer independent, which prohibits the application of standard statistical analysis techniques. Major contributions in the compositional data analysis were made by Aitchison in the 1980’s (Pawlowsky-Glahn et al., 2015). Instead of considering compositional data in the simplex, Aitchison proposed to use log-ratio for studying compositional data. Since = for two OTU i and , the effect of size factor Sj is canceled out in the log-ratio. Therefore, statistical inferences drawn from analysis of log-ratio of normalized count data are equivalent to the ones drawn from the raw count data.
Aitchison transformation connects two OTUs using log-ratio. Inspired by Aitchison transformation, we propose a new dissimilarity measurement between OTU i and OTU :
| (1) |
where ci and are the counts for OTU i and , respectively, represents the dissimilarity between OTU i and OTU with respect to their co-abundance pattern across samples and conditions. To avoid adding small number to zero counts, we only consider samples where both OTU i and OTU are none zeros when calculating Equation (1). When two OTUs are perfectly correlated, their ratio is constant, therefore , whereas the ratio of uncorrelated OTUs varies and the corresponding variance will be large. The proposed dissimilarity measurement is not only suitable for raw counts, but also applicable to pre-processed or scaling-based normalized microbiome data.
Based on Equation (1), we propose a data-driven algorithm to automatically find riOTUs for calculating size factors. We assume that most OTUs are not of differential abundance. To reduce the computation time, we only calculate the pairwise dissimilarity among top abundant OTUs. We recommend to keep OTUs observed in at least 80% of samples with average count larger than 5 (readers can also choose these values based on their application). Then the network of OTUs is constructed using hard threshold approach; there is an edge connecting two OTUs only when their dissimilarity is smaller than some threshold value h. By definition, dissimilarity between any two riOTUs should be small. Therefore, it is natural to model riOTUs as vertices of the largest clique in the network. However, there are two issues remained to be solved: (i) how to choose the optimal threshold value h and (ii) how to avoid finding a group of co-changed DA-OTUs across conditions and accidentally treat them as riOTUs. To automatically find h and to avoid the second issue, we will gradually increase h value within a range. For each h value, a network is constructed and the corresponding largest cliques will be detected. We want to exclude cliques that are formed only under large h values, and also exclude cliques that only show up under one h value and do not grow when h value increases. Therefore, the cliques are required to grow continuously from small h value to large h value. Let’s suppose h takes two values and OTUs are labeled using capital letters. The largest cliques under the smaller h value are {A, B, C}, {D, E, F} and {G, H, I}, when we increase h to the larger value, the corresponding largest cliques become {A, B, C, J}, {D, E, K, L} and {W, X, Y, Z}. In this case, only clique {A, B, C} has grown continuously to {A, B, C, J}; we would then have riOTUs to be {A, B, C, J}. We recommend possible h values to be in the range of the 0.01th to 0.1th quantile of dissimilarity distribution with 0.005 increment. If at certain h value, all current largest cliques do not include any largest clique calculated using previous smaller h value, riOTUs will be the largest clique calculated using previous h value. If cliques grow continuously from the smallest h value to largest h value, we will stop and use one of the largest cliques under the largest h value as riOTUs. Please see Figure 2 for the summary of the algorithm.
Fig. 2.
Network-based algorithm for identifying the riOTUs
After finding a group of riOTUs, the size factor for sample j is defined as:
| (2) |
where riOTUs is the group of riOTUs.
2.2 Two-stage differential abundance test
In the two-stage test, we first assume that all OTUs are not over-dispersed and fit ZIP regression model to all OTUs. The estimated parameters will be later used for testing over-dispersion. OTUs with over-dispersion will be refitted with ZINB models.
We model cij which is the count of OTU i from sample j using ZIP mixture model:
| (3) |
so that and , where πij represents the probability that a zero count is observed due to under-sampling and μij represents the mean of observed counts that are generated from Poisson distribution. The mean model for Poisson part is specified as:
| (4) |
where if sample j is from condition 1 and if sample j is from condition 2. Sj is the size factor defined in Equation (2). The parameter is an estimate of fold-change in OTU i’s mean abundance between two conditions. is the OTU-specific impact of the size factor on mean abundance level. The mean specification Equation (4) is very flexible with respect to incorporating relevant or confounding covariates. The probability of counts generated from spike 0 is assumed to be associated with sample library size and microbiome species (Paulson et al., 2013). Therefore, we model πij using the logit model:
| (5) |
The parameters can be estimated using EM algorithm combined with maximum likelihood estimation (See Supplementary File S1 Section S1 for details). The hypothesis for testing differential abundance is H0: = 0 versus H1: 0. If OTU i is differentially abundant between two conditions, we should reject H0. Here, normal approximation will be used to construct the raw P-value for each OTU i.
ZIP can incorporate the over-dispersion caused by zero inflation because E[cij] = μij(1 – πij) < Var(cij) = ) (1 + ) given . Therefore, it is suitable for OTUs whose abundance level within the same environment is stable and zero-inflation is the only source for over-dispersion. For OTUs, whose abundance varies within the same condition due to the biological replicate, the variation of counts tend to be greater than what a Poisson regression models. In this case, ZINB regression can be used to better incorporate the additional over-dispersion.
Correctly specifying the model is critical to increase power for detecting differential abundance, therefore, it is necessary to construct a test to rigorously check for over-dispersion. Here, we adopt the score test for determining the ZIP and ZINB models which is first proposed by Ridout et al. (2001). The test is operated on a per-OTU basis. Initially, we assume that none of the OTUs are over-dispersed and all OTUs are fitted using ZIP. Evidence against the null will be taken as the presence of over-dispersion and a ZINB will be used to fit over-dispersed OTUs.
ZINB is specified as follows:
| (6) |
so that and , where is the OTU-specific dispersion factor and we assume it is independent of other covariates. The mean and variance of ZINB are μij(1 – πij) and μij(1 – πij)(1 + + ). The distribution approaches to ZIP as 0. The mean specification and the logit model of πij are the same as in Equations (4) and (5). The hypothesis for testing over-dispersion is: H0: = 0 versus H1: . The score statistics is defined as S() = , where U() = is the score function of ZINB likelihood under null hypothesis and = is the information matrix evaluated at the maximum likelihood estimates under H0, where and are maximum likelihood estimates from Equations (4) and (5) under H0. Asymptotically, under H0, ∼ N(0,1). The one-sided test is appropriate for checking over-dispersion. Score test only requires to fit the model under H0, therefore, it avoids the fitting of more complex model. However, the asymptotic distribution of the score statistic approaches more slowly than that of the likelihood ratio statistic (Ridout et al., 2001). With small sample size, the significant levels based on score statistic may be misleading. Ridout et al. (2001) suggests that from a practical perspective, if a ZIP model is inappropriate at a weak level (say 10%), a ZINB model should be used to fit data. In addition to use a larger significance level (say 0.1) for score test, Jung et al. (2005) propose a parametric bootstrap method to solve the underestimation issue related to the normal approximation of score test statistic with small sample size. However, the bootstrap method usually requires heavy computation, we consider to apply it only when the number of OTUs being tested for differential abundance is relatively small.
After going through the over-dispersion test, OTUs will be divided into two groups. The group of OTUs without over-dispersion are fitted using ZIP model; the group of OTUs with over-dispersion will be fitted using ZINB. Parameters of ZINB can be estimated using BFGS algorithm. It is a quasi-Newton optimization method which only requires the first derivatives of log-likelihood function (See Supplementary File S1 Section S2 for details).
2.3 FDR control for multiple testing
Since microbiome data are usually high dimensional, even after filtering out OTUs with few observations, there are still hundreds of OTUs remained for differential abundance test. Without multiple correction of P-values, the Type I error will reach an unacceptable level. In order to control the false positive rate, we adopt the Benjamini–Hochberg (BH) procedure for multiple testing correction.
In our two-stage zero-inflated count regression model, since we use different distributions for the test with different underlying assumptions, pooling P-values together can be problematic. If one set of P-values contains a larger proportion of DA-OTUs, a combined FDR control may lack of statistical power. Auer and Doerge (2010) propose to use the BH control of the FDR separately at level q for different types of differential expression test in RNA-seq data. Here, we adopt the same procedure by applying BH FDR controlling procedure at q for each of the two sets of OTUs separately. See Supplementary File S1 Section S3 for justification of using separate multiple correction procedure.
3 Simulation
Large scale of simulation studies are conducted to compare the performance of RioNorm2 to that of DESeq, DESeq2, metagenomeSeq, RAIDA and Omnibus which all use relative log expression for normalization. Specifically, we focus on evaluating the impact of sample size, library size and effect size. We explore two simulation settings which are based on different distributions. The first one is adopted from the simulation setting B in McMurdie and Holmes (2014); the second is based on the Dirichlet–Multinomial distribution. We show the detailed simulation setup and results of the first simulation setting in the following subsections and leave the second simulation study based on the Dirichlet–Multinomial distribution to Supplementary File S1 Section S4. The simulation/evaluation codes are available on https://github.com/yuanjing-ma/RioNorm2_simulation.
3.1 Simulation setting
We adopt similar simulation setup as simulation setting B in McMurdie and Holmes (2014). To mimic OTU counts observed in the real world, we choose the real dataset ‘GlobalPattern’ in R package ‘phyloseq’ (McMurdie and Holmes, 2013) as our simulation template. ‘GlobalPattern’ dataset contains 26 samples collected from 9 different environments [feces, freshwater, freshwater (creek), mock, ocean, sediment (estuary), skin, soil and tongue] with more than 2 samples in each environment. We have three parameters: sample size per condition (25, 35 and 50), median library size (5000, 10000 and 50000) and effect size (2, 3, 4 and 5).
Firstly, OTU counts are summed across all samples of one environment in the ‘GlobalPattern’ dataset to derive a single ‘pseudo-population’ per environment. Then, we randomly pick a library size for each sample from 26 library sizes in the ‘GlobalPattern’ dataset with replacement. These library sizes are scaled to have the pre-determined median library size. Secondly, the OTU counts of each simulated sample are generated using a multinomial distribution with the OTU proportions obtained from the ‘pseudo-population’. Thirdly, to add artificial effect, the simulated samples of an OTU-table are divided into two equally-sized conditions, control and test and the effect size is multiplied to the count values of a randomly selected subset of OTUs in the test condition. Each of these perturbed OTUs is differentially abundant between two conditions. The above process for generating OTU tables will be repeated 10 times for each combination of the 3 parameters and 9 environments. Therefore, for each combination of sample size per condition, median library size and effect size, we will have 90 simulated OTU tables (10 times for each of the 9 environments) which can be used to calculate the mean and SD of evaluation metrics. Please refer to Supplementary File S1Figure S1 for a detailed diagram illustration.
3.2 Simulation results
Empirical FDR and power are used to evaluate the performance of different methods (Figs. 3 and 4). Each curve traces the mean FDR and power across all replicates and microbiome templates for various effect size (See Supplementary File S2 for the SD of FDR and power). RioNorm2 is the only approach that can control FDR under 5% across all simulation settings. RAIDA controls FDR in the most settings; other four approaches have severe FDR inflation that are near or higher than 20%. When the effect size is small, compared to other approaches, RioNorm2 constantly yields high detection power. When effect size increases, MetagenomeSeq, Omnibus, DESeq and DESeq2 all have inflated FDR. This is within our expectation since these four approaches capture the proportion change of non-DA-OTUs due to the abundance change of true DA-OTUs and tend to detect more false positives when total abundances of DA-OTUs across different conditions are large. RioNorm2 and RAIDA perform the best when the abundance change of DA-OTUs does not impact or suppress other OTUs’ abundance. They achieve high power at the same time controlling for FDR. RioNorm2 surpasses RAIDA under small effect sizes and library sizes. In general, RioNorm2 is the most robust and stable across all settings with different sample sizes, effect sizes and median library sizes. We also plot the AUC, sensitivity and specificity values, readers can refer to Supplementary File S1 Figures S2, S3 and S4 for more information. Since RioNorm2 contains two components: the network-based normalization and a two-stage differential abundance test, it is of interest to check whether the superiority of RioNorm2 is due to the two-stage test or better normalization (i.e. the size factors). Both RioNorm2 and RAIDA try to cast common size factors for the normalization. To compare the effects of normalization step of RAIDA and RioNorm2, we combine RAIDA size factors with the two-stage test of RioNorm2 to detect DA-OTUs. Supplementary Figure S5 (Supplementary File S1) shows that RAIDA’s size factors combined with the two-stage test yields a severe FDR inflation when effect size is small. However, RioNorm2 can successfully control FDR and yield comparable detection power across all simulation settings (Supplementary File S1Fig. S6).
Fig. 3.
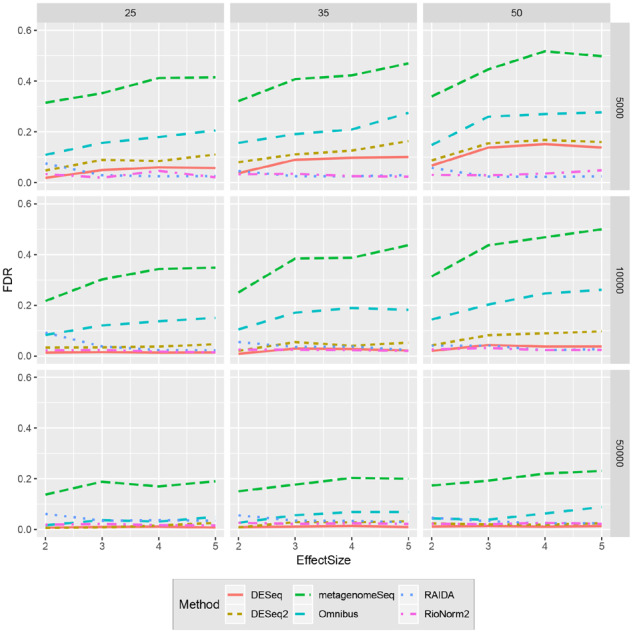
Comparisons of different methods in terms of FDR for various effect sizes. Panel rows represent the median library size, and panel columns represent the sample size per condition
In order to compare the performance of the two-stage test, we combine the RioNorm2 normalization with other differential abundance test methods such as ZIP, ZINB and t-test. To reduce the computation time, only a subset of data is used. FDR and power plots (Supplementary File S1 Figs. S7 and 8) show that ZIP-based tests cannot properly control FDR, since ZIP treats over-dispersion as differential abundance. Although t-test can control FDR, it has very low power even when DA-OTUs are easy to be detected (i.e. large effect size). In our simulation, most OTUs are over-dispersed which leads to the similar detection power of the two-stage test and ZINB. However, RioNorm2 has smaller FDR which gives the advantage of RioNorm2 for FDR control.
Besides the above mentioned five approaches, we also compare RioNorm2 to ANCOM (Mandal et al., 2015) which is becoming a standard method due to its implementation in Qiime2. Since the computation time of ANCOM is long (usually taking 20 min for an OTU table with around 1000 OTUs and 50 samples using MacBook Pro with 2.8 GHz intel Core i7), we only use a subset of simulated data. We tune the ANCOM hyper-parameter and choose the one that gives the best results. ANCOM has very low FDR value (close to 0), which trades off its ability to detect DA-OTUs. Compared to ANCOM, RioNorm2 has FDR rate close to 5% and gives high power across various effect sizes (Supplementary File S1 Figs. S9 and 10).
To summarize, in the simulation studies, we mimic the situation where some OTUs’ abundance level change in the test group without suppressing other OTUs’ abundance. This is a fairly common case in the real world. Our method works the best in the case that the absolute abundance (count) is of interest rather than the relative abundance (i.e. proportion).
3.3 Robustness of RioNorm2 with different h values for finding riOTUs
In simulation studies, in order to reduce the computation time, instead of using the iterative approach in Algorithm 1 to search for riOTUs, we fix h value as 0.03th quantile of dissimilarity distribution. To justify using the fixed h value in the simulation, we conduct the robustness analysis using a subsets of the simulated data and apply RioNorm2 with various h values from 0.02th quantile to 0.04th quantile at a 0.005 increment. FDR and power plots (Supplementary File S1 Figs. S11 and 12) show that RioNorm2 results are robust to different choices of h values. FDR are all controlled under 5% with similar powers for various level of effect sizes.
3.4 Impact of the different proportion of DA-OTUs
Figures 3 and 4 show the empirical FDR and power when the number of DA-OTUs is 30 in every simulated OTU table. We also explore the impact of different proportions of DA-OTUs on a subset of simulated data. We vary the proportion of DA-OTUs from 10% to 30% at an increment of 5%. We get similar results as shown in the Section 3.2 (Supplementary File S1 Figs. S13 and 14). RioNorm2 is the only approach that can properly control FDR at 5%. RAIDA has slightly FDR inflation when effect size is small. DESeq, DESeq2, Omnibus and MetagenomeSeq have severe FDR inflation as high as 40%. RioNorm2 is superior when the effect size is small with controlled FDR and higher detection power compared to RAIDA.
Fig. 4.
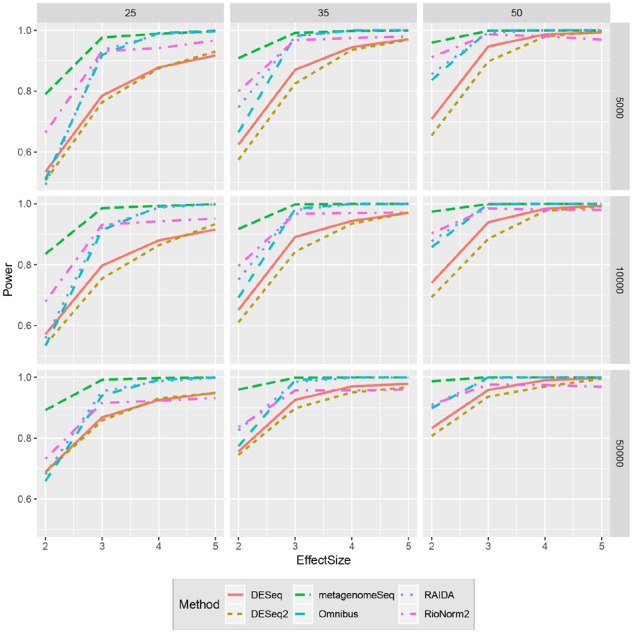
Comparisons of different methods in terms of power for various effect sizes. Panel rows represent the median library size, and panel columns represent the sample size per condition
4 Real data: metastatic melanoma cancer treatment
We apply RioNorm2 to the metastatic melanoma cancer treatment efficiency study (Matson et al., 2018). There are 10 385 OTUs and 42 samples. Among 42 patients, 16 of them have responded to the treatment while the other 26 are non-responders.
We rank OTUs reversely according to their sample counts, if a tie, based on their total count sums across samples and keep the top 1720 OTUs for differential abundance test. For finding riOTUs, we use OTUs that are observed in at least 80% of samples with average count greater than 5 to build the taxa network. Dissimilarity matrix is calculated based on Equation (1). Fourteen riOTUs are detected using Algorithm 1. We extract their taxonomy information which reflects the evolutionary relationships among various biological species (Supplementary File S1Fig. S24). It is remarkable that all 14 riOTUs share the same evolutionary paths from kingdom to genus level.
Of the 1720 OTUs that pass the filtering criterion, the score test finds that 642 OTUs are non-over-dispersed and 1078 OTUs are over-dispersed. We apply the BH control of FDR separately on ZIP and ZINB tests at level 0.05. After correction, 45 OTUs are detected to be differentially abundant; 18 of them are non-over-dispersed and 27 of them are over-dispersed. Among the 45 DA-OTUs detected by the RioNorm2 test, 29 belong to the phylum Firmicutes and 14 are taxa in the phylum Bacteroidetes (Supplementary File S1Fig. S25). The consistency of large number of Firmicutes and Bacteroidetes associations is remarkable. Besides, among these 45 OTUs, 20 OTUs are observed in at least 10 samples and 8 OTUs are observed in at least 20 samples. Box plots of top 9 abundant DA-OTUs are shown (Supplementary File S1Fig. S26). We also compare our results with those derived from the permutation test (Matson et al., 2018), RAIDA, Omnibus and DESeq2. Omnibus identifies 53 DA-OTUs while RAIDA detects 12 DA-OTUs and DESeq2 detects even fewer with 3 DA-OTUs. We record the common DA-OTUs shared by different approaches (Supplementary File S1 Section S5.1). The integration of Shotgun, 16S rRNA and PCR methods has verified Enterococcus to be more abundant in responders than non-responders (Matson et al., 2018). Enterococcus has been detected using all approaches except RAIDA, which indicates the low power of RAIDA in this real application. We run the above analysis in R using MacBook Pro with 2.8 GHz Intel Core i7 and 16 GB 2133 Mhz LPDDR3. The elapsed time for RioNorm2, RAIDA, DESeq2 and Omnibus are 5.58, 0.856, 0.101 and 0.395 min, respectively.
We also apply the RioNorm2 on another public dataset of inflammatory bowel disease which can be downloaded from Qiita with study ID 11336. We compare the RioNorm2 with other approaches such as RAIDA, Omnibus and DEseq2. Interested readers can refer to the Supplementary File S1 Section S5.2.
5 Discussion
We develop a novel framework for normalizing sparse high-dimensional marker gene microbiome data and performing differential abundance analysis. RioNorm2 relies on taxa networks to find a group of riOTUs and use the sum of their counts to construct size factors for the purpose of normalization. Since RioNorm2 does not make the assumption that counts are equivalent up to a certain quantile, it can reduce the bias by avoiding the inclusion of DA-OTUs for the construction of size factor. Another contribution of the paper is to propose a two-stage differential abundance test that takes into consideration of under-sampling and over-dispersion with flexibility. Microbiome species are divided into two different groups after over-dispersion tests and each group of OTUs are modeled separately with suitable models. Besides, by separately modeling OTUs with and without over-dispersion by a two-stage model, we largely increase the power of detecting DA-OTUs.
Simulation studies show that the performance of RioNorm2 is consistently satisfactory with controlled FDR and high power compared to other popular methods. RioNorm2’s performance is robust and comparable in all simulated settings with different levels of effect size, median library size and sample size. Since RioNorm2 contains two components: the network-based normalization and a two-stage test, we check the contribution of each component separately. Simulation results show that both components contribute to the superiority of RioNorm2. In the situation where some OTUs’ abundance level change without suppressing other OTUs’ abundance, RioNorm2, RAIDA and ANCOM are suitable. Compared to RioNorm2 and RAIDA, ANCOM has very low FDR (close to 0) which sacrifices its ability to detect DA-OTUs. When effect size is small, RioNorm2 has higher power with controlled FDR compared to RAIDA; otherwise, they have comparable performance. If the absolute abundance (count) is of interest rather than the relative abundance (i.e. proportion), it is unsuitable to use DESeq, DESeq2, omnibus and metagenomeSeq which tend to detect more false positives when the effect size increases. From the practical aspects, researchers want to avoid detecting false positives. Statistically testing differential abundance always serves as the upstream analysis; the declared positives will be further tested in the medical or biologic experiments. Therefore, including false positives will cause a large waste in the downstream experimenting analysis. In summary, our method works the best in the case that the absolute abundance (count) is of interest rather than the relative abundance (i.e. proportion).
In this article, we evaluate the performance of differential abundance analysis in the setting with two conditions. However, RioNorm2 can be easily extended to multiple conditions setting by modifying the mean specification model. Besides, the model is flexible to incorporate other covariates. For the future research, we will focus on incorporating the taxonomy information into the differential abundant analysis. Since there are biologically hierarchical structures in bacterial species, we believe that by sharing information among species with the same origin, the performance of differential abundance test can be further improved.
Supplementary Material
Acknowledgements
This research was supported through the computational resources at Northwestern University which is jointly supported by Northwestern University Information Technology.
Funding
This work was supported by National Science Foundation [DMS-1222592 to H.J.] and National Institutes of Health [R21LM012618 to Y.L].
Conflict of Interest: none declared.
References
- Anders S., Huber W. (2010) Differential expression analysis for sequence count data. Genome Biol., 11, R106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auer P.L., Doerge R.W. (2010) Statistical design and analysis of RNA sequencing data. Genetics, 185, 405–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullard J.H. et al. (2010) Evaluation of statistical methods for normalization and differential expression in mRNA-Seq experiments. Bioinformatics, 11, 94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J. et al. (2018) An omnibus test for differential distribution analysis of microbiome sequencing data. Bioinformatics, 34, 643–651. [DOI] [PubMed] [Google Scholar]
- Dethlefsen L. et al. (2008) The pervasive effects of an antibiotic on the human gut microbiota, as revealed by deep 16S rRNA sequencing. PLoS Biol., 6, e280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris J.K., Wagner B.D. (2012) Bacterial identification and analytic challenges in clinical microbiome studies. J. Allergy Clin. Immunol., 129, 441–442. [DOI] [PubMed] [Google Scholar]
- Jung B.C. et al. (2005) Bootstrap tests for overdispersion in a zero-inflated Poisson regression model. Biometrics, 61, 626–628. [DOI] [PubMed] [Google Scholar]
- Kåhrström C.T. (2012) Microbiome: gut microbiome as a marker for diabetes. Nat. Rev. Microbiol., 10, 733. [Google Scholar]
- Larsen N. et al. (2010) Gut microbiota in human adults with type 2 diabetes differs from non-diabetic adults. PLoS One, 5, e9085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Love M.I. et al. (2014) Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol., 15, 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandal S. et al. (2015) Analysis of composition of microbiomes: a novel method for studying microbial composition. Microb. Ecol. Health Dis., 26, 27663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matson V. et al. (2018) The commensal microbiome is associated with anti–PD-1 efficacy in metastatic melanoma patients. Science, 359, 104–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMurdie P.J., Holmes S. (2013) phyloseq: an R package for reproducible interactive analysis and graphics of microbiome census data. PLoS One, 8, e61217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMurdie P.J., Holmes S. (2014) Waste not, want not: why rarefying microbiome data is inadmissible. PLoS Comput. Biol., 10, e1003531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan X.C. et al. (2012) Dysfunction of the intestinal microbiome in inflammatory bowel disease and treatment. Genome Biol., 13, R79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nayfach S., Pollard K.S. (2016) Toward accurate and quantitative comparative metagenomics. Cell, 166, 1103–1116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paulson J.N. et al. (2013) Differential abundance analysis for microbial marker-gene surveys. Nat. Methods, 10, 1200–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pawlowsky-Glahn V. et al. (2015) Modeling and Analysis of Compositional Data. Wiley, Chichester, West Sussex. [Google Scholar]
- Ravel J. et al. (2011) Vaginal microbiome of reproductive-age women. Proc. Natl. Acad. Sci., 108, 4680–4687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridout M. et al. (2001) A score test for testing a zero inflated Poisson regression model against zero inflated negative binomial alternatives. Biometrics, 57, 219–223. [DOI] [PubMed] [Google Scholar]
- Robinson M.D., Oshlack A. (2010) A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol., 11, R25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah N. et al. (2011) Comparing bacterial communities inferred from 16S rRNA gene sequencing and shotgun metagenomics. Biocomputing, 165–176. [DOI] [PubMed] [Google Scholar]
- Smyth G.K. (2005) Limma: linear models for microarray data. In: Carey,V. et al. (eds.) Solutions using R and Bioconductor Bioinformatics and Computational Biology. Statistics for Biology and Health, Citeseer, pp. 397–420. [Google Scholar]
- Sohn M.B. et al. (2015) A robust approach for identifying differentially abundant features in metagenomic samples. Bioinformatics, 31, 2269–2275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turnbaugh P.J. et al. (2009) A core gut microbiome in obese and lean twins. Nature, 457, 480–484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venter J.C. et al. (2004) Environmental genome shotgun sequencing of the Sargasso Sea. Science, 304, 66–74. [DOI] [PubMed] [Google Scholar]
- White J.R. et al. (2009) Statistical methods for detecting differentially abundant features in clinical metagenomic samples. PLoS Comput. Biol., 5, e1000352. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.