Population-Specific Recombination Maps from Segments of Identity by Descent

Abstract

Recombination rates vary significantly across the genome, and estimates of recombination rates are needed for downstream analyses such as haplotype phasing and genotype imputation. Existing methods for recombination rate estimation are limited by insufficient amounts of informative genetic data or by high computational cost. We present a method and software, called IBDrecomb, for using segments of identity by descent to infer recombination rates. IBDrecomb can be applied to sequenced population cohorts to obtain high-resolution, population-specific recombination maps. In simulated admixed data, IBDrecomb obtains higher accuracy than admixture-based estimation of recombination rates. When applied to 2,500 simulated individuals, IBDrecomb obtains similar accuracy to a linkage-disequilibrium (LD)-based method applied to 96 individuals (the largest number for which computation is tractable). Compared to LD-based maps, our IBD-based maps have the advantage of estimating recombination rates in the recent past rather than the distant past. We used IBDrecomb to generate new recombination maps for European Americans and for African Americans from TOPMed sequence data from the Framingham Heart Study (1,626 unrelated individuals) and the Jackson Heart Study (2,046 unrelated individuals), and we compare them to LD-based, admixture-based, and family-based maps.

Introduction

Crossover recombination of chromosomes is essential for proper chromosome disjunction during meiosis. Recombination rates vary across the genome, tending to increase with decreasing chromosome length,¹ increase near the telomeres, particularly in males,² increase in regions with high GC content,² and increase in hotspots,³ many of which are associated with the PRDM9 motif.⁴ Recombination rates differ significantly between female and male meioses,¹ although sex-averaged maps are suitable for many analyses that involve historical recombination, including estimation of demographic history,^5,6 estimation of mutation rates,^{7, 8, 9} estimation of haplotype phase,^{10, 11, 12} genotype imputation,^13,14 and inference of local ancestry in admixed genomes.^{15, 16, 17} Recombination rates also differ by age^2,18 and by individual.^18,19

There are four primary existing approaches to recombination rate estimation. The first is analysis of family data.^2,18,20,21 In order to estimate recombination rates at high resolution, extremely large numbers of meioses are required. One of the largest sources of such meioses is the deCODE Icelandic data.² Advantages of the family-based approach are that it can estimate sex-specific rates and that it allows investigation of individual-specific factors influencing recombination rates.^2,18 A disadvantage is that the large family databases required by this approach are rare, so population-specific rates are not available for most populations.

A second approach is sperm typing, with recombination events identified by comparing haplotypes between sperm cells obtained from the same individual. This approach can be used to locate recombination hotspots^22,23 and construct individual genome-wide recombination maps in males.^24,25

A third approach uses admixed genomes such as those from African Americans.^26,27 The local ancestry (i.e., continental origin of the genetic material at each point in the genome) is inferred, and positions of change in local ancestry are positions at which post-admixture recombination has occurred. This approach can use data from unrelated individuals, and each individual provides information from multiple meioses. One limitation of this approach is that it is only applicable to admixed populations. A second limitation is that it utilizes only post-admixture meioses, which for recently admixed populations such as African Americans is around ten meioses per individual, reducing resolution of the inferred maps unless sample sizes are very large. A third limitation is that it relies on local ancestry calls which can be inaccurate in some cases.^28,29

A final approach uses population samples to infer average past rates of recombination all the way back to the common ancestors of the samples. Some such methods are based on the coalescent with recombination or an approximation to it and fit the model to the full genotype data.^{30, 31, 32, 33, 34} Other methods are based on summary statistics that capture aspects of linkage disequilibrium (LD) between loci. Some of the LD-based summary statistic methods apply population genetic modeling and likelihood-based inference,^{35, 36, 37, 38, 39, 40} while others are based on population genetic simulations and machine learning.^41,42 An advantage of this class of methods is that the results are based on very large numbers of meioses, reaching far back into the past. However, if recombination rates have changed over time, the estimates will be averages across time rather than reflecting current rates, which may be a disadvantage for applications such as local ancestry inference that are based on recombination in recent generations. Estimation with many of these methods is computationally challenging, and results can be biased when the demographic model used for analysis or simulation is incorrect.^39,40

We present a new approach based on estimated segments of identity by descent (IBD) in population samples. The endpoints of IBD segments are points at which past recombination has occurred. Since the IBD segments result from shared ancestry in the past 100 or so generations, the estimates of recombination rates reflect recent rates while incorporating information from a large number of meioses. Our approach is computationally efficient so that it can be applied to samples of thousands of individuals, resulting in highly precise estimates. When applied to samples from distinct populations, our approach provides population-specific sex-averaged rates of recombination.

Material and Methods

Method Overview

IBD segment endpoints are positions of past recombination events. The density of endpoints of IBD segments originating from common ancestors more recent than a reference time point is thus proportional to the recombination rate. We use this relationship to estimate relative recombination rates based on the endpoints of IBD segments.

There are two main challenges that must be addressed: inaccurate estimation of IBD endpoints and the unknown time to the most recent common ancestor. Because of genotype error and phasing error, IBD segment endpoints can be incorrectly determined. In our method, we apply a gap-filling strategy to address inaccurate IBD endpoints. When two or more IBD segments from the same pair of individuals are separated by only a small gap, and the gap contains very few (at most one for the analyses presented here) discordant homozygous genotypes, we merge the segments into a single segment.⁴³ This strategy is very efficient at removing incorrect IBD endpoints, even in the presence of significant genotype error (see simulation results below) and recent gene conversion.⁹

A naive algorithm for IBD-based recombination rate estimation would simply count the ends of all reported IBD segments in an interval. However, when we detect an IBD segment, we don’t generally know the number of generations to the most recent common ancestor. In some regions we may detect IBD segments due to more distant ancestry, leading to higher rates of detected IBD segments, and thus higher estimated recombination rates in those regions. If the lengths in centimorgans (cM) of the segments were known, we could filter the IBD segments by length, as a proxy for age, and thus obtain uniform rates of detected segments across the genome. But when the true recombination map is unknown, the cM lengths of the segments cannot be used as a filtering criterion. In the next paragraph we describe our approach which avoids this problem.

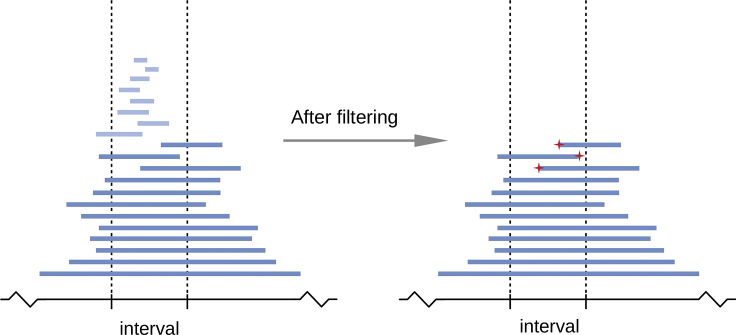
Our ideal data would include all IBD segments with cM length greater than some threshold. In such data, the distribution of ages of segments would be the same (except for sampling variation) at each point in the genome, and hence the rate of IBD endpoints along the genome would be equal in terms of cM distance and would thus allow estimation of recombination rates. Since we cannot obtain such data without knowing the recombination map, we use an iterative approach. Given the current estimate of recombination rates across the chromosome (the initial estimate has a constant rate of recombination per basepair), we obtain estimated cM lengths of all IBD segments. We then selectively remove shorter segments in regions with higher rates of IBD segments until IBD coverage across the chromosome is approximately equal. To achieve this coverage equalization, we first divide the chromosome into intervals of equal physical length and place within each interval the IBD segments that cover all or part of the interval. We determine the smallest number of IBD segments in any interval, and we remove the shortest (in estimated cM length) IBD segments from each interval to reduce the number of segments in the interval to that smallest number. After this procedure, each interval contains the same number of IBD segments (Figure 1). After the coverage equalization, we count the remaining IBD endpoints within each interval to estimate the relative recombination rate for the interval. We repeat the procedure using the updated estimates of recombination rate. We find that 20 iterations suffice for accurate estimation.

Figure 1.

An Illustration of the Procedure for Enumerating IBD Endpoints for Recombination Rate Estimation

In each iteration, IBD segments with short estimated cM length are filtered out to achieve the required level of IBD coverage in the target interval, which is delineated with vertical dashed lines. In this example, segments in light blue are filtered out and the three remaining IBD endpoints falling within the interval (marked by red stars) are counted as recombination events corresponding to this interval.

Counting IBD Ends to Estimate Recombination Rates

The IBD coverage of an interval (a genomic region of specified physical length) is the number of IBD segments covering the interval. IBD segments that partially cover the interval contribute a fractional value to the coverage equal to the proportion of the interval covered. The coverage is calculated for each interval, and the minimal value is determined. Then, in each interval, the segments with shortest cM length are removed until removing an additional segment from the interval would reduce the coverage below this minimal level. An IBD segment may be removed from one interval but retained in another.

We use a constant recombination rate (1 cM/Mb) to initiate the iterative estimation procedure. In each iteration, we re-estimate the cM lengths of the IBD segments using the current recombination map, and we re-apply the coverage threshold. We then update the recombination rates for each interval based on the number of IBD endpoints located in the interval:

$$R_i=\frac{X_i}{\sum X_j}\frac{L}{B}$$ (Equation 1)

For the i^th interval, R_i is the estimated recombination rate and X_i is the number of IBD segment endpoints in the interval (thus $\sum X_j$ is the number of IBD segment endpoints across all intervals). L is the cM length of the chromosome, and B is the physical length of the interval (which is the same for each interval). The cM length of the chromosome is obtained from an external source such as a family-based recombination map.

In order to improve convergence, we use the average of the two previous estimates as the input recombination map to the next iteration (starting with the third iteration).

Estimation at Chromosome Ends

We need to treat the ends of the chromosome differently, because IBD segments cannot continue beyond the end of the chromosome. Thus, IBD segments starting or ending at a chromosome end are shorter on average, and fewer of these IBD segments will be detected. This results in a lack of right ends of IBD segments in intervals near the left end of the chromosome, and of left ends of IBD segments near the right end of the chromosome.

When estimating the recombination rate in an interval near the chromosome end, we make several changes to the algorithm described above. In order to describe these changes, we define chromosome end regions and their neighboring adjunct regions (Figure 2). The end region starts at the chromosome end and has cM length equal to the median cM length of all IBD segments that extend to that chromosome end, plus any additional length required in order to have the end of this region correspond to a breakpoint between intervals (the cM lengths are obtained from the current estimate of the recombination map). The remaining region between the two ending regions is the mid region. The adjunct region corresponding to an end region immediately follows the end region (on the side toward the middle of the chromosome) and has the same physical length as the end region. During this procedure, we are not estimating the recombination rates of the intervals in the adjunct region. Rates in this region are estimated using the unmodified procedure described earlier. In what follows, we describe the changes to the algorithm with respect to the left end of the chromosome; the right end is analogous.

Figure 2.

Chromosome Regions for Recombination Rate Estimation

The end region has cM length equal to the median cM length of IBD segments that extend to the chromosome end, plus any additional length required to extend the end of the region to an interval boundary. The adjunct region is next to the end region and has the same basepair length as the end region.

The first change is that we count only the left ends of the IBD segments, rather than both endpoints of the IBD segments. This is because there will be a relative lack of right ends of IBD segments near the left chromosome end because many IBD segments that are censored by the left chromosome end will not be detected. In contrast, there will be no reduction in left ends of IBD segments close to the end of the chromosome.

The second change is that we need to modify the application of the IBD coverage threshold so that it has equal effect in all intervals in the end region, regardless of how close they are to the chromosome end. The left chromosome end left-censors the IBD segments that reach that chromosome end, so the visible lengths of the segments are shorter than they would otherwise be. For intervals other than the leftmost one, we can mimic this censoring by removing those parts of IBD segments that fall beyond the left boundary of the interval. This trimming reduces the lengths of the IBD segments and is performed only with respect to a given interval. The part of an IBD segment that is trimmed off when calculating segment lengths for one interval may be retained when calculating lengths for another interval. Thus, for each interval, not only for the leftmost interval, the IBD segments that intersect the interval are left-censored by the left side of the interval. These adjusted IBD lengths are used when excluding the shortest IBD segments to equalize IBD coverage in each interval.

Recombination rates calculated with our method are relative. We use a user-specified total chromosome cM length to normalize them. Since the estimation procedure for the end region and the mid region differ, we must put the two sets of results on the same scale. We do this by applying the end-region procedure for censoring IBD segments and equalizing IBD segment coverage to the adjunct region. Since we also have IBD end counts from the mid-region procedure for the adjunct region, we normalize the results from IBD endpoint counts for the end region by multiplying by the ratio of the IBD end counts in the adjunct region obtained from the mid-region and end-region methods.

Thus, for intervals in the end region, we obtain an estimate of what the two-sided end count would be if the interval was not affected by the chromosome end censoring:

$${\hat{X}}_i^E=Y_i^E\frac{\sum X_j^A}{\sum Y_j^A}$$

where $Y_i^E$ is the left-sided IBD end count for interval $i$ in the left end-region; $\sum Y_j^A$ is the total count of left-sided IBD ends for intervals in the adjunct region, applying the end-region algorithm described in this section; and $\sum X_j^A$ is the total count of IBD ends (left and right) for intervals in the adjunct region, based on the original (mid-region) algorithm. The value ${\hat{X}}_i^E$ is the adjusted end count for interval $i$ in the end-region; this is used in place of $X_i$ in the recombination rate estimation formula (Equation 1).

Fine-Scale Estimation

We have proposed a procedure for estimating recombination rates from IBD endpoints in the previous two sections. This procedure works well when the number of detected IBD segments is large due to a large sample size and the interval size is large. However, when the interval size decreases for fine-scale estimation, the coverage threshold tends to decrease, resulting in loss of information at small sample sizes. We thus improve fine-scale estimation by running our algorithm in two steps. First, we construct a recombination map at a large scale, for example with an interval size of 500 kb. We obtain estimates of cM length for each large interval, and we fix these large-scale lengths in the second step. In the second step, we divide each large interval into many smaller sub-intervals at the desired scale. For example, if results at a 10 kb scale are desired, sub-intervals of length 10 kb are used. The estimation procedure for these short intervals is slightly modified from the algorithm described above.

For the fine-scale estimation, the IBD coverage threshold is based on the minimal coverage of the sub-intervals within a large interval, rather than on the minimal coverage of intervals across the whole chromosome. The local coverage threshold tends to be larger than the global threshold used in the large-scale estimation because there is typically less variability in recombination rate across an interval than across a whole chromosome.

After the large-scale estimation, the lengths of the large intervals in the end region are known and it is no longer necessary to use an adjunct region to normalize lengths in the end region. However, we do still need to use only the one-sided IBD end counts and to censor the IBD segments intersecting each interval when applying the IBD coverage threshold in the end region. As in the large-scale step, we adjust the cM lengths by trimming off that part of the IBD segment that extends beyond the sub-interval in the direction of the nearby chromosome end.

Within each large interval (whether within an end region or not), we estimate the recombination rates of the sub-intervals using the formula in Equation 1, using the previously calculated cM length of the large interval as the region length L. For intervals that are not in the end regions, we use two-sided IBD end counts for the X_i, while for intervals within the two end regions, we replace these with the one-sided IBD end counts.

We have implemented this two-step procedure in the IBDrecomb program, and the fine-scale estimation step is automatically applied when the fine interval size parameter (for the second stage of estimation) is set to a value that is smaller than the large interval size parameter (for the first stage of estimation; 500 kb by default). For all the results presented in this paper, 500 kb was used as the interval size for the first stage of estimation, and we ran multiple analyses with different second stage interval sizes. In each case, the results shown for a given scale (e.g., 1 kb) correspond to analyses run with that interval size at the second stage.

Data Processing

We used a coalescent-based simulator, msprime,⁴⁴ to simulate genetic data under different scenarios. We set the mutation rate to 10⁻⁸ per basepair per generation in all simulations, except as otherwise noted. We removed the phase information from the simulated haplotypes and added genotype error. Given a genotype error rate ε, and considering each genotype in turn, we added an error to the genotype with probability ε. When adding an error to a genotype, we selected one of the genotype’s two alleles at random and changed that allele to its alternative form (all simulated markers are bi-allelic). Then we filtered sites to keep those with minor allele frequency larger than 5% and phased the data with Beagle 5.0^10,14 (v.04Jun18.a80).

We applied our method to TOPMed whole-genome sequence data from the Framingham Heart Study (FHS, downloaded from dbGaP, phs000974.v2.p2) and the Jackson Heart Study (JHS, downloaded from dbGaP, phs000964.v2.p1). The individuals in the FHS data are European Americans, while the individuals in the JHS data are African Americans. To control genotype error, we only used bi-allelic SNPs passing all quality filters and with minor allele frequency larger than 5%. We used Beagle 5.0^10,14 (v.04Jun18.a80) to infer haplotype phase for each dataset. We then used King v2.2.2^45,46 to select unrelated individuals separated by more than two degrees of relatedness. After filtering, we have 1,626 unrelated individuals in the FHS data and 2,046 unrelated individuals in the JHS data. The purpose of removing relatives is to improve computational efficiency. Accuracy is unchanged when relatives are included (data not shown).

We also applied our method to data from the UK Biobank (dataset accession: EGAD00010001497). We excluded 958 outliers identified by the UK Biobank and 9 samples that showed third degree or closer relationship with more than 200 individuals (indicating possible sample contamination). We also excluded the parents from 850 parent-offspring trios.⁴⁷ We estimated haplotype phase using Beagle 5.0 and randomly sampled 5,000 individuals for the IBD analysis and map estimation.

When phasing haplotypes, detecting IBD segments, and gap-filling IBD segments, we used a 1 cM/Mb recombination rate. The IBD segments for our method were obtained by applying Refined IBD⁴⁸ (LOD threshold = 1, minimum length 300 kb) with gap-filling (maximum gap distance = 500 kb, maximum number of discordant sites = 1). The thresholds (LOD 1 and minimum length 300 kb) used in Refined IBD are quite low. However, in conjunction with the gap-fill step they allow the procedure to find as much IBD as possible, some of which will have a large cM length and hence pass the subsequent filtering for IBD coverage (see the next section). The low thresholds used with Refined IBD will result in some short reported IBD segments that are actually the conflation of several shorter IBD segments.⁴⁹ However, for the purpose of estimating the recombination map, the benefit of the increased number of IBD segments is greater than the additional noise due to some IBD segment conflation. Use of a larger minimum physical length for IBD segments results in loss of accuracy (Figure S1).

The estimated recombination maps are normalized by the cM length of each chromosome from the deCODE map, or by the true total cM length for the simulated data. For comparison with our maps, we lifted over the AA map²⁶ and the AfAdm map²⁷ from build 36 to build 37 and the deCODE map from build 38 to build 37 using the following strategy. First we converted the target map to the bed interval and rate format, as “chr#:from-to rate.” Then we lifted over using the UCSC online tool (Web Resources), outputting the interval positions in bed format. We removed intervals that failed to be converted or for which the interval length changed by more than 1%. In total, 133.7 Mb was removed from the deCODE map, 139.6 Mb was removed from the AA map, and 283.8 Mb was removed from AfAdm map. Finally, we mapped the recombination rates from each original map to the remaining intervals in build 37. The intervals that were removed from one or more maps were ignored when computing the correlation coefficients between any pair of maps.

Results

Validation by Simulations

To evaluate whether our method produces unbiased estimates of recombination rate, we simulated data using a podium-like recombination map and we simulated data using the first 20 Mb region of chromosome 1 from the HapMap II combined map (Figure S2). We added genotype error to the simulated data (Material and Methods). When the genotype error rate is low (0.01%), the average across 100 replicates of the estimated recombination rate closely matches the true recombination rate; at higher error rates (0.1%–0.5%), the estimates have some bias. With high-quality sequence data, the genotype error rate for SNPs passing quality control filters is around 0.02%,⁵⁰ so in such data our method’s estimates are expected to be approximately unbiased.

Although our method accounts for censoring of IBD segments at the ends of chromosomes and provides accurate estimates of recombination rates at the chromosome ends when the genotype error rate is very low, the estimates of recombination rates are inflated at the chromosome ends when the genotype error rate is high. This is because the gap-filling step to fix breaks in IBD segments resulting from genotype errors is less effective near the chromosome ends. In our tests, the regions with inflated recombination rates at the ends of the chromosomes are generally shorter than 1 Mb when the genotype error is ≤0.1%. We recommend that normalization of relative recombination rates using an external map be calculated using the central portion of the chromosome, excluding 1 Mb on each end. For maps estimated using high-quality data, we don’t recommend removing the end regions since the amount of inflation is low.

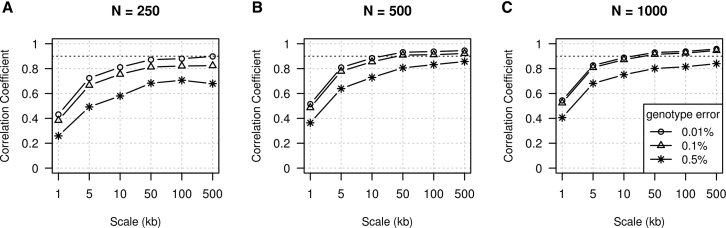
We simulated additional data to evaluate the impact of sample size and resolution on the precision of our method. The resolution, which we refer to as “scale,” is the size of the intervals in which recombination rate is estimated. For example, with a 10 kb scale, the recombination rate is estimated in intervals of size 10 kb, and the resulting map has cM positions at grid points that are 10 kb apart. We simulated 250 individuals, 500 individuals, and 1,000 individuals under a Wright-Fisher model with constant effective population size (Ne = 10,000). The recombination map used for this simulation is the Hapmap II combined LD map on chromosome 1:10 Mb–110 Mb.⁵¹ Pearson correlation coefficients between the estimated rates and the true rates across intervals increase for larger interval sizes and larger sample sizes (Figure 3). For the largest sample size, we obtain correlation coefficients over 0.9 for resolutions of 10 kb or greater and genotype error rates ≤0.1%. With smaller sample sizes, we obtain correlation coefficients over 0.9 for resolutions of 50 kb or greater and genotype error rates ≤0.1%.

Figure 3.

Recombination Rate Estimation Accuracy with Different Sample Sizes

100 Mb of data were simulated using the HapMap II combined LD map and a constant effective population size of 10,000. Sample sizes were 250 (A), 500 (B), or 1,000 (C). Genotype errors were added at three different rates. The x axis gives the estimation scale (size of intervals in which recombination rates are estimated and for which correlation coefficients are calculated). The y axis gives the Pearson correlation coefficient between the estimated and true recombination rates. The black dashed line shows a correlation coefficient of 0.9 for reference.

Comparison with Admixture-Based Recombination Rate Estimation

We simulated genotype data from an admixed African American demographic model in order to compare our IBD-based approach with RASPberry,²⁷ an admixture-based approach, and with LDhat,³⁷ an LD-based approach. In this simulation, we used demographic parameters for the reference populations from previous work,⁴³ based on a published model inferred from 1000 Genomes Project data.⁵² Then, we created an admixed population with 80% ancestry from the simulated African population and 20% from the simulated European population. The admixture occurred 6 generations before present and the admixed population grew at a rate of 5% per generation from an initial size of 30,000. We simulated 2,500 admixed individuals and 100 individuals from each reference population (representing European ancestry and African ancestry). RASPberry uses the reference individuals to call local ancestry in the admixed individuals. Because RASPberry is computationally intensive, we simulated a 20 Mb region rather than 100 Mb. The recombination map in the simulation is the HapMap II combined LD map, chr1:10 Mb–30 Mb.⁵¹ We added genotype errors to the admixed and reference individuals, removed variants with minor allele frequency < 5%, and phased the data with Beagle 5.0 (Material and Methods) before running the analyses. Our IBD-based method and LDhat were applied to the admixed data only, without the unadmixed reference individuals. The purpose of removing low-frequency variants was to reduce computing times. In previous analysis RASPberry was applied to SNP array data,²⁷ while the 1000 Genomes LDhat maps (see Web Resources) were estimated using data from an Illumina Omni SNP array rather than using the low coverage sequence data. Thus, the inclusion of low-frequency variants is not necessary for the successful application of these methods.

RASPberry uses the HapMix algorithm for ancestry inference, which analyzes each admixed individual independently and allows for parallelized computation over admixed individuals.^16,27 To reduce RASPberry’s wallclock compute time, we divided the 2,500 admixed individuals into 250 sets of 10 individuals. We analyzed the data using a compute server with two 6-core Intel Xeon E5-2630 2.6 GHz processors and 128 GB memory running CentOS Linux. RASPberry required 20.1 cpu h on average to estimate the ancestry switches for each set of 10 individuals, and hence required a total of more than 5,000 cpu h. For comparison, our method required 11.1 cpu h (1.0 h of wall clock time, multi-threaded) to call the IBD segments, fill IBD gaps, and estimate the recombination map for the whole set of 2,500 admixed individuals.

We analyzed data from 96 simulated individuals with LDhat, which is the largest number of individuals for which a pre-computed likelihood lookup table is available. Generation of new lookup tables is very computationally expensive, especially for larger sample sizes. We ran the interval³⁷ method with a block penalty of 5 and ran the method for 22.5 million iterations with a sample being taken from the MCMC chain every 15,000 iterations. The first 7.5 million iterations were discarded as burn-in. These are the same parameters that were used in the 1000 Genomes LDhat analysis (see the README file with the 1000 Genomes recombination maps; Web Resources). The computing time for this analysis was 70 min.

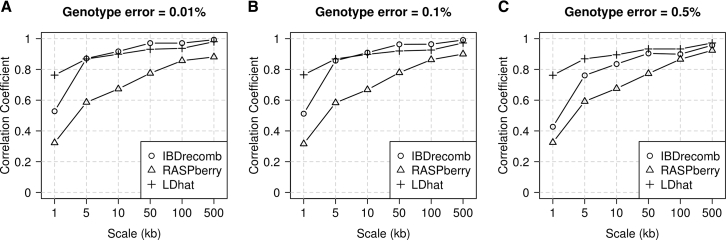
In assessing the accuracy of the estimates, we trimmed 5 Mb from each end of the simulated region (Figure 4) before computing the Pearson correlation coefficient between the estimated and true recombination rates, because accuracy is reduced near chromosome ends (results without this trim are shown in Figure S3). Estimates from our IBD-based method (IBDrecomb) have much higher correlation than RASPberry with the true recombination rates at all scales, and slightly higher correlation than LDhat with the true rates within the trimmed region at scales above 5 kb for genotype error rates of 0.01% and 0.1% and an end trim of at least 1 Mb (Figure S3). For example, with the 5 Mb trim of the ends of the region, at a 10 kb scale with 0.01% error, our method’s estimates have a correlation coefficient of 0.92, LDhat’s estimates have a correlation coefficient of 0.90, and RASPberry’s estimates have a correlation coefficient of 0.67. RASPberry’s accuracy may be lower since it can only use recombination events that occurred after admixture. When not applying any trim (Figure S3), IBDrecomb is less accurate than LDhat, indicating that LDhat has superior performance at the ends of the analyzed region due to errors in estimating IBD endpoints at the ends of the chromosome. However, results for IBDrecomb with a 1 Mb trim are indistinguishable from those with a 5 Mb trim, indicating that a 1 Mb trim is sufficient. For RASPberry, in contrast, results with a 1 Mb trim are inferior to those with a 5 Mb trim.

Figure 4.

Comparing Recombination Rate Estimation Accuracy across Methods

The results are based on simulated data from an admixed population, with different levels of added genotype error: 0.01% (A), 0.1% (B), and 0.5% (C). The IBDrecomb analysis used 2,500 admixed individuals, the RASPberry analysis used 2,500 admixed individuals and 200 reference individuals, and the LDhat analysis used 96 admixed individuals. The x axis gives the estimation scale, and the y axis gives the Pearson correlation coefficient between the estimated and true recombination rates. Each end of the region was trimmed by 5 Mb before calculating correlation coefficients.

An IBD-Based Fine-Scale Recombination Map for the Framingham Heart Study Data

We compared our map estimated from the TOPMed Framingham Heart Study data (the FHS map) to three existing recombination maps: the deCODE map based on Icelandic pedigrees² and LD-based maps for the CEU (Utah Residents with Northern and Western European Ancestry) population from the 1000 Genomes Project obtained using LDhat and pyrho.^40,53

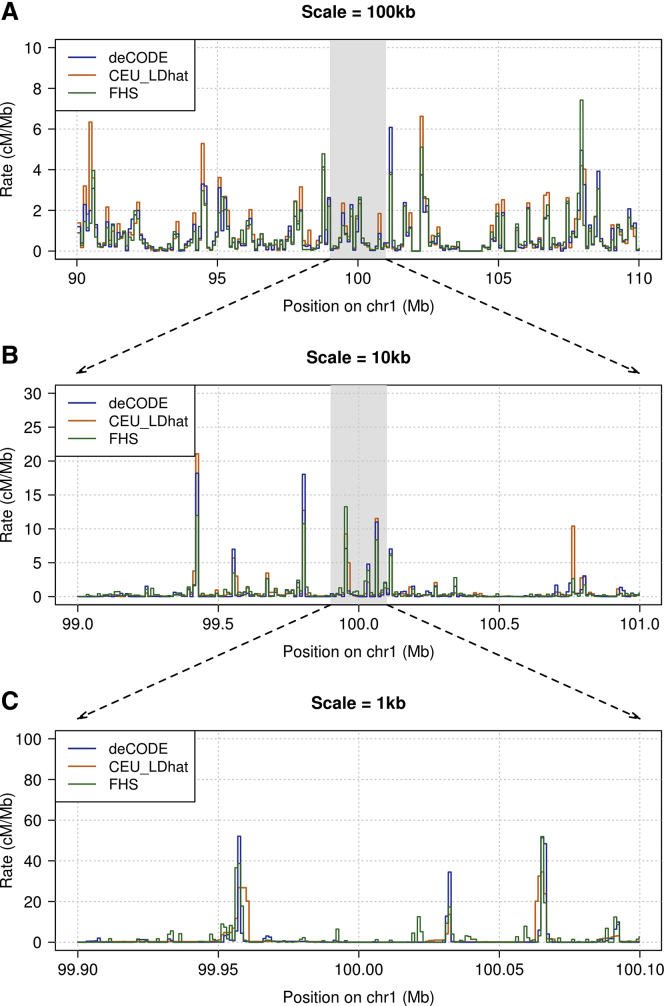
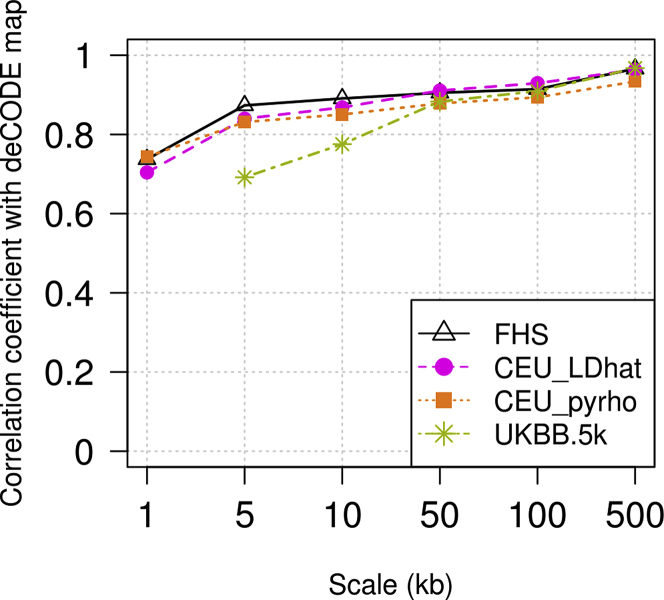
Examination of a region on chromosome 1 shows that our FHS map captures the same hotspots that are found with other methods (Figure 5). For a genome-wide comparison, we calculated correlation coefficients between maps. We regard the deCODE map as the “gold standard” in our comparison of recombination maps estimated from Europeans, because this European-specific map is based on directly observed recombination events from a very large number of meioses. We calculated the Pearson correlation coefficient between each map’s recombination rate estimates and the deCODE map’s rates. In order to calculate the correlation coefficient at a given scale (such as 1 kb), we divided the genome into intervals of this length and obtained the estimated recombination rate for each such interval for every compared map. Since each map covers a slightly different subset of the genome, we ignored intervals that are not fully covered by all maps included within a given comparison. We found that the LD-based and IBD-based maps have similar correlation coefficients to the deCODE map at all scales ranging from 1 kb to 500 kb (Figure 6).

Figure 5.

Estimated European Recombination Rates around chr1:100 Mb

Shown are (A) 20 Mb at 100 kb scale, (B) 2 Mb at 10 kb scale, and (C) 200 kb at 1 kb scale. The three maps represent three different methods: pedigree-based (deCODE), LD-based (CEU from the 1000 Genomes Project), and IBD-based (FHS). Positions on the x axes are in build 37 coordinates.

Figure 6.

Pearson Correlation Coefficients between Each Map and the deCODE Map at Different Scales

FHS is our IBD-based map from the TopMED Framingham Heart Study data. CEU_LDhat and CEU_pyrho are LD-based maps for the 1000 Genomes project Utah residents with Northern and Western European ancestry (CEU). UKBB.5k is our IBD-based map from 5,000 individuals from the UK Biobank SNP array data.

An IBD-Based Fine-Scale Recombination Map for the Jackson Heart Study Data

We constructed a recombination map for African Americans using the data from the TOPMed Jackson Heart Study data. We compared our map (the JHS map) with four other maps constructed with African American data: the AA map,²⁶ the AfAdm map,²⁷ and two LD-based maps estimated for the 1000 Genomes ASW (Americans of African ancestry in SW USA) population using LDhat and pyrho.^40,53 The AA and AfAdm maps were constructed using counts of ancestry switches in 30,000 and 2,864 admixed African Americans, respectively.

Examination again of the region on chromosome 1 shows that our JHS map includes the same recombination hotspots found by LD-based and admixture-based methods (Figure S4). For a genome-wide comparison, we calculated correlation coefficients between maps. The AA map, the JHS map, and the LD-based ASW maps are highly correlated at large scales (Pearson correlation coefficients > 0.8 at scales ≥ 50 kb) and slightly different at fine scales (Table 1, Table S1).

Table 1.

Pearson Correlation Coefficients between Estimated Recombination Rates for Five African American Recombination Maps at Different Scales

	JHS	AA	AfAdm	ASW_LDhat	ASW_pyrho
Scale: 1 kb
JHS	1.00	0.61	0.23	0.63	0.69
AA	0.61	1.00	0.26	0.65	0.60
AfAdm	0.23	0.26	1.00	0.30	0.23
ASW_LDhat	0.63	0.65	0.30	1.00	0.74
ASW_pyrho	0.69	0.60	0.23	0.74	1.00
Scale: 100 kb
JHS	1.00	0.90	0.79	0.86	0.86
AA	0.90	1.00	0.81	0.91	0.89
AfAdm	0.79	0.81	1.00	0.81	0.80
ASW_LDhat	0.86	0.91	0.81	1.00	0.94
ASW_pyrho	0.86	0.89	0.80	0.94	1.00

The JHS map is our IBD-based map, the AA and AfAdm maps are admixture-based maps, and the ASW_LDhat and ASW_pyrho maps are LD-based maps. Results at other scales from 1 kb to 500 kb can be found in Table S1.

At fine scales (1–10 kb), the JHS map and the admixture-based AA map have similar correlation with LD-based maps, while at large scales (50–500 kb) the AA map has higher correlation (Table 1, Table S1). Since the AA map is based on SNP array data, it is not surprising that it has lower relative correlations at fine scales, while its large sample size (around 15 times as many individuals as in our JHS analysis) gives it high correlations at large scales. Both the JHS map and the AA map have much higher correlations than the admixture-based AfAdm map to other maps at all scales. The AfAdm map is based on data with a sample size that is similar to that of our JHS data (2,864 individuals for the AfAdm map and 2,046 individuals for our JHS map). Hence it is notable that our JHS map has much higher correlations than the AfAdm map, which is consistent with our simulation results in which accuracy with our IBD-based method was much higher than accuracy with admixture-based estimation in admixed data.

In our simulated data, the correlation coefficient between our estimated map and the true map drops to around 0.5 at 1 kb scale (Figures 3 and 4), while the correlation between our FHS map and the deCODE map is 0.74 at this scale (Figure 6) and the correlation between our JHS map and pyrho’s ASW map is 0.69 (Table 1). In contrast, LDhat does not show such significant differences between the simulated data (Figure 4) and the real data (Figure 6). IBDrecomb has better fine-scale performance in real data than in our simulation because in real data genetic markers are not distributed evenly along the genome. Regions with high recombination rates tend to have more mutations,² which results in higher density of genetic markers. This higher marker density around recombination hotspots improves precision in estimating the endpoints of many IBD segments. In the FHS data, we found that 1 kb regions with the highest 1% of recombination rates (as determined by the deCODE map) have one third more markers than randomly selected regions (Figure S5), and removing those top recombination rate regions leads to a drop in the correlation coefficient from 0.74 to 0.47 at the 1 kb scale. We also simulated a dataset with a higher mutation rate, 2 × 10⁻⁸ per generation per basepair (compared to 10⁻⁸ in the original simulation, and resulting in a higher marker density), and found that the correlation with the true map increases to 0.69 at the 1 kb scale in the largest simulated sample size (Figure S6).

An IBD-Based Recombination Map for the UK Biobank SNP Array Data

IBD segments can be estimated from SNP array data as well as from sequence data, although the IBD segment endpoints will tend to be estimated with lower resolution in SNP array data due to lower marker density. We constructed a map using SNP array genotypes from 5,000 individuals from the UK Biobank study. Our UK Biobank map has similar correlation with the deCODE map compared to our FHS map at scales of 100 kb and higher but lower correlation at finer scales (Figure 6), as expected given the lower resolution of the SNP array.

Discussion

We have presented an IBD-based recombination rate estimation method, along with estimates of recombination rates in European Americans and African Americans. Our approach is applicable to large population-based samples with sequence data, enabling the generation of high-resolution population-specific recombination maps. Our maps constructed from the Framingham Heart Study and the Jackson Heart Study will be useful for downstream analyses that require recombination maps, including haplotype phase estimation, genotype imputation, inference of demographic history, and inference of local ancestry in admixed individuals.

As with other indirect methods (admixture-based or LD-based estimation), our method requires the total cM length of chromosomes from direct (family-based) estimation in order to convert relative recombination rates to absolute recombination rates. While family-based estimation of high-resolution recombination maps requires very large numbers of informative meioses, obtaining the approximate cM length of a chromosome requires many fewer meioses. In addition, while recombination rates may change at small scales due to changes in hotspots, large-scale rates are conserved across populations.⁵⁴ Thus, chromosome lengths from the Icelandic deCODE map (for example) or from other smaller family-based data may be used to normalize IBD-based relative recombination rates estimated in other human populations.

Generation of new maps with our method is straightforward, and we provide software to do so (Web Resources). Our method is applicable to humans and to other diploid species. With reductions in sequencing costs, it is likely that there will soon be suitable data for a variety of species, including model organisms, domesticated species, and wild species. The generation of high-resolution maps will facilitate other analyses in these populations. As input, our method requires high-quality genotype data (variant calls) on at least several hundred individuals, and a high-quality genome build for determination of physical positions. Sequence data are needed for accurate fine-scale estimation, but array data are adequate for estimation at large scales (100 kb and greater), as shown by our analysis of UK Biobank data. SNP array data should be analyzed directly, without first applying imputation, because imputed variants have lower accuracy that reduces the accuracy of IBD segment detection.

Results from simulated African American data showed that our IBD-based method gives greater accuracy than ancestry-switch based methods for constructing recombination maps from admixed individuals. This is because our method can detect recombination events that occurred before admixture, as well as those that occurred after admixture, while ancestry-switch based methods only use recombination between different ancestry segments that occurred after admixture. In addition, with 2,500 simulated admixed individuals, the IBD-based method gives similar accuracy to LDhat on 96 admixed individuals, except at the ends of the analyzed region or when the genotype error rate is high. It is not practically feasible to run LDhat with a larger number of samples, because this would require generation of a likelihood lookup table for the larger sample size, which has very high computational cost.

In real data, the true map is not known, and it is also possible that recombination rates differ across time and populations. Thus, instead of directly assessing accuracy, we can only look at correlations between results from different methods and across datasets. A map that has highest correlations with all other maps may be more accurate, although correlation between methods can be partly driven by incorporation of the same recombination events by the different methods, as many older recombination events are shared in the histories of multiple populations and utilized by different methods. While keeping these caveats in mind, we note that the correlation-based rankings of the real-data maps are largely in line with the results of the simulation study. In terms of correlation ranking, our IBD-based FHS map has similar performance to the LD-based maps, and our IBD-based JHS map outperformed an admixture-based map developed from a dataset of similar size.

Like our method, LD-based methods are based on past recombination events, but our method depends more on recent recombination events, while LD-based methods are primarily based on recombination events occurring in the much more distant past. In contrast, family-based methods use recombination events from the past few generations. Recombination rates evolve over time,⁵⁵ so restricting the analysis to more recent events is advantageous for some applications.

Current recombination rates in Europeans and other out-of-Africa populations may differ from rates in African populations because of drift that occurred in the out-of-Africa bottleneck. For example, non-African populations predominantly carry the A allele of PRDM9, while African populations carry that allele at a frequency of only around 50%.⁴ Carriers of the A allele have much higher rates of crossovers for some recombination hotspots compared to non-carriers.⁵⁶ Thus, there is a need for population-specific maps of recent recombination landscapes.

The IBD-based approach has some limitations. The major obstacle to achieving higher accuracy at fine scales for our method is the difficulty in accurately establishing the exact IBD endpoints. Wrongly placed IBD endpoints may lead to false recombination rate peaks at fine scales and may also lead to underestimation in recombination hotspots. Currently, IBD estimation methods do not provide a representation of the uncertainty around the exact IBD endpoints. A second issue is that IBD is a property of groups of haplotypes rather than just pairs of haplotypes, and as a result some IBD endpoints are shared by multiple pairs of individuals. This double-counting of some IBD endpoints increases the variability of the estimated recombination rates, particularly at fine scales. Currently, estimation of multi-individual IBD is challenging in large-scale datasets. Future work could address these issues.

Declaration of Interests

The authors declare no competing interests.

Data and Code Availability

This study made use of whole-genome sequence data obtained from dbGaP (accession numbers phs000974.v2.p2 and phs000964.v2.p1) and existing recombination maps (Web Resources). Code implementing the IBDrecomb method, as well as the maps generated in this study, are available from the IBDrecomb github site (Web Resources).

Published: June 12, 2020

Web Resources

• 1000 Genomes maps (build 37), ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/technical/working/20130507_omni_recombination_rates/

• AA map (build 36), https://www.well.ox.ac.uk/∼anjali/AAmap/aamap.tar.gz

• AfAdm map (build 36), https://www.eeb.ucla.edu/Faculty/Novembre/software/AfricanAmerican_AfricanCaribbean_recombination_maps.zip

• deCODE map (build 38), https://science.sciencemag.org/highwire/filestream/721792/field_highwire_adjunct_files/4/aau1043_DataS3.gz

• Hapmap II combined map (build 37), ftp://ftp.ncbi.nlm.nih.gov/hapmap/recombination/2011-01_phaseII_B37/genetic_map_HapMapII_GRCh37.tar.gz

• IBDrecomb (including FHS and JHS maps), https://github.com/YingZhou001/IBDrecomb

• msprime, http://msprime.readthedocs.io/en/stable

• pyrho map (build 37 and 38), https://drive.google.com/drive/folders/1Tgt_7GsDO0-o02vcYSfwqHFd3JNF6R06

• Refined IBD and Gap-filling tool, http://faculty.washington.edu/browning/refined-ibd.html

• UCSC online liftOver tool, https://genome.ucsc.edu/cgi-bin/hgLiftOver