Highlights
-
•
A new hybrid COVID-19 recognition model based on deep learning technique.
-
•
Model performance improvement with the help of chaotic optimization algorithm.
-
•
Diagnosis of COVID-19 cases by the rapid and high accuracy.
-
•
Examining the effect of curvelet transform on the performance of the model.
Keywords: Coronavirus, Covid-19, Deep learning, Curvelet transform, Chaotic salp swarm algorithm
Abstract
The novel coronavirus disease 2019 (COVID-19), detected in Wuhan City, Hubei Province, China in late December 2019, is rapidly spreading and affecting all countries in the world. Real-time reverse transcription-polymerase chain reaction (RT-PCR) test has been described by the World Health Organization (WHO) as the standard test method for the diagnosis of the disease. However, considering that the results of this test are obtained between a few hours and two days, it is very important to apply another diagnostic method as an alternative to this test. The fact that RT-PCR test kits are limited in number, the test results are obtained in a long time, and the high probability of healthcare personnel becoming infected with the disease during the test, necessitates the use of other diagnostic methods as an alternative to these test kits. In this study, a hybrid model consisting of two-dimensional (2D) curvelet transformation, chaotic salp swarm algorithm (CSSA) and deep learning technique is developed in order to determine the patient infected with coronavirus pneumonia from X-ray images. In the proposed model, 2D Curvelet transformation is applied to the images obtained from the patient's chest X-ray radiographs and a feature matrix is formed using the obtained coefficients. The coefficients in the feature matrix are optimized with the help of the CSSA and COVID-19 disease is diagnosed by the EfficientNet-B0 model, which is one of the deep learning methods. Experimental results show that the proposed hybrid model can diagnose COVID-19 disease with high accuracy from chest X-ray images.
1. Introduction
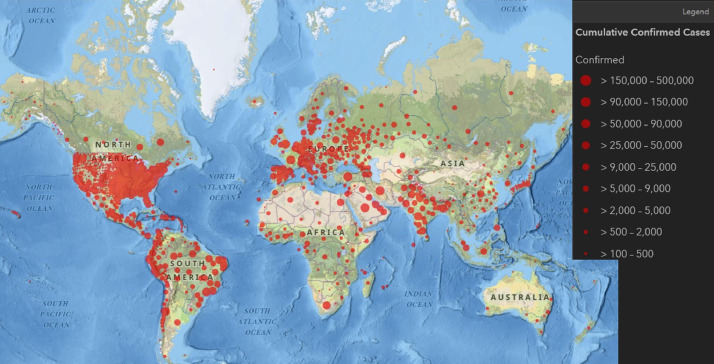
The type of pneumonia caused by the novel coronavirus disease 2019 (COVID-19) detected in late December 2019 in Wuhan City, Hubei Province, China is a highly contagious disease and is spreading very rapidly all over the world [1, 2]. According to the data of the World Health Organization (WHO) in mid-June, more than 8.86 million cases and more than 465 thousand deaths have been reported worldwide [2]. The distribution of COVID-19 cases by country in the world is shown in Fig. 1, [3]. It has been reported that COVID-19, which is still ongoing today and can be infected to people of all ages, can be characterized as a pandemic by WHO [4, 5]. The COVID-19 virus, which is zoonotic due to the ability to infect from animals to humans, is also defined as an infectious respiratory disease caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [6]. Although symptoms of high-grade fever, cough and shortness of breath are common in patients infected with COVID-19, rarely, muscle ache, headache, sputum production, chest pain, sore throat, and diarrhea symptoms are seen [7, 8].
Fig. 1.
Global cases of coronavirus COVID-19 on June 22, 2020 [3].
The mortality rate in cases infected with COVID-19 is 5.25% worldwide. This mortality rate is 7.60% in the European region, 2.24% in the Eastern Mediterranean region, 2.22% in the African region, 2.95% in the South-East Asia region, 5.07% in the region of Americas, and 3.55% in the region of Western Pacific [2]. The most deaths due to COVID-19 disease has been occurred in the United States of America (USA). According to data in mid-June, the number of deaths due to this disease has exceeded 119 thousand in the USA. The country with the highest number of deaths after the USA is Brazil with the number of deaths exceeding 51 thousand. Among the countries with more than 100 thousand cases, the first 5 countries with the highest mortality rate in cases infected with COVID-19 disease are France, Italy, the United Kingdom, Mexico and Spain with 19.13%, 14.52%, 14.00%, 11.86%, and 11.50%, respectively. Among the countries with more than 100 thousand cases, the first 5 countries with the lowest mortality rate in cases infected with COVID-19 disease are Saudi Arabia, Bangladesh, Russian Federation, Chile and Pakistan with 0.80%, 1.30%, 1.38%, 1.84% and 1.98%, respectively. When the numbers of cases infected with COVID-19 disease with the mortality rates are evaluated together, Nigeria and Philippines, which are among the countries with a population of more than 100 million, are quite stood out with their low numbers and rates [2, 9]. At the same time, it is also observed that the mortality rates in the USA and Brazil have increased very rapidly.
In China, the starting place of the epidemic, it is also known that 93.98% of cases infected with COVID-19 disease have recovered. After China and Iran, the epidemic is intensely observed in Europe. Among the European countries with more than 100 thousand COVID-19 cases, the countries with the highest recovery rate are Switzerland, Germany, Turkey, Italy and Belarus with 92.55%, 91.46%, 85.51%, 76.83% and 65.03%, respectively. The recovery rate in the USA, which is currently the center of the epidemic, is 27.68% [3].
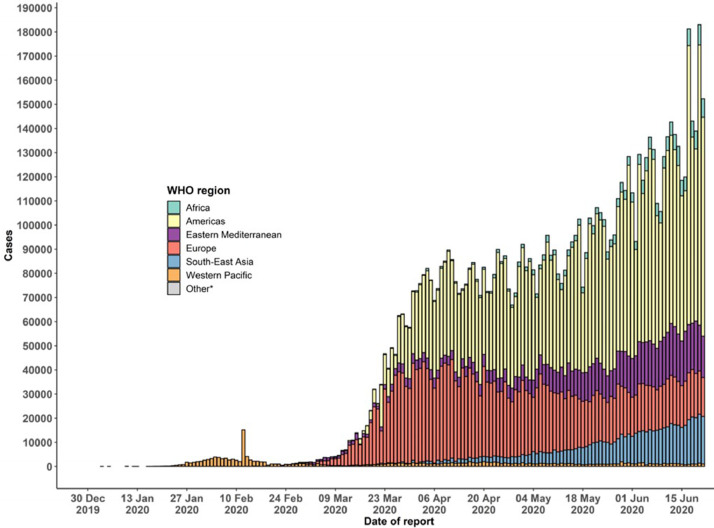
The epidemic is spreading much faster in Brazil, USA and India than other regions and countries in the world. The epidemic curve of confirmed COVID-19 in the worldwide from the beginning of the epidemic until June 22, 2020 is presented in Fig. 2 . To facilitate public health interventions and control the epidemic, it is of great importance to quickly detect cases infected with COVID-19 disease. This disease, which can be rapidly transmitted from person to person, usually by mouth droplets, also poses a great risk for healthcare workers who carry out the test for the diagnosis of the disease [10, 11]. The real-time reverse transcription-polymerase chain reaction (RT-PCR) test, which is defined by WHO as the standard test method, is widely used worldwide in the diagnosis of COVID-19 disease [12, 13]. The RT-PCR test is routinely used to detect causative viruses from respiratory secretions in acute respiratory infection [14, 15].
Fig. 2.
Epidemic curve of confirmed COVID-19 cases in the worldwide on June 22, 2020 [2].
In the absence of vaccines and specific therapeutic drugs, accurate detection of cases infected with COVID-19 disease at an early stage is extremely important in order to isolate the infected person from the healthy population and provide appropriate treatment [16]. The RT-PCR test kits are used extensively in the diagnosis of COVID-19 disease in countries where the epidemic is intense. The RT-PCR test is used to detect viral nucleotides from specimens obtained by nasopharyngeal swab, oropharyngeal swab, tracheal aspirate, or bronchoalveolar lavage [17, 18]. In countries with an epidemic, especially in China, it has been reported that the diagnosis of COVID-19 disease need to be confirmed with the help of blood specimens or gene sequencing for respiratory as the key indicator for patients' hospitalization [16]. However, the low sensitivity of RT-PCR causes many COVID-19 patients to be unidentified [19], [20], [21]. It is also reported that the results of this test are obtained from a few hours to two days. Further, the RT-PCR test may need to be repeated several times for some patients in the diagnosis of COVID-19 [16, 22]. Failure to diagnose the disease at the earliest stage causes the patient to not receive appropriate treatment on time, and given the rapid infectious nature of the virus, the risk of the disease spreading to a larger population increases. The fact that RT-PCR test kits are limited in number, the test results are obtained in a long time, and the high probability of healthcare personnel becoming infected with the disease during the test suggests that other diagnostic methods should be used as an alternative to RT-PCR test. For all these reasons, chest Computed Tomography (CT), which is used as a imaging tool for the diagnosis of pneumonia, is used as an alternative to RT-PCR test for the diagnosis of COVID-19 disease [16, 23].
In the diagnosis of COVID-19 disease, the sensitivity of chest CT is higher than RT-PCR, therefore, it is recommended to use chest CT for COVID-19 screening in patients with epidemiologic and clinical features compatible with COVID-19 infection, especially when the RT-PCR test is negative [19, 24, 25]. Chest CT is also used to assess the severity of lung involvement in cases where the COVID-19 test is positive [24]. Artificial intelligence (AI)-based studies are carried out to determine COVID-19 disease quickly and with high accuracy from chest CT [26], [27], [28]. These studies contribute to increasing the sensitivity of chest CT.
In [27], a deep learning model has been proposed to detect COVID-19 by obtaining visual features from volumetric chest CT exams. The robustness of the model has been tested by including other non-pneumonia CT exams and community acquired pneumonia. The proposed approach has been shown to distinguish COVID-19 from community-acquired pneumonia. In [28], the lesion area is accurately segmented by AI algorithms in chest CTs, which plays an important role in the diagnosis, staging and monitoring of patients with COVID-19 pneumonia. The proposed AI algorithm can compute the volume of the lesion. It is mentioned that this situation will help to provide effective treatment at an early stage, especially in cases with COVID-19 disease.
In this study, a combined model consisting of two-dimensional (2D) curvelet transformation, meta-heuristic optimization algorithm and deep learning technique is proposed to diagnose the patient infected with coronavirus pneumonia from X-ray images. Unlike the studies on this subject, the proposed model has higher accuracy and robustness compared to the studies in the literature. The remainder of this paper is organized as follows. In Section 2, the diagnosis methodology of COVID-19 disease from X-ray images is introduced in detail. The experimental results and analysis of the proposed model are presented in Section 3. The section also includes serious and concrete discussions on the accuracy, robustness and usability of the proposed model. Finally, the conclusion and future works are emphasized in Section 4.
2. Recognition methodology of COVID-19 disease from X-ray images
In this section, 2D curvelet transformation, chaotic salp swarm algorithm (CSSA) and EfficientNet-B0 methods used in the proposed model are introduced. The proposed models have been trained with 80% of the data set consisting of 1341 normal images, 219 COVID-19 positive images, and 1345 viral pneumonia images, with a total of 2905 chest X-Ray images in the training phase. The performance of the proposed model has been tested on a total of 581 chest X-Ray images, consisting of 268 normal images, 44 COVID-19 positive images, and 269 viral pneumonia images.
2.1. 2D curvelet transform
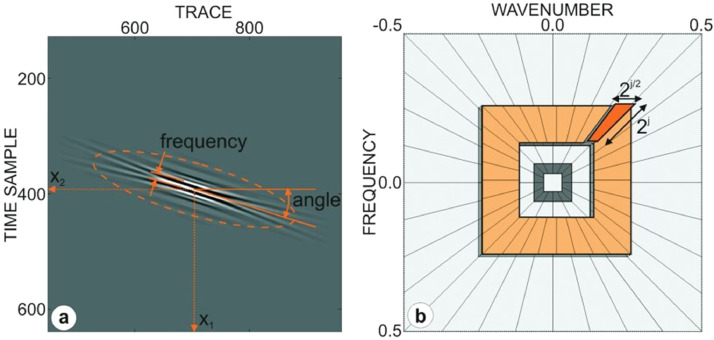
Curvelet transform, which decomposes the signals using a linear and weighted combination of basic functions called curvelets, is an extension of the 2D wavelet transform commonly used in signal and image processing. This transformation shows a very good directional dependent form that fits the multiscale, a high degree of directionality, parabolic scaling relationship, and takes the form of longitudinal needles on small scales. The curvelet transformation has directional capability and is more successful than other traditional multiscale transformations such as wavelet transformation in showing other singularities and edges along curves. A curvelet is a combination of radial and angular window in the frequency domain defined in the polar coordinate system. The angular window corresponds to Radon transformation and the radial dynamic window is similar to the band pass filter. Curvelet basics are designed to cover the frequency domain entirely, unlike other directional multiscale representations such as the Gabor transform [29]. Single curvelet in 2D can be defined as the fundamental function of angle, frequency, and two spatial coordinate variables. The parameterization of single 2D curvelet and the partitioning of the 2D frequency plane-curvelet grid produced by overlapping two types of windows are shown in Fig. 3 [30]. Firstly, 2D fast Fourier transform (FFT) is applied to the image in order to implement the curve transformation. Curvelet based functions are obtained by specifically tiling 2D Fourier spectra with the "curvelet grid". Then the 2D Fourier frequency plane is split into parabolic wedges. The curvelet coefficients for each j scale and l angle are obtained by applying inverse FFT for each wedge. The split wedges are shown in Fig. 3(b) in the Fourier frequency plane. Each wedge in spatial space corresponds to a certain curvelet at the given scale and angle.
Fig. 3.
(a) Parameterization of 2D curvelet (b) Partitioning of 2D frequency plane-curvelet grid, which is generated by overlapping two types of windows [30].
Digital curvelet transform (DCT) can be implemented in two ways, fast DCT (FDCT) via wrapping, FDCT via unequally spaced FFT. In this study, 2D FDCT via wrapping is used because it is faster, simpler and less redundant. This transform is created using wrapping, tight framing, anisotropic law and parabolic scaling. The DCT is defined as
| (1) |
where f[t 1, t 2] is an input of Cartesian arrays for 0 ≤ t 1, t 2 < n, each is a digital curvelet waveform, D indicates for “digital”, and cD(j, l, k) is curvelet coefficient. In the wrapping approach in DCT, we assume that instead of a tilted grid, there is a regular rectangular grid, and we define the Cartesian curvelets in substantially the similar way as before
| (2) |
Note that the term of b is approximately when or (3π/4, 5π/4), taking on values on a rectangular grid in Fig. 3(b). is “Cartesian” window, Sθ is the shear matrix, and the family implies a concentric tiling whose geometry is pictured in Fig. 3(b).
The structure of the FDCT by wrapping includes the following processing steps [29]:
-
i
Fourier samples of the image matrix are obtained by applying 2D FFT, , n 2 ≤ n/2.
-
ii
For each scale j and angle l, the window function and the product of Fourier samples are obtained, .
-
iii
As a result of the product, the data is re-indexed by wrapping around the origin, . Note that the range for n 1 and n 2 is now 0 ≤ n 1 < L 1, j and 0 ≤ n 2 < L 2, j. L 1, j and L 2, j are the sides of the parallelogram in the winding process.
-
iv
In order to obtain cD(j, l, k) discrete curvelet coefficients, apply the inverse 2D FFT to each .
2.2. Chaotic salp swarm algorithm
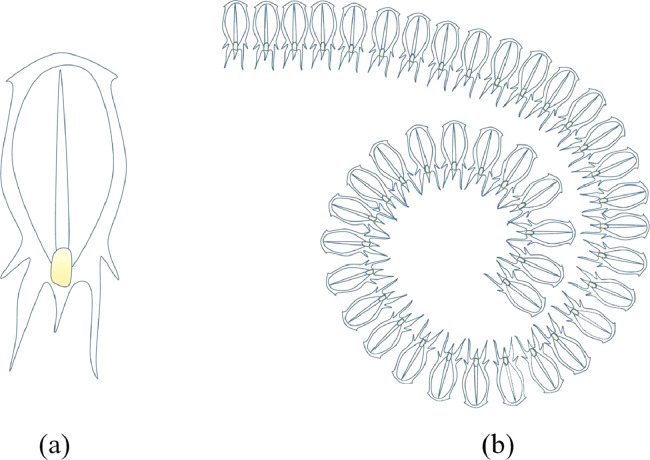
In this section, salp behavior and chaotic optimization algorithm based on salp behavior are presented. Salp swarm algorithm (SSA) is meta-heuristic random population-based algorithm based on the swarming mechanism of salps when foraging in the oceans [31]. The salps form a swarm called the salp chain in the deep oceans, and they navigate and forage in this swarm. This chain is presented in Fig. 4 . The salp in the front position of the chain shown in Fig. 4 represents the leader and guides the chain. The remaining salps are considered followers and follow the leader. As with other optimization algorithms, salp positions are represented in an n -dimensional search space. Here n represents the number of variables of the given optimization problem. Therefore, the positions of the salp are expressed by x, a two-dimensional vector. It is also assumed that there is a food source F in the search area, expressed as the target of the swarm.
Fig. 4.
(a) Individual salp (b) Salps chain [31].
The position of the leader is updated relative to the food using
| (3) |
where denotes the position of the leader in i-th dimension, Fi represents the food source at i-th dimension, ubi and lbi are upper and lower boundaries at i-th dimension, respectively. c 1, c 2 and c 3 are random numbers. c 2 and c 3 are randomly in the range (0, 1), which determines whether the next position will be towards negative infinity or positive infinity. c 1 is a balancing parameter between the exploration and exploitation stage and can be mathematically defined as
| (4) |
where M and m are the maximum number and current number of iterations, respectively. The updating positions of the remaining followers in i-th dimension are denoted by
| (5) |
where r ≥ 2, is the position of the r-th salp at i-th dimension, and is the position of the salp.
The main purpose of chaos optimization, one of the newest search algorithms, is to convert variables from chaos to solution space. The main reason for using chaos optimization algorithm in this study is local minima avoidance and rapid convergence rate. An effective and important way to overcome these problems is to use chaos theory [32]. In meta-heuristic algorithms, chaotic maps are used instead of random numbers to increase convergence. In CSSA used in the proposed model, random variables are replaced with chaotic ones. These features of chaos optimization significantly improve the performance of our COVID-19 diagnostic model and make our model robust. The advantages of the chaotic meta-heuristic optimization algorithm, such as simplicity, scalability, and reduction of computation time, have been also taken into account when using CCSA in our model.
Chaos defined as semi-randomness behavior produced by mathematically nonlinear deterministic systems has three important dynamic properties such as quasi-stochastic, ergodicity and sensitivity to original conditions [33]. The ability to replace random variables with the values of chaotic maps is described as the quasi-stochastic. The ability of chaotic variables to explore non-recurrently all states in a specified range is defined as ergodicity. The sensitivity to original conditions is characterized as any minimum change in the initial conditions can lead to different behaviors [34]. The performance of salp swarm optimization algorithm can significantly improve by including these features.
Chaotic maps generate the chaotic sequence that can be used to update the salp locations and improve the convergence speed and optimum solution. When the effectiveness of the ten chaotic maps presented in Table 1 is analyzed, it is seen that the logistic chaotic map is the most suitable map and this map has significantly improved the performance of SSA in terms of both exploration and exploitation [35]. Therefore, in order to maximize classification accuracy and find the optimal feature subset that minimizes the number of features selected, the logistic chaotic map is embedded in the optimization process in this study.
Table 1.
Definition of chaotic maps.
| No | Name | Definition | Range |
|---|---|---|---|
| 1 | Logistic | (0, 1) | |
| 2 | Singer | (0, 1) | |
| 3 | Iterative | ||
| 4 | Sinusoidal | (0, 1) | |
| 5 | Sine | (0, 1) | |
| 6 | Circle | (0, 1) | |
| 7 | Chebyshev | ||
| 8 | Gauss/mouse | (0, 1) | |
| 9 | Tent | (0, 1) | |
| 10 | Piecewise | (0, 1) |
In this study, the logistic chaotic map is employed to adjust c 2 parameter of SSA. The update of the c 2 parameter according to the chaotic map is expressed in Eq. (6).
| (6) |
According to the chaotic map, the location of a salp is defined by
| (7) |
where dt represents the obtained value of chaotic map at t-th iteration. The optimum solution that both minimizes the number of features selected and maximizes classification accuracy in each solution is determined by the following fitness function
| (8) |
where Af denotes the weight factor, Kf and Kt represent length of selected features subset and total number of features, respectively. Note that, the Af parameter is set to 0.8 to maximize classification accuracy and minimize the number of features selected. Here, Acc refers the classification accuracy obtained from k-nearest neighbor (KNN) classifier, one of the supervised machine learning algorithms.
2.3. EfficientNet-B0
Deep learning uses algorithms known as artificial neural networks (ANNs) inspired by information processing methods of biological nervous systems. Thus, it allows computers to identify what each data represents and learn models. Deep learning algorithms that are structurally more complex than ANNs are based on computation systems that mimic the functions of the human brain. Deep learning algorithms have been used frequently in the field of medical image processing recently due to their effective performance. Deep learning methods are used extensively in segmentation, classification and diagnosis of medical images obtained by medical imaging techniques such as CT, magnetic resonance imaging (MRI) and X-ray [36], [37], [38], [39]. In this study, X-ray images are classified as normal, COVID-19 positive and viral pneumonia with EfficientNet-B0 model based on convolutional neural network (CNN) in order to diagnose the patient infected with the new coronavirus pneumonia. In determining EfficentNet-B0 as the deep learning algorithm, the calculation cost, accessibility, speed, and usability parameters are taken into consideration.
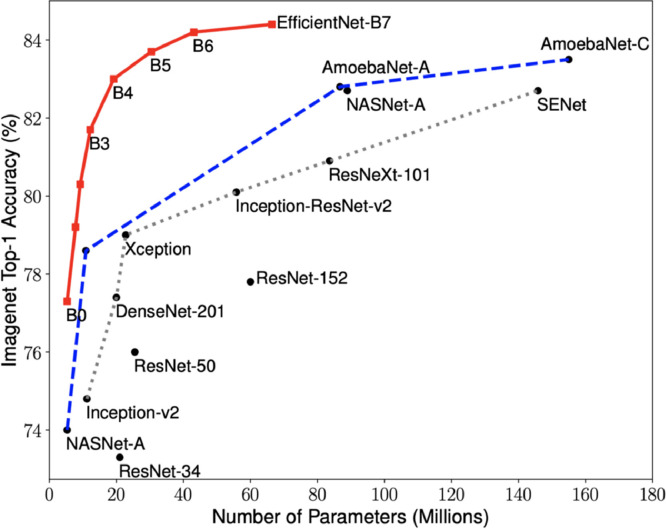
EfficientNets focus not only on improving accuracy but also on improving the efficiency of models. In addition to being 5–10 times more efficient than most models, it also displays an increase in accuracy of up to 6%. In order to increase the performance of CNNs, more layers are usually added as in ResNet34, ResNet50, ResNet152, but performance does not increase in the correct proportion. It also causes computational complexity [40]. Accuracy versus model size of deep learning methods is given in Fig. 5 .
Fig. 5.
ImageNet accuracy versus model size [40].
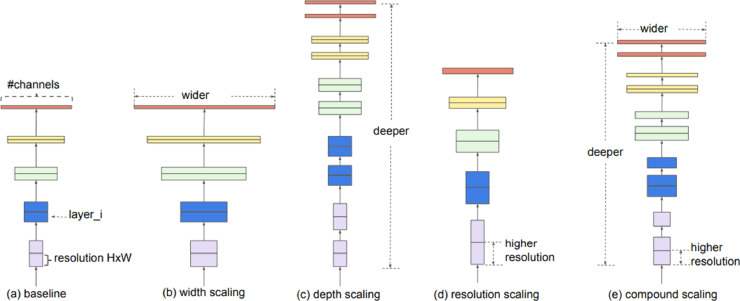
In scaling the EfficientNets model, not only depth but width and resolution parameters are taken into account. EfficientNets has been optimized by combining these three parameters to increase accuracy. One of these parameters is never allowed to be bottleneck [40]. These three scaling methods and the proposed composite scaling method that scales all three dimensions equally at a fixed rate are presented in Fig. 6 . The EfficientNet family consists of eight models between B0 and B7, and as the number grows, the calculated number of parameters and accuracy increases, but the processing load also increases. Taking into account the minimum model complexity, low calculation costs, high speed and high accuracy, it has been used in this study by choosing the basic network EfficientNet-B0 from the EfficientNets family.
Fig. 6.
EfficientNets model scaling methods [40].
2.4. Framework of proposed hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model for COVID-19 diagnostic
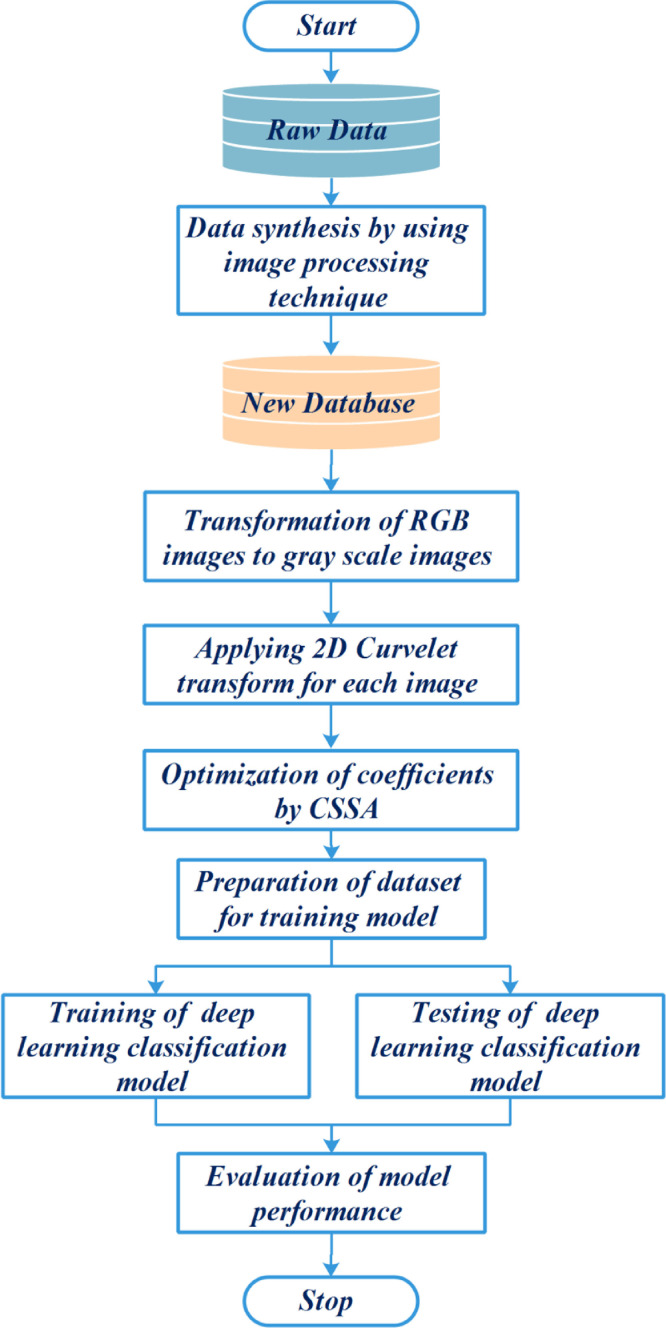
In this study, the content of the proposed a new hybrid COVID-19 disease diagnosis frame consists of data synthesis by image processing technique, transformation of RGB images into grayscale images, applying 2D curvelet transform for each image, training and testing phases of EfficientNet-B0 deep learning model, and evaluation phase of the proposed model. The overall process of the proposed hybrid COVID-19 disease diagnosis model is shown in Fig. 7 . During the data pre-processing stage, chest X-ray images are synthesized by image processing technique. The synthesized image data is transformed to grayscale images. 2D Curvelet transform is applied to each image and the feature matrix consisting of coefficients is obtained. The coefficients in the feature matrix are optimized with the help of the CSSA. EfficientNet-B0 model, one of the deep learning methods, is trained with 80% of the obtained image data set. The validity of the model is tested on the remaining 20% image dataset. The performance of the model is measured with the help of performance metrics.
Fig. 7.
Framework of the proposed hybrid model for COVID-19 disease diagnostic.
3. Experimental results and discussion
In this section, the studies performed on chest X-ray images consisting of COVID-19, normal and viral pneumonia are presented to demonstrate the classification effectiveness of the hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model proposed for the diagnosis of COVID-19. The obtained results for single EfficientNet-B0 model, combined model consisting of 2D curvelet transform and EfficientNet-B0, and hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model are compared with the results of the studies in literature. The effect of 2D curvelet transform and the CSSA, which is chaotic meta-heuristic optimization algorithm on COVID-19 diagnostic model has been examined.
3.1. Chest X-ray image dataset
In this study, data sets created by combining X-ray images consisting of 1024 × 1024 pixels taken from 219 COVID-19 patients, 1341 normal, and 1345 viral pneumonia patients are used. In total, 2905 real raw chest X-ray image data are used. 60 chest X-ray images for each class have been separated from the actual data as test data. The remaining data is used in the training phase of the model. By using image processing techniques on real raw data, 5075 synthetic image data have been produced and the chest X-ray dataset has been expanded. 472 chest X-ray images for each class have been separated from synthetic data as test data. The dataset used in the study consists of a total of 7980 chest X-ray image data; 2905 real raw and 5075 synthetic chest X-ray images. The details of the chest X-ray dataset used in the study are presented in Table 2 .
Table 2.
Details of chest X-ray the training and test dataset used in the study.
| Raw Data | Sythesis Data | Total | |||
|---|---|---|---|---|---|
| Training | Test | Training | Test | ||
| COVID-19 | 159 | 60 | 1969 | 472 | 2660 |
| Normal | 1281 | 60 | 847 | 472 | 2660 |
| Viral Pneumonia | 1285 | 60 | 843 | 472 | 2660 |
| Total | 2725 | 180 | 3659 | 1416 | 7980 |
Although there are many COVID‐19 patients infected in the world, the number of chest X-ray images that are open to the public is very small. The most important reason for using this dataset is that it has relatively more images compared to the data sets studied in the literature in terms of COVID-19 positive, normal and viral pneumonia chest X-ray images and is open to the public [41]. It is also possible to compare the proposed COVID-19 diagnostic method with other methods studied on the same data set.
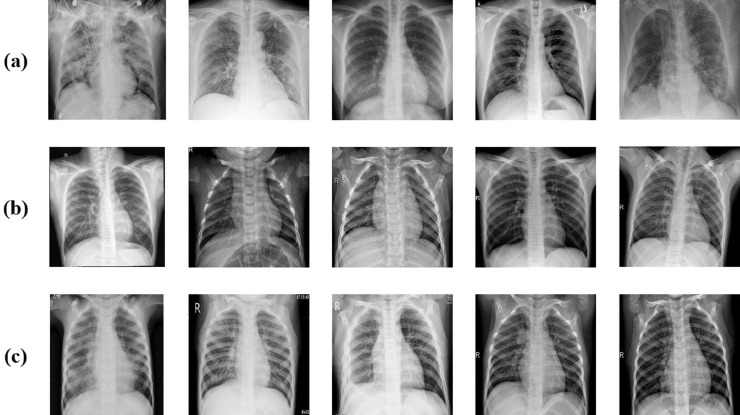
The data set has been expanded by synthesizing raw chest X-ray images with three different approaches from image processing techniques to obtain new images. The purpose of this step is to ensure that the model to be created is independent of the data and to provide data diversity during the training phase. In the first approach, rotations are applied to the images clockwise and counterclockwise, 15°, 30°, 45°, 60°, 75° and 90°. In the second approach, the process of decreasing or increasing the size of the real image is applied to the images in 2.5% steps between 2.5% and 10%. In the third approach, new pixel blocks ranging from 5% to 20% in horizontal and vertical directions are added to real images. A cross-section of the X-ray chest images of COVID-19 patients, normal and viral pneumonia patients in the dataset used in the study is presented in Fig. 8 .
Fig. 8.
Sample chest X-ray image from dataset: (a) COVID-19 cases (b) Normal cases (c) Viral pneumonia cases.
3.2. Performance metrics
The confusion matrix consists of true positive (TP), true negative (TN), false positive (FP) and false negatives (FN). TP represents samples where the actual and estimated value is 1. TN specifies samples where the actual and estimated value is 0. FP shows the samples where the actual value is 0 but the estimation model produces the value of 1. FN are samples where the actual value is 1 but the model's estimate is the value of 0. The performance metrics given in Eqs. (9)–(13) are calculated based on the confusion matrix.
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
The accuracy rate is a measure of how often the classifier correctly estimated. Specificity is the complement to sensitivity, or the TN rate, and indicates how well the negative class has been estimated. Precision is the fraction of samples assigned the positive class that belong to the positive class. Recall expresses how well the positive class has been estimated. F-measure ensures a single score that balances both recall and precision concerns simultaneously in one number.
3.3. Experimental results and analysis
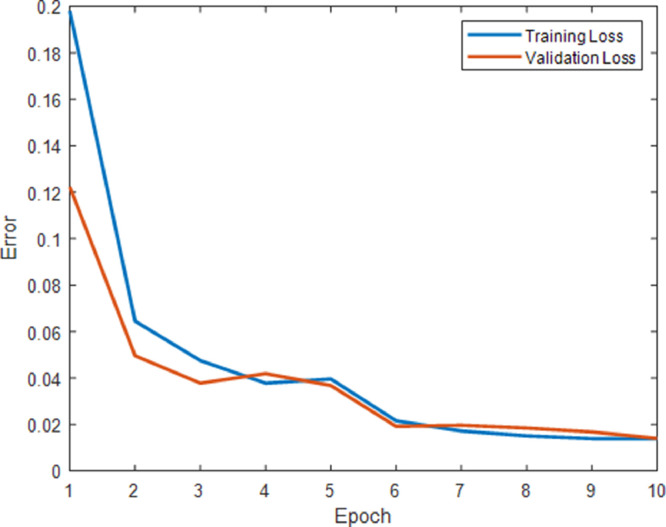
EfficientNet-B0 model, which is a pre-trained deep learning model, takes 224 × 224 pixel images at the entrance. For this reason, scaling is performed on chest X-ray images. During the training of the EfficientNet-B0 model, the learning rate per epoch is updated using the Adam optimization method. All experiments for chest X-ray images are performed on a personal computer which has Intel Core i7–3940X processor, 4 GB NVIDIA K5000 graphics card, 32 GB RAM. All codes are compiled with MATLAB 2019b. The change of error versus epoch is shown in Fig. 9 for the proposed hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model. It is seen in Fig. 9 that the training loss and validation loss values per epoch are close to each other and consistent values. It can be seen that the proposed model is not overfitting.
Fig. 9.
Change of error versus epoch for proposed model.
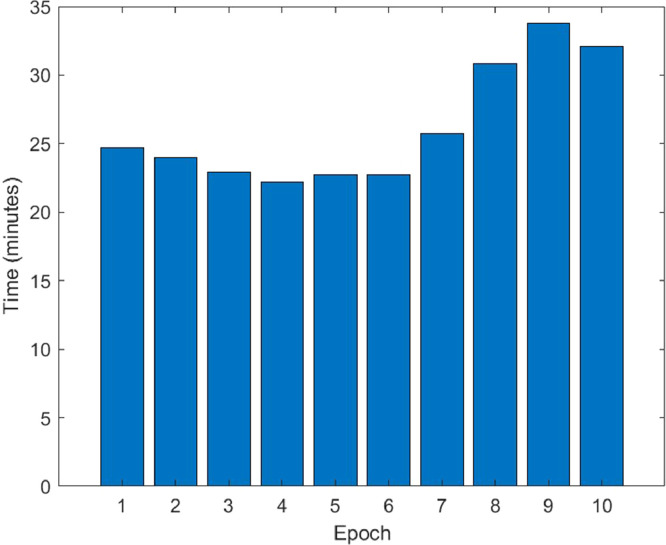
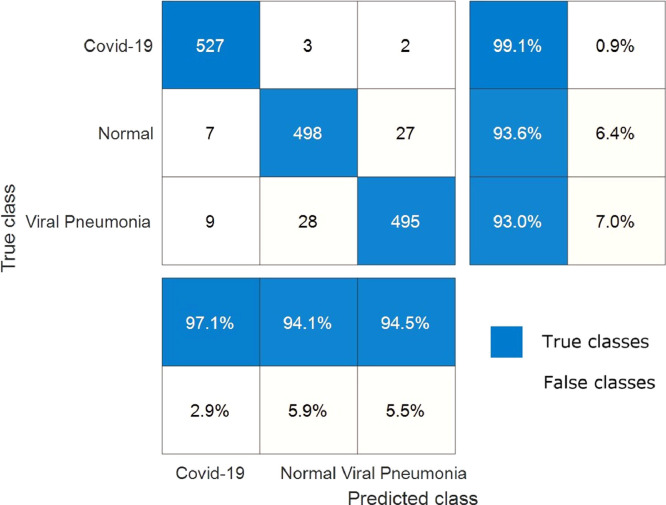
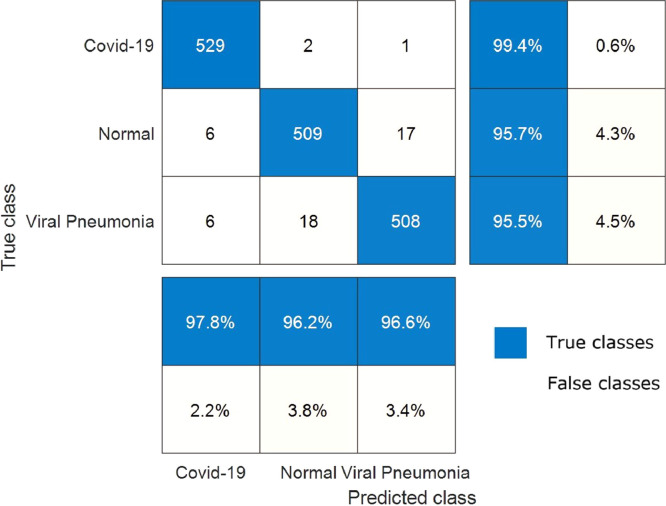
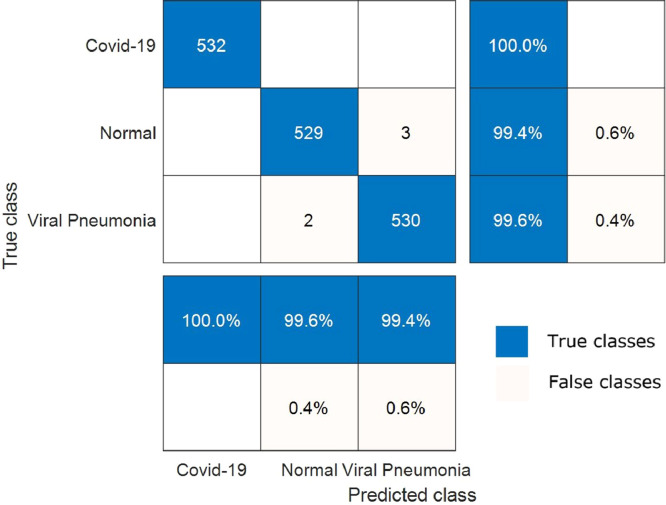
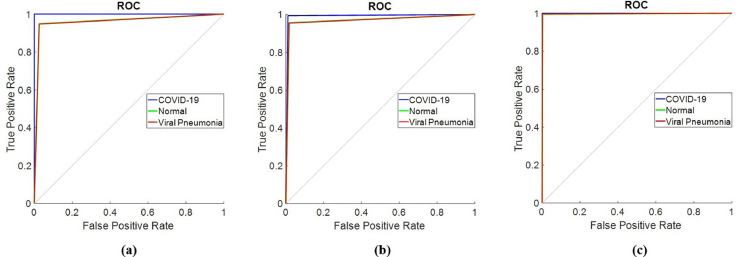
The change of training time versus epoch is demonstrated in Fig. 10 for the proposed hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model. The training time for the proposed model is an average of 27 min per epoch. The total training of the model has been completed in 4.5 h. The confusion matrix in the classification of COVID‐19, normal, and viral pneumonia of single EfficientNet-B0, 2D curvelet transform-EfficientNet-B0, and hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model are presented in Fig. 11, Fig. 12, Fig. 13 , respectively. Receiver operating characteristic (ROC) curve obtained using single EfficientNet-B0, 2D curvelet transform-EfficientNet-B0, and hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model are given in Fig. 14 (a)-(c), respectively. When the confusion matrices and ROC curves obtained for the three COVID-19 diagnostic models mentioned in the study are evaluated together, it is seen that the classification performance of the proposed hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model is quite high compared to the single EfficientNet-B0 model and combined model consisting of 2D curvelet transform and EfficientNet-B0. A significant improvement has been observed in the classification accuracy, specificity, precision, recall, and F-measure of EfficientNet-B0 model, which is trained with each image in the dataset with 2D curvelet transform applied, compared to the single EfficientNet-B0 model. It can be seen from Table 3 that CSSA has a prominent effect in improving the performance of the proposed COVID-19 diagnostic model in the study. It is seen that the proposed hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model is clearly superior to the models mentioned in the study in terms of performance metrics specified in Eqs. (9)–(13).
Fig. 10.
Change of training time versus epoch for proposed model.
Fig. 11.
Confusion matrix for classification of COVID‐19, normal and viral pneumonia using single EfficientNet-B0 model.
Fig. 12.
Confusion matrix for classification of COVID‐19, normal and viral pneumonia using combined model consisting of 2D curvelet transform and EfficientNet-B0.
Fig. 13.
Confusion matrix for classification of COVID‐19, normal and viral pneumonia using hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model.
Fig. 14.
(a) ROC curve obtained using single EfficientNet-B0 model, (b) ROC curve obtained using combined model consisting of 2D curvelet transform and EfficientNet-B0, (c) ROC curve obtained using hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model.
Table 3.
Performance results of the aforementioned models in the study.
| Accuracy (%) | Specificity (%) | Precision (%) | Recall (%) | F-measure (%) | |
|---|---|---|---|---|---|
| EfficientNet-B0 | 95.24 | 96.05 | 92.22 | 93.61 | 92.91 |
| 2D curvelet transform- EfficientNet-B0 | 96.87 | 97.46 | 94.96 | 95.68 | 95.32 |
| 2D curvelet transform-CSSA-EfficientNet-B0 | 99.69 | 99.81 | 99.62 | 99.44 | 99.53 |
The accuracy, specificity, precision, recall and F-mesure values of single EfficientNet-B0 model are 95.24%, 96.05%, 92.22%, 93.61% and 92.91%, respectively. The accuracy, specificity, precision, recall and F-mesure values of the model created by applying only 2D curvelet transformation are 96.87%, 97.46%, 94.96%, 95.68% and 95.32%, respectively. The accuracy, specificity, precision, recall and F-mesure values of the hybrid model, where the feature matrix is formed by finding optimal coefficients with CSSA optimization method, are 99.69%, 99.81%, 99.62%, 99.44% and 99.53%, respectively. The 2D curvelet transform-EfficientNet-B0 model compared to the single EfficientNet-B0 model, normal and viral pneumonia cases has been performed well in classification. The proposed model performed 100% in detecting COVID-19 cases. The proposed model also performed above 99% in the classification of normal and viral pneumonia cases. CCSA's success in determining curvelet coefficients has led to improved performance of our COVID-19 diagnostic model. So, the chaotic optimization algorithm in the study has been proven to have a local minima avoidance and rapid convergence rate. These features of CSSA significantly have been improved the performance of our COVID-19 diagnostic model and make our model robust. The minimum model complexity, high accuracy, high speed, and low calculation costs have played an important role in improving the performance of our proposed model. Further, when the confusion matrices and ROC graphs are examined, it is seen that the false estimation rate of the proposed model is lower than the other models mentioned in the study. When the proposed hybrid 2D curvelet transform-CSSA-EfficientNet-B0 model is compared with [41], which is one of the studies in the literature, it has been observed that the proposed model has higher performance in diagnosing and classifying COVID-19 cases. One of the remarkable things in our study is that the validity of the model is tested on a dataset which is approximately 9 times the dataset used in other studies. The results obtained according to the performance metrics in Table 3 clearly demonstrate the robustness of the proposed model.
4. Conclusion
It is critical to diagnose people infected with COVID-19 at an early stage, both to control the infectiousness of the epidemic and to begin treatment of the disease at an early phase. COVID-19 disease is diagnosed with high performance from the chest X-ray images by the hybrid model proposed in the study. The proposed model stands out for the diagnosis of COVID-19 disease thanks to its high performance, low cost of calculation, and robust. In order to improve the performance of the deep learning model EfficientNet-B0, which is known to have a low calculation cost, 2D Curvelet transform is applied to the images obtained from the patient's chest X-ray radiographs and a feature matrix is created using the obtained coefficients. The coefficients in the feature matrix have been optimized with the CSSA, whose processing time is relatively low, to provide that the model is robust. Our model has been tested on 1596 chest X-ray images and the test results obtained show that our model can classify COVID-19, normal and viral pneumonia with high accuracy. It is seen from obtained empirical results that the diagnose performance of the proposed hybrid model is clearly superior to the single deep learning model. The model, which has fast and low calculation cost, will help doctors to diagnose COVID-19 quickly and accurately in clinical studies. In future studies, the relationship between the chest X-ray images and symptoms of COVID-19 patients will be examined and chaotic optimization algorithms will be expanded to the multi-objective optimization area to solve this problem.
CRediT authorship contribution statement
Aytaç Altan: Conceptualization, Methodology, Software, Formal analysis, Writing - original draft, Writing - review & editing. Seçkin Karasu: Methodology, Software, Formal analysis.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Zhu N., Zhang D., Wang W., Li X., Yang B., Song J., ..., Niu P. A novel coronavirus from patients with pneumonia in China, 2019. N Engl J Med. 2020 doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.World Health Organization. (2020). Coronavirus disease 2019 (COVID-19): situation report, 154.
- 3.https://coronavirus.jhu.edu/map.html [Accessed April 11, 2020].
- 4.World Health Organization. (2020). Coronavirus disease 2019 (COVID-19): situation report, 51.
- 5.Liu Y., Gayle A.A., Wilder-Smith A., Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. Journal of travel medicine. 2020 doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Millán-Oñate J., Rodriguez-Morales A.J., Camacho-Moreno G., Mendoza-Ramírez H., Rodríguez-Sabogal I.A., Álvarez-Moreno C. A new emerging zoonotic virus of concern: the 2019 novel Coronavirus (COVID-19) Infectio. 2020;24(3) [Google Scholar]
- 7.Sohrabi C., Alsafi Z., O'Neill N., Khan M., Kerwan A., Al-Jabir A., ..., Agha R. World Health Organization declares global emergency: a review of the 2019 novel coronavirus (COVID-19) International Journal of Surgery. 2020 doi: 10.1016/j.ijsu.2020.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ahmed S.S. The Coronavirus Disease 2019 (COVID-19): a Review. Journal of Advances in Medicine and Medical Research. 2020:1–9. [Google Scholar]
- 9.https://www.ecdc.europa.eu/en/geographical-distribution-2019-ncov-cases. [Accessed June 22, 2020].
- 10.Riou J., Althaus C.L. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Eurosurveillance. 2020;25(4) doi: 10.2807/1560-7917.ES.2020.25.4.2000058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Arabi Y.M., Murthy S., Webb S. COVID-19: a novel coronavirus and a novel challenge for critical care. Intensive Care Med. 2020:1–4. doi: 10.1007/s00134-020-05955-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Salehi S., Abedi A., Balakrishnan S., Gholamrezanezhad A. Coronavirus disease 2019 (COVID-19): a systematic review of imaging findings in 919 patients. Am J Roentgenol. 2020:1–7. doi: 10.2214/AJR.20.23034. [DOI] [PubMed] [Google Scholar]
- 13.Yang W., Yan F. Patients with RT-PCR confirmed COVID-19 and normal chest CT. Radiology. 2020 doi: 10.1148/radiol.2020200702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Corman V.M., Landt O., Kaiser M., Molenkamp R., Meijer A., Chu D.K., ..., Mulders D.G. Detection of 2019 novel coronavirus (2019-nCoV) by real-time RT-PCR. Eurosurveillance. 2020;25(3) doi: 10.2807/1560-7917.ES.2020.25.3.2000045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang Y., Kang H., Liu X., Tong Z. Combination of RT‐qPCR Testing and Clinical Features For Diagnosis of COVID‐19 facilitates management of SARS‐CoV‐2 Outbreak. Journal of medical virology. 2020 doi: 10.1002/jmv.25721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ai T., Yang Z., Hou H., Zhan C., Chen C., Lv W., ..., Xia L. Correlation of chest CT and RT-PCR testing in coronavirus disease 2019 (COVID-19) in China: a report of 1014 cases. Radiology. 2020 doi: 10.1148/radiol.2020200642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu Y., Yan L.M., Wan L., Xiang T.X., Le A., Liu J.M., ..., Zhang W. Viral dynamics in mild and severe cases of COVID-19. The Lancet Infectious Diseases. 2020 doi: 10.1016/S1473-3099(20)30232-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bai H.X., Hsieh B., Xiong Z., Halsey K., Choi J.W., Tran T.M.L., ..., Jiang X.L. Performance of radiologists in differentiating COVID-19 from viral pneumonia on chest CT. Radiology. 2020 doi: 10.1148/radiol.2020200823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fang Y., Zhang H., Xie J., Lin M., Ying L., Pang P., Ji W. Sensitivity of chest CT for COVID-19: comparison to RT-PCR. Radiology. 2020 doi: 10.1148/radiol.2020200432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li Y., Yao L., Li J., Chen L., Song Y., Cai Z., Yang C. Stability Issues of RT‐PCR Testing of SARS‐CoV‐2 for Hospitalized Patients Clinically Diagnosed with COVID‐19. Journal of Medical Virology. 2020 doi: 10.1002/jmv.25786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li D., Wang D., Dong J., Wang N., Huang H., Xu H., Xia C. False-negative results of real-time reverse-transcriptase polymerase chain reaction for severe acute respiratory syndrome coronavirus 2: role of deep-learning-based CT diagnosis and insights from two cases. Korean J Radiol. 2020;21(4):505–508. doi: 10.3348/kjr.2020.0146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sheridan C. Fast, portable tests come online to curb coronavirus pandemic. Nat Biotechnol. 2020 doi: 10.1038/d41587-020-00010-2. [DOI] [PubMed] [Google Scholar]
- 23.Porcheddu R., Serra C., Kelvin D., Kelvin N., Rubino S. Similarity in case fatality rates (CFR) of COVID-19/SARS-COV-2 in Italy and China. The Journal of Infection in Developing Countries. 2020;14(02):125–128. doi: 10.3855/jidc.12600. [DOI] [PubMed] [Google Scholar]
- 24.Pan F., Ye T., Sun P., Gui S., Liang B., Li L., ..., Zheng C. Time course of lung changes on chest CT during recovery from 2019 novel coronavirus (COVID-19) pneumonia. Radiology. 2020 doi: 10.1148/radiol.2020200370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shi H., Han X., Jiang N., Cao Y., Alwalid O., Gu J., ..., Zheng C. Radiological findings from 81 patients with COVID-19 pneumonia in Wuhan, China: a descriptive study. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30086-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li M., Lei P., Zeng B., Li Z., Yu P., Fan B., ..., Liu H. Coronavirus Disease (COVID-19): spectrum of CT Findings and Temporal Progression of the Disease. Academic Radiology. 2020 doi: 10.1016/j.acra.2020.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Li L., Qin L., Xu Z., Yin Y., Wang X., Kong B., ..., Cao K. Artificial intelligence distinguishes covid-19 from community acquired pneumonia on chest ct. Radiology. 2020 doi: 10.1148/radiol.2020200905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Huang L., Han R., Ai T., Yu P., Kang H., Tao Q., Xia L. Serial Quantitative Chest CT Assessment of COVID-19: deep-Learning Approach. Radiology: Cardiothoracic Imaging. 2020;2(2) doi: 10.1148/ryct.2020200075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Candes E., Demanet L., Donoho D., Ying L. Fast discrete curvelet transforms. Multiscale Modeling & Simulation. 2006;5(3):861–899. [Google Scholar]
- 30.Górszczyk A., Malinowski M., Bellefleur G. Enhancing 3D post‐stack seismic data acquired in hardrock environment using 2D curvelet transform. Geophys Prospect. 2015;63(Hard Rock Seismic imaging):903–918. [Google Scholar]
- 31.Mirjalili S., Gandomi A.H., Mirjalili S.Z., Saremi S., Faris H., Mirjalili S.M. Salp Swarm Algorithm: a bio-inspired optimizer for engineering design problems. Adv Eng Software. 2017;114:163–191. [Google Scholar]
- 32.Zhang Y., Wang S., Ji G. A comprehensive survey on particle swarm optimization algorithm and its applications. Mathematical Problems in Engineering. 2015;2015 [Google Scholar]
- 33.Tavazoei M.S., Haeri M. An optimization algorithm based on chaotic behavior and fractal nature. J Comput Appl Math. 2007;206(2):1070–1081. [Google Scholar]
- 34.Mohanty F., Rup S., Dash B., Majhi B., Swamy M.N.S. An improved scheme for digital mammogram classification using weighted chaotic salp swarm algorithm-based kernel extreme learning machine. Appl Soft Comput. 2020 [Google Scholar]
- 35.Sayed G.I., Khoriba G., Haggag M.H. A novel chaotic salp swarm algorithm for global optimization and feature selection. Applied Intelligence. 2018;48(10):3462–3481. [Google Scholar]
- 36.Zhang J., Xie Y., Wu Q., Xia Y. Medical image classification using synergic deep learning. Med Image Anal. 2019;54:10–19. doi: 10.1016/j.media.2019.02.010. [DOI] [PubMed] [Google Scholar]
- 37.Jeyaraj P.R., Nadar E.R.S. Computer-assisted medical image classification for early diagnosis of oral cancer employing deep learning algorithm. J. Cancer Res. Clin. Oncol. 2019;145(4):829–837. doi: 10.1007/s00432-018-02834-7. [DOI] [PubMed] [Google Scholar]
- 38.Saba T., Mohamed A.S., El-Affendi M., Amin J., Sharif M. Brain tumor detection using fusion of hand crafted and deep learning features. Cogn Syst Res. 2020;59:221–230. [Google Scholar]
- 39.Vigneault D.M., Xie W., Ho C.Y., Bluemke D.A., Noble J.A. Ω-net (omega-net): fully automatic, multi-view cardiac MR detection, orientation, and segmentation with deep neural networks. Med Image Anal. 2018;48:95–106. doi: 10.1016/j.media.2018.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tan, M., & Le, Q.V. (2019). Efficientnet: rethinking model scaling for convolutional neural networks. arXiv preprint arXiv:1905.11946.
- 41.Chowdhury, M.E., Rahman, T., Khandakar, A., Mazhar, R., Kadir, M.A., Mahbub, Z.B., ... & Reaz, M.B.I. (2020). Can AI help in screening Viral and COVID-19 pneumonia? arXiv preprint arXiv:2003.13145.