Abstract
We derive an analytical connection between kinetic relaxation rate and bulk viscosity of a relativistic fluid in d spatial dimensions, all the way from the ultra-relativistic down to the near non-relativistic regime. Our derivation is based on both Chapman–Enskog asymptotic expansion and Grad’s method of moments. We validate our theoretical results against a benchmark flow, providing further evidence of the correctness of the Chapman–Enskog approach; we define the range of validity of this approach and provide evidence of mounting departures at increasing Knudsen number. Finally, we present numerical simulations of transport processes in quark-gluon plasmas, with special focus on the effects of bulk viscosity which might prove amenable to future experimental verification.
This article is part of the theme issue ‘Fluid dynamics, soft matter and complex systems: recent results and new methods’.
Keywords: relativistic hydrodynamics, quark-gluon plasma, bulk viscosity
1. Introduction
In the last decade, relativistic hydrodynamics has received renewed attention and interest thanks to major breakthroughs in condensed matter, high-energy and gravitational physics [1]. In particular, experimental data from the relativistic heavy-ion collider (RHIC) and the large Hadron collider (LHC), have triggered further developments in the study of viscous relativistic fluid dynamics, both at the level of theoretical formulations and for the development of robust numerical methods, to describe the collective behaviour of quark-gluon plasmas (QGP).
Several theoretical aspects related to a consistent formulation of dissipative relativistic hydrodynamics are still under debate in the literature [2–18], including the correct derivation of the values of the transport coefficients as a function of the parameters defined at the level of kinetic theory [19–27].
A proper understanding of transport properties is crucial for the study of the evolution and equilibration process of the QGP produced in heavy-ion collisions. The effects of shear viscosity on the elliptic flow parameters have been extensively studied by several authors [28–32]. The relevance of bulk viscosity, mostly regarded as negligible in the earlier days, has attracted significant attention in recent years [33–37]. For instance, it has been suggested that, near the critical point, bulk effects might be dominant over shear viscosity [38,39]. In this context, an accurate derivation of all transport coefficients and the availability of numerical tools capable of capturing the effects of bulk viscosity are desirable in a theoretical perspective and important also for the simulation of QGP. As a side note, we remark that a complete analysis of the role of bulk viscosity in relativistic hydrodynamics could also be beneficial for the theoretical understanding of the accelerated expansion of the universe [40–44].
In this work, we perform the Chapman–Enskog expansion to establish the analytic expression of bulk viscosity of a relativistic gas obeying an ideal equation of state and working in the single relaxation-time (SRT) approximation. The derivation is developed in a (d + 1) dimensional flat space–time. While d = 2, 3 are the most relevant physical cases, it is nevertheless interesting from a theoretical point of view to consider the general d-dimensional case. Indeed, the dependence of bulk viscosity on the relativistic parameter ζ = m c2/kB T (defined as the ratio between the particles rest energy and the thermal energy), is found to strongly depend on the dimensionality of the system.
Our analytical results are then compared and validated against numerical simulations, performed using a recently developed relativistic lattice kinetic scheme. We consider first a simple synthetic flow that we would like to suggest as a benchmark for the measurement and calibration of bulk viscosity and then a more complex flow with several features typical of QGP flows. This paper builds on previous work presented in [45], enriched with an extended set of new numerical results.
This paper is organized as follows: in §2, we briefly summarize the procedure followed to derive the analytic form of bulk viscosity working in the single relaxation time approximation. In §3, we present a numerical validation of the analytical results, also providing an example of application for which these results are relevant and of practical interest. Finally, conclusions and future developments are summarized in §4.
2. Relativistic Boltzmann equation and Chapman–Enskog expansion
We consider a (d + 1) dimensional flat space–time, in which a statistical description of a relativistic fluid is given in terms of the particle distribution function f((xα), (pα)), depending on coordinates (xα) = (c t, x), with c the light speed and momenta (pα) = (p0, p), with .
The time evolution of the system is governed by the relativistic Boltzmann equation, that we take in the Anderson–Witting [46,47] SRT approximation
| 2.1 |
with τ the relaxation (proper-) time, Uμ the relativistic fluid velocity and feq the equilibrium distribution function, for which we take the normalized Maxwell–Jüttner distribution
| 2.2 |
In the above, n is the particle number density, T the temperature, ζ (already referred to in the Introduction) is the ratio between the rest mass of the particles m and the temperature (ζ = m c2/kBT), Ki(x) the modified Bessel function of the second kind of order i and kB the Boltzmann constant.
The Anderson–Witting collisional operator ensures the local conservation of particle number, energy and momentum. Dissipative effects are described by the energy momentum tensor, which in the Landau–Lifshitz frame admits the following decomposition:
| 2.3 |
with ϵ the energy density, P the hydrostatic pressure and Δαβ the Minkowski–orthogonal projector with respect to the fluid velocity Uα
| 2.4 |
ηαβ is the metric tensor, that we define as , . Finally, and most importantly in this treatment, the pressure deviator π〈αβ〉 (here the 〈…〉 parentheses represent the traceless symmetric contribution to Tαβ) and dynamic pressure represent the non-equilibrium contribution to the energy momentum tensor, proportional to shear viscosity η and bulk viscosity μ, respectively. It can be shown [48] that bulk viscosity connects dynamic pressure and the divergence of the velocity via the relation
| 2.5 |
Asymptotic expansions are generally employed in order to establish a link between macroscopic equations and the kinetic description. In the following, we perform the Chapman–Enskog expansion [49] to determine an analytic expression putting in relation the bulk viscosity with the kinetic relaxation time parameter. Here, we confine ourselves to a summary of the main conceptual steps, while full details on the analytic procedure can be found in [45].
The starting point is an expansion of the particle distribution function f around equilibrium
| 2.6 |
with ϕ of the order of the Knudsen number Kn, defined as the ratio between the mean free path and a typical macroscopic length scale. Next, we plug equation (2.6) into equation (2.1), and retain only terms
| 2.7 |
By combining the above with equation (2.2) lengthy but straightforward calculations allow us to derive an analytic expression for ϕ
| 2.8 |
where
| 2.9 |
At this point, it is possible to use equation (2.6) to compute the energy-momentum tensor Tαβ through its integral definition. Moreover, from equation (2.3) one can single out the dynamic pressure by applying the projector Δαβ, giving
| 2.10 |
By comparing equation (2.5) with equation (2.10), and matching term by term we identify the following analytic expression for bulk viscosity
| 2.11 |
Following a similar procedure, it is possible to extract a value also for the shear viscosity η, that we show here for completeness (further details on the derivation can be found in [45])
| 2.12 |
Grad’s method of moments [50] provides an alternate procedure to connect kinetic parameters with hydrodynamics coefficients. Although there is a growing consensus on CE providing more accurate results with respect to Grad’s method [10,11,13,18,23,24,45,51,52] it is nevertheless interesting to compare the two. Following the procedure described in [48], we obtain the following expressions for the bulk and shear viscosity of a relativistic fluid in (d + 1) dimensions
| 2.13 |
and
| 2.14 |
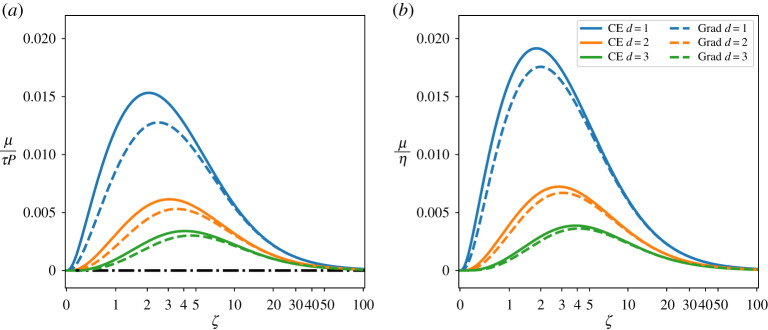
We compare the behaviour of μ obtained using CE and Grad’s method of moments in 1, 2 and 3 space dimensions in figure 1a. Both methods correctly reproduce the expected limiting behaviour for which bulk viscosity vanishes in the ultra-relativistic (ζ → 0) and non-relativistic (ζ → ∞) limit. However, there is an intermediate region for which a non-zero bulk viscosity is predicted and for which the two derivations yield different values for both the amplitude and the location of the peak. Despite the bulky analytical expressions, the position of the maximum, ζmax, is found to have a very simple linear dependence on the dimension of the system: ζmax = α1 d + α0, with α1 consistent with 1 in both cases, and α0 ≈ 0.744 for CE, α0 ≈ 1.235 for Grad. As an amusing theoretical remark, we also observe that, in the limit of infinite spatial dimensions, bulk viscosity vanishes for all values of ζ.
Figure 1.
(a) Bulk viscosity is plotted against the parameter ζ with a dependence given by the CE analysis (thick lines) and Grad’s method (dashed lines). The discrepancy between the two asymptotic expansions in more prominent in the mildly relativistic regime. The black dashed line represents the viscosity in the limit of infinite spatial dimensions, common to both CE and Grad’s method, where the transport coefficient is independent of ζ. (b) The ratio between the bulk and the shear viscosity (η) is plotted as a function of ζ. (Online version in colour.)
Finally, we conclude our analysis pointing out one important limitation of the Anderson–Witting collisional operator: since this model depends on a single mesoscopic parameter it follows that the relaxation rate will be the same for all the transport coefficients. As a consequence one cannot tune independently shear and bulk viscosity; their ratio is shown in figure 1b.
3. Numerical simulations
In this section, we make use of a recently developed lattice kinetic solver [24,53] and present results of numerical tests which aim at (i) cross-checking and validating the analytical results presented in the previous section and (ii) providing an example of a realistic application to the physics of QGP. We first give a short overview of the lattice kinetic algorithm that we have used (a detailed derivation can be found in [45]) and then proceed to present the numerical tests.
(a). I: Numerical scheme
The relativistic lattice Boltzmann method is a computationally efficient approach to dissipative relativistic hydrodynamics. It is based on a mesoscale approach, and therefore it has the advantage, with respect to other relativistic hydrodynamic solvers, that the emergence of viscous effects does not break relativistic invariance and causality, since space and time are treated on the same footing, i.e. both via first-order derivatives.
This numerical method solves a minimal version of equation (2.1), in which the discretization of the microscopic momentum vector on a Cartesian grid is coupled with a Gauss-type quadrature (see [24,45] for the formal analytic derivation) which ensures the preservation of the lower (hydrodynamics) moments of the particle distribution
| 3.1 |
In the above, are the microscopic velocities, chosen in such a way as to (i) preserve exact streaming (meaning that (pseudo)-particles travel in one time step along constant streamlines x + viΔt from a point of the grid to another point of the grid) (ii) together with an appropriate set of weights wi reproduce correctly the moments of the particle distribution up to order N. Given this two conditions, can be defined as the discrete version of a polynomial expansion of the equilibrium distribution
| 3.2 |
refer to appendix F and G in [45] for the definition of the polynomials and the projection coefficients used in the expansion. The numerical analysis presented in the coming section is based on numerical simulations making use of third-order quadratures (N = 3), which are listed in appendix H in [45].
The time evolution of equation (3.1) follows the collide-streaming paradigm typical of classic Lattice Boltzmann schemes. At each time step, and for each grid cell, we need to compute the macroscopic fields associated with the particle distribution. In order to do so we start by computing the first and second moment of distribution
From the definition of the energy-momentum tensor in the Landau frame (equation 2.3), we compute the energy density ϵ and the four velocity Uα by solving the eigenvalue problem
where ϵ corresponds to the largest eigenvalue of Tαβ. The particle density n comes from the definition of the first-order moment, while temperature and pressure follow from the ideal equation of state
| 3.3 |
At this stage, it is possible to compute the polynomial expansion of the equilibrium distribution, defined in equation (3.2), and use it to evolve equation (3.1).
(b). II: validation and calibration
Following the same approach used in previous works on the analysis of shear viscosity and thermal conductivity [24,25,52], we compare our analytical predictions for bulk viscosity with data from numerical simulations.
We consider a simple synthetic flow describing a time-decaying sinusoidal wave in a d dimensional periodic domain; this flow is characterized by sizeable velocity gradients, allowing the detection of physical effects due to a non-zero bulk viscosity. The initial conditions for the benchmark are as follows:
| 3.4 |
with v0 a given initial velocity, and with constant initial values for both particle density and temperature.
In order to numerically evaluate the dynamic pressure, we introduce the definition of the energy-momentum tensor at the equilibrium , which follows from equation (2.3):
| 3.5 |
The dynamic pressure can then be expressed as the trace of the difference between the energy momentum tensor and its equilibrium counterpart
| 3.6 |
When considering flows at sufficiently low speeds (v0 ≪ c), it is reasonable to approximate the relativistic divergence with its non-relativistic counterpart. It follows that we can numerically measure to good accuracy at each time step of the simulations, thus allowing an estimate of μ directly from equation (2.5)
| 3.7 |
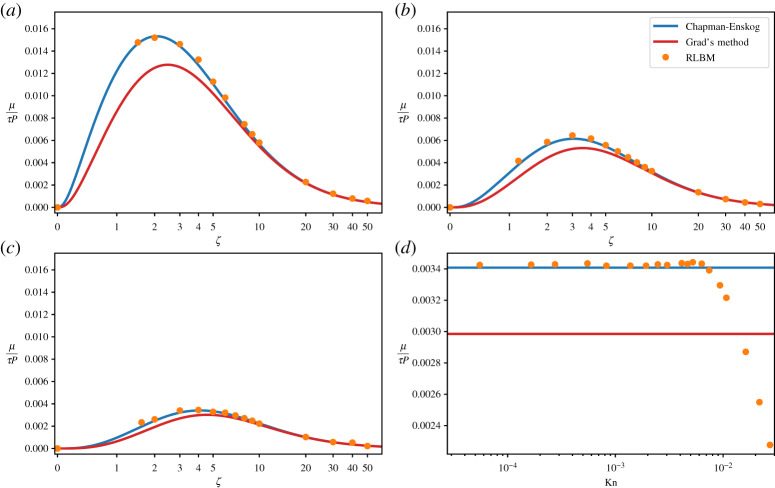
We have performed several simulations varying the mesoscopic parameters τ and ζ and extracted the expression for μ as a function of ζ in various spatial dimensions. Our results, see figure 2, confirm that the CE analysis is in excellent agreement with numerical results.
Figure 2.
Numerical estimate of the (non-dimensional) bulk viscosity for a relativistic gas in (1 + 1), (2 + 1) and (3 + 1) dimensions, shown, respectively, in (a–c). The results are in agreement with CE analysis. In (d), we consider the specific case ζ = 4 in three dimensions and show how the estimate for μ varies as a function of the Knudsen number. We estimate the Knudsen number using Kn = 〈v〉τ/L, where 〈v〉 is an estimate of the mean velocity of the particles of the relativistic fluid [48], and L the typical length scale of the system, for which we consider the wavelength of the sine wave. One can see that as Kn increases the first-order approximation given by both CE and Grad is no longer valid. (Online version in colour.)
We point out that the choice of the relaxation time τ is key to obtain accurate results. The linear relationship between μ and τ holds as long as the assumptions made in the Chapman–Enskog analysis remain valid, in particular the assumption of small Knudsen numbers. Conversely, for large values of τ, that is for regimes where a purely hydrodynamic treatment becomes questionable, the relation between the transport coefficients and the relaxation time is expected to depart from linearity [23]. This behaviour is measured in figure 2d, for a specific case in three dimensions at ζ = 4: we plot the fitted value for μ/τP against the Knudsen number Kn, clearly showing that for numerical data start to diverge from the CE prediction. One can expect better agreement when including higher order terms in the ansatz in equation (2.6), although this topic is still under debate in the literature since gradient-expansions are notoriously divergent [54,55].
(c). III: Application
In this section, we present a second simulation example where we consider a qualitative description of a relativistic elliptic flow, thus mimicking the evolution of the initial stages of heavy-ion collisions.
We adopt the same numerical setup used in a series of studies on spin-polarized relativistic flows [56–58], neglecting however quantum effects. The equation of state used in these simulations is the ideal one shown in equation (3.3). Simulations of elliptic flows with different equation of state implementations can be found, for example, in [59].
The initial conditions are given by a Gaussian distribution for both the temperature and density profiles
| 3.8 |
with σx = 1 fm, σy = 2.6 fm and σz = 2 fm. The resulting ellipsoid represents the overlapping zone in the collision between two heavy nuclei, with the fluid representing the product of such a collision, a hot, dense and strongly anisotropic ‘fireball’ of QGP. The initial temperature at the origin of the axis is T0 = 200 MeV, with n0 = 4 × 10−3 fm−3. In order to avoid numerical instabilities, we include a background temperature of T = 80 MeV and density of n = 1 × 10−3 fm−3.
The initial velocity profile is given by
| 3.9 |
with the distance from the centre of the vortex in the transverse plane, and r0 a parameter controlling the strength of the flow. This initial condition, due to the limit posed by the speed of light, is physically meaningful only inside a maximum radius R < 1/Ω; in what follows we use R = 3 fm and r0 = 6 fm. We consider a viscous regime where the ratio between the shear viscosity η and the entropy density s is kept fixed at 2/(4π), comparing simulations for different values of the rest mass of the particles in the fluid, with respectively mc2 = 0, 1, 2 GeV. All simulations pertain to a cubic domain of size 20 fm, using 1283 grid points.
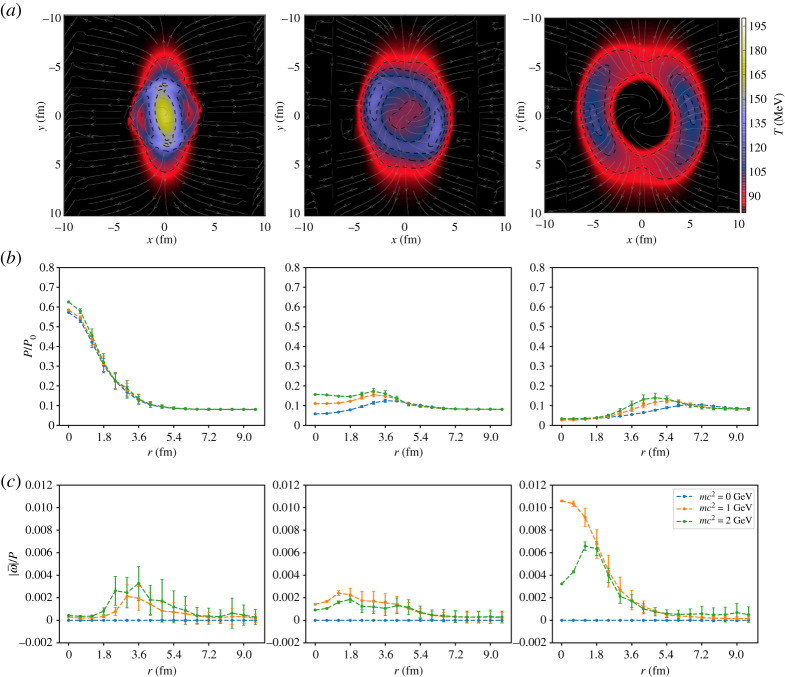
Figure 3a shows the temperature profile of the system in the x–y plane at z = 0 fm at three different time steps, from left to right t = 1, 4, 8 fm/c. In the QGP framework, one is interested in measuring the translation of the initial spatial anisotropy into a momentum space anisotropy (which can be measured in experiments). The discretization of the momentum space, upon which our numerical scheme relies, does not allow us to perform direct measurements of the elliptic flow coefficients; therefore, here we will only show that bulk viscosity effects can indeed be detected and measured, leaving a more detailed analysis to future works. With this aim, we perform measurements of macroscopic observables spatially averaged at fixed radial distance from the centre of the ellipsoid. Figure 3b,c shows, respectively, the hydrostatic pressure and the ratio between dynamic and hydrostatic pressure. Vertical bars, representing the variance, are larger at radial distances where the flow still exhibits a significant spatial anisotropy. The effect of the rest mass of the particles in the fluid is evident: the dynamic slows down when heavier particles are taken in consideration. For massless particles, the ratio between the dynamic pressure is zero up to numerical accuracy, independently of the radial distance, as expected from the analytical and numerical analysis presented in the previous sections. On the other hand, for massive particles, non-equilibrium contributions due to bulk viscosity become noticeable. In these cases, strongly varies across the domain, taking values larger than 1% of the hydrostatic pressure.
Figure 3.
Dynamic evolution of a fireball of QGP at three different time steps: t = 1 fm/c on the left panels, t = 4 fm/c on the central panels, t = 8 fm/c on the right panels. (a) The evolution of both the temperature (colour map) and the velocity (grey arrows) fields, on a slice of the system. (b,c) The time evolution of, respectively, the hydrostatic pressure (normalized respect to the initial pressure value at centre) and ratio of dynamic to hydrostatic pressure, for three different values of the particle mass m. While for m = 0 the dynamic pressure is always zero, it is not the case when m ≠ 0. This shows that in this kind of dynamic the bulk viscosity plays a subtle, but still relevant role. (Online version in colour.)
We stress here that although the dissipative dynamic in the system is inherently connected to both shear and bulk effects (and due to the single relaxation time nature of the numerical scheme a separate tuning of the two effects is not possible) the specific effects of bulk viscosity are singled out by the behaviour of the dynamic pressure via equation (2.5), since this quantity is affected only by the value of μ.
4. Conclusion
Summarizing, in this work, we have highlighted the role of bulk viscosity μ on the dynamics of a relativistic monoatomic gas. Using the Chapman–Enskog expansion and Grad’s method of moments, we have presented an analytical formulation in (d + 1) dimensions, showing the dependence of bulk viscosity on the kinetic relaxation time τ and the relativistic parameter ζ = m c2/kB T.
Our analysis shows that, at variance with both the ultra-relativistic and non-relativistic regimes, there is a region in ζ space where bulk viscosity is non-zero, whose location and extension depend on the dimensionality of the system. Next, in order to discern between the two expansion methods, a numerical validation has been presented. Once more, the correctness of the Chapman–Enskog analysis over Grad’s method has been proved, in analogy with what happens for shear viscosity and thermal conductivity; this result paves the way to the correct reproduction of viscous effects in relativistic simulations. In the same context, the measure of μ at different values of τ has allowed for testing the first-order approximations in both CE and Grad’s theory, clearly identifying the kinematic range where a hydrodynamic description is appropriate. Finally, a more realistic benchmark has been presented in the framework of QGP physics. In detail, a strongly anisotropic hot dense plasma, resulting from the Lorentz contraction of heavy-ion collisions, has been simulated, highlighting the presence of bulk-related viscous effects on the transport properties of the QGP.
One limit of SRT models is that they link multiple hydrodynamic coefficients to a single relaxation time, thus preventing the independent tuning of two viscosities. For this reason, the development of a multi-relaxation time numerical scheme, and the corresponding derivation of transport coefficients, is highly desirable for future studies of relativistic transport phenomena.
Data accessibility
This article has no additional data.
Authors' contributions
A.G. carried out the numerical simulations, participated in the design of the benchmark, realized the physical simulation and figures. D.S. carried out the analytical calculations, participated in the design of the benchmark. A.G. and S.S. and R.T. conceived and designed the study. S.S. and RT coordinated the study, drafted and critically revised the manuscript. All authors participated in the writing of the manuscript and gave final approval for publication and agree to be held accountable for the work performed therein.
Competing interests
We declare we have no competing interest.
Funding
The authors thank Victor Ambruş for useful discussions. D.S. has been supported by the European Union’s Horizon 2020research and innovation programme under the Marie Sklodowska-Curiegrant agreement No. 765048. S.S. acknowledges funding from the European Research Council under the European Union’s Horizon 2020 framework programme (grant no. P/2014-2020)/ERCgrant agreement no. 739964 (COPMAT). All the numerical work has been performed on the COKA computing cluster at Università di Ferrara.
Reference
- 1.Romatschke P, Romatschke U. 2019. Relativistic fluid dynamics in and out of equilibrium: and applications to relativistic nuclear collisions. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 2.Muronga A. 2007. Relativistic dynamics of nonideal fluids: viscous and heat-conducting fluids. I. General aspects and 3 + 1 formulation for nuclear collisions. Phys. Rev. C 7, 014909 ( 10.1103/PhysRevC.76.014909) [DOI] [Google Scholar]
- 3.Muronga A. 2007. Relativistic dynamics of non-ideal fluids: viscous and heat-conducting fluids. II. Transport properties and microscopic description of relativistic nuclear matter. Phys. Rev. C 7, 014910 ( 10.1103/PhysRevC.76.014910) [DOI] [Google Scholar]
- 4.Betz B, Henkel D, Rischke DH. 2009. Complete second-order dissipative fluid dynamics. J. Phys. G: Nucl. Part. Phys. 3, 064029 ( 10.1088/0954-3899/36/6/064029) [DOI] [Google Scholar]
- 5.El A, Xu Z, Greiner C. 2010. Extension of relativistic dissipative hydrodynamics to third order. Phys. Rev. C 8, 041901 ( 10.1103/PhysRevC.81.041901) [DOI] [Google Scholar]
- 6.Denicol GS, Koide T, Rischke DH. 2010. Dissipative relativistic fluid dynamics: a new way to derive the equations of motion from kinetic theory. Phys. Rev. Lett. 10, 162501 ( 10.1103/PhysRevLett.105.162501) [DOI] [PubMed] [Google Scholar]
- 7.Betz B, Denicol GS, Koide T, Molnár E, Niemi H, Rischke DH. 2011. Second order dissipative fluid dynamics from kinetic theory. EPJ Web Conf. 1, 07005 ( 10.1051/epjconf/20111307005) [DOI] [Google Scholar]
- 8.Denicol GS, Niemi H, Molnár E, Rischke DH. 2012. Derivation of transient relativistic fluid dynamics from the Boltzmann equation. Phys. Rev. D 8, 114047 ( 10.1103/PhysRevD.85.114047) [DOI] [Google Scholar]
- 9.Molnár E, Niemi H, Denicol GS, Rischke DH. 2014. Relative importance of second-order terms in relativistic dissipative fluid dynamics. Phys. Rev. D 8, 074010 ( 10.1103/PhysRevD.89.074010) [DOI] [Google Scholar]
- 10.Tsumura K, Kunihiro T. 2012. Derivation of relativistic hydrodynamic equations consistent with relativistic Boltzmann equation by renormalization-group method. Eur. Phys. J. A 4, 162 ( 10.1140/epja/i2012-12162-x) [DOI] [Google Scholar]
- 11.Tsumura K, Kikuchi Y, Kunihiro T. 2015. Relativistic causal hydrodynamics derived from Boltzmann equation: a novel reduction theoretical approach. Phys. Rev. D 9, 085048 ( 10.1103/PhysRevD.92.085048) [DOI] [Google Scholar]
- 12.Jaiswal A, Bhalerao RS, Pal S. 2013. Complete relativistic second-order dissipative hydrodynamics from the entropy principle. Phys. Rev. C 8, 021901 ( 10.1103/PhysRevC.87.021901) [DOI] [Google Scholar]
- 13.Jaiswal A. 2013. Relativistic dissipative hydrodynamics from kinetic theory with relaxation-time approximation. Phys. Rev. C 8, 051901 ( 10.1103/PhysRevC.87.051901) [DOI] [Google Scholar]
- 14.Jaiswal A. 2013. Relativistic third-order dissipative fluid dynamics from kinetic theory. Phys. Rev. C 8, 021903 ( 10.1103/PhysRevC.88.021903) [DOI] [Google Scholar]
- 15.Bhalerao RS, Jaiswal A, Pal S, Sreekanth V. 2013. Particle production in relativistic heavy-ion collisions: a consistent hydrodynamic approach. Phys. Rev. C 8, 044911 ( 10.1103/PhysRevC.88.044911) [DOI] [Google Scholar]
- 16.Chattopadhyay C, Jaiswal A, Pal S, Ryblewski R. 2015. Relativistic third-order viscous corrections to the entropy four-current from kinetic theory. Phys. Rev. C 9, 024917 ( 10.1103/PhysRevC.91.024917) [DOI] [Google Scholar]
- 17.Kikuchi Y, Tsumura K, Kunihiro T. 2015. Derivation of second-order relativistic hydrodynamics for reactive multicomponent systems. Phys. Rev. C 9, 064909 ( 10.1103/PhysRevC.92.064909) [DOI] [Google Scholar]
- 18.Kikuchi Y, Tsumura K, Kunihiro T. 2016. Mesoscopic dynamics of fermionic cold atoms—quantitative analysis of transport coefficients and relaxation times. Phys. Lett. A 38, 2075–2080. ( 10.1016/j.physleta.2016.04.027) [DOI] [Google Scholar]
- 19.Mendoza M, Karlin I, Succi S, Herrmann HJ. 2013. Ultrarelativistic transport coefficients in two dimensions. J. Stat. Mech: Theory Exp. 201, P02036 ( 10.1088/1742-5468/2013/02/P02036) [DOI] [Google Scholar]
- 20.Bhalerao RS, Jaiswal A, Pal S, Sreekanth V. 2014. Relativistic viscous hydrodynamics for heavy-ion collisions: a comparison between the Chapman-Enskog and grad methods. Phys. Rev. C 8, 054903 ( 10.1103/PhysRevC.89.054903) [DOI] [Google Scholar]
- 21.Florkowski W, Jaiswal A, Maksymiuk E, Ryblewski R, Strickland M. 2015. Relativistic quantum transport coefficients for second-order viscous hydrodynamics. Phys. Rev. C 9, 054907 ( 10.1103/PhysRevC.91.054907) [DOI] [Google Scholar]
- 22.García-Perciante AL, Méndez AR, Escobar-Aguilar E. 2017. Heat flux for a relativistic dilute bidimensional gas. J. Stat. Phys. 16, 123–134. ( 10.1007/s10955-017-1742-x) [DOI] [Google Scholar]
- 23.Ambruş VE. 2018. Transport coefficients in ultrarelativistic kinetic theory. Phys. Rev. C 9, 024914. [Google Scholar]
- 24.Gabbana A, Mendoza M, Succi S, Tripiccione R. 2017. Kinetic approach to relativistic dissipation. Phys. Rev. E 9, 023305 ( 10.1103/PhysRevE.96.023305) [DOI] [PubMed] [Google Scholar]
- 25.Gabbana A, Simeoni D, Succi S, Tripiccione R. 2019. Relativistic dissipation obeys Chapman-Enskog asymptotics: analytical and numerical evidence as a basis for accurate kinetic simulations. Phys. Rev. E 9, 052126 ( 10.1103/PhysRevE.99.052126) [DOI] [PubMed] [Google Scholar]
- 26.García-Perciante AL, Franco-Pérez L, Méndez AR. 2019. Bulk viscosity in 2D relativistic uids: the effects of temperature and modifications to the Rayleigh-Brillouin spectrum. J. Phys: Conf. Ser. 123, 012003 ( 10.1088/1742-6596/1239/1/012003) [DOI] [Google Scholar]
- 27.García-Perciante A, Méndez AR. 2019. Dissipative properties of relativistic two-dimensional gases. Physica A 53, 121559 ( 10.1016/j.physa.2019.121559) [DOI] [Google Scholar]
- 28.Heinz U, Song H, Chaudhuri AK. 2006. Dissipative hydrodynamics for viscous relativistic fluids. Phys. Rev. C 7, 034904 ( 10.1103/PhysRevC.73.034904) [DOI] [Google Scholar]
- 29.Romatschke P, Romatschke U. 2007. Viscosity information from relativistic nuclear collisions: how perfect is the fluid observed at RHIC? Phys. Rev. Lett. 9, 172301 ( 10.1103/PhysRevLett.99.172301) [DOI] [PubMed] [Google Scholar]
- 30.Song H, Heinz U. 2008. Causal viscous hydrodynamics in 2 + 1 dimensions for relativistic heavy-ion collisions. Phys. Rev. C 7, 064901 ( 10.1103/PhysRevC.77.064901) [DOI] [Google Scholar]
- 31.Song H, Heinz U. 2008. Multiplicity scaling in ideal and viscous hydrodynamics. Phys. Rev. C 7, 024902 ( 10.1103/PhysRevC.78.024902) [DOI] [Google Scholar]
- 32.Molnar D, Huovinen P. 2008. Dissipative effects from transport and viscous hydrodynamics. J. Phys. G: Nucl. Part. Phys. 3, 104125 ( 10.1088/0954-3899/35/10/104125) [DOI] [Google Scholar]
- 33.Denicol GS, Kodama T, Koide T, Mota P. 2009. Effect of bulk viscosity on elliptic flow near the QCD phase transition. Phys. Rev. C 8, 064901 ( 10.1103/PhysRevC.80.064901) [DOI] [Google Scholar]
- 34.Bożek P. 2010. Bulk and shear viscosities of matter created in relativistic heavy-ion collisions. Phys. Rev. C 8, 034909. [Google Scholar]
- 35.Dobado A, Torres-Rincon JM. 2012. Bulk viscosity and the phase transition of the linear sigma model. Phys. Rev. D 8, 074021 ( 10.1103/PhysRevD.86.074021) [DOI] [Google Scholar]
- 36.Noronha-Hostler J, Denicol GS, Noronha J, Andrade RPG, Grassi F. 2013. Bulk viscosity effects in event-by-event relativistic hydrodynamics. Phys. Rev. C 8, 044916 ( 10.1103/PhysRevC.88.044916) [DOI] [Google Scholar]
- 37.Kadam GP, Mishra H. 2015. Bulk and shear viscosities of hot and dense hadron gas. Nucl. Phys. A 93, 133–147. ( 10.1016/j.nuclphysa.2014.12.004) [DOI] [Google Scholar]
- 38.Karsch F, Kharzeev D, Tuchin K. 2008. Universal properties of bulk viscosity near the QCD phase transition. Phys. Lett. B 66, 217–221. ( 10.1016/j.physletb.2008.01.080) [DOI] [Google Scholar]
- 39.Meyer HB. 2008. Calculation of the bulk viscosity in SU(3) gluodynamics. Phys. Rev. Lett. 10, 162001 ( 10.1103/PhysRevLett.100.162001) [DOI] [PubMed] [Google Scholar]
- 40.Dou X, Meng X. 2011. Bulk viscous cosmology: unified dark matter. Advances in Astronomy.
- 41.Gagnon J, Lesgourgues J. 2011. Dark goo: bulk viscosity as an alternative to dark energy. J. Cosmol. Astropart. Phys. 201, 026 ( 10.1088/1475-7516/2011/09/026) [DOI] [Google Scholar]
- 42.Velten H, Wang J, Meng X. 2013. Phantom dark energy as an effect of bulk viscosity. Phys. Rev. D 8, 123504 ( 10.1103/PhysRevD.88.123504) [DOI] [Google Scholar]
- 43.Velten H. 2014. Viscous cold dark matter in agreement with observations. Int. J. Geom. Methods Mod. Phys. 1, 1460013 ( 10.1142/S0219887814600135) [DOI] [Google Scholar]
- 44.Atreya A, Bhatt J, Mishra A. 2018. Viscous self interacting dark matter and cosmic acceleration. J. Cosmol. Astropart. Phys. 201, 024–024 ( 10.1088/1475-7516/2018/02/024) [DOI] [Google Scholar]
- 45.Gabbana A, Simeoni D, Succi S, Tripiccione R. 2020. Relativistic lattice Boltzmann methods: theory and applications. (http://arxiv.org/abs/1909.04502).
- 46.Anderson J, Witting H. 1974. A relativistic relaxation-time model for the Boltzmann equation. Physica 7, 466–488. ( 10.1016/0031-8914(74)90355-3) [DOI] [Google Scholar]
- 47.Anderson J, Witting H. 1974. Relativistic quantum transport coefficients. Physica 7, 489–495. ( 10.1016/0031-8914(74)90356-5) [DOI] [Google Scholar]
- 48.Cercignani C, Kremer GM. 2002. The Relativistic Boltzmann Equation: Theory and Applications. Basel, Switzerland: Birkhüser Basel. [Google Scholar]
- 49.Chapman S, Cowling TG. 1970. The Mathematical Theory of Non-Uniform Gases. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 50.Grad H. On the kinetic theory of rarefied gases. Commun. Pure Appl. Math. 2, 331–407. [Google Scholar]
- 51.Plumari S, Puglisi A, Scardina F, Greco V. 2012. Shear viscosity of a strongly interacting system: Green-Kubo correlator versus Chapman-Enskog and relaxation-time approximations. Phys. Rev. C 8, 054902 ( 10.1103/PhysRevC.86.054902) [DOI] [Google Scholar]
- 52.Coelho RC, Mendoza M, Doria MM, Herrmann HJ. 2018. Fully dissipative relativistic lattice Boltzmann method in two dimensions. Comput. Fluids 17, 318–331. ( 10.1016/j.compfluid.2018.04.023) [DOI] [Google Scholar]
- 53.Gabbana A, Mendoza M, Succi S, Tripiccione R. 2017. Towards a unified lattice kinetic scheme for relativistic hydrodynamics. Phys. Rev. E 9, 053304 ( 10.1103/PhysRevE.95.053304) [DOI] [PubMed] [Google Scholar]
- 54.Denicol GS, Noronha J. 2016 Divergence of the chapman-enskog expansion in relativistic kinetic theory (August). (http://arxiv.org/abs/1608.07869. )
- 55.Noronha J, Denicol GS. 2017. The onset of fluid-dynamical behavior in relativistic kinetic theory. Nucl. Phys. A 967, 417–420. ( 10.1016/j.nuclphysa.2017.05.041) [DOI] [Google Scholar]
- 56.Florkowski W, Friman B, Jaiswal A, Speranza E. 2018. Relativistic fluid dynamics with spin. Phys. Rev. C 9, 041901 ( 10.1103/PhysRevC.97.041901) [DOI] [Google Scholar]
- 57.Florkowski W, Friman B, Jaiswal A, Ryblewski R, Speranza E. 2018. Spin-dependent distribution functions for relativistic hydrodynamics of spin- particles. Phys. Rev. D 9, 116017 ( 10.1103/PhysRevD.97.116017) [DOI] [Google Scholar]
- 58.Florkowski W, Friman B, Jaiswal A, Ryblewski R, Speranza E. 2019 Relativistic fluid dynamics of spin-polarized systems of particles, arXiv preprint (January). (http://arxiv.org/abs/1901.00352. )
- 59.Niemi H, Denicol GS, Huovinen P, Molnár E, Rischke DH. 2011. Influence of shear viscosity of quark-gluon plasma on elliptic flow in ultrarelativistic heavy-ion collisions. Phys. Rev. Lett. 10, 212302 ( 10.1103/PhysRevLett.106.212302) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article has no additional data.