Significance
Proper circulation of white blood cells (WBCs) in the pulmonary blood capillary network is crucial for a healthy immune watch. The remarkable mechanical properties of monocytes, a class of WBCs, allow them to gradually adapt their shape as they pass through the narrowest capillaries, ensuring a transition from a slow motion by hops at the entrance of the capillary network to a smooth and rapid circulation. The key parameters are a low cell cortical tension allowing adaptation of the cell shape, but high enough to prevent cell breakage when passing through the network bifurcations, and a high cell internal viscosity to maintain an elongated shape throughout the network.
Keywords: microfluidics, monocyte, cortical tension, pulmonary network
Abstract
Proper circulation of white blood cells (WBCs) in the pulmonary vascular bed is crucial for an effective immune response. In this branched vascular network, WBCs have to strongly deform to pass through the narrowest capillaries and bifurcations. Although it is known that this process depends on the cell mechanical properties, it is still poorly understood due to the lack of a comprehensive model of cell mechanics and of physiologically relevant experiments. Here, using an in-house microfluidic device mimicking the pulmonary capillary bed, we show that the dynamics of THP1 monocytes evolves along successive capillary-like channels, from a nonstationary slow motion with hops to a fast and smooth efficient one. We used actin cytoskeleton drugs to modify the traffic dynamics. This led us to propose a simple mechanical model that shows that a very finely tuned cortical tension combined with a high cell viscosity governs the fast transit through the network while preserving cell integrity. We finally highlight that the cortical tension controls the steady-state cell velocity via the viscous friction between the cell and the channel walls.
The efficient circulation of white blood cells (WBCs) in the microvasculature is a key factor for proper body protection. The microvasculature is a complex network of interconnected narrow capillaries, that, in many organs, have cross-sections smaller than the diameters of WBCs. A prominent example is the pulmonary bed whose capillary diameters range from 2 m to 15 m (1, 2), while those of neutrophils, the most common type of WBCs (60 to 70 of all WBCs), range from 6 m to 8 m (1, 3), and those of monocytes (7 of all WBCs), even larger, vary between 15 m and 30 m (4). WBCs must therefore deform when they transit from pulmonary arterioles to pulmonary venules, passing through 8 to 17 alveolar walls, that is, 40 to 100 alveolar capillaries of a few micrometers in diameter and length (1, 2). The deformation process, directly governed by the WBC rheological properties, is slow and results in temporary cell arrests at the entrance of the narrowest capillaries (5). This characteristic motion by hops (3, 5, 6) is associated with a prolonged transit time in the lungs compared to plasma or highly deformable red blood cells (7, 8). An increase in the rigidity of WBCs is considered sufficient for them to be trapped in the pulmonary capillaries, facilitating their subsequent adhesion and degradation on the capillary walls (9, 10). For example, neutrophils stiffened by inflammation molecules released during acute respiratory distress syndrome (10, 11) are massively trapped in pulmonary capillaries, causing fatal ischemia and lung injury (12). To date, the trapping mechanisms and, more generally, the dynamics of WBCs in pulmonary capillaries remain poorly understood. Indeed, there is no simple unified model describing the dynamical mechanical response of WBCs under various mechanical stresses. Different models have been developed (13–17) whose relevance depends on the amplitude and dynamics of the applied stress (18). Another difficulty is the lack of physiologically relevant experiments. In vivo studies are invasive and do not allow the control of cell mechanics and vascular flow parameters. Most in vitro approaches have focused on measuring the entry and transit times of individual cells in straight channels (10, 19–21) but have not addressed the dynamics of WBCs in branched capillary networks. The relationships between cell mechanics, motion by hops, retention time in network bifurcations, and transport velocity throughout the network remain unknown.
Here, we mimic the capillary bed by a microfluidic network of narrow channels whose size and applied pressure have physiological values. We show that monocytes (from THP1 lineage) have a unique adaptive dynamics in the capillary network, with a first nonstationary regime characterized by a slow movement with hops followed by a fast and smooth motion allowing efficient transport. We propose a simple mechanical model that shows how the remarkable combination of high cell viscosity and very finely tuned cortical tension induces fast and efficient transport of the cell while preserving its integrity. We show that the final cell velocity in the network is controlled by the lubrication layer between the cell membrane and the channel walls, layer itself determined by the cell cortical tension.
Results
The Biomimetic Channel Network.
Our microfluidic device consists of a network of microchannels, whose network morphology and channel geometry are similar to those of the lung bed (1, 2). An interconnected network of horizontal and diagonal channels is created by a series of 50 columns of seven pillars regularly arranged in a staggered pattern (Fig. 1 and SI Apppendix, Fig. S1 A and B). A cell enters the network on the left and exits on the right after passing through 100 channels, which is the typical number of capillaries crossed by a cell in the lung bed. At the exit of each horizontal channel, it has two choices of trajectories, mimicking the multiplicity of possible paths in the alveoli from pulmonary venules to arterioles. The channel’s dimensions are in the physiological range with a height of 9.3 m, and a length of the horizontal channels of 15 m. The width of horizontal and diagonal channels is the same and is kept constant in a given device. Various devices were prepared with varying around physiological values, from 8.6 m to m. The network unit mesh is shown in SI Appendix, Fig. S1B. The pressure drop applied between the device inlet and outlet was set to 10, 20, or 40 mbar, leading to physiological pressure drops (22) in horizontal and diagonal channels of and , respectively, where is the pressure drop in a mesh. The streamlines alternate right and left at each bifurcation (SI Appendix, Fig. S1C).
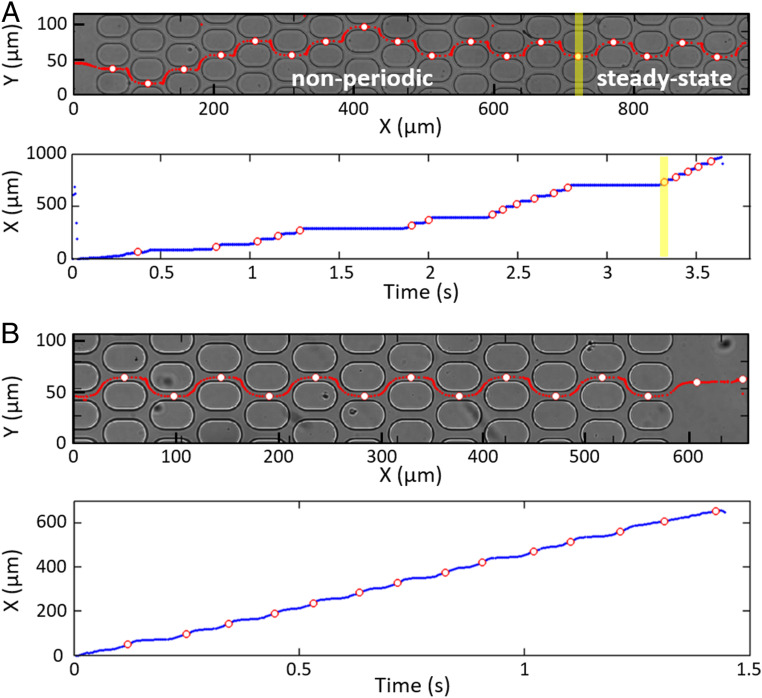
Fig. 1.
Typical behavior of THP1 cells larger than the microchannels: trajectories (red lines in A and B, Top) and X-position along the network versus time (A and B, Bottom). White dots circled in red (A and B, Top and Bottom) correspond to the cell positions when they are in the center of the horizontal channels. (A) A 15-m cell entering a 10.6-m channel network moves randomly between the pillars for the first eight meshes before alternating between two channel rows, = 40 mbar. The transit time through a mesh is still irregular (with a long stop at the exit of the 13th horizontal channel) before steady state is reached at mesh 14 (shown by the yellow line). This cell, which stays longer in the transient regime than other cells, was chosen to highlight the initial random motion. (B) A 15-m cell flowing in steady state through the last 9-m-wide channels of a network, = 20 mbar.
A Fast Periodic Monocyte Dynamics Is Achieved in the Network.
THP1 cells (14.8 1.45 m in diameter; SI Appendix, Fig. S2) are prestressed in height in the 9.3-m-high inlet channel, before reaching the network. When smaller than the channels’ width, they display a smooth periodic motion that follows the streamlines in the network. However, most cells typically have a diameter 25 larger than and are thus laterally deformed as they pass through the microchannels, leading to a very different behavior (Fig. 1 and Movie S1).
In the upstream part of the network, cells have a nonperiodic trajectory (Fig. 1A), a significant shape deformation, and a motion by hops with temporary arrests in the bifurcations at the exit of the horizontal channels, which can last up to several seconds. The time to pass through a mesh is very variable (0.1 s to a few seconds), with the cell sometimes alternating between fast and slow passage through successive meshes (SI Appendix, Fig. S3A and Movie S2). Farther downstream in the network (typically after 5 to 15 meshes), the cell motion becomes smooth, without arrests, and with a periodic trajectory characterized by alternating right and left turns at the exit of horizontal channels similarly to streamlines (Fig. 1B).
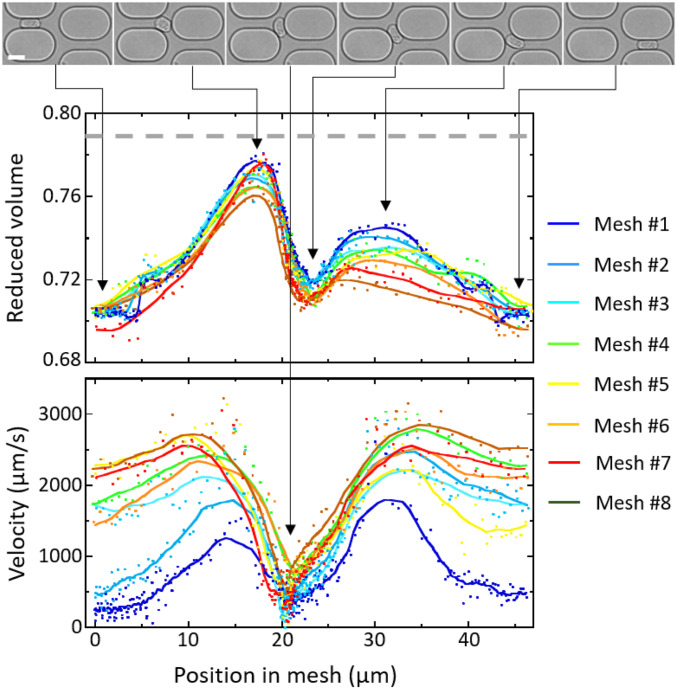
During the transient regime, cell shape and velocity vary within a mesh, but they also evolve from mesh to mesh until steady state is reached (Fig. 2). The cell deformation is characterized by its reduced volume defined as the ratio of the cell volume to the volume of a sphere with the same surface area (, for a sphere). Maximum and minimum values of are reached in the horizontal and diagonal channels, respectively, and mesh-to-mesh evolution shows that, globally, the cell progressively elongates, especially in the diagonal channel. The changes in velocity behavior mainly occur in the horizontal channels: While, in the first meshes, cells strongly slow down in both bifurcations and horizontal channels, the main slowdown then only takes place in the bifurcations. In the final steady-state regime (mesh 8, brown lines), velocity and deformation become periodic with a period of two unit meshes: The cells move fast and barely slow down at the entrance of the horizontal channels, the variation of is the lowest, and, on average, the cell is the most stretched.
Fig. 2.
Evolution of cell shape and velocity of a 13.2-m cell through the first eight meshes of an 8.6-m channel network, = 40 mbar. Reduced volume (Middle) and instantaneous velocity (Bottom) as function of the cell position in the mesh. The lines are derived from sliding averages over 11 points. Before it enters the network, the cell reduced volume is 0.79 (dashed gray line). (Top) Images of the cell through the first mesh, at minimum and maximum values of , and minimum value of . (Scale bar: 15 m.)
We compared the cell dynamics to that of giant lipid vesicles of internal viscosity close to that of the external fluid (SI Appendix, Fig. S4). Vesicles with a diameter larger than , and with sufficient excess of surface area to ensure the shape deformation required to pass through the channels without breaking, have a random trajectory over the entire network (Movie S3, and see SI Appendix, Fig. S4C for a vesicle rupture). SI Appendix, Fig. S4 A and B shows a typical vesicle motion by hops, with a residence time in the bifurcations of about 25 of the total transit time. The velocity and deformation do not evolve from mesh to mesh along the network. This highlights the remarkable adaptation of monocyte shapes along the successive meshes of the microchannel network, leading to their fast transport during the final steady-state regime.
The Mechanical Properties of Monocytes Affect Their Dynamics.
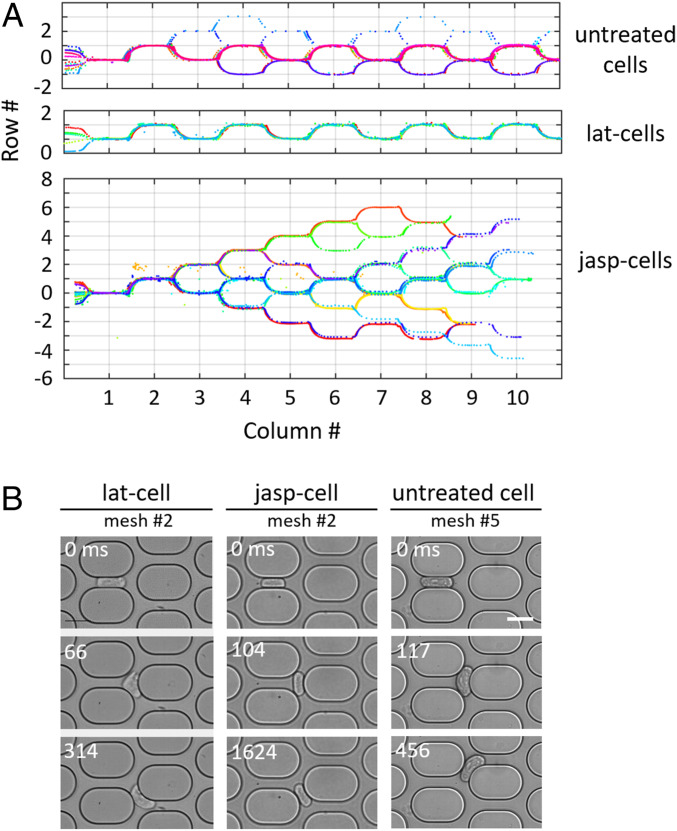
The question therefore arises of whether the adaptive monocyte behavior requires an active response of the cell or whether it can be described only in terms of complex rheological properties. This led us to modulate the cell rheology and, more specifically, to vary the elasticity of the actin cortex by treating cells with Latrunculin A (lat-cells) or Jasplakinolide (jasp-cells) that, respectively, inhibits and promotes actin polymerization. Thus, Latrunculin A decreases cell stiffness while Jasplakinolide increases it (23). Strikingly, both treatments significantly affect the cell trajectories and dynamics (Fig. 3). The percentage of cells reaching the steady state is 95, 85, and 46 for lat-cells, untreated cells, and jasp-cells, respectively. All lat-cells reach a steady-state periodic regime at very early meshes, with a trajectory alternating right and left turns and a fast traffic without arrests. In contrast, half of jasp-cells do not reach steady state over the entire network and move slowly with very irregular arrests. Untreated cells present an intermediate behavior between lat- and jasp-cells. The specific cell behaviors are illustrated in Fig. 3 (see also SI Appendix, Fig. S5 and Movies S4–S6 for a better understanding of movements).
Fig. 3.
(A) THP1 trajectories in the first 10 meshes of the network, each color corresponds to one cell. Most untreated cells display a random trajectory followed by a periodic trajectory after a few meshes; some cells still move randomly after 10 meshes (Top); lat-cells immediately display a periodic trajectory (Middle); jasp-cells never display periodic trajectory within 10 meshes (Bottom). (B) Selected images from timelapses of lat-cells, jasp-cells, and untreated cells (more details in SI Appendix, Fig. S5). (Scale bar: 15 m.)
Lat-cells gently adapt their shape as they pass through a mesh. When exiting a horizontal channel, the cells that do not present a strong shape asymmetry crash on the pillar and deform a lot in the bifurcation. The cell part closest to the entrance of a diagonal channel enters it and becomes the new cell front. The cell rear is sheared by the flow in the other diagonal channel and takes an asymmetric shape. Cells that already have an asymmetric shape in the horizontal channel immediately turn in a diagonal channel at the horizontal channel exit. It is interesting to note that in a bifurcation, the ends of the largest lat-cells may be simultaneously engaged in each of the two diagonal channels. The cells are then stretched at both ends and can possibly tear in two parts, which flow downstream (Movie S7).
In contrast, the jasp-cells that do not reach the steady-state regime are more rigid, retain their symmetrical “sausage” shape when they exit the horizontal channel, and tumble into the bifurcation in a rigid-like way. There, they often clog the two diagonal channels and hang in the bifurcation for a long and variable time. The cell elongation may increase but the cells never tear. They eventually return to circulation in one of the diagonal channels by a slight displacement of their center of symmetry in a random direction along the pillar. This randomness leads to a slow motion by hops of the cells and a frequent reversal of their direction, which results in an exchange between the cell front and rear.
Most of the untreated cells reach the steady-state regime within less than 10 meshes, few requiring more. In the transient regime (see elapsed times in Fig. 3B, and SI Appendix, Fig. S5), cells that exit the horizontal channel with a symmetrical shape crash on the pillar and may clog the two diagonal channels like a jasp-cell (hopping motion). But when they return to circulation, unlike jasp-cells, they can be asymmetrically deformed by the flow in the unobstructed diagonal channel. Farther down the network, in the steady-state regime, the cells slightly turn at the exit of the horizontal channel, thus engaging their front in a diagonal channel. Their rear tumbles over the pillar but does not clog the other diagonal channel, allowing rapid circulation. Overall, untreated cells are slower than lat-cells.
Relevant Mechanical Model for Monocyte Dynamics.
In order to highlight the mechanical parameters responsible for this very specific monocyte traffic, we analyzed the dynamics of cell entrance in the first channel (Fig. 4).
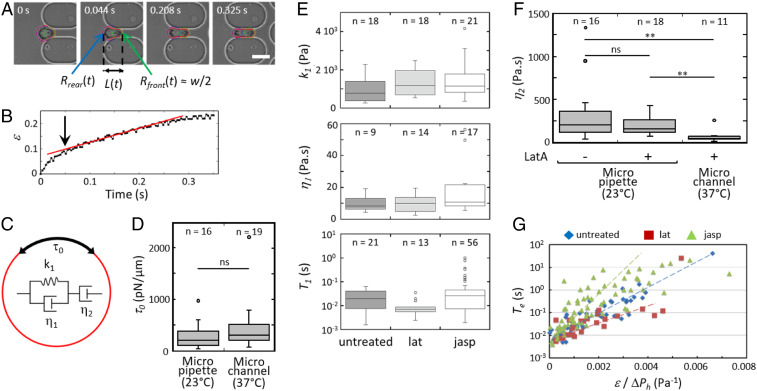
Fig. 4.
THP1 mechanical properties. (A) Time lapse of a 15.4-m cell (untreated) entering the first horizontal channel of an 8.6-m network. The total cell length is measured from the tracked cell contour (in red). The cell front and rear are approximated with circles (in green and blue, respectively). The front radius is half the channel width . (Scale bar: 15 m.) (B) Elongation ratio of the cell in A while it enters the channel. The arrow highlights the transition between the two deformation regimes. (C) Rheological model of the cell as a viscoelastic liquid combining a Kelvin–Voigt solid (, ) in series with a dashpot , and with a cortical tension . (D) measured from micropipette and microchannels experiments, at C and C, respectively. (E) Viscoelastic parameters and , and raising time of the elastic deformation. (F) Viscosity measured from micropipette and microchannels experiments at C and C, respectively. Cells were treated or not with Latrunculin A. **, ; ns, not significant. (G) Entry time into the channel as function of normalized to pressure drop, under drug treatment or not.
First, a minimal pressure drop must be applied to drive a cell into the channel, thus revealing a nonzero cell cortical tension. Above , we measured the cell elongation ratio during its entrance in the channel, where is the cell length along the channel (see Fig. 4B for a typical untreated cell). The curve initially shows a short nonlinear regime at small deformation (for ), typical of a viscoelastic material, followed by a slow viscous flow (up to ) at constant velocity. Thus, these cells are considered as viscoelastic drops with a surface tension . The internal composite material is described by the modified Maxwell model which consists of a viscoelastic Kelvin–Voigt body (dashpot of viscosity and spring of elasticity ) linked to an additional dashpot of viscosity for the long-time viscous dissipation (Fig. 4C) (24, 25).
The cell cortical tension generated by the actin cortex was determined from , the minimal pressure drop allowing a cell to enter in the network first channel (at C) or in a micropipette (at C). In the case of a cylindrical pipette of radius , relates to by the Laplace law (15, 26),
| [1] |
where is the cell radius. In the case of the network rectangular microchannel, the channel height , which is smaller than the cell diameter, defines the vertical curvature at the front and rear of the cell (Fig. 4A). thus writes as
| [2] |
where is the horizontal radius at the rear of the cell and is the microchannel width.
The median values of of untreated cells are 300 and 196 pN/m for the microfluidic and the pipette methods, respectively, and show no significant effect of temperature (Fig. 4D). They are in the range of those previously reported for THP1 cells (27). In contrast, lat-cells entered in the microchannels for applied pressure drops as low as 0.3 mbar (i.e., pN/m), confirming that Latrunculin A effectively destroyed the actin cortex. From the modified Maxwell model (24), the mechanical constitutive law of the cell is
| [3] |
where the effective applied stress for a flowing cell is determined by the pressure balance between and the pressure drop in the horizontal channel ,
| [4] |
In specific cases, the second term of the right-hand side of Eq. 4 is negligible, making constant. It happens for cells small enough to little deform because , and lat-cells for which is very small. Integration of Eq. 3 in these two cases yielded the parameters , , and by fitting curves in the first horizontal microchannel (see the example of a lat-cell in SI Appendix, Fig. S6). In the other cases, only could be estimated from the transition from elastic to viscous regime on the temporal variation of the elongation ratio (see arrow in Fig. 4B). As shown in Fig. 4E, no significant difference was found between untreated, lat-, and jasp-cells. The Voigt elasticity and viscosity are of the order of Pa and 10 Pas, respectively. The raising time for the elastic deformation is very short, of the order of 10 ms to 20 ms. The viscosity was determined on lat-cells both from the entrance in the microchannel network at C and from micropipette aspiration, together with untreated cells, at C (Fig. 4F). The median viscosity at C is 203 and 156 Pas for untreated cells and lat-cells, respectively, in excellent agreement with the values of 185 and 135 Pas reported for monocytes (27) and granulocytes (15). Also in agreement with this latter work, we observed a strong temperature dependence of the viscosity as for lat-cells decreases to 45 Pas at C.
This mechanical analysis shows that cells can undergo 1) fast small viscoelastic deformations with a characteristic time 20 ms, and 2) slow viscous deformations with a characteristic flow time , which is typically of the order of 100 ms for values of , 40 Pas, and 40 Pa. The cell cortical tension, which resists deformation, is the main parameter affected by actin drug treatment and is thus considered to be responsible for the different dynamics of lat-cells, untreated cells, and jasp-cells.
Role of Cell Cortical Tension in the Bifurcation.
As known for a long time (28), the dynamics of droplets in linear flows is determined by the nonlinear coupling of their restoring internal tension forces and the deforming hydrodynamic forces. It directly depends on the capillary number , which represents the relative effect of viscous drag forces versus surface tension, where and are the viscosity and velocity of the external fluid, respectively. The capillary number of THP1 cells increases from jasp-cells to untreated cells to lat-cells. At low , for jasp-cells and untreated cells, reduces the ability of the viscous force to deform the cells. Part of the work done by viscous force is converted into surface energy, which slows down the cell (Fig. 4G), both in the entry of the network and in bifurcations. Indeed, numerical simulations performed on droplets have clearly reported that the residence time of a droplet in a bifurcation is longer when the value of is low, until an instability drives the droplet into a daughter channel (29, 30). Interestingly, above a critical value of , a droplet is expected to split up in extensional flows (28) and in bifurcations (29, 30), the two parts flowing separately in the two daughter channels after the bifurcation, as observed in our case for some very large lat-cells (Movie S7). A low cortical tension corresponding to a high therefore increases the traffic speed of the cells, but it must remain sufficiently high to preserve the integrity of the cell as it passes the bifurcations.
Toward the Periodic Steady State.
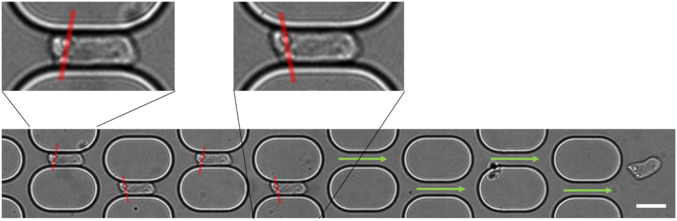
A key to the steady-state regime is that, at the exit of horizontal channels, the cells immediately turn alternately right and left to engage their front part in the next diagonal channel. This is illustrated in SI Appendix, Fig. S5 on an untreated cell in mesh 10 ( 44 ms) which, earlier, crashed on the next pillar in the transient regime (mesh 5, 51 ms). This is also shown in Fig. 5 where the cell spontaneously turns left at the exit of the network while the flow is symmetrical. This is the result of a higher friction of the cell along one of the two side walls of the horizontal channel, that is, a thinner lubrication layer along one wall, creating a torque that directs the cell trajectory. It is shown in SI Appendix, Fig. S5 on a lat-cell ( 369 ms) and in Fig. 5 on an untreated cell where the relative positions of two intracellular defects alternate in successive horizontal channels.
Fig. 5.
Asymmetric motion in the channels. Superimposed images of a cell passing through the network. Red lines drawn between two bright dots located in the cell rear (zoomed in Insets) highlight the shear effect. (Scale bar: 15 m.)
This behavior is associated with an asymmetric deformation of the cell achieved in the nonsymmetrical part of the mesh, at the bifurcation exit and in the diagonal channel, hereinafter referred to as the diag position (see circle in SI Appendix, Fig. S1B). Since the cell is viscous, the deformation needs time to be reached. Therefore, the residence time of the cell at the diag position must be long enough for the deformation to develop and/or for the fluid in the lubrication layer to be partially drained off. Furthermore, the cell transit time through the next symmetric horizontal channel must be short enough so that the asymmetry achieved at the position does not fully relax until the cell reaches the next bifurcation. As illustrated in SI Appendix, Fig. S3 C and D, and are both longer than the Kelvin–Voigt time , indicating that the cell has time to undergo a viscoelastic deformation at the diag position but also to relax this deformation in the horizontal channel. On the other hand, , therefore allowing a deformation of about 10 at the diag position, which cannot fully relax in the horizontal channel. Thus, the viscosity allows the cell to maintain an asymmetric deformation at the horizontal channel’s exit, making it turn directly toward the downstream channels.
The optimal steady-state cell deformation is obtained progressively during the transient regime by alternating rapid and slow cell transit in successive meshes (SI Appendix, Fig. S3 A and B). Indeed, a cell blocked for a very long time in the diag position (see the untreated cell at 117 ms; Fig. 3B) reaches a very high degree of asymmetry that will allow it to engage directly and efficiently at the next diag position. However, the cell will then not have time to develop the degree of mirror asymmetry sufficient to engage effectively in the next diag position and will therefore be slowed down there, and may then develop a more pronounced asymmetry again. This alternation of slow and fast passage gradually converges toward an optimal residence time and deformation in the steady state.
Steady-State. Dynamics of Cell Transport.
In the steady-state regime, a cell can be considered as progressing from mesh to mesh with an average mesh velocity . This velocity results from the balance between the driving hydrodynamic force due to the pressure difference applied in a mesh, , and the friction force of the cell membrane on the channel walls. This latter force per unit of membrane area is the shear stress exerted by the lubrication layer between the wall and the cell membrane , where is the surface area of the cell close to the walls (estimated by considering that the cell has an almost parallelepipedic shape of length , height , and width : ) and is the viscous coefficient due to the shear force in the lubrication layer between the cell membrane and the channel wall (, where is the thickness of the lubrication layer). In the steady-state regime, the sum of forces is zero,
| [5] |
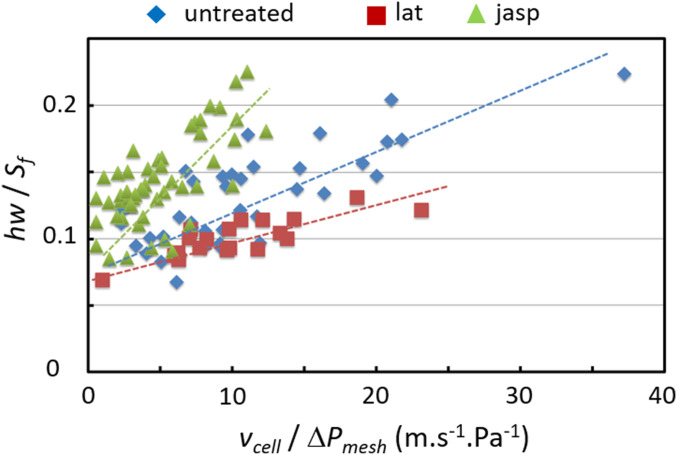
Fig. 6 displays versus for cells, treated or not, transiting through channels of width 11 m. A remarkable linear dependence is observed, validating the approach. The different slopes disclose that the friction increases from lat-cells to untreated cells to jasp-cells, resulting in a faster movement of lat-cells. Taking Pas, the values of deduced from the experimental determination of are within a reasonable range, i.e., a few hundred nanometers (Table 1). Surprisingly, the curves converge to a nonzero value when tends toward 0, equivalent to a solid friction that remains to be understood.
Fig. 6.
Experimental determination of and based on Eq. 5; is the curve slope; is the value extrapolated at .
Table 1.
Viscous friction and lubrication thickness of flowing cells
| Cells | |||
| Lat | 1.96 | ||
| Untreated | 4.19 | ||
| Jasp | 1.09 |
The lubrication theory states that the thickness of the lubrication layer is inversely proportional to the tension gradient in the membrane (31),
| [6] |
where is the tension at the cell front and is a numerical prefactor that differs only very slightly in the literature (2.123 in ref. 32 and 2.05 in ref. 33). Values of calculated from Eq. 6 with mm (Table 1) are in excellent agreement with those of measured in microchannel and micropipette experiments (Fig. 4D). These similar cortical tension values, deduced independently, strongly support our approach and confirm that the friction between the channel walls and the cell governs its speed. Note that the tension estimated from the lubrication layer is that of the cell front, higher than that of the rear. Also note that the tension of jasp-cells is twice that of untreated cells, which explains their difficulty in reaching the steady-state regime.
Discussion and Conclusion
The circulation of WBCs in the network of pulmonary capillaries is crucial for immune surveillance. Their slowed circulation leads to an increase in their concentration in the pulmonary bed, which is supposed to allow rapid release and effective response if the immune system is activated. It is known that WBC deformability is an important factor in their proper circulation. For example, neutrophils’ multilobed nuclei allow them to better squeeze into the narrowest capillaries. Here, we showed that the very fine combination of the mechanical properties of monocytes allows their rapid transport without blocking in bifurcations. First, their moderate cortical tension allows them to deform in the network. Second, thanks to their fast viscoelastic mechanical response, they adapt their shapes quickly and reversibly to local geometric variations in the capillary network. Third, their slow viscous response allows their shape to evolve from mesh to mesh and finally develop a periodic asymmetry optimized to have a smooth motion without arrests. In comparison, giant vesicles whose inner fluid is 10,000 times less viscous than monocytes immediately adapt their shape to external mechanical stresses. They thus exit the horizontal channel with a symmetrical shape, are blocked against the pillar in the middle of the bifurcation, and present a motion by hops. This work also shows that cortical tension is a key parameter. A low cortical tension allows the cell not to hang in the bifurcations and, by reducing friction between the cell membrane and the capillary wall, to increase its speed in the network. Nevertheless, the cortical tension must be high enough to preserve the integrity of the cell by preventing vesiculation and cell rupture in the bifurcations. Finally, it is worth noting that, physiologically, WBCs circulate in a highly concentrated suspension of red blood cells (SI Appendix, Fig. S7). Could the effect of red blood cells on WBC traffic just be equivalent to an increase in the effective viscosity of the suspending fluid, as often considered in hemorheology? We hope that future theoretical and experimental works will answer these questions, stimulated by the present study.
Materials and Methods
Cells and Reagents.
THP1 cells (TIB-202, ATCC) are cultured at C and under , in Roswell Park Memorial Institute (RPMI) medium supplemented with 10vol fetal bovine serum (FBS), 1 GlutaMax, Penicillin/Streptomycin, and 25 mM Hepes (RPMI 1640, HEPES, GlutaMAX 100, Pen/strep, Gibco; FBS, Lonza). During experiments, 1 bovine serum albumin (Sigma-Aldrich) is added. For actin cortex alteration, cells are treated 30 min at C with 3 g/mL Latrunculin A (Sigma-Aldrich) or Jasplakinolide (Calbiochem) before injection in the microfluidic network.
Microfluidic Device and Experiments.
The microchannel network is made of polydimethysiloxane (PDMS) (Sylgard, Dow Corning) using standard technique of microfabrication. Microfluidic experiments are performed on an inverted microscope (IX71, Olympus, 20) equipped with Photon-focus and high-speed Photron cameras up to 1,000 frames per second. The pressure between the inlet and the outlet is controlled by a flow controller (MFCS-8, Fluigent). The cells are observed at 37 C in brightfield using videomicroscopy. Note that, in comparison, micropipette experiments are performed at room temperature.
Video Analysis.
Video images are analyzed using homemade routines in Matlab (Mathworks) to automatically track the cell contour and derive its projected area, perimeter, length, and position.
Data Availability Statement.
All data are included in the manuscript and SI Appendix.
Supplementary Material
Acknowledgments
This work was supported by the French National Research Agency (Grant ANR-09-BLAN-ChipCellTrap). We warmly thank F. Beyer, A. Peignier, and K. Cosentino for experiments, and P. Tabeling, M. Reyssat, C. Vergne, F. Monti, J. Magnaudet, and M. Leroux, for very fruitful discussions.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1919984117/-/DCSupplemental.
References
- 1.Doerschuk C. M., Mechanisms of leukocyte sequestration in inflamed lungs. Microcirculation 8, 71–88 (2001). [PubMed] [Google Scholar]
- 2.Guntheroth W., Luchtel D. L., Kawabori I., Pulmonary microcirculation: Tubules rather than sheet and post. J. Appl. Physiol. 53, 510–515 (1982). [DOI] [PubMed] [Google Scholar]
- 3.Doerschuk C., Beyers N., Coxson H., Wiggs B., Hogg J., Comparison of neutrophil and capillary diameters and their relation to neutrophil sequestration in the lung. J. Appl. Physiol. 74, 3040–3045 (1993). [DOI] [PubMed] [Google Scholar]
- 4.Wang S., Mak K., Chen L., Chou M., Ho C., Heterogeneity of human blood monocyte: Two subpopulations with different sizes, phenotypes and functions. Immunology 77, 298–303 (1992). [PMC free article] [PubMed] [Google Scholar]
- 5.Gebb S. A., et al. , Sites of leukocyte sequestration in the pulmonary microcirculation. J. Appl. Physiol. 79, 493–497 (1995). [DOI] [PubMed] [Google Scholar]
- 6.Lien D., et al. , Physiologic neutrophil sequestration in the canine pulmonary circulation. J. Appl. Physiol. 62, 1236–1243 (1987). [DOI] [PubMed] [Google Scholar]
- 7.Hogg J. C., McLean T., Martin B., Wiggs B., Erythrocyte transit and neutrophil concentration in the dog lung. J. Appl. Physiol. 65, 1217–1225 (1988). [DOI] [PubMed] [Google Scholar]
- 8.Presson R., Jr, et al. , Distribution of pulmonary capillary red blood cell transit times. J. Appl. Physiol. 79, 382–388 (1995). [DOI] [PubMed] [Google Scholar]
- 9.Worthen G. S., Schwab B., Elson E. L., Downey G. P., Mechanics of stimulated neutrophils: Cell stiffening induces retention in capillaries. Science 245, 183–186 (1989). [DOI] [PubMed] [Google Scholar]
- 10.Preira P., et al. , The leukocyte-stiffening property of plasma in early acute respiratory distress syndrome (ARDS) revealed by a microfluidic single-cell study: The role of cytokines and protection with antibodies. Crit. Care 20, 8 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Preira P., et al. , Microfluidic tools to investigate pathologies in the blood microcirculation. Int. J. Nanotechnol. 9, 529–547 (2012). [Google Scholar]
- 12.Hogg J. C., Neutrophil kinetics and lung injury. Physiol. Rev. 67, 1249–1295 (1987). [DOI] [PubMed] [Google Scholar]
- 13.Herant M., Marganski W. A., Dembo M., The mechanics of neutrophils: Synthetic modeling of three experiments. Biophys. J. 84, 3389–3413 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schmid-Schönbein G., Sung K., Tözeren H., Skalak R., Chien S., Passive mechanical properties of human leukocytes. Biophys. J. 36, 243–256 (1981). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Evans E., Yeung A., Apparent viscosity and cortical tension of blood granulocytes determined by micropipet aspiration. Biophys. J. 56, 151–160 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Skalak R., Dong C., Zhu C., Passive deformations and active motions of leukocytes. J. Biomech. Eng. 112, 295–302 (1990). [DOI] [PubMed] [Google Scholar]
- 17.Tran-Son-Tay R., Kan H. C., Udaykumar H., Damay E., Shyy W., Rheological modelling of leukocytes. Med. Biol. Eng. Comput. 36, 246–250 (1998). [DOI] [PubMed] [Google Scholar]
- 18.Shirai A., Modeling neutrophil transport in pulmonary capillaries. Respir. Physiol. Neurobiol. 163, 158–165 (2008). [DOI] [PubMed] [Google Scholar]
- 19.Gabriele S., Versaevel M., Preira P., Théodoly O., A simple microfluidic method to select, isolate, and manipulate single-cells in mechanical and biochemical assays. Lab Chip 10, 1459–1467 (2010). [DOI] [PubMed] [Google Scholar]
- 20.Preira P., Valignat M. P., Bico J., Théodoly O., Single cell rheometry with a microfluidic constriction: Quantitative control of friction and fluid leaks between cell and channel walls. Biomicrofluidics 7, 024111 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yap B., Kamm R. D., Mechanical deformation of neutrophils into narrow channels induces pseudopod projection and changes in biomechanical properties. J. Appl. Physiol. 98, 1930–1939 (2005). [DOI] [PubMed] [Google Scholar]
- 22.Huang Y., Doerschuk C. M., Kamm R. D., Computational modeling of RBC and neutrophil transit through the pulmonary capillaries. J. Appl. Physiol. 90, 545–564 (2001). [DOI] [PubMed] [Google Scholar]
- 23.Gabriele S., Benoliel A. M., Bongrand P., Théodoly O., Microfluidic investigation reveals distinct roles for actin cytoskeleton and myosin II activity in capillary leukocyte trafficking. Biophys. J. 96, 4308–4318 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Guevorkian K., Colbert M. J., Durth M., Dufour S., Brochard-Wyart F., Aspiration of biological viscoelastic drops. Phys. Rev. Lett. 104, 218101 (2010). [DOI] [PubMed] [Google Scholar]
- 25.Wu P. H., et al. , A comparison of methods to assess cell mechanical properties. Nat. Methods 15, 491–498 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hochmuth R. M., Micropipette aspiration of living cells. J. Biomech. 33, 15–22 (2000). [DOI] [PubMed] [Google Scholar]
- 27.Richelme F., Benoliel A. M., Bongrand P., Aspiration of THP1 into a micropipette. Mechanical deformation of monocytic THP-1 cells: Occurrence of two sequential phases with differential sensitivity to metabolic inhibitors. Exp. Biol. Online 2, 1–14 (1997). [Google Scholar]
- 28.Rallison J., The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid Mech. 16, 45–66 (1984). [Google Scholar]
- 29.Carlson A., Do-Quang M., Amberg G., Droplet dynamics in a bifurcating channel. Int. J. Multiphas. Flow 36, 397–405 (2010). [Google Scholar]
- 30.Wang Y., Do-Quang M., Amberg G., Viscoelastic droplet dynamics in a y-shaped capillary channel. Phys. Fluids 28, 033103 (2016). [Google Scholar]
- 31.Bretherton F. P., The motion of long bubbles in tubes. J. Fluid Mech. 10, 166–188 (1961). [Google Scholar]
- 32.Secomb T. W., Skalak R., Özkaya N., Gross J., Flow of axisymmetric red blood cells in narrow capillaries. J. Fluid Mech. 163, 405–423 (1986). [Google Scholar]
- 33.Bruinsma R., Rheology and shape transitions of vesicles under capillary flow. Phys. Stat. Mech. Appl. 234, 249–270 (1996). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data are included in the manuscript and SI Appendix.