On-demand modulation of 3D-printed elastomers using programmable droplet inclusions

Significance

To manipulate extruded ink composition and properties in real time, we demonstrate the concurrent generation and deposition of textured inks with droplet inclusions. Dispersing different fluids into droplets within PDMS, we demonstrate the ability to locally impart function at the point of print, either by chemical modification resulting in mechanical compliance or by using functional nanoparticle suspensions that respond to external stimulus (e.g., B field). The present study thus introduces a strategy for facile fabrication of heterogeneous and functional structures.

Abstract

One of the key thrusts in three-dimensional (3D) printing and direct writing is to seamlessly vary composition and functional properties in printed constructs. Most inks used for extrusion-based printing, however, are compositionally static and available approaches for dynamic tuning of ink composition remain few. Here, we present an approach to modulate extruded inks at the point of print, using droplet inclusions. Using a glass capillary microfluidic device as the printhead, we dispersed droplets in a polydimethylsiloxane (PDMS) continuous phase and subsequently 3D printed the resulting emulsion into a variety of structures. The mechanical characteristics of the 3D-printed constructs can be tuned in situ by varying the spatial distribution of droplets, including aqueous and liquid metal droplets. In particular, we report the use of poly(ethylene glycol) diacrylate (PEGDA) aqueous droplets for local PDMS chemistry alteration resulting in significant softening (85% reduced elastic modulus) of the 3D-printed constructs. Furthermore, we imparted magnetic functionality in PDMS by dispersing ferrofluid droplets and rationally designed and printed a rudimentary magnetically responsive soft robotic actuator as a functional demonstration of our droplet-based strategy. Our approach represents a continuing trend of adapting microfluidic technology and principles for developing the next generation of additive manufacturing technology.

Additive manufacturing has evolved into a mainstream technology that is increasingly competitive to traditional manufacturing processes in terms of costs and process capabilities. Among the additive manufacturing technologies that have been developed, extrusion-based three-dimensional (3D) printing (e.g., fused deposition modeling and direct ink writing) is highly popular due to its relative affordability and versatility in terms of suitable materials (1, 2). In terms of performance, industrial extrusion-based 3D printers, such as those developed by nScrypt, are capable of high-precision layer-by-layer deposition of multiple inks to generate high-resolution compositionally graded 3D constructs (3–6).

Despite such capabilities, the production of fully printed functionally heterogeneous objects without resorting to a multistep assembly process remains an ongoing challenge. Some common approaches include sequential printing of different ink materials through multiple nozzles or blending ink materials at different proportions prior to extrusion (7, 8). Augmenting this material blending approach using microfluidic mixing, researchers were able to seamlessly exchange (9), homogenize (10, 11), or texturize (12, 13) ink blends at the point of printing. While these advances have demonstrated the printing of textured and heterogeneous constructs, the use of microfluidic mixers for extrusion printing has been demonstrated only in blends of miscible inks (e.g., silicone/silicone pastes and calcium/alginate aqueous solutions) and other solid additives (e.g., quantum dots and fumed silica). The application of microfluidics for multiphase or immiscible ink blends (i.e., emulsions) in a 3D-printing context remains largely unexplored.

To generate heterogeneous prints, one of the current approaches is to selectively tune the microstructural properties of extruded inks in real time. Using rotating photomasks and magnetic-field sources, researchers were able to manipulate the alignment of magnetic nanoparticle fillers in a photocurable ink, creating a structure with spatially graded microstructures and functional properties (14–16). Elsewhere, a rotating printhead was used to spatially control the orientation of short fibers in epoxy-fiber inks and to produce engineered composites (17). The multidimensional printing strategy, despite its robust control capabilities, strictly requires that fillers have high aspect ratios and are capable of responding to the stimuli provided (i.e., the applied B field and the rotational shear) (18). Thus, there still exists a need for a generalizable strategy toward generating heterogeneous prints in an extrusion-based printing context.

Here we report the in situ modulation of printed construct properties using controlled dispersion of droplet inclusions. By introducing immiscible inks in a glass capillary microfluidic device, we simultaneously generated and 3D printed highly textured emulsion inks consisting of well-organized droplets. We characterized the mechanical contribution of various droplet inclusions in printed polydimethylsiloxane (PDMS) constructs and in the process demonstrate the use of aqueous poly(ethylene glycol) diacrylate (PEGDA) droplets to chemically modify and intrinsically soften the surrounding PDMS phase. Finally, we designed and printed a primitive soft robotic actuator consisting of spatially defined mechanically compliant and magnetically responsive domains capable of instantaneous bending at desired locations in response to an external B field. Demonstrating the ability to impart functional properties at selective points across the printed construct, we anticipate the potential of our droplet-based strategy for next-generation rapid prototyping of heterogeneous and time-evolving structures.

Results and Discussion

3D Printing Emulsion Inks Using a Droplet Microfluidic Printhead.

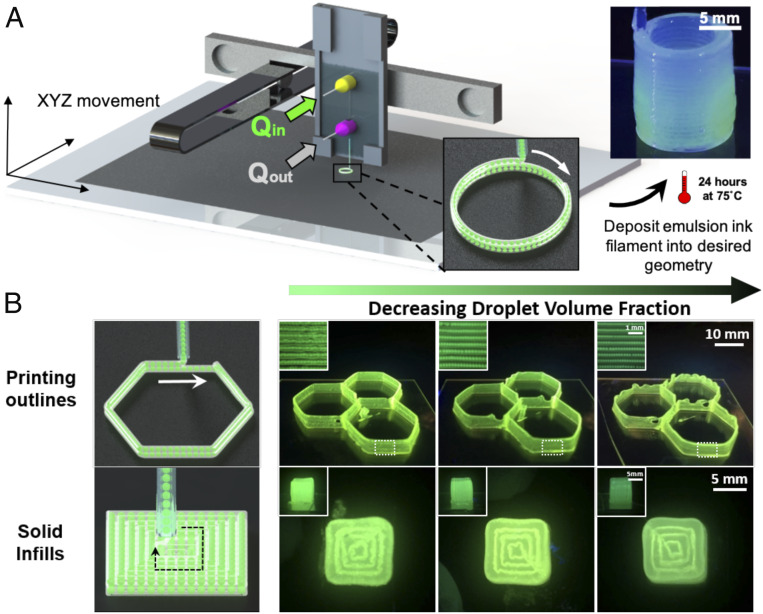
Central to our strategy of using droplet inclusions to modify the functional properties of the surrounding matrix is the ability to controllably disperse droplets within another substance. We accomplished this by introducing an aqueous inner phase with a PDMS outer phase within a standard glass capillary microfluidic device (19) while simultaneously depositing the resulting PDMS emulsion (Fig. 1A and Movie S1). The PDMS outer phase, whose rheological properties are shown in SI Appendix, Fig. S1A, consisted of Dowsil SE 1700 and silicone oil; the former is a nonflowing elastomeric paste ($\mathrm{\mu }$ = 500,000 cP) used for direct writing applications (9), and the latter is a liquid used as a thinning agent. As opposed to previous reports of embedding of individual droplets into another phase at discrete points (20–22), the flowing PDMS outer phase is sufficiently capable of continuously shearing the aqueous inner phase into monodisperse droplets. The net result is the facile generation of PDMS emulsion inks that can be 3D printed into various geometries, as shown in Fig. 1B.

Fig. 1.

In situ dispersion and 3D printing of aqueous droplets in PDMS. (A) Schematic of droplet microfluidic 3D printing process. Q_in and Q_out refer to the flow rates of the inner (aqueous glycerol) and the outer (PDMS) phase, respectively. Inset shows experimental image of a cylinder printed from PDMS with aqueous droplet (with 62 wt% glycerol) inclusions. The green glow arises from the dissolved sodium fluorescein in the aqueous inner phase. (B) Printing constructs consisting of outlines and solid infills with different droplet volume fractions, which are controlled by adjusting the ratio of Q_in and Q_out. Droplet volume fractions from Left to Right are 16.7, 9.1, and 4.8%, respectively. Top Insets and Bottom Insets are micrographs of the printed outline objects and front view images of the solid infill objects, respectively.

The use of multiple flowing streams also allows us to independently control the injected fluid flow rates and to thereby tune the resulting emulsion characteristics. In Fig. 1B, decreasing the flow rate of aqueous glycerol with fluorescein (Q_in) relative to PDMS (Q_out) caused a reduction in droplet volume fraction and droplet diameter, resulting in a visible decrease in fluorescence intensity. The relationship between Q*, where Q* = Q_in/Q_out, and droplet diameter is graphically illustrated in SI Appendix, Fig. S1B. It should be noted that the exact relationship between Q*, droplet diameter, and droplet generation frequency varies from device to device based on its key dimensions, such as the injection and collection capillary separation distance (23). While the incorporation of microfluidics for blending miscible inks prior to extrusion printing has been previously reported (9, 10), our ability to 3D print highly textured constructs by mixing immiscible fluid streams using a droplet microfluidic approach represents a budding and unique application of these same principles and tools in an extrusion-based printing context.

Mechanical Anisotropy in PDMS Constructs Made with Different Printing Paths.

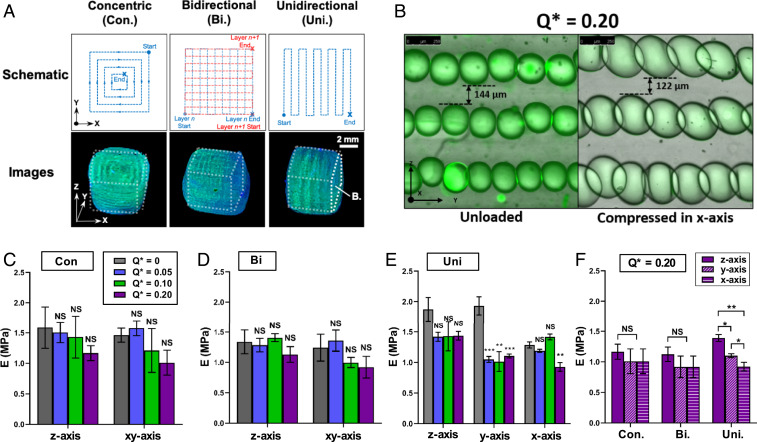
We explored the impact of choosing different 3D printing paths on the properties of these highly textured PDMS constructs. For our comparison, we printed solid cubes using concentric (Con), bidirectional (Bi), and unidirectional serpentine (Uni) printing paths. The schematic and experimental images of the constructs made using each printing path are shown in Fig. 2A. The layer-by-layer deposition of PDMS emulsion filaments results in a closer packing of droplets along the print direction compared to the vertical direction (i.e., the z axis) as shown in Fig. 2B. At Q* = 0.20, we counted five to six droplets per millimeter in the y axis, with droplets overlapping one another by several tens of micrometers. Note that the overlap becomes more pronounced under compression. In contrast, the z axis has two to three droplets per millimeter, with droplets separated by a layer of PDMS with thicknesses of 308 and 144 $\mathrm{\mu }$m at Q* = 0.05 and 0.20, respectively (SI Appendix, Fig. S2A).

Fig. 2.

Mechanical responses of PDMS constructs with droplet inclusions at various printing paths. (A) Schematic and experimental images showing three different printing paths: concentric (Con), bidirectional (Bi), and unidirectional serpentine (Uni). All PDMS constructs used here contain aqueous droplets with glycerol. (B) Representative micrograph of the face (y–z plane) highlighted in A showing multiple PDMS emulsion filament layers stacked in the z axis for Q* = 0.20. Under compression in the x axis, the droplets expand in the y–z plane and visibly overlap with one another. (Scale bar, 250 $\mathrm{\mu }$m.) (C–F) Measured elastic moduli from compressing glycerol-in-PDMS constructs show mechanical anisotropy in the Uni printing path. All printed PDMS constructs were cured for 24 h at 75 °C. *P < 0.05, **P < 0.01, ***P < 0.001, respectively, using Student’s t test. Error bars shown are SD. NS, not significant.

We hypothesized that, despite the spherical nature of the droplets, our PDMS prints would exhibit anisotropic mechanical behavior owing to differences in droplet distribution in the x, y, and z axes. Specifically, the constructs will have different elastic moduli in the z versus x and y axes. Note that the Con and Bi constructs will have identical elastic moduli in the x and y axes due to their rotational symmetry. To test our hypothesis, we subjected the cubic prints to uniaxial compression testing in all three directions and measured the mean elastic modulus of the constructs accordingly.

When the printing path and direction of mechanical loading were kept constant, the elastic modulus in the x, y, and z axes showed no significant changes as Q* increased from 0 to 0.20 in the Con constructs (Fig. 2C). The same insensitivity to Q* in all three directions was observed in Bi constructs (Fig. 2D). The Uni constructs showed no significant change in the z-axis elastic modulus with increasing Q*. However, in the y and x axes, the elastic modulus decreased by 43% (from 1.93 ± 0.30 and 1.11 ± 0.06 MPa) and 8% (from 1.28 ± 0.10 and 0.93 ± 0.14 MPa) when Q* increased from 0 to 0.20 (Fig. 2E). At Q* = 0.20, the variation in elastic moduli in the x, y, and z axes became more pronounced in the Uni constructs (Fig. 2F), with constructs being consistently stiffer in the z axis than in other directions. These results suggest that droplet organization in the Uni printing path gives rise to mechanical anisotropy in PDMS constructs. We, however, note the biphasic behavior of Uni prints in the x axis as Q* increases from 0 to 0.20 (Fig. 2E), which is likely due to poorer ink fusion in the x axis (i.e., the direction orthogonal to the print direction) as evidenced in the control when Q* = 0 (i.e., no liquid inclusions) (SI Appendix, Fig. S2B).

Previous studies have shown how droplet inclusions in solids can result in either softening or stiffening, depending on the liquid and solid properties (24–27). Specifically, the liquid droplets will mimic rigid inclusions and stiffen the surrounding solid matrix once the droplet diameter decreases below a characteristic elastocapillary length, which is defined by the relationship L = γ/E, where γ is the liquid surface tension and E is the solid elastic modulus (24). The characteristic length in this study is calculated to be O(10 nm) for a PDMS and aqueous glycerol combination, meaning our micrometer-sized droplets (50 to 200 $\mathrm{\mu }$m) soften the PDMS, consistent with the experimental observations. In addition, our results show that the extent to which droplet inclusions soften 3D-printed solids is dependent on printing path and that this softening occurs preferentially in the direction of the close-packed and overlapping droplets as in our hypothesis. For example, only the Uni constructs displayed significant softening as droplet content (or Q*) increases, and the softening was predominantly observed in the y and, to a lesser extent, x axes. We reckon that further theoretical studies are needed to corroborate our results and to determine how organizations of liquid inclusions of different length scales interact with each other and the surrounding solid matrix.

Softening PDMS Constructs Using Droplets with Different Constituents.

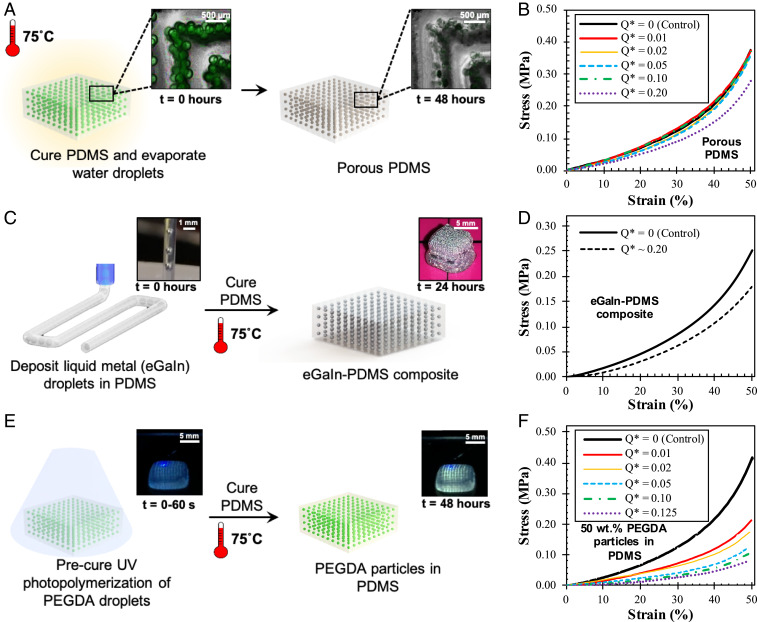
Having shown that printing path is a significant factor in softening PDMS constructs using aqueous glycerol droplet inclusions, we then pursued a different inner phase constituent that could more effectively soften the PDMS without relying on these printing parameters. At the same time, we also aimed to demonstrate the flexibility of our droplet-based strategy in handling a broad range of immiscible inks. To this end, we swapped out aqueous glycerol for other liquids including water (no glycerol), eutectic gallium-indium (eGaIn), and PEGDA prepolymer solution. Dispersing water droplets in PDMS and subsequent thermal processing resulted in PDMS with empty pores, which was visually confirmed as shown in Fig. 3A. Upon escaping the surrounding gas-permeable PDMS, the water left behind only fluorescein salt crystals that roughly outline the pores, resulting in a porous PDMS construct. The stress–strain curves obtained from compression testing of the porous PDMS cubes are shown in Fig. 3B. Analysis of the stress–strain curves reveals that the elastic modulus decreased by approximately 22.6% from 2.39 ± 0.12 to 1.85 ± 0.20 MPa as Q* changed from 0 to 0.20. Note the significantly higher elastic modulus of the Q* = 0 porous PDMS constructs compared to the Q* = 0 glycerol-in-PDMS constructs used previously (1.34 ± 0.38 MPa) was attributed to the increased thermal processing time (48 h) associated with evaporating the water droplets in PDMS.

Fig. 3.

Softening in 3D-printed PDMS constructs with different inner phase constituents. (A) Schematic of generating porous PDMS from 3D-printed PDMS with water (no glycerol) droplet inclusions. Insets are micrographs of PDMS prints containing water droplets before and after evaporation of droplets. (B) Representative compressive stress–strain curves of porous PDMS with different Q*. Controls (i.e., Q* = 0) consist of pure PDMS prints with no inner phase present. (C) Schematic of 3D printing liquid metal (eGaIn)-PDMS composites. Left and Right Insets show the dispersal of eGaIn into droplets in PDMS and a 5-mm cube of printed eGaIn-PDMS composites, respectively. (D) Representative compressive stress–strain curves of pure PDMS (control) and eGaIn-PDMS composites. (E) Schematic of converting PEGDA droplets in 3D-printed PDMS into PEGDA particle inclusions via UV photopolymerization. (F) Representative compressive stress–strain curves of PEGDA particles-in-PDMS prints with different Q*.

Next, we dispersed eGaIn in PDMS and mechanically characterized the resulting eGaIn-PDMS composite under compression. Whereas liquid metal inclusions in soft materials were previously achieved via vortex mixing or sonication (28–30), we report the simultaneous formation and 3D printing of liquid metal-PDMS composite inks (Fig. 3C). Under compression, the eGaIn-PDMS composite appeared to be softer than pure PDMS. Analysis of compression stress–strain curves in Fig. 3D revealed that including liquid metal droplets at Q* = 0.20 (or 16.7 vol%) in PDMS resulted in a decrease of 27% in elastic modulus from 1.32 ± 0.29 to 0.96 ± 0.18 MPa. A previous study reported that the mean elastic modulus of PDMS elastomers increased from 0.65 to 0.95 MPa as the liquid metal droplet content increased from 0 to 13 vol%. We attribute the stark difference between the previous results and our results to the size of the liquid metal droplets used. Whereas the eGaIn droplets in our constructs were hundreds of micrometers in diameter, the previous study used droplets that were hundreds of nanometers in diameter, which is on the same order of magnitude as the characteristic elastocapillary length for liquid metal in PDMS, thus resulting in elastocapillary stiffening (24).

Finally, we sought to include solid particles in PDMS. As shown in Fig. 3E, our strategy for realizing this involved using PEGDA prepolymer solution with 3 wt% diethoxyacetophone photoinitiator (PI) as the inner phase. Upon dispersal in PDMS, the PEGDA prepolymer droplets were exposed to UV before thermal curing of PDMS. We observed that upon successful photopolymerization of PEGDA prepolymer solution, the fluorescence intensity of the dissolved fluorescein salt increases (Fig. 3E). We attribute this to differences in fluorescein salt solvation between PEGDA prepolymer solution and solid polymer (31, 32).

The stress–strain curves for compressing PDMS with PEGDA particle inclusions are shown in Fig. 3F. At first glance, the softening effect arising from the PEGDA particles is already significantly greater compared to that arising from other inner phase constituents. Indeed, the elastic modulus between Q* = 0 and 0.125 decreased by 85% from 2.64 ± 0.56 to 0.42 ± 0.08 MPa in PDMS constructs with PEGDA particles. In contrast, aqueous glycerol droplets, porous PDMS, and eGaIn droplets at Q* = 0.20 decreased the elastic modulus only by 16, 23, and 27%, respectively (SI Appendix, Table S1). Strikingly, surface nanoindentation of these PEGDA particle-in-PDMS constructs revealed similar trends, with the mean elastic modulus decreasing by over 95% from 2.17 to 0.06 MPa as Q* changed from 0 to 0.125 (SI Appendix, Fig. S3). As the range of surface nanoindentation is less than 500 nm, this would indicate that the dramatic softening effect is not an extrinsic phenomenon arising only from bulk compression, but that the entirety of the PDMS, from the internal PDMS/PEGDA interface to the external surface, is intrinsically softer due to the introduction of PEGDA particles.

PEGDA Inclusions Soften PDMS Constructs by Chemically Modulating the PDMS Cross-Linking Process.

We then sought to understand the mechanism behind the dramatic softening of 3D-printed PDMS constructs using PEGDA particle inclusions. First, we hypothesized that the inclusion of diethoxyacetophenone as a PI in the PEGDA inner phase is primarily responsible for softening the bulk PDMS via disruption of the cross-linking process (33). To test this, we measured the swelling ratios and gel fractions of the PEGDA-in-PDMS constructs with and without PI along with stress–strain data to characterize the contributions of PDMS polymer chemistry to the observed softening effects.

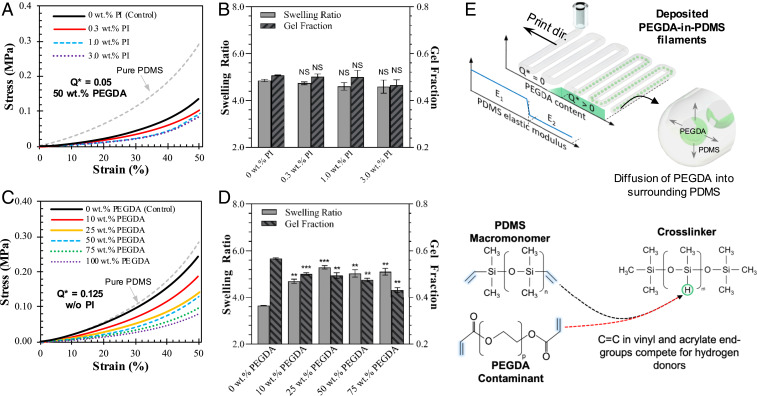
From the stress–strain curves in Fig. 4A, adding PI in the PEGDA droplet inner phase softened the bulk PDMS in a dose-dependent manner. As the amount of PI increased from 0 to 3 wt%, the mean elastic modulus of the bulk PDMS decreased by 31% from 0.77 ± 0.18 to 0.53 ± 0.24 MPa (SI Appendix, Table S2). However, we note that the elastic modulus at 0 wt% PI was already significantly lower than the pure PDMS case (1.36 ± 0.12 MPa). Furthermore, swelling ratio and gel fraction calculations show only mild changes as the amount of PI increased (Fig. 4B). When we replaced PEGDA with a glycerol solution, we found that even as the amount of glycerol droplets with 3 wt% PI dispersed in PDMS increased from Q* = 0 to 0.125, the compressive stress–strain curves remained relatively unchanged (1.23 ± 0.10 to 1.25 ± 0.27 MPa), as shown in SI Appendix, Fig. S4A. Likewise, gel fraction and swelling ratio exhibited minor changes (SI Appendix, Fig. S4B). The results thus show that PI is not wholly responsible for the dramatic softening of PDMS and that PEGDA by itself may play an essential role in the intrinsic softening of PDMS. To test this, we varied the PEGDA wt% while keeping the PI concentration at 0 wt% and dispersed the PEGDA aqueous solution in PDMS at Q* = 0.125. As seen in Fig. 4C, varying the PEGDA wt% in solution resulted in a dramatic change in the bulk PDMS compressive stress–strain behavior. As the PEGDA wt% increased from 0 to 75%, the compressive elastic modulus changed from 1.23 ± 0.41 to 0.48 ± 0.07 MPa, which corresponds to a decrease of roughly 61% (SI Appendix, Table S3). As PEGDA wt% changes from 0 to 25, the swelling ratio increased by about 40% from 3.64 ± 0.03 to 5.1 ± 0.3, while the gel fraction decreased by 7.7% from 0.567 ± 0.005 to 0.49 ± 0.02 (Fig. 4D), indicating that the presence of PEGDA by itself lowers both the cross-linking density of the bulk PDMS and the relative amount of polymer bound in the cross-link network. We deduce that these chemical changes are then reflected in the mechanical softening of PDMS as shown in the compression stress–strain curves. Altogether, PEGDA and PI work synergistically to soften the surrounding PDMS phase, with PEGDA being the more significant contributor based on its double effect on polymer chemistry.

Fig. 4.

Dose-dependent softening of PDMS constructs using PEGDA inclusions. (A) Representative compressive stress–strain curves of PDMS with 50 wt% PEGDA at various PI weight percentages. Controls refer to PDMS with 50 wt% PEGDA droplet inclusions (Q* = 0.05) without PI. The pure PDMS (i.e., no inner phase) stress–strain curve is included for comparison. (B) Plot of calculated swelling ratios and gel fractions of PDMS with 50 wt% PEGDA at various PI weight percentages, Q* = 0.05. (C) Representative compressive stress-strain curves of PDMS with droplets of different PEGDA-water solutions, Q* = 0.125. Controls refer to PDMS with water (no glycerol) droplet inclusions (Q* = 0.125). The pure PDMS (i.e., Q* = 0) stress–strain curve is included for comparison. (D) Plot of calculated swelling ratios and gel fractions of PDMS with droplets of different PEGDA–water solutions. Q* = 0.125. All constructs used here were heated to 75 °C for 24 h. (E) Schematic of the variation of PDMS elastic modulus resulting from PEGDA inclusions. Note the roles of diffusion and chemical interactions between PEGDA inclusions and PDMS cross-linker. **P < 0.01, ***P < 0.001, t test. Error bars shown are SD. NS, not significant.

Mechanistically, we infer that the PEGDA molecules are participating in side reactions with the individual PDMS constituent molecules, thereby modifying the polymer chemistry of PDMS itself, which is visualized in Fig. 4E. Standard cross-linking of PDMS involves terminal vinyl groups in the PDMS macromonomer reacting with hydrogen donors found in the cross-linker molecule. With the introduction of PEGDA molecules, the acrylate end groups which contain unsaturated carbon–carbon bonds may compete for hydrogen donors provided by the cross-linker molecules (34). As a consequence, the PEGDA molecule acts as a contaminant that adds itself to the otherwise pristine PDMS cross-link network, resulting in the softening of the PDMS network.

The occurrence of the proposed reactions is predicated upon the ability of PEGDA molecules to move beyond the PEGDA/PDMS interface and diffuse into the surrounding PDMS, as depicted in the schematic in Fig. 4E. We believe this to be the case given the results from surface nanoindentation reported earlier. This consequently suggests that the range of PEGDA movement through the PDMS and subsequent interactions is on the order of hundreds of micrometers at minimum. In addition, the movement of PEGDA through PDMS, at least in its precured state, is consistent with previous observations made in water-in-oil emulsions where hydrophobic and hydrophilic substances diffuse out aqueous droplets and through the oil continuous phase into neighboring drops (35). The out diffusion of these substances requires that the substances are capable of partitioning at the phase boundary, which is highly likely in our case due to the mildly hydrophilic nature of PEGDA by virtue of its acrylate endgroups (36). Taking this all together, we report the use of PEGDA droplet inclusions to modify the chemistry of PDMS, resulting in an elastomer that is an order of magnitude more mechanically compliant than unmodified PDMS.

Spatially Defined Softening and Magnetization in a 3D-Printed Soft Actuator.

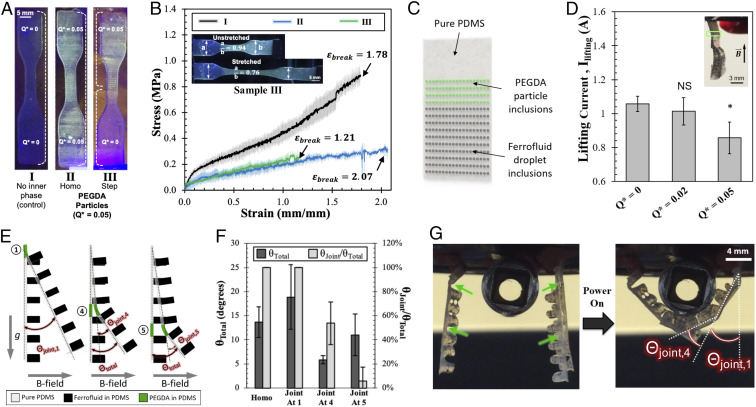
The dramatic softening of PDMS using PEGDA inclusions, combined with the ability of our setup to independently control the inner- and outer-phase fluid flow rates, constitutes a strategy for generating heterogeneous constructs. We demonstrate this by printing single-layer dog-bone–shaped tensile samples featuring a step change in the inner phase content. We chose to use PEGDA particle inclusions to soften the PDMS due to the synergy between PEGDA and PI to modulate the chemistry of PDMS. The result is a construct consisting of two distinct compositional and functional domains, depicted as sample III in Fig. 5A. We then subjected these samples to uniaxial tensile testing to produce the curves shown in Fig. 5B.

Fig. 5.

Design, optimization, and operation of a 3D-printed soft-robotic gripper arm assembly. (A) Experimental images of dog bone tensile samples consisting of (I) pure PDMS, (II) homogeneous PEGDA particles in PDMS (at Q* = 0.05), and (III) step-change PEGDA particles in PDMS at Q* = 0 and 0.05. (B) Representative tensile stress–strain curves for sample sets I, II, and III, with annotations of breaking strain (ε break). Insets are images of a step-change sample before and after stretching. The ratio of grip section widths is depicted to highlight the compositional and functional domains. All samples (n = 3) were extended at a rate of 25 mm/min. (C) A schematic of the proof-of-concept single-layer sheets with three domains: a region with no droplet inclusions, a mechanically compliant region with PEGDA particle inclusions, and a magnetically responsive region with aqueous ferrofluid droplet inclusions (Q* = 0.05). (D) Plot of lifting current (I_lifting) of sheets with different PEGDA particle content. Inset is image showing the printed sheet. The domain containing PEGDA particles is highlighted by a green box. (E) A schematic of the magnetically actuated printed soft actuators with flexible joints. The toothed portions contain ferrofluid inclusions. The possible locations of flexible PEGDA in PDMS joints (locations 1, 4, and 5) as well as the corresponding deflection angles are shown. (F) Plot of the deflection angles (θ_total and θ_joint) of each joint configuration in response to the same external B field. For the homo (homogeneous) and joint at 1 samples, the value of θ_joint is the same as θ_total. (G) Experimental images showing the whole gripper arm assembly. Three 3D-printed gripper arms with flexible joints at locations 1 and 4 attached to an electromagnet wrap around the stainless-steel socket when the electromagnet is powered (applied current = 1.0 A). Green arrows indicate where the flexible joints are located. Angles of deflection from each joint are also shown. *P < 0.05, t test. Error bars shown are SD.

Inspecting the curves, we observed that the sample with a step change in PEGDA particle content (sample III) is nearly identical to that of the sample with a homogeneous distribution of PEGDA particles (sample II) and that they are both visibly more compliant than the pure PDMS sample (sample I). This, coupled with visual analysis of stretching sample III as shown in Fig. 5B, Inset, led us to infer that the bulk tensile behavior was dominated by the mechanically compliant half consisting of PDMS with PEGDA particle inclusions. Meanwhile, the other half of the sample visibly retained the more rigid mechanical behavior of pure PDMS. Moreover, sample III had a mean breaking strain that is close to 50% of that for sample II (1.21 vs. 2.07). This is consistent with the step change in PEGDA particle content being located roughly in the middle of the sample gauge length, as well as the fact that virtually all of the strain or deformation is sustained by the mechanically compliant half.

Based on the demonstrated ability to produce constructs with mechanical heterogeneity, we conceptualized a primitive 3D-printed soft actuator that could bend or deflect at selected points in response to an external magnetic field (or B field). As a proof of concept, we first generated flat single-layer sheets (Fig. 5C) consisting of three domains: a pure PDMS portion for attachment purposes, a portion with PEGDA particle inclusions to act as a flexible joint, and a magnetically responsive portion with aqueous ferrofluid inclusions (Movie S2). We varied the Q* of PEGDA particles in the flexible joint and recorded its impact on the flexing capabilities of these samples as shown in Fig. 5D. Increasing the Q* of PEGDA particles in the flexible joint resulted in a lower lifting current (I_lifting), which is defined as the minimum current required to lift up the sheets 90° from rest. These results simultaneously indicate that the ferrofluid droplet inclusions successfully imparted magnetism and that the printed PEGDA-in-PDMS flexible joint effectively behaved as a flexural hinge to facilitate bending.

Having demonstrated our ability to incorporate mechanically compliant and B-field responsive domains into a larger printed construct, we generated a soft gripper arm whose design is illustrated in Fig. 5E. The gripper arms featured a base layer of PDMS and toothed portions consisting of PDMS with aqueous ferrofluid inclusions. On the base PDMS layer, we identified specific locations on which we could place mechanically compliant PEGDA in PDMS to maximize B-field–induced angular deflection. For subsequent range of motion testing, we prepared samples with one flexible joint located at the top (location 1), halfway down (location 4), near the bottom (location 5), or homogeneously distributed throughout the length of the gripper arm as a control (SI Appendix, Fig. S5). Note that due to the cantilever configuration of our gripper arms, the total angular deflection (θ_total) has two distinct contributions: one from the top and the other from the joint itself (θ_joint). These angles are illustrated in Fig. 5E.

Deflection angles from range of motion testing are measured and the results are shown in Fig. 5F. Placing the flexible joint at location 1 produced the highest mean θ_total, making it the best location for a flexible joint. We also considered the need to have the gripper arms deflect midway along its length (i.e., at location 4 or 5) as this would improve its ability to wrap around objects. Thus, in addition to θ_total, we also measured the distinct angular deflection contribution (or θ_joint) arising from when flexible joints are at location 4 or 5. We found θ_joint normalized by θ_total at location 4 to be 54% compared to 6% at location 5, meaning that the flexible joint at location 4 is comparatively more capable of bending in response to an external B field.

Having characterized the range of motion arising from the different flexible joint locations, we sought to demonstrate the gripping ability of our primitive 3D-printed gripper arm. To this end, we attached three gripper arms with flexible joints at locations 1 and 4 onto an electromagnet that would wrap around a stainless-steel socket upon powering the electromagnet (Fig. 5G). We observed that the gripper arm produced distinct deflection angle contributions at locations 1 and 4 as intended. With this setup, we were able to lift and hold objects weighing several hundred milligrams (Movie S3). While 3D-printed soft actuators (37, 38) or shape-changing (or 4D) constructs (39–41) have been reported previously, such results were accomplished using functional inks that are prepared beforehand with fixed composition. In contrast, our results demonstrate the ability of selectively dispersed droplet inclusions to locally tune the functional properties in printed constructs.

Conclusion

We present a versatile strategy for the modulation of printed construct properties across space using droplet inclusions. By coflowing immiscible inks in a microfluidic printhead, we could concurrently generate and extrude highly textured inks with well-organized droplet inclusions for use in extrusion-based 3D printing. The mechanical properties of the printed PDMS were found to depend on the composition and relative proportion of the inner phase, with PEGDA inclusions being especially effective at softening PDMS even at low doses via chemical modulation of the cross-linking network. We then used these insights with our printing setup to design, fabricate, and optimize the operation of soft robotic actuators, demonstrating the utility of our droplet-based strategy to impart both form and function into printed objects. Follow-up work could explore other interactions, physical or chemical, between the inner and outer phases at different length scales to generate materials with tailorable functional properties for use in soft robotics and other applications.

Materials and Methods

Experimental procedures for formulating PDMS inks; design and fabrication of the microfluidic printhead; formulating aqueous phases; printing and processing of emulsion inks; compression and tensile testing of PDMS constructs; and design, fabrication, and characterization of magnetically actuated soft robotic arm are described in SI Appendix, Materials and Methods.

Data Availability.

Raw data associated with mechanical characterization, swelling ratio and gel fraction measurements, and soft actuator characterization are available at https://doi.org/10.17632/bh6v8pcwmx.1 (42).