Ferroelectric nematic liquid crystal, a century in waiting

In PNAS, the liquid crystal group of the Soft Materials Research Center at the University of Colorado Boulder, led by N. A. Clark, reports on the discovery of a ferroelectric nematic fluid N_F, an additional state of matter (Chen et al., ref. 1) (Fig. 1A). Such a phase has been expected at least since 1916 (2), but first-principle experiments have never demonstrated its existence until now. To many, the word “nematic” is associated with the informational revolution of the 20th century and portable displays enabled by this liquid crystal. That nematic (N), shown in Fig. 1 B and C, is a nonpolar version of the discovered nematic.

Fig. 1.

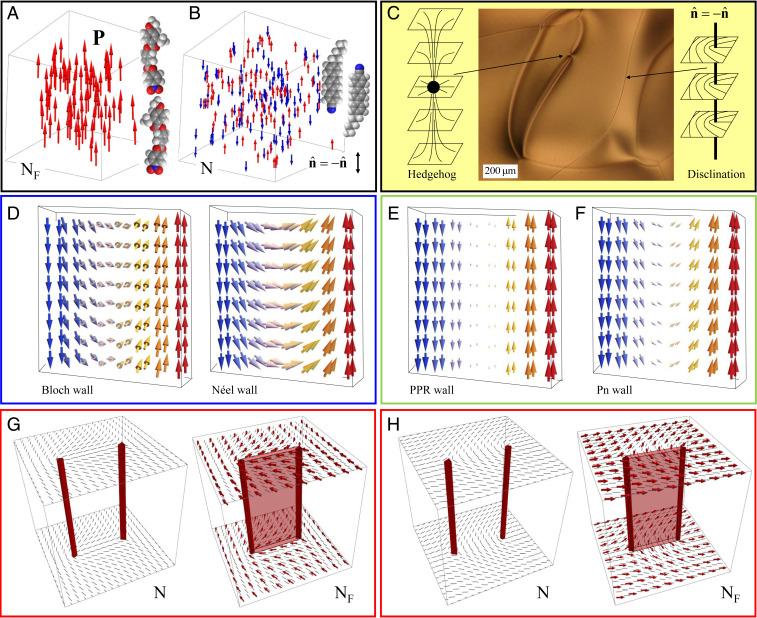
(A and B) Random selection of molecular dipoles in ferroelectric N_F (A) and dielectric N (B) nematics. (C) Topological defects, disclinations, and a point defect–hedgehog, in N. (D–F) Domain walls in ferromagnets (D) and in N_F (E and F). (G and H) Disclinations in N serve as seeds of domain walls in N_F with different orientations of the polarization vector, weakly (G) and strongly (H) charged.

Molecules of N, usually of a rod-like shape, align parallel to each other but otherwise are free to move around, showing no long-range positional order. The rods are 2 to 3 nm long, typically with chemically distinct ends, but molecular interactions do not distinguish between these ends and the fluid is nonpolar (Fig. 1B). The apolar character of N is captured by the identity property $\widehat{\mathbf{n}}\equiv -\widehat{\mathbf{n}}$ of the headless vector $\widehat{\mathbf{n}},$ called the director, which specifies the average orientation of the molecules. The nonpolarity is also reflected in the name. The term nematic derives from the Greek νεμα, which reads “nema” and means “thread.” The word was invented by Friedel in 1922 (3), who observed under a microscope an N droplet and noticed a web of “threads” (Fig. 1C). These are defect lines in the director field, called disclinations. The director rotates by 180° around a disclination, which is permissible because $\widehat{\mathbf{n}}$ and $-\widehat{\mathbf{n}}$ are indistinguishable. Disclinations are orientational analogs of dislocations in solids, cosmic strings, and vortices in superconductors and superfluids.

The property $\widehat{\mathbf{n}}\equiv -\widehat{\mathbf{n}}$ shapes an anisotropic dielectric response to an electric field. When the field $\mathbf{E}$ acts on N, positive and negative charges within the molecules shift in opposite directions, producing an electric polarization. The shifts are usually easier along the long axis than in the perpendicular directions, leading to a higher dielectric permittivity along $\widehat{\mathbf{n}},$ ${\epsilon }_{\left|\right|}>{\epsilon }_{\perp }.$ A field applied at an angle $\theta$ to $\widehat{\mathbf{n}}$ imposes a torque ${\tau }_D={\epsilon }_0\left({\epsilon }_{\left|\right|}-{\epsilon }_{\perp }\right)E^2\sin \theta \cos \theta$ that realigns $\widehat{\mathbf{n}}$ parallel to $\mathbf{E}.$ This effect, discovered by Frederics (3), is at the heart of liquid crystal displays: The realignment of $\widehat{\mathbf{n}},$ which is also the optic axis, changes the optical appearance of N pixels acted upon by the field.

This picture of N does not invoke any particular role of permanent electric dipoles that molecules with dissimilar end and head should carry. The dipoles simply contribute to dielectric permittivities. However, the very first theory of liquid crystals, proposed by Born in 1916 (2), envisioned a much stronger effect, namely the existence of a ferroelectric fluid in which all dipoles point in the same direction (Fig. 1A). Born (2) even thought that his theory was not so much a prediction but simply an explanation of the mysterious at that time state of matter, called “liquid crystals,” “anisotropic fluids,” and other names, none of which would convey what it was (3). Born knew that liquid crystals were formed by rod-like molecules. In the ferroelectric state, the dipole moments $\mu$ should be strong enough, so that their interactions withstand thermal fluctuations; tentatively, $\frac{{\mu }^2}{{\epsilon }_0\epsilon V}>k_{B}T,$ where $V$ is the molecular volume, $k_B$ is the Boltzmann constant, and $T$ is the temperature. For typical $V=1{\text{nm}}^3,$ $\epsilon =10,$ the ferroelectric should be stable at room temperature when $\mu >6$D, which is a modest requirement. And yet Born’s ferroelectric ordering (Fig. 1A), as a universal mechanism of liquid crystallinity, had not been accepted. First, no polar response to an electric field was observed at the time, and second, new liquid crystals with a weakly polar or entirely nonpolar molecular structure were synthesized (3). A different paradigm of a nonpolar N (Fig. 1 B and C) emerged in the 1920s and spearheaded the remarkable science and technology developments in the hundred years that followed.

Fast forward from 1916 to 2017. Mandle, Cowling, and Goodby (4) synthesize a highly polar rod-like material that exhibits a uniaxial N and a lower-temperature nematic with an unknown structure. Simultaneously, Kikuchi and coworkers (5) report that a different material with dipole moments ∼9.4 D shows an unusual phase with “a unidirectional, ferroelectric-like polar arrangement of the molecules.” In a continued effort, Mandle et al. (6) prepare an extended family of polar compounds. Properties of one of them, RM734 (Fig. 1A), are peculiar (7), with an anomalously small elastic constant of splay in the N phase. Mertelj et al. (7) suggest that RM734 forms a locally polar nematic upon cooling from N. This nematic is formed by periodic stripes of director splay. Each stripe accommodates polar arrangements of RM734 molecules of a slightly wedged shape. The stripes of “up” and “down” splay alternate to fill the space smoothly. Although locally ferroelectric, the “splay nematic” model implies antiferroelectricity, since the direction of polarization alternates between up and down stripes (7). The remarkable collective pursuit to understand RM734 culminates with the studies by Chen et al. (1) of how the material behaves after cooling from a uniformly aligned N and under the electric field. The work demonstrates that the discovered nematic is the ferroelectric N_F envisioned by Born and formed by macroscopic domains, within which the polarization $\mathbf{P}$ is uniform, but could adopt one of the two permissible orientations along $\widehat{\mathbf{n}},$ $\mathbf{P}$ and $-\mathbf{P}.$

A well-known feature of ferroics, a family that embraces ferromagnets, ferroelectrics, and other, mostly crystalline, materials with collectively aligned dipole moments, is the formation of domains with a different macroscopic orientation of the dipoles. These domains are separated by domain walls. Imagine that a uniform dielectric N in Fig. 1B is cooled down and transforms into an N_F by aligning all of the dipoles along a single direction. Unlike $\widehat{\mathbf{n}},$ the electric polarization is a polar vector. During the phase transition, the domains form independently of each other, and one should expect an equal probability of $\mathbf{P}$ and $-\mathbf{P}$ regions. An electric field $\mathbf{E}$ could lift the parity, forcing domains of a favorable polarity to expand and unfavorable ones to shrink. Two key observations by Chen et al. (1), namely 1) the formation of domains of opposite polarity in the absence of an electric field and 2) their polar reorientation by the field, establish the first-principle proof of a ferroelectric N_F.

The polar ordering makes N_F incredibly more sensitive to the electric field than N (1). Fields as low as ${10}^2\hspace{0.5em}\text{V/m}$ are sufficient to overcome the orientational elasticity of N_F and create a torque ${\tau }_P=PE\sin \theta$ that twists $\mathbf{P}$ by 90° from the substrate-imposed direction. The measured polarization density is very high, $P=6\times {10}^{-2}{\text{C/m}}^2$ (1). The same field ${10}^2\hspace{0.5em}\text{V/m}$ acting on N with ${\epsilon }_{\left|\right|}-{\epsilon }_{\perp }=10$ would produce a torque that is orders of magnitude weaker and incapable of causing strong twists. Note, however, that the ease with which N_F is twisted should not be assumed automatically extendable to other deformations, such as splay, since the splay produces a bound charge of density $\rho =-\text{div}\mathbf{P}.$ The space charge restricts the variations of the polarization field $\mathbf{P}\left(\mathbf{r}\right),$ a phenomenon also known for solid and smectic ferroelectrics (8). The bulk and surface charges caused by spatially varying $\mathbf{P}\left(\mathbf{r}\right)$ trigger intriguing features of domain walls, hydrodynamics, and electro-optics of N_F (1).

Domain walls are to ferroics what disclinations are to N: They showcase the intrinsic symmetry of the medium. Within a wall, the vector $\mathbf{P}$ should somehow transform into $-\mathbf{P}.$ The pathway depends on the material. In ferromagnets, the magnetization vector cannot change its magnitude. Thus the reversal is through rigid rotations, either twist or bend, known as the Bloch and Néel walls, respectively (Fig. 1D). In ferroelectrics, the physics is richer, as $\mathbf{P}$ can change its magnitude, and the polarity flip can be achieved without any reorientation, by simply diminishing $\left|\mathbf{P}\right|$ to zero on both sides of the wall, which is called an Ising wall in solid ferroelectrics (Fig. 1E). In N_F, the director could remain uniform, parallel to the wall; this is why the structure is called a pure polarization reversal (PPR) wall (1). The PPR wall tends to be parallel to $\widehat{\mathbf{n}},$ to ensure that $\mathbf{P}$ is also tangential to the wall. Any tilt $\psi$ of $\mathbf{P}$ away from the wall would create a space charge $2P\sin \psi$ (9). Since $\widehat{\mathbf{n}}\left(\mathbf{r}\right)$ = const, a PPR wall is hardly visible under an optical microscope; however, the nonpolar N character of the wall’s center should exhibit a weaker degree of orientational order compared to the domain interior. N_F also shows remarkable hybrid “Pn walls,” in which $\mathbf{P}$ and $\widehat{\mathbf{n}}$ bend together (1), as in Fig. 1F, where a decrease of $\left|\mathbf{P}\right|$ accompanies the bend. Through field-induced deformations of $\mathbf{P}$ and $\widehat{\mathbf{n}},$ domain walls in N_F can be shrunk or erased by an “order reconstruction” mechanism (1).

Imagine that an RM734 drop is cooled down from the isotropic melt into N and then into N_F. The first phase transition should produce disclinations and point defects–hedgehogs (Fig. 1C) (10, 11). The emergence of disclinations resembles the formation of cosmic strings in the Kibble model of the early Universe (12) and vortices in superfluids in the Zurek model (13). In these models, defects form at the junctions of growing and merging domains of the low-symmetry phase that carry different “orientations” of the order parameter. In N, the Kibble–Zurek mechanism is supplemented by defects formed in each nucleus regardless of mergers because of the aligning effect of the confining nematic–isotropic interfaces, called director anchoring (11). The second N–N_F transition with discrete symmetry breaking is no less intriguing. If the disclinations already exist in N, the appearance of polarization would transform each line into a seed and an edge of a domain wall (Fig. 1 G and H). A similar effect of cosmic strings seeding domain walls has been predicted for the early Universe (12). Depending on the kinetics, the walls in N_F might exhibit various $\mathbf{P}\left(\mathbf{r}\right)$ geometries and thus different physical properties, in particular a different space charge. Since the N–N_F transition is of weak first order (1), one could also expect point and wall defects brought about by anchoring of $\mathbf{P}$ and $\widehat{\mathbf{n}}$ at interfaces.

The discovery of the N_F phase by Chen et al. (1) opens another chapter in condensed-matter science and technology. It adds a distinct member to the broad group of solid ferroelectrics that hold major promise in a range of applications such as memory devices (14). An important but not an easy task in applications is to design a spatially variable polarization, as the crystalline structure anchors $\mathbf{P}$ to certain directions. The fluid character of N_F with continuously deformable $\widehat{\mathbf{n}}$ and $\mathbf{P}$ should allow a much better spatiotemporal control of polarization, for example through surface patterning (15, 16) and application of electromagnetic fields. For the liquid crystal community, N_F offers a broad range of physical effects to explore, ranging from the behavior of topological defects to surface anchoring, response to electromagnetic fields and flows, interplay of bound and free electric charges, field-controlled hydrodynamics, field-order coupling in the proper N_F state and in the pretransitional regions, and interplay of polarity and chirality. Hybrid materials involving N_F, such as polymer-stabilized, polymer-dispersed, and elastomer liquid crystals, would also be of great interest. The field of ferroelectric nematics will flourish for decades to come.