Significance
Early in embryonic brain development, progenitor cells favor proliferation—where each progenitor makes two copies of itself to expand the progenitor pool—but late in development, the progenitors prefer differentiation. In differentiation, the progenitor population finally declines as each progenitor differentiates into a pair of neurons. We discovered that the time course of proliferation to differentiation is smooth and orderly. Furthermore, neuroepithelial progenitors and the radial glial progenitors that they make simultaneously follow the same time course during development. If other animals follow the mouse model, our observations could account for the relationship between brain size and the duration of embryonic development.
Keywords: cortical development, neuroepithelial cells, radial glia progenitors, expansion coefficient
Abstract
The balance between proliferation and differentiation of stem cells and progenitors determines the size of an adult brain region. While the molecular mechanisms regulating proliferation and differentiation of cortical progenitors have been intensively studied, an analysis of the kinetics of progenitor choice between self-renewal and differentiation in vivo is, due to the technical difficulties, still unknown. Here we established a descriptive mathematical model to estimate the probability of self-renewal or differentiation of cortical progenitor behaviors in vivo, a variable we have termed the expansion coefficient. We have applied the model, one which depends only on experimentally measured parameters, to the developing mouse cortex where the expansive neuroepithelial cells and neurogenic radial glial progenitors are coexisting. Surprisingly, we found that the expansion coefficients of both neuroepithelium cells and radial glial progenitors follow the same developmental trajectory during cortical development, suggesting a common rule governing self-renewal/differentiation behaviors in mouse cortical progenitor differentiation.
The development of tissues is balanced between the proliferation and differentiation of stem cells. This balance appears to be species and tissue specific, given the unique body location and tissue size for various types of tissues. Decoding the molecular machinery regulating the process, therefore, is a key to understanding tissue size control in evolution and development. An increase in brain size, particularly that of the cerebral cortex, is believed to have been vital for enhancing the cognitive abilities of mammals and, especially, of primates. Since the number of neurons/glia strongly correlates with cortical size (1), our question can be rephrased as, What mechanisms control the species-specific neuronal/glial number during corticogenesis? All mammals evolved from a common ancestral lineage and thus share numerous developmental processes (2). However, during subsequent mammalian evolution, modification of these developmental programs must have occurred. It is these changes, particularly those underpinning brain size and neuronal/glial number, that are likely to result in species-specific alteration to brain development.
In contrast to many qualitative analyses of neuronal cell types found in higher mammals (3–5), there have been only a few quantitative studies of developmental neuro/gliogenesis. Recent work has given us key insights into the mechanisms and progenitor types that are important for cortical growth. We now know that the cortical progenitors comprise multiple subtypes (Fig. 1): 1) self-renewable neuroepithelium cells (NEs), 2) neurogenic radial glia progenitors (RGs), 3) intermediate progenitors (IPs) generating two neurons, and 4) outer/basal subventricular zone (OSVZ) radial glia-like progenitors (oRG/bRGs) recently identified as a population in gyral brains like ferret and human (3, 6, 7). These cell types are thought to generate most of the neurons and glial progenitors in embryonic stages. Later glial progenitors further proliferate after birth, contributing to the increase in the volume of the cortex. The differences in the size of the cortex for various species are therefore likely to result from the proliferative/differentiation capacities of all of these progenitor types. With techniques currently available, however, it is not feasible to obtain time-course data of in vivo embryonic cortex progenitors at a scale large enough to estimate the kinetics of progenitor expansion/differentiation throughout development. Establishing a mathematical model that is able to describe the kinetics of progenitor expansion and differentiation, therefore, is an essential step toward understanding the species-specific control of brain size. Pioneering work by Takahashi et al. (8) was based on the idea that developmental time in embryonic days can be transformed into the number of cell divisions by the measured cell cycle length. Each mother progenitor produces two daughter cells, so describing the number of cell divisions permits counting the total number of cells generated.
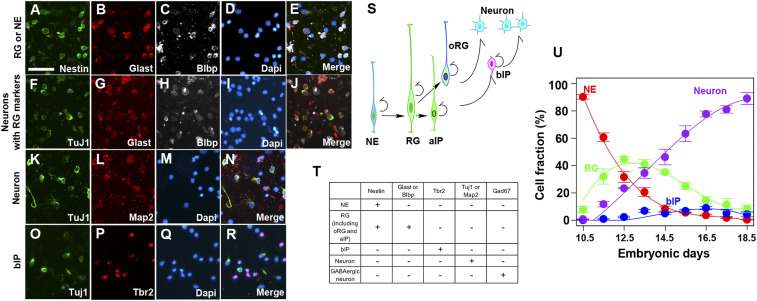
Fig. 1.
Estimation of the fraction of each cell type during mouse embryonic corticogenesis. (A–R) Immunostaining images of dissociated cells prepared from mouse cortices to distinguish the cell types. Pictures are the representative images of E14.5 dissociated cells. We counted Nestin+/Glast+, Nestin+/Blbp+, or Nestin+/Blbp+/Glast+ as RGs and Nestin+/Glast−/Blbp− as NEs (A–E). The RG fraction was further subtracted by the fraction of Tuj1+ and either Glast or Blbp+ double-positive cells (F–J). The neuronal fraction was counted as either Tuj1+ or Map2+ cells (K–N). bIPs are counted as Tbr2+/Tuj1− cells (O–R). (S) Developmental relationship of distinct progenitor types and neurons. NEs are the initial progenitors in the cortical VZ, subsequently differentiated into RGs. RGs can be further differentiated into aIPs, oRG/bRGs, bIPs, or neurons. (T) Combinatory immunostaining to delineate cell types. (U) The fraction of all of the cell types used for modeling plotted against the embryonic stage. The data are fitted with third-order polynomials. The total fraction was calculated after excluding GABAergic interneurons and glial progenitors. (Scale bar: 50 m.)
Early in development, after the neural tube closes, the neuroepithelium is formed by the division of cells in what is called the ventricular zone (VZ), a region that surrounds what will be the ventricle. The progenitors initially are NEs, but these cells generate other progenitor cell types that finally are responsible for making the brain’s neurons, a cell type that does not divide. The early-born neurons settle in the region of the cortex closest to the ventricular zone, and the late-born neurons migrate to the parts of the cortex closest to the brain surface. That is, the cortical neurons are generated in an inside-out way. During development, because of this inside-out process, the parts closest to the ventricle are called apical and the parts of the cortex closest to the surface are termed basal. NEs make a progenitor class of RGs (although they are not actually glia cells) and these fall into two classes, apical radial glia and the oRG/bRGs. The RGs also make a progenitor type of IPs that also fall into two classes, apical (aIP) and basal (bIP) progenitors.
The Takahashi et al. (8) model uses a simple assumption that cells in the VZ are one class of progenitors and cells outside of the VZ are the second class of cells. This means the theory treats the NEs, RGs, and aIPs in the VZ as one uniform progenitor type and bRGs and bIPs in the subventricular zone and neurons (which are postmitotic) as a second cell class. Here we established a model incorporating the distinct progenitor types and their kinetics. Applying our model to the mouse developing cortex led us to a surprising conclusion that the probabilities of self-renewal/differentiation of NEs and RGs follow the same kinetics. Our model revealed the existence of a common mechanism orchestrating distinct cortical progenitor types in the developing mouse cortex.
Results and Discussion
The goal of this work is a quantitative understanding of embryonic development of the mouse cortex. We carried out an experimental analysis to determine fractions of all cell types in the entire cell population every day from embryonic day (E)10.5 to E18.5 in a specific region of the developing mouse cortex, followed by a theoretical analysis of these data. Our specific focus was on how many daughter cells of the same type as their mother cell are born at different developmental stages, which we call the “expansion coefficient.” Our main conclusion is that expansion coefficients of NEs and RGs, major progenitor types in the developing cortex, follow the same quantitative rules throughout embryonic development.
Experimental Analysis.
Estimation of the fraction of all cell types in each stage of mouse cortical development.
To measure the fraction of each cell type present, we prepared dissociated cells on each of 9 d from E10.5 to E18.5 of mouse embryonic cortices and immunostained them by using the combinatorial antibodies against marker proteins to define each cell type (Fig. 1 and SI Appendix, Table S1). An example of images collected on one specific day (E14.5) is presented in Fig. 1 A–R. The cell types considered and the cells they produced (indicated by arrows) are shown in Fig. 1S. Since the marker proteins used in this study are not nuclear localized, we were unable to count labeled cells in sections. We therefore used acute dissociation of fixed cells from cortices. We judged single Nestin+ cells that are negative for RG markers (Blbp and Glast) as NEs (Fig. 1 A–E), Nestin+ cells that are either Blbp+ or Glast+ as RGs (Fig. 1 A–E), Tbr2+ cells that are Tuj1− as bIPs (Fig. 1 O–R), and Tuj1+ or Map2+ cells as neurons (Fig. 1 K–N). Although both Blbp and Glast are RG markers, we found that considerable fractions of Blbp+/Glast+ cells are costained with an early neuronal marker, Tuj1, possibly due to sustained protein expression during the transition from RGs to neurons (Fig. 1 F–J). Indeed, we detected about 20% overlapped staining fractions by the combination of Tuj1 and another proliferative marker, Ki67 at E14.5 (data not shown), supporting that the residual RG marker expression is still in the newly generated neuronal fraction. We therefore counted the double positive of Blbp+/Glast+ and Tuj1+ as neurons and subtracted them from the RG fraction (Fig. 1T and SI Appendix, Table S1). All of the cell types we considered above are the progenies of NEs. However, GABA (-aminobutyric acid)ergic interneurons which originated from the ventral telencephalon and migrated into the cortex from E13.5 onward are known to compose about 20% of total neurons in the adult brain. Since the dissociated cortical cells include this population, we subtracted the fraction of GABAergic interneurons from the neuronal fractions, as published earlier (9).
Apoptosis of progenitors, in particular during the early corticogenesis, is known to affect the final neuronal number and the brain size (10). Since we did not include dying progenitors in our cortical development model (described later), we counted the apoptotic cells by staining of activated caspase-3 from E10.5 to E14.5 to evaluate the magnitude of the cell death. We found, however, that the fraction is less than 1.5% during the stages examined (SI Appendix, Table S2). Given that the largest SEM for the NE cell fraction in our data was 3.9%, we conclude that the contribution of cell death fraction is neglectable as assumed in our model.
At the end of neurogenesis, RGs are transformed into astroglial progenitors, oligodendrocyte progenitors, or ependymal cells (11). However, the generation of these glial progenitors has been reported as 0.37% of oligodendrocyte progenitors and less than 2% of astroglial progenitors at E17 mouse cortex (12). We counted GFAP+ astroglial progenitors and confirmed that the glial fractions are approximately 2% (SI Appendix, Table S1). Given the deviation of RGs, the contribution of glial progenitors is considered as being negligible. The data of the adjusted cell fractions are fitted with third-order polynomials to provide the natural context in which to find equations that describe these data (Fig. 1U). The following theoretical analysis was applied to the data shown in Fig. 1U:
Estimation of cell cycle length of total and each progenitor population.
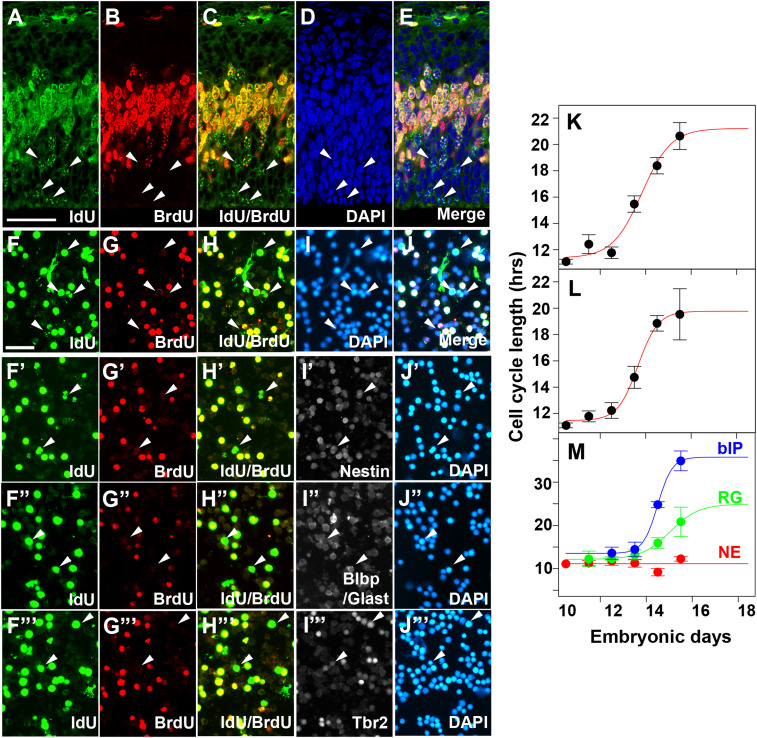
Fig. 1U presents the data needed for our subsequent theoretical analysis, but these data are not directly useful, because our model concerns cell type differentiation at each cell division, not at each embryonic day. We must convert days of embryonic development to cell divisions per day. To this end, we measured average cell cycle time for progenitors in the VZ on sections by IdU (5-iodo-2’-deoxyuridine)/BrdU (5-bromo-2’-deoxyuridine) double-labeling methods (Fig. 2 A–E) (13). The time lag between two injections of IdU and BrdU labeling of S-phase cells allowed us to calculate cell cycle length at the given embryonic stage, by calculating the ratio of cells that exit the S phase during the lag to the total number of cells, which is equal to fraction of the cell cycle that progressed during the lag at the given stage (Materials and Methods). This method yields the average cell cycle length of the entire progenitor population. The inverse of the cell cycle length is the speed of cell division (cell division number per hour), the integral of which yields cell division number at a given embryonic stage. We measured the cell cycle length using cortical sections and dissociated cortical cells. Both measurements resulted in values similar to the published data (SI Appendix, Table S3) (8). To estimate the cell cycle length at arbitrary development stages, we fitted the data with sigmoid functions (Fig. 2K).
Fig. 2.
Estimation of cell cycle length of cortical progenitors. (A–E) Representative images of E13.5 cortical sections to estimate cell cycle length by the IdU/BrdU dual-labeling method. Embryos were labeled by IdU injection followed by the BrdU 1.5 h later. Embryos were fixed 0.5 h after BrdU injection. S-phase cells in the VZ underneath (labeled by BrdU) were counted as total progenitors. Cells singly labeled by IdU (A and C, arrowheads) and those labeled by BrdU (B) were used for calculating cell cycle length as described in Materials and Methods. (F–J′) Representative images of E13.5 dissociated cortical cells to estimate cell cycle length by the IdU (F)/BrdU (G) dual-labeling method. Total cells were counted as DAPI+ cells (I). (F′–J′′′) E13.5 dissociated cortical cells were stained with IdU (F′–F′′′)/BrdU (G′–G′′′) together with progenitor markers, Nestin (I′), Blbp/Glast (I″) or Tbr2 (I′′′) for the estimation of progenitor type-specific cell cycle lengths. (K–M) Average cell cycle lengths of the entire progenitor population as a function of embryonic days, estimated from IdU/BrdU labeling of cells in sections (K) or dissociated cells (L). Those estimated for each progenitor type are shown in M. (Scale bars: A–E, 50 m; F–J′′′, 50 m.)
Since cell cycle lengths of RGs and bIPs are known to differ (14), we also estimated the cell cycle length of each progenitor type in dissociated cells by costaining with IdU/BrdU and progenitor marker: Nestin for total progenitors, Glast and Blbp for RGs, and Tbr2 for bIPs. NEs were identified as nestin+ cells that are neither RGs nor bIPs (Fig. 2 F′–J′ and SI Appendix, Table S3).
Interestingly, we found that cell cycle lengths of NEs, RGs, and bIPs follow distinct kinetics (Fig. 2M). The data of total dissociated cells are almost identical to those generated by the counting in section, indicating the consistency in both measuring methods (Fig. 2 F–J and L). Cell cycle lengths of NEs, RGs, and IPs were relatively constant until E13.5 but those of bIPs and RG cells became longer, while that of NEs largely did not change their average cell division time (Fig. 2M). We fitted the data of RG cells and bIP cells with a sigmoid function and the data of NE cells with a constant value (Fig. 2M).
bIP and RG cell cycle length data appear to be not saturated such that sigmoid fitting may not be the best estimation. However, we have a rationale for why we should employ the sigmoid fitting for these cell types as described below. While we did not measure average cell cycle length for total progenitors later than E15.5, those at E16.5 and E17.5 have been reported as 18.4 h at E16 and 19 h at E17.5 [Takahashi et al. (8) and Siegenthaler et al. (21)]. These values are close to our estimated values from sigmoid fitting (Fig. 2 K and L). Since cell cycle length of each progenitor type at a given embryonic stage constrains average cell cycle length of total progenitors, we can evaluate models of cell type-specific cell cycle length by asking whether they could reproduce experimentally measured average cell cycle length. While the second-order polynomial gave us a poor fit (SI Appendix, Fig. S1 A and A′), monotone Hermite spline interpolation provided apparently better prediction for cell cycle lengths of RGs and bIPs at later stages (SI Appendix, Fig. S1 B and B′). We compared the RG and bIP cell cycle length models by sigmoid function and spline interpolation in the estimation of average cell cycle length. We found that average cell cycle length estimated with spline interpolation fails to reproduce the experimentally measured results, in particular at later stages, while those from sigmoid function are better (SI Appendix, Fig. S1C).
Theoretical Analysis.
General observations.
In our experimental analysis, the cells considered are three progenitor types, NEs, RGs, and bIPs, together with excitatory neurons generated locally in the developing cortex (see Fig. 1S, where the arrows indicate which progenitors generate which cell types). The data used for our theoretical analysis are shown as the fractions of each of the types on each day of development from the end of E9.5 to the end of E18.5 (Fig. 1U).
Not all cell divisions are the same type. Specifically, three modes of progenitor cell division are recognized and we will later need to use this information repeatedly. Because NEs can make only NEs and RGs, we use them as an example of the three modes of division (Fig. 3B). We consider a progenitor cell population, all of which are undergoing cell divisions:
-
1)
Expansive division. Each NE can divide symmetrically to produce two new NEs (the fraction of NEs in the entire NE population that use this mode, on the th division, is denoted by with the subscript 0 indicating the number of non-NE daughter cells produced by this form of cell division).
-
2)
Asymmetric division. A NE can divide asymmetrically to make one new NE daughter cell and one RG daughter cell (the fraction of NEs that do this on the th cell division is with the subscript 1 indicating that one non-NE is made with this mode).
-
3)
Symmetric division. A NE can divide symmetrically to produce two RG daughter cells (the fraction of NEs with this fate is because two daughter cells are not NEs but RGs).
All of the progenitors we study can sometimes use each of these three modes.
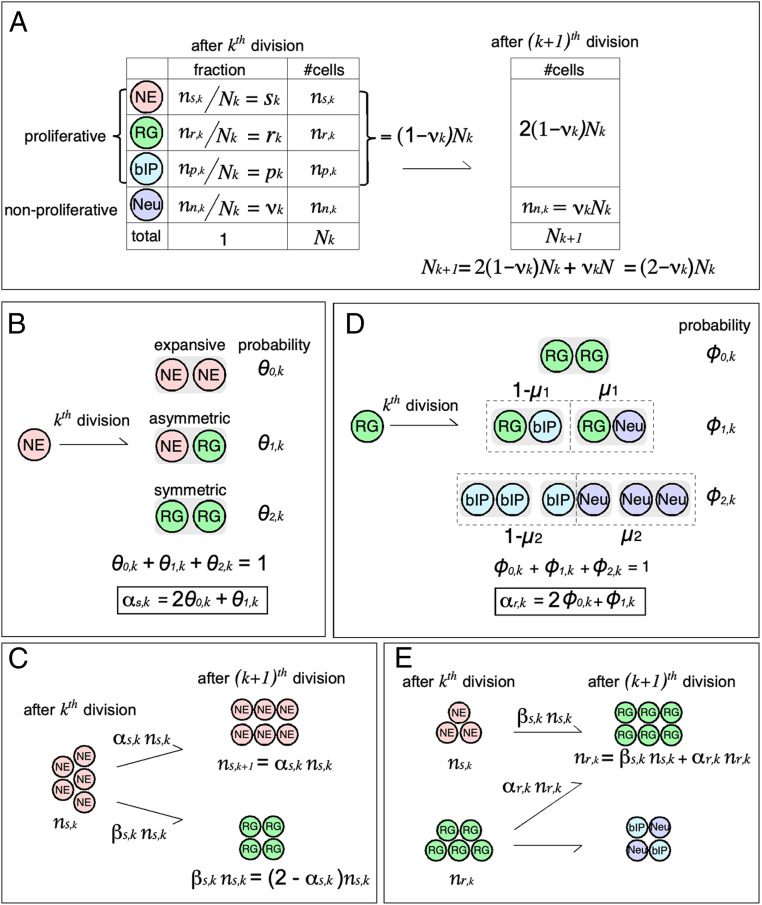
Fig. 3.
Graphical summary of the cortical development model. (A) Demographic of developing cortical neurons. The equation relating and is repeatedly used in the present theory to convert the number of each cell type to its fraction, which was experimentally measured. NE, neuroepithelium cell; RG, radial glia; bIP, basal intermediate progenitor; Neu, neuron derived from local cortical progenitor. (B) Three cell division modes of NE. A goal of the present model is estimate the average number of NEs generated by one mother NE at a given developmental stage, termed as the expansion coefficient (). (C) Differentiation of NE at a cell division. is a quantity determining change in the number of NEs at each division. (D) Cell division mode of RG. An RG yields two cells, which can be RG, bIP, or neuron. is the probability that, when an RG generates one non-RG cell, it will be a neuron. is probability that, when an RG generates two non-RG cells, either one will be a neuron (i.e., is the expected number of neurons from one RG under this division mode). The expansion coefficient of RG () is defined in the same way as that of NE. (E) Origin of RGs. Because RGs are derived from NEs and RGs, the number of RGs after the th cell division () is the sum of those from NEs () and RGs (). Note that .
Total number of cells after the th cell cycle.
We need to know , the total number of cells present after the th cell cycles. If, for example, a population of cells are all dividing with an average cell division time of 12 h, in one 24-h d, all of the population would divide twice (on average). This population of cells would then have two cell cycles per day. After cell cycles, the fraction of all cells that are neurons is (something measured), so the number of neurons present is (Fig. 3A). Because neurons do not divide, the neuron population is carried over after the th cell division. The number of progenitors (nonneurons) present after the th cell cycles is and this number of cells doubles after the th cell cycle because we assume that, on average, the population of all progenitors divides once with each cell cycle. Thus we know that is
Relation of days of embryonic development to the total number of cell cycles .
To keep the arguments as simple as possible, we start by assuming that all progenitor cells divide according to the average cell cycle time across embryogenesis as illustrated in Fig. 2L (SI Appendix, Table S3). For 9 d of development, from the beginning of day E10.5 to the end of day E18.5, d of embryonic development, and the average time of one cell division time (in hours, ) on each day is (estimated with acutely dissociated cortical neurons, Fig. 2L). If we divide 24 h/d by for each day of development, we can calculate the total number of cell cycles per day for each day of development. The result is cell cycles per day of embryonic development.
For the theory, however, we need to be able to translate days of embryonic development into a cumulative number of cell cycles on each day. If we start counting cell cycles at E10.5 and subtract 10.5 from each E between 10.5 and 18.5, we can get embryonic , and if we calculate , the cumulative sum of cell cycles per day, we get . For the 9 d of development (D = [0,1,2,3,4,5,6,7,8]), gives the corresponding cumulative number of cell cycles which is just over 12 for all of the embryonic development. We fitted (least squares) a smooth curve to the relation between and , where D and are treated as continuous variables, and find that and . Thus, the smooth polynomial relations between and can be used to convert between these variables.
Goal for Modeling of NE behavior.
Our goal in this section is to derive an equation that relates the NE expansion coefficient to the quantities (the fraction of all cells that are neurons after the th cell cycle) and and (the fraction of NEs after the th and th cell cycles):
The expansion coefficient for NEs is unknown, but the quantities , , and on the right side of the equation are all measured in the experiments. Note that the subscript stands for “stem cell” because NEs are effectively stem cells for the developing embryonic cortex we study.
Modeling of NE behavior.
First, we establish a mathematical model for the NEs, which make only NEs and RGs, and thus are particularly simple. For example, RGs make three cell types: RGs, bIPs, and neurons. Therefore, we can study the fraction of NEs present throughout embryonic development in isolation. The other progenitors we discuss later follow a straightforward elaboration of this NE model, as will be seen below.
As shown in Fig. 3B, cells in the NE population have a choice of three mutually exclusive modes of cell division (expansive = 0, asymmetric = 1, and symmetric = 2) for each cell division and so the fractions of cells using each mode for the thcell division follow the equation
Suppose that is the number of NEs present after the th cell cycle of the population, where k is the number of cell cycle steps the NE cell population has taken (one cell division per step, on average). Then, as shown in Fig. 3C, the number of NEs present after the th cell division is
Here the expansion coefficient (the subscript s indicates the expansion coefficient for NEs; other subscripts will be used for the expansion coefficient for other progenitor types) is given by . This expansion coefficient gives the average number of daughter cells from one mother cell that are identical to the mother cell type (NE).
The term is the fraction of NEs at step k that divide expansively (0 daughters different from the mother) to replace the mother cell with two new NEs, and the term is the fraction of NEs that divide asymmetrically to generate one NE and one RG. As the experimental data available will be the fraction of cells of a type present in a region of the developing cortex rather than the absolute number of cells of that type, we define the fraction of NEs present in the population as
where is the total number cells present after the th cell division (see Total number of cells after cell cycle above), and is the fraction of cells present that are NEs. The relationship between and given above is (Fig. 3A), where is the fraction of all cells present after the th cell division that are neurons (a measured quantity). Dividing the equation by this equation, we obtain the evolution equation for the measured fraction
| [1] |
The NE expansion coefficient () is unknown, but everything else in this equation is known. This means that the evolution equation can be rearranged to solve for the unknown quantity (the NE expansion coefficient )
A plot of as a function of the number of cell cycles k reveals that starts at E10.5 with a value close to 2 (Fig. 4A). Because progenitors are believed to divide in all three modes and to progress from expansive divisions to asymmetric divisions, modeling NE cell behavior is equivalent to making a model for . Because the fraction of NEs decreases steadily throughout development, starts at close to 2 and then decreases steadily (Fig. 1U).
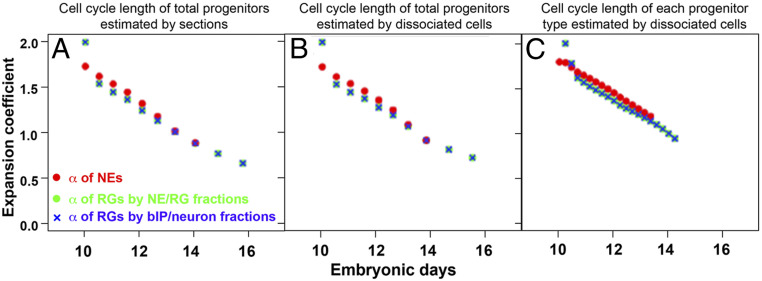
Fig. 4.
Developmental kinetics of expansion coefficients of NEs and RGs. Shown are expansion coefficients of NEs (, red circles); RGs estimated from the fraction of NEs, RGs, and bIPs/neurons (, green circles); and RGs estimated from the fraction of RGs, bIPs, and neurons (, blue cross). To estimate expansion coefficients, cell fractions as a function of embryonic stage (Fig. 1U) are converted into a function of cell division number. Compared in A–C are results of three different conversion methods. A and B use average cell cycle length of the entire progenitor population measured with cortical sections (Fig. 2K) and dissociated cortical neurons (Fig. 2L), respectively. Progenitor type-specific cell cycle lengths (Fig. 2M) are employed for C. All results shown in the plots fulfill the estimation robustness criteria (Materials and Methods), being less influenced by noise in experimental data. Expansion coefficients of NEs and RGs follow virtually identical trajectories during the corticogenesis.
The simplest theory is to have the developing cortex progress through states according to the scheme
where is the fraction of cells with division mode j at cell division k. For , gives the probability that a dividing cell will do so expansively. Similarly, would be the probability of dividing asymmetrically. These probabilities are modeled as being governed by the evolution equations
These equations, together with the requirement that , mean that the system is determined if is known. The transition probabilities in the evolution equations for must range between 0 and 1 and must increase from near 0 at early ages (to give a value of that is close to 2) to make less than 1 at E14.5. The same transition probabilities are used for both steps, and the simplest two-parameter function (one parameter to set the rate of change with k and a second parameter to set the half-rise time point) that has the right quantitative properties is a Gaussian distribution function. This model fits the measured data well so that just two parameters are needed to give , and no additional parameters except initial values are needed to generate , which is the observed value.
In summary, once we have measured cell cycle length and the fraction of each cell type, we can deduce in vivo kinetics (, the expansion coefficient of NEs) to determine whether NEs undergo self-renewal or generate differentiated cells on average at the th cell division.
Goal for Modeling of RG behavior by the fractions of NEs and RGs.
In the next section, we derive the equation for the radial glia expansion coefficient (note the subscript on the expansion coefficient for radial glia; for the NEs, this subscript is ), as related to the fraction of cells that are neurons (), the fraction that are radial glia () after the th cell cycle, and the fraction that are RGs () and the fraction that are NEs () after the th cell cycle:
The RGs expansion coefficient is unknown, but all of the quantities on the right have measured values.
Modeling of RG behavior by the fractions of NEs and RGs.
RGs are generated by NEs and by RGs themselves (Fig. 3E), and RGs also subsequently generate three different cell types, including neurons, aIPs/bIPs, and bRG/oRGs. We used an approach to estimate that depends on modifications to the equations above. The strategy is to account for the generation of RGs by RGs themselves and by NEs. As aIPs and bRG/oRGs share the histochemical markers measured empirically with RGs, we treat them as subpopulations with the overall population of RGs (15, 16).
First, we solve for from the fraction of NEs and RGs, both measured quantities. RGs are the major, if not only, cell type produced by NEs, and RGs could in turn divide expansively, asymmetrically, or symmetrically to produce both neurons and bIPs. RGs could be further differentiated into aIPs and bRG/oRGs. The evolution equation for , the fraction of all cells that are RGs after the th cell cycle, is
| [2] |
is the average number of daughter cells from one mother cell that are different from the mother cell type and given by . This equation is derived starting from the equation for the number of RGs in the same way as the NE equation above (Eq. 1). If the evolution equations for RGs (Eq. 2) and NEs (Eq. 1) are added, and if the sum of fractions for RGs and NEs () is used, the equation that results is
| [3] |
This result is gotten by noting that (i.e., two new cells of some type result from one dividing cell at each cell division) and by recognizing that . Solve Eq. 3 for to give
Goal for Modeling of RG behavior by the fractions of bIP cells and neurons.
In the this section, we calculate the RG expansion coefficient through another approach, from the fraction of RGs, bIPs, and neurons after the th cell cycle (, , and , respectively).
We derive the equation
The RGs expansion coefficient is unknown, but all of the quantities on the right have measured values.
Modeling of RG behavior by the fractions of bIP cells and neurons.
In this model, bIPs and neurons are considered together () to circumvent some complications. Because RGs generate both neurons and bIPs, we need to know what fraction of each division mode gives rise to each type. That is, for example, if an RG cell divides symmetrically, what fraction of the time does this division give a pair of neurons, and what fraction does it give a pair of bIPs? Note that asymmetric division could give one neuron and one bIP, so the fractions just specified are averages and do not necessarily apply to any specific division.
To model RG behavior that generates two different progenies, we introduced an additional parameter in the model. We denote as the probability that, when an RG yields two non-RG cells, both will be neurons, and as the probability that, when an RG yields one non-RG cell, it will be a neuron (Fig. 3D). Note that we assume, for simplicity, that these quantities do not depend on k, although they could in principle. With this notation, the evolution equations for bIPs () and neurons () are
| [4] |
and
| [5] |
where and are probabilities that RGs yield one and two non-RG cells, respectively, at the th cell division (Fig. 3D). Of note, the average number of non-RG cells from one RG () is .
Here is how these equations can be used to give another estimate for the quantity of the expansion coefficient for RGs. Simplifying this situation depends on recognizing that RGs produce just two cell types, neurons and bIPs.
If we define to be the total fraction of neurons and bIPs after the th division, then adding the two Eqs. 4 and 5 above gives
This result depends on the definition of and on recognizing that (the total cells produced per division must be two):
From experiment, , , and are known, so the average number of non-RG cells produced per cell divisions of an RG cell is
where all quantities on the right are experimental values. Because , the measured numbers of neurons and bIPs give a second way to estimate :
Modeling of bIP behavior by the fractions of RG and bIP.
Finally, we ask whether the expansion coefficient for bIPs () can be derived in the same way as and . Eq. 4 can be solved for as follows:
The equation indicates that, in addition to the fraction of the cells, depends on the probabilities concerning RG differentiation (, , , ; Fig. 3D). Therefore, to estimate , additional experiments to determine these probabilities are necessary.
The expansion coefficients of NEs and RGs follow an identical trajectory.
To estimate expansion coefficients, we first assumed that all of the progenitor types share an identical cell cycle length for simplicity. This assumption enabled the direct application of the aforementioned model of NE/RG behaviors. Before estimating expansion coefficients, the time axis of the cell fraction data was converted from the embryonic stage to cell division number, using the average cell cycle length of the entire progenitor population. Cell division number was converted back to the embryonic stage after expansion coefficients were estimated (Fig. 4). A practical challenge in expansion coefficient estimation was controlling errors due to experimental noise. Expansion coefficients we report below robustly converged to consistent values even with mild fluctuations in the cell fraction data (Materials and Methods).
To our surprise, we found that the expansion coefficients of NEs and RGs (, ) follow the same trajectory (Fig. 4 A and B). The robustness of the estimation of for RGs was confirmed by consistent results from two estimation methods; one depended on the fractions of NEs and RGs and the other on those of RGs, bIPs, and neurons. These data indicate that the NEs and RGs in developing mouse cortex produce the same average number of like daughters per mother division, suggesting common mechanisms underlying the control of self-renewing and differentiation of the two distinct cortical progenitors.
We further examined the expansion coefficients of NEs and RGs with consideration of cell cycle length of each cortical progenitor type (Fig. 2M) (14). To accommodate the progenitor subtype-specific cell cycle length in the model, we evolved the original model such that expansion coefficients were estimated per a fixed short time interval () in which cell cycle lengths of all of the progenitor types can be regarded as constants (SI Appendix, section 5). Even incorporating the progenitor-specific cell cycle length in the model, we found that the expansion coefficients of NEs and RGs ( and ) followed virtually identical kinetics (Fig. 4C, = 5 h).
These quantitative data argue that a potential common mechanism may play a role in regulating self-renewal potential across the distinct progenitor types in the developing mouse cortex. While the molecular mechanisms coordinating the differentiation kinetics of NEs and RGs are unknown, a number of known proliferation/differentiation cues such as Notch, Igf, Fgfs, Wnts, Bmps, and retinoic acids may play a role (17, 18).
Mouse is a lissencephalic species in which the brain surface is smooth, while the brains of higher mammals including humans are gyrencephalic where the oRGs are highly expandable and contribute to the expansion of the surface area (3, 4). How then is the progenitor differentiation in the gyrencephalic cortex coordinated to generate a larger neuronal population?
There are at least three ways that changes in the kinetics could lead to an increase in the absolute number of neurons in the brain. Classically, a time lag before the onset of neurogenesis is thought to account for the brain size differences (19). If that is the case, we expect the kinetics of NEs and RGs in species with larger brains would be almost the same as those for mouse but with a delayed onset for the decreasing phase of the expansion coefficient. Alternatively, if the emergence of oRGs with dedicated symmetric division explains the evolutionary increase in brain size, the kinetics of the expansion coefficient for RGs would be delayed more than those for NEs. On the other hand, we might find the expansion coefficient for both NEs and RGs has the same values through development (as it does for mouse) but is stretched out in time for animals with larger brains. In this case, if the expansion coefficient as a function of time has the same mathematical form, then we would have identified a general principle for controlling the brain size. If this were the case, the mechanism could be understood through the molecular mechanisms that describe the expansion coefficient.
Applying our model to human brain development is particularly intriguing. While direct measurement of the cell cycle length during human brain development is not technically feasible, employing the modeled cell cycle length (20) and measured dissociated cell fractions of the developing human cortex will allow us to apply our model to human cortical development. In this study, we employed established markers to distinguish cell types in a dissociated cell preparation, because not all markers have a nuclear localization signal, and cell types cannot be counted on sections. Identifying nuclear-localized markers would enable applying our approach to species that are available only in limited numbers.
Another noteworthy feature of our model is that this model is not limited to brain development but applicable to other developing tissues if they start with a stem cell population which is differentiated into further restricted progenitors and terminally differentiated cells. Exploring kinetics of stem/progenitor differentiation in various tissues may reveal a universal rule regulating stem cell behavior in tissues.
Materials and Methods
Animals.
All animal experiments were done in accordance with Institutional Animal Care and Use Committee animal protocols at the Salk Institute and the Home Office project license at King’s College London. Institute for Cancer Research (ICR) wild-type females were mated with ICR males to obtain embryos. The day of insemination and the day of birth are designated as E0.5 and postnatal day 0 (P0), respectively.
Preparation of Acute Dissociated Cortical Cells and Cortical Sections.
Dissociated cells were prepared as described previously (21). Briefly, dissected cortices were incubated for 5 to 15 min in 0.25% trypsin-ethylenediaminetetraacetic acid (EDTA)- Hank’s balanced salt solution (HBSS) with 5% glucose at C followed by mechanical dissociation by pipetting. The enzymatic reaction was stopped by adding trypsin inhibitor. A total of 0.5 106 cells were seeded into 24-well plates with poly-D-lysine–coated coverslips and centrifuged at 300 g. Cells attached to the coverslips were immediately fixed with 4% ice-cold paraformaldehyde (PFA) in phosphate-buffered saline (PBS) for 30 min and washed three times with PBS.
Embryonic brains were fixed for 1 h in ice-cold 4% PFA/PBS, cryoprotected in 25% sucrose in PBS overnight, cut at 20 m, and processed for immunostaining as described previously (21, 22).
Immunohistochemistry.
Dissociated cells on the coverslips were subjected to antigen retrieval to enhance the immunoreactivity of antigens. Coverslips were boiled for 20 min in Antigen Unmasking Solutions (Low pH; Vector Laboratories) and then cooled down to room temperature. Cells were incubated in 4% bovine serum albumin/PBS for 1 h, followed by overnight incubation with primary antibodies and subsequently with secondary antibodies to visualize the signal. The primary antibodies used in this study are as follows: Anti-BrdU (rat, 1/500; Accurate), anti-IdU/BrdU (mouse clone B44, 1/500; BD), anti-activated Caspase-3 (rabbit, 1/500; Cell Signaling), anti-GFAP (Chicken, 1/1,000; Merck Millipore), anti-Tbr2 (rabbit, 1/500; Merck Millipore), anti-Nestin (mouse, 1/500; BD), anti-Glast (guinea pig, 1/2,000; Merck Millipore), anti-Blbp (rabbit, 1/500; Merck Millipore), Tuj1 (mouse monoclonal, 1/500; Merck Millipore), and anti-Map2 (rabbit, 1/500; Abcam). Nuclei were counterstained with DAPI.
Cell Cycle Measurements of Cortical Progenitors.
Cell cycle lengths were determined by the double labeling of BrdU and IdU (15). Pregnant CD-1 females at the embryonic days indicated received thymidine analogues of 2 mg of IdU (0.2 mL of 10 mg/mL solution in 0.9% saline) intraperitoneally, followed by the same amount of BrdU 1.5 h later. We injected BrdU with a 0.5-h interval for E10.5 embryos. Animals are euthanized after 0.5 h of BrdU injection and embryonic heads are immediately fixed in 4% PFA in PBS. The sequential double labeling of IdU and BrdU allows us to determine the total cell cycle length () as follows.
Let be the number of cells labeled by IdU but not by BrdU. This population was in S phase at the time of IdU injection (), but left S phase by the time of BrdU injection (). Assuming that the distribution of progenitor cells along the cell cycle phase is constant, we found that the cell cycle progressed in 1.5 h to . Therefore,
| [6] |
where is the total number of progenitors at . can be determined from the total number of progenitors at the time of euthanizing (), which was experimentally counted by recognizing that an increase in the number of progenitors in 2 h is . That is,
| [7] |
Eliminating between Eqs. 5 and 6 yields
| [8] |
We experimentally measured the ratio of to () and determined using Eq. 8. For cell type-specific cell cycle length, we targeted our measurement onto specific cell types which were identified by additional immunostaining (Blbp and Glast for RGs, Tbr2 for bIPs). For NEs, we focused on the Nestin-positive cells in the ventricular zone which were neither RGs nor bIPs.
Image Acquisition and Analysis.
Dissociated cells were stained by the combination of Nestin/Blbp/Glast, Tuj1/Tbr2, Tuj1/Map2, GFAP, and activated caspase3 to estimate the fraction of each population. Fluorescent immunostaining images of dissociated cells were used for counting by a MatLab-based counting system. Images were taken from three to seven independent experiment sets from typically two to three embryos for preparation of dissociated cells. The number of total counted cells per stage ranged from about 500 to 5,000, depending on the age and combination of antibodies. Cortical GABAergic neurons migrating from ventral telencephalon were estimated by counting GFP-positive cells in GAD67 knock-in mice as published previously (9).
Modeling of Progenitor Behaviors.
The model of progenitor expansion and differentiation (Results and Discussion and SI Appendix, section 5) was implemented using R (http://www.r-project.org). The analysis scripts and data used in this study are available at GitHub, https://github.com/SetsukoSahara/Expansion_coefficient. Changes of the fractions of the different progenitor types over the embryonic stage were modeled with cubic polynomial functions. We first assumed that all of the progenitor types share a cell cycle length, which was measured as the average cell cycle of the entire progenitor population. By integrating the inverse of the cell cycle length (i.e., cell division number per hour), the embryonic stage was converted to cell division number, which was counted from E10.5. Expansion coefficients were calculated using the recurrence equations described in Results and Discussion. When progenitor type-specific cell cycle lengths were considered, expansion coefficients were directly estimated from the cell fraction data along the embryonic stage (SI Appendix, section 5).
To evaluate the robustness of expansion coefficient estimation, we added a small artificial noise to the cell fraction data and examined how the noise affected the estimation. Reflecting SE of the experimentally measured cell fractions (mean 0.014), uniformly distributed random noises ranging 0.01 were added to modeled cell fraction data before computing expansion coefficients. The coefficient of variation of expansion coefficients over the repetition (n = 10,000 times) reflects the robustness of the estimation against small changes in experimental data. We regarded an expansion coefficient with the coefficient of variation less than 0.1 as a robust estimation.
Supplementary Material
Acknowledgments
This work was supported by the Leverhulme Foundation (RPG-2013-313) and the Biotechnology and Biological Sciences Research Council (BB/L00562X/1) (to S.S.) and National Institutes of Health Award 1RO1DC017695 (to C.F.S.).
Footnotes
The authors declare no competing interest.
Data deposition: The analysis scripts and data used in this study are available at GitHub, https://github.com/SetsukoSahara/Expansion_coefficient.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1916665117/-/DCSupplemental.
References
- 1.Striedter G., Principles of Brain Evolution (Sinauer Associates, Inc., 2005). [Google Scholar]
- 2.Krubitzer L. A., Prescott T. J., The combinatorial creature: Cortical phenotypes within and across lifetimes. Trends Neurosci. 41, 744–762 (2018). [DOI] [PubMed] [Google Scholar]
- 3.Lui J. H., Hansen D. V., Kriegstein A. R., Development and evolution of the human neocortex. Cell 146, 18–36 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Florio M., Huttner W. B., Neural progenitors, neurogenesis and the evolution of the neocortex. Development 141, 2182–2194 (2014). [DOI] [PubMed] [Google Scholar]
- 5.Llinares-Benadero C., Borrell V., Deconstructing cortical folding: Genetic, cellular and mechanical determinants. Nat. Rev. Neurosci. 20, 161 (2019). [DOI] [PubMed] [Google Scholar]
- 6.Taverna E., Götz M., Huttner W. B., The cell biology of neurogenesis: Toward an understanding of the development and evolution of the neocortex. Annu. Rev. Cell Dev. Biol. 30, 465–502 (2014). [DOI] [PubMed] [Google Scholar]
- 7.Arai Y., Taverna E., Neural progenitor cell polarity and cortical development. Front. Cell. Neurosci. 11, 384 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Takahashi T., Nowakowski R. S., Caviness V. S., The leaving or Q fraction of the murine cerebral proliferative epithelium: A general model of neocortical neuronogenesis. J. Neurosci. 16, 6183–6196 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sahara S., Yanagawa Y., O’Leary D. D. M., Stevens C. F., The fraction of cortical GABAergic neurons is constant from near the start of cortical neurogenesis to adulthood. J. Neurosci. 32, 4755–4761 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kuida K., et al. , Reduced apoptosis and cytochrome c-mediated caspase activation in mice lacking caspase 9. Cell 94, 325–337 (1998). [DOI] [PubMed] [Google Scholar]
- 11.Kriegstein A., Alvarez-Buylla A., The glial nature of embryonic and adult neural stem cells. Annu. Rev. Neurosci. 32, 149–184 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Qian X., et al. , Timing of CNS cell generation: A programmed sequence of neuron and glial cell production from isolated murine cortical stem cells. Neuron 28, 69–80 (2000). [DOI] [PubMed] [Google Scholar]
- 13.Martynoga B., Morrison H., Price D. J., Mason J. O., Foxg1 is required for specification of ventral telencephalon and region-specific regulation of dorsal telencephalic precursor proliferation and apoptosis. Dev. Biol. 283, 113–127 (2005). [DOI] [PubMed] [Google Scholar]
- 14.Arai Y., et al. , Neural stem and progenitor cells shorten S-phase on commitment to neuron production. Nat. Commun. 2, 154 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang X., Tsai J. W., LaMonica B., Kriegstein A. R., A new subtype of progenitor cell in the mouse embryonic neocortex. Nat. Neurosci. 14, 555–561 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tyler W. A., Haydar T. F., Multiplex genetic fate mapping reveals a novel route of neocortical neurogenesis, which is altered in the Ts65Dn mouse model of Down syndrome. J. Neurosci. 33, 5106–5119 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fernández V., Llinares-Benadero C., Borrell V., Cerebral cortex expansion and folding: What have we learned? EMBO J. 35, 1021–1044 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bultje R. S., et al. , Mammalian Par3 regulates progenitor cell asymmetric division via notch signaling in the developing neocortex. Neuron 63, 189–202 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rakic P., A small step for the cell, a giant leap for mankind: A hypothesis of neocortical expansion during evolution. Trends Neurosci. 18, 383–388 (1995). [DOI] [PubMed] [Google Scholar]
- 20.Picco N., García-Moreno F., Maini P. K., Woolley T. E., Molnár Z., Mathematical modeling of cortical neurogenesis reveals that the founder population does not necessarily scale with neurogenic output. Cerebr. Cortex 28, 2540–2550 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sahara S., O’Leary D. D. M., Fgf10 regulates transition period of cortical stem cell differentiation to radial glia controlling generation of neurons and basal progenitors. Neuron 63, 48–62 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Siegenthaler J. A., Tremper-Wells B. A., Miller M. W., Foxg1 haploinsufficiency reduces the population of cortical intermediate progenitor cells: Effect of increased p21 expression. Cerebr. Cortex 18, 1865–1875 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.