Macroscopic gradients of synaptic excitation and inhibition in the neocortex

Abstract

With advances in connectomics, transcriptome and neurophysiological technologies, the neuroscience of brain-wide neural circuits is poised to take off. A major challenge is to understand how a vast diversity of functions is subserved by parcellated areas of mammalian neocortex composed of repetitions of a canonical local circuit. Areas of the cerebral cortex differ from each other in not only their input-output patterns but also their biological properties. Recent experimental and theoretical work has revealed that such variations are not random heterogeneities; rather, synaptic excitation and inhibition display systematic macroscopic gradients across the entire cortex, and they are abnormal in mental illness. Quantitative differences along these gradients can lead to qualitatively novel behaviours in nonlinear neural dynamical systems, by virtue of a phenomenon mathematically described as bifurcation. The combination of macroscopic gradients and bifurcations, in tandem with biological evolution, development and plasticity, provides a generative mechanism for functional diversity among cortical areas, as a general principle of large-scale cortical organization.

Introduction

The idea of a canonical microcircuit in the mammalian cortex is a cornerstone of neuroscience ever since the discovery of columns in the 1950s and 1960s. According to this view¹ the basic unit of cortical organization is a minicolumn, with about 100 neurons confined vertically across the cortical depth, except for the primary visual cortex (V1) where the number of neurons in a minicolumn is ~2-fold greater. Each minicolumn is dedicated to a particular neural computation, such as coding a particular orientation of visual stimuli in V1. A column consists of a number of minicolumns, and its horizontal spatial extent varies little (ranging 300–600μm in diameter) even between species whose brain volumes vary by a factor of 1,000. This expansion of cortical volumes corresponds to an increased number of columns across species².

For decades, in vitro neurophysiological studies of neocortical circuits have been largely done using slices of primary sensory areas, often with the implicit assumption that results thus obtained remain valid for all neocortical areas. By contrast, a limited number of studies have revealed marked differences between V1 and association areas such as the prefrontal cortex (PFC)^3–5 as well as between rodent and primate species^6–7, but these differences have not been systematically documented and tend to be underappreciated. As it was put some years ago: “Our view is that the rapid evolutionary expansion of neocortex has been made possible by building an ‘isocortex’ — a structure that uses repeats of the same basic local circuits throughout a single [cortical] sheet”⁸.

Of course, it is well known from neuroanatomy that spatial heterogeneity is a salient characteristic of mammalian cerebral cortex. Neuron density, pyramidal cell size, myelin content in the grey matter, cortical thickness, laminar differentiation and local circuit wiring properties all vary across the cerebral cortex^9–14. Starting with the work of Korbinian Brodmann, Constantin von Economo, Cécile Vogt-Mugnier and Oskar Vogt at the dawn of the twentieth century, these variations in cytoarchitecture and myeloarchitecture have been measured and utilized as an anatomical basis of parcellating the cortex into discrete areas and defining cortical hierarchy (see refs 13–14 for recent reviews).

Modern brain connectomics has enabled researchers to quantify cortical connectivity^15–16 . In the framework of graph theory, cortical areas are ‘nodes’ connected by ‘links’ in a structured graph. Nodes are mathematically identical even though areas are biologically heterogeneous; thus, microscale cellular variations was assessed not so much in terms of their dynamical implications as correlates of macroscale interareal long-range connections of different areas¹⁷. Similarly, in studies of functional connectivity, such as those using functional MRI (fMRI), areas are typically assumed to be identical. Functional connectivity measured by covariance matrices of the activities of pairs of areas is interpreted in terms of interareal structural connections, but the correlation between the structural and functional connections is modest^18–20. Areal differences are by and large ignored in current graph-theoretical analysis of the brain connectome, partly explaining our limited understanding of functional connectivity data, as discussed below.

From this perspective, how can one explain the different functional capabilities of such disparate areas as V1 and PFC? Differential functions of various cortical areas could emerge from their proximity to sensory peripheries, their input and output connections and synaptic plasticity. Take, for instance, the primate visual system, which is organized in a hierarchy: visual information arrives in the retina, its output is sent to the thalamus en route to V1, the output of which propagates to visual area V2 that in turn connects to V3, MT and V4, and so on^21–23. The connection patterns are determined during development and sculpted by plasticity. Along the resulting hierarchy, step-by-step there is a gradual enlargement of neuronal receptive-field sizes and selectivity for increasingly abstract stimulus features, ultimately to size- and position-invariant object recognition.

In purely feedforward architectures implemented in mathematical models of deep networks, there is no connection in the opposite direction from a higher to a lower area of a hierarchy, nor between units within each area. Such feedforward architectures have been spectacularly successful in performance of a number of tasks, and lie at the heart of the recent artificial intelligence revolution²⁴. However, the biological cortex, including early sensory areas, is endowed with an abundance of recurrent synaptic connections^25–27. Recurrent connections, sometimes also called re-entry connections, denote bidirectional interactions between neurons either within a local circuit or across different brain regions. For instance, in V1, a neuron sends signal to another neuron that in turn projects back to the first neuron. Such back-and-forth reverberation between many excitatory and inhibitory neurons is absent in networks devoid of loop connections. Most interareal connections (for example, between V1 and V2) are reciprocal, in contrast to the feedforward architecture that dominates today’s deep networks.

Moreover, brain areas differ from each other not only in inputs and outputs, but also their biological properties. For instance, consider the more than 2,400 brain-specific genes in humans: are the area-to-area variations of gene expression random heterogeneities, or does the expression of these genes vary systematically along certain well-defined axes across the cortex? The primary goal of this article is to discuss recent experimental findings in support of the notion of macroscopic gradients — namely, variations of synaptic excitation and inhibition across the cerebral cortex are not random but display macroscopic gradients primarily along a one-dimensional axis of hierarchy Importantly, strongly recurrent neural circuits are described theoretically as nonlinear dynamical systems. In such systems, quantitative changes of a property can lead to the emergence of qualitatively different behaviour, through a phenomenon mathematically called ‘bifurcation’ that is not possible in linear dynamical systems²⁸. I argue that the functional importance of macroscopic gradients can be better appreciated with the help of the theory of nonlinear dynamical systems. Bifurcations can be viewed as a mathematical engine for understanding how novel brain functions emerge, with macroscopic gradients of biological properties shaped through biological evolution, brain development and synaptic plasticity.

Below, I first present macroscopic gradients of synaptic excitation, and illustrate the idea of bifurcation that arises from such a gradient with an example of the generation of the self-sustained persistent neural activity that underlies working memory. I summarize macroscopic gradients recently reported from analyses of transcriptomic data from mouse and human cortex, and differences between the two species. Second, I show the importance of macroscopic gradients for the emergence of a hierarchy of timescales and for understanding cortex-wide functional connections. Third, I describe how synaptic excitation is balanced by inhibition, the latter of which also displays macroscopic gradients. Fourth, I briefly describe recent evidence that macroscopic gradients of synaptic excitation and inhibition are aberrant in mental disorders such as schizophrenia.

Gradients of synaptic excitation

A well-established hierarchy is that of the visual system in macaque monkey, with V1 at the bottom. Starting with the work of van Essen and his colleagues^21–22, a functional hierarchy of visual information processing has been substantiated anatomically using tract-tracing analysis. The basic observation underlying the definition of cortical hierarchy is that a feedforward projection tends to originate from neurons in superficial layers, whereas neurons that provide feedback projections reside in deep layers. According to a quantification analysis, each area in the macaque visual hierarchy was designated a position normalized between 0 and 1 along a one-dimensional hierarchy²³ For instance, a qualitative description asserts that V2 is higher than V1, V4 is higher than V2, and TEO is higher than V4 along the visual hierarchy. Quantitatively, V2, V4 and TEO were assigned hierarchical positions of 0.17, 0.42 and 0.71 respectively, with V1 at the starting position 0. To explore whether cellular or synaptic heterogeneities vary randomly or systematically along the cortical hierarchy, published spine-count data²⁹ were re-examined. Spines are small protrusions of pyramidal dendrites where individual excitatory synapses are located; therefore, spine count is a proxy of the strength of synaptic excitation per pyramidal cell. Remarkably, the spine count data display a strong positive correlation with the hierarchical position of cortical areas (Fig. 1a)³⁰. In particular, in the macaque brain, a pyramidal cell in a prefrontal area has about 10-fold more spines than a pyramidal cell in V1. By contrast, in mouse, total spine count per pyramidal cell seems to be uniform across the cortex^31–32, suggesting that the macroscopic gradient of spine counts may be a relatively recent evolutionary development.

Fig. 1 |. Macroscopic gradients of synaptic excitation and bifurcations.

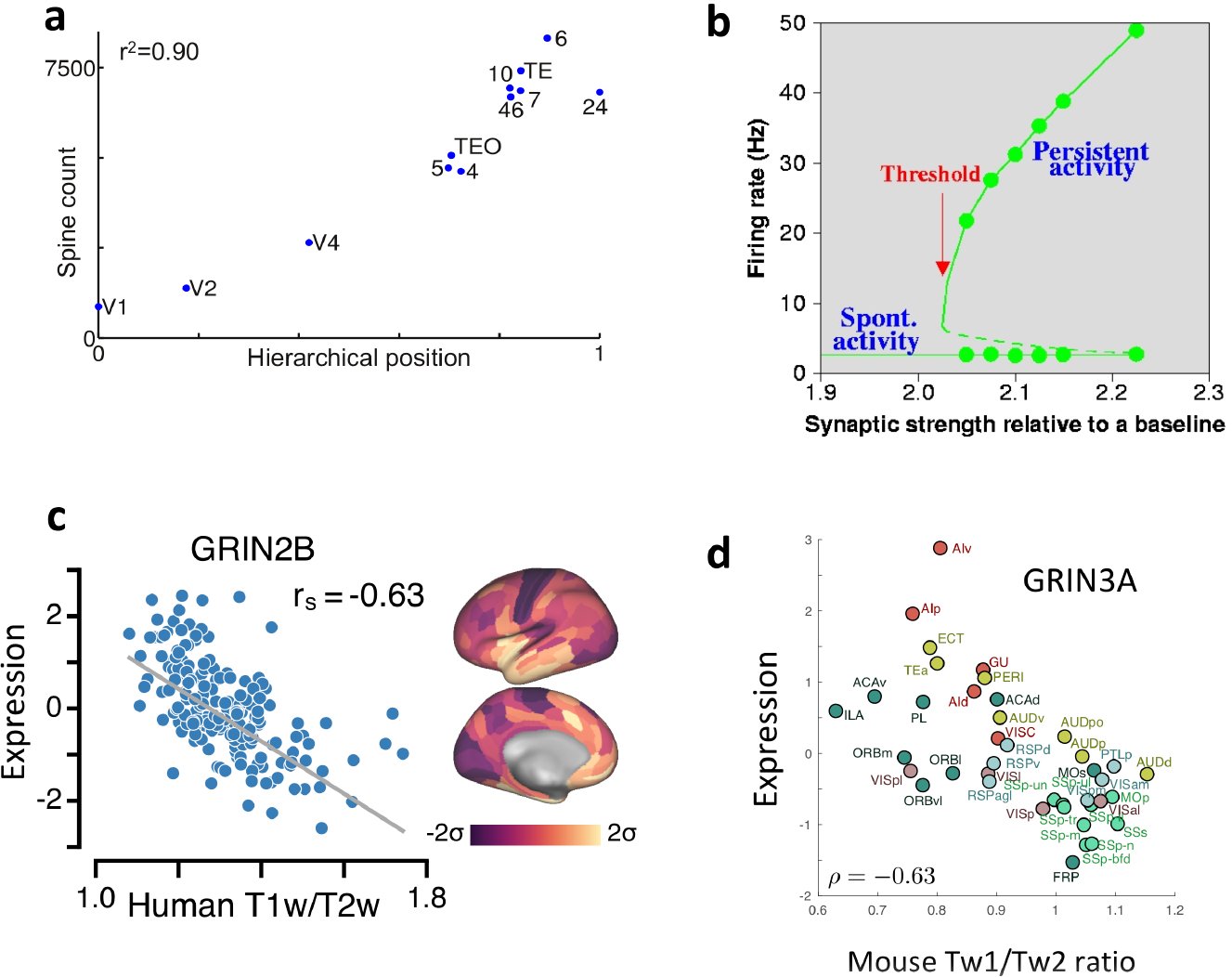
a | The number of spines on the basal dendrites of layer 3 pyramidal cells in an area of macaque cortex is strongly correlated with the area’s hierarchical position, as determined by layer-dependent projections. b | Self-sustained network states are shown by their neural firing rates (y-axis) as a function of the strength of recurrent synaptic connectivity (x-axis) in a local circuit model. Solid lines represent the spontaneous state and the mnemonic persistent memory state; dashed line: unstable states. Above a critical threshold of synaptic strength, persistent activity appears abruptly as an all-or-none bifurcation phenomenon. c | Across different areas of human cortex, the expression of GRIN2B, which encodes the NMDA receptor subunit NR2B, negatively correlates with MRI-derived T1-weighted/T2-weighted (T1w/T2w) ratio. d | In mouse cortex, Grin3a, which encodes the NMDA receptor NR3A subunit, is expressed as a function of T1w/T2w ratio. ρ, Pearson correlation coefficient; 2, somatosensory area 2; 7A, area 7A; 7B, area 7B; 7m, area 7m; 8l, lateral part of area 8; 8m, medial part of area 8; 9/46d, dorsal part of area 9/46; 9/46v, ventral part of area 9/46; 10, area 10; 24c, area 24c; TEO, area TEO; TEpd, posterior-dorsal part of area TE; r_s, Spearman rank coefficient; V1, primary visual cortex; V4, visual area 4. Parts a is adapted from ref. 30. Part b is adapted from ref. 36. Part c is adapted from ref. 43. Part d is adapted from ref. 48.

Given that 80% of all excitatory connections are intrinsic in any cortical area³³, the spine count data imply there are more recurrent excitatory connections within PFC than in V1. This is interesting functionally, because sufficiently strong excitatory connections are believed to be a mechanism for the maintenance of persistent activity in the absence of external stimulation, a neural substrate of working memory representation^34–36. Indeed, in a biologically realistic local circuit model of spiking neurons (Fig. 1b)^36–37, the strength of recurrent excitation G_EE can be varied as a parameter. When G_EE is relatively low, the system has a single stable resting state with low spontaneous activity. Neurons respond to a presented stimulus, but their firing activity rapidly decays back to the baseline after stimulation offset. As G_EE is gradually increased in a moderate range, a particular G_EE value marks a threshold level of excitatory reverberation (indicated by the red arrow) at which there is a sudden emergence of a new family of self-sustained, stimulus-selective activity states. Thus, for G_EE above the threshold, the baseline state co-exists with a number of persistent activity states (attractors), each storing a memory item. A transient stimulus can bring the system from the resting state to one of the information-selective memory states, which then persists after stimulus withdrawal.

The abrupt appearance of working memory representation is mathematically described as a bifurcation. This concept is technical, but a sudden change of behaviour as a result of graded variation of a parameter is not unfamiliar to neurophysiologists. Consider the input–output relationship of a single neuron: with a small input current, membrane potential is constant over time (a stationary attractor). When the intensity of current is increased above a threshold level, repetitive firing of action potentials (an oscillatory attractor) emerges, representing a qualitatively different dynamical behaviour from the steady state. The same holds true for recurrent neural networks. Thus, the presence of persistent neural activity in PFC but not in V1 can be theoretically explained by the strength of recurrent excitation being below the threshold in V1 and above it in PFC. This example concretely illustrates how a modest quantitative difference can produce a qualitatively novel functional capability.

Furthermore, computational modelling predicted that strong recurrent excitation is necessary but not sufficient for persistent neural activity; in addition, synaptic reverberation needs to be slow and dependent on NMDA receptors (NMDARs)³⁸. This molecular-level prediction was confirmed in a monkey physiological experiment that demonstrated a special role of NR2B-subunit-containing NMDARs in the maintenance of working memory representations³⁹. Moreover, modelling work showed that slow, NMDAR-dependent reverberation also provides a circuit mechanism for decision-making computations⁴⁰. Is there also a macroscopic gradient of NMDAR signalling along the cortical hierarchy? The answer is currently not available for macaque monkey, but relevant evidence is emerging for human and mouse. As brain-wide transcriptomic data are becoming available, one approach is to examine the expression of genes that encode NMDAR subunits — or, more generally, genes that encode receptors and other proteins of importance for synaptic excitation and inhibition — across parcellated cortical areas.

A human cortical hierarchy, as defined anatomically by tract-tracing analysis, is currently not available. However, the ratio of T1-weighted to T2-weighted MRI signal (the T1w/T2w ratio), which has been suggested to reflect myelin content in the grey matter^41–42, was noted to be high in human V1 and low in human PFC¹⁸. One study⁴³ showed that, in macaque monkeys, the T1w/T2w ratio is strongly correlated negatively (Spearman coefficient of −0.76) with the hierarchical position as defined independently using layer-dependent connections²³, in support of T1w/T2w ratio as a non-invasive index of cortical hierarchy.

Do biological properties such as gene expression levels vary systematically along the hierarchy quantified by the T1w/T2w ratio? An analysis⁴³ of published human cortical-RNA microarray data⁴⁴ revealed that multiple genes involved in synaptic transmission display macroscopic gradients along the T1w/T2w ratio axis. For example, expression of the gene GRIN2B (Fig. 1c), which encodes the NR2B NMDAR subunit, decreases with T1w/T2w ratio and thus increases with hierarchy. NMDARs are heterotetramers that each contain two copies of the obligatory NR1 subunit together with two other subunits. In V1, a ‘switch’ occurs early in development, starting near the time of eyelid opening, from NR2B to NR2A dominance in NMDARs⁴⁵. Interestingly, the expression of both NR1 and NR2A decreases rather than increases along the T1w/T2w-ratio-defined hierarchy⁴³. These results are consistent with the converging physiological evidence that differences in the abundance of NR2B-containing NMDARs mediate the appearance of the more prominent slow reverberation in PFC areas than in primary sensory areas^5,39

An analysis of genetic data among cortical areas ranked along the T1w/T2w ratio was also carried out in mouse cortex, for which hierarchy is still a matter of investigation⁴⁶. Using in situ hybridization transcriptome data⁴⁷, several macroscopic gradients were identified⁴⁸. In particular, a negative correlation of expression of NR3A-encoding gene with Tw1/Tw2 ratio (Fig. 1d) was found in mice, as in humans. By contrast, in the mouse cortex, the expression of genes encoding NR2B and NR2A positively correlates with the T1w/T2w ratio. It is worth noting that NR3A-containing NMDARs are mostly found perisynaptically, and that the functional role of NR3A in NMDAR signalling could be quite different from those of NR2A and NR2B subunits⁴⁹. Note that in vitro physiological studies showed that there is a stronger NR2B-dependent component of excitatory synaptic transmission at local pyramid-to-pyramid connections in frontal areas than in V1 of rats⁵, which appears to contradict a higher level of NR2B encoding gene expression in areas lower in the hierarchy, assuming that mouse and rat are similar. However, the relationship between gene expression of a receptor and the latter’s physiological function is an indirect one. Furthermore, the overall gene expression of a receptor does not provide information about specific locations of the encoded receptor, such as at local excitatory-to-excitatory connections in a microcircuit versus long-range interareal pathways. Nevertheless, generally, NMDAR signalling displays macroscopic gradients in both mouse and human cortices, with some similarities as well as some marked differences between species.

Global brain dynamics

Spatial dependence of network connections⁵⁰ has recently drawn attention in brain connectomic studies. In a directed- and weighted- interareal connectivity matrix of macaque monkey cortex (published in a series of articles)^33,51–52, the connection weight between pairs of areas decreases exponentially with their wiring distance (the exponential distance rule). Inspired by this work, a class of spatially embedded structural network models of the cortex has been proposed^53–54 to better describe mesoscopic cortical connectivity than purely topological networks that do not take into account spatial relationship between areas. The cortical network (Fig. 2a) endowed with this interareal connectivity matrix served as the structural basis of a large-scale dynamical model of macaque cortex, that incorporated a macroscopic gradient of synaptic excitation calibrated by the previously described spine-count data^30,55–56. In this model, spontaneous neural activity fluctuates fast in an early sensory area like V1, and much more slowly in a PFC area such as Brodmann area 9 and the dorsal part of area 46 (area 9/46d). Activity time series from each area is quantified by the autocorrelation function, which describes how the values of a neural signal between two time points decays with the temporal separation interval. A dominant time constant was extracted from each area, revealing a wide range of timescales of dynamical operation that increase from sensory to association areas (Fig. 2b).

Fig. 2 |. Timescale hierarchies and their implications for functional connectivity,

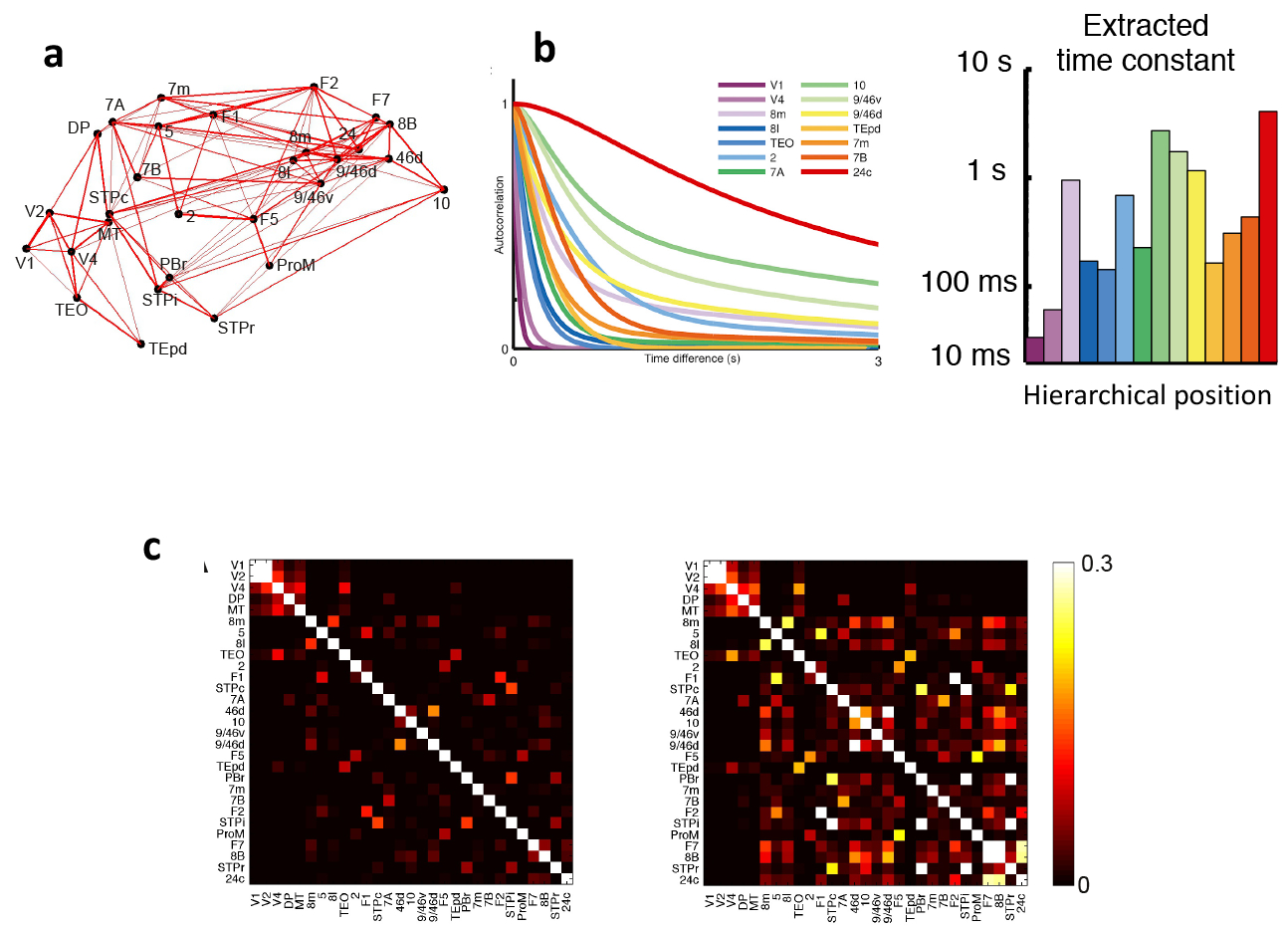
a | Connections between 29 areas in an anatomically constrained dynamical model of macaque cortex. Strong connections are indicated by lines, with line thickness determined by connection strength, b | The model shows a hierarchy of timescales, with sensory areas and association areas characterized by short and long timescales, respectively. The left graph depicts the autocorrelation function of neural activity in each of a subset of areas. From these functions, a dominant time constant was extracted (displayed as a function of the area’s hierarchical position on the right), c | The functional connectivity matrix of the macaque cortex model where areas are assumed to be identical (left) is compared to the matrix when the model includes a macroscopic gradient (right). A gradient of synaptic excitation enhances functional connectivity especially for association areas with slow time constants, whereas functional connectivity of early visual areas (upper left corner of the matrix) is similar with or without a macroscopic gradient. 2, somatosensory area 2; 5, somatosensory area 5; 7A, area 7A; 7B, area 7B; 7m, area 7m; 8B, area 8B; 81, lateral part of area 8; 8m, medial part of area 8; 9/46d, dorsal part of area 9/46; 9/46v, ventral part of area 9/46; 10, area 10; 24c, area 24c; 46d, dorsal part of area 46; DP, dorsal prelunate area; FI, frontal area FI; F2, frontal area F2; F5, frontal area F5; F7, frontal area F7; MT, middle temporal area; PBr, rostral part of the parabelt area; ProM, area ProM; STPc, caudal part of the superior temporal polysensory area; STPi, intermediate part of the superior temporal polysensory area; STPr, rostral part of the superior temporal polysensory area; TEO, area TEO; TEpd, posterior-dorsal part of area TE; VI, primary visual cortex; V2, visual area 2; V4, visual area 4. Parts a-c are adapted from Chaudhuri et al.³⁰.

This theoretically predicted hierarchy of time constants gained empirical support in analyses of single-unit activity of the monkey cortex⁵⁷ and mouse⁵⁸. It is also functionally desirable for early sensory areas to operate on fast timescales to process rapidly changing external stimuli, while association areas such as PFC display slow transients of neural activity that is appropriate for temporal integration of information in decision-making^40,59–61. The gradually expanding temporal response windows, also found in human cortex^62–64 , mirror the well-known increases of spatial receptive field size along the visual hierarchy⁶⁵. It is worth noting, however, that the dominant time constant is not a monotonically increasing function of the hierarchical position; it depends on the macroscopic gradient of synaptic excitation and the specific statistical properties of interareal connectivity including that of numerous feedback loops⁶⁶.

The existence of macroscopic gradients implies that cortical areas are not the same, in contrast to the assumption of commonly practiced graph theoretic analysis of functional connectivities. Intuitively, one expects that functional connectivity, be it measured by fMRI, magnetoencephalography or electrocorticography, would show greater correlation with anatomical connectivity if nodes were indeed identical, because in that case the global dynamics would be predominantly determined by the interactions between nodes. This was confirmed in simulations of the multi-regional macaque cortex model³⁰ in which functional connectivity was defined by co-variance of the activity of pairs of areas (Fig. 2c). Notably, the functional connectivity was dramatically altered in the absence of the macroscopic gradient, when the area-to-area variation of synaptic excitation based on the spine-count data was removed from the model (compare left and right panels of Fig. 2c). This is because the slow dynamics in association areas have a large impact on the global neurodynamical pattern. Importantly, the correlation between functional connectivity and anatomical connectivity was smaller in the presence of a macroscopic gradient (r² = 0.53) than without it (r² = 0.83)³⁰. It follows from this finding that long-range connections alone cannot predict global brain-activity patterns. Indeed, a recent study of human cortex showed that the correlation between functional connectivity and structural connectivity (measured by diffusion tensor imaging) gradually decreases from unimodal sensory areas to transmodal or association areas⁶⁷. Therefore, functional connectivity analyses that take into account a heterogeneous distribution of properties in the cortex, notably in the form of macroscopic gradients, are predicted to yield a better understanding of the relationship between functional and structural connectivity.

One study⁶⁸ addressed this matter by comparing a computational model of the human cortex with functional imaging measurements from more than 300 healthy participants. In this model, the interareal connectivity was based on the structural MRI data from the Human Connectome Project. As in previous work^69–70, the dynamics of each local area were described by a population rate model adopted from ref. 71 and BOLD signal was extracted from neural activity using the Balloon model⁷². The global brain connectivity for each parcellated area was defined as the average of its functional connectivities with all the other cortical areas, and the global brain connectivity values (one for each area) of the model were compared with those measured using human resting-state fMRI. With areas differing only in their connection patterns, the correlation (r) between the global connectivity values from the computational model and from the fMRI data was about 0.48, which is comparable comparable to that of a previous study⁷³. However, when a linear gradient of strength for local synaptic excitation as well as inhibition was introduced along the T1w/T2w axis, the correlation between the global functional connectivity from the computational model and that from the fMRI data was substantially higher (~0.74).

In a separate work, the strength of recurrent connections in a modelled cortical network was allowed to vary from area to area and was optimized to fit the model to functional connectivity data from human resting-state fMRI. The resulting model parameters revealed a macroscopic gradient of local recurrent excitation⁷⁴. However, surprisingly, the gradient that emerged from model fitting decreased rather than increased along the hierarchy. The discrepancy between the two studies^68,74 may arise from differences in the details of experimentation and modelling, and its resolution warrants future research. Regardless, these works highlight the importance of considering macroscopic gradients in network studies of large-scale brain dynamics³⁰.

Gradients of inhibition

A hallmark of cortical organization is the balance between synaptic excitation and inhibition⁷⁵. Does synaptic inhibition also display a macroscopic gradient?

Cortical GABAergic cells display remarkable diversity^76–79, and the density of various inhibitory cell types is heterogeneous across the cortex. These diverse interneuron types can be labelled with different markers. Conventionally, three major interneuron classes have been defined based on their expression of the calcium-binding proteins parvalbumin (PV⁺), calbindin (CB⁺) or calretinin (CR⁺), and their relative proportions are quite different in V1 versus PFC^80–81. More recent studies in rodents commonly divide most interneurons into three types according to their mutually exclusive expression of PV, somatostatin (SST) or vasoactive intestinal peptide (VIP); there is a large overlap between SST⁺ interneurons and CB⁺ interneurons (collectively referred to hereafter as SST⁺/CB⁺ neurons), as well as between VIP⁺ interneurons and CR⁺ interneurons (VIP⁺/CR⁺ neurons). In a disinhibitory motif initially proposed theoretically⁸² and later supported by experiments (for reviews, see Refs. 83–84), PV⁺ interneurons target the perisomatic region of pyramidal cells and control their spiking output, whereas SST⁺/CB⁺ interneurons target pyramidal dendrites and gate synaptic input flow. The third interneuron subpopulation, VIP⁺/CR⁺ neurons, preferentially project to SST⁺/CB⁺ interneurons (Fig. 3a).

Fig. 3 |. Macroscopic gradients of synaptic inhibition.

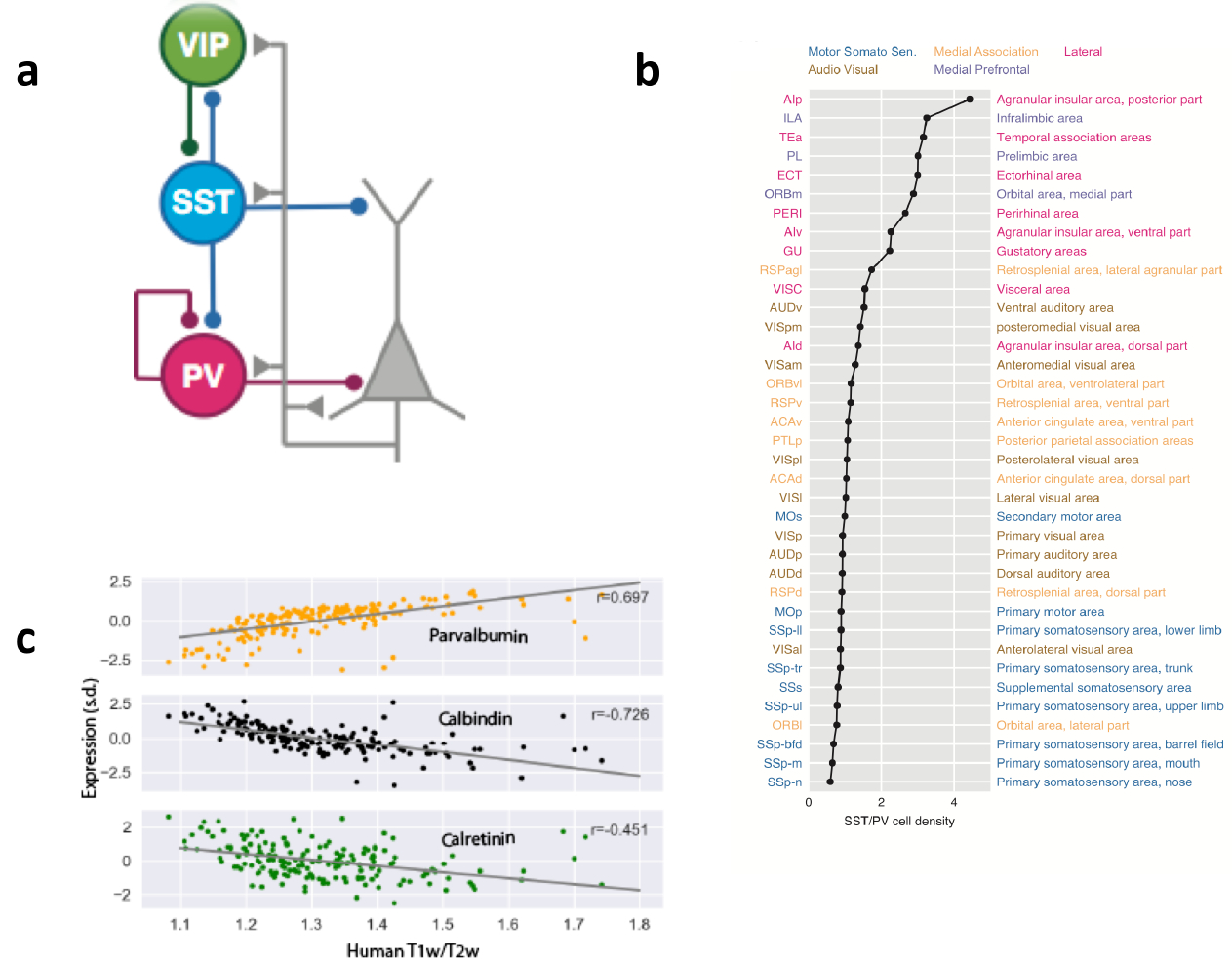
a | A disinhibitory circuit comprising a parvalbumin-expressing (PV⁺) interneuron, a somatostatin-expressing (SST+) interneuron and a vasoactive intestinal peptide-expressing (VIP⁺) interneuron. b | The ratio of SST⁺ interneuron density to PV⁺ interneuron density plotted and ranked for different areas of mouse cortex. PV⁺ neurons are abundant in primary sensory areas, whereas frontal areas are dominated by SST⁺ neurons. Areas are colour-coded to depict six types of cortical subnetwork to which they belong. c | Genes encoding calbindin (CB), calretinin (CR) and PV exhibit macroscopic gradients in the human cortex. Part a is adapted from ref. 91. Part b is adapted from an image in ref. 91 that was generated using data in ref. 85. Part c is adapted from ref. 43.

A comprehensive cell-count analysis of GABAergic cells in the mouse brain revealed that the ratio of input-controlling SST⁺ cells and output-controlling PV⁺ cells varies considerably across cortical areas⁸⁵. When areas were plotted by rank order, it became clear that the ratio of SST⁺ neurons to PV⁺ neurons is generally low in early sensory areas and motor areas, and is high in association areas including frontal areas (Fig. 3b), revealing a macroscopic gradient of synaptic inhibition in the mouse cortex. Notably, PV⁺ cells are twice as abundant as SST⁺/CB⁺ cells in V1, but SST⁺/CB⁺ cells are 4-fold more numerous than PV⁺ cells in frontal areas. This gradient of input-controlling versus output-controlling inhibition holds for primates⁸¹. Indeed, using an entirely different methodology, a separate study⁴³ found that the expression of the genes encoding PV, CB and CR all display strong correlations with the T1w/T2w ratio in the human cortex (Fig. 3c).

Synaptic inhibition is crucial for processes such as stimulus selectivity^86–87, synchronous oscillations^88–89; the functional implications of a macroscopic gradient of inhibition remains to be elucidated in future research. A particularly relevant idea is that the disinhibitory motif could serve to gate inputs into pyramidal dendrites flexibly according to behavioural demands. Specifically, when VIP⁺/CR⁺ inhibitory neurons are activated, SST⁺/CB⁺ neurons would be suppressed, thereby opening the gate for inputs into pyramidal dendrites^82,90–91. The need for such pathway gating is likely greater in association areas (as recipients of converging inputs) than in primary sensory areas along a cortical hierarchy, which I propose to be subserved by a macroscopic gradient of input-controlling versus output-controlling inhibitory neurons. Moreover, different GABAergic cell types are differentially modulated by neuromodulators in different brain states. The identification of macroscopic gradients of synaptic inhibition represents an important clue for extending our understanding of the role of inhibitory neurons, from local circuits towards multi-regional large-scale cortical systems.

Gradient deficit in mental disorders

The notion of macroscopic gradients has begun to be applied to studies of mental disorders. For instance, schizophrenia is characterized by large-scale cortical dysconnectivity (abnormally reduced or increased connectivity, depending on brain regions and task conditions, compared with health individuals)⁹². Interestingly, dysconnectivity mostly implicate the PFC and other association areas, raising the question of how such differential impairment can be explained if biological abnormalities are common across the neocortex.

This question motivated a study of brain dysconnectivity in schizophrenia that combined fMRI with a large-scale cortical network model of the human cortex⁹³. In the model and the data analysis, parcellated cortical areas were divided into association areas and sensory areas. Functional connectivity between a pair of areas was defined by the covariance of their activity, and ‘within-network connectivity’ was computed by the average of functional connectivities between association areas, or between sensory areas, separately. The computational model was used to simulate the effect of low-dose ketamine injection, which, in healthy humans, produces symptoms of schizophrenia [(94)]. The effect of ketamine was assumed to reduce NMDAR-dependent drive to inhibitory neurons, leading to weakened inhibition (the effect of ketamine on excitatory-to-excitatory connections was not included in this study). In the model, local recurrent excitation strength was scaled by a parameter W_A for association areas and W_S for sensory areas. The existence of a macroscopic gradient was incorporated in a simple way by assuming a higher recurrent excitation in association areas than in sensory areas (W_A > W_S). Reducing the strength of the excitatory-to-inhibitory connection throughout the cortex, mimicking ketamine application, produced an increase of functional connectivity in the association network, but no noticeable change of functional connectivity in the sensory network By contrast, when there was no heterogeneity in recurrent excitation between association areas and sensory areas (W_A = W_S), simulated ketamine results in increased functional connectivity similarly for the sensory network and association network. Concomitantly, resting-state fMRI measurements were carried out in 164 healthy individuals and 161 individuals with schizophrenia. The experiment revealed a differential increase of functional connectivity in association areas of individuals with schizophrenia compared with healthy individuals, but no difference in the functional connectivity of sensory areas between the two participant groups, supporting the presence of a macroscopic gradient. Therefore, macroscopic gradients offer a potential explanation for selective impairments centred around PFC and other association areas, even if biological alterations may be widespread and uniform over the entire cortex⁹⁵.

Are macroscopic gradients themselves deficient in mental illness? A recent transcriptomics study⁹⁶ investigated the expression of key markers of glutamate and GABA neurotransmission from postmortem cortical tissues of healthy individuals and individuals afflicted with schizophrenia. Four areas (V1, V2, posterior parietal cortex (PPC) and dorsolateral PFC) were chosen because of their contributions to visuospatial working memory, a cardinal cognitive function that is impaired in schizophrenia. The expression of genes encoding receptors, enzymes that synthesize transmitters, vesicular transmitter transporters, and so on, were combined into two composite measures, for glutamate signalling and GABA signalling. In the healthy controls, there were pronounced macroscopic gradients for both synaptic excitation and inhibition (Fig. 4). By sharp contrast, in individuals with schizophrenia, the gradient of glutamatergic signalling was blunted, whereas the gradient of GABAergic signaling was accentuated (Fig. 4). Although this study was limited to four areas, it suggests that macroscopic gradients of synaptic excitation and inhibition across the cortical hierarchy are aberrant in schizophrenia. Future research is needed to dissect functional consequences of abnormal macroscopic gradients associated with Schizophrenia and other mental disorders including autism⁹⁷. For instance, how does the absence of a graded increase of glutamatergic signalling along the hierarchy contribute to distributed working memory deficits? The answer requires a more complete description of differential distributions of transcripts in pyramidal neurons and various interneuron types, as well as across cortical laminae^47,98–99 . Our efforts to achieve an understanding across levels from transcripts to circuits and behaviour would benefit from continued collaborations between experiments and theoretical modelling, in a nascent field known as computational psychiatry¹⁰⁰.

Fig. 4 |. Macroscopic gradients in schizophrenia.

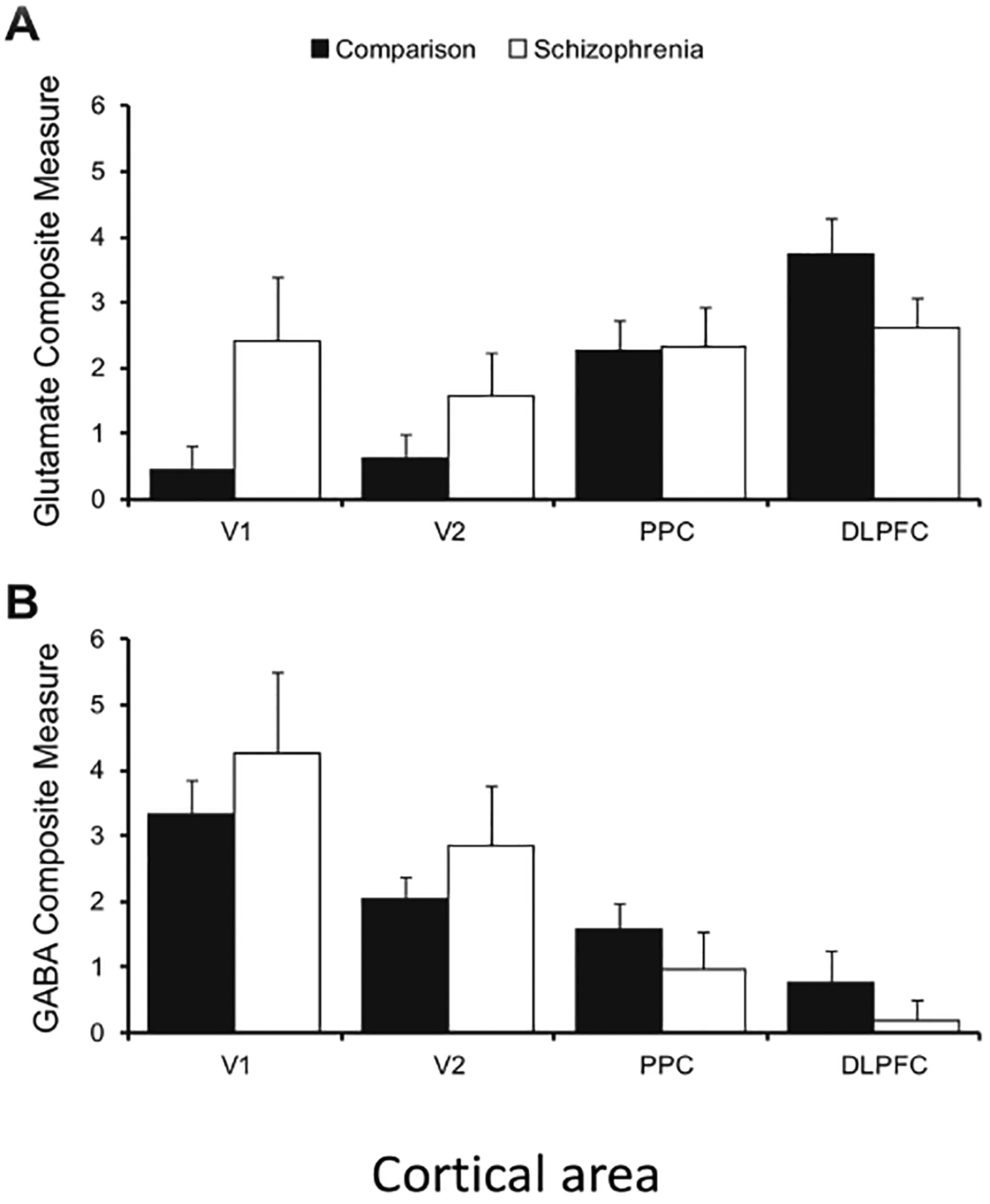
A comparison of postmortem brains of healthy controls and individuals with schizophrenia examined composite measures of glutamate-signalling-related and GABA-signalling-related transcripts in the visuospatial working-memory network. In control brains (filled bar), the composite glutamate signalling (top) and GABA signalling measures (bottom) showed marked, and opposing, caudal-to-rostral gradients. However, in individuals with schizophrenia (open bar), the gradient was lost for the glutamate-signalling measure, but enhanced for the GABA-signalling measure. Error bars represent variability across each group of 20 individuals. DLPFC, dorsolateral prefrontal cortex; PPC, posterior parietal cortex; V1, primary visual cortex; V2, Brodmann area 18. Figure reproduced from ref. 96.

Concluding remarks

Above, I have discussed work giving rise to the idea of macroscopic gradients of synaptic excitation and inhibition, which can be viewed as variations on the common theme of a canonical cortical circuit. Thus, structural differences not only serve as anatomical markers, but also have important implications for understanding distributed brain dynamics and functions. A priori, variations of biological properties in the cortical tissue could be high dimensional. Consider, for instance, a large number (N in the thousdands) of brain-specific genes in the cortex, whose expression levels in different parcellated cortical areas can be plotted as points in N-dimensional space. Analyses have revealed that variations in gene expression in the brain are not random in a space with thousands of dimensions; instead they can be accounted for largely in a low-dimensional (~10) space of principal components, with the largest component aligned with the axis of the T1w/T2w-ratio-defined hierarchy^43,48. Macroscopic gradients represent an emerging principle of large-scale cortical organization.

The main findings from the discussion above are twofold. First, there is an increasing gradient of synaptic excitation along the cortical hierarchy, which can be measured in various ways including the number of spines per pyramidal neuron, level of NMDA receptor coding genes, etc. Functionally, modelling³⁸ and experiments^5,39 point to a crucial role in cognition of NMDAR-dependent recurrent excitation, but a gradient of NMDA receptor dependent excitation in a multi-regional cortex remains to be elucidated in future research. Second, the proportion of input-controlling SST⁺/CB⁺ interneurons versus output-controlling PV⁺ interneurons increases along the cortical hierarchy. The density of PV⁺ cells may correlate with the density of pyramidal cells, but whether their ratio is constant across cortex remains to be assessed. An increase of SST⁺/CB⁺ neuronal density with hierarchy is in line with the demand of areas higher in the hierarchy to receive more converging inputs from different domains. SST⁺/CB⁺ cell density is layer-dependent, and these neurons subdivide into subgroups of cells with different targets. A comprehensive characterization of cell-type-specific connections is needed to fully understand the functional implications of this gradient of synaptic inhibition. This article covers recent analyses of gene expression, but linking gene expression to function is indirect. An important intermediate step is to quantify the labelling of receptors or their subunits that are involved in synaptic excitation and inhibition¹⁰¹.

The best descriptor for defining quantitatively a one-dimensional hierarchy in different species^{22–23,43,46,102} and that can also be confirmed by physiology^55,103–105 is a topic of active current research. Moreover, conventionally defined hierarchies are steep across sensory areas but become rather shallow in PFC. An alternative approach to quantify a hierarchy, initially derived from the analysis of PFC subregions, is based on the observation that parcellated areas show varying degrees of laminar differentiation^14,106–107. Classification on the basis of laminar differentiation has been shown to predict afferent and efferent patterns of parcellated cortical areas. The hierarchy within PFC established this way seems to be broadly consistent with a functionally revealed gradient of processing along the rostro-caudal axis of the frontal lobe, in terms of increasingly abstract representation of behavioral rules and action control^108–111.

The concept of macroscopic gradients can be extended to more than one dimension. As a matter of fact, it should, because defining a single one-dimensional hierarchy tends to be vision-centric and does not fairly consider different sensory modalities. In addition, motor areas are not readily placed in a linear framework from sensory to association areas. Decades ago, a two-dimensional diagram of cortical organization was proposed¹¹², with the radial direction along the hierarchy and the polar direction covering different sensory modalities and motor domains. This view was recently confirmed by a sophisticated analysis of interareal functional correlations of the human cortex^42,113, according to the seven-network parcellation¹¹⁴ (Fig. 5a). A two-dimensional organization of cortical areas was also reported for macaque monkey³⁰, with the radial direction defined by hierarchy and the angular distance between areas defined by the inverse of their interareal connection strength (Fig. 5b).

Fig. 5 |. Two-dimensional gradients of primate cortex.

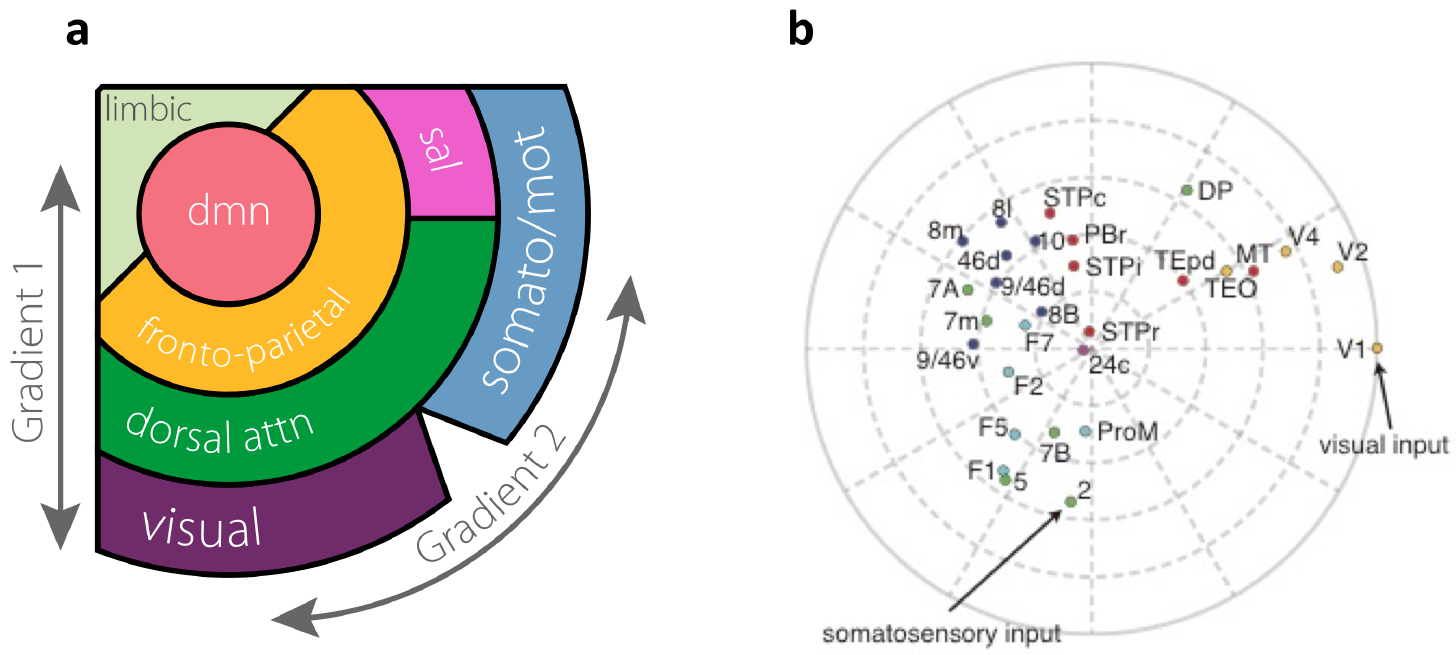
a |Spatial relationships of seven subnetworks of the human cerebral cortex.. A method called diffusion map was used to deduce two principal gradients from functional activity data in the resting state. The first (radial) gradient defines a hierarchy, with visual, somatosensory and motor areas at the bottom that are arranged along the second (angular) gradient. Association areas are in three higher levels of the hierarchy. Abbreviation: dmn, default-mode network; dorsal attn, dorsal attention network; sal, salience network; somato/mot, somatosensory/motor network. b |Two-dimensional plot of areas of macaque cortex, representing long-range connectivity and hierarchy. The distance of an area from the edge corresponds to its hierarchical position, whereas the angular distance between two areas is inversely related to their connection strength. Each color corresponds to a different cortical lobe: occipital (yellow), temporal (red), parietal (green), frontal subdivided into agranular (cyan) and granular (prefrontal proper, blue). Definitions of individual area abbreviations are included in the legend of Fig. 2. Part a is adapted from ref. 113. Part b is adapted from ref. 30.

In recurrent neural networks described by nonlinear dynamical systems, a quantitative difference in the network’s properties can lead to qualitatively different dynamical behaviour by virtue of bifurcations. The concept of bifurcations, here illustrated with a local circuit model of working memory (Fig. 1b), is widely applicable in the field of neural-network modelling^115–118 In a multi-regional large-scale system of the brain, bifurcations could arise at certain locations in space, as a result of macroscopic gradients of biological properties. This possibility points to an appealing mechanism for the generation of novel and diverse functions in different subnetworks of brain areas. It potentially offers a theoretical account of distributed cognitive processes such as working memory, which can be tested rigorously using multi-regional neurophysiology¹¹⁹ in behaving animals. Importantly, variations of biological properties, including macroscopic gradients themselves, are partly determined genetically, shaped during brain development and modifiable through plasticity in adulthood.

Variations of a canonical circuit architecture, in the form of macroscopic gradients, provide a promising approach towards understanding the vastly diverse brain functions at the biological and computational levels. The time is ripe to tackle distributed dynamics in the brain^58,120–122. Progress in this direction would help to bridge circuit neurobiology and cognitive psychology, the latter of which emphasizes the diversity of mental faculties: “Faculty psychology is impressed by such prima facie differences as between, say, sensation and perception, volition and cognition, learning and remembering, or language and thought”¹²³. A marriage of the biological concept of macroscopic gradients and the mathematical concept of bifurcations, in close interplay with experimentation, offers a concrete dynamical systems perspective in our quest of understanding distributed yet modularly organized cognitive processes in the complex large-scale neural circuits of the brain.