Abstract
FORS is the underlying hash-based few-time signing scheme in SPHINCS , one of the nine signature schemes which advanced to round 2 of the NIST Post-Quantum Cryptography standardization competition. In this paper, we analyze the security of FORS with respect to adaptive chosen message attacks. We show that in such a setting, the security of FORS decreases significantly with each signed message when compared to its security against non-adaptive chosen message attacks. We propose a chaining mechanism that with slightly more computation, dynamically binds the Obtain Random Subset (ORS) generation with signing, hence, eliminating the offline advantage of adaptive chosen message adversaries. We apply our chaining mechanism to FORS and present DFORS whose security against adaptive chosen message attacks is equal to the non-adaptive security of FORS. In a nutshell, using SPHINCS
, one of the nine signature schemes which advanced to round 2 of the NIST Post-Quantum Cryptography standardization competition. In this paper, we analyze the security of FORS with respect to adaptive chosen message attacks. We show that in such a setting, the security of FORS decreases significantly with each signed message when compared to its security against non-adaptive chosen message attacks. We propose a chaining mechanism that with slightly more computation, dynamically binds the Obtain Random Subset (ORS) generation with signing, hence, eliminating the offline advantage of adaptive chosen message adversaries. We apply our chaining mechanism to FORS and present DFORS whose security against adaptive chosen message attacks is equal to the non-adaptive security of FORS. In a nutshell, using SPHINCS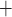 -128s parameters, FORS provides 75-bit security and DFORS achieves 150-bit security with respect to adaptive chosen message attacks after signing one message. We note that our analysis does not affect the claimed security of SPHINCS
-128s parameters, FORS provides 75-bit security and DFORS achieves 150-bit security with respect to adaptive chosen message attacks after signing one message. We note that our analysis does not affect the claimed security of SPHINCS . Nevertheless, this work provides a better understanding of FORS and other HORS variants, and furnishes a solution if new adaptive cryptanalytic techniques on SPHINCS
. Nevertheless, this work provides a better understanding of FORS and other HORS variants, and furnishes a solution if new adaptive cryptanalytic techniques on SPHINCS emerge.
emerge.
Keywords: Digital signatures, Hash-based signature schemes, Post-Quantum Cryptography, Adaptive chosen message attacks
Introduction
The current digital signature infrastructure adopts schemes that rely on the hardness of factoring or finding discrete logarithms in finite groups [12, 18, 24]. Given recent advances in physics which point towards the eventual construction of large scale quantum computers [1], these hard problems will be solved in polynomial time using Shor’s algorithm [25]. Lattice-based, coding-based, and multivariate signatures are considered quantum resilient schemes in the Q1 model [7]. However, either their exact security with respect to quantum attacks is still not clear [5, 11] or their communication/storage complexity is impractical to a multitude of applications, e.g., megabyte keys for the matrices of McEliece-based cryptosystems [27]. On the other hand, hash-based digital signatures have moderately sized keys (order of kilobytes), and their quantum security relies solely on that of hash functions based on Grover’s algorithm. They have been proven to offer simple quantum resilient security properties [26]. Note that the proofs in [26] follow the Q1 model where no superposition queries to quantum oracles are allowed [7].
Hash-based signature algorithms are comprised of two schemes, an underlying signing scheme and an extension algorithm. The former algorithm defines the main signing procedure where a key pair can be used to sign one (Lamport [19], Winternitz one time signature scheme (WOTS), WOTS++ [8, 14]) or a few messages (e.g., Biba [21], HORS [23], HORS++ [22], PORS [2], and FORS [4]), after which a new key pair should be generated to maintain security against forgery attacks. More precisely, the security of hash-based few time (HBFT) signature schemes decreases after revealing each signature, and hence their bit-security is given under the condition that re-keying is required after r signatures. Accordingly, translating this constraint to acceptable attack models implies that a maximum of r queries are allowed to the signing oracle.
The extension algorithm is a top level construction that employs several instances of underlying signing schemes (OTS and HBFT) in a Merkle tree structure. Such an algorithm enables signing multiple messages where signatures are verified with one public key (Merkle root). Extension algorithms can be stateful such as Merkle Signature Scheme MSS [20], eXtended Merkle Signature Scheme (XMSS) [9], XMSS+ [15], Multi Tree XMSS (XMSS ) [16], and XMSS with tightened security (XMSS-T) [17], or stateless such as SPHINCS [5], SPHINCS
) [16], and XMSS with tightened security (XMSS-T) [17], or stateless such as SPHINCS [5], SPHINCS [4, 6], and Gravity SPHINCS [3]. Stateless signature algorithms conform to the basic definition of digital signatures where no state updates are required to guarantee security, and only keys are needed to securely generate valid signatures at any time.
[4, 6], and Gravity SPHINCS [3]. Stateless signature algorithms conform to the basic definition of digital signatures where no state updates are required to guarantee security, and only keys are needed to securely generate valid signatures at any time.
The security of hash-based signature algorithms relies on the security of the underlying basic signing schemes. SPHINCS is a hyper-tree construction that uses WOTS and HORS trees for signing. In [2], Aumasson and Endignoux investigated the subset-resilience problem [23] and showed that HORS is vulnerable to weak-message attacks where an adaptive adversary looks for messages that produce smaller Obtain Random Subsets (ORSs). Consequently, they reported a 7-bit decrease in the expected security of SPHINCS against classical attacks. Moreover, they proposed PORS, a variant of HORS which employs a pseudorandom bit generator (PRNG) instead of a hash function to obtain random subsets with distinct elements, thus avoiding the effect of weak messages. However, PORS is not secure against adaptive chosen message attacks where an adversary is able to generate random subsets for as many messages as they want, and select a set of r message for online queries. Finally, FORS, another HORS variant, was proposed and is currently adopted in SPHINCS , a round 2 candidate in the NIST Post-Quantum Cryptography standardization competition [4, 10]. Compared to PORS, FORS mitigates weak-message attacks by increasing the size of the keys by a factor of
, a round 2 candidate in the NIST Post-Quantum Cryptography standardization competition [4, 10]. Compared to PORS, FORS mitigates weak-message attacks by increasing the size of the keys by a factor of 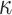 where
where 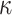 is the number of random subsets, and the overall signature size is also increased when it is integrated in a hyper-tree structure. On its own, the security of FORS against adaptive chosen message attacks decreases significantly with each signed message, which currently has no known effect on the security of SPHINCS
is the number of random subsets, and the overall signature size is also increased when it is integrated in a hyper-tree structure. On its own, the security of FORS against adaptive chosen message attacks decreases significantly with each signed message, which currently has no known effect on the security of SPHINCS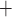 because it employs a pseudorandomly generated randomizer that is publicly sent along with the signature, and is used as a key for the hash function in FORS to obtain the random subsets. However, if cryptanalytic techniques are devised which can annihilate how this public randomizer is utilized or can break its generation procedure, then SPHINCS
because it employs a pseudorandomly generated randomizer that is publicly sent along with the signature, and is used as a key for the hash function in FORS to obtain the random subsets. However, if cryptanalytic techniques are devised which can annihilate how this public randomizer is utilized or can break its generation procedure, then SPHINCS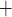 will be vulnerable to adaptive chosen message attacks. Hence, given the significance of SPHINCS
will be vulnerable to adaptive chosen message attacks. Hence, given the significance of SPHINCS as a candidate for standardization, we believe our analysis of its underlying signature scheme, FORS, is important, along with DFORS which offers a drop-in strengthened candidate.
as a candidate for standardization, we believe our analysis of its underlying signature scheme, FORS, is important, along with DFORS which offers a drop-in strengthened candidate.
Our Contribution. In what follows, we summarize the contributions of this paper.
We analyze the security of FORS against adaptive chosen message adversaries. We show that its bit security with respect to adaptive chosen message attacks decreases significantly when compared to its security in a non-adaptive setting. We adopt the adaptive chosen message attack model defined by Reyzin and Reyzin [23] and used in the analysis of HORS and PORS.
We propose a hash chaining mechanism that binds the process of generating a message ORS with signing it, which eliminates the offline adversarial advantage and makes ORS generation feasible only for the signing entity. We apply the chaining scheme to FORS and present Dynamic Forest Of Random Subsets (DFORS), a new HORS variant that resists adaptive chosen message attacks. We show that the bit-security of DFORS with respect to adaptive chosen message attacks is more than that of FORS by a factor of
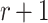 , where r is the number of signed messages per key under a given security level.
, where r is the number of signed messages per key under a given security level.We analyze the security of DFORS with respect to adaptive chosen message adversaries, discuss its limitations, and report its theoretical computational and communication performance. Finally, we compare DFORS with FORS and other HORS variants.
Preliminaries
In what follows, we provide the notation and definitions used throughout the paper. FORS can be seen as a generalized instance of HORS and it inherits most of the specifications of HORS. Accordingly, for completeness, we provide a brief overview of the HORS signature scheme.
Notation
Let n denote our security parameter. Consider a finite key space 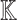 , message space of arbitrary length
, message space of arbitrary length  , the two hash families H and G where
, the two hash families H and G where 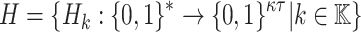 , and
, and 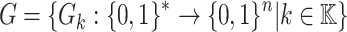 .
. 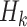 (resp.
(resp. 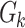 ) is an
) is an 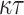 -bit (resp. n-bit) keyed one-way function. Let the
-bit (resp. n-bit) keyed one-way function. Let the 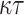 -bit message digest of an arbitrary length message
-bit message digest of an arbitrary length message 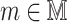 be divided into
be divided into  elements, each of length
elements, each of length 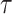 bits, such that the integer representation of a given element is a subset of
bits, such that the integer representation of a given element is a subset of 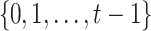 , where
, where  . We refer to the set
. We refer to the set  by T, and the subset of
by T, and the subset of 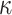 -elements of the set T is denoted by
-elements of the set T is denoted by 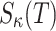 . Let
. Let  denote an Obtain Random Subset function which returns a
denote an Obtain Random Subset function which returns a 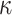 element subset from the
element subset from the 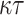 -bit hash value of a message m, formally defined as follows
-bit hash value of a message m, formally defined as follows
 |
The notion of ORS functions was introduced by Reyzin and Reyzin when HORS was proposed [23]. It has been shown that the security of the scheme is reduced to the subset resilience problem [23]. More precisely, for a given bit-security level, at most r messages can be signed before re-keying is required, otherwise an adversary can find a message whose ORS is covered by the union of the ORSs of the r messages.
Definition 1
The messages 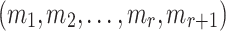 are in an r-subset-cover relation,
are in an r-subset-cover relation, 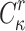 , if the Obtain Random Subset of message
, if the Obtain Random Subset of message 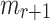
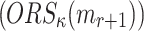 is a subset of the union of all Obtain Random Subsets of the r-messages,
is a subset of the union of all Obtain Random Subsets of the r-messages,  , formally
, formally
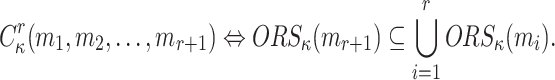 |
If finding the above cover relation for a given ORS function is infeasible, then it is said that such a function is r-subset resilient.
Definition 2
An ORS function is r-subset-resilient if for any polynomial time adversary  , the probability of finding
, the probability of finding 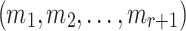 such that
such that 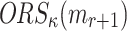 is a subset of
is a subset of 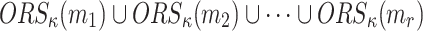 is negligible, Formally
is negligible, Formally
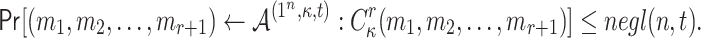 |
Definition 3
An ORS function is r-target-subset-resilient, if for any polynomial time adversary 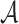 who is given the ORSs of r messages
who is given the ORSs of r messages 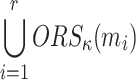 , it is infeasible to find a message
, it is infeasible to find a message  such that its
such that its 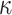 -element
-element 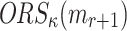 is a subset of the union of ORSs of the r messages, formally
is a subset of the union of ORSs of the r messages, formally
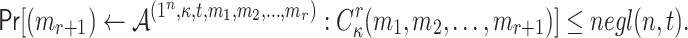 |
Hash to Obtain Random Subset (HORS) Few-Time Digital Signature Scheme
In HORS [23], the signer randomly generates t secret keys each of n-bit length, 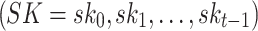 . Using a one-way function
. Using a one-way function 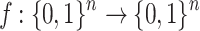 , the signer computes the public key,
, the signer computes the public key,  . For signing an arbitrary length message
. For signing an arbitrary length message  ,
,  is evaluated by dividing the
is evaluated by dividing the 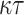 -bit message digest value of
-bit message digest value of 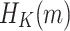 into
into 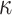 elements, each of length
elements, each of length 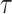 bits. Each element is represented by an integer
bits. Each element is represented by an integer 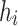 where
where  and
and 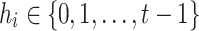 ,
,  . To generate the signature,
. To generate the signature, 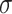 , the signer reveals the secret keys whose indices correspond to the integer representation of the
, the signer reveals the secret keys whose indices correspond to the integer representation of the 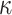 elements in the ORS, i.e.,
elements in the ORS, i.e., 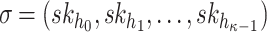 . For verification, the verifier computes
. For verification, the verifier computes 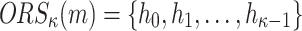 , then checks if
, then checks if 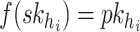 , otherwise verification fails. The description of HORS is given in Algorithm 3 in Appendix A.
, otherwise verification fails. The description of HORS is given in Algorithm 3 in Appendix A.
Security. Assuming that f is a one-way function, the security of HORS is reduced to the hardness of the (target) subset-resilience problem [23]. It has been shown that the probability of finding a message (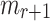 ) such that
) such that  is covered by the obtained random subsets of the r previously signed messages is
is covered by the obtained random subsets of the r previously signed messages is 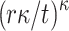 which corresponds to the probability of
which corresponds to the probability of 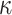 randomly chosen elements being a subset of the revealed
randomly chosen elements being a subset of the revealed 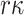 secret keys. The corresponding bit-security is then
secret keys. The corresponding bit-security is then
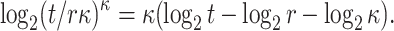 |
In [2], it was proven that the security of HORS with respect to adaptive chosen message attacks is
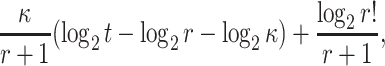 |
(see Appendix B). A practical example of a weak-message attack was also given where an adaptive adversary finds messages that map to subsets with repeated indices which results in smaller subsets, i.e., number of distinct elements 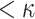 . Such subsets are easier to cover and consequently, a 7-bit decrease in the expected security of SPHINCS against classical attacks was reported.
. Such subsets are easier to cover and consequently, a 7-bit decrease in the expected security of SPHINCS against classical attacks was reported.
Variants. HORS++ [22] was introduced to provide security against adaptive attacks. A one-to-one mapping function S(m) that belongs to a cover-free family [13] is utilized to ensure that for any  messages
messages 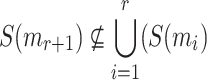 . Three constructions for S(m) based on polynomials over finite fields, error correcting codes, and algebraic curves over finite fields were presented. Consequently, HORS++ increases the signature size and the size of the secret keys to achieve the same security level of HORS against non-adaptive chosen message attacks. Moreover, the computational efficiency is decreased due to the computation of S(m). Later, PORS was suggested to replace HORS in SPHINCS where the idea of having distinct elements in subsets of weak messages was enforced by use of a pseudorandom bit generator to obtain the subsets [2]. However, although PORS mitigates weak-message attacks, it is still vulnerable to adaptive chosen message attacks under the definition given in Appendix B. Lastly, FORS was proposed and used in SPHINCS
. Three constructions for S(m) based on polynomials over finite fields, error correcting codes, and algebraic curves over finite fields were presented. Consequently, HORS++ increases the signature size and the size of the secret keys to achieve the same security level of HORS against non-adaptive chosen message attacks. Moreover, the computational efficiency is decreased due to the computation of S(m). Later, PORS was suggested to replace HORS in SPHINCS where the idea of having distinct elements in subsets of weak messages was enforced by use of a pseudorandom bit generator to obtain the subsets [2]. However, although PORS mitigates weak-message attacks, it is still vulnerable to adaptive chosen message attacks under the definition given in Appendix B. Lastly, FORS was proposed and used in SPHINCS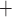 [4], where security against weak-message attacks is achieved by increasing the key size from t values to
[4], where security against weak-message attacks is achieved by increasing the key size from t values to 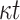 values such that each index out of the
values such that each index out of the 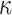 indices in the ORS reveals a secret key from a different pool of t secret keys. Accordingly, when integrated in a tree structure the size of the signature also increases.
indices in the ORS reveals a secret key from a different pool of t secret keys. Accordingly, when integrated in a tree structure the size of the signature also increases.
FORS Security Analysis
Unlike HORS which generates t secret keys from which the secret keys that are indexed by ORS(m) are released, FORS generates (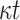 ) secret keys and dedicates t secret keys for each index out of the
) secret keys and dedicates t secret keys for each index out of the 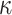 indices. By doing so, FORS mitigates weak message attacks because even if two elements in ORS(m) are equal, they index values from different secret key pools. The n-bit public key of FORS is the hash of the concatenation of
indices. By doing so, FORS mitigates weak message attacks because even if two elements in ORS(m) are equal, they index values from different secret key pools. The n-bit public key of FORS is the hash of the concatenation of 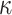 Merkle tree roots. Each root is associated with a binary hash tree whose leaves are the hashes of t secret key elements in a given pool. Accordingly, one FORS instance has
Merkle tree roots. Each root is associated with a binary hash tree whose leaves are the hashes of t secret key elements in a given pool. Accordingly, one FORS instance has  trees, each of height
trees, each of height 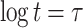 .
.
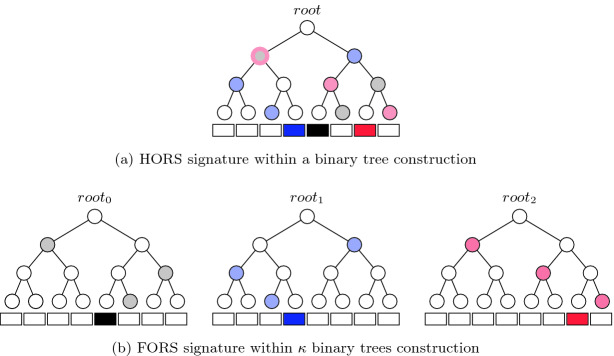
Figure 1 depicts the signatures of message 100 011 110 using (a) HORS and (b) FORS, where 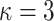 and
and 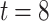 . In FORS, the first 3 bits, i.e., 100, of the message selects
. In FORS, the first 3 bits, i.e., 100, of the message selects 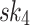 , the secret key corresponding to the 4-th leaf indexed from the left and starting from 0 in the first tree along with its authentication path to
, the secret key corresponding to the 4-th leaf indexed from the left and starting from 0 in the first tree along with its authentication path to 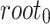 . Similarly, the second (resp. third) 3 bits of the message selects
. Similarly, the second (resp. third) 3 bits of the message selects  (resp.
(resp. 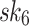 ) from the second (resp. third) tree with the authentication path to
) from the second (resp. third) tree with the authentication path to 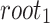 (resp.
(resp.  ). In HORS, the three 3-bit parts of the message index
). In HORS, the three 3-bit parts of the message index 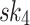 ,
, 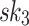 , and
, and 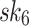 from the same tree, and with each selected secret key a 3 node authentication path is selected, hence the overlap in the node (colored in pale red and gray) at the pre-root level. More details about hash trees and authentication path calculations are provided in Sect. 4.
from the same tree, and with each selected secret key a 3 node authentication path is selected, hence the overlap in the node (colored in pale red and gray) at the pre-root level. More details about hash trees and authentication path calculations are provided in Sect. 4.
Fig. 1.
HORS and FORS signatures of the message 100 011 110 where 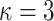 and
and 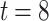 . The 8 rectangles under each tree depict the eight secret keys whose hashes are stored in the corresponding leaf nodes.
. The 8 rectangles under each tree depict the eight secret keys whose hashes are stored in the corresponding leaf nodes.
It can be verified from Fig. 1 that if two 3-bit parts of the message are equal, then the same secret key value is revealed in HORS. This fact is exploited in the weak messages attack where an adversary searches for messages that have as many repeated indices as possible, which lead to ORSs containing fewer distinct elements, and thus can be easily covered with the ORSs of the revealed r messages. However, this problem is mitigated in FORS because repeated indices select secret keys from different pools. In what follows, we investigate the security of FORS with respect to non-adaptive chosen message attacks.
FORS in a Non-adaptive Setting
Reyzin and Reyzin introduced clear attack models for analyzing HBFT signature schemes against (non) adaptive chosen message attacks [23]. Such models are used in the analysis of all HORS-variants, i.e., PORS, and FORS. Specifically, in a non-adaptive setting, also referred to by r-target subset resilience problem (see Definition 3), an adversary is required to first choose r messages 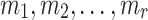 , after which they are provided with key k of
, after which they are provided with key k of  and allowed to select a message
and allowed to select a message 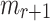 and evaluate
and evaluate 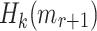 . A successful non-adaptive chosen message attack happens when the adversary is able to find
. A successful non-adaptive chosen message attack happens when the adversary is able to find 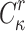 , i.e., find a message
, i.e., find a message  that is in an r-subset cover relation with
that is in an r-subset cover relation with 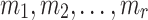 . This scenario corresponds to an attacker who is trying to forge a signature after observing all r allowed signatures per key, or an adversary who is allowed r queries at a time before being supplied with k to verify any of the returned signatures. Few-time signature schemes are expected to maintain their security against forgery attacks even after releasing all r signatures.
. This scenario corresponds to an attacker who is trying to forge a signature after observing all r allowed signatures per key, or an adversary who is allowed r queries at a time before being supplied with k to verify any of the returned signatures. Few-time signature schemes are expected to maintain their security against forgery attacks even after releasing all r signatures.
Finding
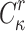 in FORS. Given an adversary who observed the signatures of r messages, finding a message
in FORS. Given an adversary who observed the signatures of r messages, finding a message 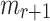 that is in an
that is in an  subset cover relation with the other r messages (
subset cover relation with the other r messages (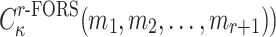 has probability of success
has probability of success 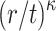 [6], which is equal to the probability that each
[6], which is equal to the probability that each 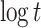 -bit element out of the
-bit element out of the  elements in
elements in 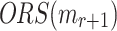 is covered by an element at the same position of the ORSs of the other r messages, i.e.,
is covered by an element at the same position of the ORSs of the other r messages, i.e., 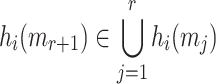 for
for 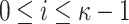 , where
, where 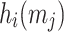 denotes the i-th ORS element of the j-th message. Accordingly, the corresponding bit-security against non-adaptive chosen message attacks is given by
denotes the i-th ORS element of the j-th message. Accordingly, the corresponding bit-security against non-adaptive chosen message attacks is given by
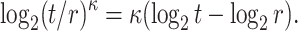 |
Adaptive Chosen Message Attack Against FORS
In this setting, an adversary is given the hash key k and allowed to evaluate 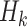 for any message of their choice before selecting
for any message of their choice before selecting 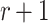 messages. This attack also indicates the r-subset resilience of the signature algorithm (see Definition 2). The definition of adaptive chosen message attack is given in Appendix B. Applying the same analysis to FORS, given the key k of
messages. This attack also indicates the r-subset resilience of the signature algorithm (see Definition 2). The definition of adaptive chosen message attack is given in Appendix B. Applying the same analysis to FORS, given the key k of 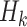 , an adversary
, an adversary 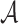 generates the ORSs of
generates the ORSs of 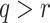 messages offline, where
messages offline, where 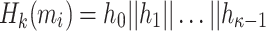 and
and  , for
, for 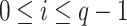
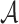 searches for all possible combinations of
searches for all possible combinations of 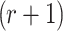 message sets from the set of q messages. For any given
message sets from the set of q messages. For any given 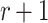 messages combination, the probability that message
messages combination, the probability that message  is covered by the remaining r messages (i.e.,
is covered by the remaining r messages (i.e.,  ), is
), is 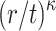 . Accordingly,
. Accordingly,  obtains
obtains  sets of
sets of  messages and each set gives
messages and each set gives 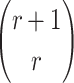 possible choices for
possible choices for 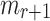 . Therefore, the probability of
. Therefore, the probability of 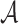 successfully generating
successfully generating 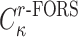 is bounded from above by
is bounded from above by
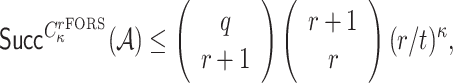 |
 |
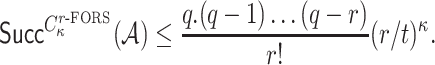 |
which can be approximated by
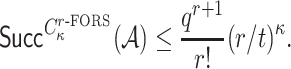 |
Assuming a success probability close to 1, the above equation can be expressed as
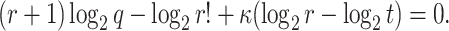 |
Then the bit security of FORS with respect to adaptive chosen message attacks is given by
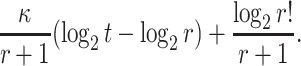 |
One may conclude that due to the offline adversarial advantage given to  (i.e., knowledge of k implies the feasibility of evaluating ORSs for more than r messages of their choice), FORS bit security against adaptive chosen message attacks decreases by a factor of
(i.e., knowledge of k implies the feasibility of evaluating ORSs for more than r messages of their choice), FORS bit security against adaptive chosen message attacks decreases by a factor of 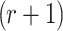 when compared to the non-adaptive setting. Note that, currently there is no attack against SPHINCS
when compared to the non-adaptive setting. Note that, currently there is no attack against SPHINCS that can utilize the offline adversarial privileges and produce
that can utilize the offline adversarial privileges and produce 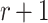 messages in an r-subset cover relation. This is because SPHINCS
messages in an r-subset cover relation. This is because SPHINCS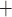 uses a fixed pseudorandom generation of the key k to get the obtained random subset
uses a fixed pseudorandom generation of the key k to get the obtained random subset  . We also note that k is message dependent and is sent in the clear with each signature so verification takes place. Accordingly, in the event of attacks on the process by which k is evaluated from m, a dramatic decrease in the security of SPHINCS
. We also note that k is message dependent and is sent in the clear with each signature so verification takes place. Accordingly, in the event of attacks on the process by which k is evaluated from m, a dramatic decrease in the security of SPHINCS will follow. Consequently, in the following section we present a technique that is robust against adaptive chosen message attacks on FORS. Our mechanism annihilates the adversarial offline advantages associated with knowing the hash key k.
will follow. Consequently, in the following section we present a technique that is robust against adaptive chosen message attacks on FORS. Our mechanism annihilates the adversarial offline advantages associated with knowing the hash key k.
Dynamic Forest of Random Subsets (DFORS)
In this section we present Dynamic Forest Of Random Subsets DFORS, a new HORS-variant that mitigates the offline advantage of an adversary which leads to the adaptive chosen message attack on FORS (discussed in Sect. 3). The main feature of DFORS is that the generation of the ORS is performed concurrently with signing such that each signature element is utilized to generate the next element of the ORS. In other words, signing and ORS generation are bound together using a chaining mechanism that utilizes the revealed secret keys. This procedure ensures that given a message, only the signer is able to efficiently generate an ORS. By doing so, even if an adversary has knowledge of k, they are not able to compute ORSs of a given message of their choice unless they have some secret key knowledge. In what follows we give a detailed specification of DFORS.
DFORS Parameters
DFORS uses the following parameters.
n : The security parameter and the bit-length of (i) the secret seed SK.seed, (ii) secret keys
 (
( ,
, 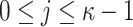 ), (iii) public key PK.root, and (iv) the output of the used one way function F, and hash function G.
), (iii) public key PK.root, and (iv) the output of the used one way function F, and hash function G.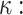 The number of (i) sub-strings of the input message, (ii) secret key pools where each contains t secret keys, and (iii) hash trees.
The number of (i) sub-strings of the input message, (ii) secret key pools where each contains t secret keys, and (iii) hash trees.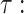 The bit length of a sub-string of the input message and the hash tree height.
The bit length of a sub-string of the input message and the hash tree height.t : the number of secret keys per pool and the number of leaves in each hash tree, t =
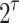 .
.
The input message for DFORS is of length 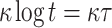 bits. To achieve n-bit security when signing r messages, we have
bits. To achieve n-bit security when signing r messages, we have  (see Sect. 5.1).
(see Sect. 5.1).
Key Generation
In what follows, we give the specifications of the secret and public key generation procedures. Moreover, DFORS is described in Algorithm 2.
Secret Key Generation. Let SK.seed denote an n-bit secret seed that is sampled at random. Given a pseudorandom function, 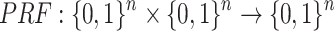 , the n-bit
, the n-bit 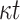 secret key values
secret key values  ,
, 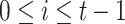 ,
, 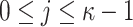 are generated by
are generated by
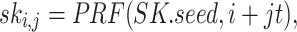 |
where each set of t secret keys belong to one of the 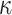 pools.
pools.
Hash Trees and Public Key Generation. Using one-way function 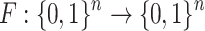 applied on the secret keys
applied on the secret keys 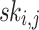 ,
, 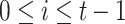 ,
, 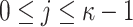 , the leaf nodes of the
, the leaf nodes of the 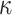 hash trees are generated,
hash trees are generated, 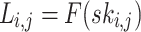 . Every t leaves,
. Every t leaves, 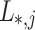 , are combined together in a Merkle tree construction to form the j-th (out of
, are combined together in a Merkle tree construction to form the j-th (out of 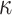 ) tree. Then, the roots of these
) tree. Then, the roots of these  trees,
trees,  , are concatenated to form an input to the hash function to get the n-bit public key expressed as
, are concatenated to form an input to the hash function to get the n-bit public key expressed as
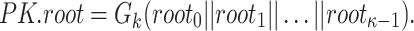 |
Binary Hash Tree. DFORS uses the XMSS binary Merkle tree construction [9]. The height of the binary hash tree is 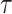 . It has
. It has 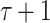 levels,
levels, 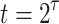 leaf nodes (each of size n bits) on level 0, i.e.,
leaf nodes (each of size n bits) on level 0, i.e., 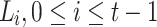 , and an n-bit root node on level
, and an n-bit root node on level 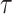 . We denote the nodes in level j by
. We denote the nodes in level j by 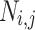 where
where 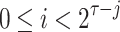 ,
, 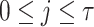 and
and 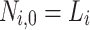 . To construct the tree, the hash function G and a 2n-bit mask, q, per hash evaluation are used. These bit masks are introduced to provide second-preimage resistance. The rationale for using different bit masks for each hash evaluation is to mitigate multi-target attacks [17]. For details on generating the hash keys
. To construct the tree, the hash function G and a 2n-bit mask, q, per hash evaluation are used. These bit masks are introduced to provide second-preimage resistance. The rationale for using different bit masks for each hash evaluation is to mitigate multi-target attacks [17]. For details on generating the hash keys  and bit masks
and bit masks 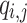 , the reader is referred to [4, 17]. Formally, for
, the reader is referred to [4, 17]. Formally, for  , a node
, a node 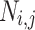 is given by
is given by
 |
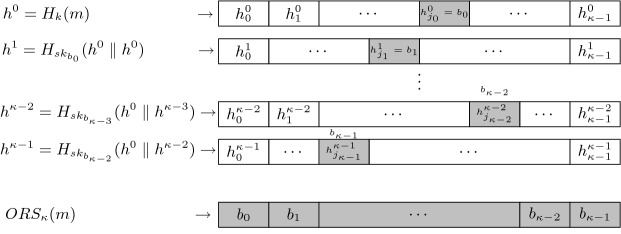
Figure 2 shows a simplified example of one of the 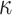 trees in DFORS with
trees in DFORS with 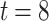 . Assuming it is the j-th tree, it depicts the nodes in the authentication path (colored in gray) associated with revealing
. Assuming it is the j-th tree, it depicts the nodes in the authentication path (colored in gray) associated with revealing  .
.
Fig. 2.
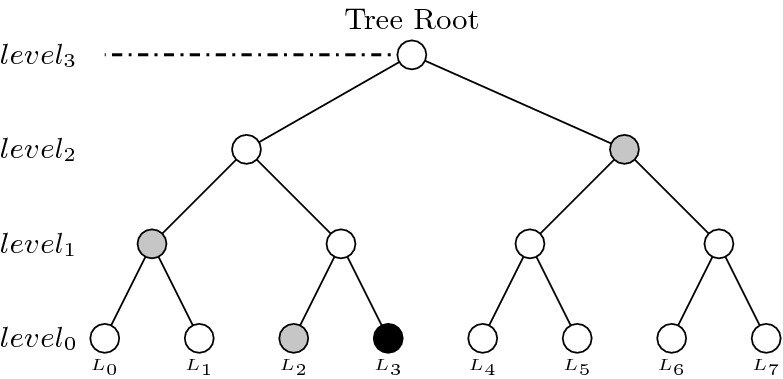
A binary hash tree with the nodes in the authentication path (colored in gray) for leaf node 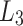 (colored in black)
(colored in black)
Signing and ORS Generation
We denote by Z(h) a function that takes as input  bits, h, and outputs the j-th
bits, h, and outputs the j-th 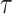 bits of h, where
bits of h, where 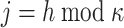 . Formally,
. Formally, 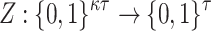 , and letting
, and letting 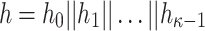 , for
, for 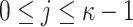
 |
The signing algorithm takes as input the message m, the secret seed SK.seed, and the hash key k. It constructs the 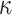 trees as explained above in Sect. 4.2. To compute the
trees as explained above in Sect. 4.2. To compute the 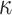 random subset
random subset 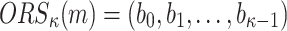 , the algorithm first evaluates
, the algorithm first evaluates 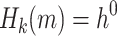 , then computes
, then computes 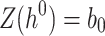 . The first element in the signature,
. The first element in the signature,  , is comprised of i) the secret key of index
, is comprised of i) the secret key of index 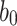 in the first pool,
in the first pool,  , and ii) the corresponding authentication path
, and ii) the corresponding authentication path 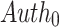 , thus
, thus  . Next,
. Next, 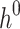 and
and  are used to choose the second random element,
are used to choose the second random element,  , where
, where 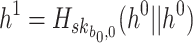 . The second signature element,
. The second signature element,  , is the secret key of index
, is the secret key of index  in the second pool,
in the second pool, 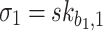 , and its corresponding authentication path
, and its corresponding authentication path 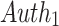 ,
, 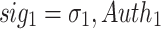 . In general, the i-th element of the
. In general, the i-th element of the  is given by
is given by 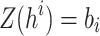 where
where  . The i-th signature element,
. The i-th signature element,  , is the secret key value of index
, is the secret key value of index 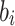 in the i-th pool and its corresponding authentication path
in the i-th pool and its corresponding authentication path 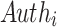 ,
, 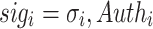 , where
, where 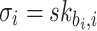 . The above process is repeated until
. The above process is repeated until 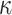 elements are generated
elements are generated  . Finally, the signature is given by
. Finally, the signature is given by
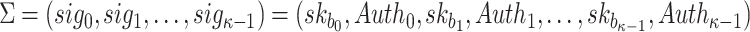 |
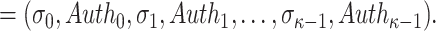 |
The ORS generation and signing process is illustrated in Fig. 3.
Fig. 3.
The DFORS procedure to compute  , where
, where 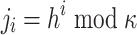 ,
, 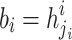 , and
, and 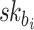 is the
is the 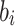 -th secret key in the i-th secret key pool.
-th secret key in the i-th secret key pool.
The authentication path of a leaf 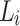 contains all the sibling nodes of the nodes in the path from the leaf
contains all the sibling nodes of the nodes in the path from the leaf 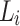 to the tree root. It is required so that the verifier can successfully generate the root in order to verify the signature element
to the tree root. It is required so that the verifier can successfully generate the root in order to verify the signature element 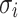 related to the leaf node
related to the leaf node  . Figure 2 shows a simple hash tree with the authentication path for leaf
. Figure 2 shows a simple hash tree with the authentication path for leaf 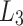 colored in black and the authentication path nodes colored in gray,
colored in black and the authentication path nodes colored in gray, 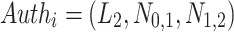 .
.
Signature Verification
The verification algorithm takes as input the message m, the public key PK.root, the hash key K, and the signature 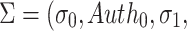
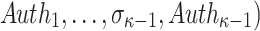 . It computes
. It computes 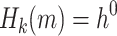 , then
, then 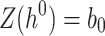 to get the leaf index of the first hash tree. Then, it applies the one-way function F to the signature element
to get the leaf index of the first hash tree. Then, it applies the one-way function F to the signature element  of the signature
of the signature 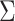 to get the leaf node
to get the leaf node  in the first tree. The authentication path
in the first tree. The authentication path  and the leaf
and the leaf 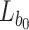 are used to compute the root of the first tree. The leaf index
are used to compute the root of the first tree. The leaf index 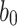 is required so that the verifier knows which node is concatenated on the right and on the left. The tree root calculation procedure is described in Algorithm 1. Generally, the verification algorithm computes the i-th tree root by applying Algorithm 1 on
is required so that the verifier knows which node is concatenated on the right and on the left. The tree root calculation procedure is described in Algorithm 1. Generally, the verification algorithm computes the i-th tree root by applying Algorithm 1 on 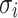 ,
, 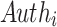 , and the leaf index
, and the leaf index 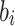 where
where 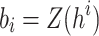 , and
, and  . This process is repeated until
. This process is repeated until 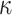 tree roots are computed which are then concatenated to form an input to the hash function G. If the output of G is equal to PK.root, the signature is valid, otherwise verification fails.
tree roots are computed which are then concatenated to form an input to the hash function G. If the output of G is equal to PK.root, the signature is valid, otherwise verification fails.

Security and Efficiency
In what follows, we analyze the security of DFORS and demonstrate the effect of the dynamic chaining on the security of FORS. Afterwards, the computational cost of the DFORS key generation, signing, and verification algorithms are presented. The bit size of the signature and keys are also given.
DFORS Security Analysis
In this section, we present a detailed analysis of DFORS with respect to weak-message attacks and r-target subset resilience adversaries. More precisely, since the proposed chaining technique does not allow an adaptive adversary who has knowledge of k to compute the ORSs of any message of their choice before asking the signing oracle for its signature, DFORS is essentially r-subset resilient. Hence, our analysis focuses on its security when an adversary is given the signatures of r messages.
Weak-Message Attacks. DFORS inherits FORS mitigation to weak-message attacks [6] because it specifies an independent key pool for each index in the ORS. Consequently, even if an ORS element is repeated, the corresponding revealed secret keys will be different.
r-Target Subset Resilience. According to Definition 3, we assume an adversary 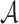 when given the ORSs of r messages will return
when given the ORSs of r messages will return 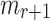 where
where  . In what follows, we show that the success probability of
. In what follows, we show that the success probability of  is bounded from above by
is bounded from above by 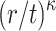 . Note that since ORS generation is secret key dependent, the ORS function of DFORS is intrinsically r-subset resilient. In other words, the value of any random ORS element,
. Note that since ORS generation is secret key dependent, the ORS function of DFORS is intrinsically r-subset resilient. In other words, the value of any random ORS element, 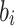 , depends on the previously revealed signature element
, depends on the previously revealed signature element  and the original message m. Accordingly, without any oracle queries,
and the original message m. Accordingly, without any oracle queries,  has no feasible function to evaluate ORSs of messages of their choice. On the other hand, if
has no feasible function to evaluate ORSs of messages of their choice. On the other hand, if 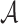 is given the signatures of r messages or they queried r messages of their choice, they need to find a message
is given the signatures of r messages or they queried r messages of their choice, they need to find a message 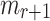 such that each element in its obtained random subset,
such that each element in its obtained random subset, 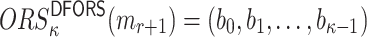 , is covered by the elements at the same corresponding positions in the ORSs of the other r messages
, is covered by the elements at the same corresponding positions in the ORSs of the other r messages
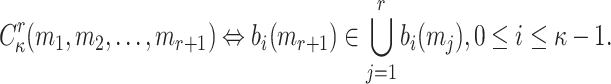 |
Due to the chaining process in generating 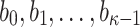 ,
, 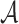 generates the ORSs sequentially. At any position i, if
generates the ORSs sequentially. At any position i, if  , then
, then  fails. In addition, they cannot evaluate
fails. In addition, they cannot evaluate 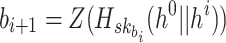 when
when 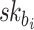 is not revealed by any of signatures of the r messages, Generally, for the i-th position in
is not revealed by any of signatures of the r messages, Generally, for the i-th position in 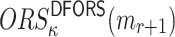
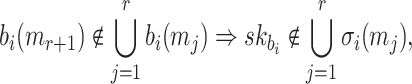 |
where 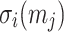 and
and  denote the i-th signature element and i-th ORS element of the j-th message, respectively. Thus, the probability that
denote the i-th signature element and i-th ORS element of the j-th message, respectively. Thus, the probability that  finds
finds  successfully is equal to their probability of finding a message
successfully is equal to their probability of finding a message 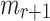 such that
such that  , each of the
, each of the  -bit
-bit  . Since
. Since  is given r messages, the probability of finding a cover for one
is given r messages, the probability of finding a cover for one 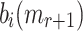 is
is  because this implies that
because this implies that 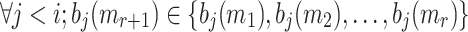 . Thus, the probability of finding a cover for all the
. Thus, the probability of finding a cover for all the 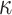 elements in
elements in 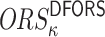 is equal to the probability of finding a cover for the last element,
is equal to the probability of finding a cover for the last element, 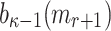 , which is
, which is 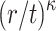 . Therefore
. Therefore
so the corresponding DFORS bit-security against adaptive chosen message attacks is
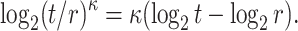 |
Compared to the adaptive chosen message attack security of FORS (See Sect. 3), the bit security of DFORS is higher by a factor of 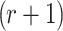 . The extra cost is performing
. The extra cost is performing  more calls to the hash function. Unlike FORS, the signing procedure cannot be parallelized because of the chaining mechanism.
more calls to the hash function. Unlike FORS, the signing procedure cannot be parallelized because of the chaining mechanism.
Theoretical Efficiency
Key Generation. This procedure requires
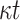 PRF function computations to generate the t secret values for
PRF function computations to generate the t secret values for  pools,
pools, 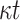 one-way function F computations to compute the leaf nodes of the hash trees, and
one-way function F computations to compute the leaf nodes of the hash trees, and  hash function G evaluations to evaluate the
hash function G evaluations to evaluate the 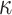 hash trees and get the public key PK.root.
hash trees and get the public key PK.root.Signing. This procedure requires
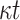 PRF function computations,
PRF function computations, 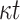 one-way function F computations,
one-way function F computations,  hash function (H and G) to compute the
hash function (H and G) to compute the 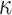 hash trees (
hash trees (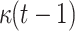 hash G calls), and
hash G calls), and 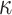 hash H calls to get
hash H calls to get  . Note that the whole tree structure is computed with each signature, otherwise, the scheme storage requirements will be huge.
. Note that the whole tree structure is computed with each signature, otherwise, the scheme storage requirements will be huge.Verification. This procedure requires
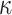 one-way function F computations that compute the trees leaves,
one-way function F computations that compute the trees leaves,  ) hash function (H and G) evaluations to reconstruct the
) hash function (H and G) evaluations to reconstruct the 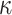 trees roots from the revealed secret values and the authentication paths (
trees roots from the revealed secret values and the authentication paths (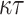 calls to G), and
calls to G), and 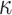 calls H to get
calls H to get  .
.Signature Size. The signature contains
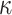 secret key elements and
secret key elements and 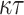 tree node for the associated authentication paths. Thus, the signature size is
tree node for the associated authentication paths. Thus, the signature size is 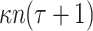 bits, where n is the bit size of each secret keys and hash tree node.
bits, where n is the bit size of each secret keys and hash tree node.Length of Keys. The size of the secret key, SK.root, is equal to that of the public key, PK.root, and it is n bits.
The computational complexities of the above procedures are given in Table 2.
Table 2.
Comparison between HORS, PORS, FORS, and DFORS
| Algorithm | KGen (# OWF)
|
Signing cost | Verification cost | Signature size
|
SK/PK size
|
Adaptive security |
|---|---|---|---|---|---|---|
| HORST | t PRF | t PRF |

|
1 | NO | |
| t OWF | t OWF |
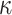 OWF OWF |
||||
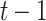 Hash Hash |
t Hash |
 Hash Hash |
||||
PORS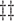
|
t PRF |
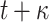 PRF PRF |
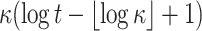
|
1 | NO | |
| t OWF | t OWF |
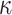 OWF OWF |
||||
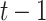 Hash Hash |
t Hash |
 Hash Hash |
||||
| FORS |
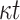 PRF PRF |
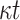 PRF PRF |
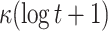
|
1 | NO | |
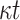 OWF OWF |
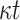 OWF OWF |
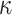 OWF OWF |
||||
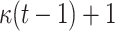 Hash Hash |
 Hash Hash |
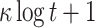 Hash Hash |
||||
| DFORS |
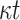 PRF PRF |
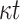 PRF PRF |
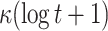
|
1 | YES | |
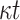 OWF OWF |
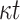 OWF OWF |
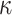 OWF OWF |
||||
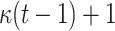 Hash Hash |
 Hash Hash |
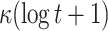 Hash Hash |
 OWF denotes one-way function.
OWF denotes one-way function.
 Size is given as a factor of n bits.
Size is given as a factor of n bits.

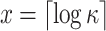 for optimal signature size in case of HORST and for the upper bound on the signature size in PORS.
for optimal signature size in case of HORST and for the upper bound on the signature size in PORS.
 Verification cost and signature size are the upper bound values.
Verification cost and signature size are the upper bound values.
Comparison with HORS Variants
DFORS inherits all the advantageous security properties of FORS. Additionally, it is secure against adaptive chosen message attacks. In fact, for the same parameters the bit-security of DFORS with respect to adaptive chosen message adversaries is equal to that of FORS under non-adaptive chosen message attacks. Table 1 gives a comparison between the bit security level of FORS and DFORS in an adaptive adversarial setting. We use the recommended parameters (i.e., n,  , and
, and 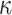 ) for all six instances of SPHINCS
) for all six instances of SPHINCS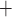 .
.
Table 1.
DFORS and FORS security levels for an adaptive chosen message attack using the SPHINCS parameters for different numbers of signed messages
parameters for different numbers of signed messages
SPHINCS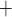 instance instance |
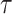 |
 |
FORS | DFORS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
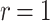 |
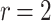 |
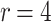 |
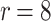 |
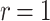 |
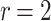 |
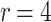 |
 |
|||
SPHINCS -128s -128s |
15 | 10 | 75 | 47 | 27 | 15 | 150 | 140 | 130 | 120 |
SPHINCS -128f -128f |
9 | 30 | 135 | 80 | 43 | 22 | 270 | 240 | 210 | 180 |
SPHINCS -192s -192s |
16 | 14 | 112 | 70 | 40 | 22 | 224 | 210 | 196 | 182 |
SPHINCS -192f -192f |
8 | 33 | 132 | 77 | 41 | 20 | 264 | 231 | 198 | 165 |
SPHINCS -256s -256s |
14 | 22 | 154 | 95 | 54 | 29 | 308 | 286 | 264 | 242 |
SPHINCS -256f -256f |
10 | 30 | 150 | 90 | 49 | 25 | 300 | 270 | 240 | 210 |
Table 1 shows the significant effect of increasing the number of signed messages, r, on the bit security of FORS. On the other hand, this effect is very reasonable with DFORS. For instance, when 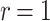 , an adaptive attack on FORS is equivalent to a collision attack on the underlying
, an adaptive attack on FORS is equivalent to a collision attack on the underlying 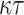 -bit hash function H which has a complexity of
-bit hash function H which has a complexity of  evaluations. However, due to the r-subset resilience of DFORS where finding a covered ORS requires successive dependency on the signature elements, an adversary must find a second preimage of the ORS in the revealed secret keys, hence the complexity is
evaluations. However, due to the r-subset resilience of DFORS where finding a covered ORS requires successive dependency on the signature elements, an adversary must find a second preimage of the ORS in the revealed secret keys, hence the complexity is 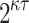 evaluations.
evaluations.
Table 2 presents a comparison between DFORSand other HORS variants with respect to their computational efficiency, signature and key sizes, and security against adaptive chosen message attacks.
Conclusion
We analyzed the security of FORS, the underlying hash-based few-time signing scheme of SPHINCS , with respect to adaptive chosen message attacks. We showed that as the number of signed messages, r, increases, its bit-security with respect to adaptive chosen message adversaries decreases significantly compared to its non-adaptive counterpart. As a solution, we proposed DFORS, which builds on FORS but utilizes a secret key dependent ORS function. Such a function binds the process of generating the ORS with signing which makes it feasible only for the signer. Accordingly, we showed that the bit security of DFORS against adaptive chosen message attacks is more than that of FORS by a factor of
, with respect to adaptive chosen message attacks. We showed that as the number of signed messages, r, increases, its bit-security with respect to adaptive chosen message adversaries decreases significantly compared to its non-adaptive counterpart. As a solution, we proposed DFORS, which builds on FORS but utilizes a secret key dependent ORS function. Such a function binds the process of generating the ORS with signing which makes it feasible only for the signer. Accordingly, we showed that the bit security of DFORS against adaptive chosen message attacks is more than that of FORS by a factor of  . Note that our analysis does not affect the claimed security of SPHINCS
. Note that our analysis does not affect the claimed security of SPHINCS but rather provides a better understanding of the security of its underlying signing scheme and offers a mechanism that can be adopted by most HORS variants to provide security against adaptive chosen message attacks.
but rather provides a better understanding of the security of its underlying signing scheme and offers a mechanism that can be adopted by most HORS variants to provide security against adaptive chosen message attacks.
Acknowledgment
The authors would like to thank the reviewers for their valuable comments that helped improve the quality of the paper.
A HORS Specification
The HORS key generation, signing, and verification procedures are given in Algorithm 3.
B Adaptive Chosen Message Attack against HORS
In [23], the following adaptive chosen message attack against HORS was defined. Let 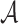 be an adaptive chosen message adversary against HORS such that given the key k,
be an adaptive chosen message adversary against HORS such that given the key k, 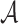 can compute the hash of any message m and
can compute the hash of any message m and 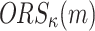 offline. Given a security parameter, n, under the birthday paradox,
offline. Given a security parameter, n, under the birthday paradox, 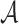 can find
can find 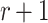 messages in a cover relation
messages in a cover relation 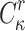 with which to query the signing oracle, formally
with which to query the signing oracle, formally
 |
Aumasson and Endignoux [2] subsequently presented an adaptive chosen message attack against HORS and proved that the security level decreases by a factor of 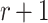 when compared to non adaptive chosen message attacks. Their attack is as follows. Given an adversary
when compared to non adaptive chosen message attacks. Their attack is as follows. Given an adversary  and a key k, the hash value
and a key k, the hash value 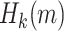 for any message of their choice can be computed, and say there are
for any message of their choice can be computed, and say there are 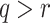 messages. For all possible combinations of
messages. For all possible combinations of 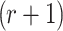 messages from the q messages,
messages from the q messages, 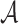 searches for
searches for 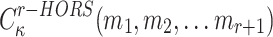 such that
such that
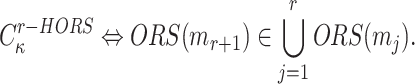 |
For any given subset, the probability of being an r-subset-cover relation is 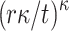 . The number of
. The number of 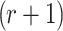 -message combinations which
-message combinations which  can construct from the q messages are
can construct from the q messages are 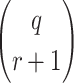 and each combination can form
and each combination can form 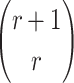 choices. Accordingly, their probability of success in defeating the r-subset resilience (SR) is given by
choices. Accordingly, their probability of success in defeating the r-subset resilience (SR) is given by
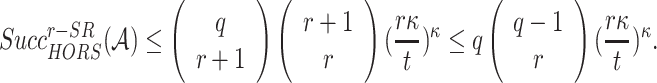 |
Assuming a success probability close to 1, the security level of HORS against an adaptive chosen message attack is
 |
Contributor Information
Abderrahmane Nitaj, Email: abderrahmane.nitaj@unicaen.fr.
Amr Youssef, Email: youssef@ciise.concordia.ca.
Riham AlTawy, Email: raltawy@uvic.ca.
References
- 1.Arute F, et al. Quantum supremacy using a programmable superconducting processor. Nature. 2019;574(7779):505–510. doi: 10.1038/s41586-019-1666-5. [DOI] [PubMed] [Google Scholar]
- 2.Aumasson, J.-P., Endignoux, G.: Clarifying the subset-resilience problem. IACR Cryptology ePrint Archive, p. 909 (2017)
- 3.Aumasson J-P, Endignoux G. Improving stateless hash-based signatures. In: Smart NP, editor. Topics in Cryptology – CT-RSA 2018; Cham: Springer; 2018. pp. 219–242. [Google Scholar]
- 4.Bernstein, D., et al.: SPHINCS+-submission to the NIST post-quantum project (2017)
- 5.Bernstein DJ, et al. SPHINCS: practical stateless hash-based signatures. In: Oswald E, Fischlin M, et al., editors. Advances in Cryptology – EUROCRYPT 2015; Heidelberg: Springer; 2015. pp. 368–397. [Google Scholar]
- 6.Bernstein, D.J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., Schwabe, P.: The SPHINCS+ signature framework. In: Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, pp. 2129–2146 (201 9)
- 7.Bonnetain X, Hosoyamada A, Naya-Plasencia M, Sasaki Y, Schrottenloher A. Quantum attacks without superposition queries: the offline simon’s algorithm. In: Galbraith SD, Moriai S, editors. Advances in Cryptology – ASIACRYPT 2019; Cham: Springer; 2019. pp. 552–583. [Google Scholar]
- 8.Buchmann J, Dahmen E, Ereth S, Hülsing A, Rückert M. On the security of the Winternitz one-time signature scheme. In: Nitaj A, Pointcheval D, editors. Progress in Cryptology – AFRICACRYPT 2011; Heidelberg: Springer; 2011. pp. 363–378. [Google Scholar]
- 9.Buchmann J, Dahmen E, Hülsing A. XMSS - a practical forward secure signature scheme based on minimal security assumptions. In: Yang B-Y, editor. Post-Quantum Cryptography; Heidelberg: Springer; 2011. pp. 117–129. [Google Scholar]
- 10.Centre, NCSR: Round 2 submissions - Post-quantum cryptography (2019). https://csrc.nist.gov/projects/post-quantum-cryptography/round-2-submissions
- 11.Ducas L, Durmus A, Lepoint T, Lyubashevsky V. Lattice signatures and bimodal Gaussians. In: Canetti R, Garay JA, editors. Advances in Cryptology – CRYPTO 2013; Heidelberg: Springer; 2013. pp. 40–56. [Google Scholar]
- 12.ElGamal T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory. 1985;31(4):469–472. doi: 10.1109/TIT.1985.1057074. [DOI] [Google Scholar]
-
13.Erdös P, Frankl P, Füredi Z. Families of finite sets in which no set is covered by the union of
 others. Isr. J. Math. 1985;51(1):79–89. doi: 10.1007/BF02772959. [DOI] [Google Scholar]
others. Isr. J. Math. 1985;51(1):79–89. doi: 10.1007/BF02772959. [DOI] [Google Scholar] - 14.Hülsing A. W-OTS+ – shorter signatures for hash-based signature schemes. In: Youssef A, Nitaj A, Hassanien AE, editors. Progress in Cryptology – AFRICACRYPT 2013; Heidelberg: Springer; 2013. pp. 173–188. [Google Scholar]
- 15.Hülsing A, Busold C, Buchmann J. Forward secure signatures on smart cards. In: Knudsen LR, Wu H, editors. Selected Areas in Cryptography; Heidelberg: Springer; 2013. pp. 66–80. [Google Scholar]
- 16.Hülsing A, Rausch L, Buchmann J. Optimal parameters for XMSSMT. In: Cuzzocrea A, Kittl C, Simos DE, Weippl E, Xu L, editors. Security Engineering and Intelligence Informatics; Heidelberg: Springer; 2013. pp. 194–208. [Google Scholar]
- 17.Hülsing A, Rijneveld J, Song F. Mitigating multi-target attacks in hash-based signatures. In: Cheng C-M, Chung K-M, Persiano G, Yang B-Y, editors. Public-Key Cryptography – PKC 2016; Heidelberg: Springer; 2016. pp. 387–416. [Google Scholar]
- 18.Johnson D, Menezes A, Vanstone S. The elliptic curve digital signature algorithm (ECDSA) Int. J. Inf. Secur. 2001;1(1):36–63. doi: 10.1007/s102070100002. [DOI] [Google Scholar]
- 19.Lamport, L.: Constructing digital signatures from a one-way function. Technical report, CSL-98, SRI International Palo Alto (1979)
- 20.Merkle RC. A certified digital signature. In: Brassard G, editor. Advances in Cryptology — CRYPTO’ 89 Proceedings; New York: Springer; 1990. pp. 218–238. [Google Scholar]
- 21.Perrig, A.: The BiBa one-time signature and broadcast authentication protocol. In: Proceedings of the ACM Conference on Computer and Communications Security, pp. 28–37 (2001)
- 22.Pieprzyk J, Wang H, Xing C. Multiple-time signature schemes against adaptive chosen message attacks. In: Matsui M, Zuccherato RJ, editors. Selected Areas in Cryptography; Heidelberg: Springer; 2004. pp. 88–100. [Google Scholar]
- 23.Reyzin L, Reyzin N. Better than BiBa: short one-time signatures with fast signing and verifying. In: Batten L, Seberry J, editors. Information Security and Privacy; Heidelberg: Springer; 2002. pp. 144–153. [Google Scholar]
- 24.Rivest RL, Shamir A, Adleman L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM. 1978;21(2):120–126. doi: 10.1145/359340.359342. [DOI] [Google Scholar]
- 25.Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings of the Annual Symposium on Foundations of Computer Science, pp. 124–134 (1994)
- 26.Song F. A note on quantum security for post-quantum cryptography. In: Mosca M, editor. Post-Quantum Cryptography; Cham: Springer; 2014. pp. 246–265. [Google Scholar]
- 27.Li YX, Deng RH, Wang XM. On the equivalence of McEliece’s and Niederreiter’s public-key cryptosystems. IEEE Trans. Inf. Theory. 1994;40(1):271–273. doi: 10.1109/18.272496. [DOI] [Google Scholar]