Machine Learning Framework to Identify Individuals at Risk of Rapid Progression of Coronary Atherosclerosis: From the PARADIGM Registry

Abstract

Background

Rapid coronary plaque progression (RPP) is associated with incident cardiovascular events. To date, no method exists for the identification of individuals at risk of RPP at a single point in time. This study integrated coronary computed tomography angiography–determined qualitative and quantitative plaque features within a machine learning (ML) framework to determine its performance for predicting RPP.

Methods and Results

Qualitative and quantitative coronary computed tomography angiography plaque characterization was performed in 1083 patients who underwent serial coronary computed tomography angiography from the PARADIGM (Progression of Atherosclerotic Plaque Determined by Computed Tomographic Angiography Imaging) registry. RPP was defined as an annual progression of percentage atheroma volume ≥1.0%. We employed the following ML models: model 1, clinical variables; model 2, model 1 plus qualitative plaque features; model 3, model 2 plus quantitative plaque features. ML models were compared with the atherosclerotic cardiovascular disease risk score, Duke coronary artery disease score, and a logistic regression statistical model. 224 patients (21%) were identified as RPP. Feature selection in ML identifies that quantitative computed tomography variables were higher‐ranking features, followed by qualitative computed tomography variables and clinical/laboratory variables. ML model 3 exhibited the highest discriminatory performance to identify individuals who would experience RPP when compared with atherosclerotic cardiovascular disease risk score, the other ML models, and the statistical model (area under the receiver operating characteristic curve in ML model 3, 0.83 [95% CI 0.78–0.89], versus atherosclerotic cardiovascular disease risk score, 0.60 [0.52–0.67]; Duke coronary artery disease score, 0.74 [0.68–0.79]; ML model 1, 0.62 [0.55–0.69]; ML model 2, 0.73 [0.67–0.80]; all P<0.001; statistical model, 0.81 [0.75–0.87], P=0.128).

Conclusions

Based on a ML framework, quantitative atherosclerosis characterization has been shown to be the most important feature when compared with clinical, laboratory, and qualitative measures in identifying patients at risk of RPP.

Clinical Perspective

What Is New?

• Computed tomography–based quantitative plaque features are the most important features to predict plaque progression, and this has been proven effectively by the machine learning method.

• The machine learning–based model, which integrated clinical, laboratory, and computed tomography–based qualitative and quantitative plaque features, demonstrated notable discrimination and reclassification for the identification of patients at risk of plaque progression.

What Are the Clinical Implications?

• The machine learning–based prediction model might be helpful to identify patients at risk of future plaque progression from a single point‐of‐time baseline noninvasive evaluation.

Introduction

Recent developments in coronary computed tomographic angiography (CCTA) have enabled reliable noninvasive assessment of coronary artery disease (CAD).1, 2 Beyond the traditional measure of diameter stenosis, CCTA has also been used to evaluate atherosclerotic plaque characteristics.3, 4 Additionally, more recent studies have demonstrated the ability of CCTA to quantify the total coronary plaque burden and to assess longitudinal changes in plaque burden by serial examinations.5, 6

Rapid progression of coronary atherosclerosis has been found to be associated with a higher risk of future cardiovascular events.7, 8 Development and progression of coronary atherosclerosis are a complex interplay of numerous factors influenced by clinical comorbidity, medication use, and baseline coronary plaque characteristics.8, 9 In addition, the changes of plaque morphology and composition are known to have dynamic variations.10, 11 As a result, the attributable individual contribution of each factor is difficult to elucidate.

Machine learning (ML) is a field of computer science based on pattern recognition and computational learning that can identify patterns and relationships formed from complex multidimensional databases.12 It relies on computer algorithms to learn and identify nonlinear and complex interactions among all variables by minimizing the error between predicted and observed outcomes. Recent studies that have incorporated ML methods into medical research have found that ML can be useful in identifying the causal factors of clinical outcomes and can effectively develop predictive models when compared with conventional statistical approaches.13, 14

To date, no method exists to identify individuals at risk of rapid plaque progression (RPP) at a single point in time. In this study we sought to evaluate the contributory role of clinical and laboratory variables, as well as qualitative and quantitative CCTA variables toward RPP in a large, longitudinal cohort. We integrate these variables within a ML framework to determine its efficacy in identifying individuals at risk of RPP. Additionally, we also evaluate the predictive and reclassification performance of these ML models against conventional methods.

Methods

The data that support the findings of this study are available from the corresponding author on reasonable request.

Study Population

This study uses data from the PARADIGM (Progression of Atherosclerotic Plaque Determined by Computed Tomographic Angiography Imaging) registry. The overall study design has been previously described.15 Briefly, PARADIGM is a prospective, open‐label, international, multicenter dynamic observational registry designed to evaluate associations between changes in serial CCTA imaging findings and clinical presentation. Between 2003 and 2015, a total of 2252 consecutive subjects underwent CCTAs at 13 centers in 7 countries. The study protocol was approved by the institutional review boards at all participating sites, and the participants gave informed consent. Among 2252 consecutive subjects, we excluded patients with coronary CCTAs of inadequate image quality for quantitative plaque analysis (n=492), prior history of coronary revascularization (n=282), major adverse cardiac events between serial CCTA scans (n=133), or 5 or more uninterpretable coronary segments (n=262). Thus, a total of 1083 patients were included in the current analysis (median interscan interval 3.3 [interquartile range 2.6–4.8] years).

CCTA Analysis

All testing, data acquisition, and image postprocessing for CCTA were in accordance with Society of Cardiovascular Computed Tomography guidelines.16 CCTA was conducted using a scanner with ≥64 detector rows in all centers. Baseline and follow‐up data sets from each center were transferred to an offline workstation for analysis using semiautomated plaque analysis software (QAngioCT Research Edition v2.1.9.1; Medis Medical Imaging Systems, Leiden, the Netherlands) with manual correction. Independent level III–experienced readers who were masked to the clinical and test results analyzed all CCTAs. Segments with a diameter ≥2 mm were evaluated using a modified 17‐segment American Heart Association model for coronary segment classification. Segments were matched between baseline and follow‐up CCTA using branch points as landmarks. For longitudinal comparisons of CCTAs, both baseline and follow‐up coronary segments were coregistered using fiduciary landmarks, including distance from ostia or branch vessel takeoffs.

Plaque characteristics were qualitatively assessed as the presence or absence of positive remodeling, low‐attenuation plaque, spotty calcification, and napkin ring sign. A remodeling index was defined as a maximal lesion vessel diameter divided by the proximal reference vessel diameter. Positive remodeling was defined as a remodeling index >1.1 and low‐attenuation plaque was defined as any voxel <30 Hounsfield units within a coronary plaque.4 An intra lesion calcific plaque <3 mm in length that composed <90° of the lesion circumference defined as a spotty calcification. Napkin ring sign was defined as a plaque core with low computed tomography attenuation surrounded by a rim‐like area of higher attenuation.3 The presence of any high‐risk plaque (HRP) feature and the number of HRP was recorded on a per‐patient level. Plaque volumes (mm³) of all coronary segments were obtained and then summated to generate the total plaque volume on a per‐patient level. Atherosclerotic plaque volume was further subclassified by composition, employing predefined intensity cutoff values in Hounsfield units (HU) for necrotic core (−30 to 30 HU), fibrofatty plaque (31 to 130 HU), fibrous plaque (131 to 350 HU), and calcified plaque (≥351 HU).17, 18 Percentage atheroma volume (PAV) was defined as total plaque volume divided by total vessel volume.19 Maximum per‐lesion PAV was defined as percentage plaque volume of the largest plaque per patient. RPP was defined as an increase from baseline PAV of more than 1% per year on follow‐up CCTA scan. This cutoff was derived in previous research with intravascular ultrasound (IVUS).20 We also observed that PAV progression at the threshold of 1% per year was associated with major adverse cardiac events and a composite of cardiac death and acute coronary syndrome.21

ML Analysis

Seventy‐seven parameters (44 clinical, 15 laboratory, 7 CCTA‐based qualitative, and 11 quantitative features) were available for the analysis (Table S1). Analysis was performed on 3 models with the following combination of variables: (1) model 1, clinical and laboratory variables only; (2) model 2, variables from model 1 and computed tomography (CT)‐based qualitative plaque features; and (3) model 3, variables from model 2 and CT‐based quantitative features. ML involved automated feature selection, splitting the entire cohort randomly into a training set (70% of data) and a test set (30% of data) (Table S2), and model building on all 3 models. Splitting of the entire cohort was done in a stratified manner so that the ratio of events (RPP) to nonevents (non‐RPP) in each split (training [20.3% RPP] and test set [20.8% RPP]) was identical to that of the entire data set [20.7% RPP] (Table S2). ML techniques were implemented in the open‐source Waikato Environment for Knowledge Analysis platform.22

Feature Selection

Feature selection was performed using information‐gain attribute ranking.23 Information gain is defined as a measure of the effectiveness of an attribute in classifying the training data. It is measured as the amount by which the entropy of the class decreases, which reflects the additional information about the class provided by the attribute. The feature selection is a standard procedure performed in ML to ensure appropriate performance of the classification algorithm. Only attributes resulting in information gain >0 were used in model building. Ten different ML classifiers (Table S3) were used to evaluate the prediction performance, and a boosted ensemble classification algorithm (LogitBoost)13 was used for the analysis due to its superior performance and also the methodological advantages as discussed below.

Model Building

Predictive classifiers for prediction of RPP were developed using an ensemble classification approach (“boosting”), employing an iterative LogitBoost algorithm24, 25 and using decision stumps (single‐node decision trees) for each feature‐selected variable as a base classifier13 on the training set (70% of the data). The hyperparameters used in the Logitboost method were (1) number of iterations (k)—the appropriate number of iterations needed to optimize the loss function was determined using 5‐fold internal cross validation while training the model on the training set (70% data) and (2) shrinkage parameter (v=0.1). The principle behind ML ensemble boosting is that a set of weak base classifiers can be combined to create a single strong classifier by iteratively adjusting their appropriate weighting according to misclassifications. A series of base classifier predictions and an updated weighting distribution are produced with each iteration. The strength of the LogitBoost algorithm is that each weak learner needs only to be slightly better than a guess, and the distribution of weights will allow the strong learner to become more influential and create accurate predictions. Further, LogitBoost algorithms use log‐likelihood loss for the binary classification (RPP versus non‐RPP) that incorporates the idea of probabilistic confidence. The predictive performance of the developed classifier from the training data set was then evaluated on the unseen test set (30% of data).

Statistical Analyses

Continuous variables are expressed as mean (standard deviation [SD]), and categorical variables are reported as counts with proportions. Both the Student unpaired t test and Pearson chi‐squared test were performed for comparison of covariates between groups. A fractional polynomial model was fitted to evaluate the pattern between high‐ranked features and changes of percentage plaque volume per year. The linear relationship between changes of percentage plaque volume per year and high‐ranked features was assessed using linear regression analyses, and the β coefficients were reported. The performance of ML (the ML model) for predicting RPP was compared with 10‐year atherosclerotic cardiovascular disease risk score (ASCVD risk score),26 Duke CAD score,27 and statistical models. Statistical modeling was performed on the same 3 models in ML analysis: (1) model 1, clinical and laboratory variables only; (2) model 2, variables from model 1 and CT‐based qualitative plaque features; and (3) model 3, variables from model 2 and CT‐based quantitative features. To avoid including highly correlated variables in statistical models, we selected 1 variable with the highest correlation coefficient with outcome (RPP) when there were significant correlations among the 77 variables (r>0.7). Then, backward stepwise logistic regression was performed on the training set with predictor‐entry and removal‐significance P values set to 0.05 and 0.10, respectively, with 1000 bootstrapped repetitions to select the predictors of outcome.28, 29 All predictors that were retained in more than 70% of the bootstrapped results were retained in the final model, resulting in 8 predictors being included in the final statistical model (Table S4). We also tested a series of statistical models with different thresholds (70%, 60%, and 50%) for the bootstrapped results in the test set (Table S5). In addition, statistical model 4 was developed using 33 important variables by the ML method (information‐gain method). Variance inflation factors were computed to assess multicollinearity in a multivariate model with a variance inflation factor <5 considered safe from multicollinearity.30 The variable with the highest variance inflation factor was removed stepwise from a multivariate model. Finally, 21 variables were included in statistical model 4 (Table S6 with all variance inflation factors <5).

Receiver operating characteristic curves were fashioned to evaluate the discriminatory ability of models for predicting RPP, and areas under the receiver operating characteristic curve (AUCs) were compared using the method described by DeLong et al.31 Additional subgroup analyses were also performed on the basis of sex and age (≥65 or <65 years). Category‐free net reclassification improvement was used to estimate reclassification performance of the ML model compared with traditional risk prediction approaches.32 Subjects were categorized as low (<7.5%) or intermediate to high (≥7.5) based on ASCVD risk score.26 Calibration was assessed by the predicted and observed proportion of RPP across quintiles of risk in ML model 3. Statistical analysis was performed using STATA (version 14; StataCorp, College Station, TX) and SAS (version 9.3; SAS Institute, Cary, NC).

Results

Baseline Characteristics

The mean age of participants was 60 (SD 9) years, and 624 (57%) were male. The baseline characteristics of participants according to plaque progression are described in Table 1. Subjects with RPP were significantly older, had higher prevalence of hypertension, diabetes mellitus, and current smoking, and showed a high rate of medication use compared with those without RPP. Patients with RPP showed lower total cholesterol and high‐density lipoprotein cholesterol level and higher ASCVD risk score and Duke CAD score than patients without RPP.

Table 1.

Baseline Characteristics of the Study Population

Variables	No RPP (n=859)	RPP (n=224)	P Value
Clinical characteristics
Age, mean (SD), y	59.5 (9)	62.3 (9)	<0.001
Male sex, n (%)	490 (57)	134 (60)	0.454
Clinical symptoms			0.190
Asymptomatic	125 (15)	20 (9)	0.028
Shortness of breath	45 (5)	16 (7)	0.271
Atypical chest pain	586 (68)	155 (69)	0.779
Noncardiac chest pain	65 (8)	22 (10)	0.269
Typical chest pain	30 (3)	10 (4)	0.492
Hypertension, n (%)	413 (48)	136 (61)	0.001
Diabetes mellitus, n (%)	152 (18)	64 (39)	<0.001
Dyslipidemia, n (%)	312 (36)	94 (42)	0.106
Current smoker, n (%)	136 (16)	62 (28)	<0.001
Aspirin use, n (%)	286 (34)	103 (47)	<0.001
β‐blocker use, n (%)	211 (25)	52 (24)	0.695
RAS inhibitor use, n (%)	213 (25)	83 (38)	<0.001
Statin use, n (%)	301 (36)	98 (46)	0.009
Total cholesterol	192.3 (38)	185.2 (39.7)	0.020
LDL cholesterol	116.9 (33.5)	113.8 (35.0)	0.245
HDL cholesterol	52.6 (14.5)	47.8 (11.7)	<0.001
ASCVD risk score	10.7 (9.7)	15.3 (12.5)	<0.001
Duke CAD score	1.3 (1.1)	2.2 (1.0)	<0.001
Qualitative CT features
No plaque at baseline scan	264 (31)	7 (3)	<0.001
No plaque at follow‐up scan	175 (18)	0 (0)	<0.001
Positive remodeling	501 (58)	208 (93)	<0.001
Low‐attenuation plaque	137 (16)	91 (41)	<0.001
Spotty calcification	131 (15)	74 (33)	<0.001
Napkin‐ring sign	5 (1)	5 (2)	0.021
Diameter stenosis >50%	15 (2)	23 (10)	<0.001
Quantitative CT features, mm3
Total plaque volume	65.9 (112.6)	240.9 (241.9)	<0.001
Fibrous plaque volume	29.4 (51.9)	110.8 (111.3)	<0.001
Fibrofatty plaque volume	13.2 (25.9)	44.6 (54.9)	<0.001
Necrotic core volume	1.8 (5.4)	5.4 (10.3)	<0.001
Calcified plaque volume	21.5 (52.4)	80.2 (135.9)	<0.001
Percentage plaque volume	2.6 (3.9)	9.2 (7.8)	<0.001

ASCVD risk score indicates 10‐y atherosclerotic cardiovascular disease risk score; CAD, coronary artery disease; CT, computed tomography; HDL, high‐density lipoprotein; LDL, low‐density lipoprotein; RAS, renin‐angiotensin system; RPP, rapid plaque progression.

The prevalence of a normal CCTA scan (no plaque) at baseline and follow‐up scan was 25% and 16% (Table 1). The prevalence of significant stenosis (diameter stenosis >50%) was 4% in the overall study population; a significantly higher prevalence was observed in patients with RPP than those without RPP (10% versus 2%, P<0.001, Table 1). With the exception of napkin ring sign, qualitative and quantitative plaque and HRP features were significantly higher in patients with RPP compared with those without RPP (Table 1, all other P<0.001).

Feature Selection

The information‐gain ranking method identified 33 variables as effectively contributing to RPP among the available total of 77 features. In the overall model, quantitative CT variables were the highest‐ranking features, followed by qualitative CT variables and, last, clinical/laboratory variables (Table 2 and Figure 1). Feature selection among clinical and laboratory variables indicated that the ASCVD risk score was the highest ranking feature, followed by age, high‐density lipoprotein cholesterol, and smoking status. Among qualitative CT features, the number of HRP was the most important feature, followed by positive remodeling, low‐attenuation plaque, and SC, respectively. With quantitative CT features, PAV was the highest contributory feature to RPP, followed by total plaque volume and fibrous plaque volume.

Table 2.

Feature Importance and Linear Regression Coefficient of High‐Ranked Features by Machine Learning Algorithm

Rank	Clinical/Laboratory			Qualitative CT Feature			Quantitative CT Feature
	Variable Name	Information Gain Value	Regression Coefficient (β)	Variable Name	Information Gain Value	Regression Coefficient (β)	Variable Name	Information Gain Value	Regression Coefficient (β)
First	ASCVD risk score	0.014	0.281	Number of HRP	0.094	0.385	Percentage plaque volume	0.193	0.529
Second	Age	0.012	0.163	Positive remodeling	0.076	0.350	Total plaque volume	0.180	0.469
Third	HDL cholesterol	0.012	−0.137	Presence of any HRP	0.074	0.345	Fibrous plaque volume	0.177	0.483
Fourth	Current smoking	0.010	0.097	Low‐attenuation plaque	0.039	0.242	Plaque burden	0.168	0.452
Fifth	RAS inhibitor use	0.008	0.115	Spotty calcification	0.022	0.199	Maximum lesion plaque volume	0.149	0.468
Sixth	Diabetes mellitus	0.008	0.135	Diameter stenosis >50%	0.020	0.179	Fibrofatty plaque volume	0.119	0.358

All P<0.01 for regression coefficient. ASCVD risk score indicates 10‐y atherosclerotic cardiovascular disease risk score; CT, computed tomography; HDL, high‐density lipoprotein; HRP, high‐risk plaque features; RAS, renin‐angiotensin system.

Figure 1.

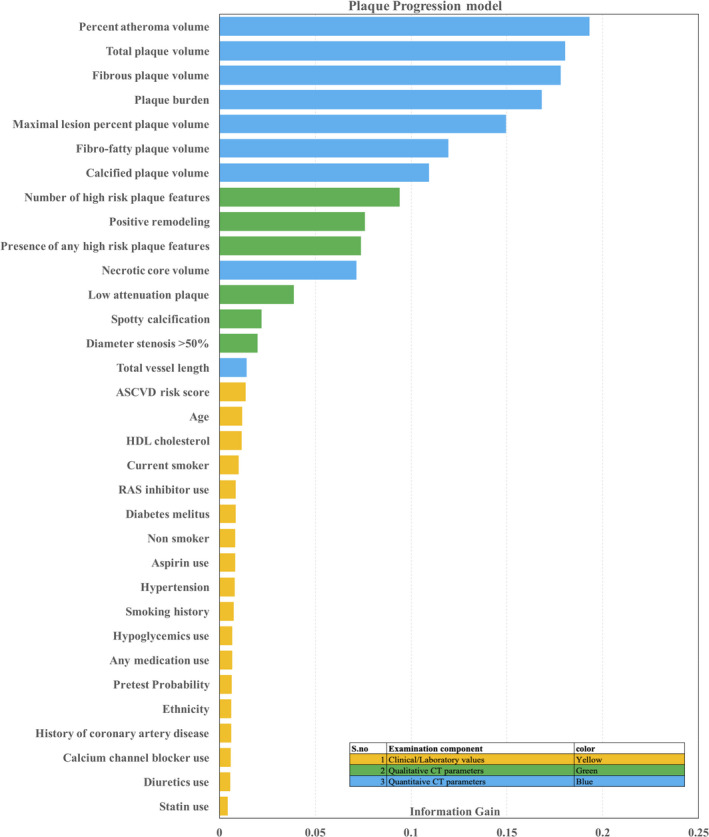
Importance of features by information‐gain method. The information gain method measured the entropy gain with respect to RPP for each variable and then ranks the attributes by their individual evaluations (from top to bottom).

There was a mostly linear relationship between more important features and RPP, especially those with qualitative and quantitative CT features (Figure S1). Regression analysis of the more important features (qualitative and quantitative CT features) and RPP also showed that there were statistically significant linear relationships (Table 2, all P<0.01 for regression coefficient β).

Predictive Performance for RPP

A calibration plot indicated good agreement between the ML model 3 and the observed risk of RPP in the internal testing cohort (Figure S2). AUC analysis indicated that the ML model 3 exhibited superior performance in predicting RPP when compared with the other ML models (model 3, 0.833 (95% CI 0.775–0.891) versus model 1, 0.618 (0.546–0.689); model 2, 0.734 (0.672–0.796); all P<0.001) (Figure 2). Further, we observed that statistical models 1, 2, and 3 had comparable predictive performance when compared with their corresponding ML models, ML models 1, 2, and 3 (P=0.897, 0.599, and 0.064; Table S7). When compared with ASCVD risk score (AUC 0.597 [95% CI 0.519–0.674]) and Duke CAD score (AUC 0.740 [95% CI 0.683–0.798]) as a traditional risk approach, ML model 3 showed significantly higher performance (both P<0.001).

Figure 2.

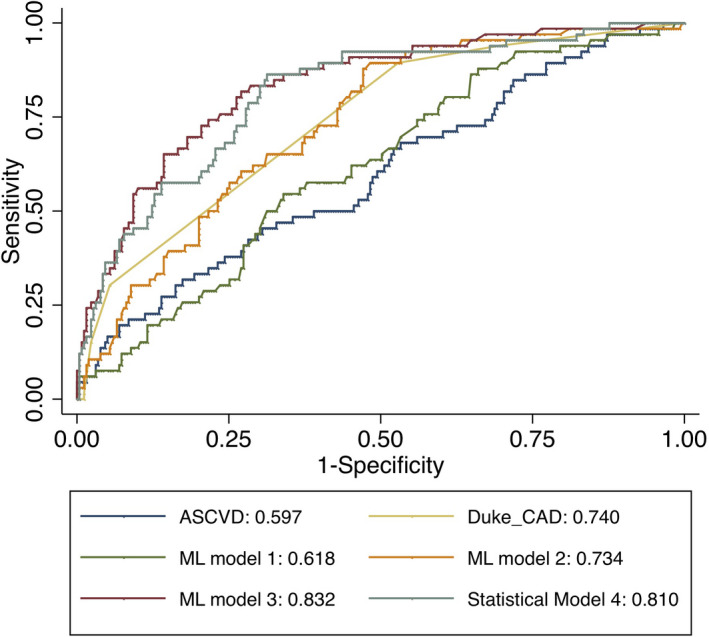
Areas under the receiver operating characteristic curves for the prediction of rapid plaque progression in test set. ASCVD indicates 10‐year atherosclerotic cardiovascular disease risk; CAD, coronary artery disease; ML, machine learning.

We also observed that statistical model 4 (AUC=0.81) with 21 variables showed slightly higher AUC compared with statistical model 3 (AUC=0.801). The AUC in ML model 3 was still higher than that in the statistical model 3 or 4 (0.833 versus 0.801 or 0.810); however, this was not statistically significant (P=0.064 and 0.128, respectively). After further stratification into subgroups of age (≥65 or <65) and sex, ML models exhibited a consistently similar trend of AUC values: ML model 3 showed a significantly higher performance than ASCVD risk score, Duke CAD score, or ML model 1 or 2 (Table 3). In addition, for model 3, there was no significant difference between older and younger patients (AUC 0.831 [95% CI 0.735–0.926] versus 0.829 [95% CI 0.752–0.904], respectively; P=0.873) as well as between men and women (AUC 0.853 [95% CI 0.778–0.932] versus 0.827 [95% CI 0.738–0.904], respectively; P=0.558) (Figure 3).

Table 3.

Comparison of Model Predictive Performance

	Age <65 y		Age ≥65 y		Men		Women
	AUC	95% CI	AUC	95% CI	AUC	95% CI	AUC	95% CI
ASCVD risk score	0.54	0.44 to 0.63	0.65	0.52 to 0.77	0.56	0.46 to 0.67	0.64	0.53 to 0.76
Duke CAD score	0.75	0.67 to 0.83	0.71	0.60 to 0.80	0.74	0.66 to 0.83	0.75	0.67 to 0.83
Statistical model 3	0.78	0.69 to 0.87	0.81	0.72 to 0.90	0.82	0.73 to 0.90	0.79	0.69 to 0.89
Statistical model 4	0.81	0.73 to 0.88	0.81	0.72 to 0.89	0.85	0.78 to 0.92	0.78	0.70 to 0.87
ML model 1	0.57	0.48 to 0.66	0.65	0.54 to 0.76	0.59	0.48 to 0.70	0.65	0.56 to 0.75
ML model 2	0.73	0.64 to 0.81	0.73	0.63 to 0.83	0.70	0.61 to 0.80	0.78	0.70 to 0.86
ML model 3	0.83	0.75 to 0.90	0.83	0.74 to 0.93	0.85	0.78 to 0.93	0.83	0.74 to 0.90

ASCVD risk score indicates 10‐yr atherosclerotic cardiovascular disease risk score; AUC, area under the receiver operating characteristic; CAD, coronary artery disease; ML, machine learning.

Figure 3.

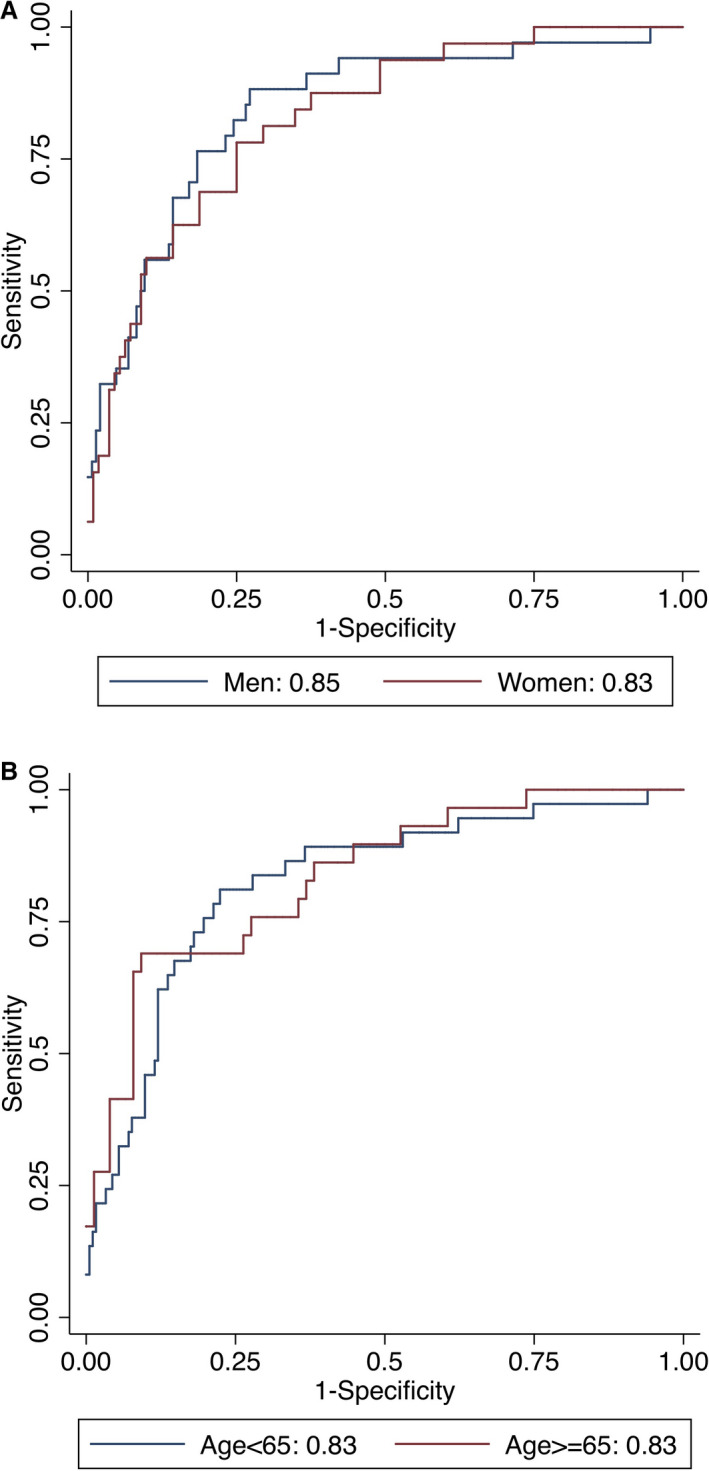
Areas under the receiver operating characteristic curves for the prediction of rapid plaque progression stratified by (A) sex and (B) age for Model 3 (P value for differences: A, 0.588; B, 0.873).

The improved reclassification of the ML model over the ASCVD risk score was significant in patients at both low and intermediate to high risk (Table 4). Notably, ML model 3 correctly reclassified patients with RPP as well as without RPP across overall, low, and intermediate to high ASCVD risk populations (all P<0.001). When the analysis was restricted to symptomatic patients, ML model 3 still displayed significantly improved reclassification over the Duke CAD score (category‐free net reclassification improvement 0.85, P<0.001, Table 5).

Table 4.

Performance of the ML Model for Reclassifying Rapid Plaque Progression Over ASCVD Risk Score

	cNRI	95% CI	P Value	% Event Classified	% Nonevent Classified
Overall
ML model 1	0.05	−0.21 to 0.32	0.700	−15%	20%a
ML model 2	0.61	0.35 to 0.87	<0.001	27%a	34%a
ML model 3	1.01	0.78 to 1.25	<0.001	42%a	59%a
Low risk (ASCVD <7.5%)
ML model 1	0.26	−0.16 to 0.69	0.232	−4%	30%a
ML model 2	0.69	0.28 to 1.11	0.002	20%	49%a
ML model 3	1.25	0.91 to 1.59	<0.001	60%a	65%a
High risk (ASCVD ≥7.5%)
ML model 1	0.15	−0.20 to 0.50	0.406	−2%	17%a
ML model 2	0.52	0.19 to 0.85	0.004	32%a	20%a
ML model 3	0.85	0.53 to 1.18	<0.001	37%a	49%a

ASCVD risk score indicates 10‐y atherosclerotic cardiovascular disease risk score; cNRI, category‐free net reclassification index; ML, machine learning.

^a P<0.05.

Table 5.

Performance of the ML Model for Reclassifying Rapid Plaque Progression Over Duke CAD Risk Score in Symptomatic Patients

	cNRI	95% CI	P Value	% Event Classified	% Nonevent Classified
Over Duke CAD risk score in symptomatic patients
ML model 1	0.21	−0.08 to 0.48	0.151	−5%	26%a
ML model 2	0.56	0.28 to 0.84	<0.001	15%a	41%a
ML model 3	0.85	0.57 to 1.13	<0.001	21%a	64%a

CAD indicates coronary artery disease; cNRI, category‐free net reclassification index; ML, machine learning.

^a P<0.05.

Discussion

In the current study we observed that quantitative CT‐based plaque features were the most important features to predict plaque progression, followed by qualitative CT‐based features and, last, clinical/laboratory features. It was also observed that ML model 3 (with clinical/laboratory and qualitative and quantitative plaque features) showed a higher predictive performance for RPP when compared with using a combination of clinical/lab and qualitative CT‐based variables (ML models 1 and 2). The ML model 3 were superior to the conventional ASCVD risk score and the Duke CAD score. Furthermore, ML model performance was robust across sex‐ and age‐based subsets. ML models 2 and 3 provided superior reclassification when compared with the ASCVD risk score and the Duke CAD risk score, across varying risk profile subsets.

The PROSPECT (Providing Regional Observations to Study Predictors of Events in the Coronary Tree) trial utilizing IVUS was performed in patients with acute coronary syndromes already undergoing percutaneous coronary intervention, and the latter study suggested that coronary atherosclerotic plaque burden was correlated with a higher incidence of adverse event rates.33 In addition, serial IVUS demonstrated the prognostic importance of plaque progression by showing an association with clinical outcomes.20 However, it should be noted that these previous IVUS studies are somewhat limited due to (1) the inclusion of only high‐risk patients at the time of the intervention and (2) limited evaluation targeted at only the lesion of interest. Additionally, compared with IVUS, CCTA can uniquely provide quantitative measures of whole‐heart atherosclerotic plaque burden and type in a clinical population in a noninvasive fashion.

In this study, we attempted to identify the important clinical and qualitative and quantitative CT features related to RPP. Although conventional risk factors such as ASCVD risk score, lipid profile, medication use, or diabetes mellitus are revealed as important features for plaque progression, CCTA features, especially those from quantitative plaque analysis, were the most important factors identified by the ML‐based feature selection algorithm. This is also consistent with previous findings from our group that identified plaque burden as an important factor for plaque progression.34 Additionally, we further extend the findings by integrating qualitative and quantitative atherosclerotic plaque characteristics within a ML framework. To our knowledge, this is first study to use ML to predict the future risk of plaque progression using single‐point‐of‐time CCTA‐based information. The ML findings identify CCTA‐based plaque features that are relevant and subsequently apportion their respective contributions toward RPP.

Previous studies applying ML in clinical research mostly focused on developing a high‐performance prediction model.13, 14, 35 In terms of developing a prediction model by ML, it is essential to compare the ML model with a reliable, well‐developed conventional prediction model, and most previous studies showed a higher performance in ML than a conventional risk score or a statistical approach.36 In the current study we use a general risk‐prediction model—ASCVD risk score and Duke CAD score—because there has been no prior published prediction model for plaque progression. The ML model showed better performance than general risk‐prediction models. However, when compared with a statistical logistic regression model, even though ML model 3 showed noticeable performance of AUC 0.83, it was not statistically significant. Further, this trend was also consistently observed when ML models 1 and 2 were compared with their corresponding statistical models (Table S6). This finding may be explained by the linear relationship between predictors and plaque progression, especially CCTA features, that played a larger role when compared with other clinical and laboratory features (Figure S1). For example, plaque volume is observed to be linearly increasing with the risk of plaque progression; a similar relationship was also noticed between HRP features and the risk of plaque progression. Furthermore, the use of ML for feature importance was obligatory in the identification of input variables for the logistic regression statistical model, which may contribute toward the statistical model's performance. In addition to this, other possible explanations for this limited result would be that, despite the PARADIGM registry being the largest available serial CCTA database, the sample size in the testing cohort was still relatively small (325 patients). To further explore these issues, we believe that models validated on external validation studies (data sets) with a larger sample size are warranted.

The current findings identify the presence and amount of coronary atherosclerotic plaque burden as the most significant factors in predicting RPP. As a result, the performance of models utilizing CCTA‐derived variables (ML model 3, ML model 2, statistical models 2 and 3, and Duke CAD score) were superior to those using clinical/laboratory variables only (ML model 1, ASCVD risk score), suggesting that a single point‐of‐time CCTA may help to better predict the risk of RPP in the future. Application of this current novel prediction tool for RPP may help to identify patients at high risk of atherosclerotic cardiovascular disease progression. Undoubtedly, further studies are needed to evaluate the performance and applicability of this model across different cohorts as well as to assess how to effectively modify the natural history of atherosclerotic cardiovascular disease progression.

Variable selection is essential for developing a prediction model. We developed 2 different statistical approaches for variable selection: stepwise selection with (1) logistic regression analysis 1000 bootstrap methods and (2) variance inflation factors to avoid multicollinearity. Although these approaches are frequently used methods to identify important predictors for developing a prediction model, there are potential limitations from overfitting and overestimation in regression coefficients and effect sizes.37, 38 In addition, we found that an increasing number of variables did not improve the AUC when we tested series of statistical models with different thresholds for bootstrap methods (50%, 60%, and 70%; Table S5). Thus, statistical models of our data should be interpreted with caution. On the other hand, ML approaches have been shown to be beneficial in feature selection over traditional statistical methods.39, 40 In addition, we employed an iterative LogitBoost algorithm using decision stumps (single‐node decision trees) for each feature‐selected variable as base classifiers to build the classifier. Tree‐based boosted ensemble models have an innate feature of being robust to correlated features and might have potential benefits in a data set with multicollinearity variables.24, 41 Further, we also used cross validation to tune the hyperparameters on the training set to prevent overfitting.

This study is not without limitations. In the current study, for the purpose of assessing plaque progression in the whole coronary tree, we included patients with high image quality and without localized artifacts. In addition, the prevalence of patients with normal CCTA was 25% at baseline, and patients who underwent revascularization before follow‐up CCTA were excluded; thus, this study population mostly consisted of low‐risk patients. Thus, the current study may be prone to potential selection bias. Although numerous clinical, medication, and laboratory variables were included in developing the ML model, the possibility of bias from unmeasured confounding factors cannot be excluded. Additionally, for a better and generalizable ML prediction model, we also need external validation in a separate independent cohort; however, currently, there is no such available serial CCTA cohort with a large enough sample size for external validation. Although ML‐based algorithms have been widely used in clinical research, we could not evaluate unnoticed potential biases from the ML algorithm in the data set, which is known as the “black‐box problem”.36 Therefore, the causal relationship between features and outcomes is not as yet known and should not be presently inferred.

Conclusions

With a ML‐based framework, the contributory variables for RPP were identified and ranked. Quantitative atherosclerotic plaque characterization was more influential when compared with qualitative CCTA variables or clinical and laboratory measures. Multidimensional reduction of coronary artery findings through ML offers a novel approach to identify patients at risk of future plaque progression from a single‐point‐of‐time baseline evaluation.

Sources of Funding

This work was supported by the Leading Foreign Research Institute Recruitment Program through the National Research Foundation (NRF) of Korea funded by the Ministry of Science and ICT (MSIT) (Grant No. 2012027176) and the Technology Innovation Program (10075266, Data Center for Korean Cardiovascular Imaging Reference) funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea). This work was also supported by Institute for Information & communications Technology Promotion (IITP) grant funded by the Korea government (MSIT) (2017‐0‐00255, Autonomous digital companion framework and application).

Disclosures

Dr Min receives funding from the Dalio Foundation, National Institutes of Health, and GE Healthcare. Dr Min serves on the scientific advisory board of Arineta and GE Healthcare and has an equity interest in Cleerly. The remaining authors have no disclosures to report.

Authors’ Affiliations

From the Division of Cardiology, Severance Cardiovascular Hospital, Yonsei University College of Medicine, Yonsei University Health System, Seoul, South Korea (D.H., J.M.S., S.‐E.L., H.‐J.C.); Department of Radiology, NewYork‐Presbyterian Hospital and Weill Cornell Medicine, New York, NY (K.K.K., S.J.A., L.B., A.R.v.R., L.J.S., F.Y.L., J.K.M.); Department of Imaging (H.G.), and Imaging and Medicine (D.S.B), Cedars Sinai Medical Center, Los Angeles, CA; Centro Cardiologico Monzino, IRCCS, Milan, Italy (D.A., E.C., G.P.); Department of Medicine, Los Angeles Biomedical Research Institute, Torrance, CA (M.J.B.); Cardiovascular Imaging Center, SDN IRCCS, Naples, Italy (F.C.); Department of Cardiology, William Beaumont Hospital, Royal Oak, MI (K.C., G.L.R.); Pusan National University Hospital, Busan, South Korea (J.H.C.); UNICA, Unit of Cardiovascular Imaging, Hospital da Luz, Lisboa, Portugal (H.M., P.d.A.G.); Department of Radiology, Casa de Saude São Jose, Rio de Janeiro, Brazil (I.G.); Department of Radiology and Nuclear Medicine, German Heart Center Munich, Germany (M.H.); Department of Medicine and Radiology, University of British Columbia, Vancouver, BC, Canada (J.A.L.); Department of Radiology, Area Vasta 1/ASUR Urbino, Italy (E.M.); Ewha Womans University Seoul Hospital, Seoul, South Korea (S.S.); Seoul National University Hospital, Seoul, South Korea (Y.‐J.K.); Gangnam Severance Hospital, Yonsei University College of Medicine, Seoul, Korea (B.K.L.); Seoul National University Bundang Hospital, Sungnam, South Korea (E.J.C.); Department of Pathology, CVPath Institute, Gaithersburg, MD (R.V.); Division of Cardiology, Emory University School of Medicine, Atlanta, GA (H.S.); Cardiovascular Division, Brigham and Women's Hospital, Harvard Medical School, Boston, MA (P.S.); Icahn School of Medicine at Mount Sinai, Mount Sinai Heart, Zena and Michael A. Wiener Cardiovascular Institute, and Marie‐Josée and Henry R. Kravis Center for Cardiovascular Health, New York, NY (J.N.); Department of Cardiology, Leiden University Medical Center, Leiden, the Netherlands (J.J.B.).

Supporting information

Table S1. Examination Components

Table S2. Baseline Characteristics of Training and Test Set

Table S3. Performance of Machine Learning Algorithms

Table S4. The Statistical Model Predictors Based on 1000 Bootstrap Samples in the Training Set

Table S5. Statistical Models Using Different Thresholds of Bootstrap Samples

Table S6. The Statistical Model 4 Predictors With Variance Inflation Factors

Table S7. Predictive Performance (AUC [95% CI]) of Statistical Models Compared With Corresponding Machine Learning Models in the Testing Set

Figure S1. Fractional polynomial graph between top 3 features in each predictor category and plaque progression. A, ASCVD risk score; B, age; C, HDL cholesterol; D, number of high‐risk plaque features; E, positive remodeling; F, presence of any high risk plaque features; G, percentage atheroma volume; H, total plaque volume; I, Fibrous plaque volume. Y axis displays changes of percentage plaque volume per year. ASCVD risk score indicates 10‐y atherosclerotic cardiovascular disease risk score; HDL, high‐density lipoprotein.

Figure S2. Calibration plot for machine learning model 3 to predict rapid plaque progression.

(J Am Heart Assoc. 2020;9:e013958 DOI: 10.1161/JAHA.119.013958.)