Mathematical modeling and the transmission dynamics in predicting the Covid-19 - What next in combating the pandemic

Abstract

Mathematical predictions in combating the epidemics are yet to reach its perfection. The rapid spread, the ways, and the procedures involved in containment of a pandemic demand the earliest understanding in finding solutions in line with the habitual, physiological, biological, and environmental aspects of life with better computerised mathematical modeling and predictions. Epidemiology models are key tools in public health management programs despite having a high level of uncertainty in each one of these models. This paper describes the outcome and the challenges of SIR, SEIR, SEIRU, SIRD, SLIAR, ARIMA, SIDARTHE, etc models used in prediction of spread, peak, and reduction of Covid-19 cases.

1. Introduction

The worldwide overwhelming number of COVID-19 infection created an emergency-like situation among the government agencies in pooling the resources and handling the epidemic at all levels. This has impacted greatly the growth and economy and the freedom in leading a happy life of all human beings. Predictions are always happening after the event has occurred. Several mathematical models and computerised simulations have cropped up as an aid in planning and designing the strategies to meet the unexpected demands of the health care system. Since the first published report on pandemic smallpox (Menninger, 1919), the progress made in this direction is still in the nascent stage. Covid-19 or any other virus or bacteria doesn’t spread on its own and the current happenings are perhaps due to our ignorance or casual attitude. The success of a mathematical prediction model depends on the type of answer we generate collectively to the question of what is the extent of the human being doesn’t intrude into the solitude of Covid type of invisible species. The majority of the statistical models currently in use are based on the basic Susceptible-Infectious-Recovered (SIR) (Kermack & McKendrick, 1927) model and its extension. The other similar models are Susceptible-Exposed-Infectious-Recovered (SEIR) predictive model (Hethcote, 2020), Auto-Regressive Integrated Moving Average ( ARIMA ) model (Arino et al., 2006), Time Series models (Kurbalija et al., 2014), Multivariate Linear Regression (Thomson et al., 2006), Grey forecasting models (Wang et al., 2018; Zhang et al., 2017), Back Propagation Neural Networks (Li et al., 2020a; Ren et al., 2013; Zhang et al., 2013), Simulation models (Nsoesie et al., 2013; Orbann et al., 2017), Phenomenological models (Roosa et al., 2020) and the latest (Giulia et al., 2020) SIDARTHE model, etc. This paper discusses the mathematical predictions since the outbreak of infection in different countries and the outcome.

2. Mathematical models and the dynamics of Covid-19

The complex behavior of voluminous transactions that happens in the financial market inspired a q-statistical functional form (Tsallis & Tirnakli, 2020) along lines similar to epidemiological models, such as the SIR. In this model, the increase and decrease in quantitative behavior was postulated in the equation

$$N=C{\left(t-t_0\right)}^{\alpha }{e}_q^{-\beta {(t-t_0)}^{\gamma }}=\frac{C{(t-t_0)}^{\alpha }}{{[1+\left(q-1\right)\beta {\left(t-t_0\right)}^{\gamma }]}^{1/(q-1)}}$$

where N is the number of active cases, t₀ the constant that indicates the first day of appearance of the epidemic, C the normalization constant that reflects the total population of a particular country, q is the exponential expression. Among the four non-trivial parameters α,β depends on the epidemiological strategy and γ,q depends on the biology of Corona virus.

The impact of the latency period was studied using SEIRU mathematical model (Liu et al., 2020a) with a constant time delay, where S is the number of individuals susceptible to infection, E is the number of asymptomatic noninfectious individuals, I is the number of asymptomatic but infectious individuals, R is the number of reported symptomatic infectious individuals and U is unreported symptomatic infectious individuals. Delay differential equations (DDE) was used in considering the latency period while keeping the duration of exposure $\delta$ as constant, time delay in the equation was defined as I(t), t ≥ t₀ is the time in days, t₀ is the beginning date of the epidemic, S(t) is the number of individuals susceptible to infection at time t, E(t) is the number of asymptomatic noninfectious individuals at time t, I(t) is the number of asymptomatic but infectious individuals at time t, R(t) is the number of reported symptomatic infectious at time t, and U(t) is the number of unreported symptomatic infectious individuals at time t. Where

S(t₀) = S₀ > 0, E(t₀) = E₀ > 0, I(t₀) = I₀ > 0, U(t₀) = U₀ > 0, R(t₀) = R₀ = 0

$$\left\{\begin{array}{l}{S}^{\prime }\left(t\right)=-\tau \left(t\right)S\left(t\right)\left[I\left(t\right)+U\left(t\right)\right],\hfill \\ I^{\prime \left(t\right)}=\tau \left(t-\delta \right)S\left(t-\delta \right)\left[I\left(t-\delta \right)+U\left(t-\delta \right)\right]-\nu I\left(t\right)\hfill \\ R^{\prime }\left(t\right)={\nu }_{1}I\left(t\right)-\eta R\left(t\right)\hfill \\ U^{\prime }\left(t\right)={\nu }_{2}I\left(t\right)-\eta U\left(t\right).\hfill \end{array}\right)$$

The exposed class is given by the integral formula and alternatively in the differential equation form

$$E\left(\text{t}\right)=\underset{t-\delta }{\overset{t}{\int }}\tau \left(\sigma \right)S\left(\sigma \right)[I\left(\sigma \right)+U\left(\sigma \right)]d\sigma .$$

$$E^{’}\left(t\right)=\tau \left(t\right)S\left(t\right)\left[I\left(t\right)+U\left(t\right)\right]-\tau \left(t-\delta \right)S\left(t-\delta \right)\left[\left(t-\delta \right)+U\left(t-\delta \right)\right].$$

The transmission dynamics model proposed (Wu et al., 2020) has a component of age-specific susceptibility to symptomatic infection sCFRs with 8 variables.

$$L\left(\theta \right)=\prod _{K=1}^8{L}_k\left(\theta \right)$$

where θ represents the set of parameters that are subject to inference.

Parameters	Description
$R_0$	Basic reproductive number, Which was linearly related to the transmission rate $\beta$

${\varphi }_0$	The relative reduction in transmissibility after vs. before lockdown of Wuhan on January 23, 2020
$z_0$	The number of infections generated by the seeding zoonotic event
sCFRi	The symptomatic case-fatality risk for age group i,i = 1, ….,m
${\alpha }_i$	The relative susceptibility to infection of age group i compared to those aged 30–39 years, i = 1, … …,m
(${\mu }_D,{\alpha }_D$)	Mean and Standard deviation for the time between onset and death
(${\mu }_{SI},{\sigma }_{SI}$)	Mean and Standard deviation of the serial interval
$\epsilon$	The proportion of human to human infections that were confirmed between December 1, 2019 and January 4, 2020

The Spatio-temporal “risk source” model (Jayson et al., 2020) derived has an index for assessing transmission risk that leverages population flow data over time for different locations. The changes in distribution and growth of epidemic overtime were derived using a Cox proportional hazards framework with a time-varying hazard rate function λ₀(t), where λ(t/x_i) is the hazard function that describes the number of cumulative confirmed cases at time t for a given population.

$$\lambda (t/x_i)=\lambda {}_{\text{o}}\left(\text{t}\right)\left(\prod _{j=1}^m{e}^{{\beta }_j{x}_{ji}}\right)e^{\sum _{k=1}^n{\lambda }_{k/ik}}$$

SEIR (Susceptible, Exposed, Infectious, and Removed) model (Wang et al., 2020a, Wang et al., 2020b) was applied to estimate the epidemic trend in Wuhan, China, by February 29, 2020. The differential equations of the SEIR model are given as:

$$ds/dt=-\beta SI/N,$$

$$dE/dt=\beta SI/N-\sigma E,$$

$$dI/dt=\sigma E-\gamma I,$$

$$dR/dt=\gamma I,$$

$$\beta =R_0\gamma ,$$

where $\beta$ is the transmission rate, $\sigma$ is the infection rate and $\gamma$ is the recovery rate. The number of infections estimated using this model was 81,393 and the actual number reported from the public domain on Feb 29 was 79,500. Using a similar model (Li et al., 2020b) forecasted 39, 000 infections in Hubei for Mar. 10, 2020 and the actual number reported was 67,760.

The simple susceptible infected-recovered-deaths (SIRD) model (Fanelli & Piazza, 2020) used an indicative rate of recovery based on the kinetic parameter, while the infection and death rate appear to be more variable.

$${\text{P}}_{\text{n}}={\alpha }^{\frac{\left(1-\beta ⁿ\right)}{\left(1-\beta \right)}}{\text{P}}_0^{{\beta }^n}$$

P = (C, R, D) where, C is the population of cumulative confirmed infected people, R is recovered people and D is the total reported deaths. This model projected 26,000 in Italy on March 21st, 2020 and the world meter showed 53,578 cases.

The heuristic model (Koczkodaja et al., 2020) proposed has an exponential curve for approximation derived from the exponential function f (.) and the proposed heuristic was

$$y_{\text{i}}=f\left({\text{x}}_{\text{i}}\text{;a,b}\right){+}_{\text{i}}\text{,}\text{i}=1\text{,}\dots \text{,n}$$

for computing parameters, a and b was considered from the exponential curve a ∗exp(b∗x) where x defines the number of cases on a specific day. The estimated COVID-19 cases in the rest of the world other than China on 31 March were 1,000,000 and the actual reported figure was 823,626 on this date as published by WHO.

The Akaike Information Criterion (AIC) model selection (Roda et al., 2020) used for comparing the standard SIR and SEIR frameworks derives the equation

$$AIC=-2\text{ln}\left(\text{L}\left({\hat{\theta }}_{\text{MLE}}\right)\right)+2\text{K}$$

where K is the number of parameters to be estimated, N is the number of time points and the L($\hat{\theta }$_MLE) is the maximum expected value. The Akaike information criterion was applied based on uniform distributions for each one of the parameters.

$$\Delta \text{i}=AI{C}_{\text{i}}\underset{i}{-\min }AI{C}_i$$

Using the calibration results of SIR and SEIR models, the corrected Akaike Information Criterion AIC_c calculated was

$$AI{C}_C=AIC+\frac{2K(K+1)}{N-K-1}$$

The numerical difference established using the data was sufficiently large and shows predictions using more complex models like SEIR have a disadvantage over a simpler model like SIR.

PASSA-ANFIS model (Al-qaness et al., 2020) is an improved adaptive neuro-fuzzy inference system (ANFIS) which uses an enhanced flower pollination algorithm (FPA) and the Salp Swarm algorithm (SSA). The purpose of SSA is to improve FPA to avoid its drawbacks (i.e., getting trapped at the local optima) thereby improving the performance of ANFIS by determining the parameters of ANFIS using FPASSA.

Patient information based algorithm [ 26] was derived for estimating the death rate of COVID-19 considering the time from severe illness. The equation was defined as

$$\text{D}=\mathrm{M\mu xW\mu }+\mathrm{M\mu }-\mathrm{\sigma x W\mu }-\mathrm{\sigma }+\mathrm{M\mu }+\mathrm{\sigma \; x\; W\mu }+\mathrm{\sigma }+\mathrm{M\mu }+2\mathrm{\sigma \; x\; W\mu }+2\mathrm{\sigma }+\mathrm{M\mu }-2\mathrm{\sigma \; x\; W\mu }-2\mathrm{\sigma }$$

where D = death rate, Mμ = mortality rate with μ days, Wμ = weight with μ days gap, μ = Mean in the normal distribution, σ = Standard deviation.

The SLIAR epidemic model (Fanelli & Piazza, 2020) (susceptible, latently infected, symptomatic, and asymptomatic infectious and removed individuals) introduced has simple variation in the classic equation from incubation to the disease propagation. The SL₁L₂I₁I2A₁A₂R epidemic model incorporates an Erlang distribution of times of sojourn in incubating, symptomatic and asymptomatic infectious compartments, and the equation was

$$S=\frac{\epsilon L_1}{\beta (\eta L_2+I_1+I_2+\xi \left(A_1+A_2\right))}=:\mathrm{\Psi }\left(\mathbf{I}\right),$$

ARIMA time series model (Benvenuto et al., 2020; Ceylan, 2020; Ting Cao et al., 2020) was used to determine the overall prevalence of COVID-19 in Italy, Spain, and France. The data of COVID-19 estimated the conformed cases on 25th April as 196,520–229,147 in Italy, 204,755–257,497 in Spain, and 140,320–159,619 in France. The actual values reported on this day were Italy 195,351 Spain 223,759 and in France 124,114.

A simple linear regression analysis (Ghosal et al., 2020) was used in the prediction of cases in India. This model predicted a death toll around 467 by April 30, 2020 and the actual reported was 1074.

The epidemic model SEIRQ (Susceptible, Exposed, Infective, Recovered) (Hu et al., 2020) (Zengyun Hu) used in prediction of the disease variations of Guangdong projected 1589 on May 13, 2020.

The mathematical model (Vega, 2020) based on Systems dynamics methodology following the SIR model has four variables that represent hospital capacity, general contacts, contacts with infected and deaths. The model was given in the following form.

$$\frac{dS}{dt}=-\frac{\beta Ci}{C}$$

$$\frac{dS}{dt}=-\frac{\beta C}{it}-\frac{I}{Dd}\square (1-Fr)$$

$$\frac{dR}{dt}=\frac{1}{dt}\square (1-Fr)$$

$$\frac{dR}{dt}=\frac{1}{Dd}\square \left(Fr\right)$$

where $it$ - incubation time, I-infected, β – infectivity, Dd-disease duration, Fr – fatality rate.

The compartmental mathematical model (Ndairou et al., 2020) that have taken into account the super-spreading phenomenon of individual and while doing so, the constant total population size N is subdivided into eight epidemiological classes such as susceptible class (S), exposed class (E), symptomatic and infectious class (I), super-spreaders class (P), infectious but asymptomatic class (A), hospitalized (H), recovery class (R), and fatality class (F) and derived the following equation

$$\text{D}\left(\text{t}\right)\text{:}=\mathrm{\delta iI}\left(\text{t}\right)+\mathrm{\delta pP}\left(\text{t}\right)+\mathrm{\delta hH}\left(\text{t}\right)=\frac{\text{dF}\left(\text{t}\right)}{\text{dt}}$$

The transmissibility (Daw & El- Bouzedi, 2020) of COVID-19 in the northern African region was evaluated using the serial interval method, with a mean of 7.5 days and a standard deviation of 3.4 days. The number of infected individuals was expected to peak in early May 2020 (80 days since initiation) was 750–1200 in Northern Africa countries Egypt Libya, Tunisia, Algeria, Morocco.

The number of COVID-19 cases in India 30 days ahead was projected using a data-driven forecasting method like long short-term memory (LSTM) (Anuradha & Gupta, 2020) model and the curve-fitting have been used to estimate the possible number of positive cases of COVID-19.

The structure of LSTM consists of four gates. The input gate, forget gate, control gate, and output gate. The input gate was defined as ${\text{i}}_t=\sigma (W_i\times \left[h_{t-1},x_t\right]+b_i)$, the forget gate $f_t=\sigma (W_f\times \left[h_{t-1},x_t\right]+b_f)$, the control gate $C_t=f_t\ast C_{t-1}+i_t\ast \widetilde{C_t}$, and the output layer gate $o_t=\sigma \left(W_o\times \left[h_{t-1},x_t\right]+b_o\right)where\sigma$ is the activation function and the scale value was −1 to 1.

The LSTM model predicted 95,000 cases by the end of Apr 2020 and the actual reported was 82,862.

The hybrid autoregressive integrated moving average model coupled with a wavelet-based forecasting model (ARIMA-WBF) (Chakraborty & Ghosh, 2020) was used to define the real-time forecast and the critical risk factor. The data derived together from the ARIMA and WBF was used in forecasting the spread of the epidemic.

The Segmented Poisson (Zhang et al., 2020) model has interventions such as stay-at-home, lockdowns, quarantines, and social distancing. By fitting the daily available new cases projected the peak time of new cases, duration, final size, and the attack rate of the outbreak. The daily new cases as a function of time t coupled with power-law and an exponential law was determined. The study incorporated the government’s interventions (stay-at-home advises/orders, lockdowns, quarantines, and social distancing to make a statistical prediction on the turning point (the time that the daily new cases peak), the duration (the period that the outbreak lasts) and the attack rate (the percentage of the total population that will be infected during the outbreak) in the countries Canada, France, Germany, Italy, UK and USA and did the predictions using the equation

$${\mathit{C}}_{\mathit{total}}\approx \sum _{\mathit{t}=1=}^{\mathit{s}}{\mathit{\alpha }}_1{\mathit{t}}^{\mathit{\beta }1}{{\mathit{e}}^{-\mathit{\gamma }1}}^{\mathit{t}}+\sum _{\mathit{t}=\mathit{s}+1}^{\mathit{N}}{\mathit{\alpha }}_2{\mathit{t}}^{\mathit{\beta }2}{{\mathit{e}}^{-\mathit{\gamma }2}}^{\mathit{t}}$$

The Stochastic susceptible, exposed, infectious, treated, and recovered (SEITR) model (Otunuga & Ogunsolu, 2020) has the input options for multiple stages of infection, treatment, and the external fluctuations in the transmission.

$$ds=ds=\left(A-\beta S\sum _{j=1}^n(h_j{I}_j+{\epsilon }_j{T}_j)-ìS\right)dt-S\sum _{j=1}^n({\sigma }_j{I}_j+{\overline{\sigma }}_j{T}_j)\circ d{C}_j\left(t\right),$$

$$dE=\left(\beta S\sum _{j=1}^n(h_j{I}_j+{\epsilon }_j{T}_j)-\left(\pi +\mu \right)E\right)+S\sum _{j=1}^n({\sigma }_j{I}_j+{\overline{\sigma }}_j{T}_j)\circ d{C}_j\left(t\right),$$

$$d{I}_1=\left(\pi E-\left(\mu +{\delta }_1+{\rho }_1+{\tau }_1+{\psi }_1\right)I_1+{\varphi }_1{T}_1\right)dt-{\overline{\tau }}_1{I}_1\circ d\psi W_1\left(t\right)-{\overline{\psi }}_1{I}_1\circ d{Z}_1\left(t\right),$$ (6.2)

$$d{I}_k=\left({\rho }_{k-1}{I}_{K-1}-\left(\mu +{\delta }_k+{\rho }_k+{\tau }_k+{\psi }_k\right)I_k+{\varphi }_k{T}_k\right)-{\overline{\tau }}_k{I}_k\circ d{W}_k\left(t\right)-{\overline{\psi }}_k{I}_k\circ d{Z}_k\left(t\right)dt,k=\mathrm{2,3}\dots ,n,$$

$$d{T}_1=({\tau }_1{I}_1-\left(\mu +{\overline{\delta }}_1+{\gamma }_1+{\varphi }_1+{\eta }_1\right)T_1)dt+{\overline{\tau }}_1{I}_1\circ d{W}_1\left(t\right)-{\overline{\eta }}_1{T}_1\circ d\overline{z}₁\left(t\right),$$

$$d{T}_k=({\tau }_k{I}_k+{\gamma }_{k-1}{T}_{k-1}-\left(\mu +{\overline{\delta }}_k+{\gamma }_k+{\varphi }_k+{\eta }_k\right)T_k)dt+{\overline{\tau }}_k{I}_k\circ d{W}_k\left(t\right)-{\overline{\eta }}_k{T}_k\circ d\overline{z_j}\left(t\right),\text{k}=2\text{,}3\text{,}\dots \dots \text{,n}$$

$$dR=\left(\sum _{j=1}^n({\psi }_j{I}_j+{\eta }_j{T}_j)-\mu R\right)dt+\sum _{j=1}^n{\overline{\psi }}_j{I}_j\circ d{Z}_j\left(t\right)+\sum _{j=1}^n{\overline{\eta }}_j{T}_j\circ d\overline{z_j}\left(t\right),$$

where ‘∘’ denotes the Stratonovich integral and $C\left(t\right),W_i\left(t\right),Z_i\left(t\right),\overline{Z_i}\left(t\right),i=\mathrm{1,2},\dots ,n$, are the standard wiener process on a filtered probability space ($\text{Ω},$(F _t)_t≥0, ℙ). The initial process $x\left(t_0\right)=(S\left(t_0\right),E\left(t_0\right),I_1\left(t_0\right),\dots ,I_n\left(t_0\right),T_1\left(t_0\right),\dots ,T_n\left(t_0\right),R\left(t_0\right))$ is independent of. $C\left(t\right)-C\left(t_0\right),W_i\left(t\right)-W_i\left(t_0\right),Z_i\left(t\right)-Z_i\left(t_0\right)and\overline{Z_i}\left(t\right)-\overline{Z_i}\left(t_0\right),i=\mathrm{1,2},\dots ,n.$

The sequential Monte Carlo simulations (Kucharski et al., 2020) incorporated the transmission rate over time in the SEIR model. The variables such as symptomatic cases reported onsets of new cases, confirmed cases, and a binomial observation process for infection prevalence on evacuation flights was used in estimating the magnitude of temporal variability in transmission.

A computational method (Liu et al., 2020b) has been validated considering four sensitive social parameters such as contacts among the individual households and the transmission within families (H), schools (S) and, physical workplaces (W), public places and communities, such as stadiums, markets, squares, and organized tours (P).

$$\text{C}=r_H{c}^H+r_S{c}^s+r_W{c}^W+r_P{c}^P$$

The iSEIR model (Yuvan, Di, Gu, Qian & Qian, 2020) (individual Susceptible-Exposed-Infective-Removed) allows conducting simulations from the individual level located on the nodes of different community networks by incorporating its uncertainty through the differential equations.

$$S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)=1$$

The behavior distribution of S, E, I and R can be numerically simulated from the iSEIR model with properly specified values of parameters on population scales based on super-saturation phenomenon when both of the super saturation variables “E(t)” and “I(t)” drop and do not increase anymore.

The SIDARTHE model (Giulia et al., 2020) broadly considers eight stages of infection. S, susceptible (uninfected); I, infected (asymptomatic or pauci-symptomatic infected, undetected); D, diagnosed (asymptomatic infected, detected); A, ailing (symptomatic infected, undetected); R, recognized (symptomatic infected, detected); T, threatened (infected with life-threatening symptoms, detected); H, healed (recovered); E, extinct (dead). The interactions among these stages are explained and omitted the probability rate of becoming susceptible after having recovered from the infection.

$$S\left(t\right)+I\left(t\right)+D\left(t\right)+A\left(t\right)+R\left(t\right)+T\left(t\right)+H\left(t\right)+R\left(t\right)=1$$

The discrete-time SIR model (Anastassopoulou et al., 2020) has the dead individuals, based on the official counts for confirmed cases. The model suggested the cumulative number of infections to reach 180,000 (with a lower bound of 45,000) by February 29. The actual figure was around 80,026.

The control-oriented SEIR model (Casella, 2020) stresses the effects of delays and compares the outcome of different containment policies. The goal, in this case, is to reduce the reproduction number Rt, which is the number of persons an infectious person infects on average. The basic SEIR model was reformulated as follows

$$\frac{{\text{dE}}_{\text{t}}\left(\text{t}\right)}{\text{dt}}=-\mathrm{\epsilon }{\text{E}}_{\text{t}}\left(\text{t}\right)+\mathrm{\beta }\left(\text{u}\left(\text{t}\right)\right){\text{I}}_{\text{t}}\left(\text{t}\right)$$

$$\frac{{\text{dI}}_{\text{t}}\left(\text{t}\right)}{\text{dt}}=\mathrm{\epsilon }{\text{E}}_{\text{t}}\left(\text{t}\right)-\mathrm{\gamma }{\text{I}}_{\text{t}}\left(\text{t}\right)$$

$${\text{I}}_{\text{r}}\left(\text{t}\right)={\text{I}}_{\text{r}}\left(\text{t}-{\mathrm{\tau }}_{\text{m}}\right)$$

the number of reported infected cases Ir(t), the average delay of Tt days between the onset of infection and the moment the swab test was taken, delay of Tr days before getting the result, $\beta$(u) is an uncertain function, ε and γ, are uncertain constant parameters, Tt, Tr is uncertain parameters and ${\mathrm{\tau }}_{\text{m}}$ = Tt + Tr is the overall measurement delay.

A simple mathematical modeling approach (Tang & Wang, 2020) was used in the US and three selected states: New York, Michigan and California. Based on the analysis, estimated the cases to reach about 1.1 million by the end of June from the number 785,000 on April 20, 2020 in US. In Michigan Predicted the total estimated cases to reach about 45,000 by end of June. In New York estimated cases to jump from 2,48,000 on 20 Apr to 320,000 by the end of June. In California the total estimated cases by June end was 47,000.

The published mathematical models not only focused on Suspected, Infectious and Recovered and further developed several hypothesis in multiple directions representing a wide category of people who are infected, likely to be infected, suspected to be infected, and the people who may or may not have symptoms and contacts with a hospital, as well as people with confirmed laboratory tests and those who are misdiagnosed. The best way to compare these models at the moment is based on what we know about the disease and what the model’s inputs are, together with some skepticism and the assumptions that accompany with each one of the model.

Discussion

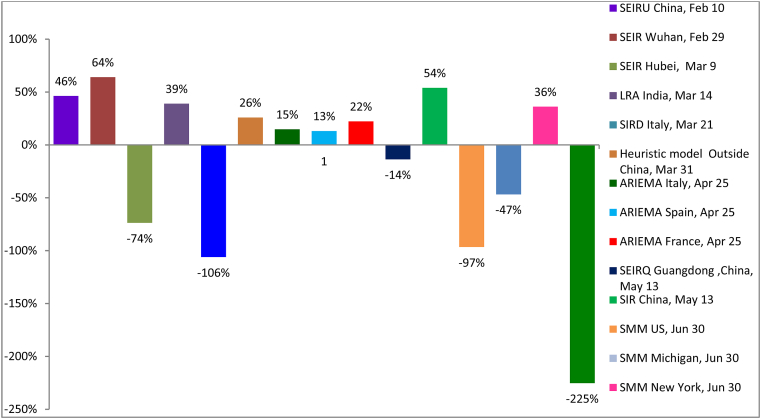
The majority of the models are the extended version of the SIR model accounting for several un-accounted parameters. The graphical data derived from some of these models is presented in Fig. 1 and the difference in prediction in Table 1. The SEIRU Model (Liu et al., 2020a) predicted three different probable turning points. The turning point of the total reported and unreported cases on February 8 February 9, February 10, (day 41), was 79,400 with approximately 63,500 reported, 15,900 unreported, and this accounts to 54% of the prediction. The susceptible-exposed-infectious-recovered model (SEIR) (Li et al., 2020b) estimated that the epidemic will end up with a total of 39, 000 infections in Hubei whereas the actual number of confirmed infections differs by 74%. The Heuristic model (Koczkodaja et al., 2020) predicted 1,000,000 COVID-19 cases in the rest of the world other than China by 31 March and the actual number was 74 % of its prediction value. The SIRD (Fanelli & Piazza, 2020) predicted value in Italy on March 21st, 2020 was 26,000 whereas the actual figure was 53,578. The ARIMA model predicted in Italy, Spain, and France differs by 13–22% of prediction and the SEIRQ model prediction in Guangdong, China by 14%. Looking at the prediction and the data the ARIMA and SEIRQ model predictions are the models which are in < ± 15% range and the others has wide difference. The success of a model depends on the thought process of experts in the field which intern depends on understanding the disease and the inputs given. The numbers in the models should not be taken at face value without considering the accuracy of inputs given to conclude what specific interventions helped and what extent they differ from others. Over-reacting to a particular model and the claim does more harm than good hence a calculated risk-based approach is necessary.

Fig. 1.

Graphical representation of the anomalies in predictions.

Table 1.

Difference in predictions of covid-19 pandemic.

MODEL	COUNTRY	% (±) DEVIATION
SEIRU	China, February 10	46
SEIR	Wuhan, February 29	64
SEIR	Hubei, March 09	74
LRA	India, March 14	39
SIRD	Italy, March 21	106
Heuristic Model	Outside China, March 31	74
ARIMA	Italy, April 25	15
ARIMA	Spain, April 25	13
ARIMA	France, April 25	22
SEIRQ	Guangdong, China, May 13	14
SIR	China, May 13	54
SSM	US, June 30	97
SSM	Michigan	47
SSM	New York	26
SSM	California	225

Challenges

Projections are yet to happen importantly with the super spreaders and other likewise situations. The need of the hour is a computerised model that best represents simply the lowest difference between the data and predictions until then we need to continue our search with several hypotheses. The simplest models like SIR and SEIR are struggling due to not accounting the impact of super spreaders, public places such as schools, public transport, crowded workplaces apart from delay in providing medical attention etc. We need to have clear answers to the questions are they just statistical models like several others, what is the importance of the model, time frame involved, short term or mechanistic, the assumptions, scale of applicability and uncertainty involved. The present-day computer science based simulation technology is promising greatly in using innovative, data-driven mathematical tools to fight the virus effectively. The purpose of a model and the prediction are the part of Good Pandemic Prevention Practice (GPP) followed by every country in containing the pandemic. The accuracy of the data generated by distinguishing the diagnosed and non-diagnosed cases should be able to explain the gap between the infection dynamics and the spread of the outbreak. The predictions are thus solely depends on the parameters of the mechanistic models and the interventions. From the lowest level of creature to the human level, one can see the less and less available to the influences around them. Covid-19 or any other virus or bacteria can’t spread on its own. It is the human mobility which is empowered the virus the way it has now if we do not control it more consciously that it is happening, nature will end up controlling us.

Summary

The outcome of continuous efforts in projecting and employing different computer simulations and mathematical models undoubtedly helped the health authorities in understanding the possible impact due to potentially overwhelming COVID-19 cases, and in addressing the limitations with the medical resources, such as hospital beds, ventilators, and life saving medicines. Several countries succeeded in planning and mobilizing the huge resources well in advance with the aid of these models and could do all the preparations ahead of time in combating the spread of epidemic through absolute planning and implementing containment policies and procedures. The type of pandemic, its existence, mobility, and persistence are absolutely in the hands of human activities and every individual must be part of government and health agencies standard operating procedures in strictly following the Good Pandemic Prevention Practice (GPP).

Declaration of competing interest

The authors declare no conflict of interest.

Handling editor: Dr. J Wu