Determining the Stoichiometry of Small Protein Oligomers Using Steady-State Fluorescence Anisotropy

Abstract

A large fraction of soluble and membrane-bound proteins exists as non-covalent dimers, trimers, and higher-order oligomers. The experimental determination of the oligomeric state or stoichiometry of proteins remains a nontrivial challenge. In one approach, the protein of interest is genetically fused to green fluorescent protein (GFP). If a fusion protein assembles into a non-covalent oligomeric complex, exciting their GFP moiety with polarized fluorescent light elicits homotypic Förster resonance energy transfer (homo-FRET), in which the emitted radiation is partially depolarized. Fluorescence depolarization is associated with a decrease in fluorescence anisotropy that can be exploited to calculate the oligomeric state. In a classical approach, several parameters obtained through time-resolved and steady-state anisotropy measurements are required for determining the stoichiometry of the oligomers. Here, we examined novel approaches in which time-resolved measurements of reference proteins provide the parameters that can be used to interpret the less expensive steady-state anisotropy data of candidates. In one approach, we find that using average homo-FRET rates (k_FRET), average fluorescence lifetimes (τ), and average anisotropies of those fluorophores that are indirectly excited by homo-FRET (r_ET) do not compromise the accuracy of calculated stoichiometries. In the other approach, fractional photobleaching of reference oligomers provides a novel parameter a whose dependence on stoichiometry allows one to quantitatively interpret the increase of fluorescence anisotropy seen after photobleaching the candidates. These methods can at least reliably distinguish monomers from dimers and trimers.

Significance

Many proteins need to form an oligomeric complex to function. Finding out of how many subunits such complexes consist is a nontrivial experimental problem. Here, we explore the use of fluorescence anisotropy measurements in determining the oligomeric state of recombinant model fusion proteins carrying green fluorescent protein. Previously, the applicability of fluorescence anisotropy measurements has been limited by the necessity of measuring time-resolved anisotropy, which requires sophisticated instrumentation in addition to steady-state measurements. Here, we facilitate the analysis by demonstrating that only certain key parameters need to be determined by time-resolved measurements of suitable reference proteins. These key parameters can then be used in combination with inexpensive steady-state measurements of candidate proteins.

Introduction

A major fraction of soluble and membrane-bound proteins exists as non-covalent dimers or higher-order oligomers (1). Formation of these higher-order structures in a cell can support the functionality of a protein by enabling its allosteric regulation, allowing multivalent ligand binding, and forming active sites at the interfaces, transmembrane signaling, etc. (1, 2, 3). Oligomerization also provides evolutionary advantages, including a reduction of genome size and of transcriptional or translational errors (1,4). In Escherichia coli, ∼80% of the oligomers consisting of 2–12 subunits are homo-oligomers (1).

The oligomeric state or stoichiometry of proteins can be investigated by a variety of techniques. These include analytical ultracentrifugation, size exclusion chromatography (SEC), native polylacrylamide gel electrophoresis (PAGE), chemical cross-linking, and the determination of high-resolution structures (5,6). Förster resonance energy transfer (FRET) can be used to examine interactions between proteins that are labeled with a fluorophore or fused to a fluorescent protein (7, 8, 9). One advantage of FRET-based methods is that they are applicable to transmembrane proteins embedded in a lipid bilayer. To characterize the homo-oligomeric state of a protein complex, FRET between identical fluorophores (homotypic FRET (homo-FRET)) can be employed. In homo-FRET, the extent to which the plane of polarization of the exciting irradiation changes during fluorescence depends on the number of subunits and can be measured via changing fluorescence anisotropy. Thereby, the anisotropy decreases with the increasing number of interacting fluorescent proteins depending on the spatial orientation of fluorescence donors and acceptors (10). Several applications have been presented in which homo-FRET has been used to gauge protein oligomerization. For example, homo-FRET was used to visualize protein clustering in vivo in which glycosylphosphatidylinositol-anchored proteins form clusters with an average size of more than two subunits (11, 12, 13). A large fraction of the epidermal growth factor receptor was found to dimerize in the plasma membrane with a small fraction of higher-order oligomers detected after stimulation with its ligand (13,14). Other applications of homo-FRET included an examination of the assembly of fluorescent proteins conjugated to scaffold-forming oligonucleotides (15,16) suggested the formation of higher oligomers of the serotonin_1A receptor in eukaryotic membranes (17) and characterized the oligomerization of fluorescently labeled lysozymes on the surface of large unilamellar vesicles, possibly up to a hexameric state (18).

The investigation of the oligomeric state of a fluorescently labeled protein requires the determination of the homotransfer rate by time-resolved anisotropy measurements on a nanosecond timescale (19). The model of Runnels and Scarlata connects these data to steady-state fluorescence anisotropy in the determination of the extent of protein oligomerization (10). The impact of homo-FRET on anisotropy can also be assessed by fractional fluorescence labeling of an oligomeric complex (17,18). It has thus been proposed by Yeow and Clayton (20) that the stoichiometry of a protein complex can be derived from steady-state anisotropy measurements gathered at different stages of fractional labeling or, conversely, fractional photobleaching. However, the applicability of the fractional labeling via photobleaching approach to the determination of the oligomeric state of a broad range of proteins has been unclear.

Here, we sought to improve the usefulness of fluorescence anisotropy-based approaches for investigating the stoichiometry of protein oligomers. As model systems, we have chosen covalently fused GFP moieties as well as non-covalently assembling coiled-coil domains. Coiled-coil domains drive the interaction of many proteins to dimers and higher oligomers (21). The repetitive sequence pattern of α-helical coiled coils is characterized by a heptad repeat motif (abcdefg) (22) in which hydrophobic residues on positions a and d form the hydrophobic interface, whereas polar residues at e and g positions support the interface by electrostatic interactions (23,24). To test our method, we use a group of de novo designed coiled-coil peptides with various oligomeric states (coiled-coil dimer (CC-Di), coiled-coil trimer (CC-Tri), coiled-coil tetramer (CC-Tet), coiled-coil pentamer (CC-Pent), etc.) (25,26) whose stoichiometry has been experimentally determined after fusing them to green fluorescent protein (GFP) (27). Crucially, we delineate ways to determine the oligomeric state from steady-state fluorescence anisotropy measurements with a minimal need of data from a more expensive time-resolved instrument. The new approach confirms the stoichiometries of the dimeric leucine-zipper GCN4 transcription factor and of its trimeric variant, GCN4-pII (22,28, 29, 30). In addition, they indicate the heptameric structure of ph3a, a novel designed coiled coil. The facilitated evaluation of steady-state fluorescence anisotropy measurements is expected to expand the future use of fluorescence anisotropy analysis in the determination of protein stoichiometries.

Theory

Determining the stoichiometry of a protein oligomer from steady state and time-resolved fluorescence anisotropy

Steady-state fluorescence anisotropy (r_SS) is experimentally determined as the following:

$$r_{SS}=\frac{I_{\parallel }-G\times I_{\perp }}{I_{\parallel }+2\times G\times I_{\perp }},$$ (1)

where $I_{\Pi }$ and $I_{\perp }$ are the fluorescence intensities measured in the parallel and perpendicular orientations relative to the plane of polarized excitation light, respectively. The grating factor, G, is a calibration factor that describes the ratio of detection sensitivity for parallel and perpendicularly polarized light. Any depolarizing effect, such as molecular rotation, leads to a decrease in anisotropy. Also, homo-FRET, i.e., FRET between the same type of fluorophore, will also lead to a decrease in anisotropy. The extent of homo-FRET depends on the spatial orientation and separation (R) between the donor and acceptor fluorophores. At the Förster distance, R₀, the homo-FRET efficiency between a pair of fluorophores is 50%. For GFP-GFP homotransfer, the Förster distance R₀ is 4.65 nm (11,31). The efficiency of homo-FRET depends on the homotransfer rate k_FRET:

$$k_{FRET}=\frac{1}{\tau }\times {\left(\frac{R_0}{R}\right)}^6,$$ (2)

where τ is the fluorescence lifetime that can be determined from the fluorescence intensity decay. R is the average distance between the fluorophores.

The homotransfer rate k_FRET can be obtained from time-resolved anisotropy measurements, which allows the discrimination between an anisotropy decrease caused by fluorophore rotation and a decrease caused by homo-FRET. Briefly, for slowly rotating large fluorescent proteins, such as GFP, the rotational correlation time ϕ_GFP (ϕ_GFP ≈ 20 ns (32)) is much longer than its fluorescence lifetime τ (τ ≈ 2.5 ns). In this case, rotational effects can be disregarded, and the time-resolved anisotropy decay r(t) is dominated by the homo-FRET rate (19,33). Thus, r(t) can be written as the following:

$$r\left(t\right)=\left(r_0-r_{\infty }\right)\times e^{\left(-2\times k_{FRET}\times t\right)}+r_{\infty },$$ (3)

where r₀ is the maximum initial anisotropy and r_∞ is the anisotropy for time t going to infinity. The average distance R between fluorophores can be determined from k_FRET, τ, and R₀ according to Eq. 2.

In a cluster of spatially close fluorophores, the steady-state anisotropy r_SS is composed of two parts: the anisotropy of the originally excited donor, r₁, plus the anisotropy of the acceptors being excited via homo-FRET, r_ET (10,13). In the case of monomeric GFP, r₁ ≈ 0.3 (34,35). The value of r_ET is dictated by the relative spatial orientation of the dipoles of the interacting fluorophores (10). This value is close to zero for small, fast-rotating fluorophores such as isolated fluorescein (10) but can be significant in slowly rotating fluorescent proteins such as GFP and higher-order complexes of GFP (13).

Runnels and Scarlata (10) quantified the contributions of donor and acceptor anisotropies (r₁ and r_ET) to the steady-state anisotropy r_SS(N) for a cluster containing N subunits. They showed that r_SS is inversely proportional to N.

$$r_{SS}\left(N\right)=r_1\times \frac{\left(1+k_{FRET}\times \tau \right)}{\left(1+N\times k_{FRET}\times \tau \right)}+r_{ET}\times \frac{\left(N-1\right)\times k_{FRET}\times \tau }{\left(1+N\times k_{FRET}\times \tau \right)}$$ (4)

Thus, N is experimentally obtained by measuring the steady-state anisotropy r_SS as well as obtaining k_FRET and τ from time-resolved measurements. r₁ is determined for the monomeric fluorophore, and r_ET is obtained by fitting Eq. 4 for reference molecules with known N. Thereby, it is assumed that r_ET is similar for fusion proteins with comparable type of fluorophore, spatial arrangement of the subunits in the oligomer as well as its symmetry, and sequence and length of linkers; these molecular properties are referred to as structural composition in the remainder of the manuscript.

Determining the stoichiometry of a protein oligomer from steady-state fluorescence anisotropy in combination with photobleaching data

Estimating stoichiometries from a single anisotropy value can be ambiguous because many factors influence the anisotropy. To circumvent this, Yeow and Clayton (20) proposed that one can estimate the oligomeric state N from the steady-state anisotropies of a fluorophore cluster after fractional labeling or fractional photobleaching of its subunits. Fractional labeling or photobleaching of a cluster of fluorophores can be envisioned as the gradual addition or removal of subunits from the cluster. Thus, photobleaching reduces homo-FRET and thereby increases steady-state anisotropy r_SS, whereas fractional labeling would have the opposite effect. In these cases, the changes in anisotropy only arise from changes due to homo-FRET. A simplified model was proposed in which the number of subunits N in the oligomer can be estimated from the response of steady-state anisotropy to fractional photobleaching (20). Accordingly, for a two-state model in which a monomer is in equilibrium with an N-mer, the minimum stoichiometry can be derived from the steady-state anisotropy as a function of the fraction of photobleached molecules, x (which is equivalent to 1−f, where f corresponds to fractional photolabeling in Eq. 8 of the original publication (20)) using

$$r_{SS}\left(x,N\right)=r_1\times \left(f_{non}+\left(1-f_{non}\right)\times x^{\left(N-1\right)}\right)=$$

$$=r_1\times f_{non}+r_1\times \left(1-f_{non}\right)\times x^{\left(N-1\right)}\text{ ,}$$ (5)

where the parameter f_non originally represented the fractional fluorescence from noninteracting fluorophores in the two-state monomer/N-mer equilibrium. The anterior term of the function, r₁ × f_non, describes the steady-state anisotropy of unbleached samples (where x = 0). The term r₁ × (1 − f_non) × x^{(N − 1)} represents the changes in anisotropy at different stages of photobleaching (0 < x < 1) of the higher-order N-mers, respectively. See Supporting Materials and Methods, Theory for a graphical depiction. This formalism was derived from purely geometrical considerations, and a particular weakness of it is the erroneous prediction that the anisotropy of any complex with a stoichiometry higher than one is zero, including fully assembled (f_non = 0) nonphotobleached (x = 0) clusters (20). As a consequence, applying Eq. 5 is expected to produce incorrect numbers for N; particularly when fully assembled (f_non = 0), clusters are investigated. Even assuming a partially assembled complex (f_non > 0), the anisotropy of nonbleached samples (x = 0), as predicted by Eq. 5, would technically not depend on stoichiometry N. This questions the original assumption that f_non represents the fractional fluorescence from noninteracting fluorophores.

To combine the approach of Runnels and Scarlata with that of Yeow and Clayton, we modified Eq. 5 by replacing f_non with the term$\frac{1+a}{1+N\times a}$. Hence, rather than representing the fraction of monomer only as it did for Yeow and Clayton, for us it represents the nonphotobleached component and needs to be modified with the reduced anisotropy of the complex (i.e., Eq. 4, where r_ET ∼ 0). The term $\frac{1+a}{1+N\times a}$ (with a = k_FRET × τ) reinstates the known inverse dependence of steady-state anisotropy of unbleached samples on N, Eq. 4 (10). The detailed derivation of this modification can be found in Supporting Materials and Methods, Theory. With this modification, the anisotropy as a function of fractional photobleaching x and the number of subunits N is given by the following:

$$r_{SS}\left(x,N\right)=r_1\times \frac{1+a}{1+N\cdot a}+r_1\times \left(1-\frac{1+a}{1+N\times a}\right)\times x^{\left(N-1\right)}=$$

$$=r_1\times \left(\frac{1+a}{1+N\times a}+x^{\left(N-1\right)}\times \frac{a\times \left(N-1\right)}{1+N\times a}\right).$$ (6)

Using Eq. 6 and reference constructs of known N, we determine the parameter a empirically by fitting the steady-state anisotropy data, r_SS, acquired at different stages of photobleaching x, as described in Results. The empirically determined a then allows us to estimate N for clusters of unknown stoichiometry after recording r_SS at different values of x. Because the parameter a is empirically determined and reflects the energy transfer rate of FRET and thus the spatial separation and orientation of fluorophores interacting via homo-FRET, its value is thought to depend on the detailed structural composition of the complex. For Eq. 6, we make the premise that the fluorescent reporter is correctly folded and that the majority of oligomerizing proteins shares a defined stoichiometry. The advantage of this method is that the unknown stoichiometry of a protein assembly can be determined from r_SS, provided that time-resolved anisotropy data can be obtained for an appropriate set of reference proteins of known stoichiometry.

Materials and Methods

Plasmid design and construction

Constructs of sfGFP are based on pET28a plasmids (Novagene, Darmstadt, Germany). The synthetic reading frame (BioCat, Heidelberg, Germany) that was used to construct 1xGFP contained 1) a variant of the Nano-tag (DVEAWLGAR) for immunoblot detection (36); 2) sfGFP (37); 3) the 22-aa-long glycine- and serine-based flexible “linker A”; 4) a TEV protease recognition site (ENLYFQG) (38); 5) a 26-aa-long glycine- and serine-based flexible “linker B”; 6) a cysteine for potential labeling; 7) a variant of the Flag-tag (YKGDYKDHDG); and 8) a polyhistidine tag (xtHis; HNHHGHHNHHHHHH) (Fig. S1). Sequences coding for all elements are separated by unique restriction sites.

Construct 2xGFP was generated by cutting an XbaI-PstI fragment from 1xGFP and inserting it into 1xGFP, previously cut with SpeI and PstI. 3xGFP, 4xGFP, and 5xGFP constructs were made similarly by successively inserting XbaI-PstI fragments.

sfGFP-GCN4-p1, sfGFP-GCN4-pII, and sfGFP-ph3a were generated by replacing the TEV site of 1xGFP by the respective coiled-coil sequences using NheI and BamHI sites. Additionally, the N-terminal Nano-tag was replaced by an N-terminal xtHis sequence via restriction-free, PCR-based cloning.

Plasmids encoding constructs EGFP, EGFP-CC-Di, EGFP-CC-Tet, and EGFP-CC-Pent (27) were a kind gift from Ajitha Cristie-David and Neil Marsh, University of Michigan, Ann Arbor, MI.

Protein expression and purification

Concatemers

Competent E. coli BL21 pLysS were transformed with the respective plasmids. The transformed cells were grown overnight at 37°C on Luria-Bertani (LB) agar with 35 μg/mL kanamycin (Kan). Individual clones were used to inoculate 5 mL LB medium containing 35 μg/mL Kan to be grown overnight under rotation for 18 h at 37°C. After diluting an overnight culture at 1:100 in LB medium with 35 μg/mL Kan and incubation at 140 rpm at 37°C until OD₆₀₀ = 0.5, expression was induced by the addition of 250 μM isopropyl-β-D-thiogalactopyranoside. After 1 h, cells were harvested by centrifugation at 4°C and washed twice with phosphate-buffered saline (PBS). Cell pellets were stored at −20°C. Protein purification was performed at 4°C or on ice. Concatemers were purified by immobilized metal ion affinity chromatography (IMAC) that was followed by anion exchange chromatography (AEX). Cell pellets were thawed and resuspended in concatemer lysis buffer (50 mM NaH₂PO₄-Na₂HPO₄ buffer (pH 8), 300 mM NaCl, 0.5 mM β-mercaptoethanol, and 1 mM EDTA). Cell lysis was performed via sonication. Cell debris was separated from the green soluble proteins via centrifugation at 20,000 × g. EDTA in the supernatant was masked by adding 20 mM MgCl₂. After 1 h and mild shaking, the supernatant was incubated with Ni-NTA resin (Macherey-Nagel, Düren, Germany) and equilibrated with concatemer IMAC buffer (50 mM NaH₂PO₄-Na₂HPO₄ buffer (pH 8), 20 mM NaCl, and 0.5 mM β-mercaptoethanol) for at least 16 h under constant rotation. The slurry was then poured into a column for protein elution. The column was washed with five bed volumes of concatemer IMAC buffer containing 20 mM imidazole and subsequently with one bed volume of IMAC buffer without imidazole. For elution, imidazole concentration was gradually increased until the GFP protein visibly dissociated from the resin where imidazole concentration was kept constant until elution appeared complete (250 mM maximum imidazole concentration). The eluate was dialyzed against concatemer AEX buffer (50 mM Na_XH_XPO₄ buffer (pH 8) and 0.5 mM β-mercaptoethanol) for 24 h to eliminate NaCl and imidazole. The sample was then applied to Q Sepharose Fast Flow (GE Healthcare Bio-Sciences, Pittsburgh, PA) and equilibrated for 3 h. The slurry was poured into a column, washed with five bed volumes concatemer AEX buffer before the concentration of NaCl was gradually increased to 500 mM NaCl. Eluate containing the target protein was dialyzed against concatemer sample buffer (flow cytometry grade PBS (pH 7.4), 0.5 mM β-mercaptoethanol, 1 mM EDTA, and 0.05% sodium azide). Purified proteins were snap frozen with liquid nitrogen and stored at −80°C.

Coiled-coil constructs

Transformed E. coli BL21 (DE3) cells were grown overnight at 37°C on LB agar with 35 μg/mL Kan (sfGFP-based fusion proteins) or 100 μg/mL ampicillin (Amp) (EGFP-based fusion proteins). Inoculated overnight cultures were grown under rotation for 18 h at 37°C in 5 mL LB medium containing 35 μg/mL Kan (sfGFP) or 100 μg/mL Amp (EGFP). After diluting an overnight culture at 1:100 in 2xYT medium (16 g/L tryptone, 10 g/L yeast extract, and 5 g/L NaCl) with 35 μg/mL Kan (sfGFP) or 100 μg/mL Amp (EGFP) and incubation at 140 rpm at 37°C until OD₆₀₀ = 0.8, expression was induced by the addition of 100 μM isopropyl-β-D-thiogalactopyranoside. The culture was incubated further for 18 h at 18°C at 140 rpm. Cells were harvested by centrifugation at 4°C and washed twice with PBS. Cell pellets were stored at −20°C. Protein purification and preparation was performed at 4°C or on ice. Cell pellets were thawed and resuspended in coiled-coil lysis buffer (50 mM HEPES (pH 7.5), 1 M urea, 300 mM NaCl, 25 mM imidazole, 5% glycerol, EDTA-free protease inhibitor, and 1 mg mL⁻¹ lysozyme). Cell lysis was performed via sonication. Cell debris was separated from soluble proteins via centrifugation at 20,000 × g. The supernatant was incubated with Ni-NTA resin and equilibrated with coiled-coil lysis buffer for at least 16 h under constant rotation. The suspension was then washed with 10 bed volumes of coiled-coil lysis buffer. Proteins were eluted using coiled-coil elution buffer (50 mM HEPES buffer (pH 7.5) containing 300 mM NaCl, 500 mM imidazole, and 5% glycerol) and dialyzed against the coiled-coil sample buffer (25 mM HEPES buffer (pH 7.5), 100 mM NaCl, 30% glycerol, and 2 mM EDTA). Purified proteins were frozen in liquid N₂ and kept at −80°C. We noted that the set of EGFP-based coiled-coil fusion proteins with their short linkers gave higher expression yield and less batch-to-batch variance in steady-state anisotropy than our sfGFP-based proteins. A future system of reference concatemers may thus be potentially based on EGFP with short linkers.

SEC

200 μL of a purified protein sample at concentrations of 20–140 μM were loaded onto a Superdex 200 10/300 separation column (GE Healthcare Bio-Sciences, Pittsburgh, PA). For equilibration and elution, 25 mM HEPES buffer (pH 7.5), 100 mM NaCl, and 2 mM EDTA was used. Proteins were eluted at 0.3 mL min⁻¹. UV₂₈₀ and fluorescence intensity (λ_ex = 488 nm; λ_em = 520 nm) were detected. The column was calibrated with standard protein solutions (β-amylase, 200 kDa; alcohol dehydrogenase, 150 kDa; bovine serum albumin, 66 kDa; carbonic anhydrase, 29 kDa; and cytochrome C, 12.4 kDa) (Merck, Darmstadt, Germany) to obtain the calibration curve to determine the molecular weights shown in the figures.

Polyacrylamide gel electrophoresis

Purified proteins were diluted to 1 μM in sodium dodecyl sulfate (SDS) sample buffer and electrophoretically separated on a 10% SDS-PAGE. 10% Native PAGE gel was used without SDS denaturation. PAGE gels were stained with Coomassie Brilliant Blue G250 (Thermo Fisher Scientific, Waltham, MA). Uncropped gel images are displayed in Fig. S7.

Steady-state anisotropy

Purified protein samples were diluted to 2 μM in 1 mL sample buffer. The sample buffer for sfGFP concatemers (1xGFP to 5xGFP) was flow cytometry grade PBS (pH 7.4), 0.5 mM β-mercaptoethanol, 1 mM EDTA, and 0.05% sodium azide. Purified coiled-coil fusion proteins were diluted in 25 mM HEPES (pH 7.5), 100 mM NaCl, 2 mM EDTA, and 30% glycerol.

To determine the steady-state anisotropy, samples were illuminated with polarized light, and the parallel and perpendicular components of emitted fluorescence (λ_ex = 488 nm; λ_em = 520 nm) were recorded with a microplate reader (POLARstar; BMG Labtech, Ortenberg, Germany). The G-factor required to calculate anisotropy was determined with the aid of fluorescein isothiocyanate as a reference. All fluorescence measurements were done in 96-well plates (nontreated back plates, Nunc; Thermo Fischer Scientific).

Photobleaching

Samples were irradiated with a 445 nm laser for repeated periods of 10–15 min. The laser power was held constant at 300 mW, as determined by an optical power meter (PM120; Thorlabs, Newton, NJ). The beam waist is 4 mm × 5 mm, yielding a power density of 15 kW/m². Accounting for the fact that only 34% of the light is absorbed, this corresponds to a light dose per hour of irradiation at 300 mW of 1.75 × 10⁷ J/m². After each bleaching step, steady-state anisotropy values were determined as described above. To reduce the day-to-day variability of anisotropy values, the data were corrected as follows: each sample was split into six to nine technical replicates for irradiation. In parallel, we measured three technical replicates without irradiation. First, the means of the nonirradiated controls were subtracted from individual values of irradiated samples. Second, the total mean of all nonirradiated samples was added back to the values obtained in the previous step. To obtain the fraction of inactive fluorophores x, the residual intensity of nonpolarized fluorescence was measured (λ_ex = 488 nm; λ_em = 520 nm) (FLUOstar; BMG Labtech, Ortenberg, Germany). The fraction of inactive fluorophores x was then calculated as residual fluorescence intensity divided by the initial intensity before photobleaching. We noticed a slight unexpected but systematical anisotropy increase upon gradual photobleaching for all investigated proteins. The increase could be visibly detected for GFP monomers as their behavior should inherently be stagnant. The monomeric increase can be described as an exponential function r_SS(x) = o × e^{(p × x)} + q. For sfGFP, r_SS(x) = 0.011 × e^{(0.974 × x)} − 0.012. In case of EGFP, r_SS(x) = 0.001 × e^{(4.056 × x)} − 0.003. To correct the bleaching data of concatemers and oligomers, we corrected Eq. 6 by simply adding this exponential relation to r_SS(x, N).

Time-resolved anisotropy and fluorescence lifetime measurements

To measure time-resolved anisotropy and fluorescence lifetime of various GFP fusion constructs, samples were measured at a concentration of 2 μM in their respective buffer systems for sfGFP (PBS) and EGFP (HEPES buffer) fusion proteins. For excitation, a polarized and pulsed 468 nm laser was used to excite the sample. Subsequently, the emitted fluorescence with polarization parallel and perpendicular to the excitation laser were recorded with a FLS1000 spectrometer (Edinburgh Instruments, Livingston, UK) equipped with photomultipliers. To resolve the time-dependent anisotropy decay, time-correlated single photon counting detection was employed (Time Harp 260; PicoQuant, Berlin, Germany). An Atto488 dye solution was used to calibrate the instrument. The grating factor, G, which corrects for the detection efficiencies for parallel and perpendicular lights, was found to be 0.78. The obtained time-resolved anisotropy data were fitted with Eq. 3. An example is shown in Fig. S4.

The fluorescence lifetime was obtained by reconvolution fitting. Briefly, first both the parallel and perpendicular florescence intensity decays, were combined together. The combined intensity decay was then fitted with a monoexponential function, convoluted with the instrument response function (IRF) to obtain the fluorescence lifetime of the various GFP fusion proteins. IRF was determined by using a scattering solution of colloidal silica (Fig. S5).

Total-internal-reflection-fluorescence-based photobleaching experiment of sfGFP ph3a peptide

A sparsely (∼5%) biotinylated polyethylene-glycol-coated glass surface was first treated with streptavidin (0.3 mg/mL). After wash, 1:1000 diluted biotinylated anti-GFP antibody (Thermo Fisher Scientific) was allowed to bind to streptavidin. After removing excess of antibody, 0.2 μM of sfGFP-ph3a was incubated with bound antibody surface for 20 min. Unbound ph3a complexes were subsequently washed with PBS buffer (Fig. S6).

A home-build total internal reflection fluorescence (TIRF) setup equipped with 488 nm laser and EMCCD camera-based detector was used to induce the bleaching and record the time points to find the bleaching steps. With a laser power of 2.5 mW after fiber and exposure time of 50 ms, data were recorded in each frame after every 200 ms.

Images were processed with ImageJ software and further analyzed with custom-written code in MATLAB (The MathWorks, Natick, MA) to get the distribution and time traces for bleached molecules (Fig. 5 I). To extract the bleaching steps accurately in the bleaching trace, we used L₁ regularization (39) to smooth the signal of the entire trace and Kalafut-Visscher algorithm (40) to find the steps with a penalty factor of 9.

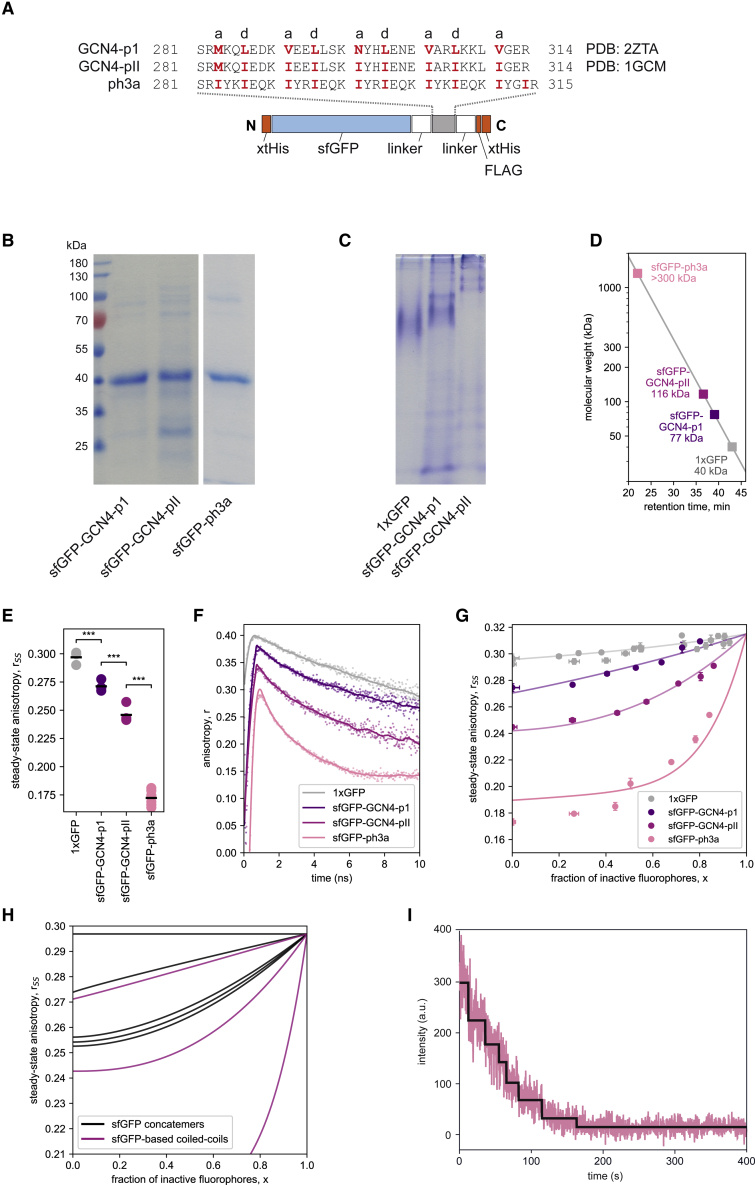
Figure 5.

Characterization of naturally occurring GCN4-based coiled-coil constructs and the multimeric ph3a. (A) Amino acid sequences of the coiled-coil elements of the GCN4-p1, GCN4-pII (30), and de novo designed peptide ph3a. The sequences were expressed in the context of a modular sfGFP-based fusion protein (see Fig. S1). (B) SDS-PAGE and (C) native PAGE separation of GCN4-based fusion proteins (2 μM in loading buffer). Note that the uncropped gel image shown in Fig. S7 reveals a very minor fraction of aggregates formed by sfGFP-GCN4-pII that does not enter the gel. The other proteins tested here, however, did not show any signs of aggregation, nor is degradation detected. Thus, the influence of such artifacts on subsequent anisotropy measurements can essentially be excluded. (D) Molecular masses derived from SEC profiles (see original elution profiles in Fig. S3). (E) The steady-state and (F) time-resolved anisotropies of GCN4 coiled-coil fusion proteins (2 μM). Measurements and evaluation were done as in Fig. 2. (G) Steady-state anisotropy was measured as a function of the fraction of photobleached fluorophores, as determined from the fluorescence intensities measured after various periods of irradiation. The data were fitted with Eq. 6. (H) A comparison of fits of photobleaching data between the sfGFP concatemers (black) and sfGFP-based GCN4 constructs (violet). For better comparability, all anisotropy values were corrected for the apparent increase of monomer values in the wake of photobleaching. (I) Number of subunits in sfGFP-ph3a assembly directly probed with TIRF microscopy. sfGFP-ph3a was immobilized on the polyethylene-glycol-passivated glass surface via anti-GFP antibody. Bleaching was induced with a 480 nm laser. For clarity, bleaching steps as detected by fitting the gradual decrease of GFP fluorescence are represented by a black line. We found seven bleaching steps that are consistent with a heptameric structure of the ph3a protein (also, see Fig. S6). To see this figure in color, go online.

Fluorescence correlation spectroscopy

Fluorescence correlation spectroscopy (FCS) measurements were performed to obtain the diffusion coefficients for the sfGFP concatemers (Fig. S2, blue data points) and to check the stability of assembled fusion proteins (Table S2). Previously described custom-build confocal microscope was used equipped with synchronized pulsed 482-nm excitation and time-correlated single photon counting capability (41). Samples were excited with ∼6 μW laser power, which minimizes photobleaching during the measurements. Data analysis was performed with PAM, a custom-written software in MATLAB (The MathWorks) (42). Obtained FCS curves were fitted with the three-dimensional diffusion model function to obtain diffusion times (τ_D${\tau }_D$). The diffusion coefficient D is then quantified via the following equation:

$$D=\frac{w_0^2}{4{\tau }_D},$$ (7)

where w₀ is the radial diameter of the confocal volume.

Einstein-Stokes model for spherical particles in a classical fluid

For spherical particles (at the very low Reynolds numbers), the diffusion coefficient is a function of absolute temperature, the viscosity of the medium, and the particle size (43):

$$D=\frac{k_B\times T}{6\pi \times \eta \times R_M}\text{ ,}$$ (8)

where k_B is Boltzmann’s constant, T is absolute temperature, η is viscosity, and R_M is the molecular radius that equates the cube root of the particle volume, ∛V_M.

To evaluate whether concatenated GFP domains are forming globular or elongated structures, we compared the measured diffusion coefficients with the hypothetical behavior of globular GFP domains. For a globular protein, the complex volume V_M is proportional to the number of GFP domains in the concatemer, N. Therefore, V_M can be replaced by N. For comparing concatemer systems of different stoichiometries, N can be written as N = (MW − MW_non)/MW_rep. Here, MW describes the molecular weight of the protein, MW_non is the molecular weight of nonrepeated elements, i.e., sequences used for protein identification and purification, and MW_rep is the molecular weight of one repeat domain, i.e., GFP and a spacer.

At constant T = 20°C and viscosity η (0.89 mPa for water at 20°C), the diffusion coefficient D of an idealized globular complex of concatenated GFP domains depends on MW according to Eq. 9:

$$D\left(MW\right)=D_1\times \frac{1}{\sqrt[3]{N}}=D_1\times \frac{1}{\sqrt[3]{\frac{MW-M{W}_{non}}{M{W}_{rep}}}}\text{ ,}$$ (9)

with D₁ as the diffusion coefficient of one single GFP moiety, MW as the molecular weight of the concatemer, MW_non as the molecular weight of nonrepetitive elements, and with MW_rep as molecular weight of repetitive elements.

To evaluate the stability of assembled sfGFP-GCN4-p1 and sfGFP-GCN4-pII proteins, the diffusion coefficients were determined after 2 min and after 90 min at a concentration of 1 nM (in PBS buffer containing 5% glycerol at room temperature) (Table S2). The observation that the diffusion coefficient, D, remains constant indicates that the oligomeric states are stable over the period of the measurement time. Increasing values for D would correspond to the dissociation of the dimer and trimer complexes into monomer and monomer/dimer, respectively.

Results

The aim of this study was to improve the usefulness of steady-state fluorescence anisotropy measurements for determining the oligomeric state of proteins. To this end, we determined the oligomeric states of three different sets of covalent or non-covalent protein assemblies in a classical way that requires the measurement of time-resolved anisotropy. The results were compared with those obtained using less expensive steady-state anisotropy instrumentation and analyzed using improved theoretical models.

Characterizing covalent and non-covalent GFP assemblies by fluorescence anisotropy

As a first test system, we engineered several GFP concatemers to serve as model oligomers with predefined stoichiometries. Similar constructs of concatenated GFP domains were used in the past to represent protein oligomers (35,44,45). The generated constructs are denoted as 1xGFP, 2xGFP, 3xGFP, 4xGFP, and 5xGFP and represent monomeric, dimeric, trimeric, tetrameric, and pentameric GFP fusion proteins, respectively. The GFP concatemers contain sfGFP domains connected by 53-aa-long glycine-serine-based flexible linkers and contain an extended polyHis-tag at the C-terminus for purification (Figs. 1 A and S1). The concatemers were expressed in E. coli and purified by metal chelate chromatography and ion exchange chromatography to near homogeneity as shown by SDS-PAGE (Fig. 1 B). The quantum yield of the sfGFP monomer, as determined from fluorescence measurements (λ_ex = 488 nm; λ_em = 512 nm) at a predetermined concentration equaled 0.70, which is close to the value from the literature (0.65 (37)). Thus, our sfGFP exists in a fully folded conformation. The diffusion coefficients of the concatemers, as assessed by FCS, decreased with an increasing number of GFP subunits, as expected (Fig. S2). We compared the experimental FCS data with predictions made on the grounds of the Einstein-Stokes equation for the diffusion of spherical particles in a classical fluid (43). The results suggest a slightly elongated shape of the different concatemers, in agreement with previous studies (35,44,45).

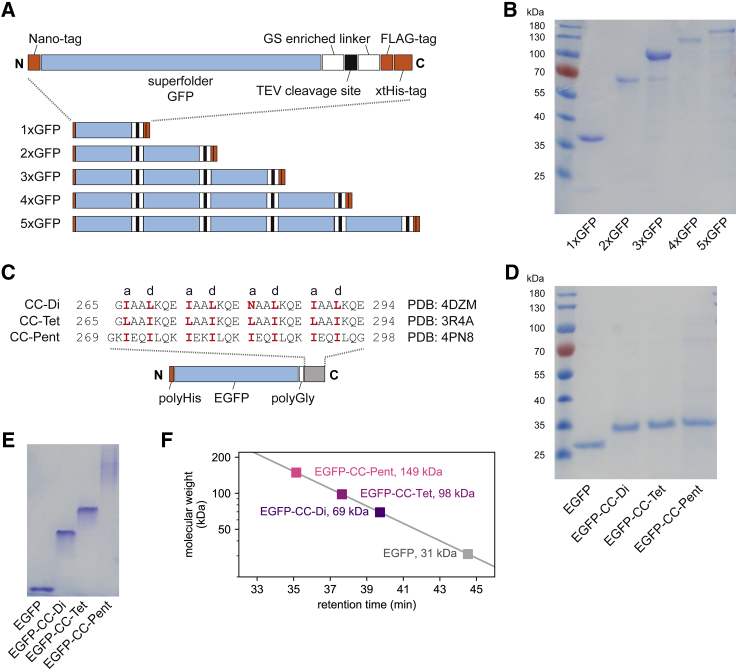
Figure 1.

Schematic structure of the test constructs and biochemical analysis of their stoichiometry. (A) Schematic structure of sfGFP concatemers. (B) SDS-PAGE of sfGFP concatemers (1 μM in loading buffer). (C) The amino acid sequences of de novo coiled-coil elements (25,26) linked to EGFP-based fusion proteins via short polyglycine linkers (27). (D) SDS-PAGE of the EGFP-based coiled-coil fusion proteins (2 μM). (E) EGFP-coiled-coil fusion proteins (2 μM) separated via native PAGE. We note that the uncropped gel image shown in Fig. S7 reveals a very minor fraction of aggregates formed by EGFP-CC-Pent that does not enter the gel. The other proteins tested here, however, did not show any signs of aggregation, nor is degradation detected. Thus, the influence of such artifacts on subsequent anisotropy measurements can essentially be excluded. (F) Derived molecular weights for EGFP-based coiled-coil fusion proteins from SEC profiles. The molecular masses were calculated relative to those of standard proteins. The data points represent ultraviolet or fluorescence intensity maxima, respectively (see details in Fig. S3). To see this figure in color, go online.

As a test system for non-covalent protein assembly, we used fusion proteins for which GFP is linked to coiled-coil domains with known oligomeric states. In these fusion proteins that were introduced by Cristie-David et al. (27), an EGFP is linked via a 6–9-aa glycine-based linker (Fig. 1 C) to various coiled-coil domains.

These coiled-coil domains were originally designed as de novo CC-Di, CC-Tet, and CC-Pent by Woolfson and co-workers (25,26). The previous characterization of these fusion proteins by SEC, ultracentrifugation, and mass spectrometry confirmed the expected dimeric structure for CC-Di, whereas CC-Tet turned out to be a trimer. Here, we will continue to refer to this construct as CC-Tet, although it is trimeric. The pentameric structure of CC-Pent could only be recovered after elongating the flexible linker to nine residues, which prevents its nonspecific aggregation (27). After expressing and purifying EGFP-CC-Di, EGFP-CC-Tet, and EGFP-CC-Pent along with the monomeric EGFP (Fig. 1 D), we could confirm their previously reported dimeric, trimeric, and pentameric structures, respectively, by native PAGE (Fig. 1 E) and SEC (Figs. 1 F and S3 A).

Fluorescence anisotropy can distinguish between subunit stoichiometries of GFP concatemers as well as fusion proteins of GFP and various coiled coils

Having expressed the test constructs, we examined to what extent we could differentiate between the different subunit stoichiometries via fluorescence anisotropy. The steady-state fluorescence anisotropy of our sfGFP concatemers, as measured at a protein concentration of 2 μM, decreased from the monomer (r_SS = 0.297) to the dimer (r_SS = 0.271) and trimer constructs (r_SS = 0.251) and then remained at similar levels for the tetrameric (r_SS = 0.250) and pentameric (r_SS = 0.254) proteins (Fig. 2 A; Table 1). The experimentally determined values for the monomeric construct thus resemble the theoretical value for GFP in solution (r_SS ≈ 0.29), as calculated from the Perrin equation (46) with parameters determined in the past (47). Time-resolved fluorescence anisotropies of our concatemers were recorded (Fig. 2 B) over a period of 10 ns, and the homo-FRET rates k_FRET (Fig. S4) as well as the average interfluorophore distance R were obtained by fitting the time-resolved anisotropy data according to Eqs. 2 and 3. The homo-FRET rate k_FRET (k_FRET,2xGFP = 0.055 ns⁻¹; k_FRET,3xGFP = 0.069 ns⁻¹; k_FRET,4xGFP = 0.071 ns⁻¹; k_FRET,5xGFP = 0.075 ns⁻¹) clearly distinguished dimers from trimers and hardly trimers from tetramers and pentamers (Table 1). Estimating the average separation between the GFP moieties in the concatemers from the FRET efficiency, we obtain distances (∼6 nm) that are somewhat larger than distances previously measured for tightly packed macrostructures of GFP proteins that range from 2.4 to 4.6 nm (48, 49, 50). Hence, we conjecture that our GFP concatemers form rather loose structures where the long linkers between the individual GFP moieties permit considerable flexibility.

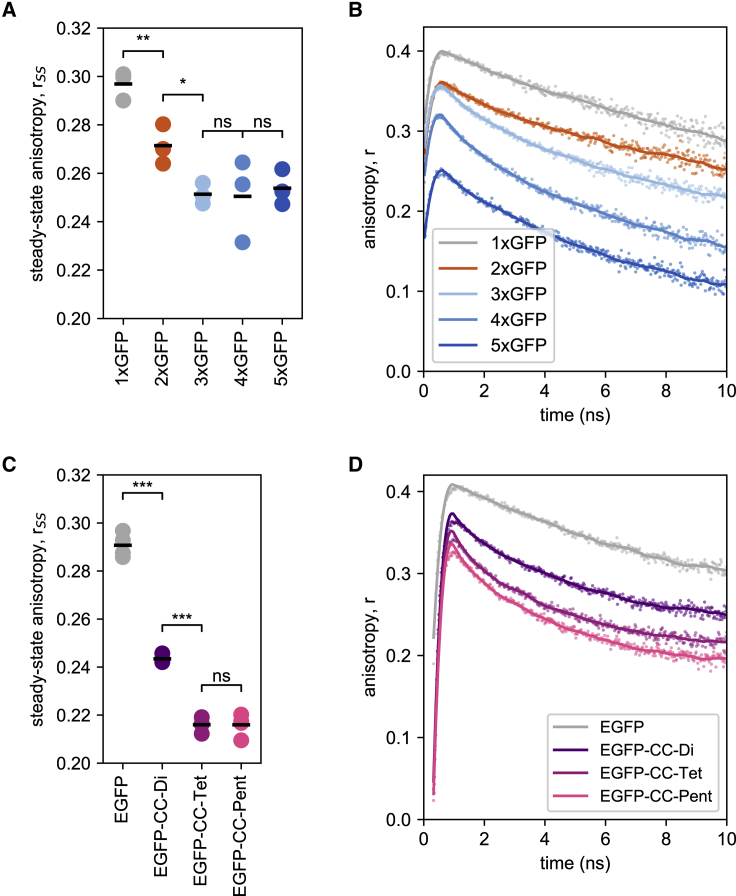
Figure 2.

Characterization of sfGFP concatemers and EGFP-coiled-coil oligomers via fluorescence anisotropy. (A) The steady-state anisotropy of sfGFP concatemers (2 μM; λ_ex = 488 nm; λ_em = 520 nm). Shown are the individual values of the steady-state anisotropy and the respective means (n = 3–6). Differences were classified with an unpaired Student’s t-test and ranked by their two-tailed p-values (p > 0.05). (B) The time-resolved fluorescence anisotropy of sfGFP concatemers (2 μM; excited with a polarized 468 nm pulsed laser, parallel and perpendicular detected fluorescence at 508 nm). (C) The steady-state anisotropy of EGFP-coiled-coil fusion protein (2 μM). Measurements and evaluation were done as in (A). (D) Time-resolved anisotropy decay of EGFP-coiled-coil fusion protein (2 μM). Measurements and evaluation were done as in (B). For the time-resolved fluorescence anisotropy measurements, samples were measured in buffer containing 30% glycerol to minimize molecular rotation (see also, Fig. S4). ^∗p ≤ 0.05, ^∗∗p ≤ 0.01, ^∗∗∗p ≤ 0.001. ns, not significant. To see this figure in color, go online.

Table 1.

Determination of Protein Stoichiometry N from Fluorescence Anisotropy

Fusion Protein	rSSa	τ (ns)b	kFRET (ns−1)c	Nss,indiv.d	Nss,stde	fnonf	Nx,fnong	Nx,ah
1xGFP	0.297 ± 0.002	2.47 ± 0.14	-	1.0 ± 0.1	1.0 ± 0.1	1.002 ± 0.003	8.2 ± 49.2	1.0 ± 0.1
2xGFP	0.271 ± 0.004	2.54 ± 0.13	0.055 ± 0.005	2.2 ± 0.3	2.0 ± 0.2	0.912 ± 0.014	1.7 ± 0.2	1.9 ± 0.1
3xGFP	0.251 ± 0.001	2.57 ± 0.20	0.069 ± 0.003	3.1 ± 0.2	3.1 ± 0.1	0.848 ± 0.009	2.3 ± 0.2	2.7 ± 0.1
4xGFP	0.250 ± 0.002	2.66 ± 0.23	0.071 ± 0.003	3.0 ± 0.2	3.1 ± 0.1	0.846 ± 0.002	2.8 ± 0.3	2.9 ± 0.1
5xGFP	0.254 ± 0.007	2.89 ± 0.25	0.075 ± 0.003	2.6 ± 0.4	2.9 ± 0.4	0.857 ± 0.011	2.9 ± 0.3	2.8 ± 0.1
EGFP	0.291 ± 0.002	2.84 ± 0.22	-	1.0 ± 0.1	1.00 ± 0.04	1.000 ± 0.005	3.7 ± 71.4	1.00 ± 0.03
EGFP-CC-Di	0.243 ± 0.001	2.92 ± 0.20	0.105 ± 0.004	2.2 ± 0.1	2.08 ± 0.03	0.846 ± 0.008	2.9 ± 0.2	2.3 ± 0.1
EGFP-CC-Tet	0.216 ± 0.002	2.75 ± 0.21	0.139 ± 0.004	2.9 ± 0.1	3.1 ± 0.1	0.75 ± 0.020	2.4 ± 0.3	2.7 ± 0.1
EGFP-CC-Pent	0.216 ± 0.002	2.89 ± 0.20	0.137 ± 0.004	2.9 ± 0.1	3.1 ± 0.1	0.759 ± 0.014	2.3 ± 0.2	2.7 ± 0.1

^aSteady-state anisotropy: the errors represent the SDs between the anisotropy measurements of the same molecule (n = 3 for sfGFP concatemers; n = 2 for EGFP-based).

^bFluorescence lifetime: the errors are the SDs between the fluorescent lifetime measurements of the same molecule (n = 3).

^cThe homotransfer rate, determined from the fit of the time-resolved anisotropy decay (Eq. 3). The errors show the square root of the diagonal entry in the covariance matrix of the fit.

^dThe oligomeric state N, as calculated via Eq. 4 from r_SS and individually measured k_FRET, τ, and r_ET. The parameter r_ET was determined with standard proteins of known N (r_ET,sfGFP = 0.111; r_ET,EGFP = 0.076). The errors were determined assuming error propagation.

^eThe oligomeric state N, as calculated via Eq. 4 from r_SS for sfGFP concatemers with $\overline{k_{FRET}}$ = 0.067 ns⁻¹, $\overline{\tau }$ = 2.62 ns, r₁ = 0.297, and r_ET = 0.105 and for EGFP-based complexes with $\overline{k_{FRET}}$ = 0.127 ns⁻¹, $\overline{\tau }$ = 2.85 ns, r₁ = 0.291, and r_ET = 0.079. The errors were determined assuming error propagation.

^ff_non was assessed with a least-square fit of the photobleached data using Eq. 5. The errors show the square root of the diagonal entry in the covariance matrix of the fit.

^gThe oligomeric state N, as calculated via Eq. 5 using f_non that was acquired from steady-state anisotropy at various stages of photobleaching. The errors show the square root of the diagonal entry in the covariance matrix of the fit.

^hThe oligomeric state N, as calculated via Eq. 6 using parameter a that was acquired from steady-state anisotropy at various stages of photobleaching (a_sfGFP = 0.10; a_EGFP = 0.21). The errors show the square root of the diagonal entry in the covariance matrix of the fit.

Next, we measured steady-state and time-resolved fluorescence anisotropies of non-covalently linked GFP assemblies. The steady-state fluorescence anisotropies of the EGFP-based coiled-coil fusion proteins, with their short flexible linkers, strongly decreased from monomeric EGFP (r_SS = 0.291) to dimeric EGFP-CC-Di (r_SS = 0.243) and trimeric EGFP-CC-Tet (r_SS = 0.216) (Fig. 2 C; Table 1). Again, trimeric, tetrameric, and pentameric concatemers displayed similar steady-state anisotropies (r_SS ≈ 0.25) (Table 1). The time-resolved measurements (Fig. 2 D) gave the homo-FRET rates k_FRET (k_{FRET,EGFP-CC-Di} = 0.105 ns⁻¹; k_{FRET,EGFP-CC-Tet} = 0.139 ns⁻¹; k_{FRET,EGFP-CC-Pent} = 0.137 ns⁻¹) (Table 1). Similar to the GFP concatemers, we can thus clearly distinguish the CC-Di from the trimer, but not the coiled-coil trimer from the CC-Pent. The estimated average relative fluorophore distance in these constructs (∼5.5 nm) was shorter than that of sfGFP concatemers but above the average distances in tightly packed GFP macrostructures (48, 49, 50).

Taken together, steady-state as well as time-resolved fluorescence anisotropy depends on protein stoichiometry in a comparable way with covalent and non-covalent GFP constructs. In the case of the EGFP-based constructs, the respective values suggest that the shorter linker between EGFP and coiled coils promote homo-FRET, resulting in lower anisotropies. The low average fluorophore distance in the EGFP-based oligomers supports this conclusion.

Calculating the oligomeric state from steady-state and time-resolved fluorescence anisotropy

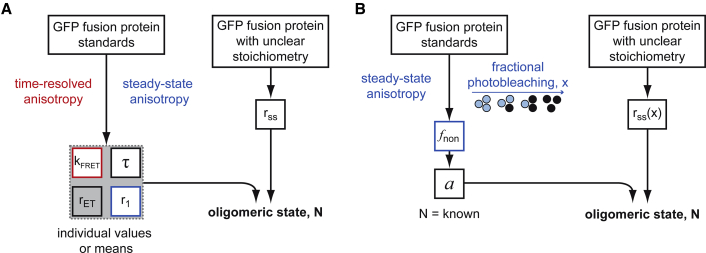
The stoichiometries of our covalent and non-covalent complexes can be calculated from a combination of steady-state and time-resolved fluorescence anisotropy data (Fig. 3 A), according to the model of Runnels and Scarlata (10), Eq. 4. These calculations require the steady-state anisotropies of the monomer, r₁, and of the different oligomers, r_SS. Values of r₁ were determined separately for sfGFP (r₁ = 0.297) and EGFP (r₁ = 0.291); the small difference between both values might be caused by subtle differences in rotational correlation times resulting from the different sizes of the constructs used (sfGFP, 36.4 kDa; EGFP, 30.0 kDa). The model comprises 1) the homotransfer rate k_FRET, as provided by time-resolved anisotropy decays; 2) the anisotropy r_ET of fluorophores that are indirectly excited after homo-FRET; and 3) the fluorescence lifetime τ as obtained from measurements of the fluorescence intensity decay. When the stoichiometry is known, the value for r_ET can be empirically determined from the experimental data using Eq. 4. Using this approach, we determined r_ET = 0.105 for sfGFP concatemers (longer linkers) and r_ET = 0.079 for EGFP fusion proteins (shorter linkers).

Figure 3.

Different approaches to determine protein stoichiometry from fluorescence anisotropy data. (A) Determination of oligomeric state N_ss,indiv or N_ss,std by time-resolved and steady-state anisotropy according to Runnels and Scarlata (10). (B) Characterization of N_x,a by steady-state anisotropy in combination with fractional photobleaching. To see this figure in color, go online.

Based on determined r_SS-, k_FRET-, and τ-values, as determined for each individual test construct, we calculated their stoichiometries N_ss,indiv (Table 1). The N_ss,indiv-values agree well with the known monomeric, dimeric, or trimeric stoichiometries of these constructs. Tetrameric and pentameric stoichiometries could not be recovered because of the resolution limit for the r_SS referred to above.

In a variation of this approach, we sought to simplify the analysis by deriving the stoichiometry from the steady-state data and using the average parameters for k_FRET, τ, and r_ET. As a consequence, the stoichiometry prediction solely requires r_SS and a standardized parameter set, as acquired by time-resolved measurements. Surprisingly, the oligomeric states N_SS,std, as calculated with the standardized parameter sets for sfGFP concatemers and EGFP-based complexes, respectively, are similar to the respective N_SS,indiv-values (Table 1). However, calculating the stoichiometries of the EGFP-based system with the parameter set for the sfGFP-based system, and vice versa, gave greatly aberrant values (Table S1). Thus, the molecular composition of a fusion protein of unknown stoichiometry has to match that of the reference proteins. In an effort to identify the factors defining a compatible reference, we found that the mean k_FRET of EGFP-based oligomers is above the mean k_FRET of sfGFP-based proteins and that r_ET is smaller for the EGFP-based (0.079) constructs than for the sfGFP-based (0.105) proteins. This can be explained by a lower average fluorophore distance in the EGFP complexes and/or differences in the spatial orientation of the subunits.

In sum, combining steady-state and time-resolved measurements permits an accurate determination of subunit stoichiometry up to a trimer. To simplify the analysis, average parameters can be used that are determined by time-resolved measurements for a compatible set of reference proteins with known stoichiometries.

Determination of subunit stoichiometry using fractional photobleaching

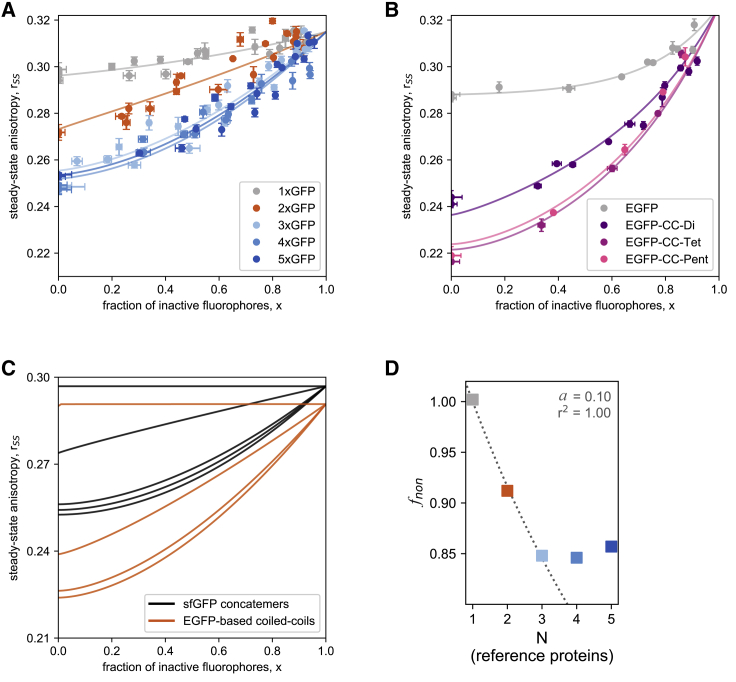
To explore alternative ways to reduce the amount of expensive time-resolved measurements and to increase the robustness of the stoichiometry analysis, we also measured the steady-state anisotropy as a function of fractional photobleaching (Fig. 3 B). It had been shown previously that fluorescence depolarization caused by energy transfer between GFP moieties successively decreases with stepwisely photobleaching the FRET acceptors (51). In the following experiments, we thus recorded steady-state anisotropies before and after fractionally photobleaching sfGFP concatemers and EGFP-based coiled-coil fusion proteins. The samples were irradiated using a blue laser in 10–15-min intervals (λ = 445 nm; 300 mW), which produced a growing fraction of inactive fluorophores, x, as determined from the decrease in fluorescence intensity. Simultaneously, the steady-state anisotropy increased to values that approach that of monomeric GFP (Fig. 4 A). The concatemers 1xGFP, 2xGFP, and 3xGFP can be readily distinguished in terms of the change in anisotropy as a function of x, whereas we could not differentiate 3xGFP from 4xGFP and 5xGFP. In a similar vein, we could distinguish between monomeric, dimeric, and trimeric EGFP-based coiled-coil proteins by fractional photobleaching (Fig. 4 B). We note that the qualitative comparison with the sfGFP concatemer data shows only limited agreement between both data sets (Fig. 4 C). Also, we unexpectedly detected a small change in the anisotropy of the monomer after photobleaching. This might originate from a potentially increasing contribution of background scattering to the signal as the fluorescence signal decreases in the wake of photobleaching. For better comparability, anisotropies were therefore corrected for the increase of monomer values.

Figure 4.

Determination of protein stoichiometry via steady-state anisotropy and fractional photobleaching. Steady-state anisotropy was measured as a function of the fraction of photobleached fluorophores, as determined from the fluorescence intensities. The data were fitted with Eq. 6 for (A) sfGFP concatemers and (B) EGFP-based coiled-coil fusion proteins. (C) A comparison of fits of photobleaching data between the two test systems, sfGFP concatemers (long linkers, black), and EGFP-based non-covalent assemblies (short linkers). For better comparability, anisotropies were corrected for the apparent increase of monomer values in the wake of photobleaching. (D) The parameter f_non, calculated for both test systems via Eq. 5, is plotted as a function of N. A nonlinear least-squares approach for f_non = $\frac{1+a}{1+N\times a}$ was used to fit the data for the samples with N = 1–3 to obtain parameter a. To see this figure in color, go online.

As proposed previously by Yeow and Clayton (20), the subunit stoichiometry of fluorophore-tagged proteins can be determined from the change in steady-state fluorescence anisotropy in response to fractional labeling (Eq. 5). As parameters, this model requires the anisotropy of the monomer, r₁, and parameter, f_non, which can be obtained from a least-squares fit of the photobleaching data. However, applying this model to our photobleaching data gave subunit stoichiometries, denoted N_x,fnon, that deviate significantly from most of the known stoichiometries of our test proteins (Table 1). The parameter f_non was close to unity in all cases, which was surprising given that f_non was originally assumed to represent the fraction of nonassembled subunits (20). By contrast, our biochemical characterization of the complexes (Fig. 1) did not detect prominent monomer fractions.

A theoretical line of reasoning argues that f_non cannot represent the fraction of noninteracting fluorophores (see Supporting Materials and Methods, Theory). Moreover, we observed here that f_non decreases with increasing subunit numbers of our complexes (Fig. 4 D). We quantitatively describe this dependence by f_non = (1 + a) × (1 + N × a) ⁻¹ (see Supporting Materials and Methods, Theory) and the parameter a_sfGFP = 0.10 for concatenated sfGFP domains, and a_EGFP = 0.21 for EGFP-coiled-coil oligomers (both values for parameter a were determined for N = 1–3 via a least-squares fit). Replacing f_non in the original formula of Yeow and Clayton (see Eq. 6) by the term (1 + a) × (1 + N × a) ⁻¹ permits us to calculate stoichiometry N from steady-state photobleaching data, denoted as N_x,a. Indeed, N_x,a are much more accurate than the N_x,fnon-values derived using the original Yeow and Clayton model, at least up to the trimers (Table 1). Again, controls in which we did the N_x,a calculations for EGFP-based oligomers with the calibration parameter a_sfGFP as well as N_x,a determinations of sfGFP concatemers using a_EGFP yielded aberrant values (Table S1). This indicates that the parameter a has to be determined from reference constructs with comparable molecular properties.

We conclude that a quantitative relationship between f_non and N can be derived from reference proteins of known stoichiometry. Furthermore, this relationship can be exploited to determine the subunit stoichiometry with reasonable accuracy from steady-state anisotropy of photobleached GFP fusion proteins, at least up to trimers. Once the reference parameter has been determined, this approach only requires inexpensive steady-state measurements.

Stoichiometry analysis of natural coiled-coil proteins and a multimeric oligomer

Here, we analyze the oligomeric state of the GCN4-p1 coiled-coil domain of the yeast leucine-zipper GCN4 (22), a natural dimer, and its GCN4-pII variant, which became trimeric by mutating the helix-helix interface (30,52). Further, we designed a de novo coiled-coil protein, ph3a, using CCbuilder, as described in Wood et al. (53). These sequences were fused to sfGFP via a flexible linker that exhibits an amino acid composition and length similar to the linker in the sfGFP concatemers. The fusion proteins contain terminal tags for immunochemical detection and purification (Fig. 5 A).

The stoichiometries of the isolated GCN4 coiled-coil peptides had previously been established by x-ray crystallography (52,54) and by nuclear magnetic resonance spectroscopy (55,56). To test whether their oligomeric states are preserved in the fusion proteins, we expressed and purified sfGFP-GCN4-p1 and sfGFP-GCN4-pII. Like the naturally monomeric 1xGFP control, they migrated as monomers in SDS-PAGE (Fig. 5 B), whereas native PAGE gave a rank order of migration of monomer < dimer < trimer for 1xGFP, GCN-p1, and GCN4-pII (Fig. 5 C). SEC produced peaks indicating a dimeric sfGFP-GCN4-p1 and a trimeric sfGFP-GCN4-pII (Figs. 5 D and S3 B). A stable diffusion coefficient, as determined via FCS at a concentration of 1 nM over a period of 1.5 h (Table S2), excludes that both proteins dissociate during measurement. The newly designed sfGFP-ph3a gave a clean protein band in SDS-PAGE (Fig. 5 B) but did not enter the gel in native PAGE (data not shown). The majority of sfGFP-ph3a eluted with the exclusion volume in SEC (Figs. 5 D and S3 B), indicating the formation of a higher-order protein complex.

The mean steady-state fluorescence anisotropies of the dimeric sfGFP-GCN4-p1 (r_SS = 0.271) and the trimeric sfGFP-GCN4-pII (r_SS = 0.246) (Fig. 5 E; Table 2) were similar to those of the dimeric and trimeric concatemers, 2xGFP (r_SS = 0.271) and 3xGFP (r_SS = 0.251), respectively (Table 1). Again, this shows that one can reliably distinguish monomers from dimers and trimers using the steady-state anisotropy of GFP fusion constructs. The steady-state anisotropy of sfGFP-ph3a is extremely low (r_SS = 0.172) (Fig. 5 E; Table 2), which supports the formation of a higher-order protein complex (Fig. 5 D). Time-resolved anisotropy measurements (Fig. 5 F) revealed distinguishable decays for the monomer, dimer, and trimer and the respective homotransfer rates k_{FRET,sfGFP-GCN4-p1} = 0.063 ns⁻¹ and k_{FRET,sfGFP-GCN4-pII} = 0.099 ns⁻¹ (Table 2). Consistent with the low steady-state fluorescence anisotropy of sfGFP-ph3a, the time-resolved measurement detected a very fast anisotropy decay (Fig. 5 F) with k_FRET = 0.230 ns⁻¹ (Table 2). The calculated average fluorophore distance equals 5.9 nm for sfGFP-GCN4 variants and 5.0 nm for sfGFP-ph3a. The significantly shorter interfluorophore distance for sfGFP-ph3a could be explained with a more condensed macromolecular structure compared with lower-order oligomers (R = 5.5–6.5 nm).

Table 2.

Determination of Protein Stoichiometry N of Non-covalent sfGFP Oligomers from Fluorescence Anisotropy

Fusion Protein	rSSa	τ (ns)b	kFRET (ns−1)c	Nss,stdd	Nx,ae
1xGFP	0.297 ± 0.002	2.47 ± 0.14	-	1.0 ± 0.1	1.0 ± 0.1
sfGFP-GCN4-p1	0.271 ± 0.003	2.50 ± 0.16	0.063 ± 0.009	2.0 ± 0.1	2.0 ± 0.1
sfGFP-GCN4-pII	0.246 ± 0.001	2.43 ± 0.20	0.099 ± 0.007	3.4 ± 0.1	3.4 ± 0.1
sfGFP-ph3a	0.172 ± 0.001	2.53 ± 0.24	0.230 ± 0.005	13.5 ± 0.3	7.1 ± 0.4

^aSteady-state anisotropy: the errors represent the SDs between the anisotropy measurements of the same molecule (n = 2).

^bFluorescence lifetime: the errors are the SDs between the fluorescent lifetime measurements of the same molecule (n = 3).

^cThe homotransfer rate, determined from the fit of the time-resolved anisotropy decay (Eq. 3). The errors show the square root of the diagonal entry in the covariance matrix of the fit.

^dThe oligomeric state N, as calculated with Eq. 4 from r_SS and with $\overline{k_{FRET}}$ = 0.067 ns⁻¹, $\overline{\tau }$ = 2.62 ns, r₁ = 0.297, and r_ET = 0.105. The errors were determined assuming error propagation.

^eThe oligomeric state N, as calculated via Eq. 6 using parameter a_sfGFP = 0.10. The errors show the square root of the diagonal entry in the covariance matrix of the fit.

Using the measured r_SS-values and the standardized parameter set for sfGFP-based constructs, we calculated N_ss,std-values that confirm that GCN4-p1 and GCN4-pII form dimeric and trimeric assemblies, respectively, when fused to GFP (Table 2). Thus, the parameter set that was determined with the sfGFP concatemers serves well in determining the stoichiometry of non-covalent oligomers.

When we fractionally photobleached sfGFP-GCN4-p1 and sfGFP-GCN4-pII (Fig. 5 G), the resulting curves were comparable with those of 2xGFP and 3xGFP (Fig. 5 H). Analyzing the photobleaching data using the newly introduced model, Eq. 6, and the calibration parameter a_sfGFP (= 0.10) yields N_x,a-values that are identical to the N_ss,std-values (Table 2). When applying the classical Runnels and Scarlata model, Eq. 4, N_ss,indiv equaling 2.1 (GCN4-p1), 2.8 (GCN4-pII), and 6.3 (ph3a) were found. These values closely agree with the respective numbers of N_ss,std and N_x,a.

For sfGFP-ph3a, N_ss,std = 13.5, which originates from the fast anisotropy decay (Fig. 5 F), and N_x,a = 7.1, reflecting the high curvature describing the data from the fractional photobleaching experiments (Fig. 5 G). These data suggest that ph3a forms a higher oligomeric assembly. In an effort to determine the stoichiometry of sfGFP-ph3a, we directly probed the number of subunits using single-step photobleaching and TIRF microscopy (Fig. 5 I). We immobilized the sfGFP-ph3a proteins on the polyethylene-glycol-passivated glass surface via an anti-GFP antibody. Assuming that each fluorescent spot consisted of an individual complex (Fig. S6 A), the number of subunits could be extracted using a step-finding algorithm on the fluorescence intensity measured during photobleaching with high laser power. The exact assignment of bleaching steps is difficult, given the limitation of signal/noise ratio in TIRF microscopy. Hence, we applied the L₁ regularization Kalafut-Visscher algorithm step-finding algorithm that we tested using simulated data with a similar signal/noise ratio (39,40). The majority of the molecules exhibited seven bleaching steps (Fig. 5 I) with minor populations showing higher complex sizes (Fig. S6 B). A subunit stoichiometry with seven subunits is highly consistent with the calculations from fluorescence anisotropy analysis after fractional photobleaching.

In conclusion, we could demonstrate that the fluorescence anisotropy-based approaches can not only resolve monomeric, dimeric, and trimeric complexes but also reveal the stoichiometry of higher-order oligomers.

Discussion

In this study, we test and expand the applicability of fluorescence anisotropy-based approaches for studying the stoichiometry of oligomeric proteins. First, we show that the steady-state anisotropy as well as the time-resolved anisotropy of various model GFP assemblies can differentiate between their monomeric, dimeric, or trimeric structures well. By contrast, differentiation between trimers, tetramers, or pentamers is difficult. The fluorescence anisotropy of a cluster of fluorophores results from the intrinsic anisotropy of the constituent subunit, the anisotropy resulting from rotation of the whole molecule as well as the fluorescence depolarization resulting from homo-FRET, depending on oligomeric state and relative spatial orientation of the subunits. Apparently, fluorescence depolarization by homo-FRET is near maximal with the tested trimeric coiled-coil oligomerization domains whose stoichiometry had previously been established. Nonetheless, analyzing ph3a, a de novo designed novel coiled-coil construct, the heptameric structure of which is indicated by TIRF microscopy, revealed that higher-order protein stoichiometries can also be resolved. Specifically, ph3a gave the highest homo-FRET rate, and hence, the lowest steady-state anisotropy of all the covalent and non-covalent oligomers investigated here. Conceivably, ph3a exhibits a structure where the GFP moieties are in closer proximity to each other, consistent with the lower GFP-GFP distance measured here. In addition, the subunits within the ph3a multimer might assume more diverse spatial orientations relative to each other than those within the other oligomers tested here. This suggests that the subunit stoichiometries that can be resolved by fluorescence anisotropy extend well beyond trimers, depending on the structure of the oligomer under question.

Quantitating subunit stoichiometries from steady-state and time-resolved fluorescence anisotropy according to Runnels and Scarlata (10) reports the correct oligomeric states of our covalent and non-covalent GFP fusion protein assemblies. Recording time-resolved fluorescence anisotropy requires advanced and expensive experimental setups. We therefore explored novel ways to systematically recover subunit stoichiometries from the more inexpensive steady-state anisotropy data. In one approach, we used a set of averaged parameters k_FRET, τ, and r_ET that were determined by time-resolved measurements of protein standards of predefined stoichiometry, i.e., sfGFP concatemers. Combining these averaged parameters with the steady-state anisotropies of individual candidate proteins yielded stoichiometries that are similar to the values obtained by using time-resolved data for each individual candidate.

In another approach, we exploited the impact of fractional photobleaching on fluorescence anisotropy of a protein cluster. Because the application of the original model (20) did not yield satisfactory stoichiometries, we extended it by exploiting the inverse relationship between parameter f_non in the original model and the stoichiometries of standard proteins, as found here. Indeed, this extension significantly improved the results when interpreting the steady-state data. What is the advantage of using the more laborious photobleaching approach in comparison with using averaged parameters from time-resolved measurements? We believe that increasing the number of data points via fractional photobleaching increases the robustness of the stoichiometry analysis. This is exemplified by our results showing that the more realistic heptameric stoichiometry of ph3a is obtained with the photobleaching method.

In sum, the approaches presented here show that protein stoichiometries can be determined with sufficient accuracy from steady-state data in combination with a few key parameters obtained from time-resolved measurements of reference proteins. Therefore, the analysis of a large number of candidates is greatly facilitated because only a limited set of reference proteins is required. We do stress that the structural composition of reference and candidate proteins has to match. Specifically, comparing calculated stoichiometries of sfGFP- and EGFP-based oligomers suggests that the length of the flexible linkers affects the homo-FRET rate and hence the anisotropy. We thus strongly recommend a uniform and streamlined molecular composition of reference and candidate proteins for optimal comparability.

Future applications of anisotropy-based determinations of oligomeric state may include membrane-bound proteins, most of which are assumed to form oligomers (3). Previously established genetic tools, such as the ToxR, TOXCAT, or BLaTM systems, cannot distinguish dimers from higher oligomers (57). Furthermore, characterizing the stoichiometry via hydrodynamic measurements, such as SEC or analytical ultracentrifugation, is prohibited by the embedding bilayer and requires detergent solubilization with unknown impacts on subunit stoichiometry. The simplified determination of stoichiometry based on fluorescence anisotropy of suitable GFP fusion proteins may thus facilitate the future characterization of homomeric membrane-bound proteins.

Editor: Jochen Mueller.