Effect of Divalent Cations on the Structure and Mechanics of Vimentin Intermediate Filaments

Abstract

Divalent cations behave as effective cross-linkers of intermediate filaments (IFs) such as vimentin IF (VIF). These interactions have been mostly attributed to their multivalency. However, ion-protein interactions often depend on the ion species, and these effects have not been widely studied in IFs. Here, we investigate the effects of two biologically important divalent cations, Zn²⁺ and Ca²⁺, on VIF network structure and mechanics in vitro. We find that the network structure is unperturbed at micromolar Zn²⁺ concentrations, but strong bundle formation is observed at a concentration of 100 μM. Microrheological measurements show that network stiffness increases with cation concentration. However, bundling of filaments softens the network. This trend also holds for VIF networks formed in the presence of Ca²⁺, but remarkably, a concentration of Ca²⁺ that is two orders higher is needed to achieve the same effect as with Zn²⁺, which suggests the importance of salt-protein interactions as described by the Hofmeister effect. Furthermore, we find evidence of competitive binding between the two divalent ion species. Hence, specific interactions between VIFs and divalent cations are likely to be an important mechanism by which cells can control their cytoplasmic mechanics.

Significance

Intermediate filaments are key structural elements within cells; they are known to form networks that can be cross-linked by divalent cations, but the interactions between the ions and the filaments are not well understood. We measure the effects that two divalent cations, zinc and calcium, have on the structure and mechanics of vimentin intermediate filaments. We show that although both have concentration-dependent effects on vimentin intermediate filaments, much more calcium is needed to achieve the same effect as a small amount of zinc. Furthermore, when mixtures of the ions are present, the results suggest that there is binding competition. Thus, cells may use the presence of different cation species to precisely control their internal mechanical properties.

Introduction

Intermediate filaments (IFs) are one of the major cytoskeletal proteins and are key contributors to the complex internal mechanics of eukaryotic cells (1,2). Vimentin intermediate filaments (VIFs) are the most abundant IFs in cells of mesenchymal origin, comprising major cytoskeletal systems in numerous cell types, including fibroblasts in connective tissues and endothelial cells lining blood vessels. Vimentin assembles into long polymeric 10-nm filaments that entangle and form complex network structures throughout the cytoplasm. Disruptions in the normal assembly and organization of VIF occur in diseases such as cataracts (3), neuromuscular disorders (4), and some cancers (5). Furthermore, the switching-on of vimentin expression is a marker of cells that are undergoing an epithelial-to-mesenchymal transition, which is accompanied by significant changes in cell stiffness and morphology (6, 7, 8). Thus, the structure and mechanics of the VIF networks are essential to their function in cells. These properties of VIFs are thought to be influenced in vivo by posttranslational modifications such as phosphorylation. However, because VIFs are highly charged polymers, charge-induced interactions may also play an important role. In fact, purified vimentin protein can be fully assembled from a soluble, tetrameric state that is stably sustained in low ionic strength buffer. Under these conditions, VIF networks can be assembled from the tetrameric state in vitro solely by tuning the monovalent salt concentration to physiological levels in a pH-neutral buffer (9,10). Thus, the intracellular ionic environment, which is actively regulated by cells, is likely to be critical in determining VIF network properties in vivo. Ion pumps in the cell membrane control the concentrations of not only monovalent ions but also some divalent ions such as calcium, whereas other divalent ions such as zinc are balanced using transporter proteins. Due to their multiple charges, multivalent ions are, in contrast to monovalent ions, more capable of mediating interactions between neighboring protein units. For example, millimolar concentrations of Mg²⁺ and Ca²⁺ have been demonstrated to effectively cross-link VIF in their C-terminal domains, and this has been shown to stiffen reconstituted VIF networks without changing their structure (11). Further increasing the Mg²⁺ concentration can induce bundling because of counterion-mediated condensation (12, 13, 14), but this has not been studied for other divalent cations. There is also evidence that Zn²⁺ may interact with a cysteine in the rod domain, C328, to regulate VIF organization in cells (15). Interestingly, divalent cation species appear to exhibit increasing effectiveness at promoting VIF aggregation according to their atomic number (14). Studies of other proteins have shown that ion-protein interactions can strongly depend on the ion species even when valency is unchanged (14,16, 17, 18, 19, 20); this is often referred to as the Hofmeister effect. Corresponding species-specific interactions have not been widely explored in VIF networks. Furthermore, the effects of exposing VIFs to multiple types of divalent cations simultaneously, which occurs naturally in the cytoplasm, are also not well known. Characterizing the exact influence that different ions have on VIF networks, both separately and together, is a necessary step toward understanding the mechanical role of IF in cells.

In this work, we investigate the effects of Zn²⁺ and Ca²⁺ cations, which have important signaling functions in cells, on VIF network structure and mechanics using VIF networks that have been assembled in vitro. We demonstrate that VIFs aggregate and align to form bundles in response to increasing concentrations of Zn²⁺ and Ca²⁺. However much higher concentration of Ca²⁺ compared to Zn²⁺ are required for bundling. Microrheological experiments show that VIF networks stiffen with increasing cation concentrations, but once bundles of VIFs form, the networks soften. Furthermore, in mixed ion solutions, we find that the network stiffness depends strongly on the relative amounts of each ion type, suggesting that there is competitive binding between ion species. Interactions between VIFs and divalent cations are likely to be an important mechanism by which cells can control their cytoplasmic mechanics.

Materials and Methods

Protein purification and reconstitution

Human vimentin protein is expressed in bacteria (Escherichia coli, strain TG1) and purified from inclusion bodies as previously described (21). The protein is stored at −80°C in 8 M urea, 5 mM Tris-HCl (pH 7.5), 1 mM EDTA, 0.1 mM EGTA, 1 mM dithiothreitol, and 10 mM methyl ammonium chloride. The purity of the protein is verified by sodium dodecyl sulfate polyacrylamide gel electrophoresis. Before use, the protein is dialyzed at 4°C into 5 mM Tris-HCl (pH 7.5), 1 mM EDTA, 0.1 mM EGTA, and 1 mM dithiothreitol in a stepwise manner using mini dialysis devices with a 20-kDa cut-off (Thermo Fisher Scientific, Waltham, MA). During dialysis, the urea concentration is decreased by 1 M every 30 min. To achieve protein concentrations appropriate for dilution, the protein stock is concentrated using a centrifuge-based filter unit (Ultra-15 Centrifugal Filter Units, Amicon; EMD Millipore, Burlington, MA). The final protein stock concentration is determined by measuring the absorption at 280 nm (Nanodrop ND-1000; Thermo Fisher Scientific Life Technologies, Wilmington, DE).

Filament assembly and electron microscopy

To improve retention of material on the transmission electron microscopy (TEM) grids and observation of individual filaments, TEM samples were prepared with 0.2 mg/mL vimentin. Assembly was initiated by the addition of a salt buffer containing a final Tris-HCl concentration of 25 mM, 160 mM NaCl, and varying amounts of CaCl₂ (Sigma-Aldrich, Burlington, MA) and/or ZnCl₂ (Sigma-Aldrich). The sample was allowed to polymerize without disturbance at 37°C for 1.5 h. A 10-μL sample was applied to a freshly glow-discharged carbon-coated copper or nickel grid and allowed to attach for 1 min. To cross-link the sample, glutaraldehyde (Electron Microscopy Sciences, Hatfield, PA) was added to a final concentration of 0.1%. Next, two brief stains of NanoVan (Nanoprobes, Yaphank, NY) were applied for 15 s each. Finally, the samples were wicked and air dried. The samples were imaged on a JEOL-2100 transmission electron microscope (JEOL, Tokyo, Japan), which uses a lanthanum hexaboride (LaB₆) thermal electron source, operated at 80 keV. Images were acquired with a digital camera (Gatan, Pleasanton, CA).

Image analysis

Because of the negative EM stain, filaments appear as two dark lines surrounding a brighter core. We obtain the filament widths by plotting the intensity profile of a thin rectangle drawn perpendicular to a filament and taking the width of the peak corresponding to the core. Within the rectangle, the intensity is averaged along the direction of the filament to decrease noise. The analysis is performed using the Fiji distribution of ImageJ (22).

Microrheology

All mechanical measurements are performed using 1 mg/mL vimentin. We coat 3.22-μm fluorescent carboxylated microspheres (Thermo Fisher Scientific) with polyethylene glycol (PEG) using an EDC/NHS (1-ethyl-3-(3-dimethylaminopropyl)carbodiimide/N-hydroxysuccinimide) reaction to covalently link amine-terminal 2-kDa PEG (Rapp Polymere, Tübingen, Germany) to the carboxyl groups on the microsphere surface as previously described (23). Briefly, we wash the microspheres in a pH-6.0 MES (2-(N-morpholino)ethanesulfonic acid) buffer, then incubate them with sulfo-NHS and EDC (Sigma-Aldrich) at 37°C for 15 min. We next wash the beads with a borate buffer and add the amine-terminal PEG, incubating for 90 min at 37°C. The coated beads are washed well and stored in the MES buffer. We incorporate the PEGylated microspheres into the vimentin assembly buffer before mixing it with the protein stock to the final working concentration. After thoroughly mixing, the solution is immediately transferred to a small well created by a double-sided adhesive silicone spacer (Life Technologies, Waltham, MA) on a No. 1.5 glass coverslip. The sample is sealed using another glass coverslip and allowed to polymerize at 37°C in the dark. The samples are kept on a slowly rotating platform to prevent settling of the beads. After 1.5 h, the samples are imaged using an epifluorescence microscope (Zeiss Axiovert; Zeiss, Oberkochen, Germany) outfitted with an LED light source (Colibri2.0) and a low-light camera (Hamamatsu Orca Flash v4; Hamamatsu Photonics, Hamamatsu, Japan). We take images of the fluorescent bead channel every 10 ms for ∼20,000 frames. For each sample condition, we make at least two samples. We track the particle positions as well as calculate the mean-squared displacements (MSDs) and rheological properties using a customized version of the MATLAB code released by the Kilfoil laboratory, which is based on the Interactive Data Language code from Crocker/Weeks (24,25).

Results and Discussion

Zn-VIF networks form bundles at high Zn²⁺ concentrations

To generate VIF networks for structural and mechanical characterization, we use recombinant human vimentin protein that is expressed in E. coli and purified from inclusion bodies as previously described (21). For reconstitution of functional complexes, the purified protein is dialyzed into a low-salt buffer, and filament assembly is induced by adding a polymerization buffer to a final concentration of 25 mM Tris-HCl (pH 7.5) and 160 mM NaCl. We view the filaments using a transmission electron microscope operated at 80 keV to minimize damage to the proteins. Using a standard assembly protocol, the resulting VIF networks form a mesh of smooth, freely organized filaments in the absence of divalent cations. The randomly oriented VIFs are entangled with each other, with many overlapping points and some looped structures, as seen in the electron micrograph in Fig. 1 A. VIFs are characterized by their length, width, and curvature. With only monovalent cations, VIFs are long and appear straight within a ∼1-μm field of view, which is consistent with previous measurements that find the persistence length of vimentin to be around 1 μm (10). To determine the widths of VIFs, we plot the intensity profile perpendicular to individual filaments at multiple locations along its length and measure the width of the bright peak that corresponds to the filament core. We find that there is some variation in the diameter along individual filaments and that they are 10.4 ± 1.6 nm wide on average (Fig. 1 B). This average width is fully consistent with previous observations of VIFs (9,10).

Figure 1.

Electron micrographs of VIF with various molar ratios of Zn²⁺ and the corresponding filament width distributions: (A and B) R = 0, (C and D) 0.054, (E and F) 0.54, and (G and H) 5.4. At the highest concentration of Zn²⁺, the average filament width increases. The scale bar represents 200 nm. Arrows indicate examples of distinct bundles. To see this figure in color, go online.

We select concentrations of Zn²⁺ based on reported values in cells, which typically contain a total of 200–300 μM of Zn²⁺ (26). However, local concentrations can be higher or lower, depending on how the ions are localized within the cytosol. In this work, we consider the cation/vimentin molar ratio, R, to facilitate comparison. When ZnCl₂ is included in the polymerization buffer at a molar ratio of R_Zn = 0.054, there are no significant changes in the overall network structure (Fig. 1 C) and the size of individual VIFs (Fig. 1 D). This is consistent with reports that when VIFs are assembled in the presence of both monovalent and divalent cations, the filaments look similar to those assembled with only monovalent cations (27). Similarly, at R_Zn = 0.54, the polymerized VIF network structure remains similar (Fig. 1 E), although individual filaments widen slightly (Fig. 1 F).

Upon increasing the Zn²⁺ concentration to R_Zn = 5.4, there is a marked difference in the network structure: the empty space between VIFs becomes much larger and the most prevalent structure is no longer comprised of individual ∼10-nm filaments. Instead, VIFs are aligned and closely packed in bundles over micron-long distances, as seen in Fig. 1 G. Interestingly, many of the bundles appear like flat sheets. Although the drying process will disrupt the three-dimensional structure of the network, and the staining process may also modify the structure, the fact that widespread bundling was visible only under the highest Zn²⁺ condition is fully consistent with lateral associations due to the ions. The bundles twist and cross over each other, as highlighted by the upper arrow in Fig. 1 G. The bundle structures are heterogeneous, containing as many as five VIFs each. Furthermore, the number of VIFs varies along the entire length of a single bundle, and individual VIFs can be part of multiple distinct bundles at different locations (see lower arrow in Fig. 1 G). The morphology of the VIF bundles is consistent with reports that multivalent ions can cause neighboring filaments to aggregate through coordinating lateral interactions of filaments along their lengths, which causes them to line up in a parallel manner (12,28). Due to the lateral alignment, individual filaments are well-defined even when they are in bundles, and thus the dimensions of individual filaments can be determined. Though bundle formation appears to be the dominant effect, we also find that the filaments widen slightly from 10.4 ± 1.6 to 12.1 ± 2.1 nm (Fig. 1 H). We cannot determine from our TEM data whether these filaments have a higher mass/length ratio or if the protofilaments are less tightly packed. However, the filaments remain very long; this observation is consistent with network formation and suggests that the bundling process does not interfere with the elongation step of filament assembly.

Networks cross-linked by Zn²⁺ are stiff but VIF bundles are soft

We use microscale measurements to characterize the impact of Zn²⁺ ions on VIF network mechanics. The network properties can be probed by observing the thermally driven motion of tracer particles within the network (29,30). To do this, we incorporate 3.22-μm PEG-functionalized particles into the vimentin solutions as they polymerize and then capture videos of the particle positions over the course of several minutes. The surface layer of PEG prevents the particles from interacting with vimentin, which could influence the structure as the network forms. Assuming a homogeneous network made from 1 mg/mL of vimentin, the expected mesh size, ξ ∼0.45 μm (11), is much smaller than the particle diameter, ensuring that the particles are fully trapped by the network. Based on the electron microscopy results, this assumption is likely to hold for R_Zn < 5.4 but may not apply to bundled VIFs.

To quantitatively understand the particle motion, we calculate the MSD for each particle. Individual (gray lines) and ensemble-averaged (black line) MSDs for a VIF network without divalent ions are plotted as a function of lag time τ in Fig. S1. There is not much variation between individual particle MSDs, indicating that the network is fairly homogeneous. The MSDs are subdiffusive and approach a plateau at larger values of τ, indicating that the particles are being influenced by the network. Embedded particles are only able to move as much as thermal energy can deform the network. Therefore, the network elasticity determines the amount of confinement. Because there are no crosslinks, this confinement likely arises from entanglements within the network, which have been shown to contribute significant elasticity to other networks of semiflexible polymers such as actin filaments (30). By plotting the particle location over time, which shows its trajectory, we find that the path covers a circular area, without specific directionality, and that it is smaller than the particle size. The trajectories of two different tracers are shown in Fig. 2 A.

Figure 2.

Sample particle trajectories for two particles in (A) VIFs without divalent cations, (B) VIFs with Zn²⁺, and (C) VIFs with Ca²⁺. The scale bar represents 1 μm, and the molar ratios are as indicated. Average MSD curves for Zn-VIF and Ca-VIF networks are shown in (D) and (E), respectively; the color of each curve corresponds to the divalent cation concentration, increasing from lightest (R_Zn = 0.027, R_Ca = 6) to darkest (R_Zn = 5.4, R_Ca = 1296). R = 0 is plotted in black as a reference. Normalized distributions of the MSDs at τ = 22 s are shown using the same color scale in (F) and (G). The distribution has a long tail to the right at R_Ca = 1296, shown in the inset of (G). To see this figure in color, go online.

When R_Zn < 5.4, the particle motion progressively covers less area with increasing Zn²⁺ concentration (Fig. 2 B). Because the network structure does not change within this concentration range, this trend reflects changes in the mechanical properties. We find that the average MSDs of Zn-VIF networks have more pronounced plateaus as R_Zn increases between 0.027 and 3.2 (Fig. 2 D). This suggests that the particles are caged by an increasingly elastic network rather than slowed down by a more viscous-like environment. Thus, changes in cation concentration significantly affect the local environment experienced by the tracer particles, even at concentrations that are too low to alter the network structure. After the VIF network bundles, however, the particle motion increases again (Fig. 2 B). The MSD curve also approaches but does not fully reach a plateau, similar to the curve obtained for a VIF network without any divalent cations (Fig. 2 D). These effects may reflect an increased mesh size, a weaker network, or a combination of both. Because we do not observe any particles that freely diffuse or hop between local microenvironments, we conclude that the mesh size here remains smaller than the particle size.

Based on particle-to-particle variations of the MSDs of individual particles, we can also gain insight into the network heterogeneity. For each particle in a Zn-VIF sample, we take the MSD at τ = 22 s and normalize it by the average of each sample to facilitate comparison between the various conditions. For all samples, we find that the distributions of normalized MSDs are nearly symmetric around 1% and have similar widths with variance between 2 and 9%, as seen in Fig. 2 F. This comparison gives a good visual sense that the networks do not have regions of significantly different material properties on the scale of the probe particles.

We measure the network rheological properties from the particle displacements. The MSDs of individual particles may be strongly influenced by a number of factors on the scale of the particle size, including variations in particle size or shape, and local heterogeneities in network structure. For this reason, we use two-point microrheology, which considers only the correlated motion of particles within a sample to probe the material over length scales much larger than the particle size (29). This method is, therefore, not dependent on the probe size or network heterogeneities and reflects the bulk mechanical properties for many soft materials, including F-actin networks (30). To perform the two-point analysis of the particle tracking data, we calculate the two-point MSD for each sample from all bead pairs for each lag time, τ. Here, we use all particle pairs that are spaced 3–20 μm apart, which represents the range in which correlated particle displacements are inversely proportional to the separation distance; this results in hundreds of measurements for each sample. We find an ensemble-averaged two-point MSD and use the generalized Stokes-Einstein relation to determine the network storage modulus, G′(ω), and loss modulus, G″(ω), which represent the elastic and viscous properties, respectively (31). In the figures, we plot G″ as solid lines and G″ as dashed lines. Without divalent cations, the VIF network is predominantly elastic, as evidenced by a dominant G′ at intermediate frequencies. The network stiffness is slightly frequency dependent, varying as G′ ∼ω ^0.2, which suggests that the VIF network consists of VIFs that are entangled but not cross-linked. It is also very soft, G′ = 0.009 Pa at ω = 1 rad/s, as shown in Fig. 3 A (black line). This value is in good agreement with semiflexible polymer theory for an entangled network, which predicts a plateau elastic modulus of ∼0.01 Pa, as given by $G_0=6\rho k_{B}T\left(l_p^2/l_e^3\right)$, where ρ is the polymer length density, l_e is the entanglement length, and the polymer persistence length, l_p, is 0.5–1 μm (32). The entanglement length is given by $l_e={\left(\alpha /8\right)}^{-2/5}{\rho }^{-2/5}{l}_p^{1/5}$ where α = 0.36 for all semiflexible polymers (33). We note here that this network stiffness is much lower than previously reported values measured by bulk rheometers (34,35). There is some evidence that bulk measurements of very soft gels that have G′ < 1 Pa may over report G′ because of elastic contributions by the interface at the exposed sample edge (36). At the highest and lowest frequencies, the limitations in the data available lead to statistical uncertainty; this is particularly evident for G′, whose value becomes much lower than that of G″ at high frequencies. The G″ scaling is roughly consistent with ω^3/4, as expected for semiflexible polymer systems.

Figure 3.

Rheological properties G′ (solid lines) and G″ (dashed lines) of the VIF networks are plotted as a function of frequency ω. Zn-VIF (A) and Ca-VIF (B) networks both behave as cross-linked networks, displaying decreased frequency dependence and increased stiffness. (C) The plateau modulus G₀ varies with molar ratio R in a similar way for both Zn²⁺ and Ca²⁺, first increasing then dropping suddenly. The standard error of the mean, indicated by the proportional error bars, is estimated to be ∼12%. (D) The data can be collapsed when R is scaled by a bundling concentration, R_c, for each ion species. To see this figure in color, go online.

Zinc cations strongly affect the mechanical properties of VIF networks. Below a molar ratio of 5.4, the VIF networks stiffen and become less frequency dependent as R_Zn is increased (Fig. 3 A), which suggests that Zn²⁺ ions effectively behave as cross-linkers of VIFs. Because the network structure does not change within this range, the differences in G′ likely reflect an increased cross-linking density. However, when R_Zn reaches 5.4, we find that the network softens dramatically such that it is similar to an entangled VIF network. The two-particle analysis considers only the portion of particle motion that is due to network fluctuations and is therefore not influenced by any uncaging events. Thus, the lower value of G′ reflects changes in the network itself, such as an altered mesh size or VIF properties. The bundled Zn-VIF network is more frequency dependent than the entangled one, falling off faster at low frequencies, and it is barely elastic within a small frequency range, likely due to the coarser network structure.

The values for G′ and G″ cross at low frequencies because of relaxation along the filaments through network constraints. The cross-linked networks appear to relax somewhat more quickly than entangled VIFs, which may reflect the transience of divalent ion crosslinks (37, 38, 39). However, the total time of the measurements does not offer enough statistics to establish any significant difference between the samples; all of the networks relax very slowly, on the order of 1–2 min, whether cross-linked or not.

Ca²⁺ affects VIFs in a similar manner as Zn²⁺ but at higher concentrations

There is some evidence that Ca²⁺ also crosslinks vimentin (34,40), but its effect has not been fully characterized, particularly at these concentrations. Thus, we incorporate CaCl₂ into the VIF polymerization buffer to determine its influence on network structure and mechanics. By using the chloride salt, we preserve the counterion identity, which facilitates direct comparisons with the effects of ZnCl₂. Although intracellular concentrations of Ca²⁺ are typically below 0.2 μM in cells at rest, they can reach millimolar concentrations during cell signaling events or in cases of cell damage (38,39). Previous work has shown that 2 mM (R ∼100) of Ca²⁺ stiffens VIF networks (11), so here, we study a range of concentrations above and below that value, spaced evenly on a log scale. Although low levels of divalent cations are not known to significantly affect the network structure (11), electron micrographs of VIF networks assembled at high molar ratios of Ca²⁺ show large bundles, thickened filaments, and a sparser mesh (Fig. S3). These results are qualitatively similar to the Zn-VIF bundles, but the concentration of Ca²⁺ used here (R_Ca ∼2000) is much larger, by over 2.5 orders of magnitude, than the concentration of Zn²⁺ at which visible bundling occurs (R_Zn = 5.4).

Particles embedded within Ca-VIF networks of varying R_Ca again reveal similar behavior as those in Zn-VIF networks, but at very different cation concentrations. As the Ca²⁺ concentration increases from R_Ca = 6–432, particle motion decreases significantly (Fig. 2 C). Interestingly, the degree of confinement is greater at R_Ca = 432 than in any of the Zn-VIF networks. The corresponding MSDs all show plateaus that reflect the constraint of particles by the surrounding network (Fig. 2 E). At R_Ca = 1296, however, particle motion increases again, and some particles can permeate through the network or jump between pores (Fig. 2 C), suggesting that the network has formed bundles and the mesh size is now close to the bead size. The shape of the ensemble-averaged MSD also changes at this molar ratio; it remains slightly subdiffusive for all lag times but continues to increase over time (Fig. 2 E). Particles in this network exhibit a broader distribution of MSDs compared with those embedded within networks at lower R_Ca, which suggests increased heterogeneity due to bundling (Fig. 2 G); furthermore, the highly motile particles cause the peak to shift left, and the long tail can be seen in the inset of Fig. 2 G. Compared to lower R_Ca networks, which have variances between 1 and 15%, the variance at R_Ca = 1296 is much higher at ∼74%.

The rheology of Ca-VIF networks is also strongly dependent on the divalent cation concentration. VIFs assembled in the presence of Ca²⁺ generally form elastic networks that are frequency independent and stiffer than entangled VIFs, reminiscent of cross-linked gels. However, the bundled Ca-VIF, like its Zn-VIF counterpart, forms the softest network, as seen in Fig. 3 B.

Because G′ exhibits little frequency dependence at intermediate frequencies, we have determined a plateau elastic modulus, G₀, at ω = 1 rad/s. In the range 0.027 < R_Zn < 0.54, we find that R_Zn directly influences G₀ according to the relation G₀ ∼R_Zn^0.51. Similarly, we find that Ca²⁺ stiffens the networks according to G₀ ∼R_Ca^0.58 in the range 36 < R_Ca < 432, which agrees with bulk rheology studies on Ca²⁺ and Mg²⁺ (34,40). Remarkably, although the exponents are similar for Zn²⁺ and Ca²⁺, their absolute concentrations differ by more than two orders of magnitude (Fig. 3 C). In fact, Zn²⁺ induces VIF bundling at molar ratios in which Ca²⁺ is only beginning to stiffen the network.

When the network is formed with Zn²⁺, G₀ appears to saturate between the R_Zn = 0.54 and 3.2. By contrast, the Ca-VIF networks do not exhibit a plateau at higher R_Ca but instead stiffen monotonically. Moreover, calcium stiffens the VIF network more than zinc does. These differences in stiffening behavior suggest subtle differences in the way each ion species binds to vimentin. VIF structure reflects a balance between the processes of lateral assembly and filament elongation, which may be influenced by both the valency and the concentration of the counterions. Here, we use a physiological concentration of monovalent ions and add several orders of magnitude fewer divalent cations. Under these conditions, divalent cations are presumed to primarily serve in a cross-linking capacity with minimal effects on VIF structure (27,34). However, it is likely that the divalent cations facilitate crosslinks or lateral interactions between vimentin tetramers even as the filaments are assembling (9,27). Such effects will affect the network mechanics in a way that depends on the comparative strengths of interaction as well as the number of interactions. Thus, although Zn²⁺ binds very strongly to vimentin, its effect on VIF network mechanics may plateau once the network branch points are saturated with crosslinks because the numbers of divalent ions and vimentin monomers are comparable. In the case of Ca²⁺, the large number of divalent ions can coordinate to stiffen the network even more.

For both ion species, a network of bundles is softer than the cross-linked networks. Because the total amount of protein is unchanged, the network of bundles must have a larger mesh size. The plateau elastic modulus of a cross-linked semiflexible polymer network can be described by G₀ = $6\rho \left(k_{B}T{l}_p^2/l_c^3\right)$ where $l_c$ is the cross-linking length and ρ is the total length of filaments per unit volume (32). In a densely cross-linked network, $l_c$ is the same as the entanglement length l_e, which scales as l_p^1/5ρ^−2/5. As bundles are introduced, the network structure is now defined by the bundles rather than by the individual filaments; thus, the new total length is ρ_bundle = ρ/N where N is the number of filaments per bundle, and l_p scales as N^x, where x represents the interfilament coupling strength. The exponent ranges between 1 and 2 for loosely- and tightly-coupled bundles, respectively (41, 42, 43). Therefore, the plateau elastic modulus scales according to G₀ ∼$N^{\left(7x-11/5\right)}$, which predicts network softening if bundles are loose (x = 1) and stiffening if the coupling is tight (x = 2). Given this relation, a loosely-bundled network should become softer whereas a tightly bundled network would stiffen. Because the G₀ of VIF networks decreases upon bundling regardless of cation species, the data suggest that the ionically-bundled filaments may be loosely coupled. To determine the exact exponent, however, would require accounting for other factors that influence network stiffness, such as the persistence length of bundles as compared to individual filaments; if the bundled filaments are very stiff, the network mechanics can become dominated by softer nonaffine deformations, which would also lead to decreases in the overall stiffness.

Overall, the shape of the G₀ versus R curves are similar for both zinc- and calcium-modified networks. We find that the points collapse and follow an exponent of ∼0.57 when the molar ratios are rescaled by a threshold molar ratio, R_c (Fig. 3 D). This suggests that the mechanism of stiffening may be fundamentally similar but that different interaction strengths could determine the relevant concentration range. From the rescaled data, we estimate the species-specific bundling thresholds to be approximately R_Zn = 5 and R_Ca = 1000.

Ionic properties affect interactions within VIF networks

The vast difference in the cross-linking and bundling concentrations suggest that Zn²⁺ and Ca²⁺ interactions with vimentin are not purely electrostatic in nature. This result is reminiscent of the Hofmeister series, in which ion species are ordered according to their ability to interact with proteins, a property that still cannot be explained from first principles (17,44,45). The Hofmeister effect is thought to be a complex balance of the many potential interactions in the system, including ion-counterion, ion-solvent, and ion-protein interactions, which necessarily depend on intrinsic properties of the ion beyond just its charge. To explore this further, we consider the effects of the solvent. A typical cytoplasm is mostly water, and the studies above are all performed in an H₂O-based buffer. However, by exchanging a fraction of H₂O for D₂O, the interactions can be influenced. For example, ion hydration is likely to decrease because of stronger hydrogen bonding in D₂O.

Therefore, to determine whether an entangled VIF network is altered by the addition of D₂O, we make microrheological measurements on pure VIF networks polymerized in a buffer that contains 45% D₂O (Fig. 4 A). At 45% D₂O, the microspheres are density-matched with the surrounding buffer. The results show that the network stiffness doubles compared with a network polymerized in H₂O, suggesting that there could be strengthening of the protein structure itself due to altered hydrogen bonding within the protein structure. Furthermore, the decreased ability of monovalent ions in D₂O to induce long-range ordering of water molecules (45) may lead to slight differences in protein assembly that affect the filament properties.

Figure 4.

The effects of changing the solvent to 45% D₂O. (A) The VIF network without divalent cations is stiffer. (B) G₀ is no longer concentration-dependent, and networks are stiffer overall. (C) Ca-VIF networks are stiffer than Zn-VIF networks. To see this figure in color, go online.

When zinc or calcium divalent cations are introduced into the system, the dependence of stiffness on the ion concentration appears to disappear in both cases; instead, the networks made with each ion species are all about the same stiffness. Notably, this stiffness is slightly higher in the Ca-VIF networks than in the ones prepared with Zn²⁺ (Fig. 4, B and C), which is reminiscent of the different maximal stiffnesses achieved by each species in a standard buffer. This provides further evidence that calcium ions are able to stiffen VIFs more but that zinc ions are highly effective at very low concentrations. At high R, the Ca-VIF network softens, likely because of bundling. Conversely, the Zn-VIF network remains stiff at high R, suggesting that D₂O may stabilize the system against counterion-induced aggregation in some cases. Despite its chemical similarity with H₂O, D₂O has significant effects on vimentin subunits, VIFs, and their interactions with ions. Whether these are effects of ion solubility or other ionic characteristics cannot be inferred at this time. Nevertheless, these results provide crucial support for the importance of hydrogen bonding and ion hydration in the interactions between VIF and divalent cations.

Competitive binding of Zn²⁺ and Ca²⁺

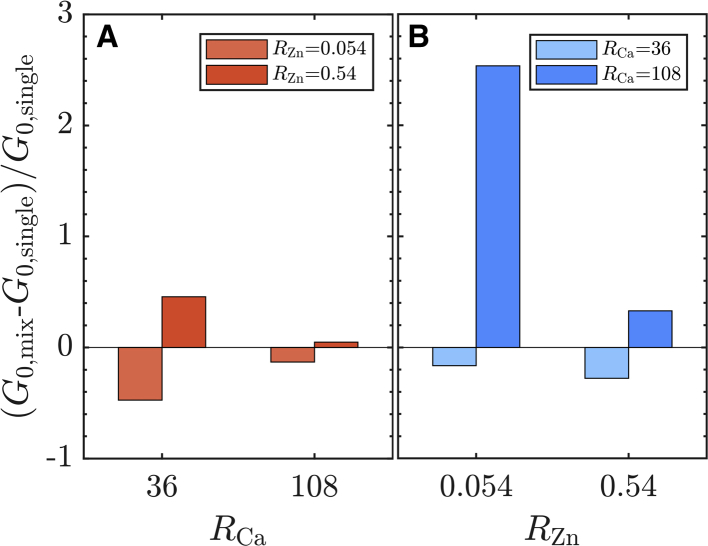
In cells, divalent ion species rarely exist in isolation; instead, the coexistence of many species is much more common. Thus, we study the network mechanics in the presence of mixed ion solutions. Holding the vimentin protein concentration constant, we vary the mixtures of Ca²⁺ and Zn²⁺ using two different concentrations of each ion within the cross-linking regime (R_Ca = 36 and 108, R_Zn = 0.054 and 0.54) and measure the microrheological properties of the resultant networks. To determine the influence of each component, we calculate the fractional change in network stiffness relative to the single-species VIF networks, (G_{0, mix} − G_{0, single})/G_0, single. For each combination, we compare G_{0, mix} with the stiffness of its components, G_{0, Zn} and G_{0, Ca}. Naively, we might expect the effects to be additive because the total divalent ion concentration increases. However, we find, instead, that the stiffness depends on the concentrations. When R_Ca = 36, the addition of either amount of Zn²⁺ changes the network stiffness by almost 50% compared to the reference Ca-VIF stiffness, as seen in Fig. 5 A. By comparison, adding Ca²⁺ at a concentration of R_Ca = 36 to Zn-VIF networks results in smaller changes to the network stiffness (Fig. 5 B). The mixed ion network stiffness is in between those of the single-species Ca-VIF and Zn-VIF networks but is closer to the Zn-VIF stiffness in both cases, suggesting that vimentin may slightly prefer to bind Zn²⁺ at these concentrations. However, at R_Ca = 108, the mixed ion networks are about the same stiffness as the reference Ca-VIF (Fig. 5 A), indicating that networks with high concentrations of Ca²⁺ are not sensitive to the presence of Zn²⁺. Correspondingly, when this amount of Ca²⁺ is added to Zn-VIF networks, it results in significant stiffening when R_Zn = 0.054 and slight stiffening when R_Zn = 0.54 (Fig. 5 B). Thus, it appears that there is competition between the ion species in two regimes: one at lower R_Ca where the single-species network stiffnesses are comparable and Zn²⁺ has a stronger influence, and another at higher R_Ca, where the effect of Ca²⁺ dominates. This result is likely related to the differences in their cross-linking behavior as well as the number of ions present because Ca²⁺ ions outnumber Zn²⁺ ions by tens to thousands of times.

Figure 5.

Mixtures of Zn²⁺and Ca²⁺ show binding competition between the ion species. The fractional change in modulus when the mixtures are viewed as (A) Zn²⁺ added to Ca-VIF networks and (B) Ca²⁺ added to Zn-VIF networks. To see this figure in color, go online.

Molar ratios of R = 36 and 108 correspond to absolute calcium concentrations of 0.67 and 2 mM, respectively. The two Zn²⁺ concentrations are equivalent to 1 and 10 μM. Compared to reported ion concentrations in the cytosol, these concentrations are likely to be on the higher end of what is typically available in a cell; however, the ions that are bound or sequestered, including those bound to VIFs, may result in high local concentrations of Ca²⁺ and Zn²⁺. By preferentially binding different ion species at different concentrations, vimentin subunits and VIFs could also serve in a regulatory or buffering role. As it interacts with the ions, the mechanical properties of the VIF network also change. For example, during a Ca²⁺ influx, the excess Ca²⁺ may further stiffen the VIF network, thereby enhancing protection of the cell against the external stress that triggered the spike. Additionally, the stiffening of VIFs has the potential to affect force propagation through the network as well as its mechanical interactions with other cytoskeletal proteins such as actin. Furthermore, intermediate-filament-associated proteins such as plectin, which can also cross-link VIFs, may have interesting effects when considered together divalent cations, and this will be an important topic for future studies. These results point to structural and mechanical adjustments of vimentin as a means by which cells can modify their internal mechanics in response to stress.

Conclusion

We have shown that the interactions between divalent cations and VIFs do affect the protein structure and mechanics in profound ways. Vimentin is a highly charged polyelectrolyte that forms very flexible polymers. Its flexibility is necessary in cellular functions that involve localizing cytoplasmic organelles and proteins (46,47), but its mechanical properties are also essential for protecting the cell from external stresses. Here, we see that divalent cations, which are ubiquitous in cells, offer a simple way for the cell to regulate their cytoplasmic properties. By carefully controlling the intracellular ionic environment, cells can tune the VIF network stiffness without changing the network structure, or they can induce bundles that significantly change the structure but are less stiff overall. Furthermore, subtle differences at ion concentrations below the bundling threshold suggest that VIF could act as a zinc-specific buffer, which may be important in some signaling events; this may be due to specific interactions between zinc and the single cysteine residue in the rod domain. Ion-specific effects may also become more important as cells experience forces on different timescales or as deformations become larger. Moreover, as vimentin is not the only filamentous protein in cells but is well integrated into the cytoskeleton, its mechanical properties are bound to affect the entire system via its interactions with the other mechanical elements.

Author Contributions

H.W. and Y.S. designed and performed experiments. H.W. and D.W. contributed analytic tools, and H.W. analyzed the data. H.W., H.H., R.D.G., and D.A.W. wrote the manuscript.

Editor: David Sept.