GAN and Dual-Input Two-Compartment Model Based Training of a Neural Network for Robust Quantification of Contrast Uptake Rate in Gadoxetic Acid-Enhanced MRI

Abstract

Purpose:

Gadoxetic acid uptake rate (k₁) obtained from DCE MRI (Dynamic, Contrast Enhanced MRI) is a promising measure of regional liver function. Clinical exams are typically poorly temporally characterized, as seen in a low temporal resolution (LTR) compared to high temporal resolution (HTR) experimental acquisitions. Meanwhile, clinical demands incentivize shortening these exams. This study develops a neural network based approach to quantification of k₁, for increased robustness over current models such as the linearized single-input, two-compartment (LSITC) model.

Methods:

30 Liver HTR DCE MRI exams were acquired in 22 patients with at least 16 minutes of post-contrast data sampled at least every 13 seconds. A simple neural network (NN) with 4 hidden layers was trained on voxel-wise LTR data to predict k₁. LTR data was created by subsampling HTR data to contain 6 time points, replicating the characteristics of clinical LTR data. Both the total length and the placement of points in the training data was varied considerably to encourage robustness to variation. A GAN (Generative Adversarial Network) was used to generate arterial and portal venous inputs for use in data augmentation based on the dual-input, two-compartment, pharmacokinetic model of gadoxetic acid in the liver. The performance of the NN was compared to direct application of LSITC on both LTR and HTR data. The error was assessed when subsampling lengths from 16 to 4 minutes, enabling assessment of robustness to acquisition length.

Results:

For acquisition lengths of 16 min NRMSE (Normalized Root-Mean-Squared Error) in k₁ was 0.60, 1.77, and 1.21, for LSITC applied to HTR data, LSITC applied to LTR data, and GAN augmented NN applied to LTR data, respectively. As the acquisition length was shortened, errors greatly increased for LSITC approaches by several folds. For acquisitions shorter than 12 minutes the GAN augmented NN approach outperformed the LSITC approach to a statistically significant extent, even with HTR data.

Conclusions:

The study indicates that data length is significant for LSITC analysis as applied to DCE data for standard temporal sampling, and that machine learning methods, such as the implemented NN, have potential for much greater resilience to shortened acquisition time than directly fitting to the LSITC model.

1. INTRODUCTION

Gadoxetic acid enhanced dynamic MRI has been shown to have promising applications in the assessment of liver function^1–6 and diagnosis of various pathologies in the liver^7–12. Gadoxetic acid provides utility as a hepatobiliary contrast, allowing interrogation of the uptake of contrast into the hepatocytes as well as liver perfusion parameters. Various pharmacokinetic parameters have been used as a measure of regional liver function^1,13–15 with gadoxetic acid uptake rate being among the most direct due to its correspondence with the number of functioning hepatocytes, making it a reasonable quantitative measure of regional liver function^6,16. Quantification of regional liver function is important in functional avoidance therapy, where radiation therapy is optimized to spare highly functional regions of the liver^17,18. Many models exist for the analysis of contrast kinetics in MRI^19–22. Fewer models are specifically applicable for determining gadoxetic acid uptake rate in the liver, including the dual-input, two-compartment (DITC) model of gadoxetic acid kinetics, and the DITC derived linearized single-input, two-compartment model (LSITC)^3,23. Most models are applicable to the high temporal resolution (HTR) dynamic, contrast enhanced (DCE), scans that collect volumes regularly enough to well characterize the concentration across time in the relevant regions, typically sampling every 5 to 15 seconds. However, the most common clinical gadoxetic acid enhanced MRI exams do not sample this comprehensively. Clinical multiphase scans are obtained for metastases detection and diagnosis. These clinical exams typically have low temporal resolution (LTR), with as few as 6 volumes irregularly sampling 20 minutes of contrast kinetics. It should also be noted that clinical demands inevitably incentivize shortening exams. If quantification accuracy can be maintained or improved while shortening total acquisition time and eliminating the need for constant acquisition (e.g. LTR style acquisitions), the patient can be given equivalent care with less inconvenience and discomfort, and minimal change to common clinical workflows.

This motivates the development of methods for accurate quantification of regional liver function from short and poorly characterized DCE MRI exams in a robust manner. This study develops an artificial neural network (NN) approach to predict k₁ from LTR data. Furthermore, this approach uses data augmentation from a generative adversarial network (GAN) implemented to allow realistic and varied simulation of gadoxetic acid dynamics from the DITC model of gadoxetic acid kinetics in the liver. These approaches are compared to least squares fitting of the LSITC model³ as applied to both HTR and LTR data. We hypothesize that the new NN approach allows faster and more convenient acquisition without a sacrifice to the accuracy of functional maps sufficient to compromise treatment guidance.

2. METHODS

A NN based approach is developed to predict k₁ from LTR data derived from DCE scans. To counter the inherent granularity of the underlying input functions a GAN is used to generate input functions for the augmentation of NN training. The NN based approaches are compared to LSITC analysis for both well characterized HTR data, and the more limited LTR data with varied acquisition duration to assess robustness of the approaches.

2.1. Models

The dual-input, two-compartment (DITC) model (Figure 1) of gadoxetic acid in the liver describes the contrast concentration dynamics in the liver at a given time as determined by the uptake rate (k₁), distribution volume (v_dis), arterial rate (k_a), portal venous rate (k_pv), and the respective portal venous and arterial blood arrival delays (T_pv and T_a)^3,23. This allows simulation of concentration for any given set of parameters and inputs, or fitting of the observed output to find the likely input parameters.

Figure 1.

A dual-input two-compartment pharmacokinetic model of gadoxetic acid in the liver.

If prediction of uptake is of chief interest, a simpler linearized single-input, dual-compartment (LSITC) model can fit to the observed data. This LSITC model is derived from the DITC model, but allows for more robust and rapid analysis over more limited datasets. Whereas fitting the DITC model involves 6 tunable parameters, with appropriate assumptions it collapses to the LSITC model described by the following 2 parameter linear equation³.

$$\stackrel{y}{\overbrace{\frac{(1-Hct)C_t\left(t\right)}{C_a\left(t\right)}}}=\stackrel{\mathit{\text{slope}}}{\overbrace{v_{dis}{k}_1}}\stackrel{x}{\overbrace{\frac{{\int }_0^t{C}_a\left(\tau \right)d\tau \mathrm{ }}{C_a\left(t\right)}}}+\stackrel{\mathit{\text{intercept}}}{\overbrace{v_{dis}}}$$ (1)

where C_t is the measured contrast concentration in the region of interest, C_a is the concentration in the arterial blood supply, k₁ is the contrast uptake rate, v_dis is the volume-normalized volume of distribution, and Hct is the hematocrit. Since C_t, C_a and Hct can be measured or estimated, the parameters to fit are k₁ and v_dis. This model applies after some point in time t₀ when the model assumptions hold. Thus, after t₀, k₁ and v_dis can be easily computed through a linear regression of the relevant data formulated as the vectors x and y.

2.2. Data acquisition

In order to assess error across analysis types and data characteristics, 3D volumetric DCE MRI of the liver were acquired during the intravenous injection of a single standard dose of gadoxetic acid using a Golden-Angle Radial sampling VIBE sequence on a 3T scanner (Skyra, Siemens Healthineer) in a prospective protocol approved by University of Michigan Institutional Review Board. 30 exams were acquired over a set of 22 patients (Age: 50 to 82 years, 6 female) with hepatocellular carcinoma. The 3D free-breathing DCE images of the liver were acquired using a 3D golden-angle radial stack-of-stars VIBE sequence. This sequence over-samples the center of k-space, and allows greater resilience to motion effects than other sequences²⁴. The time-series images were co-registered within the liver VOI using an over-determined, rigid-body transformation approach²⁵. All acquisitions continued for 16–20 minutes after injection of a single-dose gadoxetic acid contrast and had temporal resolutions of at least 5 samples per minute.

The acquired HTR data was subsampled to produce corresponding LTR data (Figure 2). This was done by interpolating (1) a pre-contrast volume, (2) 3 volumes spaced 25 seconds apart designed to capture the arterial and portal venous phases, and (3) two volumes at the end and midpoint of the acquisition (roughly 20 and 10 min, respectively).

Figure 2.

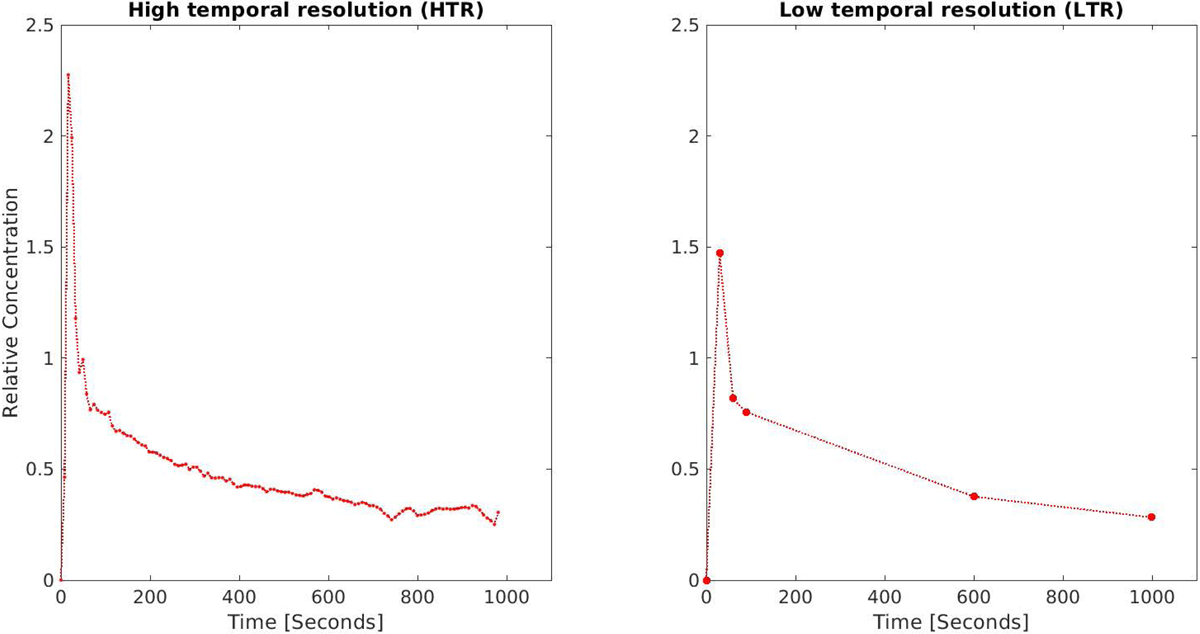
Illustration of characteristics of densely sampled high temporal resolution (HTR – left) and more sparsely sampled low temporal resolution (LTR - right) datasets. HTR data is regularly sampled at 5–10 s intervals for the duration of 16–20 min. LTR data involves the acquisition of three post contrast samples uniformly spaced at intervals of 15 to 35 seconds, followed by two points, one at roughly 10 min and another at roughly 20 min post contrast. LTR data is the clinical norm.

C_a, C_pv, and C_t were obtained as described in a prior study³. In brief, the arterial concentration (C_a) was defined by the mean 100 voxels with the maximum value just prior to the arterial peak, and selected from the three inches of aorta just prior to the aortic split to the liver.

The portal venous concentration (C_pv) was defined analogously based on a contour of the portal vein. In both cases relative enhancement was used to create the input functions:

$$C\left(iT\right)\propto \frac{S{I}_i}{S{I}_{\mathit{\text{precontrast}}}}-\mathit{1}$$ (2)

where C(iT) is the relevant concentration at time point i, given a sampling interval of T, and SI_i and SI_precontrast are the average signal intensities in the given region at time point i, and prior to contrast enhancement respectively. The same calculation was performed for each voxel in the liver to obtain the tissue concentration (C_t).

2.3. Least squares fitting of LSITC model

LSITC analysis involved linear regression for the best fit to equation (1). For HTR data t₀ was selected to maximize the linearity of the time range being fit, as described in prior work³. In the analysis of the synthetic LTR data, t₀ was chosen 75 seconds after the initial upswing of the arterial peak. In both cases the resulting estimate of the k₁ was the intercept normalized slope of the least squares linear fit from t₀ to the final point. This allowed the linear fit to incorporate 3 points for the LTR data.

2.4. Neural network – rationale and implementation

Given a reasonable set of patients with k₁ estimated from HTR data, a machine learning approach is a natural means for creating a prediction from a subset of that data, e.g., multiphase LTR data. To this end, a simple fully connected neural network (NN) with 4 hidden layers (10,10, 5 and 5 neurons) was trained on voxel-wise LTR data to predict k₁ (Figure 3). Both the total acquisition length and the placement of points in the training data were varied considerably to encourage robustness to variation. This was performed by having the arterial and portal venous phase points sampled uniformly 15 to 50 seconds apart, with uniformly distributed perturbation up to 10% of the sampling period. The endpoint t_end was randomly selected from a uniform distribution from 5 minutes after the arterial upswing until the end of the acquisition. The midpoint sample was selected from a uniform distribution from 0.25t_end to 0.75t_end. Each voxel then consisted of 5 pairs of values representing the x and y vectors calculated from equation (1) based on 5 post-contrast time points (as in the right panel of Figure 2).

Figure 3.

The design of the GAN used for the generation of C_a and C_pv curves. Parenthetical values represent the dropout rate for dropout layers, the gradient of the leaky Relu, and the number of elements for other layers.

Training was performed by randomly selecting 3 million voxels in the livers from 30 exams, holding 3/5^ths for training, 1/5^th for validation, and 1/5^th for testing. Training and validation data did not have patients that overlapped with the patients in the data held for testing.

2.5. GAN

2.5.1. GAN - rationale

No matter how many voxels are used for training, if we have only a pool of 30 exams, and 22 patients, each voxel will come from one of 30 categories defined by the precise input functions that corresponded to that exam. This inspires data augmentation for the set of input functions to ensure the training data is better spread across the reasonable space of input functions. A GAN is a reasonable choice for this generative task. This approach trains both a generator and a discriminator, who act as adversaries to one another. The generator seeks to generate artificial input functions that are in the space of real input functions. The discriminator attempts to discriminate between the real examples and those generated artificially. Eventually, the generated examples should be essentially indistinguishable from examples drawn from the true dataset. GANs have been applied in a number of circumstances, involving both temporal biological signal²⁶ and medical image^27,28 generation, including generation for data augmentation²⁹. Here we use a generative adversarial neural network to generate arterial and portal venous input functions for gadoxetic acid dynamics in the liver.

2.5.2. GAN design and implementation

The GAN consisted of a simple network for conversion of a random vector (length 20) into outputs corresponding to arterial (C_a) and portal venous (C_pv) input functions (two vectors of length 100) along with an indicator of the sampling period T. The network architecture can be seen in figure 4.

Figure 4.

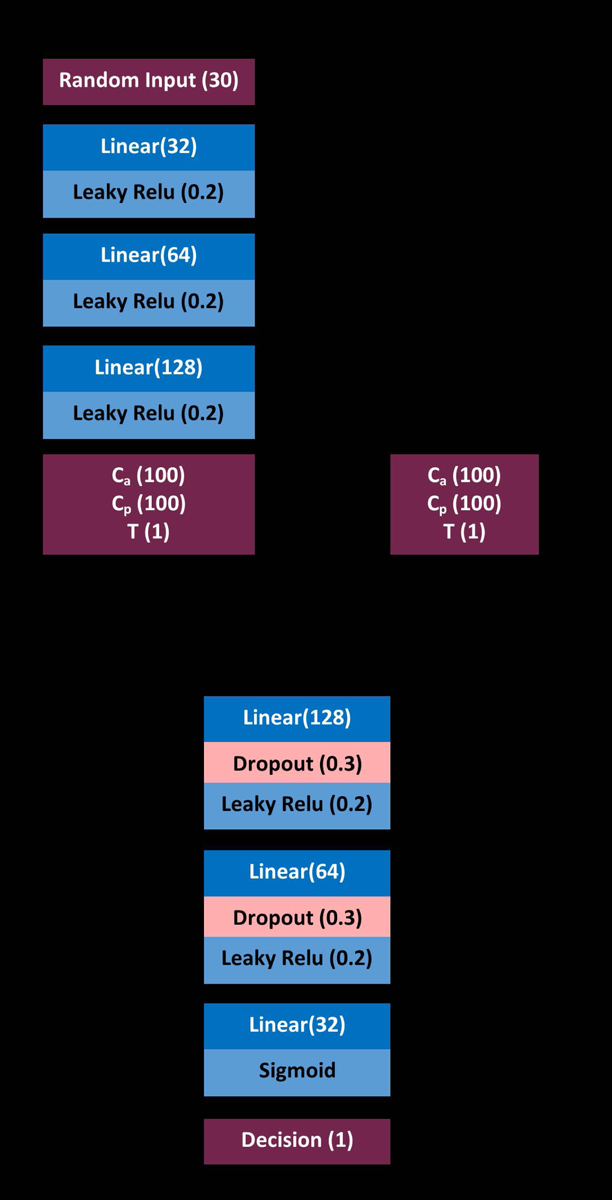
The design of the GAN used for generation of C_a and C_pv curves. Parenthetical values represent the dropout rate for dropout layers, the gradient of the leaky Relu, and the number of size for all other layers.

The generated input functions are then used as to create tissue concentration curves (C_t) using the DITC model.

2.5.3. NN augmentation from GAN data

Training using the GAN generated data serves a dual purpose – firstly it acts as a confirmation that the GAN generated data is actually representative of the real C_a and C_pv curves, secondly, it could improve prediction accuracy with comparatively minimal chance of overfitting, based on the increased variability in C_a and C_pv for the training data. This dataset then has ground truth DITC defined uptake rates with input functions replicating the variation observed empirically. This data can be used to augment the real data in training neural models to determine uptake from restricted datasets.

In order to train a network to generated C_a and C_pv curves from a random vector, training data was created by first generating 1 million random C_a and C_pv pairs with corresponding T. This was performed for 5 holdout groups of patients corresponding to the training holdout groups described in 2.4 to ensure the learned sets were not influenced by testing patients’ own data. For each of these sets of C_a and C_pv curves, k₁ and v_dis values were randomly selected from the relevant patient set (excluding holdout patients), while k_a, k_pv, T_a and T_pv were randomly selected from roughly physiologically reasonable ranges (see table 1). C_t curves were then generated from the DITC model using the GAN generated C_a and C_pv functions along with the random parameters described in table 1 as inputs to the model. Finally, gaussian distributed noise was added such that the measured SNR would be 40 dB.

Table 1.

The values used for the generation of training data using the dual-input, two-compartment model. Note that U(a,b) is the uniform distribution from a to b, and N(μ,σ²) is the normal distribution about μ with standard deviation σ. In this case the normal distribution was truncated to remove results outside the range [0,1].

Parameter	Distribution
k1,vdis	Randomly drawn from patient set	mL/100mL/min, mL/mL
kpvp+ kap	U(50,300)	mL/100mL/min
kpvp	N(0.75, (1/16)2)(kpvp+ kap),	mL/100mL/min

2.5.4. LSITC optimization from GAN data

Finally, consideration was given to minimize the error in LSITC analysis. The two obvious “tunable” parameters are t₀ and sampling time. The parameter t₀ refers to the first time point considered to satisfy the conditions of the LSITC model and thus used as the first point in the linear fit of the model. This is currently selected through a maximization of linearity as calculated by the ratio of singular values³. Determination of the sampling times is more complex, particularly if we implement irregular sampling as in LTR collection. This study uses the GAN simulated data to optimize t₀ and the sampling times, discretized in 30 second increments, for the LSITC analysis. Optimization is performed using a genetic algorithm to search for t₀ and sampling times. Breaking the signal into 30 seconds intervals increased the tractability of the problem for this discrete genetic algorithm. This resulted in each of the sampling points being chosen from 32 intervals of 30 seconds in the 16 minute datasets, where the first and last points are required. This was performed for 1 to 10 additional points, where the choice of points was optimized to minimize MSE error in a set of GAN based DITC generated synthetic voxels.

2.6. Error metric for evaluation of analysis methods and acquisition paradigms

For each method and dataset used to estimate k₁, the error was measured as NRMSE with the results of least squares fitting of the LSITC model for the full length (16–21 min) HTR dataset as the reference. NRMSE is defined here as RMSE normalized on an exam by exam basis by the interquartile range of the reference values as:

$$\mathit{\text{NRMSE}}=\frac{\mathit{\text{RMSE}}}{\mathit{\text{interquartile range}}}$$ (3)

Mean NRMSE is merely the mean across all exams analyzed.

The reference values were restricted to the values with a relative uncertainty below the 75^th percentile. This minimizes the likelihood of performing the comparison with outliers and artifacts, such as those seen on some edges, but will also tend to decrease the denominator in the NRMSE calculation.

Relative uncertainty was measured as the expected standard deviation in k₁ estimation for the fit in a given voxel divided by the predicted k₁ for that voxel. Here the variance in k₁ is estimated by the Taylor expansion of the variation of K₁/v_dis (where K₁ is the slope in equation 1) as:

$$var\left(k_1\right)=var\left(\frac{K_1}{v_{dis}}\right)\approx {{\mu }_{K_1}}^2/{{\mu }_{v_{dis}}}^2(\frac{{{\sigma }_{K1}}^2}{{{\mu }_{K1}}^2}-\frac{2Cov\left(K_1,v_{dis}\right)}{{\mu }_{K1}{\mu }_{v_{dis}}}+\frac{{{\sigma }_{v_{dis}}}^2}{{{\mu }_{v_{dis}}}^2})$$ (4)

where

$${\sigma }_{K_1}=\sqrt{\frac{\sum _{\mathit{i}:xi=x0}^{}{({\widehat{y}}_i-y_i)}^2}{(n-2)\sum _{i:xi=x0}^{}{(x_i-{\stackrel{-}{x}}_i)}^2}}$$ (5)

$${\sigma }_{v_{dis}}=\sqrt{\left(\frac{1}{n}\right){\sum }_{i:xi=x0}^{}{\left(x_i\right)}^2}$$ (6)

Where σ_a and μ_a are the respective standard deviations and means of any given measure a. x and y are defined in equation 1.

All results from five methods and datasets were compared to the k₁ estimated by fitting the LSITC model for HTR data at maximum length (at least 16 minutes and no more than 21 minutes), which are summarized in table 2.

Table 2.

The abbreviations used for each method and data pairing evaluated along with a description of the relevant method and data.

Method/Data Abbreviation	Method Description	Input Data Description
LSITC-HTR	Fitting of LSITC model with t0 chosen to maximize linearity	HTR data, with the data length truncated to a maximum length of 4 to 16 minutes
LSITC-LTR	Fitting of LSITC model with t0=75 seconds	LTR data, with the data length truncated to a maximum length of 4 to 16 minutes. The initial points spaced at 25 second intervals.
NN-LTR	Application of the NN model trained by k1 resulting from LSITC-HTR for full HTR datasets	LTR data, with the data length truncated to a maximum length of 4 to 16 minutes. The initial points spaced at 25 second intervals.
Augmented NN-LTR	Application of the NN model trained by DITC based data using input functions generated by GAN.	LTR data, with the data length truncated to a maximum length of 4 to 16 minutes. The initial points spaced at 25 second intervals.
OPT LSITC-LTR	Fitting of LSITC model with algorithmically chosen sampling times and t0	8 points selected algorithmically to minimize error in augmented dataset. Truncated to a maximum length of 8 to 16 minutes.
LSITC HTR t0 = OPT	Fitting of LSITC model with HTR data but t0 set to the optimum found in OPT LSITC-LTR	HTR data, with the data length truncated to a maximum length of 4 to 16 minutes

3. RESULTS

3.1. Fitting of LSITC model

As expected, directly fitting the LSITC model to HTR data yielded more accurate k₁ values than fitting to LTR data. For both datasets the errors grew rapidly with a decrease in the acquisition length of the data (see figure 5). At full acquisition length (16 minutes), LSTIC-HTR and LSITC-LTR resulted in an average NRMSE across exams of 0.60 (SD 0.38) and 1.77 (0.99), respectively. At an acquisition length of 10 min the average NRMSE increased to 2.59 (1.34) and 3.09 (1.54) for HTR and LTR datasets, respectively, as seen in table 3. A visual comparison at 10 minutes can be seen in figure 6.

Figure 5.

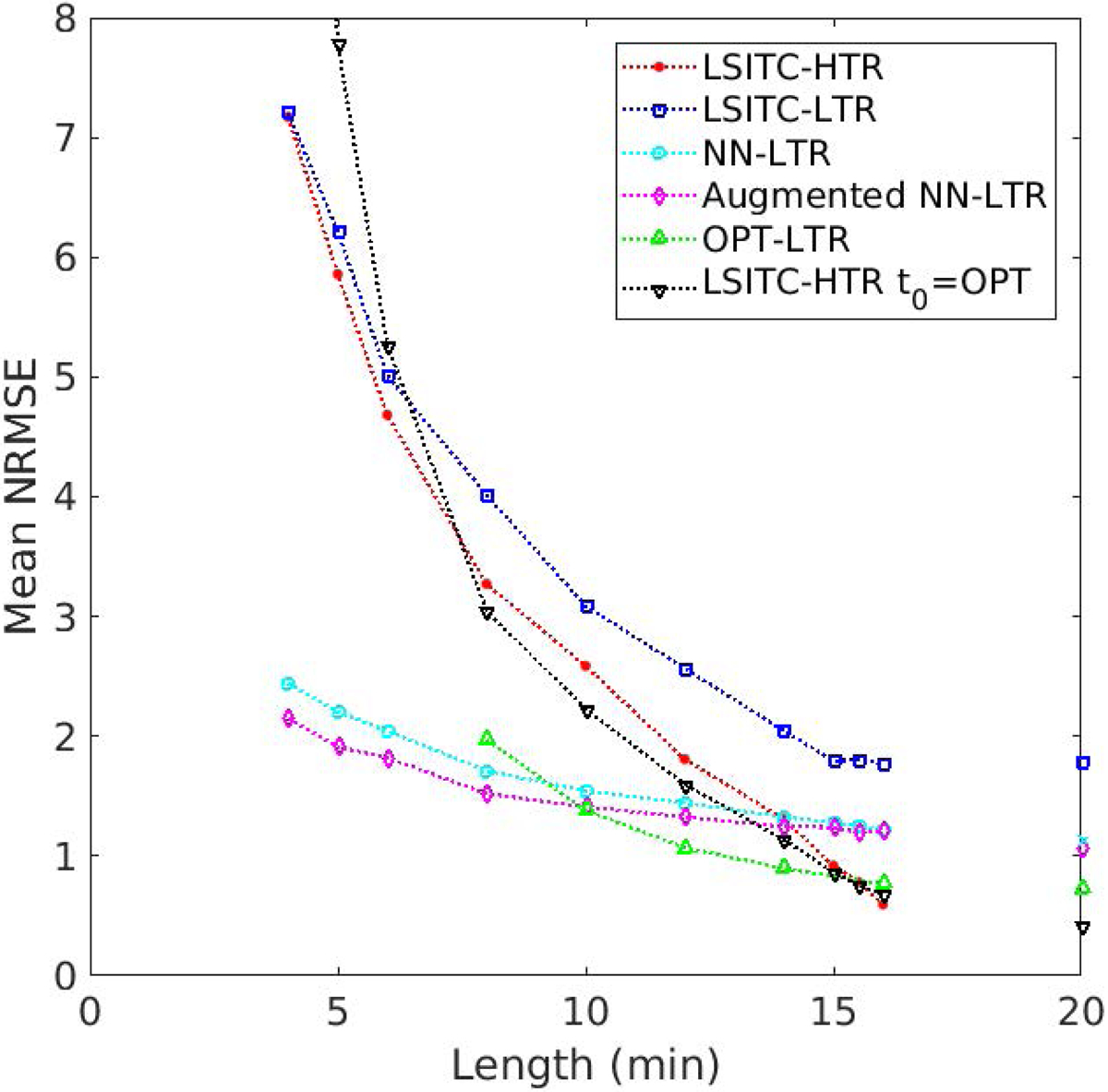
Errors of estimated k₁ values with varied acquisition lengths for the tested methods.

Table 3.

Error rates (NRMSE) for each method as function of data length. Statistically significant improvements in NRMSE over LSITC HTR are indicated by an asterisk (*). Statistically significant increases in error are indicated by a negated asterisk (⁻*). Significance was estimated based on a two sample t-test with a significance level of 0.05, except for the Max row, where a single sample t-test was used.

Series Duration (min)	NRMSE - mean (standard deviation)
	LSITC HTR	LSITC LTR	NN LTR	Augmented NN LTR	OPT LSITC LTR	LSITC HTR t0 = OPT
4	7.17 (4.39)	7.21 (3.93)	2.44 (2.06)*	2.15 (1.78)*		14.64 (9.44) −*
5	5.86 (3.47)	6.21 (3.24)	2.21 (1.79)*	1.91 (1.43)*		7.78 (4.58)
6	4.68 (2.72)	5.01 (2.95)	2.04 (1.52)*	1.82 (1.16)*		5.27 (3.18)
8	3.27 (1.79)	4.02 (2.35)	1.71 (1.15)*	1.52 (0.85)*	1.97 (1.39)*	3.05 (1.78)
10	2.59 (1.34)	3.09 (1.54)	1.54 (0.93)*	1.41 (0.75)*	1.38 (0.72)*	2.23 (1.17)
12	1.81 (1.08)	2.57 (1.39) −*	1.44 (0.79)	1.32 (0.67)*	1.07 (0.57)*	1.60 (0.99)
14	1.31 (1.01)	2.05 (1.27) −*	1.32 (0.71)	1.24 (0.62)	0.90 (0.53)	1.14 (0.90)
15	0.92 (0.61)	1.79 (1.07) −*	1.28 (0.68)−*	1.24 (0.63)		0.86 (0.62)
15.5	0.78 (0.52)	1.80 (1.02) −*	1.25 (0.64) −*	1.20 (0.58) −*		0.76 (0.54)
16	0.60 (0.38)	1.77 (0.99) −*	1.22 (0.69) −*	1.21 (0.66) −*	0.77 (0.42)	0.68 (0.50)
Max	0.00 (0.00)	1.39 (0.80) −*	1.14 (0.58) −*	1.06 (0.56) −*	0.72 (0.33) −*	0.42 (0.26) −*

Figure 6.

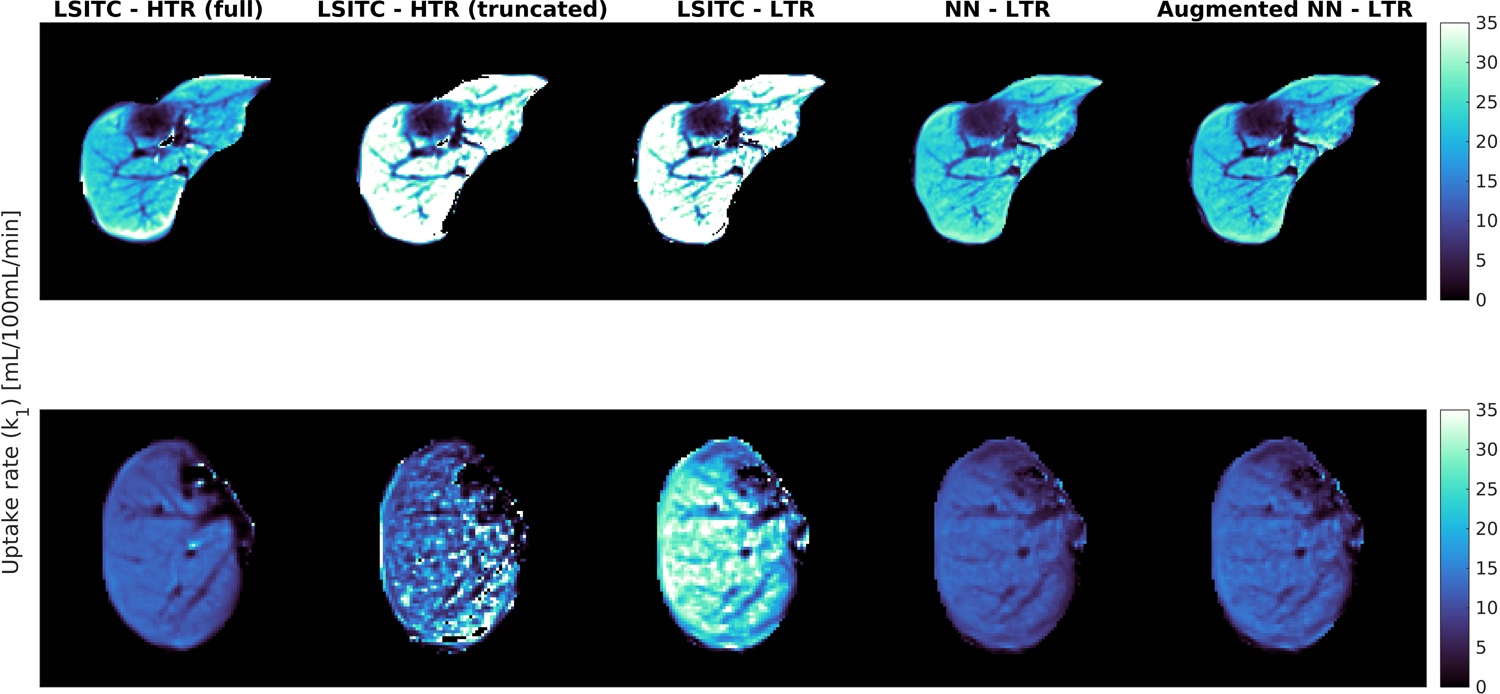
The k₁ maps created using the HTR and LTR data truncated at 10 min both from directly fitting the LSITC model (second and third columns) and from the NN and GAN augmented NN models (fourth and fifth columns respectfully). The first column displays the reference k₁ images by fitting the LSITC model to full length HTR data acquired over approximately 20 min.

3.2. NN model

The NN model yielded significantly reduced error rates in k₁ estimation over direct fitting of the LSITC model to the LTR data at all tested acquisition lengths (4–20 min). When the acquisition length was less than 14 min, the NN model applied to the LTR data resulted in the errors less than directly fitting of the LSITC model to the HTR data. This difference became significant for acquisitions of 10 minutes or less. The errors yielded by the NN model increased slowly with the acquisition length reduction, suggesting the NN model was resilient to data length. In contrast, direct fitting of the LSITC model yielded quickly increased errors with the data length reduction, regardless of the temporal resolution of the data (figure 5).

3.3. GAN augmented NN model

On visual inspection randomly selected curves generated by the trained GAN seemed to replicate the basic features of the measured curves without being direct copies of individual examples. For randomly selected GAN generated C_a curves, the nearest normalized neighbor was found from the measured set of input curves. Three examples are shown in figure 7. In each column the top plot is a randomly selected generated C_a and C_pv pair, and the bottom plot is the real C_a and C_pv pair whose normalized C_a curve is the nearest neighbor to the generated C_a curve based on a sum of squares difference. The comparisons did not show evidence of direct replication of the specifics of particular measured curves.

Figure 7.

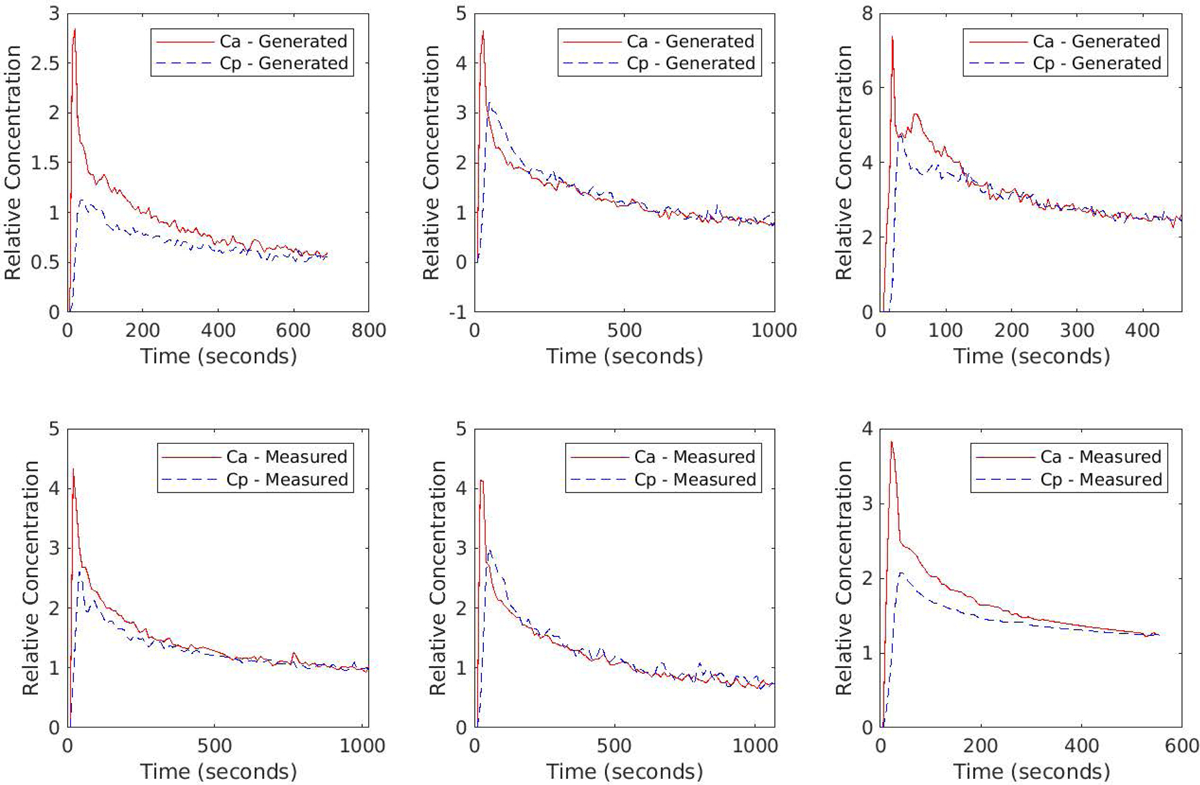
Examples of generated (top row) and nearest neighbors from the measured (bottom row) C_a and C_pv curve pairs. Nearest neighbors were calculated based on the sum of squared differences in C_a alone.

In addition to visual inspection, the distribution created by the GAN was assessed by producing histograms approximating the probability distribution of the pairwise Euclidean differences between examples within the measured data, as well as the pairwise differences in data generated by each GAN. Figure 8 displays these distributions of pairwise differences for each GAN, superimposed over the distribution of pairwise differences for the measured data. The difference between the mean distance for each GAN and the measured data is shown, along with the earth-movers-distance (EMD) to better represent the differences between distributions. In all cases the distribution of differences in GAN data visually mirrors that of the full dataset, with the smoothing we would expect from a larger number of samples from a similar dataset.

Figure 8.

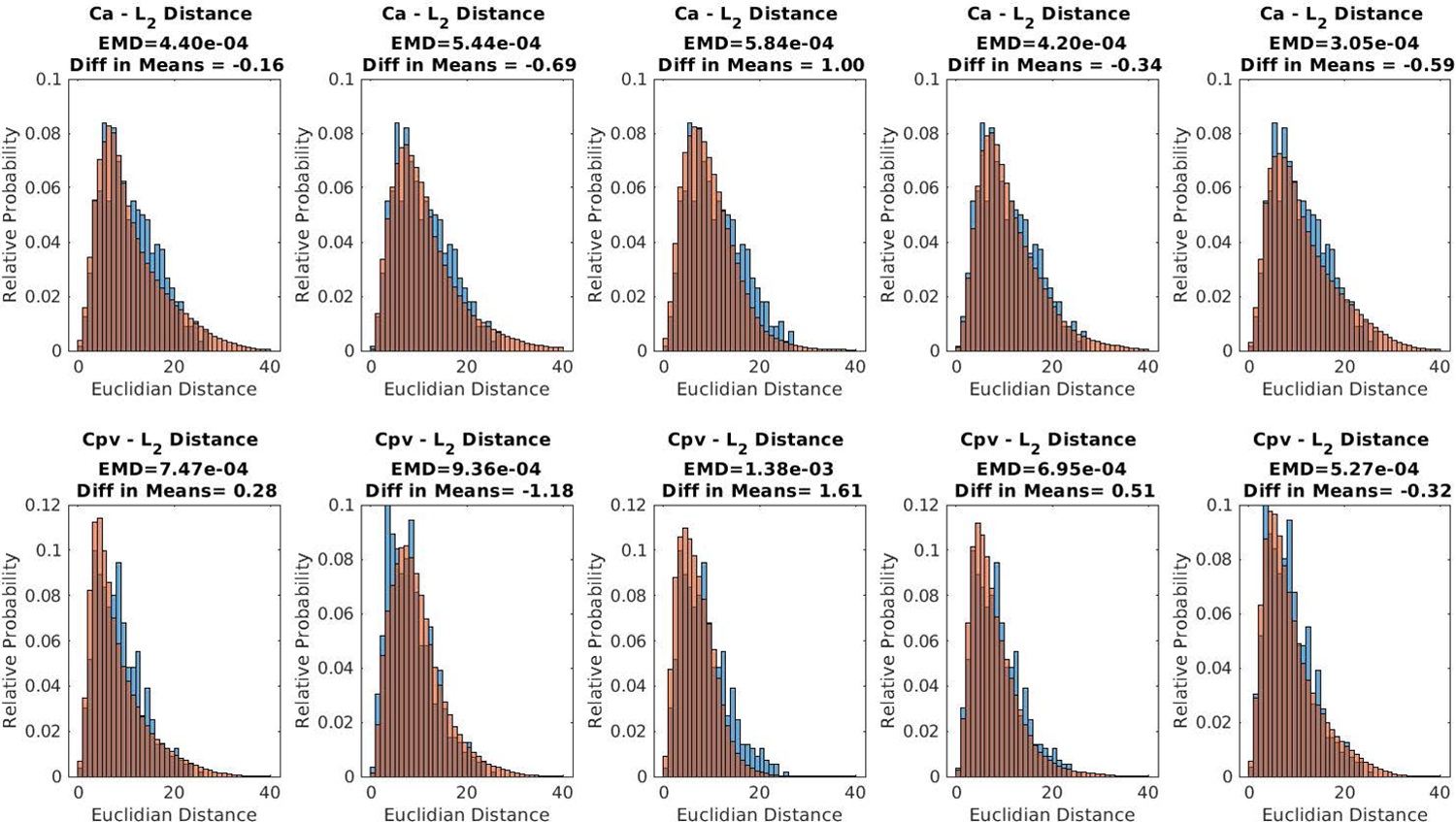
For each of the 5 GANs used, the probability distributions for L₂ norm of the distance between randomly selected C_a and C_pv curves for GAN generated data is shown in red. The probabilities for the measured data are shown in blue as reference.

Augmentation with GAN generated data gave mixed results. Training on only synthetic data resulted in improvement over prediction error from training only on real data (figure 5). With a statistically significant improvement in error over LSITC HTR for all datasets of length 12 minutes or less, and no significant drop in error up to 15 minutes. However, combining the real data with additional synthetic data did not meaningfully improve the prediction error. The results of augmented NN model trained by synthetic data only are shown in figure 5 and table 3 (Augmented NN-LTR).

3.4. Optimization of time points for the LSITC model fitting

When selecting the optimum sampling points for the LSITC model fitting, as additional points were selectively added to the set, optimization yielded a t₀ of 3 minutes in every case, without any sampling point prior to t₀. The sampling times chosen tended to group just after t₀, and near the end of the dataset. The error leveled off near 8 points in the simulated data, as seen in figure 9. As a result, 8 points were used when testing this approach, apart from the pre-contrast and final points.

Figure 9.

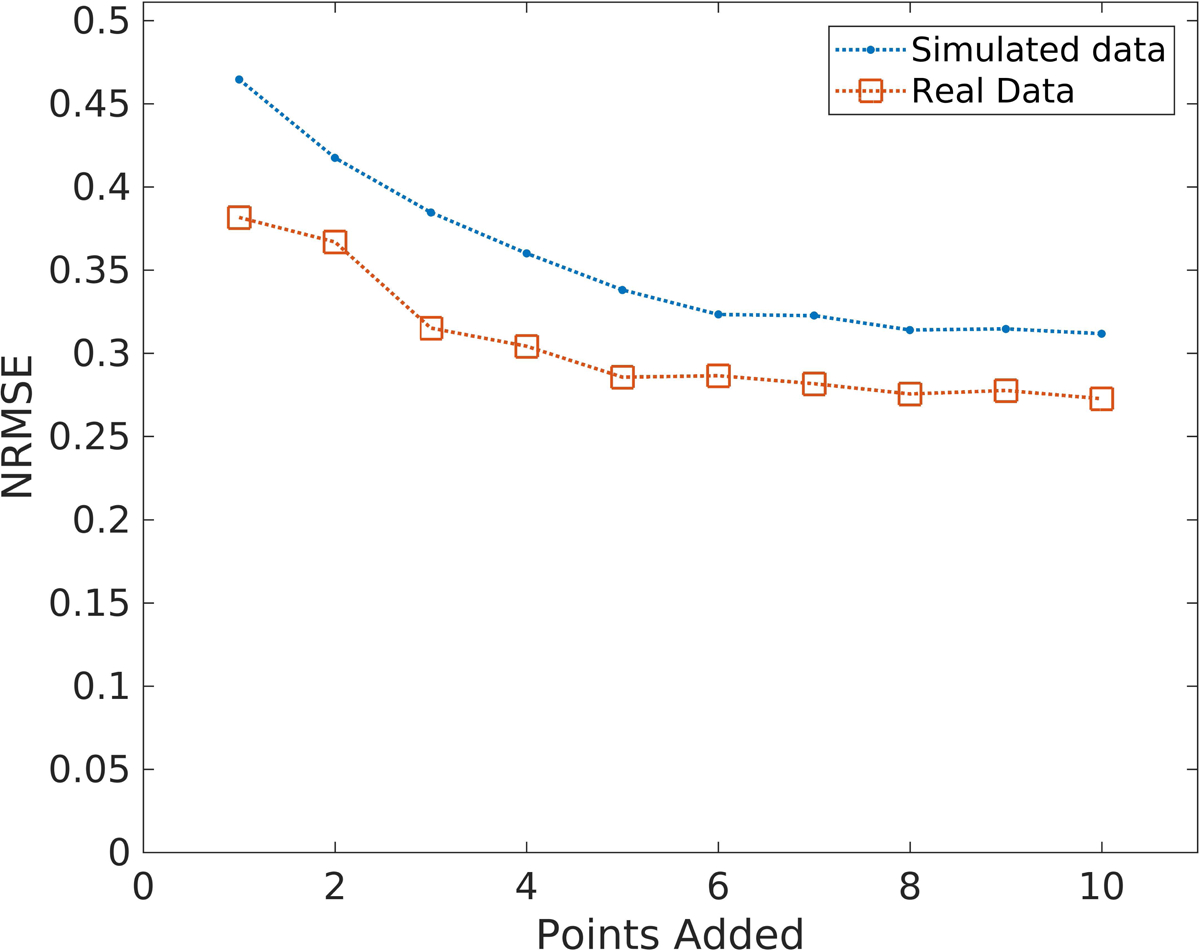
The errors in simulated and real data as a function of the number of optimum sampling points using a procedure derived from the genetic algorithm. Note that error in the data leveled off after 8 points.

Implementation of the GAN data for LSITC optimization (OPT-LSITC LTR) yielded errors significantly lower than direct fitting of the LSITC model to HTR data with acquisition lengths of 12 min or less, and lower than NN models for data lengths greater than 10 minutes (figure 5). This suggests that optimization of the time of data point acquisition could improve the performance of the LSITC model, but the NN model with non-optimized data still could perform better at a short acquisition length.

A further test of the optimal t₀ (3 min) was performed with full HTR data. As seen in figure 5, the LSITC model fitting to HTR with a dynamic t₀ (LSITC-HTR) and an optimal t₀ (LSITC-HTR t₀=OPT) yielded similar results, but worse results than the LSITC model fitting to the optimal 8-point LTR data (OPT LSITC LTR), indicating that the robustness of performance of the optimized LSITC is not merely due to the choice of t₀ but due to the particular set of points selected.

4. DISCUSSION

In this study, we developed NN models for estimation of k₁ and compared the results of the NN models to those from direct fitting of the LSITC model for various acquisition lengths and temporal resolutions of Gadoxetic acid enhanced dynamic MRI of the liver. Overall, the NN models are more resilient to the acquisition length reduction. The augmented input functions using GAN can further improve the performance of the NN models. For direct fitting of the LSITC model, ten optimized time points in the Gadoxetic acid enhanced dynamic data can significantly out-perform the HTR data (5–10 sec per volume) for acquisition lengths of 12 minutes or less, and the NN method for acquisition length not shorter than 8 minutes. Our study suggests that the NN approach can be used to enhance the performance of k₁ estimation and optimize the data acquisition.

A key element of modeling liver pharmacokinetics is obtaining arterial and portal venous input functions. These input functions have been estimated using combinations of exponentials and other simplifications, but this involves either profound simplification or the development of models of increased complexity without a guarantee of successfully capturing the relevant features of the input functions. Use of measured input functions has notable advantages in capturing the true empirical characteristics of these input functions. However, when employing data driven methods this will practically limit the researcher to a relatively small number of example cases. When machine learning methods are applied to millions of voxels but the guiding input functions consist of a few dozen examples, we may fear overlearning these limited underlying examples, rather than a more useful learning of the underlying relationships between our relevant parameters and input functions in general. Addition of noise or variation in sampling time may make this underlying granularity less starkly memorable. However, a more ideal solution would be the construction of arbitrary or random input functions from the feature space the input functions inhabit. A promising means for this generative task is a generative adversarial neural network.

One difficulty in generative networks, where the network is not cyclic (generating corresponding examples in another space rather than arbitrary or random examples in the desired space) is assessment of the quality of the generative model. One approach is the usage of these examples as augmentation data for a relevant learning task. If the augmentation helps, it is more reasonable that the generative model is representing the variation in the underlying set appropriately, or at least in a way that helps the trained network to better understand the relevant relationships. Here we used a generative adversarial neural network to generate arterial and portal venous input functions for gadoxetic acid kinetics in the liver.

The augmented NN that was trained only on GAN generated data resulted in superior results as compared to the NN trained using any fraction of the measured data with HTR-LSITC as the reference. There are various possible causes of the decrease in performance with the addition of real data. It is likely that the very few input functions were not useful in further generalizing the solution over the training from the GAN and DITC generated data. It may also have skewed the solution towards those measured input functions. It should be noted that since the GAN itself is trained from measured data, the generated examples will include characteristics caused by sampling noise, movement and other variations in the data. Because of this the input to the DITC model generated from this GAN has variation that would not be expected in the underlying input functions in reality.

In addition to the already mentioned benefits, the GAN derived data and DITC model defined reference values allowed the simulated dataset to be used to evaluate independent models relative to the DITC model. This allowed us to use references of not only our best estimate (whether DITC or LSITC) to complete (16+ min) real datasets, but also to the ground truth inputs to the DITC model without fitting error in the reference k₁ values. This helps quantify possible error in these estimates and gives a parallel reference measure for restricted methods. This is of particular interest when attempting to assess optimum, or at least improved, acquisition times for the image volumes used to estimate k₁. Use of these model defined input parameters made this optimization less susceptible to a mere reproduction of the linear fit of the LSITC model (along with any limitations or errors in this method), and helped to assess the best timing (giving the variability observed in the input functions) to acquire points for LSITC without bias to the timing used in the measured reference set.

The optimal sampling points for OPT-LSITC LTR essentially followed the expected weights for a linear regression, in that points near the end were preferred, with successive trials adding points closer to the center as those at the ends were already included. The selection of t₀ is perhaps more salient, indicating that the addition of a point near the 3 min mark would aid LSITC accuracy when applied to LTR data. This time roughly corresponds to the equilibrium phase³⁰, which would logically initiate the portion of the data where the assumptions of the LSITC model hold true. This approach resulted in lower error than even LSITC applied to HTR data from 15.5 to 8 min, for the real dataset, even though the reference was used HTR data with a variable t₀. This also casts doubt on the use of 75 seconds as t₀ in LTR data. If 3 minutes is the location of the equilibrium phase, then voxel-wise LSITC analysis of most LTR data has only 2 data points to work with, since none of the arterial or portal venous phase points will fall after that point. Without an overdetermined fit the error rates will likely be large, and concurrent error quantification will rely on assumptions regarding the similarity of nearby points. However, the selection of t₀ was not the primary factor in the improvement over other LSITC methods. This is apparent from the small difference between LSITC-HTR and LSITC-HTR where t₀ = OPT. This indicates that the specific selection of points was helpful in improving the fit. It is possible that some of the improvement came from selecting no points prior to t₀. This does not change which points are fit, but does change the x and y vectors since the integral of C_a will differ in equation 1. It may be that the discrepancy of C_a from C_pv increases the error in datasets that include pre-t₀ sampling points.

Regardless of the method used the error was greater for shorter datasets. Data length was especially significant for LSITC analysis, for both LTR and HTR data. With a fixed best t₀ and careful choice of sampling points this was reduced somewhat, perhaps making acquisitions as short as 12 minutes practical. Below this level the NN methods worked best, showing relatively little change in error with data length in time. This indicates that the underlying information is sufficient for a comparatively accurate prediction even with relatively short collection time used by the NN. However, the results did not outperform LSITC-HTR for long datasets. In each of these cases it is important not to interpret the error in absolute terms, particularly near the maximum length. Remember that the error measures will be impacted by error in the results of LSITC applied to HTR.

Use of the LSITC model as the reference allowed rapid analysis and comparison with regard to k₁, even for LTR data. In a previous study, k₁ values estimated from the LSITC and DITC have been compared and the results are very similar³. However, this model does omit parameters present in the DITC model, notably k_a and k_pv. Previous studies have correlated portal venous perfusion to liver function¹³ and arterial perfusion to tumor presence²³. Theoretically, simultaneous quantification of k₁, k_a and k_pv from a single dynamic MRI acquisition using the DITC is advantageous. Practically, there are some limitations. The FDA approved standard dose of Gadoxetic acid only contains a quarter of the Gadolinium in a standard dose of Gd-DTPA or Multihance. This results in a weak contrast enhancement and a low signal-to-noise ratio in the arterial phase signals, thereby challenging reliable quantification of arterial perfusion. Therefore, in practice, if tumor diagnosis and assessment are the primary interest, Gd-DTPA or Multihance is used. If liver function measurement is the primary interest, Gadoxetic acid is used. If both tumor assessment and liver function are of interest, a trade-off has to be made. Compared to the DITC and LSITC models, the Tofts model only considers the contrast transport between the intra-vascular and the extra-cellular space, which can only be applied for an extra-cellular contrast agent, but not an intra-cellular agent, like Gadoxetic acid.

5. CONCLUSIONS

Data length is significant for LSITC analysis as applied to DCE data for standard temporal sampling. With a fixed best t₀ and careful choice of sampling points this can be reduced somewhat, particularly for acquisitions at least 12 minutes in length. Below this level the NN worked best, indicating that NN methods may be helpful in improving the robustness of uptake analysis in temporally short datasets. Combination of a GAN with DITC model created data contributed to the training of the NN, indicating the variation in input functions was being appropriately represented. Further work should assess the impact on functional avoidance therapy dependent on the means used to create functional maps.

Table of abbreviations appearing in text with corresponding definitions.

3D

Three-dimensional

DCE

Dynamic, Contrast Enhanced

DITC

Dual-Input, Two-Compartment

EMD

Earth Mover’s Distance

GAN

Generative Adversarial Network

Hct

Hematocrit

HTR

High Temporal Resolution

LTR

Low Temporal Resolution

LSITC

Linearized Single-Input, Two-Compartment

MRI

Magnetic Resonance Imaging

MSE

Mean Squared Error

NN

Neural Network

NRMSE

Normalized Root Mean Squared Error

SD

Standard Deviation

SNR

Signal to Noise Ratio