Abstract
Selection of mutants in a microbial population depends on multiple cellular traits. In serial-dilution evolution experiments, three key traits are the lag time when transitioning from starvation to growth, the exponential growth rate, and the yield (number of cells per unit resource). Here, we investigate how these traits evolve in laboratory evolution experiments using a minimal model of population dynamics, where the only interaction between cells is competition for a single limiting resource. We find that the fixation probability of a beneficial mutation depends on a linear combination of its growth rate and lag time relative to its immediate ancestor, even under clonal interference. The relative selective pressure on growth rate and lag time is set by the dilution factor; a larger dilution factor favors the adaptation of growth rate over the adaptation of lag time. The model shows that yield, however, is under no direct selection. We also show how the adaptation speeds of growth and lag depend on experimental parameters and the underlying supply of mutations. Finally, we investigate the evolution of covariation between these traits across populations, which reveals that the population growth rate and lag time can evolve a nonzero correlation even if mutations have uncorrelated effects on the two traits. Altogether these results provide useful guidance to future experiments on microbial evolution.
Keywords: Microbial evolution, fixation probability, adaptation rate
LABORATORY evolution experiments in microbes have provided insight into many aspects of evolution (Elena and Lenski 2003; Barrick and Lenski 2013; Desai 2013), such as the speed of adaptation (Wiser et al. 2013), the nature of epistasis (Kryazhimskiy et al. 2014), the distribution of selection coefficients from spontaneous mutations (Levy et al. 2015), mutation rates (Wielgoss et al. 2011), the spectrum of adaptive genomic variants (Barrick et al. 2009), and the preponderance of clonal interference (Lang et al. 2013). Despite this progress, links between the selection of mutations and their effects on specific cellular traits have remained poorly characterized. Growth traits, such as the lag time when transitioning from starvation to growth, the exponential growth rate, and the yield (resource efficiency), are ideal candidates for investigating this question. Their association with growth means they have relatively direct connections to selection and population dynamics. Furthermore, high-throughput techniques can measure these traits for hundreds of genotypes and environments (Levin-Reisman et al. 2010; Warringer et al. 2011; Zackrisson et al. 2016; Ziv et al. 2017). Numerous experiments have shown that single mutations can be pleiotropic, affecting multiple growth traits simultaneously (Fitzsimmons et al. 2010; Adkar et al. 2017). More recent experiments have even measured these traits at the single-cell level, revealing substantial nongenetic heterogeneity (Levin-Reisman et al. 2010; Ziv et al. 2013, 2017). Several evolution experiments have found widespread evidence of adaptation in these traits (Vasi et al. 1994; Novak et al. 2006; Reding-Roman et al. 2017; Li et al. 2018). This data altogether indicates that covariation in these traits is pervasive in microbial populations.
There have been a few previous attempts to develop quantitative models to describe evolution of these traits. For example, Vasi et al. (1994) considered data after 2000 generations of evolution in Escherichia coli to estimate how much adaptation was attributable to different growth traits. Smith (2011) developed a mathematical model to study how different traits would allow strains to either fix, go extinct, or coexist. Wahl and Zhu (2015) studied the fixation probability of mutations affecting different growth traits separately (nonpleiotropic), especially to identify which traits were most likely to acquire fixed mutations and the importance of mutation occurrence time and dilution factor. However, simple quantitative results that can be used to interpret experimental data have remained lacking. More recent work (Manhart et al. 2018; Manhart and Shakhnovich 2018) derived a quantitative relation between growth traits and selection, showing that selection consists of additive components on the lag and growth phases. However, this did not address the consequences of this selection for evolution, especially the adaptation of trait covariation.
In this work, we investigate a minimal model of evolutionary dynamics in which cells interact only by competition for a single limiting resource. We find that the fixation probability of a mutation is accurately determined by a linear combination of its change in growth rate and change in lag time relative to its immediate ancestor, rather than depending on the precise combination of traits; the relative weight of these two components is determined by the dilution factor. Yield, on the other hand, is under no direct selection. This is true even in the presence of substantial clonal interference, where the mutant’s immediate ancestor may have a large fitness difference from the population mean. We provide quantitative predictions for the speed of adaptation of growth rate and lag time as well as their evolved covariation. Specifically, we find that even in the absence of an intrinsic correlation between growth and lag due to mutations, these traits can evolve a nonzero correlation due to selection and variation in number of fixed mutations.
Materials and Methods
Model of population dynamics
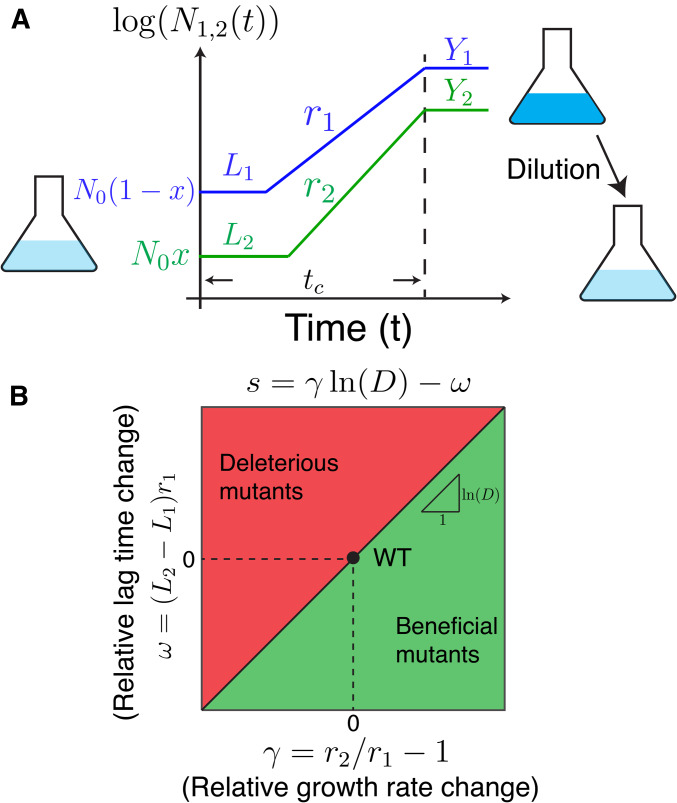
We consider a model of asexual microbial cells in a well-mixed batch culture, where the only interaction between different strains is competition for a single limiting resource (Manhart et al. 2018; Manhart and Shakhnovich 2018). Each strain k is characterized by a lag time , growth rate , and yield (see Figure 1A for a two-strain example). Here the yield is the number of cells per unit resource (Vasi et al. 1994), so that is the amount of resources consumed by time t by strain k, where is the number of cells of strain k at time t. We define R to be the initial amount of the limiting resource and assume different strains interact only by competing for the limiting resource; their growth traits are the same as when they grow independently. When the population has consumed all of the initial resource, the population reaches stationary phase with constant size. The saturation time at which this occurs is determined by which we can write in terms of the growth traits as
| (1) |
where is the total population size and is the frequency of each strain k at the beginning of the growth cycle. In Equation 1, we assume the time is longer than each strain’s lag time . Note that some of our notation differs from related models in previous work, some of which used g for growth rate and λ for lag time (Manhart et al. 2018), while others used λ for growth rate (Lin and Amir 2017). Although it is possible to extend the model to account for additional growth traits such as a death rate or lag and growth on secondary resources, here we focus on the minimal set of traits most often measured in microbial phenotyping experiments (Novak et al. 2006; Fitzsimmons et al. 2010; Levin-Reisman et al. 2010; Warringer et al. 2011; Jasmin and Zeyl 2012; Ziv et al. 2013; Zackrisson et al. 2016; Adkar et al. 2017).
Figure 1.
Model of selection on multiple microbial growth traits. (A) Simplified model of microbial population growth characterized by three traits: lag time L, growth rate r, and yield Y. The total initial population size is and the initial frequency of the mutant (strain 2) is x. After the whole population reaches stationary phase (time ), the population is diluted by a factor D into fresh media, and the cycle starts again. (B) Phase diagram of selection on mutants in the space of their growth rate and lag time relative to wild type. The slope of the diagonal line is
We define the selection coefficient between each pair of strains as the change in their log-ratio over the complete growth cycle (Chevin 2011; Good et al. 2017):
| (2) |
where is the population size of strain i at the beginning of the growth cycle and is the population size of strain i at the end. After the population reaches stationary phase, it is diluted by a factor of D into a fresh medium with amount R of the resource, and the cycle repeats (Figure 1A). We assume the population remains in the stationary phase for a sufficiently short time, such that we can ignore death and other dynamics during this phase (Finkel 2006; Avrani et al. 2017).
Over many cycles of growth, as would occur in a laboratory evolution experiment (Lenski et al. 1991; Elena and Lenski 2003; Good et al. 2017), the population dynamics of this system are characterized by the set of frequencies for all strains as well as the matrix of selection coefficients and the total population size at the beginning of each cycle. In Supplemental Material, Supplemental Methods (sections I, II, and III), we derive explicit equations for the deterministic dynamics of these quantities over multiple cycles of growth for an arbitrary number of strains. In the case of two strains, such as a mutant and a wild type, the selection coefficient is approximately
| (3) |
where is the growth rate of the mutant relative to the wild type and is the relative lag time. The approximation is valid as long as the growth rate difference between the mutant and the wild type is small (Supplemental Methods, section IV), which is true for most single mutations (Chevereau et al. 2015; Levy et al. 2015). This equation shows that the growth phase and the lag phase make distinct additive contributions to the total selection coefficient, with the dilution factor D controlling their relative magnitudes (Figure 1B). This is because a larger dilution factor will increase the amount of time the population grows exponentially, hence increasing selection on growth rate. Neutral coexistence between multiple strains is therefore possible if these two selection components balance although it requires an exact tuning of the growth traits with the dilution factor (Supplemental Methods, section III) (Manhart et al. 2018; Manhart and Shakhnovich 2018). With a fixed dilution factor D, the population size at the beginning of each growth cycle changes according to (Supplemental Methods, section I)
| (4) |
where is the effective yield of the whole population in the current growth cycle. In this manner the ratio sets the bottleneck size of the population, which for serial dilution is approximately the effective population size (Lenski et al. 1991), and therefore determines the strength of genetic drift.
Model of evolutionary dynamics
We now consider the evolution of a population as new mutations arise that alter growth traits. We start with a wild-type population having lag time and growth rate which are roughly consistent with E. coli parameters, where time is measured in minutes (Lenski et al. 1991; Vasi et al. 1994); we set the wild-type yield to be without loss of generality. As in experiments, we vary the dilution factor D and the amount of resources R, which control the relative selection on growth vs. lag (set by D, Equation 3) and the effective population size (set by Equation 4). We also set the initial population size of the first cycle to
The population grows according to the dynamics in Figure 1A. Each cell division can generate a new mutation with probability note that this rate is only for mutations altering growth traits, and therefore it is lower than the rate of mutations anywhere in the genome. We generate a random waiting time for each strain k until the next mutation with instantaneous rate When a mutation occurs, the growth traits for the mutant are drawn from a distribution where are the growth traits for the background strain on which the new mutation occurs and are the traits for the new mutant. Note that since mutations only arise during the exponential growth phase, beneficial or deleterious effects on lag time are not realized until the next growth cycle (Li et al. 2018). After the growth cycle ceases (once the resource is exhausted according to Equation 1), we randomly choose cells, each with probability to form the population for the next growth cycle.
We will assume mutational effects are not epistatic and scale with the trait values of the background strain, so that where and (Supplemental Methods, section V). Since our primary goal is to scan the space of possible mutations, we focus on uniform distributions of mutational effects where and In the Supplemental Methods, we extend our main results to the case of Gaussian distributions (section V) as well as an empirical distribution of mutational effects based on single-gene deletions in E. coli (section VI) (Campos et al. 2018).
Data availability
Data and codes are available upon request. File S1 contains the Supplemental Methods. File S2 contains data of growth traits presented in Figure S3. Supplemental material available at figshare: https://doi.org/10.25386/genetics.12194754.
Results
Fixation of mutations
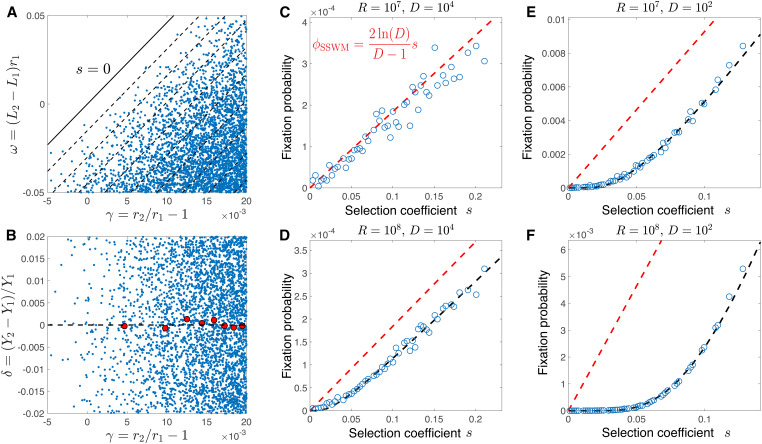
We first consider the fixation statistics of new mutations in our model. In Figure 2A we show the relative growth rates γ and the relative lag times ω of fixed mutations against their background strains, along with contours of constant selection coefficient s from Equation 3. As expected, fixed mutations either increase growth rate decrease lag time or both. In contrast, the yield of fixed mutations is the same as the ancestor on average (Figure 2B); indeed, the selection coefficient in Equation 3 does not depend on the yields. If a mutation arises with significantly higher or lower yield than the rest of the population, the bottleneck population size immediately adjusts to keep the overall fold-change of the population during the growth cycle fixed to the dilution factor D (Equation 4). Therefore mutations that significantly change yield have no effect on the overall population dynamics.
Figure 2.
Selection coefficient determines fixation probability. (A) The relative growth rates γ and the relative lag times ω of fixed mutations against their background strain. Dashed lines mark contours of constant selection coefficient with interval while the solid line marks . (B) Same as A, but for relative growth rate γ and the relative yield δ. The red dots mark the relative yield of fixed mutations averaged over binned values of the relative growth rate γ. In A and B, and . (C, D, E, and F) Fixation probability of mutations against their selection coefficients for different amounts of resource R and dilution factors D as indicated in the titles. The red dashed line shows the fixation probability predicted in the SSWM regime (Equation 5), while the black line shows a numerical fit of the data points to Equation 6 with parameters and in D, and in E, and and in F. In all panels mutations randomly arise from a uniform distribution with and
Figure 2A also suggests that the density of fixed mutations in the growth-lag trait space depends solely on their selection coefficients, rather than the precise combination of traits, as long as other parameters such as the dilution factor D, the total amount of resource R, and the distribution of mutational effects are held fixed. Mathematically, this means that the fixation probability of a mutation with growth effect γ and lag effect ω can be expressed as To test this, we discretize the scatterplot of Figure 2A and compute the fixation probabilities of mutations as functions of γ and ω (Supplemental Methods, section VII). We then plot the resulting fixation probabilities of mutations as functions of their selection coefficients calculated by Equation 3 (Figure 2, C–F). We test the dependence of the fixation probability on the selection coefficient over a range of population dynamics regimes by varying the dilution factor D and the amount of resources R.
For small populations, mutations generally arise and either fix or go extinct one at a time, a regime known as strong-selection weak-mutation (SSWM) (Gillespie 1984). In this case, we expect the fixation probability of a beneficial mutation with selection coefficient to be (Wahl and Gerrish 2001; Wahl and Zhu 2015; Guo et al. 2019)
| (5) |
This is similar to the standard Wright–Fisher fixation probability of (Crow and Kimura 1970), but with a different prefactor due to averaging over the different times in the exponential growth phase at which the mutation can arise (Supplemental Methods, section VIII). Indeed, we see this predicted dependence matches the simulation results for the small population size of (Figure 2C).
For larger populations, multiple beneficial mutations will be simultaneously present in the population and interfere with each other, an effect known as clonal interference (Gerrish and Lenski 1998; Desai and Fisher 2007; Schiffels et al. 2011; Good et al. 2012; Fisher 2013; Good and Desai 2014). Our simulations show that, as for the SSWM case, the fixation probability depends only on the selection coefficient (Equation 3) relative to the mutation’s immediate ancestor and not on the individual combination of mutant traits (Figure 2, D–F), with all other population parameters held constant. Previous work has determined the dependence of the fixation probability on the selection coefficient under clonal interference using various approximations (Gerrish and Lenski 1998; Schiffels et al. 2011; Good et al. 2012; Fisher 2013). Here, we focus on an empirical relation based on (Gerrish and Lenski 1998)
| (6) |
where A and B are two constants that depend on other parameters of the population (D, R, and the distribution of mutational effects); we treat these as empirical parameters to fit to the simulation results, although Gerrish and Lenski (1998) predicted i.e., the same constant as in the SSWM case (Equation 5). The factor in Equation 6 comes from the probability that no superior beneficial mutations appears before the current mutation fixes. Since the time to fixation scales as we expect the average number of superior mutations to be proportional to (for small s). This approximation holds only for selection coefficients that are not too small and therefore are expected to fix without additional beneficial mutations on the same background; Equation 6 breaks down for weaker beneficial mutations that typically fix by hitchhiking on stronger mutations (Schiffels et al. 2011). Nevertheless, Equation 6 matches our simulation results well for a wide range of selection coefficients achieved in our simulations and larger population sizes (Figure 2, D–F). Furthermore, the constant A we fit to the simulation data are indeed close to the predicted value of except in the most extreme case of (Figure 2F).
Altogether, Figure 2 shows that mutations with different effects on cell growth (for example, a mutant that increases the growth rate and a mutant that decreases the lag time) can nevertheless have approximately the same fixation probability as long as their overall effects on selection are the same according to Equation 3. To test the robustness of this result, we verify it for several additional distributions of mutational effects in the Supplemental Methods: a Gaussian distribution of mutational effects, including the presence of correlated mutational effects (Figure S1); a wider distribution of mutational effects with large selection coefficients (Figure S2); and an empirical distribution of mutational effects estimated from single-gene deletions in E. coli (Figure S3). In Figure S4A, we further test robustness by using the neutral phenotype (orthogonal to the selection coefficient) to quantify the range of γ and ω trait combinations that nevertheless have the same selection coefficient and fixation probability, and in Figure S4B we show that the selection coefficient on growth alone is insufficient to determine fixation probability.
While the dependence of fixation probability on the selection coefficient is a classic result of population genetics (Hartl and Clark 1997), the existence of a simple relationship here is nontrivial since, strictly speaking, selection in this model is not only frequency-dependent (Manhart et al. 2018) (i.e., selection between two strains depends on their frequencies) but also includes higher-order effects (Manhart and Shakhnovich 2018) (i.e., selection between strain 1 and strain 2 is affected by the presence of strain 3). Therefore, in principle, the fixation probability of a mutant may depend on the specific state of the population in which it is present, while the selection coefficient in Equation 3 only describes selection on the mutant in competition with its immediate ancestor. However, we see that, at least for the parameters considered in our simulations, these effects are negligible in determining the eventual fate of a mutation.
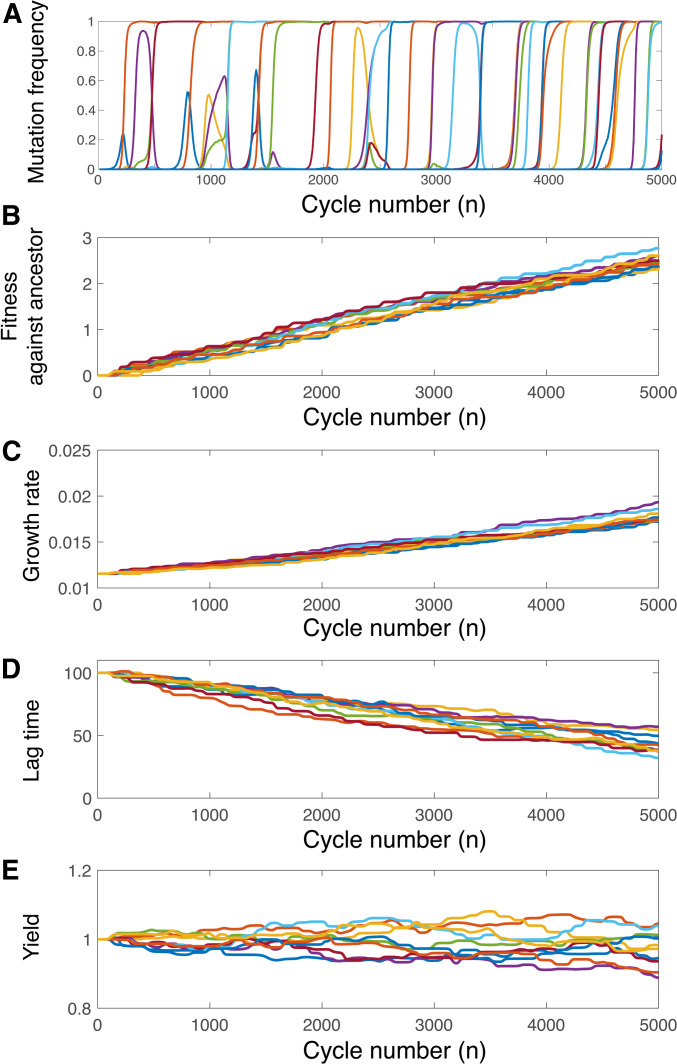
Adaptation of growth traits
As Figure 3A shows, many mutations arise and fix over the timescale of our simulations, which lead to predictable trends in the quantitative traits of the population. We first determine the relative fitness of the evolved population at each time point against the ancestral strain by simulating competition between an equal number of evolved and ancestral cells for one cycle, analogous to common experimental measurements (Lenski et al. 1991; Elena and Lenski 2003). The resulting fitness trajectories are shown in Figure 3B. To see how different traits contribute to the fitness increase, we also calculate the average population traits at the beginning of each cycle; for instance, the average population growth rate at growth cycle n is As expected from Equation 3, the average growth rate increases (Figure 3C) and the average lag time decreases (Figure 3D) for all simulations. In contrast, the average yield evolves without apparent trend (Figure 3E), since Equation 3 indicates no direct selection on yield. We note that, while the cells do not evolve toward lower or higher resource efficiency on average, they do evolve to consume resources more quickly, since the rate of resource consumption ( for each cell of strain k) depends on both the yield as well as the growth rate. Therefore the saturation time of each growth cycle evolves to be shorter, consistent with recent work from Baake et al. (2019).
Figure 3.
Dynamics of evolving populations. (A) Frequencies of new mutations as functions of the number n of growth cycles. Example trajectories of (B) the fitness of the evolved population relative to the ancestral population, (C) the evolved average growth rate, (D) the evolved average lag time, and (E) the evolved average yield. In all panels the dilution factor is the amount of resource at the beginning of each cycle is and mutations randomly arise from a uniform distribution with and
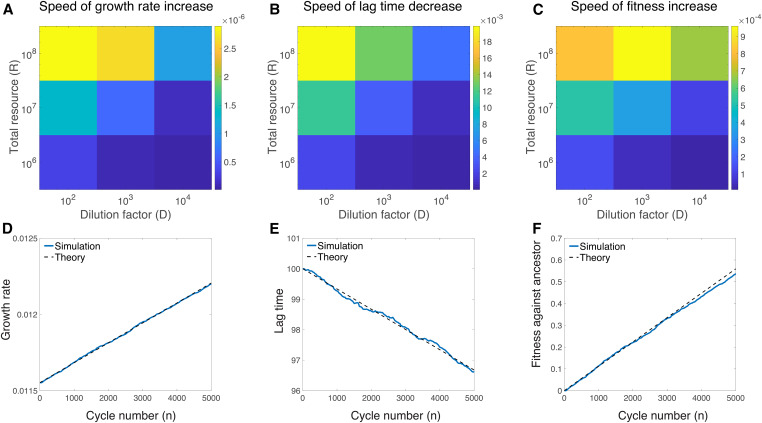
Figure 3 suggests relatively constant speeds of adaptation for the relative fitness, the average growth rate, and the average lag time. For example, we can calculate the adaptation speed of the average growth rate as the averaged change in the average growth rate per cycle:
| (7) |
where the bracket denotes an average over replicate populations and cycle number. In the Supplemental Methods (sections IX and X), we calculate the adaptation speeds of these traits in the SSWM regime to be
| (8) |
where and are the standard deviations of the underlying distributions of γ and ω for single mutations is the ancestral growth rate, and is the ancestral yield (we assume the yield does not change on average according to Figure 3E). Furthermore, the ratio of the growth adaptation rate and the lag adaptation rate is independent of the amount of resource and mutation rate in the SSWM regime:
| (9) |
Equation 8 predicts that the adaptation speeds of the average growth rate, the average lag time, and the relative fitness should all increase with the amount of resources R and decrease with the dilution factor D (for large D); although this prediction assumes the SSWM regime (relatively small ), it nevertheless holds across a wide range of R- and D-values (Figure 4, A–C), except for where the speed of fitness increase is nonmonotonic with D (Figure 4C). The predicted adaptation speeds in Equation 8 also quantitatively match the simulated trajectories in the SSWM case (Figure 4, D–F); even outside of the SSWM regime, the relative rate in Equation 9 remains a good prediction at early times (Figure S5).
Figure 4.
Speed of adaptation. The average per-cycle adaptation speed of (A) the average growth rate, (B) the average lag time, and (C) the fitness relative to the ancestral population as functions of the dilution factor D and total amount of resources R. The adaptation speeds are averaged over growth cycles and independent populations. (D) The average growth rate, (E) the average lag time, and (F) the fitness relative to the ancestral population as functions of the number n of growth cycles. The dilution factor is and the total resource is so the population is in the SSWM regime. The blue solid lines are simulation results, while the dashed lines show the mathematical predictions in Equation 8. All panels show averages over 500 independent simulated populations, with mutations randomly arising from a uniform distribution with and
Evolved covariation between growth traits
We now turn to investigating how the covariation between traits evolves. We have generally assumed that individual mutations have uncorrelated effects on different traits. Campos et al. (2018) recently systematically measured the growth curves of the single-gene deletions in E. coli. We compute the relative growth rate, lag time, and yield changes for the single-gene deletions compared with the wild type and find that the resulting empirical distribution of relative growth traits changes shows very small correlations between these traits (Figure S3, B and C), consistent with our assumptions. We note that these measurements, however, are subject to significant noise (Supplemental Methods, section VI), and therefore any conclusions ultimately require verification by further experiments.
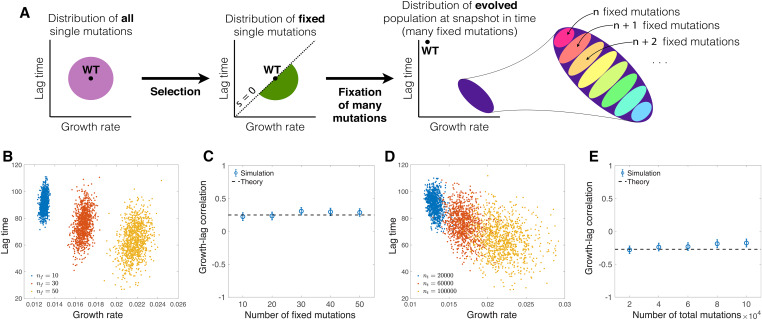
Even in the absence of mutational correlations, selection may induce a correlation between these traits in evolved populations. In Figure 5A, we schematically depict how the raw variation of traits from mutations is distorted by selection and fixation of multiple mutations. Specifically, for a single fixed mutation, selection induces a positive (i.e., antagonistic) correlation between the relative growth rate change and the relative lag time change. Figure 2A shows this for single fixed mutations, while Figure 5, B and C shows this positive correlation between the average growth rate and the average lag time across populations that have accumulated the same number of fixed mutations. For populations in the SSWM regime with the same number of fixed mutations, the Pearson correlation coefficient between the average growth rate and the average lag time across populations is approximately equal to the covariation of the relative growth rate change γ and the relative lag time change ω for a single fixed mutation:
| (10) |
where is an average over the distribution of single fixed mutations (Supplemental Methods, section IX). We can explicitly calculate this quantity in the SSWM regime, which confirms that it is positive for uncorrelated mutational effects with uniform or Gaussian distributions (Supplemental Methods, section XI).
Figure 5.
Evolved patterns of covariation among growth traits. (A) Schematic of how selection and fixation of multiple mutations shape the observed distribution of traits. The sign of the Pearson correlation coefficient between the average growth rate and lag time depends on whether we consider an ensemble of populations with the same number of fixed mutations or the same number of total mutation events. (B) Distribution of average growth rate and lag time for 1000 independent populations with the same number of fixed mutations. Each color corresponds to a different number of fixed mutations indicated in the legend. (C) Pearson correlation coefficient of growth rate and lag time for distributions in B, as a function of the number of fixed mutations. The dashed line is the prediction from Equation 10. (D) Same as B, except each color corresponds to a set of populations at a snapshot in time with the same number of total mutation events. Each color corresponds to a different number of total mutations events indicated in the legend. (E) Same as C, but for the set of populations shown in D. The dashed line is the prediction from Equation 11. In C and E, the error bars represent confidence intervals. In B–E, we simulate the SSWM regime by introducing random mutations one by one and determining their fixation from Equation 5 with
However, in evolution experiments we typically observe populations at a particular snapshot in time, such that the populations may have a variable number of fixed mutations but the same number of total mutations that arose and either fixed or went extinct (since the number of total arising mutations is very large, we neglect its fluctuation across populations). Interestingly, the variation in number of fixed mutations at a snapshot in time causes the distribution of growth rates and lag times across populations to stretch into a negative correlation; this is an example of Simpson’s paradox from statistics (Simpson 1951). Figure 5A shows this effect schematically, while Figure 5, D and E show explicit results from simulations. An intuitive way to understand the evolved negative correlation is to approximate the effects of all fixed mutations as deterministic, so that each fixed mutation increases the average growth rate and decreases the average lag time by the same amount. Therefore, populations with a higher average growth rate must have a larger number of fixed mutations and thus also a shorter average lag time, leading to a negative correlation between the average growth rates and the average lag times. In the Supplemental Methods (section XI), we calculate this evolved Pearson correlation coefficient across populations in the SSWM regime to be approximately
| (11) |
That is, the correlation of traits across populations with multiple mutations is still a function of the distribution of single fixed mutations, but it is not equal to the correlation of single fixed mutations (Equation 10). In the Supplemental Methods (section XI), we explicitly calculate in the SSWM regime for uncorrelated uniform and Gaussian distributions of mutational effects, which shows that it is negative. Furthermore, we prove that it must always be negative for any symmetric and uncorrelated distribution (Supplemental Methods, section IX).
The predicted correlations in Equations 10 and 11 quantitatively match the simulations well in the SSWM regime (Figure 5, C and E). While they are less accurate outside of the SSWM regime, they nevertheless still produce the correct sign of the evolved correlation within the parameter regimes of our simulations (Figure S6, A–C). However, the signs of the correlations can indeed change depending on the underlying distribution of mutational effects For example, in the Supplemental Methods, we explore the effects of varying the mean mutational effects (Figure S6D)—e.g., whether an average mutation has positive, negative, or zero effect on the growth rate—as well as the intrinsic mutational correlation between the relative growth rate change and the relative lag time change (Figure S6E).
Discussion
We have investigated a model of microbial evolution under serial dilution, which is both a common protocol for laboratory evolution experiments (Luckinbill 1978; Lenski et al. 1991; Elena and Lenski 2003; Levy et al. 2015; Kram et al. 2017) as well as a rough model of evolution in natural environments with feast–famine cycles. While there has been extensive work to model population and evolutionary dynamics in these conditions (Gerrish and Lenski 1998; Wahl and Gerrish 2001; Desai 2013; Baake et al. 2019; Guo et al. 2019), these models have largely neglected the physiological links connecting mutations to selection. However, models that explicitly incorporate these features are necessary to interpret experimental evidence that mutations readily generate variation in multiple cellular traits, and that this variation is important to adaptation (Vasi et al. 1994; Novak et al. 2006; Reding-Roman et al. 2017; Li et al. 2018). Wahl and Zhu (2015) determined the relative fixation probabilities of mutations on different traits and the effects of mutation occurrence time and dilution factor, but the role of pleiotropy and evolutionary dynamics over many mutations were not considered.
In this paper, we have studied a model where mutations can affect three quantitative growth traits—the lag time, the exponential growth rate, and the yield (Figure 1A)—since these three traits are widely measured for microbial populations. In particular, we have derived a simple expression (Equation 3) for the selection coefficient of a mutation in terms of its effects on growth and lag and a single environmental parameter, the dilution factor D. While previous work showed that this particular form of the selection coefficient determines the fixation probability of a single mutation in the SSWM regime (Manhart et al. 2018), here we show that this holds even in the presence of clonal interference (Figure 2, C–F), which appears to be widespread in laboratory evolution experiments (Lang et al. 2011, 2013; Good et al. 2017). Our result is therefore valuable for interpreting the abundant experimental data on mutant growth traits. We have also calculated the adaptation rates of growth traits per cycle in the SSWM regime, which turn out to increase with the amount of resource R and decrease with the dilution factor D. These results are confirmed by numerical simulations and remain good predictions even outside of the SSWM regime. Furthermore, some of these results are independent of the specific form of the selection coefficient (Equation 3), namely the fact that the fixation probability depends only on the selection coefficient (with other population parameters besides the mutant traits being held fixed) even in the clonal interference regime, and the expressions for the correlation coefficients of traits between populations (Equations 10 and 11).
An important difference with the previous work on this model is that here we used a fixed dilution factor D, which requires that the bottleneck population size fluctuates as the population evolves. In contrast, previous work used a fixed and variable D (Manhart et al. 2018; Manhart and Shakhnovich 2018). We observed two important differences between these regimes. First, in the case of fixed and variable D, the fold-change of the population during a single growth cycle, which is approximately (Manhart et al. 2018), determines the relative selection between growth and lag, since it determines how long the population undergoes exponential growth. Therefore one can experimentally tune this relative selection by varying either the total amount of resources R or the fixed bottleneck size . However, when the dilution factor D is fixed, the population fold-change is always constrained to exactly equal D, and therefore D alone determines the relative selection on growth and lag (Equation 3). The second difference is that, with fixed and variable D, the selection coefficient depends explicitly on the effective yield and is therefore frequency-dependent (Supplemental Methods, section II), which enables the possibility of stable coexistence between two strains (Manhart et al. 2018; Manhart and Shakhnovich 2018). However, for the fixed D case, the frequency dependence of is exactly canceled by (Equation 4). Therefore, there is only neutral coexistence in this case, requiring the growth and lag traits of the strains to follow an exact constraint set by D (Supplemental Methods, section III).
A major result of our model is a prediction on the evolution of covariation between growth traits. In particular, we have shown that correlations between traits can emerge from selection and accumulation of multiple mutations even without an intrinsic correlation between traits from individual mutations (Figure 5 and Figure S6). We have also shown that selection alone produces no correlation between growth and yield, in the absence of correlated mutational effects (Figure 2B and Figure 3E). This is important for interpreting evolved patterns of traits in terms of selective or physiological tradeoffs. Specifically, it emphasizes that the evolved covariation between traits conflates both the underlying supply of variation from mutations as well as the action of selection and other aspects of population dynamics (e.g., genetic drift, spatial structure, recombination), and therefore it is difficult to make clear inferences about either aspect purely from the outcome of evolution alone. For example, simply observing a negative correlation between two traits from evolved populations is insufficient to infer whether that correlation is due to a physiological constraint on mutations (e.g., mutations cannot improve both traits simultaneously) or due to a selective constraint (e.g., selection favors specialization in one trait or another).
These questions, of course, have been the foundation of quantitative trait genetics (Lynch and Walsh 1998). Historically, this field has emphasized polymorphic populations with abundant recombination as are applicable to plant and animal breeding. However, this regime is quite different from microbial populations, which, at least under laboratory conditions, are often asexual and dominated by linkage between competing mutations (Lang et al. 2011, 2013; Good et al. 2017). We therefore need a quantitative description of both between-population as well as within-population covariation of traits of microbial populations in this regime. In the present study, we focus on between-population covariation in growth traits, but recent work by Gomez et al. (2019) provides insight into the case of within-population covariation. They showed that a tradeoff across individuals within a population evolves between two quantitative traits under positive, additive selection; this suggests that while growth rate and lag time will be negatively correlated across populations (Figure 5, D and E), they should be positively correlated within populations.
Microbial growth traits should indeed be an ideal setting for this approach due to abundant data, but conclusions on the nature of trait covariation have remained elusive. Physiological models have predicted a negative correlation between growth rate and lag time across genotypes (Baranyi and Roberts 1994; Himeoka and Kaneko 2017), while models of single-cell variation in lag times also suggest there should be a negative correlation at the whole-population level (Baranyi 1998). However, experimental evidence has been mixed, with some studies finding a negative correlation (Ziv et al. 2013, 2017), while others found no correlation (Levin-Reisman et al. 2010; Warringer et al. 2011; Adkar et al. 2017). Studies of growth–yield correlations have long been motivated by r/K selection theory, which suggests there should be tradeoffs between growth rate and yield (Reznick et al. 2002). For instance, metabolic models make this prediction (Pfeiffer et al. 2001; MacLean 2007; Meyer et al. 2015). However, experimental evidence has again been mixed, with some data showing a tradeoff (Jasmin and Zeyl 2012; Jasmin et al. 2012; Bachmann et al. 2013), while others show no correlation (Velicer and Lenski 1999; Novak et al. 2006; Fitzsimmons et al. 2010; Reding-Roman et al. 2017) or even a positive correlation (Luckinbill 1978; Warringer et al. 2011). Some of this ambiguity may have to do with dependence on the environmental conditions (Reding-Roman et al. 2017) or the precise definition of yield. We define yield as the proportionality constant of population size to resource (Equation 1) and neglect any growth rate dependence on resource concentration. Under these conditions, we predict no direct selection on yield, which means that the only way to generate a correlation of yield with growth rate is if the two traits are constrained at the physiological level, so that mutational effects are correlated. In such cases yield could evolve but only as a spandrel (Gould and Lewontin 1979; Amir 2017). Ultimately, we believe more precise single-cell measurements of these traits, both across large unselected mutant libraries as well as evolved strains, are necessary to definitively test these issues (Campos et al. 2018).
Acknowledgments
We thank Christine Jacobs-Wagner for kindly sharing the data of single-gene deletions of E. coli, and we thank Yipei Guo for suggesting the proof of the sign of the evolved growth rate and lag time correlation presented in the Supplemental Methods. M.M. was supported by an F32 fellowship from the US National Institutes of Health (GM116217) and an Ambizione grant from the Swiss National Science Foundation (PZ00P3_180147). A.A. was supported by National Science Foundation CAREER grant 1752024 and the Harvard Dean’s Competitive Fund. A.A. and J.L. received support from Harvard’s Materials Research and Engineering Center (DMR-1420570).
Footnotes
Supplemental material available at figshare: https://doi.org/10.25386/genetics.12194754.
Communicating editor: L. Wahl
Literature Cited
- Adkar B. V., Manhart M., Bhattacharyya S., Tian J., Musharbash M., et al. , 2017. Optimization of lag phase shapes the evolution of a bacterial enzyme. Nat. Ecol. Evol. 1: 149 10.1038/s41559-017-0149 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amir A., 2017. Is cell size a spandrel? eLife 6: e22186. 10.7554/eLife.22186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avrani S., Bolotin E., Katz S., and Hershberg R., 2017. Rapid genetic adaptation during the first four months of survival under resource exhaustion. Mol. Biol. Evol. 34: 1758–1769. 10.1093/molbev/msx118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baake E., Casanova A. G., Probst S., and Wakolbinger A., 2019. Modelling and simulating lenski’s long-term evolution experiment. Theor. Popul. Biol. 127: 58–74. 10.1016/j.tpb.2019.03.006 [DOI] [PubMed] [Google Scholar]
- Bachmann H., Fischlechner M., Rabbers I., Barfa N., dos Santos F. B. et al. , 2013. Availability of public goods shapes the evolution of competing metabolic strategies. Proc. Natl. Acad. Sci. USA 110: 14302–14307. 10.1073/pnas.1308523110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baranyi J., 1998. Comparison of stochastic and deterministic concepts of bacterial lag. J. Theor. Biol. 192: 403–408. 10.1006/jtbi.1998.0673 [DOI] [PubMed] [Google Scholar]
- Baranyi J., and Roberts T. A., 1994. A dynamic approach to predicting bacterial growth in food. Int. J. Food Microbiol. 23: 277–294. 10.1016/0168-1605(94)90157-0 [DOI] [PubMed] [Google Scholar]
- Barrick J. E., and Lenski R. E., 2013. Genome dynamics during experimental evolution. Nat. Rev. Genet. 14: 827–839. 10.1038/nrg3564 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrick J. E., Yu D. S., Yoon S. H., Jeong H., Oh T. K. et al. , 2009. Genome evolution and adaptation in a long-term experiment with Escherichia coli. Nature 461: 1243–1247. 10.1038/nature08480 [DOI] [PubMed] [Google Scholar]
- Campos M., Govers S. K., Irnov I., Dobihal G. S., Cornet F. et al. , 2018. Genomewide phenotypic analysis of growth, cell morphogenesis, and cell cycle events in escherichia coli. Mol. Syst. Biol. 14: e7573 10.15252/msb.20177573 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevereau G., Dravecká M., Batur T., Guvenek A., Ayhan D. H. et al. , 2015. Quantifying the determinants of evolutionary dynamics leading to drug resistance. PLoS Biol. 13: e1002299 10.1371/journal.pbio.1002299 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevin L.-M., 2011. On measuring selection in experimental evolution. Biol. Lett. 7: 210–213. 10.1098/rsbl.2010.0580 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow J. F., and Kimura M., 1970. An Introduction to Population Genetics Theory. Harper and Row, New York. [Google Scholar]
- Desai M. M., 2013. Statistical questions in experimental evolution. J. Stat. Mech. 2013: P01003 10.1088/1742-5468/2013/01/P01003 [DOI] [Google Scholar]
- Desai M. M., and Fisher D. S., 2007. Beneficial mutation–selection balance and the effect of linkage on positive selection. Genetics 176: 1759–1798. 10.1534/genetics.106.067678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elena S. F., and Lenski R. E., 2003. Evolution experiments with microorganisms: the dynamics and genetic bases of adaptation. Nat. Rev. Genet. 4: 457–469. 10.1038/nrg1088 [DOI] [PubMed] [Google Scholar]
- Finkel S. E., 2006. Long-term survival during stationary phase: evolution and the gasp phenotype. Nat. Rev. Microbiol. 4: 113–120. 10.1038/nrmicro1340 [DOI] [PubMed] [Google Scholar]
- Fisher D. S., 2013. Asexual evolution waves: fluctuations and universality. J. Stat. Mech. 2013: P01011 10.1088/1742-5468/2013/01/P01011 [DOI] [Google Scholar]
- Fitzsimmons J. M., Schoustra S. E., Kerr J. T., and Kassen R., 2010. Population consequences of mutational events: effects of antibiotic resistance on the r/K trade-off. Evol. Ecol. 24: 227–236. 10.1007/s10682-009-9302-8 [DOI] [Google Scholar]
- Gerrish P. J., and Lenski R. E., 1998. The fate of competing beneficial mutations in an asexual population. Genetica 102–103: 127–144. 10.1023/A:1017067816551 [DOI] [PubMed] [Google Scholar]
- Gillespie J. H., 1984. Molecular evolution over the mutational landscape. Evolution 38: 1116–1129. 10.1111/j.1558-5646.1984.tb00380.x [DOI] [PubMed] [Google Scholar]
- Gomez K., Bertram J., and Masel J., 2019. Directional selection rather than functional constraints can shape the G matrix in rapidly adapting asexuals. Genetics 211: 715–729. 10.1534/genetics.118.301685 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good B. H., and Desai M. M., 2014. Deleterious passengers in adapting populations. Genetics 198: 1183–1208. 10.1534/genetics.114.170233 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good B. H., Rouzine I. M., Balick D. J., Hallatschek O., and Desai M. M., 2012. Distribution of fixed beneficial mutations and the rate of adaptation in asexual populations. Proc. Natl. Acad. Sci. USA 109: 4950–4955. 10.1073/pnas.1119910109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good B. H., McDonald M. J., Barrick J. E., Lenski R. E., and Desai M. M., 2017. The dynamics of molecular evolution over 60,000 generations. Nature 551: 45–50. 10.1038/nature24287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gould S. J., and Lewontin R. C., 1979. The spandrels of San Marco and the Panglossian paradigm: a critique of the adaptationist programme. Proc. R. Soc. Lond. B Biol. Sci. 205: 581–598. 10.1098/rspb.1979.0086 [DOI] [PubMed] [Google Scholar]
- Guo Y., Vucelja M., and Amir A., 2019. Stochastic tunneling across fitness valleys can give rise to a logarithmic long-term fitness trajectory. Sci. Adv. 5: eaav3842 10.1126/sciadv.aav3842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartl D. L., and Clark A. G., 1997. Principles of Population Genetics, Vol. 116 Sinauer Associates, Sunderland, MA. [Google Scholar]
- Himeoka Y., and Kaneko K., 2017. Theory for transitions between exponential and stationary phases: universal laws for lag time. Phys. Rev. X 7: 021049. [Google Scholar]
- Jasmin J.-N., and Zeyl C., 2012. Life-history evolution and density-dependent growth in experimental populations of yeast. Evolution 66: 3789–3802. 10.1111/j.1558-5646.2012.01711.x [DOI] [PubMed] [Google Scholar]
- Jasmin J.-N., Dillon M. M., and Zeyl C., 2012. The yield of experimental yeast populations declines during selection. Proc. Biol. Sci. 279: 4382–4388. 10.1098/rspb.2012.1659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kram K. E., Geiger C., Ismail W. M., Lee H., Tang H. et al. , 2017. Adaptation of escherichia coli to long-term serial passage in complex medium: evidence of parallel evolution. mSystems 2: e00192-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kryazhimskiy S., Rice D. P., Jerison E. R., and Desai M. M., 2014. Microbial evolution. Global epistasis makes adaptation predictable despite sequence-level stochasticity. Science 344: 1519–1522. 10.1126/science.1250939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang G. I., Botstein D., and Desai M. M., 2011. Genetic variation and the fate of beneficial mutations in asexual populations. Genetics 188: 647–661. 10.1534/genetics.111.128942 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang G. I., Rice D. P., Hickman M. J., Sodergren E., Weinstock G. M. et al. , 2013. Pervasive genetic hitchhiking and clonal interference in forty evolving yeast populations. Nature 500: 571–574. 10.1038/nature12344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenski R. E., Rose M. R., Simpson S. C., and Tadler S. C., 1991. Long-term experimental evolution in escherichia coli. i. adaptation and divergence during 2,000 generations. Am. Nat. 138: 1315–1341. 10.1086/285289 [DOI] [Google Scholar]
- Levin-Reisman I., Gefen O., Fridman O., Ronin I., Shwa D. et al. , 2010. Automated imaging with ScanLag reveals previously undetectable bacterial growth phenotypes. Nat. Methods 7: 737–739. 10.1038/nmeth.1485 [DOI] [PubMed] [Google Scholar]
- Levy S. F., Blundell J. R., Venkataram S., Petrov D. A., Fisher D. S. et al. , 2015. Quantitative evolutionary dynamics using high-resolution lineage tracking. Nature 519: 181–186. 10.1038/nature14279 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y., Venkataram S., Agarwala A., Dunn B., Petrov D. A. et al. , 2018. Hidden complexity of yeast adaptation under simple evolutionary conditions. Curr. Biol. 28: 515–525.e6. 10.1016/j.cub.2018.01.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin J., and Amir A., 2017. The effects of stochasticity at the single-cell level and cell size control on the population growth. Cell Syst. 5: 358–367.e4. 10.1016/j.cels.2017.08.015 [DOI] [PubMed] [Google Scholar]
- Luckinbill L. S., 1978. r and K selection in experimental populations of Escherichia coli. Science 202: 1201–1203. 10.1126/science.202.4373.1201 [DOI] [PubMed] [Google Scholar]
- Lynch M., and Walsh B., 1998. Genetics and Analysis of Quantitative Characters. Sinauer Associates, Sunderland, MA. [Google Scholar]
- MacLean R. C., 2007. The tragedy of the commons in microbial populations: insights from theoretical, comparative and experimental studies. Heredity 100: 471–477. 10.1038/sj.hdy.6801073x [DOI] [PubMed] [Google Scholar]
- Manhart M., and Shakhnovich E. I., 2018. Growth tradeoffs produce complex microbial communities on a single limiting resource. Nat. Commun. 9: 3214 10.1038/s41467-018-05703-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manhart M., Adkar B. V., and Shakhnovich E. I., 2018. Trade-offs between microbial growth phases lead to frequency-dependent and non-transitive selection. Proc. Biol. Sci. 285: 20172459. 10.1098/rspb.2017.2459 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer J. R., Gudelj I., and Beardmore R., 2015. Biophysical mechanisms that maintain biodiversity through trade-offs. Nat. Commun. 6: 6278 10.1038/ncomms7278 [DOI] [PubMed] [Google Scholar]
- Novak M., Pfeiffer T., Lenski R. E., Sauer U., and Bonhoeffer S., 2006. Experimental tests for an evolutionary trade-off between growth rate and yield in E. coli. Am. Nat. 168: 242–251. 10.1086/506527 [DOI] [PubMed] [Google Scholar]
- Pfeiffer T., Schuster S., and Bonhoeffer S., 2001. Cooperation and competition in the evolution of ATP-producing pathways. Science 292: 504–507. 10.1126/science.1058079 [DOI] [PubMed] [Google Scholar]
- Reding-Roman C., Hewlett M., Duxbury S., Gori F., Gudelj I., et al. , 2017. The unconstrained evolution of fast and efficient antibiotic-resistant bacterial genomes. Nat. Ecol. Evol. 1: 50 10.1038/s41559-016-0050 [DOI] [PubMed] [Google Scholar]
- Reznick D., Bryant M. J., and Bashey F., 2002. r- and K-selection revisited: the role of population regulation in life-history evolution. Ecology 83: 1509–1520. 10.1890/0012-9658(2002)083[1509:RAKSRT]2.0.CO;2 [DOI] [Google Scholar]
- Schiffels S., Szöllősi G. J., Mustonen V., and Lässig M., 2011. Emergent neutrality in adaptive asexual evolution. Genetics 189: 1361–1375. 10.1534/genetics.111.132027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson E. H., 1951. The interpretation of interaction in contingency tables. J. R. Stat. Soc. B 13: 238–241. [Google Scholar]
- Smith H. L., 2011. Bacterial competition in serial transfer culture. Math. Biosci. 229: 149–159. 10.1016/j.mbs.2010.12.001 [DOI] [PubMed] [Google Scholar]
- Vasi F., Travisano M., and Lenski R. E., 1994. Long-term experimental evolution in Escherichia coli. II. changes in life-history traits during adaptation to a seasonal environment. Am. Nat. 144: 432–456. 10.1086/285685 [DOI] [Google Scholar]
- Velicer G. J., and Lenski R. E., 1999. Evolutionary trade-offs under conditions of resource abundance and scarcity: experiments with bacteria. Ecology 80: 1168–1179. 10.1890/0012-9658(1999)080[1168:ETOUCO]2.0.CO;2 [DOI] [Google Scholar]
- Wahl L. M., and Gerrish P. J., 2001. The probability that beneficial mutations are lost in populations with periodic bottlenecks. Evolution 55: 2606–2610. 10.1111/j.0014-3820.2001.tb00772.x [DOI] [PubMed] [Google Scholar]
- Wahl L. M., and Zhu A. D., 2015. Survival probability of beneficial mutations in bacterial batch culture. Genetics 200: 309–320. 10.1534/genetics.114.172890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warringer J., Zörgö E., Cubillos F. A., Zia A., Gjuvsland A. et al. , 2011. Trait variation in yeast is defined by population history. PLoS Genet. 7: e1002111 10.1371/journal.pgen.1002111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wielgoss S., Barrick J. E., Tenaillon O., Cruveiller S., Chane-Woon-Ming B. et al. , 2011. Mutation rate inferred from synonymous substitutions in a long-term evolution experiment with Escherichia coli. G3 (Bethesda) 1: 183–186. 10.1534/g3.111.000406 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiser M. J., Ribeck N., and Lenski R. E., 2013. Long-term dynamics of adaptation in asexual populations. Science 342: 1364–1367. 10.1126/science.1243357 [DOI] [PubMed] [Google Scholar]
- Zackrisson M., Hallin J., Ottosson L.-G., Dahl P., Fernandez-Parada E. et al. , 2016. Scan-o-matic: high-resolution microbial phenomics at a massive scale. G3 (Bethesda) 6: 3003–3014. 10.1534/g3.116.032342 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziv N., Siegal M. L., and Gresham D., 2013. Genetic and nongenetic determinants of cell growth variation assessed by high-throughput microscopy. Mol. Biol. Evol. 30: 2568–2578. 10.1093/molbev/mst138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziv N., Shuster B. M., Siegal M. L., and Gresham D., 2017. Resolving the complex genetic basis of phenotypic variation and variability of cellular growth. Genetics 206: 1645–1657. 10.1534/genetics.116.195180 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data and codes are available upon request. File S1 contains the Supplemental Methods. File S2 contains data of growth traits presented in Figure S3. Supplemental material available at figshare: https://doi.org/10.25386/genetics.12194754.