Decision Theory Meets Explainable AI

Abstract

Explainability has been a core research topic in AI for decades and therefore it is surprising that the current concept of Explainable AI (XAI) seems to have been launched as late as 2016. This is a problem with current XAI research because it tends to ignore existing knowledge and wisdom gathered over decades or even centuries by other relevant domains. This paper presents the notion of Contextual Importance and Utility (CIU), which is based on known notions and methods of Decision Theory. CIU extends the notions of importance and utility for the non-linear models of AI systems and notably those produced by Machine Learning methods. CIU provides a universal and model-agnostic foundation for XAI.

Introduction

It seems like the term Explainable AI (XAI) dates back to a presentation by David Gunning in 2016 [13] and much recent work tends not to look at or cite research papers that are older than so. It has also been pointed out that XAI as a domain currently tends to propose methods that mainly can help experts to validate that an AI system built using Machine Learning (ML) makes sense to some extent [6]. It is rare to see methods and results that are meant to explain and justify results and actions of ML models to ‘real’ end users, such as the pedestrians who might be hit by an autonomous vehicle or the applicant of a mortgage whose request is refused by an AI system. As pointed out e.g. by Miller [20] and others [33], it is fair to say that most XAI work uses only the researchers’ intuition of what constitutes a ‘good’ explanation, while ignoring the vast and valuable bodies of research in philosophy, psychology, and cognitive science of how people define, generate, select, evaluate, and present explanations.

One truly relevant domain that seems to have been neglected in current XAI work is Decision Theory and related sub-domains such as Multiple Criteria Decision Making (MCDM). The Merriam-Webster dictionary defines Decision Theory as ‘a branch of statistical theory concerned with quantifying the process of making choices between alternatives’. However, Decision Theory is also by definition tightly connected with the domains mentioned above (philosophy, psychology, and cognitive science) because methods of Decision Theory are intended to produce Decision Support Systems (DSS) that are understood and used by humans when taking decisions. Decision Theory and MCDM provide clear definitions of what is meant by the importance of an input, as well as what is the utility of a given input value towards the outcome of a DSS. A simple linear DSS model is the weighted sum, where a numerical weight expresses the importance of an input and a numerical score expresses the utility of the current value of that input.

This paper extends the linear definition of importance and utility towards non-linear models such as those produced by typical ML methods. This non-linear extension is called Contextual Importance and Utility (CIU)1 because in many (or most) real-life situations the importance of an input and the utility of different input values changes depending on values of other inputs. For instance, the outdoor temperature has a great importance on a person’s comfort level as long as the person is outdoors. When the person goes inside, the situation (context) changes and the outdoor temperature may then have a very small importance for the comfort level. Similarly, both a very cold and a very warm outdoor temperature might have a low utility for a person’s comfort level but the level of utility can be modified by adding or removing clothes.

After this Introduction, Sect. 2 builds up the theoretical background as a combination of Decision Theory and XAI. Section 3 presents the background and definition of CIU, supported by examples and an experiment using the Iris data set, followed by conclusions in Sect. 4.

Source files for producing the results and Figures of this paper can be found at https://github.com/KaryFramling/EXTRAAMAS_2020.

Background

The rationality of human decisions (or lack of it) might be one of the oldest challenges addressed by philosophers. For instance, Socrates’ method for solving a problem in a rational way consisted in braking the problem down into a series of questions, the answers to which gradually distill the answer a person would seek. This can be thought of as ‘solve a problem by explaining your reasoning to yourself and/or someone else by starting from a high abstraction level and brake it into smaller sub-problems’. The concept of bounded rationality as proposed by Herbert Simon [28, 29] can be considered a cornerstone regarding modern theories of human decision making. The fundamental concepts and methods of Decision Theory are much older than Simon’s work. But Simon’s work can be considered to be based on Decision Theory and provides a connection from there to Artificial Intelligence and, by consequence, to Explainable AI.

Decision Theory

Decision Theory as a domain is too vast for the purposes of this article. Excellent introductions to the domain can be found for instance in [14, 18, 24] and [32], which notably focus on the sub-domain of Multiple Criteria Decision Making (MCDM). The Analytic Hierarchy Process (AHP) [26] that was originally developed in the 1970’s seems to have become the most popular MCDM method in research and practice [16, 17].

AHP is essentially based on a weighted sum, where the main selection task can be broken into sub-tasks in a hierarchical manner. The weights are typically acquired from experts using a pair-wise comparison procedure that produces a comparison matrix, which is then transformed into weights by a normalized principal Eigen vector. The utility (how good or favorable a value is for the selection) of the possible values for each leaf of the hierarchy is specified and calculated using the same principle.

MCDM problems require finding a model of the decision maker’s preferences, which may be called his or her preference function. However, the decision maker is quite often a group of people or an abstract person (society, nature, economy, ...). This makes it difficult to explicitly express the preference function, which is the reason for using machine learning methods instead. If a training set exists with labeled data on correct decisions, then it is possible to learn the preference function, no matter if the output of the model is a numerical score or a probability for one or many possible classes. A true preference function is usually non-linear and continuous, which makes its mathematical expression quite complex. Such non-linear and continuous models are mainly studied in the ML domain, which would be attractive also for MCDM if those ML methods would provide sufficient explainability.

In MCDM methods, the importances of the selection criteria are expressed by weights, while the transformation of the values of the criteria into utility values is done with utility functions. For a car selection problem, these concepts may be used for giving explanations such as ‘The car is good because it has a good size, decent performances and a reasonable price, which are very important criteria’, where words indicating utilities are underlined and only the most important criteria are presented. The fact of using a linear model makes the definition of importance and utility quite easy. However, when using non-linear models like neural nets, the task becomes challenging.

Rule-based expert systems (including fuzzy or rough rules) are a way of overcoming the linearity limitation. However, then we encounter the challenges of explainability that are known in the AI domain since its very beginnings.

Explainable Artificial Intelligence

Contrary to what many papers seem to claim, the need for explainability in Artificial Intelligence (AI) and Machine Learning (ML) has been known for about as long as AI has existed, even though the term Explainable AI (XAI) seems to have been launched only in 2016 [13]. For instance, Shortliffe et al. point out already in 1975 that ‘It is our belief, therefore, that a consultation program will gain acceptance only if it serves to augment rather than replace the physician’s own decision making processes. Gorry has reached a similar conclusion stating that one reason for the limited acceptance of Bayesian inference programs has been their inability to explain the reasoning behind their decisions’ [27]. The system described in that paper was MYCIN, an expert system that was capable of advising physicians who request advice regarding selection of appropriate antimicrobial therapy for hospital patients with bacterial infections. Great emphasis was put into the interaction with the end-user, in this case a skilled physician.

As pointed out by Shortliffe et al. in 1975, it is even more challenging to explain and understand the reasoning of numerical models, such as Bayesian inference programs. When numerical ML methods such as neural networks gained in popularity in the end of the 1980’s due to significant technological progress (e.g. in [25] and [15]), the explainability challenge was immediately identified. During the 1990’s there was extensive activity around how to make results of neural networks explainable. However, a vast majority of the work performed then was focusing on so-called intrinsic interpretability or interpretable model extraction [6], i.e. extract rules or other interpretable forms of knowledge from the trained neural network and then use that representation for explainability [2, 5, 30, 31].

Post-hoc interpretability was actually proposed as early as in 1995 [9]. However, the utility of post-hoc interpretability was not recognized by the AI community back then, as shown by the reactions of the audience at the International Conference on Artificial Neural Networks in 1995. Post-hoc interpretability was neglected to the extent that most XAI survey articles erroneously date the first post-hoc explanations much later, such as output explanation in 2006 and model inspection approach in 2002 [12]. Another example that presents outcome explanation and the use of counterfactual explanations is the article from 2002 in the Neural Networks journal [11] that is currently only cited 128 times according to Google Scholar. However, the objective of this paper is not to provide a complete overview of the history of XAI. A comprehensive survey on current trends in XAI is provided for instance in [4].

The Local Interpretable Model-agnostic Explanations (LIME) method presented in 2016 [22] might be considered a cornerstone regarding post-hoc interpretability. It emphasizes the need for outcome explanations in many real-world situations and shows good results also when applied to image recognition by deep neural networks. LIME implementations are available in several different programming languages, which has certainly increased its popularity. LIME belongs to the family of additive feature attribution methods [19] that are based on the assumption that a locally linear model around the current context is sufficient for explanation purposes. As shown in the following Section, even though such methods allow producing outcome explanations (but not model inspection explanations), they are not theoretically correct when studied from a Decision Theory point of view.

Contextual Importance and Utility (CIU)

Contextual Importance and Utility (CIU) were initially developed during Kary Främling’s PhD thesis [8]. The thesis is written in French but the method is also described in [9] and [7]. After the PhD thesis was finished, the topic was dropped for professional reasons. The popularity of neural networks and the question about their explainability also started declining at the same time. However, the recent rise in popularity of AI and the re-emergence of XAI as a research area are the reasons for the recent re-launch of the work on CIU.

The work on CIU started by a practical problem that consisted in selecting a waste disposal site for ultimate industrial waste in the region of Rhône-Alpes, France [10]. Fifteen selection criteria had been specified by experts and regional decision makers, which characterized the sites from geological, financial, social, ecological and logistic points of view. Over 3000 potential sites had been identified, together with their respective values for the 15 criteria. Tens of decision makers involved in the selection process all had their own opinions on how important different criteria are. What comes to the utility functions, there are many subjective opinions, such as how to assess recreational impact and when such an impact should be ‘too big’, ‘acceptable’, ‘negligible’ or something else.

Three methods were applied in parallel: AHP, Electre I [23] and a rule-based expert system using the tool Nexpert Object v.2.0. The weights of the 15 criteria were identified as a group work using the AHP pair-wise comparison functionality mentioned in Sect. 2.1. The same weights and utility functions were used for AHP and Electre I. For the rule-based system, the problem was divided into sub-categories, i.e. ‘Global geology’, ‘Hydrology’, ‘Access’, ‘Nuisance to population’, ‘Aesthetic values’ and ‘Agricultural value’. Explainability functionality was developed that was specific for each of the three methods, where the mentioned sub-categories were used for providing explanations with a higher level of abstraction than using the 15 selection criteria directly. Explainability of the results was a core criterion for the decision makers when they took their decision on which method to choose for taking the decision2. Since the output of all the three methods was a numeric score per potential site, what needed to be explained was why every individual site had been selected (high score) or rejected (lower score).

The waste disposal site selection problem reveals many crucial challenges related both to MCDM and XAI, such as:

• It is challenging even for one person to specify what is the importance of different selection criteria (inputs of the model) and how favorable (or not) the values of different criteria are, i.e. their utility.

• It it difficult to choose what MCDM method to use and what that choice means in practice regarding results and explainability.

• The choice of MCDM model and parameters remains subjective. It would be preferable if a ML model could learn the ‘correct’ model based on data from existing sites.

• Since explainability is a key requirement, a typical ML black-box approach is not acceptable.

• ML models, such as the ones learned by neural networks can not be supposed to be linear.

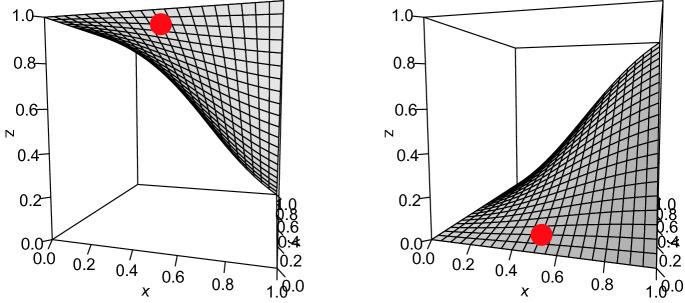
Three different kinds of MCDM models are illustrated in Fig. 1:

1. Figure 1a shows the function $z=0.3x+0.7y$. This is a weighted sum model with weights (importances) 0.3 and 0.7.

2. Figure 1b shows the result of several if-then rules that determine the z-value as a function of x- and y-values. This kind of a model is highly non-linear and is not differentiable.

3. Figure 1c shows the function $z=(x^{0.5}+y^2)/2$. This is a simple non-linear model that could have been learned by a neural net.

Fig. 1.

Examples of linear, rule-based (crisp rules, not fuzzy rules or rules involving certainty factors) and non-linear MCDM models. (Color figure online)

For the weighted sum in Fig. 1a it is obvious that the importance of each criterion is directly expressed by the corresponding weight and the utility of x and y equals their value. If such a linear model would have been learned by a ML black-box, then additive feature attribution methods should give these exact importances 0.3 and 0.7 for any point $z=f(x,y)$ because the locally linear model corresponds to the global model. Additive feature attribution methods only speak about feature importance, whereas they do not have any notion of utility.

For a stepwise model such as the one in Fig. 1b it does not make sense to apply a locally linear approximation, for two reasons: 1) the model is not differentiable and 2) the model is non-monotonic, so a local gradient does not say much about the actual importance of a feature.

The non-linear model in Fig. 1c is the most interesting to study further in the context of XAI because the main reason for using neural networks and similar ML models is to deal with non-linear but differentiable models. The next section formally describes Contextual Importance and Utility and provides the justification for why they are theoretically valid concepts for XAI. It also shows why methods based on locally linear models are not sufficiently expressive for many XAI requirements, nor theoretically sound compared to CIU.

CIU of One Input

CIU is inspired from trying to analyze how humans explain their decisions and reasoning to each other. After all, the human brain is probably the most complex black-box model on earth. But humans are still usually capable to retrospectively produce an explanation for their decisions and behaviour, even though humans do suffer from the limitations of so-called bounded rationality [29]. Bounded rationality is the idea that rationality of human individuals is limited when making decisions, by the tractability of the decision problem, the cognitive limitations of the mind, and the time available to make the decision. Humans also tend to take into account the reactions, background etc. of the audience of the explanation3. Humans would typically identify which features were the most salient for taking a decision and start the explanation with those features. In addition to explaining why a decision was taken, humans may also be asked to explain why another decision was not taken, both independently and in comparison with each other. Counterfactual “what-if” explanations are frequent when humans justify their decisions. Depending on the reactions of the audience, humans can also change the vocabulary that is used, the level of abstraction and the kind of interaction (for instance create a drawing if verbal explanation is not sufficient).

Many of these explanation capabilities are contextual. One feature might be important for taking a decision in one situation but irrelevant in another situation, as illustrated by the example mentioned in the Introduction, where the importance of the outdoor temperature depends on whether the black box (human brain and body) is indoors or outdoors.

In this paper, we will not attempt to provide a new definition of context. One definition is e.g. “Context is any information that can be used to characterize the situation of an entity. An entity is a person, place, or object that is considered relevant to the interaction between a user and an application, including the user and the applications themselves” [1]. The same source defines context-awareness as follows: “A system is context-aware if it uses context to provide relevant information and/or services to the user, where relevancy depends on the user’s task” [1]. Similar definitions are provided elsewhere, as in [21]. In general, context adds knowledge about what inputs/features/characteristics of a situation are important for the concerned entity, which in our example would be the person who is indoors or outdoors.

In order to specify Contextual Importance (CI) and Contextual Utility (CU) formally, we will study the non-linear model in Fig. 1c further. The red dot in Fig. 1c is located at $(x,y)=(0.1,0.2)$, which gives a result value $z=0.178$. Here the context is specified by the input values $(x,y)=(0.1,0.2)$, which we denote 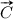. What we want to find out is the contextual importance 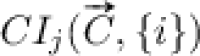of a given set of inputs $\{i\}$ for a specific output j in the context 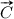. The definition of CI is

1

where $absma{x}_j$ is the maximal possible value for output j and $absmi{n}_j$ is the minimal possible value for output j. 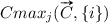is the maximal value of output j observed when modifying the values of inputs $\{i\}$ and keeping the values of the other inputs at those specified by 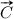. Correspondingly, 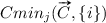is the minimal value of output j observed.

The estimation of 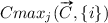and 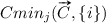is done for limited value ranges of inputs $\{i\}$. The value range to be used can be defined by the task parameters or by the input values present in the training set. The ‘safest’ option is typically to use input value ranges that are defined by the minimal and maximal values found in the training set because the behaviour of many ML models outside of that range tends to be unpredictable. It is also worth mentioning that the ‘valid’ input ranges may depend on the context C. The current implementation for estimating and 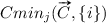uses Monte-Carlo simulation with uniformly distributed, randomly generated values within the provided value ranges of inputs $\{i\}$. More efficient methods probably exist for estimating and 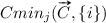if information about the black-box model or the learned function is available.

The definition of CU is

2

where 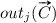is the value of the output j for the context .

The calculations of CI and CU are illustrated in Fig. 2 for the non-linear function in Fig. 1c. The values are 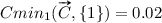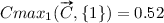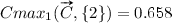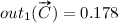$absmin=0$, $absmax=1$, , , , , , when inputs and outputs are numbered from one upwards. This gives 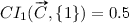and 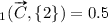, which signifies that both inputs are exactly as important for the output value. For the utilities, 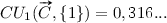and 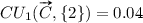, so even though the y value is higher than the x value, the utility of the x value is higher than the utility of the y value for the result z.

Fig. 2.

Illustration of calculations of CI and CU for simple non-linear model.

It is worth pointing out that an additive feature attribution method such as LIME would presumably correspond to the partial derivative, which would give importances of 0.8 and 0.24. Importances of 0.8 and 0.2 are radically different from $CI=0.5$ and illustrates to what extent CIU differs from additive feature attribution methods in the case of non-linear models. A locally linear model will provide an estimate of how much small changes in an input value affect the output value but they will not take into account what happens when modifying the input value even slightly more. Finally, additive feature attribution methods do not provide any utility concept. Such methods might produce an explanation such as ‘z has a bad value (0.18 of one), mainly because of input x (importance 0.8), whereas input y has much less importance (0.2)’.

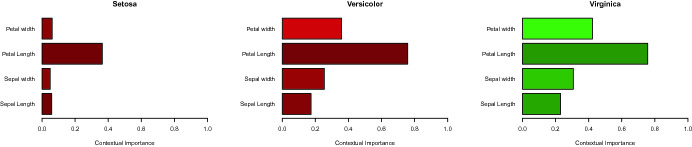
Based on CIU values, the explanation could be of the kind ‘z has a bad value (0.18 of one), where input x and input y are both quite important (0.5). The x value of 0.1 is relatively bad (CU = 0.32), while the y value is extremely bad (CU = 0.04). As a conclusion, the main reason for the bad output value is that the y value is bad’. This kind of verbal explanations are relatively straightforward to produce programmatically by dividing the maximal CI interval [0, 1] into labeled intervals with labels such as ‘insignificant’, ‘not important’, ‘some importance’, etc. The same can be done for the the maximal CU interval [0, 1]. Different intervals and vocabularies can and should be used depending on the application area and on the actual semantics and meaning for the different inputs and outputs of the black box. Examples of such programmatically generated explanations can be found in [7–9] and [3]. R and Python implementations of CIU5 also produce graphical plots as explanations, such as the one in Fig. 6 for the Iris classification task described in Sect. 3.2.

Fig. 6.

Bar plot visualisation of CIU for Iris classes. Bar length corresponds to CI value. CU values below 0.5 give red colour, otherwise green. The further away from 0.5 CU is, the darker the colour. (Color figure online)

In most existing XAI literature, the focus seems to be on answering questions such as ‘why is this a cat?’ or ‘why is this a good choice?’ but rarely answering questions such as ‘why is this not a tomato?’ or ‘why is this a bad choice?’. Classification tasks with one black-box output per possible class seem to be the most commonly used architecture in literature. However, as pointed out earlier, humans do not only explain why they choose one option. Humans are also often asked to explain why they do not choose other options. Additive feature attribution methods do not make any conceptual difference between ‘good’ and ‘bad’, so the explanations would presumably be quite similar no matter if they are for answering the question ‘why?’ or for answering the question ‘why not?’. With CIU, ‘why?’ and ‘why not?’ explanations can be quite different because the utility concept (CU) identifies which features are favorable or not for each class.

Figure 3 shows what non-linear classification models could look like for an ‘AND’/‘not AND’ classifier, with two inputs x, y and two outputs. The first output corresponds to the class ‘not AND’ and the second output corresponds to the class ‘AND’. The red dot in Fig. 3 shows the context to be studied, i.e. 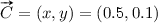. It is easy to see from Fig. 3 that modifying x will not affect the result z much and the CI of x is indeed only 0.07 for both classes, whereas the CU of x is 0.50 for both classes, which is expected. However, modifying y will modify the result z much more, which is also reflected by a CI of y of 0.50 for both classes. The CU of y is 0.93 for the class ‘not AND’ and 0.07 for the class ‘AND’, which is also expected.

Fig. 3.

Classification model learned by neural network, first output is ‘not AND’, second is ‘AND’. (Color figure online)

A simple explanation to the question ‘Why is this “not AND”?’ based on CIU would be something like ‘It is a “not AND” mainly because y is important (CI = 0.5) and has an excellent value (CU = 0.93). x is not important (CI = 0.07) but has an average value (CU = 0.5)’.

An explanation to the question ‘Why is this NOT “AND”?’ based on CIU would be something like ‘It is NOT “AND” mainly because y is important (CI = 0.5) and has an very bad value (CU = 0.07). x is not important (CI = 0.07) but has an average value (CU = 0.5)’.

This simple classification example is mainly intended to illustrate how CIU is used for classification tasks. However, the semantics of the ‘not AND’, ‘AND’, not ‘AND’ and not ‘not AND’ might not be the easiest ones to follow. Furthermore, it might be more interesting to study the joint behaviour of x and y. But since there are only two inputs in this case, the CI of both would be one because modifying both simultaneously would produce all possible z-values in the range [0, 1]. It is indeed useful to study the behaviour of the black-box also by getting CIU for all inputs at a time. However, for XAI purposes it might be more useful to calculate CIU for more than one input, as shown in the next Section.

CIU of More Than One Inputs

The definition of CI and CU is not restricted to one input. They can be calculated (or at least estimated) for any combination of inputs, as well as for all inputs simultaneously. This is useful for XAI purposes because it makes it possible to provide explanations at any level of abstraction. In a car selection case, for instance, the concept ‘Performances’ could be used to group together basic input features such as ‘Maximum power’, ‘Weight’, ‘Top speed’ and ‘Acceleration’ as in [7]. Any number of such intermediate concepts can be specified and used for explanation purposes depending on who the explanation is intended for or what level of detail is needed. There could even be different explanation vocabularies that target different audiences, such as a domain expert versus a domain novice6.

CIU for more than one input will here be studied using the simple and well-known Iris data set. The Iris set contains 150 Iris flowers, where there is 50 samples of the three different Iris species Setosa, Versicolor and Virginica. Four values are indicated for each flower: Sepal length, Sepal width, Petal length and Petal width, all measured in centimeters.

The neural network classifier used is an INKA (Interpolating, Normalising and Kernel Allocating) network [8]. INKA is a Radial Basis Function (RBF) network that is used here mainly because it tends to converge towards the average output value when extrapolating towards infinity, which can be an advantage for CIU calculations. However, since CIU is completely model-agnostic, it does not really matter what is ‘inside’ the black-box being studied. INKA also has excellent training results with the Iris data set.

For studying CIU, we will use a flower $Iri{s}_{\mathit{test}}$ that is not included in the Iris data set but that is quite a typical Virginica, so we have 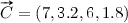as input values. The trained INKA network gives us 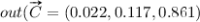for the three outputs (classes), so it is clearly a Virginica.

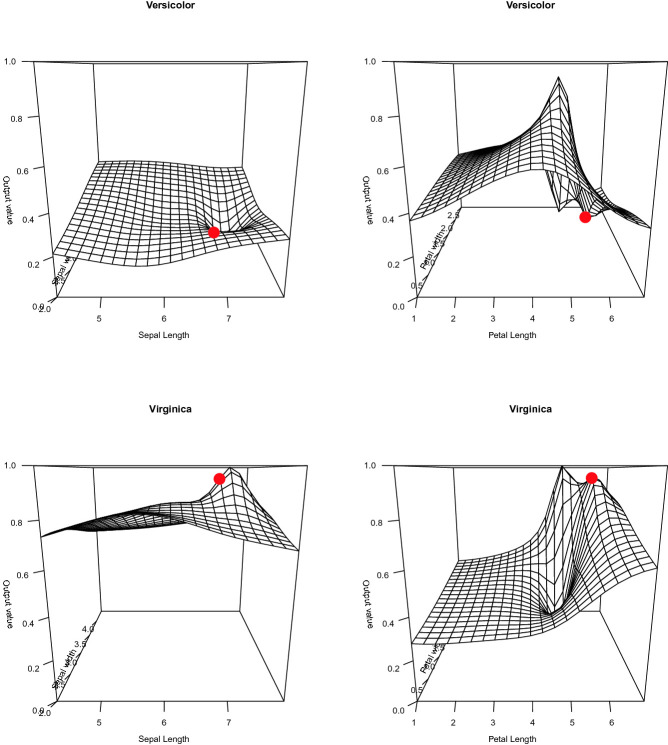
Figure 4 shows how the three outputs change as a function of each input. Table 1 shows the corresponding CI and CU values. It is clear that the flower C is very far from being a Setosa and modifying any single input will not change that classification. Figure 4 shows that the Petal length is the most important feature and that the value 6 cm makes this flower a typical Virginica (but definitely not a Versicolor). The CI and CU values in Table 1 express the same, so it is easy to provide an explanation that is clear and that corresponds exactly to the learned model7.

Fig. 4.

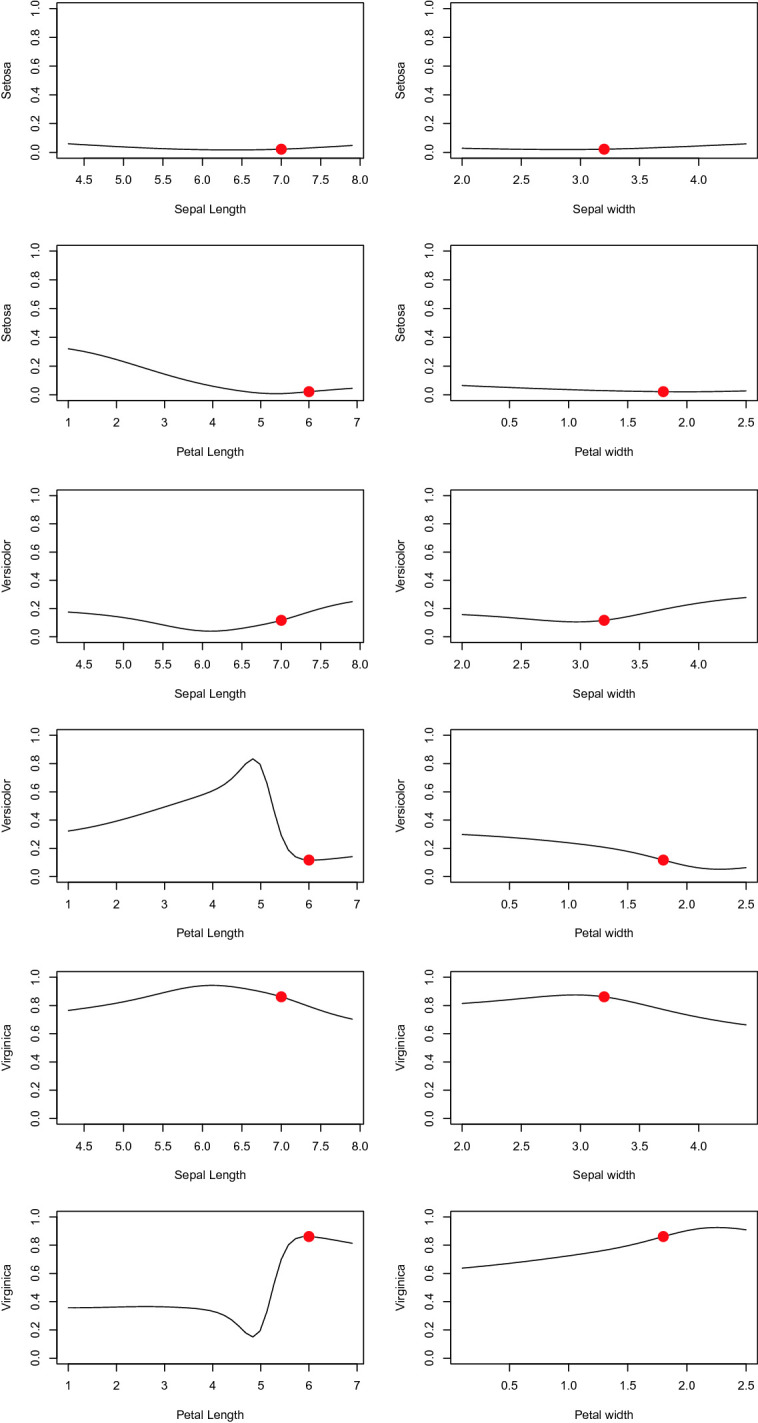
CIU as a function of the four inputs for all classes.

Table 1.

CIU values for Iris classes versus input.

Input feature	Setosa	Versicolor	Virginica
Sepal length	0.0425279	0.2085747	0.2384596	CI
Sepal width	0.03972771	0.17254086	0.21204752
Petal length	0.3124243	0.7169677	0.7113022
Petal width	0.04344366	0.24595074	0.28744096
Sepal length	0.1171743	0.3690032	0.6596097	CU
Sepal width	0.0640272	0.0644939	0.9365688
Petal length	0.0456506224	0.0006167944	0.9995161501
Petal width	0.01707707	0.26574443	0.77682899

Table 2 shows CI and CU for the intermediate concepts ‘Sepal size and shape’ (inputs one and two) and ‘Petal size and shape’ (inputs three and four), as well as CI and CU when calculated for all inputs. The CI values in Table 2 clearly show that ‘Petal size and shape’ is the most important concept for the flower studied. CI is about the same (0.91 and 0.92) for both Versicolor and Virginica but the CU values in Table 2 say that the Petal values are clearly favorable for Virginica but not favorable for Versicolor (and even less for Setosa). Figure 5 shows the probability of Virginica and Versicolor as a joint function of ‘Sepal size and shape’ and ‘Petal size and shape’.

Table 2.

CIU values for combined concepts.

Input feature	Setosa	Versicolor	Virginica
Sepal size and shape	0.07172334	0.30947848	0.36959064	CI
Petal size and shape	0.3916285	0.9102021	0.9205347
All input features	0.8240611	1.1038175	1.1122128
Sepal size and shape	0.1415141	0.4294574	0.6130286	CU
Petal size and shape	0.04523376	0.15602016	0.82909669
All input features	0.02717686	0.24984699	0.73618267

Fig. 5.

CIU as a function of the intermediate concepts ‘Sepal size and shape’ and ‘Petal size and shape’ for classes Versicolor and Virginica and $Iri{s}_{\mathit{test}}$.

When calculating CI for all input features combined, it should logically be one. The CI values in Table 2 are ‘sufficiently’ close to one in the sense that the Monte-Carlo simulation with 1000 samples for estimating 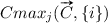and 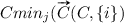only provide an estimation of the true values. However, CI for all inputs can also be used as an indicator of how reliable the learned model is. A small CI might be an indication that there are areas in the input feature space that lack in training data. A CI value over one would typically indicate that there are areas of the input space where the model is overshooting and/or undershooting so that 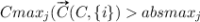and/or .

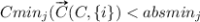On the other hand, CU for all input features combined should give a result that is similar to the different output values. In this case, , which is well in line with .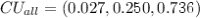

Despite the solid theoretical foundations of CIU and the consistent results presented here, there are also some challenges and topics for future research. For instance, it will take more testing and experience to learn when it might be better to use somehow normalised CI values rather than the absolute values. For instance, when dealing with saliency maps as in [22] the CI values of individual pixels will be very small so then it is only CI of each pixel relative to the other pixels that counts.

Another challenge is if the input space is not sufficiently well covered by the training set. Then the estimation of $Cmax(C,\{i\},j)$ and $Cmin(C,\{i\},j)$ might go into areas of the input space where the black-box model can be completely erroneous. Many neural networks have a tendency to go into extreme oscillations when extrapolating even slightly. However, such conditions can at least be detected using CI for all input features.

Future topics of research include detecting challenges with stability, reliability, robustness and lack of ‘self-insight’ about how certain the results of the black box are. The current CIU-based explanation features address these challenges only partially but might open new possibilities. Finally, as proposed in [8], CIU plots such as those in Fig. 4 could also be used by human experts for correcting erroneous models by augmenting the training set with pseudo-examples that would correct obvious errors in the trained model.

As CIU is applied to an increasing number of data sets and applications, it is expected that more insight will be gained into properties of the method that still tend to be intuitive. For instance, does a CU value of 0.9 for an input value indeed signify that the value is ‘as good’ as a CU value of 0.9 for an output, or for an intermediate concept? Intuition says that it should be so but it remains a topic for further research.

Conclusions

Despite all research efforts on explainability of AI systems since decades, the emergence of a new name (XAI) for the domain as recently as 2016 is an indication that XAI is still quite immature. Current XAI research notably on outcome explanation also seems to ignore the wealth of knowledge accumulated also by closely related domains for decades. This paper proposes extending the traditional MCDM concepts of importance and utility from the linear models towards the non-linear models produced by ML techniques. That extension is called Contextual Importance and Utility (CIU).

This paper provides the mathematical definition of CIU and shows how CIU is used in practice for XAI. An experiment with the Iris data set validates the approach for real-world data. The Iris data has mainly been chosen for simplicity of presentation and understanding the basics of CIU. Work is ongoing for more complex data and use cases in order to show how CIU can be used for explaining diagnostics in healthcare and machine failures, AI-performed credit assessments, control actions taken by autonomous vehicles, ....

Theoretical and practical examples were provided for showing why methods based on local linearity are not universally applicable for XAI. CIU provides the kind of universal base for XAI that is needed in the future. However, more experimental work is still needed for understanding all the possibilities, challenges and limitations of CIU.