Abstract
Objective
To examine the biomechanical stress distribution at the upper instrumented vertebra (UIV) according to unicortical- and bicortical purchase model by finite element analysis (FEA).
Methods
A T8 to Sacrum with implant finite element model was developed and validated. The pedicle screws were unicortically or bicortically inserted from T10 to L5, and each model was compared and the von Mises (VM) yield stress of T10 was calculated. According to the motion (flexion, extension, lateral bending, and axial rotation) of spine, boundary condition values were set as 15°, 15°, 10°, 4°.
Results
Although the 2 stress values did not show a significant difference between the unicortical- and bicortical purchase models in the flexion and extension, bicortical purchase model showed a larger stress distribution. However, the asymmetric behavior was significantly greater in the case of lateral bending (0.802 MPa vs. 0.489 MPa) and the rotation (5.545 MPa vs. 4.905 MPa). The greater stress was observed on the spinal body surface abutting the implanted screw. Although the maximum stress was observed around the implanted screw in the bicortical purchase model under axial loading, the VM stress of both models was not significantly different.
Conclusion
Bicortical purchase model showed a larger stress distribution than the unicortical model, especially in the case of lateral bending and the rotation behavior. Our biomechanical simulation by FEA indicates that bicortical fixation at UIV can be a risk factor for early UIV compression fracture after adult spinal deformity surgery.
Keywords: Finite element analysis, Spinal fusion, Pedicle screws, Adult spinal deformity
INTRODUCTION
Despite the developments in surgical techniques, proximal junctional failure (PJF) continues to develop after adult spinal deformity surgery. PJF is a widely recognized problematic complication of long-level arthrodesis surgery. Not a few researches reported several risk factors of proximal junctional fracture after multilevel instrumented spinal fusion surgery such as obesity, older age [1,2], osteopenia, preoperative comorbidities, and severe global sagittal imbalance including flat back posture [3].
In the previous study, we reported that bicortical fixation at the upper instrumented vertebra (UIV) is a major risk factor for early UIV compression fracture following adult spinal deformity surgery. Bicortical screw fixation at the UIV highly correlated with developing a fracture of the UIV. The average fracture rate was 0% and 42.9% in unicortical- and bicortical purchase group, respectively [4]. Based on these results, we performed a study to compare the stress levels of the anterior vertebral column at the UIV according to several behaviors after unicortical-and bicortical screw installation.
Finite element (FE) method is an engineering tool of choice for the investigation of the effect of parameters related to the geometry and to the material properties. And this FE method is advantageous in proving the differences according to the screw insertion method in increasing the risk of UIV compression fracture. The purpose of this study was to examine the biomechanical stress distribution at the UIV according to unicorticaland bicortical purchase model by finite element analysis (FEA).
MATERIALS AND METHODS
In this study, we quantified the peak von Mises (VM) stress (MPa) applied to the vertebral body when flexion, extension, lateral bending, rotation, axial weight loading was performed after spinal pedicle screw fixation. VM stress is derived from 3-dimensional (3D) status of stress. VM stress value is calculated by taking into consideration of 3 of maximum stress in 3 axis directions. That is maximum stress in X, Y, and Z directions. Principal stress is the pressure exerted on a particular point in the vertebral body in any direction [5]. For this purpose, FEA of unicortical screw purchase model and bicortical screw purchase model were performed. The FE software Abaqus ver. 6.5 (ABAQUS Inc., Johnston, RI, USA) was used to create a FE model of a T8 to Sacrum with implant model (Figs. 1, 2). The Visible human body 3D model (National Institutes of Health, Bethesda, MD, USA) was used for this analysis. After making these models, various motions were simulated to each model. UIV, which is reported to occur proximal junctional fracture frequently after spinal deformity surgery, is the target for comparing stress value. The pedicle screws were inserted into the T10 to L5 vertebral level in the FE model.
Fig. 1.

The 3-dimensional model and finite element model of the pedicle screw implant.
Fig. 2.
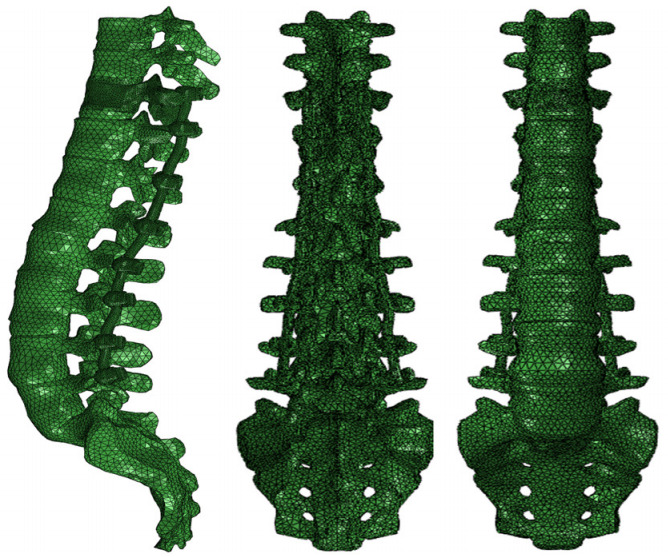
The 3-dimensional model and finite element model of T8 to Sacral spine model with pedicle screw implant.
For assuming the real condition, we added another thoracic bone as T8, T9, and Sacrum. T8 to Sacrum with implant model was used. The roof shell element of the T8 was set as rigid body and was used as moving parts. We assumed that the sacrum does not move. The sacrum was used as fixed component. Therefore, we assumed that the maximum distortion energy is applied to the T10 vertebral body (UIV in these FE models) and calculate the VM yield stress at the vertebral body. All the material properties of components mentioned earlier are listed in Table 1.
Table 1.
Material properties
| Material | Young’s modules (MPa) | Poisson’s ratio |
|---|---|---|
| Titanium Ti-6Al-4V (pedicle screw, rod) | 113,800 | 0.342 |
| Cortical bone | 12,000 | 0.3 |
| Cancellous bone | 100 | 0.2 |
| Disc | 4.2 | 0.45 |
The entire FE model of the unicortical purchase model consisted of approximately 472,950 linear tetrahedral elements. The entire FE model of the bicortical purchase model consisted of approximately 513,334 linear tetrahedral elements. The entire FE model of implant consisted of approximately 105,927 linear tetrahedral elements. Loading of the implant construct followed the recommendations of American Society for Testing and Materials (ASTM) F1717 [6]. For preclinical evaluation of a spinal device, ASTM publishes the standards describing how to evaluate and compare the surgical devices under controlled conditions. ASTM published in 1996 the first version of the F1717 standard proposing a test method useful for the assessment of the mechanical properties of posterior spinal fixator. According to the range of motion (flexion, extension, lateral bending, and axial rotation, axial loading) of lumbar spine, boundary condition and load condition was set as 15°, 15°, 10°, 4° (Fig. 3).
Fig. 3.
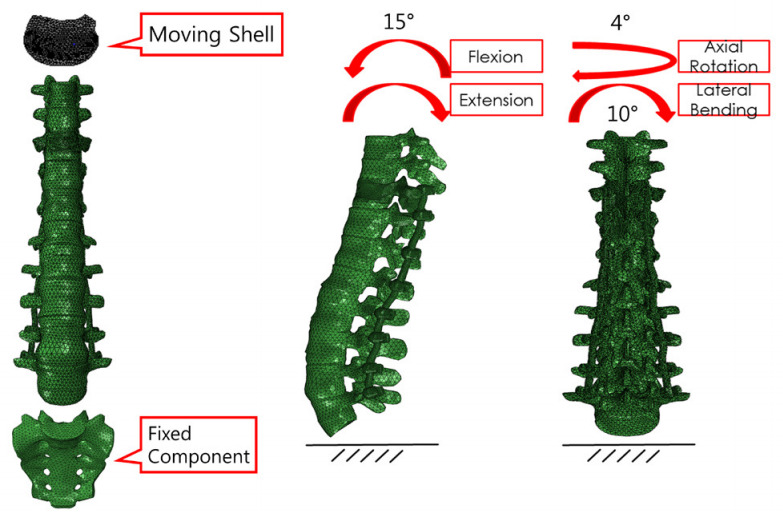
The boundary condition of T8 to Sacrum finite element model. The range of motion of spine was reflected.
RESULTS
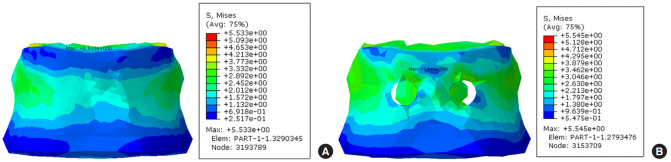
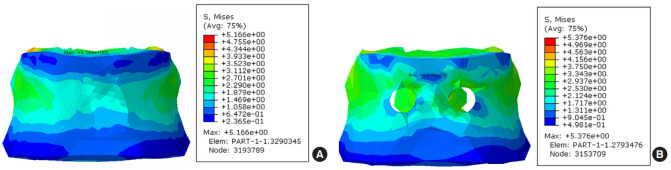
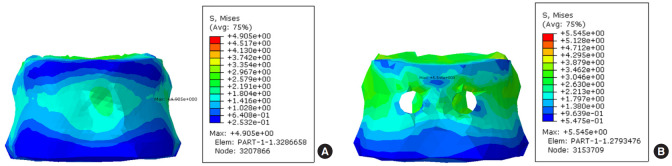
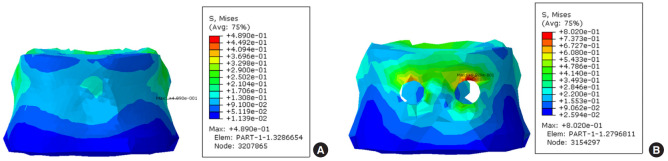
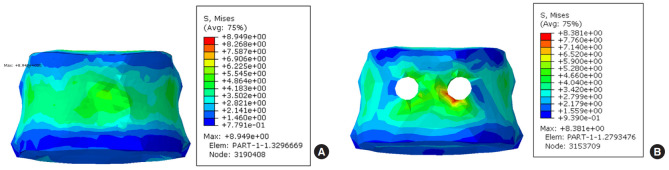
A stress simulation was performed to demonstrate the FE methodology, predict typical stress distributions within the fusion system. Previously discussed material properties and simulation conditions were used for the benchmark FE simulation. Figs. 4–8 show the predicted VM stress distribution in the FE model. It is distinguished by the color depending on the stress value and displayed the value of the largest pressure in the nonspecific point of vertebral body. VM stress is a commonly used invariant stress measure which considers all of the normal and shear stress components acting at some location in the material. We removed the shape of the pedicle screw in the contour plot to show the stress by measuring only the VM stress on the vertebral body. In a stress test using FE model, the 2 stress values (maximum VM stress and maximum principal stress) did not show a large difference in the flexion and extension behavior. In Fig. 4A and sB, the stress was increased around the area abutting the implanted screw, and the color of stress was slightly changed, but there was no significant difference in the values. This is similar in Fig. 5A and B. Especially, the asymmetric behavior was significantly greater in the case of lateral bending (5.545 MPa vs. 4.905 MPa) and the rotation behavior (0.802 MPa vs. 0.489 MPa) (Table 2). As shown in Fig. 6, the area of high stress was increased slightly and the value of the stress from lateral bending was increased by 0.6 MPa compared to the neutral position. In Fig. 7 which shows rotational behavior, the area abutting the implanted screw shows higher stress color than other surfaces. Although the maximum stress was observed around the implanted screw in the bicortical screw purchase model under axial loading, the VM stress of both models was not significantly different (8.381 MPa vs. 8.949 MPa).
Fig. 4.
Von Mises stress contour plots on the T10 from finite element analysis after 15° flexion. (A) Unicortical screw purchase fusion type. (B) Bicortical screw purchase fusion type.
Fig. 5.
Von Mises stress contour plots on the T10 from finite element analysis after 15° extension. (A) Unicortical screw purchase fusion type. (B) Bicortical screw purchase fusion type.
Fig. 6.
Von Mises stress contour plots on the T10 from finite element analysis after 10° lateral bending. (A) Unicortical screw purchase fusion type. (B) Bicortical screw purchase fusion type.
Fig. 7.
Von Mises stress contour plots on the T10 from finite element analysis after 4° rotation. (A) Unicortical screw purchase fusion type. (B) Bicortical screw purchase fusion type.
Fig. 8.
Von Mises stress contour plots on the T10 from finite element analysis after axial loading. (A) Unicortical screw purchase fusion type. (B) Bicortical screw purchase fusion type.
Table 2.
Maximum von Mises (VM) stress and maximum principal stress
| Boundary condition | Maximum VM stress of flexion | Maximum VM stress of extension | Maximum VM stress of lateral bending | Maximum VM stress of torsional rotation | Maximum VM stress of axial loading | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Specimen | Unicortical | Bicortical | Unicortical | Bicortical | Unicortical | Bicortical | Unicortical | Bicortical | Unicortical | Bicortical |
| VM stress (MPa) | 5.533 | 5.545 | 5.166 | 5.376 | 4.905 | 5.545 | 0.489 | 0.802 | 8.949 | 8.381 |
DISCUSSION
Adult long spinal instrumented fusion may be necessary for various conditions such as degenerative lumbar scoliosis, sagittal imbalance, transition syndrome, and revision cases to alleviate back pain and to achieve balance and stabilization of the fused segments [7]. However, stress concentration on the proximal junction after posterior long spinal instrumented fusion, from the thoracolumbar spine to S1 or the pelvis, has demonstrated several junctional changes: PJF including fractures, proximal junctional kyphosis, junctional disc rupture, and junctional spinal stenosis [8-11].
Several previous studies have reported various risk factors associated with PJF, known risk factors include older age, osteoporosis, female sex, high UIV angle, preoperative kyphosis adjacent to the UIV, inadequate implant systems, the level of the UIV, preoperative hyperkyphotic thoracic alignment, sagittal imbalance, and acute correction of sagittal imbalance [12-19]. We reported previously that bicortical fixation at the UIV is a major risk factor for early UIV compression fracture by examining our clinical series of patients who underwent adult spinal deformity surgery. Therefore, this study was conducted to investigate the stress load on the UIV after a bicortical screw purchase by biomechanical analysis.
While the usefulness of FEA of the spine has been demonstrated in many studies [20-23], only a few studies have analyzed long spinal instrumented fusion related fracture by FEA. Imai et al. [24] compared the results of FEA and an actual vertebral strength affect to fracture site using human fresh cadavers, and demonstrated that bone strength and fracture sites can be predicted by FEA. To simulate the FEA, modeling for implants and spines was made using a computer program. The load on the anterior wall of the UIV was evaluated after applying flexion, extension, axial rotation, lateral bending forces to the 3D-modeling made using the originally known material properties [25-28].
In the flexion and extension movements, there was almost no difference in VM stress between the 2 models, only the figures were slightly higher in the bicortical purchase model. However, in the lateral bending and rotation movements, the VM stress values were significantly greater in the bicortical screw purchase model. As shown in Figs. 4–8, it can be confirmed by color change that more stress is carried around the inserted screw in the bicortical screw purchase model, in rotational stimulation and axial loading, the change in color is more pronounced. We suggest that asymmetric movements to each pedicle screw have a substantial effect on the anterior wall of the vertebral body, which can result in mechanical overloading of the vertebral body in the bicortical screw purchase model. There was no significant difference in flexion and extension movements compared to neutral position, because the stress was distributed on both pedicle screws. In the case, the mechanical stress was loaded symmetrically. However, asymmetric stress on each pedicle screws in lateral bending and rotational movement, resulting in greater stress on one side of pedicle screw and vertebral body. With those results, unicortical screw purchase on the UIV in long spinal instrumented fusion surgery gives relatively less stress to the anterior wall of the vertebral body than bicortical screw purchase.
The present study had several limitations. First, the FEA models in this study did not consider ligaments, particularly the supraspinatus and interspinous ligaments, joint capsule, muscles, and ribs. Second, the reliability can be lower than cadaver study. Third, FE models are making an important contribution to physician’s understanding of the spine and its components. Models are being used to manifest the biomechanical function of the spine. Nevertheless, the results from FEA are not statistical values. The VM stress value is a single result through a test. The results of this study can consider as a risk factor for UIV fracture but was not a statistical conclusion. Finally, we did not make various comparisons by changing the instrumented fusion level. Future studies would need to complement these limitations.
CONCLUSION
Bicortical purchase model showed a larger stress distribution than the unicortical model, especially in the case of lateral bending and the rotation behavior. Our biomechanical simulation by FEA indicates that bicortical fixation at the UIV can be a risk factor for early UIV compression fracture after adult spinal deformity surgery.
Footnotes
The authors have nothing to disclose.
REFERENCES
- 1.O’Leary PT, Bridwell KH, Lenke LG, et al. Risk factors and outcomes for catastrophic failures at the top of long pedicle screw constructs: a matched cohort analysis performed at a single center. Spine (Phila Pa 1976) 2009;34:2134–9. doi: 10.1097/BRS.0b013e3181b2e17e. [DOI] [PubMed] [Google Scholar]
- 2.Bae J, Lee SH. Minimally invasive spinal surgery for adult spinal deformity. Neurospine. 2018;15:18–24. doi: 10.14245/ns.1836022.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Watanabe K, Lenke LG, Bridwell KH, et al. Proximal junctional vertebral fracture in adults after spinal deformity surgery using pedicle screw constructs: analysis of morphological features. Spine (Phila Pa 1976) 2010;35:138–45. doi: 10.1097/BRS.0b013e3181c8f35d. [DOI] [PubMed] [Google Scholar]
- 4.Park YS, Hyun SJ, Choi HY, et al. Association between bicortical screw fixation at upper instrumented vertebra and risk for upper instrumented vertebra fracture. J Neurosurg Spine. 2017;26:638–44. doi: 10.3171/2016.10.SPINE16535. [DOI] [PubMed] [Google Scholar]
- 5.Sin DA, Heo DH. Comparative finite element analysis of lumbar cortical screws and pedicle screws in transforaminal and posterior lumbar interbody fusion. Neurospine. 2019;16:298–304. doi: 10.14245/ns.1836030.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.La Barbera L, Galbusera F, Villa T, et al. ASTM F1717 standard for the preclinical evaluation of posterior spinal fixators: can we improve it? Proc Inst Mech Eng H. 2014;228:1014–26. doi: 10.1177/0954411914554244. [DOI] [PubMed] [Google Scholar]
- 7.Lee BH, Hyun SJ, Park JH, et al. Single stage posterior approach for total resection of presacral giant schwannoma: a technical case report. Korean J Spine. 2017;14:89–92. doi: 10.14245/kjs.2017.14.3.89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kim YJ, Bridwell KH, Lenke LG, et al. Proximal junctional kyphosis in adolescent idiopathic scoliosis following segmental posterior spinal instrumentation and fusion: minimum 5-year follow-up. Spine (Phila Pa 1976) 2005;30:2045–50. doi: 10.1097/01.brs.0000179084.45839.ad. [DOI] [PubMed] [Google Scholar]
- 9.Hyun SJ, Lee BH, Park JH, et al. Proximal junctional kyphosis and proximal junctional failure following adult spinal deformity surgery. Korean J Spine. 2017;14:126–32. doi: 10.14245/kjs.2017.14.4.126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lee BH, Hyun SJ, Kim KJ, et al. Clinical and radiological outcomes of posterior vertebral column resection for severe spinal deformities. J Korean Neurosurg Soc. 2018;61:251–7. doi: 10.3340/jkns.2017.0181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Makhni MC, Shillingford JN, Laratta JL, et al. Restoration of sagittal balance in spinal deformity surgery. J Korean Neurosurg Soc. 2018;61:167–79. doi: 10.3340/jkns.2017.0404.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dekutoski MB, Schendel MJ, Ogilvie JW, et al. Comparison of in vivo and in vitro adjacent segment motion after lumbar fusion. Spine (Phila Pa 1976) 1994;19:1745–51. doi: 10.1097/00007632-199408000-00015. [DOI] [PubMed] [Google Scholar]
- 13.Kim YJ, Bridwell KH, Lenke LG, et al. An analysis of sagittal spinal alignment following long adult lumbar instrumentation and fusion to L5 or S1: can we predict ideal lumbar lordosis? Spine (Phila Pa 1976) 2006;31:2343–52. doi: 10.1097/01.brs.0000238970.67552.f5. [DOI] [PubMed] [Google Scholar]
- 14.Lee CK. Accelerated degeneration of the segment adjacent to a lumbar fusion. Spine (Phila Pa 1976) 1988;13:375–7. doi: 10.1097/00007632-198803000-00029. [DOI] [PubMed] [Google Scholar]
- 15.Penta M, Sandhu A, Fraser RD. Magnetic resonance imaging assessment of disc degeneration 10 years after anterior lumbar interbody fusion. Spine (Phila Pa 1976) 1995;20:743–7. doi: 10.1097/00007632-199503150-00018. [DOI] [PubMed] [Google Scholar]
- 16.Phillips FM, Reuben J, Wetzel FT. Intervertebral disc degeneration adjacent to a lumbar fusion. An experimental rabbit model. J Bone Joint Surg Br. 2002;84:289–94. doi: 10.1302/0301-620x.84b2.11937. [DOI] [PubMed] [Google Scholar]
- 17.Rahm MD, Hall BB. Adjacent-segment degeneration after lumbar fusion with instrumentation: a retrospective study. J Spinal Disord. 1996;9:392–400. [PubMed] [Google Scholar]
- 18.Schlegel JD, Smith JA, Schleusener RL. Lumbar motion segment pathology adjacent to thoracolumbar, lumbar, and lumbosacral fusions. Spine (Phila Pa 1976) 1996;21:970–81. doi: 10.1097/00007632-199604150-00013. [DOI] [PubMed] [Google Scholar]
- 19.Weinhoffer SL, Guyer RD, Herbert M, et al. Intradiscal pressure measurements above an instrumented fusion. A cadaveric study. Spine (Phila Pa 1976) 1995;20:526–31. doi: 10.1097/00007632-199503010-00004. [DOI] [PubMed] [Google Scholar]
- 20.Hashemi A, Bednar D, Ziada S. Pullout strength of pedicle screws augmented with particulate calcium phosphate: an experimental study. Spine J. 2009;9:404–10. doi: 10.1016/j.spinee.2008.07.001. [DOI] [PubMed] [Google Scholar]
- 21.Hsu CC, Chao CK, Wang JL, et al. Increase of pullout strength of spinal pedicle screws with conical core: biomechanical tests and finite element analyses. J Orthop Res. 2005;23:788–94. doi: 10.1016/j.orthres.2004.11.002. [DOI] [PubMed] [Google Scholar]
- 22.Kilinçer C, Inceoglu S, Sohn MJ, et al. Effects of angle and laminectomy on triangulated pedicle screws. J Clin Neurosci. 2007;14:1186–91. doi: 10.1016/j.jocn.2006.10.008. [DOI] [PubMed] [Google Scholar]
- 23.Sairyo K, Goel VK, Masuda A, et al. Three-dimensional finite element analysis of the pediatric lumbar spine. Part I: pathomechanism of apophyseal bony ring fracture. Eur Spine J. 2006;15:923–9. doi: 10.1007/s00586-005-1026-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Imai K, Ohnishi I, Bessho M, et al. Nonlinear finite element model predicts vertebral bone strength and fracture site. Spine (Phila Pa 1976) 2006;31:1789–94. doi: 10.1097/01.brs.0000225993.57349.df. [DOI] [PubMed] [Google Scholar]
- 25.Hou FJ, Lang SM, Hoshaw SJ, et al. Human vertebral body apparent and hard tissue stiffness. J Biomech. 1998;31:1009–15. doi: 10.1016/s0021-9290(98)00110-9. [DOI] [PubMed] [Google Scholar]
- 26.Jensen KS, Mosekilde L, Mosekilde L. A model of vertebral trabecular bone architecture and its mechanical properties. Bone. 1990;11:417–23. doi: 10.1016/8756-3282(90)90137-n. [DOI] [PubMed] [Google Scholar]
- 27.Ladd AJ, Kinney JH, Haupt DL, et al. Finite-element modeling of trabecular bone: comparison with mechanical testing and determination of tissue modulus. J Orthop Res. 1998;16:622–8. doi: 10.1002/jor.1100160516. [DOI] [PubMed] [Google Scholar]
- 28.Rho JY, Tsui TY, Pharr GM. Elastic properties of human cortical and trabecular lamellar bone measured by nanoindentation. Biomaterials. 1997;18:1325–30. doi: 10.1016/s0142-9612(97)00073-2. [DOI] [PubMed] [Google Scholar]