Decrypting the Information Exchange Pathways across the Spliceosome Machinery

Abstract

Intron splicing of a nascent mRNA transcript by spliceosome (SPL) is a hallmark of gene regulation in eukaryotes. SPL is a majestic molecular machine composed of an entangled network of proteins and RNAs that meticulously promotes intron splicing through the formation of eight intermediate complexes. Cross-communication among the critical distal proteins of the SPL assembly is pivotal for fast and accurate directing of the compositional and conformational readjustments necessary to achieve high splicing fidelity. Here, molecular dynamics (MD) simulations of an 800 000 atom model of SPL C complex from yeast Saccharomyces cerevisiae and community network analysis enabled us to decrypt the complexity of this huge molecular machine, by identifying the key channels of information transfer across long distances separating key protein components. The reported study represents an unprecedented attempt in dissecting cross-communication pathways within one of the most complex machines of eukaryotic cells, supporting the critical role of Clf1 and Cwc2 splicing cofactors and specific domains of the Prp8 protein as signal conveyors for pre-mRNA maturation. Our findings provide fundamental advances into mechanistic aspects of SPL, providing a conceptual basis for controlling the SPL via small-molecule modulators able to tackle splicing-associated diseases by altering/obstructing information-exchange paths.

Graphical Abstract

INTRODUCTION

Complex and sophisticated conformational remodeling underlies the function of many types of biological systems.¹ Conformational changes are critically entwined with promotion and regulation of information exchange within biomolecules and biomolecular aggregates. Nevertheless, decrypting the pathways and the mechanisms modulating their cross-communication at the atomic-level remains challenging,^2–7 especially when tackling large macromolecular machines. Here, we address this challenge on the spliceosome (SPL), which, in eukaryotes, promotes premature-messenger (pre-m) RNA splicing, and hence is a key modulator of gene expression and diversification. The SPL is a multi-megadalton machine composed of an intricate network of hundreds of proteins and five small nuclear RNAs (snRNAs) (U1, U2, U4, U5, and U6) organized into small nuclear ribonucleoprotein subunits (snRNPs). The splicing cycle proceeds by formation of at least eight intermediate SPL states (i.e., A, B, B^act, B*, C, C*, P, and ILS), leading to the release of mature (m)RNAs upon excision of the noncoding regions (introns) from primary RNA transcripts and ligation of the protein coding segments (exons). The SPL conducts this pivotal step of gene expression by recognizing three key intronic sequences, the 5′ and 3′ splicing sites (5′SS and 3′SS, respectively), which delimit the intron boundaries, and the branch-point adenosine (BPA) lying within the branch point site (BPS). Splicing is accomplished via two subsequent transesterification reactions coadjuvated by two catalytically active Mg²⁺ ions.⁸ In the first step, a free upstream exon and an intron-lariat (IL), named hereafter as intron-lariat exon intermediate (ILE), are formed. In the second step, the exon ligation and IL release takes place. An idiosyncratic trait of the SPL is its marked structural plasticity, which promotes splicing thanks to a relentless conformational and compositional reshaping of its snRNPs. That conformational change is mediated by sophisticated and precise signaling networks. The mechanistic understanding of SPL function is burgeoning due to the cryogenic electron microscopy (cryo-EM) structures solved at near-atomic-level resolution from both human and yeast strains.⁹ All-atom molecular dynamics (MD) have supported and amplified the impact of cryo-EM data by dissecting the functional dynamics encoded into its distinct proteins/RNA components.^10–14 Here, we provide a groundbreaking advance in the field by unprecedentedly addressing the molecular origin of signal transfer within the SPL machinery, which underlays its complex functional transitions. To this end, we performed all-atom MD simulations of the C complex from the yeast Saccharomyces cerevisiae, as a prototypical example of the SPL assembly, for a cumulative statistic of 6 μs, complemented by correlation and community network analyses. Our approach allowed decrypting of the cross-talk channels for the information transfer between the distal (160 Å) Clf1 and RNase-H domain of Prp8, functional for the transition from the investigated state (C complex) toward the subsequent intermediate of the cycle (C* complex) and necessary to accurately promote gene expression. Our results are conducive to resolve the puzzling scenario underlying signal communication within the SPL and assert the critical role of computer simulations to dissect the mechanisms of complex molecular machines at the atomic level. Harnessing this knowledge may open the tantalizing perspective of identifying small-molecule modulators, able to interfere with the SPL’s signaling pathways, as a novel strategy to fight the nearly 200 human diseases associated with splicing deregulation.

MATERIALS AND METHODS

Model Construction.

The simulations were based on the S. cerevisiae C complex cryo-electron microscopy (EM) structure at a resolution of 3.8 Å on average (PDB ID: 5LJ3), with components reaching a resolution of 3.4 Å. This model is composed of three functional snRNAs (U2, U5, and U6), a 5′ exon filament, and the intron lariat-exon (ILE) junction intermediate where O2′ of the BPA has already reacted with the phosphate group of the first intron base. The model also comprised 15 proteins. In detail, the included proteins are Prp8 and Snu114 (from U5 snRNP), Cef1, Isy1, and Clf1 and the splicing factors Yju2, Cwc25, Cwc21, Cwc22, Prp45, Prp46, Cwc15, Bud31, and Cwc2, Emc2. Four Mg²⁺ ions were originally present in the structure. However, since the structure of the B^act complex (PDB id: 5GM6)¹⁵ shares an almost identical active site in which five ions are present, we recovered a fifth ion from the B^act structure. The presence of a five-metal ion motif was later confirmed in other steps of the SPL cycle,^16–18 and only in the presence of this additional metal ion we were able to achieve a stable active site architecture. Overall, also considering five Mg²⁺ ions and seven Zn²⁺ ions originally present, the counterions, and the explicit water molecules, our SPL model consists of 772 682 atoms. In order to find a compromise between system size and accuracy, we discarded all the peripheral proteins due to their incomplete chains, their low resolution, and the presence of multiple gaps. Small gaps (about 14 residues long, besides one exception of 46 residues long) in the loops within the retained regions were instead modeled with de novo model building, as implemented in Modeler 9, version 16.¹⁹ The loops were first selected among 50 models according to their DOPE (Discrete Optimized Protein Energy) score and subsequently evaluated through an accurate visual inspection.

MD Simulations.

MD simulations were carried out with the Gromacs 5.0.7 suite²⁰ using the most tested force field (FF) for proteins/RNA complexes. Namely, AMBER-ff12SB²¹ was used for proteins, whereas ff99+bsc0+χOL3 FF was used for RNAs.^22,23 This protocol has been validated in other protein/RNA macromolecular complexes.^6,7,10,11,24 For Mg²⁺ ions, we used dummy cation parameters, developed by Saxena and Sept,²⁵ since according to our benchmarks this parametrization best reproduces the structural features of sites hosting several Mg²⁺ ions in close proximity within RNA structures.²⁶ Na⁺ ions parameters were taken from Joung and Cheatham,²⁷ while Zn²⁺ ions were modeled with the cationic dummy atoms approach developed by Pang.²⁸ The system was embedded in a 12 Å layer of TIP3P water molecules leading to a box size of 196 × 220 × 200 ų and 201 Na⁺ counterions leading to 772 679 atoms. The topology was built with the tleap module of AmberTools 16 and later converted into the GROMACS format by using the acpype program. We carefully equilibrated the system to maintain unaltered the coordination of the active site. We initially performed a minimization step with the steepest descent method of 1000 steps, up to a convergence criteria of 1000 kJ/mol nm of maximum force. Next, we gradually heated the system to 300 K with an increase of 50 K every 2 ns for a total of 12 ns, keeping the entire system highly restrained (1000 kJ/mol nm²) except for the solvent and solute hydrogens. Then, we switched to the NPT ensemble, scaling the pressure to 1 bar and using two different barostats: (i) the Berendsen barostat was used for 20 ns with the same restraints on the atoms, and (ii) the Parrinello–Rahman barostat was for an additional 30 ns while leaving the side chains free of constraint. Next, we gradually decreased the restraints in 20 ns. Finally, we performed the simulations of five replicas for 1 μs each. One of the replicas was later extended to 2 μs to inspect and assess convergence issues of the principal component analysis (PCA). In each replica, we used the same starting structure, while the velocities were differently initialized. The root-mean-square deviation (RMSD), root-mean-square fluctuations (RMSF), and radius of gyration (R_g), hydrogen (H)-bond analysis, as well as covariance matrices were computed with cpptraj module of AmberTools16.²⁹

Principal Component Analysis.

This statistical technique is used to filter out the vibrational noise and redundant/nonrelevant conformational transition in MD simulations, while capturing the essential motions hidden behind an MD trajectory. These correspond to the lowest frequency motions, usually responsible of the large conformational transitions, which modulate biological functions. PCA relies on the calculation of the covariance matrix. This is calculated from the atoms’ position vectors after an RMS-fit on the first frame of the MD trajectory to remove translational and rotational motions. One average structure over the aligned trajectory is computed, and a covariance score with respect to this average is assigned to each mass-weighted Cα and P atoms, obtaining a matrix where each element represents the covariance between each pair of atoms, i and j, defining the i, j position of the matrix. The covariance is defined as

$$C_{ij}=\langle \left(\overrightarrow{r_i}-\langle \overrightarrow{r_i}\rangle \right)\left(\overrightarrow{r_j}-\langle \overrightarrow{r_j}\rangle \right)\rangle$$ (1)

where $\overrightarrow{r_i}$ and $\overrightarrow{r_j}$ are the position vectors of atoms i and j, respectively, and the brackets denote an average over the sampled time period. The matrix is then diagonalized to find the eigenvectors, or principal components (PC), and their corresponding eigenvalues. These represent the directions of the motions and their associated amplitude (i.e., the eigenvalues represent the extension of the fluctuations around the average structure along the eigenvector direction). As a result, the projection of Cartesian coordinates vectors onto the eigenvectors (i.e., by taking the dot product between the two vectors at each frame), allows reducing the dimensionality and the noise hidden behind an MD trajectory to capture and visualize the most relevant motions sampled during the simulations. The PCA has been extensively and successfully applied in many distinct applications of biological systems; however, it is well-known that limited sampling may reduce the confidence in most representative motions identified in the sampled trajectories.^30,31 At variance with previous simulations of the SPL in which the multireplica approach was employed to validate at qualitative level the reproducibility of the results,^10,11 here PCA has been conducted on single trajectories as well as on merged trajectories (Figures S1 and S2 in the Supporting Information), generated by concatenating three or five replicas^32,33 in order to increase the sampling of this large system. Nevertheless, due to their limited sampling overlap, we have also verified that the observed essential dynamics projected on both PC1 and PC2 were independent from the manipulation of the trajectory (i.e., if this pseudotrajectory was qualitatively alike to that decrypted from the single replicas). Since the main results for single replicas, the 5- and 3-replica trajectories, were similar, we discussed only the results obtained from the 3-replica pseudotrajectory due to its more portable format in postprocessing analyses. Projecting the coordinate onto the PCs and plotting PC1 and PC2 generate a scatter plot displaying how the conformational space defined by the first two modes is sampled through the MD simulations (Figure S3). The scatter plot of the 5-replica trajectory shows that each of the samples has different points of the free energy landscape. Hence, the reference structure to which all trajectories were aligned was the starting structure of the simulation, which is common to all replicas. For each replica, the matrix was calculated on 4804 Cα and 270 P atoms and considering 15 000 frames, corresponding to the last 750 ns of the MD simulations. Here, we discuss the essential dynamics obtained from PC1 and PC2 representative of most of the variance (30–50% in all single and combined replicas trajectories) (Figure S4). The Normal Mode Wizard plugin in VMD³⁴ was used to visualize PC1 and PC2 along the principal eigenvectors and to draw the arrows highlighting their direction.

Cross Correlation Matrix.

A straightforward way to normalize the covariance matrix is by using Pearson’s coefficient, giving as a result a cross-correlation matrix based on the Pearson correlation coefficient (CC_ij).

$${\text{CC}}_{ij}=\frac{\langle \left(\overrightarrow{r_i}-\langle \overrightarrow{r_i}\rangle \right)\left(\overrightarrow{r_j}-\langle \overrightarrow{r_j}\rangle \right)\rangle }{\left[\left(\langle {\overrightarrow{r}}_i^2\rangle -{\langle \overrightarrow{r_i}\rangle }^2\right)\left(\langle {\overrightarrow{r}}_j^2\rangle -{\langle \overrightarrow{r_j}\rangle }^2\right)\right]}$$ (2)

These were calculated with the cpptraj module of AmberTools 16.²⁹ This matrix allows us to qualitatively interpret the inter-residue pair correlations by measuring the linear correlations of atomic motions. These coefficients span from a value of −1, which corresponds to an anticorrelation motion between two residues, to a value of +1, which instead corresponds to a fully linearly correlated lockstep motion. Zero values indicate uncorrelated motions. In complex macromolecular systems, this matrix can be reduced into a coarse and simplified version where each pair of proteins (matrix blocks) and domains considered is averaged over the number of residues in order to find a “correlation density”, allowing one to easily decrypt the principal correlations. Due to the large size of Prp8 and Clf1 proteins, to better pinpoint their functional role, we separately considered each domain and HAT repeat, respectively.

Weighted Protein Network and Community Analysis.

The Pearson’s correlation coefficient is lacking the nonlinear contributions to pair correlations, and it is orientation-dependent; i.e., orthogonal correlated motions are completely neglected. A more accurate calculation of motion correlations is, thus, desirable for weighting protein networks⁴ based on correlated motions. To this scope, one can rely on the mutual information (MI) measure to obtain the generalized correlation coefficients.³⁵ The MI between two variables (such as the $\overrightarrow{r_i}$ and $\overrightarrow{r_j}$ position vectors) is defined as

$$\text{MI}\left[\overrightarrow{r_i},\overrightarrow{r_j}\right]=H\left[\overrightarrow{r_i}\right]+H\left[\overrightarrow{r_j}\right]-H\left[\overrightarrow{r_i},\overrightarrow{r_j}\right]$$ (3)

where $H\left[\overrightarrow{r_i},\overrightarrow{r_j}\right]$ is the joint Shannon entropy of the variables and $H\left[\overrightarrow{r_i}\right]$, $H\left[\overrightarrow{r_j}\right]$ are their marginal entropies, providing a direct link between motion correlations and information content. The MI can be conveniently converted into an orientation-independent generalized correlation coefficient (^MICC_ij, defined between 0 and 1, i.e., from uncorrelated to correlated motions) by

$${}_{}{}^{\text{MI}}\text{C}{\text{C}}_{ij}={\left(1-\text{exp}\left(-\frac{2}{d}\text{MI}\left[\overrightarrow{r_i},\overrightarrow{r_j}\right]\right)\right)}^{-1/2}$$ (4)

where d is the dimensionality of the r_i and r_j variables. The calculation of the ^MICC_ij coefficients for an extremely large system, such as that studied here, is computationally very demanding. Therefore, here we limited the calculation to the linearized version of ^MICC_ij, i.e., ^LMICC_ij, based on the linear mutual information (LMI) measure. This relies on a Gaussian approximation (i.e., the quasi-harmonic approximation to the density of the atomic fluctuations) to reduce the computational cost. This computationally efficient version of MI developed by Lange and Grubmüller,³⁵ while neglecting the nonlinear contributions to the correlation, yet still does not depend on the relative orientation of the atomic fluctuations, and it provides an excellent approximation to the generalized correlation coefficients. Using the position vectors of Cα atoms along the MD trajectories previously described, we computed the ^LMICC_ij as implemented in the GROMACS v4.6.4 package.²⁰ The CCs based on the LMI are hereafter referred as ^LMICCs. In this case, before summing ^LMICCs to generate the correlation scores (^LMICSs) in the coarse matrix, a threshold was applied to filter the noise, retaining only ^LMICCs values larger than 0.6 (Figure S5). The RMSD matrix calculated between CCM and LMI matrices (Figure S6) displays graphically how much the LMI matrix differs from the more standard Pearson-based version. In this case, LMI fills the voids of undetected orthogonal motions but still retains the correlation captured by the CCM, proving to be a complementary approach to Pearson coefficients. Whereas the former is able to more quantitatively determine the correlations, the latter adds a qualitative picture of the directions of parallel correlated motions. Remarkably, the mean RMSD value between the two matrices is 0.31. The ^LMICCs are more reliable than the Pearson’s CCs and are linked to the information content retained in the protein motions. These coefficients are then used to weight a communication network of a protein complex.^4,6,7 A protein network based on the information exchange between amino acid residues (represented by their Cα atoms) can be constructed considering residues as nodes that are connected by edges, whose lengths is related to their motion correlations.³⁶ Here, the edge lengths are weighted using the ^LMICC_ij, with the weight, w_ij, of the edge connecting nodes i and j being calculated as

$$w_{ij}=-{\text{log}}^{\text{LMI}}{\text{CC}}_{ij}$$ (5)

so that highly correlated pairs of residues are associated with efficient links for information exchange and thus lie at close distances within the (protein) communication graph. In such protein graph, two nodes are considered connected when the distance between any heavy atoms of two residues is lower than 5.0 Å (distance cutoff) for at least 75% of the frames (percentage cutoff) analyzed. These values are chosen according to previous studies on protein RNA complexes.⁷ The resulting weighted graph is, then, partitioned into communities using the Edge Betweenness (EB) criterion and the modularity measure.^36,37 The EB and the node betweenness (NB) are defined as the number of shortest (and thus more relevant) paths passing through that edge (or that node for NB). Namely, the EB (or NB) accounts for the number of times an edge (or a node) acts as a bridge in the communication flow between any pair of nodes of the network. The shortest paths used to determine EB and NB values are computed using the Floyd–Warshall algorithm.^38,39 The EB is used to partition the network (starting from a single community for the whole system) into multiple communities, using the Girvan–Newmann algorithm. The modularity parameter, defined (between 0 and 1) as the difference in probability of intra- and intercommunity connections for a given network division, is adopted to select the optimal division, i.e., the optimum community structure. The optimum community structure obtained for the SPL has a modularity of ca. 0.8, in line with the common range observed for the 3D structure (i.e., 0.4–0.7). Such definition of the network provides a coarse-grained and intuitive picture of the complex internal communication network within the macromolecular system studied here, and it allows the dissection of critical nodes and communication channels.

Electrostatic Calculations.

Electrostatic calculations were performed with the Adaptive Poisson–Boltzmann Solver (APBS) software⁴⁰ on selected frames of the C model as extracted from the cluster analysis of the MD trajectory. APBS calculations were carried out using the Linearized Poisson–Boltzmann Equation (LPBE) in the VMD software with the following settings: surface density of 10.0 points/Ų, solvent radius of 1.4 Å, system temperature of 298.15 K, solute dielectric constant of 2.0, and solvent dielectric constant of 78.54 with smoothed molecular surface.

RESULTS

Structural and Dynamical Properties of the SPL C Complex.

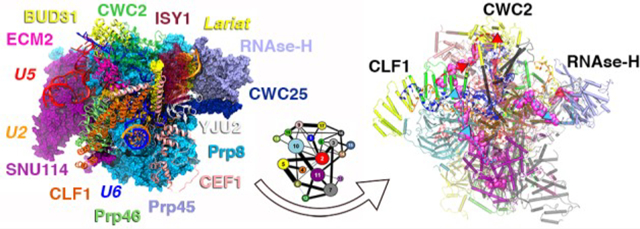
The system investigated here is based on the cryo-EM structure of the C complex SPL from S. cerevisiae, solved at an average resolution of 3.8 Å (PDB ID: 5LJ3).⁴¹ This SPL model (Figure 1, Table S1) encompasses 15 proteins, 3 snRNAs (U2, U5, and U6), the ILE intermediate, and the 5′-exon as well as 5 Mg²⁺ ions and 7 Zn²⁺ ions. Thus, in the presence of explicit water molecules, our SPL model consists of 772 682 atoms. All-atom MD simulations of 5 μs long in explicit solvent have been performed in order to trace the signaling pathways present within the SPL.

Figure 1.

(A) Model of the C complex spliceosome from the yeast S. cerevisiae cryo-EM structure (PDB entry: 5LJ3). Clf1, Prp46, Cwc2, Ecm2, Prp45, and Bud31 proteins are shown as orange, light green, green, dark pink, lilac, and yellow new cartoons, respectively. Cef1, Yju2, Isy1, and Cwc25, contributing to the intron lariat exon (ILE)’s stabilization, are depicted as pink, white, dark red (transparency), and dark blue, respectively. ILE is shown as a yellow surface, while Mg²⁺ ions are depicted as orange van der Waals spheres. U5, U2, and U6 snRNA are shown as red, orange, and blue ribbons, respectively. Prp8, its RNase-H domain, and Snu114 are displayed in light blue, lilac, and magenta surfaces, respectively. (B) Domain subdivision of Prp8, with RNase-H, endonuclease, N-terminal (Nterm), reverse transcriptase (RT), thumb, linker domains are shown in lilac, green, light blue, blue, yellow, and red surfaces, respectively.

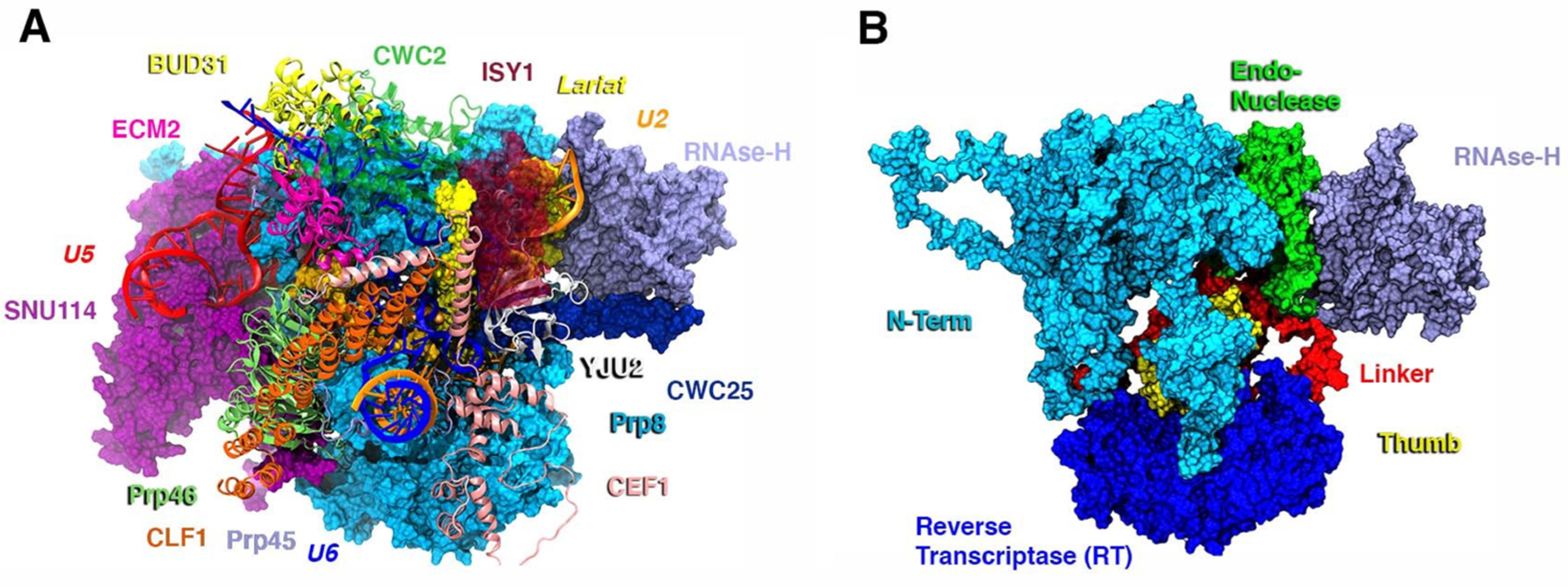
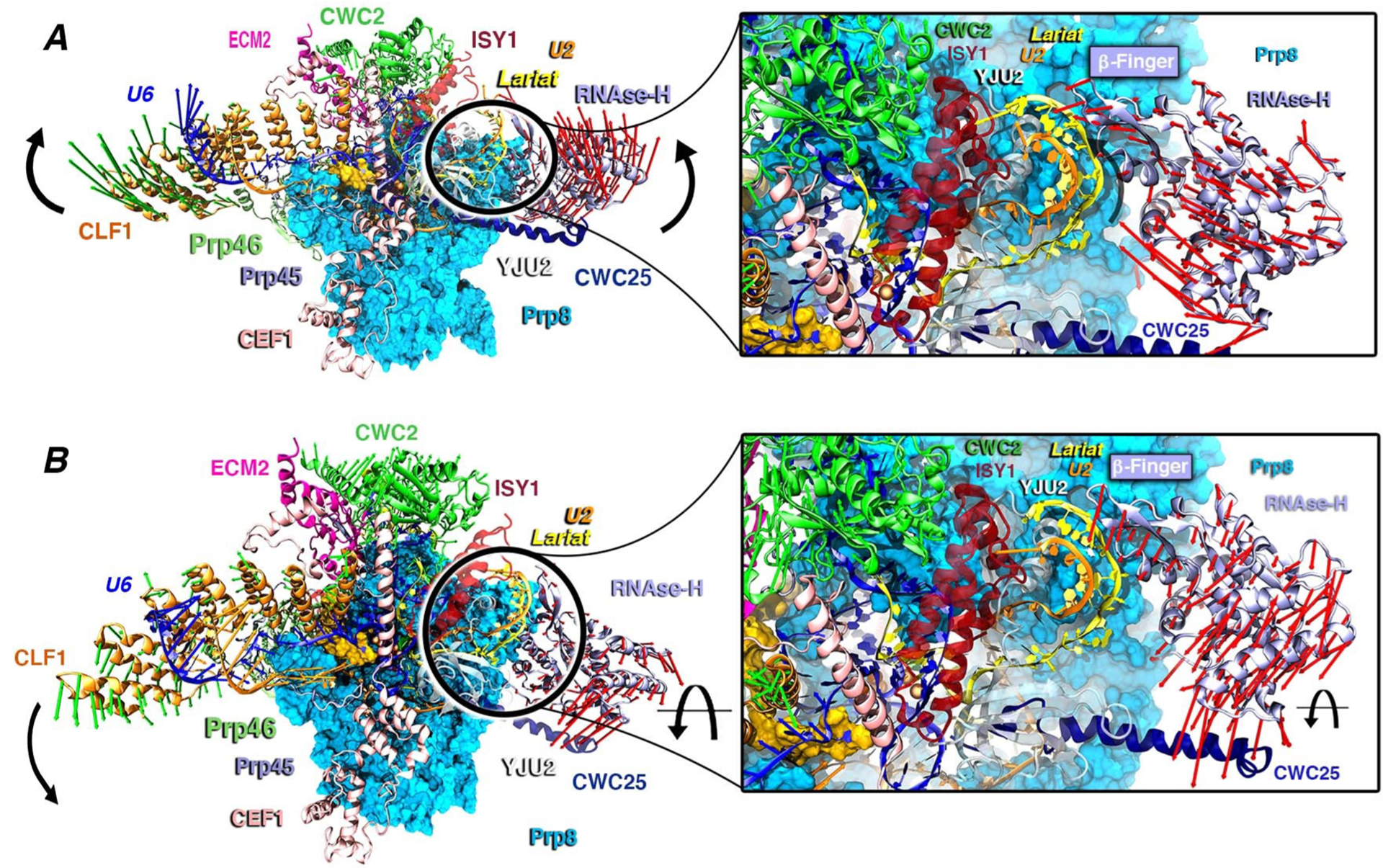
The structural convergence of the simulation was achieved in each replica within 120 ns, as shown by the analysis of the RMSD, the gyration radius, and the active site architecture (Figures S7 and S9). The SPL structure explored here catches the ILE intermediate immediately after the first splicing step has occurred (Figure S10) and the ILE is stabilized by the formation of an intricate H-bond network to U6 and U2 snRNA, respectively. To better extricate the complexity and disclose the critical proteins underlying the C complex functional dynamics, we have initially computed the cross-correlation matrix (CCM) based on Pearson’s correlation coefficient (CCs) from the combined-replicas trajectories along with its coarse-grained variant (Supporting Information Results and Figures S1 and S2) to more easily identify the dynamically coupled regions.^{6,10,11,42,43} Next, we performed PCA (Figures S3 and S4) to extract the essential dynamics of the SPL C complex from the MD trajectory. This analysis allowed us to draw out the functional motions associated with the CCM (as detailed in the Supporting Information) and to visualize which protein component/domain collectively contributed to it. The essential dynamics obtained from PC1 reveals the following: (i) Clf1 and RNase-H move lock-step in a hammerlike motion by contracting the SPL core and enabling, as a consequence, the movement of Cwc2, which acts as a mediating factor (Figure S1). (ii) The essential dynamics related to PC2 underlines a second cooperative movement of Clf1 and RNase-H domain, which undergo a twist of the α-helices and a marked rotation (Figure 2B), respectively. (iii) Additionally, by inserting its β-finger motif into the U2/IL helix (in PC1), the RNase-H domain promotes the wrapping of the U2/IL branch helix (Figure 2). This movement is regulated by electrostatic interactions, namely, N1869 from the RNase-H β-finger and K22, K26, and K30 from the Yju2 α-helix, which interact with the IL bases and the phosphate backbone of U2 (Figure S11), respectively.

Figure 2.

Essential dynamics as extracted from PCA of the combined 3-replicas pseudotrajectory. Red and green arrows depict the type and the direction of the motions. (A) Principal Component 1. Clf1 (orange) and RNase-H domain (lilac) are the arms of the hammer-like movement toward Cwc2 (green). The inset captures the wrapping of the intron-lariat (IL)/U2 double helix promoted by the β-finger motif of the RNase-H domain. (B) Principal Component 2. Clf1 and RNase-H domain perform a downward rotation. U2 and U6 snRNA are shown as orange and blue new cartoons, respectively. The inset focuses on the rotation of the RNase-H domain toward Cwc25 (dark blue). Prp8 and its RNase-H are depicted as light blue surface and lilac new cartoons, respectively. IL, Cwc2, Cwc25, Cef1, Clf1, Prp46, and U2 and U6 snRNA are shown as yellow, green, dark blue, pink, orange, light green, orange, and blue new cartoons, respectively.

Consistent with the critical importance of the β-finger pinpointed by our simulations, biochemical studies disclosed that four missense mutations of this motif (V1860D, T1865K, A1871E, and T1872E) affect the transition between first and second splicing step.⁴⁴ Among these, Val1860, Ala1871, and Thr1872 lie nearby the negatively charged RNA backbone of the U2/IL helix. Ostensibly, our simulations suggest that these mutations most likely impair the second step of SPL catalysis by altering the U2/IL wrapping and displacement. As observed in PC1 and PC2, the structural superposition of the cryo-EM structure of the C and C* complexes (Figure S12) solved by cryo-EM (PDB id: 5WSG)¹⁶ reveals that the rotation of RNase-H (PC2) and the wrapping of the IL/U2 branch helix (PC1) are clearly in line with the positions they adopt in the C* aggregate. Although the complete rotation of the β-finger motif and of the RNase-H domain is hindered in our MD simulations by the presence of the C-complex stabilizing factors (i.e., the Yju2, Cwc25, and Isy1 proteins), the β-finger motif appears to rearrange the U2/IL helix. This latter is, indeed, expected to remodel, creating the room necessary to load the second reactant (the 3′-exon) for the subsequent exon ligation step.¹⁷ Remarkably, from this structural comparison, it also clearly appears that the Clf1 helices, along with those of the Syf1 protein, create an arch connecting the large portion of Prp8 (N-term and RT domains) to U2snRNP (Lea1, Msl1, and the Sm-ring). This latter has to detach from the RNase-H domain’s surface to enable the transition from C to C* complex.¹⁷ Hence, Clf1 may act as a protruding arm connecting the SPL core to the most peripheral proteins, possibly contributing to displace the U2snRNP from the RNase-H surface via a rotation around the its own pivot located at the HAT-repeat H2–H3, as enlightened by the CCM analysis (Figures S1 and S13). As such, the hammerlike motion exerted concertedly by Clf1 and the RNase-H domain appears to be instrumental for the progression of the SPL’s cycle.

Dissecting the Pathways of Signal Transfer.

SPL is a large and highly plastic machine vitally regulated by signal transfer between the central scaffold of the snRNPs and the distal proteins. In order to decrypt the mechanism of information exchange in charge of the functional motions detailed above, we have employed protein network methods by performing a community network analysis (CNA) on our MD simulations. This approach enabled us to trace the signaling routes responsible for the communication between the critical regions of the C complex assembly (i.e., the Clf1 proteins and the RNase-H domain). The CNA methodology⁴ relies on a protein-based weighted network where the nodes, representing the Cα atoms of amino acids, are connected by edges, whose weighs depend on the correlations of residues’ pairs. Since CCM based on Pearson coefficients lacks a fraction of correlation (see Materials and Methods), we exploited the mutual information approach³⁵ to accurately compute the CNA. The aforementioned communication network, built on the basis of the ^LMICCs, can be then exploited to trace the most likely communication pathways connecting the regions critically entailed within the functional movements of the system. In fact, by identifying the protein communities, i.e., the groups of strongly correlated residues,³⁷ the CNA provides a coarse-grained picture of the intercommunications happening among the distinct regions of the SPL machinery. As shown in Figure 3A, the protein communities can be graphically displayed as groups of correlated residues (Figure 3C). The links connecting each pair of communities stand for the corresponding intercommunities edge betweenness (IEB), i.e., the sum of the EBs of the pairs of residues connecting two adjacent communities, hence indicating the strength of the communication flow between two communities.

Figure 3.

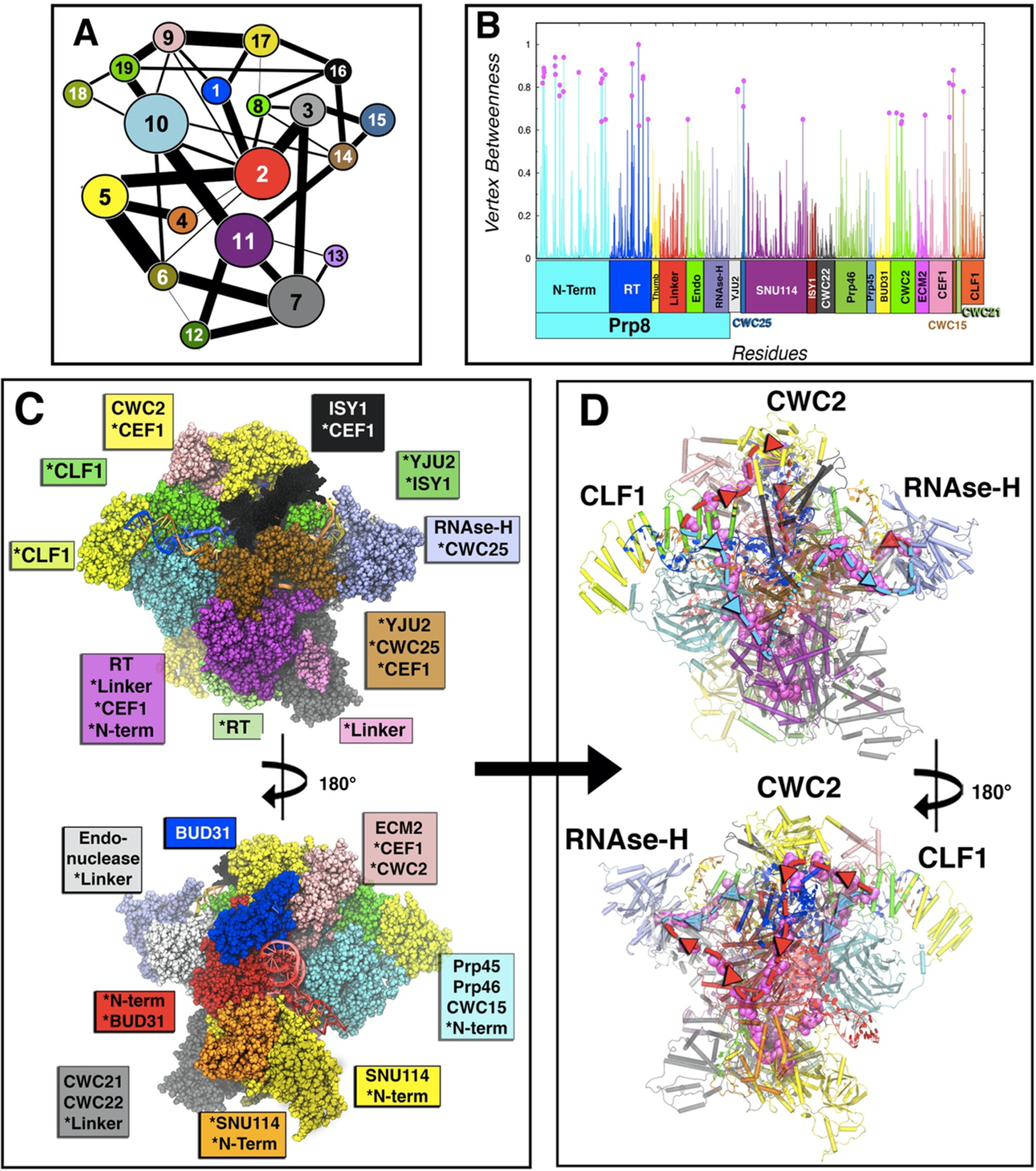
Community network analysis of the spliceosome. (A) 2D representation of the community network. The connecting links have a width proportional to the sum of all edges betweenness connecting two communities, thus measuring the corresponding intercommunities’ communication flux. (B) Normalized per-residue node betweenness (line) color coded by protein domains as in Figure 1, and points with betweenness more than 0.6 in magenta. (C) 3D-structure (front and back) of the community network, color coded with the same color of the 2D graph. Asterisks indicate domains or proteins when spread in various communities. (D) Spliceosome communication pathways (back and front). The residues with node betweenness higher than 0.6 are highlighted in magenta, thus displaying the two principal routes (path I in light blue and path II in red) for the communication flux through which most signaling occurs. In cartoon are depicted the communities with the community color code.

Strikingly, CNA (Figure 3C) reveals that Prp8 is involved in half of the totality of the SPL C complex’s communities and that five of them, i.e., communities #2, #5, #7 #10, and #11, with #2 and #11 almost fully coinciding with Prp8’s endonuclease and RT domains, are the largest and the most connected communities in the whole C complex network. This depicts Prp8 as a signals conveying platform within the SPL proteins/RNA network. To exploit the insights provided by the CNA, we tackled the communication taking place between the distinct SPL components, with a focus on the information flow between Clf1 (community #19) and the RNase-H (community #15), which are separated by 160 Å. As shown in Figure 3A, several pathways might be involved in the communication between communities #19 and #15. By considering the IEB links of community #19, the largest communication signal flows either via community #9 (comprising Ecm2 and part of Cef1) or community #10 (involving Prp46 and part of the large N-term of Prp8). Following the pathway via community #10 (Path I), the IEBs indicate that the information can easily flow through community #11 (comprising the RT domain and part of Cef1), finally reaching #15 via community #14 (corresponding to Yju2 and part of Cwc25). Alternatively, considering the pathway via community #9 (Path II), the IEB values indicate a strong communication with community #17 (located on Cwc2), from which the information flow could either remains on the same path II via communities #1 (involving Bud31), #2 (that is part of Prp8’s N-term) and #3 (corresponding to Endo domain) or heads toward Path III via communities #16 (associated with the Isy1 protein and part of Cef1) and then #14 to reach community #15. Of note, the physically shortest pathway (Path IV), i.e., the communication path along the shortest physical distance between Clf1 and RNase-H, involves just communities #16 and #14. Nevertheless, the communication flow along this path is expected to be limited by the poor IEB between communities #9 and #16, and therefore, it is unlikely. In order to extricate in more detail the communication between distinct communities, we analyzed the nodes characterized by the highest NB (see Materials and Methods) that represents the cardinal residues through which the majority of the communication travels, forming, therefore, the principal channel of information flow across the SPL components (Figure 3D). Remarkably, most of the nodes characterized by the largest NB (Figure 3D) belong to the most important communication pathways (Path I and Path II) as suggested by the CNA (Figure 3A). By this analysis, we could observe that a key point of the communication between the endonuclease and RNase-H domains (in Path II) is the specific interaction between residues Lys1912 of RNase-H and Asp1664 of Endo, located at the surface between the communities #3 and #15. A list of residues along the communication pathways (path I and II) is provided in Table S2, including the amino acids Ser13, Cys792, Asn1099, Gln558, Asn203, Thr205, Arg207, Ile209, and Leu318 which are characterized by very high node betweenness, representing good candidates for point mutation experimental studies. The communication pathways characterized across the SPL also allow one to propose potential binding sites for small molecules that could modulate the information exchange and, hence, be the target for virtual-screening studies. In particular, we have localized a possible binding pocket lying on the communication path II that is found in either open or closed state during the “hammerlike” motion described by PC1 (see Figure S16).

Both the CNA and the analysis of NB values indicate that the endonuclease and RNase-H domains strongly communicate between each other, consistently with correlation pattern observed in the CCM. A similar strong communication has been detected between Asp216 of Cef1 and Arg62 of Clf1, acting as a possible signal bridge between these two elongated proteins composed of α-helices. Noteworthy, also some residues at the core of Cwc2, i.e., Phe71, Leu106, and Lys116, are characterized by very high EB values, asserting the importance of Cwc2 in the information flow. Overall, this information opens the avenues to future computational and experimental studies aiming at exploiting signal information exchange channels for an allosteric regulation of the spliceosome.

CONCLUSIONS

The spliceosome is a huge metallo-ribozyme composed of an entangled network of proteins and RNA filaments. Protein communication over the long distances in the SPL congregate is a vital requirement to enable precise functional movements and meticulous information flow essential for faithful splicing. The characterization at the molecular level of the fundamental interactions, establishing communication channels in an immensely complex macromolecular assembly, such as SPL, is challenging and has not been previously attempted. Here, we combined all-atom MD simulations with the community network analysis to detect specific functional movements underlying internal communication of the C complex, as a prototypical case of SPL. The reported analysis unravels how information exchange is facilitated by the inner SPL conformational plasticity. In particular, the essential dynamics describes a “hammerlike” motion of two 160 Å distal proteins which most likely displaces the unneeded splicing factors for proceeding along the SPL cycle (Figure 2). The motion underlays the twisting/repositioning of the IL/U2 branching helix, possibly triggering the beginning of its conformational readjustment toward the position occupied in the subsequent SPL (C*) complex.¹⁷ The experimental evidence provided by a comparison of the cryo-EM maps of the C and C* intermediate states fully supports our findings (Figures S11–S15).¹⁷ Therefore, it is natural to conjecture that Prp8 is a key component in remodeling the substrate in the C complex, due to its β-finger motif in the RNase-H domain. Most importantly, our network analysis of MD simulations discerned the communication channels underlying these functional movements of Clf1 and the RNase-H. By connecting the nodes mostly involved in communication among different communities, we identified two most relevant paths: Clf1, Ecm2 Cwc2, Prp8’s Endo, and finally the RNase-H domain (Path I), or Clf1, Prp46, the large N-term/RT domain of Prp8, Cef1, Yju2, Cwc25 heading toward the RNase-H (Path II) (i) disclosing a critical participation of Prp8 to many strongly correlated communities, and (ii) outlining the key role of Prp8’s RNase-H, along with Clf1 and Cwc2, in conveying signals toward the functional RNase-H domain. The reported findings provide fundamental advances in dissecting pivotal mechanistic aspects of this amazing gene maturation machinery from an atomic-level perspective. Conceivably, the observed information exchange routes may be exploited to devise small-molecule modulators able to hinder the functional SPL dynamics by interfering/blocking these signaling paths. Given the mounting evidence that splicing defects are an increasingly appreciated hallmark of tumorigenesis, our outcomes may be harnessed to intervene against distinct cancer types deriving from splicing alterations.