Primary Determination of Particle Number Concentration with Light Obscuration and Dynamic Imaging Particle Counters

Abstract

Accurate number concentrations of particles in liquid media are needed to assess the quality of water, pharmaceuticals, and other liquids, yet there are limited reference materials or calibration services available with clear traceability to the International System of Units. We describe two methods, based on very simple modifications of commercial particle counter instruments, that can provide traceable number concentration measurements. One method used a light obscuration counter. Fitting a model to the data enabled correction for timing and coincidence errors, and gravimetric calibration of the syringe pump gave a traceable determination of measured volume. Other potential biases were diagnosed by analysis of the particle size distribution. The other method used a dynamic imaging particle counter (a flow imaging microscope). The instrument was intentionally configured so that each particle passing through the flow cell was imaged multiple times. Following the particle image acquisition runs, runs with a rinse solution released and counted microspheres adsorbed to tubing or flow-cell walls. Software assembled the redundant particle images into tracks, and the total number of tracks was assigned as the number of particles counted. Both light obscuration and dynamic imaging methods, when applied to polystyrene microspheres of approximately 4 μm diameter, achieved expanded uncertainties (k = 2) of approximately 2 % of number concentration and agreed to within a difference of 1.1 %.

1. Introduction

Size and number concentration measurements of particles in liquid suspensions are used for quality assessments of water [1] and pharmaceutical products [2–5] and in quantitative clinical assays [6, 7]. Common instruments for the size range 1 μm to 100 μm are based on dynamic imaging, light obscuration, or electrical sensing zone methods [8]. Microspheres of uniform size, most commonly made from polystyrene latex (PSL), are commercially available with both stated diameter and number concentration. Diameter measurements may be traceable to the International System of Units (SI) through certified reference materials available from national metrology institutes. However, the certification of number concentration for PSL microsphere reference materials is not as clear. Commercial PSL standards are often stated to have an accuracy of ±10 % in number concentration, but the confidence level of the uncertainty and the exact method used to attain traceability to the SI are not stated.

In this paper, we discuss how two different types of commercial particle counters may be characterized sufficiently to provide measurements of microsphere number concentration directly traceable to the SI. Potential uses of this method are to: (a) achieve traceability to the SI with known uncertainty, (b) attain uncertainties lower than available by commercial standards, or (c) achieve direct traceability for microsphere types that are not commercially available as certified standards.

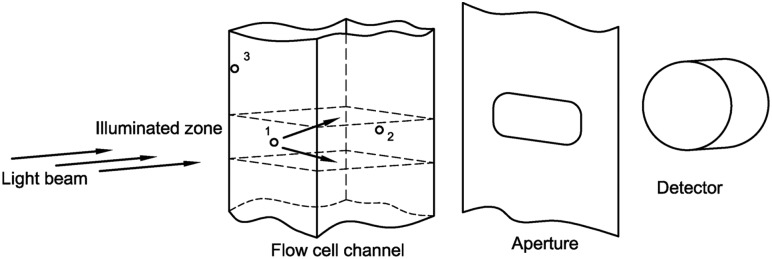
Light obscuration (LO) particle counters pass a known volume of liquid through a flow cell traversed by a light beam, as shown in Fig. 1. Scattering or absorption of light by a particle reduces the intensity of the transmitted beam, and the extent of this reduction is a measure of particle diameter. The diameter indicated by a calibrated LO counter is equal to the diameter of a PSL microsphere that gives the same reduction in intensity. Accurate counts from an LO counter require accurate knowledge of the volume sampled, and understanding of any possible biases or variance in beam-intensity reduction on detection of a microsphere. Characterization of the LO counter includes calibration of the syringe pump, assessment of timing errors in the measurement cycle, consideration of errors that can arise from optical effects, and assessment of coincidence errors arising from two microspheres flowing through the detection zone at once. Figure 1 illustrates the measurement, where microsphere 1 is in the middle of the illumination zone. If microsphere 2 enters the illumination zone, this will cause a coincidence error, where the two microspheres are counted as one particle. The illumination or collection of scattered light from microsphere 3 as it enters the illumination zone along a corner may differ from microspheres in the middle of the illumination zone.

Fig. 1.

Schematic of the image acquisition for the LO measurements. Circles denote microspheres.

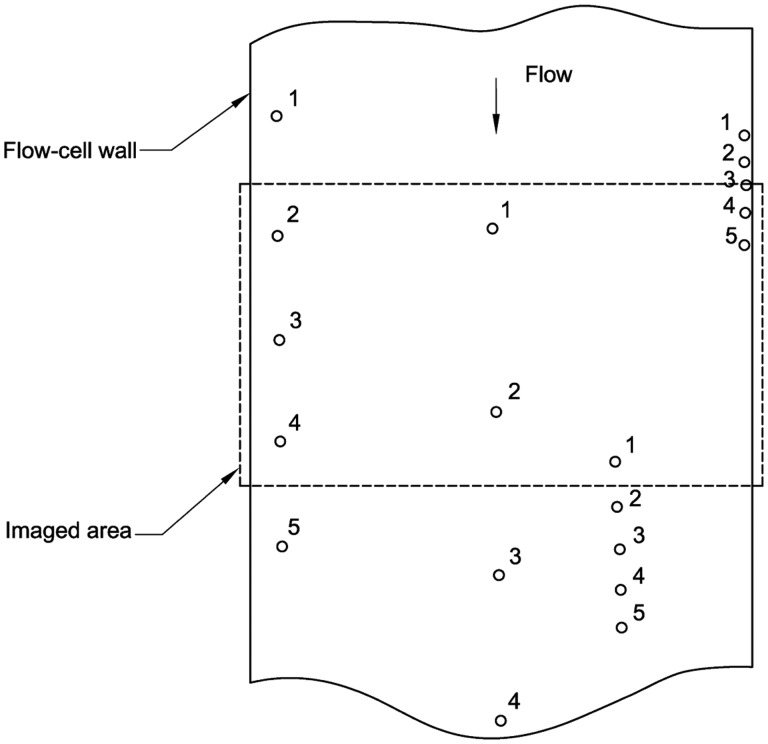
Dynamic imaging (DI) instruments for counting particles in liquid suspension are commonly referred to as flow imaging, fluid imaging, or flow microscopy systems. The DI systems used in the present work obtain microscopic images of a flowing particle suspension. Automated software analyzes those images to obtain particle images, corresponding equivalent diameters, and the concentration of particles. In standard systems, the sampled volume is inferred from the volume of the imaged fluid (equal to the nominal flow-cell thickness multiplied by the imaged area). We used a different method that eliminated the need to calibrate the flow-cell thickness or imaged area. An absolute particle count was obtained with a DI system by configuring a commercial instrument to image redundantly each microsphere passing through the flow cell, and then custom software was used to group the images corresponding to each particle into “tracks” (see Fig. 2). For this method, care is needed to understand the accuracy of the track analysis, and the parameters of the measurements are optimized to give good statistical precision and low systematic uncertainties.

Fig. 2.

Schematic of the image acquisition for the DI measurements. Circles denote microspheres, and the numbers indicate microsphere positions for five sequential images.

The results we obtained showed excellent consistency. Measurements of microsphere number concentration on two LO instruments of the same type gave results that agreed to within a difference of (0.7 ± 1.4) % (relative expanded uncertainties are given for a coverage factor of k = 2 throughout the paper). With both LO and DI methods, we obtained relative expanded uncertainties of ≈ 2 % of number concentration. A comparison of a single lot of PSL microspheres by both LO and DI measurements agreed to within (1.1 ± 1.8) % of number concentration.

Several other methods have been reported in the literature for determination of the concentration of microspheres. Kammel et al. described a custom-made flow cell that detects particles or cells by an electrical sensing zone technique [9]. Relative expanded uncertainties with this instrument are typically (1.5 to 4) % of number concentration. Sakaguchi and Ehara described a method to determine the number concentration of (10 to 20) μm microspheres with a relative expanded uncertainty of 4.4 %, using a slightly modified flow cytometer [10]. They also reported additional measurements by scanning electron microscopy (SEM) that have lower uncertainty (relative expanded uncertainty of 1.0 %), but that are arduous to perform. Schweppe et al. described another flow cytometer modification that achieves relative expanded uncertainties in the (2 to 5) % range [11].

A key advantage of our two methods is that both can be applied to a commercial instrument with only minor, temporary modifications: for the LO method, temporary modification of the sampling port for calibration of the flow rate, and for the DI instrument, slight modification of the inlet tubing. Once the instrument is calibrated, the LO measurements are faster and have reduced uncertainty relative to the method of Sakaguchi and Ehara. A limitation of our methods is that the particle concentration range for which coincidence errors are small enough for reliable corrections to be made is lower than for an electrical sensing zone or flow cytometry instrument. For the LO method, the microsphere stock being calibrated was gravimetrically diluted to number concentrations varying from (2000 to 50 000) mL⁻¹. For the DI method, measured number concentrations were approximately 7000 mL⁻¹.

Fundamentally, number concentration (or equivalently, number density) is obtained by dividing particle count by the sample volume. In its present form, the SI does not formerly recognize a dimensionless unit for particle number, although official guidance on the use of the SI states that particle count may be considered to be of dimension one, and “the unit one may instead be regarded as a further base unit [12].” Modifications to the SI have been proposed to add such a unit [13]. In this work, we conform to the present SI, stating number concentrations in dimensions of inverse volume. The uncertainty budgets include components for our confidence in the particle counts. Traceability to the SI is assured by determining the confidence that all particles within the sample volume are counted and by determining the actual sample volume.

In the LO method, the syringe pump that determines the measured volume was calibrated gravimetrically, and auxiliary experiments were conducted to confirm the sensitivity of the LO detector to particles across the whole width of the flow cell. There are several potential errors that must be addressed:

• Particle counts may be in error because of loss of particles due to microsphere aggregation or adsorption on container walls.

• Incorrectly sized particles (caused by a dirty flow cell or laser misalignment, for example) may reduce or increase the measured counts by causing particles to be incorrectly categorized as within or outside a specified diameter range.

• Transients in the flow rate or lack of synchronization between the pump and acquisition software can cause errors in the sampled volume.

• Coincidence errors (when two or more microspheres are simultaneously present in the detection zone) alter both the particle count and the particle size distribution (PSD).

Various strategies were used to address these effects. Uncertainty due to adsorption was checked by performing fluorescence imaging of the vials and transfer pipette tips used in the experiment and inspecting them for adherent beads. The effects of dirty flow-cell walls were checked by comparing measurements before and after cleaning a highly contaminated flow cell. Timing or synchronization errors were modeled by acquiring data at multiple measurement volumes and extrapolating the particle count to the point of infinite sample volume. Coincidence errors were modeled by measuring a series of diluted samples and performing an extrapolation to infinite dilution.

In addition to these effects, care must be taken to minimize bead agglomeration, contamination by foreign matter, and introduction of air bubbles. These effects are discussed below in Sec. 2, 3.1, and 4.2.2.

In the DI method, the measured aliquot of microsphere suspension is bracketed by particle-free water, so the actual flow rate of the DI instrument does not affect the measurement. Confidence in the ability of the DI instrument and custom software to identify particle tracks unambiguously was assessed by examining the variation in particle number with particle identification parameters and by manual inspection of the particle tracks. Particle adsorption effects were minimized by appropriate design of the inlet port and by running multiple rinses with particle-free water at the end of a set of runs. There are similar approaches to address counting and volumetric errors in the literature. For example, Sakaguchi and Ehara [10] avoided transient effects by bracketing a volume of particle-laden solution with clean sheath fluid during the measurement process. Kammel et al. [9] understood the exact timing of their instrument, since it was specially built for the purpose.

Highly uniform microspheres are available in several polymer types, including PSL and poly(methylmethacrylate) (PMMA), over a large range of sizes. PSL has a density very close to that of water and sediments more slowly than PMMA. The optimal size for a particle count standard requires balancing two separate effects. Large microspheres sediment at a faster rate, and the number concentration of the microsphere sample can become spatially inhomogeneous during a measurement run. For PSL microsphere diameters of 5 μm and less, sedimentation has a negligible effect (a 5 μm PSL microsphere in water falls 1 mm in 22 s). Particles with a diameter near 1 μm are near the lower detection limit of LO counters, and the number of foreign particles typically increases with decreasing diameter. As a result, PSL microspheres of diameter (3 to 5) μm are ideal as a reference material, although the method is applicable with proper sample stirring to microspheres of 2 μm diameter and up.

2. Materials

Two types of fluorescent PSL microspheres were used for this study. Microsphere type S was 4.0 μm nominal diameter, with a yellow-green fluorescence and sulfate surface modification (F8859 part number, Thermo Fisher Scientific¹, Waltham, MA). Microsphere type URB was ≈ 3.7 μm diameter, with multiple dyes incorporated in the bulk polystyrene polymer (“ultrarainbow” type; URFP-38–5A, Spherotech, Lake Forest, IL). Additional measurements were made on microspheres identical to type S, but with 2.0 μm diameter (F8853 part number, Thermo Fisher Scientific). Water to prepare the suspensions was deionized and ultrafiltered, including passage through a final-stage 0.22 μm filter. To prevent microbial growth, all microsphere suspensions contained 0.02 % mass concentration of sodium azide. To minimize aggregation, the URB suspensions also included 0.01 % mass concentration of polysorbate 80. Microsphere suspensions were stored in prewashed polycarbonate vials. Samples at different number concentration were prepared by gravimetric dilution of an initial stock solution using a calibrated mass balance. Approximately (15 to 30) min prior to measurements, the type S microsphere suspensions were shaken vigorously for 15 s and sonicated for 20 s. The URB microspheres were more sensitive to air bubble contamination due to the added surfactant. For these beads, the beads were shaken vigorously 15 min prior to measurement, and then just before the measurement, each sample was mixed by gently tipping the vials 10×, sonicating for 10 s, and waiting 10 s before commencing the measurement.

3. Methods

3.1. Preliminary Characterization of the Microsphere Lots

Measurements of microsphere suspensions in a DI system (Brightwell DPA-4200, ProteinSimple, San Jose, CA; settings: 4× objective, 100 μm thick flow cell, at set point 3) determined the proportion of microspheres that were singlet microspheres, doublets, or agglomerations of larger numbers of microspheres. For this measurement, an instrument optimized for large depth of field gives the best size resolution. Because microspheres are detected over the full plane of the imaged area, rather than one at a time through an orifice, dynamic imaging has inherently lower coincidence errors compared to light obscuration (see Sec. 4.3), and it is easy to obtain a high-resolution PSD.

Particle size distributions obtained by this system in the standard operating mode were only interpreted according to the relative populations of singlet, doublet, and higher peaks, and no use was made of the absolute number concentrations reported by the instrument. The existence of doublet peaks at a number concentration of more than a few percent of the singlet peak would indicate unacceptable microsphere agglomeration. The DI results also provided a convenient method of assessing the effect of sample handling on the introduction of air bubbles during sample mixing. Addition or alteration of surfactant in the formulation can reduce agglomeration, but it can also increase the number of air bubbles.

Fluorescence microscopy was used in a series of auxiliary experiments to better understand the location and detection response of microspheres in the measurement process. A standard microscope equipped with a Hg arc lamp and suitable filters was used for epifluorescence measurements, with an excitation wavelength of (460 to 500) nm and a detection wavelength of (512 to 542) nm. The numerical aperture of the variable-aperture stop was calibrated by measuring the integrated signal of light imaged from a white target as the stop was varied (the signal is proportional to the solid angle defined by the aperture stop and microscope objective).

To ascertain the effect of the flow-cell wall on the LO process, we used a model system consisting of fluorescent PSL microspheres laying on the bottom of an 80 μm thick glass flow cell (80 μm FOV flow cell, Fluid Imaging Technologies, Yarmouth, ME) with horizontal axis. The excitation beam travelled approximately 80 μm through the flow cell, and then the emitted fluorescence travelled an additional 80 μm back through the flow cell towards the objective. Thus, the model system simulated the behavior of an isotropically scattering microsphere located at the midpoint of a 160 μm thick flow cell, which is comparable to the likely dimensions of the LO instrument. A quantitative measurement of the effect of the wall was obtained by comparing the fluorescence emitted by microspheres adjacent to the flow-cell wall to that emitted by microspheres away from the wall.

3.2. Light Obscuration Primary Method

3.2.1. Light Obscuration Instrument and Configuration

All LO measurements were conducted with a commercial instrument representative of instruments used in the pharmaceutical industry (model SVSS-C, with a HCB-LD-25/25 sensor head, PAMAS, Leonberg, Germany). This instrument has a size range from 1 μm to 200 μm. Proper operation of the instrument was confirmed by running commercial count standards and microspheres of known diameter. The results of these checks were within manufacturer’s specifications for all runs, except as noted in the Results section for a test of a dirty flow cell.

LO measurements of filtered water and formulation blanks demonstrated that the storage vials and formulation preparation did not introduce appreciable foreign matter within the diameter range used. The washing procedure was verified to give negligible number concentrations for particles within the diameter limits used in the present work.

For measurements of the microsphere suspensions, the instrument was primed with a volume of 0.6 mL, and then readings of three samples of a fixed volume (0.2 mL to 0.8 mL) were taken in quick succession. The average of these three readings constituted one measurement. When the microsphere number concentration was changed, an additional first measurement was discarded. Measurements were conducted in triplicate for each volume.

3.2.2. Pump Calibration

The calibration of the syringe pump was straightforward. The sampling needle of the LO counter was extended using a flexible silicone tube of 1.6 mm inner diameter. The end of this tube terminated in a stainless-steel hypodermic needle (0.72 mm outer diameter and nominal 0.41 mm inner diameter) that was fixed in position passing down into a narrow-mouth, 25 mL vial placed on the pan of an analytical balance. The vial contained water plus enough vacuum pump oil to fully cover the top surface of the water. The level of the water and oil was maintained above the tip of the needle but below the top section of the vial where the side walls deviated from vertical. The vacuum pump oil greatly inhibited water evaporation, enabling accurate mass (and volume) measurements of the water volume collected in the vial. The balance gave a reading m_b referenced to conventional mass conditions (air density of 1200 kg/m³ and calibration weight density of 8000 kg/m³). Correcting these readings to true mass required an additional term for the buoyancy of the immersed needle, in addition to the standard terms for the density of the calibration weights, ρ_c, and the density of air, ρ_a:

$$m=m_{\text{b}}\frac{\left(1-{\rho }_{\text{a}}/{\rho }_{\text{c}}\right)}{\left(1-{\rho }_{\text{a}}/{\rho }_{\text{w}}\right)\left(1-A_{\text{n}}/A_{\text{v}}\right)},$$ (1)

where ρ_w is the density of pure water [14] evaluated at the temperature of the balance, A_n is the cross-sectional area of the needle, and A_v is the cross-sectional area of the water in the vial. In the present experiments, use of a small hypodermic needle and a vial of relatively large area reduced the value of A_n /A_v to 0.00025, which is negligible. Deviations of ρ_a and ρ_c from the conventional mass values were negligible relative to other uncertainties.

A simplified method of pump calibration was also used. For this method, a narrow-mouth, 60 mL vial was filled with filtered water. The full vial was weighed, water was withdrawn from the vial with 10 consecutive pump cycles on the LO instrument, and the vial was weighed again. The water temperature was measured before the first weighing and after the last weighing; the average of the two temperatures was taken as the water temperature during the measurement. The mass difference was converted to volume using literature values of the water density [14] at the given temperature.

3.3. Dynamic Imaging Primary Method

3.3.1. Instrument Configuration and Data Acquisition

In its standard operational configuration, a DI system with a liquid flow cell takes images of a particle suspension flowing through the flow cell. Each image captures a volume equal to the imaged area multiplied by the flow-cell thickness. The measured number concentration is then determined as the number of particles counted divided by the product of the total number of images multiplied by the volume imaged for each frame. In theory, one could calibrate the imaged area and flow-cell thickness, but calibration of the thickness requires special equipment and methods. We used an alternative approach. The particle suspension was intentionally measured using flow rates much lower than recommended by the instrument vendor, so that each particle would be imaged at least twice. From the set of images, custom written, open-source software [15] identified particle tracks by searching the stack of images for particles with similar diameter, direction, and pixel number in the direction transverse to flow. The total number of tracks found equals the total number of particles that passed through the flow cell, with no calibration of the flow cell needed.

The choice of the DI system was dictated by the requirements that the pump speed could be adjusted to be slow enough to give the necessary oversampling of microspheres and that the field of view could be chosen to fully span the width of the flow-cell channel. We used a FlowCam benchtop flow microscope that met these criteria (Fluid Imaging Technologies).

The image boundaries were adjusted in the FlowCam acquisition software to extend beyond the physical limits of the flow cell, ensuring that no particles would be lost at the cell edges. The flow cell was a 300 μm thick “field of view” cell, imaged with a 4× objective at a rate of 22 frames per second. The use of a 4× objective, with a numerical aperture (NA) of 0.13, gives a 5× greater depth of field and a 6.25× larger imaged area relative to a 10× objective with 0.30 NA. If the true background shifts in position relative to the acquired background image, spurious particle images will appear. We found that vibration does not cause such spurious images, but run times beyond approximately 10 min can lead to positional drift. The increased volume of fluid captured with each image by the 4× objective shortens the run times, which is both convenient for the operator and reduces drift of the optical image from the background image acquired at the beginning of the run. The velocity profile through a flat, thin cell is parabolic; microspheres near the cell wall may travel very slowly, while microspheres at the center of the cell travel most rapidly. The flow rate of 0.1 mL/min was chosen to ensure that particles at the center of the flow stream would be imaged at least two times, accounting for possible variability in illumination timing relative to the microsphere passage through the cell.

Three separate vials at a nominal number concentration of 7000 mL⁻¹ were prepared by gravimetric dilution from a stock solution of nominally 1 × 10⁵ mL⁻¹ number concentration of sulfate-functionalized PSL microspheres of nominal 4.0 μm diameter. The relatively low number concentration was chosen to minimize possible confusion (coincidence) between tracks of independent particles while still achieving acceptable statistical precision. Each of these vials was measured twice by the LO, then three times by DI, and then two more times by LO. Prior to each set of LO runs, an initial run was made to prime the instrument, and these data were discarded.

A polypropylene pipette tip was mounted with its tip directly inserted into the stainless-steel entrance tube of the field-of-view cell, to minimize any adsorption of particles to tubing, pipette tip, or cell walls. The top of the pipette tip was also cut down so that the tip could hold only 0.6 mL. Having a short-reservoir tip greatly reduced the chance of leaving a small droplet of sample on filling the reservoir.

The pipette tip was initially filled with particle-free water, and the fluid level was adjusted to a mark near the bottom of the pipette tip. The pipette tip was then loaded with sample, and the run was begun. When the liquid level reached the original mark, a 0.22 mL aliquot of particle-free water was added. This rinse step was repeated once more, and then the run was terminated. The purpose of the two rinses was to minimize the number of uncounted microspheres that could flow through the cell between runs. The next run was started without flushing any liquid through the tubing, so particles still in the system would not be discarded without counting.

When all nine measurement runs were completed, two runs were made of particle-free water. These runs captured particles that were adsorbed to the flow cell or tubing. To confirm the accuracy of the liquid transfers by pipette, the three sample vials were weighed before and after the three measurement runs for each vial. The total number of particles counted during the rinse runs was divided by the number of measurements (nine), and the result applied as a correction to the measured particle counts.

3.3.2. Data Analysis

Data from the FlowCam was exported as a comma-separated variable file, including the following fields: particle identifier, filled area, position in the image, effective diameter, and time stamp. The computer program “FlowImageTrack100.py,” written in Python 3 and available through GitHub [15], discarded particles near the top and bottom edges of the cell and then searched the remaining time-ordered data to assemble particle tracks. Beginning with a single unassigned particle image, the program searched for a particle in subsequent images with a diameter that matched the initial particle within specified limits, a center x pixel that matched within specified limits, a y pixel that was within a maximum expected travel distance, and a maximum period to look forward. When a matching particle was found, that particle became the basis for the new reference time and position. Once all tracks were obtained, a linear y versus time model was fit to each track. The root-mean-square deviation of the fit from the data was used to identify possible errors in track identification. Since the y versus time fits were only used to identify mistakes in track assignment, and were not a primary measurand, the center of the bounding image box of each microsphere had sufficient position accuracy, and we did not need to find the center of mass of the actual binary images. Assigning track numbers to each image in the initial spreadsheet assisted in manual inspection of the data for errors in track identification or particle images that were not properly assigned to a track. Section 4.3 discusses the level of errors in more detail.

4. Results

4.1. Microsphere Handling

Accurate number concentration measurements depend not only on the accuracy of the particle counters, but also on the repeatable behavior of the microsphere suspensions. In particular, the number concentration could potentially drop because of adsorption of microspheres onto pipette tips during transfer steps, or onto vial walls during storage [16]. The effect of bead adsorption on microsphere number concentration has been previously diagnosed using flow cytometry [17]. Here, we describe some additional techniques to verify that the microsphere number concentration did not vary significantly with handling. Adsorption of microspheres on the pipette tips was checked by transferring suspension samples with a pipette and then inspecting the pipette tip under a fluorescence microscope with a 5× or 10× objective. Fluorescence measurements were made with a standard epifluorescence microscope, with the addition of attenuated brightfield illumination, which was useful to visualize the edges of the pipette tip. Microspheres can be caught on the rough outer surfaces of the pipette tips; these microspheres were distinguished from microspheres on the inside of the tip by gently wiping the outside of the tip with a clean swab while the tip remained in the microscope field of view. The number of microspheres adsorbed on a pipette tip averaged less than 0.1 % of the delivered number of microspheres, as measured for five replicates at microsphere number concentrations of 9.5 × 10⁴ mL⁻¹ and 1.9 × 10³ mL⁻¹. The resulting drop in number concentration was negligible. Adsorption on vial walls was assessed by two methods. First, a vial was overfilled with microsphere suspension, so that when capped and placed on its side, no air bubbles would rise to the top. The vial was then placed under a fluorescence microscope with a 5× objective. By this method, no microspheres were observed that were truly bound to the vial wall. Some microspheres were seen near the vial wall, but over observation times of 10 min, these microspheres were always observed to move at least1 mm. Second, an experiment was conducted by preparing microsphere suspensions in two vials (at number concentrations of 4000 mL⁻¹ and 10 000 mL⁻¹), storing the suspensions for ≈ 40 h, and then transferring half the sample from each vial by pipette into two vials that had never been exposed to microsphere suspension. LO number concentration measurements were performed on both the original and transfer vials; if microspheres were adsorbed on the walls of the transfer vial, that would result in a reduced microsphere number concentration in the transfer vial relative to the number concentration in the original vial. The number concentrations for the second set of vials were within 0.5 % of the first set of vials, indicating that adsorption effects were minimal. Surprisingly, the second set of vials actually had a higher number concentration than the first set (at a significance level of 0.05), possibly as a result of hydrodynamic forces on the microspheres transverse to the fluid velocity in a shear field [18], which could lead to entrainment of additional microspheres in the volume pulled up during pipetting.

4.2. Light Obscuration Results

4.2.1. Pump Calibration

The syringe pump of the LO instrument was calibrated gravimetrically for dispensed volumes of 0.2 mL, 0.4 mL, and 0.8 mL, which were the volumes used in subsequent measurements. Plotting the deviation of the dispensed volume from the nominal volume revealed an approximately constant error as a function of nominal dispensed volume. This result suggested a linear relation between nominal and dispensed volume that included an offset:

$$V_d=A_1{V}_{\text{nom }}+A_0,$$ (2)

where A₁ and A₀ are constants. With values of A₀ = 1.48 μL and A₁ = 0.9995, the predictions of Eq. (2) agreed with measured values of dispensed volume to within a relative standard deviation of 0.04 % of the volume, for volumes ranging from 0.2 mL to 0.8 mL. The simplified method gave results that agreed to within 0.3 % of the more complex method.

4.2.2. Calibration for Timing and Coincidence

Suspensions of the two types of microspheres were measured by LO in multiple runs. The data were fit by an equation that included both a timing offset and a coincidence error [19] proportional to the microsphere number concentration:

$$DF\cdot N_{\text{m}}/A_1=N\text{exp}\left(-{\alpha }_{\text{c}}N/DF\right)\left(1+{\alpha }_{\text{t}}\cdot V_0/V\right),$$ (3)

where N_m is the measured number concentration of the diluted suspension, DF is the dilution factor, N is the actual number concentration of the stock solution, and α_c and α_t are coefficients for the coincidence and timing errors, respectively. The value of α_c equals the effective sensing volume of the counter. Note that this measurement equation includes the linear coefficient term A₁ for the syringe pump, but not the offset volume A₀. Effects of any offset volume are equivalent to the effects of a timing error, and only the single parameter α_t is needed to model both. To fit Eq. (3) to the data, it is useful to estimate the uncertainty of individual measurements. For the microsphere number concentrations and measurement volumes considered here, the uncertainties in measured number concentration arising from Poisson counting statistics [20] are much larger than the repeatability of the syringe pump. For the purpose of weighting the data for a fit of Eq. (3), the uncertainty in measured number concentration is obtained by neglecting the repeatability of the pump and assuming the uncertainty in the raw particle count n is n^1/2, giving the uncertainty in DF·N_m:

$$u\left(DF\cdot N_{\text{m}}\right)=DF{\left[N_{\text{m}}/V_{\text{t}}\right]}^{1/2},$$ (4)

where V_t is the total volume measured in the determination of N_m.

The form of Eq. (3) is chosen so that α_c and α_t are independent of the number concentration N. As a result, the equation is not a linear function of the parameters, and least squares fitting requires use of a nonlinear fitting program. Equation (3) may be recast as a linear equation for ease in fitting:

$$DF\cdot N_{\text{m}}/A_1=N+{\beta }_{\text{c}}\cdot \frac{1}{DF}+{\beta }_{\text{t}}\cdot \frac{V_0}{V},$$ (5)

where β_c = Nα_c and β_t = Nα_t. In this case, though, the values of β_c and β_t obtained are not independent of N and will vary with differences in N.

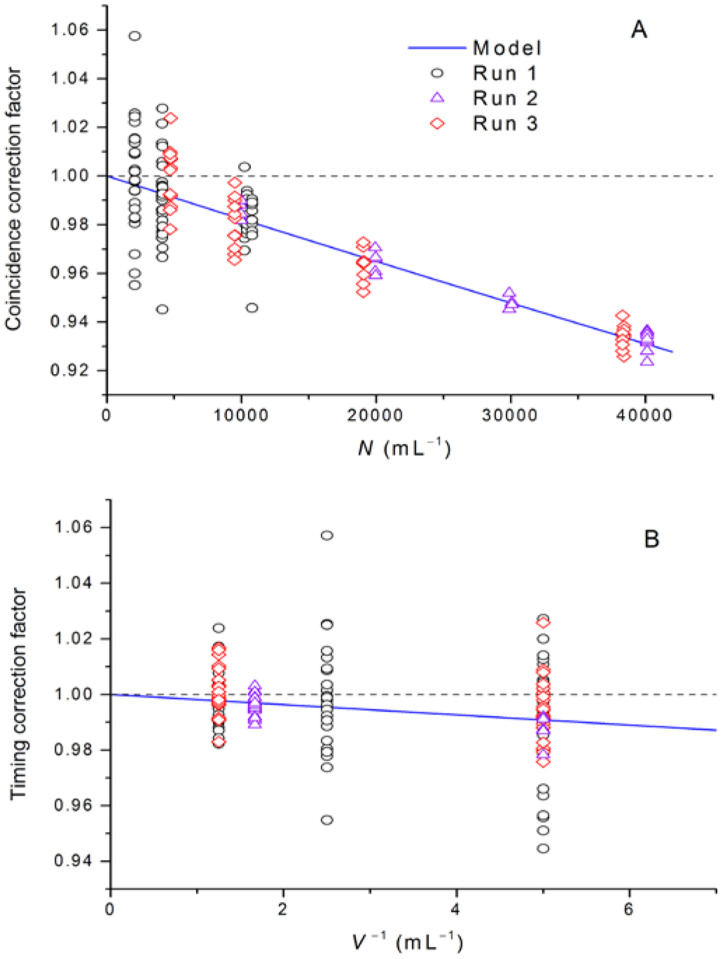
Figure 3 shows both models and data for number concentration, C_c, and timing, C_t, correction factors:

$$\begin{gathered} C_{\text{c}}=\text{exp}\left(-{\alpha }_{\text{c}}N/DF\right)=DF\cdot N_{\text{m}}/\left[N\left(1+{\alpha }_{\text{t}}\cdot V_0/V\right)\right] \\ {C}_{\text{t}}=N\left(1+{\alpha }_{\text{t}}\cdot V_0/V\right)=DF\cdot N_{\text{m}}/\text{exp}\left(-{\alpha }_{\text{c}}N/DF\right). \end{gathered}$$ (6)

Fig. 3.

For LO counter, (A) coincidence correction factor C_c versus particle number concentration and (B) timing correction factor C_t versus inverse of the sample volume.

Results of fitting Eq. (3) to the data are given in Table 1. Multiple runs were obtained with instrument A over 20 months to improve our methods and to monitor the instrument for signs of drift. Values of α_c and α_t obtained in two runs with instrument A over this period were statistically equivalent. This result confirms that the correction factors are stable in these instruments. As additional confirmation, lot URB microspheres were measured on two separate LO instruments (one instrument was new; the other instrument had five years of use), and the values of N obtained agreed to within (0.7 ± 1.4) % (k = 2). A simplified check of the syringe pump, conducted in 2016 to monitor the syringe pump accuracy, gave results within 0.3 % of the original 2014 syringe pump calibration. A check in 2017, however, showed an ≈ 2 % reduction in pump rate. Disassembly of a valve component of the syringe pump revealed deterioration of the valve seal. The stability of the instrument parameters α_c and α_t gives assurance that measurement accuracy can be maintained over an extended period with this technique provided that moving syringe parts are well maintained and the pump monitored for good performance. Fitting the linearized Eq. (5) to the data, with uniform weighting, gave number concentration values that differed by 0.3 % (root-mean-square deviation from Table 1 values), and were all higher than the corresponding weighted-fit values from Table 1.

Table 1.

Results of least squares fitting of Eq. (3) to LO data for two stock solutions of different microsphere types, on two different LO instruments of the same type. Stated uncertainties are type A standard uncertainty of the mean.

Microsphere lota	S	S	URB	URB
Instrument	A	A	A	B
Run date	28 AUG 2014	12 MAY 2016	16 NOV 2016	17 NOV 2016
Lower number concentration limit, mL−1	2,000	10,000	5,000	5,000
Upper number concentration limit, mL−1	10,000	46,000	36,000	36,000
αc, mL	(1.79 ± 0.38)×10−6	(1.76 ± 0.49)×10−6	(1.81 ± 0.07)×10−6	(1.18 ± 0.08)×10−6
αt	−0.0016 ± 0.0010	−0.0026 ± 0.0007	−0.0013 ± 0.0006	−0.00161 ± 0.0007
N, mL−1	95,377 ± 382	100,583 ± 230	96,545 ± 252	95,892 ± 281
Reduced chi-square, χv2	1.12	0.52	1.14	1.45
DF	78	27	45	45

^aS = sulfate functionalized PSL microspheres, URB = fluorescently dyed “ultrarainbow microspheres.”

The LO data obtained in 2014 were taken with the instrument set to record data only within the upper and lower diameter limits used to define the particles of interest. In hindsight, this was a mistake, because data above and below the diameter limits are critical for assessing the presence of a fouled cell (small diameters) or of significant quantities of air bubbles or large aggregated clumps of microspheres (large diameters). Since passage of an agglomeration of microspheres through the flow cell is only counted as a single count, breaking up of the agglomerate would increase the total measured number concentration. The limited 2014 data showed indications of possible small quantities of air bubbles, minor cell fouling and aggregated clumps of microspheres. We include these data only to indicate the consistency of α_c and α_t over several years. After acquiring the data in Table 1, we discovered that polycarbonate bottles have exceptionally high permeability to water vapor (in the future, we will use glycol-modified polyethylene terephthalate [PETG] bottles and refrigerate them to reduce the water vapor pressure). The observed 5 % increase in N between 2014 and 2016 is likely a result of this effect, although the breakup of aggregated clumps or of a cleaner flow cell for the 2016 data may also have contributed.

4.2.3. Impact of Flow Cell Contamination

In addition to timing errors, coincidence errors, and microsphere aggregation, microsphere counts in the LO instrument can be low if the beam extinction by a single microsphere is small enough to give a reported diameter lower than the lower diameter limit. The lower diameter limit was chosen near the minimum of the observed PSD, so that any smaller-sized debris would not be counted. Reduced extinction could result from passage of a microsphere through a portion of the cell that had substantially reduced transmission, caused either by dirt on a cell wall or by insufficient illumination of microspheres located adjacent to the cell wall. We next consider both effects.

Theoretical and experimental results for the flow of spherical microspheres in a long channel demonstrate that the number concentration of microspheres is lower near the channel walls and that there can be preferred locations within the channel [21, 22]. We confirmed this behavior with the microspheres used in the present work running through glass microcapillaries, but these results may not be applicable to microspheres running through a short channel typical of an LO particle counter. Dynamic imaging measurements of microspheres running into a rectangular-cross-section flow cell from a conical-shaped entrance (80 μm FOV flow cell, Fluid Imaging Technologies), at the same Reynolds number as used in the LO particle counter, showed no depletion of microspheres near the cell wall (data not shown). Consequently, we relied on independent measurements of fluorescent microspheres in the same flow cell as a model system to indicate whether microspheres located at the cell wall may be detected reliably.

Imaging of the model flow cell was adjusted to mimic the optics of an LO particle counter. In an LO counter, the ideal light source is a collimated sheet of light traversing the flow cell. In practice, perfectly parallel light rays are unachievable due to optical constraints. However, focused light beams have greater interaction with the flow-cell walls because of shadowing effects on the light cone. To minimize the coincidence error, the beam must be focused in the direction of the flow-cell axis. For an approximate cell width of 200 μm, a sensing zone thickness of 45 μm can be inferred from the experimentally determined value for the sensing zone volume, α_c. Gaussian beam theory predicts that a zone thickness of 45 μm requires focusing the incident beam at a half-angle of 0.014 rad. If the counter uses spherical lenses, the beam convergence in the plane of the light sheet could also be as high as 0.014 rad. Results for 4 μm microspheres in a flow cell of 80 μm depth are shown in Fig. 4 for different NA values. (Restricting the objective NA mimics the effects of different degrees of beam convergence.) At NA values of 0.12 and higher, microsphere fluorescence at the cell walls is reduced. However, at the lowest aperture attainable in our microscope (NA = 0.08), the ratio of fluorescent intensity for beads at the wall to beads away from the wall, R_w,a, was within 15 % of unity. (Some asymmetry was seen in the two sides of the optical cell in both brightfield imaging of the cell edge and in the R_w,a > 1 on one side and R_w,a < 1 on the other side.) At low numerical apertures typical of LO instruments, these data indicate that the reported diameter of microspheres at the wall will be within a small fraction of the reported diameter for microspheres away from the wall.

Fig. 4.

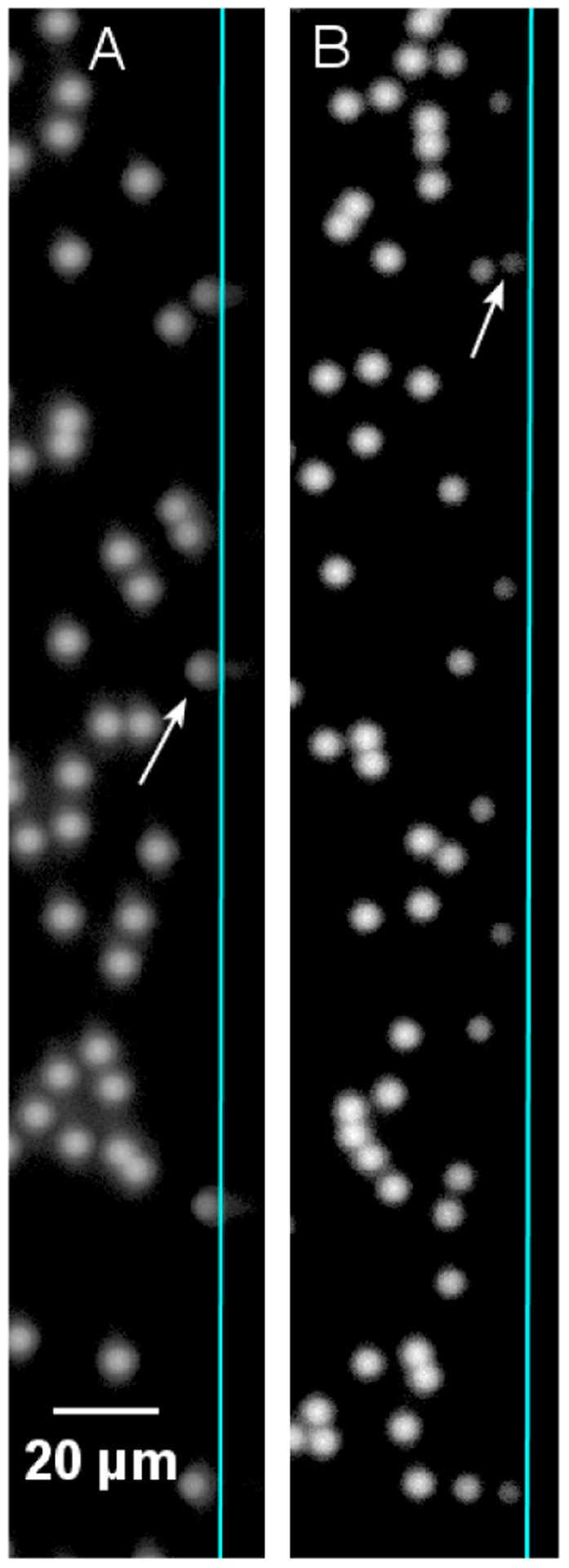
Appearance of fluorescent microspheres at the edge of a flow cell, illustrating the increase in microsphere brightness near the wall (arrows show microspheres at wall) with decreasing numerical aperture: (A) 10× objective, NA = 0.16; (B) 10× objective, NA = 0.30 (microsphere number concentration is much higher than during a number concentration measurement, to increase the number of microspheres at the wall).

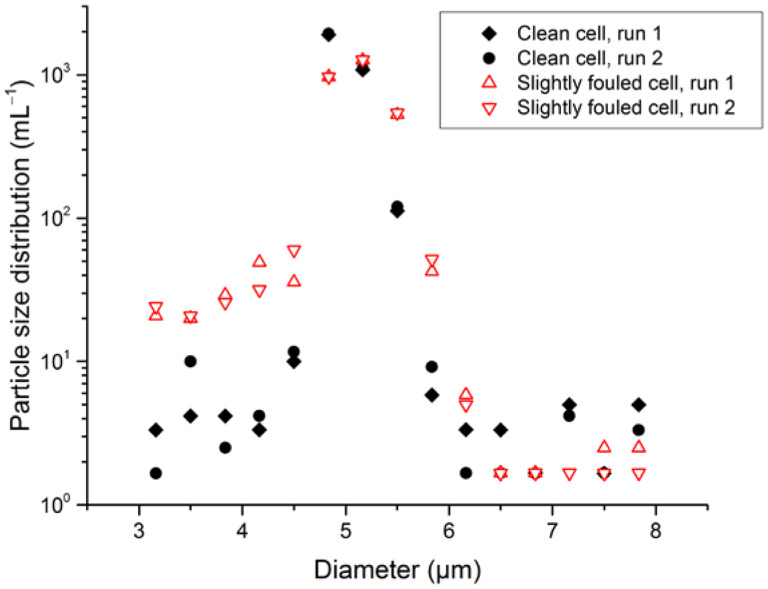
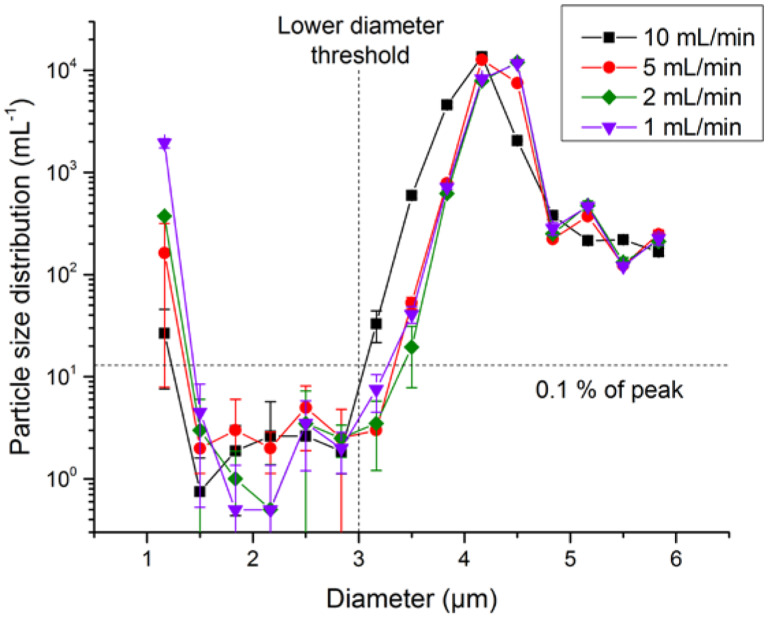
Another optical effect that must be considered is incorrect microsphere sizing due to a contaminated flow-cell wall. Fortuitously, we observed the effects of a flow cell contaminated with adsorbed protein, which resulted in reduced counts of a commercial number-concentration standard. The sample liquid still passed through the cell, and counts were within 10 % of the prior counts, confirming that the flow path was not blocked. However, comparison of the PSDs obtained before and after on the same number-concentration standard demonstrated that the PSD obtained after cell fouling had reduced counts within the nominal size window for the number-concentration standard, but increased counts at microsphere sizes below the lower limit of the window. Since the counting algorithm required the measured microsphere diameter to exceed 3 μm to be counted, any microspheres that were undersized to less than 3 μm would not be counted, leading to a reduction in count. After cleaning the instrument with detergent, enzymatic cleaner, and filtered water, the PSD returned to its original distribution, as seen in Fig. 5. For LO to have high confidence in not missing particle counts and to confirm that the levels of foreign material and air bubbles are negligible, the PSD should fall to negligible values at diameters smaller than the main peak (i.e., approximately a factor of 1000 lower than the peak value of the PSD; see Fig. 6 for an example). The presence of a shoulder at the smaller-diameter side of the distribution can indicate flow-cell fouling. Studies of this tail revealed an anomalous instrument artifact on the small-diameter side of the PSD. At the very lowest sizes attainable by the instrument (1.0 μm to 1.33 μm was the lowest bin for our configuration), there were spurious counts of ≈ 0.1% of N, as shown in Fig. 6. Unlike true particle contamination, these counts were very sensitive to syringe pump speed, were not correlated to counts in the adjacent size bin, and had a repeatability much worse than expected from Poisson statistics of the particle count. Consequently, data for the lowest size bin were discarded in analysis of the small-diameter tail of the PSD.

Fig. 5.

Apparent changes in the PSD resulting from flow-cell contamination in an LO counter. Open red symbols are two runs with slightly fouled flow-cell walls; filled black symbols are two runs after flow-cell cleaning.

Fig. 6.

PSD, evaluated for bin widths of 0.33 μm, of type S microspheres as a function of pump speed for an LO counter. Uncertainty bars indicate one standard deviation of triplicate measurements. The PSD at diameters below the main peak, but above the lowest size bin, is ≈ 3000× smaller than the peak of the PSD and is insensitive to pump speed. The PSD at the lowest size bin shows anomalous behavior.

4.2.4. Uncertainty Budget

Statistical analysis of the runs with variable volume and dilution leads to statistical uncertainties for N, α_c, and α_t. The type A uncertainty for N includes effects of variation in timing or pump volume, vial-to-vial variations, sampling errors, and Poisson statistics of the counting events. These components are all combined in the single uncertainty for N reported by the software used to fit Eq. (3) to the data.

In addition to the statistical uncertainties, there are several type B uncertainties determined by nonstatistical methods. The uncertainty of the dispensed volume is negligible, as is the uncertainty resulting from microspheres adhering to pipette tips (see Sec. 4.1). Significant sources of uncertainty include the following:

• Possible variation in the ratio of singlets to doublets: The PSDs of 2014 and 2016 results were compared, focusing on changes of the high-diameter shoulder of the main peak corresponding to doublet microspheres.

• Undersizing of microspheres (i.e., microspheres giving scattering less than the equivalent of the lower diameter limit): The PSD below the lower diameter threshold was integrated and compared to the number concentration of the main peak to estimate this component (see Fig. 6).

• Possible changes in microsphere number concentration with pipette transfer: This term was estimated from the results of the vial-transfer test described in Sec. 4.1

These uncertainty components were estimated by taking the offsets observed for each of the independent tests of these effects as the standard uncertainty. The bulleted components account for the possible variance of the particle count from the actual number of microspheres in the sampled volume, in addition to effects modeled by Eq. (3).

The combined standard uncertainty represents a confidence level equivalent to one standard deviation. Table 2 presents the uncertainty budget. Because the uncertainty budget includes a number of contributions of similar magnitude, the effective degrees of freedom is quite high, as determined by the Welch-Satterthwaite formula [23]. As a result, a coverage factor k = 2 is close to the 95 % confidence level. The coverage factor for the 95 % level of confidence given in Table 2 assumes each type B component had an effective degree of freedom of 3 (to represent our level of confidence for each of these components).

Table 2.

Relative uncertainty components for the LO determination of microsphere number concentration N.

Uncertainty component
Type A relative standard uncertainty	0.3 %
Type B components
Single/multiple microsphere variation	0.5 %
Undersizing of microspheres	0.5 %
Transfer and handling	0.5 %
Pump calibration	0.04 %
Total Type B relative standard uncertainty	0.9 %
Combined relative standard uncertainty	0.9 %
Effective degrees of freedom	11
Coverage factor for 95 % confidence level	2.2
Expanded relative uncertainty (k = 2)	1.8 %
Expanded relative uncertainty (95 % confidence level)	2.0 %

The uncertainties listed in Table 2 were obtained for microspheres of ≈ 4 μm diameter. Measurement of smaller-diameter microspheres is feasible, but it is limited by the ability of the LO instrument to discern the low-diameter tail of the PSD. Measurements on sulfate functionalized, 2.0 μm diameter microspheres (data not shown) had a PSD in the range (1.1 to 1.6) μm, which was on average 1/500 of the maximum in the PSD near 2.0 μm. This small increase in the low-diameter tail of the PSD translates to an increase of the “undersizing of microspheres” line item from 0.5 % to 0.9 % of N. The resulting expanded uncertainty is U_r(k = 2) = 2.4 % for 2.0 μm microspheres.

The value of N and its associated uncertainty provide a traceable determination of the number concentration of the microsphere suspension.

The equation used to model the data, Eq. (3), is nonlinear, and the parameters for this equation are correlated. For the analysis presented in this paper, the software used for the fitting accounted for these effects in the reported uncertainty of N. The only circumstance in which uncertainties and correlations of the Eq. (3) parameters are potentially needed is when the resulting values of α_c and α_t are used in subsequent measurements of different microsphere lots. In this case, Eq. (3) can be used to correct measurements at a single number concentration. Propagation of the resulting uncertainty in N requires knowledge of the correlation of α_c and α_t in principle, but in practice, the magnitudes of the α_t corrections are small, and these parameters are only weakly correlated (correlation coefficients between −0.06 and +0.17). Provided the volume of each measurement is 0.4 mL or larger, neglecting the correlation term in the propagated uncertainty changes the combined uncertainty u(N) by less than 1.5 % of u(N).

4.3. Dynamic Imaging Results

To assess the DI method, particle number concentrations were measured for a set of three vials having nominal 7000 mL⁻¹ number concentration of type S microspheres on a DI instrument setup as described in the Methods section. Once the tracks were identified, these data were reanalyzed with various settings to find the optimum parameters for track identification. We found that the best results were obtained by requiring the following:

• The effective particle diameter matched the previous diameter of the track to within 40 % of the previous diameter. (Microspheres that moved toward or away from the flow-cell side wall showed significant diameter variation, requiring this relatively large allowance.)

• The particle was found on an image frame acquired no more than 0.2 s beyond the previous particle. Although the nominal separation of image frames was only 0.045 s, inspection of the frame rate for very concentrated bead solutions showed multiple time gaps of 0.09 s, and a few gaps as large as 0.3 s. Microspheres on either side of a 0.3 s gap can still be detected as tracks over a limited span of y pixels.

• The x pixel for the center of the particle was within 5 pixels of the previous particle image.

• The y pixel for the center of the particle was between −5 and +500 pixels downstream of the prior particle.

A portion of the data was manually analyzed to inspect the possibility of either a single particle track being broken into two apparent tracks (which would lead to an overcount), or two tracks crossing, leading to a single particle count for two particles (a form of coincidence error). The results are not strongly dependent on the limits identified above. Altering the diameter limit to 20 % gave a change in apparent number concentration of 0.4 %; altering the range of x pixel variations from 5 to 10 gave a change in apparent number concentration of 0.1 %. These results are consistent with modeling of coincidence of the microsphere images. For a flow cell of thickness t containing microspheres at number concentration N, the probability of two microspheres being interpreted as one image by the commercial software is:

$$P_{\text{coinc}}=A_{\text{obs}}Nt,$$ (7)

where A_obs is the area of a circle with diameter equal to the minimum distance at which two microspheres appear as individual particles for the chosen instrument software parameters. For the dynamic imaging system we used, P_coinc = 0.08 % at N = 7000 mL⁻¹, which is negligible. Furthermore, because microspheres travel at different velocities due to the parabolic velocity profile inside the flow cell, two microspheres are even less likely to be in coincidence along the whole particle track.

For the DI uncertainty budget, shown in Table 3, type B components for “single/multiple microsphere variation” and “transfer and handling” are properties of the microsphere suspension and thus are the same as for the LO uncertainties. Undersizing of microspheres was evaluated by integrating the observed PSD for particle counts below the lower size threshold. Results of the manual track inspection were used to estimate the “broken or missed tracks” uncertainty component. Microsphere counts obtained on a separate lot of microspheres at a higher number concentration of 10⁵ mL⁻¹ (data not shown) were much more sensitive to the diameter and x pixel thresholds, resulting in type B uncertainties ≈ 8× larger for the first three type B uncertainty components in Table 3. At higher number concentrations, microsphere tracks are more likely to cross or interfere with one another.

Table 3.

Uncertainty components for the DI determination of microsphere number concentration N.

Uncertainty component
Type A relative standard uncertainty	0.6 %
Type B components
Single/multiple microsphere variation	0.5 %
Broken or missed tracks	0.2 %
Undersizing of microspheres	0.3 %
Transfer and handling	0.5 %
Total type B relative standard uncertainty	0.8 %
Combined relative standard uncertainty, ur,c	1.0 %
Effective degrees of freedom	16
Coverage factor for 95 % confidence level	2.1
Expanded relative uncertainty (k = 2)	2.0 %
Expanded relative uncertainty (95 % confidence level)	2.1 %

The DI and LO methods were further confirmed by comparing results from these two methods on the same set of three vials, as reported in Table 4. The reported values have been corrected for coincidence, timing, and pump biases (for LO) and for microspheres in the rinse water (DI). The uncertainties of the comparison between the two methods are given in Table 5; predominant uncertainties are the statistical error of the DI method and possible changes in the microsphere number concentration due to handling. The component for “single/multiple microsphere variation” is not included because the fraction of agglomerated microspheres does not change on the time scale of the comparison. Averaged over all three vials and all measurements, the difference between the LO and DI results is (1.1 ± 1.8) % of the number concentration (k = 2).

Table 4.

Results of LO and DI measurements of microsphere number concentration (N_LO and N_DI, respectively, all in units of reciprocal milliliters) on a single lot of type S microspheres.

	NLO, initial	NDI	NLO, final
Sample 1	7156	7070	7102
	7149	6907	7284
		7054
Sample 2	7080	6907	7140
	7110	7046	7089
		7268
Sample 3	6994	6976	7141
	7057	7175	7092
		6959
	<NLO>	7116 ± 20	mean ± ESDMa
	<NDI>	7040 ± 40	mean ± ESDM
	<NLO>/<NDI>	1.011 ± 0.009	ratio ± ur,c

^aESDM = experimental standard deviation of the mean

Table 5.

Uncertainty of comparison of LO and DI methods.

Component		ur
Di number concentration relative ESDMa	Type A	0.6 %
Lo number concentration relative ESDM	Type A	0.3 %
Transfer & handling of microspheres	Type B	0.5 %
Ambiguity of small-diameter cutoff	Type B	0.1 %
Di broken or missed tracks	Type B	0.2 %
Di correction uncertainty	Type B	0.1 %
Lo background counts	Type B	0.1 %
LO αc and αt correction uncertainty	Type B	0.1 %
Lo pump correction uncertainty	Type B	0.04 %
Relative combined standard uncertainty ur,c		0.9 %

^aESDM = experimental standard deviation of the mean

Comparing the results between LO and DI instruments required careful consideration of the upper and lower diameter limits for each instrument. For consistency, we chose to keep the LO diameter limits the same as were used for the determination of α_c and α_t: 3 μm and 8 μm. With the chosen image thresholds, the main peak on the DI instrument was slightly larger in diameter compared to the LO measurements, and the DI peak was slightly broader. Both LO and DI measurements showed a drop in the PSD to negligible levels below 3 μm, so the lower diameter limit was taken as 3 μm for both methods. For particles on the higher diameter limit, though, the PSD falls off relatively slowly. To identify the appropriate upper diameter limit for DI, we determined the fraction of LO counting events for measured diameters > 8 μm and then found the upper DI limit that would give the same proportion of counts greater than the limit. The resulting DI upper limit was set at 11.5 μm.

Initial measurements of the fluorescent URB microspheres showed significantly more scatter than measurements of the sulfate functionalized microspheres. The source of this scatter was traced to microscopic air bubbles that were entrapped in the solution upon tipping the vials to homogenize the samples, even though the tipping was gentle. The sulfate functionalized microspheres do not require surfactant to prevent aggregation and were thus resistant to bubble formation. Following these observations, we altered the sample handling procedure to: tip vial 10×; sonicate for 10 s; and wait for 10 s. A sensitive test of the presence of bubbles can be conducted by plotting the observed number concentration of apparent particles above the upper diameter limit, N_u, versus the total particle number concentration for a series of diluted samples. If N_u approaches a constant value as N decreases, bubbles are likely in the formulation, and the sample handling needs to be altered.

5. Discussion and Conclusions

Characterization of the LO instruments demonstrated that the coefficients α_c and α_t for coincidence and timing error corrections were stable over time. The timing error for the two LO instruments tested was small compared to other sources of uncertainty. The coincidence error was consistent with an accepted mathematical model, but the value of α_c was larger in magnitude than the manufacturer’s specifications for a new instrument. It is possible that variations in optical focus or assembly can give variations in the degree of optical focus in LO instruments.

The key to easy implementation of the DI method was careful optimization of the flow cell, objective, fluid velocity, and measurement protocol. Use of a low magnification objective (4×) increased the field of view and depth of field, which in turn permitted a faster flow rate. Fast flow rate reduced the total testing time to ≈ 2 h for nine samples and two rinses. A short run time, in turn, ensured that the background image acquired at the beginning of each run accurately represented the actual background throughout each sample run. The larger depth of field reduced the number of out-of-focus particles and gave better resolution of the PSD. Finally, by measuring nine samples in quick succession, the bias incurred by microspheres adsorbed to the cell or tubing walls was minimized, and the measurement time was much reduced compared to a measurement protocol requiring rinsing after each sample.

The agreement to within the stated uncertainty of two LO instruments with much different ages and between LO and DI instruments gives confidence in the number concentrations assigned by both methods and their stated uncertainties. Both methods require measurements at relatively low microsphere number concentrations (≈ 5000 mL⁻¹ to 50 000 mL⁻¹ for the LO method; ≈ 7000 mL⁻¹ for the DI method). Careful gravimetric dilution of the original stock bottle is necessary to ensure that the number concentration of the original stock bottle can be accurately inferred; care in avoiding particulate contamination is necessary to ensure that the number concentration of background particles is negligible compared to the microspheres.

An additional limitation of the LO method is the need to verify flow-cell cleanliness, through the demonstration of a PSD that drops a factor of >1000 from the main peak to the background count on the small-diameter side of the main peak. In practice, we have not found this reduction difficult to obtain with sulfate functionalized microspheres (see Fig. 6). Some microsphere lots may contain a significant number of undersized microspheres or debris at effective diameters below the mean diameter. For these lots, the PSD may vary by less than a factor of 1000, regardless of the cleanliness of the LO instrument. In this case, independent measurements of the instrument cleanliness may be made with a separate lot of microspheres that has a low level of undersized particles. Similarly, an independent test of flow-cell cleanliness will be needed if the microspheres to be calibrated are smaller than ≈ 3 μm diameter.

There are several advantages of user determination of microsphere number concentration. Commercial microsphere number-concentration standards have a relatively large uncertainty (10 % of stated concentration), a limited range of available number concentrations, and a relatively short shelf life. User determination of number concentration enables rapid assignment of particle number concentration for a stock solution of larger volume and number concentration. Repeat measurements on this stock solution give an absolute means of monitoring the stability of microsphere solutions, particularly the possible aggregation of microspheres during storage or the accumulation of extraneous particles from the solution packaging. Compared to the LO method, the DI method takes approximately the same time for initial data acquisition but requires custom software and more time for data analysis. The cleanliness of the flow cell is more readily assessed in the DI method, and a dilution series of samples is not required.

Our investigation of microsphere interactions with pipette tips and vial walls demonstrated that adsorption was not a significant problem for the microspheres used in the present study. Different microspheres and formulations may have different adsorption properties, depending on surface functionalization, the presence of hydrophobic fluorophores, and choice of formulation surfactant. It is important to quantify these effects for the microsphere type and formulation used.

The LO and DI methods proved to be practical and comparable in accuracy. Both optical methods presented here have measurement uncertainties lower than the specifications of commercially available number-concentration standards. Because neither method requires significant instrument modification, both methods are readily implemented. The LO method requires more extensive sample preparation on initial characterization of the instrument, but once α_c and α_t are determined, subsequent measurements of microsphere number concentration are easy and rapid.

Biography

About the authors: Dean Ripple is Leader of the Bioprocess Measurements Group, Biomolecular Measurement Division, National Institute of Standards and Technology (NIST). His present research focuses on the development of new standards for protein particles.

Paul DeRose is a Research Chemist in the Bioassay Methods Group, Biosystems and Biomaterials Division, NIST. His present research focuses on the development of standards for quantitative flow cytometry.

The National Institute of Standards and Technology is an agency of the U.S. Department of Commerce.