Adaptive Regulation of Motor Variability

Summary

Trial-to-trial movement variability can both drive motor learning and interfere with expert performance, suggesting benefits of regulating it in context-specific ways. Here we address whether and how the brain regulates motor variability as a function of performance by training rats to execute ballistic forelimb movements for reward. Behavioral datasets comprising millions of trials revealed that motor variability is regulated by two distinct processes. A fast process modulates variability as a function of recent trial outcomes, increasing it when performance is poor and vice versa. A slower process tunes the gain of the fast process based on the uncertainty in the task’s reward landscape. Simulations demonstrated that this regulation strategy optimizes reward accumulation over a wide range of time-horizons, while also promoting learning. Our results uncover a sophisticated algorithm implemented by the brain to adaptively regulate motor variability to improve task performance.

Introduction

Trial-to-trial variability is a pervasive feature of all movements, widely thought to be the consequence of a noisy nervous system and hence an impediment to peak performance [1–4]. However, recent studies have advanced a complementary view of motor variability, in which it is also an integral component of trial-and-error motor learning that allows the brain’s control system to explore new solutions to the task at hand, and reinforce those that improve performance [5]. These studies have shown that motor variability can be harnessed for reinforcement learning [6,7] and that its structure can predict learning rates across various tasks [8]. If motor variability is beneficial for learning but detrimental to peak performance, it should be actively controlled to meet different task demands [5]. Yet, there is currently no consensus as to whether or how motor variability is regulated by the mammalian brain [5,9].

Past studies have primarily viewed changes in motor variability as a natural consequence of motor learning [1,9,10]. Indeed, a systematic reduction of motor variability with learning is observed across many species and behavioral paradigms [11–14]. In the context of reinforcement learning, this is consistent with the nervous system acquiring information about the task’s reward landscape, then gradually settling on actions or control policies that yield the best outcomes [15]. This implies that learning-related changes in motor variability are the result of slow and adaptive changes in motor circuitry [16].

Yet, we also know from recent studies that the brain can regulate motor variability in far more dynamic and context-dependent ways. A great example comes from songbirds that learn and maintain their songs through reinforcement learning [6,7,14,17,18]. When performing for a potential partner, birds reduce the variability of their songs by about half compared to when they ‘practice’ alone [19]. This context-specific regulation of variability allows the male bird to cater to the female’s preference for stereotyped songs [20], while continuing to explore in the vocal domain to further improve its song.

For many of the tasks we face, however, learning and performance cannot be as neatly separated as in birdsong, meaning that demands for long-term performance improvement and immediate reward maximization must be satisfied at the same time. Whether and how the nervous system regulates motor variability in situations when learning and performance goals are intertwined (i.e. ‘learning on the job’) is not understood. As an example, imagine you are a tennis player trying to win points on an unfamiliar opponent with your serve. You want to figure out your opponent’s weakness (learning), while at the same time winning as many points as you can (short-term reward accrual). How should you regulate the trial-to-trial variability of your serve in this scenario? One intuitive strategy is to make it contingent on past performance. If your last few serves were unsuccessful, you would likely benefit from increasing the variability of your service motion to find ones with greater probability of success. On the other hand, if your past serves have been successful, you should reduce variability and exploit your new-found knowledge of your opponent’s weakness.

This toy example describes a strategy where variability is dynamically regulated as a function of recent outcomes. While we know that sudden changes in reward rate can modulate motor variability [21], the algorithm by which the brain regulates variability based on past performance is not understood. Unclear is also the degree to which fast fluctuations in motor variability reflect an active process for performance optimization and enhanced learning [22] versus extraneous factors, such as frustration [23]. The nature of variability regulation is also not known. Is it a binary switch between qualitatively distinct high- and low-variability states as has been proposed by studies of decision-making [24–26], or are levels of motor variability regulated along a continuum [15]? And how does task uncertainty influence motor variability? For example, when serving against a familiar opponent you may not want to overreact to occasional dips in performance, but instead continue serving in ways that you know, from extensive experience, will best exploit your opponent’s weakness [27]. Yet, whether and how regulation of motor variability is affected by the certainty in a task’s reward landscape is not clear.

Addressing how the brain regulates motor variability as a function of performance history and task uncertainty is inherently challenging. This is because reliable and quantitative measures of how motor variability (which is intrinsically measured over many trials) varies as a function of context and task parameters (e.g. reward rate) can require many thousands of trials. Furthermore, measurements of variability can suffer from statistical biases when conditioned on performance-related variables such as reward, and autocorrelations in performance can further confound analyses of causal relationships between performance and variability [28] (for details see Figures S1C–E and S2C). Thus, establishing whether and how the brain regulates motor variability would benefit greatly from having large and longitudinal datasets that can be onerous to acquire in human subjects.

To overcome these hurdles, we conducted motor learning experiments in rats, using a fully automated and high-throughput training system designed to collect datasets comprising millions of trials, including more than hundred thousand trials from each of our subjects [29]. We powered our analyses to uncover trial-by-trial relationships between motor variability and reward, and to describe the interplay between performance history, motor variability, reward accumulation, and learning. We found that rats modulate motor variability in response to the integrated outcome of the past ~10 trials. Furthermore, levels of variability are regulated as a graded function of the reward rate, a strategy that reinforcement learning simulations demonstrated to be effective for driving trial-and-error motor learning and also near-optimal for maximizing performance in our motor task. Finally, we show that motor variability is also shaped by a slower process (~5000 trials) that reflects the uncertainty of the task’s reward landscape. In line with optimal predictions from reinforcement learning simulations and similar to the regulation of exploratory behavior in decision-making tasks [30], we found that motor variability increased with increasing task uncertainty.

Results

Studying regulation of motor variability in rodents

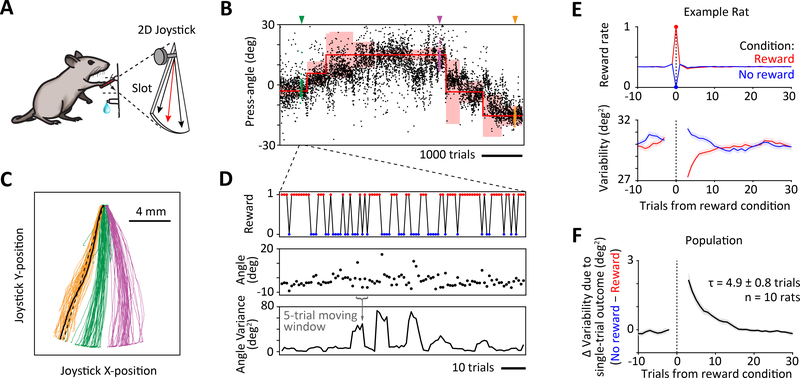
To investigate how variability is regulated by reward and its relationship with overall performance and learning, we designed a motor task in which rats were challenged to modify, through trial-and-error, a ballistic movement along a single, continuous dimension. Specifically, water-deprived rats were rewarded for pressing down a two-dimensional joystick at angles around a target (Figures 1A–C, Figures S1A–B). Three to four training sessions were scheduled per day and rats performed ~300 trials per session. The angular width of the reward zone was automatically updated between sessions to help shape the rat’s behavior towards the target angle and maintain the average reward rate between 30% and 40% (Figure 1B, see STAR Methods). To encourage subjects to continuously and adaptively update their actions, we created non-stationary reward landscapes by randomly changing the target angle as soon as animals learned the current target (defined by the reward boundaries moving to within 2.3 degrees of the target angle, Figures 1B–C). On average, it took rats 1612 ± 863 trials (median ± median absolute deviation) to learn the new target. The within-session learning rates were comparable to what has been reported for humans in analogous trial-and-error learning tasks [31] (see ‘Simulations’ in STAR Methods). Using our fully automated training system [29], we acquired large datasets totaling ~3.3 million trials from 10 rats in over 10,000 training sessions. This allowed us to perform analyses on the relationship between performance history and motor variability with unprecedented statistical power.

Figure 1: Motor variability is regulated by recent reward history.

A. Schematic of the experimental task used to study the relationship between performance and motor variability. Rats learn to press the 2-dimensional joystick close to a target angle (red) to receive water reward.

B. Example performance of a rat on the motor task. Trials are rewarded whenever the joystick press-angle (black dots) falls within the reward boundary (red shading). Reward boundaries are updated to shape rats’ press-angles towards the target (red line). Once a rat’s mean press-angle matches the target, a new target is automatically selected. Colored arrows and dots indicate example sessions whose trajectories are shown in panel C.

C. Joystick press trajectories from three example sessions indicated by arrows in panel B. The press-angle is measured between a line of best fit (dashed black line) to the joystick trajectory (example represented by solid black line) and the vertical. See also Figures S1.

D. Zoom-in of panel C showing behavioral variables of interest for our analysis: reinforcement (top), press-angles (middle) and variance of press-angles (bottom) calculated in moving windows of 5 trials.

E. Calculating a reinforcement-triggered average of motor variability for an example rat. Average reward (top) and press-angle variability (bottom), conditioned on the probabilistic outcome – reward (red) or no reward (blue) – of a single trial (at trial 0). See also Figures S1 and S2.

F. Difference between average levels of variability in response to single unrewarded and rewarded trials, averaged across the population of rats (n=10). These plots were generated by combining the results from our matching analysis and probabilistic reward manipulations. Black line indicates mean and grey shading indicates SEM across rats. τ represents the time-constant of an exponential fit to the decay of the single-trial variability effect (after trial 0). See also Figures S1 and S2.

Motor variability is regulated by recent reward history

To determine whether motor variability is causally regulated by recent trial outcomes, and if so, what its history-dependence is, we measured how the outcome (i.e. reward or no reward) on a single trial modulated motor variability in subsequent trials (Figure 1D–E). If exploratory variability is adaptively regulated by recent reward history to improve performance, we would expect greater variability following unrewarded trials than after rewarded trials. Measuring the temporal relationship between trial outcome and motor variability in accurate and unbiased ways requires controlling for several potential confounds, such as task-driven coupling between angle variability and reward, and autocorrelations in performance (Figures S1C–G).

To isolate the causal influence of trial outcome on motor variability, the outcome on the conditioned trial should be independent of past and future trials. We accomplished this using two different methods. We used a statistical matching technique (Figure S2A) to compare subsets of trials with distinct outcomes but embedded in similar reward environments. We also implemented probabilistic reward on a random subset of trials, either interspersed among regular trials (‘mini’ reward clamps) or grouped into 50–100 trial blocks (‘block’ reward clamps). On these probabilistic trials, the reward probability was clamped to constant values and reward was delivered independent of the press-angle (Figure 1E, Figure S2B, see ‘Probabilistic reward trials’ in STAR Methods). Both methods successfully removed any bias due to autocorrelations in behavior, and unequivocally demonstrated that recent reward causally modulates future motor variability, increasing it following unrewarded trials and vice versa (Figure 1E, Figure S2C). Failing to consider auto-correlations in behavior (Figure S1F) overestimated the variability response by ~200–250%, and generated artefacts such as a pronounced variability effect prior to the conditioned trial that was ~100–130% greater than the true response (Figure S2C). We also determined that single-trial outcomes affect variability by regulating the variance of the press-angle distribution rather than the drift in its mean (Figures S2D–E).

Since our two independent analysis methods yielded very similar results, both on average (Figures S2A–C) and for individual rats (correlation between average change in variability for the matching and randomization methods: r=0.9, p<10⁻⁵), we pooled the results in subsequent analyses. We observed that the effect of trial outcome on variability decayed exponentially (Figure 1F) with an average time-constant of 4.9 ± 0.8 trials (mean ± SEM, n=10 rats). This suggests that the rat brain integrates reward history in an exponentially weighted manner over the past ~10 trials to produce an estimate of the reward rate for regulating motor variability.

The relationship between variability and reward rate

We showed that rats actively modulate motor variability in response to the outcomes of recent trials, yet the specifics of how this regulation is implemented remain unclear. Our results suggest that the brain maintains a running estimate of the reward rate in the form of a weighted average of past trial-outcomes, but we do not know how variability is regulated as a function of this estimate (Figure 2A). Studies of decision making [24–26] suggest that the nervous system might regulate variability by switching between two discrete states depending on reward rate. Alternatively, variability might be regulated in a more continuous manner. To uncover the dependence of variability on the reward rate – the variability control function (see STAR Methods, eq. 11) – we analyzed the relationship between motor variability and the inferred multi-trial reward rate estimates (Figure 2A).

Figure 2: Motor variability is regulated as a graded, non-linear function of reward-rate.

A. Sequence of trial outcomes (top), reward rate estimates (middle), and variability measurements (bottom), for an example rat. Running estimates of the reward rate were computed by convolving past trial outcomes with a ‘reward rate filter’ (essentially a weighted average of past outcomes), derived from the exponential decay of the single-trial variability effect, as seen in Figure 1F.

B. Effect of single trial outcome on variability as a function of reward rate estimate. Difference in variability between rewarded and unrewarded trials (on trial 0, as in Figure 1F) for an example rat (top) which is subdivided into groups (bottom) by the reward rate estimate for the trial before the conditioned trial (trial −1 in this plot, indicated by arrow). Reward-rate estimate groups are indicated by the blue-red color scale and number ranges above each plot. Shaded regions represent SEM.

C. Average difference in the variability after an unrewarded and rewarded trial (the ‘single-trial variability effect’) as a function of the reward rate estimate on the trial prior to the reinforcement-conditioned trial, averaged across rats. The single-trial variability effect is measured as the variance over 10 trials following the reinforcement conditioned trial. Error-bars represent SEM. See also Figure S3.

D. Numerical integration of the single-trial variability effect as a function of the reward rate estimate yields ‘variability control function’, i.e. the relationship between variability and reward rate. Circles and error-bars represent mean and SEM, respectively, across the population of rats (n=10). See also Figure S3.

E. Variability control functions for individual rats, normalized by their gain (magnitude). Color indicates the gain of the variability control function, on a logarithmic scale.

Because we want to describe how reward rates affect variability and not the other way around, we again performed a causal single-trial analysis that removes the confounding effects of variability on performance (Figures S1C–G and S2C), but this time binned the data based on reward rate estimates just prior to each conditioned trial (Figure 2B). To infer the variability control function, we calculated its slope at each reward rate estimate by measuring how incremental changes in this estimate - caused by single trial outcomes - drove changes in variability. The full variability control function could then be reconstructed by integrating the slope estimates (see STAR Methods, eqns. 11–13 for details).

We found that single-trial outcomes modulate variability to a much larger degree at low reward rates (Figure 2B–C). Integrating the single-trial effects revealed that, rather than a binary switch between high- and low- variability states, rats regulate levels of motor variability as a graded, non-linear function of recent reward history (Figures 2D and S3A), decreasing it with increasing reward rates (Figure 2E). To quantify the extent to which individual rats regulated motor variability, we defined the ‘gain’ of each variability control function as the scaling factor between it and the archetypal control function (the average, normalized control function across all rats, see eqns. 13–14 in STAR Methods). These gain values (mean: 19.6 deg²) varied substantially across rats (SD: 14.2 deg², Figure 2E), revealing individual differences in the sensitivity of the variability regulation process to recent reward history.

Single-trial analyses can predict macroscopic changes in motor variability

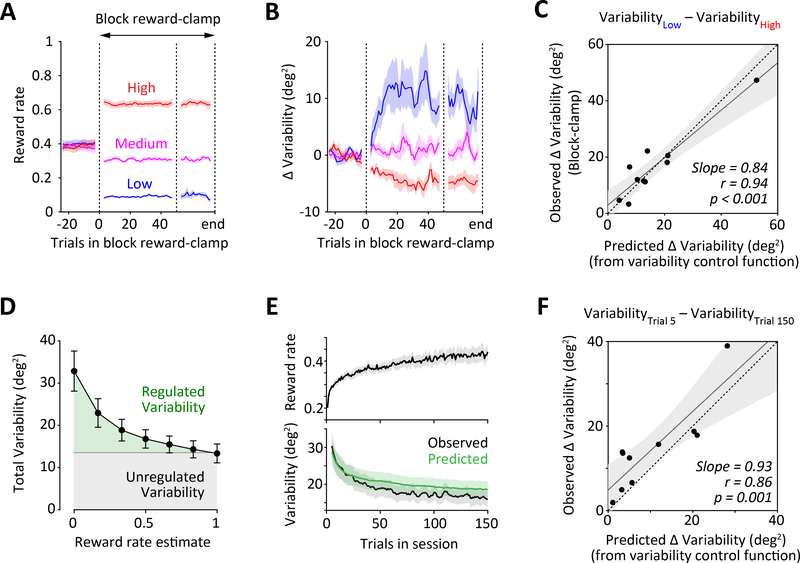
Our analyses uncovered an algorithm that can explain how motor variability is regulated in response to recent performance. However, it is unclear whether a process inferred from analyzing single trial effects is sufficient to explain longer-term changes in motor variability that could arise in response to sustained changes in reward rates over the course of a session. To probe this, we manipulated reward rates experimentally in blocks of 50–100 trials in a random subset of sessions (3 out of every 8 sessions, see STAR Methods). In these ‘block reward-clamps’, reward was uncoupled from press-angle and dispensed probabilistically on 10% (low), 31% (middle) or 63% (high) of the trials (Figure 3A, see STAR Methods). In response to these blocked reward-clamps, rats gradually increased variability when the reward-rate was low and decreased variability when it was high (Figure 3B). The time-course of the average change in variability (τ=5.9 ± 3.7 trials) was similar to that over which rats integrate past trial outcomes, as determined by our single-trial analyses (Figure 1F). Once variability reached asymptotic levels, it remained constant over the ~75 trial duration of the block clamp (Figure 3B, correlation between trial number and avg. variance: r=0.062, 0.064 and 0.002 for low, middle and high reward-clamps, respectively; p>0.05). Importantly, the degree to which the variability of individual rats differed between the low and high reward-rate clamps was well predicted by their individual variability control functions (Figure 3C), validating the accuracy of our single-trial analyses and indicating that regulation of variability is well captured by the single-trial effects.

Figure 3: Single-trial analyses can predict macroscopic changes in motor variability.

A-B. Average reward rate (A) and variability (B) during block reward clamps in which probabilistic reward was delivered over 50–100 trial segments at three different reward rates (low, medium and high – indicated by colors). The reward delivery was independent of the press-angle. Lines show 5-trial moving window measurements that were first averaged across sessions for each rat and then across rats. Shading represents SEM across rats (n=10). See also Figure S3.

C. Comparing changes in average variability between the low and high reward rate block clamps, to predictions from the variability control functions derived from single-trial analyses (as in Figure 2D). Each dot represents an individual rat. Grey line is the regression line and dashed line represents unity. Shading represents 95% confidence intervals of the regression. A significant correlation is observed even after excluding the rat with the largest difference in variability (Slope = 0.824, r=0.73, p=0.025).

D. Comparing average levels of regulated (derived from single-trial analysis, green shading) and unregulated (derived from measurements in the block reward-clamp, grey shading) variability as a function of the reward rate estimate. Error bars represent SEM.

E. Average reward rate (top) and variability (bottom, black curve) as a function of trial number in a training session. Green curve shows variability predicted from reward history by the reward-dependent variability regulating process derived from single-trial analyses of probabilistic reward trials (see STAR Methods and Figures 1–2). Measurements and predictions have been averaged over sessions for each rat and then across rats. Shading represents SEM across rats (n=10).

F. Comparing changes in average variability over the time-course of a training session (between trials 5 and 150), to predictions from the reward-dependent variability regulating process derived from single-trial analyses of probabilistic reward trials (as in panel E, bottom plot). Each dot represents an individual rat. Grey line is the regression line and dashed line represents unity. Shading represents 95% confidence intervals of the regression.

In contrast to these large reward-driven changes in the variance of the press-angle distribution, the reward manipulation did not significantly affect the drift of the mean press-angle (Figure S3B). This corroborated our previous observation (Figure S2D–E) that reward primarily regulates the variance of the press-angle distribution as opposed to the drift in its mean.

Many past studies have argued that the motor system is fundamentally noisy [2,4]. Such motor noise is thought to be uncontrollable and, hence, its magnitude should not be sensitive to reward [5]. Our single-trial analysis (Figures 1–2) cannot determine absolute levels of unregulated motor variability since it only measures changes in variability for small changes in reward rate (i.e. levels of regulated variability). In contrast, measurements of motor variability in the block-reward clamps include both reward-regulated and unregulated components. Therefore, by subtracting the variability control function at the three corresponding reward rates from asymptotic levels of variability in the block reward clamps, we can estimate levels of unregulated motor variability for individual rats (see STAR Methods). We found the ratio of regulated to unregulated variability to be 0.4 at average reward rates, and as high as 1.5 at the lowest reward rates (Figure 3D), suggesting that rats actively regulate a large fraction (between 25–75%) of their overall motor variability.

After validating our single-trial analyses using the artificial block reward-clamp manipulations, we wanted to determine if this can predict the regulation of motor variability in response to ‘natural’ changes in reinforcement contingencies. The most salient change in the reward landscape of our task occurs at the beginning of each training session when reward boundaries are updated based on the rat’s performance in the previous session. We found that, on average, reward-rates increased over the course of a session while motor variability decreased (Figure 3E). Our single-trial analysis successfully predicted the within-session coupling between motor variability and reward-rate (see ‘Predicting variability from reward’ in STAR Methods), both on average (Figure 3E), and for individual rats (Figure 3F).

These results demonstrate that the same reward-dependent process that accounts for ‘microscopic’ trial-to-trial fluctuations in motor variability can explain longer-term ‘macroscopic’ changes that occur in response to both ‘experimental’ and ‘natural’ changes in reinforcement regimes over the timescale of individual sessions.

Reward-dependent regulation of motor variability optimizes task performance

Thus far, our results have shown that rats actively regulate a large proportion of their motor variability as a graded function of recent outcomes via the variability control function (Figure 3D). But what are the benefits of such a control strategy? Traditionally, motor variability has been seen as beneficial for learning [5,7,8] but detrimental for peak performance [1–4], prompting us to ask whether the regulation strategy the brain implements is optimized for short or long-term gains, or some compromise between these seemingly competing options.

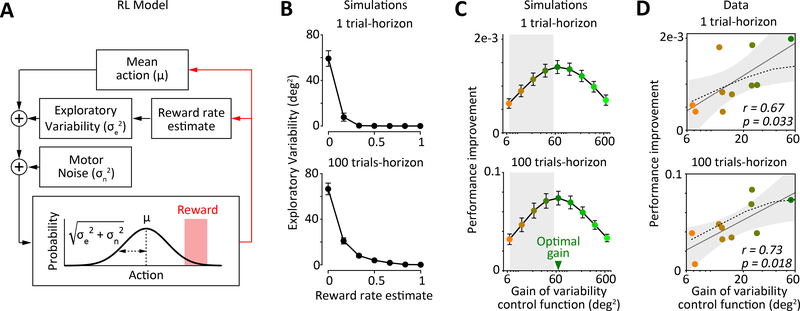
To probe this, we compared experimentally derived variability control functions to those derived from reinforcement learning simulations. We modeled rats’ behavior on the task with a class of reinforcement learning algorithms called policy gradient methods [32,33]. These algorithms can model ‘movements’ using parametrized action policies whose parameters are updated to improve performance. To generate press-angles, we sampled from a Gaussian distribution, whose mean and variance were updated by reward (Figure 4A). The hyperparameters of the algorithms, such as learning rates and levels of motor noise, were fit to data from individual rats (see STAR Methods). We used policy-gradient reinforcement learning to derive variability control functions (eqns. 6–8 in STAR Methods) that optimize performance over short (1 trial) or long (100 trials) time-horizons.

Figure 4: Reward-dependent regulation of motor variability optimizes task performance.

A. Schematic diagram of a policy-gradient reinforcement learning algorithm that implements reward-dependent modulation of motor variability. The model generates ‘movements’ from a Gaussian policy with two sources of variability – unregulated motor noise (${\sigma }_n^2$) and reward regulated variability (${\sigma }_e^2$). The latter component corresponds to exploratory variability that can drive changes to the policy mean (μ). Feedback from reinforcement updates the policy mean and the reward rate estimate, which in turn modulates levels of exploratory variability. Simulation parameters are fit to match the behavior of individual rats on the motor task (see STAR Methods).

B. Optimal variability control functions derived from reinforcement learning simulations that optimized future performance over short (1 trial, left) or long (100 trials, right) time-horizons. Optimal functions are averaged across simulated rats (n=10). Error-bars represent SEM.

C. Performance improvements as a function of changing the gain of the variability control function optimized for a 100 trial-horizon in the simulated motor task over 1 (top) and 100 (bottom) trial-horizons. Performance improvement is the difference between the average reward rate over the future trial-horizon and reward rate on the preceding trial (see STAR Methods). Error-bars indicate SEM over simulated rats (n=10). Grey shading indicates the range over which the gain of the variability control functions vary in our experimental subjects (as in Figure 2E and panel D). See also Figure S4.

D. Relationship between individual differences in rats’ performance improvement over 1 (top) and 100 (bottom) trial-horizons and the gains of their variability control functions. Each dot represents an individual rat and colors indicate gain on a log scale as in panel C. Grey line is the regression line and dashed line represents the prediction from our simulations (panel C). Shading represents 95% confidence intervals of the regression. The p-value quantifies evidence for the hypothesis that there is no relationship between the gain of the variability control function and performance improvement for individual rats. See also Figure S4.

Changing the time-horizon in our simulations allowed us to probe whether optimal strategies for regulating motor variability depend on how far into the future an agent seeks to maximize performance. For example, a tennis player serving at a crucial point in a game should optimize performance over a very short time-horizon (the next serve), and hence select the action with the highest estimated reward value – an ‘exploitative’ strategy calling for reduced exploration. In contrast, a player seeking to optimize average performance over the entire tennis match could conceivably benefit from higher levels of variability to ‘explore’ motor space and find improved solutions [34,35]. However, the variability control functions derived from our simulations were similar whether they were optimized over 1 or 100 trials (Figure 4B), suggesting no major time-horizon dependent trade-off between strategies that maximize exploitation versus those that additionally rely on exploration. Indeed, the optimal policies for both short and long time-horizons regulated motor variability as a non-linear function of the reward rate, a function that was similar in shape to the average variability control functions we uncovered experimentally (Figure 2D–E, r = 0.88 ± 0.10 and 0.95 ± 0.05, for 1- and 100-trial horizons, respectively, mean ± SD, n=10).

Optimal strategies for variability regulation are time-horizon invariant

Although strategies that optimize short- and long-term task performance are similar in how they regulate levels of motor variability (Figure 4B), the way in which variability advances the goal of each strategy differs. If the aim is to optimize performance on the very next trial, the function of variability is to achieve that objective whether or not it also results in learning. In contrast, optimizing performance over longer time-horizons could additionally benefit from having trial-to-trial variability drive motor learning. To determine whether the regulation strategy we uncovered is optimized to improve performance in the short term, or whether it additionally regulates variability to drive motor learning, we probed the relationship between the degree of variability regulation and improvements in task performance over short and long time-horizons, as well as the capacity for motor learning.

We had previously observed that the variability control functions of our experimental subjects, while similar in shape, varied in their ‘gain’ (Figure 2E), meaning that some rats regulated their variability more than others. We analyzed how the gain of the variability control function affects task performance by changing it in our simulations (Figure S4A, Methods). While optimal gain values maximized task performance over both short and long time-horizons (eq. 18 in STAR Methods; Figure 4C), lowering the gain systematically degraded performance. We also probed the relationship between the degree of variability regulation and motor learning, which we quantified as the rate at which the mean press-angle approached the reward target over the course of a session. Lowering the gain of the optimal variability control functions in our simulations reduced both learning rates (Figure S4B) and accumulation of reward (Figure S4C). In contrast, increasing the gain above optimal values further improved learning, but decreased reward accumulation, suggesting that reduction in task performance in this regime is due to a deficit in exploitation (short-term reward maximization) rather than learning-related exploration.

If motor variability is regulated to improve task performance, the gain of a rat’s variability control function should be a good predictor of how well it performs in our task. We found this to be the case whether we considered short or long time-horizons (Figure 4D), suggesting that rats use regulated variability not only to maximize reward on the next trial, but also to drive exploration and improve learning. Consistent with this, we found that the subpopulation of rats that had larger than average (closer to optimal) gains (Figure S4D) learned to a greater extent and accumulated more reward than rats with lower gains (Figure S4E–F). Furthermore, the gain of individual rats’ variability control functions was highly predictive of their learning and reward accumulation over the course of each session (Figure S4E–F). In contrast, we found no significant relationship between levels of unregulated motor variability and task performance (Figure S4G) or measures of motor learning (Figure S4H).

Taken together, our analysis suggests that regulation of motor variability can and does optimize performance on motor tasks by simultaneously enhancing short-term performance (exploitation) and by improving reinforcement learning in continuous motor spaces and consequently long-term performance.

Reward-dependent regulation of motor variability is gated by task uncertainty

Our results thus far show that motor variability is regulated as a function of recent reward history. While this strategy is optimal for reward accrual when the reward landscape is changing (e.g. when serving to unfamiliar opponents), it becomes maladaptive when it is static and known to the subject (e.g. when serving to a familiar opponent). In the latter case, it may be better not to over-react to fluctuations in performance and instead reduce variability across the board. To determine whether the nervous system takes into account the uncertainty of the reward landscape when regulating variability, we switched a subset of our rats (n=7) to a stationary reward landscape by keeping the target angle constant over several hundred experimental sessions (Figure 5A). From a rat’s perspective, the switch to the stationary reward landscape could only be inferred once the target angle for the stationary context had been reached (after 5 ± 3 sessions, median ± m.a.d.), at which point the non-stationary condition would have triggered a switch to a new target angle. As we had done for the non-stationary context, we continued to shape the width of the reward zone to maintain similar average reward rates. Over time, the change to a stationary landscape led to a significant reduction in task uncertainty as estimated by the distance between the rat’s mean press-angle and the reward zone (Figure S5A, p < 10⁻³ by paired t-test, n=7).

Figure 5: Reward-dependent regulation of motor variability is gated by task uncertainty.

A. Performance of an example rat over multiple sessions in non-stationary (green) and stationary (orange) reward landscapes. In the stationary task, the target angle (red line) is maintained at the same location (0 degrees) throughout. Dots represent the mean press-angle in individual sessions. Rats were first trained on the non-stationary task, followed by the stationary context, and finally returned to the non-stationary task until the end of training. Transitions between reward contexts are not made explicit to the rats.

B. Optimal variability control functions derived by simulation to maximize future reward over a 100-trial horizon in non-stationary (left and right panels) and stationary (middle) reward contexts. Curves represent averages across simulated ‘rats’ (n=7). Error-bars indicate SEM. See also Figure S5.

C. Variability control functions computed from experimental data acquired in the first non-stationary (left), stationary (middle), and second non-stationary (right) reward contexts. Curves are averages across rats (n=7) and error-bars represent SEM. See also Figure S5.

In the stationary context, variability control functions derived by reinforcement learning simulations for non-stationary reward landscapes (Figure 4B) performed sub-optimally. Lowering the gain of the control function improved performance (Figure S5B). Likewise, optimal variability control functions derived from simulations for the stationary context prescribed dramatically lower levels of exploratory variability compared to the non-stationary context (Figure 5B). In line with this, rats systematically reduced their mean trial-to-trial variability when switched to a stationary reward context despite seeing no increase in mean reward rate (avg. variability = 19.9 ± 3.4 deg² and 13.8 ± 3.1 deg²; avg. reward rate = 0.40 ± 0.04 and 0.30 ± 0.01, in the non-stationary and stationary reward contexts, respectively).

Since levels of unregulated motor variability were not significantly different between the two contexts (avg. unregulated variability = 13.7 ± 2.6 and 9.1 ± 2.3 in the non-stationary and stationary reward contexts, respectively; p = 0.09 by paired t-test), this indicated that rats had modified the degree to which they regulate motor variability as a function of reward history. The bias towards ‘exploitation’ in the stationary reward context was confirmed in our single-trial analyses. Although the time-course of variability decay was similar (τ = 3.7 ± 0.5 trials and 4.4 ± 0.7 trials in non-stationary and stationary reward contexts, respectively; p = 0.26 by paired t-test), the average modulation of variability by single-trial outcome was significantly lower in stationary versus non-stationary sessions (Figure S5C, p = 0.02 by paired t-test).

Notably, this reduction in regulated variability was observed for all baseline reward rates (Figure 5C and Figure S5D) with variability control functions having significantly reduced gains in the stationary compared to the non-stationary context (F_(1,96)=10.17, p=0.002). When we switched rats back to a non-stationary reward landscape (Figure 5A), they reverted to the variability control functions they had employed in the first non-stationary condition (Figure 5C, Figure S5C–D; F_(1,96)=0.25, p=0.25 implying no detectable change in gain), confirming that the gain reduction in the stationary reward context was not simply due to aging or time spent in the task.

Our finding that variability is regulated by uncertainty raised the question of whether these changes can be accounted for by a fast trial-by-trial variability regulating process or whether a different and slower process is responsible. We observed that rats had more uncertainty about the reward landscape at the beginning of a typical non-stationary task session, which then decreased with in-session learning (Figure S5E). These within-session changes in uncertainty were of similar magnitude to changes in uncertainty between the two different reward contexts (Figure S5A). Consequently, variability control functions with greater than optimal gains performed better (i.e. accumulated more reward) in the early parts (~100 trials) of the simulated sessions (Figure S4C). This led us to ask whether rats modulate the gain of their variability control functions in response to changes in uncertainty over the course of a single session. To probe this, we compared variability control functions derived from ‘early’ and ‘late’ trials in every experimental session. We found the that the variability control function remained stable over a session despite significant decreases in task uncertainty (Figure S5F; F_(1,138)=1.35, p=0.25). This implies the existence of a distinct and slower process that tunes the gain of the variability control function based on the uncertainty of the reward landscape estimated over multiple sessions.

To measure the timescale of this uncertainty-dependent process, we tracked how the average modulation of variability by single-trial outcome changed as rats transitioned from non-stationary to stationary reward contexts and vice versa. We used this metric instead of the gain of the variability control function since they are highly correlated (Figure S5G) and similarly regulated by uncertainty of the reward landscape (Figure S5C). Importantly, the single-trial variability effect can be accurately estimated using ~7 fold less data as it does not require an additional step of parsing by the estimated reward rate (Figure 2B). We found that levels of regulated variability changed gradually with an average time-constant of 18.9 ± 4.4 sessions, corresponding to ~5300 trials (Figure S5H).

If rats tune their variability as a function of uncertainty, differences in the estimates of uncertainty [36,37] could explain individual differences in variability regulation. In this case, underestimating the degree of uncertainty in the reward landscape should result in lower than optimal gains in the non-stationary task environment (Figure 4B, S4D). In support of this, we observed that the higher the gain of an individual rat’s variability control function in the non-stationary context, the more it was reduced after transitioning to a stationary reward context (r²=0.81, p=0.006, n=7 rats).

Discussion

Our finding that motor variability is causally modulated by recent trial outcomes (Figure 1E–F) is consistent with earlier reports in humans [21,22], suggesting an evolutionary conserved algorithm for reward-dependent regulation of variability in mammalian brains. By harnessing the power of our large datasets, with orders of magnitude more trials than in comparable human studies, we were able to delineate the details of this algorithm, which we show comprises two distinct processes playing out over different timescales (Figure 6). A fast reward-dependent process modulates motor variability in response to recent trial outcomes (Figures 1E–F, 2, S2), while a slower uncertainty-dependent process tunes the gain of the variability regulation function over many sessions based on the statistics of the reward landscape (Figures 5, S5). Importantly, the degree to which variability is regulated by reward (i.e. the ‘gain’ of the reward-dependent variability control function) predicted individual differences in task performance (Figure 4D, S4E–F). Reinforcement learning simulations further showed that the algorithm we uncovered regulates variability in a way that is near-optimal for improving performance both in the immediate and the long-term (Figure 4B), and for different levels of task certainty (Figure 5B). Though our analysis is focused on reward-dependent regulation of motor variability, we also found that a component of variability that is invariant to reward history and likely reflects peripherally generated motor noise (Figures 3D, S4G–H) [5,22,38].

Figure 6: A sophisticated algorithm for adaptive regulation of motor variability.

Proposed algorithm implemented by the brain to actively regulate motor variability. This algorithm comprises two processes that operate over different timescales. A fast reward-dependent process (red) integrates the outcome of recent trials to generate an estimate of the reward rate that in turn determines levels of exploratory variability via the variability control function. A slower process (green) tunes the gain of the reward-dependent process over several sessions based on the uncertainty of the reward landscape. See also Figure S6.

Contrasting regulation of variability in decision-making and motor learning paradigms

Previous studies of decision-making, including in macaques and rodents, have shown that subjects use information from previous trial outcomes to adaptively switch between qualitatively distinct exploration and exploitation ‘modes’, characterized by high and low levels of choice-variability respectively [24,26]. In contrast, we found that the brain regulates levels of motor variability as a continuous function of past performance (Figures 2D, S6). But why would the brain adopt distinct trial-and-error search strategies for decision-making and motor tasks?

In most decision-making paradigms, in which subjects choose amongst a finite set of actions, there is no relationship between the values of the different options, meaning that nothing can be inferred about the ones that are not directly sampled. This sets up an inherent antagonism between gathering information about your options (exploration) and choosing the one with the highest known value (exploitation), i.e. the explore-exploit dilemma. However, when the values of available options are correlated, as is the case for ‘structured bandits’ [39–41], an agent can learn about the value of an action that is not directly sampled – even while ‘exploiting’. In these situations, exploration and exploitation strategies can prescribe similar choices [39]. This is the case for motor tasks, which are solved in continuous motor spaces with spatially structured reward landscapes. It means that the value of a selected action carries information about the value of other actions close-by in motor space. For instance, if a selected action yielded high reward, it would imply that nearby actions are also of high value. Conversely, if a selected action did not yield reward, it would imply that high-valued areas are located farther away in motor space.

Our simulations demonstrate that decreasing motor variability when reward is plentiful, and increasing it when reward is scarce, is a prudent strategy both for increasing the likelihood of selecting higher-valued actions and thereby improving short-term performance, and for improving the odds of discovering the action with the greatest reward value and thereby enhancing learning and long-term performance. Contrasting our results to studies of decision-making suggests that exploratory search strategies are matched to the particulars of the solution space, which can be markedly different for motor and decision-making tasks. Our simulations showed that an agent that takes advantage of strong correlations in reward landscapes, such as those in our motor task, can effectively resolve the ‘explore-exploit dilemma’ (Figure 4B). This is because optimal strategies for immediate and long-term reward accumulation align rather than compete. Thus, in trial-and-error motor learning tasks immediate and long-term objectives can be reasonably achieved using the same variability regulation policy - which happens to be the one the nervous system implements.

Regulation of variability in static and dynamic task environments

The variability regulation algorithm we describe differs significantly from schemes used in machine learning and robotics to drive reinforcement learning in continuous solution spaces. While most computational studies use fixed levels of exploratory variability [32,42], some algorithms control variability as a linear function of the reward-rate [43,44], while others designate variability as an operant whose optimal level is itself determined by reinforcement learning [45]. The diversity of schemes employed by these studies implies that the regulation of variability is relatively unconstrained. This is likely a consequence of these algorithms being trained in static environments where there is typically a single end-goal for learning. Similar to the case of birdsong, this allows learning context, in which exploratory variability is useful, to be separated in time from a performance context, in which variability is detrimental and can be downregulated or simply turned ‘off’.

In contrast, the mammalian brain implements a regulation strategy optimized for ‘learning on the job’. This strategy comprises a short-term reward-dependent control process and a long-term, perhaps operant, process that tunes the control function to the statistics of the reward landscape. This scheme may provide a blue-print for designing more efficient learning solutions that balance the demands of learning and peak performance in dynamic, uncertain environments in which task goals are constantly changing.

Neural substrates for regulation of motor variability

Where and how might the sophisticated computations that underlie regulation of motor variability be implemented in the brain? The neural circuits implementing the fast variability regulation process must have information about past performance, specifically a reward rate estimate derived from integrating the outcomes of the past ~10 trials. Dynamics in this circuit must also be able to influence the circuits that generate the motor output.

The best studied example of a neural circuit that regulates motor variability is the basal ganglia-forebrain circuit of male songbirds. This pathway, which is necessary for song learning but not for expert song production, is thought to ‘inject’ variability into the main song control pathway [19,46] as a function of tonic dopamine levels in the song-specialized basal ganglia, Area X [47]. An analogous pathway in mammalian brains might be the cortico-basal ganglia circuit that comprises the prefrontal cortex and the dorsomedial striatum [48,49]. Neural activity in both structures is sensitive to past trial outcomes [50–52], and lesions of the dorsomedial striatum lessen the effects of recent performance on phenomena such as response vigor [52]. Interestingly, both dorsomedial striatum and prefrontal cortex receive extensive dopaminergic input [53]. This suggests that tonic dopamine levels, which also encode recent reward history in a graded manner [54], could be the signal through which estimates of recent performance are broadcast to cortico-striatal circuits. Along these lines, prefrontal cortex has also been implicated in the tendency to explore in decision making paradigms [24,26,55].

Active variability regulation in songbirds is implemented by switching the song-specialized basal ganglia circuit between a high and a low variability mode [56]. This raises the question of whether the graded regulation of variability we observe (Figure 2D) could be accomplished within a similar bistable circuit, or whether an intrinsically analog, ‘dial-like’, process must be invoked (Figure S6A). In the former case, the transition probability between the two discrete states must change smoothly as a function of the reward rate estimate in order to explain the graded nature of variability regulation (Figure S6A) [57]. A comparison of our data to predictions derived from both dial- and switch-models (see STAR Methods) show our observations to be more consistent with an analog mechanism (Figure S6B–D).

We found that the reward-dependent regulation of variability, which is sensitive to recent trial outcomes, is influenced by a slower process that estimates task-uncertainty over many sessions and alters the gain of the reward-dependent process in an adaptive manner (Figure 5, S5). The circuits that assess task-uncertainty, should integrate performance and movement history over days-long timescales. This could be yet another task for prefrontal cortex, which is known to encode task-uncertainty in reinforcement learning [25,27,36]. A second possibility is that the brain does not maintain an explicit representation of task uncertainty, but instead treats the gain as another operant parameter [58] and uses a reward prediction error-dependent learning process to determine optimal levels of regulated variability, similar to how we do it in our simulations (Figure 4B).

Having arrived at an algorithmic description of how the brain can regulate variability, our study sets the stage for identifying how this algorithm is instantiated in neural circuitry.

STAR Methods

Lead Contact and Materials Availability

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Bence Ölveczky (olveczky@fas.harvard.edu). This study did not generate new unique reagents.

Experimental Model and Subject Details

The experimental subjects, female Long Evans rats aged 3–5 months old at the beginning of training (n=10, Charles River Laboratories; RRID:RGD_2308852), were trained in our behavioral boxes over periods of 12–18 months. Some animals (n=4) were trained on the task but later excluded because they stopped performing before their datasets had grown to at least 100,000 trials. We note that these animals were not excluded based on any performance criterion other than the fact that their datasets were too small to yield reliable results. The care and experimental manipulation of the animals were reviewed and approved by the Harvard Institutional Animal Care and Use Committee.

Method Details

Behavioral training

Behavioral boxes

Rats were housed in a computerized, fully-automated rat-training facility, described in detail in previous work [11,29]. To construct a manipulandum that rats could press downwards in a single ballistic movement, we modified a 2-axis hall-effect sensor joystick (TS-1D1S00A-1294, APEM Inc.). We swapped its inbuilt spring with one that had reduced stiffness (II-11, Century Spring Corp.) and attached a 2-inch-long threaded rod that functioned as a lever arm (95412A870, McMaster-Carr). To provide a grip, we attached a thumb nut (95150A120, McMaster-Carr) onto the free end of the rod. The joystick was placed 14 cm above the box floor in a horizontal orientation such that the lever rod protruded into the behavioral box from the outside. The lever protruded through a triangular slot that restricted its range of motion to ~14 mm below its resting position and within ±35 degrees angles from the vertical axis. The force required to press the joystick to the bottom of the slot was under 0.02 N. To ensure that the rat only used its paw (and not its nose) to press the lever, we lined either side of the triangular slot with glass plates (2 inch by 1 inch by 1/4 inch) that protruded ~20 mm into the box such that the subject had to reach in-between the plates to access the joystick. A water-spout was placed 5 cm below the joystick within a cylindrical reward port that the rat had to nose-poke into.

Sessions

We scheduled 3 training sessions of 40 minutes duration within the 12-hour period corresponding to the animals’ subjective night-time (6 pm – 6 am), 7 nights a week. Rats performed 309 ± 172 (mean ± SD, n=10 rats) trials per session.

Motor task

All training protocols were implemented in custom software written in C# [29]. At the beginning of training, water-deprived rats were taught to press the joystick downwards to progressively greater distances for a water reward. Once rats had performed 100 successful trials (over the course of a single 40 min session) of a simple distance-pressing task in which they pressed the joystick all the way down to the bottom of the slot (typically within a week), we moved them to the main angle-press task in which rats were trained to modify the angle of their joystick presses. The task was self-paced, and trials were initiated by the rat displacing the joystick at least 2.9 mm from its starting position. To encourage rats to press the joystick in a smooth, ballistic movement, we denoted the point at which the joystick speed dropped under 44 mm/s as the end of the joystick press. At this point, we analyzed the joystick’s 2-d trajectory and determined whether the rat had pressed the joystick beyond the minimum distance (11 mm), had completed the press within the allotted time (500 ms), and if the press-angle was within the reward-bounds that surrounded the target angle. On average, rats satisfied the distance and time requirements on 81 ± 2% and 100% of trials, respectively. To calculate the angle of each press, we computed the angle (θ, measured with respect to the vertical axis) of a regression line that was fit to the joystick trajectory and constrained to pass through the starting position [x₀,y₀], (Figure S1A–B) according to the following equation.

$$\theta ={\tan }^{-1}\left(\frac{{\sum }_i\left(x_i-x_0\right)\left(y_i-y_0\right)}{{\sum }_i{\left(x_i-x_0\right)}^2}\right)$$ (Eq. 1)

…where i indexes the joystick press-trajectory from ‘start’ to ‘end’, as defined above. If the rat was judged to have pressed the joystick correctly, reward availability was signaled by a brief 5 kHz tone. Upon hearing the reward-tone, rats had to nose-poke into the reward port to trigger delivery of a 28 μl water reward. We wanted to ensure that rats approached the joystick from a similar starting position, irrespective of the outcome of the previous trial. Therefore, following completion of a joystick press, we required rats to either perform a nose-poke or wait out a 5 sec time-out before they could initiate the next trial. The time-out period was reset to 5 sec whenever the rat pressed the joystick too early.

The reward boundaries were placed symmetrically around the target angle and their function was to gradually shape the subject’s actions towards the target. The boundaries were updated following sessions in which subjects performed more than 50 trials and had an average reward rate under 30% (poor performance) or over 40% (good performance). The position of the reward boundary for the next session was determined as the 35^th percentile of the distribution of press-angles in the previous session, rank ordered by their distance from the reward target. This boundary update rule functioned to maintain an average reward rate of ~35% across all sessions. As a consequence of this rule, the reward zone was widened whenever performance was poor or a new target was selected and narrowed when performance was good.

In the non-stationary reward context, the target press-angle was updated whenever the subject learned its location, operationally defined by the reward boundaries moving to within 2.3 degrees of the target angle. The new target was randomly chosen within a range of ±20 degrees (from the vertical) with the added constraint that it be at least 2.3 degrees away from the previous target. In the stationary reward context, we switched to a 0 degree target angle and maintained it throughout. We did not present any explicit cues indicating transitions from non-stationary to stationary reward contexts and vice versa.

Probabilistic reward trials

A subset of trials were designated as ‘reward clamp’ trials. On these trials, reward was delivered probabilistically irrespective of the angle of the rat’s joystick press, provided that the press also satisfied the distance and time requirements. The reward clamp trials were administered in two ways: interspersed ‘mini’ reward clamps, or ‘block’ reward clamps lasting between 50–100 consecutive trials. ‘Mini’ reward clamps were initiated randomly on 5% of trials and, once initiated, lasted for 3 consecutive trials. In these clamps, reward was delivered with a probability of 0.5 (which, in practice, translated to a reward rate of 41.1 ± 0.9%, given the additional constraints on press distance and time). Reward probabilities on ‘block’ reward clamps were either 10%, 35% or 75% over the entire block, which translated to reward rates of 9.9 ± 0.6%, 30.8 ± 0.9% and 63.2 ± 1.9%, respectively. Block clamps were administered on a random subset of 3 out of every 8 training sessions and initiated on a random trial ranging between 50–100 trials from the start of a session. Following the end of the 50–100 trial long block clamp, normal training resumed. No mini reward clamps were administered during block clamps. Although the block reward-clamp altered the relationship between the press-angle and reward over several trials, it did not affect rat’s engagement with the task as evidenced by the number of trials performed in sessions with and without block reward-clamps (307 ± 53 and 317 ± 55 trials in non-clamp and medium reward-rate block clamp sessions, respectively; p = 0.26 by paired t-test).

Reinforcement learning simulations

Reinforcement learning model

We modeled a motor learning task in one-dimensional, continuous motor space using a policy-gradient reinforcement learning algorithm [31,32,59]. Movements (x) were drawn from a stochastic Gaussian policy with mean μ and variance comprising two components – exploratory variability ${\epsilon }_e\sim \mathcal{N}\left(0,{\sigma }_e^2\right)$ and motor noise ${\epsilon }_n\sim \mathcal{N}\left(0,{\sigma }_n^2\right)$:

$$x_t={\mu }_t+{\epsilon }_{e,t}+{\epsilon }_{n,t}$$ (Eq. 2)

where t is trial-number in a simulated session and $\mathcal{N}\left(\mu ,{\sigma }^2\right)$ references a normal distribution with mean μ and variance σ². Binary reward r ∈ {0,1} was available only within a circumscribed zone of width w centered at the origin. Due to the additional requirement for satisfying the minimum press-distance requirement, rats did not achieve 100% reward when their press-angles were within the reward zone. To reflect this, we set the probability of reward within the reward zone to a value $\mathcal{R}$ that was measured using experimental data.

$$p(r=1|x)=\{\begin{array}{ll}\mathcal{R},& -w/2\ge x\ge w/2\\ 0,& \mathrm{otherwise}\end{array}$$ (Eq. 3)

The agent updated the mean movement policy in the direction of the reward-zone using an on-policy learning rule:

$${\mu }_{t+1}={\mu }_t+{\alpha }_{\mu }{\delta }_t{\epsilon }_{e,t}$$ (Eq. 4)

where ${\delta }_t=r_t-{\overline{r}}_t$ represents the reward prediction error and α_μ is the leaning rate for the policy mean. The average reward-rate (${\overline{r}}_t$) was in turn estimated from the sequence of rewards using the following learning rule:

$${\overline{r}}_{t+1}={\overline{r}}_t+{\alpha }_r{\delta }_t$$ (Eq. 5)

where α_r is a learning-rate parameter for the average reward rate.

We implemented reward-dependent modulation of variability by designating a variability control function ($\mathit{\varsigma }\in {\mathbb{R}}_{\ge 0}^d$) to set levels of exploratory variability as a function of the reward rate estimate. We discretized the reward rate in the form of a state vector $\overline{\mathit{R}}\in {\left\{\mathrm{0,1}\right\}}^d$ (where the bin corresponding to the analog reward rate estimate ${\overline{r}}_t$ is set to 1 and the other d − 1 bins are set to 0). The variability control function was updated over several sessions to maximize future reward. To help learn optimal variability control functions, we introduced parameter space variability ${\epsilon }_{\sigma }\sim \mathcal{N}(0,{\sigma }_{\sigma }^2)$ [60]:

$${\sigma }_{e,t}^2={\mathit{\varsigma }}_t\cdot {\overline{\mathit{R}}}_t+{\epsilon }_{\sigma ,t}$$ (Eq. 6)

To regulate the time-scale over which the variability control policy optimized future reward, we introduced eligibility traces (E_σ) [32,35] which maintain a trace of parameter variations over future trials:

$${\mathit{E}}_{\sigma ,t+1}=\lambda {\mathit{E}}_{\sigma ,t}+{\epsilon }_{\sigma ,t}{\overline{\mathit{R}}}_t$$ (Eq. 7)

where λ is the decay-rate of the eligibility trace and can be set to match a specific time-scale (T ∈ {1,100}) by the formula λ = 1 − 1/T [32]. The variability control function was then modified by the learning rule:

$${\mathit{\varsigma }}_{t+1}={\mathit{\varsigma }}_t+{\alpha }_{\sigma }{\delta }_t{\mathit{E}}_{\sigma ,t}$$ (Eq. 8)

where α_σ is a learning-rate parameter for the variability control function and δ_t is the reward-prediction error ${\delta }_t=r_t-{\overline{r}}_t$. At each update, we ensured that no element of the variability control function was less than 0.

Simulations

We simulated trial-and-error motor learning on the 1-d motor task by individual rats using the reinforcement learning model described above. Sessions were 150 trials long and session-specific conditions such as the starting position relative to the reward target (μ₀), width of the reward-zone (w) and probability of reward within the reward zone ($\mathcal{R}$) were sampled from individual rat datasets. Key parameters of the policy-gradient reinforcement learning models were also derived from analysis of individual rat datasets. The magnitude of motor noise ${\sigma }_n^2$ was equated to measured levels of unregulated motor variability (Figure 3D). The learning-rate for the baseline reward-rate (α_r) was calculated from the time-scale (τ) of the experimentally observed decay of the effect of single-trial outcomes on variability i.e. the inferred memory window for reinforcement on past trials (Figure 1F) using the expression: α_r = 1 − exp(−1/τ). To fit the learning rate for the policy mean (α_μ) for individual rats, we simulated rats’ performance on the motor task for a range of learning rates using experimentally derived variability control functions (Figure 2D). We then identified the parameter value that minimized the mean-squared error between simulated policy means (μ_t) and experimentally observed press-angles (θ_t) in all experimental sessions that did not have a block-clamp condition (for our datasets, α_μ = 0.23 ± 0.19, mean ± SD across 10 rats).

To derive optimal variability control functions, we ran these simulations over 5 million, 150-trial long ‘sessions’ randomly sampled from individual rats’ experimental datasets. For the first session, the variability control function (sampled at d = 11 discrete bins) was randomly initialized to values between 0.5 and 1.5 deg². Subsequent updates to the control function over the course of each session were carried forward to the next session. To minimize the variance of these updates, we averaged updates to variability control functions from 100 independent runs for every ‘session’. Exploratory variability (σ_σ) and the learning rate (α_σ) for learning the variability control function were set to values of 0.25 and 0.05, respectively. To modulate the gain of the optimized variability control functions, we multiplied them by a scaling factor to match a desired gain value.

Quantification and Statistical Analysis

Data processing

All experimental analysis and simulations were done using custom-written scripts in Matlab (vers. 2017b and 2018b, Mathworks). The variance of press-angles was calculated in moving windows of 5 trials. To avoid errors in estimating angles of incomplete joystick presses, we excluded any variability windows that encompassed trials on which the subject did not press the joystick more than 5.5 mm from its starting position (i.e. half the press distance threshold for a successful trial). This rule excluded 2.7 ± 0.5% and 15.6 ± 2.3% of trials and variability measurements, respectively. We also excluded the first 200 sessions (~2.2 months) of training when rats were presumably familiarizing themselves with the task, from all analyses. Asymptotic levels of angle variability in the block reward clamp were computed by averaging the moving window estimates of variability after 19 trials from the start of each block clamp.

Effect of single-trial outcome on variability

To analyze the single-trial effect of reward on motor variability, we computed differences between the reinforcement triggered-averages of press-angle variability for ‘reward’ and ‘no reward’ conditions. These reinforcement triggered-averages were calculated for each rat by extracting rolling windows of angle variability measurements from all relevant sessions, grouping the windows based on the outcome (e.g. rewarded versus unrewarded) of the ‘trigger’ or ‘conditioned’ trial (numbered trial 0 in figures), and then averaging within each condition. We then subtracted the reward-triggered variability average from the no reward-triggered variability average to determine the effect of a single-trial change in outcome on motor variability. Note that these rolling windows did not cross session-to-session boundaries. Within the rolling window, we did not consider any variability measurements that included the trigger trial (i.e. those centered on trials −2 to +2 relative to the trigger trial).

Probabilistic reward analysis

When analyzing the average effect of probabilistic reinforcement, we denoted all mini and block reward clamp trials that satisfied the press-distance condition (11 mm) as trigger trials. Since average levels of variability differ between the mini-clamp and each of the 3 block-clamp manipulations, we computed single-trial changes in variability between no reward and reward conditions separately for each manipulation. We then computed a grand weighted average (weighted by number of trials) across the 4 manipulations to determine the average variability effect of single probabilistic reward trials.

Matching analysis

We used a propensity score matching analysis [61] to determine the effect of single-trial outcome on variability while statistically controlling for long-term reward context. First, we fit a logistic regression model to predict trial outcomes (r_t ∈ {0,1}) given the outcomes of 50 past and 50 future trials (r_t+s).

$$\mathrm{logit}(r_t)=\sum _{s\notin 0}{\beta }_s{r}_{t+s}+{\beta }_0$$ (Eq. 9)

where s ∈ {−50,−49,…,−1,1,2,…,50} represents the lag from trial t, logit represents the logistic function and β_s represents the coefficients of the model. We used the fitted model’s predictions of reinforcement (${\sum }_s{\beta }_s{r}_{t+s}+{\beta }_0$), termed the propensity score, as an estimator for the probability of receiving reward. Note that we used both past and future reward outcomes to compute the propensity score because of the acausal relationship between long-term reward and reinforcement on the conditioned trial (as seen in Figure S1F–G). We stratified rolling windows of variability measurements (see ‘Effect of single-trial outcome on variability’), based on their propensity scores on the trigger trial, into 20 equal-proportion bins. Then, within each propensity score bin, we computed the difference between the no reward- and reward-triggered averages of variability. Finally, we computed the average variability difference (weighted by the geometric mean of the number of rewarded and unrewarded trials per bin) across propensity score bins to measure the variability response to single-trial changes in reinforcement.

Combining probabilistic reward and matching analyses

To combine the results of probabilistic reward and matching analyses, we computed a grand, weighted average of the differences in variability due to single-trial outcome across (a) 20 propensity score bins, (b) mini reward-clamps and (c) 3 block reward-clamps (24 groups in total). When computing the grand average, we weighted each group by the geometric mean of the number of reward and no-reward trials.

Variability control functions

Regulation of variability by a multi-trial reward rate estimate

We computed a running estimate of the reward rate (${\overline{r}}_t$) for individual rats as a weighted average of past trial outcomes using the following equation.

$${\overline{r}}_t={\overline{r}}_{t-1}+\left(1-exp\left(\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.\right)\right){\delta }_{t-1}$$ (Eq. 10)

Here, τ is the time-constant of an exponential fit to the decay of the rat’s single-trial effect and ${\delta }_t=r_t-{\overline{r}}_t$ is the reward prediction error. To calculate the dependence of the single-trial variability effect on the reward rate estimate, we grouped rolling windows of variability measurements (see ‘Effect of single-trial outcome on variability’) into 7 bins based on the reward rate estimate computed just prior to the trigger trial (i.e. after trial −1 in each rolling window). Note that, unlike in the case of propensity score matching, we only used the outcomes of past trials to determine the reward rate grouping. This was done so that we could determine the causal influence of the reward rate on future motor variability. Following this, we calculated the effect of single-trial outcome on variability (using the probabilistic reward trials and matching techniques described above) using the rolling windows corresponding to each reward rate bin. Note that, due to further subdivision of data by reward rate in this analysis, we used 10 propensity score bins instead of the usual 20 (and we still used the outcomes of 50 past and 50 future trials to compute propensity scores). To summarize the magnitude of the single-trial variability effect (as in Figure 2C), we calculated the average difference in variability of press-angles on trials 1–10 after the trigger trial within each reward rate estimate group.

Calculating variability control functions

We calculated variability control functions (i.e. regulated variability versus reward rate estimate curves)

$${\sigma }_{\overline{r}}^2=f\left(\overline{r}\right)$$ (Eq. 11)

…for individual rats by integrating their single-trial variability effects as a function of the reward rate estimate ($\overline{r}$). The single-trial variability effect is essentially the average change in motor variability (Δσ²) in response to a change in single-trial outcome (Figure S3A). By calculating how much a single-trial outcome would alter a rat’s estimate of its reward rate ($\mathrm{\Delta }\overline{r}$), we can compute the slope of the variability control function ($\mathrm{\Delta }{\sigma }_{\overline{r}}^2/\mathrm{\Delta }\overline{r}$) as a function of the reward rate. Since rats weigh reinforcement on past trials in an exponential manner, altering a single-trial’s outcome from no reward to reward would change the future reward rate estimate, after a lag of s trials, by:

$$\mathrm{\Delta }{\overline{r}}_s=\left(1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-1/\tau \right)\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-\left(s-1\right)/\tau \right)$$ (Eq. 12)

where τ is the time-constant of the exponential decay of the single-trial variability effect (as in Figure 1F). Since we measured variability over multiple trials (1 through 10) after a rolling window’s trigger trial, we also averaged the resultant change in the reward rate estimate (due to change in outcome of the reinforcement conditioned trial) over delays spanning the entire variability measurement window: $\mathrm{\Delta }\overline{r}=\sum _{s=1}^{10}\mathrm{\Delta }{\overline{r}}_s/10$. Next, we divided the observed change in variability by the change in reward rate estimate due to single trial outcome to compute the slope of the variability control function at each reward rate bin ($\mathrm{\Delta }{\sigma }_{\overline{r}}^2/\mathrm{\Delta }\overline{r}$). We then computed the cumulative integral of these slope measurements with respect to the reward rate estimate (assuming the constant of integration to be 0) in order to determine the rat’s variability control function (${\sigma }_{\overline{r}}^2$). The variability control function defined in this way is essentially a look-up table corresponding to 7 discrete values of the reward rate.

Gain of variability control functions

Under the assumption that a simple scaling factor can largely account for differences in the variability control functions across rats, we computed this gain or scaling factor for individual rats. We first averaged variability control functions across rats (n = 10, indexed by i) and normalized the average function to its maximum value to yield an archetypal characteristic variability control function (${\tilde{\sigma }}_{\overline{r}}^2$).

$${\tilde{\sigma }}_{\overline{r}}^2=\frac{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.\sum _{i=1}^n{\sigma }_{\overline{r},i}^2}{\max \left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.\sum _{i=1}^n{\sigma }_{\overline{r},i}^2\right)}$$ (Eq. 13)

The gain of the variability control function was then defined for each rat (i) as the scaling factor that minimized the least-squares error between its variability control function (${\sigma }_{\overline{r},i}^2$) and the archetypal variability control function (${\tilde{\sigma }}_{\overline{r}}^2$).

$${gain}_i=\frac{\sum _{\overline{r}}\left({\tilde{\sigma }}_{\overline{r}}^2{\sigma }_{\overline{r},i}^2\right)}{\sum _{\overline{r}}{\left({\tilde{\sigma }}_{\overline{r}}^2\right)}^2}$$ (Eq. 14)

Significance test for change in gain

To determine whether the average gain of variability control functions was significantly altered by conditions such as the reward context, we used an F-test to determine whether fitting separate gain parameters (eq. 14) to the variability control functions derived in each condition resulted in significantly lower error than fitting a single gain parameter to the variability control functions from both conditions. Since we wanted to determine whether there was a significant change in the average gain between two conditions, we fit a single gain parameter to the population of variability control functions, unlike in previous analysis where we fit gains to individual variability control functions. For this analysis, we computed a single archetypal variability control function (eq.13) by averaging together the variability control functions across all rats and for both conditions.

Levels of unregulated motor variability

To determine individual rats’ levels of unregulated variability, we measured asymptotic levels of variability (following the 19^th trial from the start of the block clamp) in the low, medium and high reward rate block clamps. Measurements of variability in the block reward-clamp comprise both regulated and unregulated components. Therefore, the level of unregulated motor variability was calculated as the average difference between the variability control functions (eq. 11) and the observed levels of variability in the block clamp, at the 3 reward rates imposed in the block-clamp.

Predicting variability from reward

To generate trial-to-trial predictions of motor variability from a sequence of rewards, we first computed a running estimate of the reward rate (${\overline{r}}_t$) using equation 10 and then applied the rat’s variability control function (eq. 11) to the reward-rate estimate to yield the predicted variability (${\sigma }_{\overline{r}}^2$). Since we compute each variability control function as a look-up table for discrete reward rate estimates, we used spline interpolation to generate predictions for intermediate reward rates.

Estimating reward modulation of mean-drift rates

To minimize the interference of learning-related drifts, we measured the random drift rate of the mean press-angle during block reward-clamps in which reward is independent of the press-angle. We first measured the root mean-squared (RMS) deviation in press-angle between the first trial (trial 0) and subsequent trials (t) in the block reward-clamp, over all clamp sessions (indexed by s) within a specific reward-rate condition (i.e. low, medium or high reward rates).

$${RMSD\left(\theta \right)}_t=\sqrt{\frac{1}{S}\sum _{s=1}^S{\left({\theta }_{t,s}-{\theta }_{0,s}\right)}^2}$$ (Eq. 15)

The RMS deviation in press-angle comprises both a mean-drift component as well as a white-noise component which is due to the sum of the variance of the press-angle distribution at trial 0 and the lagged trial t ($\sqrt{{\sigma }_{t,s}^2+{\sigma }_{0,s}^2}$). To measure the white-noise contribution (W_t) to the RMS deviation, we first detrended the press-angle data by subtracting a local estimate of the median press-angle ($\overline{{\theta }_{t,s}}$, computed over a window of 11 trials) and calculated the average sum of the squared residuals at different trial lags.

$$W_t=\sqrt{\frac{1}{S}\sum _{s=1}^S{\left({\theta }_{t,s}-\overline{{\theta }_{t,s}}\right)}^2+{\left({\theta }_{0,s}-\overline{{\theta }_{0,s}}\right)}^2}$$ (Eq. 16)

Subtracting the white-noise component from the RMS deviations revealed the true drift in the mean of the angle-press distribution (D_t).

$$D_t=\sqrt{{RMSD\left(\theta \right)}_t^2-W_t^2}$$ (Eq. 17)

As the drift of a random walk process necessarily increases with trial lag, we calculated the per-trial drift-rate of the mean press-angle by regressing the squared mean-drift ($D_t^2$) against trial lag (t) and calculating the slope of the best-fit line. Note that the intercept of the best-fit line was constrained to pass through (0,0).

Measuring performance improvement

We measured performance improvement (ΔR_t) as the difference between performance on the preceding trial (i.e. reward: r_t−1), and future performance (average of temporally discounted future rewards: R_t) computed over trial-horizons T ∈ {1,10,100}.

$$\mathrm{\Delta }{R}_t=R_t-r_{t-1}=\left[\left(\sum _{s=0}^{N-t}{r}_{t+s}{\lambda }^s\right)/c_t\right]-r_{t-1}$$ (Eq. 18)

where s represents the trial lag, N is the number of trials to consider in each session (150 trials), λ = 1 − 1/T is a temporal discounting factor that sets the time-horizon of the performance measurement, and $c_t=\sum _{s=0}^{N-t}{\lambda }^s$ is a normalization factor that keeps the value of R_t between 0 and 1. We chose to measure future performance as the temporally discounted average of future rewards to align the performance improvement metric with the procedure used to derive optimal variability control functions (eqns. 7–8). Our results are essentially unchanged if we instead define future performance as a simple average of future rewards over a fixed time-horizon ($R_t=(\sum _{s=0}^{T-1}{r}_{t+s})/T$). The ΔR_t measurement was averaged over the first N − T trials in each session and over all sessions to compute the average improvement in performance for a simulation or rat. We ignored the first 2 trials of each session to disregard the initialization of simulation parameters. We restricted this analysis to experimental sessions that had at least 150 trials (74% of sessions).

Dial versus Switch analysis

To determine whether changes in motor variability are driven by an underlying continuous ‘dial-like’ or discrete ‘switch-like’ process, we narrowed our focus to press-angle differences between consecutive trials (θ_t+1 − θ_t), grouped by the reward rate estimate computed at trial t. For this analysis, we either used data from all trials or just the block reward-clamp trials. If variability was regulated by dial-like process, we would expect distributions of angle-differences within all reward rate bins to be variance-scaled versions of a common underlying distribution. However, in case of a switch-like process, we would expect distributions of angle-differences at intermediate reward rates to be mixtures of the distributions at the highest and lowest reward rates. For each model, we generated expected distributions of press-angle differences at intermediate bins of the reward rate estimate by resampling data from the maximum and minimum reward rate bins. In case of the switch model, we empirically determined the relative proportion of samples to draw from the two extreme bins in order to match the variance of the observed data distribution in the intermediate bin. In contrast, to generate predictions for the dial model, we drew equal proportion of samples from the maximum and minimum reward rate bins but only after transforming these distributions to have unit variance. We then scaled the combined, normalized distribution to have the same variance as that of the observed distribution of press-angle differences. Having generated the expected distributions of angle-differences under both ‘switch’ and ‘dial’ models, we then compared these predictions to the observed distributions of angle-differences to determine which model better fit the data. We used the Kullback-Liebler (KL) divergence as a measure of distance between the observed and predicted distributions, under each model. In each reward rate bin, we used a two-sided paired t-test to determine whether there was a significant difference in the KL divergence between the data and the switch versus dial model distributions, and then used Fisher’s method to combine these p-values across all reward rates.

Data and Code Availability

The datasets/code supporting the current study have not been deposited in a public repository because of their large size, but are available from the corresponding author on request.