Information theoretic evaluation of satellite soil moisture retrievals

Abstract

Microwave radiometry has a long legacy of providing estimates of remotely sensed near surface soil moisture measurements over continental and global scales. A consistent assessment of the errors and uncertainties associated with these retrievals is important for their effective utilization in modeling, data assimilation and end-use application environments. This article presents an evaluation of soil moisture retrieval products from AMSR-E, ASCAT, SMOS, AMSR2 and SMAP instruments using information theory-based metrics. These metrics rely on time series analysis of soil moisture retrievals for estimating the measurement error, level of randomness (entropy) and regularity (complexity) of the data. The results of the study indicate that the measurement errors in the remote sensing retrievals are significantly larger than that of the ground soil moisture measurements. The SMAP retrievals, on the other hand, were found to have reduced errors (comparable to those of in-situ datasets), particularly over areas with moderate vegetation. The SMAP retrievals also demonstrate high information content relative to other retrieval products, with higher levels of complexity and reduced entropy. Finally, a joint evaluation of the entropy and complexity of remotely sensed soil moisture products indicates that the information content of the AMSR-E, ASCAT, SMOS and AMSR2 retrievals is low, whereas SMAP retrievals show better performance. The use of information theoretic assessments is effective in quantifying the required levels of improvements needed in the remote sensing soil moisture retrievals to enhance their utility and information content.

1. Introduction

Soil moisture plays an important role in modulating the exchanges of water and energy at the land atmosphere interface and profoundly influences the spatial and temporal variability of weather and climatic conditions (Koster et al. (2004); Seneviratne et al. (2010)). Accurate characterization of soil moisture is, therefore, important for applications such as flood/drought forecasting, weather and climate modeling, agricultural and water resources management. Observations of soil moisture from ground measurements tend to be sparse and are often not sufficient to capture the spatial heterogeneity and variability of soil moisture at larger spatial scales, required for such applications. Space-borne measurements of soil moisture, primarily from microwave (MW) remote sensing, provide an alternative for developing observations of soil moisture over larger spatial extents (Jackson (1993); Njoku and Entekhabi (1995)). In the past several decades, near surface soil moisture retrievals have become available from a number of low-frequency (C, X, Ku- and L-band) passive and active microwave sensors (Wagner et al. (2003); Njoku et al. (2003); Wen et al. (2003); Owe et al. (2008); Kerr et al. (2010); Entekhabi et al. (2010)).

Microwave soil moisture sensors exploit the fact that the emission of the land surface is affected by variables such as surface temperature, roughness, vegetation and soil moisture. The influence of soil moisture is most prominent at low frequencies (~10 – 1 GHz, making it the ideal range of satellite remote sensing (Njoku and Kong (1977); Jackson et al. (1982); Ulaby et al. (1986)). Unlike the visible and infrared sensors, the microwave sensors are not limited by cloud cover and nighttime conditions. The observations can be made at any time of the day and are not dependent on solar illumination (Jackson et al. (1996)). Longer wavelengths (L-band; 1 –2 GHz) also allow for deeper penetration into the soil and reduce the influence of vegetation in attenuating the soil moisture signal (Jackson et al. (1982)). The active instruments can provide measurements at higher spatial resolutions than the passive microwave instruments, though radar systems are more strongly affected by the local topography, roughness and vegetation than passive radiometer systems (Entekhabi et al (2010); Lakshmi (2013)). However, studies such as Brocca et al (2011) have suggested that ASCAT can outperform passive microwave based retrievals over areas with moderate vegetation. Passive observations on the other hand, are more impacted by spatial heterogeneity and scaling effects because of poor spatial resolution. The spatial resolution of the passive microwave soil moisture observations is typically coarse (~25 to 50 km), with the satellite foot-print size increasing with wavelength and altitude. The presence of snow cover, frozen soil and precipitation events also limits the skill of the soil moisture retrievals (Parinussa et al. (2011)).

Due to the differences in the spatial and temporal span of different MW instruments and due to the limited availability of reliable ground measurements, a consistent evaluation of soil moisture remote sensing datasets is difficult. Land surface model climatology has often been used the reference to address the climatological differences between different retrievals when developing multi-sensor products (Liu et al. (2011b)) and for consistent evaluations of multiple products. In a recent study, Kumar et al. (2015) has shown that such approaches lead to the loss of valuable signals and cause the statistical properties of the retrieval products to be similar to that of the reference datasets. Therefore, performance measures not reliant on the availability of ancillary soil moisture data can be useful for characterizing and assessing the quality of the soil moisture retrieval datasets. As a result, studies have used indirect approaches such as triple collocation (TC; Stoffelen (1998); Dorigo et al. (2010)) and spectral fitting (SF; Su et al. (2014)) to assess the relative quality of global soil moisture retrievals. TC comparisons involve three different soil moisture products (often a mix of satellite soil moisture retrievals and land surface model estimates), with assumptions of linearity (between the true soil moisture and observations), signal and error stationarity, error orthogonality and independence of errors in the constituent datasets (Gruber et al. (2016b)). Recent studies have examined the applicability of these assumptions for soil moisture datasets (Yilmaz and Crow (2014)) and have proposed enhancements to address the limitations imposed by these assumptions, making it a powerful method for global soil moisture evaluation (Zwieback et al. (2013); Gruber et al. (2016b,a). The SF error estimator, based on the method developed by Su et al. (2013) for de-noising satellite soil moisture datasets, estimates the stochastic random errors by comparing the spectral properties of a given soil moisture time series and a linearized water balance model. This method also does not require ancillary datasets and was shown to provide error estimates comparable to those from TC.

Similar to these stand-alone assessment methods, here we present the use of information theoretic and autoregressive analysis of time series data for quantifying errors and information content of remote sensing retrieval datasets from a number of recent soil moisture missions. Information theory measures, originally proposed by Shannon (1948), consider the stochasticity in time series data as sources of information. A key information theoretic measure is entropy, which quantifies the information content or randomness associated with the probability distribution of the data. Similarly, temporal measures of complexity rooted in information theory can be used to discriminate datasets based on time series complexity. Entropy and complexity provide separate measures of information by characterizing the randomness and state changes within a given time series of the data. Entropy is a measure of uncertainty, which is low for periodic sequences and high for random processes. On the other hand, complexity is a measure that is low for both periodic and random sequences, but high for sequences that are not easy to describe with a minimal set of parameters (Lange (1999)). Such measures have been employed for comparing model outputs of soil moisture (Pachepsky et al. (2006)), space-borne soil moisture retrievals (Nearing et al. (2017)), runoff and precipitation measurements from different catchment systems (Lange (1999); Hauhs and Lange (2008)) and ecological systems (Parrott (2010)). A key advantage of information theoretic methods is that they enable the quantification of hidden patterns and structures of the data without requiring ancillary or independent data.

In addition to the use of information theoretic measures, we also employ time series red noise spectrum analysis to develop estimates of accuracy. Vinnikov et al. (1996) employed a first-order Markov process model framework to evaluate observational soil moisture data, which was extended by Dirmeyer et al. (2016) in a recent study to compare measurement errors from different in-situ soil moisture observational networks. Here we apply this method for comparing measurement errors associated with remote sensing soil moisture retrievals. Similar to the information theoretic measures, a key advantage of this approach is that it does not require specific validation or independent reference data. The simultaneous development of information theoretic and measurement error estimates allows the comparison of associated tradeoffs in accuracy, uncertainty and complexity.

The article is organized as follows: Section 2 presents the details of the datasets and the evaluation approaches. The application of the information theory methods to the remote sensing soil moisture retrievals is described in Section 3. Section 4 provides a summary and discussion of the major conclusions of this study.

2. Approach

2.1. Methods

The information theoretic measures are developed by treating the time series data as a symbol sequence with a finite number of states. The standard approach is to categorize the time series data into a binary string (“symbols”) (Lange (1999); Pachepsky et al. (2006)), by encoding values above and below the median (for time series at each grid point), as 1 and 0, respectively. The entropy and complexity measures are then computed based on the probabilities of observing patterns of states/words (a group of L consecutive symbols) within the sequence. In this article, we use three symbol states (L=3), consistent with prior studies (Pachepsky et al. (2006); Pan et al. (2011)). These include the probability of occurrence of a given state i (p_L,i) as well as the second order probability (p_L,ij) of observing state i next to j. For binary symbol sequences, there are 2^L possible words of length L. (For example, if an encoded symbol string starts as ‘0011’, then the first word is ‘001’, which transitions to the second word ‘011’ and so on.)

Shannon entropy is the expected value of the information contained in a symbol sequence. The metric entropy is specified as the normalized measure of Shannon entropy for states of size L and is defined as:

$$H(L)=-\frac{{\sum }_{i=1}^{2^L}{p}_{L,i}{\mathit{log}}_2{p}_{L,i}}{L}$$ (1)

H(L) ranges between 0 (for constant sequences) and 1 (for uniformly distributed random sequences).

The fluctuation complexity (Bates and Shephard (1993)), which measures the spread between information within a symbol string between consecutive states is expressed as:

$$C(L)=\sum _{i,j}^{2^L}{p}_{L,ij}{\left({\mathit{log}}_2\frac{p_{L,i}}{p_{L,j}}\right)}^2$$ (2)

C(L) can be thought of as a measure of the ordering of states within a symbol sequence, with high and low values associated with complex and simple orderings, respectively. The fluctuation complexity, therefore, is a measure of the extent of the changes in information gain or loss in a time series and it approaches zero for signals with limited probable states (Pan et al. (2011)).

Note that both the choice of the classification and the length of the words have an impact on the metrics that are computed. The use of a finer classifications (rather than wet and dry) and the use of larger number of words enables a more granular detection of the entropy and complexity measures, but requires longer and consistent time series. Though the use of the three-symbol states in this study limits the granularity of the soil moisture changes detected by the information theory measures, they are helpful in examining the general trends across various remote sensing datasets.

The analysis of measurement errors used in this study is based on the fact that soil moisture, due to its memory, can be described as a first order Markov process (Delworth and Manabe (1988)). The lagged autocorrelation of soil moisture (r(τ)) reduces exponentially with time:

$$r(\tau )=e^{-\text{λ}\tau }$$ (3)

where λ is decay frequency and τ is the time lag. Due to the presence of measurement errors, a linear regression of ln(r) vs τ does not pass through τ = 0, r=1. Therefore, the displacement term a of the correlation at τ = 0 can be used to compute estimates of measurement error (Vinnikov et al. (1996)). The relative measurement error (ϵ) can be expressed as the square root of the fraction of the random error variance and the variance of soil moisture, as follows:

$$ϵ=\sqrt{\left(\frac{a}{1+a}\right)}$$ (4)

In other words, ϵ is the root mean square (RMS) of the measurement error normalized by the standard deviation of soil moisture. This statistical model assumes that soil moisture evolution can be represented by a first-order ordinary differential equation (ODE) driven by white-noise precipitation forcing (Delworth and Manabe (1988)). Essentially the model assumes that noise quantified here is that which does not fit the first order ODE. In the analysis below, the error estimates are generated using autocorrelations at lags of 1, 2 and 3 days.

2.2. Data

Retrievals from five recent satellite soil moisture microwave instruments are used in this study. They include: (1) the Advanced Microwave Scanning Radiometer-Earth Observing System (AMSR-E) aboard the Aqua satellite, (2) the Advanced Scatterometer (ASCAT), a C-band active microwave remote sensing instrument aboard the Meteorological Operational (METOP) satellites, (3) the Soil Moisture Ocean Salinity (SMOS) mission, (4) the Advanced Microwave Scanning Radiometer 2 (AMSR2) onboard the Global Change Observation Mission-Water (GCOM-W) satellite, and (5) the Soil Moisture Active Passive (SMAP) mission. Except for AMSR-E, which stopped functioning in October 2011, all these instruments are currently providing measurements of surface soil moisture. Soil moisture retrievals are generated from the raw measurements using different retrieval algorithms and systems. The AMSR-E retrievals with the Land Parameter Retrieval Model (LPRM) algorithm (Owe et al., 2008) is used here as prior studies have quantified better performance of AMSR-E LPRM data relative to other available AMSR-E retrieval products (Rudiger et al. (2009); Champagne et al. (2010); Liu et al. (2011a)). The Soil Moisture Operational Products System (SMOPS; Liu et al., 2012) of NOAA/NESDIS is used for obtaining soil moisture retrievals from the backscatter measurements acquired by ASCAT and the L-band radiometer measurements of SMOS. Note that the ASCAT retrievals available through SMOPS are the same as the Near Real Time (NRT) retrievals from EUMETSAT, designed to meet the latency requirements of the operational Numerical Weather Prediction (NWP) community. The SMOS retrievals in SMOPS are produced through a single channel retrieval algorithm based on Jackson (1993). The SMOPS product is used for operational soil moisture data assimilation at several agencies around the world due to its NRT availability. The AMSR2 retrievals (Level 3 products) from the Japan Aerospace Exploration Agency (JAXA; Fujii et al., 2009; Koike, 2013) are used in this study as they have been shown to perform better compared to other available retrieval products (Bindlish et al. (2017)).

The SMAP mission consists of two instruments, a L-band high resolution radar (1 km) and a coarse-resolution radiometer (40 km). The SMAP radar encountered an anomaly a few months after launch and is currently inoperable. As a result, in this study we use the level 3, coarse resolution (36 km) passive microwave measurements (L3_SM_P; O’Neill et al. (2012); Chan et al. (2016)) available through the National Snow and Ice Data Center (NSIDC). The temporal extents of the data sets used in this study are as follows: AMSR-E data from June 2002 to October 2011, ASCAT from January 2007 to December 2016, AMSR2 from July 2012 to December 2016, SMOS from April 2012 to December 2016 and SMAP from April 2015 to December 2016. To ensure a reasonable temporal continuity in these datasets, gaps of less than 3 days are filled using a 1-d discrete cosine transform Wang et al. (2012) method, consistent with the strategy used in Su et al. (2013). Unlike Dirmeyer et al. (2016), where interpolation was used to fill gaps of less than 10 days, we used a shorter time window to ensure that the temporal interpolation itself does not significantly impact the computation of the metrics. As the temporal gaps and irregular sampling of remote sensing datasets are intrinsic to these product, we omit analyses that reconciles these differences to a common repeat period.

3. Results

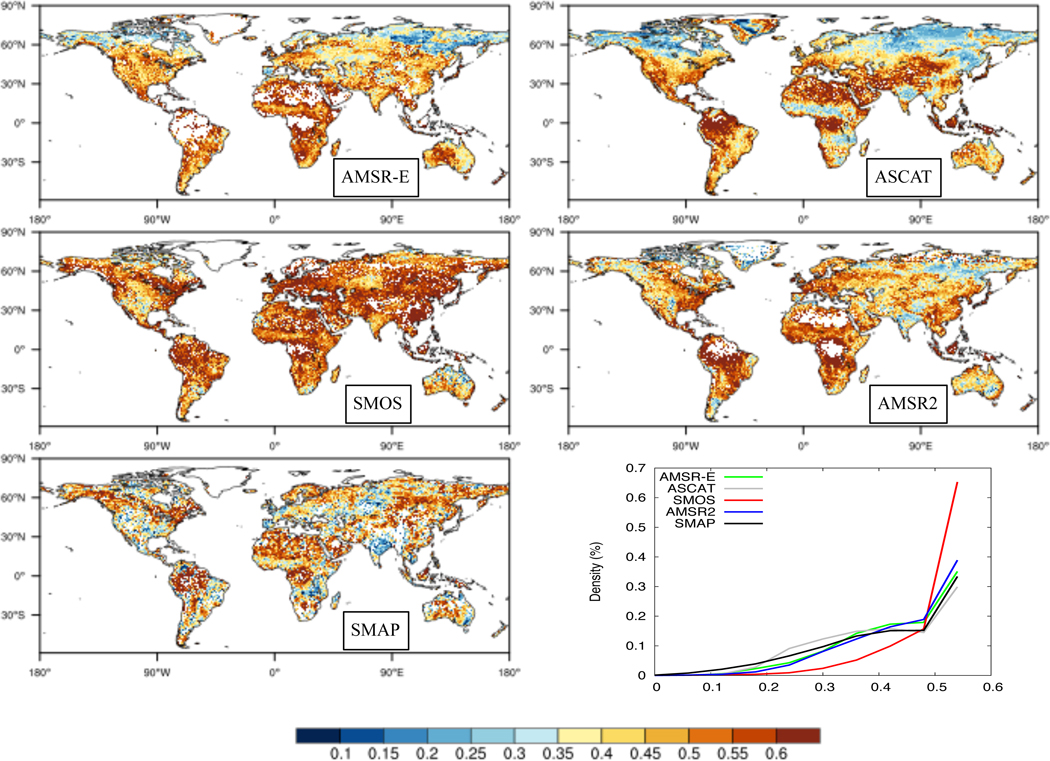
Figure 1 shows the maps of relative measurement error and its distribution for soil moisture retrievals from each sensor. The data quality flags provided with each sensor are employed in screening the data values used in the comparisons. For example, a subset of data locations that conform to the recommended Quality Assessment (QA) classifications (‘good retrievals’) of the SMOPS system is employed in the comparisons. The spatial patterns in Figure 1 show a strong signal of vegetation density with larger errors over areas with thick vegetation (e.g., Amazon, Congo, Eastern U.S.) and smaller errors over Savannas and Arid regions (e.g., India, Western U.S.). Compared to the SMOS retrievals, the ASCAT retrievals show larger errors over arid regions of the world (Sahara, Western U.S., deserts of Australia). This is consistent with prior studies (Wagner et al. (2007); Gruhier et al. (2010)) that also reported that the scatterometer retrievals are less accurate than the radiometer retrievals over dry regions. This is due to the fact that over dry environments when the soil dries out completely, the scattering contributions from surface inhomogeneities impact the soil moisture retrievals more than the soil moisture content itself (Wagner et al. (2012)). The relative measurement error computations in Figure 1 confirm these previous findings.

Figure 1:

Relative measurement error (ϵ) for soil moisture retrievals from AMSR-E, ASCAT, SMOS, AMSR2 and SMAP. The lower right figure shows the distribution of ϵ for each sensor.

The relative measurement error of in-situ soil moisture datasets reported in Dirmeyer et al. (2016) showed a range of 0.1–0.3 for most measurement systems with larger errors for systems employing sensors just above the land surface. From Figure 1, it can be seen that the errors associated with the satellite-based retrievals are generally larger, in the 0.4–0.6 range. The domain averaged relative measurement errors are 0.46, 0.44, 0.54, 0.47, and 0.42 for AMSR-E, ASCAT, SMOS, AMSR2 and SMAP, respectively. Across different sensors, SMAP based retrievals show better performance over different climatic zones and biomes, with relative measurement errors significantly reduced over areas with moderate vegetation. Some areas with notably low skill for SMAP are the Sahara and Western Australia deserts, which are likely due to factors such as the surface temperature biases used in the SMAP retrievals (SMAP science team, pers. comm.) and the deeper contributing depth of the microwave signal over arid areas. In addition, the limited dynamic range of soil moisture over deserts and forested areas also contributes to higher relative errors over these areas. Generally, the soil moisture dynamic ranges are higher over non-forested areas with moderate vegetation and SMAP retrievals show high skills over such regions. Note that such issues are also observed in retrievals from ASCAT, SMOS and AMSR-E. The comparison of the distribution of measurement errors also confirms the fact that overall, SMAP retrievals are improved relative to the skill of the retrievals from other MW sensors. The ASCAT retrievals show reduced error levels in the high latitudes, which contribute to the increased span in the medium error range (0.2–0.4) in the distribution comparisons.

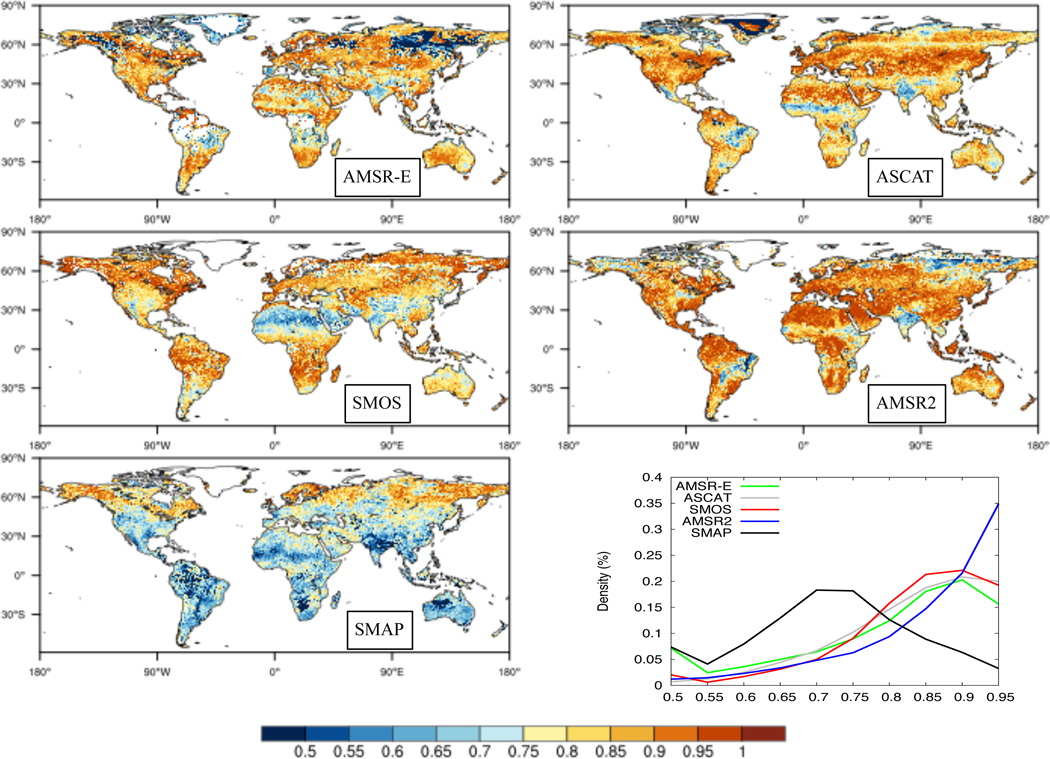
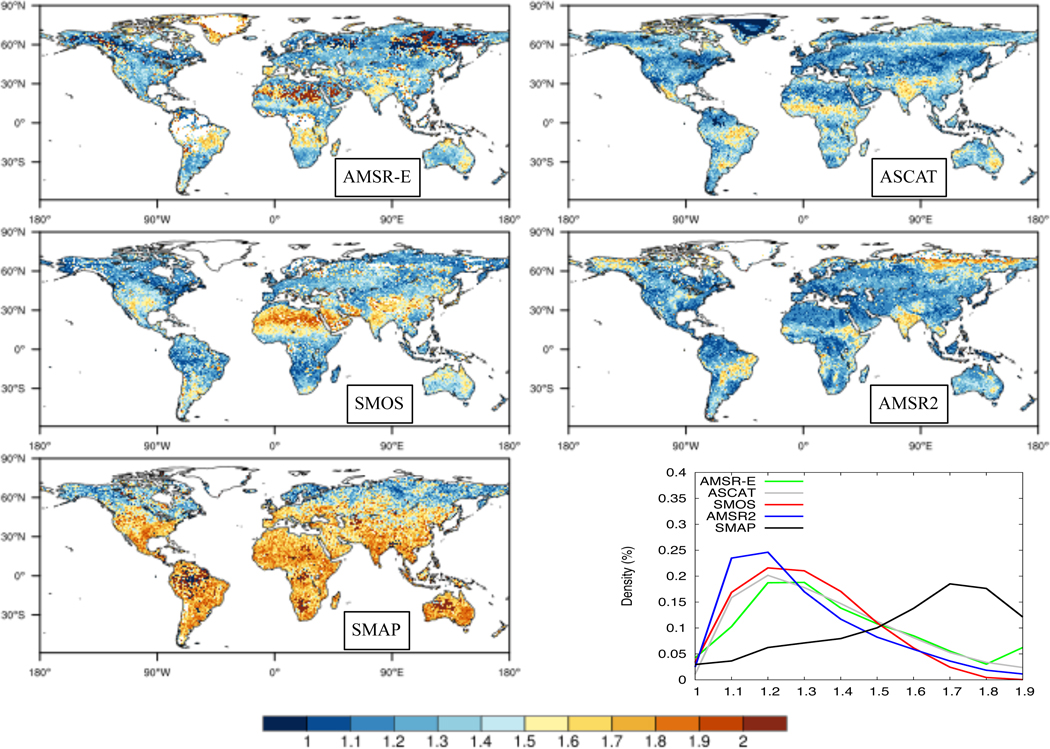
Figures 2 and 3 show comparisons of the soil moisture retrievals from the 5 sensors based on metric entropy and fluctuation complexity, respectively. The maps of metric entropy show discrimination of areas with different levels of randomness in the retrievals. For example, areas of high vegetation density show up as areas with high randomness in the retrievals, as larger H values are seen over the Amazon, Eastern U.S. and Congo. Larger uncertainty is also seen over arid regions in the Western U.S., Sahara and Western Australia, especially in the ASCAT and AMSR2 retrievals. Conversely, the fluctuation complexity maps show reduced values over these regions with larger randomness, which are indicative of low information content in the time series at these locations. Similar to the trends seen in Figure 1, SMAP shows a distinctly different behavior in these comparisons. Generally, the metric entropy values are significantly lower (reduced randomness in the SMAP time series) and fluctuation complexity values are higher (larger information content compared to a periodic or random noise signal). SMAP retrievals particularly show high information content (less noise) in the midlatitude regions in the comparisons in Figures 2 and 3. The plots of the distribution of the metric entropy and fluctuation complexity values across the whole domain also confirm these trends. The metric entropy and fluctuation complexity distributions for all sensors except SMAP are skewed to the high and low values, respectively, indicating that overall, the information content of the retrievals from these sensors have large amount of noise. The SMAP distribution spans an intermediate range, suggesting reduced levels of randomness and increased levels of complexity in the time series.

Figure 2:

Similar to Figure 1, but for metric entropy (H)

Figure 3:

Similar to 2, but for fluctuation complexity (C)

Note that the AMSR-E and AMSR2 retrieval algorithms are based on X-band passive microwave observations, whereas ASCAT uses C-band radar observations. The observations based on these channels have lower sensitivity to soil moisture and are more influenced by the presence of moderate to dense vegetation compared to the retrievals using lower frequency (L-band) channels. Nevertheless, the comparison of ASCAT versus SMOS/AMSR-E/AMSR2 presented in Figures 1 to 3 indicates that in many parts of the world, the active and passive retrievals have comparable skills. It is interesting, however, that the SMAP retrievals show higher skill and increased information content compared to SMOS, though both are L-band based retrievals. Though the SMOS and SMAP instruments are similar, they use different technologies. The SMAP instrument is a real aperture radiometer whereas SMOS uses a synthetic aperture radiometer. Previous studies (Oliva et al. (2013)) have documented that the unique SMOS brightness temperature (Tb) observations have a higher Noise Equivalent Delta Temperature (NEDT), which represents the temperature difference that would produce a signal equivalent to the internal noise of the instrument. The SMOS retrieval algorithm attempts to reduce the impact of NEDT by using Tb from all incidence angles. The error in the soil moisture retrieval is then minimized by the relationship between Tb and the incidence angles. The quality and the number of Tb samples, however, reduce as the distance from the center of the swath decreases. SMAP, on the other hand, provides observations of a particular location at a fixed incidence angle, which likely contributes to the reduced noise in the measurements, as confirmed in our analysis. Note also that though SMOS and SMAP both operate L-band radiometers, the SMOS retrievals suffer more from the man-made radio frequency interference (RFI) contamination, which were unknown before the SMOS launch. The SMAP mission, on the other hand, developed measures to mitigate the effect of RFI prior to launch, which has likely contributed to the improved performance of the SMAP retrievals relative to SMOS.

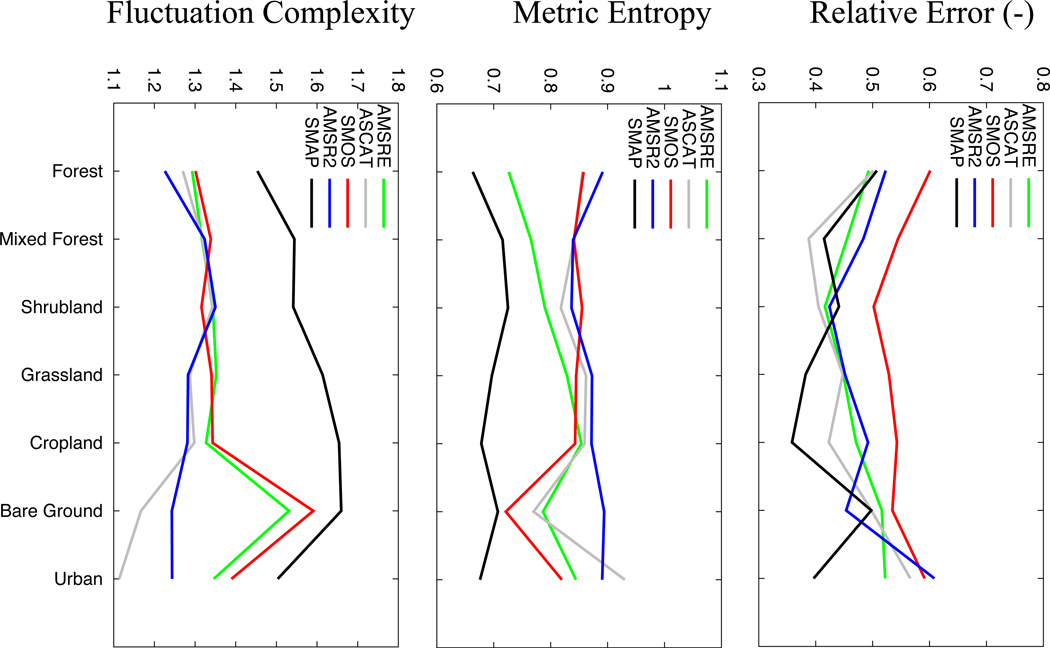
A comparison of the average values of the three metrics stratified by vegetation type is shown in Figure 4. The seven vegetation categories are derived from the modified International Geosphere-Biosphere Programme (IGBP) Moderate Resolution Imaging Spectroradiometer (MODIS) data (Friedl et al. (2010)). Similar to the patterns seen in the spatial maps, smaller errors are seen for moderate vegetation types and larger errors for bare ground and thick vegetation types. SMAP shows the smallest errors among different sensors across most vegetation types. In particular, SMAP retrievals show lowest errors over the Cropland and Grassland types. In the information theory comparisons, SMAP retrievals show reduced levels of randomness and high fluctuation complexity among the 5 sensors across all vegetation types. Generally, the stratification also indicates higher information content over moderate vegetation types compared to thick vegetation types. For other sensors, however, the obvious contrasts in the metrics between vegetation types are not always observed. For example, AMSR2 shows similar metric entropy values across all vegetation types. The performance of SMOS and ASCAT are comparable for different vegetation types, except for the low metric entropy values over bare ground areas.

Figure 4:

Stratification of metrics by vegetation type

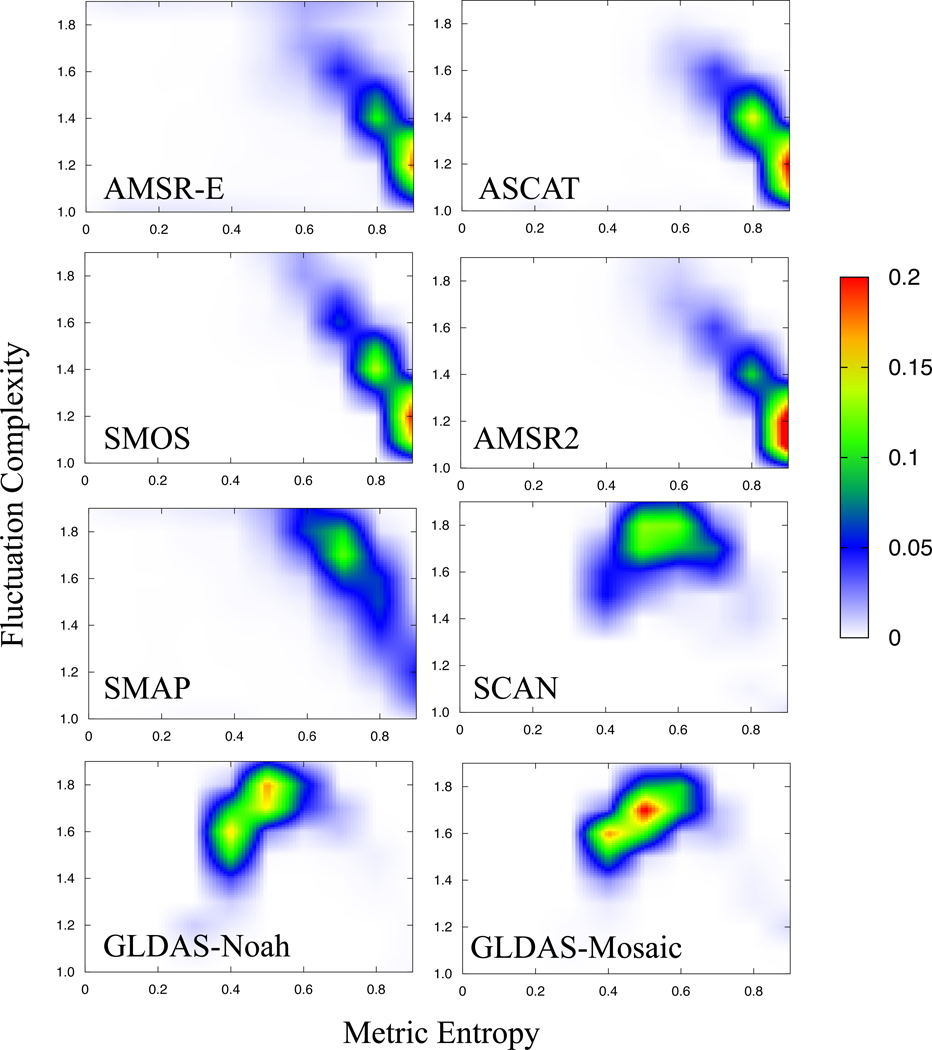
Metric entropy is a measure of the amount of uncertainty inherent in a Markov process (Gray (2011)), but it does not characterize the state changes in a time series, which can be captured by complexity measures. As a result, joint consideration of the two measures is necessary to quantify the information content of a time series in terms of its randomness and state changes within the sequences. Previous studies have shown that the functional relationship between entropy and complexity generally follows an inverse parabolic relationship (Lange (1999)), as complexity is low for periodic (low entropy) and random noise (high entropy) signals, but high for time series that are different from random or trivial sequences (intermediate entropy). Figure 5 shows “heatmaps”/density of grid points as a function of these two variables, for the 5 remote sensing retrievals. In addition, Figure 5 also includes joint evaluations of the entropy and complexity from ground soil moisture measurements and outputs from two land surface model simulations. The ground soil moisture measurements are obtained from the U.S. Department of Agriculture Soil Climate Analysis Network (SCAN; Schaefer et al. (2007)), whereas the Noah (Ek et al. (2003)) and Mosaic (Koster and Suarez (1996)) model soil moisture estimates from the Global Land Data Assimilation System (GLDAS; Rodell et al. (2004)) are used as the land surface model outputs.

Figure 5:

Density of grid points mapped as a function of metric entropy (x-axis) and fluctuation complexity (y-axis).

The comparisons shown in Figure 5 indicate the different regions of the Entropy-Complexity (E-C) space spanned by each soil moisture dataset. The remote sensing measurements AMSR-E, ASCAT, SMOS and AMSR2 show high density of grid points in the lower right part of the E-C space, the area dominated by high randomness and low complexity. This suggests that the information content of these retrievals is low. Comparatively, SMAP shows improved performance, where the density of grid points is shifted to the area with high complexity and intermediate randomness. The in-situ measurements from SCAN show high density in the E-C space in regions with high complexity, but with marginally reduced entropy (compared to SMAP). The heatmaps from GLDAS-Noah and GLDAS-Mosaic also indicate high complexity and intermediate randomness in their soil moisture time series. It can be observed that the land models, ground measurements and remote sensing datasets span different parts of the E-C space and together, they encompass the inverse parabolic relationship between entropy and complexity. Generally, entropy is lower in the land model estimates, increases marginally for the ground soil moisture measurements, and is highest for remote sensing datasets. On the other hand, complexity is comparable across land surface model and ground soil moisture estimates, but significantly lower for remote sensing measurements (except those from SMAP). If ground measurements are considered as reference, the comparison in Figure 5 shows that significant improvements to the remote sensing retrievals are required for improving their information content, to improve their utility in modeling and data assimilation environments.

As the metric entropy and fluctuation complexity measures quantify the information of the signal and are not necessarily direct assessments of the skill of the measurement itself, they should be viewed as a complementary analysis to standard validation metrics. For example, in an arid region, the soil moisture signal may not have significant variability and as a result, the complexity and entropy of the natural signal may be low. Arguably, the utility of remote sensing measurements is higher over areas where soil moisture dynamics are inherently more variable and capturing them accurately is difficult. Over such areas, the information theory metrics are useful for providing both assessments of signal quality as well as for intercomparing model, satellite and ground reference data products. The information theory based discrimination can also be used for developing merged products with improved information content.

4. Summary

Remote sensing based observations of soil moisture, primarily from passive and active microwave remote sensing, are of great value as they provide measurements across a range of spatial and temporal scales and extents. A consistent evaluation of the accuracy and information content of these products, however, is difficult since reliable, spatially coherent ground measurements of soil moisture are lacking in many parts of the world. In this article, we present a time series based information theoretic analysis for an intercomparison of recent satellite-based soil moisture products.

Soil moisture retrievals from five recent microwave remote sensing instruments, including AMSR-E, ASCAT, SMOS, AMSR2 and SMAP are used in this study. Three measures that quantify the accuracy, randomness, and the complexity of the data are used to intercompare these retrieval products. An autoregressive analysis that models soil moisture as a first order Markov process is used to develop estimates of measurement errors. Information theory measures of metric entropy and fluctuation complexity that quantify the stochasticity in time series data are used to provide comparisons of information content in these retrievals. Metric entropy measures the amount of randomness inherent in a Markov process whereas fluctuation complexity provides a measure that evaluates the level of regularity and randomness in the time series data.

The information theory measures are developed by translating the soil moisture time series to binary symbol strings and by examining the probabilities of patterns of states defined by a sequence of consecutive symbols. The article uses three symbol states, consistent with previous literature and similar applications of the information theory measures for hydrological model evaluations.

The results of the red noise spectrum analysis provide an assessment of the strengths and limitations of the soil moisture retrieval products. Generally these products have reduced measurement errors over areas with moderate vegetation density and large errors over areas with thick vegetation. In many instances, large measurement errors are also observed over bare soil areas. The estimates of measurement error also indicate that generally remote sensing retrievals have larger errors compared to that of in-situ measurements. Among the remote sensing retrieval datasets, the SMAP-based products were found to have lower errors over different climatic regimes in the world. In particular, the SMAP retrieval errors were comparable to that of the in-situ measurements over areas with moderate vegetation density (relative errors in the range of 0.2–0.3).

Comparison of the metric entropy and fluctuation complexity measures from these retrieval products also indicates similar trends. The signature of vegetation density is prominent in these information theory evaluations as the evaluations indicate larger uncertainty and lower complexity over areas of the world with thick vegetation. Comparatively, the SMAP retrievals show improved information content relative to other retrievals. The level of randomness was generally lower in the SMAP retrievals, whereas the complexity of the SMAP time series data was generally higher, compared to the AMSR-E, ASCAT, SMOS and AMSR2 products. SMAP soil moisture product is based on L-band passive microwave observations (which are most sensitive to soil moisture). Other satellites use different frequencies, which are less sensitive to soil moisture (AMSR-E and AMSR2 use X-band radiometers, ASCAT uses a C-band radar). SMOS L-band observations are affected by the presence of RFI.

A joint comparison of the metric entropy and fluctuation complexity of the remote sensing retrieval products is also presented in this study. Generally, it can be argued that a time series signal is of high information content, if it possesses intermediate entropy and high complexity. Combinations of high entropy and low complexity are symptomatic of random noise signals whereas low entropy and low complexity are indicative of periodic/trivial signals. The simultaneous assessment of entropy and complexity indicates that the majority of retrievals from AMSR-E, ASCAT, SMOS and AMSR2 have low information content. Comparatively, the performance of the SMAP retrievals is better, with higher density of grid points with increased complexity and reduced entropy. A similar evaluation of in-situ soil moisture and land surface model output data is also presented in the article. The in-situ measurements encapsulate the region of high information content in the entropy-complexity space. The land surface models also indicate marginally lower randomness with high levels of complexity in their estimates. Together, the three sets of soil moisture estimates (remote sensing, in-situ and model) span the majority of the inverse parabolic space expected in the entropy complexity comparisons. Generally, the land surface model and remote sensing datasets span mutually exclusive regions of the E-C space. This suggests that improvements in the remote sensing retrievals are necessary before including them in data assimilation environments that rely on observational information to constrain model simulations and forecasts. The results also indicate that SMAP retrievals with low entropy and increased complexity can provide valuable information for hydrologic modeling studies.