Spatial Distribution of Hydrophobic Drugs in Model Nanogel-Core Star Polymers

Abstract

Star polymers with a cross-linked nanogel core are promising carriers of cargo for therapeutic applications due to the synthetic control of amphiphilicity of arms and stability at infinite dilution. Three nanogel-core star polymers were investigated to understand how the arm-block chemical structure controls loading efficiency of a model drug, ibuprofen, and its spatial distribution. The spatial distribution profiles of hydrophobic core, hydrophilic corona, and encapsulated drug were determined by small-angle neutron scattering (SANS). SANS provides the nanometer-scale sensitivity to determine how the arm-block chemistry enhances the sequestering of ibuprofen. Validated molecular dynamics simulations capture the trends in drug profile and polymer segment distribution with further details on drug orientation distribution. This work provides a basis to study structure–function relationships in macromolecular-based carriers of cargo and represents a path toward validated and predictive simulation.

Graphical Abstract

INTRODUCTION

Polymer nanoparticles provide advanced materials for the encapsulation and targeted delivery of drugs. The loading characteristics depend on several design criteria including thermodynamic compatibility, size characteristics, and interfacial energy. Block copolymer micelles represent model structures that take advantage of relative affinity of cargo for one component, often the hydrophobic core. However, block copolymer micelles, due to their self-assembled state, upon incorporation of cargo may influence the overall micelle aggregation number—the average number of polymers forming the micelle above the critical micelle concentration. For instance, the small-angle neutron scattering (SANS) results of Foster et al.¹ and Alexander et al.² studied the uptake of ibuprofen and flurbiprofen, respectively, in Pluronic block copolymer micelles. They observed that drug loading into the micellar core increases the fraction of micellization and aggregation number. Akiba et al. measured the encapsulation of the hydrophobic retinoid antagonist drug (LE540) into the micellar core formed by poly(ethylene glycol)-block-poly-(partially benzyl-esterified aspartic acid), PEG-P(Asp(Bzl)), diblock copolymers.³ In this case, LE540 was uniformly distributed within the core with simultaneous increase in aggregation number. A slightly different behavior in the same system was observed by Sanada et al., whereby hydrophobic tetrabromocathecol distribute at the core–corona interface without changing the aggregation number.⁴ These sensitive anomalous X-ray scattering experiments, quantified by a model, demonstrate the coupled spatial distribution of cargo and block copolymer micelle aggregation characteristics.

Even slight changes in drug polarity alters the spatial distribution. Nakanishi et al. found 4-bromobenzyl alcohol was homogeneously dispersed in the hydrophobic core of block copolymer micelles while bromobenzene formed a depletion layer at the core–shell interface.⁵ Similarly, an extensive study by Valero et al.⁶ found that the drug chemical structure has a strong correlation with the spatial localization of drugs in F127 Pluronic block copolymer micelles. Therefore, the uniformity of the hydrophobic molecules distributed within polymeric micelles is affected by polarity.

One approach to decouple the polymer micelle aggregation characteristics and solute loading is to use a covalently bonded polymer nanoparticle. Recent synthetic advancements have led to increased interest in star and branched polymers as micelle replacements.^7–9 Nanogel-core star polymers offer a covalently cross-linked core surrounded by water-soluble radiating arms.^9–12 The cross-linked nanogel core is hydrophobic, and additional hydrophobic segments are incorporated via blocks on the star arms with outermost hydrophilic segments providing stabilized nanostructures in water. Since this covalently assembled macromolecule does not have a critical micelle concentration, upon infinite dilution under delivery conditions it will not revert to unimers like block copolymer micelles. The hydrophobic cross-linked core and flexible hydrophobic star-arm segments are rationalized to serve as the cargo space.

We study the effect of homopolymer, diblock, and terpolymer star arms on the spatial distribution of a model hydrophobic drug, ibuprofen. nGel-(EG₁₁₄)_f is composed of f homopolymer arms of poly(ethylene glycol) (EG₁₁₄), with degree of polymerization of 114, that radiate from the cross-linked hydrophobic caprolactone (CL) nanogel core (nGel). The diblock arms of nGel-(VL₂₃-EG₁₁₄)_f consists of an inner hydrophobic block of poly(valerolactone) (VL₂₃) and an outer hydrophilic block of EG₁₁₄. The terpolymer arms of nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f consist of an inner hydrophobic poly(valerolactone)-co-poly(4-tert-butylcarprolactone) (VL₁₁-tBuCL₁₀) and an outer hydrophilic block of EG₁₁₄. SANS measurements are combined with Pedersen’s spherical micelle scattering model to study how the star arm chemistry controls the loading and spatial distribution of ibuprofen. SANS enables us to determine the spatial distribution profiles of the hydrophobic core, hydrophilic corona, and encapsulated drugs. The experiments and analysis make simplifying assumptions that were tested by independent molecular dynamics (MD) simulation and drug loading estimates by ultraviolet (UV)–vis spectroscopy.

MATERIALS AND METHODS

Nanogel-core star polymers were synthesized and characterized as reported previously.¹² The synthetic conditions for the cross-linked caprolactone nanogel-core preparation were kept constant in order to achieve core structures and average number of arms fixed. Inhibitor-free tetrahydrofuran (THF) was purchased from Sigma-Aldrich. Deuterium oxide (D₂O, 99.9 D atom %) and d-tetrahydrofuran (d-THF, 99.95 D atom %) were purchased from Cambridge Isotope Laboratories. Ibuprofen was purchased from Spectrum Chemical Mfg. Corp. and used as received. Poly(ethylene glycol) methyl ether (number-average relative molecular mass, M_n = 5000 Da, PDI = 1.01) was purchased from Sigma-Aldrich. Deuterated poly(ethylene glycol) methyl ether (M_n = 5000 Da, PDI = 1.08) was obtained from Polymer Source. Both polymers were kept under vacuum at 50 °C for 24 h prior to use and characterized by the manufacturer for their relative number-average molar mass (M_n) and polydispersity index (PDI). Table 1 shows the chemical structures of nanogel-core star polymers studied in this work.

Table 1.

Characteristics of Nanogel-Core Star Polymers Studied^a

name	Mwb (kg/mol)	farm	A2e (mol cm3/g2)	Rg of particle (nm)e	${\overline{\mathit{R}}}_{\mathit{c}}\left(\mathbf{\text{nm}}\mathbf{\right)}$c	${\mathit{\sigma }}_{\mathbf{\text{R}}}\mathbf{/}{\overline{\mathit{R}}}_{\mathbf{\text{c}}}$c	fsol vol fracc	star arm Rg (nm)c	IBU loading efficiencyf (%)
nGel-(EG114)f	120d	27c	9.2 × 10−5	7.8	1.9 ± 0.3	0.8 ± 0.1	0.17	1.8 ± 0.1	6.0 ± 0.3
	268e	24d
		53e
nGel-(d-EG114)f	109d	21d
nGel-(VL23-EG114)f	221d	28d							23 ± 1
nGel-(VL11-tBuCL10-EG114)f	257d	28c	1.9 × 10−4	13.6	2.4 ± 0.5	0.5 ± 0.1	0.10	1.7 ± 0.5	48 ± 3
	298e	33d
	38e

^anGel = cross-linked caprolactone core. EG = (–O–CH₂–CH₂–) and d-EG = (–O–CD₂–CD₂). VL = (–O–(CH₂)₄–CO–). tBuCL = (–O– (CH₂)₂–CH(C(CH₃)₃)–(CH₂)₂–CO–). IBU = ibuprofen.

^bRelative mass-average molar mass (M_w).

^cSmall-angle neutron scattering estimate by Pedersen’s model in d-THF.

^dLight scattering GPC in THF.

^eSmall-angle neutron scattering estimate by the Zimm plot in d-THF.

^fThe value is an average of three independent measurements with uncertainties (±) estimated by one standard deviation of the mean.

Sample Preparation.

Nanogel-Core Star Polymer in d-THF.

Nanogel-core star polymers were dissolved directly in inhibitor free d-THF as clear solutions of 0.4 mass % with stirring at 40 °C for 30 min. After approximately 24 h at room temperature, the solutions were diluted to the required concentrations of 0.1%–0.4%.

Nanogel-Core Star Polymer in D₂O.

For nGel-(d-EG₁₁₄)_f and nGel-(EG₁₁₄)_f, 40 mg of nanogel-core star polymer was dissolved in 2 mL of D₂O directly. The solution was filtered through 0.45 μm PVDF syringe filter after stirring at room temperature overnight. For nGel-(VL₂₃-EG₁₁₄)_f and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f, 40 mg of nanogel-core star polymer was dissolved in 0.4 mL of inhibitor-free THF. 2 mL of D₂O was added, while stirring, and left at room temperature overnight. The mixture was filtered through a 0.45 μm PTFE syringe filter, and the obtained solution was sparged in a nitrogen stream to remove THF. The sparging process was stopped when 250 mass % of the added THF had been removed, and the solution was diluted to 2% by D₂O assuming no polymer loss. Precipitate was observed for nGel-(VL₂₃-EG114)_f.

Ibuprofen Loaded Nanogel-Core Star Polymer in D₂O.

Ibuprofen loading was accomplished by adding 4 mg of ibuprofen to 40 mg of nGel-(d-EG₁₁₄)_f, nGel-(EG₁₁₄)_f, nGel-(VL₂₃-EG₁₁₄)_f, and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f before dissolution in 0.4 mL of inhibitor-free THF and following an identical procedure to nGel-(VL₂₃-EG₁₁₄)_f and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f in D₂O.

UV–Vis Spectroscopy.

The amount of loaded ibuprofen in nanogel-core star polymers was determined using a Varian Cary 5000 UV–vis–near-infrared spectrophotometer at room temperature with quartz cuvettes of 10 mm path length. In short, 150 μL of 2% ibuprofen loaded nanogel-core star polymer in aqueous solution was first air-dried under room temperature and then redissolved in 3 mL of inhibitor-free THF to release ibuprofen into solution. The amount of loaded ibuprofen was determined by UV–vis absorbance at 264 nm referenced to a calibration curve of ibuprofen in THF over the concentration range of 12.5–400 μg/mL. The polymer absorbance at 264 nm was subtracted. Free ibuprofen was also subtracted at an amount equal to the equilibrium solubility in water, which is 0.0127 mg/mL at 25 °C.¹³ Ibuprofen loading efficiency (%) was calculated by amounts of ibuprofen loaded/amounts of ibuprofen fed × 100.

Small-Angle Neutron Scattering (SANS).

SANS measurements were performed at the National Institute of Standards and Technology, Center for Neutron Research (NCNR) NG7 SANS and NGB 10m nSOFT beamlines with cold neutrons. The scattered intensity I(q) was measured as a function of the wave vector (q) defined by q = (4π/λ) sin(θ/2), where θ is the scattering angle and λ is the neutron wavelength. For the NG7 instrument, λ was 6 Å with Δλ/λ ≈ 0.14 and used three sample-to-detector distances (1, 4, and 13 m) to provide a q range of 0.04–5 nm⁻¹. For the NGB instrument, the two wavelength settings were used across three sample–detector distances: λ = 10 Å at 5.2 m and λ = 5 Å at both 5.2 and 1.2 m with fixed Δλ/λ ≈ 0.15 leading to similar q ranges. All samples were measured in 1 or 2 mm path length Hellma quartz cells at 25 °C. Data were placed on an absolute intensity scale via direct beam flux measurement, detector sensitivity and element size, transmission, sample-to-detector distance, and sample scattering volume considerations. Standard data reduction routines and scaling to absolute intensity measurements were applied.¹⁴ Background intensity due to incoherent scattering contributions from protons and solvent scattering was experimentally estimated and subtracted using established methods.¹⁵ Uncertainties (error bars) are estimated by one standard deviation of the mean by least-squares minimization of fits to the SANS data. Modeling details of SANS data are provided in the Supporting Information.

Differential Scanning Calorimetry (DSC) Measurements.

DSC measurements were carried out with a Shimazu DSC 7 calorimeter at a heating rate 10 °C/min. Samples were first subjected to heating to 150 °C and then cooled down to 40 °C at the maximum cooling rate. The glass transition temperature (T_g) was measured in the second heating ramp.

Molecular Dynamics Simulations.

All-atom MD simulation of the nanogel core with 16 emanating star arms of VL₁₆-EG₂₄ with explicit water were performed using the LAMMPS simulation software package¹⁶ on an IBM BlueGene/Q supercomputer. The force field used OPLS-AA parameters^17,18 for ibuprofen, OPLS-AA with slight modification for the star polymer, and TIP4P-Ew for water,¹⁹ as described previously.²⁰ The simulations included 106 950 water molecules in a cubic simulation cell with an edge length of approximately 14.9 nm. Simulations were performed at 350 K using NVT ensemble, with a production phase of 50 ns after equilibration.

SANS Model Background.

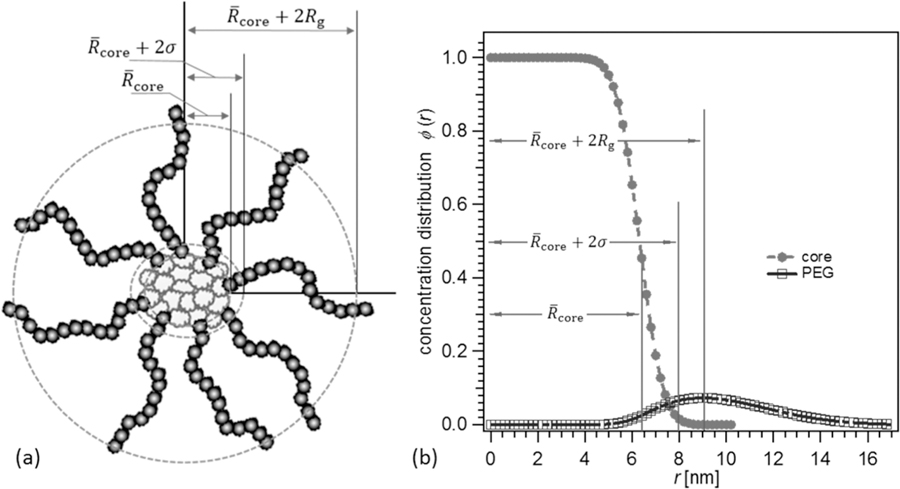
In order to understand the nanogel-core star polymer structure, we utilize the model developed by Pedersen for spherical micelles.^21,22 This model provides a molecular analysis of the micelle with a spherical core surrounded by f_arm Gaussian chains at the core surface, as depicted in Figure 1a. The details are in the original papers, but we provide a brief account relevant to the discussion. As shown in eq 1, P(q) is Pedersen’s form factor that contains contributions to the total particle scattering from self-correlations and pair-correlations

$$\begin{gathered} P\left(q\right)={\beta }_{\text{core}}^{\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2}{P}_{\text{core}}\left(q\right)+f_{\text{arm}}{\beta }_{\text{chain}}^{\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2}{P}_{\text{chain}}\left(q\right)+2f_{\text{arm}}{\beta }_{\text{core}} \\ \hspace{1em}\hspace{0.17em}\times {\beta }_{\text{chan}}{S}_{\text{core}-\text{chain}}\left(q\right)+f_{\text{arm}}\left(f_{\text{arm}}-1\right){\beta }_{\text{chain}}^{\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2}{S}_{\text{chain}-\text{chain}}\left(q\right) \end{gathered}$$ (1)

The self-correlations from the core and chain are within P_core(R_core, σ; q) and P_chain(R_g; q) that are modeled by a spherical core and a Debye chain, respectively; the parameters in these functions are core size (R_core), core–corona interfacial width (σ), and chain radius of gyration (R_g) as indicated within the function and defined in Figure 1a. The cross-correlations within the micelle between chains at the core surface are determined by S_{chain–chain}(A_chain, σ; q) while chain-core correlations by S_core–chain(A_chain, R_core, σ; q). In this case the scattering amplitude (A_chain) of corona chains are modeled by the Fourier transform of a Spline 2 chain segmental density profile (eqs 9 and 35 in ref 22). The total excess scattering lengths of the hydrophobic block in core (β_core) and hydrophilic block in corona (β_chain) are calculated based upon the specific volumes and scattering length density (SLD) differences with the solvent. The details of the SLD calculations are displayed in the Supporting Information.

Figure 1.

(a) Schematic of the Pedersen’s model parameters as applied to the nanogel-core star polymers. (b) Radial concentration distribution, ϕ(r), with length scales pertinent to the model. The total hydrophobic core radius ${\overline{R}}_{\text{core}}$ includes the cross-linked caprolactone nanogel-core and hydrophobic copolymer (HCP) arm segments.

The monodisperse form factor, P(q), was averaged over a Schulz–Zimm distribution of average core radius $\left({\overline{R}}_{\text{core}}\right)$ and polydispersity index $\rho ={\sigma }_{\text{R}}/{\overline{R}}_{\text{core}}$, where σ_R is the variance. The experimental absolute SANS intensity of I(q) is given by

$$I\left(q\right)=\frac{c}{M}{P}_{\text{poly}}\left(q\right)S\left(q\right)$$ (2)

where P_poly is the polydispersity-averaged form factor, c is the mass concentration of polymer, and M is the mass-average molecular mass of a nanogel-core star polymer. S(q) is the hard sphere structure factor to account for interparticle correlations characterized by hard sphere volume fraction and effective radius. The average radial concentration distribution ϕ(r), as shown in Figure 1b, is obtained using the method outlined by Pedersen via the Fourier transform of the combined core and corona amplitudes, A_mic, as expressed by eq 3 (also see eq 16 in ref 23 and eq 18 in ref 24). The amplitudes of A_mic for the core and corona weighted by the molar volumes are described in the Supporting Information.

$$\varphi \left(r\right)=\frac{1}{2{\pi }^2}{\int }_0^{\infty }{A}_{\text{mic}}\left(q\right)\frac{\sin qr}{qr}{q}^2\text{d}q$$ (3)

Pedersen’s micelle model was programmed into the Igor Pro software using available libraries from the NCNR data analysis packages. In organic solvent of d-THF, a global fitting method within the Igor Pro software was used to simultaneously fit the SANS data sets with common ${\overline{R}}_{\text{core}}$, R_g, f_arm, and f_solv for each nanogel-core star polymer at different polymer concentrations. In the solvent D₂O, f_arm of each polymer is set to be the same as the value in d-THF, since the star arms are covalently bonded. The strategy of isotopic substitution of hydrogen for deuterium is used to increase the sensitivity to different parts of the micelle. D₂O was used in conjunction with hydrogenous polymers to observe the whole micelle structure; select deuteration of the PEG chain in the presence of D₂O increased the sensitivity to the core–PEG interface. Common ${\overline{R}}_{\text{core}}$ and f_arm are used for nGel-(EG₁₁₄)_f and nGel-(d-EG₁₁₄)_f in the global fitting method. MD simulations of methoxypoly(ethylene glycol)-block-polycaprolactone (MePEG-b-PCL) found the PCL core excludes water.²⁵ Similarly, nuclear magnetic resonance spectra found water does not solvate VL.¹² Based on these, no solvent of D₂O was allowed ( f_solv = 0) to swell the core during SANS model fit.

Several alternative analytic SANS models are available,¹⁴ and a question may be raised regarding the curve fitting uniqueness. However, few systematically treat the correlations as outlined by Pederson. The regression results are least-squares solutions and tested for self-consistency among the core size, arm radius of gyration, organic versus aqueous solvent, and polymer concentration. The internal consistency of the parameters with independent measurements appears favorable and is discussed.

RESULTS AND DISCUSSION

Drug–Polymer Interactions and Loading Efficiency.

The thermodynamic solubility of drug in the hydrophobic core may be estimated by the Flory–Huggins parameter (χ), such that the smallest χ indicates highest compatibility.^26,27 Table 2 shows the predicted compatibility of the different polymer segments with ibuprofen and solvent (D₂O). The group contribution method of Hoftyzer and Van Krevelen^28,29 shows that ibuprofen compatibility is highest (smallest χ) for tBuCL, suggesting ibuprofen has a higher solubility within nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f than nGel-(VL₂₃-EG₁₁₄)_f. Interestingly, as shown in Table 1, the drug loading efficiency of nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f is 110% higher than nGel-(VL₂₃-EG₁₁₄)_f, which is consistent with the trend of χ parameter. However, this approach reflects only compatibility arguments, not additional interfacial packing effects. For instance, the 6% loading efficiency of nGel-(EG₁₁₄)_f shown in Table 1 may be due to less bulk cargo space because of the smaller core (bulk loading limited) or less interfacial area for drug packing (surface area limited). To explore this, SANS quantified by a detailed scattering molecular model are used to find the drug profile. These results are then compared to MD simulations.

Table 2.

Flory–Huggins Parameter χ^a

	EG	CL	VL	tBuCL	IBU
D2O	0.63	0.80	0.76	0.90	0.93
IBU	0.090	0.028	0.045	0.025

^aχ parameter was calculated from the solubility parameter estimated using the group contribution methods.^28,29 Details are provided in the Supporting Information.

Structures in d-THF.

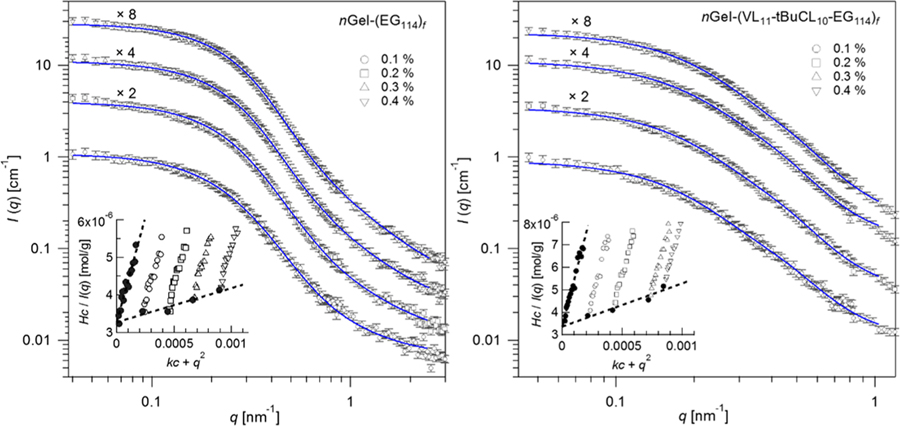
The star arms of EG₁₁₄ and VL₁₁-tBuCL₁₀-EG₁₁₄, as well as the cross-linked caprolactone nanogel core, are swollen by d-THF. In dilute solutions of d-THF, nanogel-core star polymers provide a rigorous test of Pedersen’s model. Figure 2 shows a concentration-dependent fit to nGel-(EG₁₁₄)_f and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f. The f_arm of each star polymer is shown in Table 1. The agreement of f_arm between SANS and GPC light scattering confirms the validity the model for nanogel-core star polymers. The value of f_arm obtained in d-THF may then be used in D₂O. The volume fraction of d-THF in the cross-linked caprolactone nanogel core is f_solv ≈ 13%, indicating the caprolactone nanogel core is highly cross-linked.

Figure 2.

Pedersen’s model fit to SANS data of nGel-(EG₁₁₄)_f and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f in d-THF with mass % concentrations shown by the legend. The curves are shifted vertically for clarity by factors indicated above the data. Insets show Zimm plots using data q < 0.15 nm⁻¹.

Model-independent Zimm plots are also shown in the insets of Figure 2. H is the neutron optical constant and k an arbitrary scaling factor. The molecular mass of the overall star polymer are in Table 1. In this case, the number of star arms per polymer was estimated by f_arm = M_w/M_w,arm which ignores the molecular mass of the cross-linked nanogel core. M_w and f_arm in d-THF by SANS are qualitatively in agreement with the values by GPC light scattering. This provides the confidence to extend Pederson’s model to D₂O, where quality GPC light scattering was unavailable.

Structure in D₂O.

In D₂O, cross-linked caprolactone nanogel core, VL₂₃ and VL₁₁-tBuCL₁₀ blocks become insoluble and collapse.³⁰ Representative SANS data of nGel-(d-EG₁₁₄)_f, nGel-(EG₁₁₄)_f, nGel-(VL₂₃-EG₁₁₄)_f, and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f before and after drug encapsulated are displayed in Figure 3. The data have several prominent features. All curves of protonated polymers (Figure 3b–d) follow ≈q⁻² dependence at higher q due to the Gaussian chain scattering.³¹ A peak becomes pronounced at 0.7 nm⁻¹ < q < 1.5 nm⁻¹ as the arm structure changes from EG₁₁₄ to VL₂₃-EG₁₁₄ to VL₁₁-tBuCL₁₀-EG₁₁₄. This peak results from the dense hydrophobic core with narrow size distribution. The peak shifts to lower q with added drugs that may reflect bulk core swelling or packing of drugs at the core–arm interface. The curves of deuterated nGel-(d-EG₁₁₄)_f in Figure 3a show deviation from q⁻² dependence at higher q, resulting from the low contrast between d-EG₁₁₄ and D₂O. The scattering contribution of d-EG₁₁₄ chains is lower, leading to a higher resolution of the hydrophilic and hydrophobic interphase. Further analysis by the model quantifies the behavior.

Figure 3.

SANS data of nanogel-core star polymers at a fixed concentration of 2 mass % with and without ibuprofen. The blue lines represent the best fit to Pedersen’s model. Key fit results are displayed in Table 3. Full fit results are shown in Supporting Information. The data with ibuprofen are vertically offset by ×8, for clarity.

Hydrophobic Core Structure: Before and after Ibuprofen Loading.

For nGel-(EG₁₁₄)_f and nGel-(d-EG₁₁₄)_f, the cross-linked caprolactone nanogel core provides a cargo space for partitioning of hydrophobic drugs based upon solubility parameters. The size and polydispersity of the cross-linked nanogel core and the subsequent packing of the hydrophobic segments from the emanating arms change the overall hydrophobic core size, as shown in Table 3. nGel-(EG₁₁₄)_f shows an average ${\overline{R}}_{\text{core}}=2.54\pm 0.9$ with polydispersity index of ${\sigma }_{\text{R}}/{\overline{R}}_{\text{core}}=0.53\pm 0.20$ from a Schulz–Zimm distribution. The polydispersity eliminates any expected SANS peaks from the spherical core. However, the peak becomes more pronounced in nGel-(VL₂₃-EG₁₁₄)_f and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f as the total size of the hydrophobic core increases to 5.62 ± 0.07 and 4.95 ± 0.05 nm with lower polydispersity of 0.16 ± 0.01 and 0.14 ± 0.01. Transmission electron microscopy on nGel-(VL₂₃-EG₁₁₄)_f estimates an average core size of ≈5.3 nm, consistent with SANS (Supporting Information). The fractional increase in the hydrophobic core size is from the packing of the VL₂₃ and VL₁₁-tBuCL₁₀ hydrophobic segments. These results verify recent MD simulations that show segmental packing of VL blocks upon a small cross-linked CL core.^25,32,33 MD simulations further suggest tBuCL segments pack less effectively than VL.³² This poorer packing may enhance the mobility within the hydrophobic core to reduce shape anisotropy under the interfacial tension with water.

Table 3.

Key Fit Results of Nanogel-Core Star Polymer in D₂O^a

	drug free			drug loaded
sample	${\overline{\mathit{R}}}_{\mathbf{\text{core}}}\mathbf{\left[}\mathbf{\text{nm}}\mathbf{\right]}$	${\mathit{\sigma }}_{\mathbf{\text{R}}}\mathbf{/}{\overline{\mathit{R}}}_{\mathbf{\text{core}}}$	Rg [nm]	${\overline{\mathit{R}}}_{\mathbf{\text{core}}}\mathbf{\left[}\mathbf{\text{nm}}\mathbf{\right]}$	${\mathit{\sigma }}_{\mathbf{\text{R}}}\mathbf{/}{\overline{\mathit{R}}}_{\mathbf{\text{core}}}$	Rg [nm]
nGel-(EG114)f	2.54 ± 0.9	0.53 ± 0.20	1.67 ± 0.3	3.92 ± 0.09	0.18 ± 0.02	1.85 ± 0.06
nGel-(d-EG114)f	2.54 ± 0.9	0.37 ± 0.10		3.92 ± 0.09	0.18 ± 0.01
nGel-(VL23-EG114)f	5.62 ± 0.07	0.16 ± 0.006	1.50 ± 0.06	6.46 ± 0.1	0.17 ± 0.01	1.11 ± 0.08
nGel-(VL11-tBuCL10-EG114)f	4.95 ± 0.05	0.14 ± 0.005	1.84 ± 0.08	6.40 ± 0.05	0.13 ± 0.01	1.33 ± 0.08

^aUncertainties (±) are estimated by one standard deviation to the model fit.

In Table 3, a significant increase of ${\overline{R}}_{\text{core}}$ was observed after drug loading. The packing of drug reduces the core polydispersity for nGel-(EG₁₁₄)_f, while no effect was observed for nGel-(VL₂₃-EG₁₁₄)_f and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f. Drug molecules may not swell the cross-linked core, but rather reside at the core–arm interface. The locally rough surface and core interface of nGel-(EG₁₁₄)_f could be smoothed by drug adsorption, since uniform swelling would not affect polydispersity. The z-average R_g of PEG arm chains are obtained from Pedersen’s model. As shown in Table 3, all the values of R_g are smaller than the value of 2.3 nm calculated for Gaussian coils of PEG M_n = 5 kg/mol.³⁴ After drug loading, R_g of PEG in nGel-(EG₁₁₄)_f remains constant, while it slightly decreases for nGel-(VL₂₃-EG₁₁₄)_f and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f in the presence of higher drug loading. This coil contraction effect, while small, may reflect the locally poorer solvent conditions for PEG in the presence of drug and is discussed in the context of quantifying the spatial profiles. R_g of PEG is not shown for nGel-(d-EG₁₁₄)_f because the neutron contrast between d-EG and D₂O was very low.

Concentration Profiles.

Pedersen’s model estimates the average radial concentration distribution ϕ(r) via modeling the core and corona in a piecewise manner and then Fourier transforming the combined form factor amplitude A_mic(q). In our case, the Spline 2 model was used that smoothly connects the polymer segmental profile to the uniform density core by an interfacial width. Since D₂O did not swell the hydrophobic core (f_solv = 0), one may normalize the concentration profiles as described by Pedersen and Gerstenberg.³⁵

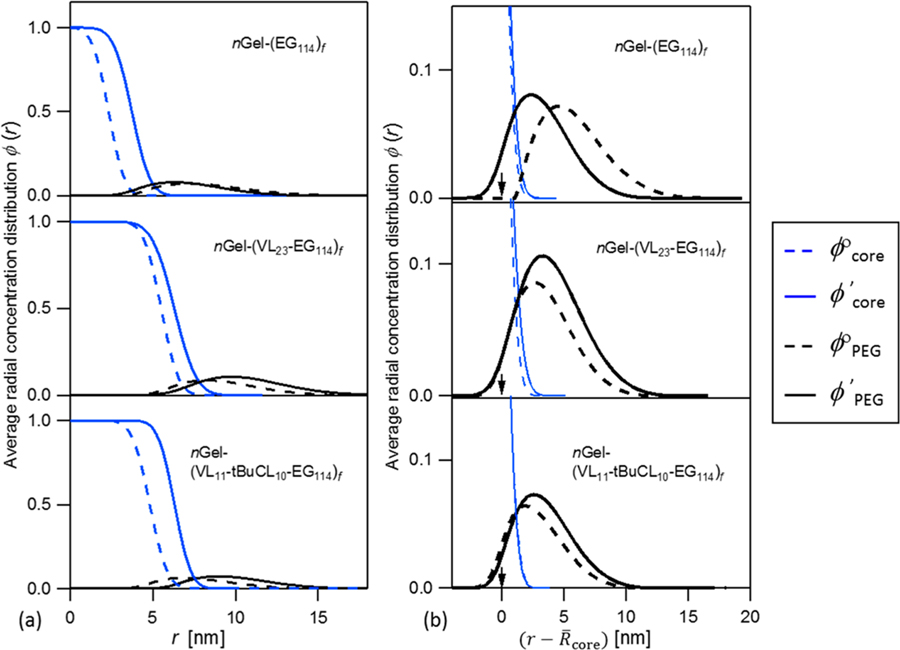
Figure 4 shows the total hydrophobic core, ϕ_core(r), and PEG, ϕ_PEG(r), concentration profiles for nanogel-core star polymer before and after ibuprofen loading. Figure 4a shows the hydrophobic core with unit normalized volume fraction with diffuse core to star arm interface characterized by the interfacial width (σ). After drug loading, the spatial distribution of the hydrophobic core expands with values shown in Table 3. The loaded drugs are considered as a part of ϕ′_core(r), since neutrons cannot distinguish drug molecules and hydrophobic segments unless one of them is deuterated. As shown in Figure 4b, the hydrophobic core overlaps with the PEG profile due to the covalent connectivity.

Figure 4.

(a) Radial concentration distribution ϕ_core(r) of total hydrophobic core, including cross-linked caprolactone nanogel core, VL and tBuCL segments, and encapsulated ibuprofen. (b) Radial concentration distribution ϕ_PEG(r) of PEG in corona. The abscissa scaling of $\left(r-{\overline{R}}_{\text{core}}\right)$ is calculated by subtracting corresponding values of ${\overline{R}}_{\text{core}}$. The arrows indicate the hydrophobic core–arm interface where the position of $\left(r-{\overline{R}}_{\text{core}}\right)=0$. In the legend, superscripts degree and prime are used to represent drug free and drug loaded state, respectively.

In Figure 4b, the segmental concentration of PEG reaches a maximum of ≈10%, consistent with highly swollen star arms at relatively low graft density. This level of PEG hydration agrees with SANS results of F127 Pluronic micelles modeled as a core–shell, not by Pedersen’s model.⁶ The abscissa is normalized by the total hydrophobic core radius $\left({\overline{R}}_{\text{core}}\right)$ to show how the tethered PEG chains shift as drug is encapsulated. Figure 4b shows ϕ°_PEG(r) of nGel-(EG₁₁₄)_f has the lowest overlap with ϕ°_core(r), indicating the cross-linked caprolactone nanogel core is impermeable. As drug is encapsulated, no spatial expansion of the cross-linked core could be permitted thus drugs could only locate at the cross-linked core–arm interface. The anchored end of PEG to the cross-linked core surface does not shift since the cross-linked core does not swell. The encapsulated drugs at the cross-linked Core–arm interface contribute to ϕ′_core(r). The total hydrophobic core of nGel-(EG₁₁₄)_f increases, and the anchored ends of PEG chains are buried. When normalized by the total core radius, ϕ′_PEG(r) of nGel-(EG₁₁₄)_f shifts toward the interior of the hydrophobic core compared to ϕ°_PEG(r), as shown in Figure 4b. This result confirms the prediction³⁰ that for nGel-(EG₁₁₄)_f the drug resides at the interface of the core-PEG without substantial swelling of the core by mobile drug molecules. In contrast, ϕ_PEG(r) of nGel-(VL₂₃-EG₁₁₄)_f and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f shows that the anchored ends of PEG chains shift away from the core center spontaneously with the expansion of total hydrophobic core. This is observed by the nearly constant tail of the distribution at $\left(r-{\overline{R}}_{\text{core}}\le 0\right)$. This does not lead to substantially different PEG swelling or PEG spatial extent profile but corresponds to spatial expansion of mobile hydrophobic blocks (VL₂₃ or VL₁₁-tBuCL₁₀) as drug is encapsulated. Based on these results, the drug penetrates to the interior of hydrophobic core enabled by the repartitioning of the VL₂₃ or VL₁₁-tBuCL₁₀ segments in nGel-(VL₂₃-EG₁₁₄)_f and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f, while the cross-linked core remains unchanged.

Estimate for Spatial Distribution of Drug.

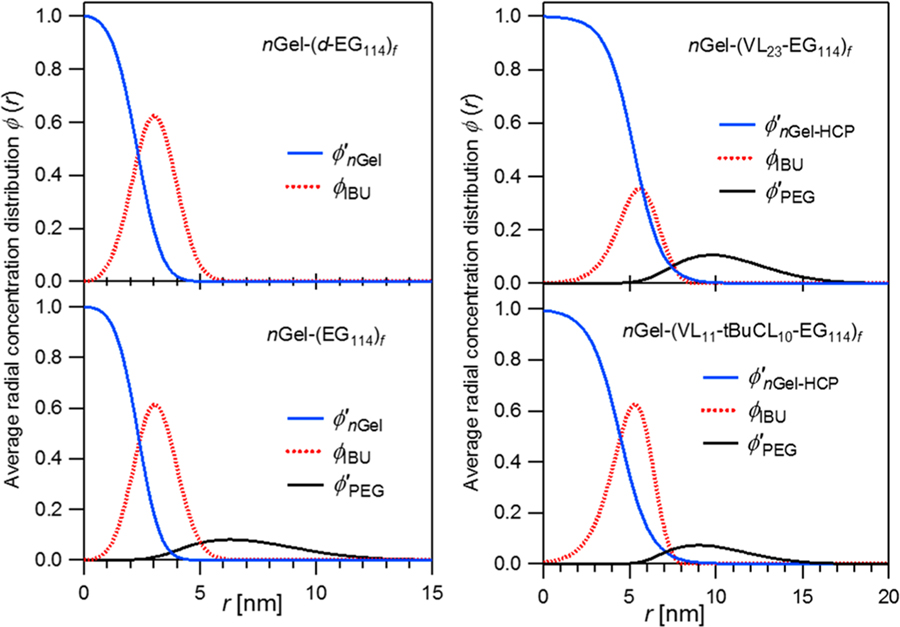
For nGel-(EG₁₁₄)_f and nGel-(d-EG₁₁₄)_f without ibuprofen, the total hydrophobic core concentration profile $\left({\varphi }_{\text{core}}^{\circ }\left(r\right)\right)$ is the same as the cross-linked caprolactone nanogel core $\left({\varphi }_{n\text{Gel}}^{\circ }\left(r\right)\right)$, ${\varphi }_{n\text{Gel}}^{\circ }\left(r\right)={\varphi }_{\text{core}}^{\circ }\left(r\right)$. As ibuprofen is loaded, the total hydrophobic core $\left({\varphi }_{\text{core}}^{\text{'}}\left(r\right)\right)$ contains two additive-by-volume parts, such that ${\varphi }_{\text{core}}^{\text{'}}\left(r\right)={\varphi }_{n\text{Gel}}^{\text{'}}\left(r\right)+{\varphi }_{\text{IBU}}\left(r\right)$, where ${\varphi }_{n\text{Gel}}^{\text{'}}\left(r\right)$ is the concentration profile of the cross-linked caprolactone nanogel core after ibuprofen loaded, and ϕ_IBU(r) is the concentration profile of loaded ibuprofen. Since the nanogel cross-linked caprolactone core does not change in the presence of ibuprofen ${\varphi }_{n\text{Gel}}^{\text{'}}\left(r\right)={\varphi }_{n\text{Gel}}^{\circ }\left(r\right)$, the concentration profile of loaded ibuprofen in nGel-(EG₁₁₄)_f and nGel-(d-EG₁₁₄)_f may be estimated by the difference in profiles, ${\varphi }_{\text{IBU}}\left(r\right)={\varphi }_{\text{core}}^{\text{'}}\left(r\right)-{\varphi }_{n\text{Gel}}^{\text{'}}\left(r\right)$.

For nGel-(VL₂₃-EG₁₁₄)_f and nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f, the total hydrophobic core concentration profiles can be generalized in the presence of the hydrophobic copolymer (HCP) arm segments before drug loading, ${\varphi }_{\text{core}}^{\circ }\left(r\right)={\varphi }_{n\text{Gel}}^{\circ }\left(r\right)+{\varphi }_{\text{HCP}}^{\circ }\left(r\right)$ and after drug loading ${\varphi }_{\text{core}}^{\text{'}}\left(r\right)={\varphi }_{n\text{Gel}}^{\text{'}}\left(r\right)+{\varphi }_{\text{HCP}}^{\text{'}}\left(r\right)+{\varphi }_{\text{IBU}}\left(r\right)$, where ${\varphi }_{\text{HCP}}^{\circ }\left(r\right)$ and ${\varphi }_{\text{HCP}}^{\text{'}}\left(r\right)$ are the concentration profiles of hydrophobic copolymer arm segments before and after drug loading, respectively. For nGel-(VL₂₃-EG₁₁₄)_f, HCP represents VL₂₃, while for nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f, HCP is VL₁₁-tBuCL₁₀. As ibuprofen is loaded, the collapsed HCP segments are swollen and spatial distribution of HCP segments changes, but the total numbers of HCP segments and cross-linked nanogel core remain constant. Therefore, by conservation of mass of the cross-linked nanogel core and total HCP segments, m_nGel + m_HCP are related to the concentration profiles before and after loading by

$$\begin{gathered} m_{n\text{Gel}}+m_{\text{HCP}}={\int }_0^{\xi }\left[{\varphi }_{n\text{Gel}}^{\circ }\left(r\right)+{\varphi }_{\text{HCP}}^{\circ }\left(r\right)\right]r^2\hspace{0.17em}\text{d}r \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\int }_0^{\xi }\left[{\varphi }_{\hspace{0.17em}n\text{Gel}}^{\text{'}}\left(r\right)+{\varphi }_{\hspace{0.17em}\hspace{0.17em}\text{HCP}}^{\text{'}}\left(r\right)\right]r^2\hspace{0.17em}\text{d}r \end{gathered}$$ (4)

where the integration cutoff (ξ) is taken to be the core size plus the core-corona interfacial full width $\left({\overline{R}}_{\text{core}}+2\sigma \right)$. SANS cannot separate ϕ_nGel(r) and ϕ_HCP(r) unless one of them is deuterated. Deuterated VL and tBuCL monomer were not available. Here, we use ϕ_nGel–HCP(r) to represent ϕ_nGel(r) + ϕ_HCP(r). It is observed that the shape of ϕ_core(r) in Figure 4a can be approximately described by a tanh function. In order to solve for the final hydrophobic core profile of ${\varphi }_{n\text{Gel}+\text{HCP}}^{\text{'}}\left(r\right)$, we assume that ${\varphi }_{n\text{Gel}+\text{HCP}}^{\text{'}}\left(r\right)$ has a similar tanh shape to ϕ_core(r). More details of ${\varphi }_{n\text{Gel}+\text{HCP}}^{\text{'}}\left(r\right)$ calculation are presented in the Supporting Information. After integration by eq 4, the concentration profile of ibuprofen is obtained by difference ${\varphi }_{\text{IBU}}\left(r\right)={\varphi }_{\text{core}}^{\text{'}}\left(r\right)-{\varphi }_{n\text{Gel}+\text{HCP}}^{\text{'}}\left(r\right)$. This analysis assumes little to no water is distributed within the nanogel core or hydrophobic copolymer.

Figure 5 shows that the radial spatial distribution of ibuprofen is not homogeneously distributed in the hydrophobic core. The extent of loading is dependent upon the star arm chemistry as predicted by the loading efficiencies. For nGel-(EG₁₁₄)_f and nGel-(d-EG₁₁₄)_f due to the nearly impenetrable cross-linked caprolactone nanogel core, the drug appears at the core surface. For nGel-(VL₂₃-EG₁₁₄)_f, the drug is confined to the hydrophobic core region with maximum of ϕ_IBU ≈ 34%. In contrast, the maximum of ϕ_IBU ≈ 62% for nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f with majority within the hydrophobic domain.

Figure 5.

Average radial concentration distribution, ϕ(r), of hydrophobic core, PEG, and ibuprofen. The concentration profiles are shown after ibuprofen loading for the nanogel core (ϕ′_nGel), ibuprofen (ϕ_IBU), corona PEG chains (ϕ′_PEG), and the nanogel core combined hydrophobic copolymer arm segments (ϕ′_nGel–HCP) for the four systems under study.

On the basis of the average radial concentration distribution shown in Figure 5, one may estimate the amount of ibuprofen. However, we found an overestimate of IBU based upon either the volume expansion of the total hydrophobic core or estimates from the concentration distribution, when compared to the model-independent UV–vis loading data. We attribute the overestimate of the total hydrophobic core after IBU loading as possibly due to EG segments appearing at the core–corona interface. This may reconcile the smaller R_g of PEG in Table 3 after IBU loading, such that PEG adsorbs or associates with the hydrophobic core. This would be consistent with the decrease of R_g after drug loading. The increment of ${\overline{R}}_{\text{core}}$ is somehow overestimated and not entirely due to the IBU loading. This is not an artifact of Pedersen’s model as an independent estimate of the core size by fitting a sphere form factor to the peak feature at 0.7 nm⁻¹ < q < 1.5 nm⁻¹ in Figure 3d reveals the same core size consistent with the model and consistent with $q{\overline{R}}_{\text{core}}=4.493$ at the first form factor minimum as discussed for block copolymer micelles.³⁶ Therefore, we believe that some PEG segments may be preferentially adsorbed to the core/corona interface. The trend of IBU loading amount obtained from SANS qualitatively agrees with the loading efficiency by UV–vis measurement as shown in Figure S2 that the loading extent follows nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f > nGel-(VL₂₃-EG₁₁₄)_f > nGel-(EG₁₁₄)_f. In order to better estimate the IBU spatial distribution, the mass density profiles of IBU were normalized by the amounts per particle determined by UV–vis and shown in Figure 6a.

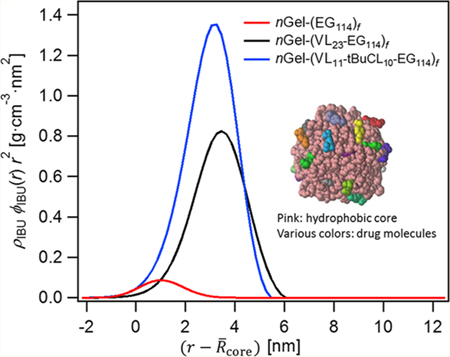
Figure 6.

(a) Average radial mass distribution, ρ_IBUϕ_IBU(r)r², of nanogel-core star polymer studied. ρ_IBU is the mass density of ibuprofen. ρ_IBU = 1.03 g/cm³. In the x-axis of $\left(r-{\overline{R}}_{\text{core}}\right)$, ${\overline{R}}_{\text{core}}=2.54\hspace{0.17em}\text{nm}$, equal to the radius of the cross-linked caprolactone nanogel core. (b) The analogous mass distribution is shown for the simulated system with ${\overline{R}}_{\text{core}}=2.4\hspace{0.17em}\text{nm}$.

Figure 6a summarizes the probability mass distribution of ibuprofen with abscissa in units of distance from the surface of the cross-linked caprolactone nanogel core to permit comparison. These results show that the probability to observe ibuprofen is peaked at the nanogel-core interface in the homopolymer arm case but then peaked within the interphase formed by the packing of mobile diblock and terpolymer hydrophobic segments. This allows us to compare the trends in ibuprofen distribution with the validated MD simulations.

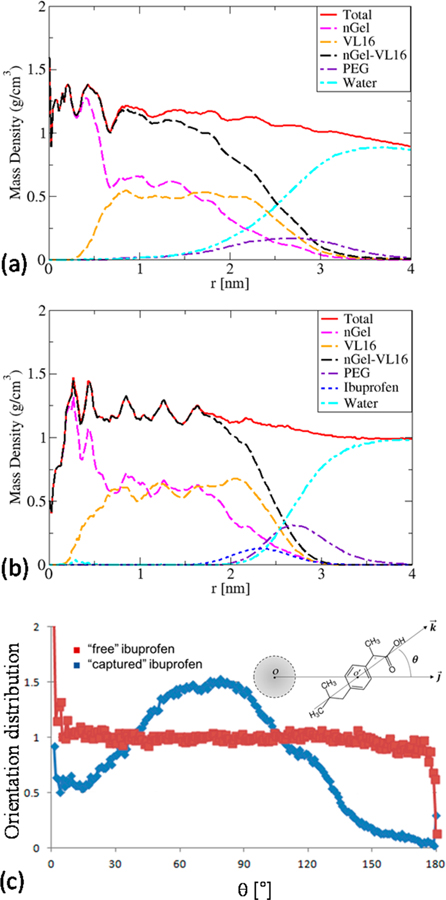
MD Simulations of Composition Profiles.

In order to test the conclusions based upon SANS and UV–vis, simulations were performed using models for nanogel star polymers prepared as described in previous work.²⁰ These models were constructed in a way that mimics the synthetic process of the formation of the core in order to obtain a realistic core cross-linking topology.²⁰ The nanogel star polymer constructed in this way had 16 diblock arms nGel-(VL₁₆-EG₂₄)₁₆ and was simulated in the liquid phase using an atomistic model for water. Two long simulations were performed: one with 24 ibuprofen molecules included in random starting positions within the simulation cell and another without any ibuprofen molecules. In the simulation that included ibuprofen, after only about 40 ns, 23 of the 24 drug molecules became associated with the star polymer and subsequently remained associated, suggesting that significantly greater loading could be possible. The resulting orientationally averaged mass density profile is shown in Figure 7, for comparison with Figures 4 and 5. There are striking similarities even though the simulated system is significantly smaller than the polymers used in experiments. The simulated system has a hydrophobic core with radius of approximately 2.4 nm compared with about 5.62 nm for the actual molecules of nGel-(VL₂₃-EG₁₁₄)_f. Each component of the diblock arms is shorter, and there are fewer arms. Upon addition of the ibuprofen molecules, the core in the simulation does not exhibit as much core expansion as illustrated in Figure 4a, but there is a slight reorganization of the core with enhanced core density in the vicinity of the ibuprofen. The addition of the ibuprofen pushes the PEG away from the core, exactly as is seen in the experimental systems with diblock and terpolymer arms. As seen in Figure 7b, the simulations show that the ibuprofen is rather well localized, inside the PEG layer, slightly inside the core, but also having significant contact with both PEG and water as well as the core, i.e., at the interface between the hydrophobic core and the PEG–water layer. Figure 6b shows that the simulated system has a very narrow and well-localized ibuprofen layer (approximately 1 nm thick) compared to the experimental system (approximately 4 nm) and that it is nearer to the surface of the core, but this may be due to the much lower ibuprofen loading used in the simulation.

Figure 7.

Orientationally averaged mass density as a function of distance from the center of mass of a small simulated nanogel-core star polymer nGel-(VL₁₆-EG₂₄)₁₆ without (a) and with (b) ibuprofen. Different material is represented by different line color: black (total hydrophobic core nGel-VL₁₆), magenta (nGel), orange (VL₁₆), purple (PEG), cyan (water), blue (ibuprofen), total (red). (c) Relative orientation distribution of ibuprofen defined by the angle between the vector $\overrightarrow{k}$ from the center of mass of the polymer and the vector $\overrightarrow{j}$ defined along the ibuprofen from the methyl to carboxylic acid group.

The relative orientation of the ibuprofen molecules can be determined from the simulation results. When the distance from the center of the polymer to the center of the ibuprofen is <2.5 nm, the ibuprofen is considered to be captured by the star polymer. When this distance is >3 nm, ibuprofen is considered free. The relative orientation of ibuprofen and the polymer was analyzed by computing the distribution of angles measured between two vectors: a vector $\left(\overrightarrow{k}\right)$ from the hydrophobic methyl end to the acid end of ibuprofen, defining the axis of the ibuprofen molecules, and a position vector $\left(\overrightarrow{j}\right)$ from the center of the polymer to the center of ibuprofen. The projected angle (θ) varies from 0° to 180°. At 0°, the acid end points out away from the star polymer toward solvent. At 180°, the acid end points toward the interior of the star polymer. If θ is 90°, ibuprofen appears tangential or lying flat to the star polymer surface. The angle distribution is normalized by sin(θ) so that it is flat if there is no preferred orientation. Figure 7c shows that for the free, unbound, ibuprofen outside of the interface (>3 nm) no orientation preference is observed. However, an enhanced probability occurs for θ between 45° and 105° (lying flat) and diminished probability for perpendicular to the surface (0° and 180°). However, it is more probable for the acid end to pointing toward the solvent, since the peak is located below 90°.

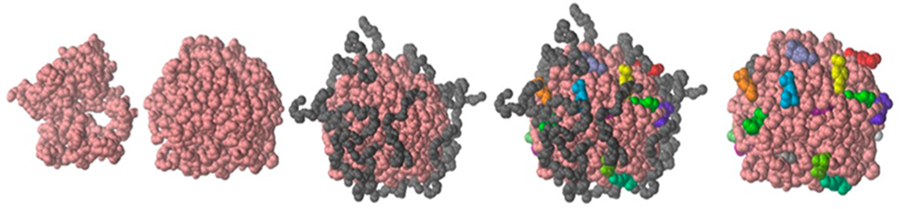
Comparing the homopolymer, diblock, and terpolymer star arms, the packing of the VL₁₁-tBuCL₁₀ make the hydrophobic core most accessible to ibuprofen loading. This may lead to the highest segmental mobility as supported by DSC results, where the T_g was found to be −17.8 and 36 °C for VL₁₁-tBuCL₁₀-EG₁₁₄ and VL₂₃-EG₁₁₄, respectively. Further, the hydrophobic core is more regular in shape in the diblock and terpolymer arms as easily shown by the SANS peak and by the simulation sequence of structure in Figure 8. Lastly, because of the low rigidity, it is easier for drug to penetrate, and ϕ_IBU(r) is the highest for the terpolymer arms enabled by the lowest Flory–Huggins interaction parameter. These experimental results support the recent consideration by Yamamoto et al.³⁷ on the role of mobility/rigidity of the hydrophobic core on drug incorporation.

Figure 8.

Simulated nGel-(VL₁₆-EG₂₄)₁₆ system showing successive layers of (left to right): cross-linked gel core region (pink); hydrophobic region consisting of gel core region and the PVL block of each arm (both pink); entire star polymer consisting of the hydrophobic region (pink) and the PEG block of each arm (gray); entire star polymer (pink and gray) and adsorbed ibuprofen (various colors); star polymer without the PEG block (pink) and the adsorbed ibuprofen (various colors).

Currently, we do not have experimental data on release profiles of the star polymers; the evaluation is underway. However, we anticipate the rate of cargo release will be fastest for the nGel-(EG₁₁₄)_f star polymer and slowest for the nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f star polymer. Our prediction is based on the accessibility of the cargo and the hydrophobic core by water molecules. Two factors come into play: concentration gradient driven release and hydrolytic degradation of the star polymer. Both factors are present in the case of nGel-(EG₁₁₄)_f, where cargo molecules are located at the surface of a hydrophobic core and hence readily exposed to the aqueous environment. In addition, this cross-linked core is more susceptible to hydrolytic degradation under basic or acidic conditions. In the case of nGel-(VL₁₁-tBuCL₁₀-EG₁₁₄)_f cargo is buried inside of the hydrophobic core and hence has a “harder” time escaping. In addition, the presence of a pendant alkyl functionality increases the overall hydrophobicity of the core, driving water molecules away and hence suppressing the hydrolytic degradation.

CONCLUSION

The spatial distribution of ibuprofen can be controlled by the hydrophobic inner-block segments of emanating star arms in cross-linked nanogel core star polymers. Bulkier hydrophobic block substituents (VL and tBuCL) improve the loading efficiency as independently confirmed by UV–vis spectroscopy. The loading efficiency also correlates to solubility parameter/interaction parameter compatibility arguments. While the absolute loading of the drug was improved in the presence of the diblock and terpolymer arm substituents, the reason appears to be caused by a thicker and mobile interphase between the cross-linked caprolactone nanogel core and the emanating hydrophilic PEG arms, rather than bulk loading within the nanogel core. This interphase accommodates a few molecular layers of ibuprofen preferentially lying flat to the hydrophobic core with acid end pointing toward the solvent. Therefore, a design criteria worthy of study is the relationship between the projected interfacial area for adsorption of drug. This could be optimized with respect to the loading efficiency, which is of practical interest in formulations. Importantly, calorimetry provides a simple estimate as to the mobility of the bulky segments within the interphase that guides the spatial distribution of ibuprofen. The validated MD simulations recover the spatial distribution of drug at the nanogel core/arm interphase and provide the first step to develop predictive models toward improved polymers for nanomedicine.