Landscape simplification shapes pathogen prevalence in plant-pollinator networks

Abstract

Species interaction networks, which play an important role in determining pathogen transmission and spread in ecological communities, can shift in response to agricultural landscape simplification. However, we know surprisingly little about how landscape simplification-driven changes in network structure impact epidemiological patterns. Here, we combine mathematical modeling and data from eleven bipartite plant-pollinator networks observed along a landscape simplification gradient to elucidate how changes in network structure shape disease dynamics. Our empirical data show that landscape simplification reduces pathogen prevalence in bee communities via increased diet breadth of the dominant species. Furthermore, our empirical data and theoretical model indicate that increased connectance reduces the likelihood of a disease outbreak and decreases variance in prevalence among bee species in the community, resulting in a dilution effect. Because infectious diseases are implicated in pollinator declines worldwide, a better understanding of how land use change impacts species interactions is therefore critical for conserving pollinator health.

Graphical Abstract

We combined mathematical modeling and data from eleven plant-pollinator networks observed along a landscape simplification gradient to elucidate how changes in network structure shape disease dynamics. Our empirical data show that landscape simplification reduces pathogen prevalence in bee communities via increased diet breadth of the dominant species. Furthermore, our empirical data and theoretical model indicate that increased connectance reduces the likelihood of a disease outbreak and decreases variance in prevalence among bee species in the community, resulting in a dilution effect.

INTRODUCTION

Landscape simplification driven by agricultural expansion is one of the most significant anthropogenic changes to the planet, influencing resource availability, biodiversity, and ecosystem functioning (Tscharntke et al. 2005). An important but often overlooked consequence of landscape simplification is the deterioration of interaction patterns across trophic levels, including host-parasitoid and plant-pollinator networks (Fortuna & Bascompte 2006; Tylianakis et al. 2007; Spiesman & Inouye 2013). These interactions between species are essential for maintaining ecosystem function and stability (Thébault & Fontaine 2010), and they also shape how pathogens are transmitted and spread. Moreover, the predictive power of disease spread models is often improved when interaction patterns are considered (White et al. 2017). Yet we currently do not understand how landscape simplification impacts disease dynamics via changes to interaction networks. This is an important knowledge gap given increasing global dependence on pollinators for ecosystem service provisioning (Aizen et al. 2008) and the documented links between pathogens and bee declines worldwide (Goulson et al. 2015).

The impacts of landscape simplification on network structure have been generally attributed to species turnover and reduced specialization (Grass et al. 2013). Plant-pollinator networks are characterized by diverse bee species assemblages with frequently overlapping visitation patterns (Petanidou et al. 2008; Pocock et al. 2012). Given that generalist floral visitors are typically less susceptible to habitat loss (Fortuna & Bascompte 2006), pollinator communities in simplified landscapes could be dominated by generalist species. In such a scenario, we would expect interaction networks with high proportions of realized links between bee and flower species (high connectance), in which interactions occur evenly throughout (low modularity), and with few specialists present to interact with generalists (low nestedness), which has been found in some (Spiesman & Inouye 2013; Vanbergen et al. 2014), but not all systems (Redhead et al. 2018; Traveset et al. 2018). Moreover, all of these metrics have been highlighted as potential key mediators of disease transmission (i.e. connectance/nestedness (Wei et al. 2015), modularity (Sah et al. 2017), and abundance/diversity (Johnson et al. 2015)). Ultimately, how changes to network structure influence pathogen prevalence in plant-pollinator communities is largely unknown, limiting our understanding of how agricultural expansion impacts the health of bee communities.

Dominant species often disproportionately influence ecosystem functions, including disease transmission dynamics (Keesing et al. 2010), due to their high abundance, broad diet breadth, and/or dispersal abilities. Focusing on dominant species can provide an initial assessment of the impact that landscape simplification has on network stability (Hagen et al. 2012). These dominant species could influence encounter probabilities, subsequent exposure to pathogens, and ultimately, disease spread dynamics at the community level (Keesing et al. 2010). Thus, the way in which dominant species respond to landscape simplification and influence plant-pollinator network structure could have significant implications for pathogen transmission and prevalence at the community level.

Pathogen transmission can occur among multiple bee species when susceptible individuals forage on contaminated flowers (Durrer & Schmid-Hempel 1994). Furthermore, bees can simultaneously vector multiple pathogens onto flowers, even without developing active infections (Graystock et al. 2015). Recently, pathogens known to infect honey bees and bumble bees have been detected in a broad array of bee species, including social and solitary taxa (Cordes et al. 2012; Evison et al. 2012; Ravoet et al. 2014), highlighting the existing knowledge gap in the host range of these pathogens and more generally in bee inter-species transmission dynamics. Moreover, differences in pathogen prevalence in bee communities across land use gradients (Theodorou et al. 2016; Piot et al. 2019) suggest that changes in host density and interaction patterns may be key mediators in how communities respond to landscape simplification.

Here, we characterized plant-pollinator networks and bee pathogen prevalence in 11 replicated wildflower plots established across a landscape simplification gradient in order to address three major questions. First, does landscape simplification shape pathogen prevalence in bee communities mediated by changes in network structure? Specifically, we used structural equation modeling to quantify the role of network connectance, modularity, and nestedness, as well as bee abundance, species richness, and diet breadth of the dominant bee species. Second, does the role of a bee species in the network predict its likelihood of harboring pathogens? To address this question we computed species-level network descriptors such as centrality and diet breadth, as well as pairwise interactions between bee species mediated by shared floral resources. Finally, what mechanisms underpin the empirical relationship between network structure and pathogen prevalence in bipartite plant-pollinator networks? To shed light on this question, we developed mathematical models using empirically derived parameters from our data and additional literature to determine drivers of pathogen prevalence and spread.

MATERIAL AND METHODS

Field sites, sample collection, and network assessment

We evaluated the plant-pollinator networks of 11 replicated wildflower plots in upstate New York from June 10 to September 26, 2015 (Fig. S1). Each 10 × 15 meter planting was established with native perennial wildflower species in 2012 following regional guidelines for species that encompass a broad phenological range and are known foraging resources for wild bees (Tuell et al. 2008; Grab et al. 2018). Not all plant species established equally well at each of the sites, and the parentheses indicate the number of sites that included each species: Silphium perfoliatum (11), Solidago canadensis (11), Penstemon digitalis (11), Veronicastrum virginicum (10), Lobelia siphilitica (10), Coreopsis lanceolata (5), and Agastache nepetoides (4). Sites were also invaded by weedy species: Erigeron annuus (9), Trifolium repens (9), Medicago sativa (7), Trifolium pratens (7), Daucus carota (5), and Cirsium arvense (3). Plant species richness was assessed within the planted wildflower plots at each site.

We characterized each network by conducting weekly ten-minute visitation surveys at each site, where all bee-flower interactions occurring within the site were recorded to the finest taxonomic resolution possible. Each site was surveyed 8 to 12 times throughout the summer from 08:00 to 17:00 hrs on sunny and low wind days, with temperatures ranging from 16 to 33 °C, and visited in rotating sequence. During the visitation surveys we recorded 28 bee morphogroups via visual assessments, 17 of which were identifiable at the species level, 10 to genus only, and a few unidentified bees. After each visitation assessment, we collected bees actively foraging on the flowers for 1.5 ± 0.5 person hours, depending on foraging activity levels. Bees were collected by hand from flowers into sterile vials and a sample of each observed flower species was also collected using sterilized 50 ml falcon tubes. Samples were immediately placed on dry ice in the field, transported to the laboratory and stored at –80 °C until processing. Collected bees were used for subsequent pathogen screening and species determination using reference materials located in the Cornell University Insect Collection, published keys, and barcoding methods (Appendix 2).

Overall, 91% of bee samples were identified to species (46 species). Rarefaction analyses indicated sufficient sampling of the pollinator communities (Fig. S2). We compared analyses with networks constructed at the taxonomic resolution possible in the field (“unresolved”) and those that were later fully resolved to species in the laboratory (“resolved”), finding no significant differences for any of our analyses (Table S1); here we present unresolved data to minimize assumptions. We screened 12 of the 13 flower species found in the wildflower sites for bee pathogens (Appendix 3).

DNA extraction and pathogen screening

We surface sterilized each bee to ensure only pathogens inside of the bees were detected (Lacey 1997). The pathogens screened (trypanosomes, neogregarines, Nosema ceranae, and Nosema bombi) display broad tissue tropism (Schmid-Hempel 1998), therefore we extracted gut, fat body, and Malpighian tubules in each sample. To maximize the amount of nucleic acid collected, we also pipetted 20 μl UltraPure™ water (ThermoFisher, Grand Island, NY, USA) into the abdomen during dissection. The dissected bee organs and water mixture were placed in sterile vials containing two sterilized 2.4 mm steel beads, 100 μl of sterilized 0.1 mm zirconia beads, and 800 μl of TRIsure™ reagent (BIOLINE, Boston, MA, USA). Samples were homogenized for 30 seconds at 6.5 m/s using a bead mill homogenizer (Omni International, Kennesaw, GA, USA), then immediately placed on ice. The solution was transferred to a new sterile vial, taking care to not pipette beads or large tissue fragments. DNA extraction from the TRIsure™ reagent then proceeded using the manufacturer’s protocol. Each extraction batch included a negative control. Pathogen DNA on 100 mg of floral tissue per species per site was similarly extracted (Appendix 3) using established PCR primers (Appendix 3, Table S3 – S4).

Landscape characterization

The 11 replicated wildflower sites were established along a landscape simplification gradient in the fall of 2012 (Fig. S1). We used ArcGIS v10 (Environmental Systems Research Institute, Redlands, CA, USA) and the 2015 Cropland Data Layer (30 m resolution, USDA NASS) to evaluate the landscape composition within a 500, 750, and 1,250 meter radius of each site, encompassing the typical foraging range of most wild bees (Greenleaf et al. 2007). In North American farmlands, pasture management frequently includes mowing and herbicide use (Singh et al. 2006), both of which can affect the distribution of flowering plants available for bees at the landscape scale. Thus, we evaluated the proportion of agricultural cover (defined as corn, soy, barley, wheat, vegetable crops, alfalfa, orchards, hay fields, and grass/pastures) at each of the 11 sites. Agricultural cover was positively correlated with cropland (defined as corn, soy, barley, wheat, vegetable crops, alfalfa, and orchards: F_1,9 = 22.39, P = 0.001; F_1,9 = 51.12, P < 0.001; and F_1,9 = 55.67, P < 0.001, for the 500, 750, and 1,250 meter scales, respectively) and negatively correlated with natural area (defined as deciduous, evergreen and mixed forest, woody and herbaceous wetlands, old fields, and shrub lands, as well as open and low intensity developed lands, such as roadside edges: F_1,9 = 10.2, P = 0.011; F_1,9 = 3.39, P = 0.100; and F_1,9 = 6.33, P = 0.033, for the 500, 750, and 1,250 meter scales, respectively). As such, we analyzed the effect of agricultural cover on network metrics and pathogen prevalence in our system.

Network characterization and statistical analyses

Network characterization and statistical analyses were conducted in R version 3.5.1 using the bipartite, vegan, epiR, lme4, ape and piecewiseSEM packages (Paradis et al. 2004; Oksanen et al. 2007; Dormann et al. 2008; R Development Core Team 2008; Bates et al. 2015; Lefcheck 2016), unless otherwise stated. Qualitative and quantitative network indices were calculated using the networklevel function in bipartite: connectance, nestedness (weighted NODF), and bee species richness (Dormann et al. 2008). Modularity (Q) was estimated using the QuaBiMo algorithm (computeModules function; (Dormann & Strauss 2014)). Module membership, indicating similarity in visitation patterns, was categorically determined for each bee morphogroup at each site, hereafter referred to as species (Table S5). In modular networks, pathogen transmission is much more frequent within modules than in the overall community (Sah et al. 2017). As such, we hypothesized that module membership would predict bee pathogen prevalence given the higher likelihood of indirect pathogen exposure via flowers for bee species in the same module as those with pathogens. Taxon-specific network indices (betweenness centrality and degree) were calculated for bee species at each site using the specieslevel function in bipartite. Betweenness centrality, by measuring the frequency of shortest paths that pass through a species, can indicate likely “hotspots” of pathogen transmission. We expected bee species that most closely connected the greatest number of other bee species to have the highest likelihood of harboring a pathogen. Bee abundance was calculated by summing the total number of interactions observed at each site throughout the summer (Vázquez et al. 2005; Vázquez et al. 2007; Fort et al. 2016).

We evaluated relationships in bee community composition via non-metric multidimensional scaling (NMDS with the Bray-Curtis dissimilarity measure on the species-abundance matrix following Wisconsin double standardization (Oksanen 2015)). We investigated how the proportion of agricultural cover related to the ordination by fitting the agricultural landscape variable to the ordination axes (envfit function with 999 permutations to determine significance).

Prior to analyses, degree, betweenness centrality, nestedness (weighted NODF), and modularity (Q) were standardized based on comparisons to null models (Dormann et al. 2009; Dormann 2011). We selected the vaznull null model because by maintaining the number of links and marginal totals in the null model equal to those of the real world network it can more closely mirror real ecological and/or evolutionary processes, including the existence of trait mismatching that impedes interactions from occurring (Dormann et al. 2009). We computed 1000 null models for each network index at each site using the vaznull method, which first creates a binary matrix with randomized interaction probabilities proportional to each species’ relative abundance, constrained by the connectance of the original network. Once the matrix was created with the same number of filled cells as the original network, the remaining interactions were distributed among the filled cells, thus constraining connectance while including interaction frequency (Vázquez et al. 2007). We then calculated the z-score for the network indices observed at each site by comparing to the mean and standard deviation of the computed null models. The resulting z-scores were the values employed in subsequent statistical analyses. The z-score of connectance was not calculated because vaznull constrains connectance.

We employed structural equation models to evaluate the hypothesized indirect effects of landscape simplification on pathogen prevalence via network metrics (Appendix 5). Our models evaluated whether landscape simplification (proportion agricultural cover at either 500, 750, or 1250 meters) predicted network-level metrics (connectance, modularity, nestedness, bee species richness, and scaled bee abundance), as well as the diet breadth (degree) of the dominant species in our system, Bombus impatiens, which is known to vector pathogens on flowers and is linked to pathogen spillover from commercial colonies to wild bees (Otterstatter & Thomson 2008). All network metrics (including B. impatiens diet breadth) were modeled to co-vary a priori because directionality was unclear. The landscape and network metrics were based on linear regression of values for each of the sites (n = 11); we evaluated model assumptions using the olsrr package (Hebbali 2017). The role of landscape simplification and each network metric on pathogen prevalence (trypanosomes, neogregarines, Nosema bombi, and/or Nosema ceranae) was evaluated using a Generalized Linear Mixed Model (GLMM), which included pathogen presence in individual bees as the binary response, all network metrics and proportion of agricultural cover as predictor variables, as well as bee species and site as random effects (n = 575). We then simplified our model by removing non-significant terms (Appendix 5). Our simplified model, presented in the main text, included proportion of agricultural cover at the 500-meter scale, B. impatiens diet breadth (degree), network connectance, overall bee abundance, and presence of pathogens in individual bees (Table S1). Results from the full model and the three spatial scales are presented in Table S6.

To determine whether each bee species’ position in the network predicted its likelihood of harboring pathogens, we conducted a GLMM that included three taxon-specific indices: module membership, diet breadth (degree), and betweenness centrality. We calculated the variance inflation factor for a model including all three indices and found that module membership greatly increased estimate variances; therefore, the impact of module membership was analyzed separately from the other two factors. The taxon-specific network metrics were evaluated as the explanatory variable for presence of pathogens in bees using a binomial GLMM that included site and bee species as random effects. We conducted a likelihood ratio test to determine the significance of coefficients by comparing against a null model that only included the random effects. The taxon-specific analyses were conducted only on bee species for which we had both pathogen and visitation data at a site (14 species). Furthermore, we tested the hypothesis that similarity in foraging patterns between bee species in a given network predicted similarity in pathogen prevalence using Mantel tests, but found that number of shared floral partners was a poor predictor (Appendix 6).

Modelling pathogen transmission in bipartite networks with varying connectance

Existing theoretical models have generally suggested that increasing network connectance results in higher rates of disease transmission (Shirley & Rushton 2005; Moslonka-Lefebvre et al. 2009; Strona et al. 2018), contrasting with our empirical findings (see Results). However, previous models generally assume that a host’s contact rate scales with its network degree, corresponding to the niche breadth. This is unlikely to be true for plant-pollinator networks, unless floral resources are so scarce that foraging rates become search-time limited, and hence warrants a re-evaluation of existing results under a different set of assumptions. As such, we developed a new theoretical model parameterized with empirically derived values to understand how connectance could impact a pathogen’s basic reproductive number (R₀), linearized prevalence growth rate (λ), and steady state prevalence based on realistic assumptions for the plant-pollinator system.

We considered a simple deterministic susceptible – infected – susceptible (SIS) model with demography, assuming no latent period for exposed bees, and that bees and flowers become susceptible again after clearing infection. We assumed constant population sizes (equal birth and death rates), and that bees emerged uninfected as adults. Here, “infected” bees included host and non-host vectors that carry pathogens. Transmission of pathogens was assumed to occur only from fecal deposition of infected bees on uncontaminated (“susceptible”) flowers, and from susceptible bees ingesting pathogens while foraging on contaminated (“infected”) flowers (Figueroa et al. 2019). Within-hive transmission and demographic processes were ignored (i.e., we assumed that the population of each bee and flower species remained constant).

With the above assumptions, the SIS model was described by the system of equations (definitions provided in Table 1):

$${\dot{y}}_q=\sum _{k=1}^K{\beta }_{q,k}\cdot s_q\cdot c_k-\left({\gamma }_q+{\mu }_q\right)\cdot y_q,s_q=1-y_q,$$

$${\dot{c}}_k=\sum _{q=1}^Q\frac{{\alpha }_{q,k}\cdot M_q}{N_k}\cdot y_q\cdot u_k-{\zeta }_k\cdot c_k,u_k=1-c_k,$$

Table 1. Variables, parameters, and their definitions in the SIS system of equations.

Parameter values are realistic for plant-pollinator networks. The only exception is N_k, which was adjusted to reproduce realistic values of R₀, λ, and mean steady-state prevalence in the models. The value of N_k is much higher than the observed floral abundance in the wildflower plots, due to the fact that the SIS model assumes a closed system, whereas the bees observed did not forage exclusively inside the plot. Therefore, the correct N_k should be one where the plot area has been sufficiently extended to support the population of bees.

Variables and parameters	Short description	Central value, comments, and reference
yq and ck	Fractions of infected/contaminated individuals of bee species q and flower species k
sq and uk	Fractions of susceptible/uncontaminated individuals of bee species q and flower species k
Q and K	Bee and flower species richness	Mean from empirical data
q and k	Labels for bee and flower species
Mq and Nk	Abundance of bee species q and flower species k	Bee abundance 50, order-of-magnitude estimate based on observations at the wildflower plots. Flower abundance 2000 (see caption).
1 / (γq + μq)	Reciprocal of the sum of bee recovery and mortality rates	3 days. Central value between species that are non-host vectors (recovery time < 1 day) and species that can develop active infections (if chronic, life expectancy of ~1 month; however, not all exposed individuals become infected, so we chose an intermediate value of 10 days).
1 / ζk	Flower decontamination time	3 hours (Figueroa et al. 2019)
αq,k	Rate at which uncontaminated flowers of species k become contaminated when foraged on by an infected bee of species q	Combination of other parameters ${\alpha }_{q,k}={\eta }_{q,k}\cdot f_q\cdot r_q\cdot {\varphi }_{q,k}$
βq,k	Rate at which a susceptible bee of species q becomes infected when foraging on contaminated flowers of species k	Combination of other parameters ${\beta }_{q,k}={\eta }_{q,k}\cdot f_q\cdot r_q\cdot {\psi }_{q,k}$
ηq,k	Fraction of foraging time a bee of species q spends on flowers of species k	We require that $\sum _{k=1}^K{\eta }_{q,k}=1$
fq	Fraction of day bee species q spends foraging	2 hours / day (Otterstatter & Thomson 2008)
rq	Foraging rate for a bee of species q	5 flowers / minute, order-of-magnitude estimate based on observations
q,k	Bee-to-flower transmission: probability of an infected bee of species q contaminating a single flower of species k when foraging on it	0.01 (Otterstatter & Thomson 2008)
ψq,k	Flower-to-bee transmission: probability of a bee of species q becoming infected when foraging on a contaminated flower of species k	0.01 (Truitt et al. 2019)

We generated 100,000 random plant-pollinator networks as follows: for each network, we sampled the degree of each bee or flower species from a zero-truncated binomial distribution, with one binomial proportion used for bees and a different one for flowers. The zero-truncated binomial distribution was chosen for its simplicity and because it fit the observed degree distributions well, albeit being slightly over-dispersed. The Gale-Ryser criterion (Krause 1996) was used to check whether a bipartite network could be constructed using the two sampled degree sets; if not, the flower degree set was re-sampled until the criterion was satisfied. Edges from bee and flower species were then joined at random while ensuring that no parallel edges were created. Changes to the two binomial proportions used in the zero-truncated binomial altered the expected degree of each bee or flower species, hence allowing connectance to vary. The bee binomial proportions fit from the empirically observed degree distributions ranged from 0.13 to 0.31, so we allowed the bee proportion in each network to vary between 0.05 and 0.4. The corresponding flower proportion was chosen such that the expected value for the sum of flower degrees equaled that of the bee degrees. We fixed the number of bee and flower species at Q = 13 and K = 7, based on the mean from our empirical networks. Missing edges in each network hence indicated that transmission parameters α_q,k and β_q,k were zero. The two transmission parameters α_q,k and β_q,k in the SIS model were combinations of other parameters defined in Table 1; importantly, both contain a multiplicative factor η_q,k, where $\sum _{k=1}^K{\eta }_{q,k}=1$, to account for the division of total foraging efforts among multiple flower species, a departure from existing theoretical models on the effects of connectance.

The SIS model depended on four combination of parameters α_q,k · M_q / N_k, β_q,k, γ_q + μ_q, and ζ_k. Therefore, to account for heterogeneity among bee and flower species, for example between bee species that are non-host vectors versus those that can develop active infection, we first calculated reference values of these combinations (Table 1), except without η_q,k for the first two combinations. Next, we allowed the values of these combinations for each q and k to fluctuate about the reference values by a multiplicative factor of $\sqrt{10}$ in either direction, so that the range of values spanned one order of magnitude. Finally, to complete the first two combinations, we randomly generated η_q,k for each bee species q, with the requirements that $\sum _{k=1}^K{\eta }_{q,k}=1$ and that they were zero if the corresponding edges between q and k were missing in the network. This process was repeated for each random network.

To quantify disease transmission, we defined two matrices T and Σ of dimensions $\left(Q+K\right)\times \left(Q+K\right)$ with matrix elements

$$T_{i,j}=\left\{\begin{array}{ll}{\beta }_{q,k},\hfill & \begin{array}{l}i=q\hfill \\ j=Q+k\hfill \end{array}\hfill \\ \frac{{\alpha }_{q,k}\cdot M_q}{N_k},\hfill & \begin{array}{l}i=Q+k\hfill \\ j=q\hfill \end{array}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\right\},{\text{Σ}}_{i,j}=\left\{\begin{array}{ll}-{\gamma }_q,\hfill & i=j=q\hfill \\ -{\zeta }_k,\hfill & i=j=Q+k\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\right\},$$

For each random network, we then calculated three metrics:

• Reproduction number R₀, given by the dominant eigenvalue of the next-generation matrix -TΣ⁻⁻¹ (Diekmann et al. 2009).

• Linearized prevalence growth rate λ, given by the dominant eigenvalue of the time evolution matrix T + Σ.

• Distribution of steady-state pathogen prevalence among the bee species.

Note that while we have used an SIS model, many pollinator pathogens are believed to cause chronic infections. Nonetheless, both SIS and SI models can give similar results once we include population dynamics (mortality and reproduction) in the SI model, so that reproduction in the SI model plays the same role as recovery in the SIS model in terms of recruiting new susceptibles. Therefore, for species that can develop active infection, mortality rates replace recovery rates in our model (assuming constant population to balance reproduction rates).

All computations were performed in R using the packages extraDistr (Wolodzko 2018) for zero-truncated binomial distributions and rootSolve (Soetaert & Herman 2009) for numerical evaluation of the steady-state prevalence.

RESULTS

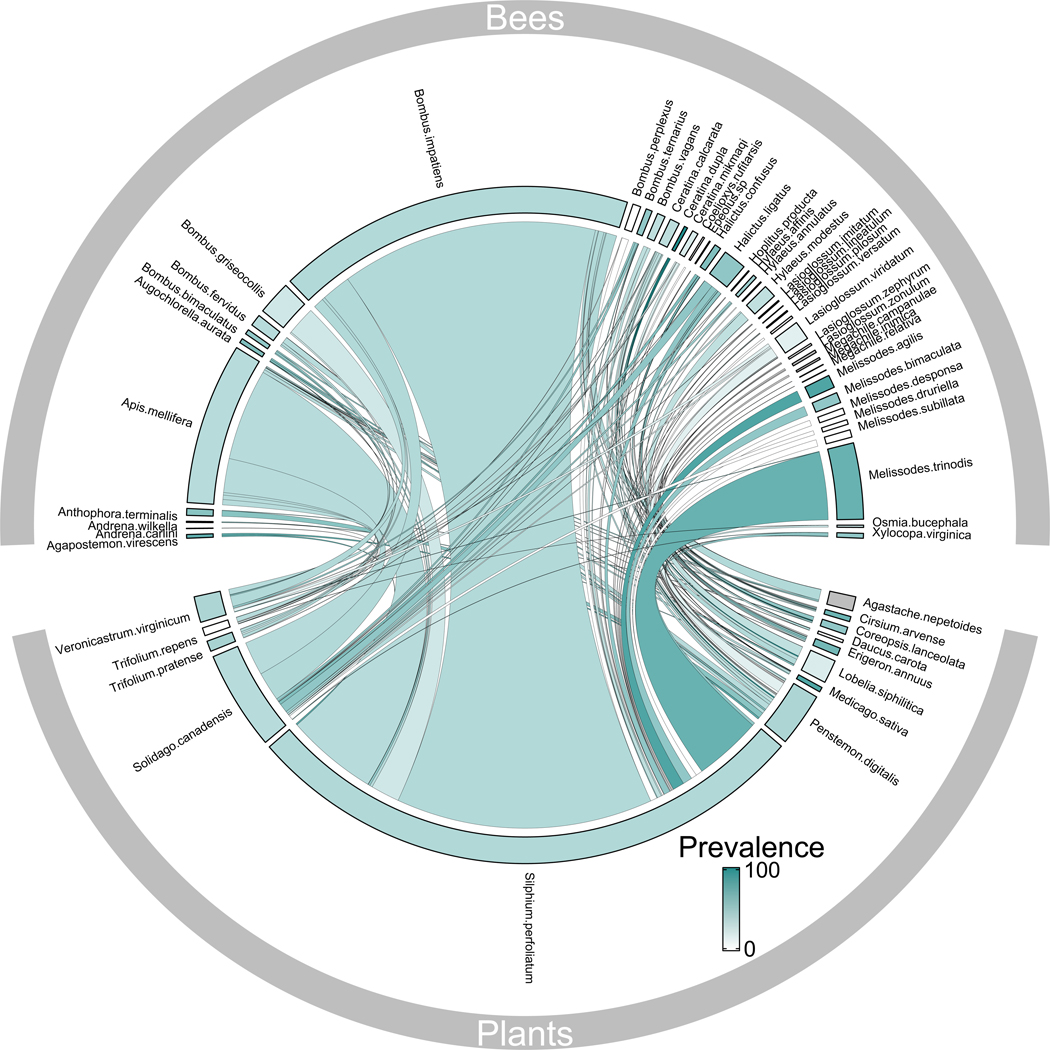
We recorded 2,936 bee visits across 143 plant-pollinator interaction pairs and screened 575 bees (46 species) and 81 flowers (12 species), finding that 65% of bee species (39% of bees; 95% Confidence Interval (CI), 35 – 44%) and 75% of flower species (31% of flowers; 95% CI, 20 – 43%) harbored at least one of the three pathogen groups (trypanosomes, neogregarines, Nosema bombi, and/or Nosema ceranae; Fig. 1, Fig. S3 & S4).

Fig. 1. Pathogen prevalence is widespread in plant-pollinator networks.

Composite quantitative bipartite network of f3"interactions (links) between bees (top bars) and flowers (bottom bars). Width of bars reflects relative abundance of bees and flowers, and width of links indicates interaction frequency. Color intensity of bars indicates pathogen prevalence in bees and on flowers (links colored according to prevalence in bees). Gray bars indicate species that were not screened. At least one screened pathogen (trypanosomes, neogregarines, Nosema ceranae, and Nosema bombi) was present in 65% of bee species and 75% of flower species. There were 42 bee species in the resolved network and 28 bee morphogroups in the unresolved network. Fig. S3 provides pathogen-specific depictions of prevalence across networks.

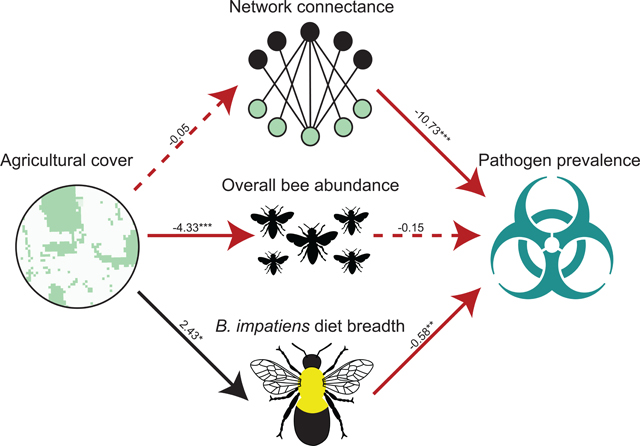
We employed structural equation models to evaluate the role of landscape simplification on network metrics, diet breadth of the dominant bee species, and, subsequently, on pathogen prevalence at the community level. In more simplified agricultural landscapes, there were fewer foraging bees and the dominant bee species, Bombus impatiens, visited more plant species (higher degree: broader diet breadth) (Table S1). Bee species richness did not vary along the landscape gradient (Table S6), nor did species composition (NMDS stress = 0.62, R² = 0.07, P = 0.79), indicating that landscape simplification affected interaction patterns rather than interaction partners per se (Tylianakis et al. 2007). Consequently, we infer that species loss was not the mechanism by which landscape simplification altered interaction patterns.

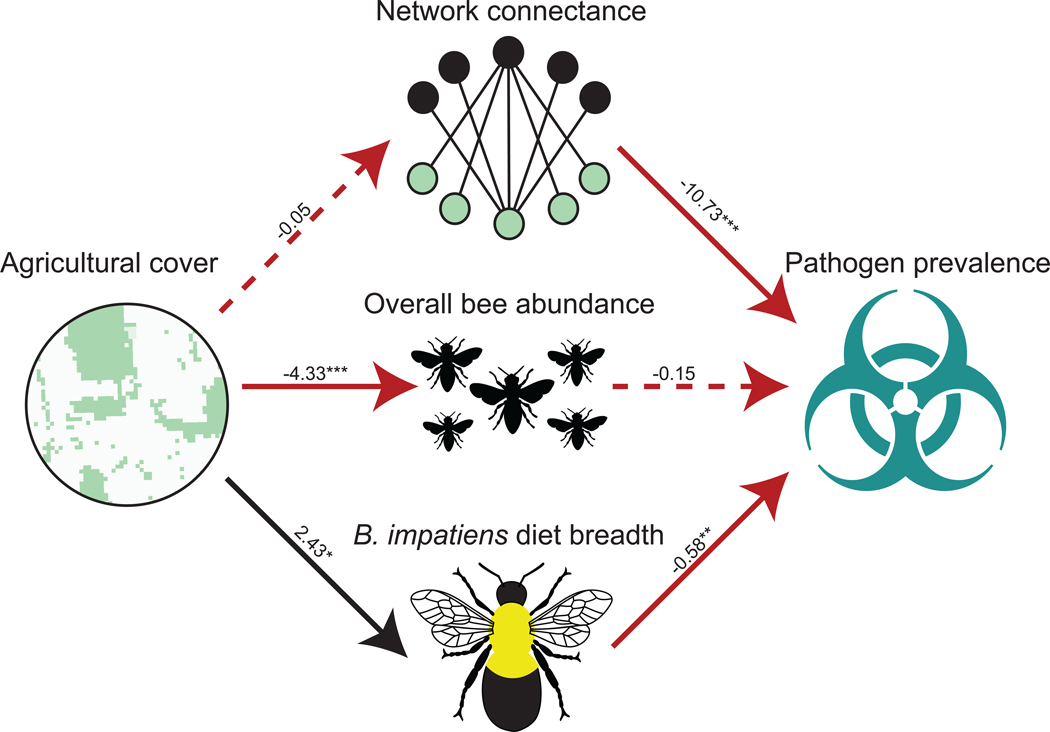
At sites where B. impatiens visited more plant species, pathogen prevalence in the community was lower (Fig. 2 bottom; Table S1). Conversely, bee abundance did not explain pathogen prevalence in the bee community (Fig. 2 center; Table S1). We found that in more connected networks, bees were less likely to harbor pathogens (Fig. 2 top; Table S1), a pattern not driven by landscape simplification. There was no direct relationship between agricultural cover and pathogen prevalence in the bee communities (Fig. 2 & Fig. S5). Instead, the relationship between landscape simplification and pathogen prevalence was mediated by B. impatiens diet breadth (Fig. 2).

Fig. 2. Landscape simplification indirectly influences pathogen prevalence in bee communities by altering the diet breadth of the dominant species, Bombus impatiens.

Unstandardized coefficients are shown for each path due to differences in sample sizes (n =11 for site-level comparisons compared to n = 575 for pathogen prevalence calculations). Solid lines indicate significant relationships (P < 0.05), dashed lines indicate a non-significant relationship (P > 0.05), black indicates positive relationships, and red indicates negative relationships. Ultimately, 76% of overall bee abundance, 40% of Bombus impatiens diet breadth (degree), 12% of overall pathogen prevalence, and 6% of network connectance variance was explained by the model. * P < 0.05, ** P < 0.01, * ** P < 0.001.

We found that modules differed in pathogen prevalence, suggesting that groups of bee species with similar interaction patterns were more likely to share pathogens (χ²₂₉ = 48.1, P = 0.01; Fig. S6). However, bee species’ centrality (degree and betweenness centrality) did not explain likelihood of harboring pathogens (χ²₂ = 0.98, P = 0.61), nor did similarity of pairwise species interaction partners explain similarity in prevalence (number of shared interaction partners: $\overline{r}=-0.31,P=0.76$, Jaccard index: $\overline{r}=0.30,P=0.77$, and weighted Jaccard index: $\overline{r}=0.35,P=0.73$). Furthermore, network modularity did not predict pathogen prevalence at the community level (Table S6).

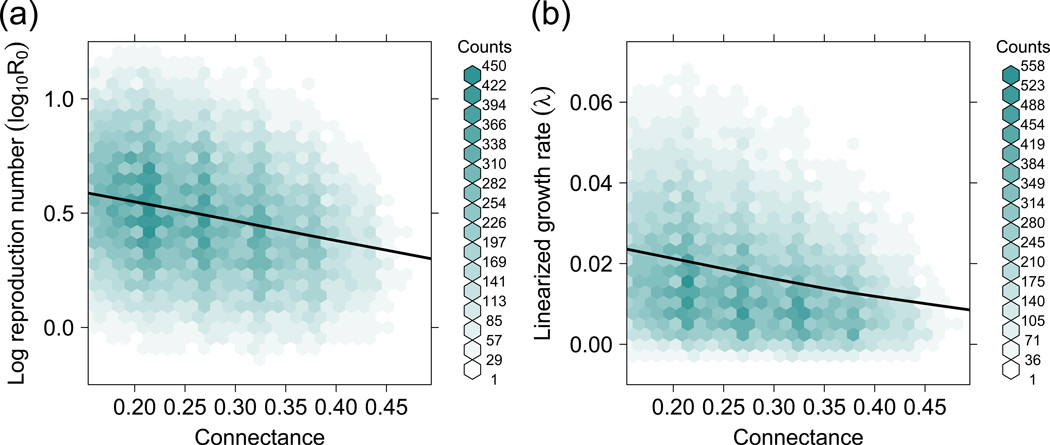
From our theoretical model with empirically derived parameter values, we found that the rate of pathogen spread in the bee community, as measured both by pathogen reproduction number (R₀) and linearized prevalence growth rate (λ), decreased with connectance in bipartite networks (Fig. 3). In the initial pathogen spread phase, before steady-state prevalence had been reached, lower R₀ and λ in more connected networks suggest reduced prevalence. These results are in agreement with our empirical data, which found a negative relationship between connectance and pathogen prevalence in the community (Fig. 2). We also examined the steady-state pathogen prevalence of each bee species in the networks, finding that the outcome was highly dependent on changes to model parameter values within realistic ranges. Pathogen prevalence of the most infected species was consistently lower in well-connected networks, while prevalence of the least infected species was consistently higher (Fig. 4).

Fig. 3. (a) Connectance reduces pathogen reproductive number (R₀).

Based on results from a SIS model run on 100,000 random networks of varying connectance. (b) Connectance reduces pathogen linearized prevalence growth rate (λ). Results from a SIS model run on 100,000 random networks of varying connectance show that λ decreases with increasing connectance. Lower R₀ and λ imply lower pathogen prevalence during the early stages of an outbreak. The solid line is a smoothing curve fitted through median values of R₀ and λ for each connectance bin.

Fig. 4. Connectance reduces variance in the distribution of steady-state pathogen prevalence within a network.

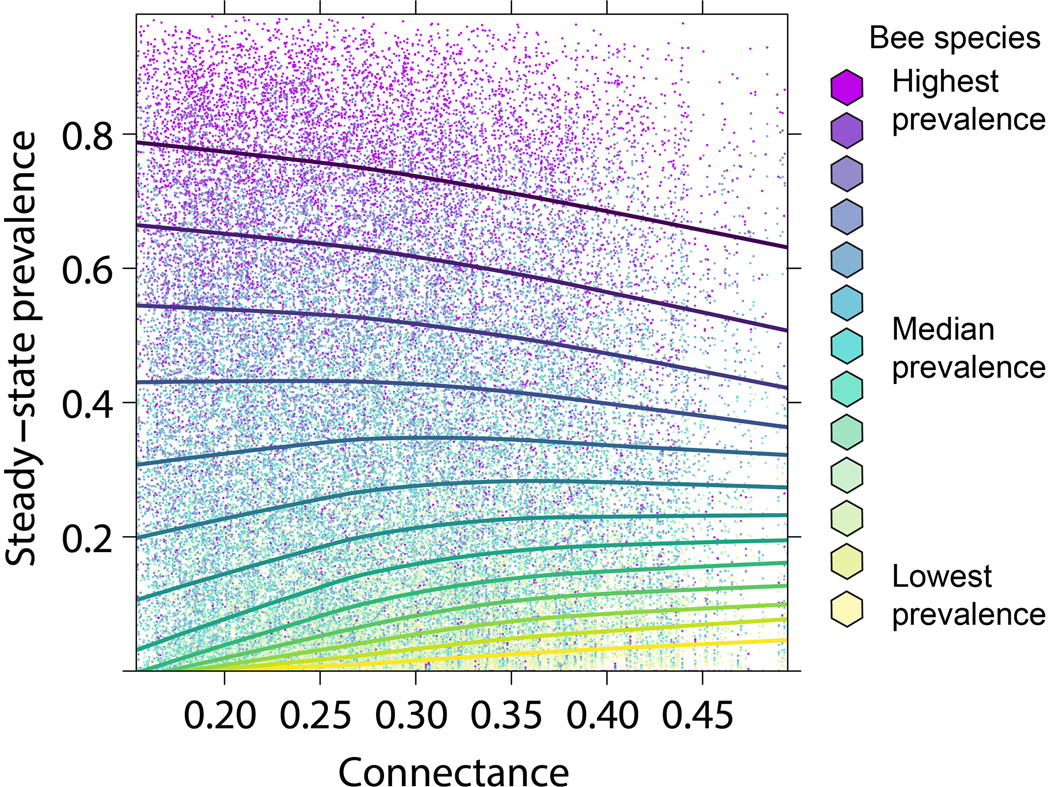
Steady-state pathogen prevalence of all bee species from a sample of 5,000 networks are shown, with the more infected species in each network shown as points in purple (top) and the less infected species in yellow (bottom). Points are slightly jittered in the horizontal direction to reduce overlap. For each bee species, a smoothing curve of the same color is fitted through the median prevalence values for each connectance bin. Connectance decreases the prevalence level of the more infected species while increasing that of the less infected ones.

DISCUSSION

In this study, we found widespread pathogen prevalence in plant-pollinator networks along an experimentally established agricultural landscape gradient. We found that landscape simplification can impact pathogen prevalence by altering the visitation patterns of the dominant bee species, Bombus impatiens. Empirical and theoretical model results indicate that more diverse plant-pollinator interactions dilute pathogen prevalence. In the field, networks that were more connected and had dominant species with broader diet-breath had lower pathogen prevalence in the bee communities. Similarly, in our newly developed and realistically-parameterized SIS models, more connected networks had lower rates of pathogen spread and reduced variance in steady-state prevalence within the communities.

The dominant species in our system, Bombus impatiens, visited more plant species in simplified landscapes. Others have found that along experimental gradients of floral abundance, increased resource availability decreased B. terrestris diet breadth (Fontaine et al. 2008). Thus, along our landscape simplification gradient, the dominant bumble bee species may have foraged more generally due to reduced abundance of floral resources at the landscape scale (Tscharntke et al. 2005) or within the wildflower plantings (see Appendix 5 for further discussion). Both possibilities have the potential to alter disease dynamics. For example, a recent study found that increases in floral abundance in old-field communities reduce prevalence of bee pathogens on flowers, thus decreasing the potential for transmission (Graystock et al. 2020). Given that landscape context can differentially influence diet breath across bee species (Cusser et al. 2019) and that life histories, including diet breadth, dispersal ability, and body size, shape how species respond to habitat fragmentation (Hagen et al. 2012), evaluating whether and how these functional traits in diverse bee communities mediate the effect of landscape simplification on pathogen transmission and spread is highly warranted.

When Bombus impatiens visited more plant species, we found lower pathogen prevalence in the community. Others have estimated that infected B. impatiens deposit pathogens on only 1% of flowers visited (Otterstatter & Thomson 2008), and that bumble bee species differ in their transmission potential on flowers (Ruiz-González et al. 2012). The low deposition rate may therefore underlie the negative relationship between B. impatiens diet breadth and pathogen prevalence. Determining which bee traits, such as deposition rate and host competence, contribute to differential dynamics among species is an important future direction in pollinator epidemiology. Furthermore, this pattern supports the importance of dilution, as a known host visiting a broader array of plants and not concentrating exclusively on one hub of disease transmission may have reduced the overall encounter likelihood for the next incoming foraging bee.

Land use change is often associated with a reduction in specialists, which are disproportionately lost along habitat fragmentation gradients (Hagen et al. 2012). On this basis we had expected an increase in network connectance in simplified habitats. However, we did not see a change in bee species richness or composition along our landscape gradient, nor in network connectance. Our results are in agreement with recent studies showing that network connectance does not always respond to landscape simplification (Redhead et al. 2018). Evaluating the importance of land use histories, ecoregions, and gradients of landscape simplification are important future directions in the field of plant-pollinator network ecology.

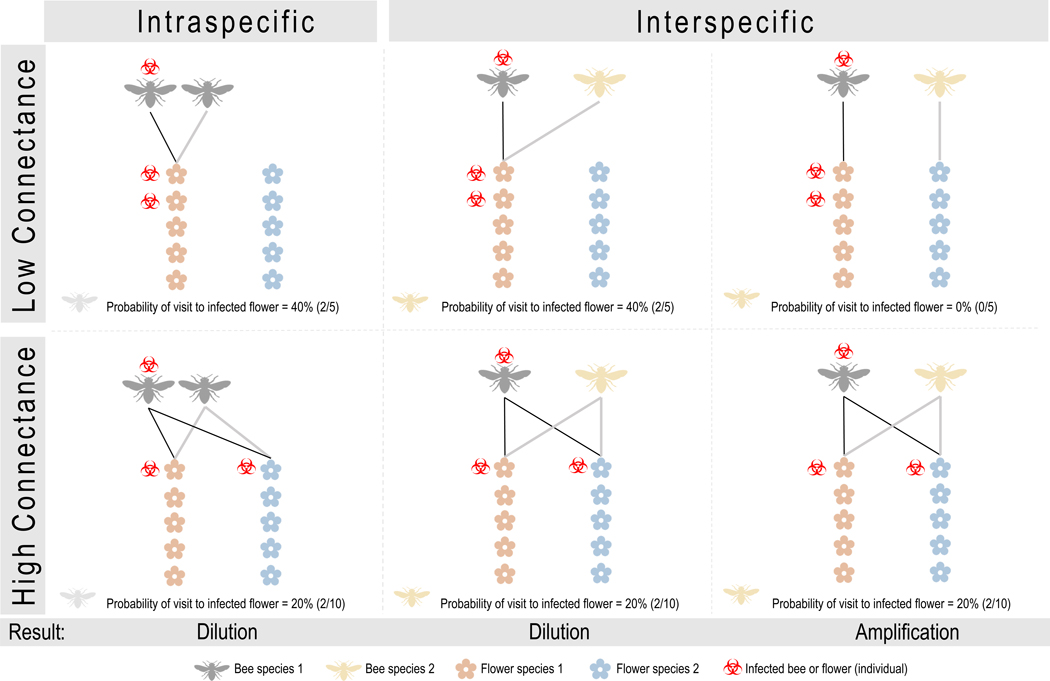
Our model found that greater connectance decreased both the rate of pathogen spread as well as variance in the prevalence distribution across species (Fig. 3 – 4). Given that steady-state prevalence is sensitive to the non-linear structure of the model, rates of pathogen spread are likely better indicators of observed prevalence. Thus, our theoretical prediction that increased connectance leads to slower pathogen spread is in agreement with the negative relation between connectance and prevalence in our empirical results (Fig. 2). Both theoretical results can be explained as follows. First, in a highly connected network, an infected bee would visit and hence contaminate more plant species; however, assuming a constant contact rate, the contamination would be distributed among more flowers, thus decreasing the probability that a susceptible bee will encounter a contaminated flower (“dilution”; Fig. 5). This slows disease spread among the competent host species that usually drive disease growth rate. We note that others (Moslonka-Lefebvre et al. 2009; Strona et al. 2018) have predicted opposite patterns, where increased connectance enhances transmission. However, existing models assume that a host’s contact rate scales with its degree, hence undoing any dilution. Given that we expect the foraging rate of an individual pollinator to remain roughly constant regardless of diet breadth (assuming similar search and handling times), our model is more appropriate for plant-pollinator networks. Second, high connectance facilitates pathogen transmission from competent hosts to other species within the network by increasing indirect interactions via flowers (“amplification”; Fig. 5); this raises the prevalence in other species toward that of the competent hosts, thus reducing the variance across species (Fig. 4).

Fig. 5. Conceptual diagram illustrating how connectance can influence bee pathogen transmission in bipartite plant-pollinator networks.

Low connectance networks (top row) are represented by two realized links between bees and plants, while high connectance networks (bottom row) have four realized links. Bees of the same species always forage on the same set of plant species (left column), while bees of different species can have either overlapping (center column) or non-overlapping (top right column) visitation patterns. Here, the bee vectoring pathogens will “infect” two flowers before clearing the infection. Under dilution scenarios (left and center columns), connectance reduces the probability that an incoming susceptible bee will encounter an infected flower because the total number of possible flowers increases. Conversely, under the amplification scenario, connectance increases diet overlap between infected and uninfected bees, resulting in greater encounter probability (right column).

Modules often form in ecological networks, within which interactions occur more frequently than in the overall community. Highly modular networks have the potential to structurally suppress pathogen spread (Gilarranz et al. 2017). While we found that modules differed in pathogen prevalence (Fig. S6), network modularity did not predict overall pathogen prevalence nor did bee species’ centrality predict likelihood of harboring pathogens. Furthermore, pairwise similarity between bees’ interaction partners did not explain similarity in prevalence. Our data and models suggest that an understanding of how all species interact (e.g., network connectance) is more informative than the interaction patterns of any given pair. Disentangling the role of foraging behavior, phylogeny, and susceptibility to infection in diverse bee communities is an important future direction for pollinator epidemiology.

The development of cost-effective pollinator conservation strategies across landscapes is of pressing global concern given documented bee declines and increasing dependence on crop pollinators (Aizen et al. 2008; Goulson et al. 2015). Our data and model illustrate that while pathogens can spread more slowly in highly connected plant-pollinator networks due to a “dilution” effect, resulting pathogen prevalence varies among bee species. These results suggest that management for species of conservation concern may differ from community-wide approaches and those targeting dominant species. Currently, one of the predominant strategies for promoting pollinators is the establishment of wildflower plantings (Williams et al. 2015). Given our results showing that connectance is a key mediator of pathogen spread in bee communities, we recommend evaluating this metric in bee communities vulnerable to disease outbreaks, for example those in wildflower strips near apiaries or commercial bumble bee operations (Otterstatter & Thomson 2008; Furst et al. 2014), and adjusting seed mixes accordingly. Thus, wildflower plantings promoting pollinator health could be designed to maximize food resources while minimizing disease spread.